Aprende en Casa III SEP: 27 de abril TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 27 de abril de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Martes 27 de abril, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Método suma y resta
Aprendizaje esperado: Resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.
Énfasis: Resolver problemas mediante el planteamiento y la solución de sistemas de dos ecuaciones lineales con dos incógnitas utilizando el método de suma y resta.
¿Qué vamos a aprender?
Se te recomienda participar activamente, anotar las ideas principales del tema y las dudas que surjan.
En esta sesión, resolverás problemas que se pueden modelar con sistemas de dos ecuaciones lineales con dos incógnitas. En la resolución de esos sistemas se usará el método de suma y resta.
¿Qué hacemos?
Para comenzar, lee detenidamente el siguiente ejercicio:
La suma de dos números es 30 y su diferencia es 6. ¿Cuáles son los números?
Una vez leído el problema, estima qué números cumplen con las condiciones descritas y anota la estimación en tu cuaderno.
A continuación, se resolverá el ejercicio con base en un sistema de dos ecuaciones lineales con dos incógnitas.
Para eso, primero plantea dicho sistema. Puedes utilizar como guía las siguientes preguntas o consideraciones:
1. ¿Cuáles son las cantidades desconocidas o incógnitas del ejercicio?
2. Asigna una letra o literal distinta a cada una de las incógnitas.
3. Con base en lo anterior, ¿cómo se puede representar algebraicamente el enunciado “la suma de dos números es 30”? ¿Y el enunciado “y su diferencia es 6”?
En la primera pregunta se solicita identificar las incógnitas del ejercicio. Léelo nuevamente:
“La suma de dos números es 30 y su diferencia es 6. ¿Cuáles son los números?”. Se pueden identificar como incógnitas dos números.
En la segunda pregunta, se solicita asignar letras a las cantidades desconocidas identificadas. Aquí, se asignará la letra “x” a uno de los números y la letra “y” al otro número.
En la tercera pregunta, se solicita representar algebraicamente el ejercicio. El enunciado “La suma de dos números es 30”, se puede representar con la expresión “x” más “y” igual a 30. En donde “x” representa un número y “y” representa el otro número.
El enunciado “su diferencia es 6”, se puede representar con la expresión algebraica “x” menos “y” igual a 6. En donde la letra “x” representa un número, y la letra “y”, el otro número, que son los mismos números utilizados en la expresión anterior.
De acuerdo con lo anterior, el sistema de dos ecuaciones lineales con dos incógnitas que resuelve el ejercicio es:

Una vez planteado el sistema, a continuación, se resolverá por el método de suma y resta.
Antes de exponer los pasos de ese método, se estudiarán algunos conceptos para darle un significado a esos pasos.
Observa que el sistema se compone de dos igualdades. Primero, analiza las igualdades por separado.
Comienza por la igualdad: “x” más “y” igual a 30, ¿qué valores de “x” y de “y” hacen de la igualdad un enunciado verdadero?
Por ejemplo, si “x” toma el valor de 30 y “y” toma el valor de cero, se cumple la igualdad “x” más “y” igual a 30, porque 30 más cero da como resultado 30.
Se dice entonces que el par ordenado 30 coma cero hace que se cumpla la igualdad.
Otro par ordenado que hace que se cumpla la igualdad es 29 coma 1, porque 29 más 1 es igual a 30.
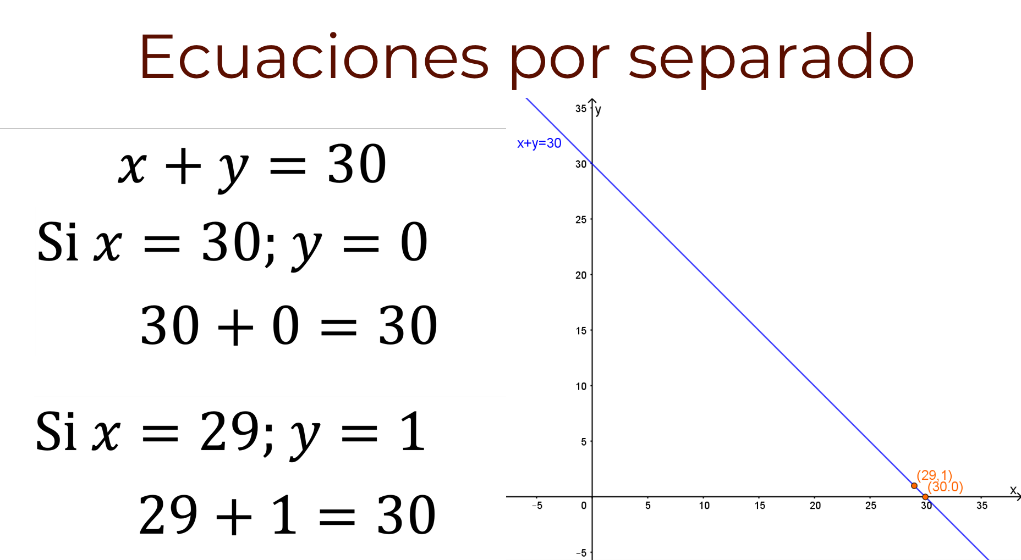
En un plano cartesiano, ¿cómo se pueden representar los valores de “x” y “y” que hacen que se cumpla la igualdad?
En un plano cartesiano, cada pareja ordenada que hace que se cumpla una expresión lineal, se puede representar con un punto.
En el caso de la igualdad “x” más “y” igual a 30, cada par ordenado que hace de la igualdad un enunciado verdadero, se puede representar con un punto sobre la recta “y” igual a 30 menos “x”.
Si se realiza un análisis similar para la igualdad, “x” menos “y” igual a 6, se llega a la conclusión de que los pares ordenados que cumplen con la igualdad se pueden representar como puntos sobre la recta “y” igual a “x” menos 6.

En resumen, si cada expresión lineal se analiza por separado, se pueden encontrar una infinidad de pares ordenados que hacen que se cumpla la igualdad.
Ahora bien, ¿qué es la solución de un sistema de ecuaciones lineales como “x” más “y” igual a 30 y “x” menos “y” igual a 6?
La solución de un sistema de ecuaciones se refiere a los pares ordenados que satisfacen. al mismo tiempo, todas las ecuaciones que lo conforman.
Por ejemplo, ¿el par ordenado 29 coma 1 es solución del sistema “x” más “y” igual a 30; “x” menos “y” igual a 6?
Se advierte que, si se sustituye “x” por 29 y “y” por 1, en la ecuación “x” más “y” igual a 30 se cumple la igualdad porque 29 más 1 es igual a 30.
Sin embargo, si se sustituye “x” por 29 y “y” por 1 en la ecuación “x” menos “y” igual a 6, no se cumple la igualdad porque 29 menos 1 es distinto de 6.

Así, el par ordenado 29 coma 1 no es solución del sistema porque al sustituirlos en las dos ecuaciones, no se verifican todas las igualdades al mismo tiempo.
Cada ecuación lineal del sistema, se representa en el plano por una recta. Todos los puntos de la recta representan los pares ordenados que hacen que se cumpla la igualdad.
Pero, al analizar las rectas como la representación de un sistema de ecuaciones, se buscan los pares ordenados que se encuentren en las dos rectas al mismo tiempo.
Por ejemplo, si se grafica el sistema “x” más “y” igual a 30; “x” menos “y” igual a 6, ¿qué punto o puntos se encuentran en las dos rectas al mismo tiempo?

Se observa que, en este caso, las rectas coinciden en el punto 18 coma 12. Por tanto, el par ordenado 18 y 12 es solución del sistema.
Si sustituyes estos valores en las ecuaciones se observa que se cumplen las igualdades de 18 más 12 igual a 30 y 18 menos 12 igual a 6.
¿Cómo se puede encontrar ese punto algebraicamente? A continuación, se expondrá el método de suma y resta, y se le dará significado con base en lo que has aprendido.
En primera instancia, se puede observar que cada ecuación del sistema “x” más “y” igual a 30; “x” menos “y” igual a 6, contiene dos literales de las que se desconoce su valor llamadas incógnitas.
De acuerdo con lo que has estudiado en este grado ¿cómo consideras que se puede resolver el sistema de ecuaciones?
Uno de los métodos además del que acabas de utilizar es buscar un nuevo sistema de ecuaciones de tal forma que una de las ecuaciones sólo tenga una incógnita, pero al mismo tiempo, que tenga las mismas soluciones que el sistema original. Cuando dos sistemas tienen las mismas soluciones, se dice que son equivalentes.
¿Cómo se puede encontrar un sistema de ecuaciones que tenga las mismas soluciones que el sistema “x” más “y” igual a 30; “x” menos “y” igual a 6? En otras palabras ¿cómo se pueden encontrar sistemas equivalentes?
Una opción puede ser multiplicar ambos miembros de una de las ecuaciones del sistema por cualquier número distinto de cero.
Por ejemplo, considera nuevamente el sistema “x” más “y” igual a 30; “x” menos “y” igual a 6. Considera también que su representación gráfica consiste en dos rectas que se cortan en un punto.
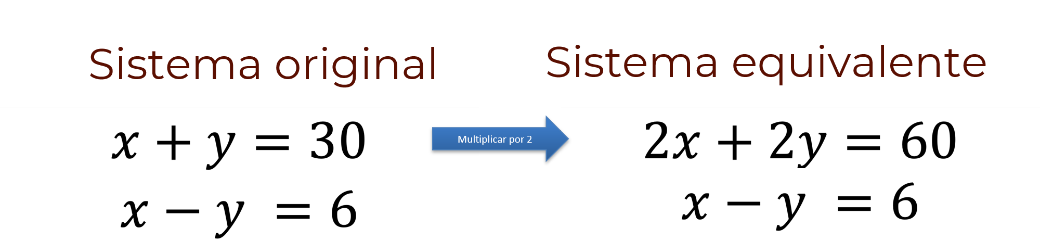
Ahora bien, si en el sistema, la ecuación “x” más “y” igual a 30 se multiplica por dos, se obtiene la expresión 2 “x” más 2 “y” igual a 60.
Aunque algebraicamente, las expresiones “x” más “y” igual a 30 y 2 “x” más 2 “y” igual a 60 puedan parecer dos ecuaciones distintas, los pares ordenados que hacen de las igualdades un enunciado verdadero son los mismos para ambas ecuaciones. Verifica esto para algunos valores.
En la gráfica, se puede observar que se trata de la misma recta y que, por tanto, el nuevo sistema tiene las mismas soluciones que el original, es decir, es equivalente.

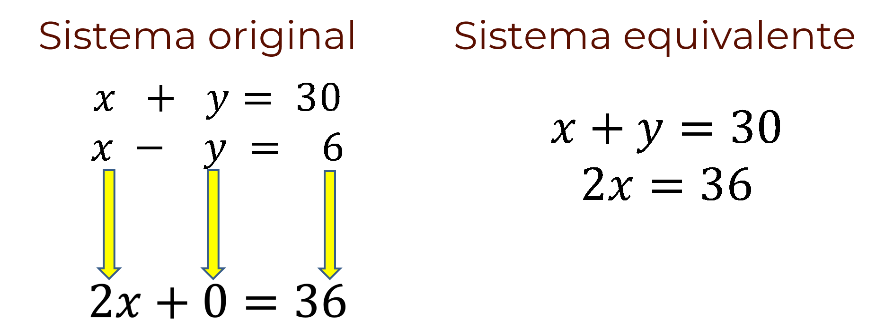
Otra opción consiste en sustituir una de las ecuaciones del sistema por la suma de ella con la otra.
Por ejemplo, en el sistema “x” más “y” igual a 30, “x” menos “y” igual a 6; realiza la suma de “x” más “y” igual a 30 y “x” menos “y” igual a 6.
Operando uno “x” más uno “x” da como resultado 2 “x”. Luego, uno “y” menos uno “y” es igual a cero “y”; por otro lado, 30 más 6 igual a 36. Por lo tanto, se obtiene la expresión 2 “x” igual a 36.
Ahora bien, si en el sistema “x” más “y” igual a 30, “x” menos “y” igual a 6; se sustituye la ecuación “x” menos “y” igual a 6 por la suma de las ecuaciones que se obtuvo: 2 “x” igual a 36; se obtiene el nuevo sistema “x” más “y” igual a 30, 2 “x” igual a 36.
Observa que este nuevo sistema tiene las mismas soluciones que el original, es decir es un sistema equivalente al original. En la gráfica, se observa que las rectas del nuevo sistema se cortan en el punto 18 coma 12, como en el sistema original.
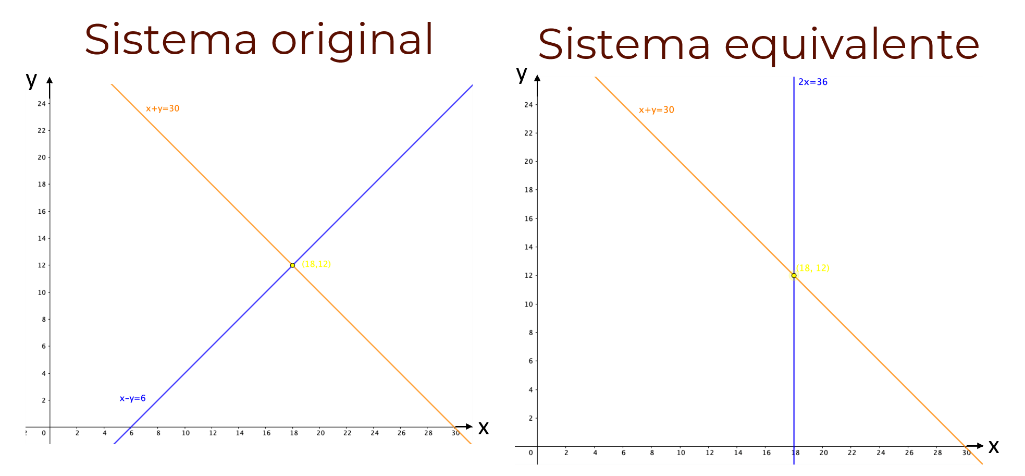
¿Qué ventajas tiene realizar las operaciones antes mencionadas para obtener sistemas lineales con la misma solución o soluciones?
Al elegir de manera adecuada las operaciones permitidas entre las ecuaciones, se puede obtener un nuevo sistema que contenga una ecuación lineal con una sola incógnita.
Esa ecuación se puede resolver con los métodos conocidos.
Por ejemplo, al realizar las operaciones permitidas entre las ecuaciones del sistema original, se obtuvo el nuevo sistema “x” más “y” igual a 30; 2 “x” igual a 36. En ese nuevo sistema, la ecuación 2 “x” igual a 36 se puede resolver con las propiedades de la igualdad:
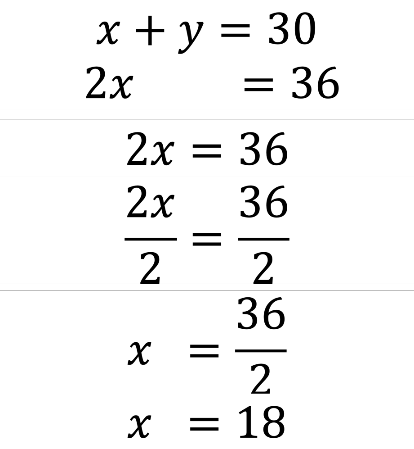
Se dividen ambos miembros de la igualdad entre el coeficiente de “x” que es 2, por lo tanto, se obtiene 2 “x” entre 2 igual a 36 entre 2. Si se realizan operaciones en el miembro izquierdo de la ecuación se tiene 2 “x” entre 2 es uno “x” que es igual a “x”. La ecuación que resulta es “x” igual a 36 entre 2. Si se realizan operaciones en el segundo miembro de la ecuación se divide 36 entre 2 y el cociente es igual a 18.
Así obtienes el valor de “x”, que es igual a 18.
Una vez que se conoce que el valor de “x” es 18, se puede conocer el valor de “y”. Para esto, se puede sustituir ese valor de la incógnita “x” en la primera ecuación del sistema: “x” más “y” igual a 30.
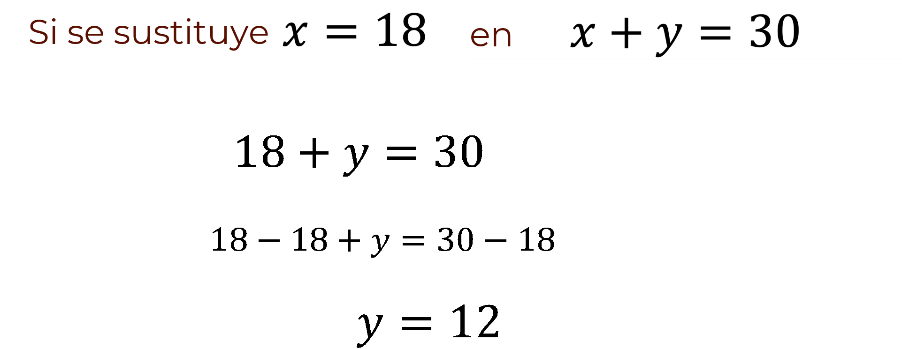
Sustituyendo, se tiene que 18 más “y” es igual a 30.
Por las propiedades de la igualdad, se puede restar 18 en ambos miembros de la ecuación, quedando 18 menos 18 más “y” es igual a 30 menos 18.
Al operar en el primer miembro, se obtiene 18 menos 18 da como resultado cero, más “y”, es decir, se obtiene únicamente “y”. Al operar en el segundo miembro se obtiene, 30 menos 18, es igual a 12.
Así, el valor de la incógnita “y” es igual a 12.
Entonces, la solución del sistema es:
“x” igual a 18 y “y” igual a 12
Por lo tanto, un número es 18 y el otro es 12.
Has aprendido que, se pueden realizar operaciones permitidas entre las ecuaciones de un sistema, de forma que, por un lado, se pueda obtener uno nuevo con las mismas soluciones que el original y que, por otro lado, el sistema obtenido tenga la ventaja de que una de las ecuaciones se encuentre en términos de una sola incógnita.
Al resolver esa ecuación, es posible conocer el valor de una de las incógnitas. Una vez que se obtiene dicho valor, se puede sustituir en la otra ecuación del sistema para obtener el valor de la otra incógnita.
Este método, suele presentarse en forma de pasos:
1. Multiplicar ambas ecuaciones del sistema por números, de tal forma que se tengan términos iguales con la misma incógnita, pero con signos opuestos.
2. Sumar las ecuaciones.
3. Resolver la ecuación obtenida.
4. Sustituir el valor hallado en una de las ecuaciones para obtener el valor de la otra incógnita.
Ahora que ya has dado un significado a esos pasos. Responde, ¿en qué casos utilizarías este método?
Una vez que se hallan los valores de las incógnitas, se sustituirán en las ecuaciones del sistema de dos ecuaciones lineales con dos incógnitas, para verificar que las igualdades se cumplen.
Se sustituye el valor numérico de “x” igual a 18 y “y” igual a 12 en las dos ecuaciones.
Se comenzará sustituyendo los valores numéricos de “x” y de “y”, en la primera ecuación, que es: “x” más “y” igual a 30.
Sustituyendo los valores se obtiene: 18 + 12 = 30. Si se realiza la suma de 18 + 12 se obtiene como resultado 30. Se observa que 30 es igual a 30.
En segundo lugar, se sustituyen los valores numéricos de “x” y de “y” en la segunda ecuación, que es: “x” menos “y” igual a 6.
Al sustituirlos, se obtiene: 18 menos 12 igual a 6. Al realizar la operación se obtiene 6. Se observa que 6 es igual a 6.
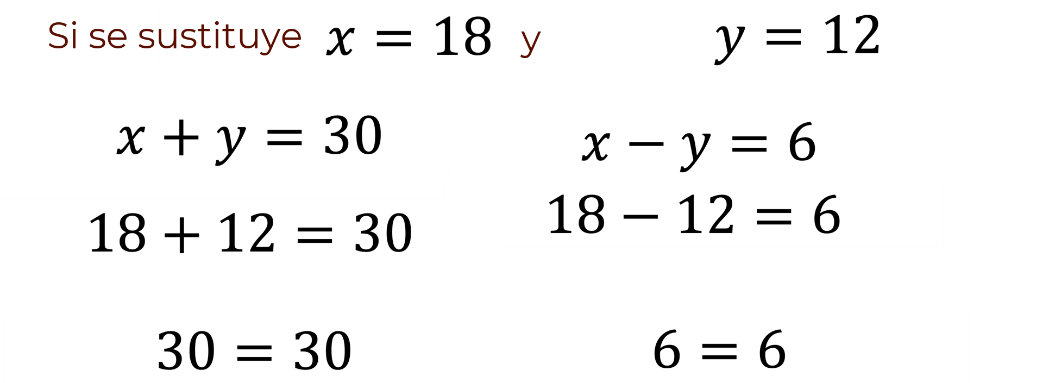
Así, se verifica que los valores numéricos de las literales “x” y “y”, satisfacen ambas ecuaciones del sistema.
A continuación, resuelve el siguiente ejercicio para aplicar lo aprendido.

Primero realiza una estimación: ¿Se llenaron más botellas con una capacidad de 5 litros que de 2 litros?
Ahora, procede a modelar el ejercicio con un sistema de dos ecuaciones lineales con dos incógnitas.
Se asignará la letra “x” al número de botellas con capacidad de 5 litros, y “y” al número de botellas con capacidad de 2 litros.
La primera ecuación del sistema es “x” más “y” igual a 323, donde “x” representa el número de botellas con capacidad de 5 litros, “y” el número de botellas con capacidad de 2 litros y 323 el número total de botellas.
La segunda ecuación del sistema se puede representar como 5 “x” más 2 “y” igual a mil, donde 5x representa la cantidad total de detergente envasada en las botellas de 5 litros, mientras que 2x representa la cantidad total envasada en botellas de 2 litros y 1,000 litros es la cantidad total de detergente.
El sistema de dos ecuaciones con dos incógnitas queda:
La primera ecuación: “x” más “y” igual a 323.
La segunda ecuación: 5 “x” más 2 “y” igual a 1,000.

Una manera de continuar con la resolución del problema consiste en encontrar un nuevo sistema de ecuaciones que sea equivalente al original, pero que contenga una ecuación con únicamente una incógnita.
¿Qué operaciones están permitidas para encontrar el sistema equivalente?
Como se dijo anteriormente, una operación permitida consiste en multiplicar ambos miembros de una de las ecuaciones del sistema por cualquier número distinto de cero.
Otra operación permitida consiste en sustituir una de las ecuaciones del sistema por la suma de ella con la otra. Esa otra ecuación se puede multiplicar por cualquier número.
Reflexiona, ¿qué operaciones permitidas pueden realizar entre las ecuaciones del sistema “x” más “y” igual a 323; 5 “x” más 2 “y” igual a 1 000, para encontrar un nuevo sistema de ecuaciones equivalente, pero que contenga una ecuación con únicamente una incógnita?
Una opción es multiplicar la ecuación “x” más “y” igual a 323 por 2 negativo.
Realizando la operación, se obtiene: 2 negativo por uno “x” dando como resultado 2 “x” negativo; luego, 2 negativo por uno “y” da como resultado 2 “y” negativo y al multiplicar 2 negativo por 323 se obtiene 646 negativo.
Así, se obtiene el nuevo sistema conformado por las ecuaciones 2 “x” negativo menos 2 “y” igual a 646 negativo y 5 “x” más 2 “y” igual a mil.

Recuerda que, al realizar las operaciones permitidas, este nuevo sistema tiene las mismas soluciones que el original. Es decir, este sistema es equivalente al original. Pero todavía no se obtiene un sistema en el que una de las ecuaciones contenga únicamente una incógnita.
De acuerdo con las operaciones permitidas, en el sistema conformado por las ecuaciones 2 “x” negativo menos 2 “y” igual a 646 negativo y 5 “x” más 2 “y” igual a 1,000, una de las ecuaciones se puede sustituir por la suma de ella con la otra ecuación del sistema.

Al sumar 2 “x” negativo menos 2 “y” igual a 646 negativo más 5 “x” más 2 “y” igual a 1,000, se tiene que, 2 “x” negativo más 5 “x” da como resultado 3 “x”; 2 “y“ negativo más 2 “y” igual a cero; y 646 negativo más 1,000 es igual a 354. Por lo tanto, se obtiene la ecuación 3x igual a 354.
En el sistema conformado por las ecuaciones, dos “x” negativo menos dos “y” igual a 646 negativo y 5 “x” más 2 “y” igual a 1,000, se puede sustituir la ecuación 5 “x” más 2 “y” igual a 1,000 por la ecuación 3 “x” igual a 354.
Así, se obtiene un nuevo sistema conformado por las ecuaciones dos “x” negativo menos dos “y” igual a 646 negativo y 3 “x” igual a 354. Ese sistema es equivalente al original, pero tiene la ventaja de que contiene una ecuación con únicamente una incógnita.
En ese nuevo sistema, se puede resolver la ecuación 3 “x” igual a 354 aplicando las propiedades de la igualdad:
Se divide ambos miembros de la ecuación entre el coeficiente de “x” que es 3, por lo tanto, se obtiene 3 “x” entre 3 igual a 354 entre 3. Al dividir 3 “x” entre 3 se obtiene uno “x” igual a “x”. Al dividir 354 entre 3, el cociente es igual a 118.
Así, se obtiene el valor de la incógnita “x” es igual a 118.
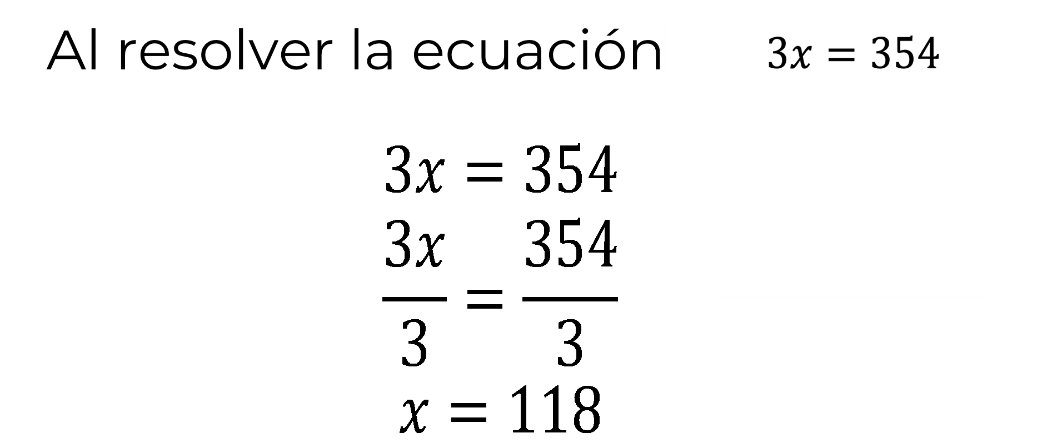
Ahora, una vez que ya se obtuvo el valor de la incógnita “x” se puede calcular el valor de la incógnita “y”.
Piensa ¿qué harías para obtenerla?
Se puede sustituir el valor obtenido para “x” en la otra ecuación del sistema equivalente que es 2 “x” negativo menos 2 “y” igual a 646 negativo o en la ecuación original x + y = 323.
Resuelve la ecuación que resulta para calcular el valor de “y”. Se obtiene “y” igual a 205.
La solución del sistema es:
“x” igual a 118
“y” igual a 205
Esto significa que, el número de botellas de 5 litros que se ocuparon es igual a 118 y el de 2 litros es igual a 205.
Comprueba estos resultados. Observa las ecuaciones originales:
“x” más “y” igual a 323 y 5 “x” más 2 “y” igual a 1,000.
Al sustituir los valores obtenidos para “x” y para “y” se tiene, para la primera ecuación: 118 más 205 igual a 323. 118 más 205 es igual a 323. Observa que se cumple la igualdad.
En la segunda ecuación se tiene 5 por 118 más 2 por 205 es igual 1,000. Al calcular los productos se obtiene que 5 por 118 es igual a 590 y que 2 por 205 es igual a 410. Al sumar 590 más 410 se obtiene 1,000. En esta ecuación también se cumple la igualdad.
Regresa a la estimación que hiciste al inicio de este problema, ¿qué tanto te aproximaste a la respuesta correcta? Ahora, ya sabes que las botellas de dos litros se ocuparon más en el envasado.
Una vez que ya se encontraron los valores de las literales, puedes verificar que, al sustituir esos valores en el sistema de dos ecuaciones lineales con dos incógnitas, se obtienen igualdades.
En ella, se modelaron problemas con sistemas de ecuaciones lineales con dos incógnitas, los cuales se resolvieron por el método de suma y resta.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Lo que la canción quiso decir
Aprendizaje esperado: Analiza críticamente el contenido de canciones de su interés.
Énfasis: Analizar mensajes de canciones.
¿Qué vamos a aprender?
Aprenderás sobre: “Lo que la canción quiso decir”, con esto se refiere a: “Analizar los mensajes que contienen las letras de las canciones”.
Así podrás entender mejor el mensaje que las letras de una canción buscan transmitir.
Los materiales que necesitarás son tu cuaderno, y lápiz o bolígrafo para que puedas tomar notas, así como tu libro de texto.
Se te recomienda llevar un registro de las dudas, inquietudes o dificultades que surjan, pues muchas de éstas las podrás resolver al momento de consultar tu libro de texto y revisar tus apuntes.
¿Qué hacemos?
Las canciones han acompañado desde tiempos inmemoriales a la humanidad, a través de ellas es posible comunicar ideas y sentimientos de una forma única. Y, a pesar de la cantidad de géneros musicales, cada persona siente predilección por alguno, ¿qué música te gusta escuchar cuando estás feliz?
Las canciones forman parte de la educación sentimental. ¿Cuántas veces, al escuchar una canción, te has sentido identificado con su mensaje? ¿Has llegado a dedicar canciones?
Seguramente lo has hecho, pues una canción puede transmitir de mejor manera las emociones.
En efecto, no a todas las personas se les facilita comunicar lo que sienten. Y también es recomendable buscar en un diccionario las palabras que desconoces, para saber lo que estás dedicando o cantando.
Para concretar la idea escucha el extracto de una canción del cantautor, poeta y músico mexicano Alejandro Filio, quien pertenece al movimiento conocido como nueva canción. ¿Cuál crees que es el mensaje de la canción “De los enamorados”?
- “De los enamorados”
Puedes pensar que el mensaje es acerca del recuerdo de una mujer que crea muchas emociones en el hombre que la recuerda.
Observa qué papel juega el mensaje, por ejemplo, en un proceso de comunicación, ya que las letras de una canción además de tener una finalidad se insertan en un contexto, es decir, en una situación.
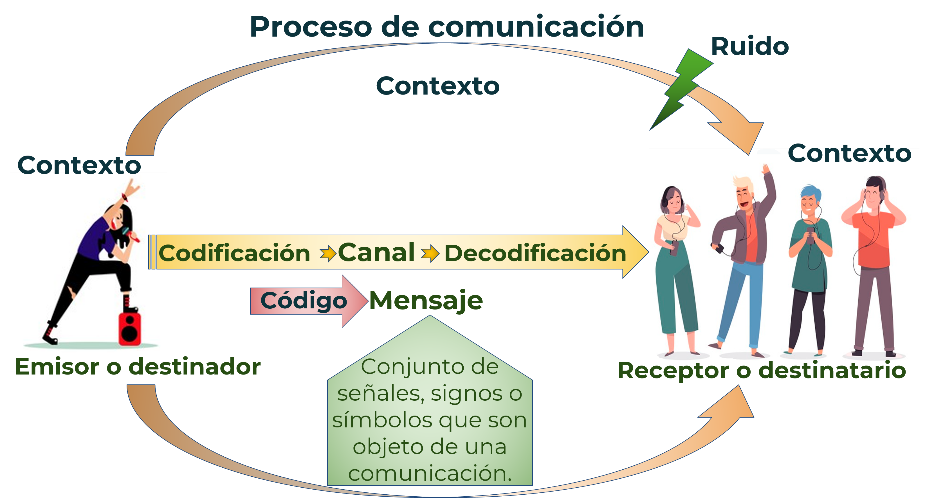
Todo proceso de comunicación tiene alguien que envía un mensaje y quien lo recibe, y se realiza a través de una canal o medio. En este caso una canción y ésta lleva un mensaje, que es un conjunto de señales, signos o símbolos encerrados en un código, que es el tipo de lenguaje utilizado para crear el mensaje.
El contexto es el momento en el que se comunica algo y que cada emisor y receptor tienen su propio contexto y a partir de ello decodifican el mensaje, es decir, lo interpretan.
Y el ruido es una interferencia, es decir, un desconocimiento acerca de algo que se dice en el mensaje, por ejemplo, si determinada canción la escucha un niño de 6 u 8 años, quizá se le dificulta entender el mensaje por completo.
Dicho lo anterior, rescata algunas frases del fragmento del cantautor Alejandro Filio para entender el mensaje.
Inicia con las primeras estrofas, trata de identificar las oraciones que se están usando con un significado distinto al que se utilizan normalmente.

Como puedes observar, lo subrayado en verde se refiere a la tarde que llega al mismo tiempo que una mujer; en lo subrayado en amarillo se manifiesta que se ha dejado la voz de la mujer, guardada en el enamorado y, en lo subrayado en rojo, se indica que, por ello, la busca y la inventa.
La palabra “ceniza”, no tiene un significado literal o realista, pues la canción dice: “tarde color de ceniza”.
Esto ocurre con frecuencia en las canciones, muchas palabras no se usan de forma habitual y esto puede generar ciertas confusiones.
Para entender más cómo funcionan estos aspectos, observa el video en el que da su opinión el cantautor mexicano Fernando Delgadillo, quien es creador de la canción informal. Obsérvalo del inicio al minuto 03:20.
- Fernando Delgadillo
Fernando Delgadillo señala que hay acordes que pueden ayudar a entender por dónde va la letra y el mensaje de una canción y en la canción de “No me pidas ser tu amigo”, es probable que muchos hayan estado en esa situación.
Observa el extracto de esa canción y presta atención al mensaje.

¿Qué observas en este extracto?
El mensaje es contundente: Él no quiere ser su amigo, sino su novio.
A eso le conocemos como lenguaje denotativo porque dice tal cual las cosas.
Conoce los tipos de mensaje:
El denotativo aporta el valor informativo o referencial de un término o palabra, es decir, el significado literal de un diccionario, por ejemplo, “es muy sentimental y por todo llora”; en el caso del extracto de la canción de Delgadillo, todo es denotativo.
En cambio, en el connotativo, hay un uso figurado del lenguaje. Nuevos sentidos o valores que puedes agregar al significado, por ejemplo, “Anda chipil” o “Tiene corazón de pollo”.
En el denotativo se dicen las palabras o las oraciones tal cual, y en el connotativo se agregan otros sentidos que, quizá, no todos pueden entender.
Se identifican unas con lenguaje connotativo:
- Hoy me vino la gana que no las musas…
- Y descolgarte desde aquí hasta las ganas de la mañana…
- Mientras esta mujer rompe el espacio…
¿Por qué son connotativas en lugar de denotativas?
Porque usa palabras para darle al mensaje otro sentido, por ejemplo, indicar que no le “vinieron las musas” pero sí las ganas es un mensaje figurado; lo mismo “descolgarte desde aquí hasta las ganas”, pues las ganas no se descuelgan y “esta mujer rompe el espacio” hace alusión a que se hace presente.
Como puedes darte cuenta, al entender los tipos de mensajes su interpretación adquiere sentido.
Ahora observa, de nuevo, a Fernando Delgadillo, quien habla acerca de los mensajes en una canción y escucha el extracto de su composición “Hoy hace un buen día”.
Intenta localizar el tipo de mensaje que tiene y si es denotativo o connotativo. Obsérvalo y escúchalo del minuto 03:21 al 06:31.
- Fernando Delgadillo
Como pudiste escuchar, el extracto tiene una serie de mensajes denotativos y connotativos. Escucha lo que logró identificar su compañero Camilo.
- Camilo
Esas observaciones son correctas.
Ahora escucharás otro género musical para que observes que los mensajes también se pueden identificar en otras canciones.
Escucha a Juan Manuel Campechano, él es miembro del grupo de soneros Mono Blanco, quienes han llevado su música por todo el mundo.
Escucha atentamente para poder identificar el mensaje que trae el extracto que cantará.
- Juan Manuel Campechano Yan

¿Cuál es el mensaje de la primera estrofa?
¿Detectas el lenguaje denotativo o es connotativo?
¿Qué lenguaje sería el de la segunda estrofa?
Con lo que has aprendido seguramente podrás responder a las preguntas. No olvides revisar diccionarios especializados para poder identificar las palabras “vide” o “nubería”.
El Reto de Hoy:
No olvides revisar tus libros de texto y buscar el Aprendizaje esperado. Ahí podrás encontrar más ejemplos de canciones. Recuerda que puedes acudir a tu maestra o maestro para que disipe tus dudas.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Visitando otros planetas
Aprendizaje esperado: Describe cómo se lleva a cabo la exploración de los cuerpos celestes por medio de la detección y el procesamiento de las ondas electromagnéticas que éstos emiten.
Énfasis: Reflexionar sobre los avances tecnológicos que han permitido la exploración no tripulada de planetas como Marte.
¿Qué vamos a aprender?
Ten a la mano tu cuaderno, lápiz o bolígrafo para que puedas tomar notas de las ideas principales, de tus reflexiones y de las dudas que te puedan surgir durante el desarrollo del tema.
Además, puedes recurrir a tu libro de texto para profundizar más o resolver tus dudas.
¿Alguna vez has pensado en lo interesante que sería la visita a otros planetas?
Seguramente da curiosidad como serían, y la curiosidad siempre te lleva a averiguar, a tratar de comprender lo que desconoces.
¿En qué piensas cuando vas a visitar a alguien?, quizá planeas lo que vas a comer, o cuánto tiempo estarás allá, si la gasolina del automóvil te alcanzará para ir y regresar de ese viaje.
También puedes pensar en si habrá otros visitantes, en cómo vas a pasar el tiempo y si surge un problema ayudar a resolverlo; sin duda alguna, se piensa en disfrutar la visita o por lo menos estar lo más cómodo posible al igual que con las personas que se comparte el momento.
Ese es un pensamiento científico, porque te estás formulando preguntas, pero además se busca la forma de responderlas, así como lo hace todo el equipo que está detrás de una misión espacial.
Imagina todo lo que necesitarías atender si es que la visita fuera a la Luna o a Marte, donde las condiciones de tu cuerpo y la comida son completamente distintas, además de que el tiempo de estancia sería aún mayor.
¿Qué hacemos?
El primer destino fue la Luna.
La Unión Soviética y los Estados Unidos se propusieron dirigir sus naves hacia la Luna, sin que estas impactaran catastróficamente sobre el satélite natural. Se crearon dos sondas que lograron tal propósito. En enero de 1966, la sonda soviética Luna 9 consiguió alunizar suavemente y enviar fotografías a la Tierra.
La cámara que tenía la Luna 9 contaba con un sistema de espejo que podía orientarse, con el fin de tener una visión más amplia de la superficie del astro, gracias a sus giros.
Era una tecnología muy avanzada para esa época. Además, qué importante debió haber sido la información que se obtuvo de esas fotografías.
La primera imagen tardó siete horas en llegar a la Tierra, y fueron un total de nueve imágenes adquiridas en cinco panoramas. Gracias a las imágenes que captó la cámara de la sonda se obtuvo información relacionada con las características de la superficie lunar, más específicamente sobre la cantidad y distribución de los cráteres.
Es importante conocer, por lo menos en foto, el lugar que se va a visitar, porque eso permite prepararte sobre cómo debes ir vestido o las provisiones que debes llevar.
En ese momento el descubrimiento más importante que se hizo fue lograr comprobar la dureza del suelo lunar, es decir, que la Luna pudiera soportar en su superficie un objeto sin que este se hundiera.
Pero el hombre aún no era tripulante en ninguna de esas misiones, la prioridad era conocer la mayor cantidad de detalles posibles de la Luna. Antes se habían enviado a algunos animales para saber si un ser vivo podía soportar un viaje de este tipo. Entonces, hasta el momento eran misiones no tripuladas
En junio de 1966, los norteamericanos enviaron la sonda Surveyor 1, que logró el primer aterrizaje suave en la superficie lunar.
Los principales propósitos del programa Surveyor fueron una serie de vuelos robóticos dirigidos hacia la Luna, con el fin de alunizar exitosamente para poder apoyar los demás arribos del programa Apolo y lograr, además, el desarrollo y la validación de la tecnología necesaria para el descenso suave en la Luna, el suministro de datos sobre la compatibilidad de la estructura del Apolo con las condiciones observadas en el suelo lunar y la incrementación de la información concerniente a este hermoso astro.
Eso quiere decir que la información de las sondas espaciales es sumamente importante, pero ¿qué son?
Una sonda espacial es un dispositivo tecnológico que ayuda a la exploración del universo. Estos dispositivos han llegado a todos los planetas y suelen ser, generalmente, más pequeños que un cohete. Así van desplazándose por el espacio con un equipo de cámaras y sensores que arrojan información valiosa sobre los sitios que visitan.
Entre las sondas espaciales más famosas se encuentran:
La Voyager 1 y 2, lanzadas en 1977, que visitaron los planetas Júpiter, Saturno, Urano y Neptuno. La misión de la Voyager 1 es localizar los límites del Sistema Solar.
Actualmente es el objeto de fabricación humana más alejado de la Tierra, ya que continúa viajando por el universo.
¿Puedes imaginar todo lo que la sonda espacial ha visto? Imagina todo lo que ha podido encontrar a su paso. Te has preguntado, ¿qué sucedería si una de estas sondas encuentra formas de vida en otra región del universo?
Se debe precisar que la ciencia se basa en hechos, se debe comprobar para poder tomarlo como válido. Cuando se habla de formas de vida se refiere a vestigios o a condiciones favorables para ella en planetas lejanos.
Para ejemplificar lo que has aprendido realiza la siguiente actividad.
Imagina que tu maestra visitará una escuela en África, y a ti se te pidió que prepares algunos objetos para llevarlos con ella, con el propósito de que los estudiantes africanos conozcan más sobre la vida de los estudiantes mexicanos.
La limitante es que todos los objetos deben caber en una caja de zapatos y no es posible incluir aparatos electrónicos. ¿Qué objetos enviarías para cumplir el objetivo? y ¿por qué?
Un ejemplo puede ser un libro de ciencia, quizá alguna planta pequeña, tal vez algún fruto típico de la región. ¿En qué objetos pensaste?
El astrónomo Carl Sagan se enfrentó a un problema similar a este, pues le solicitaron que preparara un disco con información del planeta Tierra para incluirlo en una de las sondas espaciales Voyager, en caso de que alguna civilización extraterrestre las encontrara.
Sagan seleccionó fotografías de personas, animales, plantas y paisajes de nuestro planeta. También incluyó saludos en muchos idiomas y canciones, entre ellas un son jarocho titulado “El cascabel”.
Así que en esas sondas va un pedacito de la humanidad viajando por el espacio.
Puedes conocer el contenido de este disco visitando el siguiente enlace:
http://goldenrecord.org/#discus-aureus
Se han enviado cientos de sondas espaciales. Las más importantes de los últimos años han sido la sonda Cassini-Huygens y New Horizons.
La sonda Cassini-Huygens tenía como objetivo explorar el planeta Saturno, sus anillos y varias de sus lunas, particularmente Titán. Terminó su vida útil en 2017. Como era imposible regresar la sonda a la Tierra y existía cierta posibilidad de que cayera en algún satélite del planeta, se decidió quemarla por fricción en la atmósfera de Saturno, lo que se hizo para evitar contaminar con objetos terrestres a un astro.
La sonda New Horizons fue lanzada en 2006, visitó Júpiter y llegó a Plutón en 2015. La información que envió sobre el planeta enano tardó en llegar a la Tierra alrededor de cinco horas y media.
En enero de 2019 también sobrevoló Ultima Thule, el planeta enano más lejano del sistema solar. Las señales del encuentro tardaron seis horas en recorrer, a la velocidad de la luz, los más de 6,600 millones de kilómetros que lo separan de la Tierra. Las mejores imágenes que se tienen de los confines del sistema solar las tomó esta sonda.
La mirada siempre ha estado puesta en el cielo, pero regresa al alunizaje.
Fue así que el 21 de julio de 1969, el planeta entero tenía puestos los ojos sobre las transmisiones por televisión que se hacían de dos astronautas caminando sobre la Luna, quienes, además, contemplaban el amanecer terrestre desde el satélite natural.
De esta manera, tres norteamericanos, Neil Armstrong, Buzz Aldrin y Michael Collins subieron a una nave espacial, el Apolo 11, situada en el extremo norte de Cabo Kennedy e impulsada por el cohete Saturno, que los pondría fuera de la Tierra y de esta manera empezarían a orbitar la Luna.
Pero la Luna no fue el único objetivo, había más cuerpos celestes por los que la humanidad sentía curiosidad, como el planeta rojo.
El planeta marciano, es decir Marte. De esta manera, los primeros intentos por llegar a pisar suelo marciano se llevaron a cabo por la Unión Soviética en octubre de 1960, con dos sondas del programa Marsnik. No obstante, fue hasta 1963 que una sonda de origen ruso orbitaría Marte. La Mars 1 giró alrededor del planeta rojo por unos días, y luego la base central en Tierra perdió contacto con ella.
Pero fue Estados Unidos quien en 1965 envió la sonda Mariner 4, que fue la primera en conseguir llegar a Marte luego de un vuelo de casi ocho meses, y fue además la primera en tomar fotografías de la superficie de este planeta.
Las expediciones a Marte apenas iniciaban. Como evidencia de ello, en 1971, los soviéticos lanzaron la sonda Mars 2. Esta vez, gracias a la corrección de algunos errores que se produjeron en la primera sonda enviada, logró orbitar el planeta rojo. La Unión Soviética no quería quedarse atrás y para finales del mismo año enviaron la sonda Mars 3, que se creía sería un éxito total al tocar suavemente la superficie marciana. Sin embargo, decepcionó a todos cuando perdió comunicación con Tierra instantes más tarde de haber llegado al suelo del planeta rojo.
Los soviéticos habían tomado de nuevo la delantera en la competencia.
Por lo tanto, el 19 de julio de 1976, los norteamericanos lanzaron al espacio la sonda Viking 1, seguida casi inmediatamente por la Viking 2. Ambos objetos significaron un total orgullo para la nación norteamericana, ya que ambos artefactos lograron tomar y enviar imágenes a la Tierra.
Estas sondas se encontraban equipadas con dispositivos que permitirían realizar análisis de temperatura y composición al suelo marciano. Luego de esta última misión, la exploración en Marte se detuvo por casi dos décadas.
Fue hasta 1992 que continuaron las misiones a Marte, lideradas por la NASA, con el lanzamiento del Mars Observer, cuyo propósito era entrar en órbita de Marte. Sin embargo, la comunicación con la sonda se perdió. Sólo fue hasta 1997, con la puesta en órbita marciana de las sondas Mars Global surveyor y del Mars Pathfinder que se logró observar, por medio de imágenes transmitidas por las sondas desde la superficie del planeta rojo, el característico desierto rocoso que conforma la capa externa del suelo marciano.
Estas misiones son una excelente oportunidad para conocer el planeta rojo y saber si algún día se pueden habitar esos planetas.
Y es así como se llama una misión para explorar el planeta rojo, la Misión Opportunity. El Opportunity Mars Rover fue lanzado el 7 de julio de 2003, con un aterrizaje exitoso en Marte el 25 de enero de 2004. Opportunity es un vehículo con seis ruedas, un brazo robótico y una pequeña pala que le permite tomar muestras del polvo que cubre el suelo marciano. Este vehículo lleva herramientas científicas más avanzadas que las de las misiones anteriores.
Esta misión fue diseñada para resistir 90 días marcianos, un día solar marciano solamente es un poco más largo que un día solar terrestre, y para recorrer unos 1000 metros de distancia, pero viajó más de 45 kilómetros.
Esta estructura tenía cuatro objetivos principales: determinar la existencia de vida en Marte, definir su clima, diagnosticar la composición de su suelo y tomar información que contribuya a la exploración humana del planeta rojo en un futuro.
No obstante, los hallazgos del Opportunity no se limitaban a las tomas de muestras señaladas. Este explorador de 174 kg de peso y un tamaño similar a un carrito de golf ha tenido que viajar sobre rocas y cantos rodados, bajar al interior de cráteres, atravesar cauces secos de antiguos ríos y escalar pendientes de grava con 32 grados de inclinación, todo un récord fuera de la Tierra.
La misión Opportunity finalizó oficialmente el 13 de febrero de 2019. La histórica misión del rover Opportunity en Marte finalizó tras 15 años en la superficie marciana. La tormenta de polvo bloqueó tal cantidad de luz solar que el día se convirtió en noche para el Opportunity, localizado cerca del centro de la tormenta, en el Valle de la Perseverancia.
Después de más de 1.000 órdenes para restablecer el contacto, los ingenieros de la Instalación de Operaciones de Vuelo Espacial en el Laboratorio de propulsión a chorro de la NASA realizaron el martes un último intento por resucitar el Opportunity, pero fue en vano.
La NASA destaca los siguientes logros del Opportunity: el 20 de marzo de 2005, en un solo día, recorrió 220 metros; envió a la Tierra más de 200 mil imágenes; dejó al descubierto las superficies de 52 rocas, revelando superficies minerales frescas para el análisis, y despejó 72 objetivos adicionales con un cepillo y los preparó para la inspección con espectrómetros y para un examen microscópico; encontró hematita, un mineral que se forma en el agua, en el lugar de aterrizaje; y halló fuertes indicios de la acción de agua antigua en el cráter Endeavour, similar al agua potable de un estanque o lago en la Tierra.
Es muy importante la labor de esa misión y del pequeño rover, pero, ¿qué es un rover?
Es un vehículo electromecánico que sirve para desplazarse y recoger muestras minerales, entre otras cosas, de una superficie, ya sea lunar o marciana. El diseño y las funciones de los rover han ido cambiando, ahora son robots que se encuentran completamente computarizados, de tal manera que los dispositivos modernos ya no se envían sólo a la Luna, sino también a Marte.
Por ejemplo, para que el Rover Opportunity se tomara una foto a sí mismo en Marte o una vista panorámica, tuvo que recibir instrucciones de un ser humano a través de una computadora.
Seguramente las señalas tardan mucho en llegar por la distancia que deben recorrer.
Realiza la siguiente actividad. Imagina que tienes que dar indicaciones a distancia a otra persona, y para ello has construido un mecanismo que conoces muy bien, pero con un gran inconveniente: cualquier indicación que le des tardará 15 minutos en llegar, y cualquier pregunta que te haga tardarás otros 15 minutos en recibirla.
En otras palabras, la comunicación no será inmediata ni fluida. Piensa, ¿qué estrategia sería la mejor para que la comunicación sea eficiente? Considera también qué sucedería si das una indicación errónea.
Podría ser enviar códigos muy breves con indicaciones precisas o almacenar información en una memoria para que tenga la programación básica.
Esta actividad te ayuda a simular lo que sucede al manipular robots rover que se encuentran en Marte, ya que la señal que se les envía desde la Tierra puede tardar entre 5 y 21 minutos en llegar, por lo que las indicaciones que se les dan deben ser precisas y muy bien planeadas, con tal de optimizar el tiempo de comunicación.
Para recapitular, lo que has aprendido observa el siguiente video del inicio al minuto 02:26.
- Estación espacial internacional y exploración con rovers
El Reto de Hoy:
Se te invita a nunca dejar de hacerte preguntas, aún falta mucho por conocer y explorar en el universo, tú puedes ser ese futuro científico que asombren con nuevos hallazgos o descubrimientos.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
¿Quién aplica las leyes?
Aprendizaje esperado: Valora la aplicación imparcial de las normas y leyes por parte de las autoridades y analiza situaciones en las que no se cumple este criterio.
Énfasis: Reconocer al funcionariado público que aplica las leyes de manera imparcial.
¿Qué vamos a aprender?
Aprenderás sobre la aplicación de las leyes de manera imparcial; para ello, reflexionarás con relación al papel de las y los funcionarios públicos para llevar a cabo esta labor tan importante al momento de hacer valer una normativa o ley.
Para trabajar en esta sesión, necesitarás tu cuaderno o una hoja, un bolígrafo o un lápiz para anotar las ideas y conceptos relevantes del contenido que se desarrollará.
Recuerda que a lo largo de la sesión deberás anotar por lo menos cinco ideas generales sobre el tema, así como todo lo que consideres relevante, ya que te servirá de insumo para la elaboración del reto al final de la sesión.
¿Qué piensas cuando escuchas la palabra “autoridad”?
Puede ser: policías, poder, personas encargadas de hacer cumplir las leyes.
Todo eso es correcto; pero ¿qué pensarías si te pidieran que comenzaras a reconocer como primeras autoridades a tus padres y familiares?, ¿creerías que es posible?
En el hogar existen normas que se deben cumplir, como los quehaceres, hacer la comida, realizar las tareas escolares, todo ello significa un conocimiento de reglas que rigen el lugar donde vives. Ahora piensa ¿qué sucede cuando estas reglas se rompen o no se cumplen? ¿Existen sanciones? ¿Cuáles son?
La familia es la primera autoridad con la que se convive desde pequeños, enseña ciertas pautas de comportamiento y también implementa “sanciones”, como no salir con las amistades o utilizar algún dispositivo electrónico.
Ahora piensa en las reglas que existen en tu escuela, como llegar a tiempo, respetar las salidas del aula o el uso de las áreas comunes, ¿existen sanciones si se rompe alguna regla?, ¿son las mismas sanciones que suceden en tus hogares?, ¿las sanciones se acumulan, es decir, existen sanciones en la escuela que dan lugar a recibir sanciones de tu madre, padre o tutor?
Este mismo razonamiento lo aplicas a tus relaciones personales, te puedes dar cuenta de que también existen reglas que no necesariamente están escritas, pero que se siguen y regulan el comportamiento del grupo de amistades.
En esta ocasión te centrarás en las reglas que son obligatorias para el buen funcionamiento de la sociedad, también conocidas como leyes, que como bien has reconocido, existen en todos los ámbitos de la sociedad en la cual te desarrollas; además de la importancia de conocerlas, es importante identificar a las personas encargadas de su aplicación, las autoridades que se definen como poder que gobierna o ejerce el mando.
Una de las funciones de las autoridades y de las y los representantes populares consiste en realizar acciones de gobierno en beneficio de la población sin hacer ningún tipo de distinción o dar privilegios a alguien. También tienen la obligación de aplicar las leyes, con base en principios que ya has revisado en sesiones anteriores.
Pero, ¿qué es una ley y qué significa aplicar las leyes?
Una ley, según la Real Academia Española, es un precepto o mandato dictado por la autoridad competente, en que se manda o prohíbe algo en consonancia o relación con la justicia y para el bien de los gobernados, o sea, el pueblo, implica llevarlas a la realidad o hacerlas efectivas en el terreno de lo práctico.
¿Qué sucede en nuestro país y en otros lugares del mundo cuando no se aplican las leyes con imparcialidad?
Se parte por definir a la imparcialidad como actuar de manera equitativa, sin tomar partido por una de las partes en perjuicio de otra.
Si bien es cierto que casi siempre buscas lo mejor para ti y para tus seres queridos, cuando no eres imparcial puedes cometer injusticias contra las y los demás y lastimar la relación con ellas y ellos.
En la convivencia escolar pueden darse casos en los que no se actúa de manera imparcial, por ejemplo, cuando algún profesor o profesora tiene algún alumno o alumna preferida, a quien le exige menos o le pone altas calificaciones sin merecerlo.
¿Qué pasaría si esto ocurre en un partido de fútbol? Analiza el siguiente ejemplo.
¿Por qué es tan difícil ser árbitro o árbitra de fútbol?
Es reglamentario:
- Tener conocimiento de reglas y normas, e
- Interpretar dichas normas.
Aspecto moral
- Posee una serie de valores que le otorgan superioridad moral
- Por ejemplo, honradez, lealtad y firmeza
Posee capacidad de juicio
- Decidir bajo presión
- Tener templanza
- Calificar y sancionar
Dotes de liderazgo
- A esto se le debe añadir las críticas y presiones mediáticas
Reflexiona mediante las siguientes preguntas:
- ¿Qué pasaría si un árbitro o árbitra de futbol realiza su trabajo sin basarse en un reglamento?
- ¿Es posible ser árbitro o árbitra sin seguir ciertos lineamientos?
- Imagina un caso en el que la árbitra o el árbitro opten por una decisión contraria al valor de honradez, ¿de qué manera esa actitud negativa deteriora su imagen y afecta a otras personas?
- ¿Se le puede reconocer como autoridad y tener confianza a una persona deshonesta?
Entonces, tomando en cuenta que las y los árbitros toman decisiones polémicas, como la expulsión de jugadoras o jugadores que cometen faltas graves y que éstas pueden provocar enojos y reclamos de los equipos y seguidores, se podría considerar que es lo mismo que hacen las autoridades.
Una función esencial de las autoridades políticas es aplicar la ley y, en general, todas las normas contenidas en la Constitución Política de los Estados Unidos Mexicanos, los tratados internacionales y los demás textos normativos vigentes.
Este principio se llama principio de legalidad. Y tiene que ver con el principio de división de poderes, que establece que corresponde al Poder Legislativo elaborar las leyes, mientras que su aplicación corresponde a los otros dos Poderes, el Ejecutivo y el Judicial.
Lo anterior lo puedes observar en el siguiente esquema.
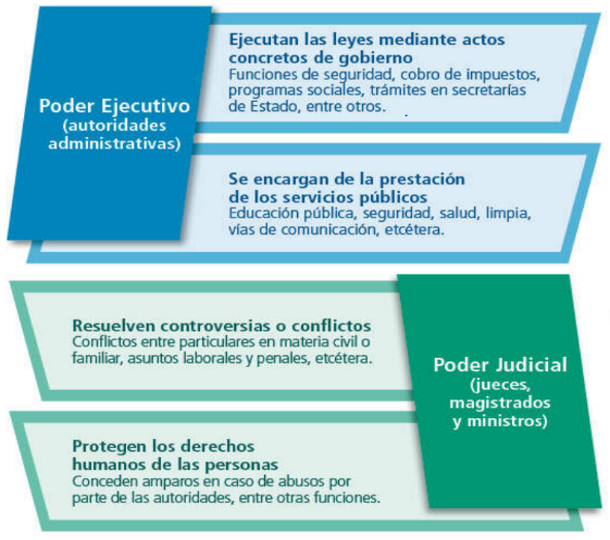
El Poder Ejecutivo, es decir, las autoridades administrativas, ejecutan las leyes mediante actos concretos de gobierno, como funciones de seguridad, cobro de impuestos, programas sociales, trámites en secretarías de Estado, entre otros.
También se encargan de la prestación de los servicios públicos, como la educación pública, seguridad, salud, limpia, vías de comunicación, etc.
Mientras que el Poder Judicial, que es representado por jueces, magistrados y ministros, resuelven controversias o conflictos, ya sea entre particulares en materia civil o familiar, asuntos laborales y penales, etc. También protegen los derechos humanos de las personas, conceden amparos en caso de abusos por parte de las autoridades, entre otras funciones.
Para seguir con la explicación, observa y escucha el siguiente video del minuto 01:41 al 03:43 que te ayudará a profundizar más sobre las funciones de las y los servidores públicos.
- Las autoridades, los servidores públicos y la aplicación imparcial de la ley
https://www.youtube.com/watch?v=U7AYCrFT8kU&t=3s
Es importante reconocer la importancia de las funciones de las y los servidores públicos, pues como ciudadanas y ciudadanos es su deber.
La ciudadanía tiene la responsabilidad de aceptar y respetar las instituciones públicas, sus decisiones y las resoluciones que emiten, cuando esto ocurre se alcanza el bien común. Recuerda que, para poder pedir justicia, primero debes conocer tus derechos.
Las autoridades encargadas de aplicar las leyes tienen la obligación de actuar de acuerdo con el principio de imparcialidad, de manera neutral, justa y equitativa, sin conceder privilegios indebidos ni discriminar a persona alguna. El desempeño imparcial de las autoridades a las ciudadanas y ciudadanos genera la certidumbre de que serán tratadas y tratados como iguales.
Anteriormente has escuchado el término “imparcialidad”, y para profundizar un poco más observa y escucha el siguiente video del 03:45 al 04:52.
- Las autoridades, los servidores públicos y la aplicación imparcial de la ley
https://www.youtube.com/watch?v=U7AYCrFT8kU&t=3s
Las autoridades son responsables de aplicar las leyes de manera imparcial, así como el árbitro del primer ejemplo.
Puedes reconocer que las figuras de autoridad se encuentran en todos los ámbitos en los que se convive, puedes incluso pensar que el primer acercamiento con la aplicación de normas es tu madre y padre, vistos como una primera figura de autoridad, como se mencionó al inicio de la sesión.
Lo cual tiene mucho sentido, pues son mamá y papá quienes ponen las reglas en casa y tratan igual a tus hermanas, hermanos, existen sanciones, pero hay que estar atentas y atentos para que no haya injusticias y así todas y todos cooperar por igual en las labores del hogar.
Del mismo modo funciona la aplicación de leyes y normas en la sociedad, debes conocerlas para exigir justicia y conocer a quienes las aplican para saber a qué instancias recurrir en caso de ser necesario, así se puede decir que aplicar las leyes imparcialmente significa que las autoridades:
- No conceden ventajas injustas al prestar los servicios públicos o al distribuir los beneficios de las acciones de gobierno.
- No toman partido ni tienen predilección por alguna de las partes en un conflicto o controversia.
- Resuelven los asuntos con objetividad, haciendo a un lado sus simpatías, antipatías y prejuicios.
Esas mismas cualidades las encuentras también en las autoridades de la escuela, con tus profesoras, profesores y personal directivo, todos deben actuar con imparcialidad.
A continuación, analizarás dos imágenes que te ayudarán a ejemplificar el punto anterior.
Observa detenidamente las imágenes y responde las siguientes preguntas:


- ¿Crees que las autoridades actúan con imparcialidad?, ¿por qué?
- Desde tu perspectiva, ¿cómo deberían actuar las autoridades para asegurar que todas y todos tengan los mismos derechos y oportunidades?
- ¿Qué beneficios tiene la población a la actuación imparcial de las autoridades?
- ¿De qué manera estas situaciones te afectan o te benefician?
- *¿Cuál crees que sería la mejor solución? ¿Por qué?
Esas situaciones resultan muy conocidas, sin embargo, es posible que logres un cambio en los resultados si haces el compromiso de conocer y hacer valer las leyes que nos rigen como ciudadanas y ciudadanos.
Se puede cambiar el comportamiento desde tu actuar diario, en tu casa con tu familia, con tus amistades, en tu escuela y demás espacios de convivencia.
Si conoces las normas de cada uno de los espacios en donde te desarrollas, seguramente lograrás una mejor armonía; a esto se le conoce como cultura de la legalidad.
Para conocer más sobre este término y su importancia, observa el siguiente video del minuto 01:47 al 03:34.
- Los desafíos de los servidores públicos en la aplicación de la ley
https://www.youtube.com/watch?v=oHjrPt1ULh8
Como pudiste observar y escuchar en el video, la legalidad te permite regular la forma en la que socializas con las y los demás, pues regula, orienta, limita y encausa las acciones de un colectivo, lo que evita que vivas aplicando la ley del más fuerte.
También sirve como medida para saber qué tanto las ciudadanas y ciudadanos conocen, respetan y aplican las leyes que les rigen.
No se puede ignorar que existen personas que, sin duda, violan las leyes de forma intencionada para sacar ventaja, debido a ello, ¿crees que es posible lograr vivir en una cultura de la legalidad?
Eso es posible si se construye una sociedad congruente con sus leyes y su cumplimiento, empezando por respetar las normas que te rigen en el hogar y en la escuela, pues todas ellas tienen un para qué de su existencia. Debes saber que no hay esfuerzos pequeños, cada regla que respetes es un paso más hacia un país con mejores oportunidades para todas y todos.
Para finalizar, identifica tres normas o leyes de acuerdo con el ámbito en el que te desarrollas; recuerda que son tu hogar, tu escuela y la sociedad, así como las sanciones que ocurrirán si se rompe alguna de ellas.
Con base en tus respuestas, elige alguna de esas normas o leyes junto con su sanción, con la que no estés de acuerdo y reescríbela como creas que funcionaría mejor.
Discute tus respuestas con tus padres, madres o tutores, recuerda que un buen argumento que surja desde la razón puede lograr grandes cambios.
Recapitula:
Reconociste el significado de autoridad y la relación tan cercana que tienes hacia ella desde muy temprana edad, como con nuestras madres y padres en el ámbito del hogar o un árbitro o árbitra en el ámbito social.
Recordaste el principio de imparcialidad y su importancia en la aplicación de normas y leyes por parte de las autoridades competentes.
También recordaste cuáles son algunas de las funciones que realizan las autoridades encargadas de aplicar la ley, específicamente las del poder ejecutivo y del poder judicial, así como la obligación moral y civil que tienen como sociedad en conocer las leyes que nos rigen.
Por último, revisaste cuál es el significado de vivir en una cultura de la legalidad, sus ventajas y su viabilidad.
El Reto de Hoy:
Consulta tu libro de texto para informarse más del tema y retomar los aprendizajes que favorezcan la construcción de una cultura de la legalidad, así como resolver tus dudas con tu profesora o profesor de la asignatura.
Continúa reforzando el diálogo con tus familiares, compañeras, compañeros de clase y amistades respecto a estos temas, su opinión puede enriquecer la tuya de manera favorable, además de que podrás ampliar tu panorama con respecto a los temas siguientes.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Las necesidades de la comunidad y la gestión técnica
Aprendizaje esperado: Planifica y organiza las acciones técnicas según las necesidades y oportunidades indicadas en el diagnóstico.
Énfasis: Reflexionar sobre la importancia de la gestión técnica y el diagnóstico.
¿Qué vamos a aprender?
No olvides tomar nota en tu cuaderno de lo que consideres más importante a lo largo de la sesión.
¿Qué hacemos?
Recuerda que en sesiones anteriores analizaste en qué consiste la gestión técnica y el diagnóstico de las necesidades para la ejecución de los procesos técnicos.
Aprendiste que la gestión técnica permite ordenar y distribuir todos los recursos que se tienen disponibles como medios técnicos, insumos e implementar criterios de eficiencia, para elaborar un producto o generar un servicio.
El desarrollo de la gestión técnica, conlleva una serie de fases ordenadas: planeación, organización, ejecución, control y evaluación de los procesos técnicos, y éstos se definen como un conjunto de operaciones que producirán un bien o un servicio.
La gestión técnica está integrada por la:
Planeación.
Comienza con el diagnóstico para la identificación de necesidades, también implica la identificación de los materiales, medios técnicos y energía que se utilizará, así como el o los procesos técnicos que se deben llevar a cabo, para poder satisfacer esta necesidad con un producto o un servicio.
Organización.
Permite determinar la secuencia de las acciones que intervienen en un proceso técnico, tiempos para realizarlas y los responsables de llevarlas a cabo.
Ejecución.
Consiste en llevar a cabo las acciones programadas en la fase de organización.
Control.
Se refiere a la supervisión de las diferentes acciones que conforman el proceso técnico que se lleva a cabo.
Evaluación.
Se refiere a la valoración del producto o servicio generado respecto a sus propósitos e implicaciones en la naturaleza y la sociedad.
Observaste un ejemplo de cómo la familia de la maestra Esmeralda, planea y organiza el proceso técnico de la elaboración de cuadernos de manera artesanal.
Se sabe que el cuaderno no es el único producto que satisface la necesidad de escribir, pero sí el que está al alcance de la familia de la maestra.
Para llevar a cabo el control de la elaboración de los cuadernos, es necesario dar seguimiento al proceso, para supervisar que todas las acciones se hagan correctamente, en tiempo y forma, corrigiendo las posibles fallas que surjan.
Registran todas las actividades que se llevan a cabo, para ello utilizan instrumentos de control que les ayudan a visualizar los procesos para analizarlos y corroborar que se están cumpliendo los objetivos.
Con respecto de la necesidad de comunicarse de manera escrita, existen diferentes tipos y maneras de hacerlo, cada sociedad ha encontrado diversas formas de cubrirla, de acuerdo a sus ideas, costumbres, tradiciones, y el espacio geográfico en el que habitan.
Las necesidades y las formas de satisfacerlas se van modificando constantemente y con ellas también los procesos y los objetos técnicos que buscan satisfacerlas.
Sólo que en muchos de los casos no todos los objetos técnicos y servicios que se comercializan responden a necesidades básicas. También existen otras que se han generado al ser influenciadas por imitación, publicidad, moda o mercadotecnia.
Observa el siguiente video, donde la mercadotecnia y la publicidad hacen que un producto se vuelva una necesidad convirtiéndolo en moda.
- TEC2_B4_PG1_V1_SEM31_b240221_Moda Ropa
Ya no es sólo satisfacer una necesidad básica, sino también han creado otras, como tener una condición social o estar a la moda.
Recuerda que, al adquirir algún artículo, debes preguntarte:
- ¿De verdad lo necesitas?
- ¿Qué otro producto puede suplirlo?
- Si no lo adquieres, ¿qué otras opciones tienes?
Más allá del tipo de necesidades, es esencial, como primer paso en la planeación de cualquier proceso técnico, hacer un diagnóstico de necesidades de la comunidad, para tener conocimiento de ellas, con el fin de satisfacerlas con un producto o servicio.
Para ello, es necesario recabar información de las necesidades que tiene esa comunidad, por medio de las técnicas de observación, encuesta y entrevista.
Mediante la observación puedes adquirir información a partir de lo que observas y escuchas, así como obtener datos de manera rápida, es esencial al realizar una investigación y para analizar gran parte de los conocimientos científicos y tecnológicos.
La encuesta es una técnica que permite obtener y registrar información de manera rápida y concisa, por medio de preguntas cerradas y abiertas, de manera presencial o con aplicaciones digitales a través de redes sociales o sitios web.
En muchas ocasiones se piensa que la encuesta y la entrevista no tienen importancia para el análisis de necesidades y, al no realizarlas se cometen errores al acelerar la presentación de un producto en el mercado, suponiendo que satisfará una necesidad.
Estas técnicas cuentan con diversos instrumentos para poder obtener datos que ayuden a identificar claramente las necesidades.
Ahora bien, toda la información recabada se concentra en un informe técnico, el cual es un documento donde se exponen con claridad los resultados del diagnóstico, se analizan las necesidades identificadas y los problemas derivados de ellas. Además, se plantean algunas ideas como posibles soluciones y algunas recomendaciones.
En la planeación técnica, también es muy importante fijar objetivos para alcanzar la o las metas establecidas, definir las estrategias a seguir durante un cierto tiempo y crear una buena comunicación con el personal involucrado en la producción del producto o servicio.
En la planeación, también se pueden identificar a tiempo posibles problemas en los procesos por lo que la toma de decisiones en esta fase es indispensable.
Dentro de la gestión técnica es muy importante planear, organizar, controlar y evaluar los procesos técnicos para lograr los fines establecidos, que es elaborar un producto o generar un servicio. De manera general, observa que es necesario:
- Realizar un diagnóstico de necesidades e investigar todo lo relacionado a la necesidad para poder satisfacerla.
- Establecer estrategias y secuencias de las acciones del proceso de producción.
- Considerar costos, insumos, medios técnicos y participantes. Se refiere a la cantidad y calidad de los insumos, maquinaria, herramienta y personal especializado.
- Elaborar un plan de trabajo para el desarrollo del proceso técnico del bien o servicio; a fin de que no haya retrasos.
- Elaborar un cursograma para visualizar la planeación de las acciones, así como los tiempos que se invertirán en ellas.
- Supervisar el transporte o traslado del producto o servicio, carga, descarga y almacenamiento.
- Evaluar todo el proceso para garantizar que la producción sea exitosa certificando la calidad y la eficiencia, que solicitan las normas y estándares de la localidad o país.
Los productos o servicios deben cumplir con la Norma Oficial Mexicana, que está constituida de una serie de reglas.
Un ejemplo de esto, es que la norma establece que toda prenda de vestir, debe llevar etiquetas con información determinada.
Realiza la siguiente actividad que consiste en contestar un crucigrama, debes de estar listos con la respuesta.
- Comienza con el diagnóstico para poder identificar las necesidades, también implica la identificación de los materiales, medios técnicos y energía que se utilizará, así como el o los procesos técnicos que se deben llevar a cabo.
- TEC2_B4_PG1_V1_SEM31_d240221_Planeación

La respuesta es Planeación.
- Comprende la planeación, organización, control y evaluación de los procesos técnicos, para producir de manera adecuada un bien o un servicio.
La respuesta es la gestión técnica.
- Es una técnica que se utiliza en el diagnóstico de necesidades y que ayuda a analizar gran parte de los conocimientos científicos y tecnológicos.
- TEC2_B4_PG1_V1_SEM31_f240221_Observación
La respuesta es la observación.
- Se refiere a la valoración del producto o servicio generado, respecto a sus propósitos e implicaciones en la naturaleza y la sociedad.
La respuesta es la evaluación.
- Permite determinar la secuencia de las acciones que son parte del proceso técnico, tiempos para realizarlas y los responsables de éstas.
- TEC2_B4_PG1_V1_SEM31_h240221_Organización
La respuesta es la organización.
- Es una fase en la que se supervisan las diferentes acciones que conforman el proceso técnico.
La respuesta es el control.
- Es una técnica que permite obtener y registrar información de manera rápida y concisa, por medio de preguntas de manera presencial o por medio de redes sociales, sitios web o formularios.
- TEC2_B4_PG1_V1_SEM31_j240221_Encuesta
La respuesta es la encuesta.
- Identifica necesidades de varias personas o de una comunidad, a través de las técnicas de observación, encuesta y entrevista
Es el diagnóstico de necesidades.
- Es un documento donde se exponen con claridad los resultados del diagnóstico, se analizan las necesidades identificadas y los problemas derivados de ellas.
Es el informe técnico.
- Se trata de una necesidad básica, que se satisface con prendas de vestir y con la publicidad ha cambiado el enfoque de la necesidad.
La necesidad es abrigarse.

Para concluir, retoma el concepto de gestión técnica, los aspectos que la integran, la planeación, organización, ejecución, control y evaluación de los procesos técnicos.
Así también la identificación de las necesidades de la comunidad.
Realiza una recapitulación de los programas pasados para que recordaras los elementos más importantes de la gestión técnica.
- TEC2_B4_PG1_V1_SEM31_n240221
El Reto de Hoy:
Escribe en tu cuaderno las preguntas y replica el crucigrama que trabajaste.
Se te invita a que comentes tus respuestas con tu maestra o maestro de Tecnología y pongas en práctica con tu familia lo que aprendiste durante la sesión.
No se olvides de anotar la palabra de esta sesión que enriquecerá tu glosario técnico que es:
Gestión Técnica.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario