Aprende en Casa III SEP: 21 de abril TAREAS y ACTIVIDADES de 3° de secundaria
A continuación dejamos los temas vistos el 21 de abril de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 3° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Miércoles 21 de abril, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Reales o imaginarios, todos son personajes
Aprendizaje esperado: Reconoce algunos de los valores de la época en que fue escrita la obra leída.
Énfasis: Explorar personajes en obras de teatro.
¿Qué vamos a aprender?
Aprenderás sobre: reales o imaginarios, todos son personajes, y con esto se refiere a explorar personajes.
Conocerás y recordarás a algunos de los personajes más importantes de la historia del teatro. Como a Hamlet, Blanche Dubois, Medea, Antígona, Segismundo.
Avanza poco a poco por el apasionante mundo de la ficción teatral.
Está sesión será muy útil, puesto que aprenderás a identificar los tipos de personajes que pueden aparecer en una obra de teatro y también conocerás las características que predominan en algunos de ellos.
Los materiales que necesitarás para esta sesión son tu cuaderno y lápiz o bolígrafo para que tomes notas, así como tu libro de texto.
Recuerda que todo lo que aprendas te servirá para fortalecer tus conocimientos, por lo que se te recomienda llevar un registro de las dudas, inquietudes o dificultades que surjan durante el desarrollo de la sesión, pues muchas de éstas las podrás resolver al consultar tu libro de texto y revisar tus apuntes.
¿Has escuchado acerca de Hamlet? Es el protagonista de la obra que lleva ese mismo nombre y que fue escrita por Shakespeare.
Hamlet es uno de los personajes más célebres del teatro universal. Él revela muchas características del Renacimiento, la época en la que vivió su autor.
El rey, que era el papá de Hamlet, fue un gran soldado medieval, pero Hamlet era poeta y filósofo. Ese detalle demuestra la ruptura entre la época de los guerreros que peleaban en batallas religiosas y los jóvenes renacentistas, que se preocupaban más por el intelecto que por los músculos.
¿Alguna vez has sentido que eres muy diferente de tus papás? ¿No te preguntas a veces “quién eres y por qué te gustan las cosas que te gustan”? Pues eso mismo le pasaba a Hamlet.
Lo cual demuestra que un personaje importante puede reflejar las características de una época y, al mismo tiempo, mantener su vigencia en cualquier lugar y tiempo.
¿Alguna vez has asistido a una obra de teatro o representado alguna?
En esta sesión te enfocarás en una parte primordial de las obras de teatro, en los personajes. Si alguna vez has visto una obra, analiza lo siguiente: ¿Qué personaje te ha llamado la atención y por qué?
¿Si tuvieras la oportunidad de representar alguno, cuál sería y por qué?
Estas y otras preguntas las resolverás en el transcurso de la sesión.
¿Qué hacemos?
Los personajes son indispensables en cualquier obra de teatro. Los actores son quienes les dan vida a estos entes ficticios de los que depende la trama de cualquier historia.
Conforme pasa el tiempo, también los personajes y sus características se van rediseñando.
Cada personaje tiene características diferentes en cuanto a su forma de hablar, caminar, vestir y comportarse.
Por ejemplo, en el Siglo de Oro, los personajes se repetían tanto que se volvieron personajes-tipo. ¿Cómo te imaginas que era un galán de esa época?
Por ejemplo, en algunas obras se habla de un hombre joven, guapo, valiente, honesto y justo. Llevaba a cabo hazañas heroicas para conquistar a su dama y superar varios conflictos.
Pero también se tiene a la dama, que es una mujer joven, hermosa y amable. Al gracioso, hombre ingenioso, que brinda una perspectiva práctica al conflicto central. El rey o príncipe, quien representa la autoridad máxima, defiende el honor, a su pueblo y la religión. Otros personajes recurrentes son el sacristán, el hambriento, el estudiante, el pícaro, quienes dan cuenta de la sociedad y costumbres de la época.
Cabe señalar que los personajes de una obra de teatro son ficticios, son imaginarios, surgen en la mente de los dramaturgos, aquellas personas que escriben obras de teatro para que después cobren vida al ser representadas ante un público.
Algunos personajes tienen características tan detalladas y realistas que, al verlos en acción, se siente que no son del todo imaginarios. ¿Alguna vez te has sentido identificado con algún personaje?
¿Recuerdas la pregunta del inicio de la sesión?
Están los protagonistas, que son los personajes centrales, aquellos de los que depende por completo la trama. Sin ellos, la historia no avanzaría. Así pues, el protagonista es el personaje principal y actúa para resolver el conflicto planteado en la obra. Sus características cambian dependiendo del género.
Pero, para que el conflicto sea interesante, es necesario que exista un personaje que se oponga a los deseos del protagonista.
Al personaje que obstaculiza las acciones del protagonista, se le llama antagonista. Existen obras en las que este rol no lo desempeña un personaje específico, sino una situación adversa. Por ejemplo, puedes ver a un hombre que está tratando de salvar a su familia de una catástrofe natural. En ese caso, las fuerzas de la naturaleza representan el papel antagónico. El antagonista no tiene que ser malvado, en ocasiones es una persona semejante al protagonista, pero con necesidades o intereses opuestos.
También están los personajes secundarios, son importantes, ya que influyen en las decisiones o acciones del protagonista o antagonista. Además, ayudan a complementar el tema o a evidenciar diferentes aspectos del carácter del protagonista.
Los individuos que representan un grupo social, una nación u otra población son personajes colectivos.
Existen más personajes, pero los que se mencionaron son los más recurrentes.
Seguramente has leído la obra Romeo y Julieta, una de las piezas teatrales más conocidas de William Shakespeare.
En esta obra Romeo Montesco y Julieta Capuleto son los protagonistas. La pregunta que se plantea para descubrirlo fue: ¿Quién enfrenta un conflicto y busca resolverlo?
Y entonces ¿quién es el antagonista?
Para esto puedes guiarte con la pregunta: ¿Quién se opone a qué los protagonistas logren su objetivo o resuelvan el conflicto?
En esta obra, según se sabe, el papel antagónico lo representan las familias de ambos personajes, porque estas se oponen a que los jóvenes se unan y expresen su amor.
Y, por último, ¿quiénes son los personajes secundarios? Para identificarlos puedes hacerte la pregunta: ¿Quiénes influyen en las decisiones o acciones del protagonista o antagonista?
Fray Lorenzo, Mercurio.
Cómo lo mencionaba anteriormente, cada personaje tiene características diferentes, pero también denotan actitudes, valores y sentimientos.
Existe una infinidad de personajes del teatro universal que han dejado una huella imborrable en la historia del teatro.
Mujeres y hombres con actitudes y valores diversos, entre ellos: Medea, de Eurípides; Edipo, de la obra Edipo Rey de Sófocles; Hamlet de la obra Hamlet de William Shakespeare; Segismundo de La vida es sueño de Pedro Calderón de la Barca; Julieta de Romeo y Julieta de William Shakespeare; Laurencia de Fuenteovejuna de Lope de Vega; Bernarda Alba en la obra La casa de Bernarda Alba de Federico García Lorca, entre otros personajes.
Analizarás algunos de los personajes mencionados. Todos ellos son apasionantes.
Inicia con el ilustre Segismundo.
Segismundo, protagonista de La vida es sueño, ha vivido encerrado en una cárcel casi toda su vida, puesto que su padre, el rey, temía ser destronado por su hijo. El rey se arrepiente de haber mantenido cautivo a Segismundo y lo libera. Cuando Segismundo se ve rodeado de lujos, se convierte en un patán violento y lo vuelven a encerrar. Entonces es cuando él se pregunta si todo fue un sueño.
Es un personaje interesante, se pregunta si su reinado fue sólo un sueño y si la vida no es más que una ilusión. Cuando unos soldados vuelven a liberarlo, se convierte en un rey justo y amable.
Aunque existe una reflexión filosófica muy importante en la obra, no es aburrida ni lenta. Segismundo llora, grita, se conmueve, se enamora y demuestra muchas emociones con las que te puedes identificar.
¿Te han castigado alguna vez injustamente? ¿Y te has enojado por eso? ¿Le has gritado a alguien y después te has arrepentido? ¿Has pensado alguna vez que un sueño es real o que la realidad es un sueño? Todos se parecen un poco a Segismundo.
Observa la siguiente entrevista realizada a Alma Claudia Velázquez Torices, Licenciada en literatura dramática y teatro y compartirá experiencias actriz y también como personaje.
Entrevistador: Maestra, ¿cómo logra representar las características emocionales y psicológicos de un personaje?
Alma Claudia: Muy buena pregunta, lo más importante al momento de encarnar a un personaje es que, a través de sus acciones, se revelen su mundo interior. deseos, su forma de pensar y sus miedos. Algunos de sus deseos, creencias y temores se expresan por medio de los diálogos, pero, como ocurre en la vida real, los personajes no siempre dicen todo lo que piensan. Por eso, los actores debemos revelar muchos detalles a través de movimientos, posturas y reacciones gestuales.
Entrevistador: ¿Qué hace para analizar con mayor profundidad, las características del personaje que deberá interpretar?
Alma Claudia: Una vez que he leído el texto, intento descubrir las situaciones que reflejan el conflicto principal de la obra. Me es de gran utilidad buscar información sobre el autor y acerca de la época en la que se escribió el texto, pues estos detalles me permiten imaginar el contexto en el que se encuentra el personaje.
Después inicia la etapa de exploración en la que comienzo a jugar con las principales herramientas: mi cuerpo y mi voz. Es un proceso creativo de búsqueda. Después de descubrir cómo habla y cómo se mueve mi personaje, empiezo a relacionarme con el espacio y con los demás actores.
De ese modo van apareciendo las reacciones y actitudes que requiere cada parte de la obra. Se trata de entender desde cómo despierta hasta cómo se va a dormir. Aunque el público sólo verá un momentito en la vida del personaje, el actor debe conocerlo completamente para que cada acción resulte creíble y sincera.
Entrevistador: Alguna vez le ha pasado que se mete tanto en el papel del personaje que ya no puede desprenderse de él. Puede hablar de eso por favor.
Alma Claudia: Claro. La creación de un personaje implica vivir otra vida, crearla integralmente. Tuve la oportunidad de concebir un personaje desde cero y explorar situaciones realistas que no se relacionan con mi vida directamente y que no conocía por experiencia propia.
Aunque la mujer a la que interpreté aparecía sólo 3 minutos y la temporada iba a durar únicamente dos semanas, yo tenía que concentrarme profundamente cada vez que intervenía en la obra. La experiencia fue tan intensa y trascendente, que el personaje me persiguió después de la temporada. A veces hablaba y me comportaba como ella. Por eso es importante que los actores entrenen sus emociones, para poder abandonar la ficción una vez que finaliza la obra.
Entrevistador: Cómo pudiste apreciar ésa es la voz y el porte de la maestra que respondió como actriz, ahora cómo sería si le diera vida a un personaje, por ejemplo, a Bernarda Alba.
Alma Claudia: Será un placer. ¿Qué le gustaría saber?
Entrevistador: Por ejemplo: ¿Quién es Bernarda Alba?
Alma Claudia: Soy una viuda sin mancha, una mujer digna. Ésa soy yo.
Entrevistador: Pero dígame, Bernarda ¿Cuál es su mayor miedo?
Alma Claudia: ¿Miedo? ¿Ha dicho usted “miedo”? Una viuda honrada no puede tener miedo de nada; la gente habla porque tiene lengua, pero ninguna me toca porque no hay quien se me asemeje.
Entrevistador: Por lo que sé, usted es madre de familia, ¿qué es lo que significa ser madre y qué siente por sus hijas?
Alma Claudia: Ser madre es el sino de toda mujer decente, nace una mujer, se casa, se guarda y ya. Una cumple.
Cuando una está al frente, la responsabilidad de guardar la honra es lo único que cuenta; siento por ellas lo mismo que siento por mi madre.
Entrevistador: ¿Cuál es la actitud de Bernarda hacia los novios de sus hijas?
Alma Claudia: Mis hijas no tienen “novio” ¿cómo se atreve? No hay en la comarca ninguno digno ni me iría a otro pueblo a venderlas. Aquí no hay hombres, sólo gañanes.
Entrevistador: Muchas personas tienen miedo al qué dirán, usted ¿Qué es lo que piensa acerca de esa frase “el qué dirán” y qué importancia tiene?
Alma Claudia: Una mujer decente no anda en habladurías, ni mira de ellas ni las hace.
Entrevistador: ¿Qué siente y piensa sobre las mujeres?
Alma Claudia: “Cada una sabe lo que piensa por dentro. Yo no me meto en los corazones, pero me gusta la buena fachada y la armonía familiar”. La honrada a su casa, la que no, que pague lo que debe. A fin de cuentas, las cosas son como una se las propone. Una no debe preguntar y casada, menos. Habla si él te habla y míralo cuando te mire, así no tendrás disgustos. No procures descubrir lo que oculta un hombre, no preguntes y que no te vea llorar jamás.
Entrevistador: Estoy impresionado, maestra, verdaderamente es usted una profesional, la vi tan metida en el personaje que creí que estaba hablando con la verdadera Bernarda.
Alma Claudia: Claro que hablas con la verdadera Bernarda, si no soy una ilusión, pero me tendrás que disculpar porque me tengo que retirar, tengo unos asuntos que tratar.
Entrevistador: Le agradezco, señora Bernarda.
Entrevistador: ¿De qué manera identifica las características de los personajes?
Alma Claudia: Por ejemplo, si el personaje aparece en un texto dramático, en una obra ya hecha, debes leerlo con atención y captar el subtexto de cada diálogo. Fíjate en la réplica de la madre:
Novio: Déjalo. Comeré uvas. Dame la navaja.
Madre: ¿Para qué?
Novio: (Riendo) Para cortarlas.
Madre: (Entre dientes y buscándola) La navaja, la navaja... Malditas sean todas y el bribón que las inventó.
Novio: Vamos a otro asunto.
Madre: Y las escopetas, y las pistolas, y el cuchillo más pequeño, y hasta las azadas y los bieldos de la era.
Novio: Bueno.
Sólo con eso puedo saber que la madre tiene un asunto no resuelto, en conflicto propiamente con las navajas y todo tipo de arma; los invito a leer Bodas de sangre de Federico García Lorca para que se enteren del asunto completo. No es una madre cualquiera y tiene sus razones para iniciar así la obra.
Ahora, si deseas crear un personaje que no aparece en ningún texto dramático, puedes determinar su historia personal, sus posibles antecedentes biográficos, el lugar en el que vive y el trabajo que desempeña. Esas características particulares ayudan a la actriz o al actor a establecer una forma de hablar, de caminar y de comportarse en distintas situaciones.
Entrevistador: Esta pregunta posiblemente sea complicada, pero ¿qué diferencia existe entre los personajes basados en personas reales y aquellos que han sido creados por los autores?
Alma Claudia: El personaje es una creación colectiva, el autor y el director tienen una concepción acerca de él, pero quien le da cuerpo, voz, expresión y vida es quien lo interpreta.
Los integrantes de un equipo creativo comparten sus perspectivas y colaboran para entender lo que el autor quiso decir, el rumbo que el director quiere darle al montaje y las ideas que los actores proponen para que los personajes cobren vida.
Por ello, no hay una diferencia real entre los personajes que se basan en seres humanos reales y aquellos que son estrictamente ficticios. De cualquier modo, cada montaje exige que los artistas interpreten a su manera la historia que se contará.
Entrevistador: ¿Qué sugiere a los alumnos para identificar las características de los personajes?
Alma Claudia: Que los observen con mucha atención. Si, en vez de ver una obra, la leen, fíjense bien en los diálogos, pero también en el contexto que lo rodea.
En Los sueños de Paco del mexicano Carlos Corona, Paco es un niño de casi 10 años que vive en sus sueños, en su imaginación consciente. Sus padres se separaron y no son capaces de ver lo que se revela frente al público. Ellos sólo saben que se orina en la cama o que no come. El público lo ve todo, comprende al personaje y se convierte en su cómplice, pues comprende que sus padres no se dan cuenta de lo que en realidad él siente.
Entrevistador: ¿Cómo es que se prepara al interpretar a un personaje?, ¿qué es lo que hace para conferirle características creíbles y conmovedoras?
Alma Claudia: La preparación es diaria, cuidar la salud mental y física es parte del entrenamiento. Leer toda clase de libros, escuchar música variada, observar el mundo ayuda a ampliar las perspectivas de un actor. Aunque no me encuentre en un proceso creativo, no dejo de prepararme mental y emocionalmente para el siguiente reto. Creo que el secreto está en conocer al personaje, fijarte en los detalles e ir jugando con diferentes posibilidades que te permitan acercarte a él e interpretarlo dignamente.
Entrevistador: ¿Hoy nos visitará otro personaje?
Alma Claudia: Será un placer, mi nombre es Laurencia, soy habitante de la región de Fuenteovejuna, señor, hija del alcalde Esteban. Y soy una mujer sensata y firme.
Entrevistador: Mucho gusto, señorita Laurencia, todos tenemos perspectivas diferentes sobre el amor, usted qué opina acerca de eso y qué es lo que ama.
Alma Claudia: ¡Pardíez! Amo mi propio honor. Y lo que pienso sobre el amor es que es un deseo de hermosura que se procura para gozarla, es un bien que contenta.
Entrevistador: Para Laurencia ¿Qué es la cortesía?
Alma Claudia: Un vocabulario que, en lenguas descorteces, se torna mucho peor: así se le llama a la verdad, imprudencia, cobardía a la paciencia, y culpa a lo que es desdicha, necia a la mujer honesta; mal hecha a la hermosa y casta, y a la honrada… pero basta, que esto basta por respuesta.
Entrevistador: Hace rato platicábamos con Bernarda y ella tiene una idea sobre los hombres, usted ¿Qué piensa de ellos?
Alma Claudia: En momentos de suma diligencia, sois cobardes pastores, ovejas, piedras, liebres cobardes, bárbaros, gallinas, medio hombres…
Entrevistador: Bueno, ya entendimos, muchas gracias, prosigamos con otra pregunta, coméntenos por qué se atreve Frondoso a ayudarla, enfrentando al comendador, a la autoridad.
Alma Claudia: Porque dice que es su intención es desear ser mi esposo, que por mis desdenes no bebe, duerme ni come y que no comprende el rigor en angélico rostro. ¡Vive el cielo, que es lenguado!
Entrevistador: ¿Qué actitud toma ante la vida?
Alma Claudia: Soy decidida, me resuelvo a que no haya más ultrajes por la tiranía, que la obediencia sola es al rey que cuida de su pueblo, no al que agravia y ofende, ni al que ufana y pretende disponer de personas como de licores. Si con los hombres no se cuenta para el cuidado y atención, convoco a la ocasión, que solas mujeres cobren la honra destos tiranos y torne aquel siglo de amazonas eterno espanto del orbe.
Entrevistador: Fue algo increíble, maestra, le agradezco mucho el brindarnos tan valiosa información para las y los estudiantes.
Alma Claudia: Es un placer.
Los personajes son piezas fundamentales en las obras de teatro, puesto que alrededor de ellos girará toda la historia. Cada personaje es diferente, dependiendo de si se trata de una obra cómica o trágica.
Aunque dos actores distintos encarnen a un mismo personaje, cada actor le confiere un estilo propio a su interpretación. No existen dos interpretaciones iguales. A través de la expresión vocal y las acciones físicas, los personajes conmueven y transmiten emociones muy variadas y poderosas.
Muchas veces se dice que se comparte la misma idea que tiene dicho personaje, te sientes identificado y piensas que de alguna forma los personajes no son del todo imaginarios.
El Reto de Hoy:
Observa una obra de teatro y céntrate en los personajes, identifica sus características y define cuál es su papel. Escribe qué similitudes comparten y posteriormente comparte tu análisis con amigos y familiares.
Si quedaron dudas, consulta tu libro de texto y busca el Aprendizaje esperado de esta sesión: “Reconoce algunos de los valores de la época en que fue escrita la obra leída”.
El Propósito de nuestra sesión fue: “Explorar personajes”.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Sistema de ecuaciones. Método de igualación
Aprendizaje esperado: Resuelve y plantea problemas que involucran ecuaciones lineales, sistemas de ecuaciones y ecuaciones de segundo grado.
Énfasis: Resolver problemas que implican un sistema de ecuaciones lineales utilizando el método de igualación.
¿Qué vamos a aprender?
Ten a la mano tu cuaderno, lápiz y goma.
El método de igualación es una de las varias formas de encontrar los valores de las incógnitas en un sistema de dos ecuaciones lineales con dos incógnitas.
En este método de solución es importante considerar, que, en un sistema de ecuaciones lineales, las incógnitas tienen el mismo valor para ambas ecuaciones, pero quedan representadas de manera distinta.
¿Qué hacemos?
Comienza el análisis de una situación cotidiana.
Imagina que vas al parque a pasear un rato. La primera ocasión vas con 2 amigos y compras 3 botellas de agua y un coctel de frutas en el kiosco del parque. La cuenta asciende a $125.

Después, vas en pareja y compras 2 botellas de agua y 2 cocteles de frutas. En esta ocasión, se pagan $110.

Se considera que el precio es la suma de cada producto. Y aunque no se sabe cuánto cuesta cada producto por separado, se tienen los suficientes elementos para calcularlo. En ambas ocasiones, los productos conservaron su precio y presentación.
En el primer caso, 3 botellas de agua más 1 coctel de frutas cuestan $125.
En la traducción algebraica, la expresión “3b” representa el costo de las 3 botellas de agua más “c”, el valor del coctel de frutas, igual a 125.
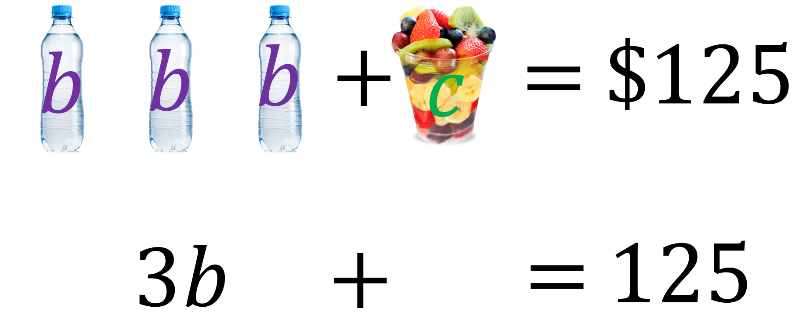
En el segundo caso, 2 botellas de agua más 2 palomitas cuestan $110.
En la traducción algebraica se tiene “2b” para el valor de las dos botellas de agua más “2c”, el costo de dos cocteles de frutas, igual a 110.
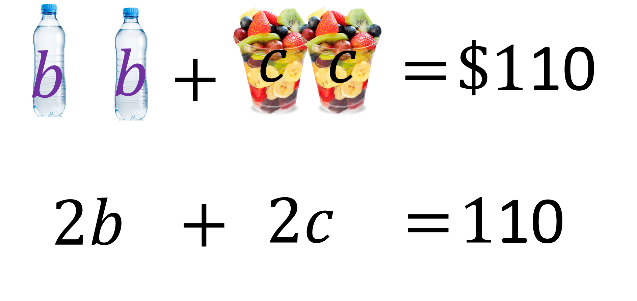
En este caso se aprovecha que, se tiene un único coctel de frutas para calcular su valor.
El costo de este coctel es igual al total de la compra menos el valor de las 3 botellas de agua. Así, el valor de un coctel de frutas se representa como “c” igual a 125 pesos menos “3b”.

Para el segundo caso, el precio de dos cocteles es el costo total menos el valor de dos botellas de agua.
Si se representa de forma algebraica: “2c” igual a 110 menos “2b”.

Y si ése es el costo de dos cocteles de frutas, uno de estos sólo costará la mitad. Es decir, 55 menos el valor de una botella de agua.

Ahora se tienen las condiciones necesarias para usar el método de igualación.
Ya se tienen dos expresiones para una misma incógnita: el valor de un coctel de frutas.
Se tiene que “c” es igual a 55 menos “b”, y también es igual a 125 menos “3b”.
Entonces, se hace una igualdad con 55 pesos menos el valor de una botella de agua, que es equivalente a 125 pesos menos el valor de 3 botellas de agua.

De esta manera ya se tiene una igualdad en la que sólo está involucrada una incógnita a la vez. Pero, ¿cuánto vale una botella de agua?
Analizando la igualdad:
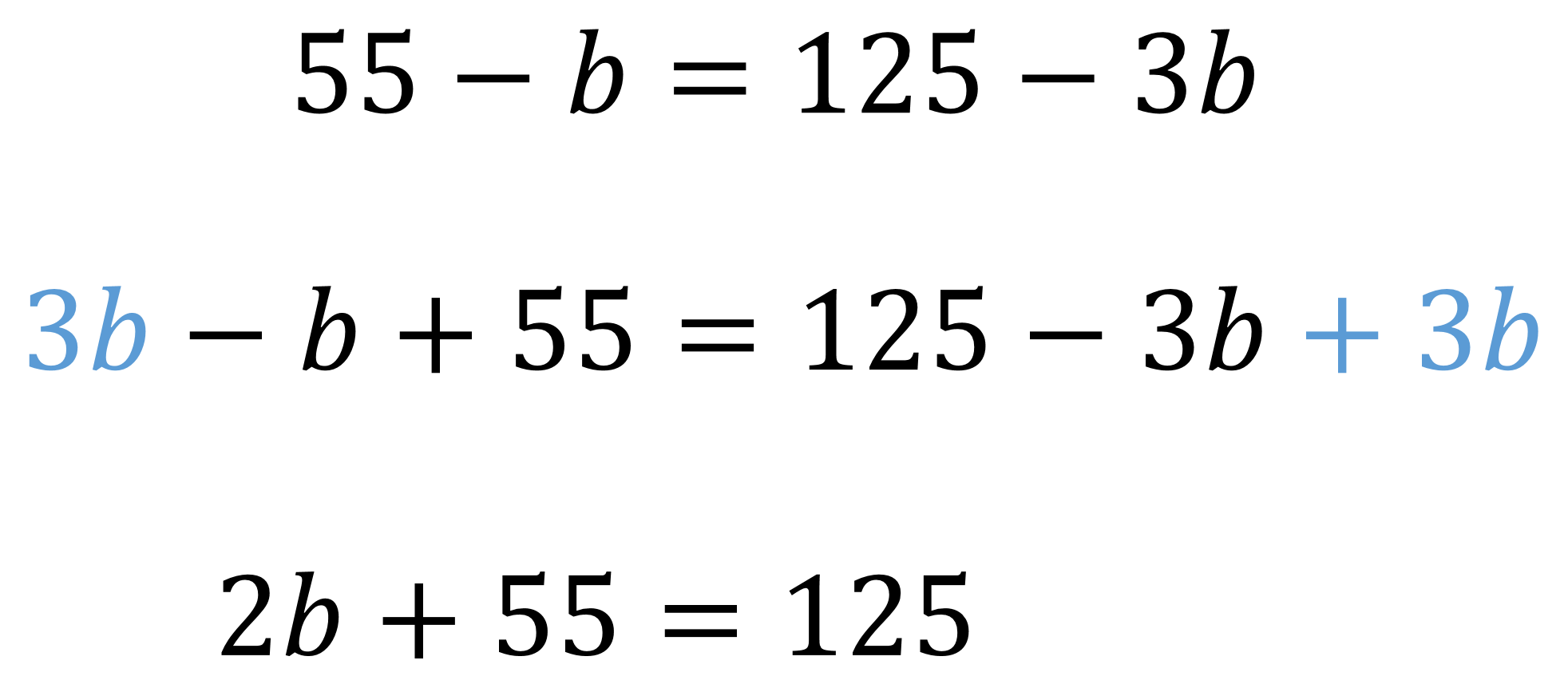
Se resta 55 en ambos lados de la igualdad y se obtiene:

Y si 2 botellas de agua valen 70 pesos, una sola botella de agua vale 35 pesos.
Se tiene el valor de una botella de agua y a partir de este, se calcula el valor de los cocteles. Para ello, se escoge una de las dos expresiones ya despejadas.
“c” igual a 55 menos “b”
o la segunda equivalencia
“c” igual a 125 menos “3b”
En cualquiera de ellas se obtiene el mismo resultado.
Al escoger la primera igualdad y sustituir el valor de la botella de agua, 55 pesos menos 35 pesos, el coctel de frutas vale 20 pesos.

Si se escoge la segunda igualdad, al sustituir el valor de la botella de agua, 125 pesos menos tres botellas de agua de 35 pesos, es igual a 125 menos 105; el coctel de frutas vale 20 pesos, que coincide con el primer cálculo.
De esta manera, se sabe el valor de cada producto de forma independiente: Las botellas de agua cuestan 35 pesos y el coctel de frutas 20 pesos.

Para la segunda situación que trabajarás, el contexto es una función de teatro a la que asistieron 270 personas.
Se recaudaron en total 24,800 pesos
Si los boletos de estudiante cuestan 80 pesos y los boletos para público en general cuestan 100 pesos.
¿Cuántos boletos de estudiante y cuántos de público general se vendieron?
El sistema de ecuaciones asociado a este problema es el siguiente:
Según los datos, el total de estudiantes “x”, más el público en general “y”, es en total 270 personas.
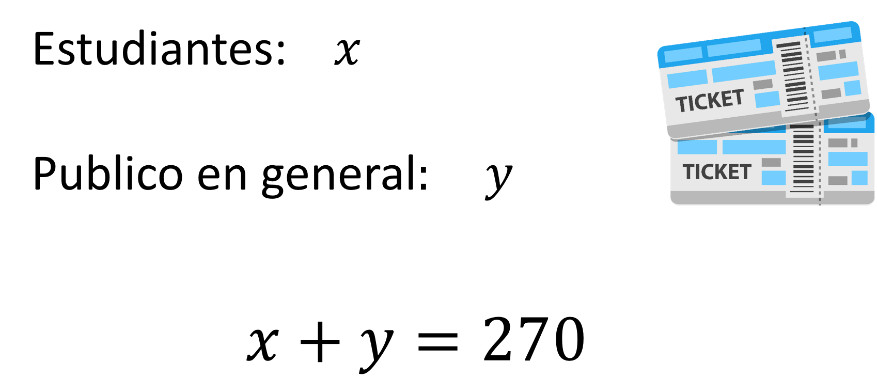
Los boletos de estudiante valen 80 pesos y asistieron “x” número de personas.
Con relación a los boletos de 100 pesos, asistieron “y” número de personas y el ingreso total es de 24,800 pesos.

Ya se tiene el sistema de ecuaciones que describe la situación. Para usar el método de igualación, se despeja la misma incógnita en ambas igualdades.
Se escoge la incógnita “y”, que representa el número de personas que pagaron el boleto general de la obra.
En la primera expresión: “x” más “y” igual a 270, se despeja la incógnita “y”.
Se resta “x” en ambos lados de la igualdad y se obtiene: “y” igual a 270 menos “x”.
En la segunda ecuación:
“80x” más “100y”, igual a 24,800.
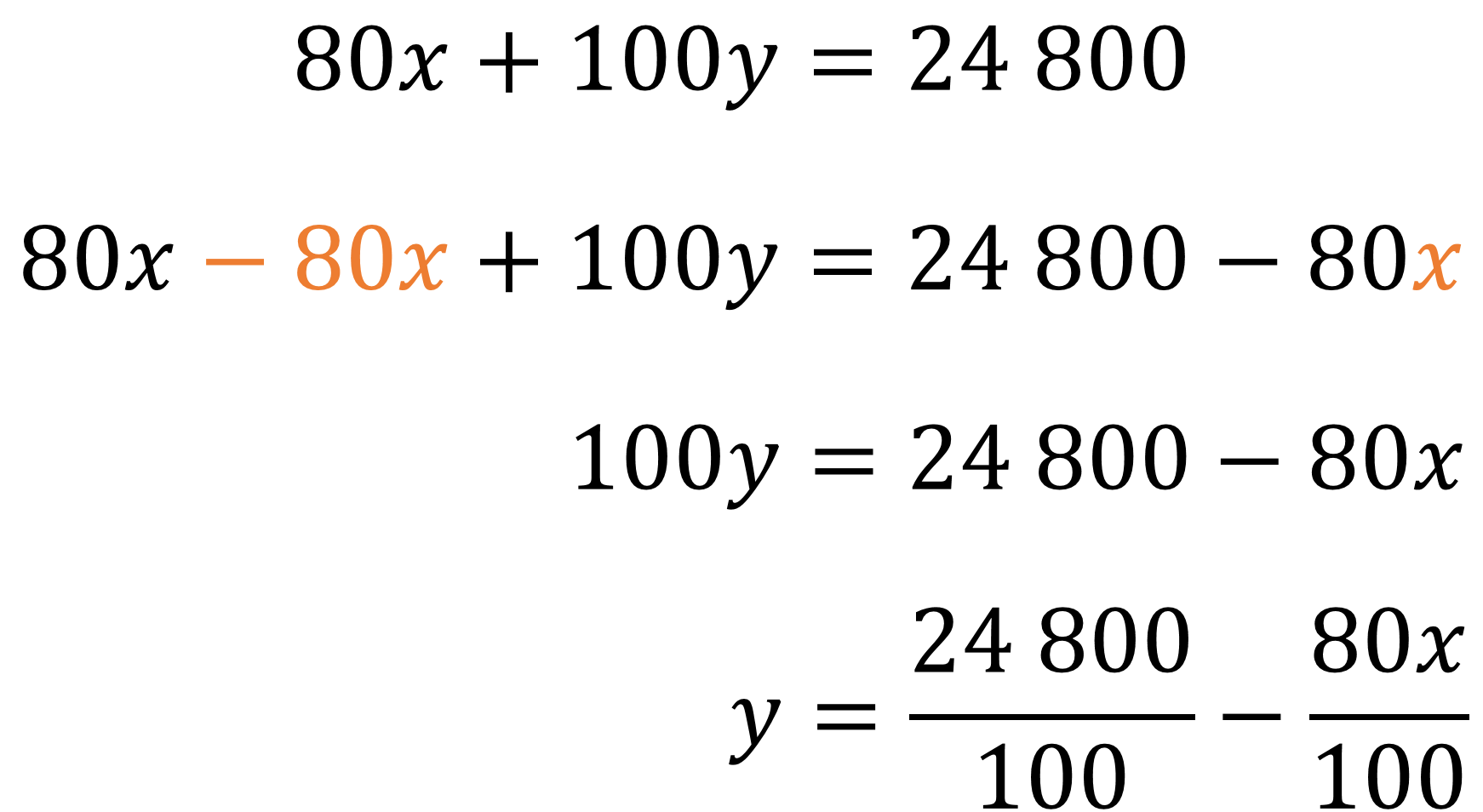
Se resta “80x” en ambos lados de la igualdad para obtener que “100y” es igual a 24,800 menos 80x.
Y se divide toda la expresión entre 100, teniendo como resultado: “y” igual a 24,800 entre 100 menos “80x” entre 100.
Para agilizar el cálculo, se reducen las fracciones a su mínima expresión. Así 24,800 centésimos es igual a 248, y 80 centésimos de “x” es igual a 8 décimos de “x”, que también es equivalente a 4 quintos de “x”.
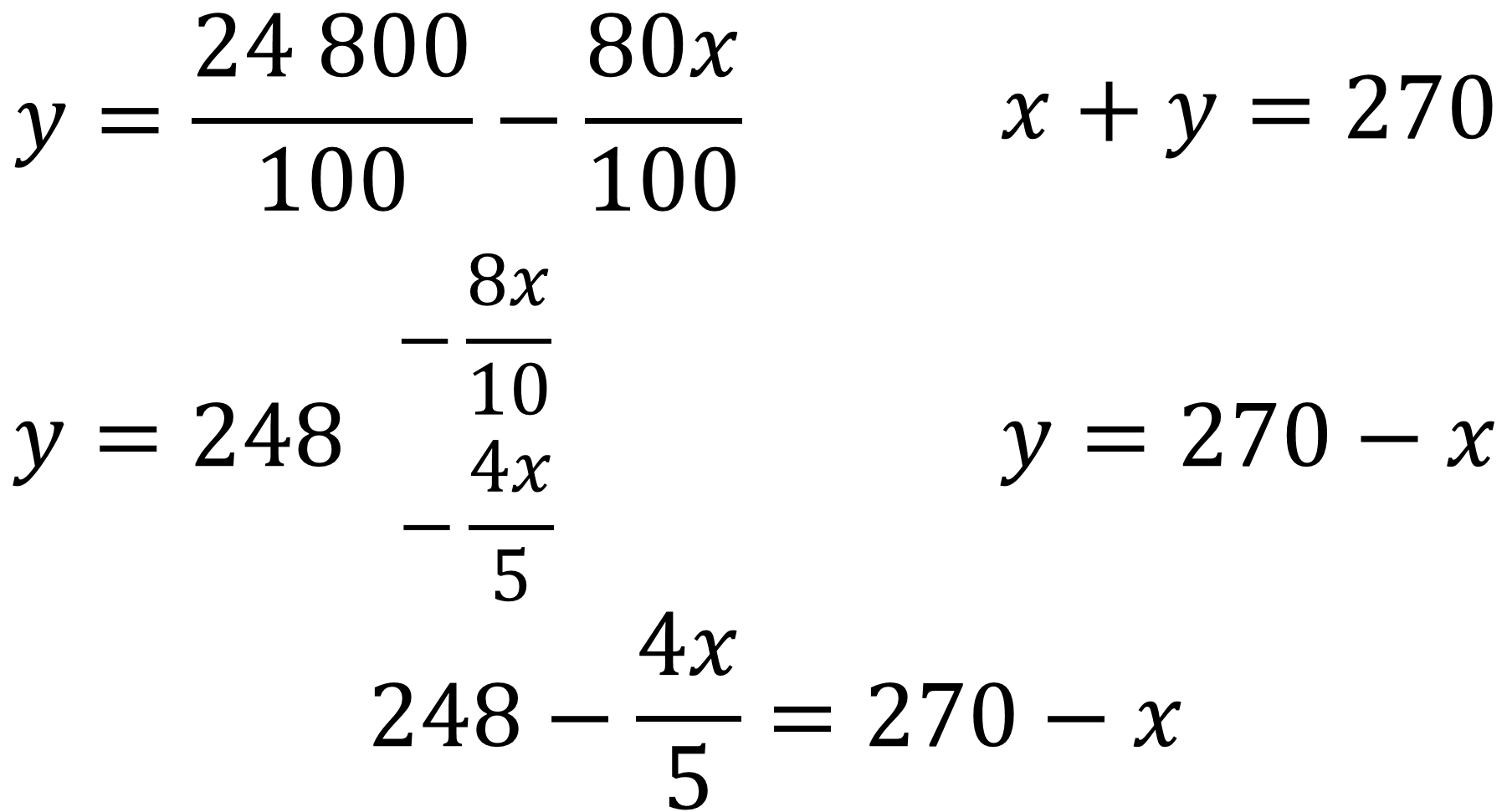
De este modo, ya se tiene despejada la misma incógnita en ambas ecuaciones.
Entonces, se tiene que 248 menos 4 quintos de “x” es equivalente a 270 menos “x”.
Se suma “x” en ambos lados de la igualdad y se obtiene que “x” menos 4 quintos de “x” más 248 es igual 270 menos “x” mas “x”.
Al reducir términos semejantes, para los términos “x” menos 4 quintos de “x”, se puede sustituir un entero por su equivalente 5 quintos.
Y queda, 5 quintos de “x” menos 4 quintos es igual a un quinto de “x”, y en el segundo miembro de la igualdad, “x” menos “x” es igual a cero.
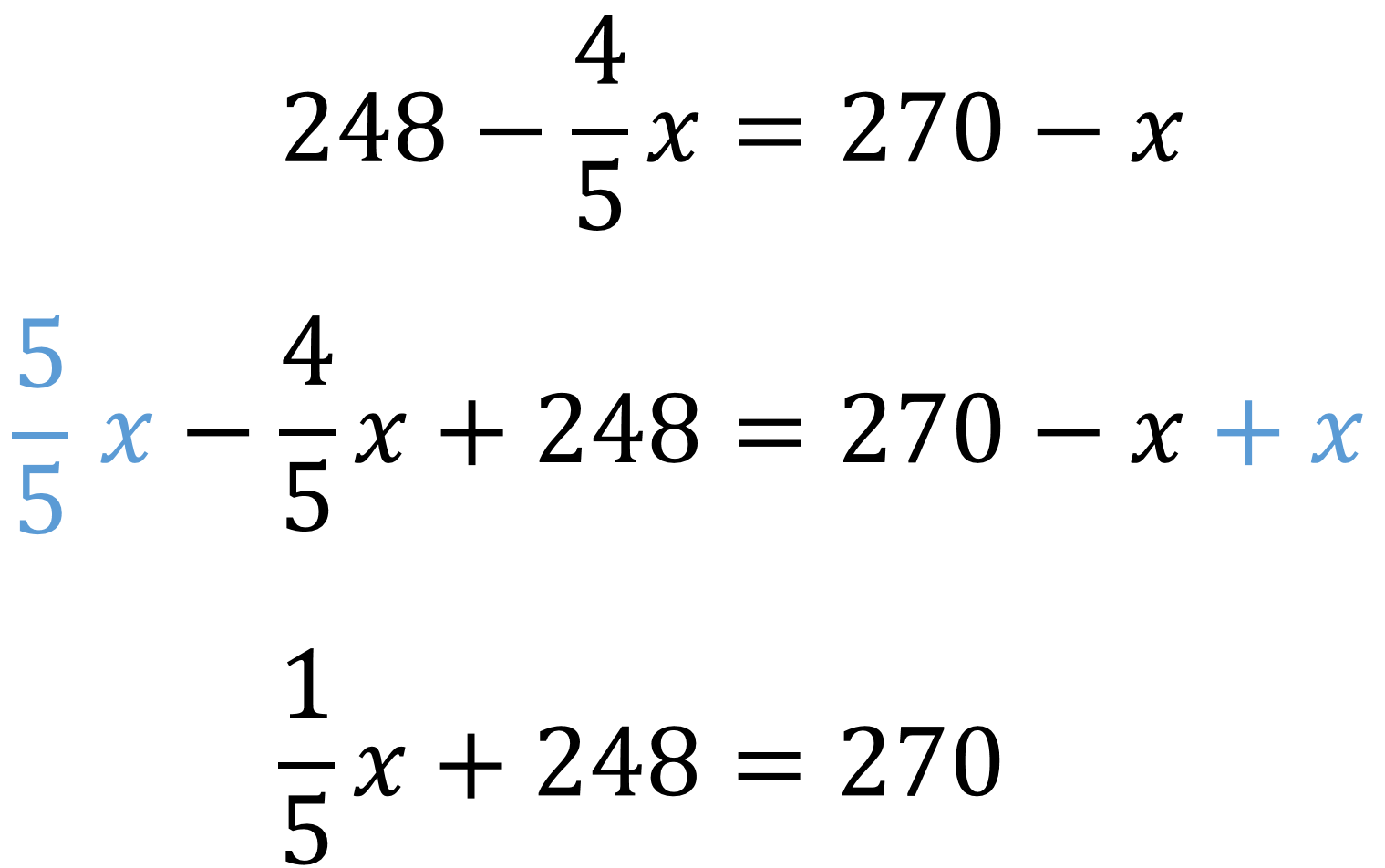
Después, se restan 248 en ambos lados de la igualdad; en el lado izquierdo 248 menos 248 es igual a cero, y del lado derecho 270 menos 248 es igual a 22.
Y para finalizar, si un quinto de “x” es igual a 22, entonces el valor de “x” es cinco veces 22, que es igual a 110.
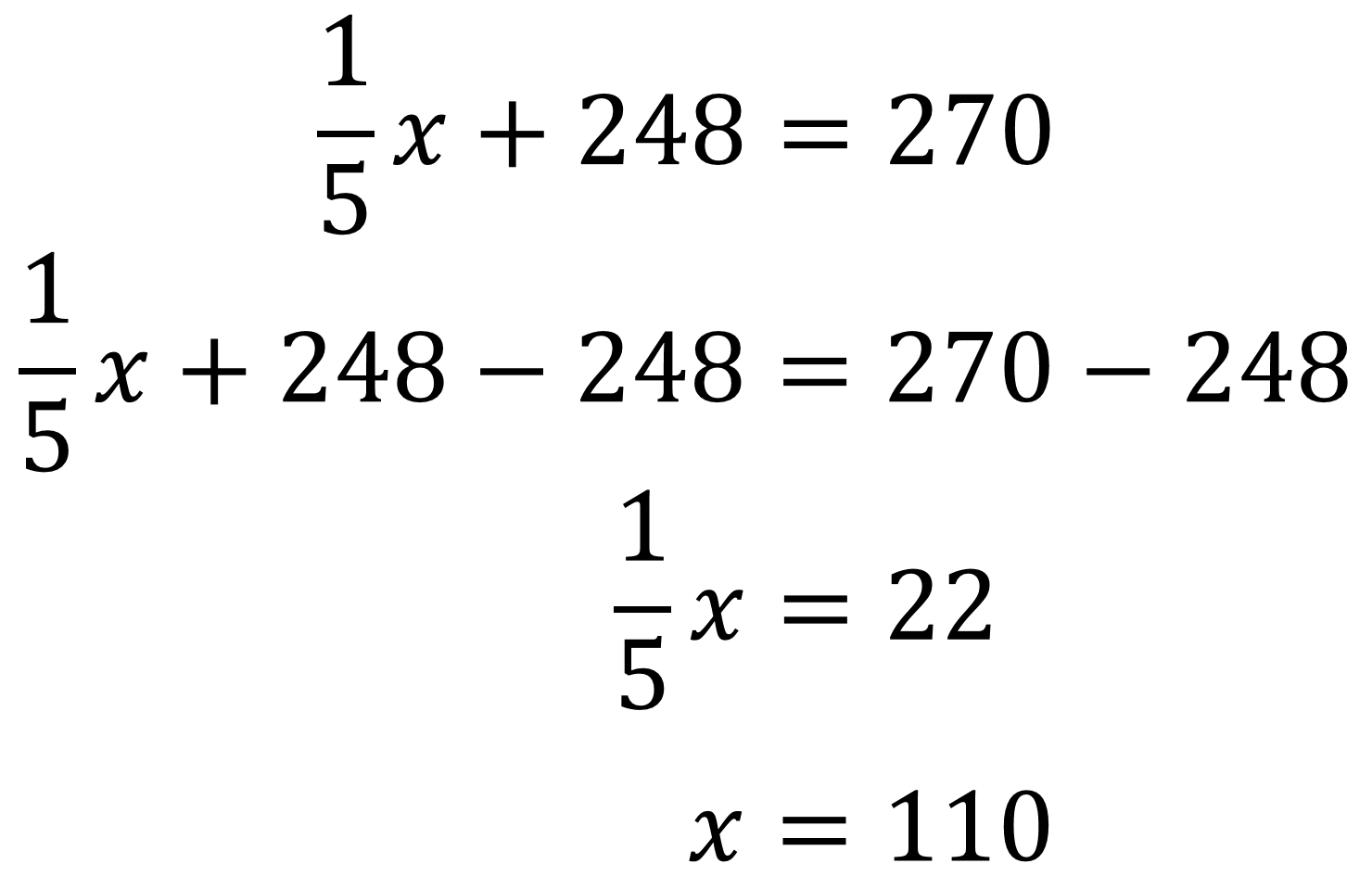
Con el valor de “x” igual a 110 se sabe que fueron 110 boletos para estudiantes los que se vendieron en la taquilla del teatro.
Entonces, para completar las 270 entradas de ese día, se compraron 160 boletos de entrada general.
Para comprobar los valores obtenidos, se sustituyen en la expresión del problema.
La venta de 110 boletos de estudiante, más 160 boletos de entrada general, coincide con las 270 entradas vendidas ese día.
Después, se comprueba que el dinero recaudado por la venta de 110 boletos de 80 pesos, más 160 boletos de 100 pesos, deben de sumar 24,800 pesos.

110 boletos por 80 pesos cada uno, es igual a 8,800 pesos.
160 boletos por 100 pesos de cada uno, es igual a 16,000 pesos.
La suma de 8,800 pesos de los boletos de estudiante más 16,000 pesos, de los boletos de entrada general, es igual a los 24,800 pesos recaudados ese día.

Se lograron encontrar las incógnitas en dos diferentes situaciones donde los datos permitieron usar un sistema de dos ecuaciones lineales con dos incógnitas. Además, en cada situación planteada, el sistema de ecuaciones tenía una única solución.
A continuación, se analizarán dos sistemas en donde no hay una solución o, por el contrario, existen múltiples soluciones que, al resolverlos con el método de igualación, se presentan resultados característicos.
En el sistema: “2x” menos “3y” igual a cero, y “4x” menos “6y” igual a 9.
Se despeja la incógnita “x” de ambas ecuaciones, y se obtiene que en la primera:
“x” es igual a “3y” entre 2
En la segunda ecuación:
“x” es igual a “6y” más 9, todo dividido entre 4.
Por lo tanto, “3y” sobre 2 debe ser igual a la cuarta parte de la suma de “6y” más 9.
Para simplificar la expresión, se multiplican ambos lados de la igualdad por 4, que es el mínimo común múltiplo de los denominadores. Tras realizar las operaciones, se obtiene 2 que multiplica a “3y”, igual a “6y” más 9.

El resultado de las multiplicaciones es “6y”, igual “6y” más 9.
Desde este punto, ya se puede observar que la expresión no es una igualdad, porque 6 multiplicado por cualquier número, no puede ser igual a 6 multiplicado por el mismo número, y todavía sumarle 9 unidades más.
Pero se sigue para conocer la resolución de la situación planteada.
Si se restan “6y” en ambos lados de la igualdad, se obtiene “6y” menos “6y” es igual a 9.
Operando, “6y” menos “6y” es igual a cero, y cero no es igual a 9.
Cuando sucede este tipo de situación, se dice que el sistema no es compatible. Es decir, que no tiene solución.
El otro caso se analiza con el siguiente sistema de ecuaciones:
“2x” más “3y” es igual a 6, con
“4x” más “6y”, es igual a 12.
Se despeja el valor de la incógnita “x” en ambas ecuaciones.
Para la primera ecuación, “x” es igual a un medio de la suma de “3y” negativo más 6.
En la segunda ecuación, “x” es igual a la cuarta parte de la suma de “6y” negativo más 12.
Entonces, se tiene que la mitad de la suma “3y” negativo más 6 es igual a la cuarta parte de la suma de “6y” negativo más 12.
Para simplificar la igualdad, se multiplica por 4, que es el mínimo común múltiplo de los denominadores.
Como resultado de las multiplicaciones, se obtiene: “6y” negativo más 12, es igual a “6y” negativo más 12.
En este punto se puede reconocer que la igualdad tiene los mismos términos, lo que es una identidad. De este modo, se reducen términos semejantes para obtener que cero es igual a cero.
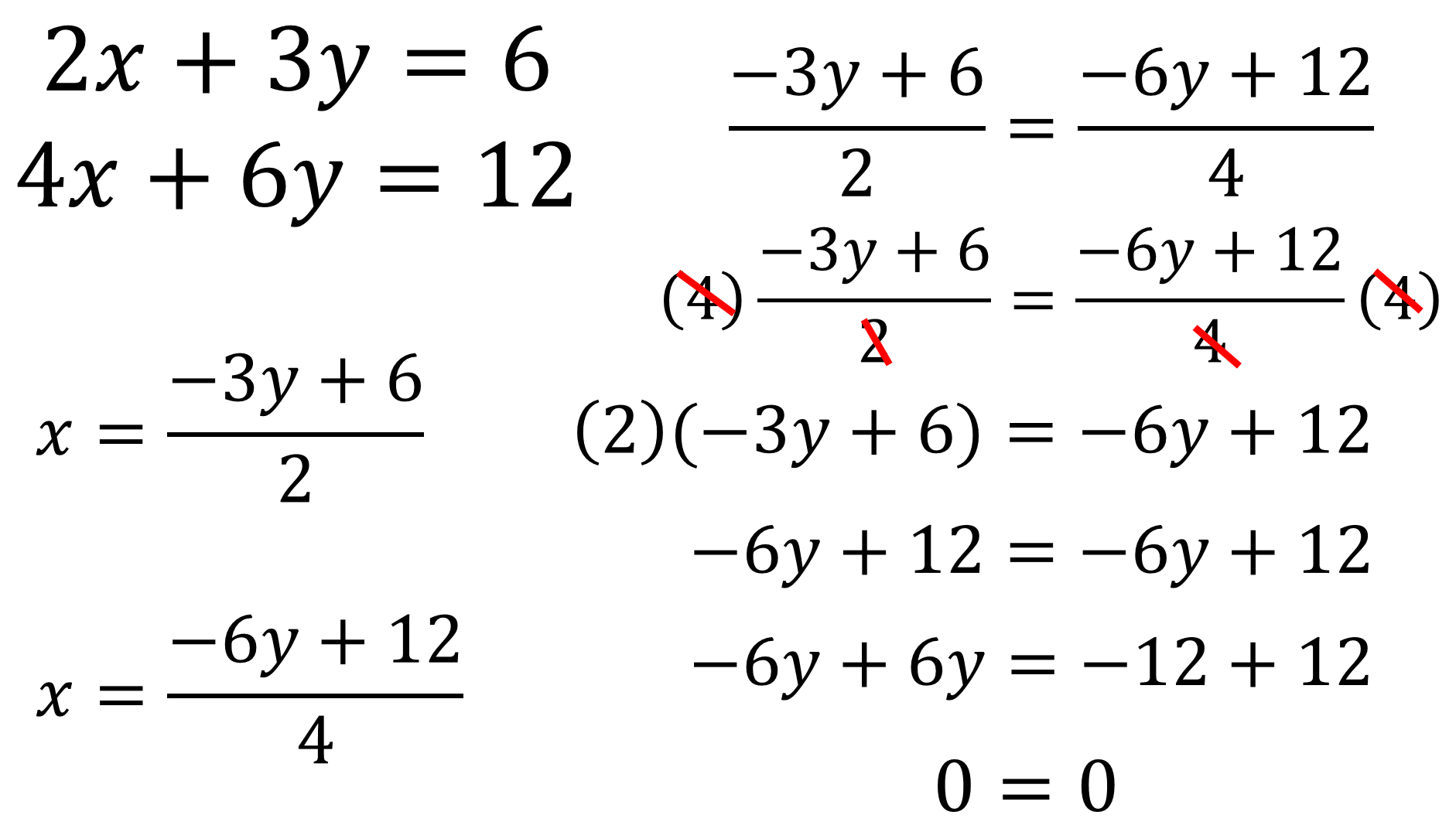
Para este caso, la igualdad es cierta porque cero si es igual a cero, pero no se obtuvo el resultado de la incógnita que se está buscando.
A este tipo de sistemas de ecuaciones se les conoce como “Sistema compatible indeterminado”, es decir, que tiene infinitas soluciones.
Se verifica lo anterior con un par de datos enteros para las incógnitas.
Se asigna el valor de cero a “x” y valor de 2 a “y”; en ambas ecuaciones el resultado es correcto.
2 por cero más 3 por 2 sí es igual a 6
4 por cero más 6 por 2 sí es igual a 12
Y para demostrarlo, se le asigna otro par de valores:
Para “x” igual a 6 y “y” igual a 2 negativo, se tiene 2 por 6 más 3 por 2 negativo, que es igual a 12 menos 6, igual a 6.
En la segunda ecuación:
4 por 6 más 6 por 2 negativo, es igual a 24, menos 12 es igual a 12
Y así como se han empleado estos resultados para “x” y “y”, existen una infinidad de resultados, pero no cualquier combinación, que cumplen con las dos ecuaciones al mismo tiempo.
Después de analizar los casos anteriores, en donde el sistema no tiene solución o existen infinitas soluciones, se estudia una situación que implica el planteamiento de un sistema de ecuaciones en donde también se expresa una ecuación cuadrática.
¿Cuáles son las dimensiones de un terreno rectangular cuyo perímetro es 50 metros y de área cubre 156 metros cuadrados?
Al ser un terreno rectangular se tienen únicamente 2 medidas, el largo y el ancho del terreno que no son iguales, de lo contrario sería un cuadrado.
El perímetro es igual a la suma de todos sus lados, y se tiene en el esquema:
“x” más “y” más “x” más “y” igual a 50 metros.

Al agrupar términos semejantes, se obtiene “2x” más “2y”, igual a 50 metros. Esta expresión representa el perímetro.
El área del rectángulo se obtiene multiplicando el valor del largo “x” por el ancho “y”, que es igual a 156 metros cuadrados.
De esta forma, ya se tienen expresadas dos ecuaciones con dos incógnitas.
Se despeja “x” de la primera ecuación de la que se obtiene “x” igual a 25 menos “y”.
Mientras que al despejar “x” de la segunda ecuación, se obtiene “x” es igual a 156 entre “y”.
Es así como se obtiene la igualdad:
25 menos “y” es igual a 156 entre “y”.
Se comienza a operar la igualdad, multiplicando ambos miembros de la igualdad por “y” para eliminar el denominador, se debe considerar a y diferente de cero.

“y” que multiplica a 25 menos “y” es igual a 156 entre “y”, que multiplica a “y”. Realizando la multiplicación se obtiene que: “y” cuadrada negativa más “25y” es igual a 156.
Al igualar la expresión a cero, se multiplica toda la expresión por 1 negativo, para obtener una ecuación de segundo grado.
“y” cuadrada menos “25y” más 156 es igual a cero.

25 negativo se descompone en dos sumandos, de manera que permita factorizar la expresión.
Se elige “12y” negativo y “13y” negativo.
Se calcula el factor común de “y” cuadrada y “12y” negativo, que es “y”, y lo mismo se realiza para “13y” negativo y 156 que es 13.
De este modo se tiene:
“y” que multiplica a “y” menos 12, menos 13, que multiplica a “y” menos 12 es igual a cero.
Se factoriza nuevamente la expresión, ahora utilizando como factor común a “y menos doce) y se obtiene: “y” menos 12 que multiplica a “y” menos 13 es igual a cero.
Se considera ahora que, si el producto de varios factores es igual a cero, entonces al menos uno de los factores es igual a cero.
Esto implica que “y” menos 12 es igual a cero, o “y” menos 13 es igual a cero.
Por lo tanto, las respuestas a estas dos igualdades son: “y” igual a 12, o “y” igual a 13.
Para calcular el valor del lado “x”, se sustituyen los dos valores de “y” en uno de los dos despejes de “x”.
Por ejemplo, en “x” igual a 25 menos “y”.
Para “y uno”, “x” es igual a 25 menos 12, que es igual a 13, y para “y dos”, “x” es igual a 25 menos 13, que es igual a 12.
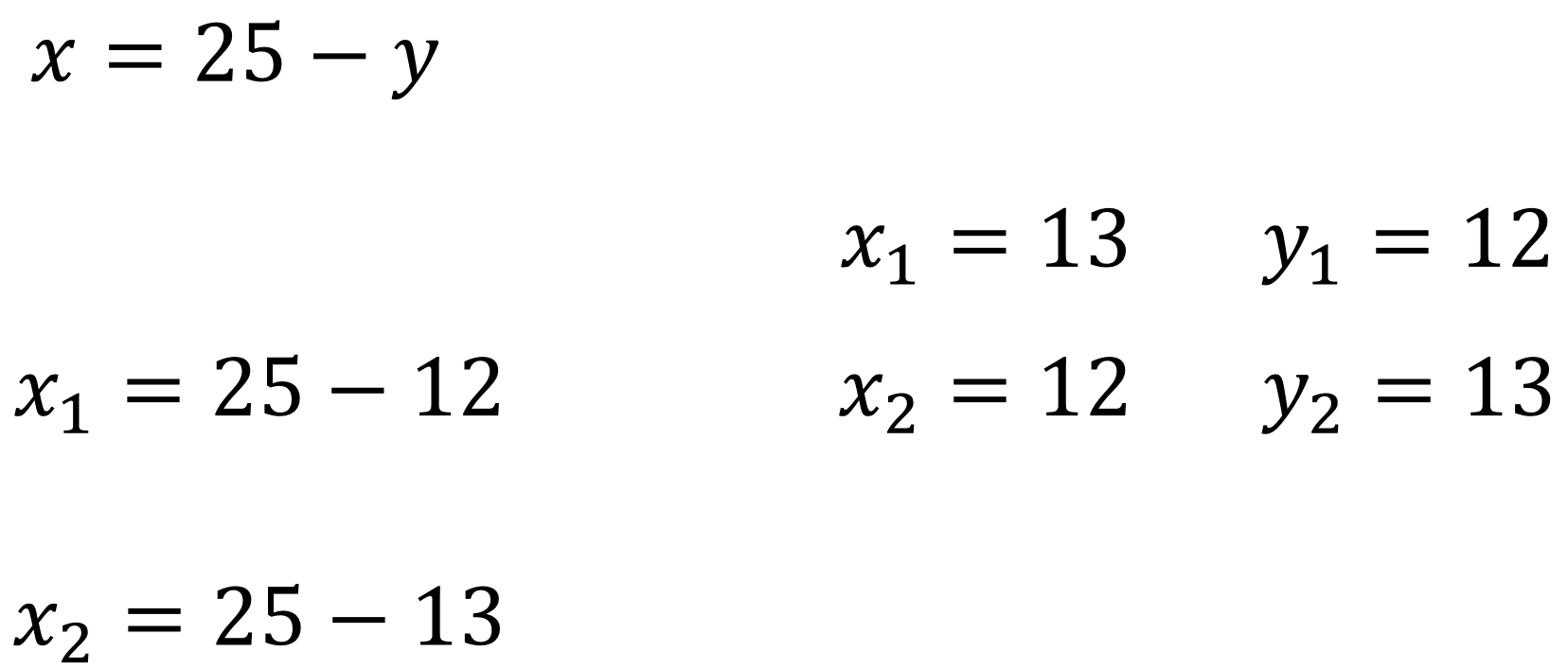
Analizando los resultados, el terreno mide 13 metros de largo por 12 de ancho.
También se puede medir 12 metros de largo por 13 de ancho, que se logra al cambiar la orientación del terreno en el esquema.
En el problema anterior, además de ocupar el método de igualación, también se necesitó de la factorización de una ecuación de segundo grado para poder obtener el resultado.
Como se ha observado durante la sesión, el método de igualación consiste en despejar la misma incógnita de ambas ecuaciones, lo que permite igualar ambas expresiones, (de ahí el nombre del método). Con lo anterior, se genera una ecuación con una incógnita y se evita el manejo de las dos al mismo tiempo.
Para concluir analiza la siguiente situación hasta el punto de la traducción algebraica, y el despeje de la misma incógnita en ambas ecuaciones, para que en casa obtengan la solución utilizando el método de igualación.
Escribe en tu cuaderno los datos necesarios para realizar el ejercicio.
Con dos camiones, cuyas capacidades de carga son respectivamente de 3 y 4 toneladas, se hicieron en total 23 viajes para transportar 80 toneladas de arena. ¿Cuántos viajes realizó cada camión?
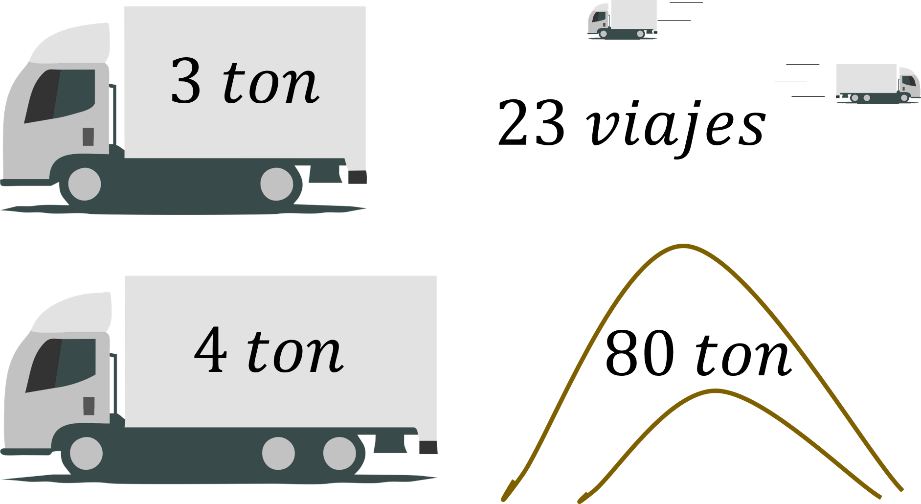
Se asigna la variable “x” a la cantidad de viajes que realizó el primer camión; “y” a la cantidad de viajes que realizó el segundo camión. Y se expresan algebraicamente los datos:
La suma de los viajes del primer camión “x”, y el segundo camión “y”, es igual a 23, el total de viajes realizados.
Ahora, se considera que el camión 1 transporta 3 toneladas por cada viaje; la representación algebraica es 3 (toneladas), que multiplica al número de viajes “x”.
Para el camión número 2, cada viaje lleva una carga de 4 toneladas; la representación algebraica es 4 que multiplica al número de viajes “y”.
Finalmente, la suma de la cantidad de arena que transportó el camión 1 (“3x”) más la cantidad de arena que transportó el camión 2 (“4y”) es igual a las 80 toneladas en total.
Se despeja una de las 2 incógnitas en ambas expresiones; para esta se escoge la “y”.
En la expresión “x” más “y” igual a 23 se resta el valor de “x” de ambos lados de la igualdad, y se obtiene que “y” es igual a 23 menos el valor de “x”.
En la segunda expresión, “3x” más “4y” igual a 80, se resta “3x” en ambos lados de la igualdad. Después, se divide entre 4 para obtener que “y” es igual a la cuarta parte de 80 menos “3x”.
Y se aplica el método de igualación para resolver la pregunta: ¿Cuántos viajes realizó cada camión?
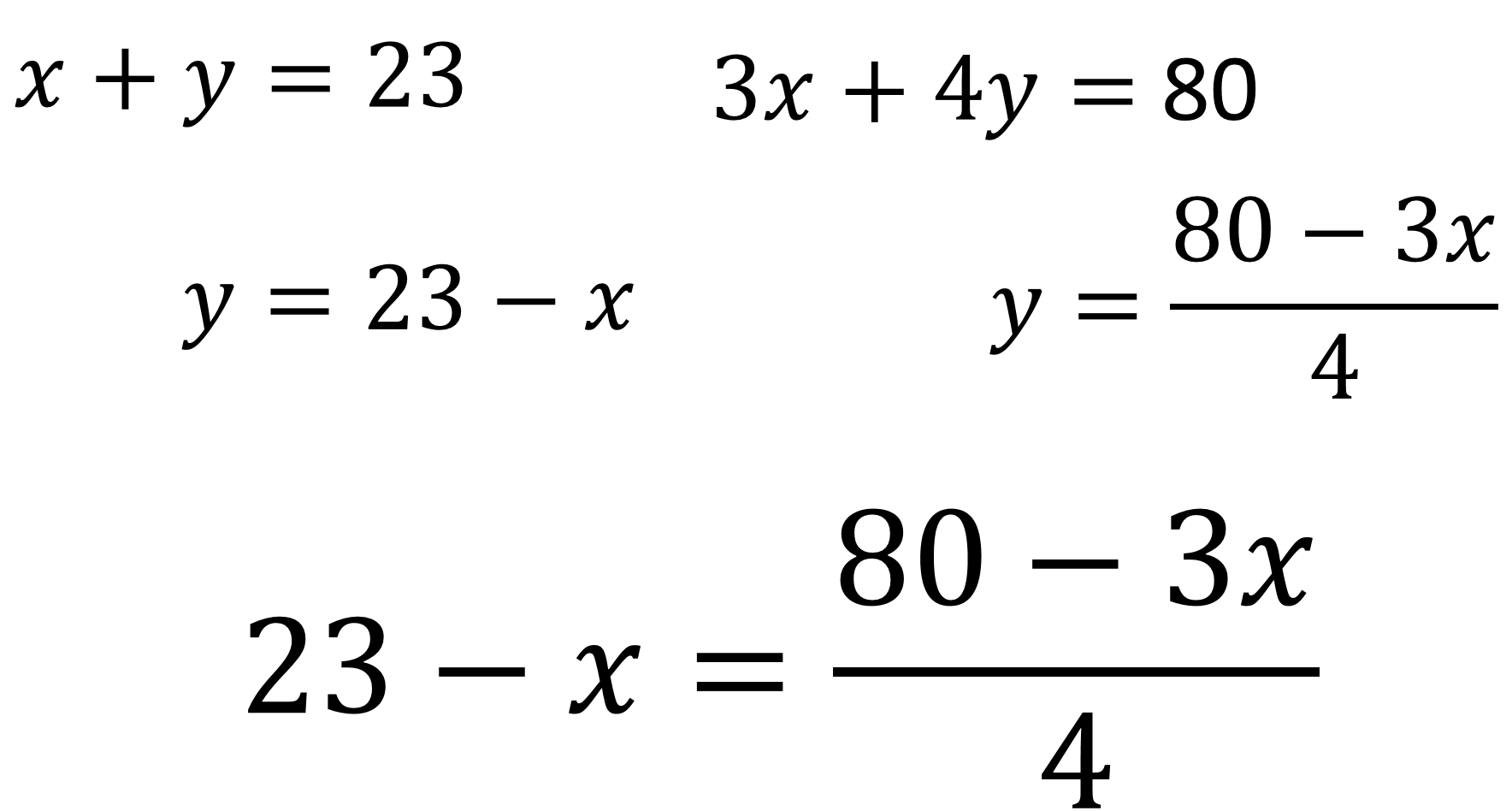
Para ejercicios como los anteriores, existe varios métodos de solución; el método de igualación es el más viable cuando el coeficiente de alguna incógnita es 1, lo que favorece mucho el proceso.
El Reto de Hoy:
Busca ejercicios o problemas ya resueltos en tu libro del año anterior para repetirlos con el método de igualación, y así verificar cómo se obtiene el mismo resultado con este método.
Y para resolver dudas o ejercitar lo aprendido, te puedes apoyar en tu libro de texto.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Panorama del periodo II
Aprendizaje esperado: Ordena secuencialmente hechos y procesos desde la Revolución mexicana hasta las décadas más recientes. Identifica las instituciones revolucionarias que se crearon en este periodo.
Énfasis: Ubicar temporal y espacialmente los acontecimientos nacionales e internacionales que caracterizaron a México entre 1920 y 1980.
¿Qué vamos a aprender?
Después de diez años de conflicto armado, la sociedad mexicana sufrió diversas transformaciones, como la migración provocada por la violencia, la inestabilidad económica y social ante la constante sucesión de líderes políticos. En este contexto urgía crear un proyecto de gobierno sólido.
El propósito que guiará esta sesión es: ubicar temporal y espacialmente los acontecimientos nacionales e internacionales que caracterizaron a México entre 1920 y 1980.
Recuerda que para realizar anotaciones sólo necesitas lápiz o bolígrafo, cuaderno y tu libro de texto para profundizar y ampliar tus conocimientos acerca del tema.
¿Qué hacemos?
Durante la segunda mitad del siglo XX se vivieron en México distintos movimientos sociales, como el magisterial en 1958, el de ferrocarrileros entre 1958 y 1959 y el de los médicos entre 1964 y 1965, a estos se sumaron movimientos estudiantiles como el de 1968 y el de 1971.
Lee algunos testimonios del llamado “Movimiento del 68”, que se encuentran compilados en el libro La noche de Tlatelolco, de la escritora Elena Poniatowska.
El primero es de Raúl Álvarez Garín. Profesor de la Escuela Nacional de Ciencias Biológicas del Instituto Politécnico Nacional, preso en Lecumberri:
No es que yo me "metiera" al Movimiento Estudiantil; ya estaba adentro desde hace mucho […]. Yo soy del Poli; allá tengo mi casa; allá están mis cuates, los vecinos, el trabajo. Allá nacieron mis hijos. Mi mujer también es del Poli.
El Movimiento lo traemos dentro desde hace muchos años. ¡Aquí no hay improvisación! […] No se trata de eso. Se trata de defender todo aquello en que creemos, por lo que siempre hemos luchado y antes de nosotros nuestros padres y los padres de nuestros padres...
Provenimos de familias de obreros, de gente que siempre ha trabajado, y trabajado duro.
El siguiente es de Carolina Pérez Cicero, estudiante de la Facultad de Filosofía y Letras de la UNAM:
Pienso que la fuerza y la importancia del Movimiento Estudiantil se la dio la represión. Más que ningún discurso político, el hecho mismo de la represión politizó a la gente y logró que la gran mayoría participara activamente en las asambleas.
Se decretó que en cada escuela habría paros y allí mismo surgió la idea de las brigadas y de los comités de lucha en cada Facultad. Los brigadistas eran muchachos y muchachas de la base estudiantil que realizaban todo tipo de actividades, desde recolectar dinero hasta hacer mítines relámpago en la calle, en los barrios más alejados, en las colonias proletarias. Las grandes manifestaciones fueron una de las armas políticas más eficaces del Movimiento.
Ahora el de Mercedes Olivera de Vázquez, antropóloga:
¡Les dije a todos que la plaza era una trampa, se los dije! ¡No hay salida! ¡Más claro lo querían ver! Les dije que no había ni por dónde escapar, que nos quedaríamos todos encajonados allí, cercados como en un corral. ¡Se los dije tantas veces, pero no!
Finalmente, el de Margarita García Flores, jefa de prensa de la UNAM:
Cuatro bengalas verdes lanzadas a las 18:10 fueron la señal para que elementos del Batallón Olimpia, vestidos de civil, iniciaran el fuego esta tarde contra estudiantes y obreros que se manifestaban en Ciudad Tlatelolco.
El periodo que estudiarás es un lapso clave en la historia, pues moldeó el presente no sólo de nuestro país, sino de todo el mundo.
Entre 1920 y 1980 la humanidad, y desde luego México, afrontó una de las peores crisis económicas: la Gran Depresión de 1929, dentro de un periodo que los historiadores han llamado el periodo de entreguerras; vio también la avanzada del nazismo y fascismo, que llevaría a múltiples naciones a enfrentarse en la Segunda Guerra Mundial, entre 1939 y 1945; después la humanidad experimentó la angustia del periodo de la posguerra que en pocos años se presentó como la Guerra Fría; esto es, un mundo bipolar en el que dos ideologías, la capitalista representada por Estados Unidos de América y el comunismo representado por la Unión Soviética, se enfrentaron, y en el que el avance de la tecnología y la fuerza militar pudieron haber acabado con la vida en el planeta.
En materia nacional, este periodo se caracteriza por la construcción de un nuevo Estado y la consolidación del Partido Revolucionario Institucional.
Nuestro país inició la década de 1920 de forma tensa. El presidente Venustiano Carranza fue asesinado el 21 de mayo de 1920 en Tlaxcalantongo, Puebla. Adolfo de la Huerta asumió el poder como presidente interino. Álvaro Obregón se presentó como candidato y después de su triunfo se creó una alianza denominada el Grupo Sonora, encabezada por Obregón en la presidencia, De la Huerta como secretario de Hacienda, y Plutarco Elías Calles, como secretario de Gobernación.
En 1923, Francisco Villa fue asesinado y al año siguiente Calles triunfaría en la elección presidencial. Los mandatos del Grupo Sonora, es decir, de Obregón de 1920 a 1924 y Calles de 1924 a 1928 se caracterizaron por un fuerte interés en la educación, la persecución política contra sus adversarios y conflictos con las organizaciones católicas.
Un acontecimiento fundamental en esta década fue la creación de la Secretaría de Educación Pública, en 1921. Además de las “Misiones culturales” que tenían como objetivo alfabetizar a la población; importante también fue el proyecto educativo muralista liderado por figuras como Diego Rivera, José Clemente Orozco y David Alfaro Siqueiros.
Conoce más sobre el muralismo en México a través del siguiente video del inicio al 01:34.
- Contexto y expresión
https://www.youtube.com/watch?v=sZ25qMHxa6Y
Otro proceso histórico relevante fue la “Guerra Cristera” que se prolongó de 1926 a 1929, debido a medidas anticlericales adoptadas por el gobierno y a la persecución contra las prácticas religiosas católicas. Obregón se reeligió y fue asesinado en 1928 antes de tomar posesión.
Prácticamente todos los líderes revolucionarios habían sido asesinados en la última década, por lo que Calles se convirtió en el “Jefe Máximo de la Revolución”; intentó mantener el poder creando el Partido Nacional Revolucionario (PNR), antecedente del actual PRI, por medio del cual se postulaba a los candidatos. A los años que comprenden de 1929 a 1935 se les conoce como “Maximato”, periodo en que Calles impuso a los presidentes: Emilio Portes Gil, Pascual Ortiz Rubio y Abelardo L. Rodríguez.
En la década de 1930, Genaro Estrada formularía su célebre “Doctrina Estrada”, es decir, el principio de no intervención. Destacan en esta década las figuras de Lázaro Cárdenas del Río, presidente de México de 1934 a 1940 y de Vicente Lombardo Toledano, líder sindical. Cárdenas no sólo sustituyó a los funcionarios callistas, sino que expulsó a Calles del país hacia 1936. Llegando así el fin de la hegemonía de los sonorenses sobre el Estado mexicano.
Con Cárdenas, el reparto agrario tuvo su momento más destacado. Asimismo, el 18 de marzo de 1938, expropiaron las empresas petroleras extranjeras con el fin de mejorar las condiciones de los trabajadores mexicanos. Por otra parte, se fundó el Instituto Politécnico Nacional (IPN) en 1936 y la Escuela Nacional de Antropología e Historia en 1938.
En el plano internacional, durante la Guerra civil española que tuvo lugar de 1936 a 1939, el gobierno de Cárdenas concedió asilo, primero a niñas y niños y después a exiliados españoles. Esta sería la semilla de un significativo florecimiento en el plano cultural; por ejemplo, se crearon instituciones como El Colegio de México.
También, durante este periodo el PNR se convirtió en el Partido de la Revolución Mexicana (PRM), antecedente directo del PRI. Con Cárdenas iniciaría el presidencialismo, es decir, un modelo en el que el poder está depositado en un presidente, que tiene la facultad de realizar nombramientos, convocar consultas ciudadanas y vetar leyes.
Posteriormente, Manuel Ávila Camacho fue electo presidente para el periodo 1940 a 1946, para entonces ya había comenzado una de las páginas más oscuras en la historia de la humanidad con la Segunda Guerra Mundial. La entrada de México ocurrió en 1942, cuando submarinos alemanes hundieron en el Golfo de México los buques petroleros Potrero del Llano y Faja de Oro. México declaró la guerra a las potencias del Eje: Alemania, Italia y Japón.
En 1945, México participó en el frente del Pacífico, bajo el liderazgo estadounidense y acompañado de australianos y filipinos, con el Escuadrón 201 de aviación. Éste ejecutó acciones de combate para la liberación de Filipinas, ocupada por Japón. También destacaron diplomáticos como Luis Rodríguez y Gilberto Bosques, quienes en Europa salvaron a miles de perseguidos políticos extranjeros.
Debido a la guerra, Estados Unidos de América convirtió sus industrias metalúrgicas y de ensamblaje en fábricas de armamento, esto favoreció que México acelerara su industrialización para producir y exportar bienes al vecino del norte. Además, bajo el “Programa Bracero” que se desarrolló de 1942 a 1964, más de 4 millones de mexicanos fueron contratados para trabajar en Estados Unidos de América.
Al finalizar la guerra, en 1945, México fue uno de los fundadores de la Organización de las Naciones Unidas (ONU) y envió al diplomático Isidro Fabela como juez en la Corte Internacional de Justicia de la Haya.
La década de los cincuenta fue fundamental para la economía, México siguió beneficiándose del comercio con Estados Unidos de América, este periodo, que incluso abarcaría hasta la década de 1970, es conocido como “el milagro mexicano” o del “crecimiento económico sostenido”. De acuerdo con la historiadora Soledad Loaeza, entre 1949 y 1958, el Producto Interno Bruto (PIB) creció a una tasa anual promedio de 6.6 %, uno de los más altos del mundo en ese entonces. Al mismo tiempo la población aumentaba a una elevada tasa de 3.1 % al año.
Algunas legislaturas estatales, como las de San Luis Potosí y Chiapas, reconocieron el derecho al voto femenino en 1925 y 1927, respectivamente; sin embargo, dichas medidas fueron eliminadas un par de años después de haber sido promulgadas.
En 1947 se reconoció el derecho al voto de la mujer, pero sólo para el ámbito municipal. Y no sería sino hasta el 17 de octubre de 1953 cuando se reformaría el artículo 34 constitucional. México fue de los últimos países del mundo en otorgar el voto a las mujeres. Esto permitió que, después de décadas de lucha, las mexicanas pudieran ser al fin ciudadanas plenas, con el derecho de votar y ser votadas. Destacaron sufragistas como Hermila Galindo y Elvia Carrillo Puerto.
También durante este periodo, el mexicano Luis Ernesto Miramontes sintetizó la sustancia activa de la primera píldora anticonceptiva en 1951 y se comercializó en 1964. Heberto Castillo inventó la tridilosa, un sistema constructivo que ahorra el 66 % del concreto y aligera las estructuras.
Antonio Camargo descubrió el cráter de Chicxulub en 1970, que aclaró la extinción de los dinosaurios. En el ámbito educativo, en 1960, por iniciativa de Jaime Torres Bodet se creó la Comisión Nacional de Libros de Texto Gratuitos (Conaliteg) que, desde entonces, brinda material educativo sin costo para todos los estudiantes del Sistema Educativo Nacional.
En el plano internacional, Estados Unidos de América y la Unión Soviética entraron en un conflicto que generó divisiones económicas y políticas entre los países que se agruparon entre el bloque occidental, capitalista y el bloque del este, comunista, este proceso es conocido como Guerra Fría.
México se alió a la ideología capitalista y con el pretexto de combatir al comunismo, Miguel Alemán Valdés, presidente de 1946 a 1952, creó la Dirección Federal de Seguridad, una agencia que perseguía el delito de disolución social, que se cometía al realizar propaganda a favor de algún gobierno extranjero y pudiera producir “rebelión, tumulto, sedición o escándalo”.
La tensión de la Guerra Fría siguió creciendo hasta 1968. En muchos países hubo protestas, en Estados Unidos de América por la lucha por los derechos civiles de los afrodescendientes y contra la Guerra de Vietnam. En distintos países de Europa por la invasión soviética de la República Checa.
Ese año, con Gustavo Díaz Ordaz como presidente, México era sede de las Olimpiadas, cuatro meses antes de ser inauguradas, estudiantes de educación media y superior en muchas partes de México se fueron a huelga y protestaron en las calles ante la represión sufrida. Organizaciones obreras y campesinas también se unieron. El ejército tomó varios planteles y el Zócalo. El 2 de octubre, diez días antes de iniciar las Olimpiadas, un mitin realizado en la plaza de las Tres Culturas en Tlatelolco acabó con la represión ejercida en contra de los estudiantes.
Durante el gobierno de Luis Echeverría Álvarez, presidente de 1970 a 1976, una manifestación de estudiantes del IPN fue atacada el 10 de junio de 1971 por un grupo de choque del gobierno infiltrado en la protesta, llamado “los halcones”; a este hecho se le conoce como “el halconazo”.
Ante la cerrazón de las vías políticas institucionales y como la participación pacífica no daba resultados, surgieron movimientos guerrilleros como el de los maestros Genaro Vázquez y Lucio Cabañas en Guerrero y la Liga Comunista 23 de septiembre.
Conoce más sobre estos levantamientos a través de la siguiente entrevista, del minuto 01:00 al 05:25 y del 06:15 l 07:35, a quien fuera uno de sus principales estudiosos: Carlos Montemayor.
- Protestas e inconformidades: movimientos sociales en México
https://www.youtube.com/watch?v=hqmaBxFeUZM
Para 1979 inició la participación femenina en puestos políticos federales con Griselda Álvarez, como primera gobernadora por el estado de Colima; y Rosa Luz Alegría Escamilla, como la primera secretaria federal de Turismo en 1980.
México tuvo gran atención del mundo por haber sido anfitrión de las Olimpiadas del 1968 y la Copa Mundial de fútbol varonil de 1970. El país se endeudó para ampliar a Pemex y programas sociales, cada vez se debía más y las ganancias del gobierno no eran suficientes. De acuerdo con Loaeza, “entre 1960 y 1968, la deuda externa aumentó de 813 a 2 500 millones de dólares”.
Los años de 1970 también los puedes caracterizar por un gran crecimiento de la población. Según cifras del historiador Ariel Rodríguez Kuri, “México pasó de poco más de 25 millones en 1950 a unos 81 millones de habitantes en 1990”. También es una década en la que los medios de comunicación masiva, radio y televisión fueron un eje importante en la vida nacional, generalmente en concordancia con los intereses del gobierno.
El Reto de Hoy:
Continua con el reto de la semana: la elaboración de la segunda parte de tu línea del tiempo que en esta ocasión comprende de 1920 a 1980. Recuerda que además de los hechos nacionales debes colocar los eventos internacionales que tuvieron impacto en nuestro país, como la Segunda Guerra Mundial y la Guerra Fría.
Ilústrala. Puedes apoyarte en tu libro de texto. Además, se te recomienda leer las novelas históricas Guerra en el Paraíso, Las armas del alba o Las mujeres del alba de Carlos Montemayor.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Valoremos la mediación
Aprendizaje esperado: Valora la mediación como un recurso que permite intervenir en los conflictos entre personas o grupos para impedir o detener la violencia y encontrar soluciones justas.
Énfasis: Valorar el papel de la mediación como un recurso para lograr soluciones justas ante diferentes conflictos.
¿Qué vamos a aprender?
Lo que necesitarás para esta sesión es tu cuaderno de notas, para realizar los registros que consideres importantes.
Como has revisado, la mediación es una estrategia que implica varios procesos y habilidades que se desarrollan para la resolución satisfactoria y justa de conflictos.
Es un recurso que favorece la comprensión, la empatía, el dialogo, la solidaridad, la conciliación y los acuerdos de dos partes en conflicto, con la participación de un tercero quien tiene la disposición de ayudar a destrabar el conflicto, para lo cual debe conocer el problema, los factores que dieron lugar al conflicto, sus posibles consecuencias, la disposición de las personas involucradas y el nivel de compromiso que cada una tiene con respecto al problema.
Los conflictos se pueden presentar en la cotidianidad, como resultado de las diferentes formas de pensar y actuar que dificultan resolver uno o varios problemas que se convierten en conflicto.
En esta diversidad, como resultado de la pluriculturalidad y la multiculturalidad, se convive todos los días en diferentes espacios, con personas que tienen aspiraciones, ideología, personalidad, cultura, costumbres y preferencias diferentes a la que se poseen.
Pero con respeto, tolerancia y escucha activa, se puede convivir e interactuar favorablemente con todas y todos los integrantes de la familia, en la escuela, el empleo o comunidad con la oportunidad de aprender, conocer particularidades, formas de vida que enriquecen el conocimiento y fortalecen las relaciones con las y los demás.
Cuando estas diferencias entre los seres humanos propician, como respuesta, actitudes violentas, y no se vislumbra una posible solución, es el momento de buscar formas pacíficas de resolución de conflictos.
¿Qué hacemos?
Una manera de resolver el conflicto es a través de la negociación, donde las partes involucradas acuerdan directamente el modo de resolverlo.
Cuando las partes han agotado las posibilidades de solución por sí mismas o la violencia impide la comunicación, es conveniente recurrir a la mediación. Esta se entiende como la intervención de una persona ajena al conflicto que tiene la habilidad de propiciar condiciones de comunicación entre las partes involucradas, con el propósito de alcanzar acuerdos que beneficien a todas y todos.
Para poder realizar la mediación se debe considerar algunos aspectos importantes, como si el conflicto ha llegado al momento de requerir la mediación, o si las partes no pudieron encontrar una solución por sí solas. Por ello.
Se requiere:
- La voluntad de las personas involucradas.
- Confidencialidad para evitar que en el conflicto se involucren más personas.
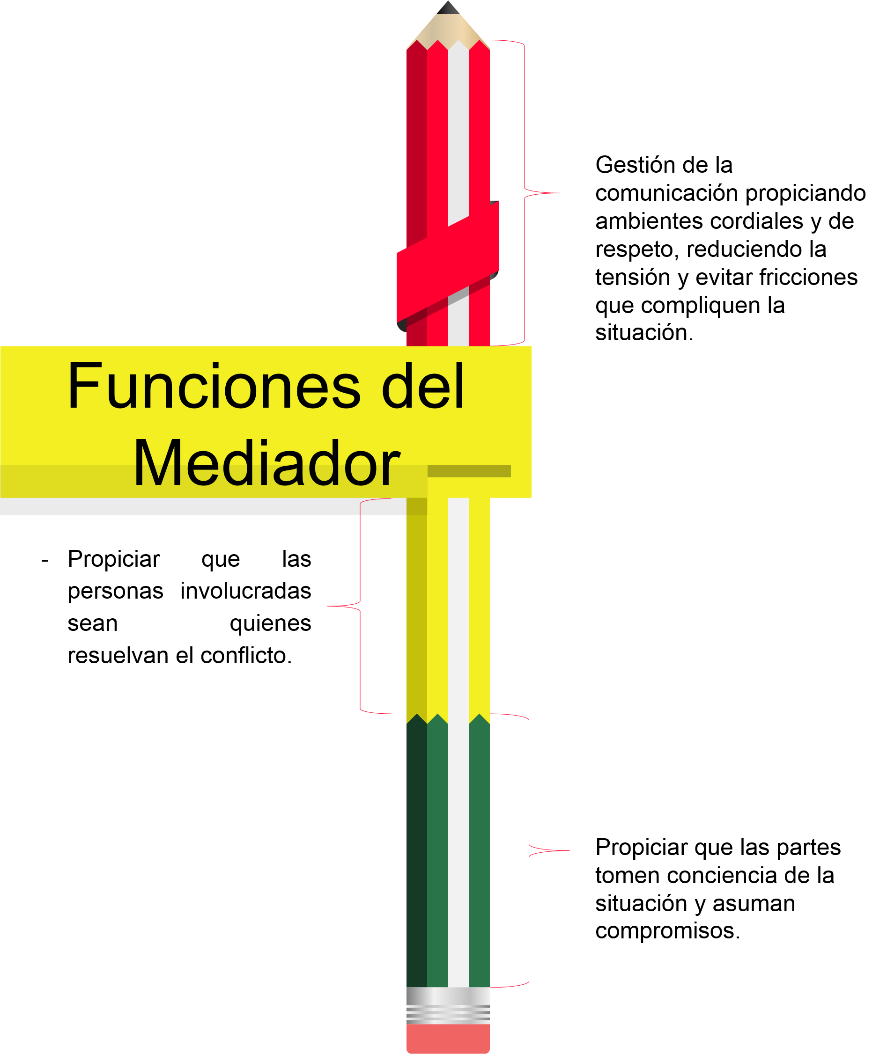
Dentro de las funciones del mediador destacan:
- Gestión de la comunicación, propiciando ambientes cordiales y de respeto, reduciendo la tensión y evitando fricciones que compliquen la situación.
- Propiciar que las personas involucradas sean quienes resuelvan el conflicto.
- Y propiciar que las partes tomen conciencia de la situación y asuman compromisos.
Las funciones y gestión del mediador permiten alcanzar los siguientes beneficios:
- Desarrollo de actitudes, cooperación.
- La toma de decisiones en las y los involucrados.
- Asumir responsabilidades en el cumplimiento de los compromisos.
- Favorece el dialogo y la negociación.
Como ejemplo, uno de los mejores mediadores de la historia fue Nelson Mandela, observa algunos datos acerca de él en el siguiente video del minuto 3:55 a 4:20.
- La mediación en la solución de conflictos
https://www.youtube.com/watch?v=-lsifcMK9oQ
Como pudiste observar, Nelson Mandela fue un activista y político que participó en diversos movimientos contra la opresión. A pesar de ser encarcelado, dedicó su vida a la lucha contra la segregación racial en Sudáfrica, específicamente, contra el apartheid, esta separación que había entre negros y blancos se llevó a cabo durante el siglo XX.
Nelson Mandela ha sido y seguirá siendo reconocido como el principal mediador en la historia debido a sus habilidades innatas de conciliador, motivador, hombre de escucha activa, que dialogaba e intervenía de forma prudente, logrando acuerdos y cooperación.
Reflexiona acerca de la siguiente pregunta:
¿En qué situaciones has tenido que recurrir a la mediación para solucionar un conflicto?
Los conflictos pueden presentarse en los diferentes ámbitos, familiar, escolar, laboral, comunitario; a nivel nacional o internacional. Por lo tanto, la mediación puede realizarse de forma civil, es decir, de forma voluntaria y conciliatoria; si el conflicto es en la familia, escuela o colonia, participan la familia, los responsables escolares, los vecinos.
Sin embargo, también puede realizarse de manera jurídica, en situaciones que se presentan en la sociedad, en instituciones, gobiernos y naciones, cuando es necesaria la aplicación de la norma legal y la intervención de la justicia.
Otro ejemplo es el papel que juegan las instituciones, organizaciones de la sociedad civil, líderes religiosos o morales para mantener el dialogo, respeto, acuerdos y compromisos; en otros casos, las acciones que realizan organismos internacionales y gobiernos del mundo para mantener la paz entre las naciones.
Después de la familia, la escuela es un ámbito donde converge una diversidad de formas de pensar, sentir y actuar; las y los adolescentes interactúan y aprenden a socializar, tomar decisiones y resolver conflictos.
Es en este espacio que las y los estudiantes tienen la posibilidad de fortalecer el dialogo, la escucha activa, respeto, tolerancia y participar en la mediación como herramienta para evitar la violencia y favorecer espacios de sana convivencia.
Observa la siguiente situación entre Karla y Liliana, pon atención a la intervención del profesor, del minuto 0:50 a 2:41.
- Solucionar los conflictos de manera no violenta
https://www.youtube.com/watch?v=_Zq96d_9sMk
- ¿Cuál es la actitud que muestran Karla y Liliana?
- ¿Cuál es el motivo aparente que originó el conflicto?
- ¿Qué actitud adopta el profesor?
Todos los conflictos tienen siempre una solución, lo importante es proponer formas no violentas para resolverlos. Recuerda que no puedes perder de vista la necesidad de aprender a aceptar las diferencias en la forma de pensar, sentir y actuar, lo que permitirá reconocer a las y los demás y estar dispuesta o dispuesto a mantener y fortalecer una Cultura de Paz.
Si pensaras en todo momento que es posible encontrar la salida a los problemas de forma pacífica y mantener la paz, y aprender a respetar los derechos humanos utilizando el diálogo, la empatía, la solidaridad y la justicia, las personas no saldrían lastimadas, por el contrario, se construiría un ambiente seguro, tolerante, respetuoso y libre de toda forma de violencia.
Ante la existencia de un conflicto, es necesario conciliar a las partes para armonizar los intereses poniendo en práctica la mediación y propiciando la disposición de las y los involucrados. Además, es muy importante la tolerancia para poder y querer resolver el problema.
En este caso, el profesor pudo asumir el rol de mediador pues Karla y Liliana son estudiantes de su grupo y al tener información acerca del contexto escolar, la relación de amistad que existe entre ellas pudo sugerir un espacio para dialogar y que cada una planteara su sentir. Para poder realizar una mediación efectiva es importante desarrollar algunas cualidades:
A continuación, se te propone un acróstico para que puedas recordar las cualidades de las que se abordaron:

El acróstico es una composición de letras con las que se puede formar una palabra o frase, este ejercicio lo puedes realizar de forma recurrente para recordar algunas palabras o conceptos relevantes y recuperarlos con facilidad.
Observa a la profesora Paola Oviedo Tiscareño, quién comparte la importancia de valorar la mediación en el aula escolar.
- Testimonio de la profesora Paola Oviedo Tiscareño
Después del ámbito familiar es en el espacio escolar donde las y los jóvenes experimentan diferencias y desacuerdos; sin embargo, son las y los profesores quiénes tienen la oportunidad de aprender a mediar cuando el conflicto se presenta en la escuela.
La responsabilidad ética es fungir como mediadores, fomentando el diálogo, así como encaminar a las y los estudiantes a aprender a resolver conflictos mediante la práctica de valores y habilidades comunicativas.
La empatía es una herramienta básica para construir ambientes favorables para la conciliación. La o el profesor mediador tiene la función de escuchar y ayudar a las y los involucrados a resolver, pues las y los jóvenes tienen la capacidad de proponer y establecer acuerdos de solución.
Las y los jóvenes pueden participar como mediadores entre pares. Al entenderse y reconocerse como iguales, pueden apoyarse y proponer soluciones ante las diferencias, desacuerdos o malos entendidos.
Observa cómo participan las y los adolescentes mediadores en la solución del conflicto entre Karla y Liliana, del minuto 8:37 a 13:11.
- Solucionar los conflictos de manera no violenta
https://www.youtube.com/watch?v=_Zq96d_9sMk
Tienes la oportunidad de colaborar con tu familia, amistades, vecinos y con tu comunidad en la solución de diferencias y conflictos. Tú puedes hacer la diferencia mediando, en la construcción de una Cultura de Paz.
Reflexiona acerca de las siguientes preguntas:
¿Consideras que la forma en que mediaron las y los adolescentes para ayudar a Karla y Liliana a resolver su desacuerdo fue asertiva?
¿El papel del profesor como mediador y observador durante el dialogo y la participación de las y los jóvenes contribuyó para crear un ambiente empático, tolerante y de respeto para la solución del conflicto?
Recupera el acróstico de las cualidades del mediador para contestar la siguiente pregunta:
• ¿Qué otras acciones sugieren para realizar una mediación efectiva, lograr acuerdos y compromisos en un conflicto?
Registra en tu cuaderno las respuestas con la finalidad de compartirlas posteriormente con tu profesora o profesor.
Lee la descripción de un conflicto entre Clara y Alicia:
Clara y Alicia son compañeras de grupo, la profesora de Orientación Educativa les asignó una actividad en binas, la cual debían organizar y presentar; como se encuentran a distancia se distribuyeron las tareas para integrar posteriormente la actividad; sin embargo, Clara no realizó lo que le correspondía y ello originó que las dos estudiantes tuvieran un intercambio de agresiones durante la clase. La profesora les solicitó que esperaran un momento al concluir para conocer los motivos de su conducta.
Completa el siguiente organizador como se muestra en la imagen, registra a la izquierda las acciones que pueden realizar las adolescentes con la participación de la profesora y las ventajas de la intervención.
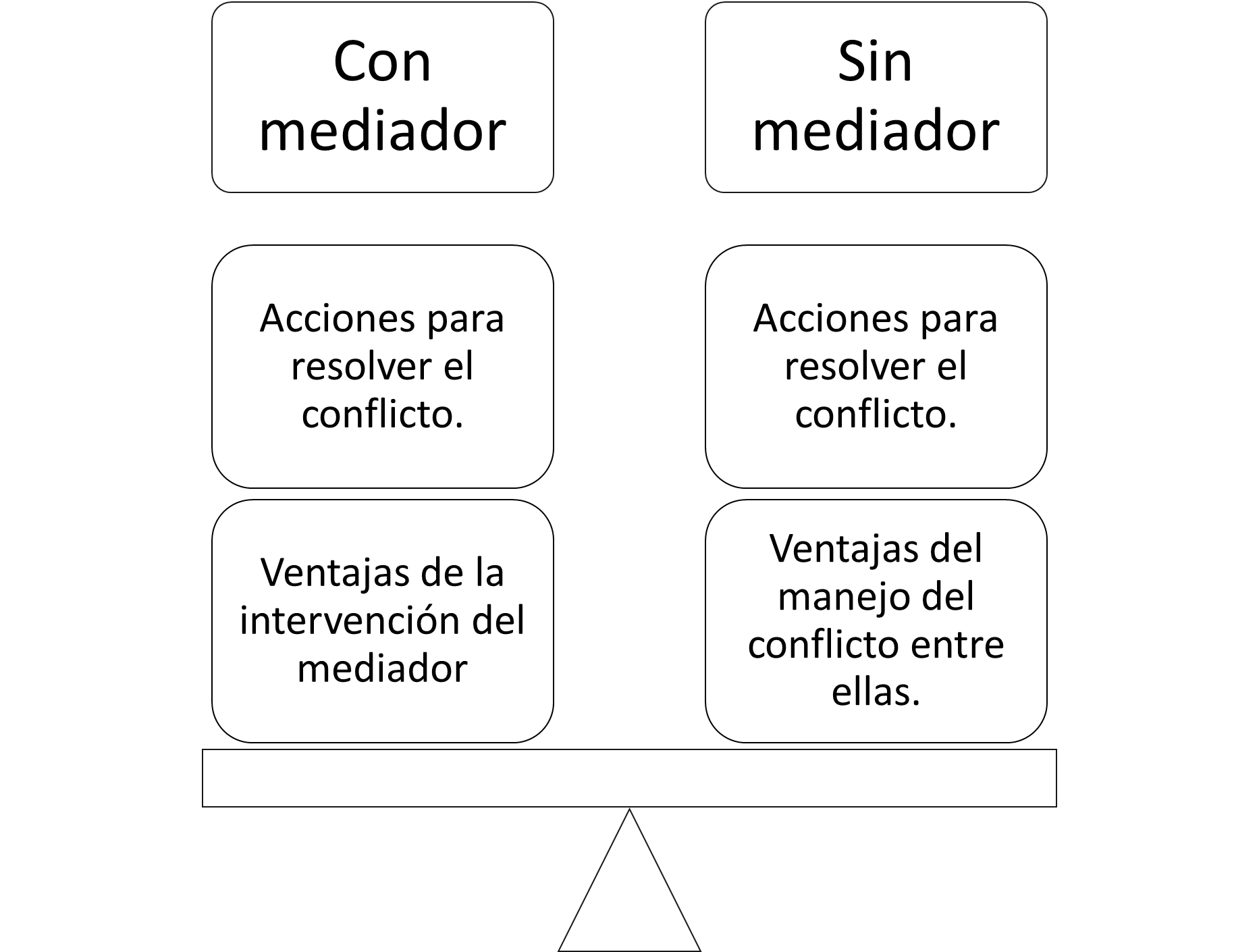
Registra, a la derecha, las acciones que pueden realizar las adolescentes sin la intervención del mediador y las ventajas de resolver de forma justa para ambas.
La participación del mediador es un recurso para llegar a acuerdos.
La lucha por alcanzar una Cultura de Paz ha sido una tarea incansable que debe continuar. Mujeres y hombres sobresalientes, como Nelson Mandela, dedicaron y dedican su vida a mediar para construir sociedades tolerantes y lograr soluciones justas ante los conflictos.
Revisaste videos y situaciones donde las y los jóvenes son capaces de resolver diferencias y malentendidos participando como mediadores. Escuchaste el testimonio de la profesora Paola, resaltando la responsabilidad de las y los profesores como mediadores para lograr soluciones pacíficas entre las y los jóvenes.
Y realizaste una actividad para poner en práctica los aprendizajes correspondientes a la sesión.
El Reto de Hoy:
Revisa tu libro de texto para ampliar la información y las reflexiones que hiciste a lo largo de la sesión para valorar el papel de la mediación para lograr soluciones justas.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
¡Planteemos una solución técnica!
Aprendizaje esperado: Plantea mejoras en los procesos y productos a partir de los resultados de la evaluación de los sistemas tecnológicos.
Énfasis: Representar las mejoras a un proceso o producto considerando la evaluación previa del sistema tecnológico.
¿Qué vamos a aprender?
Ten a la mano tu cuaderno y lápiz o bolígrafo para anotar las ideas principales, preguntas y reflexiones que surjan a partir del tema.
Además de tener tu listado con todos los conceptos relacionados con tecnología que has aprendido hasta ahora.
Éstos te facilitarán la comprensión del tema.
Recuerda lo que abordaste en la sesión anterior.
¿Qué hacemos?
Un problema técnico es una situación que surge de alguna necesidad insatisfecha y que puede tener una solución técnica.
Normalmente se encuentra una explicación sobre cuál es el contexto en el que tiene lugar la situación a la que hace referencia e incluye la necesidad insatisfecha, la situación a resolver y las condiciones que debe cumplir la solución.
Por eso, para darle solución, es necesario analizar la necesidad insatisfecha, identificar claramente el problema y distinguir las condiciones y requerimientos planteados para la solución. Así ya queda delimitado y es momento de buscar alternativas de solución.
Una vez que las tengas, es necesario revisarlas de una en una, en cuanto a sus requerimientos e implicaciones, tanto en la naturaleza como en la sociedad. Con ello, puedes valorar qué tan viable es llevarla a cabo.
Ya una vez seleccionada la alternativa más pertinente haces un boceto o diagrama de cómo quedará y puedes mostrarla para discutirla con los involucrados en el problema.
Y puedes quedarte hasta ahí o puedes desarrollar un proyecto. En el segundo caso habría que establecer los objetivos, un plan de trabajo, ejecutarlo, evaluarlo y comunicar los resultados.
Observa el siguiente video:
- Justificación y objetivos de un proyecto
Este video te da una idea más clara de lo que se debe considerar para iniciar la solución de un problema técnico, una vez que ya se eligió la solución más viable.
Empieza por la necesidad insatisfecha de la que se deriva cierto problema y plantea de manera clara la situación problemática elegida. De esa manera podrás plantear tus objetivos con claridad.
Además, es importante que tu plan de trabajo contenga la programación de actividades.
De acuerdo con las actividades requeridas ir asigna un responsable para ejecutarlas, para lo cual también necesitas de un cronograma para establecer tiempos.
Para que te queden más claros los pasos de un proyecto, observa el siguiente video.
- Acciones o metas para llegar al objetivo planteado
1. La justificación.
2. Los objetivos.
3. El plan de trabajo.
4. Programación de actividades.
5. El cronograma.
Esos son algunos de los pasos generales para desarrollar un proyecto; sin embargo, puedes ampliar, pues depende hasta dónde quieras llegar con tu proyecto.
Pero estos pasos son muy generales, porque si hablas de un proyecto tecnológico todavía falta la evaluación y la comunicación de resultados, así como algunos puntos específicos dentro de cada fase.
Dentro de algunas sesiones conocerás con todo detalle de qué se trata el proyecto tecnológico.
Regresa al problema de Pedro, para darle una solución.
Como recordarás, Pedro es un alumno de tercero de secundaria que vive en una comunidad del estado de Morelos y le gusta mucho andar en bicicleta.
Su papá es jardinero, oficio que a Pedro le gusta, y cada que puede le ayuda. A él le agrada mucho manejar las herramientas, como las tijeras de podar, la hoz, la pala y el pico, entre otras. Además, tiene la posibilidad de conocer gente, lo cual le ha permitido hacer muchos amigos.
Pedro estaba preocupado por un problema relacionado con el oficio de su papá. Éste tenía que ver con que el proceso de afilado de sus tijeras es muy lento y le gustaría generar un producto o servicio que le permita hacerlo más rápido, económico, que evite el uso de energía eléctrica proveniente de fuentes fósiles o lo disminuya y que no utilice materiales como el acero, en la medida de lo posible.
De este modo, el papá de Pedro podrá tener su herramienta lista en poco tiempo y podar más jardines en menos tiempo.
Esto será muy benéfico para Pedro y su familia, pues su papá tendrá más ingresos y con ello tendrá la posibilidad de comprar una computadora y contratar el internet que requieren.
Entonces el producto o servicio que genere contribuirá a disminuir los daños en la naturaleza al usar energías limpias y tendrá implicaciones sociales directamente en su familia, pues logrará tener conectividad de internet en casa.
Cómo solucionó este problema Pedro.
Primero, buscó alternativas de solución para mejorar el proceso de afilado de herramientas.
- ¿Qué alternativas de solución crees que encontró Pedro?
- ¿Qué información crees que encontró respecto a herramientas y equipo de afilado?
- ¿Qué información y alternativas encontraste?
Descubre lo que Pedro encontró, observa el siguiente video.
- Herramientas y equipo para afilar
Siempre puedes encontrar más y más información conforme vas buscando. Lo importante es ir revisándola para ver qué puedes considerar para solucionar tu problema.
¿Cuáles de estas alternativas considerarías?
En el caso de Pedro, consideró tres alternativas de solución.
La primera alternativa de Pedro fue comprar más herramienta, para cuando una de ellas pierda el filo se pueda utilizar otra y afilarla llegando a casa.
La segunda alternativa fue comprar un esmeril de banco para afilar la herramienta cada que lo requieras de manera rápida.
La tercera fue diseñar y construir un mecanismo similar al esmeril de banco, pero con funcionamiento mecánico utilizando los pedales y rueda de su bicicleta.
¿Alguna alternativa de Pedro se parece a las tuyas?
Como siguiente paso, Pedro analizó las ventajas y desventajas de sus alternativas.
Y concluyó lo siguiente:
La primera alternativa no es tan viable, pues se lo comentó a su papá y le respondió que era mucha inversión. Además, no tenía mucho sentido, pues al regresar a casa después de una larga jornada, todavía tendrían que afilar sus herramientas para el día siguiente y el proceso sería igual de lento. Incluso Pedro terminaría tan cansado que no tendría energía para tomar sus clases de Aprende en casa III en la mañana. Así que fue descartada esta opción.
En la segunda alternativa, aunque es muy veloz el afilado, el papá de Pedro le comentó que hay que hacer una inversión alta. Además, el esmeril de banco sólo funcionaría con energía eléctrica, por lo que el afilado tendría que ser en casa y tendría implicaciones en la naturaleza.
Sin duda, es mejor propuesta que la primera, pero no cumple con los requerimientos que conociste del problema.
La última alternativa fue plantear el diseño y construcción de un esmeril de banco, pero con un funcionamiento mecánico, y para ello pensó en su bicicleta, Pedro le vio varias ventajas:
Con el uso de la bicicleta que ya tiene, no necesitaría energía eléctrica, sino mecánica, pues con el movimiento de los pedales haría girar la polea de la rueda y ésta a su vez, por medio de una banda, giraría las piedras del esmeril mecánico. Al tener ya su bicicleta, la inversión resultaría más económica, así como su operación, pues no requiere de energía eléctrica y podría llevársela a los servicios de jardinería para realizar el proceso de afilado en sitio.
Y esto sí que le agradó a su papá.
Además, puede generar algunas ganancias extra afilando herramientas de otras personas a un costo más bajo que en otros lugares, pues no utiliza energía eléctrica.
Al acondicionar su bicicleta como herramienta de afilado, él podrá prestar servicios a diferentes usuarios como: jardineros, carniceros, polleros, o incluso en cualquier casa que requieran estos servicios de afilado.
¿Cuál es la más viable desde tu punto de vista?
La alternativa 3 es la mejor, pues cumple con todos los requerimientos que conociste en el problema técnico; es económica, contribuye al ahorro de tiempo y dinero, no usa energía eléctrica y el esmeril no está hecho de acero.
¿Te animarías a diseñarla y construir esta solución?
¿Cómo convertir tu bicicleta en una herramienta para afilar?
Esto es lo que realizó Pedro:
Primero investigó cómo podía construir este mecanismo y le pidió ayuda a su maestra de Tecnología. Una vez que supo cómo lograrlo, mandó a hacer con el herrero una base para elevar la rueda trasera y que ésta le permitiera mantener estática la bicicleta, aunque estuviera girando la llanta, como se muestra en la imagen.
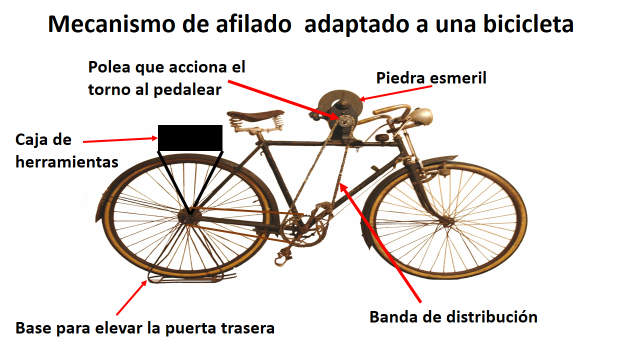
Después, consiguió un esmeril de banco que ya no funcionaba, lo desarmó y adaptó el torno o eje rotatorio en el frente de su bicicleta colocándole a un costado una polea superior con su tensor correspondiente para ajustar la posición, como se muestra en la imagen.
Luego, en la llanta trasera le adaptó una polea inferior para que tuviera movimiento junto con el rin de la llanta.
Posteriormente, buscó una banda de distribución de automóvil con una longitud similar a la distancia que hay entre su polea inferior y superior para lograr que con el movimiento de la rueda trasera girara el eje de las piedras de afilar con una velocidad considerable para un buen y eficiente afilado.
Hasta en la parrilla de la bicicleta adaptó una caja para guardar y transportar las herramientas que requiere.
Pedro hizo un gran trabajo. Con su bicicleta, entonces, no sólo puede transportarse sin contaminar, sino también puede afilar las herramientas de su papá con todos los requerimientos que planteó desde el inicio.
Ahora que has aprendido cómo se resolvió el problema técnico de Pedro, ya podrás plantear tus problemas técnicos, buscar alternativas de solución, elegir la más adecuada y representarla en un boceto, como el de la bicicleta con afilador de Pedro.
El Reto de Hoy:
Si tienes interés en adaptar tu bicicleta como Pedro, consulta a tus familiares y a tu maestra o maestro de Tecnología.
Además, recuerda compartir con tu grupo y tu familia algún problema técnico que identifiques en tu casa o en tu comunidad. Seguramente podrás analizarlo y resolverlo conjuntamente.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario