Aprende en Casa III SEP: 28 de abril TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 28 de abril de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Miércoles 28 de abril, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Método gráfico
Aprendizaje esperado: Resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.
Énfasis: Resolver problemas mediante el planteamiento y solución de sistemas de dos ecuaciones lineales con dos incógnitas utilizando el método gráfico.
¿Qué vamos a aprender?
Esta sesión será práctica, profundizaremos en el estudio de los métodos de solución para un sistema de ecuaciones de 2 incógnitas con 2 ecuaciones, concretamente estudiaremos el método gráfico.
Durante el estudio de las matemáticas en segundo grado de secundaria, concretamente con el estudio del álgebra, existen varios métodos para resolver un sistema de 2 ecuaciones lineales con 2 incógnitas.
Si en cada paso de cualquiera de esos métodos, realizamos las operaciones correctamente, llegaremos a las soluciones que cumplen adecuadamente las condiciones de las 2 ecuaciones. En esta sesión realizaremos trazos, leeremos la solución del sistema de ecuaciones en una gráfica, incluso podemos utilizar colores en los trabajos escolares.
¿Qué hacemos?
En esta sesión vamos a trazar varias rectas para encontrar las soluciones a los sistemas de ecuaciones lineales 2 por 2. Así que alumnas y alumnos, les recomendamos que tengan cerca de ustedes 2 colores distintos, uno para cada recta que se trazará.
¿Por qué vamos a trazar 2 rectas en un sistema de 2 ecuaciones con 2 incógnitas?
Vamos a trazar 2 rectas porque representaremos cada ecuación del sistema con una recta en el plano cartesiano.
¿Cómo podemos encontrar la solución de un sistema de 2 por 2 por el método gráfico?
¿Qué le parece si nos propone un sistema de ecuaciones y entre todos lo resolveremos?
Comencemos con un sistema que por sus características puede ser considerado sencillo de resolver y gradualmente aumentaremos la dificultad de ellos.
La primera ecuación del sistema es “y” más “x” es igual a 13 y la segunda, “y” más 6 “x” igual a 38.
Podemos resolver el sistema por diferentes caminos y diferentes métodos, pero, como les mencionamos anteriormente, en esta ocasión utilizaremos el método gráfico y el camino que nosotros les proponemos, es el siguiente:
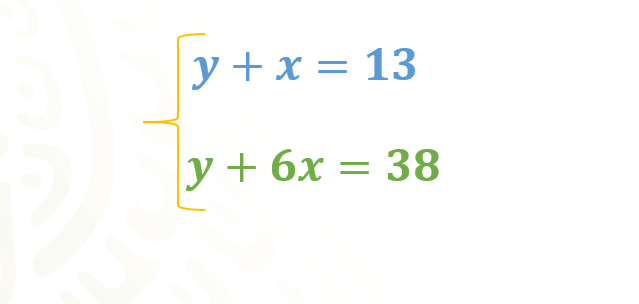
En ambas ecuaciones despejamos a “y”, es decir, la dejamos sola en un lado de la ecuación, haciendo uso de las propiedades de la igualdad.
Esto lo hacemos para que tengamos expresiones equivalentes a esas ecuaciones, pero de manera que las podamos observar como una relación donde el valor “y” está en función del valor de “x”.
Para la primera ecuación, primero, sustraemos “x” en ambos miembros de la igualdad, por lo que la ecuación ahora es “y” más “x”, menos “x”, igual a 13 menos “x”.
Reducimos los términos semejantes en el primer miembro de la ecuación, con lo que las “x” se eliminan entre sí dado que su suma es cero.
Con lo anterior, obtenemos “y” igual a 13 menos “x”.

De la misma manera, despejamos “y” en la segunda ecuación.
Haciendo uso de las propiedades de la igualdad, sustraemos 6 “x” en ambos miembros de la igualdad, por lo que tenemos “y” más 6 “x”, menos 6 “x” igual a 38 menos 6 “x”.
Al reducir los términos semejantes en el primer miembro de la igualdad, se eliminan entre sí 6 “x” dado que su resultado es cero.
Con ello ya hemos despejado a “y”, como “y” igual a 38 menos 6 “x”.

Ahora, podemos hacer uso de una tabla para organizar los valores de las coordenadas que vamos a calcular. La tabla permitirá diferenciar visualmente las coordenadas que corresponden a cada recta.
Puedes elaborar su tabla como gustes, te sugerimos el siguiente orden, observa la tabla.

En la primera columna colocaremos los valores de “x”.
En la segunda columna las operaciones que se generan al sustituir el valor de “x” en el despeje de “y” en la primera ecuación.
En la tercera columna las operaciones que se generan al sustituir el valor de “x” en el despeje de “y” para la segunda ecuación.
En la cuarta columna las coordenadas que se forman con el valor de “x” y el valor calculado de “y”, para la recta de la primera ecuación.
En la quinta columna las coordenadas que se forman con el valor de “x” y el valor calculado de “y”, para la recta de la segunda ecuación.
Pueden asignar los valores que ustedes gusten para “x”, es muy común que se asignen valores positivos, negativos y el cero para “x”, con la finalidad de observar el comportamiento de las rectas para valores dados. Nosotros asignamos valores enteros desde 3 negativo a 3 positivo.
|
|
|
|
Primera ecuación
|
Segunda ecuación
|
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
Sustituiremos los valores de “x” en el primer despeje, para encontrar el valor de “y” en cada caso de esas sustituciones.
Para “x” igual a 3 negativo, sustituimos y obtenemos “y” igual a 13 menos 3 negativo. Al resolver las operaciones el resultado es 16.
Para “x” igual a 2 negativo, tenemos “y” igual a 13 menos 2 negativo y al resolver las operaciones el resultado es 15.
Para “x” igual a uno negativo, la sustitución queda como “y” igual a 13 menos uno negativo de donde se obtiene que “y” es igual a 14.
|
|
|
|
Primera ecuación
|
Segunda ecuación
|
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
Para “x” igual a cero, “y” es igual a 13 menos cero lo que hace que “y” es igual a 13.
Para “x” igual a uno, al sustituir tenemos que “y” igual a 13 menos uno y al resolver las operaciones el resultado es 12.
Para “x” igual a 2, “y” es igual a 13 menos 2 con lo que se obtiene que “y” es igual a 11.
Por último, para “x” igual a 3, sustituimos con lo que tenemos que “y” es igual a 13 menos 3, por lo que “y” es igual a 10.
De la misma manera que en el paso anterior, sustituiremos los valores de “x” en el despeje de “y” de la segunda ecuación, para obtener el valor de “y” que corresponde a cada valor propuesto de “x”.
Iniciemos entonces, con el primero valor de “x”. Para “x” igual a 3 negativo, “y” es igual a 38 menos, 6 por 3 negativo, lo que hace “y” igual a 38 más 18, de donde se obtiene “y” igual a 56.
Para “x” igual a 2 negativo, “y” igual a 38 menos, 6 por 2 negativo, lo que hace “y” igual a 38 más 12, de donde se obtiene “y” igual a 50.
Para “x” igual a 1 negativo, “y” igual a 38 menos, 6 por 1 negativo, lo que hace “y” igual a 38 más 6, de donde se obtiene “y” igual a 44.
Para “x” igual a cero, tenemos que “y” igual a 38 menos 6 por cero, entonces “y” es igual a 38.
En el caso de “x” igual a uno, se tiene “y” igual a 38 menos, 6 por uno, con lo que se tiene “y” igual a 38 menos 6, entonces “y” es igual a 32.
Para “x” igual a 2, “y” es igual a 38 menos, 6 por 2; luego, “y” es igual a 38 menos 12, y al resolver la operación obtenemos que “y” es igual a 26.
Finalmente, para “x” igual a 3, tenemos “y” igual a 38 menos, 6 por 3, de donde se tiene “y” igual a 38 menos 18 por lo que “y” es igual a 20.
|
|
|
|
Primera ecuación
|
Segunda ecuación
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
Ya que hemos calculado los valores de “y”, formaremos con los valores de “x” y de “y” las coordenadas de cada uno de los puntos que corresponden a cada ecuación, ya que por dichos puntos pasarán las rectas, que son sus gráficas.
Los puntos de la primera recta, que corresponde a la ecuación “y” más “x” igual a 13, son los siguientes:
3 negativo coma 16.
2 negativo coma 15.
1 negativo coma 14.
Cero coma 13.
Uno coma 12.
2 coma 11.
3 coma 10.
|
|
|
|
Primera ecuación
|
Segunda ecuación
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Los puntos de la segunda recta, que corresponde a la ecuación “y” más 6 “x” igual a 38, son los siguientes:
3 negativo coma 56.
2 negativo coma 50.
1 negativo coma 44.
Cero coma 38.
Uno coma 32.
2 coma 26.
3 coma 20.
|
|
|
|
Primera ecuación
|
Segunda ecuación
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¿Qué piensan que debemos hacer a continuación?
Debemos ubicar estos puntos en un plano cartesiano para trazar las rectas que corresponden al sistema que queremos resolver.
Para que nosotros no confundamos los puntos de cada recta, ubicaremos las coordenadas de la primera recta y posteriormente, las de la segunda.
La primera coordenada es 3 negativo coma 16, por lo que nos desplazamos 3 lugares hacia la izquierda sobre el eje de las “x” o de las abscisas a partir del origen. Posteriormente, desde ahí nos desplazamos 16 lugares hacia arriba paralelamente al eje de las “y” o de las ordenadas. Ésa será la coordenada 3 negativo, coma 16.
La segunda coordenada es 2 negativo coma 15, por lo que nos desplazamos 2 lugares hacia la izquierda sobre el eje de las “x” o de las abscisas a partir del origen. Luego, y desde ese lugar, nos desplazamos 15 lugares hacia arriba paralelamente al eje de las “y” o de las ordenadas. Ésa será la coordenada 2 negativo, coma 15.
La tercera coordenada es uno negativo coma 14, por lo que nos desplazamos un lugar hacia la izquierda sobre el eje de las “x” o el eje horizontal a partir del origen. Desde ahí, nos desplazamos 14 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada uno negativo, coma 14.
La cuarta coordenada es cero coma 13, por lo que no nos desplazamos sobre el eje de las “x” o el eje horizontal. Luego partimos del origen, desde ese lugar, nos desplazamos 13 lugares hacia arriba sobre el eje de las “y”. Ésa será la coordenada cero, coma 13.
Para la quinta coordenada, que es 1 coma 12, nos desplazamos un lugar hacia la derecha sobre el eje de las “x” a partir del origen. Ahora, desde ahí, nos desplazamos 12 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 1, coma 12.
La sexta coordenada es 2 coma 11, por lo que nos desplazamos 2 lugares hacia la derecha sobre el eje de las “x” a partir del origen. Posteriormente, a partir de ahí, nos desplazamos 11 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 2, coma 11.
Finalmente, para la séptima coordenada que calculamos para la primera ecuación, que es 3 coma 10, nos desplazamos 3 lugares hacia la derecha sobre el eje de las “x” a partir del origen. Luego, desde ese lugar, nos desplazamos 10 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 3, coma 10.

Una vez ubicados los puntos trazaremos una recta que pase por todos ellos. Con ello simbolizaremos a la recta que pasa por todas las coordenadas que colocamos y que representa a la primera ecuación.

Ya que hemos ubicado las coordenadas de la primera recta y trazado su representación gráfica, colocaremos de la misma manera las coordenadas de la segunda ecuación.
La primera coordenada es 3 negativo coma 56, por lo que nos desplazamos 3 lugares hacia la izquierda del origen sobre el eje de las “x”. Desde ese lugar, nos desplazamos 56 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 3 negativo, coma 56.
La segunda coordenada es 2 negativo coma 50, por lo que nos desplazamos 2 lugares hacia la izquierda del origen sobre el eje de las “x” y posteriormente, a partir de ahí, nos desplazamos 50 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 2 negativo, coma 50.
La tercera coordenada es 1 negativo coma 44, por lo que nos desplazamos un lugar hacia la izquierda del origen sobre el eje de las “x”. Luego, desde ese lugar, nos desplazamos 44 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 1 negativo, coma 44.
La cuarta coordenada es cero coma 38, por lo que no nos desplazamos sobre el eje de las “x” y sí lo hacemos sobre el eje de las “y”, desde el origen, 38 lugares hacia arriba. Esa será la coordenada cero, coma 38.
Para la quinta coordenada que es 1 coma 32, nos desplazamos un lugar hacia la derecha del origen sobre el eje de las “x”. Posteriormente, desde ahí, nos desplazamos 32 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 1, coma 32.
Para el caso de la sexta coordenada que es 2 coma 26, nos desplazamos 2 lugares hacia la derecha del origen sobre el eje de las “x”. Luego, desde ese lugar, nos desplazamos 26 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 2, coma 26.
La séptima coordenada es 3 coma 20, por lo que nos desplazamos 3 lugares hacia la derecha del origen sobre el eje de las “x”. Posteriormente, a partir de ahí, nos desplazamos 20 lugares hacia arriba paralelamente al eje de las “y”. Ésa será la coordenada 3, coma 20.

¿Qué hacemos para continuar?
Trazamos una recta que pase por todos los puntos que acabamos de localizar, prolongando sus extremos.
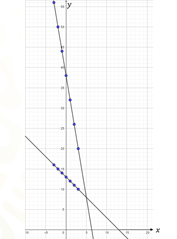
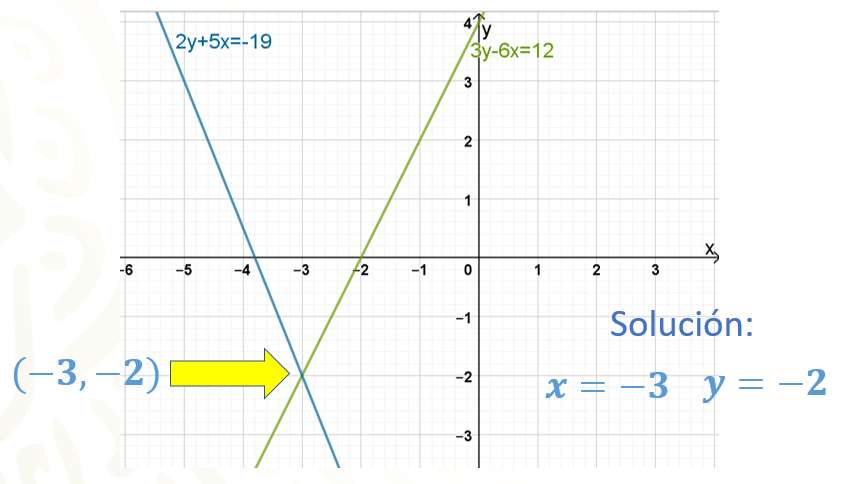
Observa el plano que aparece en sus pantallas, donde ya fueron trazadas las 2 rectas que genera el sistema de ecuaciones de 2 por 2 que estamos resolviendo.
¿En dónde podemos observar la solución al sistema? Es decir, el valor de “x” y el valor de “y”, que satisfacen las condiciones de las 2 ecuaciones al mismo tiempo.
Exacto, ya se dieron cuenta que la solución se encuentra en el punto donde las rectas se intersecan, es decir, el punto donde se cortan, esto es en la coordenada 5 coma 8.
Esto quiere decir que “x” es igual a 5 y que “y” es igual a 8.
Pero, ¿cómo podemos estar seguros que esos valores de las incógnitas son la solución del sistema de ecuaciones motivo de esta actividad?
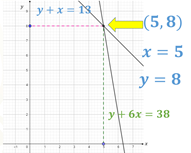
Esto lo podemos averiguar sustituyendo los valores obtenidos para “x” y para “y” en las ecuaciones iniciales y observar si se cumple la igualdad.
Vamos a hacerlo.

Si sustituimos en la primera ecuación que es “y” más “x” igual a 13 obtenemos 8 más 5 igual a 13. Al sumar comprobamos la igualdad, 13 igual a 13.
En la segunda ecuación, “y” más 6 “x” igual a 38, sustituimos y obtenemos 8 más, 6 por 5 igual a 38. Al realizar la multiplicación resulta 8 más 30 igual a 38 y, al sumar obtenemos la igualdad, 38 igual a 38.
De esta manera, al comprobar que los valores que obtuvimos, “x” igual a 5 y “y” igual a 8, hacen verdaderas las igualdades de ambas ecuaciones, podemos afirmar que son las soluciones del sistema formado por “y” más “x” igual a 13 y “y” más 6 “x” igual a 38.
Así es, maestro, ¿qué le parece si resolvemos, junto con las alumnas y los alumnos, un problema?
Resolvamos el siguiente problema.
El doble de un número más el quíntuple de otro es igual a 19 negativo. Se sabe que el triple del primero menos el séxtuple del segundo es 12. ¿Cuáles son esos números?

Para la primera ecuación: 2 “y” más 5 “x” igual a 19 negativo y para la segunda ecuación 3 “y” menos 6 “x” igual a 12.
Resolver este sistema involucrará pasos adicionales comparado con el que respondimos anteriormente, ya que como seguramente ya se dieron cuenta, la “y” no está del todo sola. En ambos casos tiene un coeficiente distinto de uno.
Sin embargo, de manera general, seguiremos los mismos pasos que en el caso anterior.
Comencemos despejando la “y” en ambas ecuaciones.
Para la primera ecuación restamos 5 “x” en ambos lados de la ecuación. Al reducir términos semejantes resulta 2 “y” igual a 19 negativo menos 5 “x”. Como la “y” aún no está sola dividiremos los dos miembros de la igualdad entre 2, este es el paso adicional que no hicimos en el sistema anterior.
Al dividir entre 2, ya tenemos despejada a la “y”, como “y” igual a 19 negativo menos 5 “x”, entre 2.
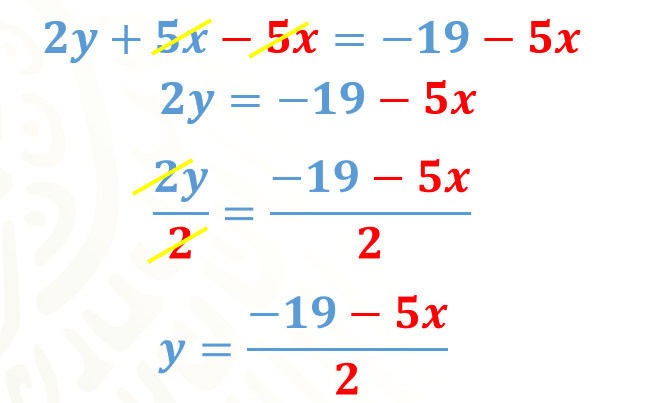
Una manera de despejar “y” en la segunda ecuación, es sumar 6 “x” en ambos miembros de la igualdad, con ello tenemos 3 “y” es igual a 12 más 6 “x”.
Como la “y” aún no está despejada, dividimos entre 3 a ambos miembros de la igualdad, con lo que obtenemos “y” es igual a 12 más 6 “x”, entre 3.
¿Qué hacemos para continuar?
Podemos continuar dando valores para “x” y determinar el que le corresponda para “y” en ambos despejes realizados anteriormente.

Para organizar los datos que nos llevarán a trazar las gráficas, usaremos una tabla similar a la del sistema anterior, pero ahora no usaremos tantos valores. Así que usaremos 3 valores, un valor positivo, uno negativo y el cero.

De la misma manera que en el procedimiento anterior, sustituimos los valores de “x” en el primer despeje de “y”.
Para “x” igual a 3 negativo, sustituimos y obtenemos “y” igual a 19 negativo, menos, 5 por 3 negativo, entre 2, y al resolver las operaciones obtenemos 2 negativo.
Ahora, para “x” igual a cero, sustituimos y obtenemos “y” igual a 19 negativo, menos, cinco por cero, entre 2, lo que da como resultado 9 punto 5 negativo.
Por último, para “x” igual a 3, al sustituir tenemos “y” igual a 19 negativo, menos 5 por 3, entre 2, y al resolver las operaciones obtenemos que “y” es igual a 17 negativo.
|
|
|
|
Primera ecuación
|
Segunda ecuación
|
|
|
|
|||
|
|
|
|||
|
|
|
Ahora, sustituimos los valores de “x” en el despeje de “y” de la segunda ecuación:
Para “x” igual a 3 negativo, tenemos “y” igual a 12 más, 6 por 3 negativo, entre 3 y al resolver las operaciones obtenemos “y” igual a 2 negativo.
|
|
|
|
Primera ecuación
|
Segunda ecuación
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
En el caso de “x” igual a cero, “y” igual a 12 más, 6 por cero, entre 3 y al resolver las operaciones determinamos que “y” es igual a 4.
Por último, para “x” igual a 3, “y” es igual a 12 más, 6 por 3, entre 3, de donde obtenemos “y” igual a 10.
Con lo anterior obtenemos las coordenadas asignadas a algunos puntos de ambas rectas.
¿Qué notas al comparar los puntos de ambas rectas?
A partir de los datos de la tabla, ¿podemos saber si habrá un punto en común para ambas rectas?
Vayamos a la representación de las gráficas del sistema para resolverlo.
|
|
|
|
Primera ecuación
|
Segunda ecuación
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Observa las rectas que representan el sistema. ¿En dónde se observa la solución a este sistema?
Seguramente ya identificaste que la coordenada en donde se cortan las rectas es la 3 negativo coma 2 negativo, y esto significa que la solución del sistema es “x” igual a 3 negativo y “y” igual a 2 negativo.
El Reto de Hoy:
Como reto te corresponde realizar la comprobación de estos valores.
Con esto hemos llegado al final de esta sesión. Recuerden que este es un material de apoyo y que, para complementar lo estudiado, pueden consultar otras fuentes, como su libro de texto de matemáticas de segundo grado.
Si quieres volver a ver los programas de Aprende en casa transmitidos en semanas previas, los puedes encontrar en la página: youtube.com/aprendeencasa
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
La canción es cultura
Aprendizaje esperado: Analiza críticamente el contenido de canciones de su interés.
Énfasis: Identificar elementos culturales en las canciones.
¿Qué vamos a aprender?
El tema que abordaremos es la canción es cultura, en esta sesión identificaremos aspectos culturales de las canciones indígenas, lo que permite comprender el entorno en que fueron creadas.
¿Qué hacemos?
Escuchemos el siguiente poema en lengua Tutunaku.
- VIDEO: POEMA TOTONACO. MUERE MI ROSTRO
El canto no muere nunca.
La música tradicional y las canciones han sido un instrumento de comunicación fundamental, como saben, según el Instituto Nacional de Lenguas Indígenas, tenemos 68 agrupaciones lingüísticas, y han utilizado las canciones para socializar y son parte de nuestro patrimonio cultural.
Observamos la siguiente cápsula del minuto 04:51 al 05:18:
- VIDEO LOS DERECHOS CULTURALES EN LA MÚSICA
La música de los pueblos indígenas es un patrimonio cultural porque tiene valor histórico y expresa sentimientos, vivencias y costumbres que están vigentes en sus comunidades.
Observa esta foto de músicos Warárikas conocidos en español como Huicholes. ¿Qué les evoca?

Imagino que es una canción de su pueblo y que están vestidos así porque, quizá, es un festival. Por otro lado, tienen integrantes menores de edad porque buscan preservar los cantos transmitidos de generación en generación.
Recuerden que vivimos en un país plurilingüe y multicultural donde conviven una gran cantidad de lenguas, tradiciones y costumbres.
Observa el siguiente video del minuto 03:26 al 4:06 para que quede más claro.
- VIDEO LOS DERECHOS CULTURALES EN LA MÚSICA
En la música se manifiesta la cultura a través de todo.
Ahora observa estas imágenes, ¿qué te evoca el vestuario y la situación?

Esta imagen es de danzantes Guaguas o Quetzales de la cultura totonaca. Portan un pantalón de terciopelo rojo, acompañado de una camisa blanca con bordados en chaquira, canutillo y lentejuela. Sus penachos están hechos de carrizo, tejido con listones de colores vistosos y plumas blancas. El caporal viste camisa y pantalón blanco, acompañado de un pañuelo bordado de flores, él guía al grupo de danzantes, a través de la flauta y el tambor que imitan el canto del quetzal. Asimismo, utilizan una cruceta que simboliza la reverencia hacia los cuatro puntos cardinales.

En esta otra imagen observamos a otros danzantes totonacos, conocidos como Los Negritos, su vestimenta es vistosa: con sus bellos bordados y con sombreros adornados con flores.
Como observaste, la vestimenta aporta un sentido de identidad y cada región se caracteriza por portar sus trajes típicos, los cuales reflejan su cultura y el medio que les rodea.
¿Cómo podrías ver reflejado el legado cultural en una canción?, ¿cuál es la importancia de transmitir la música totonaca?
Escuchemos al profesor Romualdo Santiago Ramírez, de la localidad de Puente de Piedra, municipio de Papantla, de origen totonaco, promotor y profesor de lengua tutunaku.
- VIDEO PROF. ROMULO IMPORTANTE TRASMITIR LA MÚSICA TOTONACA
Escuchemos la canción de la que habla el maestro para conocer su letra y su sentido:
- AUDIO 01 LA TOTONAQUITA
La lengua tutunaku, significa tres corazones y que este pueblo se ubica en los estados de Veracruz y Puebla.
¿Qué reflejan las canciones?

Pues reflejan y expresan nuestras emociones; comunican sentimientos y vivencias que no se pueden expresar por medio del lenguaje común.
Ahora escuchemos el extracto de “Papantla mi pueblo querido”, escrita y cantada por José Antonio Pallares Castañeda.
- AUDIO 02 PAPANTLA MI PUEBLO QUERIDO
Como escuchaste, la letra habla sobre el orgullo de pertenecer a un pueblo con riqueza cultural y rescata la diversidad de personas, su color de piel, el vestuario, entre otras. Esto es porque:
Las canciones son un medio de comunicación, mediante el cual se transmiten emociones, sentimientos; son construidas culturalmente, reflejan la cultura a la que pertenecen.
Algo interesante es que esta cultura se ha transformado, pues la música tradicional era exclusiva de los hombres y ahora participan mujeres.
Ahora, ahondemos más:

¿Cómo se reflejan esos elementos en la vida diaria de los pueblos?
Pues eso se observa en los contenidos. Por ejemplo:

Escuchemos nuevamente al maestro Romualdo Santiago Ramírez, quien también es promotor de la lengua Tutunaku, del Centro de las Artes Indígenas en Papantla, Veracruz.
- VIDEO 02 PROF. ROMUALDO HACIA LAS Y LOS ADOLESCENTES SOBRE LA IMPORTANCIA DE CONOCER LA MÚSICA TRADICIONAL
Con esto queda clara la importancia de conocer y valorar las canciones emanadas de diferentes culturas y cantadas en diversas lenguas originarias.
La cultura totonaca tiene fama mundial, por sus voladores de Papantla, declarados por la UNESCO como patrimonio inmaterial de la humanidad.
El Reto de Hoy:
El reto es escuchar la música de estos pueblos o acercarse a canciones de Tlen Huicani, con sus famosas interpretaciones de La Bruja, El Cascabel y sus sones o huapangos; al grupo Mono Blanco o al grupo Cojolites, entre otros, que le han dado fama a Veracruz.
Recuerda que es posible conocer más sobre las canciones y su aporte cultural de los 68 pueblos indígenas que habitan en nuestro país. Y les invitamos a adentrarse en este mundo fascinante y que está al alcance de ustedes.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
El actuar imparcial de la autoridad con apego a las leyes
Aprendizaje esperado: Valora la aplicación imparcial de las normas y leyes por parte de las autoridades y analiza situaciones en las que no se cumple este criterio.
Énfasis: Valorar el ejercicio de la autoridad bajo el principio de imparcialidad y apego a las leyes.
¿Qué vamos a aprender?
En esta ocasión, hablaremos sobre cuestiones que les permitirán analizar sus ideas, conductas y acciones de la vida cotidiana. Es un tema de suma importancia para todas y todos.
Resulta muy interesante conocer cómo es el funcionamiento del mundo de la política y las autoridades del Estado, sin embargo, para dedicarse a ello, es necesario estudiar asuntos como leyes, derecho, economía y otras disciplinas sociales que parecen muy complicadas, o bien tener muchas habilidades para hablar y decir discursos que convenzan a la gente.
Pero ¿Cuál es la función de la autoridad? ¿Qué se requiere para dedicarse a esa profesión?
Lo que define a una profesión u oficio no muy sencillo, que es el de las y los servidores públicos y las autoridades del gobierno.
No cualquiera puede ocupar un puesto así, no sólo porque para ejercer un cargo público es necesario tener una gran preparación académica y tener una trayectoria de servicio social, sino que, además de todo esto, es necesario reunir una serie de habilidades, virtudes éticas y valores morales como son honradez, honestidad, empatía, solidaridad, legalidad e imparcialidad.
De todo ello tendremos oportunidad de hablar en esta sesión.
¿Qué hacemos?
Cuando hablamos de autoridad, inmediatamente pensamos en alguien que da órdenes a las demás personas y a quien tenemos que obedecer, porque se le confiere saber o poder. También hemos visto que, en un país democrático, el poder lo tiene el pueblo, por lo que no me queda muy claro cuál es el poder de las autoridades que gobiernan.
La democracia es un concepto no tan sencillo de comprender, es una forma muy evolucionada y moderna de gobierno, si lo vemos desde la perspectiva histórica. Mucho más fácil es comprender, por ejemplo, que un faraón o un rey se dedique a mandar sobre sus esclavos o vasallos, mientras que el pueblo sólo obedece a esa voluntad ajena.
Pero, en la democracia, el pueblo es el soberano, no hay nadie por encima de su voluntad, y eso hace mucho más complejo todo, porque el pueblo es, al mismo tiempo que gobernante, el gobernado que obedece a sus autoridades.
En la democracia el pueblo manda.
El filósofo griego Aristóteles decía sobre esta doble función de gobernantes y gobernados en el sistema democrático que…
“[…] se manda a los de la misma clase y a los libres. Ése decimos que es el mando político, que el gobernante debe aprender siendo gobernado, como se aprende a ser jefe de caballería habiendo servido en la misma […] Por eso se dice y con razón que no puede mandar bien quien no ha obedecido. La virtud de éstos es distinta, pero el buen ciudadano debe saber y ser capaz de obedecer y mandar; y ésa es la virtud del ciudadano: conocer el gobierno de los hombres libres bajo sus dos aspectos a la vez” Aristóteles Pol. III 4, 1227b 13-15.
Esta idea fundamenta la necesidad de que un o una buena gobernante, además de saber mandar sobre las ciudadanas y ciudadanos, debía poder también obedecerles y, principalmente, a las leyes del Estado.
También aplica al revés esa responsabilidad, y es que las ciudadanas y ciudadanos de un Estado democrático como el nuestro, debemos tener la capacidad de mandar sobre las y los gobernantes a través de las instituciones y leyes, para que ellas y ellos, a su vez, puedan conducir el país.
Suena un poco enredado esto, pero si lo pensamos detenidamente, tiene mucho sentido, ya que, en una democracia, el que gobierna es el pueblo, y también se sabe que alguna parte de la población está dedicada especialmente a desempeñar cargos de autoridad, desde la policía hasta quien presida la República. Pero supongo que unas personas tienen más autoridad que otras.
Cada puesto del gobierno tiene distintas capacidades o facultades y también diferentes obligaciones de acuerdo con su rango de responsabilidad, sin embargo, todas y todos son, finalmente, servidoras y servidores públicos, y están obligados a una serie de normas, reglamentos y leyes especiales que regulan su campo de acción y responsabilidad.
Para ayudar a saber qué tipo de obligaciones tienen las y los servidores públicos, así como las ciudadanas y ciudadanos mexicanos, les invitamos a ver y escuchar con atención el siguiente video del minuto 03:44 a 04:52:
- Las autoridades, los servidores públicos y la aplicación imparcial de la ley
https://www.youtube.com/watch?v=U7AYCrFT8kU&t=3s
Como vimos y escuchamos en el video, todas las personas, tanto ciudadanía como autoridades, tenemos el compromiso de respetar las leyes y actuar con ética y responsabilidad.
En una democracia todas y todos debemos ejercer el poder ciudadano, que es el de tomar decisiones y, como hemos visto en otras sesiones, tomar decisiones acertadas requiere de una serie de habilidades y valores que, si bien debemos poseer como ciudadanía, cuando se trata del servicio público, toman mayor importancia.
Creo que queda claro lo importante que es ser una o un buen servidor público y por qué esos puestos deben ser ocupados por personas muy bien preparadas y de gran calidad ética. ¡Y cómo no, si en sus manos están las vidas de todas y todos los mexicanos!
Sin duda, tienen una enorme responsabilidad en la vida de todas y todos. Recordemos que muchas de las funciones de las autoridades tienen que ver con asuntos como la salud, la seguridad, la economía, la vivienda, el trabajo, la educación, la alimentación, la comunicación, el transporte, la organización política, en fin. Los aspectos más sensibles de la vida de los pueblos están en manos de sus autoridades.
Es por todo esto que es tan importante elegir bien a quienes estarán representándonos o sean nuestras autoridades. Pero no sólo escoger a los mejores, sino vigilar su actuar y, ¿por qué no?, apoyarles por medio de la participación ciudadana, para que puedan realizar mejor sus encargos, como lo hemos visto en casos de emergencia, en donde la ciudadanía respalda a sus autoridades y así las y los servidores públicos pueden ser más eficaces y eficientes.
Un ejemplo, en esta situación de emergencia que hemos vivido estos meses, la participación general de la gente al quedarse en casa, usar cubrebocas y no hacer caso a la información falsa ha ayudado. Estamos actuando conjuntamente autoridades y ciudadanía, y con ello hemos podido controlar la epidemia y hasta la infodemia.
Escuchemos al maestro Renato Jiménez, que nos presenta a servidores públicos que nos causan orgullo por su heroica labor.
- Valores Servidores Públicos:
¿Qué te ha parecido? ¿Qué otros requisitos consideran deben ser necesarios para ser una o un buen servidor público?
Las autoridades están obligadas a conducirse bajo todos estos principios y hacer su trabajo de la mejor forma para el bien de todas y todos.
Gobernar y administrar el Estado para todas las personas por igual es la principal función de las instituciones democráticas. Así como no se debe discriminar a unas personas, tampoco se debe privilegiar a otras. Esto se llama imparcialidad.
Cuando acudimos a una oficina del gobierno para hacer cualquier trámite o solicitar atención, esperamos ser tratados con respeto, dignidad e igualdad.
Esto también tiene que ver con la imparcialidad.
Fallar en esto es especialmente grave cuando se trata, por ejemplo, de autoridades que imparten justicia pues, como se dice, “no se puede ser juez y parte”, o sea que no es posible fungir como autoridad cuando se tiene preferencia por alguna de las personas que están en conflicto.
Para ser una servidora o un servidor público se tienen que priorizar los intereses generales a los intereses particulares.
Cuando el interés particular de una servidora o un servidor público entra en conflicto con un interés público, se dice que hay “conflicto de intereses”. En este caso, lo más recomendable es que esa autoridad declare su conflicto y permita que alguien neutral e imparcial haga justicia o administre ese servicio. De lo contrario, siempre quedará la idea de que la resolución a la que llegue afecte a una u otra parte, ya sea por privilegiar lo privado o por hacer injusticia contra alguien, en el afán por compensar.
Es todo un reto para los ciudadanos que administran el Estado poder mantener la imparcialidad.
¿Y tú qué opinan? ¿Cuál consideran que sea el reto más difícil de las y los servidores públicos?
Veamos y escuchemos el siguiente video del minuto 00:35 a 1:47, en el que nos ampliará lo que aquí hemos expuesto.
- Los desafíos de los servidores públicos en la aplicación de la ley
https://www.youtube.com/watch?v=oHjrPt1ULh8
En un principio parece una labor muy complicada la de desempeñar un cargo en el gobierno, pero reflexionando un poco más, también es algo que debe dar mucha satisfacción, pues siendo fiel a los principios democráticos y obedeciendo las leyes, se puede ayudar a que muchas personas disfruten plenamente de sus derechos y tengan una mejor calidad de vida.
Cuando una servidora o un servidor público se comporta de forma imparcial y ética, su trabajo tiene un impacto positivo en la vida de las personas y engrandece al país.
Pero para esto debe existir una cultura de la legalidad en todas las ciudadanas y ciudadanos del país, que es el apego a las normas para tomar decisiones y realizar acciones, procurando que todo se haga con orden y racionalidad.
La cultura de la legalidad es para todas y todos, no sólo para las y los servidores públicos y autoridades o jueces. Esto quiere decir que, incluso desde la escuela, nosotros debemos practicarla haciendo caso a las normas de nuestro reglamento del salón o en nuestra familia, respetando los tiempos y espacios de todas y todos. Así como en la calle, respetando las señales de tránsito y las normas de cortesía y amabilidad que nuestra sociedad ha establecido, como ceder el paso o cruzar con precaución.
Es imprescindible seguir estos principios de forma cotidiana, recordemos que la escuela es el paso intermedio entre la casa y el espacio público y que la cultura de la legalidad comienza en el hogar y continúa en las calles.
Para apoyar lo que decimos, observen y escuchen con atención el siguiente video del minuto 01:48 a 3:13
- Los desafíos de los servidores públicos en la aplicación de la ley
https://www.youtube.com/watch?v=oHjrPt1ULh8
Es necesario reconocer que existen acciones negativas entre algunas servidoras y servidores públicos que no cumplen con estos requisitos que mencionamos.
Como malas prácticas, e incluso delitos, debemos identificar…

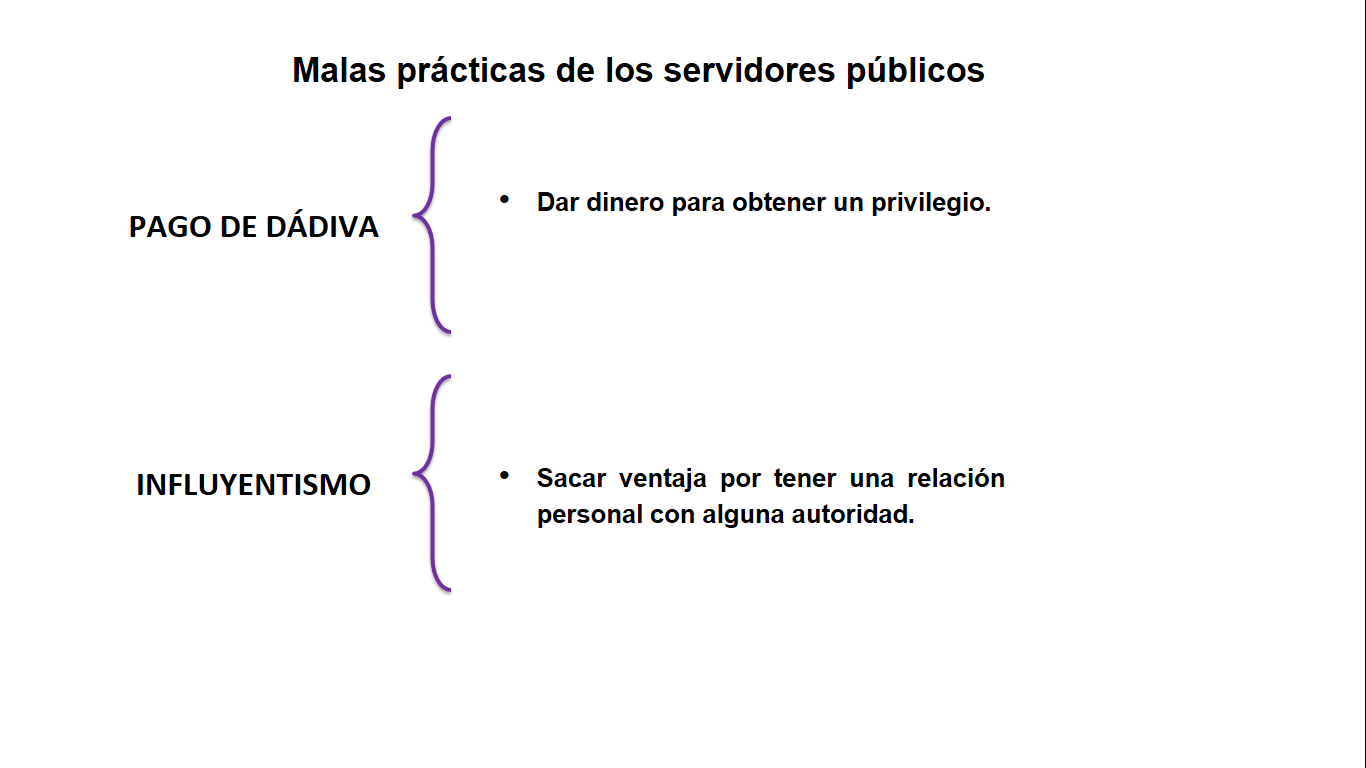
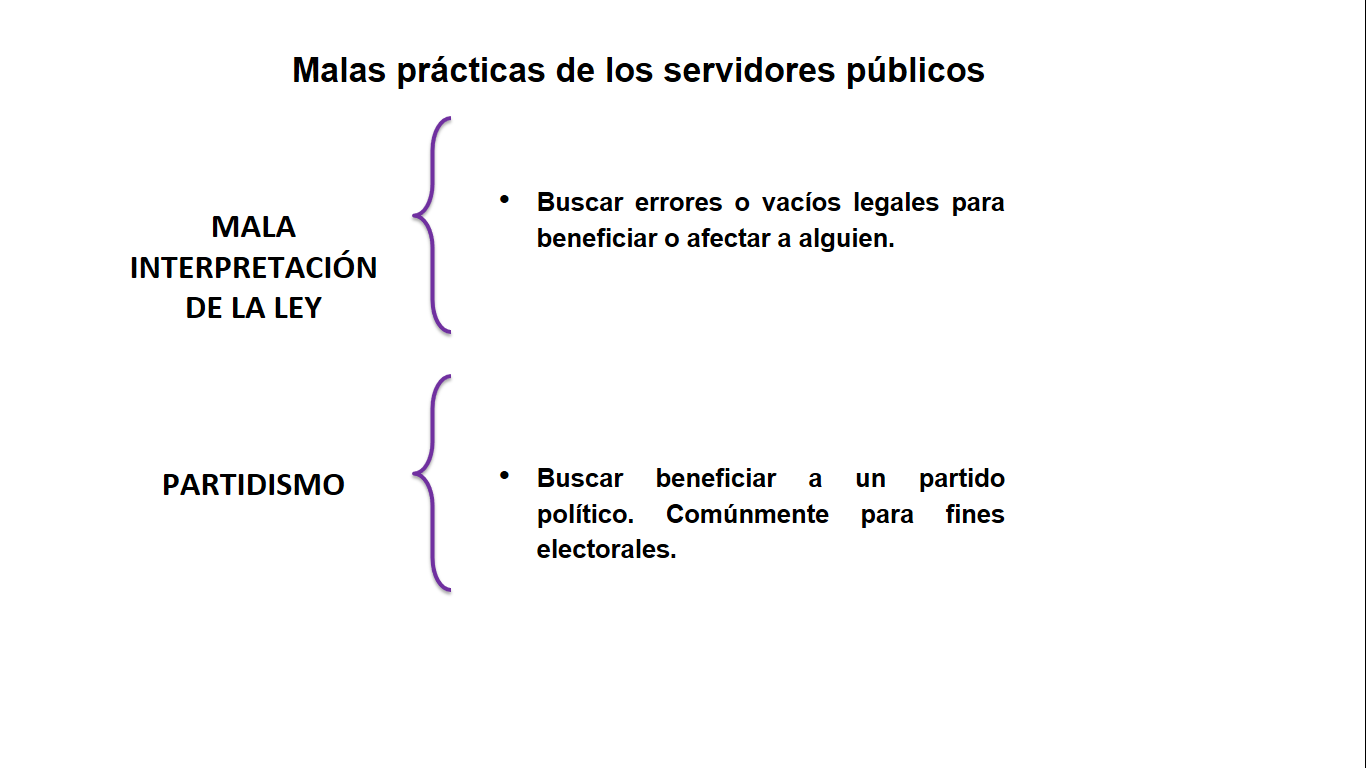

Está muy claro que, como ciudadanía, tenemos que estar muy atentos al actuar de nuestras y nuestros gobernantes, autoridades y, en general, de todas y todos los servidores públicos y también privados que participan en asuntos públicos, para que cumplan con todos los principios éticos que se requieren.
Es una tarea de todas y todos. Volviendo a la parte positiva de nuestro tema, les invito a ver el siguiente video, que nos explica cómo podemos contribuir a construir una cultura de la legalidad en las y los servidores públicos para que actúen con imparcialidad, legalidad, ética y apego a los derechos humanos.
Pongamos atención en el siguiente video del minuto 03:36 a 4:46
- Los desafíos de los servidores públicos en la aplicación de la ley
https://www.youtube.com/watch?v=oHjrPt1ULh8
Reflexionamos sobre las virtudes necesarias en autoridades y ciudadanía en el sistema democrático.
- Destacamos la enorme responsabilidad que tienen las servidoras y servidores públicos frente a todas y todos los mexicanos de conducirse con imparcialidad y ética.
- Explicamos lo que significa la cultura de la legalidad y su importancia en todos los ámbitos.
- Finalmente, resaltamos la importancia de identificar las amenazas más comunes a la legalidad e imparcialidad, así como del conocimiento y obediencia a los códigos éticos.
El Reto de Hoy:
Consulta tu libro de texto de Formación Cívica y Ética para saber más acerca de la cultura de la legalidad y valores democráticos.
Dialoga con sus familiares, amigas y amigos acerca de las diversas formas en las que pueden ejercer el poder ciudadano.
Si quieres volver a ver los programas de “Aprende en Casa III” transmitidos en semanas previas, los puedes encontrar en la siguiente página: youtube.com/aprendeencasa
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Agricultura y ganadería en la Nueva España
Aprendizaje esperado: Conoce la formación de áreas productoras de granos y cría de ganado, y su relación con los centros mineros.
Énfasis: Comprender la transformación de la producción agropecuaria en la América conquistada.
¿Qué vamos a aprender?
El tema que abordaremos es la Agricultura y ganadería en la Nueva España. Nos centraremos en comprender la transformación de la producción agropecuaria en la América conquistada.
¿Qué hacemos?
Imagina el paisaje de lo que hoy es México antes de la llegada de los españoles: piensa que en América no había especies animales como caballos, cerdos, ovejas, cabras o gallinas; tampoco había cultivos de trigo, cebada, arroz o caña de azúcar. Todas estas especies fueron introducidas en América por los españoles y tuvieron un impacto profundo en las actividades agropecuarias de la región.

Tras la conquista de los españoles, la introducción de nuevas especies vegetales y animales, hasta entonces desconocidas en Mesoamérica, produjo una serie de cambios no sólo en los medios de producción agrícola y en la alimentación de la población, sino también en el paisaje.
La introducción de especies animales y vegetales que tuvo lugar entre los siglos XV y XVI se produjo en dos sentidos: de Europa hacia América y viceversa. Algunos especialistas han denominado a este proceso intercambio colombino.
Para darnos una idea de las trasformaciones que produjo el intercambio colombino en la Nueva España, veamos y escuchemos el siguiente video.
- El paisaje de Nueva España a mediados del siglo XVI. Tercer grado. Historia II. Bloque 1
https://www.youtube.com/watch?v=hH8C2YC7WXM&list=PLNoT1XYbIfIl5RND7J9qhpQzeMteQpMvN&index=9
Gracias a la enorme extensión territorial de la Nueva España, los productos tradicionales mesoamericanos se cultivaron a la par de los introducidos por los europeos. De manera tal que los indígenas continuaron cultivando maíz, frijol, chile y calabaza para su consumo, y aprendieron a sembrar trigo, caña de azúcar, habas, garbanzo, lentejas, arroz, avena, cebada, café.
Las condiciones climáticas y la variedad de los suelos determinaron la conformación de zonas de producción.
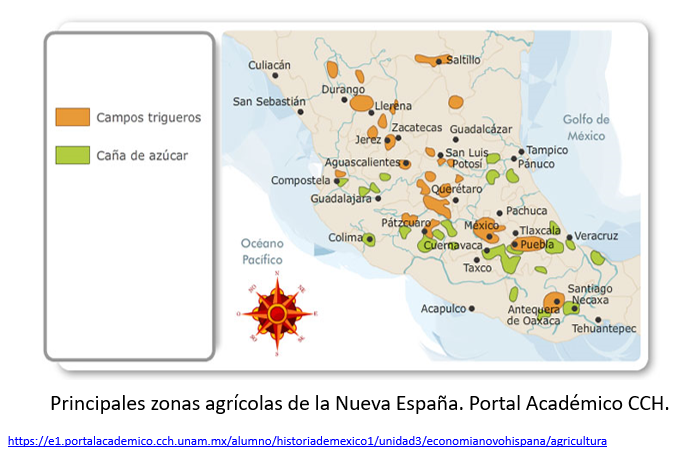
Hacia la segunda mitad del siglo XVI se desarrollaron cuatro grandes zonas trigueras: una en los valles de Atlixco y Puebla, otra en el valle de México y Toluca, otra más en el Valle de Oaxaca y la última en algunas regiones de Jalisco, Michoacán, Guanajuato y Zacatecas.
También se desarrollaron cultivos tropicales, como el plátano y la caña de azúcar en las zonas cálidas de sierras y costas. Esta última fue un producto de gran demanda que se cultivó principalmente en Cuernavaca, Atlixco, Puebla, Orizaba, Jalapa, Córdoba, Michoacán y, en menor medida, en Oaxaca y Chiapas.

Debido a la brutal explotación que padecieron los indígenas en las plantaciones de caña de azúcar, la Corona prohibió en 1631 que se empleara su mano de obra y la sustituyó por esclavos negros traídos de África.

Con la llegada de los españoles, la producción agrícola sufrió una enorme transformación, no sólo por la introducción de estos productos, sino también por el desarrollo de nuevas formas de trabajo y técnicas para la siembra, como la yunta, el arado y otros aperos de labranza. Sin embargo, esto no significa que los antiguos instrumentos indígenas y los sistemas de cultivo de milpa y chinampa dejaran de emplearse.
Recordemos que el intercambio colombino fue recíproco. Algunos de los productos indígenas que comenzaron a exportarse al mundo fueron la vainilla, el cacao y la grana cochinilla.
Este es un insecto que se cría en las nopaleras, del que se obtiene un potente colorante rojo; se utilizaba para teñir textiles, papeles y mobiliarios. Como explica el Dr. Bernardo García Martínez, la grana cochinilla se situó como la exportación más valiosa de la Nueva España después de la plata e hizo la riqueza de muchos comerciantes e intermediarios. Su cultivo se dio principalmente en los actuales estados de Tlaxcala y Oaxaca.

Observa detenidamente la siguiente imagen. Intenten responder estas preguntas:
- ¿Qué especies animales fueron introducidas por los europeos en la Nueva España?
- ¿Qué impacto tuvo la ganadería en las actividades económicas novohispanas en comparación con la época mesoamericana?

En la imagen pueden apreciar algunas actividades agropecuarias como el arado de la tierra y la cosecha de trigo; los animales que observamos son caballos y toros, pero los españoles también introdujeron ovejas, cabras, mulas, cerdos y gallinas. La introducción de estas especies permitió el desarrollo de la ganadería, gracias a la cual se transformaron la agricultura, la alimentación y los medios de trasporte. Recordemos que, durante la época prehispánica, los productos eran llevados de un lugar a otro por los tamemes.

Las principales zonas ganaderas novohispanas se concentraron en el centro y norte de la Nueva España. La introducción del ganado menor (cerdos y ovejas) y el ganado mayor (las reses) fue paulatina, y se inició desde los primeros años de la conquista.

Además de las transformaciones ya señaladas, la industria agropecuaria también impactó en las formas de tenencia de la tierra, es decir dio origen a dos tipos de propiedad en constante pugna: por un lado, estaba la propiedad comunal, que correspondía exclusivamente a los pueblos indígenas, heredada de los calpullis; y por otro, la propiedad privada de los españoles.

Agropecuario: De la agricultura y la ganadería o relacionado con ellas.
Debido a que el pastoreo y el cultivo de productos como el trigo, base de la alimentación española, requerían de grandes extensiones de tierra, fue común la práctica de apropiación de territorios pertenecientes a comunidades indígenas. Los españoles llegaron a formar verdaderos latifundios dentro de los cuales construyeron sus haciendas.
¿Quieren saber más sobre la industria agropecuaria novohispana y cómo se procesaban algunos productos? Acompáñennos a ver y escuchar el siguiente video.
- Molinos novohispanos. INAH TV.
https://www.youtube.com/watch?v=O6lXN63Gb-k
Para darnos una idea de cómo funcionaban las haciendas novohispanas, y como parte de nuestra sección de Leer para Reconocernos, les voy a leer un fragmento del texto “El abasto urbano: caminos y bastimentos”, de Ivonne Mijares, contenido en el tomo II de Historia de la vida cotidiana en México. Dice así:
“La hacienda era ante todo una unidad de producción autosuficiente, ya que junto con los artículos comerciales producía prácticamente todos los insumos que necesitaba para su funcionamiento: maíz, chile, frijol, carne y productos lácteos para alimentar a sus trabajadores, animales de tiro y de carga para las labores agrícolas y transporte, además de cueros, lana, sebo, leña y carbón que cubrían otras necesidades.
Esto era posible porque las haciendas abarcaban grandes extensiones territoriales en las que había tierras de regadío, que generalmente se reservaban para los cultivos comerciales; tierras de temporal, donde se sembraba maíz y otros productos de consumo interno, además una zona de pastizales que, en el caso de las haciendas de ganado mayor, llegaba a ser enorme; a esto se podían agregar montes, bosques, canteras, manantiales o ríos.
También disponían de una amplia infraestructura que solía comprender canales de riego, represas, trojes, graneros, molinos, establos, caballerizas, corrales, ingenios, obrajes y talleres de diferentes clases, además de la iglesia y las casas de cal y canto para el dueño y su mayordomo, y de abobe para sus trabajadores.
[…] Las grandes haciendas contaban con tiendas en las que se vendía de fiado a los trabajadores todo tipo de mercancías; se les llamaba “de raya” porque se marcaba con ese símbolo las deudas que se iban adquiriendo. Estos establecimientos, que dependían del hacendado, podían constituir una verdadera ayuda para las familias campesinas o convertirse en el instrumento para mantenerlas atadas a la propiedad.
Las haciendas operaban con diferentes tipos de trabajadores. En primer lugar, estaban los peones o trabajadores permanentes, por lo general, de origen indígena, que vivían con sus familias en casas especialmente construidas para ellos dentro de la hacienda; se dedicaban sobre todo a las labores agrícolas, y el pago de sus salarios se hacía en dinero, en especie o en una combinación de ambos; también podían recibir una parcela para sembrar y complementar sus ingresos. Después estaban los trabajadores especializados, como cañaveleros (expertos en la siembra de caña), cacahueros (cultivadores de cacao), vaqueros, arrieros, herreros, carpinteros, curtidores, etc., que vivían un poco mejor que los anteriores y podían ser desde españoles pobres hasta negros esclavos, pasando por mestizos, negros libres y mulatos.
[…] Cuando los dueños no administraban personalmente su propiedad, lo cual era bastante frecuente, la responsabilidad del funcionamiento de la hacienda era dejada en manos de mayordomo, persona de toda la confianza del hacendado, quien, con ayuda de capataces y otros sirvientes, controlaba todo lo que sucedía en su interior.”
Después de leer el texto, podemos inferir que las haciendas conformaban verdaderos pueblos habitados por cientos de personas. La vida para los trabajadores no era fácil, muchos fueron forzados a permanecer en ellas por las prácticas de endeudamiento. El sistema de explotación que se vivía al interior de las haciendas se perpetuó, casi sin cambios, hasta el Porfiriato.
Antes de finalizar, debemos recordar que el intercambio colombino ocurrió entre los siglos XV y XVI, y consistió en la introducción de nuevos cultivos y especies animales a la Nueva España y en la exportación hacia Europa de otros productos de origen mesoamericano. Dicho intercambio dio paso a una serie de transformaciones en las técnicas de cultivo, en la alimentación, en la tenencia de la tierra y en el paisaje.
La industria agropecuaria fue fundamental para el desarrollo económico de la Colonia, y estuvo estrechamente relacionada con la minería, la actividad económica más importante de la Nueva España.
El Reto de Hoy:
Te recordamos que el reto planteado la sesión anterior fue la redacción de una receta que recupere elementos tanto de la tradición indígena como de la hispana.
Ya que han elegido el platillo típico de su región, e identificado el origen de los ingredientes a través de un cuadro de doble entrada como el que ven en pantalla, es hora de escribir la receta, para ello pueden recurrir a su familia.

Además de describir los ingredientes, las cantidades y el procedimiento para la elaboración de su platillo, incluyan un apartado en el que expliquen cómo se transportaban y/o producían los ingredientes. Es decir, en el caso de productos importados, deberán especificar si provenían de Asia o de Europa y a través de qué ruta llegaban a la Nueva España; si se trata de un ingrediente procedente del interior del virreinato, deberán señalar las condiciones alrededor de su producción, como el funcionamiento de las haciendas.
No olviden compartir su receta con su maestra o maestro. Estamos seguros de que, con esta actividad, les sorprenderá descubrir lo diversa y variada que es nuestra gastronomía.
¿Quieren saber mientras tanto qué pasaba en el mundo?
En 1542, tras la caída del Imperio inca, se estableció el virreinato del Perú. Al igual que ocurrió en la Nueva España, la minería fue la base de su economía, en torno a las minas peruanas florecieron las haciendas agropecuarias. Algunos de los productos originarios que se continuaron cultivando tras la conquista fueron el olluco y la coca.
Además de su libro de texto y el tomo II de Historia de la vida cotidiana en México, los invitamos a consultar otras fuentes bibliográficas, digitales y audiovisuales que tengan a la mano, por ejemplo, pueden acceder al portal académico del Colegio de Ciencias y Humanidades, en la sección de “Economía novohispana”, específicamente les recomendamos los apartados de agricultura y ganadería.
Otro texto que les recomendamos leer es Animales del nuevo mundo, de Miguel León Portilla, que podrán encontrar en los Libros del Rincón. En él, el autor recupera las descripciones de siete animales del siglo XVI hechas por los mismos indígenas. Tengamos en cuenta que no sólo llegaron nuevas especies animales a la Nueva España, los europeos también se encontraron con especies que nunca habían visto.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Gestión y vida cotidiana
Aprendizaje esperado: Usa diferentes técnicas de planeación y organización para la ejecución de los procesos técnicos.
Énfasis: Reflexionar sobre las situaciones de la vida cotidiana en las que se utiliza la gestión técnica.
¿Qué vamos a aprender?
Es tiempo de reflexionar de cómo utilizar las técnicas de planeación y organización para la ejecución de los procesos técnicos.
Tendremos una sesión muy interesante ya que hablaremos de gestión y vida cotidiana, recordando lo que ya hemos visto en diferentes sesiones.
Podremos reflexionar sobre las situaciones de la vida cotidiana en las que se utiliza la gestión técnica.
¿Qué hacemos?
Realizaremos una actividad de preguntas y respuestas con las alumnas y alumnos; a dicha actividad la llamaremos, “historia de la gestión técnica”.
La dinámica es la siguiente:
Realizaremos una pregunta asociada al tema y posteriormente, las alumnas y los alumnos darán respuesta a la pregunta planteada.
¿Qué es un cursograma?
- VIDEO. TEC2_B4_PG2_V1_SEM31_a030321 Cursograma.mp4
Efectivamente, en el cursograma podemos señalar paso a paso el proceso técnico de un producto o servicio.
Además, nos ayuda para que, si en un futuro se requiere repetir el proceso de la elaboración de un producto o servicio, se pueda controlar sin ningún problema.
Siguiente pregunta: En un cursograma ¿Cuáles son las diferentes fases de un proceso y con qué símbolos se representan?
- VIDEO. Respuesta de Ademar, veamos qué nos dice:
Sigamos con la siguiente pregunta:
¿Qué tipos de cursograma conoces y cuáles son sus características?
- VIDEO Respuesta de Lesly.
Continuemos, ¿Qué es una lista de cotejo?
- VIDEO. Yaretzi nos dice que:
Nos mandó un ejemplo, de la que utilizan en su clase de Tecnología con énfasis en Confección del Vestido e Industria Textil.
¿Cuál es la utilidad de la planeación?
- VIDEO. María Fernanda nos dice que:
Un ejemplo de planeación, sería el de una empresa de ropa de playa que quiere incursionar en la fabricación de ropa deportiva, primero tiene que hacer un diagnóstico de necesidades para detectar qué es lo que se requiere en este rubro, qué problemas está generando y después escoger la más viable para dar solución a este problema, se tendrá que definir el objetivo, y todo lo que se necesita para elaborar el sistema técnico: los insumos, herramientas, recursos humanos, maquinaria. Realizar la representación gráfica del producto, y elaborar el diagrama del proceso técnico.
¿Para qué nos sirve un plan de trabajo?
- VIDEO. Osiel, veamos qué nos dice:
¿Cuáles son los elementos del plan de trabajo?
- VIDEO. Martha nos envía un mensaje de texto y nos dice que son:
- Objetivo
- Representación gráfica
-Definición de etapas del proceso técnico
- Definición de responsables
- Presupuesto
- Cronograma
- Materiales y proveedores
La siguiente pregunta es ¿Cuáles son los instrumentos para el control del proceso técnico?
- VIDEO. Ángel y nos dice que son:
Para que nos quede más claro veamos una imagen de un cursograma sinóptico y otro ejemplo de la lista de cotejo.


Ya casi terminamos, veamos ésta: ¿Que son las normas de seguridad e higiene?
- VIDEO: Miguel nos mandó un mensaje de audio con la respuesta. Escuchémoslo:
¿Qué es un proceso técnico?
- VIDEO. Elizabeth nos manda la siguiente respuesta por correo electrónico:
¿Cuál es la utilidad de las normas de higiene y seguridad en el trabajo?
- VIDEO_ utilidad de las normas
“Menciona 5 posibles causas de accidentes durante el desarrollo de un proceso técnico”.
- VIDEO. Fernanda y nos dice lo siguiente:
Además, son muy útiles porque permiten controlar los tiempos en los que cada acción debe ser realizada, pues, una actividad que no tiene fecha de entrega no se termina.
¿Qué significa la simbología OTIDA utilizada en el cursograma?
Respuesta de Yima, nos manda un video donde nos muestra los apuntes que ha hecho en su cuaderno, ¡adelante! Veámoslo:
- VIDEO Yima:
Veamos el siguiente video para que nos quede más claro.
- OTIDA.pptx
Repasamos algunos puntos de la gestión técnica, recordando que ésta tiene como propósito organizar y coordinar todos los recursos disponibles, humanos, insumos y tiempos para la producción de un producto o servicio y se deben seguir una serie de pasos, como la planeación, organización, ejecución, control y evaluación del proceso técnico, para obtener un bien o servicio con éxito.
También recordemos que, dentro de los procesos, surgen algunos imprevistos y que tenemos que prever alguna solución, y estar preparados para ello.
Veamos por ejemplo cómo en Confección del Vestido e Industria Textil se utiliza la gestión técnica, ya que se planea, organiza, controla y evalúa cada uno de los procesos de la confección de una prenda. Es necesario tener conocimiento del campo tecnológico, posteriormente se hace la elección de la vestimenta que se ve a confeccionar: vestido, falda, blusa entre otros.
Ya que se seleccionó la prenda y el modelo, se enlistan todos los insumos que se van a utilizar, elección de la tela para la prenda, hilos, botones, cierres entre otros; se seleccionan los medios técnicos que intervendrán en el proceso como tijeras, máquinas de coser y se enumeran las acciones que conforman cada uno de los procesos técnicos como el trazo de la prenda, elaboración de patrones, corte de piezas, marcado de costuras, hilvanado de piezas, prueba de prenda, costura a máquina y terminados, se destinan tiempos y responsables y se desarrolla un plan de trabajo con todos estos elementos.
Después de que se ha planeado el proceso técnico, se organiza para poder llevarlo a cabo y se controla mediante un cursograma o lista de cotejo, así las alumnas y alumnos conocen el orden de las acciones y los tiempos para cada una de ellas, cumpliendo con éxito el objetivo.
Otro ejemplo, es la planeación de una fiesta donde tenemos que partir desde la fecha, el lugar donde se realizará el evento, presupuesto, organización, invitados, entre otros.
O la planeación de unas vacaciones, donde tenemos que ver qué lugar visitaremos, presupuesto, cuántos días, a dónde vamos a llegar a hospedarnos, que recorridos haremos, etcétera.
O la construcción de una casa donde tenemos que partir del terreno, necesidades de la familia, presupuesto, proyecto arquitectónico, permisos, materiales, tiempo de ejecución entre otros.
Te invitamos a integrar a su glosario técnico, los conceptos que vimos en la sesión de hoy, que no hayan agregado anteriormente. Te recuerdo cuáles son:
- Cursograma
- Plan de trabajo
- Proceso técnico
- Higiene y seguridad
El Reto de Hoy:
Si quieres volver a ver los programas de Aprende en casa transmitidos en semanas previas, los puedes encontrar en la página: youtube.com/aprendeencasa
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon




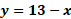

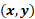





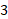





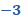


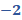


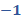



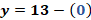
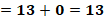

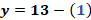


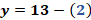
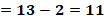

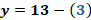







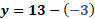
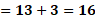
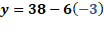
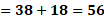
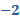


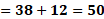

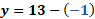
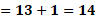
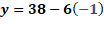
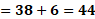
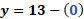

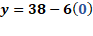


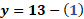
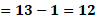

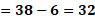

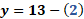

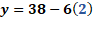


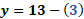
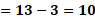
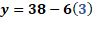
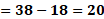






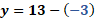
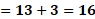
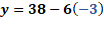

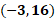

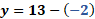

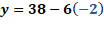
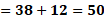


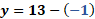

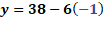


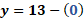
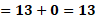


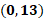

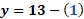

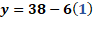

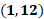


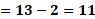


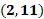


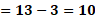

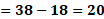
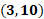






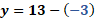


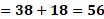

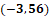
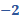
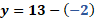
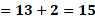

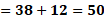
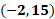
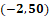


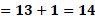


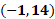
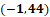

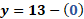

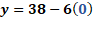
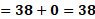
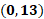
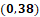


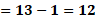
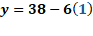
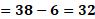

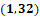

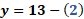

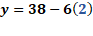
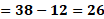
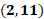
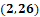

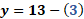

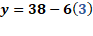
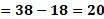

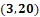

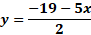


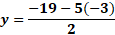
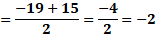

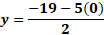
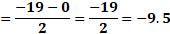

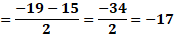

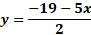
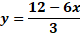
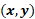

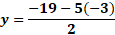

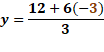

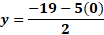
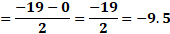
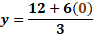

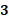


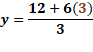
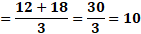

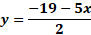
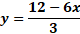
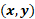
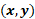
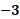


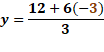
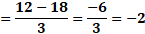
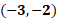
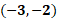

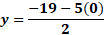
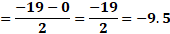
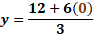
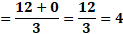
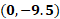
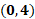
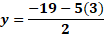
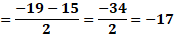
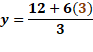
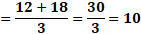
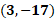
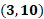








Publicar un Comentario