Aprende en Casa III SEP: 6 de mayo TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 6 de mayo de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.
Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Jueves 6 de mayo, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa III:
https://aprendeencasa.sep.gob.mx/#
El método adecuado III
Aprendizaje esperado: Resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.
Énfasis: Resolver problemas mediante sistemas de dos ecuaciones lineales con dos incógnitas.
¿Qué vamos a aprender?
En esta sesión continuarás aprendiendo a resolver sistemas de dos ecuaciones lineales con dos incógnitas, ahora mediante el método más conveniente.
Ten a la mano tu cuaderno u hojas para tomar notas y tú lápiz o bolígrafo y una goma.
Para fortalecer lo aprendido, ampliarás el conocimiento y se aclararán dudas. Asimismo, se precisarán algunos aspectos necesarios para resolver un sistema de dos ecuaciones lineales con dos incógnitas mediante el método más conveniente.
Has aprendido que los valores desconocidos de un sistema de dos ecuaciones lineales con dos incógnitas se pueden representar mediante las literales “x” y “y”, entre otras. El valor de cada una de las incógnitas, en este caso de “x” y de “y”, debe ser el mismo en ambas ecuaciones para que se cumplan las igualdades.
Recuerda que durante el ciclo escolar se han modelado situaciones mediante sistemas de dos ecuaciones lineales con dos incógnitas y resuelto esos sistemas empleando el método gráfico, el método de sustitución, el de igualación, así como el de suma y resta, algunos de los cuales se retomarán en esta sesión.
Se iniciará con la primera situación.
También sabes que debes plantear el sistema de ecuaciones lineales con dos incógnitas, con base en los datos identificados en el problema propuesto.
Revisa el siguiente problema:
La suma del cuádruple de un número y el cuádruple de otro es igual a 100; se sabe que el cuádruple del primero menos el cuádruple del segundo es igual a 60. ¿Cuáles son esos dos números?
Primero se plantea el sistema que representa al problema y así se obtiene el sistema:
4 “x” más 4 “y” igual a 100.
4 “x” menos 4 “y” igual a 60.
En donde “x” representa al primer número y “y” representa al segundo número.
Ya que tienes identificadas las incógnitas “x” y “y”, así como el sistema de ecuaciones lineales con dos incógnitas, a partir de este paso el procedimiento será diferente, ya que dependerá del método que elijas utilizar para la resolución de ese sistema.
¿Cuál método de resolución elegirías y por qué?
Toma notas de tus dudas y consúltalas con tu profesora o profesor, si te es posible.
Ahora, se resolverá un problema mediante el planteamiento de un sistema de dos ecuaciones lineales con dos incógnitas, y se decidirá cuál es el método más apropiado para determinar los valores de las incógnitas.
Piensa en la siguiente situación:
Se construye un cuadro con tiras de madera iguales. Se desconocen las medidas del largo y del ancho de esas tiras. Así que se le llamará “x” a la medida del largo y “y” a la del ancho.
Las tiras se acomodan como se muestra en la siguiente figura, se sabe que el perímetro del cuadrado exterior es de 100 centímetros y el del cuadrado interior de 60 centímetros. ¿Cuánto mide el largo de las tiras? ¿Y cuánto mide el ancho de las tiras?
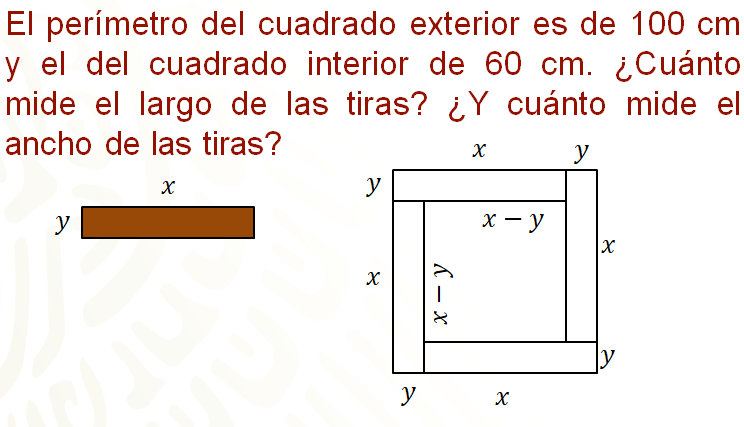
Una manera de iniciar la resolución del problema es responder primero la pregunta: ¿cuánto miden los lados del cuadrado exterior y cuánto los del interior?
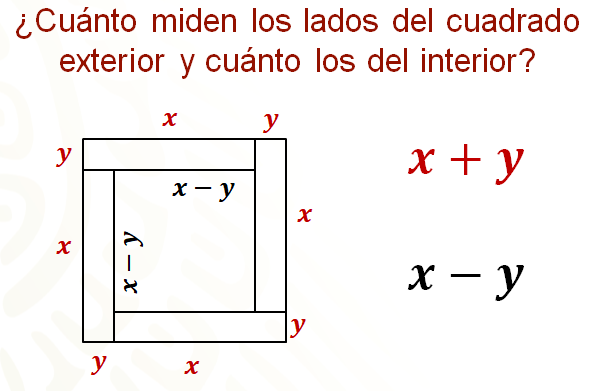
Seguramente, ya sabes cómo resolver el problema.
Al observar la figura, con las tiras de madera de “x” centímetros de largo y “y” centímetros de ancho, puedes ver que los lados del cuadrado exterior miden “x” más “y” y los del cuadrado interior “x” menos “y”.
¿Cómo representarías el perímetro de ambos cuadrados?
Como uno de los datos que se tienen es la medida del perímetro, tanto del cuadrado exterior como del interior, se tomará esa medida para plantear las ecuaciones del sistema. Recuerda que una manera de calcular el perímetro de un cuadrado es usando la fórmula perímetro igual a 4 por lado.
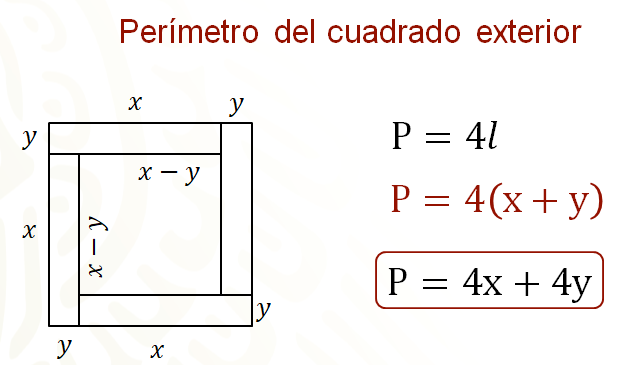
Al sustituir “x” más “y” en la fórmula tienes: perímetro igual a 4 por, abre paréntesis, “x” más “y”, cierra paréntesis. Entonces el perímetro es igual a 4 “x” más 4 “y”.
La expresión anterior representa el perímetro del cuadrado exterior.
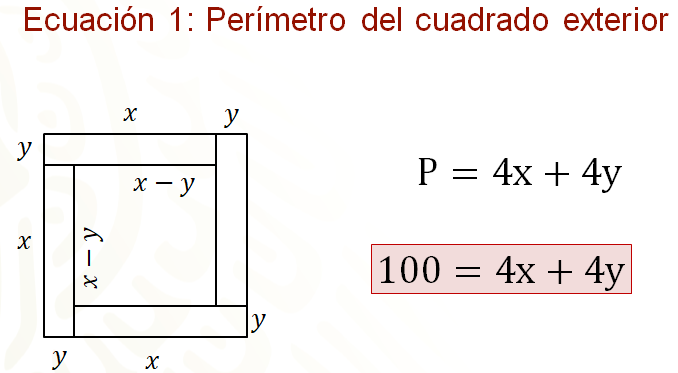
Recuerda que el perímetro del cuadrado exterior es de 100 centímetros; por lo tanto, la ecuación 1, que representa el perímetro del cuadrado exterior queda 100 igual a 4 “x” más 4 “y”.
Ahora, se va a representar el perímetro del cuadrado interior.
A partir de la fórmula para calcular el perímetro del cuadrado, que es perímetro igual a 4 por lado, se sustituye lo que representa el lado y se tiene que el perímetro es igual a 4 por, abre paréntesis, “x“ menos “y“, cierra paréntesis. Luego, perímetro igual a 4 “x“ menos 4 “y”.
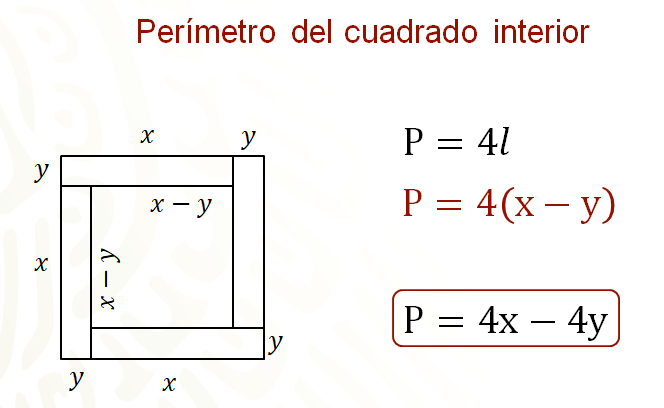
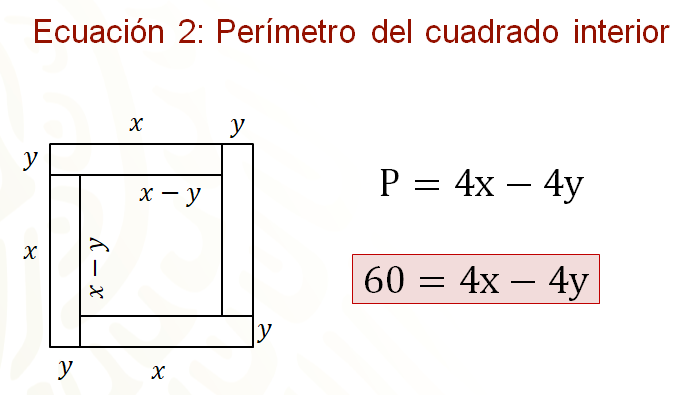
Entonces, esta expresión representa el perímetro del cuadrado interior, pero no olvides que el perímetro del cuadrado interior es de 60 centímetros, por lo tanto, la ecuación dos queda definida como 60 igual a 4 “x” menos 4 “y”.
¿Cuál es el sistema de ecuaciones que representa ambos perímetros?
Seguramente ya tienes la respuesta, compara, analiza y registra tus dudas e inquietudes para que las compartas con tu maestra o maestro de esta asignatura.
El sistema de dos ecuaciones lineales con dos incógnitas que permite resolver esta situación es: 4 “x” más 4 “y” igual a 100, que es la ecuación uno y 4 “x” menos 4 “y” igual a 60, que es la ecuación dos.
Ahora, se encontrarán los valores de “x” y “y” para saber las dimensiones de las tiras de madera que son los lados de los cuadrados.
¿Qué método utilizarías para resolver el sistema de ecuaciones? ¿Por qué?
Al observar las ecuaciones puedes darte cuenta de que la variable “y” tiene coeficientes simétricos, por lo que se puede eliminar rápidamente dado que su suma es cero. De acuerdo con lo anterior, se puede decir que el método más conveniente para resolver este sistema es el de suma y resta.
Una vez decidido este método para resolver el sistema, se suma la ecuación uno más la ecuación dos, de donde se tiene 4 “x” más 4 “x” igual a 8 “x”; 4 “y” menos 4 “y” igual a cero; 100 más 60 igual a 160. De esta manera se obtiene la ecuación 8 “x” igual a 160.
Ahora, divides ambos miembros de la ecuación entre 8 para obtener 1 como coeficiente de “x”. Por lo tanto, tienes 8 “x” entre 8 igual a 160 entre 8. De esto se obtiene que “x” es igual a 20.
¿Recuerdas qué representa “x” en esta situación?
“x” representa la medida del largo de las tiras de madera con que se formó el cuadrado.
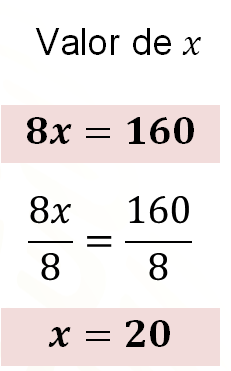
Ahora, puedes sustituir el valor de “x” igual a 20 en cualquiera de las ecuaciones originales. Se hará en la ecuación 1, que es 4 “x” más 4 “y” igual a 100. De donde se obtiene la expresión 4 por 20 más 4 “y” igual a 100.
Como 4 por 20 es igual a 80 se tiene 80 más 4 “y” igual a 100. Ahora suma el inverso aditivo de 80 en ambos miembros de la ecuación, de donde se obtiene 80 negativo más 80, más 4 “y” igual a 100 más 80 negativo. De lo anterior se obtiene 4 “y” igual a 20. Luego, divides ambos miembros de la ecuación entre el coeficiente de “y” que es 4; por lo tanto, ahora se tiene “y” igual a 5.
¿Recuerdas qué representa “y” en esta situación?
“y” representa la medida del ancho de las tiras de madera con que se formó el cuadro.
Ahora, se determinará si los valores obtenidos para “x” y “y” son correctos. Para ello, se sustituyen los valores de “x” y “y”, en la ecuación 1, que es 4 “x” más 4 “y” igual a 100, quedando 4 por 20 más 4 por 5 igual a 100. De acuerdo con la jerarquía de las operaciones, primero se resuelven las multiplicaciones, por lo que se obtiene 80 más 20 igual a 100. Al sumar 80 más 20 se obtiene 100; por lo tanto, se obtiene una identidad y se puede afirmar que dichos valores hacen verdadera la ecuación 1.
Para la ecuación 2 se tiene 4 “x” menos 4 “y” igual a 60, se sustituyen los valores de “x” y “y” quedando 4 por 20 menos 4 por 5 igual a 60. De esto se obtiene 80 menos 20 igual a 60. Al restar 80 menos 20 se obtiene 60; por lo tanto, también se obtiene una identidad y se puede afirmar que dichos valores hacen verdadera la ecuación 2; es decir, los valores de “x” y “y” son correctos.
Para finalizar esta situación, recuerda que el largo de las tiras fue representado por “x” y el ancho por “y”.
Ahora, responde las preguntas:
¿Cuánto mide el largo de las tiras?
Se puede afirmar que el largo de las tiras mide de 20 centímetros.
¿Cuánto mide el ancho de las tiras?
El ancho de las tiras mide 5 centímetros.
Se ha resuelto el sistema de dos ecuaciones lineales con dos incógnitas, usando el método de suma y resta. Pero, ¿qué hizo que se tomará la decisión de utilizar este método y no otro?
Por lo que se decidió utilizar este método es que una de las incógnitas, en este caso “y”, tiene coeficientes simétricos en las ecuaciones originales, lo que permitió eliminarlas al sumar ambas ecuaciones para obtener una ecuación con una incógnita.
De manera general, se puede decir que para aplicar el método de suma y resta al resolver un sistema de dos ecuaciones lineales con dos incógnitas es necesario ver si alguna de esas incógnitas tiene coeficientes simétricos, o realizar cálculos para que esto ocurra.
Ahora, hay que resolver otra situación problema.
Se tienen dos cartulinas rectangulares con las dimensiones que se muestran en las siguientes figuras.
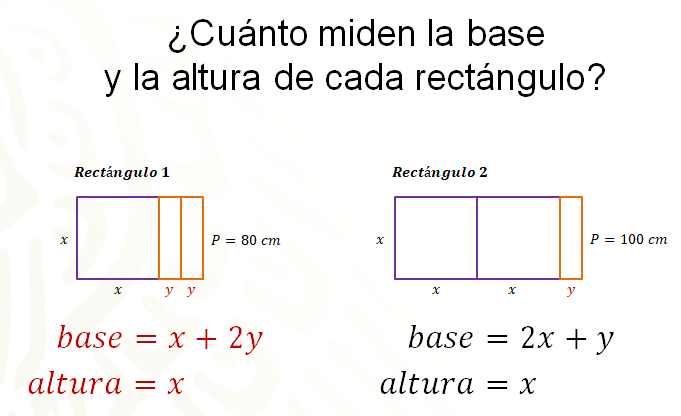
Si el perímetro de la primera es de 80 centímetros y el de la segunda es de 100 centímetros, ¿cuánto miden la base y la altura de cada rectángulo?
Por el momento, al observar las figuras sabes que la base del rectángulo 1 es igual a “x” más 2 “y” y su altura es igual a “x” para el rectángulo 2, la base es igual a 2 “x” más “y” y su altura es igual “x”.
Ahora, se representará algebraicamente el perímetro de cada rectángulo.
Primero, se hará la representación algebraica del perímetro del rectángulo 1. Utiliza la fórmula de perímetro igual a 2 por base más 2 por altura.
Entonces, el perímetro es igual a 2 por, abre paréntesis, “x” más 2 “y”, se cierra paréntesis, más 2 por “x”.
De esto se obtiene que el perímetro es igual a 2 “x” más 4 “y”, más 2 “x”, y al reducir términos semejantes el perímetro del rectángulo 1 es igual a 4 “x” más 4 “y”.
Como sabes que el perímetro de esta figura es de 80 centímetros; entonces, la ecuación uno del sistema, que te ayudará a encontrar las dimensiones de las figuras, queda definida como 4 “x” más 4 “y” igual a 80.
Ahora, la representación algebraica del perímetro del rectángulo 2 queda como perímetro igual a 2 por, abre paréntesis, 2 “x” más “y”, se cierra paréntesis, más 2 por “x”. De aquí se obtiene que perímetro es igual a 4 “x” más 2 “y” más 2 “x”. Luego, reduciendo términos semejantes, se obtiene que el perímetro del rectángulo 2 es igual a 6 “x” más 2 “y”.
Como sabes que el perímetro de esta figura es de 100 centímetros; entonces, la ecuación dos del sistema, que te ayudará a encontrar las dimensiones de las figuras, queda definida como 6 “x” más 2 “y” igual a 100.
Pero, ¿cuál es el sistema de ecuaciones que representa ambos perímetros?
Seguramente ya tienes la respuesta. Compara y analiza tus respuestas, registra tus dudas e inquietudes para que las compartas con tu maestra o maestro.
El sistema de dos ecuaciones lineales con dos incógnitas que permite resolver esta situación es: 4 “x” más 4 “y” igual a 80, que es la ecuación 1, y 6 “x” más 2 “y” igual a 100 que corresponde a la ecuación 2.
Ahora, hay que encontrar los valores de “x” y “y” para saber las dimensiones de los rectángulos.
Para ello, ¿qué método utilizarías para resolver el sistema de ecuaciones? ¿Por qué?
Recuerda que algo a considerar para elegir el método con el cual resolver un sistema de dos ecuaciones lineales con dos incógnitas es observar las características de las ecuaciones para decidir lo que puedes hacer.
En este sistema, por ejemplo, se puede observar que todos los términos, en ambas ecuaciones, son múltiplos del menor coeficiente que aparece en cada una de ellas.
Para la ecuación 1, todos los términos son múltiplos de 4, que es el coeficiente menor y que corresponde a “x” y a “y”. En el caso de la ecuación 2, todos los términos son múltiplos de 2, que es el coeficiente menor, y que corresponde a “y”. Por ello, al despejar la incógnita con el coeficiente menor, en este caso “y”, en esas ecuaciones se tendría una igualdad con coeficientes enteros, lo que facilitaría los cálculos.
Considerando lo anterior, ahora se elegirá el método de igualación en el que se debe despejar la misma incógnita en ambas ecuaciones para luego igualar las expresiones obtenidas en esos despejes. Entonces, despejando “y” en ecuación 1 se tiene que 4 “x” más 4 “y” igual a 80, sumas el inverso aditivo de 4 “x” en ambos miembros de la ecuación. Al operar se obtiene 4 “y” igual a 80 menos 4 “x”. Luego, se dividen ambos miembros de la ecuación entre el coeficiente de “y” que es 4, de donde se obtiene “y” igual a “x” negativa más 20.
Ahora, despejando “y” en la ecuación 2, que es 6 “x” más 2 “y” igual a 100, se suma el inverso aditivo de 6 “x” en ambos miembros de la ecuación y se reducen los términos semejantes, por lo que se obtiene 2 “y” igual a 100 menos 6 “x”. Luego, divides ambos miembros de la ecuación entre el coeficiente de “y”, que es 2, por lo que se obtiene “y” igual a 3 “x” negativa más 50.
Ahora, se debe igualar lo obtenido en los despejes de “y”, por lo que se tiene “x” negativa más 20 igual a 3 “x” negativa más 50.
Aplicando la transposición de términos, es decir, la manipulación algebraica para despejar la incógnita, se obtiene “x” negativa más 3 “x” igual a 50 menos 20. De donde se obtiene 2 “x” igual a 30.
Ahora, se dividen ambos miembros de la ecuación entre el coeficiente de “x” que es 2, por lo que se obtiene que “x” es igual a 15.
Ahora, sustituyendo el valor de “x” en la expresión “y” igual a “x” negativa más 20, que es una igualdad obtenida de la ecuación 1, se tiene que “y” es igual al simétrico de 15, más 20, por lo que “y” es igual a 5.
Por lo tanto, el valor de “x” es igual a 15 y el valor de “y” es igual a 5.
Pero, ¿cómo puedes estar seguro de que esos valores son correctos?
Hay que comprobarlo, sustituyendo los valores en ambas ecuaciones.
En la ecuación uno, 4 “x” más 4 “y” igual a 80, se tiene 4 por 15 más, 4 por 5 igual a 80.
Al multiplicar obtienes 60 más 20 igual a (80). Sumando 60 más 20 se obtiene 80, por lo tanto, se tiene una identidad y se puede afirmar que dichos valores hacen verdadera la ecuación uno.
Para la ecuación dos, 6 “x” más 2 “y” igual a 100, sustituyes los valores de “x” y “y”, ahora tienes 6 por 15 más 2 por 5 igual a 100. Luego de calcular los productos, la igualdad es 90 más 10 igual a 100.
Como 90 más 10 es igual a 100, se obtiene una identidad y se puede afirmar que los valores de “x” y “y” también hacen verdadera la ecuación dos, por lo tanto, se puede decir que los valores obtenidos para “x” y para “y” son correctos.
Siempre se recomienda hacer la comprobación en ambas ecuaciones para estar seguro de que los valores de “x” y “y” sean correctos.
Entonces, ¿cuánto miden la base y la altura de cada rectángulo?
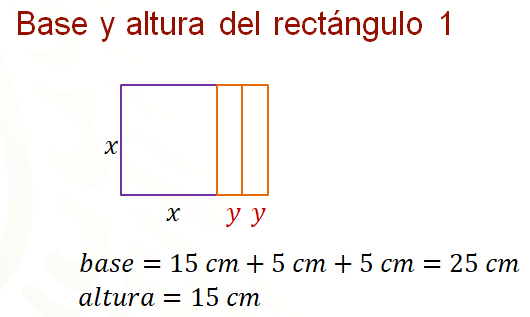
Sustituyes los valores de “x” y de “y”, de manera que para el rectángulo 1, la base es igual a 15 centímetros más 5 centímetros, más 5 centímetros igual a 25 centímetros y la medida de la altura, que es igual a “x” es de 15 centímetros.
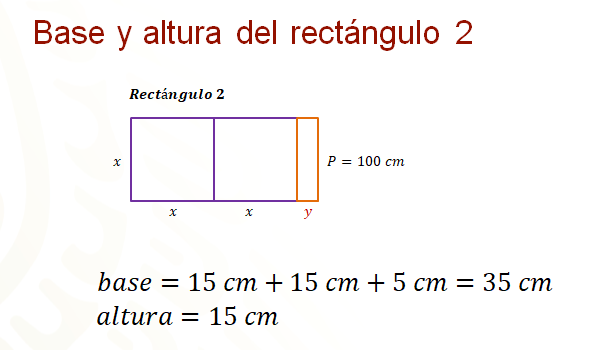
Para el rectángulo 2, la base es igual a 15 centímetros más 15 centímetros, más 5 centímetros. De donde se obtiene que la base mide 35 centímetros y la medida de la altura es de 15 centímetros.
Se ha resuelto la situación problema, registra tus dudas, inquietudes y dificultades que hayan surgido y no olvides compartirlas con tu profesora o profesor.
Ahora, se mostrarán tres sistemas de dos ecuaciones lineales con dos incógnitas para analizar cuál método sería más adecuado utilizar para resolverlos. Las cuales se presentan en la siguiente tabla, donde se debe colocar los sistemas de ecuaciones en la primera columna y el método más conveniente en la segunda.
Se iniciará con el sistema de ecuaciones formado por 4 “x” menos 2 “y” igual a cero y “y” igual a “x” más 3.
¿Qué método piensas que es el más adecuado para resolver este sistema?
Dado que en una ecuación ya se encuentra despejada la “y” puedes pensar que el método más conveniente para resolver este sistema es el método de sustitución.
Ahora, para el sistema formado por 3 “x” menos 2 “y” igual a 1 negativo y 8 “x” más “y” igual a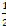 
, ¿qué método piensas que es el más adecuado para resolverlo?
Puedes pensar que el método de sustitución podría ser el más adecuado, y habría que despejar una de las incógnitas en una ecuación para sustituir su valor en la otra.
También se podría utilizar el método de suma y resta, y para aplicarlo podrías multiplicar una ecuación por un número que te arrojara una ecuación equivalente con un coeficiente simétrico en uno de los términos de la otra ecuación para la misma incógnita. Por ejemplo, se puede multiplicar por 2 la segunda ecuación.
Hay que revisar un tercer sistema. Se trata de “y” igual a “x” más 3 y “y” igual a “x” negativa más cinco. ¿Qué método utilizarías para resolverlo?
El método de igualación dado que en ambas ecuaciones se encuentra despejada la misma incógnita. Pero, también podrías utilizar el método de suma y resta porque se observa que los términos con “x” tienen coeficientes simétricos.
Por otro lado, se podría utilizar el método gráfico, dado que se pueden asignar valores a “x” y encontrar su correspondiente para “y”, lo que determinaría coordenadas que, al unirse, generan las rectas que son las gráficas asociadas a esas ecuaciones.
Como ves, un mismo sistema de dos ecuaciones lineales con dos incógnitas puede ser resuelto usando cualquier método, lo importante es observar las características de ese sistema para decidir qué método utilizar. También es importante considerar las habilidades de cada persona para decidir sobre el método más adecuado.
El Reto de Hoy:
Realiza las actividades de tu libro de texto, correspondientes a resolver problemas que implican la resolución de sistemas de dos ecuaciones lineales con dos incógnitas.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
La asamblea dice...
Aprendizaje esperado: Diseña una campaña escolar para proponer soluciones ante un problema de la escuela.
Énfasis: Conducir una asamblea escolar.
¿Qué vamos a aprender?
En esta sesión profundizarás en el aprendizaje esperado: diseña una campaña escolar para proponer soluciones a un problema de la escuela, y sabrás como conducir una asamblea escolar.
Ten a la mano tu cuaderno, lápiz o pluma para tus anotaciones. También tu libro de texto para cualquier consulta.
¿Qué hacemos?
En esta sesión se va a hablar sobre las asambleas escolares.
Por ejemplo, tu compañero Pablo hace un par de días participó en una asamblea familiar que su hermano Eduardo organizó para solucionar un problema doméstico: el lavado de platos. Pablo pensaba que Eduardo pensaba que su hermana Diana pensaba que a él le tocaba lavar los platos los lunes y los miércoles, pero Eduardo pensaba que Pablo pensaba que su hermana Diana era a quien le tocaba lavarlos.
Quizás con tantos pensamientos ya te confundiste.
Ahora se te presentará otra forma de ejemplificar lo anterior.
Hay un calcetín blanco que es Eduardo, Pablo es el calcetín café. Y llegó la hora de iniciar la asamblea, aunque no están aún su hermana Diana, ni su papá, ni su abuela.
Pero ni modo.
Aunque no se puede decir “ni modo”. No puede haber una asamblea, si no se reúnen los participantes, pues el lavado de platos involucra a toda la familia.
Cuando por fin se dio la asamblea, se empezaron a pelear entre todos, porque no estaban de acuerdo. Eduardo gritaba, Pablo gritaba más fuerte, su papá los trata de calmar y todos se desesperaron y se fueron cada uno por su lado.
Como verás con este ejemplo, hace falta que esta familia aprenda a organizar una asamblea.
Por ello, en esta sesión se te explicará que pasos debes seguir para lograr que una asamblea funcione bien, sin gritos, ni enojos.
Ahora, revisarás un video en donde se realiza una asamblea escolar.
- VIDEO 01_APERTURA ASAMBLEA.
Como observaste en el video, la presidenta a través del pase de lista se aseguró de que existiera quórum. Aparte de esto, ¿lograste notar algunas características de la asamblea?
Tal vez, el perfil de los participantes. Ahora, quizás entiendas la función que desempeña cada uno.
En esta asamblea escolar las y los alumnos se reunieron por iniciativa personal y en forma autónoma para dialogar, debatir y tomar acuerdos acerca de la organización de su campaña escolar.
Cada uno tuvo una función en la actividad, pero todos fueron miembros importantes.
Así es, aunque Frida, Luisa y Miranda organizan y conducen la reunión, la opinión de todos se respeta y juntos establecen acuerdos.
Pero, sería importante saber ¿qué es una asamblea escolar?, ¿cuáles son los tipos de asamblea?, ¿qué momentos existen dentro de ella?, ¿cuál es la función de cada uno de sus miembros? y ¿cómo se levanta un acta de acuerdos en ella?
Son interesantes los cuestionamientos, para ello recordarás qué es una asamblea.
- VIDEO 12. UNA ASAMBLEA ESCOLAR.
Revisa del tiempo 01:26 al 01:47.
Como viste en el video, en las asambleas escolares se informa y se debate sobre distintas cuestiones comunes a los participantes. Es importante enfatizar que, a través de ellas, se favorece la participación colectiva en términos de igualdad y respeto.
Sí, todos tienen la misma oportunidad de expresar sus opiniones y puntos de vista, ¿las asambleas se programan al inicio del ciclo escolar o pueden realizarse en cualquier momento?
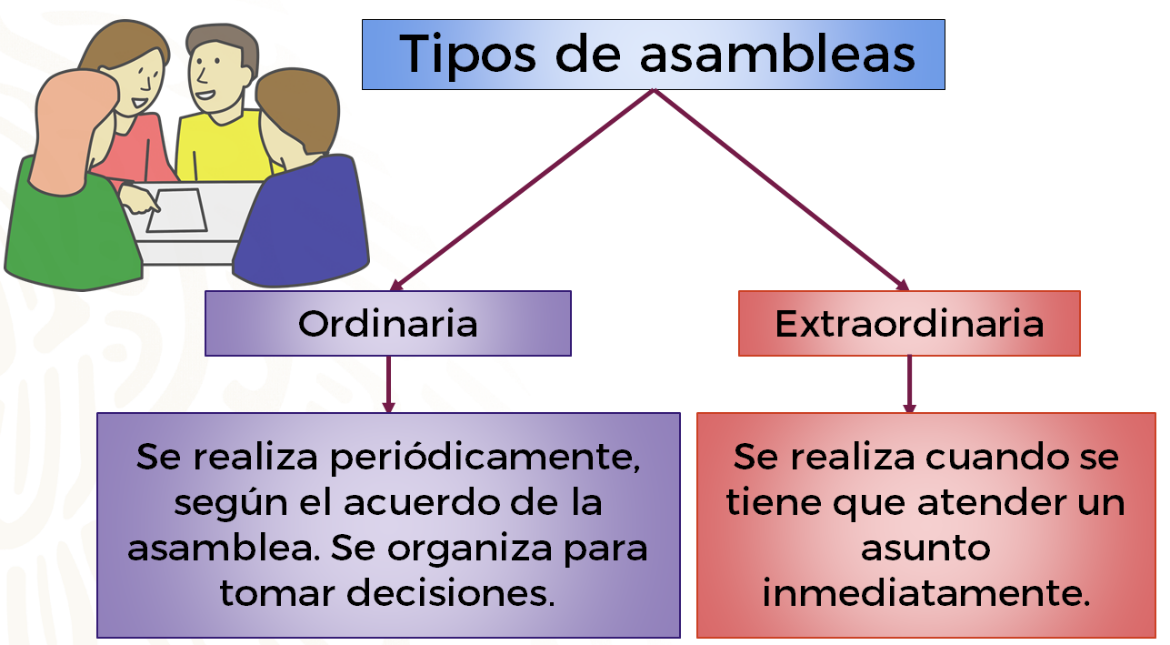
Existen asambleas extraordinarias, en ese caso se organizó una para hablar sobre la campaña escolar. Éstas son de carácter emergente, pues atienden situaciones imprevistas y no tienen fecha programada. En cambio, las asambleas que se programan y se realizan periódicamente se llaman ordinarias.
¿Quiénes participan en una asamblea escolar?
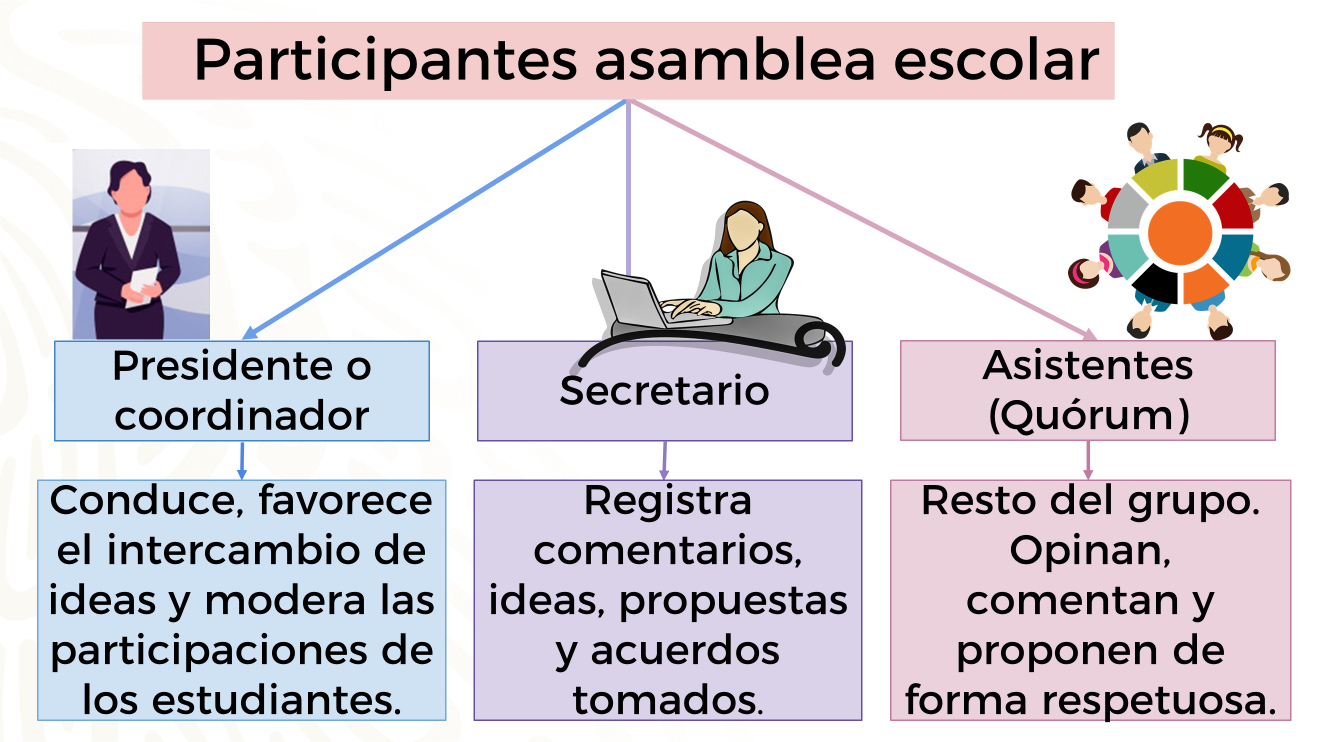
En la asamblea que observaste, Frida desempeña el rol de presidenta o coordinadora, su función es relevante, otorga la palabra y guía la discusión de los temas en la asamblea.
El secretario de la asamblea, que en este caso es Luisa, anota los puntos importantes, las ideas, las propuestas y los acuerdos a los que llegan los participantes.
En las asambleas escolares es necesario que alguien asuma la función del escrutador, éste se encarga de contar los votos que emiten los participantes durante el desarrollo de la asamblea. En la asamblea que revisaste, esta función la desempeña Miranda.
Y, por supuesto, los participantes fundamentales son los socios, pues ejercen su derecho al voto con el objetivo de participar en la toma de decisiones y acuerdos.
Pero, ¿cómo se sabe que esos acuerdos son legales?
Lo sabes desde el primer momento de la asamblea escolar, a través del pase de lista, pues la asistencia te lo indica.
¿Entonces la cantidad de asistentes indica si existe el quórum necesario para su realización?
Así es, revisa la definición de quórum en la siguiente imagen para resolver tus dudas.
Entonces, cuando se apertura la asamblea escolar se procede al pase de lista de los participantes. Si existe quórum se puede proseguir con el orden del día, con el tema o los diferentes puntos a tratar.
Pero, ¿qué pasa si no hay quórum?
De no haber quórum habrá que esperar a que se incorporen otros participantes a la reunión o, de lo contrario, se suspende la asamblea. Normalmente se considera que existe quórum cuando el 50 % de los miembros de la asamblea más uno, se encuentran presentes en ese momento.
Cuando se comprueba que existe quórum, se procede a la lectura del orden del día para presentar el tema y los puntos a debatir. Ese es el primer momento de la asamblea.
En la reunión realizada por el grupo de Frida, el orden del día tuvo como finalidad tomar acuerdos para la organización de la campaña escolar.
Observa los datos principales del orden del día que utilizaron en el grupo de Frida.
Después del título, se anota la ubicación en la cual se lleva a cabo la asamblea, la fecha, hora y los puntos que componen el orden del día que en esta ocasión se compone de:
- Establecimiento de quórum.
- Aprobación de las reglas del debate.
- Aprobación de la agenda.
- Asunto 1 (problemática a tratar).
- Clausura de la asamblea escolar.
¿Te parece si continúas observando el video de la asamblea realizada por las y los alumnos de segundo grado para organizar una campaña escolar?
- VIDEO 02_DESARROLLO ASAMBLEA.
Durante el desarrollo de la asamblea escolar, las y los alumnos primero discuten la estrategia al interior de los equipos, así como el tiempo de duración del trabajo para organizar la campaña escolar, expresando cada uno su opinión y consensuando la propuesta del equipo para presentarla.
Es durante el desarrollo de la asamblea escolar cuando hay una participación equitativa por parte de los alumnos a través de un debate, es decir, discuten respetuosamente acerca del tema para, posteriormente, emitir los votos según sus opiniones e intereses.
Observa también cómo se realiza la votación de forma organizada, ordenada y planeada para elegir una de las opciones que fueron propuestas durante la asamblea. La sugerencia que obtiene un mayor número de votos es la que se toma en cuenta.
¿Te percataste de que, durante el desarrollo de la asamblea escolar, los participantes dialogaron para tomar acuerdos?
Así es, se mantuvo el orden y todos respetaron la opinión de los demás compañeros, el diálogo los llevó a la toma de acuerdos. Pero ¿qué puedes entender por diálogo?
El diálogo es una conversación entre varias personas, quienes expresan sus ideas, puntos de vista, emociones y sentimientos con el fin de lograr entendimiento y llegar a acuerdos pacíficos para resolver conflictos mediante el diálogo; es importante desarrollar la inteligencia emocional, que permite identificar y manejar las emociones, así como la asertividad, que ayuda a las personas a expresarse sin afectar a otros.
Algo que también se notó durante la asamblea es que, en los momentos en los que las y los alumnos no participan activamente, se muestran atentos a los comentarios de sus compañeras y compañeros.
Durante las asambleas no todos pueden hablar al mismo tiempo. Escuchar ayuda a ampliar las perspectivas en relación con el tema abordado y considerar las coincidencias o las diferencias que existen entre formas de pensar. De ese modo se podrán tomar mejores decisiones al final de la asamblea.
Revisa cómo se entabla el diálogo para la toma de acuerdos en los equipos, en el siguiente video.
- VIDEO 03_EQUIPO ACUERDOS.
Como observaste en el video, todos tienen la oportunidad de expresarse de manera creativa y propositiva; sin embargo, durante la toma de acuerdos en la asamblea, hubo momentos en los que las y los participantes se arrebataron la palabra para hacer oír su opinión.
Así es, de ahí la importancia de la figura del coordinador, quien, además de estimular la confianza, el diálogo y la interacción, también debe estar presente dentro de los equipos en las asambleas, de este modo se asegura la participación ordenada y respetuosa de todos los miembros del equipo.
¿Cómo se cierra una asamblea escolar?
Para responder tu duda, observa el siguiente video.
- VIDEO 04_CLAUSURA ASAMBLEA.
En la clausura de la asamblea escolar se recapitulan los acuerdos tomados y se imprime el acta para que todos los asistentes puedan firmar.
Como viste en el ejemplo, el secretario de la asamblea da lectura en voz alta al acta de acuerdos y se formaliza el establecimiento de éstos mediante la firma de todos los participantes.
¿Notaste que al finalizar la reunión Benjamín no estuvo conforme con los acuerdos establecidos en el acta?
Hay que ver, cómo quedó estructurada el acta final de esta asamblea.
En el acta se puede observar que todos firmaron, aunque Benjamín lo hizo con reservas.
En este caso, ¿qué acciones podrían servir para solucionar estos desacuerdos y evitar conflictos entre los miembros de la asamblea escolar?
Se puede permitir que el inconforme exprese su punto de vista y sea escuchado con respeto y tolerancia.
Ahora revisa las opiniones de algunas y algunos alumnos acerca de las asambleas escolares, en el siguiente video.
- VIDEO 05_ENTREVISTA ESTUDIANTES.
Son muy acertados los comentarios de las y los alumnos. Efectivamente, la asamblea escolar es un espacio en donde prevalece el diálogo respetuoso para la toma de acuerdos. ¡Ahora entenderás muy bien, qué pasos se deben seguir para organizar una asamblea!
Se te invita a revisar las sugerencias que aparecen en tu libro de texto de Lengua Materna. Y no olvides practicar lo aprendido en esta sesión. Puedes elaborar una lista de los problemas de la escuela para organizar la asamblea.
Has concluido el tema del día de hoy.
El Reto de Hoy:
Elige una problemática escolar a la cual quisieras darle solución.
Escribe en tu libreta la justificación de tu elección, esto te servirá para debatir. Anota los nombres de las y los compañeros que pueden realizar las funciones de presidente y secretario durante la asamblea escolar. Complementa la siguiente tabla en tu cuaderno de notas.
En la primera columna coloca los aspectos que se analizarán y en la segunda columna completa la información: definición de la asamblea escolar, participantes, función de cada participante y momentos de la asamblea.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Igualdad ante la ley y democracia
Aprendizaje esperado: Reconoce que la igualdad ante la ley es condición para la construcción de una sociedad justa y equitativa.
Énfasis: Considerar que una sociedad democrática promueve la igualdad ante la ley en la ciudadanía.
¿Qué vamos a aprender?
Identificarás 11 tipos de igualdad, se explicará que un país democrático promueve la igualdad de las personas ante la ley; la cual debe ser incluyente, equitativa e imparcial en su aplicación. También se brindarán ejemplos de prácticas democráticas en las que está presente la igualdad ante la ley.
Ten a la mano tu cuaderno, un lápiz o bolígrafo, para anotar algunas ideas o inquietudes que surjan durante la sesión, así como colores. Si tienes una discapacidad visual, prepara tus hojas leyer, punzón y regleta.
¿Qué hacemos?
La igualdad se puede definir como el trato idéntico entre personas, aunque también hace referencia a la expresión de equivalencia entre dos cantidades.
Como punto de partida, revisarás las siguientes frases que retoman algunas ideas acerca de la igualdad, como valor para la convivencia.
- La libertad es un valor importante para la convivencia, porque te recuerda que todas y todos tienen dignidad y ésta debe respetarse.
- En la convivencia diaria, el valor de igualdad no se respeta cuando se menosprecia o se deja fuera a alguien de tu escuela o comunidad, por alguna característica.
- Una condición para que exista igualdad es respetar las distintas formas de ser, pensar y vivir.
Es importante saber que, dentro de una sociedad, la equidad significa que los recursos, las posibilidades de desarrollo y el poder se distribuyen entre todas las personas, tomando en cuenta sus necesidades y características particulares.
Sólo cuando esto ocurre es posible hablar realmente de igualdad de derechos. Cuando algunas personas o grupos sociales concentran el poder, se benefician de los recursos que las y los demás generan y tienen más posibilidades de desarrollarse, se puede decir que es una sociedad inequitativa, donde sólo unas cuantas personas se ven beneficiadas.
Entonces, con la finalidad de que reflexiones con relación al tema, se te pregunta:
- ¿Qué significa para ti ser iguales ante la ley?
- ¿Opinas que existen grupos que no merecen el derecho a la igualdad ante la ley?
- En este momento de tu vida, ¿te das cuenta de que existen grupos sociales con privilegios?
- ¿Eso te parece justo?
Se hacen estas preguntas, ya que hay sectores de la sociedad que aún piensan que algunas personas no merecen ser tratadas como tal y, mucho menos, merecen ser tratadas con igualdad; argumentan que no todas las personas tienen los mismos derechos.
Este comportamiento afecta a las y los demás, es un peligro para la paz, la economía, el bienestar y el desarrollo de la sociedad. Hay quien considera que solamente quienes cumplen con determinadas características parecidas a las que tienen los grupos con privilegios tendrán derecho de pertenecer o de verse favorecidas por las leyes.
En esta sesión se contará con la colaboración del licenciado Germán Bautista, especialista en derechos humanos, quien apoyará en dar una explicación sobre la importancia de la democracia para garantizar que todas las personas sean iguales ante la ley.
Pon atención lo que dice, ya que te dará elementos clave para entender el tema, y responderá a la pregunta: ¿de qué manera un país democrático promueve que todas las personas sean iguales ante la ley?
Revisa el siguiente video.
- FCE_B3_PG2_SEM32_VIDEOS 1_GERMAN.
Revisa del tiempo 00:05 al 01:19.
Como observaste, es importante reconocer que la igualdad ante la ley no sólo debe promoverse, también debe garantizarse, lo cual será una condición para construir una sociedad equitativa y justa.
Por eso es muy importante que tú observes tu entorno y te des cuenta de que la desigualdad afecta las posibilidades de vivir con dignidad y sin discriminación. Debes asumir que el pleno cumplimiento de la igualdad ante la ley es responsabilidad de la sociedad y del gobierno.
Es importante recordar que todas las personas son dignas, merecen respeto y que en una sociedad democrática deben ser reconocidas y valoradas.
Se te invita a revisar el siguiente video que te habla de la importancia de vivir en democracia y aplicar las leyes por igual.
- Los desafíos de los servidores públicos en la aplicación de la ley.
https://www.youtube.com/watch?v=oHjrPt1ULh8
Revisa del tiempo 00:59 al 01:31.
Como observaste, la democracia obliga a adoptar una cultura cívica o de legalidad, ya que, por ejemplo, para construir paz con justicia, se requiere que quienes integran la sociedad cuenten con las mismas oportunidades para desarrollarse, tengan protección por las leyes, cero privilegios y puedan ejercer sus derechos sin discriminación.
Esto se relaciona con los principios fundamentales para la vida democrática, que son la imparcialidad y la igualdad ante la ley.
Al respecto, es importante señalar que existen dos concepciones distintas en términos de igualdad; una es la formal o de contexto normativo y la otra real o práctica y que la aspiración en una sociedad democrática es que se logren ambas y se lleven a cabo en el mismo tiempo.
A continuación, revisa en voz de las y los adolescentes de la sección La voz de la juventud, 4 tipos de igualdad ante la ley que se fundamentan en la existencia y respeto al trato imparcial y justo que se debe dar a toda la población.
Como has revisado, para una sociedad democrática esto es una condición necesaria.
- Audio 1.
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202104/202104-RSC-9d9sRDUngI-3.Audio1.mp3 
- Audio 2.
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202104/202104-RSC-ipKgP53JYF-4.Audio2.mp3
- Audio 3.
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202104/202104-RSC-Ghhzwy5K36-5.Audio3.mp3
- Audio 4.
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202104/202104-RSC-0QVPbV2kWB-6.Audio4.mp3
Como viste la igualdad de género, igualdad por ser miembro del género humano, igualdad social e igualdad de accesos públicos, así como las otras que se enunciarán más adelante, son formas necesarias y urgentes a aplicarse y mantenerse en una sociedad democrática, entendida como dice el Artículo 3º de la Constitución Política, no sólo como una estructura jurídica y un régimen político, sino como un sistema de vida fundado en el constante mejoramiento económico, social y cultural del pueblo.
Al respecto, el Lic. Germán responde la pregunta ¿de qué manera un país democrático es incluyente y equitativo en la aplicación de la igualdad ante la ley?
Observa en el siguiente video, la importancia de ello.
- FCE_B3_PG2_SEM32_VIDEOS 2_GERMAN.
Revisa del tiempo 01:24 al 03:26.
Como observaste, además de la revisión del concepto de democracia, el abogado habla de la importancia del reconocimiento de las diferencias y sus características, y que un país democrático debe dar atención específica a la igualdad, otorgando tratos justos y apoyos necesarios para la plena participación de las personas, recordándote que la inclusión requiere de la capacidad de reconocer la diversidad y hacer lo necesario para que todas las personas participen, aprendan en igualdad de circunstancias y tengan las mismas oportunidades que el resto de la población.
Se entiende, entonces, que en un sistema democrático debe florecer de manera plena el derecho a la no discriminación, lo que mejorará la economía, la sociedad y la cultura de un Estado; implica asumir valores como la solidaridad, el respeto a la diversidad y la empatía para eliminar desigualdades y barreras que no favorecen los derechos de todas las personas.
A continuación, se enunciarán otros 4 tipos de igualdad con sus respectivos ejemplos, los cuales, de la misma manera que los anteriores, se clasifican dependiendo del contexto de vida de las personas que se busca equilibrar.
- Audio 5.
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202104/202104-RSC-GKWrZGnicr-8.Audio5.mp3
- Audio 6.
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202104/202104-RSC-lcyctgamFt-9.Audio6.mp3
- Audio 7.
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202104/202104-RSC-YavL4b0nhm-10.Audio7.mp3
- Audio 8.
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202104/202104-RSC-6CtiglHFzh-11.Audio8.mp3
La igualdad de justicia, personal, matemática y jurídica que acabas de revisar, clarifican que, la igualdad ante la ley, es el principio que reconoce que todas las personas deben ser tratadas de la misma manera y de forma imparcial, lo que se conoce como: principio de isonomía o igualdad ante la ley, lo que implica que estén sujetas a las mismas leyes de justicia, también conocido como: principio de debido proceso, lo que reconoce la equiparación igualitaria de todas las ciudadanas y ciudadanos en derechos civiles y políticos. Revisa tres formas más de igualdad con ejemplos de prácticas democráticas en las que está presente la igualdad ante la ley.
- Audio 9.
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202104/202104-RSC-QR5rfzmXFs-12.Audio9.mp3
- Audio 10.
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202104/202104-RSC-FKMdMbiv19-13.Audio10.mp3
- Audio 11.
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202104/202104-RSC-GTbTbet8AH-14.Audio11.mp3
Después de escuchar estas 3 últimas formas, se enlistarán los 11 tipos de igualdad ante la ley para facilitar tus notas en casa:
- Igualdad de género.
- Igualdad por ser miembro del género humano.
- Igualdad social.
- Igualdad de accesos públicos.
- Igualdad de justicia.
- Igualdad personal.
- Igualdad matemática.
- Igualdad jurídica.
- Igualdad política.
- Igualdad de oportunidades para personas con discapacidad.
- Igualdad de derechos para las personas mayores.
Es importante señalar que, para alcanzar todas las anteriores formas de igualdad, se han dado pasos hacia la plena igualdad, pero el camino que queda por recorrer aún es largo y difícil, pues depende a la vez de factores, sociales, económicos y culturales, y es responsabilidad de la sociedad y de todos los niveles de gobierno, realizar acciones que faciliten su práctica; sin embargo, muchas veces es necesario iniciar con lo primero, que es identificar los propios requerimientos en función de la identidad que se tiene.
Ahora se realizará una recapitulación de lo revisado el día de hoy.
En la sesión identificaste 11 tipos de igualdad ante la ley, revisaste su vínculo con la equidad, con la justicia, y se mencionaron algunos ejemplos de cómo se llevan a la práctica.
Revisaste que un país democrático, se promueve que todas las personas sean iguales ante la ley y que la igualdad está vinculada estrechamente con el principio de imparcialidad y con la inclusión.
Se te invita a que consultes tu libro de texto para informarte más sobre el tema.
Recuerda que, una forma de iniciar un proceso de transformación de un país democrático, puede darse a partir del reconocimiento de tu propia identidad, tus requerimientos de igualdad y tus derechos.
Para lograr la igualdad ante la ley, es indispensable estar alerta a la manera en cómo se distribuyen las oportunidades y las posibilidades para el ejercicio de los derechos; por lo tanto, debes hacer lo que te corresponde como parte de la sociedad para exigir sin violencia lo necesario para que no exista discriminación.
El Reto de Hoy:
El reto del día de hoy, consiste en que: con relación a la identidad que tienes, la describirás brevemente, te dibujarás y contestarás las siguientes preguntas:
- ¿Qué tipos de igualdad ante la ley necesitas para ejercer tu derecho a ser incluida o incluido socialmente? y ¿por qué?
Un ejemplo es el siguiente:
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
¿Cuáles son las fuentes de luz?
Aprendizaje esperado: Describe la generación, diversidad y comportamiento de las ondas electromagnéticas como resultado de la interacción entre electricidad y magnetismo.
Énfasis: Reflexionar sobre la importancia de los diferentes tipos de fuentes naturales y artificiales de luz.
¿Qué vamos a aprender?
Reflexionarás acerca de la importancia de los diferentes tipos de fuentes de luz.
Es importante que tengas a la mano tu cuaderno, libro de texto y lápiz o bolígrafo, para que puedas anotar las ideas principales que identifiques, así como dudas que pudieran surgir a lo largo de la sesión. Si tienes alguna discapacidad visual, prepara hojas leyer, punzón y regleta para hacer tus anotaciones en sistema braille.
¿Qué hacemos?
Para iniciar, se dirá que la luz es un fenómeno que ha intrigado a la humanidad desde siempre. Se sabe que los filósofos griegos ya elaboraban teorías acerca de la naturaleza de la luz.
Efectivamente, varios filósofos griegos se interesaron en su estudio, entre los que se pueden mencionar a Euclides, quien describió formas en las que la luz rebotaba en los objetos de manera matemática, y Empédocles de Agrigento, quien sostenía que los ojos producían rayos de luz que tocaban los objetos y se podía así verlos.
¿Rayos que salían de los ojos?
Eso suena como de película de ciencia ficción.
Puede ser que así te parezca ahora, pero todo esto tiene un gran valor, ya que, mediante el planteamiento de hipótesis como ésta, su comprobación y las conclusiones derivadas de los resultados, se construye el conocimiento.
Aunque esta sesión se centre en las fuentes de luz y su importancia, como se mencionó en un inicio, vale la pena recordar algunas de sus características. Así que se iniciará por esa parte.
La luz es una manifestación de energía y es una de las formas principales mediante las cuales se interactúa con el mundo que te rodea. Durante miles de años se han creado diferentes explicaciones acerca de su naturaleza, las cuales han conducido a la noción de que la luz puede comportarse tanto en forma de partícula como en forma de onda. Las partículas de luz se llaman fotones.
Los fotones son partículas elementales que siempre están en movimiento y lo hacen a una velocidad aproximada de 300 000 kilómetros por segundo en el vacío. Por otro lado, la luz también son ondas electromagnéticas, las cuales transportan energía y en su conjunto forman el espectro electromagnético. Parte de este espectro es invisible al ojo humano y parte es visible.
¿La luz que puedes ver mediante tus ojos es entonces sólo una parte del espectro electromagnético?
Así es, y una pequeñísima parte del espectro en realidad, como puedes ver en la siguiente imagen.
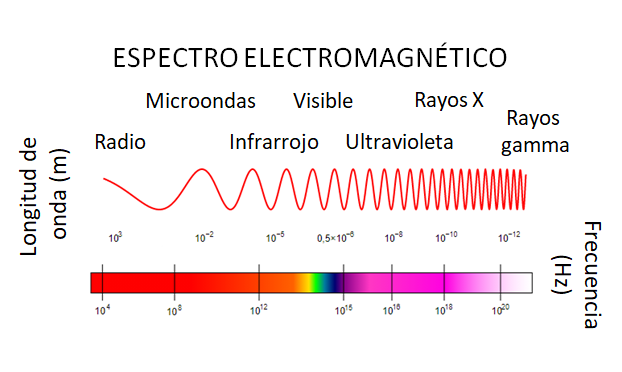
Como ves, las ondas correspondientes a luz blanca o espectro de la luz visible están al centro de todo el espectro; las ondas invisibles al ojo humano son las ondas de radio, las infrarrojas, las ultravioletas, los rayos X y los rayos gamma.
¿Por qué las ondas están acomodadas en ese orden en el espectro electromagnético?
El acomodo que puedes ver es debido a la longitud de onda.
La longitud de onda es una propiedad que tienen todas las ondas, es la distancia que existe entre dos de sus valles o dos de sus crestas que son consecutivas. Las ondas de radio son las ondas electromagnéticas con longitudes de onda mayores, por eso se sitúan en el extremo izquierdo del espectro electromagnético, mientras que los rayos gamma son las ondas con menor longitud, y por eso se ubican en el extremo derecho.
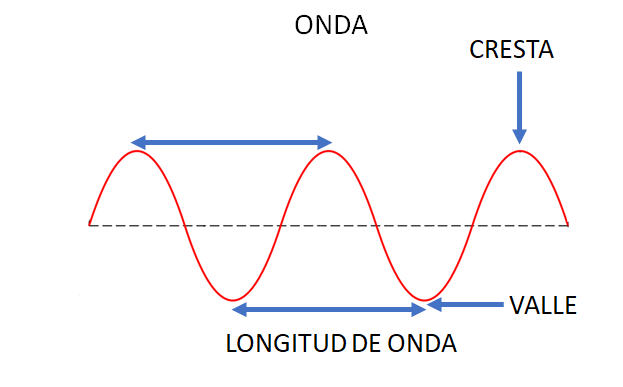
Revisa el siguiente video, para seguir aprendiendo más acerca de la luz.
- Electricidad, luz y espectros.
https://www.youtube.com/watch?v=4VDU5j3Ex0o&t=80s
Revisa del tiempo 05:41 al 07:00.
Pero, ¿por qué se mencionó en el video que existen luces de diferentes colores?
La respuesta es que, los diferentes colores están dados por las longitudes de onda de las que se hablaba antes. Además, éstas son distintas debido a las características de los elementos o materiales que las emitieron, es decir, a las fuentes de luz que las produjeron.
¿Qué son las fuentes de luz?
Las fuentes de luz son objetos que emiten luz o que reflejan la luz emitida por otra. Revisa el siguiente video, para introducirte más en el tema.
- Un poco de luz.
Revisa del tiempo 05:33 al 06:16.
Con esto te quedará más claro, las fuentes de luz emiten o reflejan la luz.
Ciertamente, las fuentes de luz que la emiten directamente son conocidas como fuentes primarias, mientras que aquellas que reflejan la luz de fuentes primarias son llamadas fuentes secundarias. De acuerdo con esto, todos los objetos que perciben tus ojos son fuentes de luz secundarias, ya que si no hubiera luz que rebotara sobre los objetos, no podrías verlos.
Todos los objetos que puedes ver y que no emiten luz por sí mismos son fuentes secundarias, mientras que las primarias siempre tienen que producir su propia luz.
Entonces, ¿un ejemplo de fuente primaria de luz sería el Sol?
Efectivamente, el Sol es una fuente primaria de luz y es la principal con la que se cuenta en la Tierra. El Sol irradia luz en el espectro electromagnético de la luz ultravioleta, la luz visible y el infrarrojo.
Observa el siguiente video, para conocer más acerca de esta importantísima fuente de luz y calor.
- El sol como fuente de energía.
https://www.youtube.com/watch?v=T8dlzBQUIIM
Revisa del tiempo 00:48 al 02:05.
Como viste en el video, ¡qué sorprendente es el Sol!
Además de ser la fuente principal de luz para los seres humanos, ha sido fundamental para el planeta y la vida que aquí se ha desarrollado. La luz solar permite a las plantas llevar a cabo el proceso de la fotosíntesis, mediante el cual producen su propio alimento y como consecuencia de éste, liberan el oxígeno que todos los seres humanos respiran.
La energía trasmitida por las ondas electromagnéticas provenientes del Sol es aprovechada en forma de calor para mantener la temperatura de la Tierra y que ésta pueda sostener vida. Esta luz solar es semejante a la emitida por otras estrellas de esta galaxia, aunque claramente la luz de éstas no llegan a la Tierra con la misma intensidad dada su lejanía.
¿Qué otras fuentes primarias como el Sol existen?
Las fuentes primarias y secundarias pueden ser, a su vez, clasificadas en fuentes naturales y artificiales de luz.
Las fuentes de luz primarias naturales producen luz por sí mismas y tienen un origen natural, es decir, el ser humano no intervino en su proceso.
¿Puedes pensar en otras fuentes de luz naturales además del Sol?
Para apoyarte con la respuesta, se puede decir, que otras fuentes de luz de origen natural pueden ser el fuego y los rayos eléctricos. Efectivamente, ésas también son fuentes naturales de luz.
El fuego es un fenómeno producido al aplicar calor a un combustible, como un tronco, en presencia de un comburente, el oxígeno. La luz y calor son producidos a partir de esta combustión, la cual durará mientras estén presentes estos tres elementos, el calor, el combustible y el comburente. La parte visible del fuego es la llama. Para los antiguos filósofos griegos, el fuego era uno de los cuatro elementos, junto con el agua, el aire y la tierra. El fuego te sirve para iluminar el espacio en el que te encuentras, en especial, en ausencia de la luz solar, es decir, durante la noche, así como para calentarte y cocinar tus alimentos.
¡Qué importante ha sido el fuego en la historia de la humanidad!
Sí, así es. Por otra parte, los rayos eléctricos también son una fuente de luz primaria y natural, ya que son un fenómeno natural de la Tierra.
Los rayos son producidos por una diferencia de potencial eléctrico entre nubes y el suelo. Cuando se condensa gran cantidad de vapor de agua en las nubes, se producen colisiones; dichas colisiones ocasionan una separación de cargas eléctricas y cuando la diferencia de potencial con el suelo o con otra nube aumenta, se produce el rayo o descarga eléctrica. Los rayos van acompañados del relámpago, que es la radiación electromagnética en el rango visible, es decir, la luz que observas, y el trueno, que es la emisión de energía sonora o el ruido estruendoso que percibes.
Ciertamente un conjunto de relámpagos o uno muy intenso pueden iluminar la noche, y quizás los has observado. Son fenómenos naturales de gran energía, lo mejor es que los observes desde una distancia segura y en espacios techados.
Otras fuentes de luz primarias de origen natural son el magma de un volcán, algunos animales que producen luz como las luciérnagas y algunas medusas. Es verdad, también algunos animales producen luz.
¿Y qué se puede decir de la Luna?
La Luna es también una fuente natural, pero es una fuente natural secundaria, ya que recuerda que la Luna no produce su propia luz, sino que la ves gracias a la luz del Sol que se refleja en ella.
Debido a esto y dependiendo de la posición relativa de la Luna y la Tierra, puedes verla de diferentes formas: a veces la ves como una Luna llena cuando la luz del Sol se refleja en toda la cara que queda de frente a la Tierra; una Luna creciente o menguante cuando sólo rebota en una parte, y una Luna nueva cuando no es posible verla, ya que se encuentra situada entre la Tierra y el Sol, de tal forma que su hemisferio iluminado no se encuentra en dirección a la Tierra.
Cuando la Luna se encuentra completamente alineada con el Sol es cuando se produce un eclipse solar. Mediante este fenómeno natural es posible que se oscurezca por completo durante el día, ya que el Sol está bloqueado por la Luna durante un periodo de tiempo y la sombra de ésta se proyecta en una región determinada de la Tierra.
Ahora se hablará sobre las fuentes de luz artificial. Estas involucran la intervención del ser humano.
Efectivamente. El ser humano, desde siempre, ha intentado imitar las fuentes naturales de luz para poder tener control sobre ésta a su conveniencia. En un inicio dominó el fuego, ya podía encenderlo a su voluntad en fogatas y antorchas, cuyos combustibles eran leña y fibras vegetales, y posteriormente, en velas de cera.
Revisa el siguiente video para conocer más acerca del funcionamiento de una vela.
- Electricidad, luz y espectros.
https://www.youtube.com/watch?v=4VDU5j3Ex0o&t=80s
Revisa del tiempo 08:19 al 09:34.
Como viste en el video, el combustible de la vela es la cera, grasa o parafina. Las velas se utilizaron por muchísimo tiempo en los hogares y edificios, también se colocaron en la calle en forma de farolas para iluminar los caminos. Posteriormente se fabricaron lámparas de queroseno, un tipo de combustible líquido derivado del petróleo.
También se llegó a utilizar el gas natural como combustible de fuentes artificiales de luz. La desventaja que se tenía con estos métodos es que eran muy inseguros y a menudo se generaban incendios que no eran fácilmente controlables. Todo esto cambió radicalmente a finales del siglo XIX e inicios del XX.
¿Qué sucedió entonces?
A partir de aquel momento, se comenzó a generar energía eléctrica de manera masiva, y dicha energía eléctrica fue utilizada para iluminar las casas, comunidades y ciudades por medio de lámparas.
Las lámparas son consideradas fuentes primarias de luz artificial.
Efectivamente. Ahora se tienen otras fuentes primarias de luz artificial que también funcionan con energía eléctrica provista por pilas y baterías, como las linternas, los leds e incluso dispositivos electrónicos como los celulares y tabletas.
¿Cuál es la importancia de los diferentes tipos de fuentes naturales y artificiales de luz?
Las fuentes de luz naturales, particularmente el Sol por el tiempo de exposición que tiene éste, son sumamente importantes.
Como se comentaba anteriormente, la luz solar es esencial para que las plantas lleven a cabo el proceso de fotosíntesis, y éste es de gran importancia para el equilibrio de diversos ecosistemas biológicos de manera directa y, en general, para toda la vida del planeta. En verdad que este proceso es crucial.
Además, la luz solar es también necesaria para diversas funciones de los seres vivos.
Por ejemplo, los seres humanos requieren de la luz solar directa para producir la vitamina D que necesitan.
La vitamina D ayuda al cuerpo a fijar el calcio en los huesos y está también relacionada con el sistema inmunológico que ayuda a prevenir enfermedades.
Es por esto que en lugares de la Tierra en los que no hay gran exposición de luz solar, las personas requieren tomar suplementos de esta vitamina.
También la luz solar influye en el estado anímico de los seres humanos, ya que provoca la liberación del neurotransmisor llamado serotonina, el cual también afecta al sistema inmunológico y brinda la sensación de felicidad.
Por otra parte, controla también en gran medida los ritmos biológicos del cuerpo humano, como el ciclo del sueño.
¡Qué sorprendente es todo lo que se comenta acerca de la luz solar! ¡Sin lugar a duda es vital!
En general todas las fuentes de luz, tanto naturales como artificiales, son importantes ya que, sin luz, no se podría ver el mundo que te rodea.
Revisa ahora un video para reforzar este tema de la observación de los objetos.
- ¿Existe la luz invisible?
Revisa del tiempo 08:43 al 09:57.
Después de revisar el video, se te invita a reunirte con tu familia para reflexionar sobre las diferentes fuentes de luz.
El Reto de Hoy:
El reto de hoy consiste en que busques fuentes de luz en tu hogar y que realices un listado. Después elabora un mapa mental en el que destaques las fuentes de luz primarias, secundarias, naturales y artificiales, y brindes ejemplos a partir de tu lista y de las que conociste el día de hoy.
También, subraya las ideas principales de tu libro de texto y, si deseas profundizar en el tema o resolver dudas, puedes recurrir a fuentes de información confiables.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Publicar un Comentario