Aprende en Casa III SEP: 17 de mayo TAREAS y ACTIVIDADES de 2° de secundaria

¿Cuáles fueron los temas del día?

A continuación dejamos los temas vistos el 17 de mayo de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Aprende en Casa III SEP: TAREAS y ACTIVIDADES de 2° de secundaria 17 de mayo

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Lunes 17 de mayo, así como las dudas que se plantearon.

La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en Casa III:

https://aprendeencasa.sep.gob.mx/#

Prismacolor M1799879 Premier - caja 150 lápices de colores

Compra en Amazon

Polígonos regulares II

Aprendizaje esperado: Deduce y usa las relaciones entre los ángulos de polígonos en la construcción de polígonos regulares.

Énfasis: Construir polígonos regulares con algunos datos proporcionados.

¿Qué vamos a aprender?

Analizarás la construcción de polígonos regulares y estrellas.

¿Qué hacemos?

En sesiones anteriores has visto la manera de construir polígonos regulares a partir de algunos de sus datos, ya sea el tamaño de su lado o a partir de alguno de sus ángulos que los caracterizan.

Si observas las imágenes, verás que en todas ellas aparecen diversas figuras geométricas. Hoy aprenderás cómo construir algunas de esas figuras para que puedas echar andar tu imaginación y así, poder realizar configuraciones parecidas a éstas.

Para ello, primero verás otras construcciones geométricas para construir algunos polígonos regulares, usando de manera particular, las simetrías que tienen cierto tipo de polígonos.

Inicia construyendo un hexágono regular.

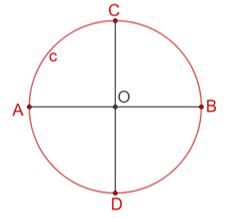
Señala un punto “O”, el cuál será el centro del hexágono. Abre el compás con una apertura cualquiera; que llamaremos “L” y que será la longitud de los lados del hexágono. Se traza la circunferencia “c” con centro en “O” y radio de longitud “L”.

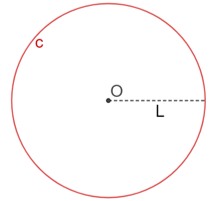
Traza dos diámetros perpendiculares u ortogonales de la circunferencia “c”, los cuales la intersecan en los puntos “A” y “B” y en los puntos “C” y “D”, respectivamente.

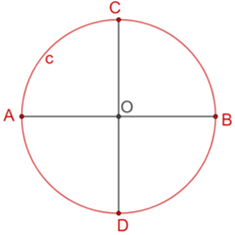
Con centro en el punto “C” y mismo radio igual al de la circunferencia “c”, traza otra circunferencia, que interseca a la circunferencia “C” en los puntos “P subíndice 1” y “P subíndice 2”.

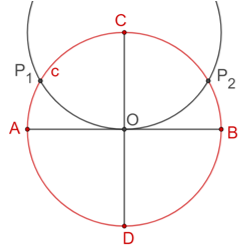
De manera análoga, con centro en “D” y radio igual al de la circunferencia “c”, traza una circunferencia que interseca, en los puntos “P subíndice 3” y “P subíndice 4”, a la circunferencia “c”.

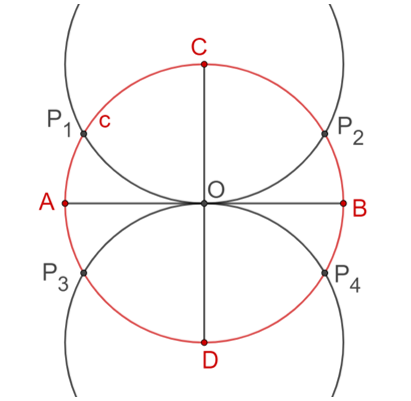
Ahora, une con segmentos de recta los siguientes puntos: el punto “C” con el punto “P subíndice 1”, el punto “P subíndice 1” con el punto “P subíndice 3”, el punto “P subíndice 3 “con el punto “D”, el punto “D” con el punto “P subíndice 4”, el punto “P subíndice 4” con el punto “P subíndice 2” y finalmente el punto “P subíndice 2” con el punto “C”. De esta manera has trazado un hexágono regular de lado “L”.

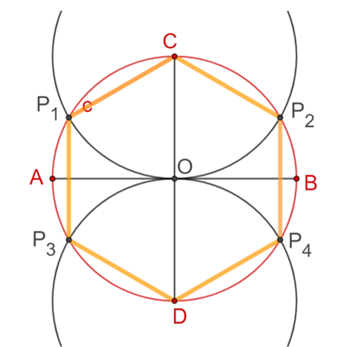
Analizando con mayor detenimiento la construcción anterior, y aprovechando las simetrías del hexágono, se puede hacer también partiendo del diámetro “AB” de la circunferencia “c”, sólo que ahora las circunferencias que determinan los otros vértices del hexágono “P subíndice uno”, “P subíndice dos”, “P subíndice tres” y “P subíndice 4” tendrán como centro los puntos “A” y “B” respectivamente, como se muestra en la figura.

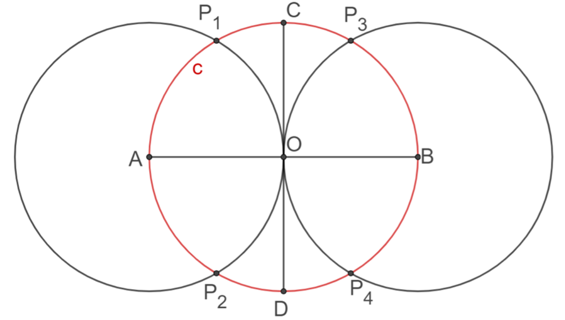
Ahora, une con segmentos de recta al punto “A” con el punto “P subíndice 1”, el punto “P subíndice 1“ con el punto “P subíndice 3”, el punto “P subíndice 3 “con el punto “B”, el punto “B” con el punto ”P subíndice 4”, y así sucesivamente hasta obtener un hexágono.

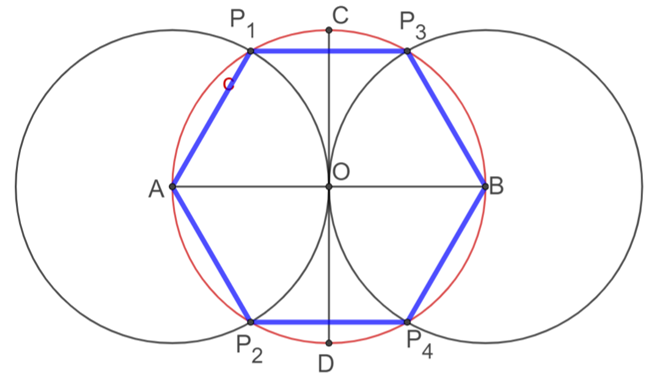
Compara las dos construcciones hechas del hexágono. Observa que los hexágonos que se obtienen en ambas construcciones son iguales, sólo que uno es la rotación o giro del otro, alrededor del punto O.

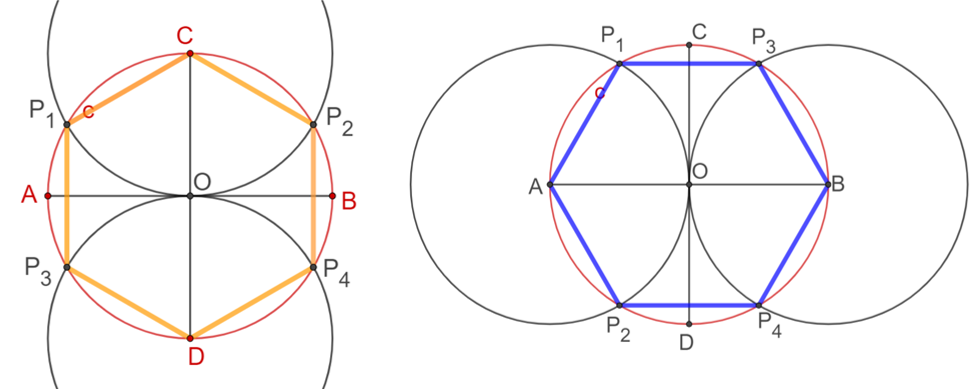
Al realizar ambas construcciones sobre una misma circunferencia “c” se obtiene una construcción como la siguiente. Recuerda que todas las circunferencias que trazaste tienen el mismo radio, que es igual a la longitud de los lados del hexágono que vas a construir. En esta construcción vas cambiando el centro de cada una de las circunferencias, al considerar como centro de ellas, uno a uno los extremos de los diámetros perpendiculares de la circunferencia “c”.

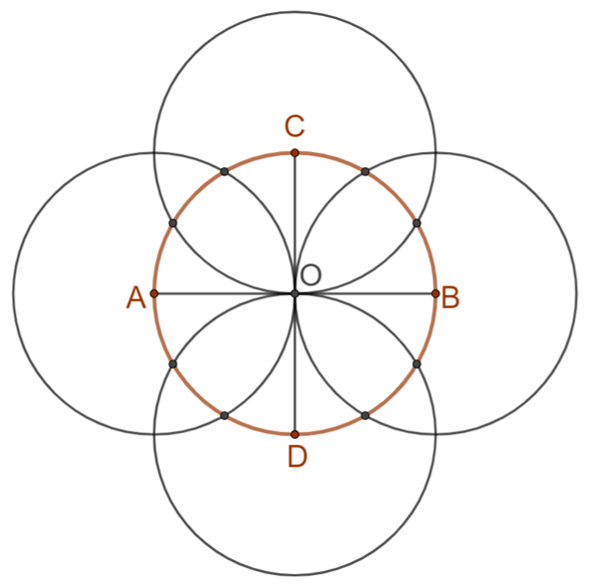
Considerando los puntos extremos “A”, “B”, “C” y “D” de los diámetros perpendiculares de la circunferencia central, así como los puntos de intersección de las circunferencias externas con la circunferencia inicial, ve uniendo consecutivamente con segmentos de recta dichos puntos para obtener los lados de un polígono regular del doble de lados que el hexágono, es decir, un dodecágono o polígono de doce lados.

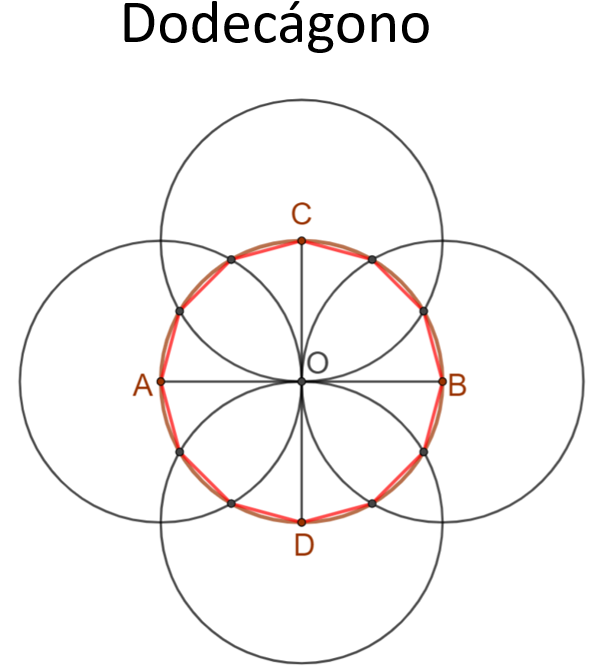
Como puedes observar, ya no sólo tienes la construcción de un hexágono regular sino has obtenido también un procedimiento para trazar un dodecágono regular, es decir, un polígono de doce lados y doce ángulos iguales. Pero recuerda que esta construcción surgió al cambiar de diámetro para iniciar el trazo del hexágono. Ahora, verás otra forma sobre cómo se van uniendo los vértices en la construcción del dodecágono.

Parte ahora de la ubicación de los puntos en la construcción que ha hecho para trazar al dodecágono. Para trazar el dodecágono, uniste con segmentos de recta, uno a uno, los puntos contiguos en la configuración obtenida. Pero, si ahora vas uniendo los puntos de manera alternada, es decir, de dos en dos, partiendo del punto “A”, lo unes con el punto “P subíndice 1”, de nuevo, repitiendo el proceso une con un segmento de recta el punto “P subíndice 1” con el punto “P subíndice 2”, después une el punto “P subíndice 2” con el punto “B” y así sucesivamente, hasta que vuelves a encontrar el punto “A”, del cual partiste, nota que obtienes de nuevo el hexágono.

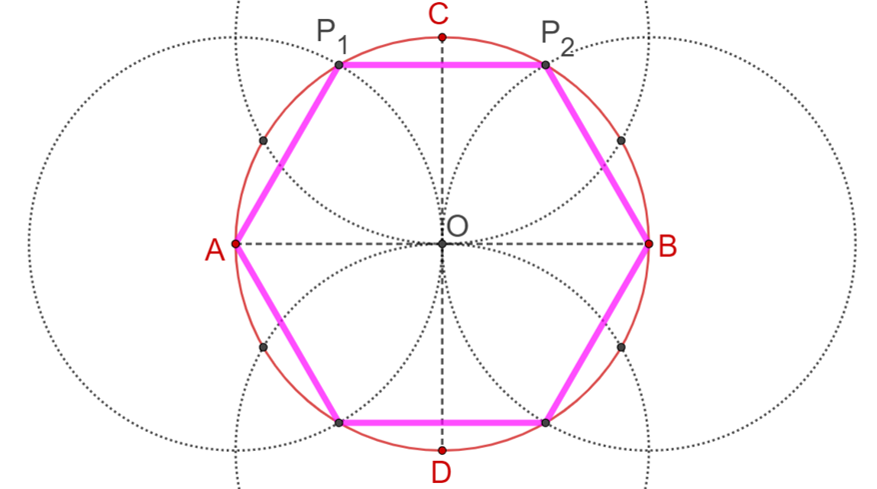
Ahora, si vas uniendo los vértices del dodecágono de tres en tres, es decir, traza el segmento de recta del punto “A” al punto “C”. Luego, traza el segmento del punto “C” al punto “B”, el segmento del punto “B” al punto “D” y finalmente el segmento del punto “D” al punto “A”, del cual partiste. Puedes notar que obtienes un cuadrado, que también es un polígono regular.

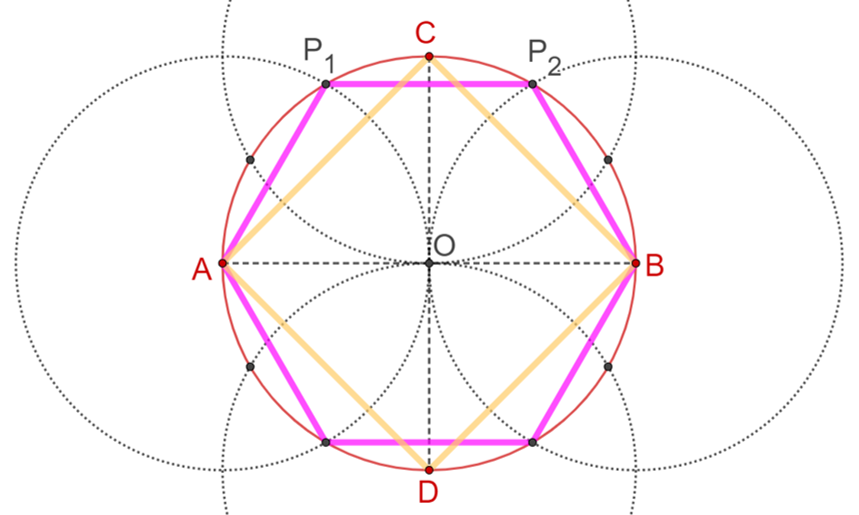
Realiza una construcción más, pero ahora uniendo los vértices del dodecágono de cuatro en cuatro.

Traza el segmento que parte del punto “A” al punto “P subíndice 2”. Luego, de este punto, traza un segmento al cuarto punto, contado desde ahí en sentido horario, para finalmente, unir este punto con el punto “A”. Así, has obtenido un triángulo equilátero.

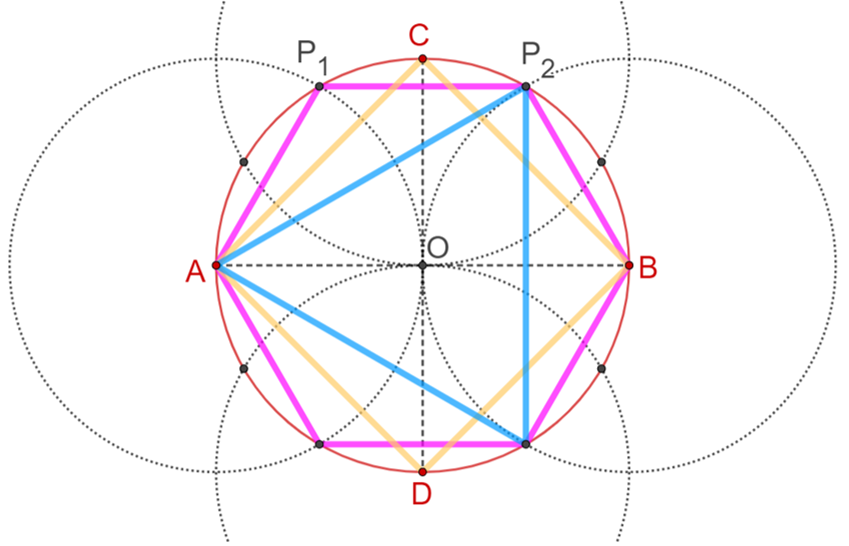
Hasta ahora, has estudiado una construcción geométrica con regla y compás para el hexágono regular, de donde, luego, obtuviste el dodecágono regular, el cuadrado y el triángulo equilátero. Analizando la forma en que se van uniendo los vértices del dodecágono descubriste que se van obteniendo distintos polígonos, lo cual puedes organizar en la siguiente tabla, donde en la primera columna se coloca el valor de “n”, en la segunda columna se indica de cuánto en cuánto vas eligiendo los vértices del dodecágono para ir trazando los segmentos que los unan y, en la tercera columna, el nombre del polígono que vas obteniendo.

De esta manera, cuando los 12 puntos se unieron consecutivamente, es decir, de 1 en 1, se obtuvo un dodecágono. Cuando los puntos se unieron alternadamente de 2 en 2, se obtuvo un hexágono. Luego, al unir los puntos de 3 en 3, se obtuvo un cuadrado. Posteriormente, al unirlos de 4 en 4, se obtuvo un triángulo equilátero.

¿Qué polígono regular se obtiene si ahora tratas de unir los vértices del dodecágono de 5 en 5?

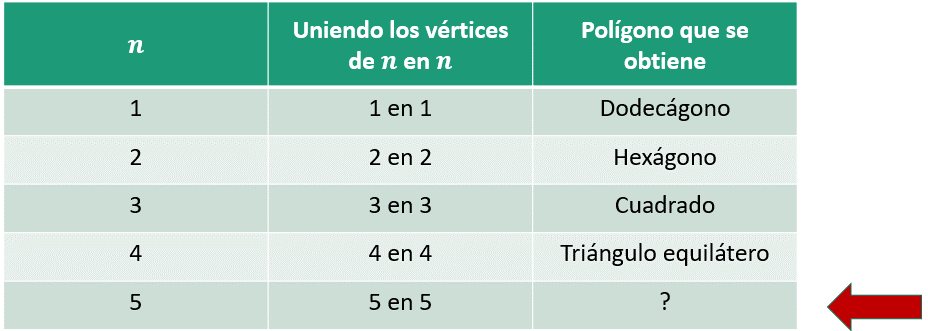
1, 2, 3 y 4 son divisores de 12, que son los vértices del dodecágono y 5 no es divisor de 12, por esto, no se pueden unir los vértices del dodecágono de 5 en 5 para obtener un polígono regular. Pero, ¿no habrá alguna manera de poder unir todos los vértices del dodecágono de 5 en 5?

Vuelve a considerar los vértices del dodecágono a partir de la construcción que ya conoces, así que ahora irás contando los vértices del dodecágono de cinco en cinco siguiendo un solo sentido ya sea en dirección de las manecillas del reloj o en dirección contraria, pero una vez que elegiste una de esas direcciones la vas a mantener para el resto de la construcción, por ejemplo, une el vértice “A” con el vértice “P subíndice 1” siguiendo la dirección de las manecillas del reloj o sentido horario.

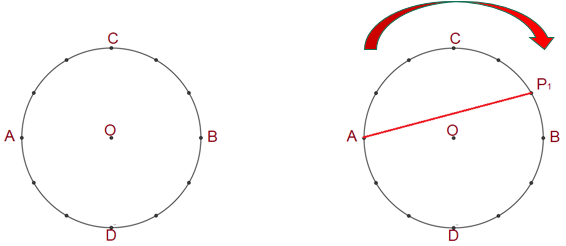
Continuando de la misma manera siguiendo la dirección de las manecillas del reloj, a partir del punto “P subíndice 1” cuenta 5 vértices para llegar a ubicar el vértice “P subíndice 2” para proceder a trazar el segmento de recta que los une y así obtienes un lado más del polígono que buscas construir. Continuando de la misma forma para ubicar el siguiente vértice, debemos unir el vértice “P subíndice 2” con el vértice “C”. De esta manera hemos trazado el tercer lado del polígono.

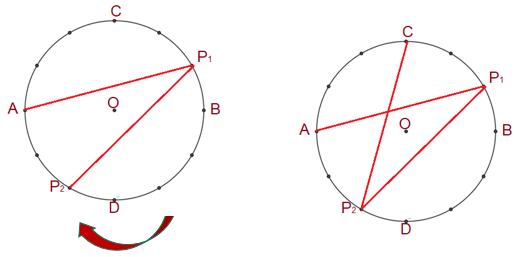
A partir del punto “C” cuenta 5 vértices en dirección de las manecillas del reloj, para llegar al vértice “P subíndice tres”. Traza el segmento que une al vértice “C” con el vértice “P subíndice tres”. ¿Ya puedes empezar a identificar qué figura vas obteniendo?

Pareciera que vamos a obtener una estrella. Continua.

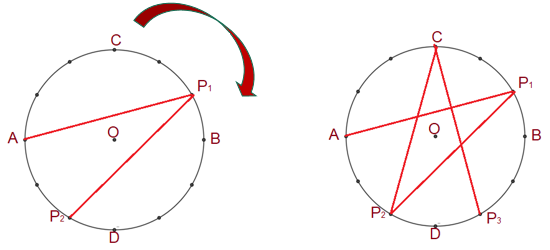
Pues bien, continuando con el conteo sobre los vértices del dodecágono de 5 en 5 en dirección de las manecillas del reloj, vas obteniendo más y más lados, al unir el vértice “P subíndice 3” con el vértice “P subíndice 4”, obtienes otro lado del polígono, para después unir el vértice “P subíndice 4” con el vértice “B” para obtener un lado más del polígono. Hasta aquí, si vas observando, estas recorriendo uno a uno los vértices del dodecágono. Continua de la misma manera en la que estas trazando los segmentos obtienes ¡una estrella!

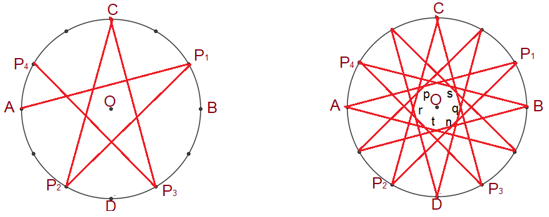
Has construido una estrella conformada por 12 puntas al realizar un recorrido por cada uno de los vértices del dodecágono, contados de 5 en 5. A esta figura que has construido se le conoce con el nombre de polígono estrellado.

Aquí algunos ejemplos de tal polígono estrellado que se obtuvieron jugando con los contrastes de color en sus lados, o en las regiones que ella abarca. Esto depende de tu imaginación para que vaya teniendo una estética visual tu obra de arte.

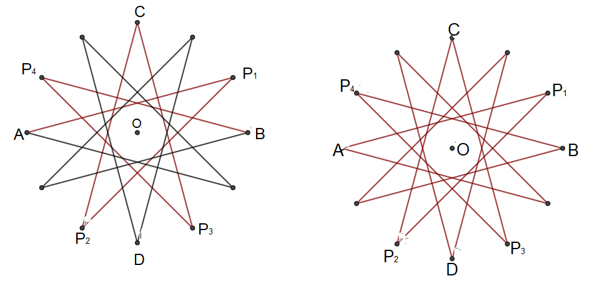
Analizando nuevamente los polígonos que obtuviste a partir de la manera como trazaste los lados al ir uniendo los vértices del dodecágono, puedes notar que el polígono estrellado es el único que cumple con la característica que sus lados pasan por todos los vértices del dodecágono, además de éste claro, pero lo más interesante consiste en que, conforme vas uniendo los vértices, también puedes hacerlo sin levantar el lápiz de la hoja de papel, es decir, los lados se trazaron de manera consecutiva. Este polígono estrellado de doce picos se puede hacer con un solo trazo.

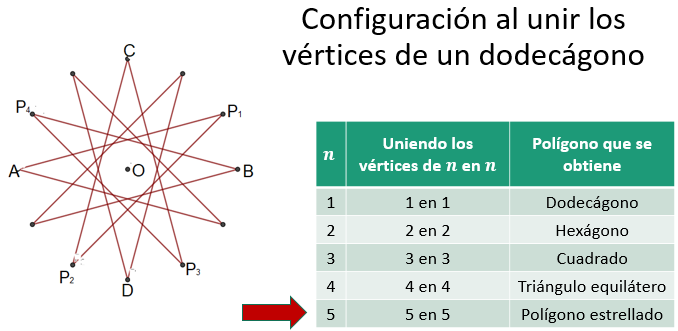
¿Para qué valor de “n” puedes seguir eligiendo la unión de los vértices del dodecágono?, ¿cómo puedes saber cuándo vas a obtener un polígono estrellado?

Una forma de descubrir las respuestas de nuevo está en la relación que existe entre el número de vértices o lados del dodecágono “L” y el valor “n” que indica como fuiste uniendo los vértices del dodecágono, observa la siguiente tabla:

Al considerar nuevamente la tabla donde anotaste los polígonos construidos previamente, y agregaste una columna al final en la cual anotaste las razones con numerador “L”, que es el número de vértices del polígono regular base, y denominador igual a “n” que indica la manera en que vas uniendo los vértices del polígono regular base. De esta manera obtienes las razones “12 sobre 1”, “12 sobre 2”, “12 sobre 3”, ”12 sobre 4 " y “12 sobre 5”. De las razones anteriores, solamente “12 sobre 5” no se puede reducir. Las demás dan como resultado, 12, 6, 4 y 3 respectivamente. “12 sobre 5” no se puede simplificar, la razón es irreducible, es decir, 12 y 5 son números primos relativos entre sí.

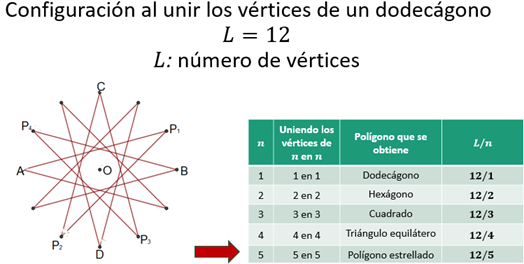
Dado un polígono regular de “L” vértices, obtendrás un polígono estrellado cuando la razón “L sobre n” es irreducible.

¿Para qué valor de “n” puedes seguir eligiendo la unión de los vértices del dodecágono?

Si sigues el mismo proceso en el dodecágono, cuando eliges los vértices de 6 en 6, obtienes un segmento de recta que es un diámetro, por lo que no se forma ningún polígono. A partir de ese momento, si se continua con la elección de los vértices para cantidades mayores a la mitad del número de vértices el polígono base, volverás a obtener los polígonos que ya tienes descritos en la tabla.

Para continuar con las construcciones específicas de polígonos regulares, verás ahora un procedimiento para la construcción de un octágono regular.

Inicia con el trazo de una circunferencia “c minúscula” con centro en el punto “O” y con una apertura cualquiera del compás. Luego, traza dos diámetros perpendiculares de dicha circunferencia. Nombra a esos diámetros AB y CD, como se muestra.

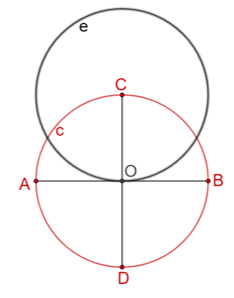
Posteriormente, se trazan las bisectrices a cada uno de los ángulos cuatro ángulos que se forman con los diámetros. Para ello, traza la circunferencia “e minúscula” con centro en el punto “C” y de radio igual a la circunferencia “c minúscula”, que trazaste primero.

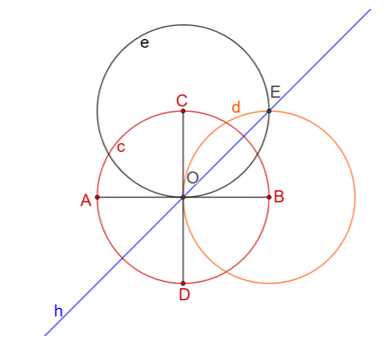
Ahora, traza la circunferencia “d minúscula” con centro en el punto “B mayúscula” con radio igual al de las otras dos circunferencias trazadas. Llamaremos “E mayúscula” al punto de intersección de las circunferencias “e minúscula” y “d minúscula”. Luego, traza la recta que une al centro “O” de la circunferencia “c minúscula” con el punto “E mayúscula”, para obtener la bisectriz “h minúscula” del ángulo “C mayúscula, O, B mayúscula”. Esta misma recta es bisectriz del ángulo “A mayúscula, O, D mayúscula”.

Para el trazo de la otra bisectriz, traza la circunferencia “k minúscula” con centro en el punto “A” y con radio igual al de las otras circunferencias trazadas. De esta manera se ubica el punto de intersección “F mayúscula” de las circunferencias “e minúscula” y “k minúscula”. Traza la recta que pasa por los puntos “F mayúscula” y el centro “O” de la circunferencia “c minúscula” que será la bisectriz “i minúscula” del ángulo “A mayúscula, O mayúscula, C mayúscula” y también del ángulo “D mayúscula, O mayúscula, B mayúscula”.

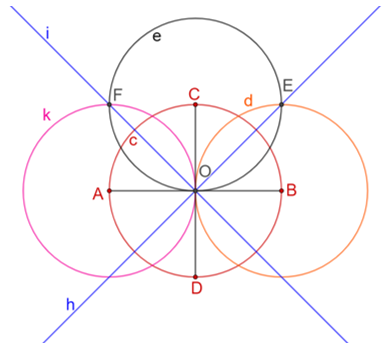
Marca los puntos de intersección “P subíndice uno”, “P subíndice dos”, “P subíndice tres” y “P subíndice cuatro” de las bisectrices “i minúscula” y “h minúscula” con la circunferencia “c” minúscula. Estos puntos, junto con los extremos de los diámetros perpendiculares, serán los vértices del octágono.

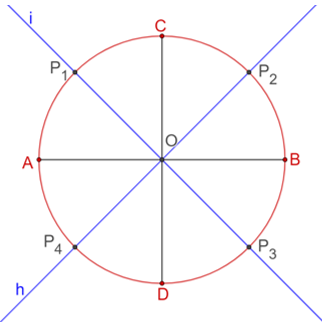
Partiendo del punto “A mayúscula”, traza un segmento de recta al punto “P subíndice 1”, para obtener el primer lado del octágono. Ahora, une el punto “P subíndice uno” con el punto “C mayúscula” para obtener otro lado del octágono y así sucesivamente vas obteniendo los demás lados del octágono, uniendo de 1 en 1 los puntos marcados sobre la circunferencia “c minúscula”.

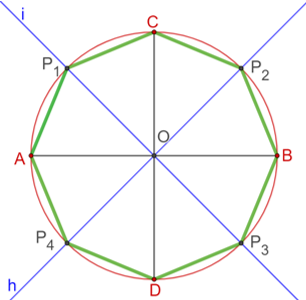
Como te puedes dar cuenta, los lados del octágono se fueron uniendo de 1 en 1 para así obtener esa figura. Ahora, ¿Existe un polígono estrellado inscrito en el octágono?

Para responder a esta pregunta vas de nuevo a organizar los datos en una tabla. Recuerda que L es igual a 8, dado que L corresponde al número de vértices del octágono.

Construye una tabla con cuatro columnas donde en la primera columna aparece el valor de “n”. En la segunda columna se indica de qué manera se unen los vértices del octágono. En la tercera columna aparece el nombre del polígono regular que se obtiene y en la última columna las razones entre el número de vértices “L mayúscula” y el valor de “n minúscula”. Como las razones “8 sobre 1” y “8 sobre 2” se pueden reducir, esto indica que de esa manera se pueden construir polígonos regulares, un octágono y un cuadrado, respectivamente.

Cuando los vértices se van uniendo de 3 en 3, se obtiene la razón “8 sobre 3”, que es irreductible. Esto nos indica que, uniendo los vértices de esa manera, siguiendo un mismo sentido, es posible construir un polígono estrellado. Por otro lado, al querer unir los vértices de 4 en 4, lo que se obtiene es una recta.

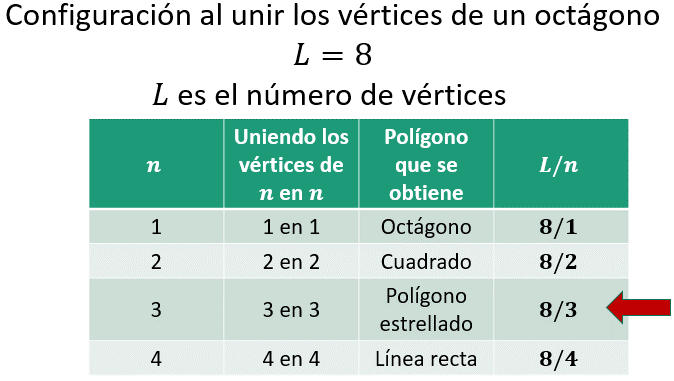
Ahora realiza la construcción del polígono estrellado.

Para trazar el primer lado del polígono estrellado, que se encuentra inscrito en el octágono, traza el segmento de recta para unir al vértice A con el punto “P subíndice 2”, como se muestra en la imagen. Como la ubicación de los puntos anteriores se hizo siguiendo el sentido de las manecillas del reloj, así continuaras uniendo los vértices del octágono. Para trazar el segundo lado traza el segmento de recta que une al vértice “P subíndice dos” con el vértice “D mayúscula”.

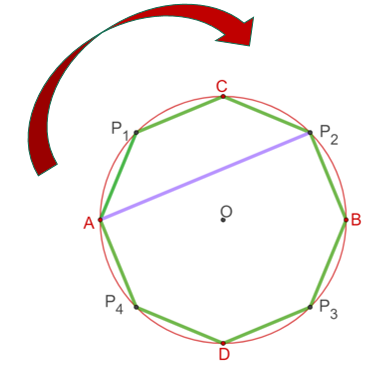
A continuación, se une el vértice “D mayúscula” con el vértice “P subíndice uno”. Luego, une el vértice “P subíndice uno” con el vértice “B mayúscula” para obtener un lado más del polígono estrellado.

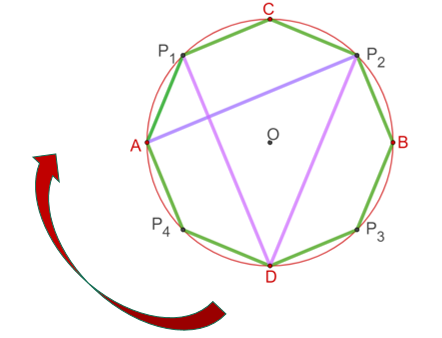
Al seguir uniendo todos los vértices del octágono de la misma manera, obtienes el polígono estrellado correspondiente a la razón “8 sobre 3”. Puedes hacer con tus trazos una composición como la que se muestra en la siguiente imagen.

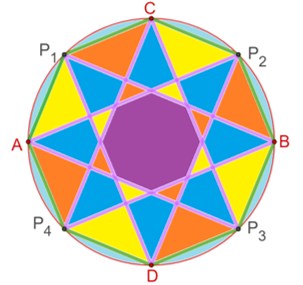
Recuerda que éste es un material de apoyo y que puedes consultar otras fuentes para complementar lo que aprendas aquí.

El Reto de Hoy:

Trazar un pentágono regular por cualquiera de los métodos de construcción vistos en su curso de Matemáticas II.
Construir una tabla para determinar los polígonos estrellados que se pueden formar a partir de un pentágono regular.
Trazar los polígonos estrellados que obtuvieron en el paso anterior.
Hagan una composición usando el pentágono regular y los polígonos estrellados que se forman. No olviden que pueden hacer contrastes de color, ya sea en los lados de los polígonos o las regiones que delimitan sus lados, cuando estos se encuentran sobrepuestos. ¡Echen a volar su creatividad e imaginación!

Recuerda que puedes elaborar tus notas, considerando las ideas más importantes del tema de hoy, y sobre todo, anota tus dudas y posibles dificultades.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

Compra en Amazon

Campaña evaluada

Aprendizaje esperado: Diseña una campaña escolar para proponer soluciones a un problema de la escuela.

Énfasis: Evaluar campañas.

¿Qué vamos a aprender?

En esta sesión, aprenderás a evaluar campañas, es decir, valorar el impacto de aquellas campañas escolares que has realizado o realizarás durante el ciclo escolar.

Esto es importante, pues te permite saber si la campaña escolar cumplió su objetivo.

¿Qué hacemos?

Seguramente has identificado, te han platicado o has vivido problemáticas que pueden estar presentes en tu escuela o en tu comunidad. Por ello, dialogar, tomar decisiones y fomentar la participación para crear nuevos hábitos para vivir en armonía, con el entorno natural y social, a partir de campañas escolares, permite visibilizar y sensibilizar ciertos problemas que afectan a una comunidad.

También es cierto que, generalmente, se decide realizar una campaña escolar, pero al final, aunque ésta atienda asuntos importantes para la comunidad escolar, no se realiza una evaluación, a partir de una asamblea, para saber si ésta funcionó o surtió efecto.

Una campaña es un conjunto de actividades que hace una persona o un grupo de personas para alcanzar un fin en un plazo determinado o hasta que se logre el objetivo propuesto. En nuestra cotidianidad hay muchos problemas por resolver, y hay que hacer conciencia y actuar de inmediato.

Antes de entrar en materia recuerda que los pasos para realizar una campaña son:

Organizar una asamblea en el salón para identificar los problemas de la comunidad escolar.
Formar equipos en asamblea para que elijan un problema y analicen sus causas.
Diseñar en equipo una campaña para resolver el problema elegido.
Revisar en asamblea las campañas y organizar la forma de difundirlas.
Evaluar en asamblea los resultados de las campañas

Analiza el siguiente ejemplo; en una secundaria ubicada al norte de Veracruz, existe un problema recurrente de basura y en una asamblea se decidió realizar una campaña para darle solución y el eslogan fue: “Por una comunidad sin basura”.

En la actualidad existen escuelas en contextos rurales con presencia de grupos culturales originarios o indígenas que trabajan de forma colaborativa como el tequio. Es decir, trabajan en conjunto, se ayudan mutuamente. Esto es muy importante porque cuando se realizan campañas escolares la comunidad también se involucra.

Medir estas campañas suele ser sencillo, porque toman acuerdos y cada cual trabaja con ahínco para lograr lo que le corresponde.

Para evaluar la campaña se debe realizar una asamblea. Una asamblea escolar es la reunión de un grupo para informar, debatir y solucionar temas de interés común, y esto favorece la participación colectiva en términos de igualdad y respeto.

También se toman acuerdos que son importantes. En la secundaria que se muestra en el ejemplo, asisten alumnas y alumnos que hablan náhuatl, tutunaku y español, ellos asumen con formalidad los acuerdos, porque en esas campañas escolares se involucran las madres, padres de familia y la comunidad en general.

Una asamblea se conforma por:

El coordinador que es el que da la palabra a las y los participantes.
Secretario. Es quien registra las participaciones y los comentarios.
Y los participantes son el resto del grupo, que se expresan de manera respetuosa, libremente, opinan, comentan y hacen propuestas argumentadas.

En algunas asambleas escolares en zonas rurales donde asisten alumnas y alumnos de diferentes grupos culturales, se conservan las formas organizativas de sus pueblos indígenas u originarios.

Es importante tener esto presente al momento de realizar la evaluación, ya que permite ver desde distintas perspectivas el impacto de la campaña realizada. Sobre todo, para que las y los participantes logren acuerdos de manera ordenada.

La evaluación permite no sólo corroborar si surtió efecto nuestra campaña escolar, sino que permite trabajar, en un futuro, en la efectividad de la misma o, en su defecto, dirimir en una asamblea si se requieren hacer ajustes de más tiempo u otras tácticas para que, de verdad, el cambio se vea reflejado en las acciones.

Para esa campaña escolar se realizaron carteles en tres lenguas: tutunaku, náhuatl y español. Para buscar estrategias concientizando a las y los alumnos de la comunidad. También se realizaron audios para perifoneo.

AUDIO 01 TUTUNAKU

DURACIÓN: 00:05

https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202104/202104-RSC-ec6x2x3kJv-AUDIO01CARTELTUTUNAKU.mp3

AUDIO 02 TUTUNAKU

DURACIÓN: 00:05

https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202104/202104-RSC-OE46uA3NsT-AUDIO02CARTELTUTUNAKU.mp3

En la imagen del cartel en tutunaku de la sierra norte de Puebla puedes observar que se utilizaron algunos elementos regionales como las hojas de plátano, con el fin de envolver o empaquetar algún producto de consumo, por ejemplo: el queso o la carne. Para productos líquidos utilizan los guajes, las jícaras, el cántaro y en lugar de bolsas de plástico para hacer sus compras utilizan un morral de ixtle. Estos métodos los rescataron desde la voz de sus abuelas y abuelos, porque les contaron que antes no se usaba el plástico.

Muchas comunidades locales e indígenas han desarrollado modos de vida y prácticas íntimamente ligadas a la naturaleza, que son respetuosas con el medioambiente. Los valores espirituales que se atribuyen han ayudado a proteger la biodiversidad de nuestro país. Si bien las personas mayores son las principales depositarias del patrimonio. Cada miembro de la comunidad juega un papel en la protección de los recursos naturales.

En los carteles que se diseñaron, el lema fue: “Yo cuido, tú cuidas, todas y todos cuidamos”. El objetivo era disminuir la cantidad de desechos que se generan en la escuela y la comunidad. Buscando sensibilizar y concientizar sobre el uso del plástico, usando otros recursos que no causen daño al medio ambiente.

Un valor social que rescatan es el respeto y el compromiso de cada alumna y alumno, así como la participación de los habitantes de la comunidad para tener un lugar limpio, el mensaje central fue: Todas y todos somos responsables de los desechos que producimos y somos responsables de ello.

AUDIO 03

https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202104/202104-RSC-kLIkzehiat-AUDIO03CARTELNAHUATL.mp3

Una campaña debe ir acompañada de elementos visuales que llamen la atención. Esto se observa en los carteles, pues se incluyen recursos naturales para dar a entender que hay elementos que pueden utilizar para cuidar el medio ambiente, y evitar el uso del plástico. También es importante utilizar elementos de audio.

Para saber cómo evaluar una campaña primero tienes que saber que la evaluación es un medio que se realiza de forma ordenada, encaminada a identificar, obtener y promocionar información suficiente para emitir un juicio o valor.

La evaluación es el medio por el cual puedes darte cuenta de los resultados obtenidos, si se necesita restructurar algunas actividades de la campaña, por ejemplo, elaborar más carteles, colocarlos en espacios donde las personas puedan leerlos, entre otros, y el impacto que generó, ya sea positivo o negativo.

Recuerda que es importante organizarse para examinar los efectos de la campaña y una técnica que ayuda es la reunión en asamblea.

Se dialoga sobres los pros y contras de la campaña.
Con los resultados obtenidos en la difusión de los carteles durante los dos meses de promoción o el tiempo que se decida ocupar, se empiezan a realizar algunas encuestas y entrevistas.
Posteriormente, se reúnen para llevar a cabo el análisis de datos y gráficos en grupo. Platicando los efectos obtenidos.

Otra manera de obtener información podría ser a través de opiniones, pláticas, encuentros, votos y observaciones, pero lo importante es hacerlo a partir de preguntas precisas o cuestionamientos que inviten a la reflexión de si hubo o no cambios.

Se utilizan dos tipos de evaluación: la primera, que es cualitativa, utiliza la observación, la entrevista, las notas, las opiniones y los comentarios. La segunda, que es la cuantitativa, se realiza por medio de cuestionarios con preguntas cerradas, permitiendo realizar conteos y estadísticas de las respuestas emitidas por un cierto número de población.

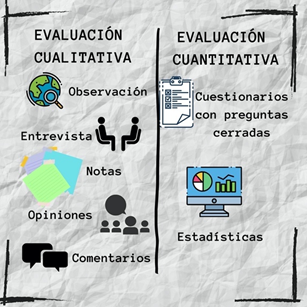
Si quisieras, entonces, evaluar una campaña, primero deberías hacerte las siguientes preguntas:

¿A quién dirigirías la entrevista?
¿Qué tipo de preguntas realizarías?

Recuerda que puedes hacer cuestionarios con preguntas abiertas y con preguntas cerradas, como en el siguiente ejemplo:

En las preguntas abiertas, las personas pueden opinar a partir de su punto de vista y en las preguntas cerradas sólo pueden elegir entre las opciones que se presentan, ya sea marcando con una “x”, subrayando o escribiendo “sí” o “no”. También se podría hacer una evaluación que valore la participación individual de los responsables de la campaña, es decir, si participaron en la identificación del problema, se comprometieron al momento de implementarla y si realizaron las tareas encomendadas. A esta evaluación personal se le conoce como autoevaluación.

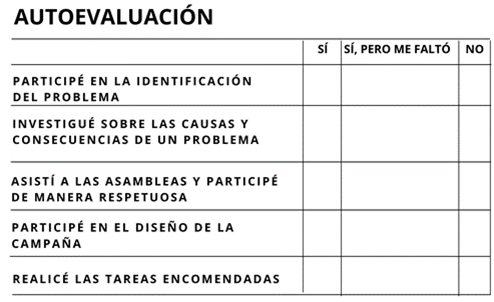
Esta evaluación es personal, cada uno puede evaluar su contribución y el desempeño logrado en la campaña, desde su propia perspectiva.

Hay otro tipo de evaluación conocida como coevaluación este tipo de evaluación se caracteriza porque el grupo evalúa la participación de las y los integrantes de manera individual, pero no para señalar todo el tiempo de manera negativa, sino resaltando lo positivo y las áreas de oportunidad.

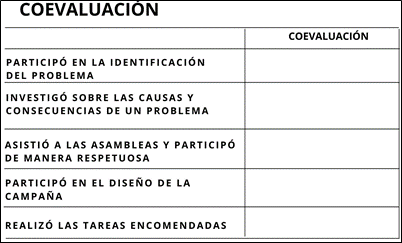
La evaluación es importante ya que permitirá valorar el éxito de la campaña o dará información sobre lo que faltó, por lo que las preguntas o aseveraciones deberán ser muy precisas para no confundir al entrevistado. Y, además, estas acciones deben aplicarse a la mayor cantidad de alumnas y alumnos, pues de otra manera los resultados no estarán respaldados de forma amplia.

En las asambleas para la evaluación de la campaña escolar es importante valorar la participación de las y los miembros de la comunidad educativa en las acciones organizadas que se realizaron. Éstas son valiosas porque con ellas se logra influir y transformar el entorno. Observa el siguiente video que muestra como al organizarse, se pueden obtener grandes logros no sólo para la escuela sino para la comunidad en general.

Acciones organizadas

Formación Cívica y Ética, Primer grado, Bloque 3

Del minuto 01:04 al 03:41

https://youtu.be/74e3tGlgiPo

Como observaste, las acciones que realizaron las y los alumnos, no sólo resultaron efectivas, sino que con el premio que ganaron realizaron mejoras comunitarias, con esto se puede decir que la evaluación de la misma resultó ser todo un éxito.

Además, pusieron de manifiesto sus saberes, experiencias, conocimientos, habilidades y actitudes necesarias para el diálogo y la escucha, buscando la construcción colaborativa de propuestas que respondieran a sus necesidades y contextos, éstas son habilidades que deben manifestarse en el momento de diseñar, pero sobre todo evaluar campañas escolares.

Es muy importante evaluar los alcances cuantitativos y cualitativos de la misma. Es decir, no solo se evalúa el posible éxito de la campaña en cuestiones que pudieran parecer subjetivas como lo son la colaboración y el trabajo en equipo, sino que además hay campañas como la que acabamos de ver, que se pueden evaluar con números, por ejemplo: El número de baños ecológicos que fueron instalados en la escuela a partir del éxito de la campaña, entre otros.

Estos son alcances cuantitativos y es muy importante que sean considerados en cualquier evaluación de una campaña y aún más importante y necesario que en la planeación de la campaña se proyecten esos posibles alcances, así, al momento de hacer la evaluación de dicha campaña, se podrá saber si los objetivos en cuanto a números se alcanzaron.

Así como es importante poder evaluar la participación de las y los miembros de la comunidad educativa, también lo es evaluar los resultados y los objetivos cumplidos de cada campaña. Y la manera más clara de lograrlo es a través de una valoración cuantitativa y cualitativa de esos objetivos y resultados.

Con esto queda clara la importancia de evaluar las campañas, ya que esto permite conocer el impacto que tienen y, sobre todo, crear conciencia y cambios en nuestra sociedad para mejorar nuestra calidad de vida.

El Reto de Hoy:

A partir de la experiencia de campaña del siguiente video, evalúa los resultados. Escribe en tu cuaderno cómo se llamó la campaña, cuáles fueron sus resultados, y cómo podrías evaluar el efecto en la comunidad escolar.

Cuidado del medio ambiente: reduce, recicla, reutiliza

Geografía, Primer grado, Bloque 3

Del minuto 00:22 al 1:15

https://www.youtube.com/watch?v=oIkl1bTkI8o&t=140s

Te invitamos a que participes en las asambleas de evaluación de las campañas que se realizan en tu escuela para que puedas ver los resultados obtenidos durante su desarrollo.

También te proponemos hacer una campaña con las problemáticas que hay en tu escuela o comunidad. No olvides que pueden ser diversos temas como el uso de las lenguas en el espacio escolar, la falta de agua, entre otros.

Por último, te invitamos a que investigues y revises los resultados de las campañas realizadas en tu escuela o en tu comunidad. Sobre todo, que profundices en los cambios que hubo en la población y revises tu libro de texto, pues ahí encontrarás aspectos de las campañas escolares.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

Compra en Amazon

InteriorizARTE

Aprendizaje esperado: Experimenta las propiedades del cuerpo, el tiempo y el espacio para crear atmósferas inmersivas que relaciona con obras o manifestaciones artísticas.

Énfasis: Relacionar una memoria o experiencia pasada con el significado interpretado en una obra o manifestación artística para recrearla mediante una atmósfera inmersiva.

¿Qué vamos a aprender?

El propósito de esta sesión es que relaciones una experiencia propia con el significado interpretado de una obra artística ya existente para recrear una memoria.

¿Qué hacemos?

El movimiento puede definir sensaciones, ilustrar un momento en particular o ayuda a decir lo que con palabras no nos es posible. Trata de hacer memoria, de encontrar alguna posición que te recuerde algo en particular, algún gesto o movimiento.

Desde que nacemos, el cuerpo va adquiriendo memoria, es decir, va guardando aquellos movimientos, posturas, gestos, sensaciones y emociones que nos permiten expresarnos. En el arte no solo nos expresamos de manera verbal, también lo podemos hacer a partir del cuerpo, de la voz, del movimiento.

El cuerpo guarda memorias a partir de las emociones y sensaciones que hacen que éste se mueva, muchas veces de manera involuntaria, pero que sirven como recurso expresivo.

Te invitamos a colocarte, si es posible, en un espacio donde te puedas desplazar sin obstáculos, para evitar chocar con algo a la hora de realizar la dinámica que te propondremos en esta sesión. Con la ayuda de tu imaginación, vas a recordar memorias, es decir momentos y circunstancias en determinados lugares. Esto será de gran utilidad para desarrollar esta actividad.

Justo estas memorias te llevan a preguntar: ¿cómo es que se mueve mi cuerpo solo?, ¿cómo se mueve cuando se relaciona con otros cuerpos?, ¿qué hace que tenga movimiento?

Detente un momento y recuerda que posición suele adoptar tu cuerpo cuando pasa algo que te pone triste o enojada o enojado, cuando viajas en el transporte público o vas caminando por la calle, cuando miras tu programa favorito o estás realizando tu tarea.

El día de hoy, vas a buscar en tus memorias corporales, recuerda y lleva tu cuerpo a esa acción.

¿Te has dado cuenta que el cuerpo todo el tiempo está expresando algo a partir de las actividades y emociones que realizamos día con día?

Una situación, un contexto, te puede llevar a identificar lo que sucede en ese momento, gracias a lo que tu cuerpo dice con sus posturas y movimientos. A eso se le conoce como “lenguaje no verbal”, el cual permite transmitir un mensaje mediante posturas, gestos faciales y movimientos voluntarios e involuntarios del cuerpo y rostro.

Haz una exploración de movimientos y genera una secuencia coreográfica. Lo primordial es hacer consciente tu movimiento, es decir, poner atención y sentir como reacciona tu cuerpo con cada movimiento, pero antes, vas a preparar tu cuerpo para el trabajo expresivo. Colócate en una posición neutra y ahora:

Respira profundamente y con cada respiración ve sintiendo como entra el aire a tu cuerpo. Pon atención ya desde ahora en cómo se mueve tu cuerpo con cada inspiración y exhalación y ve guardando esa sensación en tu mente.

Destensa cada parte del cuerpo sin perder la atención a tus movimientos y donde sientas tensión, permite que el aire se la lleve con cada exhalación. Vas a trabajar el cuerpo en tres niveles, el nivel bajo, el nivel medio y el nivel alto.

Flexiona un poco tus rodillas, deja caer tus brazos y piernas, y comienza a balancearte de un lado a otro para relajar cada parte de los músculos, inhalando y exhalando en todo momento. Cambia de peso de una pierna a otra.

Recuerda ubicarte en un espacio donde puedas moverte libremente. Pero, si las circunstancias no te lo permiten, puedes hacerlo solo con tus manos, un movimiento expresivo, o solo con gestos. Recuerda que no hay obstáculos para la creatividad.

Como sugerencia te proponemos utilizar algún elemento sonoro para ir generando tu propuesta de movimientos. Puedes utilizar por ejemplo botellas rellenas de piedritas o con algún tipo de semillas, también puedes también utilizar el sonido del ambiente que hay en el lugar donde te encuentres para interpretarlo con movimientos corporales.

De igual manera puedes agregar un elemento más que adorne el movimiento como palitos de madera con listones de es. Explorando en tu memoria, podrías representar con tu cuerpo cuando llegas a una fiesta, o cuando entras a un lugar donde todos están muy serios. Intenta representar esas atmosferas con tu cuerpo.

Tu cuerpo de verdad tiene memoria, recordar es revivir momentos y situaciones no solo de forma visual sino corporal. Te invitamos a que, a partir de este momento, recuerdes no solo a través de la memoria, sino con todo el cuerpo: siente, percibe, entiende y reflexiona tus pasos al andar.

Por ejemplo, ahora que debemos permanecer encerrados, suele ser un poco frustrante, probablemente te haga sentir atrapado. No poder salir o quizá moverte con más libertad puede causar muchas emociones, las cuáles a través de los movimientos se pueden ir liberando.

El Reto de Hoy:

Te invitamos a que, realices este proceso de secuencia de movimientos, lo dejes plasmado en tu cuaderno, añadiendo ahí como te sentiste al realizarlo o que emoción resulto de ello. Y si no pudiste realizarlo, igual describe o dibuja lo que te produce imaginarlo.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

Compra en Amazon

¿Por qué el cielo es azul?

Aprendizaje esperado: Describe la generación, diversidad y comportamiento de las ondas electromagnéticas como resultado de la interacción entre electricidad y magnetismo.

Énfasis: Analizar el fenómeno de dispersión de Rayleigh que, en conjunto con la atmósfera terrestre, hace que veamos el cielo de azul.

¿Qué vamos a aprender?

Reflexionarás sobre el del cielo, con base en lo que se ha tratado en sesiones anteriores. Para esta sesión el propósito es: Analizar algunos fenómenos luminosos, que ocurren en la atmósfera terrestre, y cómo intervienen en la percepción del del cielo.

¿Qué hacemos?

Inicia por reflexionar un momento acerca de lo que sabes respecto a la pregunta plateada: ¿a qué supones que se debe el del cielo?

En ese caso tenemos que considerar cómo interactúa la luz con la materia. En sesiones anteriores ya se habló de esto, ¿recuerdas qué fenómenos se relacionan con el comportamiento de la luz?

Se trata de los fenómenos de la reflexión y la refracción de la luz.

La reflexión es el cambio de dirección de los haces de luz que ocurre en un mismo medio, después de incidir sobre una superficie.

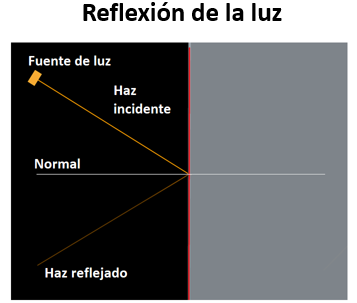
En la refracción también hay un cambio de dirección de los rayos de luz, pero ocurre al pasar de un medio a otro en el que la luz se propaga con distinta velocidad.

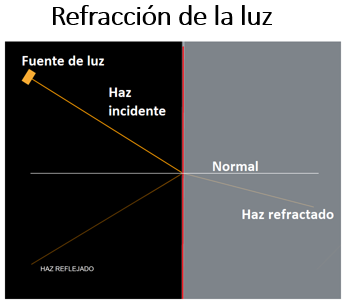
Retomarás estos fenómenos a lo largo de toda la sesión para que elabores una explicación a la pregunta.

Asimismo, hay que considerar que la luz se propaga en línea recta y al interactuar con algún medio, puede desviar su dirección, como sucede en los fenómenos de reflexión y refracción.

La luz del Sol está compuesta por luz de los es que identificamos en el arcoíris. Cuando vemos luz blanca, estamos percibiendo, al mismo tiempo, la luz de los es que la conforman. La belleza del cielo y del arcoíris es el resultado de la interacción de la luz del Sol con la atmósfera. Una cantidad de humedad, relativamente pequeña es suficiente para provocar en el cielo las múltiples manifestaciones de , entre ellas el arcoíris.

Es posible descomponer la luz blanca en los diferentes es que la forman, mediante un prisma. La luz se abre en un abanico de es, ya que al refractarse se obtiene una gama de es: violeta, azul, verde, amarillo, naranja y rojo.

Se trata de la dispersión de la luz visible, que forma parte del espectro electromagnético, que se relaciona con el comportamiento de onda de la luz. Te invitamos a observar el siguiente video para hacer un recordatorio de estos fenómenos y puedas relacionarlos con el del cielo.

Ondas electromagnéticas

Ciencias y Tecnología. Física, Segundo grado, Bloque 2

Del minuto: 01:28 al 02:00, del 02:22 al 03:21 y del 03:35 al 04:05

https://youtu.be/kULLeGOQOyo

La luz blanca está compuesta por ondas que corresponden a los distintos es, En el vacío la luz viaja a la misma velocidad, pero ¿qué sucede al pasar por un medio?

Recuerda lo que ocurre en la formación del arcoíris: los es de la luz visible, cada uno tiene diferente longitud de onda y al incidir en las partículas de agua se refractan, pero de manera diferente.

Y al refractarse cambia su velocidad en ese medio. Por eso se dispersan y forman los diferentes es del arcoíris.

Es importante señalar que en la atmósfera terrestre hay pequeñas partículas de gases, como el oxígeno, así como dióxidos de carbono y de nitrógeno que absorben y reemiten la luz. Además, hay partículas de polvo y gotas de agua. Cuando la luz solar llega a nuestro planeta, las pequeñas partículas de la atmósfera causan que la luz de algunos es se desvíe y que la de otros es siga su curso.

Observa el siguiente video que elaboró el Instituto de Astronomía y la Facultad de Ciencias de la UNAM, en el que participa la doctora Julieta Fierro, quien explica de manera muy sencilla ¿por qué el cielo es azul?

¿Por qué el cielo es azul? Clase de astronomía para la primaria con Julieta Fierro.

Ciencias TV

Del minuto 00:45 al 03:49

https://www.youtube.com/watch?v=-yXY4YL3_7A&ab_channel=CienciasTV

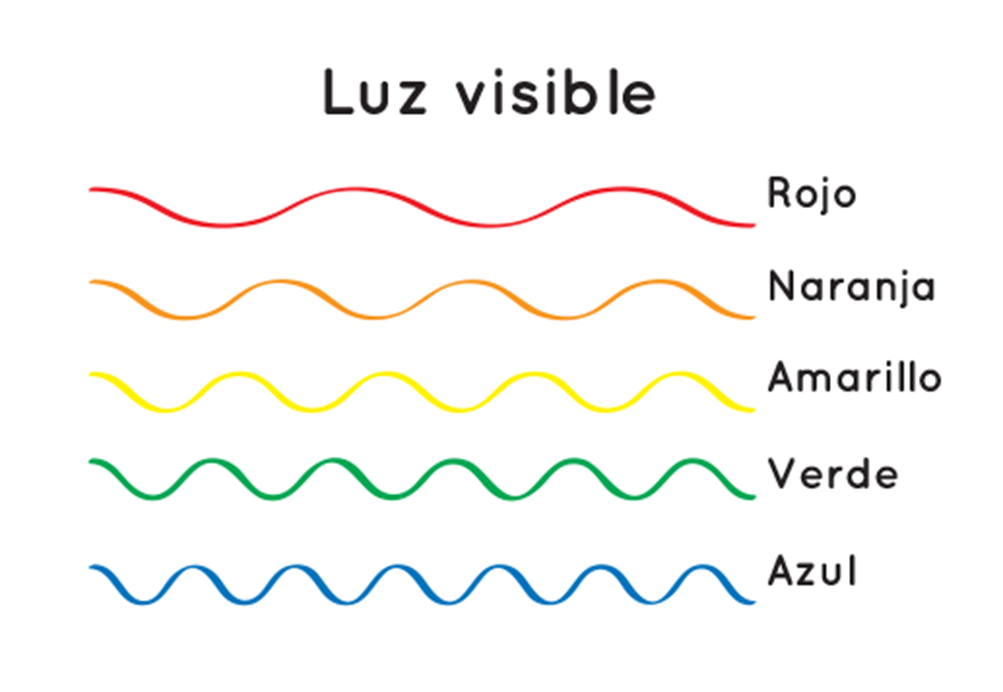
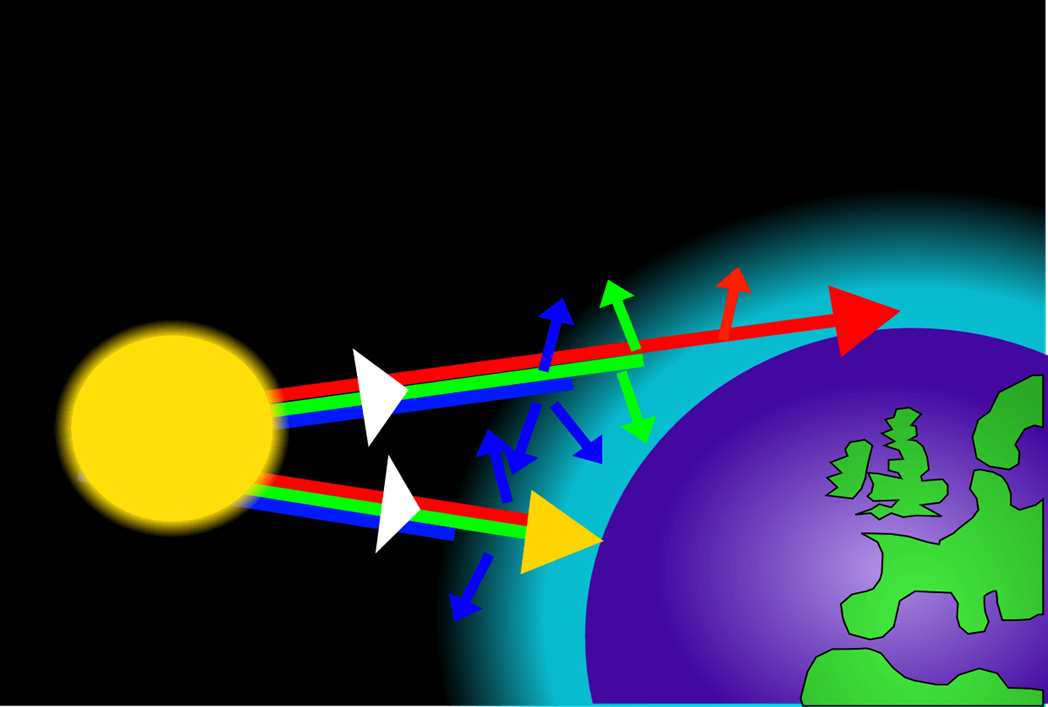
Los distintos es que forman la luz del Sol, se comportan diferente al interactuar con las partículas de la atmósfera. Esto se debe a las características de los diferentes es que conforman la luz blanca. Como se puede observar en la imagen, la luz roja tiene una longitud de onda mayor y la luz azul tiene menor longitud de onda.

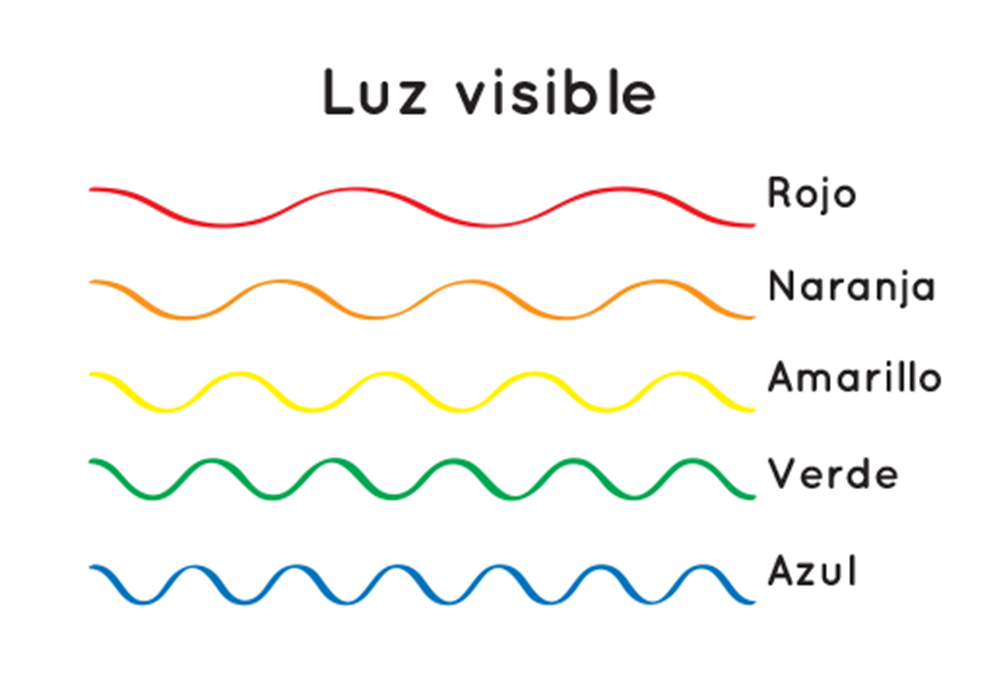
La longitud de onda de los diferentes es de la luz influye en el del cielo. La luz que tiene longitudes mayores como la roja, naranja, amarilla y verde, se propaga sin ser perturbada; mientras que la luz de longitud menor, como la azul y la violeta, cambia su curso al encontrarse con partículas que tienen un tamaño menor a la décima de una micra.

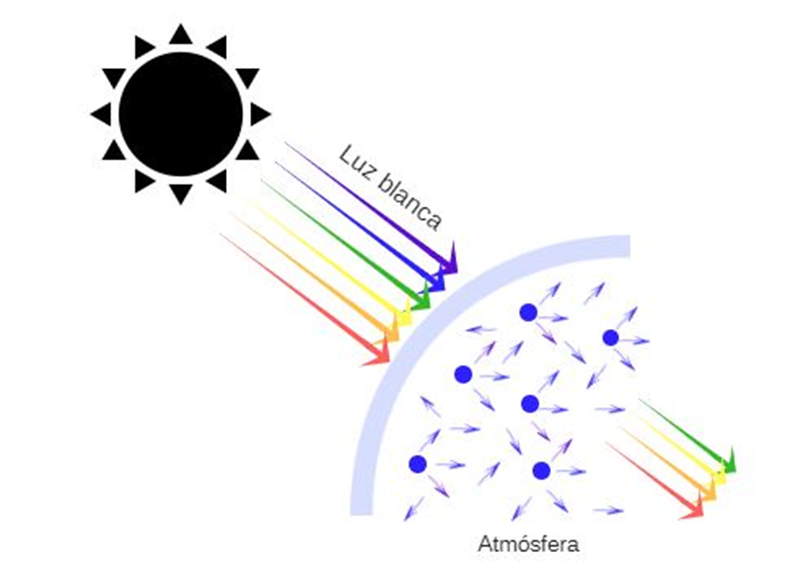
Finalmente, nosotros percibimos la luz azul que ha sido dispersada y reflejada, y por diferentes procesos, por muchas partículas de la atmósfera terrestre.

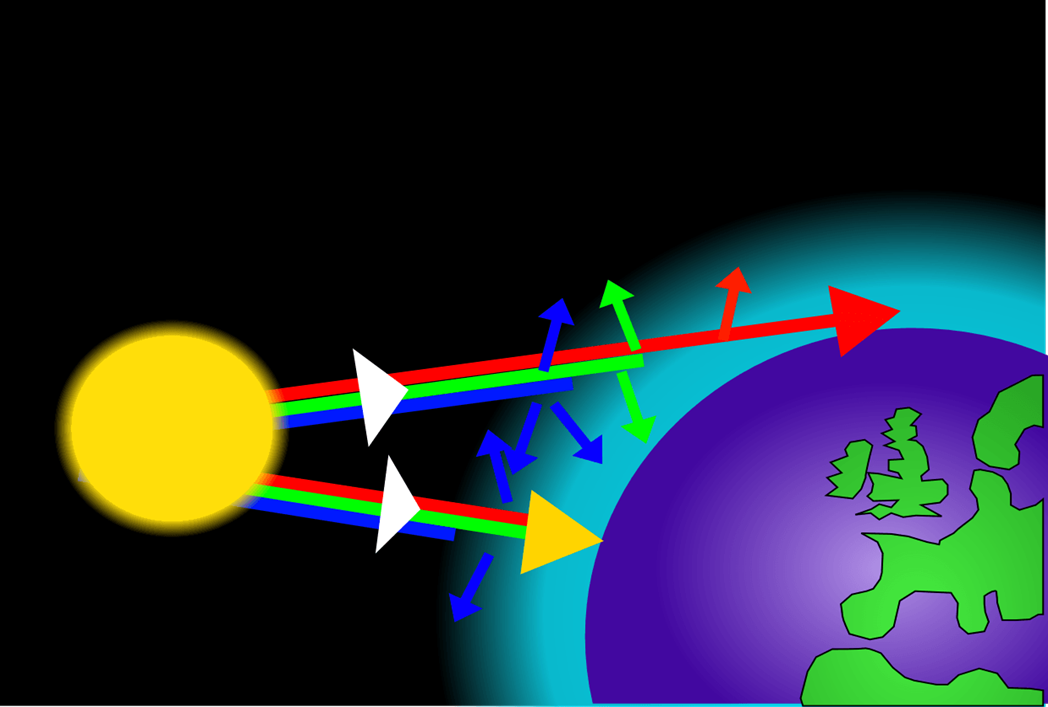
La luz de mayor longitud de onda tiene poca interacción con las partículas de la atmósfera, y nos llega directamente del Sol. Por lo tanto, los haces de luz verdes, amarillos, naranjas y rojos no se dispersan en la atmósfera. La suma de la luz verde, amarilla, naranja y roja es lo que hace que percibamos al Sol como si fuera amarillo, además de que nuestro sistema de visión tiene una mayor sensibilidad a las longitudes de onda de tonos amarillo y verde.

Entonces el fenómeno de dispersión de la luz en la atmósfera no sólo es causante de que veamos el cielo de azul, también de que veamos al Sol de amarillo.

Esta explicación del del cielo debido a la dispersión de la luz al interactuar con las partículas de cierto tamaño que conforman el aire fue propuesta en 1871 por el físico matemático inglés John William Strutt, quien tenía el título de tercer barón de Rayleigh. En honor a este científico, el fenómeno se le conoce como dispersión Rayleigh.

Vemos el cielo azul, ya que la longitud de onda de este , al ser menor, rebota en las partículas que son parte de la atmósfera, pero, aunque la longitud de onda del violeta es menor, no vemos el cielo de ese , porque intervienen otros factores, uno de ellos es que hay menor cantidad de luz violeta que azul en la luz del Sol; además, la luz violeta se dispersa en las capas superiores de la atmósfera. Por otra parte, nuestro ojo es mucho más sensible al azul que al violeta y no percibimos longitudes de onda de luz ultravioleta. Por ello, no importa a qué lugar del cielo mires, lo que verás serán distintos tonos azules. Mientras que el Sol aparece de amarillo, ya que los rayos amarillos y rojos son poco desviados.

En conclusión, quiere decir que el ojo humano solamente puede distinguir ciertas ondas del espectro electromagnético, de ahí que a un rango de longitudes de onda de luz, que corresponden a los es del arcoíris, se le llame luz visible o espectro visible.

Las nubes no son de azul porque están formadas por partículas de mayor tamaño, bastante más grandes que las longitudes de onda de la luz del Sol. Entonces estas partículas se comportan como un espejo dispersando todos los es. Cuando miramos una nube, a nuestros ojos están llegando, al mismo tiempo, las ondas de diferentes longitudes de la luz visible. Por ello, se suman las longitudes de onda y percibimos las nubes blancas. Las nubes reflejan la luz blanca.

Cuando el vapor de agua se condensa en las nubes por la gran cantidad de gotas de agua que acumula, se vuelven más densas, lo que impide el paso de la luz y las vemos grises.

En el amanecer o el atardecer, cuando el Sol está cerca del horizonte, la luz debe atravesar una porción de atmósfera cada vez mayor.

El del Sol va cambiando porque se van dispersando cada vez más las longitudes de onda cortas, es decir, la azul y la verde; y solo nos llega la luz con tonalidades rojas.

Esa es la razón de porqué el cielo es azul en determinados momentos del día y rojizo o anaranjado en otros. Asimismo, el tipo de partículas presentes en la atmósfera, como en el caso de la contaminación del aire, varía el del cielo que vemos.

Con esta información, se puede deducir que: En ausencia de luz, es decir que no hay ondas o fotones, no hay nada que choque contra las partículas de la atmósfera, por lo tanto, vemos el cielo oscuro.

Te proponemos una demostración muy sencilla que te permita observar el que se forma mediante la interacción de la luz con un líquido, para hacer una analogía con el del cielo. Los materiales que vas a utilizar son los siguientes:

Un recipiente transparente con agua.
Una linterna o lámpara de luz blanca.
Leche.
Una cartulina blanca.
Un agitador.

Como primer paso, coloca la cartulina como fondo. Ahora enciende la linterna. Después, dirige la luz hacia el agua. La luz va a pasar a través del agua y se va a reflejar en la cartulina, aunque también se va a refractar. Observaras que la luz se refracta, y se descompone en los distintos es del arcoíris.

El agua cumple el efecto de desviar la luz, como si fuera un prisma que la refracta. Es así como puedes observar este fenómeno.

Ahora vas a colocar un poco de leche al agua y disolverla con ayuda del agitador. Repite el procedimiento con la luz.

Observarás que, al iluminar con la linterna, se ve de azul, La leche simula la atmósfera, por lo tanto, cuando se acerca la luz de la linterna y se ilumina directamente, se ve azul porque choca con las partículas de la leche, se dispersan y reflejan, haciendo que se vea el azul.

El del cielo en otros planetas depende de la atmósfera del astro, para ser más precisos de su densidad y composición. Entonces la atmósfera es el punto clave en el del cielo.

En la Luna prácticamente no hay atmósfera. El cielo allí siempre es negro. La luz del Sol llega sin impedimentos hasta la superficie, es por eso que ésta siempre se ve de blanco.

Con base en las investigaciones actuales, se sabe que Marte tiene una atmósfera poco densa, compuesta sobre todo por dióxido de carbono y pequeñas partículas de óxido de hierro. Esto hace que en Marte se vea el cielo amarillo-rojizo, lo que se ha podido comprobar con las imágenes que se han tomado en el planeta con la ayuda de sondas espaciales y robots.

Conociendo la composición de cada planeta podríamos deducir el del cielo que se observaría desde su superficie.

El Reto de Hoy:

Realiza un mapa mental de por qué el cielo es de azul, identificando cada una de sus características.

No olvides consultar tu libro de texto o bien, otras fuentes confiables de información, como páginas de internet, para profundizar acerca del tema e indagar los asuntos de interés que surgieron a lo largo de esta sesión

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

Compra en Amazon

La ciencia en la Nueva España

Aprendizaje esperado: Aprende los rasgos principales de las ciencias y artes novohispanas entre los siglos XVI y XVII. Además, reconoce las características del periodo Barroco.

Énfasis: Conocer la actividad científica novohispana: los inventarios del Nuevo Mundo.

¿Qué vamos a aprender?

En la sesión del día de hoy revisarás algunos de los inventarios que se realizaron sobre el Nuevo Mundo y cómo se desarrolló la actividad científica en la Nueva España durante los siglos XVI y XVII.

¿Qué hacemos?

Te imaginas: ¿qué pensarían los españoles de las plantas y animales de América? Seguramente estarían muy impresionados y asombrados de la gran variedad, además de desconcertados, pues mucha fauna y flora les eran totalmente desconocidas.

Para comenzar lee el siguiente texto que se encuentra en el Códice Florentino y que ha sido adaptado por Felipe Garrido:

“El Ahuítzotl”

“Hay un animal en esta tierra que vive en el agua, nunca [antes] oído, el cual se llama ahuítzotl. Es del tamaño de un perro pequeño.

Tiene el pelo muy suave y corto. Tiene las orejitas pequeñas y puntiagudas. Tiene el cuerpo negro muy liso. Tiene la cola larga, y en el cabo de la cola una mano, como mano de persona. Tiene pies y manos, las manos y pies como mono.

Habita este animal en los profundos manantiales de las aguas; si alguna persona llega a la orilla donde él habita, lo jala con la mano de la cola y lo mete debajo del agua y lo lleva a lo profundo.