Aprende en Casa III SEP: 14 de mayo TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 14 de mayo de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Viernes 14 de mayo, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en Casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Polígonos regulares I
Aprendizaje esperado: Deduce y usa las relaciones entre los ángulos de polígonos en la construcción de polígonos regulares.
Énfasis: Construir polígonos regulares con GeoGebra.
¿Qué vamos a aprender?
Analizarás la construcción de polígonos regulares a partir de diferentes datos.
¿Qué hacemos?
¿Alguna vez te has puesto a observar la naturaleza, un cuadro, una fotografía o una construcción? te han preguntado ¿qué tienen que ver todo esto con las matemáticas?

Seguramente lo que puedes notar es que son elementos geométricos, como una flor, una semilla, la piel de una serpiente, la fachada de un edificio, la forma de una pirámide.
Como habrás observado, en los ejemplos anteriores aparecen distintas formas geométricas dentro de las que destacan los polígonos regulares, es decir, que con ayuda de estas figuras puedes representar distintos objetos en la vida cotidiana; por ejemplo, en la estrella de mar y en la flor se observa un pentágono, o en las celdas del panal de abejas y en los mosaicos se pueden ver hexágonos. En esta sesión vas a trabajar cómo hacer esas construcciones geométricas, con las cuales la naturaleza, los arquitectos y artistas nos maravillan.
Por ello, necesitas recordar algunos conceptos, elementos y propiedades de los polígonos regulares que serán útiles en su construcción.
La palabra polígono proviene de la composición de dos palabras griegas, polys que significa mucho y gonos, que significa ángulos; así que un polígono es una figura geométrica de muchos ángulos, aunque en la práctica a los polígonos los identificamos más por sus lados.
Ahora que tienes claro el concepto de polígono recuerda algunos de sus elementos.
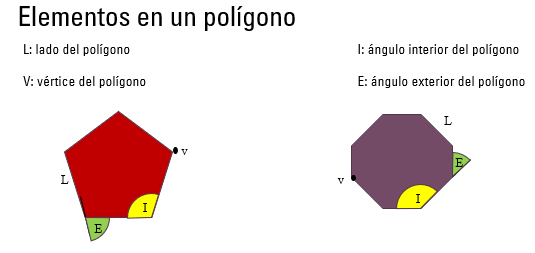
Un lado, “L”, de un polígono es un segmento que conforma el polígono.
Un vértice, “V”, es el punto de intersección de dos lados consecutivos.
Un ángulo interior, “I”, se forma por dos lados consecutivos y es interno al polígono. En las figuras se muestran con color amarillo.
Un ángulo exterior, “E”, se forma por un lado del polígono y la extensión del lado consecutivo, siendo externo al polígono. En las figuras se encuentran en color verde.
Los polígonos pueden tener distintas formas dependiendo del número y tamaño de sus lados, así como de sus ángulos interiores.
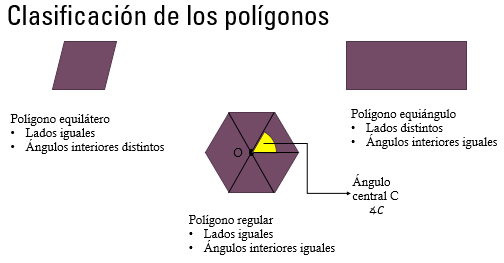
Un polígono es equilátero cuando todos sus lados son iguales, como el cuadrado o el triángulo equilátero. Mientras que un polígono es equiángulo cuando sus ángulos interiores son iguales, como el rectángulo y o el triángulo equilátero.
Puede haber polígonos con lados iguales y ángulos desiguales, como el rombo, y viceversa, con lados desiguales y ángulos iguales, como el rectángulo.
Cuando un polígono tiene sus lados y ángulos iguales decimos que es un polígono regular. En este tipo de polígonos, notamos sus ejes de simetría con los cuáles podemos obtener su centro “O”, que es la intersección de dos de sus ejes de simetría; asimismo se forma un ángulo “C” con dos segmentos que parten del centro “O” a los extremos de uno de los lados. Este ángulo es un ángulo central.
Por cierto, los polígonos regulares aparecen en nuestro entorno con mucha frecuencia, por ello, verás algunos métodos geométricos para su construcción.
Ahora que has recordado brevemente cómo se clasifican los polígonos, te vas a centrar en la construcción de polígonos regulares.
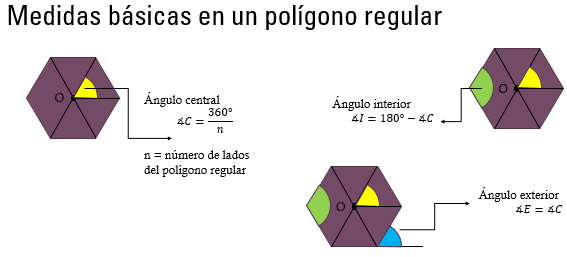
Para lo anterior, ten presentes algunas relaciones métricas para el cálculo del valor de los ángulos que los constituyen. De esta manera, tenemos que el valor del ángulo central “C” es igual a 360 grados entre “n”, siendo “n” el número de lados del polígono. La medida del ángulo interior “I” en un polígono regular es igual a 180 grados menos la medida del ángulo central “C” y la medida del ángulo exterior “E” es la misma que la del ángulo central “C” del polígono regular.
No olvides registrar los aspectos que consideres más relevantes para que los puedas utilizar en el transcurso de la sesión.
Ahora verás cómo puedes trazar polígonos regulares a partir de algunos de sus elementos; por ejemplo, si te piden simplemente trazar un pentágono regular o un hexágono regular, sin darte más información. Ello significa que en principio no se conoce el tamaño del lado “L” del polígono, pero recuerda el significado etimológico de la palabra, polígono significa varios ángulos, y ahí está la clave. Para las construcciones te vas a apoyar en sus ángulos, en particular en el ángulo central “C”. Aquí se nota la importancia de entender el significado de las palabras.
Para trazar un pentágono regular sin más información, puedes iniciar con el cálculo de la medida de ángulo central de esa figura.
Recuerda que en los polígonos regulares la medida del ángulo central “C” es igual a 360 grados entre “n”, en donde “n” es el número de lados. Como en un pentágono regular “n” vale 5, se sustituye este valor y se tiene que el ángulo central es igual a 360 grados entre 5, lo que resulta 72 grados, que es la medida del ángulo central de un pentágono regular.

Con ello vas a trazar un pentágono regular.
Primero, elige un punto arbitrario “O”. Con ayuda del compás, traza una circunferencia de cualquier radio o abertura que tenga como centro el punto “O”. Con el centro “O” de la circunferencia como vértice y con ayuda del transportador, mide un ángulo central “C” de amplitud 72 grados, marcando sobre la circunferencia las intersecciones “A” y “A” prima de los lados del ángulo.
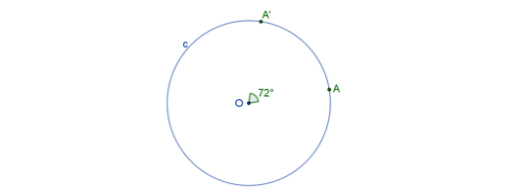
Ahora ve trazando más ángulos centrales de amplitud “72 grados”, uno junto al otro, con la ayuda del transportador. Conforme se van trazando marca los puntos de las intersecciones de los lados de los ángulos centrales con la circunferencia. Llamamos a esos puntos de intersección, “A” prima, “A” doble prima, “A” triple prima y “B”. Estos puntos serán los vértices de la figura que debes trazar.

Posteriormente, se unen los puntos de intersección de manera consecutiva con segmentos de recta para ir formando los lados del polígono.
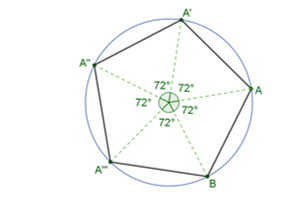
Para la construcción del hexágono regular procede de manera análoga. Primero vas a determinar el valor del ángulo central “C” que es igual a “360 grados entre “n”, donde “n” es el número de lados. Como en el hexágono “n” es igual a 6, se sustituye obteniendo 360 grados entre 6, lo que resulta 60 grados, que es la medida del ángulo central “C”.
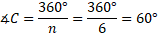
Con dicha amplitud del ángulo central vas a trazar tu hexágono regular. De nuevo, vuelve a elegir un punto “O”. Con ayuda de un compás, traza una circunferencia de cualquier radio o abertura, que tenga como centro el punto “O”. Luego, con ayuda del transportador, vas a trazar el ángulo central “C” de amplitud 60 grados, que tenga como vértice el centro de la circunferencia. Marca sobre la circunferencia los puntos de las intersecciones de los lados del ángulo con ella. Nombramos a esos puntos como “A” y “A” prima.
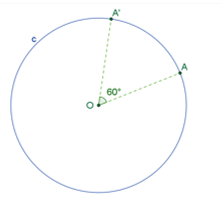
Ahora ve trazando más ángulos centrales de amplitud 60 grados, uno junto al otro con la ayuda del transportador. Conforme vas trazando estos ángulos, marca las intersecciones “A” doble prima, “A” triple prima, “B” y “B” prima. Estos puntos serán los vértices del hexágono que se desea construir.
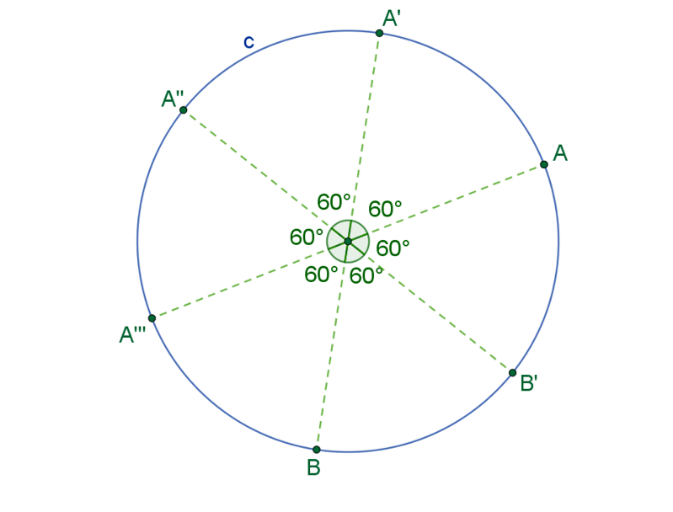
Posteriormente, ve uniendo los puntos que marcaste sobre la circunferencia, de manera consecutiva. Los segmentos de recta que unen esos puntos son los lados del hexágono regular.
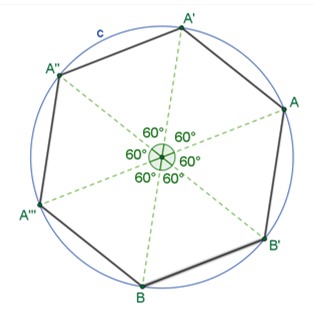
Ahora, vas a trazar polígonos regulares con otras condiciones. Anteriormente construiste los polígonos regulares a partir de conocer el número de sus lados. Ahora verás la manera de construir polígonos regulares conociendo la longitud de sus lados. Para las construcciones con esta condición, también usarás alguno de los ángulos existentes en los polígonos regulares. De esta manera, una construcción la harás usando el ángulo interior y para la otra, el ángulo exterior.
Analiza entonces otro método de construcción de polígonos regulares a partir de conocer la medida de sus lados usando su ángulo interior.
Volverás a construir un pentágono y un hexágono, ambos regulares.
Como viste al principio de la sesión, el valor o la amplitud del ángulo interior “I” en un polígono regular es igual a “180 grados menos el valor del ángulo central “C” de ese polígono. Para el caso del pentágono regular, sabes que el ángulo central “C” es igual a 72 grados, entonces sustituyendo ese valor en la expresión anterior, se tiene que el ángulo interior “I” en el pentágono regular es igual 180 grados menos 72 grados, por ello, el valor del ángulo interior “I” en un pentágono regular es igual a 108 grados.

Por otro lado, repitiendo el mismo procedimiento para el hexágono regular, se tiene que el ángulo central “C” del hexágono es igual a 60 grados, y sustituyendo en la expresión para calcular el ángulo interior “I” se tiene que el ángulo “I” es igual a 180 grados menos 60 grados. Por ello, el valor del ángulo interior “I” en un hexágono regular es igual a 120 grados.
Recuerda que esta construcción se hará conociendo la medida de los lados. Esta medida puede ser cualquiera que tu decidas o que te sea indicada; en este caso, la llamaremos “L”.
Una vez que tienes el valor del lado “L” y el valor del ángulo interior procede a la construcción del pentágono regular.
Primero, traza un segmento con la longitud dada para el lado “L” o lado “AB”. Con uno de los extremos del lado “L” como vértice y haciendo uso del transportador se traza un ángulo de amplitud igual a 108 grados; Este ángulo será un ángulo interior del pentágono regular. Luego, a partir del vértice y sobre el otro lado del ángulo, localiza el punto “A” prima que determina el segmento “BA” prima, de igual longitud que el lado “L”. Este segmento será el segundo lado del pentágono, y se llamara “L” prima.
Para la construcción del siguiente lado del pentágono regular se considera el extremo libre del lado “L” prima como vértice para trazar un nuevo ángulo de 108 grados, respetando la orientación hacía donde se quiere el interior del pentágono. Luego ubica el punto “A” doble prima sobre el nuevo lado de este ángulo de manera que se determine un segmento de igual medida a la del lado “L”. De esta manera se obtiene un nuevo lado del pentágono, al que llamaremos “L” doble prima.
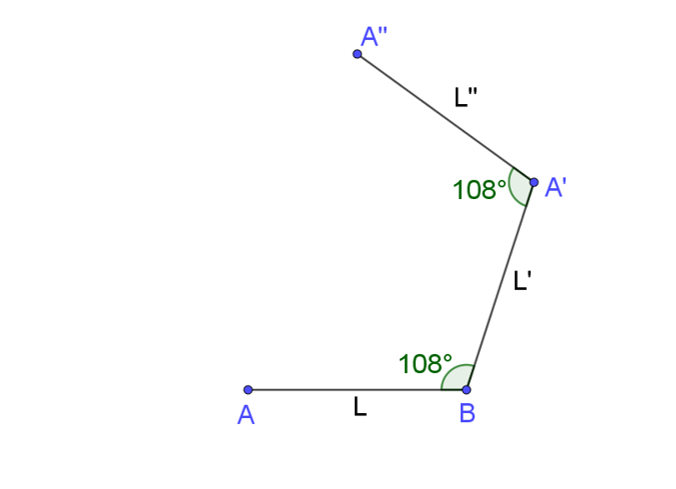
Procediendo de la misma manera para la construcción de los ángulos interiores y los lados de esta figura, ve construyendo los lados faltantes hasta completar el pentágono regular.
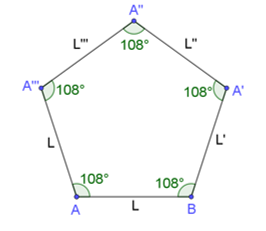
Ahora procede a la construcción del hexágono con lado “L” igual al del pentágono.
Puedes realizar los mismos pasos que para el pentágono regular, pero de acuerdo con las medidas correspondientes al hexágono regular. Si tienes la oportunidad de utilizar el software GeoGebra también puedes realizar los trazos con esta herramienta tecnológica.
Por un cálculo previo, sabes que el valor del ángulo interior para un hexágono regular es de 120 grados.
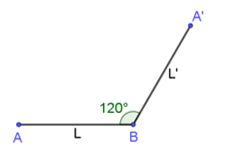
Primero traza un segmento con la longitud dada para el lado “L”, aquí llamado lado “AB”. Con uno de los extremos del lado “L” como vértice y haciendo uso del transportador, se traza un ángulo interior de amplitud igual a 120 grados; se hemos trazado el ángulo con vértice en “B”. Este ángulo será un ángulo interior del hexágono regular. Luego, a partir del vértice y sobre el otro lado del ángulo, localiza el punto “A” prima que determina el segmento “BA” prima, de igual longitud que el lado “L”. Este segmento será el segundo lado del hexágono, que llamaremos “L” prima.
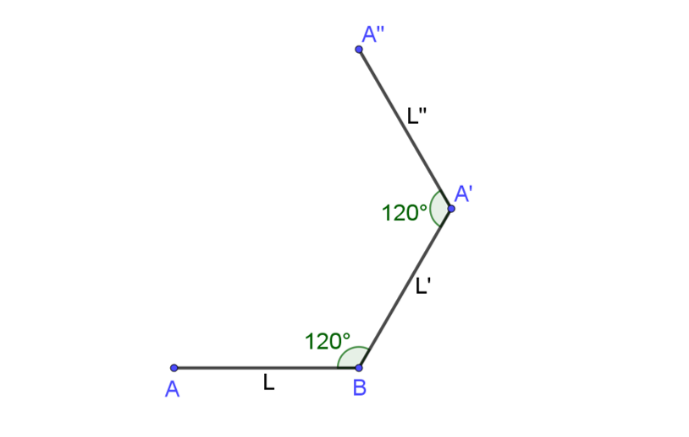
Para la construcción del siguiente lado del hexágono regular se considera el extremo libre del lado “L” prima como vértice para trazar un nuevo ángulo de 120 grados, respetando la orientación hacía donde quieres el interior del hexágono. Luego, ubica el punto “A” doble prima sobre el nuevo lado de este ángulo, de manera que se determine un segmento de igual medida a la del lado “L”. De esta manera se obtiene un nuevo lado del hexágono, al que llamaremos “L” doble prima.
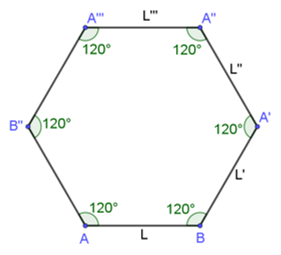
Procediendo de la misma manera para la construcción de los ángulos interiores y los lados de esta figura, ve construyendo los lados faltantes hasta completar el hexágono regular.
Hasta aquí llevas dos métodos para construir polígonos regulares. En el primero partiste del ángulo central “C”, y en el segundo usaste el ángulo interior “I”, una vez que la longitud del lado “L” del polígono está dada.
Ahora continua con otro método utilizando el otro ángulo asociado, es decir, el ángulo exterior.
Sabes por lo que viste al inicio de la sesión, que la amplitud del ángulo exterior “E” en un polígono regular es igual a la de su ángulo central “C”. A partir de lo anterior, puedes encontrar que para el pentágono regular, como su ángulo central “C” es igual a 72 grados, sustituyendo en la expresión anterior, se tiene que su ángulo exterior “E” es igual a 72 grados.

Por otro lado, para el hexágono regular su ángulo central tiene una amplitud de 60 grados, de donde el ángulo exterior “E” es igual también a 60 grados.
Estos trazos los puedes hacer con regla, compás y transportador o como en este caso, lo haremos con el uso de GeoGebra. Una manera de iniciar es trazar el lado “L” con la longitud dada, aquí representado por el segmento “AB”.
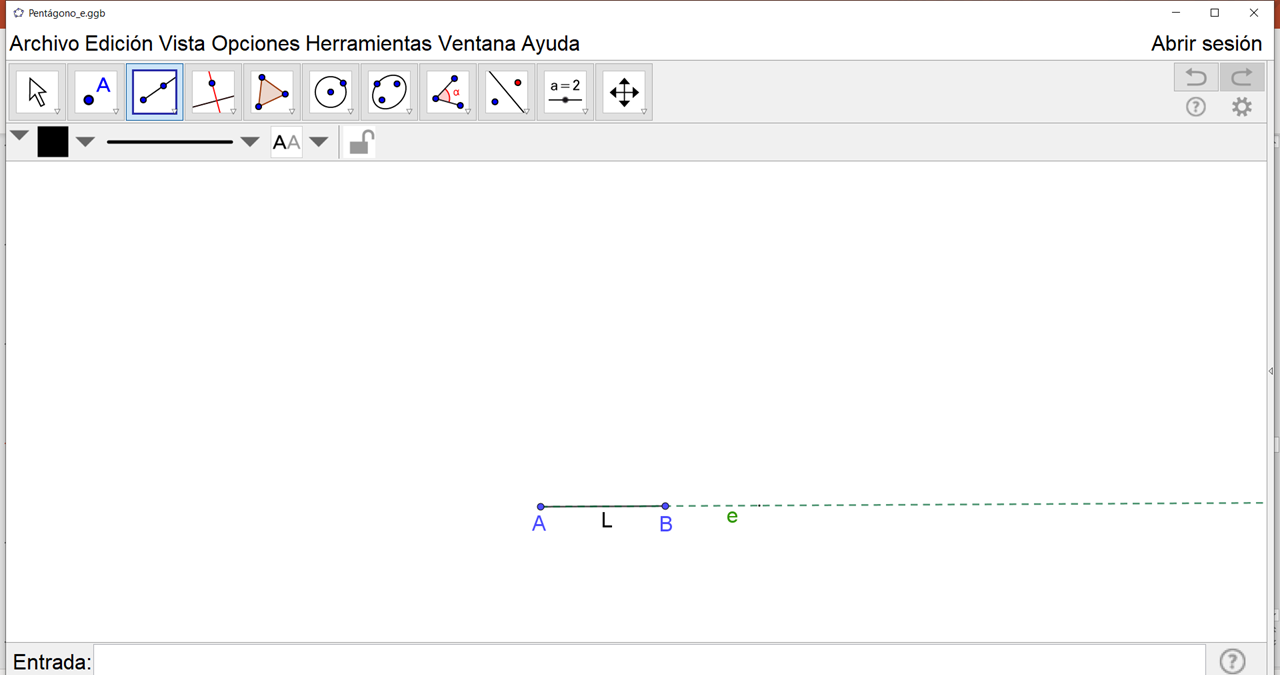
En la imagen se muestra con la flecha roja en la barra de herramientas, el ícono con el cual pueden trazar el segmento “AB”; para seleccionarlo, deben hacer clic con el botón izquierdo del ratón en él. Se procede al trazo.
Por uno de sus extremos, desde “A” hacia “B”, prolonga dicho lado con una línea “e” punteada o tenue. Para prolongarlo en GeoGebra traza una semirrecta seleccionándola de la barra de herramientas y procediendo al trazo.
Haciendo uso de un transportador mide el ángulo exterior “E” de amplitud igual a 72 grados, con vértice en “B” y cómo lado inicial la prolongación del segmento “AB”. Esto porque dicho ángulo debe ser externo al polígono y por ello hay que cuidar su orientación para ubicarlo en el exterior del polígono. Para trazarlo con GeoGebra se utiliza de la barra de herramientas el ícono ángulo dada su amplitud.

Sobre el lado final del ángulo trazado, se mide una longitud igual al lado “L” a partir del vértice “B”, con lo que se determina el segmento “B”, “C” prima. De esta manera se determina el segundo lado del pentágono regular, que llamaremos “L” prima.
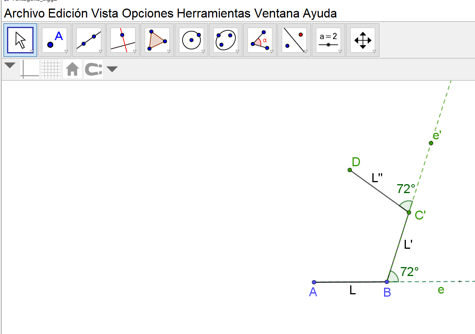
Una vez trazado el lado “L” prima, prolongamos este lado, lo que aquí se muestra con la línea punteada “e” prima. Nuevamente, tomando como lado inicial esta prolongación, haz uso de un transportador para trazar otro ángulo exterior de 72 grados y, repitiendo los pasos anteriores, construye otro lado del pentágono, que llamaremos “L” doble prima. En GeoGebra puedes utilizar de la barra de herramientas para prolongar el lado con el ícono de semirrecta y para medir el ángulo exterior usamos el ícono de ángulo dada su amplitud.
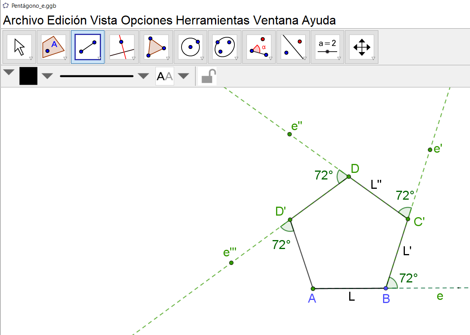
Para continuar con la construcción del resto de los lados del pentágono regular procede de manera análoga, es decir, extendiendo cada nuevo lado del pentágono regular y, sobre dicha extensión, se traza el ángulo exterior de 72 grados, y así vas trazando los lados faltantes.
Ahora realiza la construcción del hexágono regular usando este método de construcción a partir de la medida del ángulo exterior “E”. Como ya calculaste anteriormente, la medida de dicho ángulo es igual a 60 grados.
Puedes iniciar de la misma manera que la construcción anterior, es decir, traza el lado “L” pero ahora con una la longitud de 5 cm, aquí representado por el segmento “AB”. Por uno de sus extremos, “B”, prolonga dicho lado con una línea “e” punteada. Recuerda que si quieres usar GeoGebra, primero debes usar el ícono “segmento”, y para prolongar ese segmento puedes usar el ícono “semirrecta”.
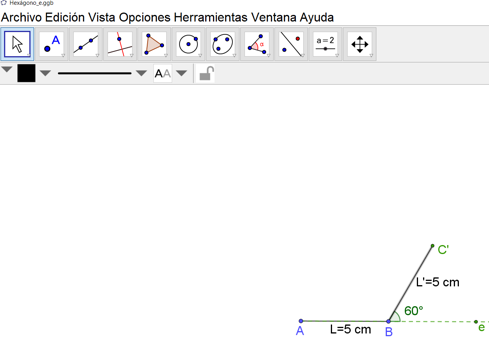
Luego, haciendo uso de un transportador medimos el ángulo exterior “E” de amplitud igual a 60 grados, con vértice en “B” y como lado inicial la prolongación del segmento “AB”. Esto porque dicho ángulo debe ser externo al polígono y por ello hay que cuidar su orientación para ubicarlo en el exterior del polígono.
Para trazarlo con GeoGebra, busca en la barra el icono de ángulo dada su amplitud y traza el ángulo exterior.
Sobre el lado final del ángulo trazado, se mide una longitud igual al lado “L” a partir del vértice “B”, con lo que se determina el segmento “B”, “C” prima. De esta manera, se determina el segundo lado del hexágono regular, que llamaremos “L” prima.

Una vez trazado el lado “L” prima, prolonga este lado, lo que aquí se muestra con la línea punteada “e” prima. Nuevamente, tomando como lado inicial esta prolongación, haz uso de un transportador para trazar otro ángulo exterior de 60 grados y, repitiendo los pasos anteriores, construye otro lado del hexágono, que llamaremos “L” doble prima.
Para continuar con la construcción del resto de los lados del hexágono regular procede de manera análoga, es decir, extendiendo cada nuevo lado del hexágono regular y, sobre dicha extensión, se traza el ángulo exterior de 60 grados, y así vas trazando los lados faltantes.

Ahora conoces algunos métodos para construir polígonos regulares. Unos son más accesibles que otros, dependiendo de los datos que te den, pero todos tienen algo en común, se apoyan en algún tipo de ángulos de los polígonos. Además de la medida de lados, cuando ésa es una condición de la construcción.
Así que cuando tengas que trazar un polígono regular, el método que decidas va a depender de los datos que te proporcionen y de las herramientas tecnológicas con las que cuentes.
Así ha llegado al final de esta sesión, recuerda que éste es un material de apoyo y que puedes consultar otras fuentes para complementar lo que aprendas aquí, como tu libro de texto.
El Reto de Hoy:
El reto de hoy es que contestes las siguientes preguntas.
Los métodos de construcción de polígonos regulares que has estudiado en esta sesión, ¿se pueden aplicar para construir cualquier polígono, independientemente de su número de lados?
¿Cualquier polígono regular se puede construir usando sólo regla y compás?, ¿por qué?
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Campañas en seguimiento
Aprendizaje esperado: Diseña una campaña escolar para proponer soluciones a un problema de la escuela.
Énfasis: Generar planes de seguimiento a campañas
¿Qué vamos a aprender?
En esta sesión el aprendizaje esperado es: “Diseña una campaña escolar para proponer soluciones a un problema de la escuela”, y específicamente te centrarás en el propósito de: “Generar planes de seguimiento a campañas”.
¿Qué hacemos?
Al momento de planear una campaña, es importante considerar cómo se va a evaluar su eficacia y cómo se le va a dar seguimiento.
Para iniciar, recuerda qué son las campañas escolares.
Las campañas escolares las pueden realizarse por varios organismos, pero en este caso hablaremos de las creadas por las y los alumnos para:
- Tratar asuntos de índole escolar que afectan o inciden en el alumnado.
- Generar conciencia, influir en la conducta o atención ante ciertas situaciones.
- Utiliza carteles, folletos, historietas o materiales audiovisuales para lograr su fin.
Observa el siguiente video donde unas alumnas presentan sus dudas sobre el tema.
- VIDEO 01 ALUMNOS
Para poder realizar el seguimiento de una campaña, lo primero que se debe establecer es el objetivo, es decir, qué se pretende al realizar esa campaña y a qué público va dirigida, para ser coherente con el segmento de población elegida.
Para saber el impacto que tuvo es necesario identificar el alcance, el cual se medirá de acuerdo con el número de personas que podrán ver la campaña y el medio de difusión que se usará. Después puedes elaborar encuestas o entrevistas que muestren si los resultados obtenidos fueron los que se esperaban, o bien si es necesario corregir o mejorar la estrategia para el impacto de la campaña.
Podemos decir que se puede realizar una encuesta de seguimiento o encuesta de varias rondas, o encuesta de múltiples fases, pues son instrumentos que se pueden utilizar para saber si el mensaje de la campaña ha sido claro, o si se requieren modificaciones para llegar al fin que persigue. En este tipo de encuestas, los participantes son entrevistados una o más veces para obtener información sobre eventos vitales del mensaje e impacto de la campaña.
Gracias a que se elaboran varias encuestas a lo largo del tiempo, se cuenta con más datos sobre los cambios percibidos y los resultados de la campaña, y esto ayuda al seguimiento.
Más adelante analizarás de manera más detallada cómo recuperar la información que proporcionan las encuestas. Por lo pronto, observa el siguiente material de la maestra Esther Garduño Siciliano para saber más acerca de qué aspectos se deben tomar en cuenta para una entrevista.
- ANEXO 02 VIDEO 02 ESPECIALISTA
Una entrevista serviría para conocer la opinión de la comunidad escolar sobre la campaña. Y se puede complementar con el uso de una encuesta.
Para que quede más claro, tomando como ejemplo una campaña de secundaria del uso de la biblioteca, ¿cómo realizarías una encuesta para saber si funcionó?
La encuesta podría incluir como opciones de respuesta “Sí” y “No” a preguntas como:

Como observas, la encuesta debe llevar un título; el propósito, es decir, cuál es su finalidad; los datos de quien contesta y las instrucciones. También debemos señalar que esta encuesta es de preguntas cerradas, es decir, cuando se responde “Sí” o “No”; por el contrario, las preguntas abiertas permiten todo tipo de respuestas. Aunque ninguna es incorrecta, lo cierto es que las cerradas permiten más control y las abiertas más variación en las interpretaciones.
Esta encuesta tendría que haberse realizado a toda la comunidad escolar, pues todos son usuarios potenciales de la biblioteca, y se les tendría que preguntar antes, durante o al final de la campaña.
Ahora piensa en cómo harías la entrevista. Puesto que es un proceso más tardado, tendrías que seleccionar a un grupo de alumnas y alumnos que respondan una serie de preguntas.
Observa el formato y las preguntas. Como ves, se pregunta el nombre de quien será entrevistado y el grado escolar al que pertenece, y luego se redactan las preguntas, dejando espacio suficiente para que quien responda se sienta en la libertad de dar respuestas extensas.

Una entrevista consta de preguntas abiertas y puede aplicarse a un número reducido de personas que responde todo lo que desea y expresa su opinión sobre un tema. Por otro lado, la encuesta se aplica a más personas, contiene, sobre todo, preguntas cerradas, y quienes responden tienen que elegir entre una cantidad limitada de respuestas.
Observa la siguiente imagen con las características de ambas.

Deben aplicarse en distintas situaciones, pero ambas te pueden dar información de los alcances e impacto de la campaña. Cabe señalar que las preguntas deben ser pertinentes y responder, en lo general y lo particular, qué tan efectiva fue la campaña. ¿A ti se te ocurren otras preguntas? Podrían ser:
- ¿Les cambiarías o agregarías algo a los carteles, trípticos e infografías de la campaña para visitar la biblioteca? ¿Por qué?
- ¿Los carteles de la campaña te han inspirado o creado curiosidad para ir a la biblioteca?
- ¿Te parece efectivo el mensaje de la campaña?, ¿puedes decirnos si sí o no, y explicarlo?
Esto parece adecuado, porque lo que se quiere saber es la efectividad de la campaña. Y hay más beneficios de estos recursos pues nos permiten realizar análisis cualitativos y cuantitativos.
El análisis cuantitativo te ayuda a recopilar datos y proporciona cifras o cantidades que puedes medir, mientras que el cualitativo te ayuda a comprender las respuestas obtenidas de los encuestados o entrevistados.
Con el enfoque cuantitativo puedes graficar los resultados, mientras que el enfoque cualitativo te permite interpretar la información obtenida a través de recursos como la entrevista; al analizar las respuestas de los entrevistados, puedes encontrar elementos comunes que te ayuden a formar un panorama de sus puntos de vista.
Los enfoques cuantitativos y cualitativos te darán resultados que ayudarán a saber:
- El impacto del mensaje en nuestra campaña.
- La opinión que se tiene sobre nuestro material de difusión.
- Mejorar las estrategias de contenido, creación y difusión de nuestra campaña.
El seguimiento a las campañas se debe hacer de manera muy organizada, a esto se le llama pensamiento estratégico. Cuando realizas un proyecto, como la campaña escolar, no puedes hacerlo de manera desordenada, sino que debes trabajar con orden para asegurar que tus esfuerzos y los recursos que utilices rindan la mayor cantidad de frutos posible.
Es importante tener una estrategia y que todo el equipo la conozca. Esto ayuda a trabajar enfocados en un objetivo común y a que cada decisión se tome pensando en ese objetivo final. Es más fácil cumplir bien, a tiempo y evitando desilusiones porque las cosas no salieron como se quería.
Recuerda que las campañas no dependen de una sola persona, sino de un equipo de trabajo que deberá colaborar de manera conjunta.
El trabajo en equipo es una parte fundamental de la campaña. Para que funcione mejor, es recomendable organizar una reunión y elaborar un cronograma de trabajo en donde se establezcan las tareas de seguimiento a realizar, por ejemplo:
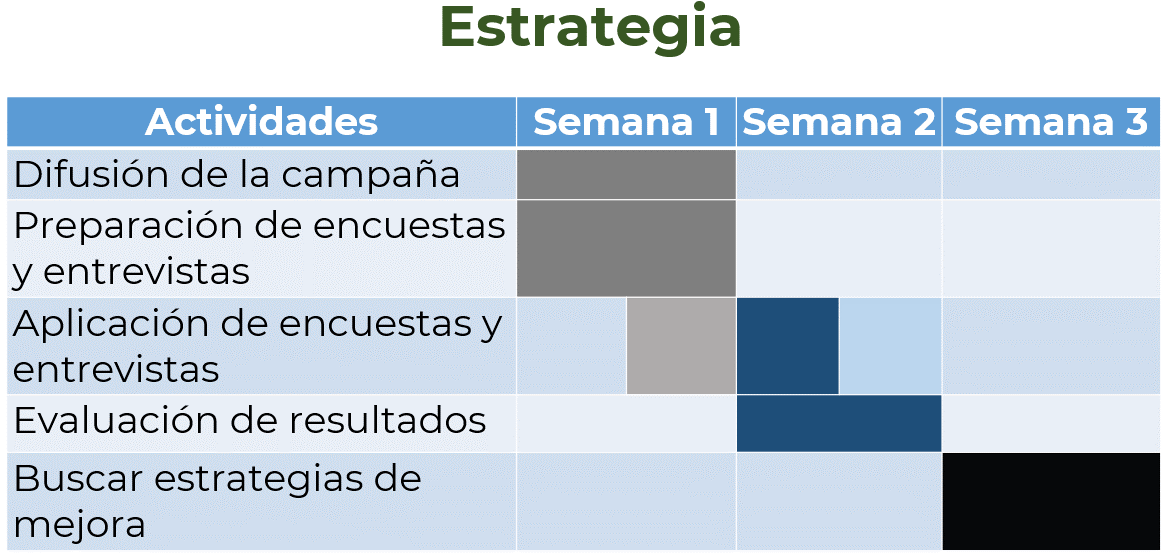
Como puedes ver, un cronograma es indispensable porque así sabes qué actividades se realizarán y en qué tiempos estimados deben llevarse a cabo. También es importante establecer quiénes serán los responsables de cada una de las acciones.
Y a esto todavía hay que aplicarle un análisis FODA.

Es una herramienta de evaluación muy conocida. FODA significa: Fortalezas, Oportunidades, Debilidades y Amenazas, y nos ayuda a analizar situaciones internas y externas de una situación que deseamos mejorar.
En este tipo de análisis se puede vaciar la información que se haya obtenido con las entrevistas y las encuestas. Porque las opiniones y puntos de vista del público que responda se suman a los de los miembros del equipo, lo cual permitirá dibujar un panorama más amplio de aquello con lo que se está enfrentando.
Con el ejemplo de la campaña de la biblioteca escolar, un análisis FODA seria:
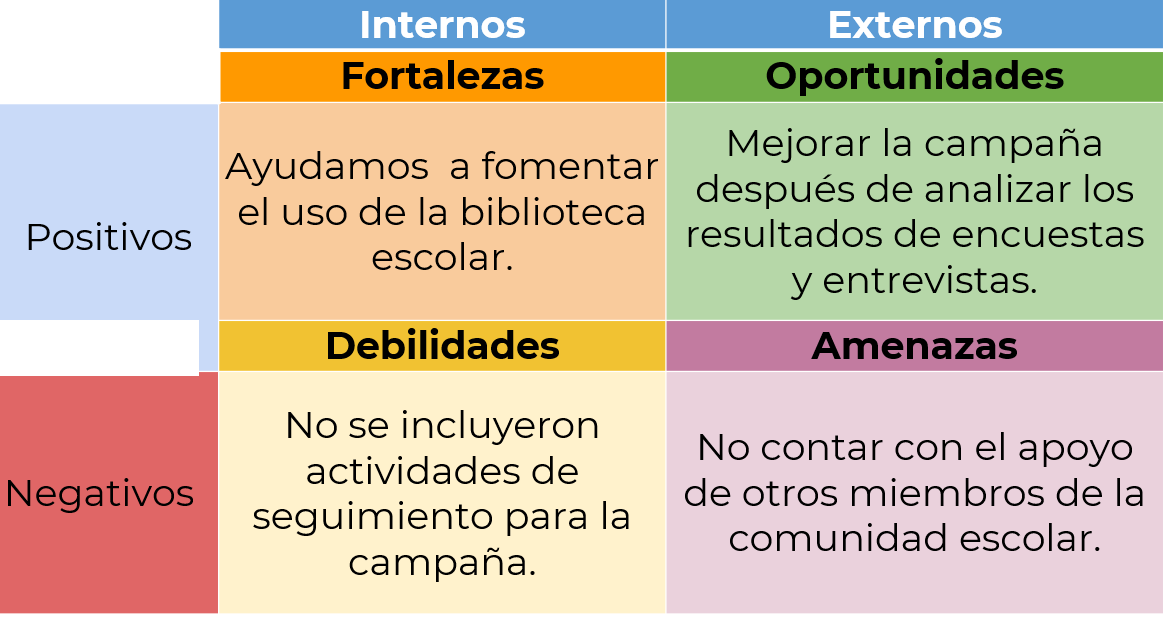
Considera qué aspectos se podrían mejorar de la campaña a partir del análisis FODA. Recuerda tomar notas de todo lo que suceda durante el proceso de conceptualización y desarrollo de la campaña, ya sea con un listado de ideas, como has hecho en esta sesión, o a través de preguntas.
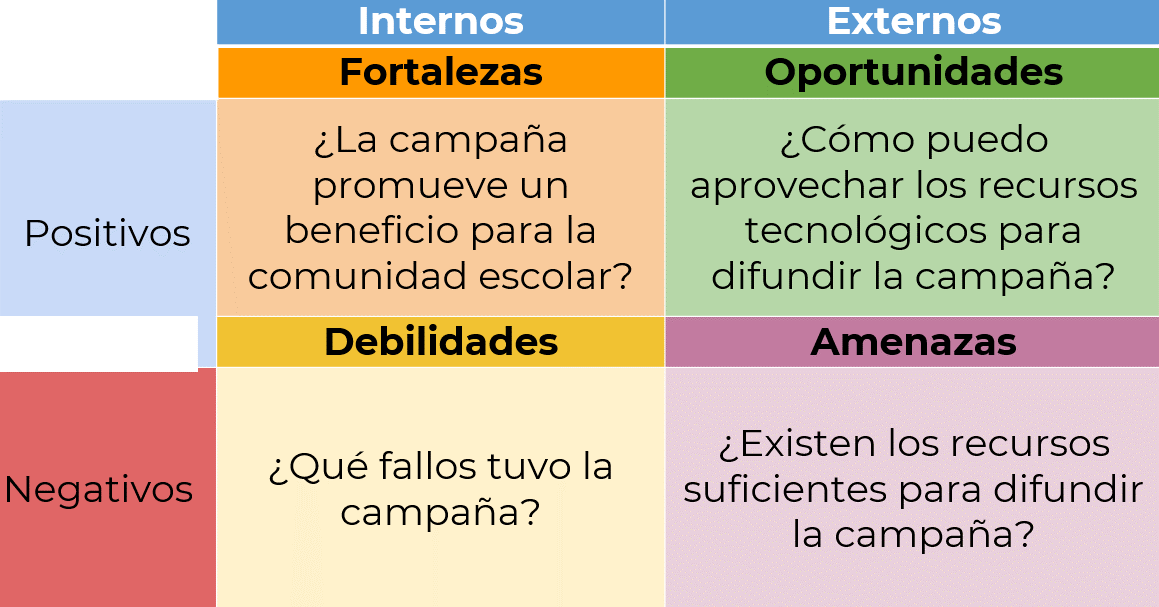
Recuerda que puedes plantearte las preguntas que necesites para analizar los factores positivos y negativos. Ten en cuenta que FODA es una herramienta útil para conocer la situación real de una campaña y planear una estrategia a futuro que ayude a mejorarla.
Ya que trabajaste con todos estos contenidos, te invitamos a que veas la campaña de convivencia escolar “Juntos aprendemos”, que realizaron algunos alumnos, con el objetivo de concientizar a los padres de familia, estudiantes y maestros de realizar un trabajo colaborativo a favor de su proceso de enseñanza.
- VIDEO 03 CAMPAÑA DE CONVIVENCIA
No olvides revisar tu libro de texto a partir del aprendizaje esperado y el propósito; puedes también buscar información para reforzar en internet.
El Reto de Hoy:
A partir del ejemplo del último video que observaste, de la campaña “Juntos aprendemos”. Piensa cómo difundirías esa campaña escolar y cómo le darías un seguimiento adecuado.
Utiliza los recursos que has aprendido en esta sesión para crear tu propia estrategia de trabajo, puedes usar:
- Las acciones de tu cronograma de trabajo.
- Las preguntas que podrías aplicar en una entrevista o encuesta para saber el impacto de esta campaña.
- Las fortalezas, debilidades, oportunidades y amenazas de la campaña.
También puedes aplicar el pensamiento estratégico a alguna campaña escolar en la que hayas colaborado, y piensa de qué manera podrías realizar un seguimiento para medir los alcances del trabajo y cómo mejorar los resultados.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Del recuerdo al re-creo
Aprendizaje esperado: Ejerce su derecho a la vida cultural del país y del mundo mediante el acceso, disfrute y valoración de las manifestaciones del arte.
Énfasis: Recrear manifestaciones del arte para distinguir su importancia como parte de la memoria histórica de nuestro país y del mundo.
¿Qué vamos a aprender?
Observa el siguiente video:
- Video 1. La sobremesa con Giovanna y Maggali
Esta es la “sobremesa” de Giovanna y Maggali.
¿Recuerdas el recreo escolar: desayunando y compartiendo junto con tus amigos?
En esta sesión, estará de invitada Giovanna Cavasola, quien es narradora del programa “Alas y Raíces”.
Ella invita a reflexionar en torno a la importancia de la narración y, en especial, cómo éstas recuperan las memorias.
Prepara tu cuaderno, lápices, colores, bolígrafo y, por supuesto, dispón de todo el poder de tu imaginación, creatividad y sensibilidad.
¿Qué hacemos?
Observa el siguiente video:
- Cuentos y tradición oral
Provoca un encuentro en la mesa de tu casa, con todas las personas que en ella habiten. Si quieres invitar a más personas, hazlo a través de la virtualidad.
Puedes tomarte un café o un té, y al terminar “en la sobremesa” invítales a compartir diversas historias que para ellos sean importantes y que valga la pena recordar.
Observa el siguiente ejemplo:
- Anécdota del abuelo
Como puedes darte cuenta, las narraciones de la sobremesa también permiten recuperar "las memorias", ya sean de nuestros familiares o personas importantes que ya no están.
Pero, también, se puede compartir y recuperar la “memoria histórica” de nuestro país; es decir, aquellos sucesos que han marcado a México y que se han plasmado de distintas formas. Esto ayuda a no olvidar lo que nos conforma como nación.
Observa el siguiente video:
- Con música
Escribir las memorias del futuro, es una buena idea. Imagínate qué tipo de narraciones se podrían compartir en la “sobremesa" en 10 o 20 años. Por ejemplo: ¿qué platicarás sobre esta contingencia sanitaria por COVID-19, u otro acontecimiento que aún no ha ocurrido y que quisieran incluirlo en esas memorias?
Así que, lo que harás será imaginar una situación ya sea real (como este acontecimiento) o imaginaria, por ejemplo: la creación de un nuevo invento.
Por ejemplo, se te sugieren estos temas:
- “Recordar” cómo fue el regreso a clases cuando acabó la pandemia.
- “Recordar” cómo fue tu último día en la secundaria (tratar de generar anécdotas muy específicas: a dónde fuiste a celebrar, qué comiste, etc.).
- Una colaboración artística que realizaste con un colega de otro país.
- Una charla profunda con algún miembro de tu familia.
- El día que te mudaste de casa.
Ahora observa algunos ejemplos de “memorias del futuro” creadas por tus compañeros.
- Anécdotas del futuro
Es interesante lo que los alumnos comparten. Ahora es momento de escribir tu memoria del futuro. Recuerda tomar en cuenta las sugerencias anteriores.
Otra forma para compartir tu memoria del futuro es utilizando algún otro lenguaje artístico.
Piensa con qué lenguaje artístico o elementos de las artes consideras que lo puedes compartir.
- Memoria del futuro
Cuántas miradas distintas se tienen sobre el futuro y cuántas formas diferentes para representar estas “futuras memorias”.
El Reto de Hoy:
Comparte tus producciones con tus profesoras y profesores, y con tus compañeras y compañeros de grupo.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
¿Qué es la refracción de la luz?
Aprendizaje esperado: Describe la generación, la diversidad y el comportamiento de las ondas electromagnéticas como resultado de la interacción entre electricidad y magnetismo.
Énfasis: Conocer y reflexionar sobre el fenómeno de la refracción de la luz.
¿Qué vamos a aprender?
En esta ocasión, continuaras con el análisis acerca del comportamiento de la luz, en relación al fenómeno de la refracción.
¿Qué hacemos?
Desde sesiones anteriores, se han tratado algunos aspectos relacionados con la luz y su comportamiento. Analizaste la reflexión de la luz que ocurre en los espejos. Viste el uso de los telescopios en el estudio del Universo y cómo la luz se desvía en las lentes y espejos que utilizan estos aparatos para formar imágenes cercanas, de objetos lejanos. También se abordó cómo es el arco iris.
En esta ocasión, continuarás el análisis acerca del comportamiento de la luz. Para empezar, piensa un momento lo que sabes acerca de la luz, a partir de las siguientes preguntas:
- ¿Cómo viaja la luz?
- ¿Qué pasa con la luz cuando incide en un espejo o un material transparente como el de una lupa?
- ¿Cómo se ve un cuerpo dentro del agua, por ejemplo, una persona en una alberca o los peces en un estanque? ¿A qué suponen que se debe?
La idea es recuperar lo que sabes y lo puedas relacionar con lo que tratarás el día de hoy. Iniciaras con una experiencia sencilla con la finalidad de analizar cómo se ve un objeto dentro del agua.
Necesitaras: un vaso de cristal transparente y liso, una moneda y un poco de agua.
- Primero, coloca la moneda dentro del vaso de cristal. ¿Qué piensas que ocurrirá con la moneda?
- Con cuidado vierte el agua en el vaso y observa la moneda por un lado del vaso ¿Qué sucede?
- ¿La moneda aumentó de tamaño? Retira el agua para verificar.
La moneda tiene su tamaño original, pero se veía más grande dentro del agua esto se trata de un fenómeno relacionado con el comportamiento de la luz, pero no es el caso de la reflexión que ocurre en espejos, sino de la refracción. Observa el siguiente video acerca del comportamiento de la luz en diferentes materiales:
- ¿Existe la luz invisible?
Ciencias II. Énfasis en Física, Segundo grado, Bloque 4
Del minuto 06:17 al 08:38
- Ondas electromagnéticas
Ciencias y Tecnología. Física, Segundo grado, Bloque 2
Del minuto 03.09 al 03:34
La luz produce diferentes fenómenos dependiendo de las características del material con el que esté en contacto. El fenómeno que se produce en el caso del lápiz que se coloca en el vaso con agua, se trata de la refracción, que sucede cuando la luz atraviesa dos medios diferentes, como el aire y el agua, y desvía su dirección.
La refracción de la luz también tiene que ver con la velocidad con que viaja en los diferentes medios transparentes. La luz viaja en línea recta, con una velocidad de 300 000 km/s pero hay que precisar que tiene esa velocidad en el vacío. Por otra parte, cuando la luz se propaga en medios transparentes, su velocidad cambia, dependiendo de la densidad de los materiales; de esta manera, los haces luminosos son más rápidos en medios poco densos; y más lentos en medios de mayor densidad; al cambiar la velocidad, cambia de dirección.
Si el aire es menos denso que el agua, entonces, la luz viaja más rápido en el aire que en el agua. La velocidad de la luz en el aire es de 299 900 km/s, en tanto que en el agua se propaga a 250 000 Km/s.
Para ejemplificar esto vamos a recurrir a la representación gráfica de los rayos de luz, que se ubican en un plano. Distinguimos los dos medios que atraviesa la luz, divididos por una línea horizontal. Con una flecha, representamos el rayo incidente que se propaga en el medio 1, y avanza hacia en el segundo medio, a partir del cual continua, pero cambia de dirección, formando el rayo refractado.
Ubicamos una línea media vertical punteada, como referente para identificar la desviación del rayo refractado, comparado con el que incide, en relación a los ángulos que se forman. De manera cualitativa se puede distinguir si el ángulo de cada rayo es menor cuanto más se acerque a la línea normal, o es mayor al alejarse de la misma.
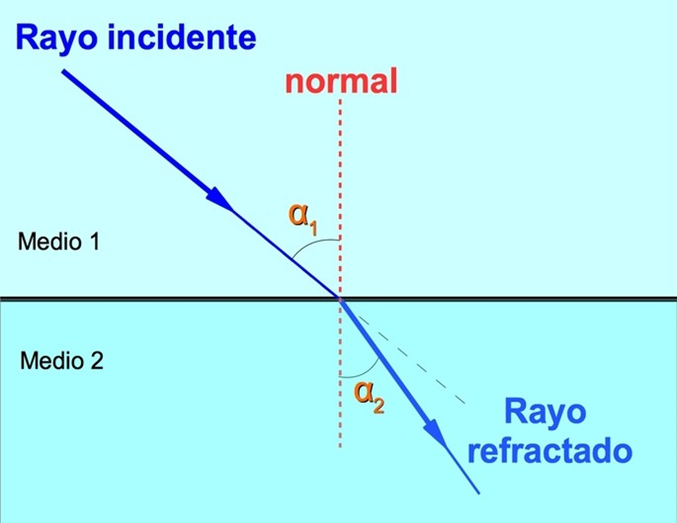
Es una representación similar a la empleada en la reflexión de la luz; la diferencia es que considera dos medios.
Supón que la luz viaja en el vacío y atraviesa un cristal de zafiro, utilizado en joyería. Representa un rayo incidente que viaja en el vacío y desvía su dirección al propagarse en el zafiro, representada en el rayo refractado. ¿En qué caso la luz viaja más lento?, ¿cuál es el medio más denso?
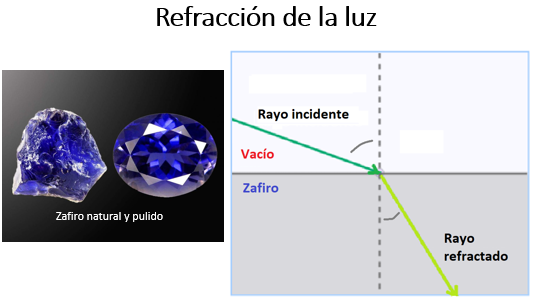
Considerando que la luz viaja más rápido en el vacío, se desplaza más lento en el zafiro; entonces este material es el medio más denso, representado en la zona inferior. En este caso, el ángulo del rayo refractado ¿Es mayor o menor que el ángulo del rayo incidente?
Se aprecia que el rayo refractado está más cerca de la “normal”, comparado con el ángulo del rayo incidente, por tanto, es menor que éste.
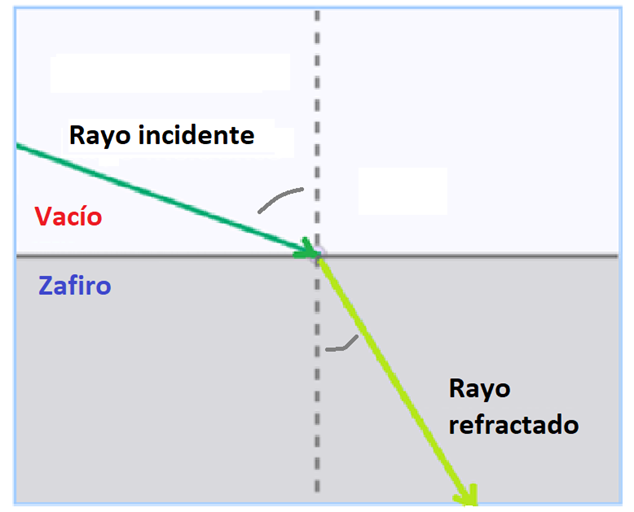
¿Qué supones ocurrirá con la refracción de un rayo que viaja en el vacío, pero continúa su propagación por un material más denso que el zafiro, como el diamante?
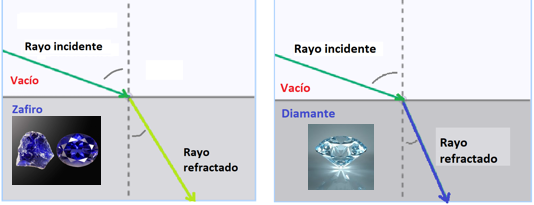
En el caso del diamante, el ángulo del rayo refractado será menor que el formado en el zafiro. Como se ve en la representación, se ubica más cerca de la normal, en comparación con el rayo refractado en el zafiro.
Este mismo caso a la inversa seria de la siguiente manera, el rayo de luz pasa de un medio más denso, como el diamante; a otro de menor densidad como un cristal de aguamarina, también utilizado en joyería ¿En qué medio viaja más rápido la luz? ¿Cómo supones que será el ángulo del rayo incidente en relación al del rayo refractado?
La luz viaja más rápido en el medio menos denso, que en este caso es el de la aguamarina. El rayo refractado se aleja de la “normal”, esto es que su ángulo es mayor respecto del que presenta el rayo incidente.
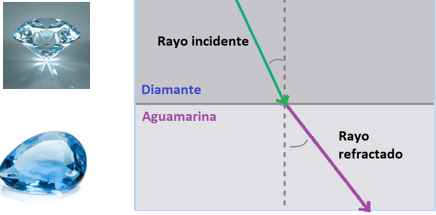
Si la luz pasa del diamante al vacío ¿En dónde viaja a mayor velocidad? ¿Cómo será el ángulo del rayo refractado, comparado con el del ejemplo del cristal de aguamarina?
La luz viaja más rápido en el vacío; el ángulo del rayo refractado que se propaga en el vacío será mayor que el ángulo del rayo refractado en la aguamarina.
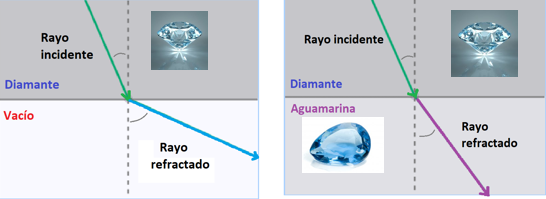
¿Qué pasaría con la luz, en el caso de que el rayo incida de manera perpendicular a la superficie de otro medio? La luz no se desviaría, esto es, no ocurriría la refracción; sin embargo, sí cambia la velocidad de propagación de la luz, considerando que la velocidad disminuye en los medios más densos. La velocidad de la luz varía en los diferentes medios por los que se propaga. Se ha determinado una medida denominada índice de refracción que expresa cuánto se reduce la velocidad de la luz al pasar por determinado material.
El índice de refracción relaciona la velocidad de propagación de la luz en el vacío y la de la luz en un medio determinado, mediante la siguiente expresión matemática:
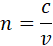
Donde la letra “c” corresponde a la velocidad de la luz en el vacío; la “v” es la velocidad de la luz en un medio determinado; y la “n” refiere el índice de refracción del medio en cuestión.
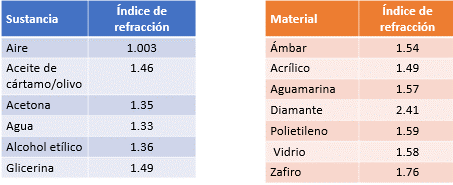
En la tabla se muestran valores para el índice de refracción de diferentes medios.
El índice de refracción del vacío es. Entonces, al aumentar el índice de refracción de un material, la velocidad de la luz será menor y viceversa.
Realiza una actividad para observar la refracción de la luz. Retoma el caso del lápiz en el agua.
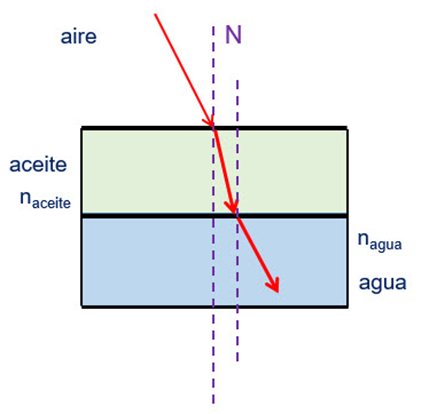
¿Cuáles son los medios por el que pasa la luz en esta situación?
El primer medio es el aire y el segundo es el agua, observa que ocurre al agregar un tercer medio: El aceite.
Para realizar esta actividad, necesitaras:
- Un vaso de cristal transparente, liso
- Un popote o lápiz
- Aceite comestible, y
- Agua
Primero, agrega agua hasta una tercera parte del vaso. Luego vierte otra parte de aceite ¿Qué supones se observará al introducir el popote o el lápiz en el vaso que contiene el aceite y el agua?
De acuerdo con lo que has analizado, se puede deducir que el lápiz o el popote se verán cortado, en cada uno de los medios, debido a que se refracta ya que las sustancias tienen diferente densidad.
Ahora vas a introducir el objeto en el vaso y comprobar la suposición.
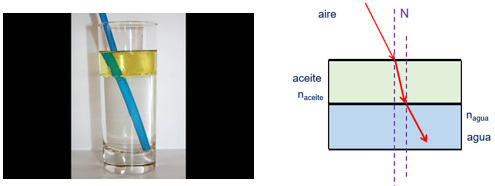
Parece que el popote se hubiera roto en tres partes. Si observas el vaso desde arriba, da la apariencia que el popote se flexiona. Al ver de lado, la imagen del popote se amplifica.
Esto se debe a que el aire, el agua y el aceite tienen distinta densidad y es diferente su índice de refracción, lo que hace que la luz se refracte en cada sustancia, de manera diferente. La desviación de la luz en el aceite es mayor, debido a que el índice de refracción de esta sustancia es mayor que el del agua; que a su vez es mayor al del aire.
Si el rayo de luz pasa del aire, que es el medio de menor densidad, a otro medio de mayor densidad, que en este caso es el aceite; el rayo refractado se acerca a la normal, por eso el popote se ve más cerca del centro del vaso. Pero si la sustancia es más densa como en el caso del aceite y pasa a una menos densa como el agua, el rayo refractado se va a desviar alejándose de la normal.
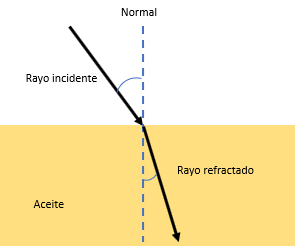
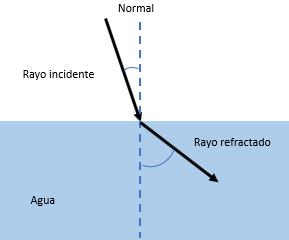
Por eso el popote en el agua se ve más separado del centro del vaso.
La refracción es un comportamiento de la luz que podemos observar en diversas situaciones. Por ejemplo, produce, los espejismos que se observan al viajar por una carretera, debido a que el aire al calentarse tiene diferente densidad, por lo que cambia su velocidad y produce el cambio de dirección de la luz.
Se aprovecha la refracción en el funcionamiento de algunas tecnologías modernas como cámaras fotográficas, microscopios, binoculares y telescopios refractores, que utilizan lentes para refractar la luz y formar imágenes con ciertas características.
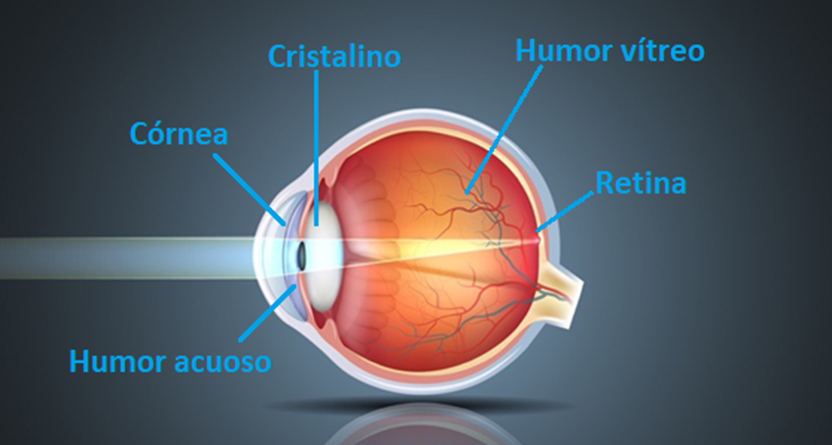
Otro ejemplo ocurre en el mecanismo de la visión: Nuestros ojos tienen una lente natural llamado cristalino, además de contener líquidos; cuando la luz pasa por esos medios que tienen diferente densidad, se refracta y concentra en la retina, lo que nos permite percibir las imágenes.
La refracción también se aprovecha en los anteojos o gafas, mediante los cuales se desvía la luz para corregir defectos de la visión. También ocurre la refracción de la luz en la formación del arcoíris. Isaac Newton estudió este hermoso fenómeno a partir de la observación de los colores que se forman al descomponer la luz blanca del sol, mediante un prisma; colores que se producen de manera natural en el arcoíris.
Un prisma es un medio transparente con caras triangulares. Al incidir, la luz blanca en una de sus caras se refracta, esto es, cambia de dirección y, por la otra cara, sale luz de distintos colores del arcoíris, cada uno tiene distinta longitud de onda y frecuencia.

La luz blanca está formada por ondas de diversa longitud, que al pasar por el prisma se refractan, desviándose más la luz de menor longitud de onda, cercanas al violeta; y desviándose menos la luz con longitud de onda más larga, como el rojo.
En el arcoíris se produce la dispersión de la luz blanca del Sol al pasar por millones de gotas de agua suspendidas en la atmósfera o en las gotas de lluvia, y al refractarse con diferente dirección, forman el espectro de siete colores: rojo, naranja, amarillo, verde, azul, índigo y violeta.
En el siguiente video observaras una descripción sencilla de este proceso
- Ondas electromagnéticas
Ciencia y Tecnología. Física, Segundo grado, Bloque 2
Del minuto 03.35 al 04:25)
Una manera sencilla de formar un arcoíris, la podemos realizar cuando regamos el jardín con una manguera, al medio día, de tal manera que los rayos de luz solar pasan a través de las gotitas de agua.
También, si tienes un atomizador en casa, puedes llenarlo con agua y en un día soleado, a medio día, dar varias atomizaciones, verás que bonito arcoíris formas.
El Reto de Hoy:
Para terminar, te sugerimos una actividad en la que se produce un efecto curioso, debido a la refracción de la luz: Lograr que aparezca una moneda oculta. Puedes compartirla con tus familiares y explicarla, con base en la información que revisaste en la sesión de hoy.
Requerirás de una taza que no sea transparente, una moneda y agua.
Primero, pon la taza sobre una mesa y coloca la moneda en el centro del fondo de la taza.
Observa la moneda, por encima de la taza y, poco a poco, cambia el punto de observación, frente a la taza, de tal modo que la pared del recipiente impida que veas la moneda. Luego, sin mover la taza ni cambiar de posición, vas a verter agua en la taza muy despacio y… de repente… ¡Ya está! ¡Aparece la moneda oculta!
Aunque no muevas la taza ni cambies tu punto de observación. Parece cosa de magia, pero no, se trata de la reflexión de la luz, un fenómeno que tiene una explicación científica.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
El arte novohispano
Aprendizaje esperado: Aprende los rasgos principales de las ciencias y artes novohispanas entre los siglos XVI y XVII. Además, reconoce las características del periodo Barroco.
Énfasis: Conocer las características del Barroco y su expresión mexicana. Asimismo, conocer a Sor Juana Inés de la Cruz y su obra como ejemplo de la literatura del Barroco novohispano.
¿Qué vamos a aprender?
En la sesión de hoy enfocarás la mirada en el arte novohispano, en particular revisarás el estilo denominado Barroco, y abordarás a una de las más grandes poetisas de esta época, auténtico símbolo de la cultura virreinal: Sor Juana Inés de la Cruz.
¿Qué hacemos?
Barroco es una palabra que proviene del vocablo portugués barroco, en español su equivalente es barrueco. Término utilizado para designar a las perlas que no tienen un perímetro regular, es decir, que tienen protuberancias y deformaciones. La palabra barroco también se emplea para nombrar a aquello que está excesivamente recargado u ornamentado.

Perla barrueca
https://europeomodernoula.wordpress.com/2018/03/21/comentario-a-proposito-de-la-clase-de-hoy-barroco-y-clasicismo/
Sin embargo, la acepción que nos ocupa es aquella que hace referencia a un movimiento cultural ampliamente extendido desde 1600 hasta 1750, aproximadamente. Para comprender qué es el Barroco debemos remontarnos a la Europa occidental del siglo XVI.
En Alemania, las ideas del fraile agustino Martín Lutero dieron lugar al movimiento conocido como Reforma Protestante. Lutero dirigió una serie de críticas y señalamientos en contra de la iglesia católica, particularmente reprochó la venta de indulgencias para financiar la construcción de la Basílica de San Pedro en Roma. Por su parte, la iglesia católica emprendió la Contrarreforma.

Martín Lutero. Obra de Lucas Cranach el Viejo, 1529.
https://es.wikipedia.org/wiki/Mart%C3%ADn_Lutero#/media/Archivo:Martin_Luther_by_Cranach-restoration.tif
Estos enfrentamientos religiosos, que desembocaron en una ruptura al interior de la cristiandad, enfrentaron a familias, localidades, regiones, naciones e incluso imperios entre sí. Además de sangrientas batallas, el conflicto se desarrolló en el ámbito artístico:
Por un lado, las ideas reformistas se inclinaban por el retorno a un cristianismo primitivo; rechazaban la utilización de imágenes religiosas y consideraban que el arte sacro debía ser austero y sobrio.

Vista de la nave principal de la Iglesia de San Olaf, Tallin, Estonia.
https://es.wikipedia.org/wiki/Iglesia_de_San_Olaf_(Tallin)#/media/Archivo:Iglesia_de_San_Olaf,_Tallinn,_Estonia,_2012-08-05,_DD_02.JPG
Por otro lado, la iglesia católica, sujeta a la jurisdicción papal, empleó el arte como un medio de propaganda religiosa, surgió así el Barroco, un estilo artístico que se reprodujo en la pintura, la escultura, la arquitectura, la música y la literatura.

Vista de la nave central de la capilla de la Virgen del Rosario, Puebla, México.
https://twitter.com/PueblaEsChula/status/1238172488112226305/photo/1
El Barroco apelaba a la contemplación de la obra artística como una experiencia sensorial que involucraba la vista, el tacto y el oído. Este estilo se caracterizó por su dinamismo en la forma, su excesiva ornamentación, así como por su inclinación a lo espectacular y monumental. La idea era comunicar la fe al mayor número de creyentes y consolidar el catolicismo a través de los sentidos.
Observa el siguiente video acerca del arte y la contrarreforma en la Nueva España.
- El arte y la contrarreforma en la Nueva España
Historia, Segundo grado, Bloque 2
https://www.youtube.com/watch?v=jY5AKBpGBG8
Cómo pudiste observar, el Barroco fue el estilo artístico predominante durante el siglo XVII en la Nueva España. Pero el Barroco fue más que un género artístico, ya que se pude comprender como el periodo histórico que abarcó todo el siglo XVII y la primera mitad del XVIII, el Barroco permeó todas las actividades de la sociedad, por tanto, se consolidó como un "modo de vivir". Como explica el filósofo Bolívar Echeverría en su texto “La modernidad de lo barroco”:
“extender el calificativo de "barroco" de las obras de arte definidas como tales al conjunto de los fenómenos culturales que las rodean, e incluso a la región o la época en que ellas fueron producidas, es una tendencia tan vieja como la idea misma de lo barroco”.
Bolívar Echeverría. La modernidad de lo barroco. México, Era, 2000.
De acuerdo con Echeverría, el Barroco tuvo un desarrollo particular en América, fue practicado tanto por indígenas como por los demás grupos sociales novohispanos como una forma de apropiarse de la cultura occidental y redefinirse como mestizos.
El arte barroco novohispano se caracterizó por la producción de obras religiosas de gran ornamentación en las que se fusionaron elementos indígenas con formas e ideas europeas, africanas y asiáticas.
Dentro de la arquitectura barroca, se puede señalar la Catedral Metropolitana de la Ciudad de México como una de sus expresiones más bellas. Destaca en particular el Retablo de los Reyes, obra del escultor español Jerónimo de Balbás. También son obras barrocas el convento jesuita de Tepotzotlán, en el Estado de México y el templo de Santa Prisca de Taxco en Guerrero.




Una manifestación dentro de la arquitectura y escultura barrocas fue el churrigueresco. Este estilo recibe su nombre por una familia española de arquitectos de apellido Churriguera. Fue introducido a la Nueva España por Jerónimo de Balbás, se caracteriza por una saturación exacerbada de elementos decorativos. Ejemplos del arte churrigueresco son la Catedral de Zacatecas o la cúpula de la Iglesia de Santa María Tonantzintla en Puebla.


Por su parte, la pintura barroca novohispana se caracterizó por la representación de temas tanto religiosos como profanos, las formas son voluptuosas y exageradas, las figuras cobran expresividad y movimiento y el contraste de luces y sombras imprime realismo a las obras. Entre los pintores novohispanos más destacados se encuentra Cristóbal de Villalpando.
Algunas de sus obras se pueden apreciar en las catedrales de la Ciudad de México, Puebla y Guadalajara, así como en el convento de Tepotzotlán. Una de sus piezas más reconocidas es el retrato de La Plaza Mayor de México pintado en 1695.

Otro representante de la pintura barroca novohispana fue Juan Correa. Una de las obras más conocidas de este pintor de ascendencia africana es La asunción de la Virgen.

Por último, destacaremos a Miguel Cabrera, quien además de retratar temas religiosos dejó constancia de costumbres y espacios de la realidad cotidiana en los cuadros de castas que pintó. Fue un artista prolífico, su obra se compone de más de 300 piezas.
Entre las que destaca el Retrato de Sor Juana Inés de la Cruz. Observa con detenimiento el cuadro de Cabrera que aparece en pantalla. ¿Qué aspectos de la vida y personalidad de Sor Juana crees que destaca el pintor?

Para responder esta pregunta lee la participación de una alumna de secundaria.
“Observo que el pintor retrató a Sor Juana portando su hábito de monja, sentada frente a un escritorio, detrás de ella se puede ver un gran librero. Creo que el artista quiso resaltar su gran inteligencia, su gusto por el estudio y su devoción religiosa”.
El pintor novohispano representó a sor Juana Inés de la Cruz en una celda amplia, llena de libros para destacar la sabiduría y amor por el estudio que la caracterizaron.

Cabrera realizó la pintura más de medio siglo después de la muerte de Sor Juana, para elaborarla se inspiró en un retrato de 1713 del artista español Juan de Miranda. Se puede observar la Décima Musa, apelativo con el que también se conoce a la monja, portando el hábito de la Orden de las Jerónimas en el pecho, se ve el llamado “escudo de monjas”, se encuentra sentada en un sillón de respaldo alto; su mano derecha se posa sobre un libro, mientras que en la mano izquierda sostiene un rosario en alusión a su piedad.
Sin lugar a dudas, Sor Juana Inés de la Cruz es una de las mujeres más ilustres de la historia de nuestro país y una de las exponentes más importantes de la literatura barroca hispanoamericana. Juana Inés de Asbaje Ramírez de Santillana nació en San Miguel Nepantla, localizado en el actual Estado de México, un 12 de noviembre; sobre el año de su nacimiento hay algunas dudas, ella declaró haber nacido en 1651, pero en su fe de bautismo se asienta que fue en 1648.
Los datos que se conocen sobre la vida de Sor Juana están basados principalmente en dos fuentes: la carta autobiográfica que envió a Manuel Fernández de Santa Cruz, obispo de Puebla, conocida como Respuesta a Sor Filotea de la Cruz; y la obra Vida de la madre Juana Inés de la Cruz, religiosa profesa en el convento de San Jerónimo de la Ciudad Imperial de México, del sacerdote jesuita Diego Calleja, quien fuera su primer biógrafo.
Sor Juana pasó los primeros años de su vida en la hacienda de su abuelo materno en Amecameca, Estado de México. Allí aprendió a hablar náhuatl con los indígenas que laboraban en la propiedad.

A los tres años de edad ya sabía leer, aprendió a escondidas de su madre, y cuando tenía ocho años compuso su primera loa con la que ganó un concurso local.
Su gusto por el estudio era tal que llegó a pedir a su madre que la enviara a la Ciudad de México vestida de hombre para que pudiera asistir a la Universidad, pero ésta no accedió. Su deseo de mudarse a la capital del virreinato se realizó en su adolescencia, cuando tras la muerte de su abuelo su madre la envío a vivir con unos parientes.
Estando ya en la Ciudad de México aprendió latín en tan sólo diez lecciones. Pronto, la fama de su inteligencia y belleza llegó a la corte del marqués de Mancera, virrey de la Nueva España. La virreina Leonor de Carreto se convirtió en su mecenas y protectora.

Durante su estancia en el palacio virreinal, por instrucciones del virrey, fue examinada por un grupo conformado por 40 hombres, los más sabios e ilustres de la ciudad. La joven Juana Inés salió triunfante de la prueba, gracias a la agudeza de sus argumentos y réplicas ganó admiración y respeto.
Por consejo del padre jesuita Antonio Núñez de Miranda, a quien conoció en la corte y más tarde se convertiría en su confesor, ingresó a la vida religiosa. Primero lo hizo en el convento de San José con las carmelitas descalzas, pero salió debido a que la regla era demasiado estricta.
En un segundo intento, en 1669, ingresó al convento de San Jerónimo, eligió esta orden, por un lado, porque le daba la posibilidad de comprar una celda particular con un amplio espacio para instalar su biblioteca personal. Y por otro porque disponía de tiempo y privacidad para dedicarse a sus estudios y escritos. Además, sin quebrantar la regla conventual, podía disponer de gente a su servicio.

Tras convenirse en jerónima, fue que Sor Juana escribió la mayor parte de su obra narrativa, la cual es muy variada porque incluye versos sacros y profanos, villancicos para festividades religiosas, autos sacramentales y dos comedias teatrales: Los empeños de una casa y Amor es más laberinto.
Gracias a su talento literario, Sor Juana pudo hacerse de recursos, escribía textos por encargo y, a cambio, recibía un pago, el dinero lo invirtió en instrumentos musicales y científicos que le gustaba coleccionar y en ampliar su biblioteca. A decir de la propia Sor Juana, por gusto sólo escribió un “papelillo” llamado “El sueño”.
Se trata de su poema más célebre, fue publicado en 1692 bajo el título de Primero sueño, en él la autora relata el viaje del alma al separarse del cuerpo. Octavio Paz dedicó un análisis profundo a esta pieza poética en su obra Sor Juana Inés de la Cruz o Las trampas de la fe.

La publicación de gran parte de la obra de Sor Juana se la debemos a la virreina Luisa Manrique de Lara y Gonzaga, condesa de Paredes, quien instó a la monja a reunir sus poesías con la finalidad de publicarlas en España. Ser una mujer de letras en una época donde el ámbito intelectual era reservado sólo para los hombres, le significó a Sor Juana varias dificultades, no faltaron quienes se empeñaron en reprocharle su dedicación al estudio y a temas mundanos, como lo hicieran su confesor Núñez de Miranda, el arzobispo de México Francisco de Aguiar y Seijas y el obispo de Puebla Manuel Fernández de Santa Cruz.
Con este último sostuvo una disputa luego de que, en 1690, el obispo publicara, bajo el título de Carta atenagórica, una crítica que Sor Juana había formulado a propósito de un sermón del sacerdote jesuita Antonio Vieyra.

Retrato de Manuel Fernández de Santa Cruz. Autor Anónimo. Museo Nacional del Virreinato, Tepotzotlán, México.
https://commons.wikimedia.org/wiki/File:Obispo_Manuel_Fern%C3%A1ndez_de_Santa_Cruz.jpg
Se desconocen los motivos por los que el obispo Fernández de Santa Cruz difundió el texto de Sor Juana sin su consentimiento, también publicó una carta que él mismo escribió bajo el seudónimo de Sor Filotea de la Cruz, en la que asegura que ninguna mujer debería esforzarse por aprender ciertos temas filosóficos y sugería a la monja jerónima enfocarse en temas más sagrados.
En su defensa, Sor Juana escribió el texto conocido como Respuesta a Sor Filotea de la Cruz.
Lee algunos fragmentos de la Respuesta a Sor Filotea de la Cruz, el texto ha sido modificado para facilitar su lectura y comprensión. Dice así:
“[…] Yo no estudio para escribir, ni menos para enseñar (que fuera en mí desmedida soberbia), sino sólo por ver si con estudiar ignoro menos.
[…] Empecé a aprender gramática, en que creo no llegaron a veinte las lecciones que tomé; y era tan intenso mi cuidado, que siendo así que en las mujeres -y más en tan florida juventud- es tan apreciable el adorno natural del cabello, yo me cortaba de él cuatro o seis dedos, midiendo hasta dónde llegaba antes, e imponiéndome ley de que si cuando volviese a crecer hasta allí no sabía tal o cual cosa que me había propuesto aprender en tanto que crecía, me lo había de volver a cortar en pena de la rudeza. Sucedía así que él crecía y yo no sabía lo propuesto, porque el pelo crecía aprisa y yo aprendía despacio, y con efecto le cortaba en pena de la rudeza: que no me parecía razón que estuviese vestida de cabellos cabeza que estaba tan desnuda de noticias, que era más apetecible adorno.

[…] Yo confieso que me hallo muy distante de los términos de la sabiduría y que la he deseado seguir, aunque [de lejos]. Pero todo ha sido acercarme más al fuego de la persecución, al crisol del tormento; y ha sido con tal extremo que han llegado a solicitar que se me prohíba el estudio.
Pues si vuelvo los ojos a la tan perseguida habilidad de hacer versos, que en mí es tan natural […] he buscado muy de propósito cuál sea el daño que pueden tener, y no le he hallado […].

Interpretación moderna del retrato de Sor Juana del pintor mexicano Mauricio García Vega.
Pues si está el mal en que los use una mujer, ya se ve cuántas los han usado loablemente; pues ¿en qué está el serlo yo? Confieso desde luego mi ruindad y vileza; pero no juzgo que se haya visto una copla mía indecente”.

“Lo que sólo he deseado es estudiar para ignorar menos: que, según San Agustín, unas cosas se aprenden para hacer y otras para sólo para saber […] Pues ¿en qué ha estado el delito?”.
Sor Juna no sólo hace una defensa de su capacidad intelectual, sino que también cuestiona el impedimento impuesto a las mujeres para acceder a la educación.
En 1693, un par de años después de la publicación de su respuesta, Sor Juana dejó de escribir, las razones no son claras, hay quienes señalan que se debió a la renovación de sus votos religiosos y hay quienes ven una conjura misógina para obligarla a abandonar su labor intelectual. Lo cierto es que, meses antes de su muerte, Sor Juana firmó el libro del convento como “yo, la peor del mundo”, ésta se volvería una de sus frases más célebres.
A principios de 1695, se desató una epidemia en la Ciudad de México, probablemente se trataba de tifus o fiebre amarilla, la enfermedad llegó al convento de San Jerónimo causando grandes estragos. Sor Juana se contagió y murió el 17 de abril de ese año.
Además de la religiosa jerónima, Carlos de Sigüenza y Góngora y Juan Ruíz de Alarcón fueron grandes exponentes de la literatura barroca en la Nueva España.


Mientras tanto, en otras partes del mundo Mientras en Europa y las colonias españolas se desarrollaba el Barroco en 1682, el navegante francés Robert de La Salle exploró las aguas del río Mississippi y lo reclamó para Francia, junto con las tierras circundantes. Esto daría inicio al expansionismo francés en América. El territorio adjudicado sería conocido como Luisiana, nombrado así en honor del rey Luis XIV.

Además de las obras mencionadas a lo largo de la sesión, puedes consultar otras fuentes bibliográficas, digitales y audiovisuales que tengas a la mano, por ejemplo, para saber más acerca de Sor Juana Inés de la Cruz, visita la página de la Secretaría de Gobernación.
Si quieren profundizar en la época barroca novohispana, te invitamos a leer México durante el virreinato, de Antonio Rubial, texto que encontrarás en la colección de los Libros del rincón.
También puedes consultar Monjas, cortesanos y plebeyos. La vida cotidiana en la época de Sor Juana, del mismo autor.

Antonio Rubial García. Monjas, cortesanos y plebeyos. La vida cotidiana en la época de Sor Juana. México, Taurus, 2005.
El Reto de Hoy:
Escribe un párrafo en el que expliques cómo Sor Juana defendió su derecho a la educación. Incluye una reflexión propia acerca de la igualdad de derechos y oportunidades que debe existir entre mujeres y hombres.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario