Aprende en Casa III SEP: 13 de mayo TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 13 de mayo de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Jueves 13 de mayo, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Proporcionalidad inversa VII
Aprendizaje esperado: Analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.
Énfasis: Interpretar y resolver problemas que se modelan con este tipo de variación en diferentes contextos.
¿Qué vamos a aprender?
Hoy continuarás con el análisis y resolución de problemas de variación proporcional inversa. En esta ocasión resolverás problemas que se presentan en diversos contextos y que se modelan con este tipo de variación.
Ten a la mano tu cuaderno u hojas para tomar notas y tú lápiz o bolígrafo y una goma.
¿Qué hacemos?
Para iniciar, lee y analiza cuidadosamente el enunciado de cada uno de los problemas que se presentarán y piensa en una estrategia para resolverlos. Antes de aplicar un procedimiento, también es importante reflexionar sobre cuál es la propiedad o propiedades que se están usando para resolverlo.
Seguramente has escuchado acerca de las carreras de autos de la Fórmula 1. El primer problema que analizarás se ubica en ese contexto.

Una forma de iniciar la resolución del problema es reflexionar sobre las siguientes preguntas. Tú en casa, toma un tiempo para contestarlas.
¿La revisión la harán más o menos de 15 mecánicos?
Bien como vez, la revisión la harán menos de 15 mecánicos.
Los 5 mecánicos ¿deberían tardar más o menos de 600 segundos?
Los 5 mecánicos tardarán más de 600 segundos, que es lo que tardan 15 mecánicos.
¿La consigna y la pregunta se refieren a las mismas unidades de tiempo?
No. En los datos del problema se refiere a segundos y se pregunta por minutos.
¿Qué procedimiento pueden seguir para resolver el problema?
Anota lo que harían en tu cuaderno y resuelve el problema.
Ahora se revisarán dos maneras de resolver este problema.
Uno de los procedimientos es utilizar la constante de proporcionalidad inversa. Sin embargo, para estar en posibilidad de utilizarla es preciso que primero recuerdes qué es la constante de proporcionalidad inversa y cómo se obtiene.
El otro procedimiento es utilizar una proporción inversa. En este caso, debes saber lo que es una proporción de este tipo y cómo plantearla correctamente, incluso debes recordar qué es una proporción directa, porque se puede partir de ésta para facilitar el planteamiento de la inversa.

Se te invita a que reflexiones en lo que has aprendido a lo largo de este tema para responder las preguntas que se te plantean. Una vez que hayas reflexionado al respecto hay que aplicar ambos procedimientos.
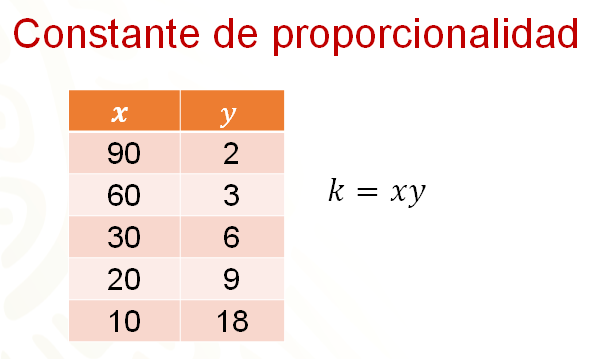
En toda proporción inversa, al multiplicar los valores de la primera magnitud por su correspondiente de los de la segunda, se obtiene una constante, que se simboliza con la letra “k”.
En la siguiente tabla se muestran los valores de “x” y “y” de una proporción inversa. Ahí puedes ver que los productos de los valores correspondientes de cualquier fila, es 180; por ejemplo, 90 por 2, 30 por 6 y 10 por 18. Entonces 180 es la constante de proporcionalidad inversa para estos valores.
De manera general, la constante “k” es igual a “x” por “y”.
Primero se presentará el procedimiento utilizando la constante de proporcionalidad inversa. Hay que organizar los datos en una tabla, en donde anotas en la primera columna el número de mecánicos, que será la variable independiente, o sea “x”; en la segunda columna anotas el tiempo en segundos que tardan los mecánicos en hacer el trabajo; ésta será la variable dependiente, es decir, “y”.
Como la fórmula de la constante de proporcionalidad inversa es “k” igual a “x” por “y”, se sustituyen en ella los valores conocidos de “x” y “y”, por lo que “k” es igual a 15 por 600, lo que arroja como producto 9 000, que será el valor de la constante en este caso.
De la fórmula de la constante “k” igual a “x” por “y” se obtiene que “y” es igual a “k” entre “x”. Al sustituir en esta igualdad la constante y el valor de “x” igual a 5, se tiene que “y” es igual a 9000 entre 5, cuyo cociente es 1 800.
Con esto se puede afirmar que 5 mecánicos tardarían 1 800 segundos en hacer el mismo trabajo que 15 mecánicos realizan en 600 segundos.

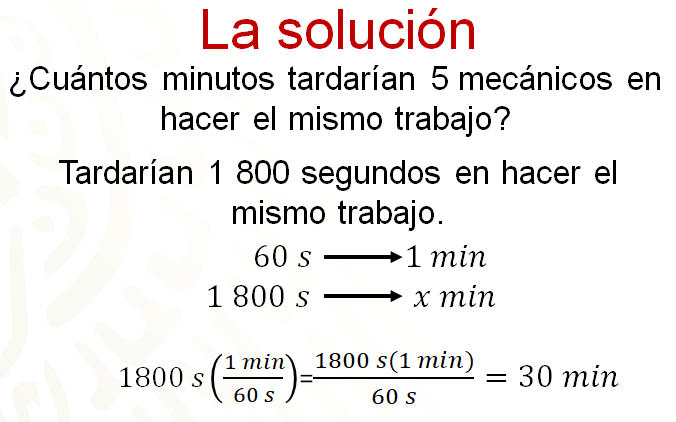
Ahora se pude dar solución al problema, es decir, contestar la pregunta ¿cuántos minutos tardarían 5 mecánicos en hacer el mismo trabajo?
Anteriormente se encontró que los 5 mecánicos tardarían 1 800 segundos en hacer el mismo trabajo.
Sin embargo, se pregunta por el tiempo en minutos, por lo tanto, se deben convertir los segundos en minutos. Sabes que 60 segundos equivalen a un minuto y quieres saber cuántos minutos son 1 800 segundos. Al resolver esta proporción directa, se multiplica 1 por 1 800 y el resultado se divide entre 60. Este último resultado es el número de minutos equivalentes a 1 800 segundos. Entonces, ¿cuántos minutos tardarían 5 mecánicos en hacer el mismo trabajo?
La respuesta es que tardarían 30 minutos.
Otro procedimiento que puedes usar es el que consiste en plantear dos razones para conformar una proporción inversa. Para facilitar formar la proporción inversa se puede partir de formar la proporción como si fuera directa. Así que, 15 es a 5 como 600 es a “y”, pero enseguida debes proceder a dejar la primera razón tal como está y se invierte la segunda, en lugar de escribir 600 es a “y”, escribes “y” es a 600. De esta manera se forma la proporción 15 es a 5 como “y” es a 600.
Para encontrar el valor de “y” se multiplica 15 por 600, entre 5. El resultado es 1 800, que es el mismo resultado al que se llega con el procedimiento anterior.

Es común cometer errores a la hora de plantear la proporción inversa. Para evitar confundirte, se puede plantear la proporción como si se tratara de una proporcionalidad directa, esto sólo con la finalidad de facilitar formar la proporción.

Revisa el caso de este problema. En la expresión del inciso “A” está planteada la proporción como si se tratara de proporcionalidad directa; luego, en el inciso “B” está formada la proporción inversa de forma correcta, ya que se mantuvo la primera razón y se invirtió la segunda.
Sin embargo, en el inciso “C”, aunque la proporción planteada es equivalente a la del inciso “A”, en el inciso “D” al invertir correctamente la segunda razón del inciso “C” la proporción inversa está mal planteada. El error surge porque en el inciso “C”, al plantear la proporción directa, no se respetó el colocar la misma clase de magnitud en la primera razón, en este caso, el número de mecánicos, sino que se formó con mecánicos y tiempo, por consecuencia, la proporción inversa planteada es incorrecta.
Dadas dos magnitudes inversamente proporcionales, la razón entre dos cantidades de la primera magnitud es igual a la razón inversa de las cantidades correspondientes de la otra. En la proporción del inciso “B” se observa que mientras una magnitud disminuye, la otra debe aumentar, por eso una flecha va hacia abajo y la otra hacia arriba.

Otra propiedad de la variación proporcional inversa es que la razón entre dos cantidades de la primera magnitud es igual a la razón inversa de las cantidades correspondientes de la otra.
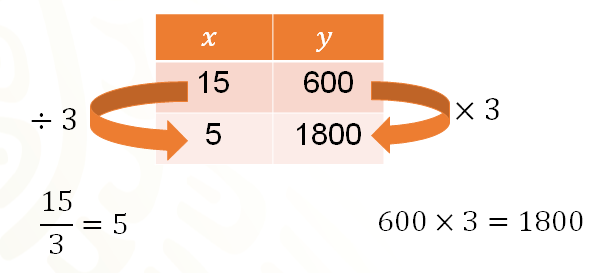
La siguiente tabla muestra cantidades que varían de manera inversamente proporcional. En ella se puede ejemplificar la propiedad enunciada anteriormente, ya que si “x” es igual a 15 y se divide entre 3 se obtiene “x” igual a 5, entonces a “y” igual a 600, que corresponde a “x” igual a 15, se multiplica por 3 para obtener el valor de “y” correspondiente a “x” igual a 1 800, como lo indican las flechas anaranjadas.
La razón inversa de 3 es  , que es lo mismo que dividir entre 3 o viceversa.
, que es lo mismo que dividir entre 3 o viceversa.
Al resolver el problema de carreras de la Fórmula 1, se obtuvo que 5 mecánicos tardarían 30 minutos en hacer la revisión completa de uno de sus automóviles. Ahora se quiere saber ¿cuántos minutos tardarían 4, 8, 10 y 12 mecánicos en realizar el mismo trabajo?
Una forma de resolver el problema es construir una tabla donde, en la primera columna, se escriba el número de mecánicos que trabajarán en la revisión del automóvil y en la segunda, el tiempo (en minutos) que tardarán en hacer ese trabajo.
En el problema dice que 15 mecánicos realizan el trabajo en 600 segundos, que equivalen a 10 minutos, por eso, en la tabla se registró 10.

Se usa la fórmula de la constante “k” igual a “x” por “y” y si multiplicas cualquiera o las dos parejas de valores conocidos para “x” y “y”, es decir, 5 por 30 y 15 por 10, se obtiene que “k” es igual a 150.
Por otro lado, de la fórmula de la constante se obtiene que “y” es igual a “k” entre “x” se tiene que “y” igual a 150 sobre “x”. Entonces se utiliza esta expresión para obtener los valores correspondientes de “y” dividiendo 150 entre el valor de “x”, es decir, entre el número de mecánicos.
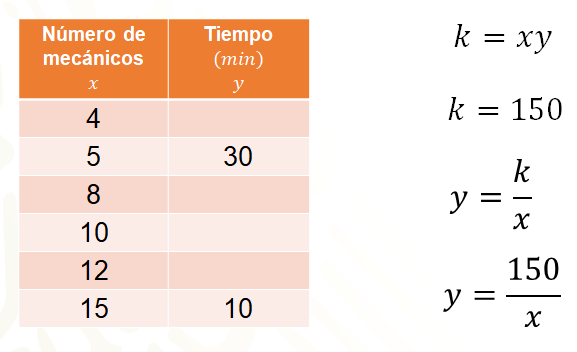
De esta forma se puede completar la tabla. Para 4 mecánicos “y” es igual a 150 entre 4, cuyo cociente es 37 punto cinco. Es decir, 4 mecánicos tardarían 37 punto 5 minutos en realizar el mismo trabajo.
En casa completa los datos que faltan en la tabla.
Ahora, compara tus resultados con los mostrados aquí y, en caso necesario, corrígelos.

- 8 mecánicos realizarían ese trabajo en 18 punto 75 minutos.
- 10 mecánicos realizarían ese trabajo en 15 minutos.
- 12 mecánicos realizarían ese trabajo en 12 punto 5 minutos.
Te puedes preguntar ¿qué procedimiento elegir?
Al resolver un problema de proporcionalidad inversa, utilizar la constante de proporcionalidad “y” igual a “k” entre “x”, o bien plantear una proporción inversa como la equivalencia de dos razones.
De hecho, es indistinto aplicar cualquiera de esos procedimientos, sin embargo, se debe notar que el problema inicial de las carreras de la Fórmula 1 se pedía un sólo valor, el correspondiente a la cantidad de tiempo que tardarían en la revisión 5 mecánicos, así que usar cualquier procedimiento es indistinto; sin embargo, en la segunda versión del problema, se pedían varios valores de la cantidad de tiempo, en esta última situación se vuelve más ágil utilizar la constante de proporcionalidad, ya que sólo se divide el valor de “k” entre los valores de “x” para encontrar los valores requeridos para “y”. Sería menos ágil formar proporciones inversas para cada valor.

Has revisado dos procedimientos con los cuales es posible resolver problemas de proporcionalidad inversa.
A continuación, se analizará y resolverá otro problema de este tipo de proporcionalidad a través de otro procedimiento.

Piensa en una estrategia para resolver este problema.
¿Ya la tienes?
Este problema puede resolverse con alguno de los dos procedimientos que ya se han utilizado, sin embargo, se revisará otra manera de resolver este tipo de situaciones.
En el problema que se está resolviendo, puede extraerse sólo lo matemático del enunciado, o sea, repartir 590 300 en partes inversamente proporcionales a 6, 8, 12 y 18. Ahora bien, recuerda una de las propiedades de la proporcionalidad inversa que dice: “dadas dos magnitudes inversamente proporcionales, la razón entre dos cantidades de la primera magnitud es igual a la razón inversa de las cantidades correspondientes a la otra”.
Utilizando esta propiedad sabes que repartir 590 300 en partes inversamente proporcionales a 6, 8, 12 y 18, equivale a repartir 590 300 en partes directamente proporcionales a un sexto, un octavo, un doceavo y un dieciochoavo.

Para resolver las proporciones directas se deben convertir las fracciones un sexto, un octavo, un doceavo y un dieciochoavo en sus equivalentes con igual denominador, éstas pueden ser, un sexto igual a 12, 72avos; un octavo igual a 9, 72avos; un doceavo igual a 6, 72avos, y un dieciochoavo igual a 4, 72avos.
Al sumar las fracciones, se obtiene 31/72, que es el total que hay que repartir entre los 4 hijos de forma directamente proporcional a las fracciones obtenidas. De ahí se forma la razón 590 300 es a 31/72, con las que se va a calcular la proporción directa.

Usando la primera fracción, 12, 72avos para plantear la proporción directa 590 300 es a 31/72 como “x” es a 12/72. Al resolver esta proporción directa, se obtendrá la cantidad que le corresponde a la primera fracción, es decir al hijo de 6 años.
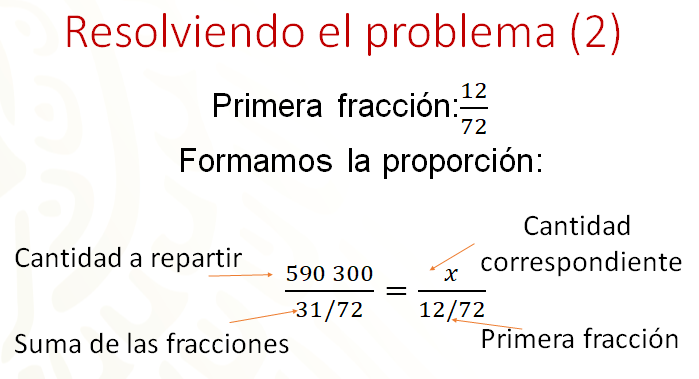
Para resolver la proporción directa que se ha planteado, en la siguiente imagen se tiene del lado izquierdo el procedimiento que conoces como regla de tres y que se basa en los productos cruzados, es decir, multiplicar 590 300 por 12/72 y dividirlo entre 31/72, de esa manera se obtiene 228 503 punto 22.
Del lado derecho se han usado los productos cruzados para formar una ecuación lineal, donde, al despejar “x” se encuentra el mismo resultado que en el procedimiento de la izquierda. Comparando ambos procedimientos te puedes dar cuenta que el procedimiento de la regla de tres se basa precisamente en el planteamiento de la ecuación.

Ambos procedimientos tienen su fundamento en una propiedad de las proporciones, el cual dice que el producto de los extremos es igual al producto de los medios, considerando a 590 300 y a 12/72 como los extremos, y a “x” y 31/72 los medios.
De esta manera, se puede decir que al hijo que tiene 6 años, le corresponden 228 503 pesos con 22 centavos.
Pon en práctica el procedimiento que has desarrollado para obtener la cantidad de dinero que le toca a cada uno de los demás hijos.
Recuerda que originalmente se está resolviendo una proporción inversa, pero en este caso se ha convertido en una proporción directa con el inverso de la segunda razón para llegar a la solución.
Ahora, se resolverá un último problema.

Cabe mencionar que se desea colocar toda la pintura en un sólo tipo de envase. En la tabla se muestran las diferentes capacidades que tendrán los envases, la idea es saber cuántos comprar, de acuerdo con la capacidad de los envases.
¿Qué harías para resolver este problema?
Podrías iniciar identificando ¿cuál es la consigna del problema?
Tienes que encontrar el número de recipientes de varias capacidades que se necesitan para envasar toda la pintura.
Por otro lado, ¿qué datos o condiciones se te proporcionan?
Primero, que hay 80 envases, cada uno con 5 litros de pintura. Luego, que se debe repartir toda la pintura en envases de dos, uno, medio o de un cuarto de litro.

Un procedimiento que se puede utilizar para resolver el problema es el uso de la constante “k”, que se obtiene multiplicando dos valores correspondientes conocidos, en este caso 5 por 80. El resultado de esta multiplicación es 400 por lo que se puede afirmar que “k” es igual a 400.
¿Qué representa el valor de “k” en el contexto de este problema?
Es el total de litros de pintura que se ha decidido colocar en envases de menor capacidad que en los que se encuentran.
Por otro lado, también se sabe qué “y” es igual a “k” entre “x”. Entonces sólo queda sustituir los valores que se tienen de “x”, es decir las diferentes capacidades, una por una, en esta expresión de “y”, para encontrar los diferentes valores de “y”, que es el número de envases requeridos. Por ejemplo, para “x” igual a 2 se tiene que “y” es igual 400 entre 2 igual a 200. Con esto, se sabe que se requieren 200 recipientes de 2 litros para envasar toda la pintura.
¿Cuántos envases de 1 litro se necesitan para envasar toda la pintura?
Se necesitan 400 envases de 1 litro.

Ya sabes que para envasar toda la pintura en recipientes de 2 litros se necesitan 200 de ellos. También se determinó que, si los envases son de 1 litro, entonces se requieren 400 de ellos.
Ahora, se va a calcular la cantidad de envases de medio litro que se necesitan para colocar en ellos toda la pintura.
Para ello, en “y” igual a 400 entre “x” se sustituye la “x” por un medio, por lo que tienes que “y” es igual a 400 entre un medio. Para resolver esta división, puedes utilizar el algoritmo de la división de fracciones y colocas un uno como denominador del 400. A continuación, se multiplica 400 por 2 y el resultado, que es 800, lo divides entre el resultado de uno por uno, es decir, entre uno. En este caso, “y” es igual a 800. Esto significa que, si se envasan los 400 litros de pintura en envases de medio litro, se necesitarán 800 envases de esta capacidad.
¿Cuántos envases se necesitan para envasar los 400 litros en envases de a un cuarto de litro?
Realiza los cálculos necesarios. ¿Cuánto obtuviste?
Para envasar toda la pintura en envases de un cuarto de litro se necesitan 1 600 de estos recipientes.

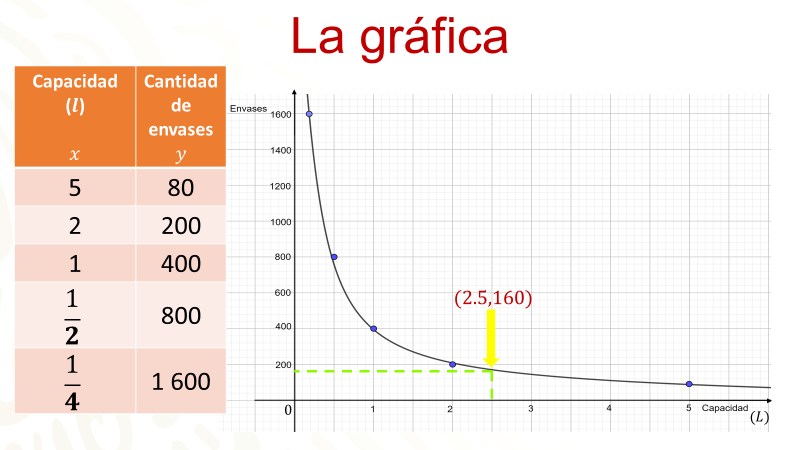
Es posible presentar en una gráfica el problema de los envases. Se hace a partir de los valores de la capacidad de los envases y el número de ellos que se requieren. Estos valores se representan en una tabla.
La gráfica que representa este problema, llamada hipérbola, se comporta de esta manera: mientras la capacidad del envase aumenta, la cantidad de envases disminuye, esto equivale a decir que mientras la curva se acerca más al eje “x”, los valores en el eje “y” serán menores. En el eje “y”, mientras mayor es la cantidad de envases, la capacidad de ellos será menor, es decir que mientras más se acerca la curva al eje “y”, los valores de “x” serán menores.
Pero, ¿tiene sentido envasar pintura en recipientes de capacidad cero litros? La respuesta es no, y por ello la curva no toca el eje “y”, porque la “x” seria cero, y esto no tendría sentido.
En la misma gráfica se muestra la coordenada 2 punto 5 coma 160. ¿Qué significa esta coordenada en el contexto del problema?
Es cuando una coordenada se puede determinar exactamente en la gráfica, es posible encontrar otros valores para “x” y para “y”, en este caso, esa coordenada indica que, cuando los envases tienen una capacidad de 2 punto 5 litros, se requieren 160 de ellos para colocar 400 litros de pintura.
Si necesitas aclarar dudas, recurre a otras fuentes de información acerca del tema, sobre todo, consulta tu libro de texto.
El Reto de Hoy:
El reto del día hoy, consiste en que utilices el mismo procedimiento que se usó en el problema de la herencia para obtener la cantidad de dinero que le corresponde a cada uno de los hijos que faltó calcular. Recuerda que sólo se calculó la cantidad que le corresponde al hijo de 6 años y que es de 228 503 pesos con 22 centavos.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Si lo veo y escucho, entiendo mejor
Aprendizaje esperado: Diseña una campaña escolar para proponer soluciones a un problema de la escuela.
Énfasis: Preparar recursos audiovisuales.
¿Qué vamos a aprender?
En esta sesión revisarás las herramientas audiovisuales que te ayudarán a difundir con claridad y contundencia un mensaje. De este modo lograrás integrar recursos creativos a tus campañas escolares para que tengas un mayor alcance y te ayuden a solucionar diversas problemáticas.
Ten a la mano tu cuaderno, lápiz o pluma para tus anotaciones. También tu libro de texto para cualquier consulta.
¿Qué hacemos?
Para iniciar, revisa la siguiente ejemplificación.
Fernando se reunión con algunos vecinos para crear un huerto comunitario en un jardín público que está en su calle. Para fertilizar la tierra usarán desechos orgánicos, por lo que instalarán botes de basura para que las personas puedan separar los desperdicios.
Y, aunque suene raro, se le ocurrió escribir un rap, para explicarles a los vecinos dónde deben tirar la basura y por qué es importante separarla. Como en esta sesión se hablará sobre recursos audiovisuales para campañas escolares, Fernando lo recitará, pues lo piensa grabar con un celular para difundirlo por internet.
Eso parece creativo ¿verdad?, lee el mensaje con ritmo de rap, que escribió Fernando.
No lo olvides, buen vecino,
necesitas muy buen tino:
si quieres tirar tus latas
para que no atraigan ratas.
Hemos puesto aquí tres botes,
esperamos que los notes.
Uno es verde como el pasto,
¡úsalo, no dejes rastro!
Si comes un platanito
ajusta muy bien tu buen tino,
tira la cáscara al verde,
ve, sin miedo, que no muerde.
Las latas van en el negro
si le atinas, yo me alegro.
Plásticos van en el blanco
el que queda junto al banco.
De todos será la huerta.
¡No te duermas, ponte alerta!
Como viste, la letra estuvo bastante creativa. Si en su video de Fernando, aparecen los botes de basura, sus vecinos entenderán bien el mensaje. Esta estrategia, como la que se acaba de proponer, puede funcionar también en una campaña escolar.
Recuerda que las campañas escolares son necesarias, puesto que ayudan a solucionar problemáticas diversas. Ahora bien: ¿por qué utilizarías un recurso audiovisual en una campaña?
La respuesta es, porque en la actualidad casi todos tienen acceso a medios de comunicación digitales o televisivos, por lo que es útil valerse de esos canales de difusión para informar a más personas.
Las herramientas digitales te permiten comunicarte de forma directa e inmediata.
Ahora, se revisarán algunas de estas herramientas.
Existen las cámaras digitales, tabletas, laptops o los propios celulares, estos son recursos que permiten crear materiales audiovisuales para campañas.
Fernando comenta que, mientras estaba buscando material para desarrollar la campaña de reciclaje, encontró una imagen que puede servir.

Como observas, dice: “Deposita la basura donde corresponde: reciclable, inorgánica y orgánica”. Esta imagen puede formar parte de una campaña.
Es probable que así sea. Sin embargo, se puede ver que a la imagen le hacen falta elementos que podrían ayudar a fortalecer el mensaje. Tal vez, como se mencionó, esta campaña podría apoyarse en algún recurso audiovisual.
Así es, existe una gran diversidad de recursos, por ejemplo, las infografías, los breves videos sin sonido que presentan imágenes cíclicas, los tutoriales y demás métodos de persuasión visual y sonora.
¿Lograste detectar el problema que aborda la campaña cuya imagen observaste?
Si te pudiste percatar, a las y los alumnos les preocupa el que la basura no sea tirada en un contenedor específico.
Para determinar los aspectos que conforman esta problemática, revisa la siguiente lista:
- No existen recipientes para clasificar la basura.
- Faltan señalamientos que indiquen los lugares para depositar los desperdicios.
- Se detectó un exceso en el uso de plásticos y desechables.
- Falta un grupo de alumnas y alumnos que promuevan el cuidado del ambiente.
A partir de este listado, se puede constatar que es importante resolver el problema a partir de acciones precisas y efectivas.
Recuerda que las campañas que se difunden en las escuelas tienen una duración breve. Deben ser claras y de fácil lectura para que se comprenda el mensaje.
Por ejemplo, en una escuela secundaria utilizaron el siguiente recurso audiovisual como parte de su campaña escolar titulada “Reciclando ando”. Revisa el audiovisual.
- Cápsula 11: Medio ambiente. Reciclaje de basura.
¿Te diste cuenta de que el recurso audiovisual que utilizaron en la campaña escolar fue atractivo, claro y directo?
Así es. Pero, ¿qué es un recurso audiovisual?
Los recursos audiovisuales, son materiales y equipos que registran, reproducen, difunden mensajes visuales y sonoros con el fin de facilitar conocimientos y motivar aprendizajes y actitudes, y generalmente se valen de videos, spots, gifs, infografías con movimiento, entre otros.
Observa algunos aspectos relevantes a considerar para que tu recurso audiovisual sea efectivo.
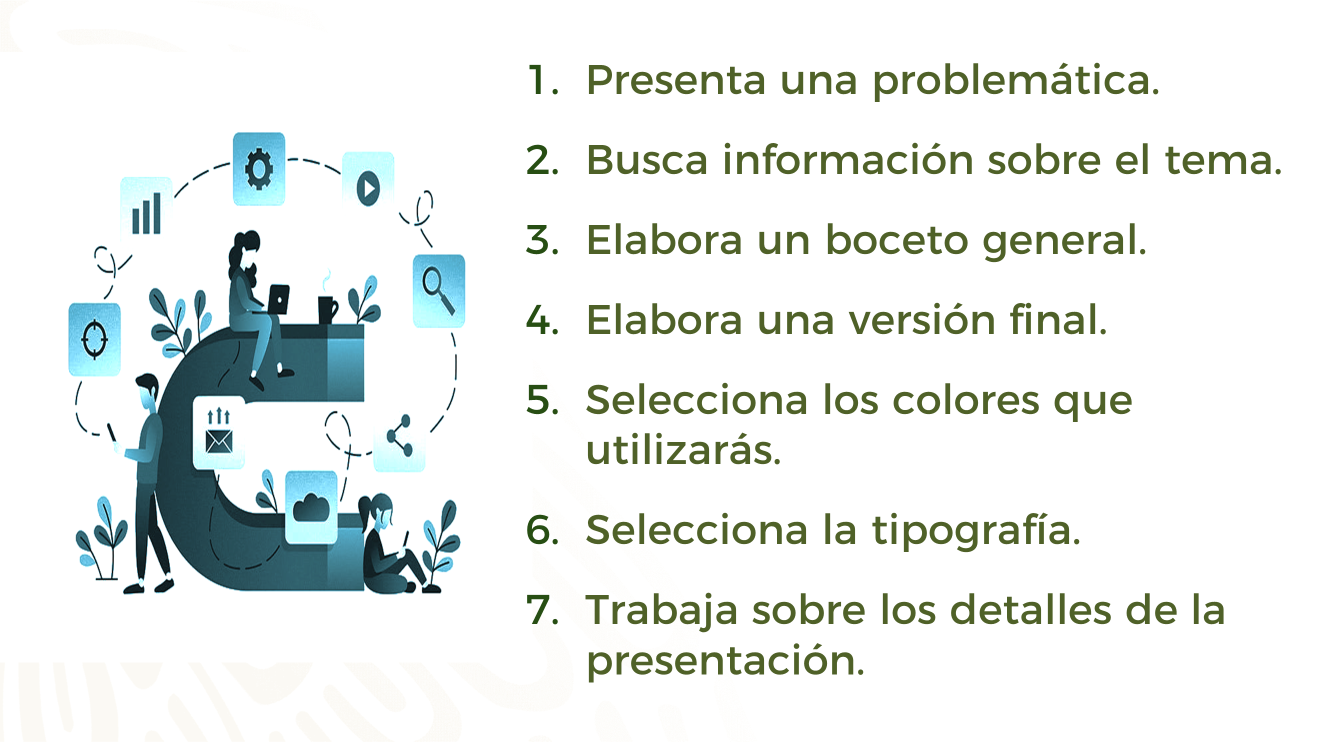
- Se debe precisar tu tema y reducir al mínimo las palabras que acompañarán las imágenes.
- Hay que buscar información sobre el tema y transcribirla coloquialmente.
- Debes elaborar un boceto general del que partirá la versión final.
- Elaborar una versión final.
- Necesitas seleccionar los colores que utilizarás
- Es recomendable elegir una tipografía que se adecue a los gustos del sector poblacional que quieres atraer.
- Trabajar sobre los detalles de la presentación.
Tal como se han enumerado, estos son los pasos que puedes seguir al elaborar el material audiovisual de apoyo para una campaña.
Ahora se mostrará cómo puedes crear una campaña a través de recursos audiovisuales.
Ya se tiene una problemática definida, como la del interés de abordar en la campaña vecinal. Ahora sería importante saber: ¿cuál es la finalidad que buscan?
El propósito sería crear una cultura del cuidado del ambiente y generar un espacio escolar más limpio.
Así es, ahora, ¿qué aspectos se pueden incluir en el audiovisual?
Quizás los tres que se señalaron. El primero sería ubicar los recipientes donde se pueden depositar los desechos, separados por categorías. El segundo, disminuir el uso de plásticos y desechables. Finalmente, colocar y reconocer los señalamientos para depositar la basura.
Con esas tres ideas centrales se puede ir haciendo un boceto del video. ¿De qué recurso audiovisual podrías valerte?
Se podría hacer un video con el celular o en la computadora. Existen algunas aplicaciones que pueden ayudar a editar las imágenes.
Es cierto, se puede utilizar un editor de video, que puede instalarse en casi cualquier computadora portátil.
Las imágenes que se utilicen deberán considerar las características de la comunidad escolar. Quizás las siguientes podrían servir.

Se pensó en estas imágenes porque una se refiere a los contenedores de plástico, orgánico, vidrio, papel y cartón. Las otras, por el plástico y los desechables.
También las fotografías gratuitas de internet pueden funcionar. Algunas de ellas ilustran la separación de desechos.
Ahora se podrán guardar en una carpeta o álbum para utilizarlas en el editor de video. ¿Qué observas que sucede con él?
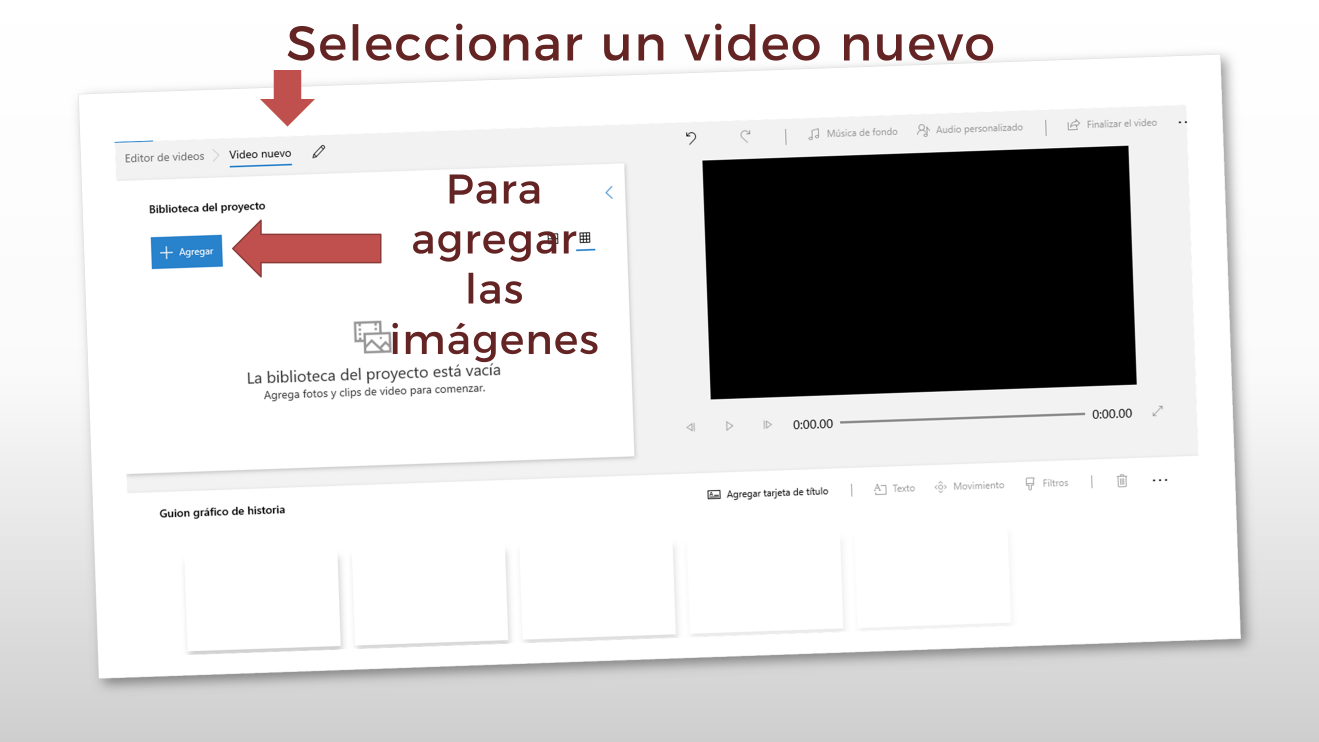
Este es el primer paso para comenzar a hacer el video: seleccionar la creación de un nuevo video e ir agregando las imágenes elegidas.
Así es, después de integrar las imágenes, habrá que darle un sentido, es decir, una secuencia; pero debes pensar en tu título de campaña y el mensaje que buscas enviar.
La campaña se podría titular: “Bote pronto: La basura, al bote correcto, pronto”.
Tal vez, puede funcionar la expresión “bote pronto”; la campaña adquiere un tono atractivo. Observa cómo se integra el título al editor de videos.
Claro, muchos de los recursos para editar videos permiten agregar títulos y manejar diversos tipos de letras.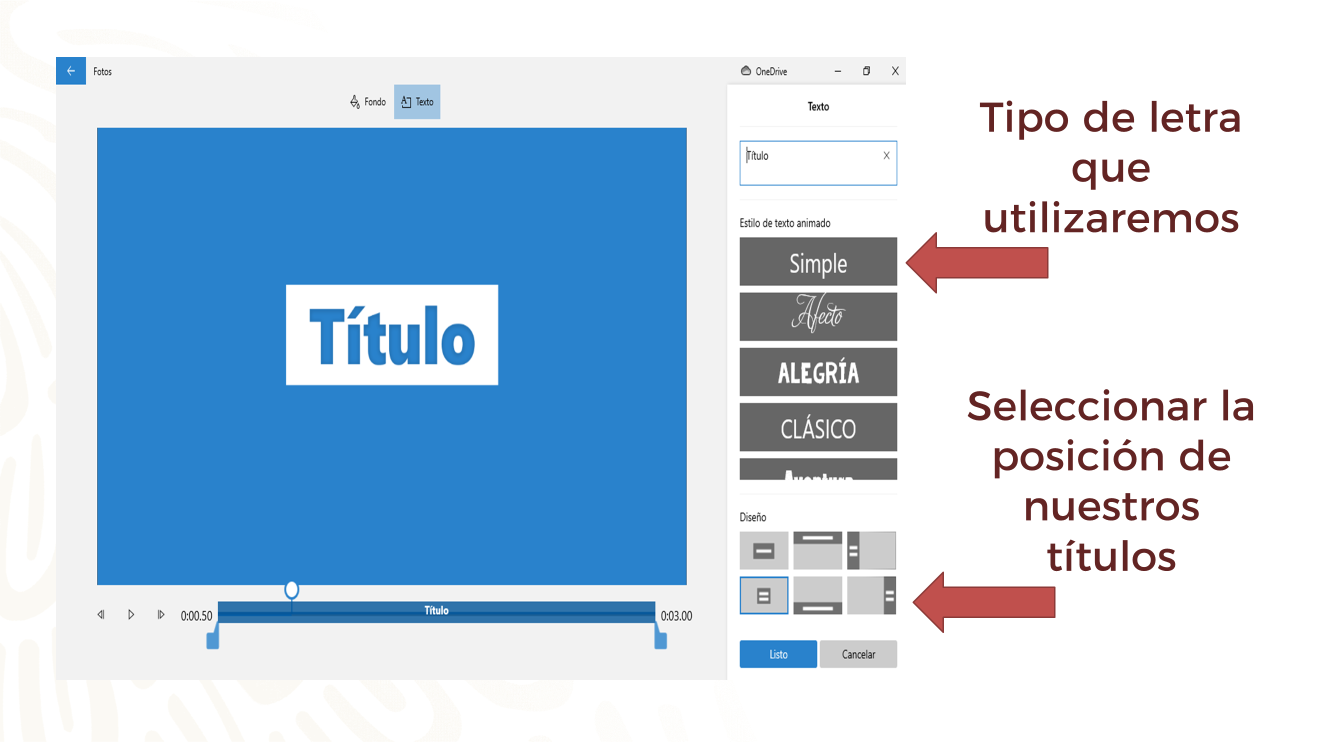
Esto significa que debes seleccionar la que más te convenga para crear tu audiovisual de manera llamativa.
Si es un video formal, quizá lo más correcto sería utilizar una letra simple o clásica, en esta ocasión se usará la opción “alegría”.
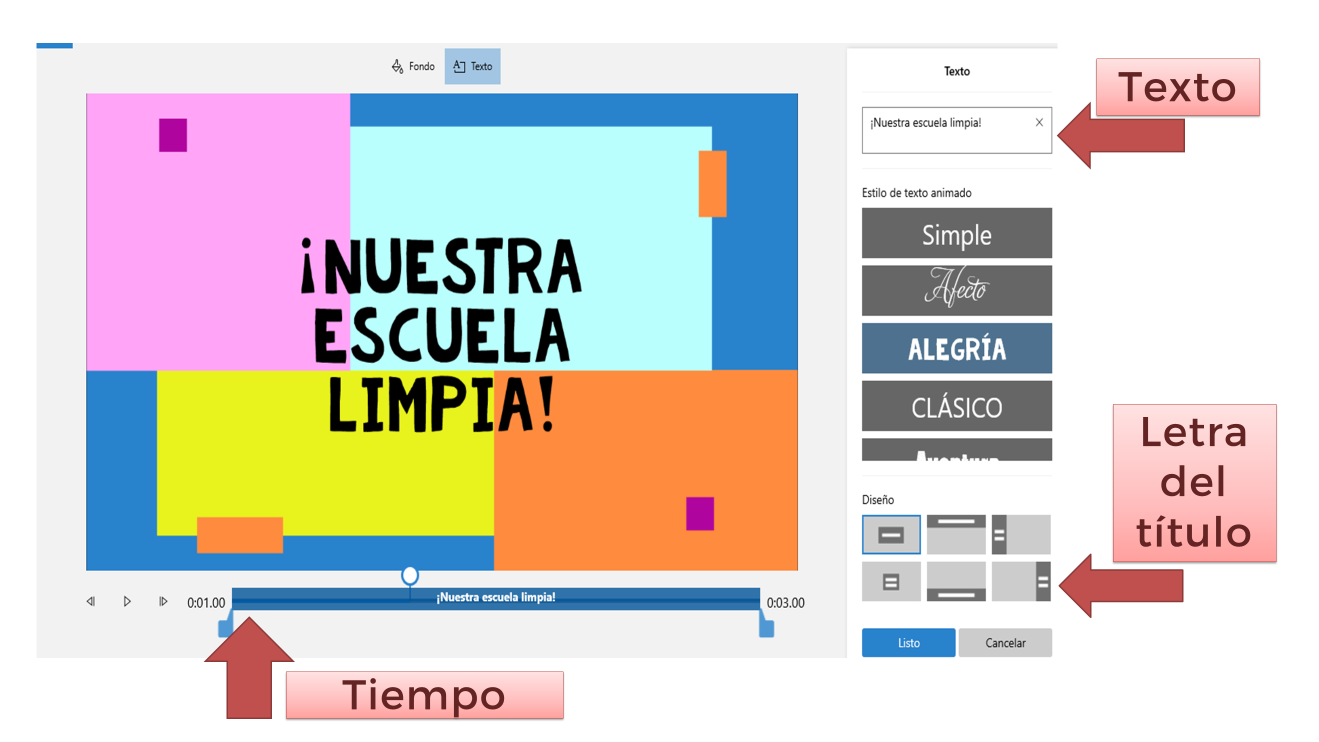
En el editor de video debes buscar la sección donde puedas agregar el texto y el tiempo de la presentación del título. Además, como se mencionó, el tipo de letra.
Los titulares o mensajes que buscas transmitir también tienen un grado de importancia, dependiendo de su intención. Por ejemplo, si es el título de la campaña, debería ir al centro; y si es una sugerencia, podría ubicarse en la parte final de la imagen.
Hay que pensar en el color y es uno de los aspectos que también deben considerarse.
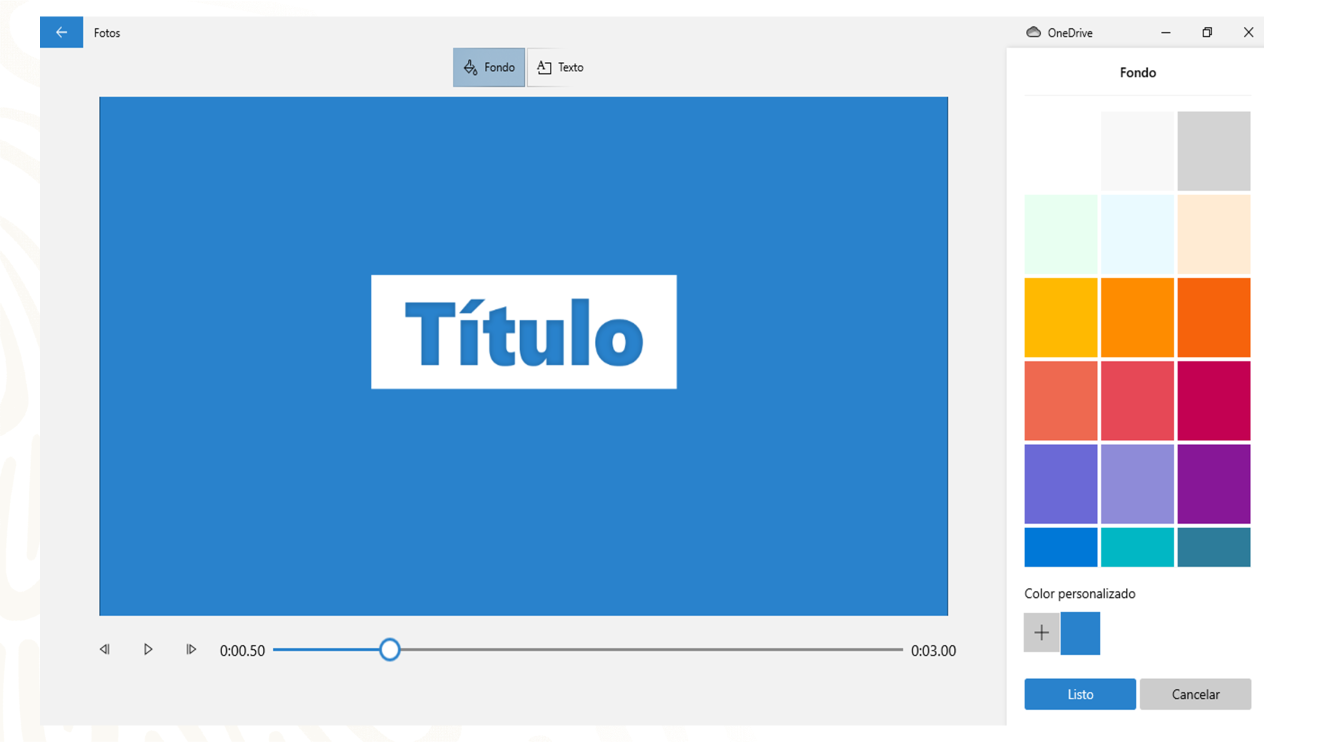
También revisa la paleta de colores, pues tal vez sea necesario usar colores más intensos como rojo o naranja, pero si transmiten una información más delicada, quizá lo pertinente sea elegir colores pastel. En este caso, que el interés es mantener el cuidado de las áreas comunes, se puede recurrir al verde o al azul. Así es, pues también se está pensando en el tipo de mensaje que se está transmitiendo.
Por otro lado, el sonido es otro de los factores importantes en la elaboración del material audiovisual, ya que te hace recordar, reconocer o reforzar una campaña. Revisa lo siguiente.
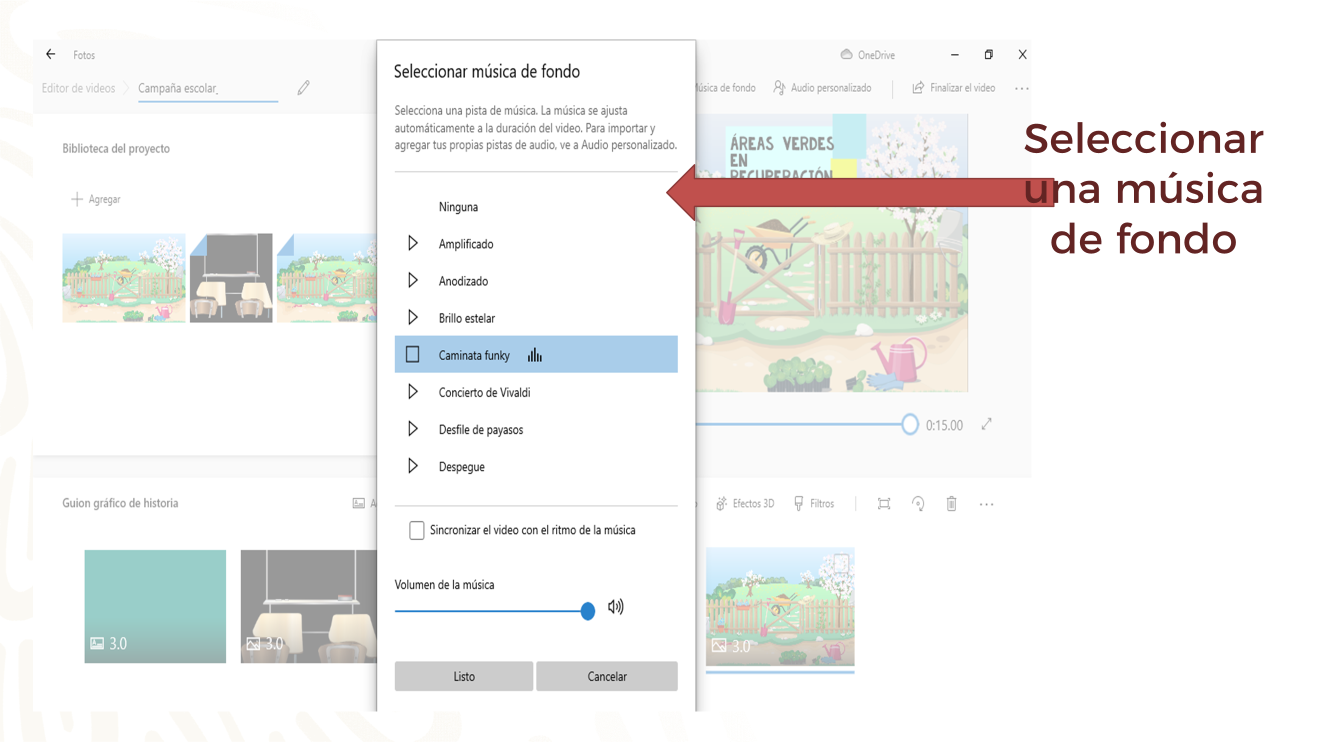
El editor de video puede proporcionar una serie de pistas que se pueden seleccionar. Algunas son más dinámicas que otras. También algunos editores permiten agregar música de tu preferencia. Así es, dependiendo de la campaña que estás realizando, deberás elegir la música adecuada.
En este caso, un sonido más dinámico sería lo más indicado, pues la campaña va dirigida a la comunidad escolar.
Ahora revisa cómo quedaría el video a través de imágenes.
- VIDEO 01 ESCUELA LIMPIA.
Esta es una manera sencilla de generar tus recursos audiovisuales.
Otra manera de generar material audiovisual es a través de algunas aplicaciones, como el stop motion, que es la grabación cuadro a cuadro del movimiento de un objeto o figura.
Como esa técnica se basa en edición de fotos que se enlazan unas con otras para generar la sensación de movimiento, las imágenes podrían elaborarse a partir de materiales reciclados o con utensilios de casa. Revisa algunas ideas.
- VIDEO BALLENA / VIDEO ESPECIERO.
Como has revisado, debes considerar tu tema de campaña y la forma en que crearás el desarrollo.
Recuerda que debes limitar tu tiempo de 10 a 30 segundos, pues eso te permitirá mantener la atención de la audiencia. Tomando en cuenta a tus personajes, materiales e historia, ¿qué podrías hacer para elaborar su stop motion?
Para comprenderlo, revisa el siguiente video.
- Hagamos una animación Stop motion. 3/5.
Es un buen recurso con el que puedes trabajar de forma creativa.
Ahora, revisa con cuál herramienta digital lo puedes elaborar.
- Hagamos una animación Stop motion. 4/5.
Ya que revisaste los pasos, herramientas y recursos que serán de utilidad para generar productos audiovisuales. Observa el video que se desarrolló para difundir el mensaje de la campaña.
- VIDEO 02 CAMPAÑA “BOTE PRONTO”
Se espera que te haya gustado.
Con estos nuevos aprendizajes ahora puedes realizar tu propio material audiovisual acerca de una problemática particular de tu escuela y complementar tu campaña escolar.
Además, puedes buscar en tu libro de texto de Lengua Materna, segundo grado, algunos otros ejemplos para reforzar lo aprendido.
El Reto de Hoy:
Es momento del reto del día de hoy. ¿Te parece si se te propone un esquema de planeación?
Aquí podrás plantear tu problemática, el medio audiovisual con el que quieres elaborar tu campaña, la situación que se presenta, el tipo de sonidos que utilizarás y la duración del video.
Ahora se te propone una posible campaña.

Esta campaña escolar se titula “Almuerzo sano”. El mensaje es la importancia de preparar los alimentos en casa y consumirlos durante el receso escolar.
Ahora observa cómo podrías completar el esquema.
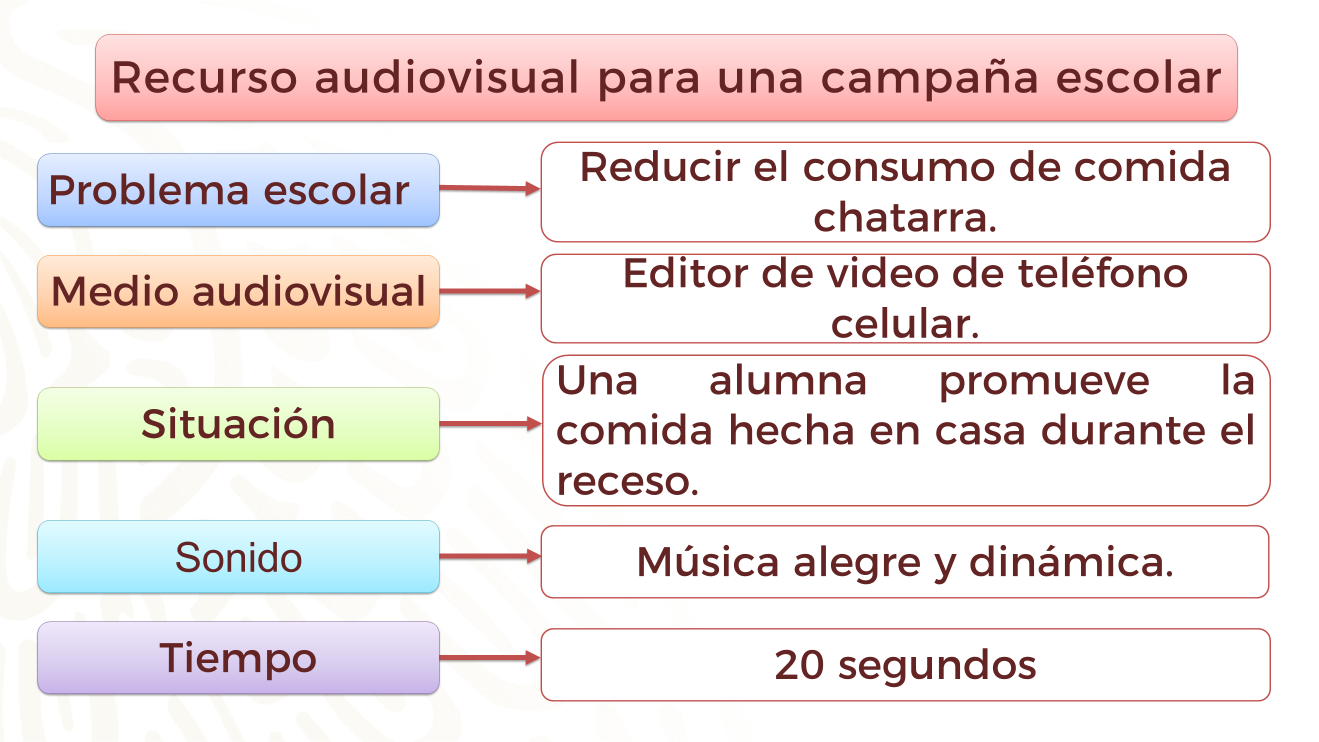
El problema escolar: el consumo de comida chatarra. El medio audiovisual: el editor de video de su teléfono celular. La situación: una alumna promueve la comida hecha en casa durante el receso. Podrías utilizar música alegre y dinámica. Finalmente, el tiempo de duración sería de 20 segundos.
Intenta realizarlo en casa.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Igualdad entre mujeres y hombres
Aprendizaje esperado: Reconoce que la igualdad ante la ley es condición para la construcción de una sociedad justa y equitativa.
Énfasis: Reconocer acciones para avanzar hacia la igualdad sustantiva como derecho entre mujeres y hombres.
¿Qué vamos a aprender?
En esta sesión titulada “Igualdad entre mujeres y hombres” revisarás cuestiones que te permitirán analizar sus ideas, conductas y acciones de la vida cotidiana.
¿Existe igualdad entre hombres y mujeres?
Si se cuenta con un marco legal que ampara que mujeres y hombres son iguales ante la ley. Pero, ¿Por qué no se manifiesta en el día a día?
Haciendo un poco de historia sobre el tema. La igualdad como derecho surgió, apenas, a finales del siglo XVIII, tras la Revolución Francesa y no fue sino hasta 1948, con la Declaración Universal de los Derechos Humanos, que en su Art. 1° se establece que:
“Todos los seres humanos nacen libres e iguales en dignidad y derechos y, dotados como están de razón y conciencia, deben comportarse fraternalmente los unos con los otros”.
Pero todavía se está en el proceso de llevar esa declaración a la realidad, lo que requiere de educación, concienciación y el compromiso de todas y todos. De esto se hablará en esta sesión.
Ten a la mano tu cuaderno, un lápiz o bolígrafo, para anotar algunas ideas o inquietudes que surjan durante la sesión. Si tienes una discapacidad visual, prepara tus hojas leyer, punzón y regleta.
¿Qué hacemos?
Para comenzar, revisa una situación que comenta Marisol, una compañera tuya de una secundaria del estado de Oaxaca.
- VIDEO 1. SITUACIÓN PROBLEMÁTICA.
Después de escuchar la situación que plantea Marisol, entenderás perfectamente cómo se sentiría cualquier persona, si le negaran aquello que quiere hacer por el hecho de ser mujer u hombre.
Esta es una de las formas de discriminación más común que, desafortunadamente, está presente en todos los ámbitos.
En la escuela has aprendido que la igualdad es un valor muy importante para tener una convivencia sana y respetuosa. Esto te permite considerar que los rasgos propios de mujeres y hombres no les hacen valer más ni menos, porque todas las personas, como seres humanos, tienen dignidad.
Además de ser un valor, la igualdad debe ser una condición que permita poder exigir su reconocimiento, lograr la justicia y una vida democrática.
Por lo tanto, en el caso de Andrea, no se le debe negar su inscripción al taller de electricidad y se debe fomentar, tanto en sus compañeras y compañeros como entre maestras y maestros, que las diferencias enriquecen y enseñan a convivir con las y los demás, dejando atrás los prejuicios y estereotipos de género.
Para saber más sobre el derecho a la igualdad, se te invita a revisar con atención el siguiente video de algunas alumnas y alumnos de secundaria del estado de Oaxaca.
- VIDEO 2. YO SOY.
- ¿Qué te pareció la opinión de las alumnas y alumnos?
- ¿Te parece que tienen razón?
- ¿Consideras que es una utopía?
Se te invita a que escribas tu opinión al respecto en tu libreta de notas. Si te percataste, en las opiniones de Karen, José Antonio, Karol y Jesús hay una coincidencia: Todas y todos hablaban de igualdad de género ante la ley y la sociedad.
Es importante reconocer que, a pesar de las aparentes diferencias entre ambos géneros, se reconoce la necesidad de recibir un trato con igualdad en la convivencia diaria, por lo que se te invita a que consideres que demandar la igualdad de género no implica fomentar la competencia y ver a la otra u otro como alguien inferior, recuerda lo que viste al inicio: “Todos los seres humanos tienen el mismo valor por el simple hecho de existir.”
En la Constitución Política de los Estados Unidos Mexicanos, se encuentra garantizado el derecho a la igualdad entre hombres y mujeres en los siguientes artículos:
Art. 1. Todas las personas gozarán de derechos humanos reconocidos en la Constitución.
Art. 4. Mujeres y hombres son iguales ante la ley.
También en la Declaración Universal de los Derechos humanos y los tratados internacionales, se establece el principio de igualdad de género.
Art. 1. Todos los seres humanos, al nacer, son libres e iguales en dignidad y derechos.
Art. 16. Los hombres y las mujeres, a partir de la edad núbil, tienen derecho, sin restricción alguna por motivos de raza, nacionalidad o religión, a casarse y fundar una familia, y disfrutarán de iguales derechos en cuanto al matrimonio, durante el matrimonio y en caso de disolución del matrimonio. Sólo mediante libre y pleno consentimiento de los futuros esposos podrá contraerse el matrimonio.
El pacto internacional de Derechos Civiles y Políticos también establece:
Art. 3. El estado se compromete a garantizar la igualdad entre hombres y mujeres en el ejercicio de sus derechos civiles y políticos.
Art. 23. En el matrimonio, ambos esposos tienen las mismas responsabilidades y derechos.
Existen, además, instituciones que protegen estos derechos.
En el país, se cuenta con el Instituto Nacional de las Mujeres (INMUJERES), el Consejo Nacional para Prevenir la Discriminación (CONAPRED) y la Comisión Nacional de los Derechos Humanos (CNDH).
Como instituciones internaciones se encuentra a la Organización de las Naciones Unidas o el Programa de las Naciones Unidas para el Desarrollo.
Contar con estas leyes es una forma de reconocer que tanto hombres como mujeres merecen respeto y tienen dignidad humana, pero, al mismo tiempo, son diferentes.
Una forma de definir la justicia es dar a cada quien lo que le corresponde.
Por esto, la igualdad ante la ley significa reconocer, para todas las personas, los mismos derechos, pero también garantizar que cada persona recibirá el mismo trato y oportunidades, sin importar su género ni el entorno en el que se encuentre.
La igualdad sustantiva son normas y acciones orientadas a la aplicación de todos los derechos humanos sin distinción, es decir, que las leyes que están plasmadas se cumplan y apliquen en el diario vivir.
Como todas las personas saben, en este país, tanto hombres como mujeres, gozan de los mismos derechos. Pero, ¿qué pasa en el día a día?
La realidad es otra.
El hecho de que estas formas de igualdad se encuentren en las leyes no garantiza que se cumplan, pero sí marca el camino de aquello que tiene que ser respetado y construido.
Para continuar profundizando en el contenido, revisa lo que dice la maestra Esmeralda Martínez, del estado de Oaxaca, quien comparte algunas reflexiones al respecto, en el siguiente video.
- VIDEO 3. MAESTRA ESMERALDA MARTÍNEZ.
Interesante lo que dice la maestra sobre este tema. Ahora, se presenta la participación de la alumna Irla, que desea compartir su opinión, en el siguiente video.
- VIDEO 4. YO TENGO UN SUEÑO
¿Qué te ha parecido? ¿Estás lista o listo para hacer estos cambios en la cultura para la igualdad?
Hasta aquí, se entiende que la igualdad entre hombres y mujeres es un principio constitucional que estipula que mujeres y hombres son iguales ante la ley, lo que significa que todas las personas, sin distinción alguna, tienen los mismos derechos y deberes frente al Estado y la sociedad, en su conjunto.
Se han logrado grandes avances en materia de salud, trabajo, educación y política. Por ejemplo, en las elecciones de 2018, los partidos políticos estuvieron obligados al mismo número de candidaturas para mujeres y hombres en las elecciones para diputados y senadores federales.
Construir entornos de igualdad es una tarea que impacta y que involucra a todas y todos. Un aspecto que contribuye a la igualdad, es que cada persona reconozca a las demás como iguales en dignidad y merecedoras de derechos. La igualdad es un derecho humano, es una demanda social y un objetivo común.
Así como en todo momento, y en todas partes, ves ejemplos de desigualdad, puedes hacer mucho en todos lados, todo el tiempo, para hacer valer este derecho.
Por lo que has visto es un gran reto lograr la igualdad, pero vale la pena luchar por ella. Revisa el siguiente video que te ampliará lo que aquí se ha expuesto.
- Género e identidad sexual.
https://www.youtube.com/watch?v=cCgFd05QBoY
Revisa del tiempo 00:32 al 04:34.
Ahora se recapitulará lo visto en esta sesión, para ello observa lo que dicen alumnas y alumnos de segundo grado, quienes darán algunas conclusiones.
- VIDEO 5. CONCLUSIONES.
Como viste en el video. En la sesión del día de hoy, se ha abordado cómo surge el derecho a la igualdad y las diferentes leyes que respaldan los derechos de mujeres y hombres en nuestro país y en el mundo, además de algunas instituciones nacionales e internacionales a las cuales se puede acudir en caso de requerirlo.
Las leyes respaldan los derechos y se establecen bajo el principio de equidad y justicia, protegen las garantías de mujeres y hombres. Se debe respetar la diversidad, no discriminar por ninguna situación y ser inclusiva o inclusivo.
También te diste cuenta de los retos que se tiene como sociedad para dejar a un lado los roles y estereotipos que no permiten lograr la igualdad sustantiva.
Se te invita a consultar tu libro de texto de Formación Cívica y Ética para saber más acerca de la igualdad entre mujeres y hombres.
Has concluido el tema del día de hoy.
El Reto de Hoy:
Como actividad complementaria, se te pide que escribas tus propias conclusiones acerca de este tema, donde incluyas las situaciones de tu vida diaria donde hay igualdad y en las que se requieren cambiar patrones de comportamiento, leyes o ideas para lograrla. Puedes retomar para ello las siguientes preguntas:
- ¿Qué opinas?
- ¿Cuál consideras que sea el reto más difícil para lograr la igualdad sustantiva?
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
¿Qué es la reflexión de la luz?
Aprendizaje esperado: Describe la generación, la diversidad y el comportamiento de las ondas electromagnéticas como resultado de la interacción entre electricidad y magnetismo.
Énfasis: Conocer y reflexionar sobre el fenómeno de la reflexión de la luz.
¿Qué vamos a aprender?
Conocerás y reflexionarás sobre el fenómeno de la reflexión de la luz.
Es importante que tengas a la mano tu cuaderno, libro de texto y lápiz o bolígrafo, para que puedas anotar las ideas principales. Si tienes alguna discapacidad visual, prepara hojas leyer, punzón y regleta.
¿Qué hacemos?
Para iniciar, contesta las siguientes preguntas y al final compara tus respuestas. Esto con la finalidad de que compruebes lo que has aprendido en esta sesión.
Las preguntas son:
- ¿Por qué puedes mirar tu imagen en un espejo?
- ¿Todos los objetos que observas tienen luz propia?
- ¿Puedes predecir en donde aparecerá una imagen al reflejarse en una superficie?
- ¿Será igual el reflejo de la luz en un espejo plano, que en uno cóncavo?
Vives en un mundo visual, rodeado de imágenes como la del arcoíris, el reflejo de tu persona en un espejo, en el agua cristalina de un lago o un recipiente con agua. Al observar un haz de luz reflejando en un reloj o en los lentes de una persona.
Muchas de estas imágenes las consideras como cotidianas porque estás acostumbrado a verlas, hasta que observas algo que no resulta fácil de explicar.
La mayoría de los objetos que ves no emiten su propia luz, son visibles porque reflejan la luz de otro objeto, que sí puede emitirla, como el sol, una lámpara o la flama de una vela.
Para entender mejor el tema de la reflexión, hay que recordar el concepto de Luz.
La Luz, es una forma de energía que se propaga a través de ondas electromagnéticas, aunque en ocasiones se comporta como partícula, a la que se le llama fotón.
La rama de la física que se encarga de estudiar el comportamiento y las propiedades de la luz es la óptica. Generalmente, la óptica describe el comportamiento de la luz visible.
En particular, la óptica geométrica se encarga de estudiar a la luz como una colección de rayos que viajan en línea recta y se desvían cuando atraviesan o se reflejan en alguna superficie.
En esta sesión, se explicará el fenómeno de la reflexión de la luz.
Para que te formes una idea sobre la reflexión de la luz, revisa el siguiente video.
- ¿Existe la luz invisible?
Revisa del tiempo 01:22 al 06:37.
Después de haber visto el video, ahora se explicará cómo se produce tu imagen, cuando te miras en el espejo.
Los espejos son superficies pulidas que tienen en su reverso una capa metalizada de plata o estaño que refleja casi totalmente la luz.
Cuando te colocas ante un espejo, los rayos luminosos que refleja tu cuerpo llegan a su superficie y se vuelven a reflejar, viajando en sentido contrario, es decir, del espejo a ti.
Al estimular las células receptoras en tus ojos, las señales luminosas son transmitidas al cerebro, que se encarga de ordenarlas y reconstruir la imagen captada, que es simétrica a la tuya.
Por esto, precisamente, si ante el cristal mueves la mano derecha, parecerá que tu figura reflejada ha movido la izquierda, y viceversa.
También si pones un papel con un texto ante el espejo, se verá reflejado al revés, de forma que casi no podrás leerlo.
Algo que puede parecer obvio, es que, para poder ver tu reflejo es necesario contar con una fuente de luz natural o artificial. Para comprobarlo, en la noche puedes apagar la luz e intentar ver tu reflejo en un espejo.
¿Piensas que podrás observar tu imagen en la oscuridad?
Se te invita a realizar este sencillo experimento y obtener tu propia conclusión. Para poder ver una imagen, es necesario contar con una fuente de luz.
Además de este ejemplo tan cotidiano de verte en un espejo, ¿crees que se podría realizar algún experimento para conocer más sobre el fenómeno de la reflexión de la luz?
La respuesta es sí.
Ahora, se realizará un experimento, para el cual necesitarás el siguiente material:
- Un cuadrado de papel aluminio de 20 centímetros por lado.
- Una lámpara de mano.
- Un espejo.
- Una regla.
- Un transportador.
- Cartulina negra.
Revisa el procedimiento a seguir.
Haz bolita el papel aluminio y lo vuelvas a extender. Cuidando de que no se rompa.
Justo frente al cuadrado de aluminio, coloca la cartulina negra, y haz incidir un rayo de luz sobre el papel aluminio.
¿Qué observas?
Podrás ver que la luz casi no ilumina en la cartulina.
A este fenómeno se le llama reflexión difusa, se debe a que la superficie del papel aluminio es irregular y la luz se refleja en todas direcciones.
Ahora, vas hacer incidir un haz de luz sobre el espejo, colocando en el extremo contrario la cartulina negra. Puedes observar que el haz de luz se refleja sobre la cartulina.
La reflexión sucede cuando se hace que un rayo de luz, al que se llamará rayo incidente, choque sobre una superficie reflejante, en este caso el espejo. Este medio, que es el espejo, hace que el haz de luz cambie de sentido y dirección, es decir, que el haz de luz se refleje en sentido contrario, a este fenómeno se le llama reflexión especular o reflexión regular.
Como sabes en la física existen leyes, el fenómeno de la reflexión de la luz no podría ser la excepción.
|
La primera ley de la reflexión de la luz dice que: El rayo incidente, el rayo reflejado y la normal se encuentran en un mismo plano. |
La normal es una línea imaginaria perpendicular a la superficie reflectora.
|
La segunda Ley de la Reflexión de la Luz dice que: El ángulo que se forma entre el rayo incidente con la normal y el ángulo que se forma entre la normal y el rayo reflejado es igual. |
Para comprobar estas leyes, ahora vas a utilizar, el siguiente material:
- Una cartulina.
- Un transportador.
- Un espejo.
- Una lámpara.
Procedimiento a seguir.
Colocas la cartulina en posición horizontal, junto con el transportador.
En la cartulina trazas una línea a la mitad para que funcione como la normal, en seguida colocas el espejo en posición vertical sobre la base del transportador, con una lámpara haces incidir un rayo de luz sobre el espejo a 45º, observa lo que sucede.
Con lo anterior se quiere decir, que si tú te paras frente al espejo y enciendes la luz, los rayos incidentes serán los rayos que emite el foco, los rayos reflejados son los rayos de luz que chocan sobre tu cara, hacia el espejo, la normal es la línea recta imaginaria que existe entre tu cara y el espejo y a su vez los rayos reflejados componen la imagen que se refleja hacia tus ojos, sin importar el ángulo al que se emita el rayo de luz siempre se reflejará a los mismos grados pero en sentido opuesto.
Ahora, se realizará un experimento que ejemplifique mejor la reflexión de la luz.
El material que vas a usar es el siguiente:
- 2 espejos planos del mismo tamaño, pueden ser chicos o grandes.
- Cinta adhesiva.
- Bolígrafo de color, que no sea transparente.
- Transportador.
- Un plumón de color.
Procedimiento a seguir.
Colócate frente al espejo, como a un metro de distancia. ¿Qué observas?
Podrás ver tu reflejo en el espejo, pero notarás algo que quizás nunca te habías fijado, que la distancia a la que te reflejas en el espejo, es la misma a la que te encuentras fuera de este, pareciera que la distancia de la imagen atravesara el espejo y saliera hacia atrás.
Así es, se te explicará lo que sucede. A ese fenómeno se le llama imagen virtual.
Esta imagen virtual, son los rayos reflejados que se proyectan detrás del espejo y está en la posición en donde se unen los rayos reflejados o líneas punteadas en la imagen.
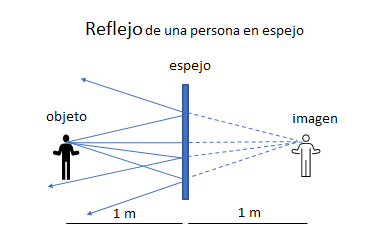
Esto quiere decir, que la distancia de tu imagen está a la misma distancia que hay entre tú y el espejo.
Hay que seguir con el experimento, ahora vas a unir dos espejos planos del mismo tamaño. Los vas a colocar en posición vertical y a 180º.
Coloca un objeto frente a la unión de los espejos, por ejemplo, un bolígrafo.
Observa de frente dentro de los espejos ¿Cuántas imágenes ves?
Sólo verás una imagen.
Ahora, vas a cambiar el ángulo a 135º, ¿cuántas imágenes observas?
Podrás ver 2 imágenes.
¿Y si colocas los espejos a 90º?
Se verán cuatro bolígrafos, uno real y tres imágenes.
¿Cuántas imágenes cuentas con los espejos a 60º?, ¿Y a 45º?
Anota tus respuestas.
Es interesante ¿verdad?
Pero, ¿a qué se debe este fenómeno?
Te puedes dar cuenta que a medida que se reduce el ángulo, se va incrementando el número de imágenes.
Si haces pruebas en otros ángulos y quieres saber el número de imágenes que se forman lo puedes obtener con la siguiente fórmula:
|
360 entre el ángulo al que están los espejos, y al resultado le restamos uno. |
Como verás es sencilla está fórmula y si no tienes los espejos y quieres saber cuántas imágenes se ven reflejadas en estos, en un ángulo de 36º puedes usar esa fórmula.
Revisa el siguiente ejemplo.
Para calcular el número de imágenes si colocas los espejos a 36°, tienes que dividir 360° entre 36° y restarle uno.
Entonces 360° entre 36° es igual a 10, 10 menos 1 te da 9. Lo que significa que si colocas los dos espejos a 36° uno del otro, observarás 9 imágenes.
A continuación, se realizará una tercera actividad.
Vas a colocar dos espejos en forma paralela, o sea uno frente al otro, si es posible que algún familiar te ayude a sostenerlos, mientras tú vas a poner el plumón entre ellos. Ahora cuenta el número de imágenes que se forman.
Como verás son muchísimas, no podrás contar todas las imágenes que se forman.
¿A qué se debe esto?
Se debe a que la imagen del plumón que se forma al reflejarse la luz en un espejo, rebota en el otro, y la imagen resultante, a su vez se refleja en el primer espejo. Este ciclo se repite una infinidad de veces.
Hay que realizar un último experimento.
Vas a elaborar un caleidoscopio, para demostrar la formación de imágenes en los espejos por medio de la reflexión.
Para construir tu propio caleidoscopio necesitarás:
- Tres espejos de 3 cm de ancho y 10 cm de largo.
- Un tubo de cartón, puede ser el que queda de los rollos de papel, o de las servilletas para la cocina.
- Dos círculos de vidrio con un diámetro igual al del tubo de cartón.
- Un círculo de vidrio opaco o esmerilado que deje pasar la luz.
- Trozos pequeños de cristales de colores o canicas en trocitos.
- Cinta adhesiva.
Como vas a utilizar espejos y vidrios en esta actividad, es recomendable que, si decides replicarla en casa, cuentes con la supervisión de un adulto, para que no sufras ningún accidente.
Ahora sí, para tener tu propio caleidoscopio, vas a seguir los siguientes pasos:
- Primero, vas a unir los tres espejos con cinta adhesiva formando un triángulo, trata de que al unirlos queden derechos y al mismo nivel.
- Después introducirás el triángulo de espejos que acabas de armar, dentro del tubo de cartón.
- En seguida colocarás uno de los círculos de vidrio, apoyándolo sobre los espejos.
- Con cuidado de no cortarte, vas a agregar los trocitos de cristal de colores, también los puedes sustituir por trozos de papel de colores o lentejuelas o chaquira.
- Colocas el círculo de cristal opaco, dejando un espacio entre los cristales y este, fíjalo con cinta adhesiva.
- En el extremo contrario colocarás el otro círculo transparente pegándolo con cinta adhesiva, debes tener cuidado de dejar una abertura pequeña, equivalente a un círculo de 1 centímetro de diámetro, para que se pueda observar a través de él.
Listo, ya puedes observar a través de él.
Si lo replicas en casa, rótalo lentamente para que puedas apreciar todas las figuras que se forman, producidas por la reflexión de las imágenes en los espejos.
Ahora se responderá la duda que tiene una de tus compañeras llamada Sandy, ella dice que cuando se ve en una cuchara, observa su imagen reflejada, pero está deformada, ¿a qué se debe eso?
La respuesta es que ambas caras de la cuchara forman lo que se llaman lentes cóncavas o convexas, dependiendo de cómo la esté sosteniendo.
Los espejos cóncavos se caracterizan porque cuando incide sobre ellos un haz de luz de rayos paralelos, los refleja haciéndolos convergir en un punto denominado foco.
Lo que hace que la imagen reflejada se vea más grande, como algunos espejos que se suelen utilizar para magnificar la imagen reflejada.
Un espejo convexo, hace divergir a los rayos reflejados, de modo que las prolongaciones de la luz de los rayos pasan por el foco, haciendo la imagen más pequeña en el centro y grande en sus extremos, como en los espejos retrovisores de los autos.
Con los diferentes tipos de espejos se produce el fenómeno de reflexión, cuando un rayo luminoso choca con su superficie, proyectando una imagen virtual, simétrica y derecha, cuando el espejo es plano o invertida y reducida cuando es cóncavo o convexo.
La reflexión se usa en muchos dispositivos, algunos ejemplos son los telescopios, periscopios, caleidoscopios, espejos dentales o espejos retrovisores, espejos de salones de belleza y espejos que usan los dermatólogos, por mencionar algunos.
Para finalizar esta sesión, se te pide que revises lo que respondiste a las preguntas que se realizaron al inicio.
Las preguntas fueron:
- ¿Por qué puedes mirar tu imagen en un espejo?
- ¿Todos los objetos que observas tienen luz propia?
- ¿Puedes predecir en donde aparecerá una imagen al reflejarse en una superficie?
- ¿Será igual el reflejo de la luz en un espejo plano, que en uno cóncavo?
No olvides consultar tu libro de texto, así como otras fuentes de información confiables, para ampliar la información si lo consideras necesario o es de tu interés.
Se te recomienda reunirte con tu familia para comentar lo que aprendiste en esta sesión.
El Reto de Hoy:
En caso de no contar aún con las respuestas a las preguntas que se te realizaron al principio y final de la sesión, resuélvelas.
Si estás en posibilidad y es de tu interés, realiza los experimentos que revisaste en la sesión del día de hoy.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario