Aprende en Casa III SEP: 13 de mayo TAREAS y ACTIVIDADES de 1° de secundaria
A continuación dejamos los temas vistos el 13 de mayo de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 1° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Jueves 13 de mayo, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en Casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Distintas ecuaciones para un mismo problema
Aprendizaje esperado: Resuelve problemas mediante la formulación y solución algebraica de ecuaciones lineales.
Énfasis: Identificar y resolver diferentes ecuaciones que pueden representar a un mismo problema.
¿Qué vamos a aprender?
En esta sesión trabajarás con problemas que se pueden resolver con más de una ecuación lineal, a través del planteamiento de situaciones en diversos contextos.
Se te recomienda tener a la mano tu cuaderno, o en su defecto, hojas reutilizables, lápiz, goma y regla, Así como tu libro de texto.
¿Qué hacemos?
Para iniciar, analiza la siguiente situación-problema y reflexiona sobre los puntos importantes que se vayan mencionando.
Si la suma de dos números es 180 y uno es el triple del otro, ¿cuáles son esos números?
Para dar respuesta a la pregunta, lo primero que debes hacer es traducir la situación a lenguaje algebraico para, posteriormente, dar respuesta a la situación planteada.
En este caso, tienes el primer número, que se representará con la literal “x”.
El triple de ese número lo escribes como: 3x.
Ahora, representas el enunciado “la suma de los dos números es igual a 180”, lo escribes algebraicamente como la ecuación lineal: x + 3x = 180.

Ya tienes la ecuación que modela la situación; es momento de resolverla respetando las propiedades y las reglas de la igualdad que ya conoces.
Primero, debes simplificar los términos semejantes en el primer miembro de la ecuación: x + 3x es igual a 4x; así, tienes la ecuación equivalente 4x = 180. Para despejar a “x” divides ambos miembros entre 4, dando 4x/4 = 180/4. Resolviendo las operaciones, obtienes el valor de “x” que es igual a 45.

Ahora sí, ya tienes elementos suficientes para poder responder la pregunta y solucionar la situación. La suma de dos números es 180 y uno es el triple del otro, ¿cuáles son esos números?
Como “x” es el primer número, de acuerdo con la representación algebraica, tienes que x = 45, que es el primer número.
Como el triple del número es 3x y “x” vale 45, tienes que 3 por 45 es igual a 135, que es el segundo número.

Hay que hacer la comprobación, sustituyendo el valor de “x” en la expresión que modela la situación trabajada: x + 3x = 180.
Al sustituir el valor de “x”, se tiene que:
45 + 3 (45) = 180
45 + 135 = 180
180 = 180
La igualdad entre ambos miembros indica que el resultado obtenido para “x” es correcto. De esta forma, queda comprobado que la respuesta es correcta.
Se ha resuelto satisfactoriamente la situación planteada, pero ¿será la única ecuación lineal que se puede plantear, a partir de la situación-problema?
Piénsalo un momento.
En algunas situaciones se puede plantear más de una ecuación, la cual puede modelar el problema y que, al ser resuelta, se encuentren los mismos resultados. Observa.
En la situación anterior se puede considerar que el primer número es el triple del segundo, el cual se representa con la letra “a”; entonces, se puede representar al segundo número con la expresión a/3, es decir, un tercio de “a”. Así, la condición no cambia, puesto que queda entendido que un número es el triple del otro; o bien, el segundo número es un tercio del primero, es decir, a/3 + a = 180.

Ya se tiene la nueva ecuación que representa el mismo problema. Revisa lo que sucede. No olvides tomar nota de lo que consideres importante y escribir las dudas que vayan surgiendo durante el proceso.
Primero, se reducen los términos semejantes del primer miembro, así que se procede a sumar: a + a/3, lo puedes escribir como 1/3”a” + 3/3”a” = 4/3”a"; así tienes que: 4/3”a” = 180.
Para despejar la incógnita, como 4/3 está multiplicando a “a”, se puede dividir ambos términos entre 4/3, quedando 4/3”a” entre 4/3 = 180/4/3.
Al resolver las operaciones, 4/3”a” entre 4/3 es igual a “a”; y, por otro lado, 180 entre 4/3 es igual a 540/4 a su vez igual a 135. Con esto se tiene que a = 135.
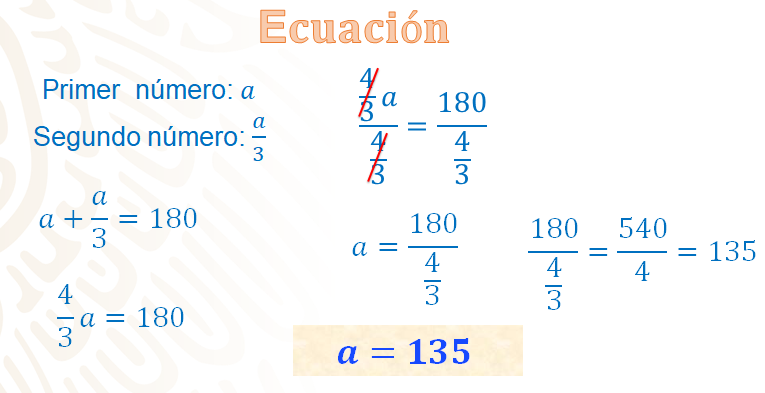
Ahora, relaciona los valores obtenidos con la incógnita “a” para comprobar la respuesta. Esto es a = 135, que es el primer número; y, para obtener el segundo número, utiliza la expresión a/3; sustituyendo “a”, resulta que 135/3 = 45, que es el valor del segundo número.
Comprobando el valor obtenido de “a” en la ecuación, se ve que cumple con la igualdad. Para comprobar la respuesta, se sustituye el valor de “a”, y tienes que 135 + 135/3 = 180; al resolver 135/3 = 45 y, si sumas 135 + 45 = 180; y 180 es igual a 180, lo cual indica que la solución de la ecuación es correcta.

Se ha logrado trabajar con dos ecuaciones diferentes para resolver una misma situación.
A continuación, analiza y resuelve la siguiente actividad.
Vicente compró dos camisas y un pantalón, por los que pagó 350 pesos. Aunque desconoce el precio de cada prenda, sabe que el precio de cada pantalón es 50 pesos más que el de una camisa.
¿Cuál es el precio de cada prenda?
Considera que, para resolver el problema, es necesario traducir a lenguaje algebraico la situación–problema, como se muestra a continuación.

Se representa el precio de la camisa con la literal “c” y el del pantalón con la literal “p”.
Como el precio del pantalón es 50 pesos más que el de una camisa, puedes expresarlo algebraicamente como: p = c + 50.
La situación está determinada por la siguiente relación: el precio de 2 camisas + un pantalón = 350 pesos, esto es 2c + p = 350.
Tienes dos ecuaciones y dos literales, entonces para trabajar con una sola ecuación y una sola literal debes realizar lo siguiente:
Como el precio del pantalón “p” algebraicamente es igual a “c + 50”; entonces, en la expresión 2c + p = 350, sustituye “p” por “c + 50” y te queda la ecuación: 2c + c + 50 = 350.
Ahora ya tienes la ecuación con una incógnita, la cual vas a resolver aplicando las propiedades de la igualdad.
Tienes que: 2c + c + 50 = 350. Primero, reduces términos semejantes del lado izquierdo de la igualdad, obteniendo la ecuación 3c + 50 = 350.
Posteriormente, restas 50 en ambos miembros de la igualdad, quedando: 3c + 50 – 50 = 350 – 50 y, al simplificar, queda: 3c = 300.
Por último, tienes a 3 que multiplica a “c”; así que procedes a dividir ambos miembros entre 3, para que no se altere la igualdad, quedando: 3c/3 = 300/3. Al resolver las operaciones, resulta que c = 100; es decir, el precio de cada camisa es de $100.
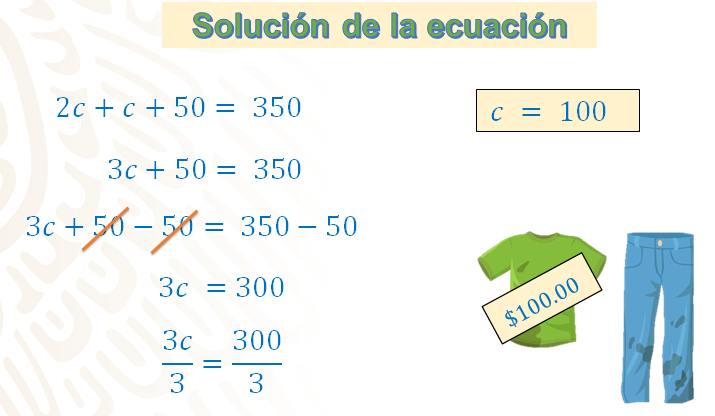
Con este resultado ya se puede calcular el precio del pantalón, resuélvelo algebraicamente.
Sustituye el valor de “c” en la expresión: 2c + p = 350, para obtener el precio del pantalón; es decir, el valor de “p”. Al sustituir “c”, tienes: 2 por 100 más p es igual a 350. Resuelve la multiplicación 2 por 100 y queda la ecuación: 200 + p = 350.
Para despejar “p”, observa que se está sumando con 200; así que resta 200 en ambos miembros de la ecuación, para que la igualdad se mantenga y tienes: 200 + p – 200 = 350 – 200. Al simplificar la ecuación, obtienes: p = 150; es decir, el precio del pantalón es de 150 pesos.

Con lo anterior ya se dio respuesta a la pregunta: ¿cuánto vale cada prenda de vestir?
Para comprobar los resultados, suma el precio de las prendas: 2 por 100 más 150 es igual a 200 más 150, igual a 350, que es la cantidad que pagó Vicente por las tres prendas.
Con el fin de ir consolidando lo que has realizado al resolver los problemas anteriores, en los que el uso de ecuaciones lineales ha sido importante, analiza la siguiente situación y resuélvela.
Sonia fue a la papelería para comprar 5 cuadernos y 3 bolígrafos por los que pagó 301 pesos. Se sabe que el precio de un cuaderno es igual al precio de ocho bolígrafos; es decir, ocho veces mayor.
¿Cuál es el precio de cada cuaderno y de cada bolígrafo?

Si asignas la literal “c” al precio de los cuadernos y la “b” al de los bolígrafos, ¿cuál sería la expresión algebraica que modela el problema? Escríbela en tu cuaderno.
Revisa si lo que escribiste es parecido a lo siguiente: 5c + 3b = 301.
Esta expresión algebraica servirá de base para encontrar los precios de los artículos. De la lectura del problema, se sabe que el precio de un cuaderno es ocho veces el precio de un bolígrafo. ¿Cómo se representa algebraicamente esto?
Intenta hacerlo.
La expresión algebraica es: c = 8b.
Si en la expresión algebraica 5c + 3b = 301, sustituyes a “c” por “8b”, obtienes una ecuación con una sola incógnita y queda lo siguiente: 5 por 8b + 3b = 301.
Observa que 5 multiplica a 8b; al resolver, el producto es 40b, por lo que queda la ecuación: 40b + 3b = 301. Ahora se deben agrupar términos semejantes para simplificar la ecuación: 40b + 3b = 43b; así, queda la ecuación: 43b = 301.
Para despejar a “b” divides ambos miembros de la ecuación entre 43; de donde resulta: 43b/43 = 301/43.
Al realizar las divisiones te queda que b = 7.
Esto quiere decir que cada bolígrafo tiene un precio de 7 pesos.

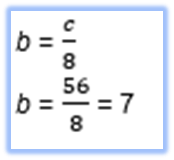
Al sustituir el valor de “b” en la expresión c = 8b, obtienes el precio de cada cuaderno. Realízalo.
c = 8 por (7), de donde resulta que c = 56; esto es que cada cuaderno tiene un precio de 56 pesos.

Hay que comprobar estos valores en la ecuación inicial: 5c + 3b = 301.
Al sustituir los valores encontrados obtienes:
5(56) + 3(7) = 301. Realizando las operaciones, 5 por 56 y 3 por 7 queda, 280 + 21 = 301. Tras realizar la suma del primer miembro, resulta que 301 = 301, con lo que queda comprobado que esos valores son el precio de cada cuaderno y de cada bolígrafo.

¿Habrá otra manera de resolver este problema?
La respuesta es sí.
Otra forma de resolverlo es a partir de relacionar, de otra manera, el precio de cada cuaderno con el de cada bolígrafo.
De los datos que se proporcionan en el problema, se tiene que cada cuaderno vale ocho veces el precio de un bolígrafo. Ya viste que la expresión que los relaciona es: c = 8b y de ella puedes obtener que el precio de cada bolígrafo es la octava parte del de un cuaderno, esto es: b = c/8.
Si sustituyes esta expresión en la ecuación de base, se tiene que: 5c + 3(c/8) = 301.
Observa que en el primer miembro se tiene una suma de fracciones y, para realizarla, es necesario obtener fracciones que tengan denominador común. Expresa a 5 enteros en octavos que es igual a 40/8, por lo que queda: 40/8 c + 3/8 c = 301.
Al realizar la suma de cuarenta octavos más tres octavos, se obtiene que: 43/8 c = 301.
Despeja “c” para obtener su valor; para hacerlo aplica la propiedad uniforme de la igualdad, que indica que lo que se haga en un miembro de la ecuación, tiene que hacerse en el otro. Divide ambos miembros de la ecuación entre 43/8:
43/8 c entre 43/8 es igual a 301 entre 43/8, por lo que “c” = 301 entre 43/8, de donde resulta: c = 301 por 8 entre 43, en donde “c” = 2408 entre 43. Al resolver la división, c = 56, es decir, que, efectivamente, cada cuaderno tiene un precio de 56 pesos, lo que ya se había obtenido previamente.
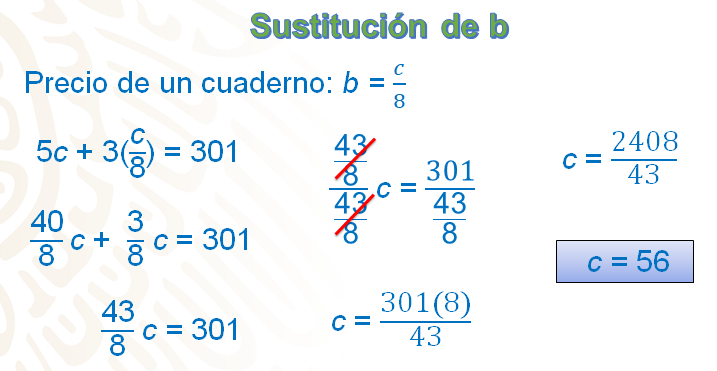
Al sustituir este valor en la expresión b = c/8, tienes que b = 56/8; es decir que b = 7, y así corroboras que el precio de cada bolígrafo es de 7 pesos.
Ahora se resolverá el siguiente acertijo.
La edad de Memo es el doble de la de Luis, pero la mitad de la de Juan. Si las tres edades suman 77 años, ¿cuál es la edad de cada uno?
Hay que recabar la información que proporciona el problema y plantear las expresiones algebraicas y la ecuación que permitirá resolver la situación.
Se tomará la edad de Memo como la incógnita y se le asigna la literal “x”. Como la edad de Memo es el doble de la de Luis, entonces la edad de Luis es la mitad de la edad de Memo, quedando la expresión: edad de Luis x/2.
Ahora, hay que representar la edad de Juan. Como la edad de Memo es la mitad de la de Juan, se puede decir, entonces, que la edad de Juan es el doble de la edad de Memo, quedando la expresión: edad de Juan 2x.
Enseguida, hay que relacionar las expresiones para plantear la ecuación lineal; así, tienes que la suma de las tres edades es igual a 77, es decir, x + x/2 + 2x = 77, que es la ecuación que modela la situación.

Ahora, hay que resolverla. Pon mucha atención y no olvides hacer tus anotaciones.
Observa que, en el primer miembro, todos los términos son semejantes, ya que todos tienen la misma literal con el mismo exponente; entonces, puedes simplificarlos sumando los coeficientes: 1 + 1/2 + 2 = 3 un medio = 7/2, así obtienes la ecuación: 7/2x = 77.
Para despejar “x”, observa que 7/2 está multiplicando a “x”, así que procede a dividir tanto el primer miembro como el segundo por 7/2, quedando la expresión: 7/2x entre 7/2 = 77 entre 7/2.
Al resolver las operaciones, te queda que 7/2x entre 7/2 = x, y 77 enteros entre 7/2 = 154/7 = 22; así, se tiene que la solución de la ecuación es: x = 22.

Ahora sí, con este resultado, estas en condiciones de determinar las edades de cada persona.
La edad de Memo, “x”, es igual a 22 años; como la edad de Luis, es la mitad de la edad de Memo; es decir, x/2, que es igual a 22 entre 2, igual a 11 años. Y la edad de Juan es del doble de la edad de Memo, es decir, 2x, que es igual a 22 por 2 igual a 44 años.
|
Edad de Memo: 22 años. Edad de Luis: 11 años. Edad de Juan: 44 años. |
Pero, ¿ésta será la única manera de plantear la ecuación que resuelve el problema?
En este caso, al igual que en otros similares, se puede obtener una ecuación distinta para resolver la situación.
Estudia otra ecuación que te permita resolverla, considerando la edad de otra de las personas como la incógnita. Reflexiona, si consideras la edad de Juan como la incógnita, ¿qué ecuación permitiría resolver el problema?
Observa que sucede.
Hay que desarrollar las expresiones, pero ahora considerando a Juan como la incógnita; tienes las expresiones para cada uno de los personajes de la siguiente manera:
La edad de Juan es igual a “j”. Como Memo tiene la mitad de la edad de Juan, queda como ½ de “j” y, como Memo tiene el doble de la edad de Luis, ½ de “j” es el doble de ¼ de “j”, que es la edad de Luis. Ahora ya puedes representar la ecuación (la suma de las edades es igual a 77), quedando de la siguiente manera: j + ½ j + ¼ j = 77.

Para resolver la ecuación sigues el mismo procedimiento que en el caso anterior. Como en el primer miembro todos son términos semejantes, los sumas como fracciones equivalentes en cuartos, y para simplificar la ecuación obtienes 7/4 de “j” = 77.
En esta ocasión, vas a operar con números decimales; por ello, 7/4 lo conviertes en su representación como número decimal y tienes que 7/4 de “j” es igual a 1.75” j”.
Para despejar “j” debes dividir entre 1.75 a ambos miembros de la ecuación, quedando: 1.75j entre 1.75 igual a 77 entre 1.75. Al resolver las operaciones, tienes que 1.75j entre 1.75 es igual a “j” y 77 entre 1.75 es igual a 44; es decir, j = 44.
Esto indica que la edad de Juan es de 44 años.

Con esto se puede obtener las edades de Memo y Luis, que son: para Memo la mitad de la edad de Juan; es decir, j/2, que es igual a 44 entre 2, igual a 22 años; y para Luis se tiene que su edad es igual a ¼ de j, que es igual a 44 entre 4, igual a 11 años.
|
Edad de Juan: 44 años Edad de Memo: 22 años Edad de Luis: 11 años |
Así, se comprueba que esta nueva ecuación te permitió obtener los mismos resultados, por lo que ambas representaciones de la situación son correctas.
El Reto de Hoy:
El reto de hoy consiste en lo siguiente:
Retoma del último ejercicio del acertijo de las edades, como resolverías las siguientes preguntas:
- ¿Qué sucedería si la edad de Luis representa la incógnita del problema y usas la literal ele?
- ¿Cuáles serían las expresiones que representarían las edades de Memo y Juan?
Se te invita a que encuentres las edades de estos tres personajes usando una nueva ecuación.
Comparte tus resultados con tu maestra o maestro de esta asignatura, a la distancia para recibir retroalimentación.
Asimismo, revisa en tu libro de texto el tema que estudiaste en esta sesión y realiza las actividades que ahí se te sugieren.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Diferentes formas de adornar el lenguaje
Aprendizaje Esperado: Lee y compara poemas de diferentes épocas sobre un tema específico.
Énfasis: Indagar formas literarias en poemas.
¿Qué vamos a aprender?
En esta sesión revisarás: diferentes formas de adornar el lenguaje, con esto se hace referencia a: indagar formas literarias en poemas. Esto te ayudará a analizar las formas literarias de la poesía y comprender lo que al autor quiso decir.
Conocer las formas literarias te servirá no sólo para comprender poemas, sino también para comprender otros textos donde, de igual manera, se utilizan las formas literarias.
Los materiales que vas a necesitar para esta sesión son: tu cuaderno, y lápiz o bolígrafo para que puedan tomar notas. Asimismo, tu libro de texto de Lengua Materna.
¿Qué hacemos?
Para iniciar, piensa y responde las siguientes preguntas:
- ¿Recuerdas algún poema que hayas leído?
- ¿Recuerdas algunas frases que no hayas comprendido porque utilizaba una figura o forma literaria?
- ¿Recuerdas lo que es una figura o forma literaria?
Quizás cuando se leen algunos poemas, hay algunas frases que cuestan trabajo comprender, pues están escritas de manera figurada y a veces comparan a personas con objetos o elementos de la naturaleza y causa confusión, pero se puede notar que así se expresan muchos escritores; seguramente a muchas personas les sucede lo mismo, sobre todo cuando se están iniciando en la lectura.
Cuando se lee un texto, como un poema, encontrarás que algunas palabras o frases son poco usuales, pero que sirven para dar mayor expresión, belleza y emotividad, y para que el autor pueda motivar al lector, a través de esta manipulación del lenguaje. Eso es lo que revisarás en el transcurso de esta sesión, para qué sirve expresarse con este recurso literario, cuál es la clasificación y ejemplos, y también analizarás un poema escrito en una lengua materna que es el náhuatl, para que puedas entender mejor.
Sobre todo, revisarás varios ejemplos, porque así es más fácil comprender los conceptos.
Lo primero que debes hacer es conocer cómo está escrito el poema. Para poder comprenderlo y para comprender la poesía debes tener en cuenta que el autor se expresa en dos sentidos: en sentido literal, es decir, que lo escrito debe entenderse tal cual, en su sentido original, que no debe de darse otra interpretación ni doble sentido; y en sentido figurado, que se refiere a que lo escrito tiene que entenderse con un mayor valor expresivo; y para que esto suceda se utilizan las formas o figuras literarias.
Ahora. leerás un poema de Carlos Edmundo de Ory.
Hipérbole del amoroso
Te amo tanto que duermo con los ojos abiertos.
Te amo tanto que hablo con los árboles.
Te amo tanto que como ruiseñores.
Te amo tanto que lloro joyas de oro.
Te amo tanto que mi alma tiene trenzas.
Te amo tanto que me olvido del mar.
Te amo tanto que las arañas me sonríen.
Te amo tanto que soy una jirafa.
Te amo tanto que a Dios telefoneo.
Te amo tanto que acabo de nacer.
¿Qué te pareció el poema?
Quizás, te suceda que a veces te enfrentas al problema de no entender lo que quiso expresar el autor, porque éste, uso el sentido figurado.
No te preocupes, hay muchas personas que se enfrentan a este tipo de problemas al leer un poema, pero para que puedas entender lo que el autor quiso expresar se analizarán algunas figuras literarias que, aunque son muchas las clasificaciones, verás las que más se utilizan.
Se empezará con las siguientes formas literarias: la hipérbole, la metáfora, la comparación y la rima:
Hipérbole: es cuando se aumenta o disminuye, a manera de exageración, un aspecto o una característica. Ejemplo: Te amo tanto que hablo con los árboles.
Como te puedes dar cuenta, en el poema el autor exagera la emoción, lo que le produce el amor: que ama tanto que es capaz de realizar acciones imposibles.
Las hipérboles, en este poema, parecen más complejas, pero si las analizas detenidamente una por una podrás saber qué acción, aspecto, o característica está exagerando. Por ejemplo, cuando dice: “Te amo tanto que soy una jirafa”. Quiere decir que el amor lo hace sentir diferente, pero lo exagera con esta hipérbole.
Incluso, el autor sabe muy bien qué figura está utilizando, por eso tituló a su poema “Hipérbole del amoroso”.
Un ejemplo de hipérbole que se utiliza cotidianamente es cuando le dices a alguien: te llamé mil veces; es muy improbable que le llamemos mil veces a alguien.
Aunque, te pueden parecer metáforas, algunas lo son, pero en este poema se clarifica el uso de la hipérbole porque se tiene algo claro: que se ama tanto que… se exagera lo que esa emoción produce.
Es como como la expresión: “estoy tan enojado que voy a explotar”.
La metáfora es una analogía o semejanza entre dos ideas. También se utiliza para referirse a algo, pero sin mencionarlo específicamente. Un ejemplo es: tus labios son pétalos perfumados.
Lee el siguiente fragmento del poema de Pablo Neruda e identifica las metáforas.
Te recuerdo como eras en el último otoño.
Eras la boina gris y el corazón en calma.
En tus ojos peleaban las llamas del crepúsculo.
Y las hojas caían en el agua de tu alma.
¿Por dónde comenzamos?
Hasta aquí el poema.
Si se revisa por partes, es más fácil. Observa una de estas partes.
|
Eras la boina gris y el corazón en calma. |
Ésta es una metáfora del recuerdo que tiene de la persona. En lugar de decir: recuerdo que traías una boina gris y me producías tranquilidad, el autor la evoca como la boina y como el sentimiento que le producía.
Revisa con otra.
|
Y las hojas caían en el agua de tu alma. |
Aquí, la mención a las hojas cayendo se refiere al otoño, la temporada en donde las hojas pausan su producción de clorofila, es decir, se detienen, como los recuerdos. ¿Has visto qué pasa cuando cae una hoja al agua?
Produce ondas. Así es, el agua significa un estado de calma, y las hojas pueden ser recuerdos que desestabilizan esa tranquilidad. A veces cuando se recuerda algo doloroso se puede sentir tristeza o ansiedad.
Entonces, en lugar de decir: los recuerdos te perturbaban, el poeta dice: “Y las hojas caían en el agua de tu alma”.
Parece complejo, pero no lo es. Más adelante se clarificará esto con ejemplos más sencillos.
Ahora se analizará lo que es la comparación:
La comparación es cuando se relacionan dos elementos entre sí para expresar de otra manera la semejanza. Ejemplo: se sentía un estruendo como de fieras al combate.
Otros ejemplos serían:
Su sonrisa brillaba como la luna en la oscuridad.
Resucitó de las cenizas cual ave fénix.
Analiza la siguiente estrofa escrita por Antonio Machado e identifica la comparación.
Yo amo los mundos sutiles,
Ingrávidos y gentiles,
Como pompas de jabón.
El “como” es lo que marca o establece la comparación.
¿Cómo interpretas esto?
Se ve la comparación cuando se dice: en mundos ingrávidos, es decir, mundos flotantes, y, en esta estrofa, es comparado con las pompas de jabón, que es otra forma de llamarle a las burbujas. Éstas flotan y caen lentamente como si no les afectara la gravedad.
Así es, esa es la comparación o símil, como también se le llama.
Ahora analiza la rima.
Rima. Es la coincidencia de sílabas finales de los versos entre sí.
Lee el siguiente poema de José Martí que ya has visto en sesiones pasadas, pero esta vez identificarás las rimas.
Cultivo una rosa blanca
en junio como enero
para el amigo sincero
que me da su mano franca.
Y para el cruel que me arranca
el corazón con que vivo,
cardo ni ortiga cultivo;
cultivo la rosa blanca.
¿Puedes identificar las rimas?
Las rimas de la primera estrofa están en el verso 1 y 4, que serían las palabras: blanca y franca. En el dos y el tres: enero y sincero.
En la segunda estrofa, los versos 1 y 4: arranca y blanca, y nuevamente el 2 y el 3: vivo y cultivo.
Ahora, se ejemplificará estas figuras con frases simples, para que queden más claras.
Cuando se dice: “Es muy lejos a dónde vas, llegarás mañana”, es una exageración, en este caso, es una hipérbole, porque es común decir esto cuando se va a un lugar que está distante, pero no es exacto decir que te tomará un día, quizá te tomará un par de horas.
Al decir, “estudia tanto que se le queman las pestañas”, esto es una metáfora porque cuando estudias mucho no se te queman las pestañas, pero ya es un dicho popular mexicano. Cuando se dice “come frutas y verduras para que crezcas alto y fuerte como un árbol” es una comparación o símil porque se compara el tamaño y fortaleza de una persona con la de un árbol. Y al decir “imaginando y creando, llegaré muy lejos trabajando” es una rima, puesto que en las palabras “imaginando y trabajando” riman sus dos últimas sílabas.
Ahora, verás otras formas o figuras literarias: la anáfora, prosopopeya o personificación, onomatopeya y el oxímoron. Se te mostrará a que se hace referencia con cada una de ellas:
Kema kanantlajki titeiljuis o titepouilis, moneki axkana san ma mitskakikaj, moneki ma kuali kikuamachilikaj, nojkia ijkino ma eli kema mochiua se tlajkuiloli.
Para empezar la anáfora: es la repetición rítmica de determinados sonidos o palabras al iniciar un verso o una frase.
Identifica esta repetición en el siguiente fragmento del poema “A un hombre de gran nariz” de Francisco de Quevedo.
Érase un hombre a una nariz pegado,
érase una nariz superlativa,
érase una nariz sayón y escriba,
érase un peje espada muy barbado.
Éste es más fácil de identificar. La anáfora se percibe en la palabra “érase”.
Se podría sustituir esta palabra por comas, pero la anáfora se utiliza para resaltar las imágenes.
A continuación, se seguirá con la prosopopeya o personificación.
Prosopopeya o personificación: es cuando se dan características humanas a animales, objetos o fenómenos.
Lee el siguiente poema de Federico García Lorca.
"El lagarto está llorando.
La lagarta está llorando.
El lagarto y la lagarta
con delantaritos blancos.
Han perdido sin querer
su anillo de desposados.
¡Ay, su anillito de plomo,
ay, su anillito plomado!
Un cielo grande y sin gente
monta en su globo a los pájaros.
El sol, capitán redondo,
lleva un chaleco de raso.
¡Miradlos qué viejos son!
¡Qué viejos son los lagartos!
¡Ay cómo lloran y lloran!
¡Ay! ¡ay!, ¡cómo están llorando!"
Aquí se pone una característica humana a los lagartos. Pero ¿acaso no lloran?, ¿y cuando se dice de alguien que llora lágrimas de cocodrilo?
En realidad, los cocodrilos lloran por cuestiones biológicas y no por una emoción. Por eso aquel dicho “lágrimas de cocodrilo” se refiere a lágrimas falsas, es decir, fingidas, no nacidas de una emoción genuina.
Otro ejemplo sería “La luna me sonríe”, pues la sonrisa es una forma de expresión propia de los humanos que no puede hacer la luna.
Ahora se seguirá con la onomatopeya, que son los sonidos reales, de manera escrita y con el oxímoron, que es cuando dos términos de significado opuesto se complementan.
Hay que identificar las onomatopeyas en el siguiente poema.
Este es un poema para niños de la poeta María Alonso Santamaría.
¡Toc toc!
¿Hay alguien ahí?
Brrrrr, ¡qué frío hace aquí!
Uuuuhhhh, ¡cómo sopla el viento!
Ploc, ploc, ¡empieza a llover!
Tictac, tictac, da el reloj las tres.
Ñam ñam ¡Me voy a comer!
después en silencio, shisss, shisss
he dormido un rato. Zzzzz, Zzzzz
Riiiing, riiiing, riiiing
(suena el teléfono)
¡Miau! y ha maullado el gato.
¡Puf! ¡Se acabó el descanso!
Quedó muy claro. Ya que fue fácil identificar a qué sonidos se refería. El próximo ejemplo es un oxímoron.
Lee el siguiente poema de Julia Uceda:
Y no dejéis
que los grifos abiertos
inunden las estancias:
que el pétalo amarillo
de las horas encienda
de frío sol los ámbitos vacíos.
Hasta aquí el poema.
¿Dónde notas el oxímoron?
En donde dice: En frío sol, ya que el sol no es frío.
Ahora lee el siguiente:
En las noches claras,
resuelvo el problema de la soledad del ser.
¿En dónde se encuentra?
En: Noches claras. Las noches no son claras. Ahí está lo opuesto.
Como puedes ver, se trata de calificar algo con un sentido opuesto, como en estos ejemplos.
Fuego helado.
Luz oscura.
Vista ciega.
Débil mármol.
Ahora, para reforzar las figuras que has visto hasta ahora, se pondrá un ejemplo con un poema llamado “Ahí donde el aire reposa”, en español y en náhuatl “Kampa ejekatl san tlamajtok”. Habla sobre la vida en el campo. Lee el siguiente fragmento que se analizará.
|
“Ahí donde el aire reposa”
Ahí donde el aire reposa Ahí donde el aire reposa y en la flor la mariposa y el sol duerme cada tarde cobijado por las nubes blancas como las canas de mi madre.
|
Kampa ejekatl san tlamajtok
Kampa ejekatl san tlamajtok Nopaya kampa ejekatl san tlamajtok papalotl ipan ne pilxochitsi kampa ne tonati kochi se teotlak kipijtok chipauaj mixtli ken ne ikuaich nonana.
|
Este poema es muy bonito y tiene varias formas literarias.
Se empezará analizar en español.
Ahí donde el aire reposa. Es una personificación o prosopopeya, pues las personas son las que reposan o descansan.
Ahí donde el aire reposa y en la flor la mariposa. Es una rima, pues coinciden las últimas sílabas.
y el sol duerme cada tarde. Es una personificación, las personas son las que duermen.
cobijado por las nubes blancas
como las canas de mi madre
Los dos párrafos anteriores, son metáforas, pues es una analogía o semejanza entre dos ideas.
Con este análisis del poema, ¿está más claro tu aprendizaje?
Mientras más leas poesía, podrás poner en práctica este contenido e identificarás las figuras literarias revisadas el día de hoy y quizás tengas otra percepción al leer poesía.
Pero, ¿hay algo más que se pueda recomendar que se lea al respecto?
Algunas recomendaciones que se pueden dar, además de las formas literarias que ya revisaste, es que investigues en la web, en libros, en bibliotecas virtuales: si existen poetas en tu comunidad o con tus conocidos, pues ellos te pueden aportar más información sobre las distintas formas literarias utilizadas en los poemas, ¡ellos conocen mucho sobre el tema!
Por otra parte, se puede decir que las formas y figuras literarias están presentes, en los poemas y canciones que te encuentras en la escuela y en la vida diaria, pero también en el habla que se escucha y producen los hablantes del español y de todas las lenguas mexicanas. Solo hay que tener los oídos abiertos para reconocerlas y valorarlas.
Recuerda que para comprender mejor la idea que el autor quiso plasmar al escribir su poema, debes leer detenidamente e identificar a cuál forma literaria corresponde cada uno de sus versos, y verás que poco a poco te será más sencillo comprenderlos; además de que harás volar tu imaginación.
Si quieres saber más sobre las lenguas nacionales de nuestro país, se te invita a revisar en la página del INALI: https://www.inali.gob.mx
Y en la página web de la UNAM, para que puedas escuchar poesía, también encontrarás en dicha página, poesía indígena, la dirección electrónica es: https://descargacultura.unam.mx/
El Reto de Hoy:
En tu cuaderno, anota la forma literaria que no conozcas, e investiga a qué tipo pertenece. Nunca dejes de investigar.
Recuerda que, si tienes dudas o quieres profundizar sobre este contenido, puedes buscar el aprendizaje esperado en tu libro de texto, además de realizar las actividades que ahí se te proponen.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Libertades y limitaciones del poder
Aprendizaje esperado: Explica las implicaciones de la autoridad y el poder público en un régimen democrático.
Énfasis: Comprender las libertades y limitaciones en el ejercicio del poder público en el régimen democrático.
¿Qué vamos a aprender?
Conocerás las libertades y limitaciones en el ejercicio del poder público, en un régimen democrático. Durante la sesión, con ayuda de algunas de tus compañeras y compañeros; así como de docentes, se profundizará sobre el poder y su ejercicio en el ámbito público y privado.
Ten a la mano tu libro de texto de la asignatura, tu cuaderno u hojas blancas, un lápiz o bolígrafo. Si tienes discapacidad visual, prepara tus hojas leyer, punzón y regleta.
¿Qué hacemos?
En una democracia, la organización del gobierno responde a la soberanía popular, para así representar los intereses y necesidades de la ciudadanía. Asimismo, requiere garantizar el respeto de los derechos humanos de toda la población: De las mayorías y las minorías.
En este caso, el poder político, es decir, el poder para gobernar y tomar decisiones sobre la vida pública de toda una región o un país, se comparte con la ciudadanía.
Este poder político es público porque las y los gobernantes, y la ciudadanía, tienen la posibilidad de interactuar para dar forma a las decisiones y las acciones que se tomen para la población, relacionadas con los asuntos comunes y sus derechos.
Para ayudarte a ampliar tu conocimiento sobre el tema de la autoridad y el poder público, revisa la entrevista realizada por tu compañera Lilia al Mtro. Jorge Jiménez, en el siguiente video.
- VIDEO 1.
Revisa del tiempo 00:35 al 07:11.
Según lo expuesto en el video por Jorge Jiménez, se puede definir al poder público o los poderes públicos como un conjunto de órganos e instituciones del Estado, que se agrupan en torno a tres diferentes poderes: Poder legislativo, ejecutivo y judicial.
Con la organización del gobierno en tres poderes se busca la distribución del poder político. Cada uno requiere actuar con autonomía y debe haber un equilibrio entre ellos.
Para que te quede más claro considera el siguiente esquema sobre la división del poder público.
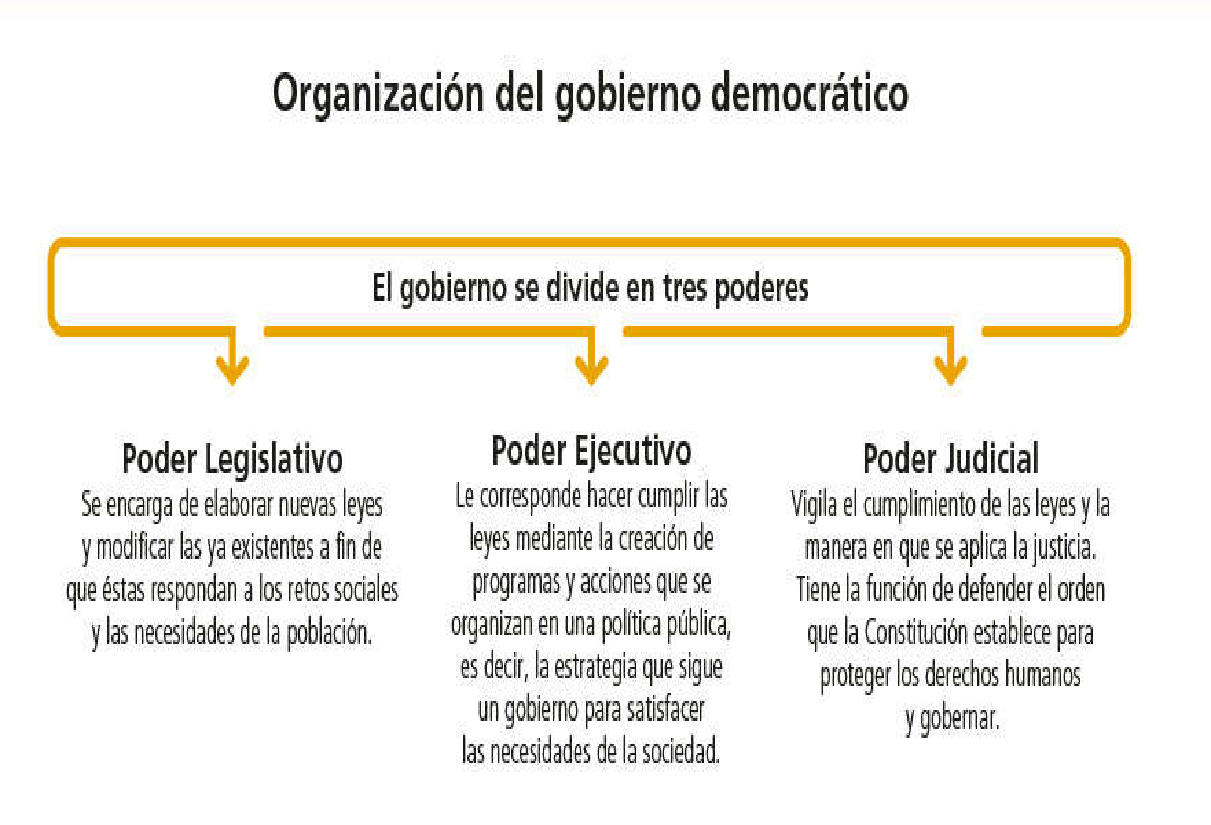
Como se ha mencionado, la organización del gobierno democrático se divide en tres poderes:
- Poder legislativo: Se encarga de elaborar nuevas leyes y modificar las ya existentes a fin de que éstas respondan a los retos sociales y las necesidades de la población.
- Poder ejecutivo: Le corresponde hacer cumplir las leyes mediante la creación de programas y acciones que se organizan en una política pública, es decir, la estrategia que sigue un gobierno para satisfacer las necesidades de una sociedad.
- Poder judicial: Vigila el cumplimiento de las leyes y la manera en que se aplica la justicia. Tiene la función de defender el orden que la Constitución establece para proteger los derechos humanos y gobernar.
Asimismo, las autoridades que integran cada uno de los tres niveles de gobierno (legislativo, ejecutivo y judicial) se organizan de la siguiente manera:
|
A nivel federal: |
A nivel estatal:
|
A nivel municipal: |
|
Se integran por:
|
||
|
|
|
A las figuras antes mencionadas se les llama servidoras y servidores públicos. Como recordarás, una servidora o un servidor público es una persona que brinda un servicio de utilidad social. Las y los servidores públicos prestan servicios al Estado, a través de instituciones federales o estatales públicas. Por ejemplo:
Los hospitales, las escuelas o las fuerzas de seguridad, que están encargadas de hacer llegar el servicio público a la comunidad. En otras palabras, buscan el bienestar y la creación de las condiciones para el ejercicio de derechos entre la población.
Pero, ¿qué pasa cuando una servidora o servidor público no cumple con sus funciones?
El incumplimiento de los deberes por parte de una empleada o empleado público, implica sanciones, que consisten en: amonestaciones, suspensión del empleo, suspensión del cargo o comisión, entre otras.
No está por demás recordar que los valores y principios que toda y todo servidor público deben observar en el desempeño de su empleo, cargo, comisión o función son los siguientes:
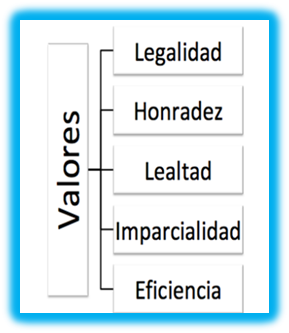
Mientras que los principios que deben guiar su actuar son los siguientes:
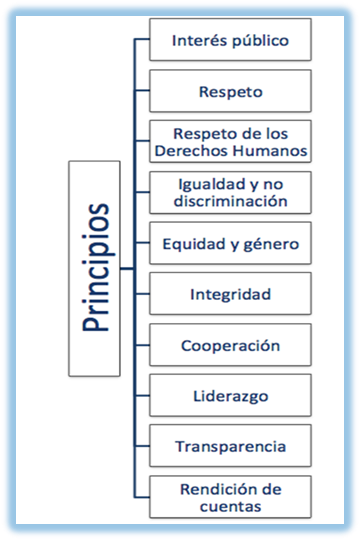
Ahora bien, para saber más sobre este tema y las leyes que regulan las responsabilidades de las y los servidores públicos, revisa con mucha atención el siguiente vídeo, realizado por la alumna de secundaria María José.
- FCYE1_B3_SEM33_PG2_VIDEO 2.
Como viste, María ha señalado un punto muy importante, y es que una servidora o servidor público es aquella persona que se encarga de realizar una tarea con el fin de generar un bienestar para la sociedad.
Así es, uno de los rasgos que debe sobresalir en una servidora o servidor público es proceder con ética, ya que las consecuencias de sus acciones suelen llegar a un conjunto mayor de la sociedad.
Para poner en práctica los conocimientos adquiridos hasta ahora sobre los poderes legislativo, ejecutivo y judicial, y las servidoras y servidores públicos que los conforman, se realizará el siguiente ejercicio.
Desde casa observa con mucha atención las indicaciones. El ejercicio consiste en relacionar las columnas sobre las funciones de los poderes del gobierno para la satisfacción de las necesidades de la población.
A continuación, analizarás los reactivos y anotarás la opción que corresponde con el enunciado, después verificarás si tus respuestas fueron correctas.

Ya has dado respuesta, verifica si lo que anotaste fue lo correcto.

Se espera que hayas acertado correctamente en todas tus respuestas.
Ahora se te compartirá el siguiente cuento, contado por Clauzzia Gómez, acerca de la división de poderes. Revísalo atentamente.
- VIDEO 3
Después de revisar el vídeo te quedará más claro que la mejor forma de gobierno es la división de poderes, ya que evita que un jefe de Estado se convierta en un dictador o en un tirano, pues al administrar el poder público, unas personas se encargan de elaborar leyes, otras de aplicarlas y otras de interpretarlas y resolver los conflictos derivados de su aplicación.
Y frente al poder público también se encuentra el poder popular, que implica el ejercicio de manera democrática y participativa por parte de las ciudadanas y los ciudadanos en las distintas esferas de la vida social; en la búsqueda del establecimiento de relaciones humanas, sociales y políticas justas e incluyentes.
A continuación, se realizará una recapitulación de lo visto en esta sesión.
Aprendiste que los poderes públicos son el conjunto de los poderes del Estado: el Ejecutivo, el Legislativo y el Judicial. El poder público es necesario para la organización de grupos sociales que confluyen en un espacio geográfico, social, político, cultural e histórico. La división de poderes democráticos se origina como una necesidad de asegurar la convivencia humana.
Asimismo, se resaltó que un funcionario es quien desempeña profesionalmente un empleo público. En México existe una Ley Federal de responsabilidades de los servidores públicos, que reglamenta su trabajo.
Se llegó a la conclusión de que el poder popular puede provocar una transformación progresiva, que como fuerza política posee en su centro la participación ciudadana.
El Reto de Hoy:
Para continuar fortaleciendo tus saberes se te invita a consultar tu libro de texto de Formación Cívica y Ética de primer grado y localizar las secciones de repaso o evaluación de los temas de diversidad e igualdad.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
La guerra de los Balcanes
Aprendizaje esperado: Favorece el reconocimiento de procesos relacionados con el fin del sistema bipolar.
Énfasis: Examinar algunas de las consecuencias del final del socialismo en la conformación del nuevo mapa europeo.
¿Qué vamos a aprender?
En esta sesión examinarás algunas de las consecuencias del final del socialismo en la conformación del nuevo mapa europeo.
Ten a la mano tu libro de texto, cuaderno u hojas blancas y de colores, pegamento, así como lápiz o bolígrafo y colores para registrar las ideas principales, así como dudas y reflexiones.
¿Qué hacemos?
Para iniciar, como parte de la sección “Leer para conocer”, realizarás la lectura de un fragmento de la historia de Mirsada Buric, corredora que entrenaba entre las bombas y los disparos durante el sitio de Sarajevo.
Dice así:
“Casi todos los días, Mirsada Buric salía a las devastadas calles de Sarajevo y realizaba un sencillo acto de valor que algunos calificaban de locura: corría.”
Sí, corría entre el fuego de los francotiradores y los bombazos de los morteros, junto a las construcciones acribilladas y a medio derruir de su ciudad. No tenía más escudo contra las balas y la metralla que su valentía, ni más sustento espiritual que el anhelo de competir en los Juegos Olímpicos. Su inquebrantable espíritu inspiró a sus compatriotas y le robó el corazón a un joven que vivía al otro lado del mundo.
Era un domingo de verano, en 1992, y Eric Adam, soltero de 34 años, estaba en la cocina de su pequeño apartamento, en Prescott, Arizona, haciendo lo que muchos solteros hacen el fin de semana: separar la ropa para la lavandería y empaquetar periódicos.
Tenía prendida la televisión en la sala y alcanzaba a oír las noticias. En eso, comenzaron a hablar de una corredora bosnia de media distancia que estaba entrenándose para los Juegos Olímpicos. Su pista eran las calles de una ciudad azotada por la guerra: Sarajevo, capital de Bosnia-Herzegovina. Todos los días la atleta corría entre los cráteres dejados por las bombas, desafiando el fuego de los morteros y el de los francotiradores. Eric fue a la sala para verla.
En la pantalla aparecía una joven de figura grácil, vestida con un traje deportivo elástico, que avanzaba con paso ligero moviendo los brazos cadenciosamente. Llevaba la cabeza en alto, como en calculado desafío a los tiradores serbios que la tenían en la mira.
El locutor decía que la corredora pretendía obtener un lugar para la bandera bosnia en los Juegos Olímpicos, y recordarle al mundo que su patria aún existía, por abatida y asediada que estuviera. La joven siguió corriendo en dirección a la cámara y luego su imagen desapareció.
Eric se quedó de una pieza.
Desde hacía varios años, aturdido por la muerte de su novia, iba por la vida como sonámbulo. Entonces, de buenas a primeras, la insólita imagen de una joven valerosa lo sacaba de su estupor. Invadido por un sentimiento que iba más allá de la razón y el sentido común, quiso conocer en persona a esa mujer, que estaba dispuesta a arriesgarlo todo por una causa noble. […]
“Mirsada ganó la prueba de su categoría de edad en el torneo anual de carrera a campo traviesa de Sarajevo. A los 20 años ya era una corredora de calidad internacional y se contaba entre las mejores de su país. “[…]
“Entonces estalló la guerra civil en lo que hasta ese momento era Yugoslavia. A Mirsada la desterraron de su pueblo natal y la llevaron a un campo de concentración, de donde, al cabo de dos semanas, la enviaron a Sarajevo.”
Fiel a su sueño, comenzó a entrenarse una semana después de su llegada. Como el estadio, situado al pie de los cerros arbolados que dominan la ciudad, estaba al alcance de los francotiradores serbios, no le quedó más remedio que correr en las calles dos veces al día. […]
En todo Sarajevo no había un solo lugar seguro. Los francotiradores disparaban a sangre fría contra todo aquel que tuviera la mala suerte de pasar frente a la mira de sus fusiles, fuese hombre, mujer o niño. Mientras Mirsada corría, oía silbar las balas a su lado y las veía incrustarse en los árboles y en las paredes; sentía en los pies el retumbar del suelo por los cañonazos y morterazos; percibía el penetrante olor a pólvora que impregnaba la ciudad.
A pesar de todo, seguía corriendo. "Es lo que me mantiene cuerda", dijo a los periodistas que la entrevistaron […].”
Hasta aquí la lectura.
¿Qué te pareció?
Una terrible guerra involucró a familias y pueblos que, durante décadas, habían convivido pacíficamente y que tuvieron que adaptarse y sobrevivir.
A continuación, observa la siguiente imagen.

Se conoce como “Otoño de las Naciones” al último trimestre de 1989, cuando las naciones de Europa del Este dejaron de pertenecer al bloque comunista, cambiaron el equilibrio de poder en el mundo y marcaron el final de la Guerra Fría.
El "Otoño de las Naciones" refiere a las revoluciones que sucedieron en Europa del Este y marcaron el fin del comunismo en esos países. A partir de 1989, después de la caída del Muro de Berlín, surgieron movimientos en varios países que reclamaban su independencia.
Al igual que la URSS, Yugoslavia también se desintegró, y este proceso estuvo marcado por la intolerancia hacia las otras etnias y religiones.
Ahora, observa el siguiente video.
- Los mapas de la segunda mitad del siglo XX.
https://www.youtube.com/watch?v=hgjJssemufI&t=36s
Revisa del tiempo 03:12 al 05:32.
Como observaste en el video, los países socialistas del Este de Europa, también conocidos como satélites porque estaban fuertemente controlados por la URSS, fueron afectados profundamente después de la caída del Muro de Berlín.
Los países que estuvieron bajo la influencia de la Unión Soviética ahora veían un marco favorable para que surgieran los nacionalismos, y surgieron movimientos que reclamaron su deseo de independencia.
En esta sesión se hablará del conflicto en la península de los Balcanes, que originalmente estuvo habitaba por diversos grupos étnicos y religiosos, primero bajo el Imperio Austro Húngaro y posteriormente por Yugoslavia.
Comenzarás por revisar los antecedentes históricos.
Los reinos de Serbia y Montenegro, de religión cristiana ortodoxa debido a su legado bizantino, obtuvieron su independencia del Imperio Otomano, mientras que Croacia se fusionó con Eslovenia.
Ante la caída del imperio Austro Húngaro en 1918, Croacia quedó incluida, contra su voluntad, en el Reino de los Serbios, Croatas y Eslovenos, formando un estado parlamentario que adoptó la religión católica.
Durante el último periodo de su reinado (1929-1934), Alejandro I, tras haber contemplado la incapacidad del régimen parlamentario para acabar con las disputas y llevar a cabo reformas necesarias, intentó lograr la unificación efectiva de Yugoslavia.
Su intento de unificación forzada fracasó, dejando sin resolver los graves problemas políticos que amenazaban al país.
Disolvió el parlamento y acumuló poder bajo un sistema de monarquía constitucional. Cambió el nombre a Reino de Yugoslavia, que permaneció hasta 1941 cuando fue ocupado por Alemania durante la Segunda Guerra Mundial.
En 1945, después de la liberación de la ocupación nazi, el Ejército Popular Partisano de Yugoslavia, al mando del Mariscal Tito, comenzó a liberar partes del territorio.
Josip Broz Tito se convirtió en presidente de la República Federal Socialista de Yugoslavia, en donde instauró un régimen comunista, pero a diferencia del resto del bloque fue independiente tanto de la OTAN como del Pacto de Varsovia.
Durante su gobierno logró unificar los territorios de Yugoslavia integrando las seis repúblicas socialistas de Bosnia y Herzegovina, Croacia, Macedonia, Montenegro, Eslovenia y Serbia.
Serbia contenía dos provincias autónomas: Voivodina y Kosovo.
Las diferentes repúblicas que la conformaban eran autónomas en materia de lengua y personal administrativo, aunque en Belgrado se tomaban las decisiones económicas y políticas del país.
De la misma manera que la URSS, Yugoslavia tuvo un crecimiento económico notable entre 1953 y 1965, pero el desarrollo se estancó, la inflación y el desempleo se dispararon hacia la década de los 80.
En 1980, tras la muerte de Tito, varios movimientos nacionalistas comenzaron a exigir un cambio en la federación yugoslava: por un lado, se hablaba de una “Gran Serbia”, por otro de independencia.
Todo esto llevó al comienzo de la Guerra de los Balcanes, llamada así por la península donde se encuentran los países implicados.
En 1986, Slobodan Milosevic, un nacionalista serbio, llegó a la presidencia de la liga de comunistas de Serbia, combatió los alzamientos albaneses en Kosovo purgó el aparato comunista kosovar y sometió a votación una medida para reintegrar Kosovo y Voivodina al territorio serbio. Además, apoyó las protestas de las minorías serbias en Croacia y Bosnia.
Bajo un marcado nacionalismo, recogía una antigua idea de reunir a las minorías serbias en un solo territorio, la Gran Serbia.
A principios de la década de 1990, tres estados de los seis que formaban parte de Yugoslavia decidieron independizarse:
Eslovenia, en 1991, fue la primera en autoproclamarse independiente.
Tras la guerra de los 10 días, una guerra rápida y poco sangrienta, lo consiguió.
El territorio no era muy extenso y lo más importante, la mezcla étnica era prácticamente nula.
Después de la proclamación de independencia de Eslovenia, otro país solicitó su salida de la Federación Socialista Yugoslava: Croacia.
En este caso, la guerra sería más larga y cruel. En un bando luchaba el Ejército Croata, que intentaba proclamar su independencia y, por el otro, el Ejército Popular Yugoslavo que reivindicaba territorios croatas con mayoría de población de origen serbio.
Bosnia-Herzegovina siempre fue un estado particularmente complejo y al mismo tiempo absolutamente tolerante, puesto que convivían pacíficamente bosnios, musulmanes, serbios ortodoxos y bosnio croatas católicos.
Tras la declaración de independencia de Eslovenia y Croacia, los líderes bosnios creyeron conveniente celebrar un referéndum para conocer si el pueblo estaba a favor o no de la independencia.
Sin embargo, los diputados serbo-ortodoxos, contrarios a la independencia, decidieron abandonar el parlamento en señal de protesta y boicotear el referéndum, que finalmente se llevó a cabo el 1 de marzo de 1992 con 60% de la población a favor de la independencia.
Los serbios de Bosnia, apoyados por el gobierno central de Belgrado, se opusieron con fuerza a esta consulta, poniendo bajo sitio a Sarajevo.
Las tropas de los serbios de Bosnia iniciaron inmediatamente un asedio de la capital de Bosnia, Sarajevo, que duraría 44 meses, ¡más de tres años!
Los 350,000 residentes de la ciudad lucharon por satisfacer sus necesidades básicas y al menos 10,000 murieron por los disparos y bombardeos de los serbios.
Se cortaron la electricidad, el agua, el suministro de comida y de medicamentos.
En mayo de 1992, los serbios de Bosnia controlaban dos tercios del país, fue así como se iniciaron los enfrentamientos entre musulmanes bosnios, serbios y croatas. Gran parte del país rápidamente quedó bajo la ocupación de los serbios de Bosnia.
El túnel de Sarajevo.
A mediados de 1992, la ONU mandó ayuda humanitaria a Sarajevo. En 1993 construyó un túnel desde las montañas, fuera del control serbio, hasta la ciudad, que permitía la entrada de alimentos, medicamentos y armas. Hoy en día es un museo.
Limpieza étnica.
Durante la guerra en Yugoslavia y después de su desintegración, tuvo lugar en el territorio de los Balcanes un proceso de limpieza étnica.
El objetivo era “limpiar” una zona forzando a los habitantes de una etnia a marcharse. Si se resistían eran torturados y matados.
La finalidad era crear estados 100% puros étnicamente. También se procedía a eliminar cada símbolo cultural y religioso: lugares de culto y cementerios fueron derribados sin piedad. El caso más famoso fue el genocidio de Srebrenica, donde unos 8,000 musulmanes fueron asesinados.
Fue Bill Clinton quien dio un paso al frente para ayudar a Bosnia cuando, tras el genocidio de Srebrenica, decidió enviar tropas de la OTAN que comenzaron a bombardear Serbia, esto fue fundamental para el fin de la guerra.
Con la independencia de Eslovenia, Croacia, Bosnia Herzegovina y Macedonia, la República Federal Socialista de Yugoslavia llegó oficialmente a su fin el 27 de abril de 1992.
Con la firma de los acuerdos de Dayton, en 1995, Bosnia quedó dividida en dos partes (la República Srpska con 49 % del territorio donde viven bosnios-serbios y la Federación Croata-musulmana (Federación de Bosnia y Herzegovina) con 51% del territorio, dividida en 10 cantones, donde conviven sin mezclarse bosnios musulmanes y bosnios croatas.
Si bien el tratado de Dayton permitió el fin de una guerra, no ayudó a favorecer una integración de las tres partes implicadas (Bosnia, Croacia y Serbia).
En 1998 surgió otro enfrentamiento, esta vez en la provincia de Kosovo, al sur de Serbia. El conflicto se desarrolló entre los rebeldes de etnia albanesa, que buscaban la independencia y las fuerzas armadas de Serbia.
Los combates terminaron en 1999 después de una campaña de bombardeos de la OTAN de 11 semanas. Unas 13,000 personas habían muerto y cientos de miles habían huido de sus hogares.
Kosovo declaró su independencia en 2008.
Como viste a lo largo de la sesión, la Guerra de los Balcanes fue un conflicto bélico que tuvo lugar entre 1992 y 1995. Muchos factores provocaron un movimiento militar a gran escala debido a la situación tras la desaparición de la URSS.
Tras la caída del socialismo soviético, el sentimiento de independencia de los distintos grupos étnicos se manifestó con fuerza; esto provocó una larga guerra civil entre serbios, bosnios, croatas y albaneses que condujeron a la desintegración de Yugoslavia en 2003.
En los cuatro años que duró el conflicto, murieron más de 130,000 personas (no hay cifras oficiales) y dos millones tuvieron que huir de sus casas.
La Corte Penal Internacional para la ex Yugoslavia, establecida en 1993, ha seguido procesando a los responsables de crímenes de guerra desde el final de los conflictos.
Ha procesado a 161 personas, condenado a 83 y absuelto a 19. Entre los condenados se encuentra el líder de los serbios de Bosnia, Radovan Karadzic, mientras que Slobodan Milosevic murió en prisión antes de ser juzgado.
La corte se disolvió el 31 de diciembre de 2017 y se ha establecido un tribunal separado para manejar las apelaciones restantes y otros asuntos.
Este tema lo podrás encontrar en tu libro de texto de la asignatura. También puedes consultar otras fuentes bibliográficas, digitales y audiovisuales que tengas a la mano.
Se te recomienda la lectura de Volver a Bosnia, de Juan Cruz Iguerabide, libro que narra la huida de un joven y su familia durante la guerra de Bosnia.
El Reto de Hoy:
Es momento de continuar con el reto que comenzaste al inicio de la semana:
El noticiero.
Recuerda que deberás organizarlo de manera clara y precisa. Podrás presentar y redactar la información que se vio en estas sesiones en forma de una entrevista. Esto le dará a tu noticiero un tinte más serio.
Por ejemplo, puedes buscar y entrevistar a un profesor que ofrezca su opinión sobre el tema a presentar; o exponer las distintas opiniones que hubo en la época estudiada.
Finalmente, no olvides redactar un buen titular para tu noticia. Tienes que crear impacto o misterio, siempre dependiendo del tipo de noticia.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario