Aprende en Casa III SEP: 12 de mayo TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 12 de mayo de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Miércoles 12 de mayo, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Proporcionalidad inversa VI
Aprendizaje esperado: Analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.
Énfasis: Interpretar y resolver problemas que se modelan con este tipo de variación, incluyendo fenómenos de las ciencias sociales.
¿Qué vamos a aprender?
En esta sesión estudiarás la resolución de problemas de proporcional inversa. Las situaciones que se presentan son de tipo social, algunas de las cuales se presentan en nuestra realidad.
¿Qué hacemos?
Lee cuidadosamente el enunciado del siguiente problema, analiza la información que se presenta y la pregunta que se plantea.
El problema se trata de la relación inversa entre llamadas telefónicas y distancia entre ciudades. Es oportuno aclarar que, aunque este problema es de carácter social, podría existir en algún momento dado.
Las llamadas telefonicas
En cierta región, el número promedio de llamadas telefónicas entre dos ciudades es directamente proporcional a cada una de sus poblaciones, e inversamente proporcional al cuadrado de la distancia entre ellas. La distancia entre la ciudad de Crestview y Cedar es de 40.2 kilómetros. Los registros telefónicos indican un promedio de 200 llamadas diarias.
¿Cuál es el promedio de llamadas diarias de la ciudad de Crestview a Palmas, una ciudad situada a 160.3 kilómetros de Crestview?
Antes de resolver el problema, identifica algunas propiedades de la variación proporcional inversa. Para ello analizara la siguiente tabla, en donde los números no refieren a ninguna situación en particular, sólo son dos variables relacionadas a las que llamamos “A” y “B”.

¿Qué pasa con los valores de la variable “A”?, ¿aumentan o disminuyen?
Van aumentando desde uno hasta 6.
¿Qué sucede con el valor de la variable “B”?, ¿aumenta o disminuye?
La variable “B” disminuye de 60 hasta 10.
De lo anterior podemos enunciar una de las propiedades de proporcionalidad inversa.
Si llamamos a los valores de la columna “A”, la primera magnitud, y los de la columna “B” la segunda magnitud, entonces decimos que en una relación de proporcionalidad inversa entre dos magnitudes, si aumentan los valores de la primera magnitud, los valores de la segunda magnitud disminuyen en la misma proporción, o viceversa, si disminuyen los valores de la primera magnitud, los de la segunda aumentan también en la misma proporción.
Continúa analizando la tabla para identificar otra característica de la proporcionalidad inversa. ¿Qué sucede si multiplicamos cada uno de los valores de la columna “A” con el valor correspondiente en la columna “B”?

El producto es constante. En este caso se obtuvo como resultado 60. Este valor, producto de cada magnitud de la columna “A” con la magnitud correspondiente en la columna “B”, se denomina constante de proporcionalidad inversa y se representa con la letra “k”.
De esta manera podemos enunciar otra propiedad de la variación proporcional inversa, en una relación de proporcionalidad inversa, el producto de las cantidades de la primera magnitud por su correspondiente de la segunda magnitud es constante.
Ahora bien, a los valores de la primera y segunda columna de la tabla podemos llamarlos “x” y “y”, en lugar de “A” y “B”, esto con la finalidad de relacionarlos más adelante con los ejes coordenados. Entonces si denominamos las magnitudes “x” y “y”, y a la constante de proporcionalidad “k”, podemos establecer la relación de las magnitudes con la constante y observamos que se relacionan de la siguiente forma

Una vez teniendo la fórmula de la constante, podemos despejar cada una de las variables. De ahí tenemos que.

Estas tres formas de la misma relación te pueden ayudar a resolver diversas situaciones de proporcionalidad inversa. Por ejemplo.
Supón que quieres completar los valores de la magnitud “y”, de la siguiente tabla, sabiendo que se trata de una proporcionalidad inversa. Se tienen algunos valores de la magnitud “x” y únicamente uno de los valores de la magnitud “y”, como se observa. ¿Cómo se utiliza la constante de proporcionalidad para completar la tabla?

Como la “k” es igual “x” por “y”, entonces se puede obtener el valor de “k” multiplicando los valores conocidos correspondientes de “x” y de “y”.

Después, como “y” es igual a “k” entre “x”, y “k” es igual a 180, entonces “y” es igual a 180 entre cada uno de los valores de “x”. Se presentan dos valores de “y”, el primero resulta de dividir 180 entre uno y el segundo, de dividir 180 entre 2.
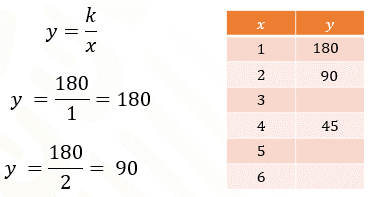
Te invitamos a encontrar los demás valores de la tabla.
Regresando a la situación problemática planteada al principio. En el problema se dice que las llamadas y el cuadrado de la distancia, en kilómetros, se relacionan de manera inversamente proporcional.
Una manera de iniciar la resolución del problema es realizando una tabla donde se coloquen las ciudades involucradas en la primera columna, la distancia entre ciudades en la segunda columna, en la tercera columna el cuadrado de las distancias entre ciudades, y finalmente, en la última columna el número de llamadas. Como es precisamente el promedio de llamadas que se realizan entre la ciudad de Crestview y la ciudad de Palmas el que no se conoce, se escribe la letra “y”.

Al tratarse de una situación de proporcionalidad inversa, puedes obtener la constante de proporcionalidad inversa. En este caso llamemos “x” al cuadrado de la distancia y “y” al número de llamadas “y”. La constante de proporcionalidad se obtiene multiplicando los valores correspondientes conocidos, en este caso 1 616 x 200 lo que resulta 323,200.

Anteriormente viste que en la proporcionalidad inversa “y” es igual a “k” entre “x”. Entonces sustituye en la fórmula la constante “k” por 323 200 y “x” por 25 696, y al hacer la división se obtiene el resultado para “y”, que es 12.5, que se puede redondear a 13, y entonces se puede decir que entre la ciudad de Crestview y la ciudad de Palmas, se realizan aproximadamente 13 llamadas diariamente.

Analiza en una tabla de datos otra propiedad que pertenece a la variación proporcional inversa.

Las cantidades que se presentan en la tabla varían de manera inversamente proporcional. Una manera de comprobar esta afirmación, incluso mentalmente, es multiplicar los valores de la primera magnitud con los correspondientes de la segunda magnitud, en este caso todas las multiplicaciones dan por resultado 60, que es la constante de proporcionalidad de esta situación.
Otra propiedad de la variación proporcional inversa es que la razón entre dos cantidades de la primera magnitud es igual a la razón inversa de las cantidades correspondientes de la otra magnitud. Por ejemplo, en la primera tabla si multiplicas 1 por 3 resulta 3 en los valores de “x”, como lo señala la flecha en azul, y si dividimos 60 entre 3, como lo señala la flecha en rojo, el resultado es 20.
Ahora en la segunda tabla si se divide 5 entre 5, resulta 1, como se muestra con la flecha negra, y si se multiplica 12 por 5 el resultado es 60, como se puede notar, 12 y 60, son los valores de “y” que corresponden inversamente proporcionales a 5 y 1 como valores de “x”.
Ahora analiza otra situación que se presenta también como un fenómeno social. Se trata de lo siguiente:
Cierto día en una clínica sólo había tres médicos para atender a 56 pacientes. El director de la clínica decide repartirlos proporcionalmente, de tal forma que a mayor antigüedad del médico en la clínica fuera menor el número de pacientes que le tocaría atender. ¿Cuántos pacientes le toca atender a cada médico si tienen 2, 4 y 8 años de antigüedad?
De esta manera, quien lleva trabajando 2 años atenderá más pacientes que aquel que lleva 4 u 8 años trabajando en esa clínica.
Lo que se trata es de repartir 56 de forma inversamente proporcional a los números 2, 4 y 8, y esto equivale a repartir el número 56 de forma directamente proporcional a los números un medio, un cuarto y un octavo, como veras a continuación.
Resolver el problema equivale dividir el número 56 en partes inversamente proporcionales a los números 2, 4 y 8, pero al mismo tiempo esto equivale a repartir el número 56 en partes proporcionales a un medio, un cuarto y un octavo.
Para realizar esto último, primero se obtienen fracciones comunes a un medio, un cuarto y un octavo. En este caso se decidio que el denominador común sea 8. Entonces convirtiendo las fracciones mencionadas a sus equivalentes con denominador 8 se obtienen las fracciones.

Una vez teniendo estas fracciones, repartiremos al número 56 en partes directamente proporcionales a 4/8, 2/8 y 1/8. El procedimiento para obtener proporciones directas nos permite plantear entonces una regla de tres simple, para conocer cuánto le toca al número 4/8, que es la fracción que le corresponde al médico de 2 años de antigüedad. En esta proporción el 56 es el número de pacientes, estableciendo la proporción tenemos que 7/8 es a 56 como 4/8 es a “x”.

Obtenemos 32, es decir, que al médico con dos años de antigüedad le corresponde atender a 32 pacientes.
Inicialmente, descontextualizamos el problema, es decir, resolvimos la proporción sólo con números con la finalidad de entender el procedimiento. Ahora daremos la solución al problema respondiendo la pregunta ¿cuántos pacientes les tocan a tres médicos que tienen 2, 4 y 8 años de antigüedad?
Con el procedimiento anterior obtuvimos que el médico con 2 años de antigüedad debe atender 32 pacientes. Entonces a partir de este dato podemos afirmar que: el médico con 4 años de antigüedad debe atender 16 pacientes, ya que tiene el doble de años de antigüedad que el médico anterior, por lo que le corresponde atender la mitad de los pacientes que al primer médico. Por otra parte, el médico con 8 años de antigüedad, debe atender 8 pacientes, ¿por qué afirmamos esto?

Una manera de afirmarlo es porque tiene el cuádruplo de años de antigüedad que el médico con 2 años de antigüedad, por lo tanto, le corresponde atender la cuarta parte de pacientes que, a dicho médico, esto es 32 / 4 = 8 pacientes.
Revisa un problema más donde los valores de las magnitudes varían de forma inversamente proporcional.
Un campamento de la Cruz Roja que alimenta a 1 800 refugiados tiene víveres para 3 meses si se distribuyen raciones de 800 gramos por día.
¿Cuántos gramos contendrían las raciones si aumenta el número de refugiados a 2 100, 2 400, 2 700 y 3 000 para el mismo periodo de tiempo?
La siguiente gráfica muestra una parte de la curva que relaciona el número de refugiados en el eje “x”, con la cantidad de gramos por ración diaria en el eje “y”.

Una manera de iniciar a dar respuesta a la pregunta del problema es a través del análisis de la gráfica. Si analizas la gráfica puedes ver que hay cantidades que es posible ubicar con precisión y otras solamente se pueden ubicar de manera aproximada. Por ejemplo, la coordenada (2,400,600) puede observarse claramente e indica que si hay 2 400 refugiados las raciones diarias serían de 600 gramos de víveres. Sin embargo, esto no ocurre con otras cantidades.
Continuando con el análisis de la gráfica, observamos que la cantidad de gramos por ración diaria de los víveres correspondiente a 2,100 refugiados, sólo pueden obtenerse de manera aproximada, de acuerdo con la escala a la que se trazaron las unidades en cada uno de los ejes. Teniendo esto en cuenta, podemos afirmar que al ser 2 100 refugiados entonces las raciones diarias serán de un poco menos de 700 gramos.

Entonces, ¿qué hacer para encontrar las cantidades exactas en gramos de víveres que corresponden a las otras cantidades de refugiados?
Una manera de calcular las cantidades que faltan para contestar completamente la pregunta planteada en el problema es recordar que, en la proporcionalidad inversa, la constante es el resultado de multiplicar los valores de una magnitud por los valores correspondientes de la otra, en este caso los valores de la cantidad de refugiados por la de la cantidad de gramos de la ración diaria de víveres.
También podemos organizar los datos de la tabla, donde en la primera columna anotaremos el número de refugiados y en la segunda los gramos de cada ración.

De las cantidades correspondientes que se tienen podemos calcular la constante de proporcionalidad de esta situación, ya que la constante es el producto de cantidades que corresponden.

Se puede decir que la constante, es decir, “k” es igual a 1 440 000.
Ahora utiliza la expresión “y” igual a “k” entre “x”, donde se sustituirán los valores conocidos, es decir, el valor de “k” y la cantidad de refugiados que ya conoces.
De esta forma, para 2 100 refugiados tenemos:
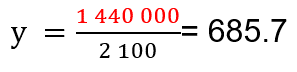
Para 2 700 refugiados tenemos:

Y para 3 000 refugiados:

Ahora puedes terminar de dar respuesta al problema porque encontraste que a 2 100 refugiados corresponden 685.7 gramos por ración diaria de víveres; a 2 700 refugiados le tocan 533.3 gramos por ración diaria de víveres, y a 3 000 refugiados le corresponden 480 gramos por ración diaria de víveres.
Como recordarás, este problema se resolvió recurriendo en primer lugar a la gráfica, de donde se extrajeron datos que se organizaron en una tabla. Esto no significa que, si se tuviera sólo el enunciado del problema, éste no se pueda resolver. Una forma de hacerlo es analizar el enunciado. De ahí se puede afirmar que este problema es de proporcionalidad inversa ya que, si aumenta el número de refugiados, disminuirá la cantidad de gramos de víveres que les corresponden diariamente. Con este análisis y recordando que una propiedad de la proporcionalidad inversa es que la constante se obtiene multiplicando los valores de ambas magnitudes o variables que se corresponden, en este caso, multiplicando el número de refugiados por el número de gramos de víveres, se obtiene la constante, que en esta situación es “k” igual a 1 440 000.

Luego se utiliza la expresión “y” igual a “k” entre “x” para obtener las cantidades de los gramos diarios de víveres solicitadas. A continuación, se muestran las que corresponden a 2 100 y 2 400 refugiados.

Otra forma de resolver el problema es establecer una proporción inversa. Para entender cómo se formula una proporción de este tipo, primero se plantea como si fuera una proporción directa, donde en la primera cantidad aumenta, es decir, el número de refugiados de 1 800 a 2 100 y por lo tanto la otra cantidad también aumenta, es decir, la cantidad de víveres de 800 a “x”.
Sin embargo, como no se trata de una proporcionalidad directa, sino inversa, mantenemos la primera razón como la planteamos e invertimos la segunda razón.

Luego, sabiendo que, en una proporción, los productos cruzados son iguales, es decir que 1 800 por 800 es igual a 2 100 por “x”, formamos la ecuación 2100 “x” es igual a 1800 por 800. Al resolver dicha ecuación obtenemos la cantidad gramos diarios de víveres que corresponde a 2 100 refugiados. Realizando el mismo procedimiento se pueden obtener la cantidad de víveres para las otras cantidades de refugiados.

La forma anterior como se resolvió el problema, se basa en la propiedad que dice:
Dadas dos magnitudes inversamente proporcionales, la razón entre dos cantidades de la primera magnitud es igual a la razón inversa de las cantidades correspondientes a la otra.

A continuación, realizarás algunas observaciones en relación con la gráfica, recuerda que otra propiedad de la variación proporcional inversa es que su grafica es una curva. Si continuaras el trazo de la gráfica con los valores para el número de refugiados y la cantidad de gramos de víveres, la gráfica continuaría como la que se muestra.

Este tipo de grafica recibe el nombre de hipérbola y es característica de las variaciones proporcionales inversas.
Si imaginas el plano cartesiano mucho más grande, se podría pensar que la curva cruzará a los ejes “x” y “y”, sin embargo, una propiedad de la hipérbola es precisamente que por más valores que se continúen asignando al eje “x” y se obtengan los correspondientes de “y”, la curva se irá acercando más y más a los ejes, pero nunca los tocará. Los ejes “x” y “y” son las asíntotas de la hipérbola de esta situación.
Las asíntotas son las dos líneas rectas a las que se aproxima cada vez más la hipérbola, pero no se tocan. Este tipo de curva, la hipérbola, es una propiedad más de la variación proporcional inversa.

Para comprender por qué la hipérbola no puede tocar los ejes “x” y “y” es preciso recordar que en la proporcionalidad inversa “y” es igual a “k” entre “x”, así como “x” es igual a “k” entre “y”.
Dicho esto, para que algún punto de la curva tocara al eje “y”, se necesitaría que el valor de “x” fuera cero, entonces se dividiría “k” entre cero. Por otro lado, como “k” puede tomar cualquier valor, en este caso consideramos a “k” igual a 45, a 1 000 y a 1.
Entonces para encontrar el valor de “y” cuando “k” es igual a 45, se divide 45 entre cero. Resuelve esta división. Puedes hacer uso de tu calculadora.

¿Qué obtuviste? Bien. El mensaje que te envía la calculadora significa que esa división no está definida.
¿Qué obtienes si divides 1 000 entre cero y 1 entre cero?
Encuentras el mismo resultado que para 45 entre cero. Esto quiere decir que no existe un punto de la hipérbola en el cual la coordenada en “x” sea igual a cero.
Ahora, ¿qué pasaría si se desea encontrar la coordenada donde la hipérbola cruzara el eje “x”, es decir cuando “y” es igual a cero? Para ello puedes utilizar la expresión “x” igual a “k” entre “y” y dar los mismos u otros valores para “k” y dividirlos entre cero, que es lo que debe valer “y”.
Sucede lo mismo que para cuando “x” es igual cero.
El Reto de Hoy:
Para finalizar, contesta ¿cuál es el significado en este problema que “y” sea igual a cero o que “x” sea igual a cero? Y compártelo a la distancia con tus compañeras, compañeros y docentes.
No olvides anotar tus dudas acerca del tema y consultarlas con tu docente a distancia.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Entre revisión y revisión, la campaña queda mejor
Aprendizaje esperado: Diseña una campaña escolar para proponer soluciones a un problema de la escuela.
Énfasis: Revisar textos para una campaña.
¿Qué vamos a aprender?
El día de hoy revisarás textos para una campaña. Revisarás diversos textos multimodales, como carteles, infografías, posts de redes sociales, donde también se incluyen audio y video; y que puedes usar para el diseño y realización de tu campaña escolar.
¿Qué hacemos?
En la escuela y aulas es común que se vivan de manera cotidiana situaciones problemáticas, pues convivir y, sobre todo, ponerse de acuerdo, no siempre resulta fácil. Sin embargo, para lograr una sana convivencia escolar es indispensable la resolución de algunas situaciones y, en varias ocasiones, las soluciones se encuentran con un cambio de actitud.
¿Qué opinas?, ¿los problemas que se viven dentro de las escuelas son fáciles de resolver?, ¿qué estrategias se han utilizado dentro de tu escuela para resolverlos?
En un problema común como el tiradero de basura que queda en el salón al final de la jornada de clases. Y quizá una manera de crear conciencia y un cambio de actitud ante el problema es a partir de una campaña escolar.
Seguramente durante el trayecto de tu vida escolar has visto o has participado en la realización de campañas. Y quizá, las campañas que más recuerdas son aquellas cuyos textos bien escritos y creativos lograron impactar a la comunidad escolar.
Por ejemplo, este cartel se usó en esta campaña.

Vamos a usar este ejemplo para hacer nuestro primer reto. En tu cuaderno ve respondiendo las preguntas que se te van a ir planteando.
¿Qué mensaje transmite la imagen?, ¿consideras que coincide con el texto, se complementa o se contradice?, ¿es claro el mensaje del texto?
El mensaje de la imagen no queda muy claro, pues el ver un cesto de basura con papeles a su alrededor no indica que hay que ponerlos dentro de éste, por lo que la imagen no coincide mucho con el texto.
¿No crees que el enunciado que se está usando parece más una orden que un lema que va más acorde para convencer?
Se visualiza primero en los signos de exclamación y, sobre todo, en el uso excesivo de mayúsculas.
Una campaña pro limpieza y conservación de aulas y espacios escolares funcionaría muy bien, siempre y cuando el diseño y textos impacten, sean breves, claros y persuasivos, y que lleguen a toda la comunidad escolar.
Se podrían utilizar herramientas que combinan lo visual, lo escrito e, incluso, en otras ocasiones, audios o videos. ¿Qué otros aspectos se podrían utilizar?
Esas herramientas que se aplican en los materiales visuales de una campaña escolar, como el cartel, un tríptico, un audio, video, entre otros, hacen que éstos sean textos o materiales audiovisuales multimodales.

Con el uso de las redes sociales, se han popularizado, con las nuevas tecnologías se han desarrollado nuevas, efectivas y masivas formas de comunicación y, por lo tanto, nuevos modos de hacer llegar los mensajes. Para explicarlo de una manera más sencilla: cuando se combina más de un modo de comunicación, estamos hablando de textos multimodales.

Las infografías, los carteles y los videos son algunos de los textos multimodales que se pueden elaborar para la realización de una campaña escolar.
Utiliza el cartel del inicio de la sesión para ir revisando los elementos que están dificultando su comprensión.
Obsérvalo de nuevo, para ir analizando cómo hacer este texto multimodal. Te presentaremos unas preguntas que deberás ir contestando en tu cuaderno.

Recuerda que un texto multimodal combina al menos dos formas diferentes de lenguaje. En el cartel se combina el lenguaje escrito y el visual. No olvides que esta combinación no puede visualizarse por separado o de manera fragmentada. La intención en este tipo de textos es que estos dos lenguajes, cada uno distinto del otro, se conviertan en un solo texto que a primer golpe de vista logre captar la atención y casi de inmediato haga llegar el mensaje propuesto. ¿En este cartel se logran complementar estos dos lenguajes?
En ese primer golpe de vista, evidentemente no. La imagen debe complementar el texto y el texto debe complementar la imagen para que ambos logren un solo texto.
Piensa en imágenes y textos que se complementen. Antes, recuerda que el objetivo de esta campaña es que los salones queden sin basura al salir de clases.
Observa estas tres imágenes y estos dos enunciados. ¿Cuál imagen y enunciado consideras que se complementan mejor?, ¿por qué? No olvides ir tomando notas en tu cuaderno.

Recuerda que, para hacer una correcta selección de los elementos que deben integrar al cartel, debes considerar el objetivo específico perseguido.
De los dos enunciados, ¿cuál consideras que pueda convencer o llamar más la atención?, ¿por qué? Ahora, ¿qué imagen consideras pueda lograr un buen impacto en el cartel?, ¿por qué?
El primer enunciado es imperativo. Y tal vez una orden no logre convencer mucho a un cambio de actitud. En cambio, el segundo es una afirmación que de manera implícita indica que hay que dejar limpio.
En cuanto a las imágenes, en la primera se observa el ícono de prohibición; pero no es una buena forma de convencer, y más al final de un día en el que, por lo general, las y los alumnos ya están cansados. La segunda imagen muestra a un personaje tirando la basura en el cesto, pero es una señalización que puede ser utilizada en cualquier contexto, incluido el escolar, pero en este caso, un cartel de campaña escolar debe usar imágenes más cercanas a las y los alumnos.
A partir de esto, la imagen tres nos indica, sin ser impositiva, un salón limpio, que es como debe quedar al final de la jornada. Entonces estos dos elementos son los que podrían quedar en este cartel. ¿Qué piensas tu?

Ahora sí, vas a producir un cartel con una herramienta digital que te permitirá que este texto multimodal pueda estar a la vista dentro del salón de clases, y también distribuido masivamente a través de redes sociales.
Después de haber seleccionado los componentes de este texto multimodal: el texto visual, la imagen; y el texto escrito, el lema, vas a usar el programa para elaborar diapositivas electrónicas. Éste te permite realizar diapositivas para una presentación, diseñar infografías y carteles.
Cuando abres el programa para realizar diapositivas, se observa que el diseño de la hoja está en horizontal, y para hacer un cartel, por lo general, se usa un diseño de hoja en vertical. Para saber como realizar esta modificación, observa el siguiente video:
- VIDEO 01. GRABACIÓN DE PANTALLA.
Ahora les mostraré cómo pueden insertar texto multimedia.
- ¿Cómo hacer una presentación en PowerPoint?
Lengua Materna. Español, Primer grado, Bloque 3
Del minuto 02:18 al 04:19
Ahora que ya, puedes empezar a distribuir los dos elementos para ponerlos en el cartel.

¿Consideras que las dimensiones de la imagen y el texto logran un buen equilibrio visual?
El tamaño de la imagen no está muy equilibrado visualmente con el texto, ¿qué podrías hacer para equilibrar visualmente estos elementos?
Puede hacerse más grande la imagen y quizá darle un formato diferente al borde para suavizar sus esquinas. Observa el siguiente video para saber cómo editar la imagen.
- VIDEO 02. GRABACIÓN DE PANTALLA.
También se puede agregar audio y video, observa el siguiente video para saber cómo.
- ¿Cómo hacer una presentación en PowerPoint?
Lengua Materna. Español, Primer grado, Bloque 3
Del minuto 04:54 al 05:24
Ahora debes buscar un tipo de letra que haga resaltar el texto. Así como los colores e imágenes transmiten emociones y sensaciones, la tipografía, es decir, el tipo de letra, también lo hace ejerciendo influencia en el mensaje que queremos comunicar. Por lo tanto, es indispensable considerar el objetivo que perseguimos para así hacer una selección bien pensada de la tipografía y lo que queremos proyectar con el texto.
Para que quede claro cómo hacer una selección precisa de la tipografía, realiza el siguiente reto.
Primero observa con atención el mismo texto con tres diferentes tipos de letra. Contesta en tu cuaderno ¿qué impresión te transmite cada tipografía?, ¿cuál consideras que sea la más apropiada para este texto multimodal? y ¿por qué?

Cada tipo de letra transmite diferentes sensaciones. La que utiliza la tipografía Impact aporta una sensación de amontonamiento porque las letras están muy juntas y esa falta de espacio no proyecta el mensaje de orden y limpieza que se intenta comunicar.
La segunda es una tipografía, “bonita”, que se podría utilizar en un poema, por ejemplo, pero para los fines de este mensaje, no llama mucho la atención. En cambio, la tercera tipografía, Arial, da la sensación de claridad, pues la separación entre cada letra hace que la pueda leer con más facilidad, y resulta asertiva al mensaje de orden y limpieza que se quiere proyectar.
Anota en tu cuaderno todas las impresiones que te causa cada una de las tipografías para que vayas encontrando la selección más idónea para el propósito de este texto multimodal.
Ahora lo que falta es distribuir el texto a lo largo del cartel. Ve contestando en tu cuaderno las respuestas a las preguntas planteadas. Piensa: ¿cómo podrías distribuir el texto para que se pueda complementar con la imagen?

En una opción está el texto centrado en la parte superior de la imagen, y en la otra se encuentra el texto dividido en los extremos de la imagen. Recuerda que, en un texto multimodal, como este cartel, se deben complementar los dos elementos para volverse uno. Por lo tanto, ¿cuál opción consideras la más apropiada?
En la opción donde el texto se encuentra en la parte superior de la imagen hace que nuestra vista se enfoque primero al texto y luego a la imagen, por lo que nos hace ver por separado estos dos elementos.

En la otra opción, al estar dividido el texto en los extremos de la imagen, engloba ambos elementos al primer golpe de vista y se ve como un solo texto. Así, en este texto multimodal, los dos elementos se pueden observar como un solo texto. Yo creo que pudieron obtener la misma conclusión.
Ahora ya tienes tu cartel, se puede colocar dentro de los salones o lo puedes distribuir a través de las redes sociales como parte de la campaña escolar.
Después de haber revisado algunos textos multimodales que pueden formar parte de una campaña escolar, ya puedes seleccionar y, sobre todo, realizar tus propios textos multimodales.
Como has visto, las campañas escolares constan de diferentes pasos para su planeación y su desarrollo, y lo que hoy has aprendido es cómo los textos multimodales pueden ser útiles en el desarrollo y presentación de éstas.
Te recomendamos acudir a tus libros de texto y buscar el aprendizaje esperado. Ahí podrás encontrar más ejemplos de estos textos para revisar. También puedes buscar en fuentes confiables de internet para reforzar tus conocimientos.
Para tener una idea más clara de qué fuentes puedes consultar para tener más ejemplos con textos multimodales, y así poder enriquecer tus ideas para las campañas escolares. Observa las siguientes infografías, que es un recurso más que puedes utilizar.



Cada una tiene su propia lógica y da una idea clara del sector al que se dirigen y la finalidad de cada uno. Las tres infografías pertenecen a la plataforma Conagua, y están dirigidas al público en general, son coloridas en su diseño y en la elección de sus fuentes. Además de valerse del recurso de personajes afines al imaginario colectivo.
Como puedes ver, cumplen con el fin de informar sobre las medidas del cuidado del agua valiéndose de diferentes medios. Además, son para toda la población
El Reto de Hoy:
Tu reto será poner manos a la obra y empezar a producir sus propios textos. Quizá ahora pueden hacer textos para una campaña que promueva el buen uso del agua y distribuirlos por redes sociales a sus compañeros de la escuela.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Diferencias entre equidad e igualdad
Aprendizaje esperado: Reconoce que la igualdad ante la ley es condición para la construcción de una sociedad justa y equitativa.
Énfasis: Reconocer la diferencia entre equidad e igualdad.
¿Qué vamos a aprender?
Conocerás la diferencia entre las nociones de equidad e igualdad, ya que son muy parecidas y, en muchas ocasiones, son tomadas como palabras sinónimas, cuando no lo son, debido a que cada una se ejerce de diferente manera. Para ello, analizarás algunas ideas y ejemplos que te permitan identificar la diferencia y reflexionar si estas llevando a cabo esos valores en la sociedad.
Estos dos valores tienen mucha importancia en nuestra manera de conducirnos y en los principios éticos que compartimos en la sociedad en que vivimos. Más en estos tiempos de contingencia sanitaria, donde compartirnos el autocuidado y cuidado de las demás personas como compromiso colectivo, bajo el reconocimiento de que todas las personas valemos por igual en dignidad y derechos.
Como has venido analizando en sesiones anteriores, la igualdad es un valor que nos otorga los mismos derechos a todas y todos, independientemente de las circunstancias sociales, o económicas en la que nos encontremos. No se puede pensar en igualdad sin asumir que somos diversos, lo cual implica valorar las diferencias como un aspecto que nos enriquece como sociedad y que debemos respetar siempre.
¿Qué hacemos?
Para iniciar, observa las siguientes imágenes.

Libro para el Alumno, 1° Telesecundaria, Formación cívica y ética, p. 70
http://telesecundaria.sep.gob.mx/Content/Repositorio/Alumno/Libros/1/FCYE/TS-LPA-FCYE-1/#p=72
En la primera imagen se encuentran tres personas jugando cartas, un niño y dos mujeres, los tres con diferentes vestimentas y color de piel.

Libro para el Alumno. 2° Telesecundaria, Formación cívica y ética, p. 46
http://telesecundaria.sep.gob.mx/Content/Repositorio/Alumno/Libros/2/FCyE/TS-LPA-FCYE-2-V2-BAJA/#p=48
En la segunda imagen, todas las personas que se encuentran pertenecen a distintas clases sociales y diferentes costumbres.
¿Qué pudiste identificar en las imágenes?, ¿qué significa para ti ser iguales?
¿Alguna vez has sentido que alguien te ha tratado de manera diferente por algún rasgo o cualidad?
Debemos saber que todas y todos tenemos el mismo valor como personas y, por lo tanto, debemos acceder a las mismas oportunidades para desarrollarnos integralmente, sin que seamos prejuzgados.
Para hablar un poco más al respecto, observa el siguiente video, para recordar a qué nos referimos con “igualdad ante la ley”.
- El derecho a la igualdad
Formación Cívica y Ética, Primer grado, bloque 1
Del minuto 1:15 al 1:55
https://www.youtube.com/watch?v=nEHaHyRBqyc
Es interesante es saber a qué se refiere y distinguir la igualdad ante la ley y poder ejercer ese derecho en la sociedad. Decir que somos iguales no significa que todas y todos somos idénticos o que tenemos los mismos gustos, sino que tenemos el mismo valor como personas y, por lo tanto, debemos tener iguales oportunidades para desarrollarnos integralmente. Por ejemplo: Podemos observar una caja de colores; todos son de diferentes tonalidades, algunos muy parecidos, pero en esa diferencia cada color cumple su función cuando con ellos hacemos un hermoso y colorido dibujo.

FCYE. 1ER GRADO. P. 178
Para entender mejor, es necesario revisar la definición de igualdad.
Es un principio muy importante para proteger y defender la dignidad humana. A partir de él, se deben elaborar leyes en nuestro país que aseguren a las personas el goce y ejercicio de sus derechos fundamentales.
En México, el Artículo 1º de la Constitución Política de los Estados Unidos Mexicanos protege el derecho a la igualdad y el respeto a las diferencias cuando menciona:
“Queda prohibida toda discriminación motivada por origen étnico o nacional, el género, la edad, las discapacidades, la condición social, las condiciones de salud, la religión, las opiniones, las preferencias sexuales, el estado civil o cualquier otra que atente contra la dignidad humana y tenga por objeto anular o menoscabar los derechos y libertades de las personas”
Es necesario conocer nuestras leyes y su contenido. Para seguir reflexionando sobre el tema, Para ello, observa el siguiente video.
- La igualdad, nuestro desafío
Formación Cívica y ética, Tercer grado, Bloque 2
Del minuto 1:50 al 2:07
https://www.youtube.com/watch?v=t7iceLlHMj4&t=113s
¿Qué diferencias hay entre la igualdad y la equidad?, ¿ambos son derechos?
Es normal llegarlos a confundir. Para que todo quede claro hablaremos de la equidad, la cual es una cualidad, un valor que promueve en dar a cada persona lo que necesita de acuerdo a sus circunstancias.
Equidad, alude a la distribución de recursos, oportunidades y poder al interior de una sociedad. Podemos decir que la equidad se da cuando las niñas, los niños, las y los adolescentes y las personas adultas:
- Reciben los beneficios del desarrollo y tienen acceso a bienes y servicios sin discriminación o exclusión.
- Eligen su forma de vivir y disponen de oportunidades para ello.
- Reciben atención a sus necesidades, tomando en cuenta sus diferencias. Este punto es importante para entender que la equidad no es dar a todos lo mismo, sino a cada quien lo que necesita.
- Tienen un poder equilibrado al interior de la sociedad y, por tanto, la posibilidad de ejercer derechos igual que otros sectores. Esto implica combatir desequilibrios, algunos de ellos históricos (como en el caso de las niñas y las mujeres).
Hasta el momento sabes sobre la Igualdad y la Equidad, que son valores éticos, que no son palabras sinónimas, y ya conoces sus definiciones. Ahora: ¿Cómo puedes saber si tu derecho a la igualdad y a la equidad no está siendo violentado?
Recuerda que el derecho a la igualdad no está a merced de la buena voluntad de las personas, sino que está amparado por las normas jurídicas. Para ampliar más los conocimientos, observa el siguiente video donde la maestra Gabriela Noya, de Oaxaca explica qué son las normas jurídicas.
- VIDEO 1. MAESTRA GABRIELA NOYA
Las normas jurídicas son una clasificación de las garantías individuales y una de ellas es la de igualdad, la cual implica la eliminación de toda distinción entre individuos, como nacionalidad, religión, posición económica o social, entre otras. Y se encuentran en el artículo 1° de nuestra Constitución, así como también en el:
- Artículo 2. El cual prohíbe la esclavitud y
- El artículo 4. Que establece la libertad jurídica entre hombres y mujeres y dicta que toda persona tiene derecho a la protección de la salud.
Por otro lado, la Ley General para La Igualdad Entre Mujeres y Hombres menciona que tenemos que regular y garantizar la Igualdad de oportunidades y de trato entre mujeres y hombres, por ejemplo: En la impartición de justicia, todas las personas tenemos derecho a recibir un trato digno en las cuestiones judiciales, bajo los principios de legalidad e imparcialidad. También aquí podemos considerar el principio de equidad, que implica no favorecer a alguien en detrimento de otra.
La equidad de género significa distribuir de forma justa los beneficios, el poder, los recursos y las responsabilidades entre las mujeres y los hombres; para ello se necesitan reconocer las posiciones de desigualdad y subordinación que han vivido las mujeres a lo largo de la historia en comparación con los hombres, para así, identificar las inequidades de género.
Un ejemplo de equidad de género es garantizar que mujeres y hombres tengan las mismas oportunidades para acceder a la escuela, en el caso de las y los adolescentes a la educación secundaria, es decir, que no sólo debe garantizarse el derecho a la educación, sino considerar las diferencias de género para garantizar que las mujeres, además de ingresar a la escuela, permanezcan y puedan decidir, con libertad, lo que deseen estudiar.
Podemos decir que para lograr la igualdad y equidad de género se debe garantizar, por un lado, la igualdad de trato, lo cual se aspira a conseguir con el principio de igualdad ante la ley; y por otro lado, es necesario señalar que como sociedad aún nos falta consolidar la igualdad de oportunidades para mujeres y hombres.
Después de esta comparación, te invitamos a observar el siguiente video para concretar lo que has aprendido.
- El derecho a la igualdad
Formación Cívica y Ética, Primer grado, Bloque 1
Del minuto 1:56 al 3:13
https://www.youtube.com/watch?v=nEHaHyRBqyc&t=15s
Recapitulando:
Muchas veces podemos llegar a confundir la igualdad con la equidad, ya que las dos defienden que todas las personas tengan acceso a las mismas oportunidades. Contar con las leyes que reconocen que todas las personas son merecedoras de respeto, pero al mismo tiempo que son diferentes y tienen necesidades particulares, permite reconocer el principio de igualdad ante la ley, así como, marca la diferencia entre los valores de igualdad y equidad.
Existe una línea muy delgada entre la igualdad y la equidad. Una forma de definirlas como dos componentes distintos ante la ley; es que la igualdad significa reconocer a todas las personas con los mismos derechos y obligaciones sin importar su género, raza, color de piel o clase social. Por lo consiguiente la equidad es que cada persona o grupo reciba lo que necesita y merece de acuerdo a sus circunstancias, para que pueda ejercer sus derechos. Que reciban los beneficios del desarrollo y servicios.
Para mayor información sobre el tema, consulta tu libro de texto e identifica qué otros ejemplos y acciones pueden favorecer la igualdad y la equidad en nuestra sociedad.
El Reto de Hoy:
Observa las siguientes imágenes, las cuales están numeradas del uno al seis.

- En la imagen uno hay dos personas adultas y un niño, cada quien está parado en un banco que tiene la misma altura, pero el niño queda más abajo que las personas adultas.
- La imagen dos es una balanza equilibrada en forma de planeta tierra.
- La imagen tres muestra unas manos que, unidas, forman un circulo.
- En la imagen cuatro aparece un árbol con manos de diferente color, donde el tronco es la imagen de una señora solicitando apoyo.
- La imagen cinco, son dos mujeres indígenas que están votando.
- La imagen seis, son las dos personas adultas y el niño, ahora parados en un banco de diferentes tamaños, donde el niño queda a la misma altura que las personas adultas.
Ahora, elabora una tabla con dos columnas, en una anota como título “igualdad” y en la otra “equidad”, la tabla tendrá 6 filas, las cuales corresponden a la cantidad de imágenes presentadas y descritas. Escribe el número en la columna que consideres corresponde a la imagen que describen y expresan los derechos y valores que son la igualdad y la equidad.

Como segundo reto de la sesión, reflexiona sobre nuestra vida y convivencia con las demás personas e identificar en qué momentos ejercemos el derecho a la igualdad y cuando son acciones equitativas. Para ello puedes guiarte de las siguientes preguntas:
- ¿Consideras que se respeta el derecho a la igualdad en tu localidad y salón de clases? Argumenta tu respuesta
- ¿Qué acciones tomarías para ejercer el derecho a la igualdad dentro de tu localidad y salón de clases?
- ¿Qué significaría para ti lograr la equidad e igualdad en tu localidad y salón de clases?
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Las órdenes religiosas
Aprendizaje esperado: Aprende los rasgos principales de las ciencias y artes novohispanas entre los siglos XVI y XVII. Además, reconoce las características del periodo Barroco.
Énfasis: Conocer el papel de las órdenes religiosas en la enseñanza y la construcción de conventos como centros de enseñanza.
¿Qué vamos a aprender?
Continuarás con el recorrido por el Virreinato de la Nueva España. En esta ocasión verás el papel de las órdenes religiosas en la educación y en la construcción de conventos, los cuales fueron la punta de lanza para la evangelización.
¿Qué hacemos?
La justificación española de la conquista de territorios en América era que llevaba el cristianismo a las poblaciones originarias que no lo conocían. A la conquista militar seguía la conquista espiritual, iniciada de forma masiva con la llegada de 12 franciscanos en 1524. Dos años después llegaron frailes dominicos y, en 1533, arribaron los agustinos. Estas órdenes religiosas construyeron grandes conventos donde realizaron su labor evangelizadora. En 1572, llegaron los primeros jesuitas, quienes fundaron colegios en las ciudades y misiones en áreas aisladas del noroeste novohispano.
Como parte de la sección “Leer para ReConocerNos” lee el siguiente texto escrito por Pablo Escalante y Antonio Rubial sobre el rol educativo de las órdenes religiosas.
“En la base de la empresa mendicante en la Nueva España, se encontraban las escuelas. Según los testimonios de los frailes, había en ellas cerca de 5000 niños (entre los 7 y los 15 años) para 1531[…]
El tema central de varias cartas de franciscanos de esta época y de la siguiente es la educación de los niños en los conventos, su vida ejemplar y la ayuda que esos niños les prestaban en el aprendizaje de los idiomas nativos y en la destrucción de los santuarios antiguos y de la religión [que ellos consideraban] demoniaca.

https://www.codices.inah.gob.mx/pc/contenido.php?id=40
Fray Diego Valadés indica que las escuelas estaban a un costado de los templos; a los jovencitos que asistían a ellas se les enseñaba el modo de hablar y escribir correctamente, a cantar y tocar instrumentos de cuerdas y viento, a pintar y a dibujar y todas las otras artes mecánicas

https://es.wikipedia.org/wiki/Diego_de_Valad%C3%A9s#/media/Archivo:Houghton_Typ_525.79.865_-_Rhetorica_christiana,_Diego_Valad%C3%A9s,_211.jpg
Señala además que se les reunía y despedía tocando unas campanillas, que asistían a las ceremonias ordenadamente y permanecían en el templo con gran compostura. Durante las primeras décadas, dice Sahagún, “dormían en la casa que para ellos estaba edificada… donde los enseñábamos a levantarse a media noche, y los enseñábamos a decir los maitines de Nuestra Señora… y aún les enseñábamos que de noche se azotasen”.

https://arqueologiamexicana.mx/mexico-antiguo/el-conjunto-conventual-de-san-miguel-de-huejotzingo-puebla
Cuarenta años después, el mismo fraile señalaba que los había echado de los dormitorios que en un principio habían construido para ellos y les habían mandado dormir con sus padres y “desde entonces sólo venían a la mañana a aprender a leer y escribir”.

https://arqueologiamexicana.mx/mexico-antiguo/el-venerado-padre-sol-en-la-parroquia-de-ixmiquilpan-0
Aunque los principales testimonios que tenemos sobre el tema son franciscanos, sabemos que los agustinos y los dominicos tenían prácticas similares. […] Sin embargo, sólo los franciscanos se dedicaron a la instrucción de las niñas nobles, colaboradoras después en la catequesis de las mujeres. En las escuelas las niñas no estudiaban música, pero las exalumnas de esas casas, aun estando casadas, asistían en las mañanas a decir las horas de Nuestra Señora.
La idea de los frailes era formar a las esposas de los jóvenes egresados de sus conventos y formar familias cristianas nobles que fueran modelo para los macehuales.

https://mxcity.mx/2021/03/ariel-guzik-el-artista-mexicano-que-descifro-la-voz-de-ballenas-y-plantas/
Sin embargo, Zumárraga asegura que los matrimonios entre egresados de los conventos y las jóvenes educadas por los frailes no fueron comunes pues los muchachos alegaban que ellas “se criaban ociosas y a los maridos los tenían en poco, ni los querrían servir según la costumbre suya [de] que ellas mantienen a ellos, por haber sido criadas y doctrinadas de mujer de Castilla”.
Pablo Escalante Gonzalbo y Antonio Rubial García. “La educación y el cambio tecnológico”, en Historia de la vida cotidiana en México I. Mesoamérica y los ámbitos indígenas de la Nueva España. México, FCE / Colegio de México, 2004.
La labor evangelizadora y educativa de las órdenes mendicantes fue fundamental para determinar el carácter social de la Nueva España, como una sociedad que se adapta a las costumbres de la metrópoli española.
Para conocer más sobre el trabajo realizado por las órdenes religiosas, observa el siguiente video.
- Crónicas de las Indias. Documentos antiguos de la Biblioteca Nacional de Antropología e Historia
INAH TV
https://www.youtube.com/watch?v=sGVlnvwPZi4
Un punto a destacar sobre el conocimiento que se tiene de los señoríos prehispánicos, es la labor que realizaron las órdenes monásticas para rescatar las costumbres y formas de vida previos a la conquista, para poder realizar de una forma más efectiva su labor evangelizadora.
Los conventos fueron los lugares donde no sólo se evangelizaba a la población indígena, sino que se les enseñaba español, artes y oficios europeos.
En este grabado de Diego Valadés se ve el atrio de un convento donde los frailes enseñaban a los naturales y en el que están representados diversos aspectos de la tradición cristiana, como el bautismo y el matrimonio.

Fray Pedro de San José Betancourt, grabado
Colección Culhuacán - Fototeca Nacional
Fototeca Nacional INAH
https://www.mediateca.inah.gob.mx/islandora_74/islandora/object/fotografia%3A401015
Para conocer más sobre la educación en la época colonial observa el siguiente video.
- Iglesia y sociedad en la Nueva España
UNAM – Históricas
Del minute 02:23 al 02:58
https://www.youtube.com/watch?v=xCRw2FBJmDY
Las órdenes monásticas o mendicantes pertenecen al clero secular, una división dentro de la organización de la iglesia, que dedican su vida por completo a la enseñanza y el cuidado de los grupos susceptibles de ayuda, que, en el caso de la Nueva España, son los indígenas.
Estas órdenes empiezan a llegar a los territorios recién conquistados a partir de 1524 con los franciscanos, seguidos de los dominicos en 1526, los agustinos en 1533 y los jesuitas en 1572. El primer reto que enfrentan las órdenes religiosas al evangelizar a los nativos americanos es el lenguaje. Como te puedes imaginar, resultó más sencillo que un grupo reducido de frailes aprendiera las lenguas de los indígenas a que cientos o miles de ellos lo hicieran con el castellano.
Precisamente en esta labor evangelizadora es que destacamos el rescate de la lengua de los naturales y las nociones más tempranas que se sabe sobre la forma de vida en Mesoamérica.

Bautizo de la nobleza tlaxcalteca
Museo Nacional de Historia, Castillo de Chapultepec
https://mediateca.inah.gob.mx/islandora_74/islandora/object/pintura%3A3979
Muchos frailes se destacaron por sus actividades en la vida política y cultural de la Nueva España, hubo catedráticos en universidades, confesores de la autoridad Virreinal, calificadores y consultores del tribunal del santo oficio. La mayor parte de los más notables escritores de obras teológicas, doctrinales, místicas, históricas, hagiográficas, lingüísticas y científicas pertenecieron a las órdenes mendicantes.
La construcción de conventos fue una labor encabezada por las órdenes religiosas; primero para tener un lugar donde vivir y, en segundo plano, para consolidar el proceso de evangelización, convirtiéndose en un símbolo de la misión ya consumada. Como lo define Jessica Ramírez Mendoza, “eran fortalezas de la fe que mostraban simbólicamente el triunfo de Dios sobre los demonios de las idolatrías”.
Lee la siguiente cita de Fray Pedro de Gante en donde justifica la construcción de templos y ermitas en los poblados de naturales en la Nueva España:
“solían tener ellos los principales templos de sus ídolos en tiempos de su infidelidad y, pareció convenir, que a donde hubo particular memoria y adoración de los demonios, la hubiera ahora de Jesucristo y veneración de los santos”.

Fray Pedro de Gante
Pintura de caballete
Óleo sobre tela
Museo Nacional de Historia, Castillo de Chapultepec
https://mediateca.inah.gob.mx/islandora_74/islandora/object/pintura%3A3984
La gran cantidad de templos, ermitas y conventos se relaciona con la misma cantidad de construcciones prehispánicas que existían en Mesoamérica y, durante la transición a Nueva España, fueron sustituidas por las órdenes religiosas.
De la misma forma en que los frailes fueron modificando las creencias religiosas de los indígenas, los arquitectos del viejo continente, principalmente españoles, edificaron los palacios, monasterios e iglesias católicas al estilo europeo. Sin embargo, el estilo arquitectónico tuvo que adecuarse a los usos y costumbres de los naturales y las características físicas de cada región; así, el Barroco adquiere una nueva denominación “Barroco Novohispano”, donde los adornos no dejan espacios vacíos en los retablos

El Barroco novohispano es un movimiento artístico cuyas expresiones las encontramos en la arquitectura, la literatura y la pintura; tuvo su máximo desarrollo durante los siglos que duró la Colonia, del siglo XVI a mediados del siglo XVIII.
https://e1.portalacademico.cch.unam.mx/alumno/historiademexico1/unidad3/culturanovohispana/arquitectura
La influencia de las órdenes religiosas sobre la población novohispana fue creciendo con el tiempo, a tal punto que generó tensión con el clero secular y la confrontación fue inevitable. El Rey Fernando VI en 1749 y 1753 expide dos cédulas reales para traspasar las parroquias de regulares a seculares para limitar los privilegios de esta corporación a favor del estado.
Para complementar esta información, observa el siguiente video sobre la labor de una de las órdenes religiosas que llegan a la Nueva España: los jesuitas.
- Guía infantil del Museo Nacional del Virreinato
INAH TV
https://www.youtube.com/watch?v=_oZS8oPGAi0
Con base a lo que acabas de ver, sabrás que las órdenes religiosas en la Nueva España dejaron huella en la educación, la cultura y arquitectura que hasta la actualidad puedes apreciar. Su actividad fue de vital importancia para el desarrollo social y cultural de los siglos XVI al XIX y el periodo virreinal no se podría explicar sin su aportación cultural y científica. A continuación, veras otro video para conocer el interior de un exconvento y conocer cómo vivían las órdenes religiosas, en este caso los agustinos en el actual municipio de Acolman en el Estado de México.
- Acolman, arquitectura de los Agustinos
INAH TV
https://www.youtube.com/watch?v=3X9YAP1mE3Q&t=2s
Mientras tanto, en lo que hoy es Estados Unidos, se fundó el asentamiento de Jamestown, en la actual Virginia. Fue la primera comunidad permanente inglesa en América del norte y la fundadora de lo que serían las 13 colonias.

Jamestown en el siglo XVII.
https://destinoinfinito.com/jamestown/
En 1620 llegó otro grupo de migrantes de religión protestante a las costas de lo que sería Nueva Inglaterra, a bordo del barco MayFlower.

De William Halsall - Pilgrim Hall Museum, Dominio público: https://commons.wikimedia.org/w/index.php?curid=308115
Paralelamente al proceso de conquista y evangelización de la Nueva España, se fundan las 13 colonias británicas, que en un futuro llegarán a ser los Estados Unidos.
Al término de la conquista militar, inicia el proceso de conquista espiritual, la que va a ser realizada por las órdenes religiosas. Estas agrupaciones realizaron una muy valiosa labor en educar a los naturales, protegerlos de los encomenderos y rescatar algunos elementos de la tradición mesoamericana e introducirlos en la nueva religión. Las órdenes religiosas realizaron una importante aportación a la vida social y cultural de los novohispanos.
Como testigos del trabajo realizado en la evangelización, podemos observar las iglesias, ermitas y conventos construidos por las gestiones de estos grupos, para tener un lugar para vivir y enseñar a los indígenas, que reflejan el estilo arquitectónico del barroco novohispano, caracterizado por una exageración en los ornamentos de las construcciones.
El Reto de Hoy:
Investiga con tus familiares o en el portal de la localidad donde vives si es que existe algún exconvento cerca y a qué orden religiosa pertenece o pertenecía. Cuando sea posible, ya que termine la contingencia, visítalo, será otra forma de vivir y aprender la historia.
También puedes consultar otras fuentes bibliográficas, digitales y audiovisuales que tengas a la mano, por ejemplo, puedes acceder al recorrido virtual del exconvento de Tepoztlán, sede del Museo Nacional del Virreinato.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Gestión y vida cotidiana
Aprendizaje esperado: Usa diferentes técnicas de planeación y organización para la ejecución de los procesos técnicos.
Énfasis: Reflexionar sobre las situaciones de la vida cotidiana en las que se utiliza la gestión técnica.
¿Qué vamos a aprender?
Es tiempo de reflexionar de cómo utilizar las técnicas de planeación y organización para la ejecución de los procesos técnicos.
Tendremos una sesión muy interesante ya que hablaremos de gestión y vida cotidiana, recordando lo que ya hemos visto en diferentes sesiones.
Podremos reflexionar sobre las situaciones de la vida cotidiana en las que se utiliza la gestión técnica.
¿Qué hacemos?
Realizaremos una actividad de preguntas y respuestas con las alumnas y alumnos; a dicha actividad la llamaremos, “historia de la gestión técnica”.
La dinámica es la siguiente:
Realizaremos una pregunta asociada al tema y posteriormente, las alumnas y los alumnos darán respuesta a la pregunta planteada.
¿Qué es un cursograma?
- VIDEO. TEC2_B4_PG2_V1_SEM31_a030321 Cursograma.mp4
Efectivamente, en el cursograma podemos señalar paso a paso el proceso técnico de un producto o servicio.
Además, nos ayuda para que, si en un futuro se requiere repetir el proceso de la elaboración de un producto o servicio, se pueda controlar sin ningún problema.
Siguiente pregunta: En un cursograma ¿Cuáles son las diferentes fases de un proceso y con qué símbolos se representan?
- VIDEO. Respuesta de Ademar, veamos qué nos dice:
Sigamos con la siguiente pregunta:
¿Qué tipos de cursograma conoces y cuáles son sus características?
- VIDEO Respuesta de Lesly.
Continuemos, ¿Qué es una lista de cotejo?
- VIDEO. Yaretzi nos dice que:
Nos mandó un ejemplo, de la que utilizan en su clase de Tecnología con énfasis en Confección del Vestido e Industria Textil.
¿Cuál es la utilidad de la planeación?
- VIDEO. María Fernanda nos dice que:
Un ejemplo de planeación, sería el de una empresa de ropa de playa que quiere incursionar en la fabricación de ropa deportiva, primero tiene que hacer un diagnóstico de necesidades para detectar qué es lo que se requiere en este rubro, qué problemas está generando y después escoger la más viable para dar solución a este problema, se tendrá que definir el objetivo, y todo lo que se necesita para elaborar el sistema técnico: los insumos, herramientas, recursos humanos, maquinaria. Realizar la representación gráfica del producto, y elaborar el diagrama del proceso técnico.
¿Para qué nos sirve un plan de trabajo?
- VIDEO. Osiel, veamos qué nos dice:
¿Cuáles son los elementos del plan de trabajo?
- VIDEO. Martha nos envía un mensaje de texto y nos dice que son:
- Objetivo
- Representación gráfica
-Definición de etapas del proceso técnico
- Definición de responsables
- Presupuesto
- Cronograma
- Materiales y proveedores
La siguiente pregunta es ¿Cuáles son los instrumentos para el control del proceso técnico?
- VIDEO. Ángel y nos dice que son:
Para que nos quede más claro veamos una imagen de un cursograma sinóptico y otro ejemplo de la lista de cotejo.


Ya casi terminamos, veamos ésta: ¿Que son las normas de seguridad e higiene?
- VIDEO: Miguel nos mandó un mensaje de audio con la respuesta. Escuchémoslo:
¿Qué es un proceso técnico?
- VIDEO. Elizabeth nos manda la siguiente respuesta por correo electrónico:
¿Cuál es la utilidad de las normas de higiene y seguridad en el trabajo?
- VIDEO_ utilidad de las normas
“Menciona 5 posibles causas de accidentes durante el desarrollo de un proceso técnico”.
- VIDEO. Fernanda y nos dice lo siguiente:
Además, son muy útiles porque permiten controlar los tiempos en los que cada acción debe ser realizada, pues, una actividad que no tiene fecha de entrega no se termina.
¿Qué significa la simbología OTIDA utilizada en el cursograma?
Respuesta de Yima, nos manda un video donde nos muestra los apuntes que ha hecho en su cuaderno, ¡adelante! Veámoslo:
- VIDEO Yima:
Veamos el siguiente video para que nos quede más claro.
- OTIDA.pptx
Repasamos algunos puntos de la gestión técnica, recordando que ésta tiene como propósito organizar y coordinar todos los recursos disponibles, humanos, insumos y tiempos para la producción de un producto o servicio y se deben seguir una serie de pasos, como la planeación, organización, ejecución, control y evaluación del proceso técnico, para obtener un bien o servicio con éxito.
También recordemos que, dentro de los procesos, surgen algunos imprevistos y que tenemos que prever alguna solución, y estar preparados para ello.
Veamos por ejemplo cómo en Confección del Vestido e Industria Textil se utiliza la gestión técnica, ya que se planea, organiza, controla y evalúa cada uno de los procesos de la confección de una prenda. Es necesario tener conocimiento del campo tecnológico, posteriormente se hace la elección de la vestimenta que se ve a confeccionar: vestido, falda, blusa entre otros.
Ya que se seleccionó la prenda y el modelo, se enlistan todos los insumos que se van a utilizar, elección de la tela para la prenda, hilos, botones, cierres entre otros; se seleccionan los medios técnicos que intervendrán en el proceso como tijeras, máquinas de coser y se enumeran las acciones que conforman cada uno de los procesos técnicos como el trazo de la prenda, elaboración de patrones, corte de piezas, marcado de costuras, hilvanado de piezas, prueba de prenda, costura a máquina y terminados, se destinan tiempos y responsables y se desarrolla un plan de trabajo con todos estos elementos.
Después de que se ha planeado el proceso técnico, se organiza para poder llevarlo a cabo y se controla mediante un cursograma o lista de cotejo, así las alumnas y alumnos conocen el orden de las acciones y los tiempos para cada una de ellas, cumpliendo con éxito el objetivo.
Otro ejemplo, es la planeación de una fiesta donde tenemos que partir desde la fecha, el lugar donde se realizará el evento, presupuesto, organización, invitados, entre otros.
O la planeación de unas vacaciones, donde tenemos que ver qué lugar visitaremos, presupuesto, cuántos días, a dónde vamos a llegar a hospedarnos, que recorridos haremos, etcétera.
O la construcción de una casa donde tenemos que partir del terreno, necesidades de la familia, presupuesto, proyecto arquitectónico, permisos, materiales, tiempo de ejecución entre otros.
Te invitamos a integrar a su glosario técnico, los conceptos que vimos en la sesión de hoy, que no hayan agregado anteriormente. Te recuerdo cuáles son:
- Cursograma
- Plan de trabajo
- Proceso técnico
- Higiene y seguridad
El Reto de Hoy:
Si quieres volver a ver los programas de Aprende en casa transmitidos en semanas previas, los puedes encontrar en la página: youtube.com/aprendeencasa
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario