Aprende en Casa III SEP: 14 de mayo TAREAS y ACTIVIDADES de 1° de secundaria
A continuación dejamos los temas vistos el 14 de mayo de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 1° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Viernes 14 de mayo, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en Casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Problemas de ecuaciones lineales
Aprendizaje esperado: Resuelve problemas mediante la formulación y solución algebraica de ecuaciones lineales.
Énfasis: Plantear y resolver una ecuación a partir de un problema dado y viceversa.
¿Qué vamos a aprender?
En esta lección, ampliarás los conocimientos sobre cómo plantear y resolver una ecuación lineal de la forma ax + b = cx + d, a partir de un problema dado y viceversa.
Para esta sesión utilizarás:
- Cuaderno de Matemáticas o en su defecto hojas reutilizables para tomar notas.
- Lápiz, goma, sacapuntas y
- Tu libro de texto de Matemáticas de primer grado.
En esta sesión darás continuidad al tema, solución de ecuaciones de la forma “ax + b = cx + d”.
Debes recordar que una igualdad es la equivalencia entre dos expresiones algebraicas relacionadas, a través del signo igual.
¿Qué hacemos?
Antes de iniciar con el tema de hoy, te invito a resolver el siguiente reto:
Observa las operaciones de figuras y números:
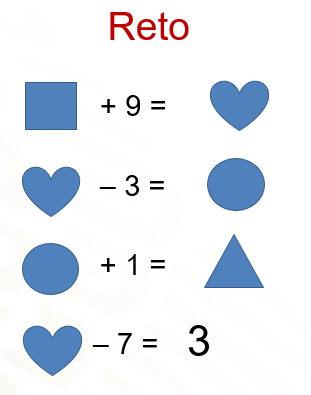
Un cuadrado más 9 es igual a un corazón.
El mismo corazón menos 3 es igual a un círculo; a su vez, el círculo más uno es igual al triángulo y finalmente, el corazón menos 7 es igual a 3.
El reto consiste en encontrar el valor que representa cada figura, de manera que se cumplan todas las igualdades.
Al final de esta sesión se dará respuesta a este reto.
Comienza analizando la siguiente situación:
“Martha y Alberto tenían la misma cantidad de dinero y compraron lápices del mismo precio. Martha compró 5 lápices y le quedaron $15.00 y Alberto compró 3 lápices y le sobraron $29.00. ¿Cuánto cuesta cada lápiz?
Iniciemos por traducir la situación al lenguaje algebraico. Nuestra incógnita, que es el costo de cada lápiz, la representamos con la letra “x”. Por lo que, para el caso de Martha la expresión algebraica es: 5x + 15, se realiza una suma, porque 15 pesos es lo que le quedó en dinero.”
Para el caso de Alberto la expresión algebraica es: 3x + 29.
Como ambos tenían la misma cantidad de dinero, ahora igualas ambas expresiones para formar la ecuación que represente la situación, que es:
5x + 15 = 3x + 29
Observa que la ecuación representa una igualdad, por lo tanto, lo que haces de un lado, ya sea sumar, restar, multiplicar o dividir, tienes que hacerlo del otro lado, para conservar la igualdad.
Empieza a despejar la incógnita “x”; para ello, vas a utilizar el inverso aditivo. Recuerda que el inverso aditivo de un número es su opuesto, de tal manera que, al sumarlos, se obtiene cero. En este caso, para eliminar a la incógnita del lado derecho, sumarás 3x negativo en ambos lados, obteniendo:

5x + (-3x) + 15 = 3x + (-3x) + 29, reduciendo términos semejantes queda: 2x + 15 = 29.
Ahora, en el primer miembro de la ecuación, el término que tiene a la incógnita se está sumando con 15. Para lograr que la incógnita quede sola, se debe restar primero 15 en ambos miembros de la ecuación o se suma el inverso aditivo de 15, que es 15 negativo, de la siguiente manera:
2x + 15 +(-15) = 29 +(-15).
Ahora, simplifica y obtienes la ecuación:
2x = 14.
Como el coeficiente 2 está multiplicando a “x”, se multiplica por el inverso multiplicativo de 2 en ambos miembros de la ecuación que es un medio, o bien, se divide entre 2. De ahí obtienes 2x entre 2 es igual a 14 entre 2. Al resolver, se sabe que “x” es igual a 7; es decir, cada lápiz cuesta 7 pesos.
A partir de los resultados obtenidos, ¿puedes saber cuánto dinero tenían Martha y Alberto?
Al comprobar la solución de la ecuación, puedes responder la pregunta.
Si sustituyes a la incógnita por el valor encontrado en la ecuación inicial: 5x+15=3x+29, se tiene que 5 por 7 + 15 igual 3 por 7 más 29; al aplicar la jerarquía de las operaciones, se tiene: 35 + 15 = 21 + 29. Al simplificar ambos lados de la igualdad, se tiene 50 es igual a 50.

Queda comprobado que 7 es el número que satisface a la ecuación. Y con esto, puedes responder la pregunta, ¿cuánto dinero tenían Martha y Alberto?
La respuesta es que cada uno tenía 50 pesos.
Como te pudiste cuenta, puedes resolver ecuaciones en situaciones cotidianas y con más frecuencia de lo que te das cuenta.
Observa otra situación que te permita utilizar ecuaciones de primer grado.
“Patricia y Carmen son dos amigas que decidieron guardar sus ahorros, cada una en una alcancía que se habían ganado en una feria. Se pusieron de acuerdo y decidieron ahorrar una cantidad fija mínima, cada semana; pero, si querían, podían ahorrar un poco más. Empezaron a ahorrar en diferentes momentos, hasta la semana 5 tenían los siguientes ahorros:
Carmen ahorró, cada semana, durante 2 semanas, 8 cuotas fijas más 5 pesos. Y Patricia ahorró, cada semana, durante 5 semanas, 3 cuotas fijas más 4 pesos.
Si tienen los mismos ahorros, ¿qué cantidad acordaron ahorrar como cuota fija semanal? ¿Cuánto dinero han ahorrado?”
¿Qué es lo primero que tienes que hacer para saber cuánto dinero ahorraron Patricia y Carmen?
Lo primero que harás, es traducir a lenguaje algebraico la información, con una ecuación de la forma “ax + b = cx + d”.
Representa a la cuota fija de ahorro semanal con la letra “c”. La representación algebraica de esta situación queda: Carmen, 2 veces, 8 cuotas fijas más 5 pesos. Algebraicamente es: 2 por la suma 8c + 5. Patricia, 5 veces, 3 cuotas fijas más 4 pesos, que algebraicamente es: 5 por la suma 8c + 4. Al igualar las expresiones, obtenemos la ecuación: 2 por la suma (8c + 5) igual a 5 por la suma (3c + 4).

Como puedes observar, obtuviste una ecuación que incluye paréntesis; así que, lo primero que harás, será aplicar la propiedad distributiva, que dice que: la multiplicación de un número por una suma, es igual a la suma de las multiplicaciones, de dicho número, por cada uno de los sumandos
Para despejar a la incógnita “c”, primero multiplica 2 por 8c y 2 por 5 y 5 por 3c y 5 por 4, obteniendo la ecuación: 16c +10 = 15c + 20.

Ya que eliminas los paréntesis, aplicas el procedimiento visto antes para despejar a la incógnita. Sumarás el inverso aditivo de 10, en ambos lados de la ecuación, quedando: 16c+10 +(-10) = 15c +20 + (-10). Reduciendo términos semejantes obtienes: 16c = 15c + 10; ahora, sumas en ambos lados el inverso aditivo de 15c, para dejar a la incógnita de un solo lado de la igualdad, resultando: 16c + 15c negativo = 15c + 15c negativo + 10, reduce términos semejantes, nuevamente, lo que da como resultado c = 10.
Con esto, obtienes la solución de la ecuación y se concluye que la cuota que fijaron Patricia y Carmen fue de 10 pesos semanales.
¿Cómo puedes saber qué cantidad ha ahorrado cada una?
Lo primero que tienes que hacer es comprobar el resultado de la ecuación, que es el último paso en el procedimiento; y con esto, puedes saber la cantidad que cada una tiene ahorrado.
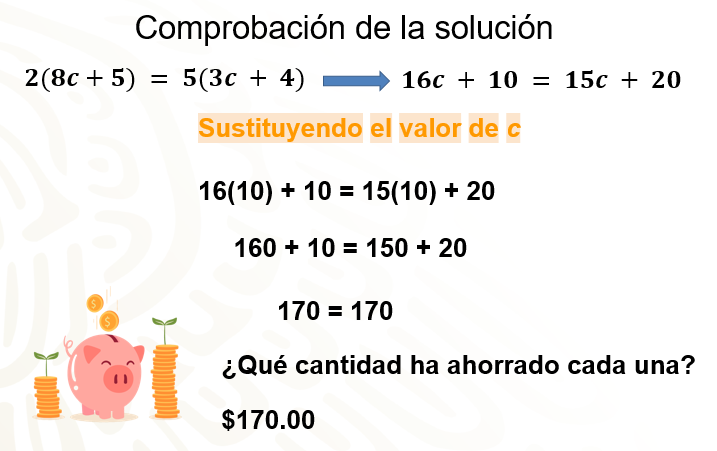
Observa, sustituyes el valor que se encontró para “c”, en la ecuación que obtuviste al aplicar la propiedad distributiva: 16c + 10 = 15c + 20, como c = 10, entonces: 16 por 10 más 10 es igual a 15 por 10 más 20. Resuelve las multiplicaciones y obtienes la igualdad: 160 más 10 igual a 150 más 20. Al simplificar, nos queda que 170 es igual a 170; por lo que la solución es correcta. Ahora ya sabes que cada una tiene ahorrados 170 pesos.
Ahora, resuelve la siguiente ecuación de la forma ax + b = cx + d.
El reto para ti, será plantear un problema que se resuelva con dicha ecuación, que es:
3.5x + 8 = 6.5x – 4.
¿Qué situación-problema podría relacionarse con esta ecuación?
“La edad de Luis es igual a 3.5 veces la edad de Eduardo, más 8. pero también, la edad de Luis también es igual a 6.5 veces la edad de Eduardo, más 4 años: es decir, Si la edad de Luis es “x”; entonces, 3.5x + 8 = 6.5x – 4.”
Así se tiene que el problema cumple con la ecuación dada.
Ahora, habría que resolverla para conocer la edad de Luis y de Eduardo.
¿Recuerdas qué es lo primero que hay que hacer?
Se tiene que despejar la incógnita en uno de los miembros de la igualdad; en este caso, lo harás del lado derecho. Primero, como a 6.5x se le restan 4; entonces, sumas 4 en ambos lados de la igualdad, obteniendo la ecuación: 3.5x + 8 + 4 = 6.5x – 4 + 4, que al simplificar queda: 3.5x + 12 = 6.5x.
Ahora, se resta 3.5x en ambos lados para tener a la incógnita únicamente del lado derecho, 3.5x + 12 - 3.5x = 6.5x - 3.5x, al simplificar queda: 12 = 3x
Finalmente, para despejar la incógnita se divide entre 3 a ambos miembros de la ecuación.
Quedando 12/3 igual a 4 y 3x entre 3 igual a x, dando como resultado 4 igual a x o lo que es lo mismo aplicando la propiedad reflexiva o simétrica x es igual a 4.

Ya se tiene la solución de la ecuación y se sabe que la edad de Luis es de 4 años.
Pero, como en toda ecuación, se tiene que comprobar la solución del problema, lo que te permitirá conocer la edad de Eduardo.
En casa, comprueba la solución de la ecuación y comprueba que Eduardo tiene 22 años.
Para ahondar en la resolución de problemas que llevan a ecuaciones de la forma antes mencionada, analiza y resuelve la siguiente situación.
Se tiene la ecuación 10x - 5 + 3x - 6 = 10x + 10. ¿Qué observas en esta ecuación?
Para poder desarrollar todo el proceso ya conocido, primero se deben de reducir los términos semejantes del lado izquierdo de la igualdad, obteniendo 10 x + 3x = 13x y resuelve las restas de 5 y 6 obtienes a 11 como sustraendo. Muy bien, ahora ya tienes la ecuación de la forma que has trabajado en esta sesión: 13x – 11 = 10x + 10
Ahora puedes iniciar el despeje de nuestra incógnita en uno de los lados de la igualdad. Como a 13x se le resta 11; entonces, se suma 11 en ambos lados de la igualdad, obteniendo la expresión: 13x – 11 + 11 = 10x + 10 + 11, que al simplificar queda como: 13x = 10x + 21.
Ahora, se resta 10x en ambos lados para tener al término que tiene a la incógnita únicamente del lado izquierdo: 13x - 10x = 10x + 21 - 10x, que, al simplificar, queda como: 3x = 21.
Por último, para despejar la incógnita, se divide entre 3 a ambos miembros de la ecuación, resultando que “x” es igual a 7.

Una vez que se ha encontrado el valor de la incógnita “x”, se comprueba que el valor obtenido es correcto en la ecuación inicial:
10x - 5 + 3x - 6 = 10x + 10
Al sustituir el valor que se obtuvo de la “x”, se tiene que: 10 (7) - 5 + 3 (7) - 6 = 10 (7) + 10
Se realiza la operación en el miembro izquierdo y se obtiene:
70 - 5 + 21 - 6 = 80
Al efectuar las operaciones en el miembro derecho se tiene que: 70 + 10 = 80
Por lo que se obtiene finalmente que 80 = 80

Resuelve la siguiente situación problema:
La edad de Antonio es el doble de la edad de Ramiro.
Dentro de 6 años la edad de Antonio será 5/3 la edad de Ramiro.
La pregunta es: ¿Cuáles es la edad actual de ambos?
Iniciemos planteando la ecuación. Si la edad actual de Ramiro la presentamos con “x”; entonces, la edad de Antonio es 2x.
Dentro de 6 años la edad de Ramiro será x + 6 y la de Antonio 2x + 6. Como sabemos que en seis años la edad de Ramiro será 5/3 la edad de Antonio; entonces, se plantea la ecuación: 2x + 6 = 5/3 por (x + 6)

Si observas, la expresión tiene una fracción en el miembro derecho. Como es más práctico operar con números enteros, multiplicas ambos miembros de la ecuación por 3.
Y queda la ecuación: 3 por el binomio 2x + 6, igual a 3 por 5/3, por el binomio x + 6; como 3 por 5/3, es igual a 5, la siguiente ecuación que se obtiene es: 6x + 18 = 5 por el binomio x + 6. Al eliminar los paréntesis, tienes que: 6x + 18 es igual a 5x + 30.
Ahora, restas 5x en ambos miembros de la ecuación, para lograr que la incógnita esté únicamente del lado izquierdo: 6x + 18 - 5x = 5x + 30 - 5x. Simplificando se obtiene x + 18 = 30. El siguiente paso es restar 18 en ambos miembros de la ecuación, para que los términos independientes o constantes se encuentren sólo del lado derecho: x + 18 - 18 = 30 - 18, reduciendo se tiene x = 12;
¿Recuerdas qué representa a “x”?.
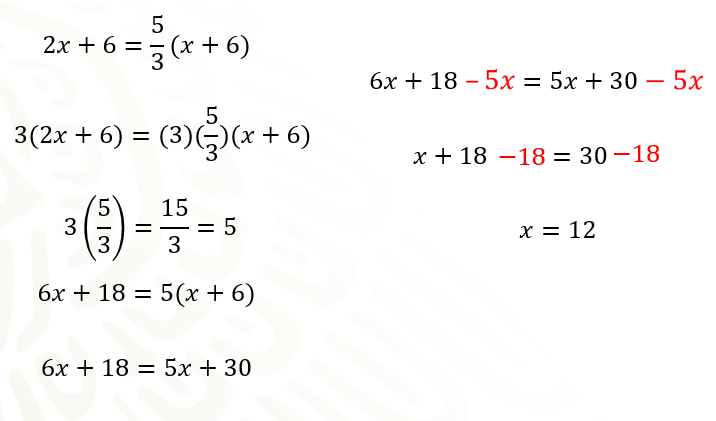
Para poder saber las edades de Ramiro y de Antonio, sustituyes el valor de la incógnita x encontrada en la expresión algebraica.
Ramiro tiene 12 años y Antonio, 12 por 2, igual a 24 años y, dentro de seis años, Ramiro tendrá 12 más 6 igual a 18 años y Ramiro 24 más 6 igual a 30 años.
Con esto se demuestra que en 6 años la edad de Ramiro será 5/3 la edad de Antonio, ya que 30 es 5/3 de 18.
Observa la última situación problema.
Un recipiente tiene una cierta cantidad x en litros de agua. Si se le añaden 160 litros de agua tendría la miasma cantidad total en litros de agua que si a esa cierta cantidad x se le añadieran 10 litros y se triplicara.
¿Cuántos litros de agua hay en el recipiente?
¿Cuál es esa cantidad inicial de agua en el recipiente?
¿Lo tienes?, ¿Ya sabes cuál es la ecuación que representa a este problema?
En este caso, se desconoce la cantidad en litros inicial de agua que contiene el tanque, por lo que este dato será la incógnita a encontrar. Nuevamente, la se expresará con la literal “x”, obteniendo la ecuación:
x más 160 litros es igual a el triple del binomio x más 10, es decir, x + 160 = 3(x + 10).
Si observas tienes que emplear del lado derecho la propiedad distributiva para eliminar los paréntesis. Se multiplica el 3 por x y 3 por 10, al resolver tienes la ecuación: x + 160 = 3x + 30.
Ahora, se procede a despejar la incógnita “x”. En este caso, lo hrarás del lado derecho, entonces, en ambos lados de la igualdad restas x, y nos queda:
x + 160 – x = 3x + 30 – x, que al simplificar se obtiene:
160 = 2x +30.
Ahora, se restan 30 en ambos de la igualdad, 160 – 30 = 2x + 30 – 30, simplificando da: 130 = 2x.

Finalmente, para despejar la incógnita y encontrar su valor, se divide entre 2 ambos miembros de la ecuación, resultando que: 130 entre 2 = 2x entre 2, lo que da “x” igual a 65.
Ahora, ya puedes dar respuesta al cuestionamiento ¿Cuál es esa cantidad inicial x de agua en el recipiente?
La respuesta es 65 litros.
Y ¿Cuántos litros de agua hay en el recipiente?
Hay 65 más los 160 litros que se agregaron, es decir 225 litros.
En casa, comprueba que el resultado es el correcto sustituyendo a “x” por el valor obtenido y resolviendo las operaciones. Si tienes oportunidad, comparte con tu maestra o maestro tus resultados.
¿Qué te parece si, antes de terminar esta sesión, te das un momento para anotar lo más importante del tema que desarrollaste el día de hoy? Realiza en tu cuaderno tus anotaciones.
Recuerda que en la solución de ecuaciones se debe tener en cuenta lo siguiente:
- Leer detenidamente para comprender la situación que se plantea.
- Traducir el problema al lenguaje algebraico.
- Resolver la ecuación empleando la propiedad uniforme de la igualdad; es decir, encontrar el valor de la incógnita.
- Realizar la comprobación de la solución.
- Dar respuesta a los cuestionamientos de la situación problema, si es que existiera.
Es importante no omitir algún paso mencionado anteriormente; de esta manera, obtendrás un aprendizaje certero y un resultado algebraico correcto.
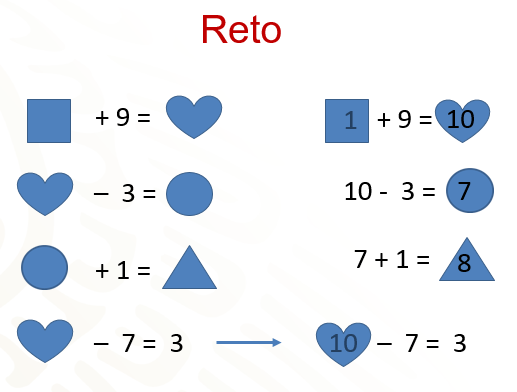
Si observas las operaciones, la cuarta nos indica que el resultado es 3; por lo que puedes considerar al corazón como la incógnita de una ecuación, entonces, sumas 7 en ambos lados y el resultado es corazón igual a 10. Ya tienes el primer valor de las figuras.
Conociendo el valor del corazón, ya puedes resolver la primera operación, cuadrado más 9, igual a corazón, es decir a 10; entonces, el número sumado con 9 da como resultado 10, es el 1. Entonces, el cuadrado vale 1.
La segunda operación indica el corazón menos 3 igual a círculo, como ya conoces el valor del corazón sustituyes su valor quedando 10 - 3 = a círculo. Al realizar la operación, obtienes 7, que es el valor del círculo. Vas por la última operación: círculo más 1 es igual a triángulo. Nuevamente, sustituyes el valor de círculo, que es 7, más 1, es igual a 8. El triángulo tiene como valor 8.
¿Qué tal? ¿Ya tenías las respuestas? Seguramente lograste obtener el mismo resultado.
En caso de que tengas dudas o deseen profundizar, te recomiendo apoyarte en tu libro de texto de Matemáticas de primer grado: o bien, volver a ver esta lección.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Espacios y ambientes en poemas
Aprendizaje esperado: Lee y compara poemas de diferentes épocas sobre un tema específico.
Énfasis: Argumentar sobre la relación entre espacios y ambientes en poemas
¿Qué vamos a aprender?
En esta sesión se hablará sobre Espacios y ambientes en poemas y, particularmente, te concentrarás en el propósito de “Argumentar sobre la relación entre espacios y ambientes en poemas”. Es decir, que revisarás la forma en que los poetas reconstruyen ambientes y espacios a través de sus palabras.
A lo largo de esta sesión, te dedicarás a “argumentar sobre la relación entre espacios y ambientes en poemas”, lo cual implicará leer varios textos poéticos y revisar de qué manera su autor o autora construye o reconstruye espacios reales o imaginarios.
Los materiales que vas a necesitar para esta sesión son: cuaderno, y lápiz o bolígrafo para que puedas tomar notas. Y, por supuesto, tu libro de texto.
Además, en esta sesión trabajarás con los siguientes poemas:
- “Estoy aquí, sentada, con todas mis palabras”, de Rosario Castellanos;
- “Viento”, de Octavio Paz;
- “Luz de Chile”, de Gabriela Mistral;
- “Suave Patria”, de Ramón López Velarde;
- “Oda al perro”, de Pablo Neruda, y
- “Ataraxia”, de Matías York Castro Slim
Recuerda que todo lo que veas es para reforzar tu conocimiento, así que te recomiendo llevar un registro de las dudas, inquietudes o dificultades que surjan al resolver los planteamientos, pues muchas de éstas las podrás resolver al momento de consultar tu libro de texto y revisar tus apuntes.
¿Qué hacemos?
A veces es difícil comprender los poemas, si no entiendes los poemas es posible que no hayas encontrado el poema que te hable a ti, o no has escuchado una explicación que te sirva, por ejemplo, ¿qué te viene a la mente si te digo…
“Estoy aquí, sentada, con todas mis palabras
como una cesta de fruta verde, intactas”?
Es posible que no es algo real, porque las palabras no se ven, no son algo como la fruta verde, que sí se puede tocar y poner en una canasta. Pero al mismo tiempo, se escucha bien, y a veces así pasa de pronto a los seres humanos, que están llenos de palabras, sólo esperando decirlas.
Ahora revísala con más calma. Antes, observa lo que trata de los dos primeros versos de un poema más extensos de la poeta chiapaneca Rosario Castellanos.
Y, para seguir hablando del tema y centrar en los contenidos para esta sesión, ¿qué te parece si revisas un video para justamente, entender cuál es la diferencia entre el lenguaje literal y el lenguaje figurado en la poesía?
Observa del minuto 00:58 al 02:24.
- Crear textos poéticos con formas gráficas
https://www.youtube.com/watch?v=uuPD36vkxPE
Igual que Rosario Castellanos dice que tiene sus palabras en una canasta, Octavio Paz dice que el aire hace que las peras bailen y las hojas canten. Eso es lenguaje figurado
El lenguaje literal es el que se usa a diario para comunicarse, y el figurado es del que se alimenta la poesía para construir imágenes y evocar sentimientos y atmósferas. Y, por supuesto, para construir o reconstruir espacios que quienes leen o escuchan el poema no puedes ver directamente, pero puedes ver en la mente gracias a las palabras que da la poeta.
¿Cómo que lo puedo ver en la mente?
Por ejemplo, cuando yo se repiten los versos
“nubes y nubes
flotan dormidas”
¿Qué te imaginas?
Podrían ser unas nubes, muy tranquilas, flotando contra un cielo azul.
Eso es la poesía: la capacidad de elegir ciertas palabras y ordenarlas para que quien te las lee o te escucha sea capaz de sentir e imaginar algo.
¿A ti te ha ocurrido algo como que no puedes expresar algo que en tu mente estabas recordando?
¿Te has sentido incapaces de recrear con palabras una emoción o una experiencia?
No te preocupes, mientras sigas leyendo poesía y aprendiendo nuevas palabras y formas retóricas, te será más sencillo comprender y expresar lo que sientes y piensas; de hecho, en un momento más verás un ejemplo de un poema escrito por un alumno a partir de una imagen, pero antes, observa un ejemplo más parecido a lo que se está abordando ahora.
El alumno Lluis Emiliano Fuentes viajó a un lugar apartado del estado de Tlaxcala, y se encontró con este paisaje. Como él es muy aficionado a la fotografía, lo retrató y lo comparte:

Hace recordar en un poema de Gabriela Mistral que se llama “Luz de Chile”, a continuación el poema.
¿Qué tendrán las piedras pardas
y los pedriscos y el légamo
que al más cascado lo llevan
alácrito de ardimiento?
Es como que el valle hace
de camino y de viajero
y nos lleva liberados
de jornada y de aceceo.
Se entiende que habla de un paisaje, por lo de las piedras y el valle y el camino, pero hay otras palabras que son difíciles de comprender.
Légamo: Según el Diccionario de la lengua española, el légamo es un “barro pegajoso que se forma en el suelo con el agua de lluvia”, o sea lodo.
Alácrito: Cuando se conduce con alacridad, que según el mismo diccionario, es “alegría y presteza del ánimo para hacer algo”. Es decir, que va muy contento, con mucho entusiasmo.
Acezar: La poeta Gabriela Mistral utiliza muchos regionalismos y juega constantemente con las palabras, pero una buena hipótesis sería que viene del verbo “acezar”, cuya segunda acepción es “sentir anhelo, deseo vehemente o codicia de algo”.
Es interesante porque hace una descripción no sólo del paisaje, con las piedras pardas y el légamo, sino también de lo que siente la persona que lo va recorriendo. Igual que en la foto de Lluis, que transmite paz, el poema nos permite sentir la alegría de quien va por ese camino.
¿Te diste cuenta cómo la poesía no es difícil? Sólo es cosa de leerla con cuidado, con los ojos bien abiertos y con un diccionario al lado.
Con esta explicación hace pensar en todos los poemas que has leído y estudiado en la vida escolar, y que puedes volver a ellos para encontrar las descripciones que hacen las y los poetas de los espacios y las atmósferas.
Piensa siempre que la poesía es algo completamente natural para el ser humano, aunque no te propongas escribir poesía, los hablantes están constantemente produciendo metáforas, comparaciones, rimas y todo tipo de textos poéticos en el habla cotidiana. Y si lees con cuidado los poemas, verás que sí, quienes los escriben tienen un talento muy especial, pero muchas veces ese talento reside en encontrar dos palabras usuales y juntarlas de manera inusual, como cuando Ramón López Velarde, en su poema largo “Suave Patria”, habla del “relámpago verde de los loros”
Esa palabra tan sencilla da idea de un movimiento rápido, como si pasara el loro volando.
Los textos poéticos son para todo aquello que le interese y le emocione al ser humano, o sea, para todo. Precisamente, otro poeta chileno, Pablo Neruda, escribió una serie de obras llamadas “odas elementales”, donde hace poemas a objetos tan cotidianos como el pan, la cebolla y, a su perro.
Lee un par de fragmentos de la “Oda al perro”, de Pablo Neruda. Pon mucha atención y procura localizar qué palabras utiliza el poeta para recrear el espacio en el que está.
“El perro me pregunta
y no respondo.
Salta, corre en el campo y me pregunta
sin hablar
y sus ojos
son dos preguntas húmedas, dos llamas
líquidas que me interrogan…”
Es interesante la forma en que describe los ojos del perro como preguntas húmedas y llamas líquidas, profesora. Porque hay muchos perros así, que miran con mucha intensidad, y sus ojos siempre están húmedos.
Y habrás observado que describe los paseos que dan por el campo el perro y el humano. Observa ahora cómo describe el espacio en el que se encuentran. Pon atención a ver si tú te has topado con un lugar similar.
“A campo pleno vamos
hombre y perro.
Brillan las hojas como
si alguien
las hubiera besado
una por una,
suben del suelo
todas las naranjas
a establecer
pequeños planetarios
en árboles redondos
como la noche, y verdes…”
¿Alguna vez has estado debajo de un árbol de naranjas, o de manzanas?
Se siente exactamente, como si las ramas cubrieran todo y formaran un techo sobre tu cabeza.
Observa cómo dice que “brillan las hojas como si alguien las hubiera besado una por una”, y piensa en esas hojas de naranjo de verde muy oscuro, que se ven lustrosas al sol. Las y los poetas, como ya se dijo, ven lo que observan todos, pero buscan afanosamente las palabras adecuadas que ayuden al lector o a quien escucha el poema a mirar con otros ojos lo que ven todos los días. Piensa en este poema, en estas hojas que brillan “como si alguien las hubiera besado una por una” la próxima vez que te encuentres con un naranjo o un árbol cualquiera.
Ahora lee el siguiente poema que escribió un alumno, Matías York Castro Slim, un día en que, al igual que Pablo Neruda, salió a pasear con su perrita y el atardecer era deslumbrante.
Descansa tranquila,
Frente a mí posando.
Mientras la luz brilla
y tú pensando.
Paisaje azul,
azul como el mar.
Recuerdos en un baúl
que he de recordar.
Inamovible canela,
imperturbable porte.
Mi alma anhela,
que esa flor no se corte.
¿Ya viste como un poema tan bello puede estar escrito por alguien que es un alumno? Sólo necesitas inspirarte y pensar un poco en algo que te guste, en el caso de Neruda y el alumno Matías, fueron sus perritos.
Ahora, te propongo un reto. Observa tres preguntas y respóndelas tomando en cuenta lo que acabas no sólo de leer, sino de sentir y evocar con las palabras de Matías.
Las tres preguntas son:
1. ¿Qué sentiste al leer el poema?
2. ¿Cómo es el lugar donde se desarrolla el poema?
3. ¿Cómo se sienten los personajes?
Por ejemplo: El poema dio paz y tranquilidad, porque utiliza palabras como “posando”, “descansa”, “pensando”, “imperturbable” e “inamovible”, que todas dan idea de quietud, de reposo. Y el lugar donde se desarrolla es, sobre todo, azul, que es un color que se relaciona con lo claro, lo limpio y lo tranquilo. Y, justamente, lo que transmite es que tanto el perro como el humano están tranquilos, en paz.
La palabra “ataraxia”, que da título al poema, significa estar tranquilo e inamovible. Se supone que también que fuiste leyendo el poema te diste cuenta de la descripción de color “canela” de la perrita y de la tranquilidad que tienen en medio del paraje.
Seguramente notaste que, a pesar de que Matías se siente muy feliz y tranquilo al lado de su perra, cuando aparecen los versos que rezan:
“Mi alma anhela,
que esa flor no se corte.”
Hace referencia a que la vida de un ser humano o de una mascota es efímera, es decir, breve y que Matías no quisiera que la vida de su perrita se extinguiera.
La maravilla de los poemas y de todos los textos es que se puede volver a ellos una y otra vez, y en cada ocasión el texto revelará algo nuevo, algo que no habías notado o que no habiías entendido en lecturas previas.
Recuerda que el lenguaje puede ser literal o figurado.
Literal cuando describe exactamente la realidad, figurado cuando utiliza formas poéticas como metáforas o hipérboles para expresar no sólo la realidad, sino una opinión o una interpretación de ella.
El lenguaje figurado es del que se alimentan las y los poetas para construir sus textos, y los lectores deben poner mucha atención para entender qué quieren expresar o construir los autores cuando eligen una palabra u otra.
Por otro lado, la poesía evoca y recrea la realidad, y una parte de la realidad muy importante tiene que ver con los espacios, las atmósferas y los ambientes. A partir de la elección de palabras, los poetas pueden llevarte de inmediato a un lugar, o hacer recordar una experiencia.
Se mencionó que como lectores deben poner atención a la elección de palabras del autor o la autora, pues pueden utilizar términos poco usuales para ayudar a construir una imagen vívida.
Y, sobre todo, que la escritura de la poesía no está limitada a quienes se llaman a sí mismos poetas, sino a todos los que hablan y escriben.
El Reto de Hoy:
Recuerda algún espacio, algún ambiente que te haya parecido interesante por alguna razón; puede ser algo que veas diariamente de camino a la escuela, o algún rincón que hayas visto en la televisión o que te hayan platicado, y piensa con qué adjetivos lo describirías, cómo construirías un poema al respecto. Si no se te ocurre nada, puedes buscar imágenes como las siguientes.

Y escribir a partir de ellas.
Ten en cuenta que lo importante no es tanto describir el espacio, sino describir los sentimientos, el ambiente, la sensación que genera en ti. Cuando hayas terminado, comparte tus poemas o tus textos con tus familiares o amigos y pregúntales si experimentaron lo que mismo que ustedes o algo distinto. Será un experimento muy interesante.
Busca en tu libro de texto el Aprendizaje esperado y realiza las actividades que ahí te propongan. Además, puedes buscar poemas en tu libro o en repositorios digitales o bibliotecas, para encontrar los textos poéticos que te hablen directamente a ti y te resulten interesantes. No olvides tener siempre cerca tu diccionario y tu libreta de apuntes.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
La distribución de las actividades económicas primarias en el mundo
Aprendizaje esperado: Compara la producción agrícola, ganadera, forestal y pesquera en diferentes regiones del mundo.
Énfasis: Identificar la distribución de las actividades económicas primarias en el mundo.
¿Qué vamos a aprender?
“La distribución de las actividades económicas primarias en el mundo”.
Y el propósito será identificar la distribución de estas actividades a nivel mundial.
Estudiando su clasificación según el tipo de producto, su volumen de producción y las condiciones geográficas que favorecen su desarrollo.
¿Qué hacemos?
¿De dónde provienen todos los recursos que consumes? Y…
¿En qué partes del mundo hay mayor disponibilidad de éstos recursos?
Con esto se refiere a la extracción de esos recursos naturales de los que se derivan productos. Mismos que se obtienen por medio de actividades como: la agricultura, la ganadería, la pesca y la actividad forestal.
Pocas veces con esto se detiene a pensar de dónde provienen esos recursos y la importancia que adquieren en la vida diaria.
En esta sesión tendrás la oportunidad de conocer la distribución de las diferentes actividades económicas primarias; además de identificar la producción agrícola, ganadera, pesquera y forestal en diferentes regiones del mundo.
La agricultura, considerada como base de la alimentación humana; y la cual tiene una gran demanda en todo el mundo.
Existe una gran relación entre la producción agrícola y las condiciones del clima, relieve y tipo de suelo, pero también -debido a los avances tecnológicos-, se practican técnicas que ayudan a producir este recurso.
Como: el riego artificial, el uso de fertilizantes y plaguicidas; e invernaderos que permiten cultivar en regiones áridas.
Por ejemplo, en Almería, España; se practica la agricultura intensiva con técnicas modernas que superan el obstáculo que el entorno árido representa para la actividad.
Utilizando estas técnicas es posible cubrir la demanda de la creciente población mundial.
¿Qué hay del cuidado de estos recursos?
Es un aspecto muy importante; en el que debes generar consciencia de los recursos que utilizas, ya que mientras mayor sea el consumo, también mayor será la sobreexplotación de los recursos.
Por ejemplo, en años más recientes, la agricultura también ha incorporado técnicas más amigables con el medioambiente, como la hidroponía, en la que ya no se requiere suelo y los nutrientes se agregan directamente al agua donde crecen los cultivos.
En el supermercado, he observado que existen algunos productos etiquetados que dicen: hidropónicos; y esto quiere decir que son cultivados en agua.
Comparte esta información con tu familia, y contribuye al cuidado del medioambiente; consumiendo estos productos, y sin desperdiciar alimentos, sólo utilizando lo necesario.
Por otro lado la actividad agrícola se clasifica según sus métodos de producción en:
1. Tradicional, en donde se cultivan productos locales aprovechando el clima, el suelo y el relieve; por ejemplo, en la alcaldía Milpa Alta de la Ciudad de México.
2. Industrial, basada en sistemas intensivos, con maquinaria, riego artificial, fertilizantes químicos y plaguicidas, que permiten producir grandes cantidades de alimentos en menos tiempo y espacio, aunque con mayor daño al medioambiente. Un ejemplo es el cultivo de cereales en Estados Unidos de América.
Y 3. La agricultura ecológica, la cual impulsa la producción de alimentos ocasionando menor impacto ambiental, pues se distingue por no agregar productos químicos a los cultivos.
¿Cuáles son las principales regiones de producción agrícola en el mundo?
Estas regiones coinciden con las mayores densidades demográficas.
Estados Unidos de América, Canadá y Países Europeos como Rusia y Ucrania, destacan por su producción de alimentos debido al avance tecnológico para desarrollar la agricultura comercial a gran escala.
Observa la siguiente imagen.
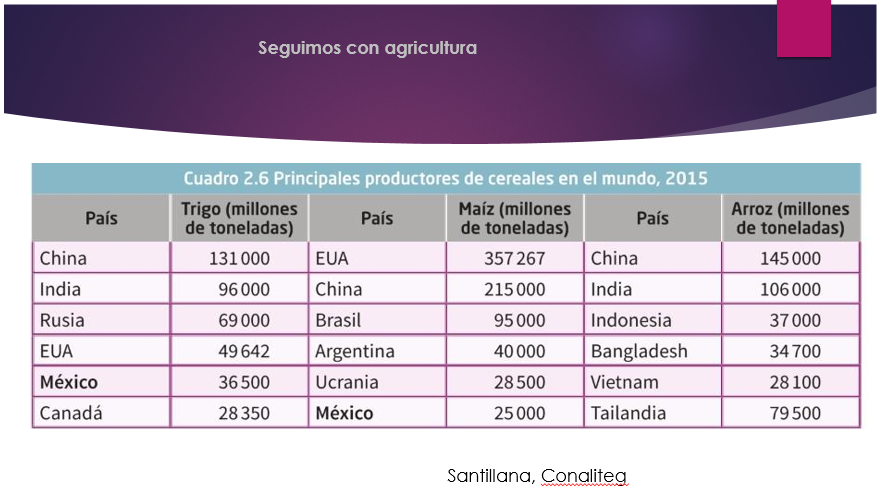
Como puedes observar, estos son los países con mayor producción de granos básicos en el mundo.
¿Esto significa que los países que cuentan con climas tropicales en sus territorios aprovechan esta condición para practicar la agricultura? Y producir cultivos tropicales que son de gran demanda en países desarrollados.
Está relacionado a nivel mundial, las regiones más sobresalientes por su producción agrícola presentan las siguientes condiciones geográficas:
Grandes llanuras, climas tropicales y templados, así como disponibilidad de agua. Por ejemplo: Estados Unidos de América, el sureste de Canadá, el centro del continente Asiático, así como el este y oeste de Europa.
Esto con respecto a la agricultura.
La ganadería, se refiere al manejo y explotación de animales domesticables con fines de producción.
Se puede dividir a la ganadería en dos tipos, según su volumen de producción:
La actividad pecuaria, relacionada con la producción de ganado, puede ser de autoconsumo, cuando se lleva a cabo principalmente en espacios rurales, y se refiere principalmente a la cría de animales para consumo familiar.
Y la ganadería comercial, la cual tiene como propósito la venta de los productos en los mercados nacionales o extranjeros.
La ganadería comercial, se divide en: ganadería extensiva y ganadería intensiva.
La extensiva se desarrolla principalmente en países como México, Argentina, Estados Unidos de América y Nueva Zelanda. Utilizan grandes superficies para la alimentación del ganado, y aprovechan el crecimiento natural de la vegetación.
Por otro lado, en la ganadería intensiva, los animales se mantienen en establos o granjas, utilizando tecnología de punta para obtener mayor producción; como en el norte de nuestro país y en lugares del mundo como Bélgica y Países Bajos.
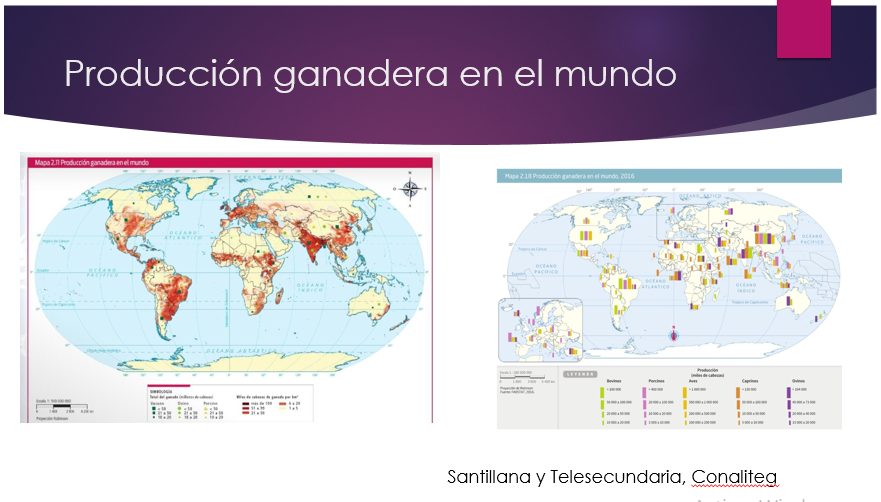
Los principales países productores de leche y huevo son Estados Unidos de América, India y China, como se observa en la tabla.
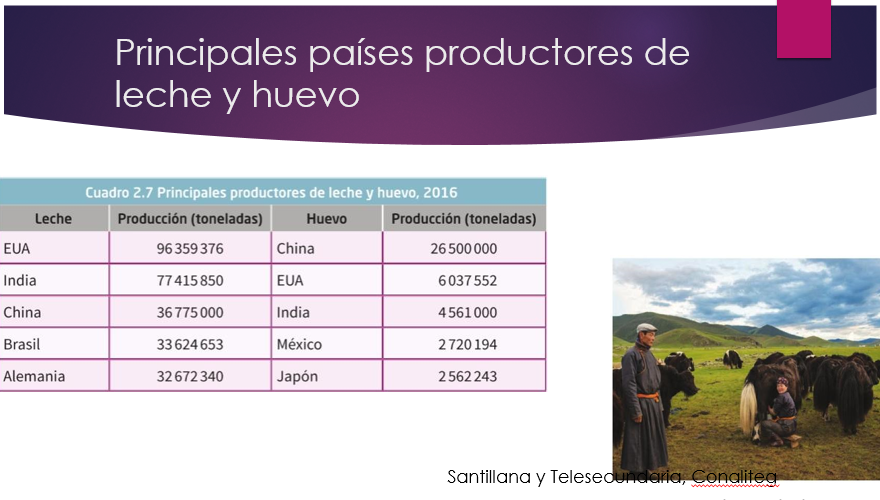
Distingue con la ayuda de los mapas, la distribución de la actividad ganadera en el mundo, destacando que los países cercanos a los trópicos aprovechan su clima, suelo y disponibilidad de agua para la crianza de animales.
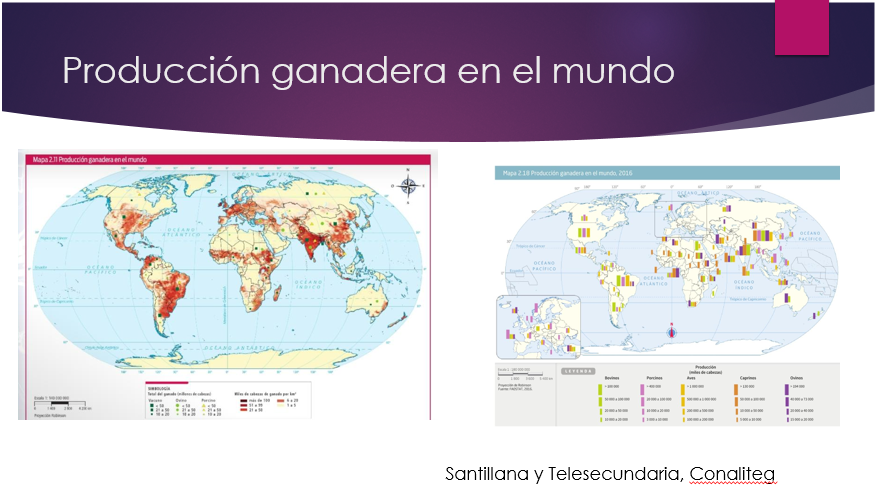
En cuanto a la producción pesquera en el mundo, e muy interesante conocer su distribución; ya que esta actividad dio lugar al desarrollo de grandes puertos pesqueros en las costas de Europa, en el mar Mediterráneo, en las costas occidentales de Estados Unidos de América y México. Y también en las costas Orientales de China y Japón.
Un dato muy interesante, es que Japón, Noruega y Canadá, tienen la mayor capacidad industrial de pesca, almacenaje y procesamiento de las especies capturadas, para posteriormente comercializarlas en diferentes regiones del mundo.
En el siguiente cuadro podrás identificar cuáles fueron los países con mayor producción pesquera en el año 2017.
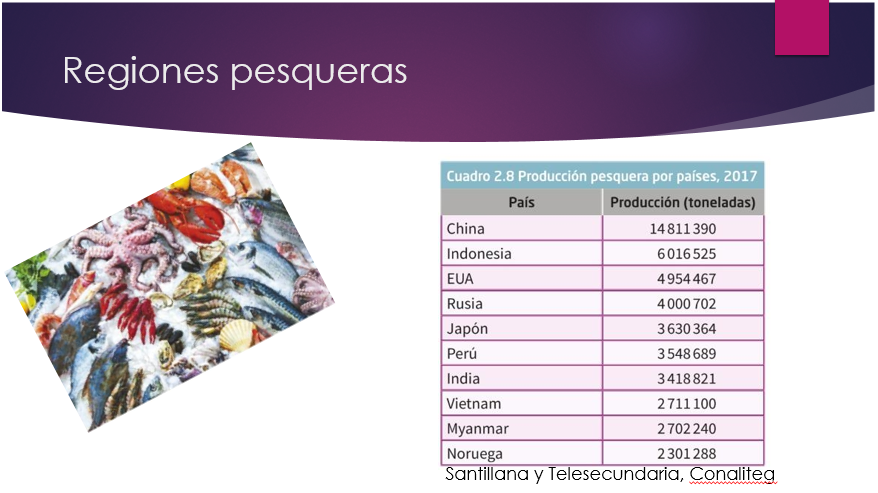
Observa que en los primeros lugares se encuentran China, Indonesia y Estados Unidos de América.
¿Qué factores influyen para que esto suceda?
Son varios: las corrientes marinas frías, pues transportan una gran cantidad de plancton, que es el principal alimento de los peces; la forma de las costas y la extensión de la plataforma continental.
Analiza el siguiente mapa sobre la distribución de la producción pesquera en el mundo:
Como puedes ver en el mapa, las principales regiones pesqueras se ubican en los océanos Pacífico y Atlántico, algunas de las zonas más productivas coindicen con las corrientes frías de Kuroshivo y de Humboldt, frente a las costas orientales de Japón y las costas de Chile y Perú, en Sudamérica.
Debido a la pesca excesiva en altamar, se ha provocado desequilibrio en los ecosistemas y la desaparición de grandes bancos de peces.
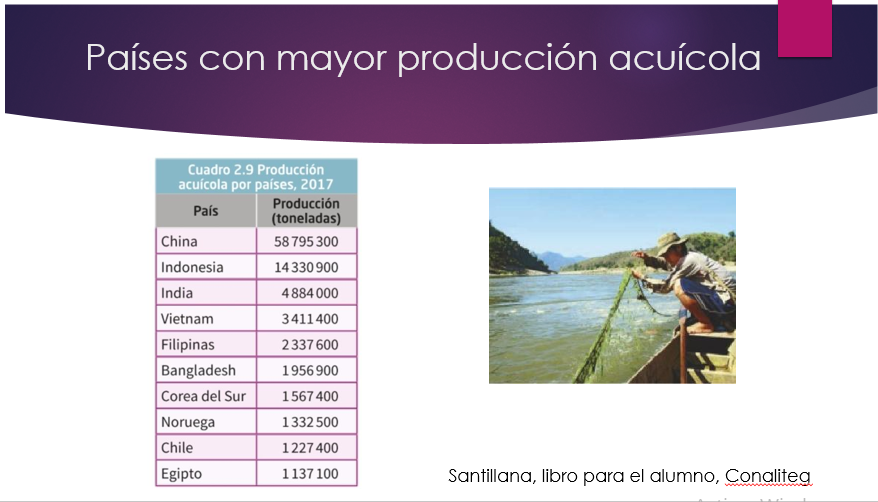
La acuicultura es una de ellas, que garantiza el acceso a los recursos pesqueros, practicando la crianza de peces, moluscos y crustáceos, en ríos, lagos, lagunas y granjas acuícolas.
Como la granja acuícola de cobia, un pez de alto valor comercial en Vietnam.
La acuicultura ha sido una actividad que ha ganado terreno a nivel mundial y se practica principalmente en países como China, Indonesia, India y Vietnam. Como puedes ver en la tabla.
¿Y qué pasa con la actividad forestal y su distribución en el mundo?
Recuerda que las regiones forestales se clasifican según su producto: en maderables y no maderables.
Las regiones forestales más productivas del mundo comprenden los bosques templados y fríos del hemisferio norte. Sobresalen países como Estados Unidos de América, China y Canadá, como los mayores productores de madera de pino y celulosa para papel.
Por otro lado, los bosques tropicales son una fuente de recursos forestales de alto valor comercial, ya que incluyen maderas preciosas como el ébano, la caoba y el cedro rojo. Y de estos bosques también se obtienen ceras, aceites, caucho y otros productos utilizados en la industria; por ejemplo, algunas de las cremas corporales que se utilizan contienen esos recursos.
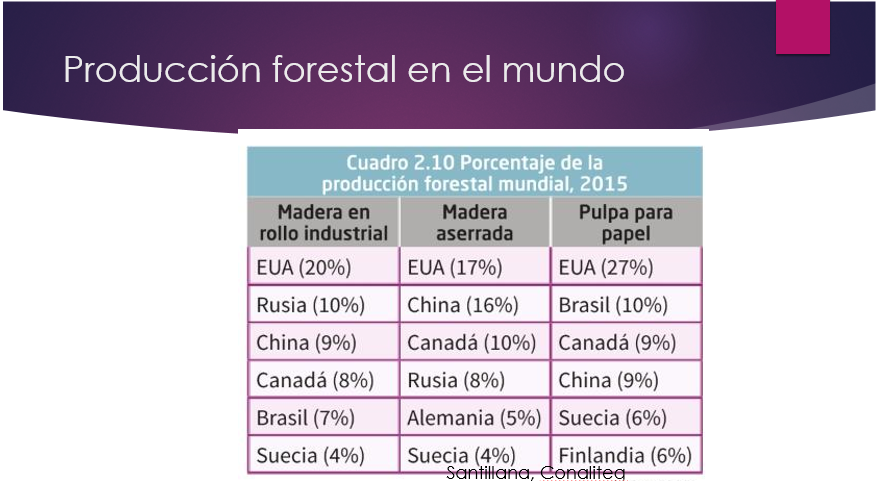
Como puede observar en la tabla, Estados Unidos de América, China, Rusia, Canadá y Brasil; entre otros países, presentan el mayor porcentaje de la producción forestal mundial.
En las regiones áridas no hay recursos maderables, sólo algunos árboles pequeños, cuyos troncos y ramas se utilizan como combustible; sin embargo, estas regiones son ricas en productos no maderables, como plantas de uso medicinal, esencias, colorantes y fibras que se utilizan para la ropa.
¿Esto quiere decir que hasta la ropa que utilizas puede provenir de la actividad forestal?
Si lo piensas detenidamente, y contestando a la pregunta inicial, todo, absolutamente todo lo que utilizas tiene su origen en los recursos que se obtienen por medio de las actividades económicas primarias.
Es por eso la importancia de las actividades económicas primarias y por qué no se pueden practicar en todo el mundo.
Observa el mapa sobre la producción forestal a nivel mundial.
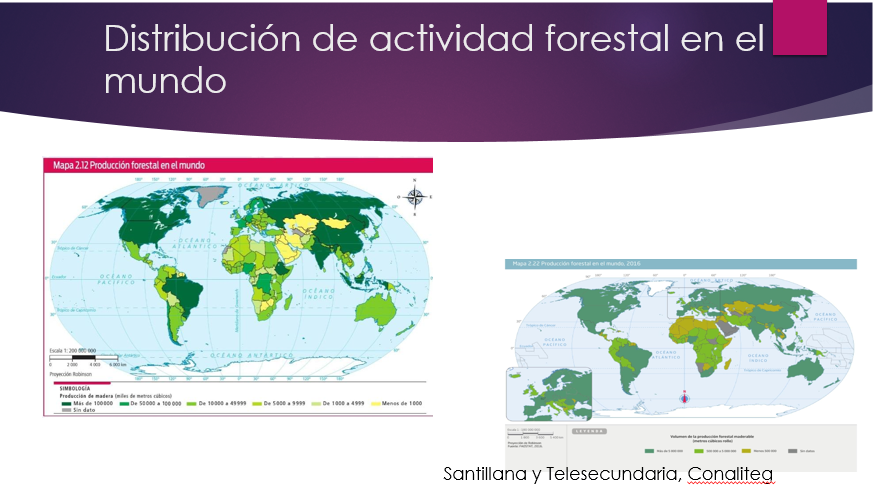
Hay algunas partes del mundo que tienen muy poca o nula producción forestal; pero ahora se puede explicar que es por su localización geográfica, y su tipo de clima, que no es favorable para el desarrollo de esta actividad; o no hay cuerpos de agua que favorezcan al crecimiento de árboles y pinos.
Por ejemplo, las regiones áridas, como puedes observar en el mapa, son una fuente muy importante de recursos no maderables; y recuerda que de ahí se obtienen otros recursos económicos, de la explotación de las plantas con las cuales se pueden elaborar cremas, shampoos y jabones, entre otras cosas.
Es increíble la importancia que tienen estos productos en la vida de todos.
Observa a tu alrededor y descubre de dónde proviene todo lo que consumes.
Y para dar seguimiento a lo que has estudiado y ampliar tus conocimientos sobre la distribución geográfica de las actividades económicas primarias, te comparto el siguiente material audiovisual.
- Dr. Álvaro Sánchez
https://drive.google.com/file/d/1icTr80xHGORdSxXn5Y11UNAnC0bV01rT/view?usp=sharing
Como bien lo explicó el Doctor Álvaro, la distribución de las actividades primarias es desigual en el mundo, debido a la diversidad de condiciones geográficas como el relieve; la ubicación, que influye en los climas; el tipo de suelo; entre otros factores que favorecen la diversidad de recursos disponibles.
Y en conclusión, eso explica por qué hay más agricultura, ganadería, pesca o actividad forestal en algunos lugares del planeta que en otros.
El Reto de Hoy:
Analiza las siguientes preguntas e intenta contestarlas para movilizar tus conocimientos.
1. Se caracteriza por tener la mayor producción de arroz en el mundo, aprovechando sus condiciones de clima y suelo para el desarrollo de la actividad agrícola, ¿qué país es?
R= China
2. Es considerado el país con mayor producción de leche y huevo a nivel mundial, esto debido al aprovechamiento de su entorno físico y al alto desarrollo tecnológico…
R= Estados Unidos de América, pues sus condiciones geográficas y su desarrollo económico le permiten el aprovechamiento de sus recursos naturales.
3. ¿Qué países ocupan los primeros lugares en el mundo por su producción pesquera?
R= China, Indonesia y Estados Unidos de América. Y por lo que se pudo ver en las imágenes, en países con mayor desarrollo practican pesca de altura, y Japón es una región pesquera muy importante a nivel mundial.
4. Una alternativa para garantizar el acceso a los recursos pesqueros, frenando la desaparición de grandes bancos de peces, ¿es?
R= La acuicultura, y se practica en países como Vietnam.
5. ¿Qué importancia tiene conocer la distribución de las actividades económicas primarias en el mundo?
R= Es muy importante reconocer la desigual distribución de los recursos naturales en el mundo, pues de ello depende el desarrollo de las actividades económicas primarias que nos proporcionan todo lo necesario para vivir.
En esta sesión lograste: Identificar las actividades económicas primarias y su distribución en el mundo.
Considerando sus características, y las condiciones geográficas que intervienen en su desarrollo: relieve, clima, suelo y agua.
Y tomando en cuenta el desarrollo tecnológico en países con mayor capital, el cual ha contribuido al aprovechamiento de los recursos, en esos países.
Sin perder de vista, que se ha incrementado la preocupación por el cuidado y conservación del medioambiente, buscando alternativas amigables para no dañar los recursos naturales.
Recuerda que todo lo revisado en esta sesión lo puedes seguir investigando en tu libro de texto de Geografía de México y del Mundo. O consultando la página de CONALITEG, en donde puedes encontrar información que enriquezca tus conocimientos, con respecto a este tema.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Por una mejor salud, sumemos nutrientes y restemos calorías.
Aprendizaje esperado: Explica cómo evitar el sobrepeso y la obesidad con base en las características de la dieta correcta y las necesidades energéticas en la adolescencia.
Énfasis: Reconocer las necesidades energéticas en la adolescencia.
¿Qué vamos a aprender?
En la sesión de hoy trabajarás con el aprendizaje esperado:
Explica cómo evitar el sobrepeso y la obesidad con base en las características de la dieta correcta y las necesidades energéticas en la adolescencia.
Y el propósito es:
Reconocer las necesidades energéticas en la adolescencia.
En esta sesión titulada: Por una mejor salud, sumemos nutrientes y restemos calorías.
Para ello, debes recurrir a tus materiales escolares y tener a la mano tu “Abecedario biológico”, imprescindible en cada sesión.
¿Qué hacemos?
Observa lo que dice el maestro Raúl de Tonalá, Jalisco, quien estará participando en esta sesión mediante una serie de videos.
- Maestro Raúl 3
Se debe mencionar que esto no implica por sí mismo la disminución o eliminación de los problemas de sobrepeso y obesidad, sino que solamente contribuye a la creación de un ambiente saludable que fomente un mejor estilo de vida.
- Maestro Raúl 4
Observa la duda que planteó un alumno con respecto a la alimentación.
“He visto que algunos de mis familiares eligen productos bajos en azúcar o en grasas, ya que comentan que son más saludables y que a la vez nos ayudarán a evitar el sobrepeso y la obesidad ¿Esto es cierto?”
Recuerda que al hablar de dieta correcta se refiere al consumo de alimentos con cantidades adecuadas de proteínas, carbohidratos, lípidos, vitaminas, minerales y agua simple potable.
Además, es cierto que en el mercado existen muchos productos que se promocionan como “dietéticos”, “bajos en azúcares” y bajos en grasas o lípidos, lo cual realmente no significa que sean bajos en energía.
Por lo que podrías comentarles a tus familiares están en lo correcto al elegir productos bajos en azúcares o en grasas, pues efectivamente son más saludables. Sin embargo, también conviene recordar que no hay nada mejor que el consumir alimentos basados en el Plato del Bien Comer, realizar actividad física con regularidad, de tal manera que las kilocalorías que ingieras estén acordes con dicha actividad, tu edad y sexo, esto les permitirá mantener un estilo de vida saludable y un peso correcto.
- Maestro Raúl 6
Y para reconocer si un producto procesado como una bebida azucarada o cualquier otro alimento influirá en el desarrollo de enfermedades alimentarias, debes recordar que el cuerpo en todo momento requiere de la energía de los alimentos para su funcionamiento, aunque no se esté haciendo ejercicio alguno, ya que el respirar, digerir o dormir también representa un gasto de energía.
Cualquier alimento que se consuma, tendrá energía, excepto el agua simple potable. La energía contenida en los nutrientes de los alimentos se mide en calorías (cal), aunque es más frecuente la kilocaloría (kcal). Un gramo de carbohidratos y de proteínas contienen 4 kilocalorías de energía, en cambio un gramo de lípidos contiene 9 kilocalorías.
- Maestro Raúl 7
Para reconocer cuánta energía es la que necesita, se han creado tablas que estiman la cantidad aproximada de kilocalorías que requerirían consumir de acuerdo a su edad, sexo, estatura y peso.
Observa la tabla que se muestra a continuación e identifiquen la cantidad de energía que necesitan según su edad y actividad física.
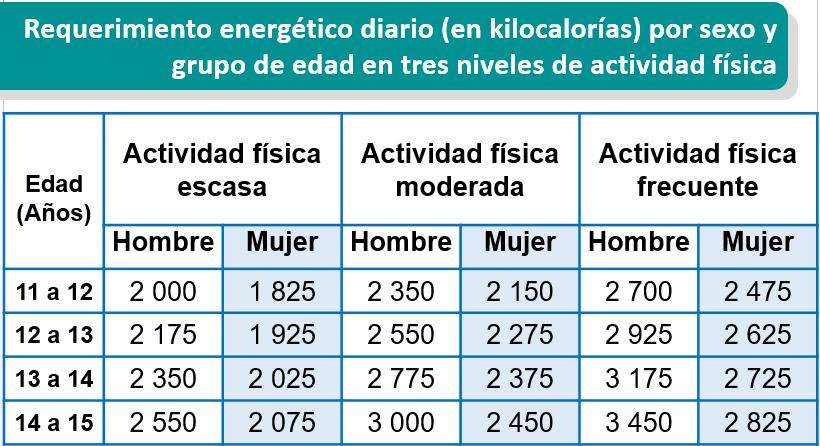
Por ejemplo, puedes ver que en la primera columna se muestran los rangos de edad en los cuales te puede ubicar. Después, se muestran tres columnas que clasifican la actividad física diaria en tres tipos: Escasa, Moderada y Frecuente.
- Maestro Raúl 8
¿Ya identificaste cuál es tu tipo de actividad física?
Observa de nuevo la tabla.
Debajo de cada uno de los tipos de actividad física se encuentra el sexo de la persona y al cuadrar la edad, con la actividad física y el sexo, podrás identificar la cantidad de kilocalorías que necesitarías para mantener el correcto funcionamiento del organismo.
Debes tomar en cuenta que estos valores pueden variar de persona a persona, ya que la genética, la estructura corporal y distintas enfermedades pueden hacer que estos valores sean diferentes para cada persona.
- Maestro Raúl 9
Por lo tanto, es mejor buscar otras opciones como las aguas de sabores naturales como limón o jamaica, que además de ser bajas en azúcares y calorías, ayudarán a tu cuerpo a metabolizar mejor los azúcares de una fruta de temporada que el de un edulcorante artificial.
Observa otra pregunta que realizó otro alumno.
“He visto que en la televisión promocionan muchos productos para bajar de peso, como pomadas, fajas o pastillas. ¿Me podría decir si estas son opciones recomendables para bajar de peso para nosotros los adolescentes?”
- Maestro Raúl 11
Ahora, para llevar un seguimiento aproximado de la cantidad de kilocalorías que consumirías por los alimentos que conforman tu dieta, observa la siguiente tabla, en la cual muestra el aporte kilocalórico aproximado por cada porción de alimentos.
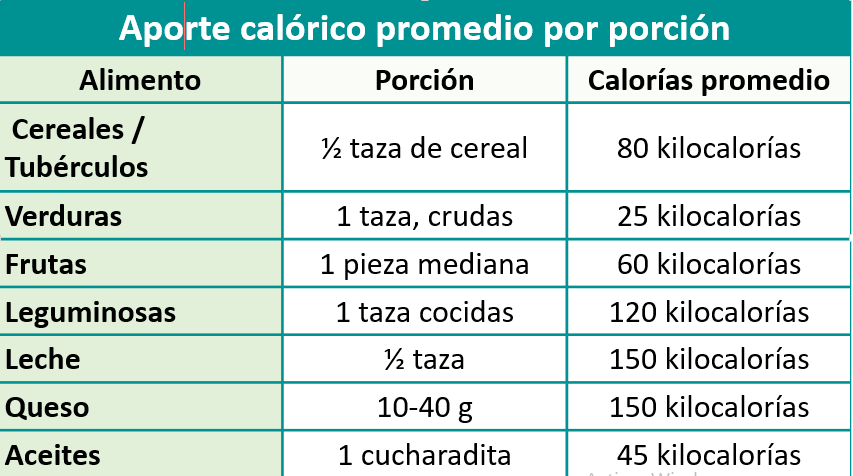
Como puedes observar, en el caso de los cereales y leguminosas, como el arroz, el maíz, la avena o el trigo, en forma de sopa, tortillas, cereal de caja, granola, barras energéticas, nos aportan 80 kilocalorías por media taza. En el caso de que desees comer un poco más, la energía se multiplicaría.
Piensa entonces ¿Cuántas porciones de cada alimento estás consumiendo? ¿Serán las sugeridas para esta etapa de tu desarrollo?
- Maestro Raúl 12
Ahora, para identificar cuánta energía gastas en las actividades que realizas al día o en la semana, observa las siguientes imágenes que muestran la cantidad de kilocalorías que una persona de 50 o 60 kilogramos gastaría en 30 minutos continuos de ejecución.
Para dormir necesitarías 26 kilocalorías, al ver la televisión sólo se utilizarían 27 y para estudiar sólo se requerirían 30. Para lavar trastes necesitaríamos 56 kilocalorías por 30 minutos.
Si durante el día realizas actividades físicas más intensas, puedes reconocer que caminar lento necesita 77 kilocalorías, trapear 98, bailar 152 así como el caminar rápido nos consume 146 kilocalorías.
En caso de que la actividad física sea intensa o vigorosa, se sabe que el jugar futbol o basquetbol te resultará un gasto energético de 210 kilocalorías, el andar en bicicleta a una alta velocidad requiere de 250, el correr 227 y el subir escaleras 381.
¿Cuáles de ellas son las que realizas frecuentemente? y ¿Cuántas kilocalorías estarías gastando para realizar estas actividades?
- Maestro Raúl 13
Es de suma importancia que las y los adolescentes consuman suficiente vitamina A, vitamina D, vitaminas del complejo B, calcio, hierro y zinc, por lo que se recomienda la ingesta diaria de algunos vegetales verdes y alimentos de origen animal como la carne, huevo y lácteos.
- Maestro Raúl 14
En esta sesión identificaste los requerimientos calóricos que necesita el cuerpo según tu sexo, edad y el tipo de actividad física que desarrolles.
Recuerda que una dieta correcta debe ir acompañada de actividad física; por ello es necesario que acumules 30 minutos al día. Puedes iniciar con periodos de cinco a diez minutos e incrementar poco a poco el tiempo.
Ahora, es momento de agregar una nueva palabra al “Abecedario biológico”
La palabra es “kilocaloría”, recuerda anotar su definición, así como ilustrarla.
El Reto de Hoy:
- Maestro Raúl 16
Si un día decidieras consumir los tres productos súper procesados que más te agradan, ¿Cuántas kilocalorías te aportarían? ¿Qué actividades físicas deberías hacer y por cuánto tiempo para poder quemar éstas kilocalorías? ¿De qué manera esta información te ayudaría a mejorar tus hábitos de consumo?
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario