Aprende en Casa III SEP: 8 de febrero TAREAS y ACTIVIDADES de 1° de secundaria
A continuación dejamos los temas vistos el 8 de febrero de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 1° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Lunes 8 de febrero, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en Casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
¿Dónde busco lo que digo?
Aprendizaje esperado: Recopila y comparte refranes, dichos y pregones populares.
Énfasis: Definir y emplear fuentes escritas para consultar refranes, dichos y pregones.
¿Qué vamos a aprender?
Repasarás cómo y dónde puedes consultar refranes de manera escrita. Asimismo, los localizarás en textos literarios, para que los puedas entender mejor.
¿Qué hacemos?
En esta ocasión aprenderás a identificar refranes, dichos y pregones en fuentes escritas. Estas frases forman parte de la sabiduría popular y pueden ser utilizadas en una infinidad de situaciones cotidianas. Existen tantos refranes y dichos, y muy probablemente encontrarás los apropiados para muchísimos momentos de tu vida.
En esta sesión se revisarán esas frases sabias que fueron acuñadas hace mucho tiempo y que forman parte de la riquísima herencia cultural.
¿En todos los países tienen refranes, dichos y pregones?
Así es, los hay en todos los idiomas del mundo, porque las situaciones sobre las que éstos hablan son universales.
¿Tú has escuchado refranes en tu casa? ¿Recurren a ellos con frecuencia?
Son muy útiles para comunicar una idea, dar un consejo u ofrecer y recibir un servicio.
¿Alguna vez has escuchado ese refrán que dice: “El que busca encuentra”?
No sólo se refiere al hecho de averiguar algo que se temía descubrir, sino también a la posibilidad de encontrar algo muy esperado. En esta sesión “se buscará para encontrar” fuentes escritas que contengan dichos, refranes y pregones.
Pero, ¿los refranes, los dichos y los pregones son igualitos?
La respuesta es que es muy importante que conozcas las diferencias entre estos tres tipos de consejos populares. Cabe mencionar que, al transmitirse de persona en persona y de generación en generación, a través del tiempo pueden modificarse, aunque sea mínimamente.
Todos tienen una característica particular: son fáciles de recordar. Revisa las definiciones de refrán, dicho y pregón, en el siguiente video.
- Refranes dichos y pregones.
Con este video te quedará clara la diferencia entre refrán, dicho y pregón, pero ¿es posible encontrar ejemplos de estas expresiones en libros y demás fuentes impresas?
¡Claro! Incluso existen escritoras y escritores que han dejado testimonio de ellas a través sus obras literarias.
Ahora bien, para que puedas hacer tu compilación, es necesario saber dónde buscar; esta sesión está centrada precisamente, en fuentes escritas: libros, revistas e internet.
Pero antes, reflexiona.
- ¿Alguna vez has buscado refranes, dichos y pregones?
- ¿Sabes dónde buscarlos?
- ¿Sabes qué fuentes escritas puedes consultar para su compilación?
Antes de reunir el material que necesitarás para crear tu compilación, ¿qué te parece si primero rastreas la antigüedad de los refranes, dichos y pregones en el español de México? Después se realizará la búsqueda en fuentes escritas.
Para iniciar se dirá que cada cultura tiene su propia manera de expresar parte de su sabiduría popular a través de proverbios, dichos y refranes, pero ¿cómo y cuándo es que éstos se crean?
Aunque cada una de estas frases populares surgió en alguna época, a partir de la cual comenzó a propagarse por medio de la repetición, no es posible determinar la fecha específica en la que se originó. El hecho de que se transmitan de generación en generación las somete a muchas variantes.
Se puede afirmar que los refranes que se encuentran en el léxico provienen de España y de algunas partes de Europa. Con la llegada de los españoles se mezcló la lengua de los conquistadores con las lenguas originarias del país, es decir, se dio una fusión cultural que modificó el habla. Las aportaciones extranjeras referentes a los refranes, dichos y pregones se quedaron en el país y se enriquecieron con la cultura de los pueblos indígenas.
Cabe mencionar que, en ocasiones, estas expresiones conllevan una historia implícita; por ejemplo, tú seguramente llegaste a escuchar el dicho: “Salvado por la campana” en el salón de clases. Si una maestra o maestro te invitaba a participar o te exigía la entrega de una tarea y en ese preciso instante tocaban el timbre para el cambio de clase o salida, no faltaba quien decía: “Te salvó la campana”.
La popularidad del dicho ha hecho que se generen diversos mitos sobre su origen; uno de ellos, desde luego, erróneo, remite a la existencia de campanas dentro de los ataúdes, mismas que podían ser usadas en caso de que, por error, alguien fuera enterrado vivo. Sin embargo, como ya se dijo, esta versión es falsa. El verdadero origen de la frase tiene que ver con el boxeo, en donde como sabes, se marca con una campana el final de cada round.
Pero, ¿dónde se puede encontrar esta información?
Qué te parece si escuchas las voces del ayer, en donde se preguntó a varias personas, lo siguiente:
- ¿Sabe algún dicho, refrán o pregón?, ¿cuál?
- ¿Sabe qué significa?
- ¿Quién se lo enseñó o dónde lo aprendió?
- ¿Sabe dónde puede encontrar refranes, dichos y pregones en fuentes escritas?
Escucha y lee las respuestas.
- Audio 1.
|
Sí, sé el refrán que dice: “Dios aprieta, pero no ahorca”; significa que Dios no nos dará más cosas de las que no podamos soportar. Mi abuela lo decía mucho cuando era niña, pues a veces no teníamos dinero para comer. No sé en dónde, probablemente en internet.
|
- Audio 2.
|
Por supuesto que me sé varios, desde dichos y refranes hasta pregones. El que dice: “A darle que es mole de olla” significa que hay que hacer las cosas bien, rápidas y sin quejas. Mi familia lo dice mucho. Cuando mi papá nos daba una orden, lo teníamos que hacer, y cuidado pusiéramos alguna cara. En los refraneros o libros, ahí debe haber bastante información.
|
- Audio 3.
|
Sí, me sé el dicho que dice: “No des tu brazo a torcer”; significa que una persona debe tener carácter o debe ser firme con la decisión que haya tomado. Mi mamá se lo dice a mi hermana cuando castiga a mi sobrina porque luego va a chillar con la intención de que le quite el castigo. Hay libros que tienen refranes, dichos y hasta chistes, creo que los pueden consultar en una biblioteca o comprarlos.
|
- Audio 4.
|
Sí, conozco los pregones del ropavejero: “Colchones que vendan, ropa que vendan”. Cuando alguien pasa gritando o con una música, se puede escuchar de fondo lo que ofrece al público; por ejemplo, cuando voy al mercado, los que venden, gritan. En este caso, el ropavejero pide que le vendan lo que ya no se necesita. Cuando era niño, mi mamá me decía que, si no me portaba bien, me llevaría con el ropavejero o el señor del costal, eso me daba miedo y cada que lo escuchaba, me escondía. Supongo que debe existir algo escrito o se copian las palabras de manera que todos las conocemos.
|
Como leíste y escuchaste, la mayoría de los entrevistados saben y conocen refranes, dichos y pregones, ya sea porque los han escuchado de personas mayores que los usaban en situaciones específicas o porque forman parte de la tradición oral propia del lugar donde viven; sin embargo, no identifican con certeza en qué fuentes escritas los pueden encontrar.
El primer tipo de texto donde puedes iniciar tu búsqueda son los llamados refraneros. ¿A qué te suena este nombre? Sí, precisamente son libros que resguardan entre sus páginas refranes de diversas temáticas. Existen refraneros modernos y otros más antiguos.
¿Sabes quién fue Gonzalo Correas?
Gonzalo Correas fue autor de un refranero clásico en español. Él nació en Jaraíz Vera, España, en el año 1571. En Salamanca estudió teología, latín, hebreo y griego; esa razón lo llevó a estudiar la lengua castellana, por lo que hizo aportaciones al vocabulario de refranes y frases proverbiales en el libro Vocabulario de refranes y frases proverbiales y otras fórmulas comunes de la lengua castellana en que van todos los impresos antes y otra gran copia.
Es importante mencionar que es uno de los libros más antiguos que versan sobre este tema, su valor es incalculable debido a que la mayoría de los refranes que se conocen hoy en día datan de esa época; además, al consultar este libro, puedes conocer otros refranes que quizás ya estén en desuso. Pero, ¿es fácil conseguirlo o hay que zambullirse en alguna librería donde venden volúmenes antiguos?
Una buena noticia es que este libro lo puedes encontrar en internet.
Al asentar por escrito esta información, los refraneros permiten echar un vistazo a las costumbres de las sociedades que los engendraron, a los enfoques políticos y a la visión religiosa de la época a la que pertenecen. Si no se contará con esos invaluables testimonios, se hubiera perdido en el tiempo un material altamente significativo.
Debido a que los refranes, dichos y pregones no siempre tienen un autor, se recopilaba la información, y las personas como Gonzalo Correas se encargaban de transcribirla para hacerla perdurar en la sociedad y en el tiempo.
Para poder consultar este refranero, puedes buscarlo en internet o, si hay condiciones seguras, puedes asistir a una biblioteca. Para ello:
- Coloca el título de la obra en el buscador, en este caso será: Vocabulario de refranes y frases y otras fórmulas comunes de la lengua castellana en que van todos los impresos antes y otra gran copia.
- Verifica que el autor sea Gonzalo Correas.
- Si estás en internet, probablemente encuentres el libro en formato PDF, así que podrás descargarlo.
- Si estás en una biblioteca, verifica si puedes solicitar el libro en préstamo a domicilio. En caso de ser de uso interno, puedes solicitar fotocopiar algunas páginas, o bien sacar fotos con algún dispositivo digital.
Ahora tienes la compilación más antigua de refranes, la cual podrás utilizar para ensamblar tu propia colección de refranes, dichos y pregones.
“Para muestra un botón”, dice el dicho, así que, a continuación, se presentará un refrán contenido en este maravilloso refranero. El cual se interpretará y se buscará equivalentes de refranes actuales.
El refrán es: “A Azuaga por aceite y a La Granja por naranja”.
Fíjate que Azuaga y La Granja están escritos con mayúscula inicial. Esto es porque son nombres de dos ciudades en Extremadura, España. La clave para entender este refrán está en que en estas ciudades antiguamente no se encontraba ni aceite ni naranjas.
Por lo tanto. ¿Cuál sería su equivalente moderno?
- No le busques tres pies al gato.
- Echar la casa por la ventana.
- Consultar algo con la almohada.
La respuesta correcta es la a. Es imposible pedirle algo a alguien cuando sabes de antemano que no lo va a lograr, o simplemente no se puede pedir algo que no se puede hacer. Sería como buscarle tres pies al gato, sabiendo que tiene cuatro. Como dato curioso, Correas hace alusión en casi todos los refranes a los gatos.
Otro escritor perteneciente a la misma época es Melchor de Santa Cruz, nacido en Toledo, España, y es reconocido por ser el autor de la miscelánea popular: “Floresta española, de apotegmas, o sentencias, sabia y graciosamente dichas, de algunos españoles”, escrita en 1574. Hay que recordar que no sólo llevan como nombre refranes, pues en la antigüedad también se les llamaba aforismos, proverbios o sentencias.
Nuevamente, se te invita a que busques este refranero, ya sea en bibliotecas o internet. Para ello, bastará con seguir los pasos que se mencionaron anteriormente. Se espera que puedas encontrarlo, pues tendrás un libro que no sólo contiene refranes o dichos, sino también chistes, anécdotas y cuentos cortos que podrás consultar para tu compilación.
Probablemente el lenguaje no sea tan fácil de comprender debido a la época en la que se escribió; puedes consultar el Diccionario de la Lengua Española para entenderlo mejor.
Gracias a la tecnología con la que se cuenta hoy en día, universidades e instituciones dedicadas al estudio de la lengua ponen al alcance de todos bases de datos que recopilan refranes y dichos clasificados por temas, no sólo en español, sino de otras lenguas del mundo, tanto modernos como antiguos. Si tienes la posibilidad de consultar estas bases de datos, no dudes en hacerlo.
De una de estas bases se tomó el siguiente refrán: “A la noche y con aguacero no es bueno traer sombrero”.
Este refrán hace alusión a la meteorología, pero para poder entenderlo tendrías que estar familiarizado con los barcos antiguos y con la navegación en altamar.
¿Cuál crees que es el “sombrero” del barco?
La respuesta es las velas, las cuales ayudan a mover al barco por la fuerza del viento. Imagínate que, en plena tormenta, en la noche, con fuertes vientos, a la tripulación se le ocurriera tender las velas extendidas, probablemente el barco estaría a merced de las fuertes ráfagas y de la mar agitada. Por ello, se solía decir que: “A la noche y con aguacero no es bueno traer sombrero”.
No es común escuchar este refrán en la cotidianidad, por lo tanto, se podría decir que es un refrán en desuso. Si no lo hubieran registrado en un texto escrito, probablemente se hubiera perdido en el olvido.
Así es. Esta es una razón más para valorar las fuentes escritas. Hasta este momento has explorado fuentes escritas, como refraneros, ahora se revisará una fuente más: las obras literarias.
Por ejemplo, el libro de Miguel de Cervantes Saavedra, El ingenioso hidalgo don Quijote de la Mancha. Como dato curioso, este libro tiene más de 381 104 palabras y es una gran fuente para obtener dichos o proverbios, pues muchos refranes de amplio uso aún en estos días se pueden encontrar en esta novela. Si ya has leído el libro, notarás que quien ahonda más en el tema es Sancho Panza. Ahora se citarán algunos ejemplos.
|
“Al buen entendedor, pocas palabras.”
Significado: una persona que sabe observar y escuchar bien, no necesita que le digan las cosas dos veces.
|
|
“Al buen pagador, no le duelen las prendas.”
Significado: explica que, si una persona hace lo que debe, no le importa proporcionar una garantía.
|
|
El refrán hace alusión al poder de las palabras: no es necesario mencionar tantas para que se entienda un mensaje.
|
|
Este refrán se refiere a que una persona que está segura de poder cumplir con sus responsabilidades, no teme ofrecer una garantía para asegurar la fiabilidad de su palabra. |
Pero ¿es cierto que Miguel de Cervantes Saavedra escribió su novela mientras estaba en la cárcel, debido a que fue injustamente castigado al negarse a pagar los excesivos impuestos que se recaudaron para costear la Armada Invencible?
Es cierto. Además, la novela no sólo cuenta con una parte, sino con dos. Es un libro que ha tenido más de 500 millones de copias y es, sin duda, una de las obras cumbre escritas en lengua española.
Otra novela que aporta refranes es El Periquillo Sarniento; esta obra clásica data de 1816 y fue escrita por el mexicano José Joaquín Fernández de Lizardi. Reflexiona y lee algunos fragmentos sobre los modismos que vienen en esta novela.
|
“Acercarse a todo trapo.”
Significado: sin temor y rápidamente.
|
|
“Cuajar un rato.”
Significado: charlar por un buen rato.
|
|
El primer refrán se refiere a que se debe hacer algo a toda prisa. |
|
El segundo simboliza cuando alguien se queda platicando durante un buen rato.
|
Probablemente algunos de los refranes y dichos mencionados los has leído en las obras de diversos escritores mexicanos de los siglos XIX, XX y XXI: José Tomás de Cuéllar, en Baile y cochino; Agustín Yáñez, en Ojerosa y pintada, y Armando Ramírez, en varias de sus obras que tienen como escenario el célebre barrio de Tepito, en la Ciudad de México.
Por último, no se puede dejar de lado los estudios académicos sobre refranes, dichos y pregones. Varios investigadores, especialistas en literatura, etnografía, antropología, sociología, historia y otras disciplinas, tanto mexicanos como de otros países, han basado su obra en el estudio de los refranes, de los dichos y los pregones. En sus artículos académicos ellos suelen tener recopilaciones que a veces incluyen en apéndices de sus trabajos de investigación.
Para acceder a estos estudios académicos, explora los repositorios digitales de las universidades públicas y centros de investigación del país. Otra manera es explorar los catálogos digitales de los sistemas bibliotecarios de estas mismas instituciones. Asimismo, puedes recurrir a los buscadores académicos.
Para acceder a ellos, en la barra de navegación de tu explorador de internet pon las palabras “buscador académico”. El buscador te arrojará entre los primeros resultados sitios de buscadores académicos. Da clic para entrar a la página y ya que estés ahí, escribe: “refranes”, “dichos” o “pregones”. Es recomendable añadir el origen o el periodo; por ejemplo, “refranes siglo XX” o “pregones mexicanos”, para ayudar a precisar la búsqueda. Así, el buscador te dará acceso a diversos trabajos académicos donde puedes conseguir diversos refranes, dichos y pregones. Después de este repaso por fuentes escritas, ¿ya sabes cuáles consultarás para conformar tu compilación de refranes, dichos y pregones?
Para ello, se te aconseja que explores fuentes escritas y selecciones algunos refranes, dichos y pregones. Léelos y elije los que incluirás en tu compilación. Y no olvides indicar la referencia bibliográfica.
Ahora, se recapitulará lo visto en esta sesión.
Recordaste las definiciones de refrán, dicho y pregón, considerando que cada uno tiene sus propios elementos y características que los hacen únicos; además, se mencionó que cada pueblo tiene distinta cultura que conlleva su forma de expresarse y su manera de usar los refranes, dependiendo del contexto y sus costumbres; escuchaste y leíste la opinión de varias personas, las cuales mencionaron su conocimiento sobre los refranes, los dichos y pregones; exploraste y realizaste paso a paso la búsqueda de información en fuentes escritas; se ejemplificó con libros recomendados para la compilación de tu trabajo, refranes y dichos, así como la recomendación de libros para los pregones. Y finalmente, aprendiste que no sólo se conocen de esa manera, también se les llama sentencias, aforismos o proverbios.
Recuerda que el fomento de la escritura es importante, pues gracias a ella se puede preservar la cultura, costumbres y conocimiento para las generaciones venideras. Es parte del patrimonio cultural.
Has concluido la sesión del día de hoy.
Revisa en tu libro de texto el aprendizaje esperado: “Recopila y comparte refranes, dichos y pregones populares”, ubica la sección dedicada a explorar fuentes escritas y realiza las actividades que se te proponen. También, para ampliar la información, puedes buscar en internet.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Multiplicación con números decimales
Aprendizaje esperado: Resuelve problemas de multiplicación con fracciones y decimales y de división con decimales.
Énfasis: Resolver problemas de multiplicación con números decimales en contextos científicos.
¿Qué vamos a aprender?
Durante esta sesión realizarás cálculos matemáticos que te permitan la resolución de problemas en contextos cotidianos y científicos.
Para esta sesión utilizarás:
- Cuaderno de matemáticas o en su defecto hojas para tomar notas.
- Lápiz, goma, sacapuntas y
- Su libro de texto de matemáticas.
¿Qué hacemos?
Observa la siguiente situación.
“Luisa tiene una bicicleta. Al pasear en ella, le dio curiosidad saber cuántas vueltas darían las ruedas para recorrer cierta distancia, así que midió y se dio cuenta que cuando la rueda da una vuelta completa, recorre 0.8 metros.”
Con esto en mente, ella quiere saber cuántos metros recorrerá si la rueda de su bicicleta da 3 vueltas, 100 vueltas, 0.75 vueltas, un medio de vuelta y 1/10 de vuelta.
¿Cuántas vueltas darán las ruedas para llegar de su casa a la tienda de la esquina que está a 80 metros de distancia?
Comienza ordenando los datos en una tabla, como la que se muestra a continuación:
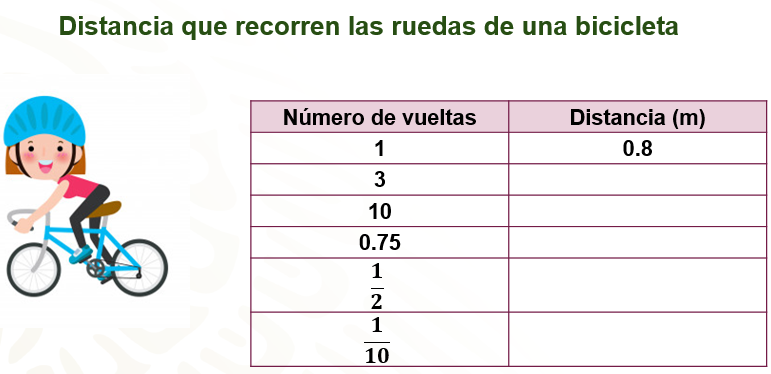
Elabora una tabla con dos columnas, en la primera coloca los datos referentes al número de vueltas que dan las llantas, en este caso son una, tres, 10, 0.75, media y un décimo de vuelta.
En la segunda columna colocamos la información referente a la distancia recorrida por las ruedas, en cada caso, ya sabemos que en una vuelta las ruedas recorren 0.8 metros.
¿Ya sabes qué operaciones tiene que hacer Luisa para calcular las distancias?
Si la rueda de la bicicleta da una vuelta y recorre 0.8 metros, entonces para saber la distancia que recorre en 3 vueltas, podemos sumar 0.8 tres veces, es decir, 0.8 + 0.8 + 0.8, que es igual a 2.4
Con esto ya sabes que la rueda recorre 2.4 metros cuando da tres vueltas.
Para saber la distancia que recorren las ruedas en 3 vueltas, resolviste una multiplicación de un número natural por uno decimal.
En el caso anterior, 3 por 0.8, multiplicaste 3 por 8 que es igual a 24 y como 0.8 tiene una cifra decimal, en el producto se recorre anterior se recorre el punto decimal una cifra a la izquierda.
En el caso de la multiplicación 1.22 por 6, multiplicamos 122 por 6, cuyo resultado es 732. Después, recorres el punto decimal dos cifras a la izquierda, así 1.22 por 6 es igual a 7.32
¿Cómo puedes resolver la multiplicación para saber la distancia que recorren las ruedas en 100 vueltas?
En ese caso, lo que tienes que resolver es una multiplicación de una potencia de 10 por un número decimal. ¿Sabes cómo resolver este tipo de operaciones?
Al multiplicar una potencia de 10, es decir, números como 10, 100, 1 000, etcétera, por un número decimal, únicamente se recorre el punto decimal a la derecha tantas cifras como ceros tenga el número, si es necesario se agregan ceros. Por ejemplo, 10 por 0.8, como 10 tiene un cero, en 0.8 recorremos el punto decimal una cifra a la derecha, así tenemos que el resultado es 8.
Para 100 por 1.54, recorremos el punto dos cifras a la derecha que son los ceros que tiene 100, así el resultado es 154
Retomando el caso de Luisa, observa nuevamente la tabla.

Ahora ya sabes que en 3 vueltas las ruedas recorren 2.4 metros y que, en 10 vueltas, recorren 8 metros.
¿Cómo puedes completar el resto de la tabla? ¿Qué procedimiento permite multiplicar dos números decimales? ¿Y una multiplicación de un número decimal por un número fraccionario?
Para resolver este tipo de multiplicaciones, puedes convertir las fracciones en números decimales, para operar con este tipo de números. Es importante, considerar que cuando las fracciones no tienen un número decimal finito equivalente, es mejor operar con fracciones, que no son el caso de los datos de la tabla.
En estos casos, también operas como si fueran números naturales y en el resultado recorremos el punto decimal a la izquierda tantas cifras como cifras decimales tengan los números involucrados, como pueden ver en los ejemplos:
2.3 por 0.8 es igual a 1.84 y 1.22 por 1.4 es igual a 1.708
Para el caso en el que la rueda da 0.75 vueltas, multiplicamos 0.75 por 0.8 que es igual a 0.6 metros; Como 1/2 es igual a 0.5, multiplicamos 0.5 por 0.8 que es igual a 0.4 metros y finalmente, 1/10 que es igual a 0.1 lo multiplicamos por 0.8 y el resultado es 0.08 metros.
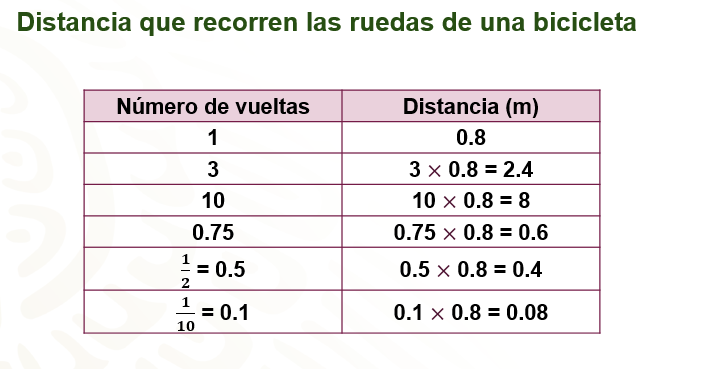
Por lo tanto, si la tienda se encuentra a 80 metros de la casa de Luisa, entonces las ruedas de su bicicleta tienen que dar 100 vueltas para llegar, porque 100 por 0.8 es igual a 80
Con estos conocimientos ya podrás resolver otro tipo de situaciones en las que se involucren multiplicaciones de números decimales. Observa la siguiente situación.
“Un médico familiar en el invierno pasado recetó a varios pacientes de la misma familia jarabe para la tos. Las indicaciones del medicamento mostraban que tenían que tomar una cucharada de 1.5 mililitros por cada 25 kilogramos de masa, cada 8 horas.
De acuerdo con su masa Toño debió tomar 3 cucharadas; su hija Lupe el equivalente a tres cuartos de cucharada y a su hijo Pablo, cuatro quintos de cucharada.”
De acuerdo con la información que se muestra, ¿cuántos mililitros de jarabe consumía cada persona en cada toma?
Para resolverlo puedes utilizar nuevamente una tabla y ordenar los datos. ¿Qué tipo de operaciones tienes que resolver? ¿Qué procedimiento se sigue en cada caso?
Observa la siguiente imagen:
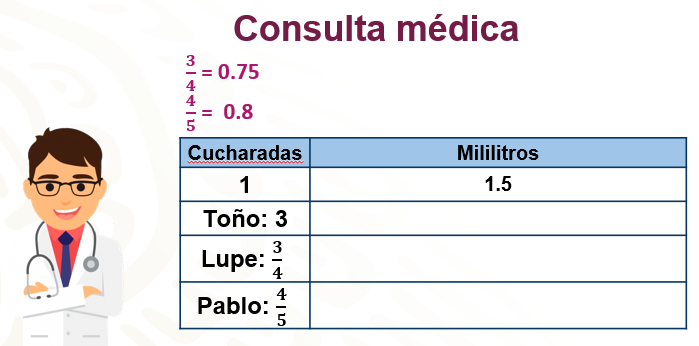
En la primera columna pones las cucharadas de las personas en cada toma: 3, 3/4 y 4/5 y en la segunda columna, los mililitros que consumía cada uno, sabes que una cucharada equivale a 1.5 mililitros.
Tienes nuevamente que resolver multiplicaciones de números naturales por decimales y de decimales por fracciones. En estos casos, operarás con números decimales, por lo que convertirás las fracciones a su representación decimal.
Para el caso de Toño, multiplica 3 por 1.5, cuyo resultado es igual a 4.5, que es la cantidad de mililitros de jarabe que toma. En el caso de Lupe, convierte 3/4 a número decimal, dividiendo el numerador entre el denominador, cuyo resultado es 0.75, multiplicamos 0.75 por 1.5, que es igual a 1.125 mililitros de jarabe, y para Pablo, convierte 4/5 a número decimal, 4/5 es igual a 0.8 y multiplicamos: 0.8 por 1.5 es igual a 1.2 mililitros.

Ahora ya sabes la cantidad de jarabe que toma cada uno.
A partir de esta información, ¿podrías encontrar la masa de Toño, Lupe y Pablo? ¿Cómo lo harías?
Si toman el medicamento 3 veces al día, y lo tienen que hacer durante 5 días, ¿cuántos mililitros tomará cada uno durante su tratamiento?
¿Sabías que la Tierra gira alrededor del Sol a una velocidad de 29.7 kilómetros por segundo?
Comparado con la velocidad de la Tierra, Marte gira a 0.81 veces la velocidad de la Tierra.
De lo anterior surgen dos preguntas:
¿Cuál de los dos planetas gira más rápido: Marte o la Tierra? ¿A qué velocidad gira Marte?
Seguramente ya sabes que la Tierra gira más rápido que Marte, ya que 0.81 es un número menor a una unidad.
En el caso de la segunda pregunta, para saber la velocidad la que gira Marte alrededor de la Tierra, multiplica 29.7 por 0.81, siguiendo el procedimiento que ya conoces, operas como si fueran números naturales y en el resultado colocas el punto considerando las tres cifras decimales que suman 29.7 y 0.81
Por lo que 29.7 por 0.81 es igual a 24.057
Marte gira alrededor del Sol a 24.057 kilómetros por segundo.
Reflexiona: ¿Qué relación tiene el número 0.81 con que el resultado de la multiplicación haya sido menor que 29.7?
Ahora analiza y responde lo siguiente:
La velocidad de Plutón al girar alrededor del Sol es de 4.8 kilómetros por segundo y la de Venus, es 7.5 veces la velocidad de Plutón. ¿A qué velocidad gira Venus?
¿Cómo lo resolverías?
Para saber a qué velocidad gira Venus, multiplica la velocidad a la que gira Plutón, por las veces que representa dicha velocidad la de Venus, es decir, 7.5 por 4.8
Al resolver la operación mediante el algoritmo convencional de la multiplicación, observa que 7.5 por 4.8 es igual a 36; es decir, Venus gira alrededor del Sol a una velocidad de 36 kilómetros por segundo.
Como pudiste observar en los casos anteriores, no siempre el producto de una multiplicación debe ser mayor que los factores. En el problema de la Tierra y Marte, una de las cantidades es un número decimal menor que uno, por lo tanto, el producto de la multiplicación es menor que uno de los factores. Mientras que, en el problema de Plutón y Venus, como ambos factores son mayores a uno, el producto es mayor que ambos factores.
¿Qué sucede con el producto cuando se multiplican dos números decimales menores que la unidad?
Analiza el siguiente problema:
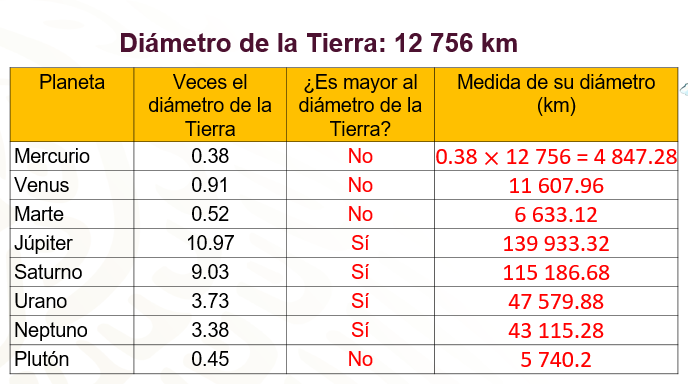
“El diámetro de la Tierra es igual a 12 756 km, averigua cuánto mide el diámetro de los otros planetas del sistema solar. Antes de calcularlo, deberás anticipar qué planetas son más grandes y cuáles más chicos que la Tierra.”
Observa la siguiente tabla:
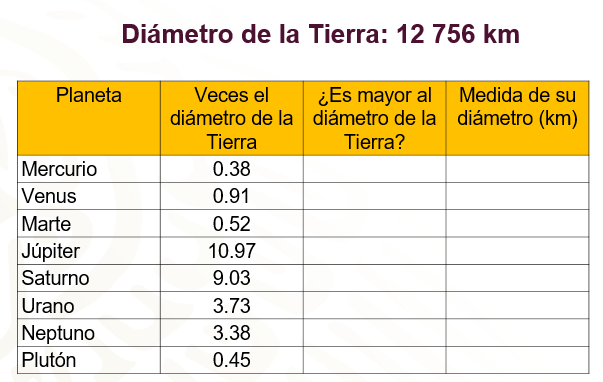
En la tabla se muestra el nombre de los planetas y las veces que su diámetro equivale al diámetro de la Tierra que es de 12 756 kilómetros.
Mercurio, 0.38 veces; Venus, 0.91; Marte, 0.52; Júpiter, 10.97; Saturno, 9.03; Urano, 3.73; Neptuno, 3.38 y Plutón, 0.45 veces. En la tercera columna deben anticipar y escribir si el diámetro es o no mayor al diámetro de la Tierra, y en la cuarta columna, la medida del diámetro de cada planeta.
¿Ya sabes qué planetas son más grandes y cuáles más pequeños que la Tierra?
Seguramente ya sabes que planetas son mayores que la Tierra, pues en esos casos, el diámetro es más de una vez el diámetro de la Tierra, y en los casos en los que el diámetro es menor, las veces el diámetro de la Tierra es menor a uno.
En el caso de la última columna, ¿qué operaciones permiten obtener las medidas?
Como sabes, la operación que permite saber las veces que es una cantidad de otra, es una multiplicación; por ejemplo, “n” de “m” es igual a “n” por “m”. En el ejemplo, multiplica el diámetro de la Tierra por las veces que dicho diámetro representan el de cada planeta.
En el caso de Mercurio, como su diámetro es 0.38 veces el diámetro de la Tierra, entonces mide 12 756 por 0.38, que es igual a 4 847.28 kilómetros. Para Venus, después de resolver la multiplicación, vemos que su diámetro mide 11 607.96 kilómetros; el diámetro de Marte mide 6 633.12 km; el de Júpiter, 139 933.32 km; el diámetro de Urano mide 47 579.88 km; el de Neptuno, 43 115.28.y el de Plutón, 5 740.2 km.
Como puedes ver, las multiplicaciones con decimales se encuentran en situaciones de la vida cotidiana y científica. Muchos de los estudios que realizan los astronautas, tanto para viajar al espacio como en el espacio mismo, se realizan con cantidades que involucran a los números decimales.
¿Has observado que muchas veces el cielo tiene una especie de niebla grisácea? Es una forma de contaminación del aire muy común y evidente, ésta es generada por varios tipos de contaminantes en el aire, en su mayoría por la quema de combustibles provenientes del carbono, petróleo y gases, como el dióxido de carbono.
¿Sabías que las emisiones de dióxido de carbono en exceso pueden generar grandes daños sobre los ecosistemas y la biodiversidad? Este gas en exceso, crea el efecto invernadero, lo que provoca un mayor calentamiento de la Tierra.
Los automóviles generan una parte del dióxido de carbono que va al medio ambiente, es por ello que equipos de ingenieros ya trabajan en prototipos de automóviles de tecnología híbrida.
“Se espera que este tipo de automóvil recorra 32.57 km por cada litro de gasolina, lo que los hacer ahorradores de combustible y, por consiguiente, mucho menos contaminante que un automóvil normal.”
¿Cuántos kilómetros recorrerá un automóvil de este tipo con tres cuartos de litro? ¿Con 0.3 litros? ¿Y con 1.6 litros de gasolina?
Para resolver esta situación realiza la conversión de tres cuartos a una cantidad decimal, y ahora sí, realiza el procedimiento de la multiplicación que ya conocen, para colocar el punto decimal vamos a contar de derecha a izquierda tantas cifras, como cifras decimales tengan los factores.
Tres cuartos equivalen a 0.75, así que al multiplicar 32.57 por 0.75, el resultado es 24.4275, como hay cuatro cifras decimales en los factores, se cuentan cuatro cifras a la izquierda en el producto.
Para el caso de 0.3 litros, el automóvil puede recorrer 0.3 por 32.57, igual a 9.771 kilómetros.
¿Qué distancia recorrerá con 1.6 litros de gasolina? En casa realicen las operaciones para responder esta pregunta.
El Reto de Hoy:
Si las emisiones de dióxido de carbono de ese prototipo son 12.06 kilogramos por cada 100 kilómetros, ¿cuántos kilogramos de dióxido de carbono emitirá en un año en el que recorrió 15.345 kilómetros?
Y si las emisiones de dióxido de carbono de un automóvil convencional son de 17.73 kilogramos por 100 kilómetros, ¿cuántos kilogramos de dióxido de carbono emitirá en un año si en ese año recorrió 15.345 kilómetros?
Repasa el tema:
La multiplicación es una suma abreviada, por lo que puedes sumar el decimal, el número de veces que indica el número natural, o realizar el procedimiento de la multiplicación.
Para multiplicar un número natural por un número decimal, se multiplica como si los dos números fueran naturales, siguiendo el procedimiento que conocen. En el resultado se coloca el punto decimal contando de derecha a izquierda tantas cifras como cifras decimales tengan los factores decimales, por ejemplo: 32.52 por 8 260.16
En la multiplicación con decimales menores que la unidad el producto es menor que los factores y en la multiplicación con decimales mayores a la unidad el producto puede ser mayor.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Bioconstruyéndola célula procarionte y eucarionte
Aprendizaje esperado: Identifica las funciones de la célula y sus estructuras básicas (pared celular, membrana, citoplasma y núcleo).
Énfasis: Distinguir entre células procariotas y células eucariotas.
¿Qué vamos a aprender?
En esta sesión revisarás un divertido juego que te permitirá conocer más sobre los tipos de células. De esta manera se continuará con el desarrollo del aprendizaje esperado: Identifica las funciones de la célula y sus estructuras básicas (pared celular, membrana, citoplasma y núcleo). Teniendo como propósito: Distinguir entre células procariotas y células eucariotas.
¿Qué hacemos?
Hay dos tipos de juego, uno es Bioconstruyendo la célula eucarionte y el otro se llama Bioconstruyendo la célula procarionte.
Si recuerdas en sesiones anteriores, se explicó que en la naturaleza existe una gran diversidad de formas de vida que va desde las microscópicas unicelulares hasta organismos muy grandes, pluricelulares.
Fue Robert Whittaker quien propuso la clasificación en cinco reinos, la cual se basaba en el tipo de célula, el número de células y el tipo de nutrición.
En la sesión anterior se mostró que, aunque los organismos son muy diferentes, a nivel celular, se comparten varias características. Para comprenderlo se puede retomar la teoría de Darwin que menciona que todos los seres descienden de un ancestro común.
Asimismo, Lynn Margulis en colaboración con Karlene V. Schwartz mantuvieron, con algunas modificaciones, el sistema de cinco reinos. Y, tomando en cuenta la evolución biológica, los biólogos han construido varios árboles filogenéticos. Derivado de lo anterior, se puede mencionar que todos los organismos de los cinco reinos tienen un “ancestro universal común”.
Los biólogos señalan que el ancestro común, denominado LUCA, por sus siglas en inglés, lo cual traducido al español significa "Último Ancestro Común Universal”, fue un organismo unicelular del que probablemente evolucionaron, durante miles de millones de años, todos los seres vivos que existen actualmente, formados por células procariotas y eucariotas.
¡Así es! Fue con el descubrimiento y uso constante del microscopio que los biólogos reconocieron la existencia de dos tipos de células: procariotas y eucariotas. La característica que se tomó en cuenta para denominarlos es la presencia o ausencia de núcleo. De ahí surge el nombre procariota, es decir, antes del núcleo, representado por el reino Monera. Y eucariota, que significa núcleo verdadero. Constituyen a los reinos Protista o Protoctista, Fungi, Plantae y Animalia.
Interesante el origen de estos conceptos y su clasificación. Tomando en cuenta esta información: ¿qué te parece si revisas una ejemplificación del juego Bioconstruyendo la célula procarionte”?
Imagina que hay dos personas que llevarán a cabo este juego una es Rodolfo y la otra persona es Jaqueline:
Rodolfo:
Vamos a sacar el juego de su caja.
Jaqueline:
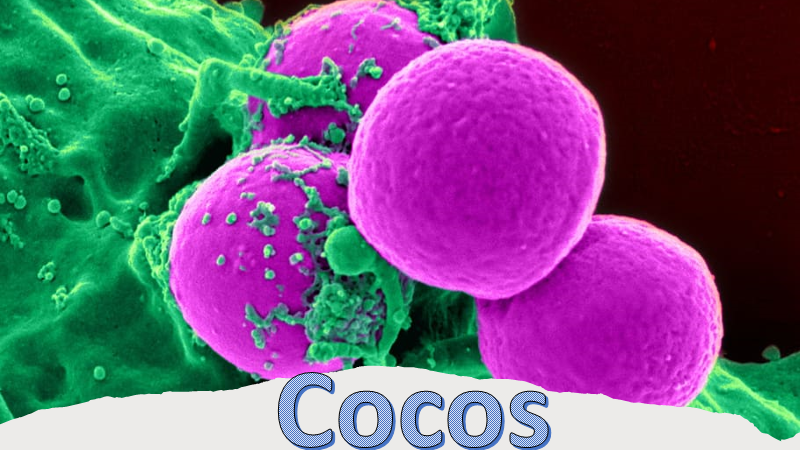
La tapa dice: “se calcula que las células procariotas existen desde hace más de 3,500 millones de años y fueron las únicas habitantes por más de 2,000 millones de años; actualmente, son los organismos más abundantes en la Tierra. Es en el reino Monera donde se encuentra una diversidad de formas de bacterias, como: bacilos, espirilos y cocos”.
|
|
|
|
Rodolfo:
¡Muy buen dato! Vamos a pegar tu tablero en una pared, para que se pueda observar la membrana de la célula; que tiene la función de aislar el contenido celular del entorno y regular la entrada y salida de materiales de la célula.
Jaqueline:
El juego también incluye las imágenes de las diferentes estructuras, las cuales se van a ir pegando cuando se logre sacarlas del Bioconstruyendo.
Rodolfo:
¡Listo! ¿Gustas empezar, Jaqueline?
Jaqueline:
¡Gracias!, pero he de advertir que mi pulso no es nada estable.
(Toma unas pinzas y se prepara para sacar la primera pieza).
Rodolfo:
Entonces deberás tener mucho cuidado, pues recuerda que debes ir sacando las partes de la célula sin tocar los bordes. En caso de que los toques se escuchará un sonido. Y perderás tu turno.
Jaqueline:
Bueno, lo haré lentamente.
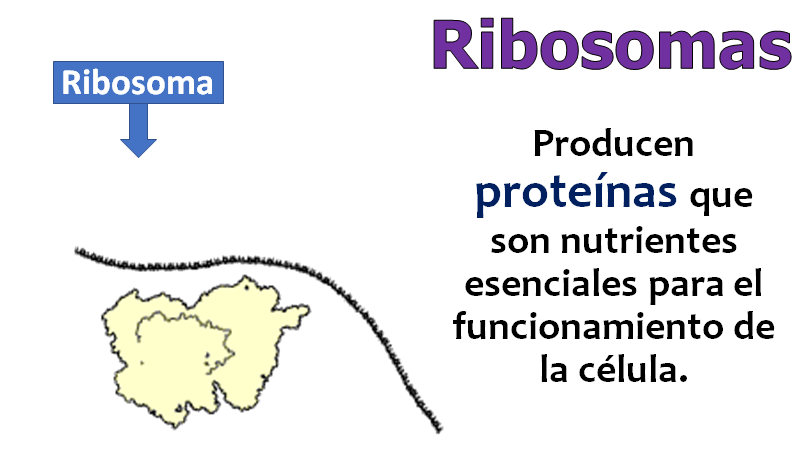
(Se acerca al juego y saca al ribosoma).
¡Qué bien! Pude obtener los ribosomas.
Rodolfo:
¡Lo hiciste muy bien!
(Toma una tarjeta del ribosoma y lee la información).
Jaqueline:
Pega la imagen en el tablero.
Rodolfo:
En la tarjeta de información se menciona que en esta estructura se producen proteínas que son nutrientes esenciales para el funcionamiento de la célula. Se encuentran flotando en el citoplasma, aunque en las células procariontes son más pequeños que en las eucariontes.
Jaqueline:
¡Interesante!, y hay muchos dispersos en todo el citoplasma.
Ahora es su turno, Rodolfo.
Rodolfo:
(Toma las pinzas y saca la pieza del ADN).
¡Sí! He obtenido el ADN o ácido desoxirribonucleico, que es el material genético.
Jaqueline:
(Toma la tarjeta y lee la información, mientras Rodolfo pega la imagen en el tablero).
En esta tarjeta se menciona que el ADN contiene toda la información para elaborar proteínas que controlarán las funciones del organismo procarionte. Tienen un cromosoma circular único que consta de dos largas cadenas enrolladas de ADN, el cual no cuenta con una membrana que lo recubra.
Rodolfo:
Así es, cabe mencionar que la reproducción de la célula procariota es asexual, usualmente por fisión binaria. La célula primero duplica su material genético, después aumenta su tamaño y finalmente se divide en dos.
Jaqueline:
¡Es mi turno!
(Toma las pinzas e intenta obtener la pared celular, pero suena el timbre que marca error).
¡Noooo, perdí!
Rodolfo:
Ni hablar, al parecer sí te falló el pulso. Ahora me toca a mí.
(Toma las pinzas y saca la pared celular).
¡Sí! Obtuve la pared celular.
Jaqueline:
(Toma la tarjeta y lee la información, mientras Rodolfo pega la imagen en el tablero).
Esta estructura protege y da soporte a la célula.
Rodolfo:
Claro y, como una de las partes básicas, permite que los organismos procariotas habiten ambientes extremos: con poca agua, con temperaturas muy elevadas, muy ácidos, entre otros.
Jaqueline:
(Observa el juego bioconstruyendo).
No puede ser, ya sólo quedan dos estructuras, espero que pierdas en tu siguiente turno Rodolfo, de lo contrario creo que me vas a ganar.
(Toma las pinzas e intenta obtener el flagelo).
Sólo espero no volver a equivocarme.
(Suena el timbre de error).
¡Nooo! Otra vez perdí mi oportunidad.
Rodolfo:
Ay, Jaqueline, no te preocupes. A veces se pierde y a veces se gana.
(Toma las pinzas e intenta obtener la pared celular y suena el timbre de error).
¡No puede ser! También toqué los bordes.
Jaqueline:
¡Siiií! Aún tengo oportunidad de ganar.
(Toma las pinzas saca el flagelo).
¡Qué bien!, pude sacar el flagelo.
Rodolfo:
(Toma la tarjeta y lee la información, mientras Jaqueline pega el flagelo).
De acuerdo con la información de la tarjeta, éste permite que la célula se mueva en un medio acuoso.
Ahora es mi turno.
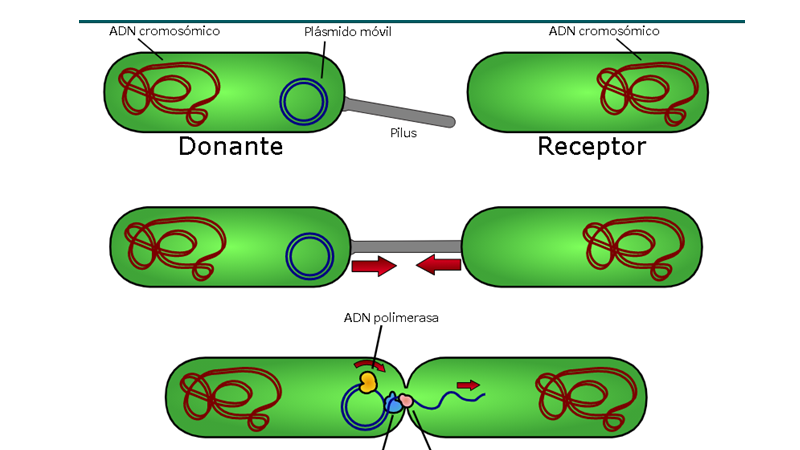
(Toma las pinzas saca el plásmido).
¡Qué bien!, pude sacar el plásmido.
Jaqueline:
La tarjeta dice: son elementos extracromosómicos del ADN bacteriano. Están formados por una doble cadena de ADN, sólo que no siempre son circulares, hay especies en los que éstos son lineales.
Rodolfo:
Los plásmidos pueden contener información sobre la fertilidad, resistencia a un tipo de medicamentos o sustancias dañinas para las células. Esto permite explicar la resistencia de las bacterias a algunos medicamentos.
Mira Jaqueline, se completó el tablero, así que por nuestro gran trabajo en equipo lo declaramos como un empate.
Jaqueline:
¡Tienes razón! Creo que es lo justo.
Qué interesante ver sus estructuras, con las cuales puede realizar todas las funciones de los seres vivos, como nutrirse, respirar, relacionarse con el entorno y reproducirse.
Rodolfo:
Así es, ahora para identificar en qué se parecen y en qué son diferentes las células procariontes y eucariontes, vamos a ver mi juego de “Bioconstruyendo la célula eucarionte”.
Jaqueline:
¡Me parece perfecto, Rodolfo! Te ayudo a pegar tu tablero.
Rodolfo:
En mi caja también viene un dato.
Considerando la teoría endosimbiótica de la bióloga Lynn Margulis, las células eucariotas se originaron, probablemente, a partir de las células procariotas, por lo que se consideran las antecesoras de los organismos pluricelulares. Esta teoría está basada en el hecho de que las mitocondrias y los cloroplastos tienen su propio ADN, membranas y ribosomas para poder producir sus propias proteínas y reproducirse.
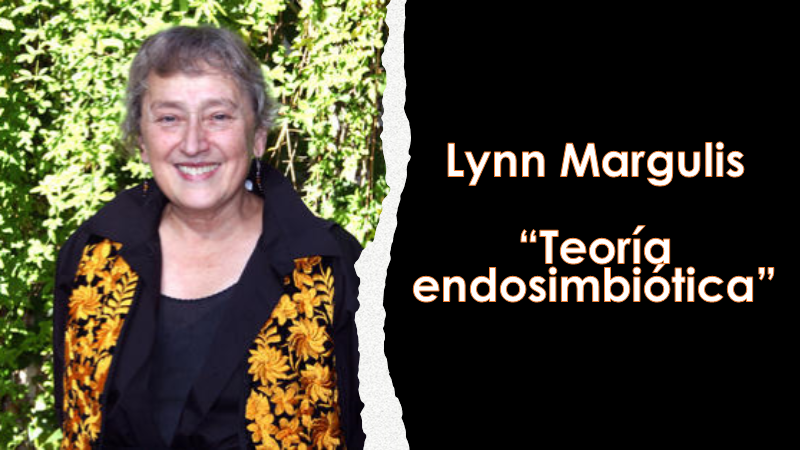
Jaqueline:
¡Woow! entonces eso quiere decir que, probablemente, una célula procarionte ¡fue absorbida por otra célula más grande! Ahora entiendo por qué es mayor el tamaño de tu tablero.
Rodolfo:
¡Así es! De acuerdo con los datos con los que cuentan los científicos, proponen que fue un evento casual de una mala digestión, es decir, que ciertos organismos procariotas absorbieron a otros procariotas más pequeños, pero no fueron capaces de digerirlas.
Así, probablemente, quedaron atrapadas dentro de la célula precursora de las eucariotas. Con el tiempo se hicieron simbióticas, es decir, ¡una dependía de la otra para sobrevivir!

Jaqueline:
Seguramente estás ¡impactado con esta información! Ya que, de esa forma, probablemente surgieron los organelos celulares de la célula eucarionte.
Rodolfo:
Esta interacción produjo el surgimiento de los primeros seres unicelulares eucariontes y continúa hasta estos días debido a la capacidad hereditaria de esta asociación endosimbiótica.
Jaqueline:
Muy interesante, ¡ya quiero ver las partes de tu célula!
Rodolfo:
¡Perfecto! Vamos a sacar las piezas para identificar qué estructuras contienen. Mira, aquí está la membrana celular.
(Señala el tablero).
Jaqueline:
Al igual que en la célula procarionte, es la que permitirá delimitar a la célula eucarionte, y como ya lo mencionamos, va acompañada del citoplasma, líquido importantísimo, que en este caso contendrá los organelos celulares.
Rodolfo:
¡Así es! Y precisamente aquí se tienen algunos organelos, como el núcleo, la mitocondria y el cloroplasto.
Jaqueline:
De manera muy general se puede decir que el núcleo contiene el ADN, rodeado por una membrana, toda la información genética se encuentra ahí. Pero, además, coordina la división celular, que puede dar origen a dos o cuatro células hijas, dependiendo del tipo de célula y el proceso que realice: mitosis o meiosis.
Rodolfo:
Por otro lado, la mitocondria también es un organelo ¡muy importante! ¿Te acuerdas del ATP, la moneda energética de los seres vivos? Pues bien, es la encargada de organizar esa transformación de la energía es la mitocondria.
Jaqueline:
El último organelo del Bioconstruyendo es el cloroplasto, estructura que se encuentra en células eucariotas de organismos productores que realizan fotosíntesis, es decir, el proceso por el cual logran transformar la energía luminosa en energía química.
Rodolfo:
Este proceso es muy importante, ya que es la base para el desarrollo de las cadenas y redes tróficas.
Jaqueline:
Se nos olvidan los ribosomas. Estos se encuentran en todas las células, y dentro de organelos, como las mitocondrias, cloroplastos y adheridos al Retículo Endoplásmico Rugoso. Estos pequeños paquetes son muy importantes para la síntesis de proteínas.
¡Ahora sí se tiene ambos tableros completos!
Rodolfo:
¡Woww! Son tan diferentes, pero también tienen similitudes.
Bien, después de haber revisado la ejemplificación anterior. Qué te parece si revisas el modelo de célula del proyecto de Ciencia escolar para identificar semejanzas y diferencias entre estos tipos de células.
Continuando con la elaboración, y enfocándose en algunos elementos que permiten diferenciar a las células procariontes de las células eucariontes.
¿Cuáles te imaginas que pueden ser?
La forma en cómo se presenta el material genético (ADN). En el caso de las células eucariontes, este elemento está almacenado en el núcleo, rodeado por una membrana. Pero en las procariontes, como se mencionó, se encuentra disperso en el citoplasma en forma circular sin contar con una membrana nuclear que lo delimite.
Para representar el material genético se utilizarán limpiapipas de dos diferentes colores. Al entrelazarlos te quedará una figura que integrarás a tu modelo. También puedes representar los plásmidos, formados por una doble cadena de ADN, más pequeña, que puede ser circular o lineal. Asimismo, se integra al ribosoma, ya que es una de las pocas estructuras con las que cuenta la célula procarionte.
Para la elaboración de esta estructura, puedes utilizar hojas de papel o periódico, café soluble y agua.
Con estas estructuras tienes los elementos mínimos para que tu modelo pueda representar a una célula procarionte. Como lo puedes ver. Teniendo tu modelo listo, ahora, se realizará una síntesis de lo estudiado en la sesión.
Entre las semejanzas se tiene, que tanto la célula eucarionte y procarionte poseen membrana celular, citoplasma y ribosomas. Y ambas células realizan todas las funciones vitales, como son la respiración, nutrición, relación con el entorno y reproducción, entre otras.
Por otro lado, para las diferencias podemos resaltar que la célula procarionte tiene ribosomas y plásmidos dispersos en el citoplasma. Y no cuenta con organelos rodeados por membranas. Además de que es mucho más pequeña que una célula eucarionte.
Así mismo, el material genético (ADN) se encuentra en forma circular y disperso en el citoplasma sin una membrana nuclear que lo delimite, mientras que en la eucarionte se encuentra dentro de la membrana nuclear.
De acuerdo con la teoría endosimbiótica propuesta por Margulis, las células eucariontes surgieron a partir de las procariontes. En esta propuesta se describe que posiblemente las mitocondrias y los cloroplastos fueron células procariontes independientes que en algún momento fueron absorbidas por otra célula más grande.
De esta manera surgieron los organelos celulares, que generaron la aparición de los primeros seres unicelulares eucariontes. En otras palabras, una célula vive dentro de otra célula y ambas se benefician de esta relación endosimbiótica.
Para concluir con esta síntesis revisa la siguiente lectura de Martín Bonfil Olivera del año 2004, titulada “¿Somos bacterias?”
“La idea puede parecer extraña. Después de todo, estamos acostumbrados a pensar en las bacterias, esos invisibles, microscópicos vecinos con quienes compartimos el planeta, como fuente sólo de enfermedades o de descomposición de los alimentos. O, en todo caso, como el último eslabón en el ciclo natural por el que la materia orgánica de los cadáveres regresa a formar parte del suelo.
Pero las bacterias son mucho más antiguas que nosotros. Estuvieron aquí en un principio, cuando no había ningún otro ser vivo sobre el entonces joven planeta. Sin duda los primeros organismos eran primitivas bacterias, con células de tipo procarionte: simples, sin un núcleo definido por una membrana, con su material genético en contacto directo con el citoplasma. En el origen fueron las bacterias. o sus ancestros.
Y es que, a su vez, las bacterias son nuestros ancestros. De nosotros los eucariontes, plantas, animales, hongos y ese quinto reino en que se agrupa a los organismos que no caben en los otros cuatro: los protistas.
La historia es simple. A lo largo de años, siglos, milenios y millones de años, las bacterias han venido creciendo, dividiéndose y multiplicándose. En este proceso también han cambiado. Evolución significa cambio. El azar de la mutación y el rigor de la supervivencia las han obligado a adaptarse a los ambientes más variados.
En algún momento de esta larga historia evolutiva, la competencia dejó de ser el único recurso, y la colaboración entró en escena. Quizá fue un accidente, quizá un intento fallido de conquista; lo cierto es que hoy las células eucariontes tienen en su interior lo que parecen ser antiguas bacterias…”.
Si quieres saber en qué concluye la lectura, se te invita a buscar este artículo en internet, ya que es de acceso libre. Así es, sólo coloca el nombre del autor en tu buscador de internet, “Martín Bonfil Olivera”, seguido del título “¿Somos bacterias?” y encontrarás la lectura. Se te invita leer y disfrutar de esta excelente lectura.
Como observaste, hoy se estudiaron dos conceptos importantes a lo largo de la sesión, pero se te invita a añadir uno de ellos a tu “Abecedario biológico”. El concepto de “célula procarionte” es el que se te pide que incluyas. No olvides: integrarlo, definirlo e ilustrarlo.
Has concluido el tema del día de hoy.
El Reto de Hoy:
Realiza el siguiente reto:
En tu libreta escribe dos semejanzas y dos diferencias entre la célula procarionte y eucarionte. Si tienes la posibilidad, compártelo con tu profesora o profesor, así como con tu grupo de trabajo.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
La dinámica de la población en México
Aprendizaje esperado: Argumenta implicaciones ambientales, sociales y económicas del crecimiento, la composición y la distribución de la población en el mundo.
Énfasis: Distinguir las características demográficas de la población mexicana y sus implicaciones.
¿Qué vamos a aprender?
El propósito de esta sesión, es distinguir las características de la población mexicana, las cuales se refieren a su distribución, crecimiento y composición. Asimismo, reconocerás algunos de los desafíos que enfrenta la población mexicana actual.
Ten listos tus materiales, cuaderno de notas, libro de texto y bolígrafos y toma nota de lo más importante.
¿Qué hacemos?
¿Tú sabes en dónde se localiza la población mexicana y por qué?
En las sesiones anteriores observaste que la población tiende a concentrarse en los espacios urbanos.
Para el año 2020 la población total de la República Mexicana se contabilizó en 127 575 529 habitantes. Debido a la cantidad de población que se encuentra en el territorio México ocupa la posición número 10 a nivel mundial entre los países más poblados y en Latinoamérica se posiciona en el segundo lugar sólo después de Brasil.
Es importante mencionar que el Estado de México es la entidad con la mayor cantidad de población pues cuenta con 16 187 608 habitantes y, el estado de Colima es el que tiene el menor número de población, ya que cuenta con 711 235 habitantes.
A lo largo del siglo XX y a principios del siglo XXI, el crecimiento de la población en México cambió mucho. En el año de 1970 México tenía una población de 51 millones de habitantes y siguió incrementando de manera muy rápida en años posteriores, por lo que desde los años 70´s a la actualidad han transcurrido 50 años y se ha aumentado al doble el número de personas que se tenía en esos años.
Ahora, la densidad de población que posee nuestro territorio mexicano es de 65 habitantes por kilómetro cuadrado, siendo las zonas urbanas las que concentran 80% de sus habitantes, mientras que otro 20% vive en los espacios rurales.
¿Es cierto que en México hay más mujeres que hombres?
Así es, de la población total que alberga México, 51.1% de las personas son mujeres, mientras que el 48.9% son varones.
Es importante saber que 26.6% de los habitantes está conformado por niños, 66.4% personas que oscilan entre los 15 y 65 años de edad, y nuestros adultos mayores de 65 años representan 7% de la población total.
Ahora ve y escucha el siguiente video, en donde conocerás como es que se distribuye la población en México:
- La población Mexicana.
https://www.youtube.com/watch?v=e-YDXbM3cwA
Como pudiste observar en el video, la concentración de la población se da principalmente en zonas urbanas; las zonas rurales las que concentran menos población.
¿A qué se debe que hay habitantes que vienen de otros estados a la Ciudad de México?
Esto se debe a que la población de las comunidades rurales muchas veces migra a las ciudades en busca de mejores oportunidades de empleo; esto hace que la población tienda a disminuir en las zonas rurales e incremente en las zonas urbanas.
En México la población se distribuye de manera heterogénea, esto quiere decir que, en algunos espacios, como los urbanos, se concentra, y en otros, como los rurales, se dispersa.
Observa el mapa que se muestra en la imagen:
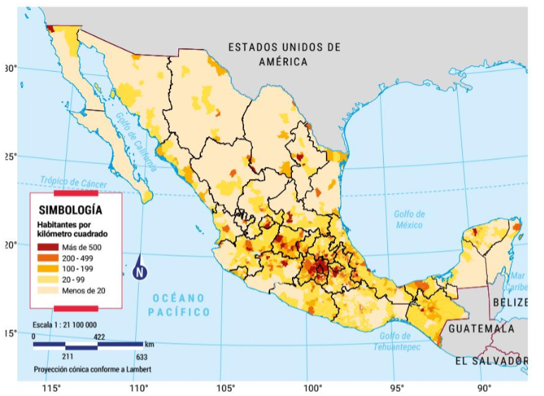
En el mapa se observa la densidad de población según los municipios de las entidades. Los colores crema y amarillo, corresponden a bajas densidades de población, esto es, de menos de 99 habitantes por km2, el color amarillo presenta entre 100 y 199 habitantes por km2, el anaranjado va de 200 a 499 y el rojo indica más de 500 habitantes por km2.
Nota que la población se concentra en los municipios y entidades del centro del país.
Como la Ciudad de México y el Estado de México (1), Morelos (2), Puebla (3), Tlaxcala (4), Hidalgo (5), Querétaro (6) y Guanajuato (7).
Asimismo, identifica que las densidades de población más altas en el oriente y norte de nuestro país, corresponden con dos de los espacios urbanos más importantes: Guadalajara, en Jalisco, y Monterrey, en Nuevo León, respectivamente.
¿A qué se debe la concentración de la población en estos espacios urbanos?
En el caso del centro del país, la alta densidad de población se debe a razones históricas y geográficas, ya que los primeros poblamientos de las culturas prehispánicas se asentaron ahí debido a la disponibilidad de agua y la fertilidad de los suelos volcánicos; a partir de entonces, el crecimiento demográfico y urbano ha conformado las ciudades de la región como las conocemos hoy en día.
En el caso de Monterrey, esto se debe a razones históricas y económicas, ya que fue ahí en donde se estableció el cabildo colonial de Santa Lucía, que correspondía al Nuevo Reino de León de la Corona española, y posteriormente se convirtió en una ciudad industrial estratégica al ubicarse cerca de la frontera entre México y Estados Unidos de América.
Y en cuanto a Guadalajara, la ciudad más importante del oriente del país, la densidad de población también se debe a razones histórico-geográficas, ya que la Villa de Guadalajara, se fundó al margen del río San Juan de Dios debido a la disponibilidad de agua, y se derivó de la expansión de las colonias de la Nueva España en ese territorio.
Ahora bien, los estados de la República Mexicana con menor densidad de población son Sonora (1), Chihuahua (2), Durango (3) y Coahuila (4), que se ubican en el norte del país, así como los estados de las penínsulas de Baja California: Baja California (5) y Baja California Sur (6) y la de Yucatán: el estado del mismo nombre (7), Quintana Roo (8) y Campeche (9).
En el caso de los estados del norte del país, la baja densidad de población se debe a las condiciones de aridez y gran extensión del territorio, mientras que, en la península de Yucatán, la baja o nula accesibilidad que propicia la selva, así como las condiciones climáticas, son los principales factores.
Para conocer más respecto de este tema y para poder observar los mapas de distribución de la población México con mayor detalle, visita el siguiente sitio web, que es del Inegi.
https://www.inegi.org.mx/temas/estructura/#Mapas
Recuerda que el Inegi es el encargado de realizar los censos y conteos de la población en el país.
Lee las siguientes preguntas:
¿Qué lugar ocupa México en Latinoamérica por la cantidad de habitantes?
R= México se ubica en segundo lugar, después de Brasil.
¿Cuál es el medio donde se concentra la mayor cantidad de población?
R= El medio que cuenta con mayor cantidad de población es el medio urbano, o la ciudad, pues concentra el 80% de la población total.
¿Qué tipo de población predomina en el territorio mexicano?
R= La población que predomina son personas de 15 a 65 años.
Bien has concluido el tema del día de hoy.
El Reto de Hoy:
Elabora un pequeño censo con tu familia, puedes registrar tus datos en una tabla como la que se muestra a continuación.
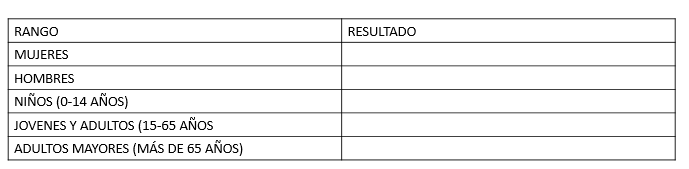
Registra cuántos son hombres y cuántas mujeres; también cuenta el rango de edades que hay en tu familia.
Una vez que termines de realizar tu registro, comparte los resultados con tu familia y reflexiona en lo siguiente:
- ¿Qué hay más, mujeres u hombres?
- ¿A qué crees que se debe?
- ¿Cuál es la población predominante?
- ¿Por qué es así?
- En 5 años, ¿crees que tu población familiar aumente de manera considerable? ¿Por qué?
Como habrás notado México es un país que ha tenido un crecimiento poblacional considerable en los últimos 50 años, incrementando al doble su población en comparación con la que se registró en el año de 1970.
Son las zonas urbanas o las ciudades las que albergan la mayor densidad de población, pues se crea un fenómeno social, ya que en las zonas rurales la población migra a la ciudad; de esta manera la población en el campo disminuye, e incluso hay comunidades llamadas “comunidades fantasmas”, se les ha llamado así porque su población ha desaparecido casi por completo a causa del movimiento migratorio.
Por otra parte, la población en las ciudades incrementa, debido a la llegada de personas migrantes del campo.
Por ello es importante que el gobierno, otorgue las mismas oportunidades tanto en comunidades rurales como urbanas, para que de este modo disminuya la cantidad de migrantes de las comunidades rurales a las ciudades.
¿Te gustaría saber cuánta población hay en su comunidad, localidad o ciudad?
Te invito a que visites la página “Cuéntame de México”; en esta página podrás encontrar información de tu entidad y podrás realizar actividades interactivas relacionadas con el tema de la población.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
La vuelta al día en 80 mundos
Énfasis: Jugar con los objetos cotidianos y los elementos del arte para representar distintas situaciones cómicas de su día a día.
¿Qué vamos a aprender?
Representarás situaciones que posiblemente has vivido habitualmente, lo harás jugando con los elementos del arte en distintas formas expresivas.
Tu acontecer en el día está lleno de muchas situaciones que puedes transformar en un juego, incluso jugando e imaginando puedes hacer que los objetos cobren vida.
¿Qué hacemos?
Esta sesión amerita dar vida a todos los objetos que te rodean aun cuando no los toques: puedes observar una cama o el jarrón de cristal y así la magia aparecerá.
Revisa la siguiente ejemplificación:
Alma usa una olla de barro como elemento cotidiano para el ejemplo Víctor tiene un huaje. Estos objetos los usarán para contar historias graciosas que les han pasado.
Víctor cuenta su historia con movimientos y sonidos, en donde representa que está preparando chocolate caliente.
Alma adivina diciendo: ¡Ah, ya sé! Estás haciendo chocolate con un molinillo.
Víctor comenta que sí, y en su historia relata que estaba en la casa de una amiga queriendo quedar bien, y que se le antoja un chocolate a su abuelita y que decidió prepararlo. Desde niño se maravilló con el sonido de las burbujas, tanto le gustan que las distingue en cualquier alimento.
Alma le dice que no exagere, que las burbujas de la comida suenan igual.
Pero Víctor dice que no, suenan diferente. No es lo mismo el sonido del maíz fermentado para el tesgüino, que para una salsa agria. Que se fije bien y que lo va a entender.
Víctor continua con su historia, y relata lo siguiente: pues estaba yo duro y dale al molinillo, con ritmo, ya sabes, para darle sabor; y la espuma del chocolate caliente en la estufa empezó a subir cada vez más y yo, encantado, perdido en el sonido.
Recuerdo el sonido del chocolate hirviendo y el sonido del molinillo para hacer espumoso el chocolate, la espuma flotando. Ese sonido burbujeante invitándome a deleitarme.
En eso dice Alma: ¡ay cuidado, cuidado, ya está hirviendo! Ya se tiró todo el chocolate y la espuma que tanto te gusta… ¡Ah! Ya sé lo que te pasó.
Víctor le responde: exacto, lo que pasó es que me perdí tanto en los sonidos, el ritmo del molinillo, el olor, la forma de la olla, que cuando reaccioné mi amiga me estaba empujando lejos de la estufa para limpiarla. Y es que sí, así como lo imite ahorita, se me derramó el chocolate de tanto hervor.
Alma sonriendo le dice: pues ahora sí que “bájale de espuma a tu chocolate” ja ja ja ja. Disculpa que me ría, sé que no es gracioso lo que te pasó, pero, es que, ahora que lo cuentas, pues me dio risa. Bueno, cambiemos de tema, fíjate que me llamó la atención lo que dices, que las burbujas suenan diferente.
Interrumpiendo la ejemplificación, ¿tú lo has notado?, que las burbujas suenan diferente.
Si no lo has hecho, detente a disfrutar los sonidos, escucha con atención, los sonidos son distintos.
Tal vez has encontrado en las burbujas de la comida una forma expresiva y eres tú quien ayuda a que esas burbujas surjan y con ello estás creando nuevas maneras de comunicarte.
Ahora se va representar una situación que te deje dar la vuelta al día en 80 mundos, así como leíste. Pero ¿cómo se dará esta vuelta?
Bien, imagina que es de mañana y vas por agua a un pozo y entonces, ¿por qué no mejor lo representas? En este caso toma nota para ver cómo lo harías con tu propia representación.
Por ejemplo, Alma se imagina que va por agua al pozo, canta, se distrae y se gacha de más y casi se va para adentro, pero un muchacho que pasa por ahí le lanza un aro para lazarla y tratar de ayudarla, pero a la olla, no a la muchacha.
Como viste, se acaba de jugar con los elementos para darle un tono cómico. Pues lo coherente hubiera sido salvarla a ella primero; pero al salvar primero a la olla, se rompe con lo lógico y resulta cómico por lo inesperado.
Quizás el ejemplo te pareció chistoso, que en vez de una cuerda se usará un aro, con eso no se atrapa a nadie porque cualquiera se puede salir fácilmente.
Precisamente ahí está el juego y se espera que juegues con el objeto que tengas a la mano, para crear situaciones que puedan hacer reír retomando tus experiencias cotidianas y aceptando la propuesta del juego.
Recuerda que para jugar se debe aceptar lo que propone tu imaginación, la persona con quien estas y también las circunstancias.
En casa, ¿qué situaciones identificas que causen risa? Ahora que las reflexionas, ¿son o no son chistosas? ¿Por qué dan risa?
En lo que lo piensas, ¿qué te parece si exploras otra forma expresiva a partir de una situación que te haya pasado, dando vida a los objetos? Así que vas a ver al Doctor Misterio para que cuentes con más ideas.
- Actuar a ser tu juguete favorito.
Revisa del tiempo 0:16 al 1:11.
Como viste, es divertido actuar como un juguete. Hacer con tu cuerpo el cuerpo del juguete. ¿Y si le das cuerpo a la olla de la que se habló?, o, ¿cómo hablaría el molinillo? Inténtalo con algún objeto que tengas a la mano, primero observa tu objeto y trata de imitarlo con tu cuerpo.
Considera que, si no te gusta tanto eso de actuar, puedes realizar la actividad con otros recursos expresivos, como dibujar.
Con el objeto elegido, trata de capturar su esencia, dibuja el objeto en tu libreta o en una hoja que tengas. Puede ser la olla, el molinillo o lo primero que veas en este momento. Sólo captura la imagen con la vista, nada de agarrarlo.
¿Qué forma tiene tu objeto?
Al dibujar estas usando otra forma expresiva de tu objeto. Estas reinterpretando la realidad. Lo primero es observar y después plasmar. Y si le sumas tu interpretación, tus recuerdos, tu cosmovisión, estas dando una nueva vida a los objetos, otra personalidad; vaya que los objetos tienen personalidades variadas.
Una vez que tengas la forma de tu objeto, puedes pintarlo con colores o tinturas, o en su caso podrías escribir sobre tu experiencia, escribir sobre el objeto más que pintarlo.
¿De qué manera representarás el objeto que elegiste?
Al escribir sobre el objeto, tal vez te cuesta trabajo no relacionarlo con situaciones; con una anécdota quizás que sea chistosa en tu familia u otras situaciones.
Como ves, los objetos tienen una personalidad y pareciera que también se expresan.
Por ejemplo, Van Gogh pintó una silla. A primera vista se ve estática, pero tal vez a ti te diga la imagen, que la silla es fuerte a pesar de ser delgada. Podrías imaginarte un asiento suave y que huele a palma con madera.

Con una silla, como la de Van Gogh o una normal, quizás puedas recordar cuando se fue al piso algún familiar o amigo tuyo. Le pudieron estar advirtiendo que se bajará, que no se parará o sentará en ella, y ¡zaz! Azotó en el suelo. Afortunadamente no pasó nada, pero te reíste, quizás él lloró o se río.
Y la silla toda seriedad, inerte, fuerte, tal vez te la imagines que su voz es grave y lenta.
Bien, en artes, recordarás, que se ha dicho que lo cómico es gracioso porque es sorprendente, porque rompe con lo cotidiano, por ser inesperado. Lleva lo extraño o lo adverso a un plano de juego.
Así es, tal vez si lo ves a primera vista, no te cause nada de risa, pero detrás de tu representación, dibujo o escrito hay una historia, y si conoces esa historia te hace sentido y tal vez te parezca gracioso, como lo viste con algunos de los ejemplos que revisaste.
Así es, ahora tú en casa trata de dibujar la historia cómica detrás del objeto para que tenga ese sentido expresivo y así te vayas a otros mundos o a otros días, o le des la vuelta al día en 80 mundos.
Bueno, ahora revisa el ejemplo de la historia del objeto de Alma, que es un Molinillo y dice así:
Paren, paren, ya estoy mareado, quiero vomitar. Ah, pero qué vida la mía. No estoy solo, disculpen que no los saludara, soy Modesto Linderos Hillo, por eso todos me dicen Molinillo. En realidad, no muelo, pero hazlos entender. Una mañana, una persona que según iba a hacer la dieta de la avena, ¡catapum!, me sumerge en un vaso lleno de hojuelas crujientes, pero por más que intentó no se molieron; pues no, me dicen molinillo, pero no soy molino chiquito, soy más bien como un batidor. Otro día les cuento más, conste que no me voy, me llevan.
¿Qué te parece esta historia?
Observa como tal vez te reíste o causo gracia el ridículo que hace el personaje, porque te acercaste a él. Así es, lo cómico permite que las personas liberen temores, miedos o recuerdos desagradables, como vergüenzas que has pasado, porque al reír liberas tensión y eso te permite sentirte mejor.
Ahora, revisa el siguiente video. Considera que las personas tienen tantas maneras para expresarse, que la imaginación no tiene límites, así como lo enseña Tanya Covarrubias. Es un video tan breve que requiere toda tu atención.
- Hacer una nanodanza.
Como viste puedes hacer una historia con tus manos; algo que te haya pasado ahora o hace mucho tiempo.
Cuando ríes no siempre sabes de qué, igual que cuando algo te gusta, casi no te detienes a pensar en las razones de por qué te gusta o no, simplemente lo aceptas en tu vida y lo disfrutas.
Es importante que recuerdes que, de vez en cuando, conviene reflexionar para revalorar tus ideas, porque con el tiempo se pueden formar prejuicios. Hoy sabes que existen chistes que no lo son porque lastiman a las personas a las que se refieren.
El humor siempre debe estar acompañado de reflexión e inteligencia. Si tu risa lastima a alguien, sea o no vulnerable, entonces no es una risa sanadora. Hay una regla muy sencilla: me puedo reír si no lastimo a nadie.
Lo importante es que siempre utilices tu imaginación y tu inteligencia. Y entonces podrás crear todo tipo de historias, ya sea con objetos, con dibujos, con objetos o siendo tú mismo el personaje de la historia.
Historias hay muchas y muy graciosas por el enredo que se genera, por ejemplo, en un triángulo amoroso.
Ahora, se te invita a que revises la obra “Las bodas de Fígaro”, tiene música compuesta por Mozart y hay tantas versiones que, seguro encontrarás una que sea de tu agrado.
Wolfgang Amadeus Mozart es de los grandes compositores que sobresale por su gusto y trabajo en el género bufo o cómico y es de los más interpretados en todo el mundo, por eso abundan versiones de sus obras.
Ya que has jugado con los objetos, que te has inspirado en los sonidos y has jugado con ellos al representar situaciones que podrían considerarse cómicas, es hora de concluir.
Esta sesión fue inspirada en el libro de Julio Verne La vuelta al mundo en 80 días y la obra de Julio Cortázar La vuelta al día en 80 mundos. Así que, ya sabes, puedes dar la vuelta a tu mundo a través de las historias que cuentes de él. En esta ocasión el tema fue centrado en lo cómico como parte de la vida cotidiana vinculando diversas formas expresivas como el dibujo, la representación corporal y la música.
El Reto de Hoy:
Cuenta una historia graciosa sólo con tus manos o una parte de su cuerpo. Asimismo, se te invita a que juegues con los objetos que tienes en casa para generar situaciones sorpresivas, que te distraigan gratamente en compañía de tus familiares. Se espera que hayas descubierto ese mundo de posibilidades que te rodean a cada instante, ya sea con objetos o con momentos o situaciones sencillas pero divertidas.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario