Aprende en Casa III SEP: 26 de febrero TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 26 de febrero de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Viernes 26 de febrero, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en Casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Proporcionalidad inversa y sus representaciones
Aprendizaje esperado: Analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.
Énfasis: Comparar situaciones de proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica.
¿Qué vamos a aprender?
Continuarás con el estudio de la variación lineal y la proporcionalidad inversa. En esta sesión, abordarás algunas situaciones para analizar sus propiedades a través de la resolución de problemas.
¿Qué hacemos?
Para iniciar, es importante que realices un ejercicio de concentración y memoria.
Cierra los ojos y reflexiona sobre todo lo que has aprendido acerca de la proporcionalidad inversa. Puedes apoyarte respondiendo las siguientes preguntas:
- ¿Qué es la proporcionalidad inversa?
- ¿Cómo es la gráfica de una proporcionalidad inversa?
- ¿Cuál es la expresión algebraica que permite saber el valor de la constante de proporcionalidad inversa?
- ¿Cuál es la expresión algebraica que permite calcular los valores de la variable independiente y de la variable dependiente?
La proporcionalidad inversa es la relación que existe entre los valores de dos magnitudes tales que, si al multiplicar el valor de una de ellas por cualquier número, su valor correspondiente de la otra magnitud queda dividido por el mismo número y viceversa. Es decir, si un valor de una magnitud es dividido por un número, el valor correspondiente de la otra magnitud es multiplicado por el mismo número.
Por ejemplo, en la siguiente tabla se puede observar que al multiplicar el primer valor de la magnitud (largo) por el número 2, se obtiene como resultado 2. Entonces, ¿qué operación se debe realizar al primer valor de la magnitud (ancho) para comprobar que es inversamente proporcional a su valor correspondiente?
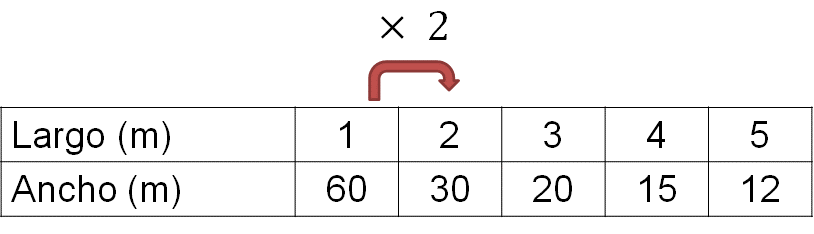
Habrá que dividirlo entre 2. Así se comprueba que las magnitudes de la tabla son inversamente proporcionales.
La gráfica que define una proporcionalidad inversa está representada en el plano cartesiano por una hipérbola. Observa el ejemplo.

En la gráfica puedes ver, para el mismo ejemplo, cómo a medida que aumentan sus valores en el eje “x”, sus valores en el eje “y” disminuyen. También se observa el caso inverso: a medida que los valores en el eje “y” aumentan, los valores en el eje “x” disminuyen. La gráfica que representa una situación de proporcionalidad inversa es una curva llamada hipérbola.
Por otra parte, en una relación de proporcionalidad inversa, la constante de proporcionalidad se representa con la expresión algebraica:
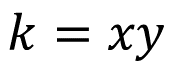
Es decir, “k” es el producto de cada pareja de valores correspondientes de ambas magnitudes “x” y “y”, y el resultado siempre será el mismo, en otras palabras, es constante. Observa el siguiente ejemplo.
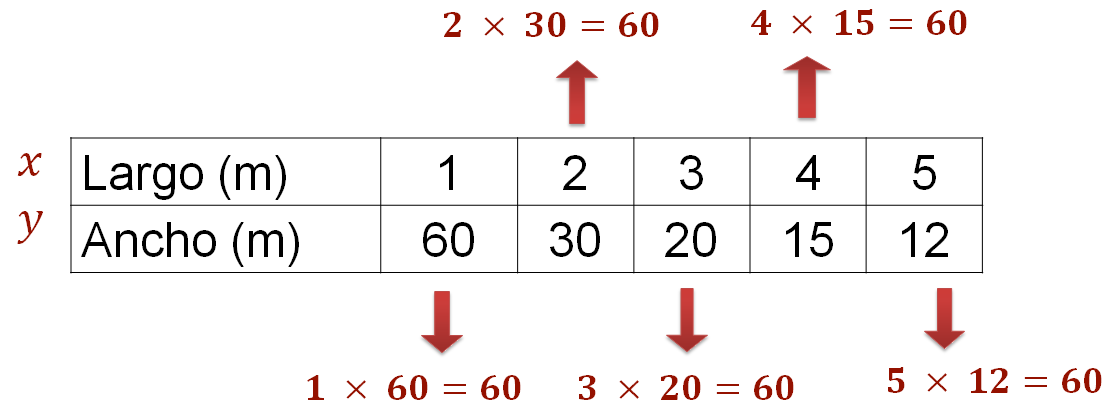
Para saber cómo calcular los valores faltantes en una proporcionalidad inversa, se puede utilizar la expresión algebraica que determina la constante de proporcionalidad y despejar “x” o “y”, según las necesidades del problema.
Para calcular la constante de proporcionalidad “k”:
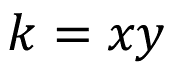
Para calcular la variable “y”:

Para calcular la variable “x”:
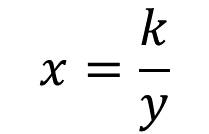
Hasta este momento, has recapitulado todo lo necesario para poder resolver problemas de proporcionalidad inversa. Así que manos a la obra. Analiza y resuelve la siguiente situación.
Situación-problema: velocidad-tiempo de un auto
Se quiere saber los diferentes tiempos y las diferentes velocidades a las que un auto debe circular para recorrer una distancia fija de 50 kilómetros.
Observa y analiza la tabla. Calcula los valores faltantes de la variable dependiente y de la variable independiente. También elabora una gráfica que represente la situación.

En la tabla se puede observar que faltan valores para el tiempo, es decir, la variable independiente “x”. También faltan valores para la velocidad, es decir, la variable dependiente “y”. Para calcular los valores faltantes se puede hacer uso de las expresiones algebraicas anteriores. Realiza los cálculos.
Es conveniente definir cuál es la expresión algebraica para calcular el tiempo y cuál es la expresión algebraica para calcular la velocidad. Toma un momento para pensar y decidir.
Seguramente identificaste que, para calcular el tiempo o la velocidad, se necesita el valor de “k”, es decir, de la constante de proporcionalidad inversa. ¿Ya sabes cuál es su valor?
Es 50, porque el problema dice que el auto deberá recorrer una distancia fija, además, en la tabla se puede comprobar que al multiplicar las parejas de valores correspondientes que están completas, el resultado es 50
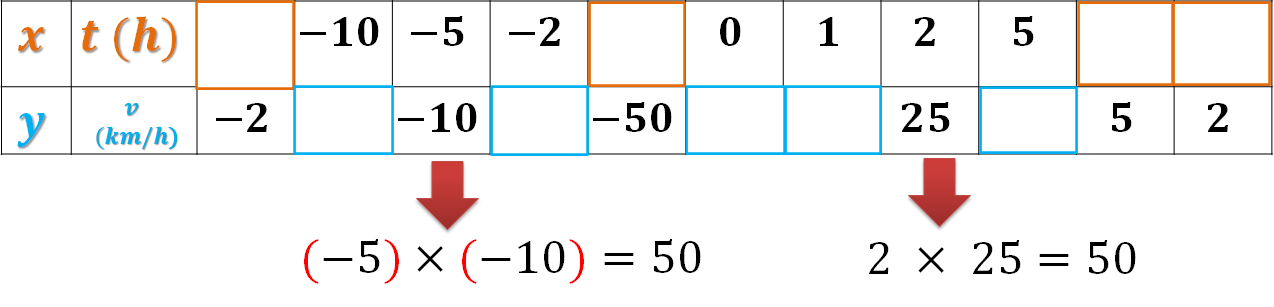
Ya cuentas con los datos para realizar los cálculos.
El primer valor para calcular corresponde al tiempo cuando la velocidad es 2 negativo, por lo que se puede usar la expresión algebraica:

Es decir, el tiempo es igual a la constante de proporcionalidad inversa entre la velocidad. Se sustituyen los valores

El resultado es 25 negativo y se registra en la tabla.
Ahora se calcula el valor correspondiente a la velocidad cuando el tiempo es 10 negativo. Se usa la expresión algebraica:
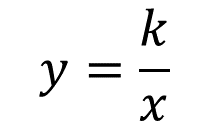
Es decir, la velocidad es igual a la constante de proporcionalidad inversa entre el tiempo. Se sustituyen los valores y la velocidad es igual a 50 entre 10 negativo.
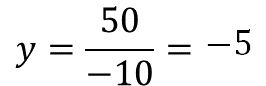
El resultado es 5 negativo.
Después se aplica el mismo procedimiento para calcular el valor correspondiente a la velocidad cuando el tiempo es 2 negativo. Se sustituyen valores y se resuelven las operaciones:

El resultado es 25 negativo.
Para calcular el valor correspondiente al tiempo cuando la velocidad es 50 negativo, se sustituyen los valores y se realizan los cálculos

El resultado es 1 negativo cuando la velocidad es 50 negativo.
Se ha calculado una parte de los datos, pero ¿habrá alguna otra forma de saber los valores faltantes sin realizar todo ese procedimiento?
Otra forma de conocer los valores faltantes es a través de la constante de proporcionalidad inversa. Se sabe que, si se multiplican los valores correspondientes del tiempo y la velocidad, el resultado siempre debe ser 50. Entonces, para calcular los valores que faltan, se puede hacer mentalmente, buscando un número que, multiplicado por el valor conocido, dé como resultado 50. Continúa con los datos faltantes.
De acuerdo con la tabla, el tiempo vale 1, entonces, para calcular la velocidad en ese momento, se determina un número que multiplicado por 1 dé como resultado 50. El resultado es 50. Para calcular la velocidad cuando el tiempo es 5, se determina un número que multiplicado por 5 sea 50. El número es 10. El valor del tiempo cuando la velocidad es 5, es 10. El valor del tiempo cuando la velocidad es 2, es 25.
Aún nos falta calcular el valor de la velocidad cuando el tiempo es cero. Se puede aplicar la fórmula o determinar un número que multiplicado por cero sea 50
Toma unos instantes para hacer los cálculos y reflexiona:
¿Cuál fue el resultado?
¿Realmente “x”, es decir, el tiempo puede valer cero?, ¿por qué?
¿Qué significa que el tiempo valga cero?
¿Son necesarios los números negativos en el contexto de este problema?, ¿por qué?
Piensa unos instantes para responder cada una de estas preguntas.
Ya sea que hayas dividido 50 entre cero a mano, en calculadora, en el celular u hoja de cálculo, no fue posible determinar un resultado; lo mismo pasa si intentas buscar un número que multiplicado por cero de como resultado 50. Simplemente no es posible calcular el resultado, esto se debe a que la división por cero no está definida y no es posible interpretarla a través de la aritmética.
Entonces ¿realmente “x”, es decir, el tiempo, puede valer cero? Después de haber realizado los cálculos, la respuesta lógica es no, pero ¿qué significa que el tiempo valga cero? Una interpretación es que no se requiere tiempo para recorrer esa distancia y eso es imposible físicamente.
Por último, ¿realmente son necesarios los números negativos en este problema?, ¿por qué? La respuesta es no, porque en el contexto de este problema no existen velocidades ni tiempos negativos. Por ejemplo, no existe un auto que viaje a -30 kilómetros por hora, o que tarde en llegar a alguna parte -2 horas negativas. Analizar el contexto de un problema permite tomar decisiones sobre los datos a utilizar para su resolución.
Observa cómo queda la tabla:

Es momento de elaborar la gráfica. Y con la información anterior, te puedes dar cuenta de que no es necesario utilizar los valores negativos, porque el contexto del problema limita su uso.
Lo primero será trazar el cuadrante del plano cartesiano; después, escribir los valores de la variable independiente tiempo y de la variable dependiente velocidad; determinando la escala en cada eje, en este caso de 5 en 5 para el eje “y” y de 2 en 2 para el eje “x”
Después se marca con un punto dónde se ubica en el plano cartesiano cada pareja de valores correspondientes. Una vez marcados todos, se traza la línea que define la gráfica. Queda de la siguiente manera:
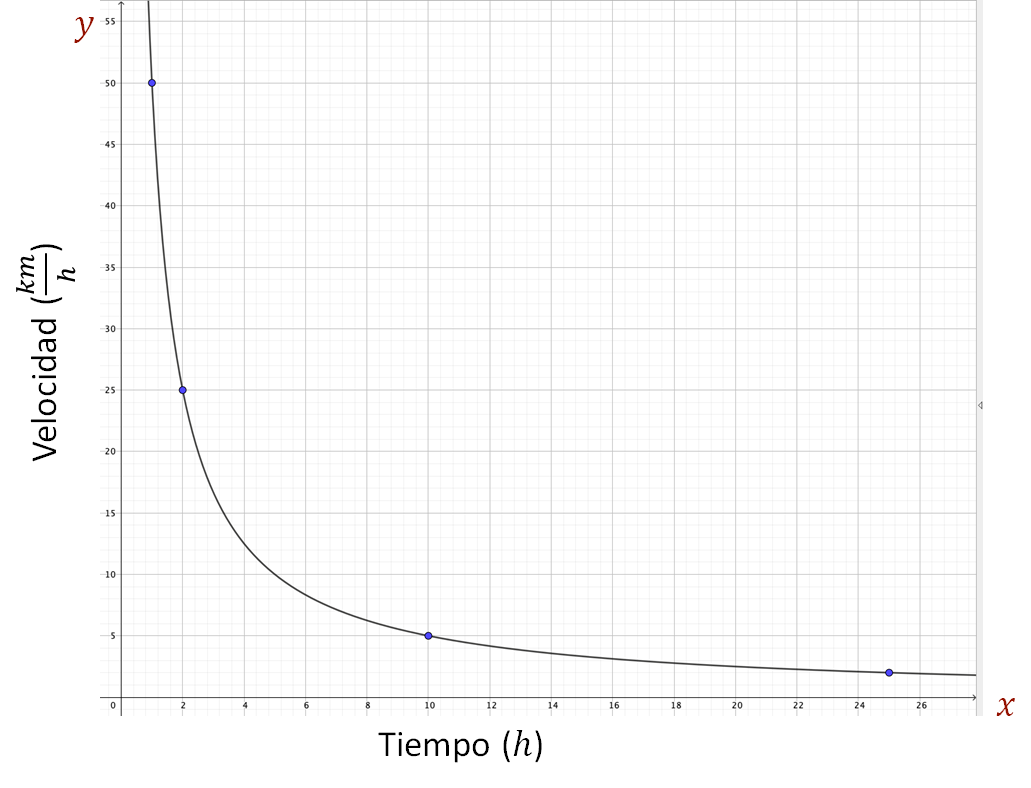
Ahora, ¿qué se puede decir acerca de la gráfica?
Se puede ver que a mayor tiempo, menor velocidad y viceversa.
Finalmente, reflexiona:
¿Qué pasa con el cero?
En el recorrido de la línea, ¿en algún momento pasa por el cero?
¿A qué se supone que se deba?
Toma un momento para pensarlo, y en tu cuaderno escribe una conclusión al respecto.
Ahora fortalecerás lo que has aprendido sobre gráficas haciendo la interpretación y comparación de un par de ellas.
Las siguientes gráficas y expresiones algebraicas representan la proporcionalidad inversa. Analízalas y encuentra puntos en común o de diferencia.
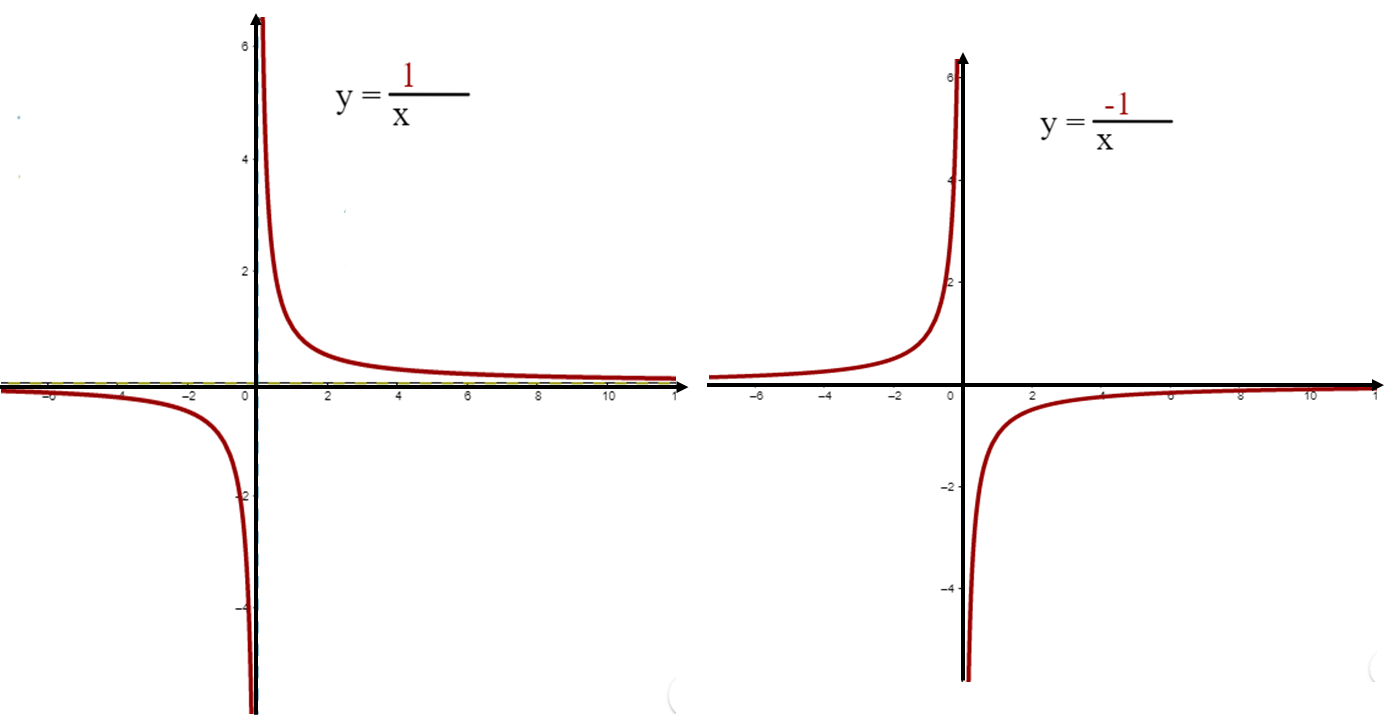
Se pueden ver dos gráficas que tienen los mismos valores en el eje “x” y en el eje “y”. También que en ambas aparecen líneas curvas que definen la gráfica, las cuales, se sabe, se llaman hipérbolas. Otra cosa que se nota es una expresión algebraica en cada gráfica, que como seguramente ya identificaste, se trata de la expresión que permite calcular los valores de la variable dependiente. En el denominador aparece “x”, es decir, los valores que puede tomar la variable independiente, mientras que en el numerador aparece el número 1. Pero en una expresión el número 1 es positivo y en la otra es negativo.
¿Qué valor representan el 1 y 1 negativo en cada expresión algebraica?
¿Cómo influye en la gráfica el signo que pueda tomar la constante de proporcionalidad inversa?
¿Qué tiene que ver el cero con todo esto?
Para responder estas preguntas, analiza los siguientes ejemplos.
Para responder la primera pregunta, se necesita comparar las expresiones algebraicas que aparecen en las gráficas con la expresión algebraica que se usa para calcular los valores que puede tomar la variable dependiente, es decir, “y”.

Como puedes observar, el número 1 y el 1 negativo se encuentran situados en el mismo lugar donde aparece la letra “k”. En otras palabras, el numerador; en esa forma de la expresión algebraica de la proporcionalidad inversa, siempre será el valor que representa la constante de proporcionalidad inversa.
Para responder la segunda pregunta: ¿cómo influye en la gráfica el signo que pueda tomar la constante de proporcionalidad inversa?, es necesario analizar varias gráficas simultáneamente, en donde la constante de proporcionalidad inversa represente valores negativos y positivos. Observa los ejemplos.
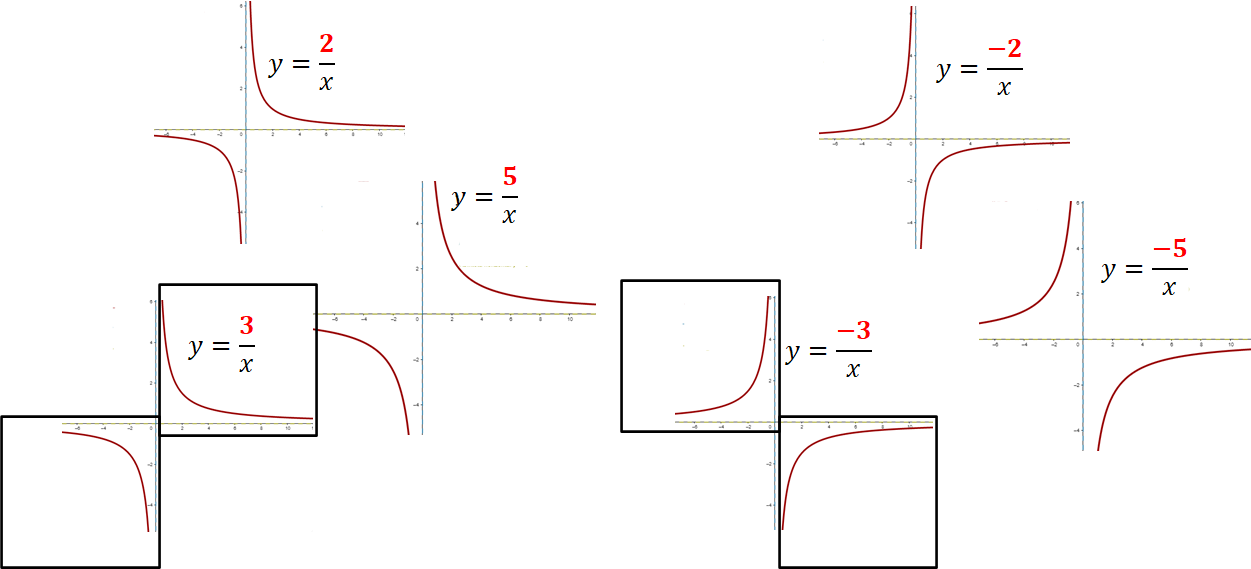
Hay seis gráficas de funciones de proporcionalidad inversa, tres de ellas con constante de proporcionalidad negativa y otras tres con constante de proporcionalidad positiva. ¿Qué puedes decir sobre el lugar que ocupan las líneas en cada gráfica y cómo se relaciona con el signo de la constante de proporcionalidad?
Cuando la constante de proporcionalidad inversa tiene valores negativos, la línea que define la gráfica siempre se encontrará en la parte superior izquierda si los valores de “x” son negativos, y en la parte inferior derecha si los valores de “x” son positivos; es decir, en los cuadrantes dos y cuatro de un plano cartesiano, respectivamente.
Por otro lado, cuando la constante de proporcionalidad inversa tiene valores positivos, la línea que define la gráfica siempre se encontrará en la parte superior derecha si los valores de “x” son positivos, y en la parte inferior izquierda si los valores de “x” son negativos. Es decir, en los cuadrantes uno y tres de un plano cartesiano.
Para responder la pregunta: ¿qué tiene que ver el cero con todo esto? Se sabe que, en las gráficas de proporcionalidad inversa, la línea que las define no pasa nunca por el cero, entonces, el cero será el punto de referencia y de partida para el análisis.
Las gráficas de proporcionalidad inversa pueden crecer o decrecer y que esto suceda depende directamente del signo de la constante de proporcionalidad.
Si la constante de proporcionalidad es menor que cero (negativo), entonces la gráfica es creciente. Pero ¿esto qué quiere decir? Que una gráfica de proporcionalidad inversa sea creciente significa que al aumentar la variable independiente “x”, aumenta también la variable dependiente “y”

Por otro lado, en una relación de proporcionalidad inversa, siempre que la constante de proporcionalidad sea mayor que cero (positivo), la gráfica siempre será decreciente, entonces, al aumentar la variable independiente “x”, la variable dependiente “y” disminuirá.

Hasta ahora, has resuelto problemas que involucran funciones de proporcionalidad inversa, también has analizado algunas de sus propiedades. Por lo tanto, se puede concluir que:
- En una relación de proporcionalidad inversa, su gráfica es creciente si la constante de proporcionalidad es menor que cero o negativa, y es decreciente si la constante de proporcionalidad es mayor que cero o positiva.
- La gráfica de una proporcionalidad inversa es creciente o decreciente a través del lugar en donde la línea que define la gráfica se ubique. Si la línea se ubica en los cuadrantes 1 y 3, la gráfica es decreciente, y si se ubica en los cuadrantes 2 y 4, la gráfica es creciente.
- La línea que define la gráfica de una relación de proporcionalidad inversa puede estar muy cerca del cero, pero jamás pasará por él.
Has finalizado esta sesión, dedicada al análisis de las propiedades de la proporcionalidad inversa a través de la resolución de problemas.
Recuerda que este es un material de apoyo, y para complementar lo estudiado puedes consultar otras fuentes, como tu libro de texto de Matemáticas de segundo grado.
El Reto de Hoy:
Ahora que ya conoces más sobre las propiedades de la proporcionalidad inversa, resuelve el siguiente problema.
El producto de dos números es 24. ¿Cuáles son los valores que pueden tomar estos números?
Si se elabora la gráfica de cada pareja de los números obtenidos, ¿la gráfica es creciente o decreciente?
Argumenta tu respuesta.
Analiza la situación y escribe en tu cuaderno un breve procedimiento sobre cómo resolverlo.
Para resolver este problema se deben formar parejas de números cuyo producto siempre sea 24, es decir, el 24 es un valor constante y representa el valor de la constante de proporcionalidad.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Diversas formas de modelar un poema
Aprendizaje esperado: Crea textos poéticos con formas gráficas.
Énfasis: Explorar elementos plásticos en poemas.
¿Qué vamos a aprender?
En esta sesión, conocerás la manera en que los textos juegan con las palabras y las letras para crear formas y nuevos sentidos. Es decir, las diversas formas de modelar un poema, para ello, profundizarás en los elementos plásticos.
¿Qué hacemos?
Reflexiona en la siguiente información.
La poesía se encuentra presente en la vida cotidiana, sólo es cuestión de estar atenta o atento a esos momentos donde se puede expresar, y puede surgir cuando despiertas, al desayunar, al disfrutar una fruta o algún aspecto que rodea tu vida.
Los actos de la poesía visual en la vida cotidiana están presentes en los anuncios, por ejemplo, ya que suelen jugar con la tipografía, con los colores y tamaños de las letras, con los espacios entre las palabras. Lo mismo ocurre en otras prácticas como el grafiti, los cómics y novelas gráficas, los créditos de las películas y las películas mismas. Los periódicos y las revistas suelen poner en letras más grandes los encabezados de las noticias para llamar la atención.
Pero no sólo eso, sino aspectos de la oralidad, pues toda la escritura traslada elementos de la oralidad. Con recursos como el tamaño de las letras y los espacios entre las palabras; quien escribe, puede dar tono a sus textos y hacer que se lean como si se hablara más alto (si la tipografía es más grande o si se utilizan mayúsculas) o más bajito (si se usan paréntesis, por ejemplo). Hay muchos textos que se escriben para ser leídos en voz alta o representados de alguna forma (como las obras de teatro o los guiones de programas de televisión). Son como las partituras musicales, en las que se escriben notas que los músicos deben de interpretar a su manera.
Para entenderlo mejor, explora cómo las palabras y la plástica conviven y se relacionan en un poema visual.

Como puedes observar, existe un diálogo que comienza con la pregunta: ¿podrías esbozar aquí algunos de los personajes de tu novela?; y la frase "Y ver cómo se desarrolla…". ¿Qué crees que podría significar cada imagen?
Esta obra corresponde al pintor y escultor español Vicente Rojo, quien ha relacionado el arte plástico y el dibujo con las letras como parte de su creación que entra en el terreno poético. Algunas de sus colecciones retoman la exploración de los alfabetos con el arte plástico; eso se observa, por ejemplo, en esta pieza de su “Alfabeto primitivo”.
Observa otra imagen.

Si se atiende a este código, se podrían tener varias posibilidades para traducirlo; por ejemplo: ¿qué letras o símbolos alcanzas a ver y cómo esto se transforma en otras figuras? ¿Logras verlas?
Más allá de descifrar su significado o darle una sola definición, lo importante es que transmita alguna emoción, pues depende del momento en que se observa.
Continúa con otro ejemplo.

Esta maqueta: ¿a qué se parece o qué te trae a la mente?, ¿qué te hace decir o pensar al verla?
Éste es un trabajo de Vicente Rojo a partir de la obra poética "Circo de noche", de José Emilio Pacheco, para crear su versión titulada “Circo”, donde la poesía y la imagen se conjugan y fusionan.
Aunque parezca que se pierde la manera tradicional de la poesía, se experimenta con otros lenguajes y expresiones, y se retoman aspectos como el ritmo, la imagen, la metáfora, el espacio y la forma para lograr una composición.
Analiza ahora el siguiente poema plástico del artista y arquitecto Mathias Goeritz.

Este poema plástico, como lo titula el autor, muestra relaciones directas con la poesía, ¿puedes, aunque no entiendas lo que dice, identificar la estructura?, ¿a qué se parece? Por ejemplo, las estrofas y los versos están ahí y permiten apreciar la forma de este poema.
Como observaste con los ejemplos anteriores, el punto de vinculación es la poesía y la forma. Ese efecto se logra por las imágenes que se consiguen crear a través de la percepción.
Esta poesía plástica se inspiró en lo que la pintura hacía, es decir, ¿cómo lograr pintar con palabras?, ¿cómo conseguir lo que una imagen visual consigue? Existe una respuesta muy fácil a esta pregunta y es que las palabras, en vez de escribirse siguiendo un renglón, sigan otras formas. Por ejemplo, que sigan la forma de una taza o de un sapo, como hizo José Juan Tablada en "Li-po y otros poemas".
Estos poemas se derivan de una tradición muy antigua, los “Carmen figuratum” (siglo VII a. C. en el mundo clásico), que se conservó durante el Renacimiento y se trata de textos que presentaban una imagen sagrada, normalmente en letras rojas sobre un fondo negro, para resaltar una figura y volver más fácil la meditación.
Algo parecido a esto puede verse en el siguiente poema de George Herbert (1593-1633), que se llama, en la traducción que hizo José Luis Rivas al español, “Alas de Pascua de Resurrección”.
"Señor, tú que creaste al hombre en la opulencia,
Aunque él, necio, todo lo gastara,
Cada vez más hundiéndose
Hasta volverse
Mísero:
Déjame
Elevarme contigo,
Cual una alondra, en armonioso vuelo,
Y cantar ese día tus victorias:
Entonces la caída al vuelo ha de lanzarme.
Mi tierna edad en tristeza empezó;
Y con enfermedades y vergüenza
Castigaste hasta tal punto mi pecado
Que me volví
Grácil.
Deja
Que me incorpore a ti
Y ese día comparte tu conquista:
Pues si en tu ala herida injerto el ala mía,
La pesadumbre al vuelo ha de impulsarme".
¿Identificaste la figura que se forma?
La poesía visual no fue inventada en las vanguardias del siglo XX ni en el XIX. En realidad, es tan vieja como la poesía escrita. Por ejemplo, se considera que el inicio de la poesía figurada en verso fue con los caligramas atribuidos al poeta griego Simmias de Rodas por el año 300 a.C. Su caligrama “Huevo” es una muestra.

En términos estrictos, toda poesía escrita es visual, ya que requiere de verla para entenderla. Sin embargo, el término se usa para referirse a las formas particulares de poesía impresa en las que la forma visual del texto se vuelve un objeto que se debe entender en propios términos. Además de la tipografía (su estilo, color y tamaño), estos poemas utilizan de manera particular el interlineado, la longitud del verso, los espacios y la puntuación para lograr sus efectos.
En diferentes momentos históricos, se han hecho poemas visuales, y se les ha llamado de diferentes formas. Otro ejemplo son los versus intertexti, que se hicieron desde el siglo IV y que tienen como representante principal a Rabano Mauro, quien en el siglo IX compuso poemas en una cuadrícula de 35 por 35 cuadrados; en cada uno colocaba una letra de algún tamaño, estilo o color particular que permitía identificar distintas palabras con diferentes propósitos, en su caso, religiosos.
Durante el Renacimiento, por su parte, fueron muy comunes los emblemas; esto es, textos que incluyen una imagen y un poema que la explicaba. Por ejemplo, algunos que incluyen abejas, entre los que destaca el de Alciato, que es el autor más conocido.
También se tienen los acrósticos, una forma muy antigua que subvierte la convención de leer de izquierda a derecha y de arriba abajo únicamente. Un acróstico muy famoso en español es “El bachiller”, de Fernando de Rojas.
Durante el siglo XX, diferentes artistas y autores se basaron en este tipo de tradición para hacer sus obras. El poeta francés Apollinaire llamó “caligramas” a los poemas que hizo, retomando algunas de las características mencionadas anteriormente.
En este mismo tenor se puede pensar en el llamado “Letrismo”, un movimiento vanguardista, fundado por el rumano Isidore Isou en París, que buscaba reducir el lenguaje a sus constituyentes más fundamentales. Otros letristas fueron Maurice Lemaitre y Jean-Paul Curtay. Hacían libros en los que colocaban letras junto a fotografías, signos diversos e imágenes pictóricas realmente interesantes.
El más famoso poeta visual de México es José Juan Tablada. Sin embargo, hay muchos otros. Hay una antología de Carlos Pineda, llamada "Poesía visual. La palabra transfigurada", que compila alrededor de cuatrocientos poemas visuales en cinco tomos con ejemplos de más de 300 diferentes autores.
También ha habido y hay muchas artistas y poetas mujeres importantes que suelen quedarse al margen en esta forma convencional de referirse a lo pasado. Observa lo que algunas mujeres escritoras hacen con la poesía visual.

Ahora, analiza cómo la forma y la palabra se juntan en esta creación del poeta y escritor cubano Guillermo Cabrera Infante, en el “Texto que se encoge”.
Guillermo Cabrera Infante
“Y el dueño se achicó, si es que podía hacerlo todavía y
fue el hombre increíblemente encogido, pulgarcito
o meñique, el genio de la botella al revés y
se fue haciendo más y más chico,
pequeño, pequeñito, chirriquitico
hasta que desapareció por
un agujero de ratones al
fondo-fondo-fondo,
un hoyo que
empezaba
con
o”
Lo que se observa aquí es una pirámide invertida y el texto poético que ayuda y refuerza la imagen. Pero no es la única variante. Otro elemento que se puede identificar en la poesía es la combinación de letras y dibujos. Observa el siguiente ejemplo.

En esta imagen de la palabra imperdible, se puede contemplar al texto separado, de tal forma que el alfiler lleva las letras «perdible» y el «Im» se queda en lo que abrocha el objeto.
Si observas con atención, esta imagen se vale de las dimensiones y las formas para dar fuerza o impactar al lector.
Pero ¿por quéÌ la poesía del siglo XX utiliza más estos elementos plásticos y gráficos? Una de las razones es la multiplicación y el alcance de diferentes medios debido a la cultura de masas, que comenzó a surgir desde el siglo anterior. Se pudieron hacer muchos más libros con más facilidad, y entonces se empezó a jugar con los materiales que constituyen los libros. Las letras son uno de esos materiales.
También tiene que ver con lo que las vanguardias artísticas se proponían: romper con lo que había antes, encontrar nuevas formas de escribir y de hacer arte, además de hacer que la separación entre la poesía y otros ámbitos de la vida desapareciera. Por ejemplo, los poetas concretos de Brasil decidieron que no debía haber separación entre la escritura y el diseño gráfico e hicieron cosas como la que se muestra en la siguiente imagen.

En este ejemplo, la palabra ‘lluvia’ se escribe con la letra ‘i’ al revés como si el punto fuera una de las gotas de agua que caen al llover.
Otro aspecto del porqué hay una diferencia muy marcada en el ámbito visual de este tipo de poesía, es que, hubo una multiplicación de los libros debido a la cultura de masas, las búsquedas vanguardistas (surrealistas, concretas) por hacer algo nuevo. Además, había más gente que sabía leer y entonces se hicieron más libros para ellos y se buscaron otras formas de llamar su atención. Una de esas formas de expresión se observa a continuación.

Se podría decir que es un tipo de poema visual que combina la imagen y palabras, e intervienen otros elementos como el color, lo que le da un efecto de pintura y poesía
Esto lleva a preguntar, ¿por quéÌ para los poemas visuales la tipografía de letras puede ser un recurso muy importante?
La tipografía de letras puede ser un recurso muy importante para los poemas visuales, porque con ella se pueden enfatizar muchas cosas. Varias ya están mencionadas antes. Por poner otro ejemplo, hay tipografías que se asocian con estilos particulares. Por ejemplo, las tipografías góticas, suelen asociarse con lo oscuro y lo raro, que son características relacionadas con este estilo y quienes escriben poesía pueden aprovechar esas asociaciones.
La historia de cada una de las tipografías también es algo muy interesante para estudiar. La Garamond llega desde el siglo XVI.
En la poesía visual, como en cualquier otro texto escrito, la tipografía, las dimensiones y el grosor de las letras o los espacios entre las palabras, pueden cargar de expresividad a lo escrito. Una tipografía muy sencilla produce efectos distintos a otra más rebuscada.
El tamaño de la letra puede llamar más la atención en algunas partes del texto. Incluso puede evitar que se lea, por ejemplo, cuando el tamaño de la letra es muy pequeño y quien lee no ve bien. Si algunas partes del texto tienen letras más grandes, se verán antes que las otras partes. Lo mismo puede lograrse con letras de diferentes colores. Los espacios entre las letras y las palabras también pueden hacer que quien lea, lo haga más rápido o más lento.
Un ejemplo de lo anterior es el poema del artista y creador Mathias Goeritz, quien utilizó la siguiente idea.

Es decir que, la poesía concreta pasó a otra forma de expresión como es la arquitectura. La frase que utilizó es: “Pocos cocodrilos locos”, que al leerla juega con las expresiones “Locos cocodrilos pocos”. Este poema mural fue creado en 1967, pero con el temblor de 1985 sufrió daños. Hoy se puede encontrar una reproducción parcial en el Museo del Eco.
También existen otras formas de creación poética, los medios audiovisuales. Es decir, la poesía se ha trasladado del papel a los objetos y a otros medios como el video. Su plasticidad y la exploración con el lenguaje ha permitido que otros espacios, sonidos e imágenes sirvan para trasmitir un mensaje. Observa el siguiente video sobre una de las posibilidades poéticas.
- Chispazos: poemas (antipoemas) visuales.
https://youtu.be/3DLzxmkswFk
Lo que observaste en el video anterior, fue un juego con la imagen, el sonido y la posición de los objetos; además, los colores, tamaños, formas, movimiento, imágenes y sonidos como elementos de exploración para crear diversos efectos.
Esta poesía tiene tantas clasificaciones que no vale la pena pensar en sólo una. Los ejemplos anteriores te pueden dar una idea de las posibilidades de este tipo de poesía. Asimismo, ha sido una corriente muy popular porque al mismo tiempo que permite explorar con la materialidad de lo que constituye la poesía, es divertida, además de sencilla y aparentemente fácil de entender.
Con todos estos elementos, ya puedes aventurarte a explorar los poemas plásticos. Para ello, observa las siguientes imágenes e identifica algunos aspectos que brinda la plasticidad de la poesía.
Comienza la obra del poeta visual de Joan Brossa.

¿Qué título crees que tendría? ¿Cuáles serían las características que puedes observar en ella?
Esta pieza la trabajó el autor en el espacio público. Revisa el título de la obra, y compara tus respuestas y las características que observaste.
El título de la obra es “Letras Gimnastas”, y sus características son:
- Letras iguales en tamaño y forma.
- Tienen el mismo color.
- Están simulando una barra de equilibro.
Esta representación puede hacerte pensar o imaginar cómo otros son parecidos a ti. Ahora revisa otro poema de este autor.

¿Qué figuras utiliza? ¿Qué significados o intenciones descubriste?
El autor utiliza algunas formas convencionales como el círculo, el cuadro y la letra. Pero también refiere a algo común, el hilo y la sensación de laberinto.
La oportunidad que brindan estos poemas es crear nuestros propios significados. Este poema podría acercar al mito del minotauro y el laberinto. Alguna vez también te podrías haber sentido así, en un laberinto, buscando la salida.
Has concluido la sesión. Si deseas saber más del tema, puedes consultar tu libro de texto de Lengua Materna, Español.
El Reto de Hoy:
Investiga, lee y analiza otros poemas y autores en otros libros o soportes electrónicos. Recuerda que lo importante es la exploración y el desarrollo de tu creatividad. Incluso podrías crear tu propio poema gráfico.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Caleidoscopio de mi comunidad
Aprendizaje esperado: Representa acontecimientos importantes vinculados a la historia de su comunidad mediante distintas formas expresivas.
Énfasis: Generar prácticas artísticas que modelen una mirada hacia el arte ambiental en su comunidad.
¿Qué vamos a aprender?
En esta sesión, representarás a través de diversas formas expresivas acontecimientos importantes, generando experiencias artísticas y vínculos dirigidas hacia el arte ambiental de tu comunidad. Para ello, explorarás la magia del caleidoscopio.
El ambiente es un conjunto de elementos naturales, emocionales y sociales que están estrechamente relacionados con lo que está en tu alrededor.
¿Qué hacemos?
Trabajarás para construir y reconstruir tu ambiente, en esta ocasión lo realizarás desde la magia de tu imaginación, recuerdos, memorias, historias y jugando.
Los materiales que necesitarás son: un lugar donde anotar lo más importante, lápices, colores, material reciclado, regalos que algún familiar te haya dado. Asimismo, piensa en un lugar importante o significativo que exista donde vives, donde estás en este momento, o que recuerdes de alguna parte, y toda tu imaginación, creatividad y disposición.
Ya que cuentes con estos elementos, comienza con este caleidoscopio de tu comunidad.
El caleidoscopio es un objeto óptico que está construido con tres espejos y cristales de colores; estos cristales los colocas dentro de un tubo, y si miras en su interior, verás diversas formas geométricas diferentes y llenas de color.
Para conocer más sobre este sorprendente caleidoscopio y cómo realizarlo, observa el siguiente video.
- Video. Alumno realizando un caleidoscopio con material reciclado.
Si te es posible, construye tu propio caleidoscopio. El caleidoscopio es mágico e importante porque cuando se observa a través de él, no sólo encontrarás formas geométricas, este artefacto te contará historias y visiones de muchas personas.
Tienes que mirar con atención, más allá de las figuras que se van formando en cada giro. Abre tu mente, tu corazón y tus "sentipensares".
A continuación, observa el siguiente video sobre lo importante de aprender a ver las miradas y cómo ven las cosas los demás. Presta mucha atención.
- Video. Abuela.
Con lo que se menciona en el video anterior, puedes reflexionar sobre las historias importantes que nos cambian y transcienden de generación en generación, de darle un significado e importancia a los lugares e historias que se crean en la comunidad, aprendiendo a escuchar a los demás.
Continúa con el siguiente video para seguir profundizando en este caleidoscopio de la comunidad.
- Video. Regina.
El juego y la imaginación son los poderes de la magia. Ahora, realizarás lo siguiente:
Con toda información que ya cuentas, crea una historia. Inspírate e imagina. Puedes pedir ayuda a un familiar y construir juntos una historia. Mientras alguno actúa otro puede producir los efectos de sonido o ser el narrador. Todo depende de tu creatividad.
Para inspirarte lee el siguiente ejemplo:
"Soy un nahual, soy un hombre sabio, protector de los demás, con poderes sobrenaturales y me puedo trasformar en diferentes animales y fenómenos atmosféricos".
"El aire me ayuda a llevar mi poesía a través de las montañas, siembro memorias y ayudo a que crezcan las ramas con conocimiento…".
Existen varias formas de hacerlo, por ejemplo, observa nuevamente por tu caleidoscopio o los videos anteriores, pero ahora no sólo abrirás bien los ojos, también vas a abrir bien tu sentido del oído, para escuchar las historias y “su esencia”.
Ahora, realiza la siguiente actividad.
Abre muy bien todos sus sentidos y también tu corazón y alma para ver más allá. Busca un lugar, un rinconcito especial de tu agrado, en tu casa o donde ahora te encuentres.
El espacio que elijas, lo transformarás con plantas, decoraciones, dibujos, objetos, fotografías, sonidos, canciones, movimientos, leyendas, historias, comida.
Y si deseas, compártelo con tu familia o con quienes estés cerca, creando en comunidad lazos.
Si no cuentas con ese espacio, podrías también darle un significado especial a la construcción de un árbol elaborado por ti, iniciando con las raíces formadas de las historias relatadas por los abuelos. El tronco se formará con recuerdos, momentos valiosos que surgieron de estas historias. Puedes incluir tus pinturas, las canciones favoritas de mamá o papá. No hay límite para la imaginación y construcción del arte.
Para inspirarte, observa el siguiente video sobre las historias de algunas y algunos alumnos.
- Video. Historias alumnos.
El Reto de Hoy:
Realiza las actividades que se presentaron en esta sesión, y si está en tus posibilidades, construye tu propio caleidoscopio y mira a través de él para reconocer otros puntos de vista y otras formas de vivir.
Además, busca un lugar que te pueda dar un nuevo significado y modifícalo con aspectos positivos que transformen el ambiente, utilizando tu sentir, tu pensar, tus "sentipensares".
Finalmente, comparte tus manifestaciones artísticas con tu familia.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
¿Conoces el Sistema Solar?
Aprendizaje esperado: Describir las características y la dinámica del sistema solar.
Énfasis: Reflexionar sobre algunas ideas previas que se tienen acerca del sistema solar.
¿Qué vamos a aprender?
En esta sesión, explorarás el sistema solar. Para ello, conocerás algunas de sus características y las ideas previas que se tienen acerca de este, considerando las aportaciones de cada astrónomo y físico que contribuyo a descubrir lo que conocemos.
¿Qué hacemos?
Inicia con la siguiente pregunta:
¿Conoces el sistema solar?
Actualmente se habla de 8 planetas, pero hace muchos años, cuando tus padres eran estudiantes, se decía que el sistema solar lo conformaban 9 planetas. Sin embargo, esta clasificación cambio en el año 2006, ya que la Unión Astronómica Internacional determinó que Plutón no tenía la masa suficiente para ser considerado un planeta, por lo que se le dio la clasificación de planeta enano.
Observa el siguiente video para descubrir más cosas sorprendentes del sistema solar.
- El sistema solar.
https://www.youtube.com/watch?v=5S6yGtsDMrE
Cómo pudiste observar, nuestro sistema solar está formado por los siguientes planetas:
- Mercurio
- Venus
- Tierra
- Marte
- Júpiter
- Saturno
- Urano
- Neptuno
A los planetas se les puede clasificar por su composición y por su distancia al Sol. Considerando la composición de cada planeta, se tienen dos clasificaciones: planetas rocosos y planetas gaseosos.
Los planetas rocosos, también llamados telúricos o terrestres, están formados principalmente por materiales rocosos y metálicos, y con un tamaño relativamente similar. Mercurio, Venus, Tierra y Marte pertenecen a esta clasificación.
Por otro lado, los planetas gaseosos se caracterizan por sus atmósferas densas, rápidos movimientos de rotación, campos magnéticos intensos, por contar con sistemas de anillos y con muchos satélites orbitando a su alrededor. Júpiter, Saturno, Urano, y Neptuno cumplen con estas características, por lo que se les clasifica como planetas gaseosos.
Según su distancia al Sol los planetas se clasifican en interiores y exteriores. Los planetas interiores son los que se encuentran entre el Sol y el cinturón de asteroides. Mercurio, Venus, Tierra y Marte pertenecen a esta clasificación. Los planetas exteriores son los que se encuentran después del cinturón de asteroides. Júpiter, Saturno, Urano y Neptuno pertenecen a esta clasificación de planetas.
Curiosamente, todos los planetas interiores como Mercurio, Venus, Tierra, y Marte, también son planetas rocos, mientras que los exteriores como Júpiter, Saturno, Urano, y Neptuno, son planetas gaseosos.
Ahora que conoces más sobre los planetas, es hora de que descubras lo que es el sistema solar. Hasta donde se puede inferir, recibe su nombre a partir del sol y los cuerpos celestes que giran a su alrededor, pero también se puede entender como un sistema planetario que se compone de una estrella central y uno o más planetas que giran a su alrededor.
Si embargo, no siempre fue de esta forma, antes de llegar a eso, las observaciones que se hacían en diferentes partes del mundo y dentro de las diferentes culturas que miraban hacia el cielo, se creía que la tierra era el centro del universo, a esto se le conoce como la teoría geocéntrica o geocentrismo, e incluso no se utilizaba el termino de sistema solar, ya que en esta teoría ponían a la tierra como el centro del universo y eran el Sol y el resto de los planetas los que giraban alrededor de la Tierra.
Esta teoría la postuló Claudio Ptolomeo en el siglo II de nuestra era. El modelo de Ptolomeo estuvo en vigor hasta el siglo XVI, ya que poco después apareció el famoso Nicolás Copérnico.
Los trabajos de observación astronómica que hizo Copérnico lo llevaron a concluir que el Sol se encontraba en el centro del universo y la Tierra, que giraba una vez en torno a su eje, completaba cada año una vuelta alrededor de él. Además, afirmaba que el resto de los planetas conocidos hasta ese entonces, Mercurio, Venus, Marte, Júpiter y Saturno, también giraban en torno al Sol.
Al ser nueva la teoría que planteaban, no fue bien recibida de momento. Casi medio siglo después de que Copérnico publicara su teoría heliocéntrica, Galileo Galilei fabricó el telescopio; y con sus observaciones contribuyó a lo dicho por Copérnico.
Incluso, hay una leyenda de Galileo Galilei, donde menciona una frase en el momento que le piden que se retracte de su apoyo a la teoría:
“Y sin embargo se mueve”.
Giuseppe Baretti, un escritor y crítico de la ilustración italiana, afirmó que, después de la abjuración, Galileo dijo la famosa frase, pero es poco probable que Galileo pronunciara esa famosa frase en ese momento, ya que no se encontraba en situación de libertad y sin duda era desafiante hacerlo ante el tribunal de cardenales de la Inquisición.
Para conocer otros elementos del sistema solar, observa el siguiente video del minuto 3:04 al 5:40.
- Las leyes de Kepler.
https://www.youtube.com/watch?v=pJZox-Wo2og&t=52s
El estudio del sistema solar ha cambiado en diferentes etapas del tiempo. Y cada uno de los astrónomos que has conocido en esta sesión, aporta elementos nuevos. Estas teorías se van nutriendo, con el tiempo y con observaciones.
Gracias a la fuerza de gravitación universal, es posible que los planetas giren alrededor del sol, con una órbita elíptica como mencionó Kepler. Esta fuerza tiene que ver con la masa de los cuerpos y la distancia a la que se encuentran uno del otro, por lo tanto, es importante considerar este descubrimiento de Newton. Hoy en día, se puede afirmar que el sol es más grande que cualquier planeta de nuestro sistema solar; en otras palabras, la masa del sol es incluso más grande que la masa junta de los 8 planetas juntos, por lo tanto, ejerce una gran fuerza de atracción.
Por la forma en que se mueven los planetas en orbitas elípticas y la aceleración que llevan al moverse, éstos desarrollan una forma esférica.
Entre los planetas y el sol hay elementos que se van a encontrar en el sistema solar, pero la diferencia es que acorde a las características de cada uno, se encontrarán con mayor abundancia.
Si se habla del sol, encontrarás que está compuesto principalmente de hidrogeno y helio, pero abundara en un 73% el hidrógeno en su composición.
Ahora, si se habla de los planetas rocosos, encontrarás que Mercurio tiene una composición de hierro entre un 65% a 70%, y esto lo convierte en el planeta con más hierro del sistema solar. Por otro lado, Venus tiene una atmósfera compuesta principalmente de dióxido de carbono y gruesas nubes de ácido sulfúrico.
Mientras que la Tierra tiene una atmósfera relativamente delgada, 78% de la atmósfera es nitrógeno, el 21% es oxígeno y el resto lo componen argón, dióxido de carbono y vapor de agua. Por último, Marte tiene una atmósfera extremadamente delgada compuesta en un 95% de dióxido de carbono y el resto es una mezcla de nitrógeno, argón, oxígeno y metano.
Una particularidad en el suelo de Marte es que es muy similar al de la Tierra, pero como éste contiene mucho óxido de hierro, se ve de color rojizo.
Continúa con los planetas gaseosos. Júpiter, al ser un planeta gaseoso, no es claro dónde termina la atmósfera del planeta y donde comienza el interior del planeta. Se sabe que la atmósfera de Júpiter está compuesta principalmente por hidrógeno molecular y helio, aunque se han encontrado pequeñas trazas de metano, amoniaco y ácido sulfhídrico.
Si se compara con Saturno, notarás que son muy similares en su composición ya que la atmósfera de Saturno está compuesta de hidrógeno, helio y una mezcla de metano, amonio, vapor de agua y otros gases.
La atmósfera de Urano está compuesta de hidrógeno y helio, como Júpiter y Saturno, pero además tiene metano, lo cual le da el color azul al planeta.
Neptuno es muy parecido a Urano. Está compuesto de una espesa mezcla de agua, amoniaco y metano sobre un centro sólido del tamaño de la Tierra. Su atmósfera se compone de hidrógeno, helio y metano. El metano le da a Neptuno el mismo color azul de Urano.
De lo que se sabe de los planetas, se puede concluir que sí hay una gran similitud entre los elementos que forman a los planetas del sistema solar.
Otros elementos importantes del sistema solar son las estrellas y los asteroides. Una estrella es una masa de materia gaseosa incandescente que flota en el espacio. La estrella más cercana a nosotros es el Sol, pero cualquier estrella que se pueda observar en el universo cumple las mismas características. Por lo que son descritas como cuerpos celestes que emiten luz, a diferencia de los planetas que son objetos que no la emiten.
Mientras que los asteroides, son pequeños objetos rocosos, más pequeños que un planeta y estos orbitan entre marte y júpiter. Si dos asteroides chocan entre sí y salen pedazos más pequeños estos se convierten en un meteoroide.
Si ese meteoroide se acercara lo suficiente a la Tierra y entra en la atmósfera terrestre, éste se evaporaría para convertirse en un meteoro, que se vería como un hermoso haz de luz en el cielo y si el meteoro logra llegar al suelo después de entrar a la atmosfera, este será un meteorito.
Una estrella fugaz es realmente un meteoro que desde el espacio roza en la atmósfera de la Tierra, y se mueve tan rápido que se calienta y se quema, produciendo un brillo que permite verla, sin embargo, éstas no llegan al suelo.
Con esta información, has concluido la sesión. Si deseas saber más del sistema solar, puedes consultar tu libro de texto u otras fuentes confiables.
El Reto de Hoy:
Realiza una cronología de cómo fue cambiando el concepto de sistema solar, considerando las aportaciones de cada astrónomo y físico que contribuyo a descubrir lo que hoy conocemos.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Europa en América
Aprendizaje esperado: Reconoce hechos ocurridos en Europa y América antes y durante los viajes de exploración. También estudia la relación entre la defensa de la religión cristiana y el proceso de conquista española.
Énfasis: Conocer los viajes de Colón y los primeros europeos que llegaron a América.
¿Qué vamos a aprender?
En esta sesión, estudiarás sobre los viajes de exploración de los primeros europeos que llegaron al continente americano, como Cristóbal Colon. Asimismo, profundizarás en qué fue lo que los alentó y cómo lo lograron.
¿Qué hacemos?
Para iniciar, lee los textos que redactó Cristóbal Colón durante el viaje a lo que él pensó que eran las Indias, así como algunas cartas posteriores, que fueron compilados en el Diario de a bordo de Cristóbal Colón.
“Diario de a bordo de Cristóbal Colon”
"Más me pareció que era gente muy pobre de todo. Ellos andan todos desnudos como su madre los parió, y también las mujeres […]. Y todos los que yo vi eran todos mancebos, que ninguno vi de edad de más de 30 años. Muy bien hechos, de muy hermosos cuerpos y muy buenas caras. Los cabellos gruesos casi como sedas de cola de caballos, y cortos. Los cabellos traen por encima de las cejas, salvo unos pocos detrás que traen largos, que jamás cortan. Ellos no traen armas ni las conocen, porque les mostré espadas y las tomaban por el filo, y se cortaban con ignorancia. No tienen algún hierro. Sus azagayas son unas varas sin hierro, y algunas de ellas tienen al cabo un diente de pece, y otras de otras cosas […].
Ellos todos a una mano son de buena estatura de grandeza y buenos gestos, bien hechos. Yo vi algunos que tenían señales de heridas en sus cuerpos, y les hice señas que era aquello, y ellos me mostraron como allí venían gente de otras islas que estaban cerca y los querían tomar y se defendían. Y yo creí y creo que aquí vienen de tierra firme a tomarlos por cautivos. Ellos deben ser buenos servidores y de buen ingenio, que veo que muy presto dicen todo lo que les decía. Y creo que ligeramente se harían cristianos, que me pareció que ninguna secta tenían. Yo, placiendo a Nuestro Señor, llevaré de aquí al tiempo de mi partida seis a Vuestra Alteza para que aprendan a hablar. Ninguna bestia de ninguna manera vi, salvo papagayos en esta Isla.
Sobre el paisaje, contó:
“Hay palmas de seis u ocho maneras, que es admiración verlas, por la deformidad hermosa de ellas, mas, así como los otros árboles, hierbas y frutos […]. Hay pinares a maravilla y hay campiñas grandísimas, y hay miel, y de muchas maneras de aves, y frutas muy diversas. En las tierras hay muchas minas de metales […] las tierras tan hermosas y gruesas para plantar y sembrar, para criar ganados de todas suertes, para edificios de villas y lugares. Los puertos de la mar aquí no habría creencia sin vista, y de los ríos muchos y grandes, y buenas aguas, los más de los cuales traen oro”.
Ahora, anota las siguientes preguntas que guiarán esta sesión:
¿Qué fue lo que alentó a portugueses y españoles a explorar nuevas rutas marítimas?
¿Qué consecuencias tuvo la exploración de nuevas rutas comerciales?
En 1453, los otomanos conquistaron la ciudad de Constantinopla. Esta ciudad, en la actual Turquía, era el punto más importante en las redes comerciales entre Europa y Asia. A través de ella se obtenían especias, como la pimienta, la canela y el clavo, mismas que eran muy apreciadas por los europeos. En la actualidad las usamos para dar sabor a los alimentos, pero en ese momento eran empleadas como conservadores, es decir, permitían que los alimentos se mantuvieran frescos durante más tiempo. También adquirían de Asia porcelana, incienso, seda y metales.
Con la caída de Constantinopla, los europeos perdieron el acceso a los productos asiáticos que tanto ansiaban. Como consecuencia de este bloqueo, los comerciantes y gobernantes europeos tuvieron que buscar nuevas rutas hacia el continente asiático para seguir obteniendo los productos provenientes de China e India, principalmente.
Los portugueses empezaron rodeando el continente africano para llegar por el sur del océano Índico. Una segunda ruta la propuso el genovés Cristóbal Colon. Él planteó la posibilidad de dirigirse al occidente, atravesar el océano Atlántico y así llegar a las Indias. Pero desembarcó en un continente hasta ese momento desconocido por los europeos: América.
Colón conocía que la Tierra era esférica, pero creía que era menos grande de lo que decían varios astrónomos de aquella época, y pensaba que si navegaba hacia el este de Europa no iba a demorar en llegar al lejano oriente; entonces, presentó su propuesta ante los reyes de España por primera vez en 1486.
Los reyes consultaron esta petición con astrónomos, marinos, pilotos y filósofos, quienes dictaminaron los aspectos técnicos del viaje, lo rechazaron, muchas veces entre burlas, una y otra vez durante los siguientes seis años. Hasta que Luis de Santángel se dirigió a la reina Isabel:
“Señora serenísima, este negocio es de calidad, si lo que tiene Vuestra Alteza por dificultoso a otro Rey se ofrece, y si lo acepta y sale próspero, qué inconvenientes y daños a vuestros reinos vendrían”.
Ante la intervención de Santángel, los reyes aceptaron financiar el viaje. El viernes 3 de agosto, en San Jorge, Palos, embarcaron la Santa María, la Pinta y la Niña. Después de dos meses de navegación, hacia las 2:00 am del 12 de octubre, con luna menguante, Rodrigo de Triana, vigía de la proa de la Pinta, gritaría: “¡Tierra! ¡Tierra!” Esa tierra era la costa de una isla de Guanahani en las Bahamas. A quien Colón dio por nombre San Salvador.
Luego del desembarco, el almirante salió a tierra desplegando el estandarte real; lo mismo hicieron los capitanes de la Pinta y la Niña, Martín Alonso Pinzón y Vicente Yáñez Pinzón. Colón tomó posesión de la isla en nombre de los reyes católicos. En el primer viaje, que realizó entre 1492 y 1493, recorrió el noreste del Caribe. También llegó a Cuba y a la isla de La Española, donde hoy están República Dominicana y Haití.
Cuando Colón regresó a España se presentó ante los reyes que habían financiado el viaje. Sobre este encuentro se tiene un relato del cronista Francisco López de Gómara.
«Presentó a los reyes el oro y las cosas que traía del otro mundo; y ellos y cuantos estaban delante se maravillaron mucho en ver que todo aquello […]. Elogiaron los papagayos, por ser de muy hermosos colores: unos muy verdes, otros muy colorados, otros amarillos, y pocos de ellos parecían a los que de otras partes se traen. Los conejos eran pequeñitos, orejas y cola de ratón, y el color gris. Probaron el ají, especia de los indios, que les quemó la lengua, y las batatas, que son raíces dulces […]. Maravillándose que no hubiese trigo allá, sino que todos comiesen pan de aquel maíz. Lo que más miraron fue los hombres, que traían cercillos de oro en las orejas y en las narices.
Después de ese encuentro, Colón reunió 1,500 voluntarios y emprendió un segundo viaje, que duró de 1493 a 1496. Los viajeros fundaron una colonia, llamada La Isabela, en la actual República Dominicana. Colón continuó su exploración hacia la isla de Jamaica. Su tercer viaje comenzó en 1498 y se prolongó dos años, hasta el 1500. En esa ocasión llegó a la actual Venezuela. En un cuarto viaje llegó a los actuales Costa Rica, Honduras y Nicaragua, pero nunca logró encontrar un paso marino para continuar rumbo a Asia.
Mientras esto ocurría, otro navegante, Américo Vespucio, descubrió que Colón no había llegado a Asia, sino a un nuevo continente.
La llegada a América, como casi todos los procesos históricos, fue multicausal, es decir, que tuvieron relación distintas causas. La principal: la necesidad de nuevas rutas para reestablecer los lazos comerciales con Asia. Otra serían los avances científicos y tecnológicos, que experimentó Europa desde el siglo XII como consecuencia de la presencia árabe, y que se vieron reflejados en las embarcaciones e instrumentos de navegación.
Las carabelas eran embarcaciones muy resistentes en mar abierto. Para moverse usaban velas triangulares y cuadradas, lo cual les permitía atravesar grandes distancias. Las naos se habían inventado copiando los barcos grandes que se usaban en el Mar del Norte. Por lo general eran más grandes que las carabelas. Su gran tamaño les permitía cargar muchas más cosas, por lo que podían utilizarse para hacer largos viajes, por ejemplo, cruzar el océano Atlántico, aunque no eran tan agiles como las carabelas y requerían más gente para conducirlas. También utilizaban dos o tres velas que les permitían navegar aprovechando la fuerza del viento.
Los principales instrumentos de navegación fueron: la brújula y el astrolabio. La brújula se descubrió en China y algunos investigadores creen que fueron los árabes quienes la llevaron a Europa, donde se sabe que existía hacia el año de 1200.
Originalmente, la brújula no era más que una aguja imantada que se ponía dentro de un cubo lleno de agua, sin embargo, con el paso de los años se inventaron brújulas que no requerían de agua para funcionar, estas cambiaron para siempre la forma en que se navegaba en Europa. El astrolabio se usaba para seguir el movimiento de los astros. Fue hasta el siglo XV que algunos marineros se dieron cuenta de que también había que mirar hacia el cielo para ubicarse en el mar.
Observa el siguiente video para profundizar en lo anterior.
- Divididos por un océano.
https://www.youtube.com/watch?v=3Ja4FdiQwAU&t=196s
A partir de los viajes de Cristóbal Colón, diversos navegantes comenzaron a explorar Centroamérica. Entre 1492 y 1519 muchas de las islas del Caribe fueron exploradas y conquistadas; islas como Puerto Rico, Jamaica o Cuba pasaron a formar parte del Imperio español entre 1500 y 1519, donde comenzaron a explorar también tierra firme. Los exploradores, además de conseguir el permiso de los reyes, les tenían que entregar una quinta parte de todo lo que consiguieran.
En el año de 1511 Gonzalo Guerrero y Jerónimo de Aguilar fueron los primeros españoles que se conoce que llegaron a las costas del actual México y vivieron en estas tierras. Llegaron a la península de Yucatán por un naufragio y su participación, años después, sería determinante.
Las primeras expediciones que llegaron a nuestro actual territorio fueron las de Francisco Hernández de Córdoba en 1517, quien zarpó desde Cuba y la de Juan de Grijalva en 1518. El gobernador de Cuba, Diego de Velázquez, con el objetivo de aumentar su poder y riqueza, envío estas tripulaciones para explorar los territorios y elaborar un informe sobre las riquezas.
Francisco Hernández de Córdoba salió de Cuba el 8 de febrero de 1517 y para principios del mes de marzo ya habían llegado a Isla Mujeres, a la que le pusieron así porque en los templos encontraron muchas estatuas de la diosa maya Ixchel. De ahí siguieron por la costa de la península de Yucatán, empezando por Cabo Catoche.
Continuaron su camino por la costa y llegaron al actual estado de Campeche, en Champotón los españoles bajaron a tomar agua y explorar la zona; arribo que preocupó a los mayas-chontales, quienes decidieron atacarlos para ahuyentarlos de sus tierras.
A pesar de las armas de los españoles, los mayas ganaron la batalla y los europeos tuvieron que regresar a sus barcos y volver a Cuba. Cabe señalar que, en uno de esos enfrentamientos, Hernández de Córdoba fue herido y murió en Cuba poco después.
Una vez que regresaron y le contaron a Diego de Velázquez lo que habían encontrado, el gobernador de Cuba decidió que tenía que enviar otra expedición, ahora encabezada por Juan de Grijalva, al mando de cuatro navíos bien equipados.
Los primeros puntos a los que llegaron fueron la isla de Cozumel y la bahía de la Ascensión, en la reserva de la biósfera de Sian Ka’an. Posteriormente continuaron su expedición por la costa yucateca y de Campeche, hasta llegar a la desembocadura de un gran río en el actual Tabasco, hoy conocido como Río Grijalva. La expedición navegó río arriba, pero sólo encontraron tierras cada vez más altas y montañas. Eso demostró que no había paso hacia el mar.
La expedición siguió su camino por la costa, llegando a San Juan de Ulúa. Ahí fueron visitados por emisarios de Moctezuma II, gobernante de los mexicas, quienes les dieron regalos. Grijalva en vez de avanzar decidió que era mejor avisar a Diego de Velázquez de todo lo que había descubierto y ver cuáles eran sus instrucciones, siguió explorando la costa hasta llegar al río Pánuco y de ahí regresó a Cuba.
Una tercera expedición zarpó en febrero de 1519, liderada por Hernán Cortés. Según el cronista Bernal Díaz del Castillo, se embarcó con menos de 700 hombres, 11 navíos, 16 caballos y armas de fuego hacia la península de Yucatán como sus antecesores, pero a diferencia de éstos, la expedición concluiría con la caía de México-Tenochtitlan.
Para recapitular lo que has estudiado en esta sesión, observa el siguiente video.
- Del posclásico a mediados del siglo XVII.
https://www.youtube.com/watch?v=zoTvnDShgKc&t=271s
Unos cuantos años después del primer viaje de Cristóbal Colón, los españoles exploraron y colonizaron las islas del Caribe y el resto del continente. Pronto otros países europeos lo hicieron con otras partes de América. Portugal se apropió de la región que hoy es Brasil; Francia e Inglaterra de América del Norte; Holanda de algunas islas del Caribe.
Además de explorar estas regiones, los europeos las colonizaron, este es un concepto que estudiarán más adelante.
Los malos tratos, la violencia y las enfermedades hicieron que comenzaran a morir muchos indígenas, hasta el punto de que desaparecieron poblaciones enteras, como los taínos en el Caribe.
El Reto de Hoy:
Realiza un mapa donde señales las rutas de exploración que estudiaste en esta sesión.
Finalmente retoma y responde las preguntas que anotaste:
¿Qué fue lo que alentó a portugueses y españoles a explorar nuevas rutas marítimas?
¿Qué consecuencias tuvo la exploración de nuevas rutas comerciales?
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario