Aprende en Casa III SEP: 23 de febrero TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 23 de febrero de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Martes 23 de febrero, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Proporcionalidad directa e inversa
Aprendizaje esperado: Analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.
Énfasis: Analizar y comparar situaciones de proporcionalidad directa e inversa a partir de sus representaciones tabular, gráfica y algebraica.
¿Qué vamos a aprender?
En esta sesión, estudiarás la variación proporcional directa y la variación proporcional inversa. Para ello, analizarás y resolverás problemas que se modelan con este tipo de variación a partir de sus representaciones algebraica, tabular y gráfica.
¿Qué hacemos?
Para iniciar, resuelve el siguiente problema.
Situación-problema: fabricación de tornillos
En una fábrica de tornillos, una máquina produce 30 tornillos cada 10 minutos, si la producción es siempre en el mismo tiempo y en la misma cantidad, ¿cuántas piezas produce en media hora?, ¿cuántas en una hora?, ¿en dos horas? y ¿en ocho horas?
Analiza la relación que se establece entre los datos del problema para responder las preguntas. Justifica y anota tus procedimientos.
Para responder las preguntas de la situación planteada es posible organizar la información en una tabla como la que se muestra, que consta de dos columnas con nueve renglones.

En la tabla se registran los datos que se relacionan, es decir, el tiempo en minutos y la cantidad de tornillos que se producen.
Como la producción depende del tiempo, se tiene entonces una variable que depende de otra. El tiempo es la variable independiente y la producción de tornillos es la variable dependiente. Para construir la tabla se nombra cada columna con las magnitudes involucradas, en la primera columna se ubica la variable tiempo, que está dada en minutos, en la segunda columna se anota la variable que corresponde al número de tornillos que se producen de acuerdo con el tiempo transcurrido.
En el segundo renglón y en lo sucesivo se registran los datos que proporciona el problema, es decir, en el segundo renglón se escribe 10, que hacen referencia a los 10 minutos mencionados en el problema. Posteriormente, a la derecha, el número de tornillos, en este caso 30. Las columnas permiten relacionar los datos, cada 10 minutos se producen 30 tornillos.
Ahora, contesta las siguientes preguntas:
Si en 10 minutos se producen 30 tornillos, ¿cuántos tornillos se producirán en 20 minutos?
Si 20 minutos es lo doble de 10 minutos, ¿también se producirá el doble de tornillos?
Si la cantidad de minutos aumenta al triple, ¿la producción de tornillos también aumentará al triple?
¿Qué pasará con la cantidad de tornillos producidos si el tiempo aumenta cinco veces?
Elabora tu tabla y trata de completarla.
Una manera de completar la tabla de la producción de tornillos es la siguiente.
Como la producción es de 30 tornillos cada 10 minutos, entonces a los 20 minutos se producen 60 tornillos; en 30 minutos se producen 90 tornillos; en 40 minutos se producen 120 tornillos; en 50 minutos se producen 150; en 60 minutos, es decir, 1 hora, se producen 180 tornillos; en 2 horas, es decir, 120 minutos, se produce el doble, 360 tornillos.
Compara los valores de la siguiente tabla con los tuyos y contesta: ¿los valores son iguales?
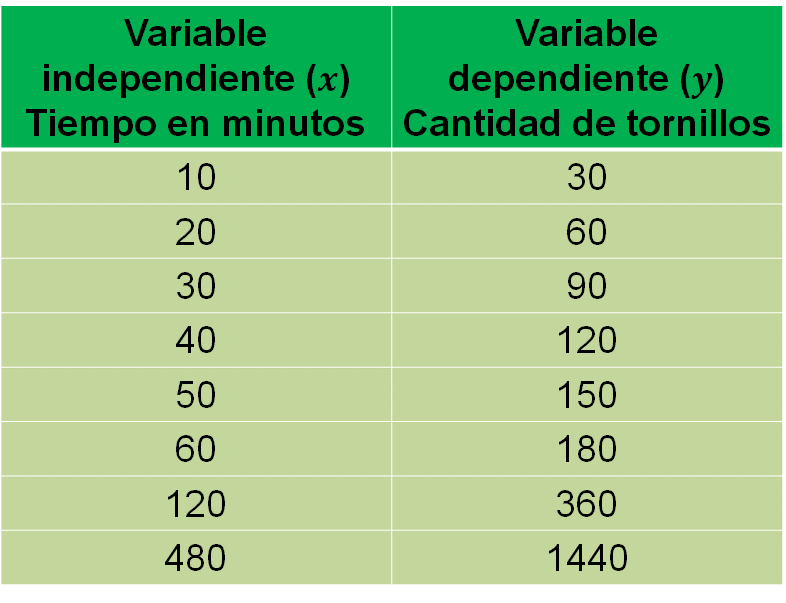
Verifica que cada valor de la variable dependiente aumenta en la misma proporción que la variable independiente, es decir, si “x” aumenta al doble, “y” aumenta al doble, si “x” aumenta al triple, “y” aumenta al triple y así sucesivamente. ¿Ocurre esto con los valores correspondientes en esta tabla?
Observa que las magnitudes varían de manera proporcional, y con la información de la tabla, se puede dar respuesta a las preguntas del problema inicial.
En media hora se producen noventa tornillos, en una hora se fabrican ciento ochenta tornillos, en dos horas se producen trescientos sesenta tornillos, y finalmente, en ocho horas la producción total será de mil cuatrocientos cuarenta tornillos.
Ahora, realiza algunas divisiones. En éstas, calcula el resultado de dividir cada valor de la variable dependiente “y”, entre el valor de la variable independiente “x”, que le corresponde. De esta manera, la primera división será:

La segunda división es:

Realiza las divisiones faltantes y contesta: ¿en todos los casos se obtiene el mismo resultado?
Como lo habrás notado, el resultado de las divisiones de los valores correspondientes de “y” entre “x” siempre es el mismo, esto hace que la variación de las magnitudes sea proporcional. A ese valor se le llama constante de proporcionalidad y se denota con una literal "k". En este caso la constante de proporcionalidad es igual a 3, que es el cociente obtenido en todas las divisiones de los valores correspondientes de “y” entre “x”

A partir de la expresión “k” igual a “y” entre “x”, se puede determinar que, “y” es igual a “k” por “x”. ¿Qué es lo que permite afirmar esto?, ¿cómo harías para establecer esta igualdad?
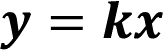
La manera de encontrar que “y” es igual a “k” por “x” es despejando la “y” de la expresión “k” es igual a “y” entre “x”. En este caso, la expresión adquiere la forma “y” igual a tres por “x”, dado que se conoce el valor de la constante de proporcionalidad “k”, que es igual a 3

Esta expresión permite calcular cualquier valor de la variable “y” a partir de un valor de la variable “x”. Por ejemplo, si quieres saber cuántos tornillos se producen en cuatro horas, es decir, en doscientos cuarenta minutos, se multiplica tres, que es el valor de “k” por doscientos cuarenta, que es el tiempo dado en minutos. Así se obtienen setecientos veinte, que es el número de tornillos que se producen en cuatro horas.
En la tabla se puede observar que cuatro horas corresponden al doble de dos horas, por lo que la producción de tornillos en cuatro horas debe ser el doble de los que se producen en dos horas, pero también corresponden a la mitad de los que se fabrican en ocho horas.
Continúa con otra situación alrededor de la misma fábrica de tornillos. Recuerda anotar todos los procedimientos para verificarlos, y si tienes alguna duda, anótala.
Situación-problema: fabricación de tornillos 2
La fábrica tiene un pedido de 15,000 tornillos. Para la entrega, se tiene la posibilidad de empacarlos en cajas de diferentes capacidades, pero colocando siempre el mismo número de tornillos en cada caja.
Determina el número de cajas que se van a utilizar dependiendo de los tornillos
que contienen, esto de acuerdo con los datos de la tabla que se muestra.

Antes de iniciar el llenado de la tabla, piensa y contesta:
Si aumenta el número de tornillos en cada caja, ¿aumenta o disminuye el número de cajas necesarias para empacarlos?; si disminuye el número de tornillos en cada caja, ¿aumenta o disminuye el número de cajas necesarias para empacarlos?; si el número de tornillos disminuye a la mitad, ¿el número de cajas también disminuye a la mitad? o ¿aumenta al doble?; por ejemplo, para empaquetar 500 tornillos, ¿se requiere la mitad de cajas o el doble de cajas que para empaquetar 1000 tornillos?
Se representarán en la tabla los datos variables, es decir, el número de cajas será la variable dependiente “y”, porque depende de la cantidad de tornillos que se acomoden en ellas, así que la cantidad de tornillos es la variable independiente, es decir, “x”
De acuerdo con los datos de la tabla, se necesita conocer el número de cajas para 1,500, 1,000, 750, 500, 250, 150 y 100 tornillos por caja.
¿Ya lo resolviste? ¿qué hiciste para calcular los datos que faltan? Una manera de encontrar los datos que faltan es dividir el total de tornillos a empaquetar, 15000, en este caso, entre el total de tornillos por caja.
Así, para 1500 tornillos, se determina el cociente de 15000 entre 1500 y se obtienen 10, lo que significa que para empaquetar 15000 tornillos en cajas de 1500 cada una, se requieren 10 cajas.
Con el mismo procedimiento se obtiene el resultado de utilizar 15 cajas cuando son 1000 tornillos por caja. Entonces, si disminuye el número de tornillos en cada caja.
Esta situación presenta un cambio entre las variables, que no es igual a la que observaste anteriormente con la producción de tornillos en esa fábrica.
Ahora, completa los datos faltantes de la tabla. Si se utiliza la misma manera de calcular el número de cajas de acuerdo con la cantidad de cajas, se obtiene que: para colocar 750 tornillos en cada caja, se necesitan 20 cajas. Si se colocan 500 tornillos por caja serán necesarias 30 cajas, para cajas con 250 tornillos se necesitan 60 de ellas, para colocar 150 tornillos en cada caja se requieren 100 cajas y para ubicar tornillos en cajas con 100, serán necesarias 150 cajas.
Analiza lo que ocurre con los valores correspondientes de las variables. ¿Piensas que existe algún valor constante? Para ello, observa con atención la tabla completa.
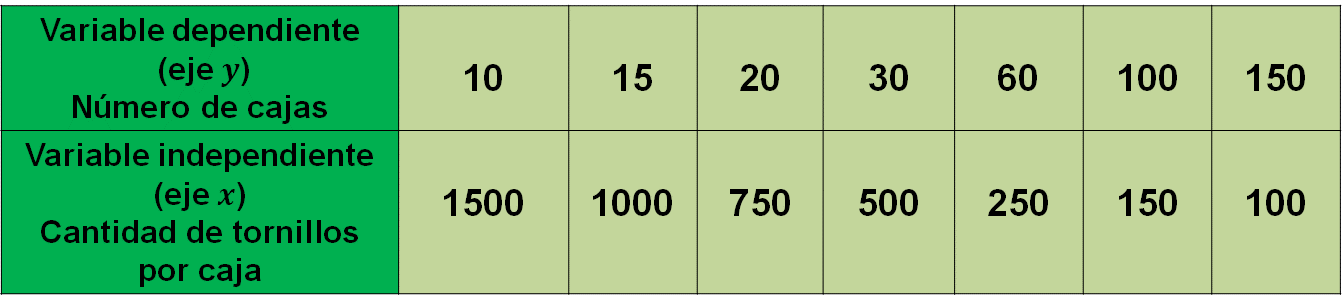
Calcula el producto de dos valores que se correspondan en la tabla. Es decir, multiplica un valor de “x” por el valor de “y” que le corresponde. Por ejemplo, 1500 por 10, ¿cuánto se obtiene? ¿se obtendrá el mismo resultado para cualquier par de valores en la tabla?
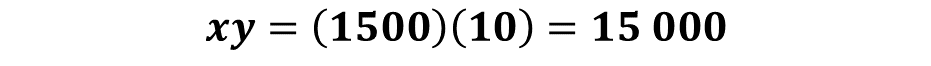
Sucede que se encuentra el mismo producto para todos los valores correspondientes de las variables en esta tabla.
En la tabla que corresponde a esta situación es posible identificar que cuando los valores de la variable independiente disminuyen, los valores de la variable dependiente aumentan, es decir, cuando la cantidad de tornillos por paquete disminuye, la cantidad de cajas aumenta, pero lo hacen en la misma proporción.
De esta manera, si los valores de “x” disminuyen a la mitad, los valores de “y” aumentan al doble, si los valores de “x” disminuyen a la tercera parte, los datos correspondientes de “y” aumentan al triple. Se trata de una variación proporcional, pero inversa.
Asimismo, al multiplicar los datos del primer renglón por los datos que les corresponden en el segundo renglón se obtiene el mismo valor, es decir, un valor constante, "k", en este caso, 15000
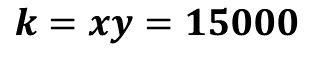
Todo lo anterior permite afirmar que esta situación representa una relación de proporcionalidad inversa. La constante “k” en una relación de proporcionalidad inversa es el producto de “x” por “y”
De aquí se puede obtener la expresión algebraica de una relación de proporcionalidad inversa que es:
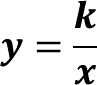
A partir de lo anterior, se puede afirmar que el valor de la constante en esta situación es 15000. También se puede afirmar que la expresión algebraica que corresponde a esta situación es, “y” es igual a 15000 entre “x”
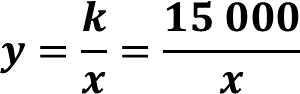
Ahora, compara lo obtenido en las dos situaciones anteriores.
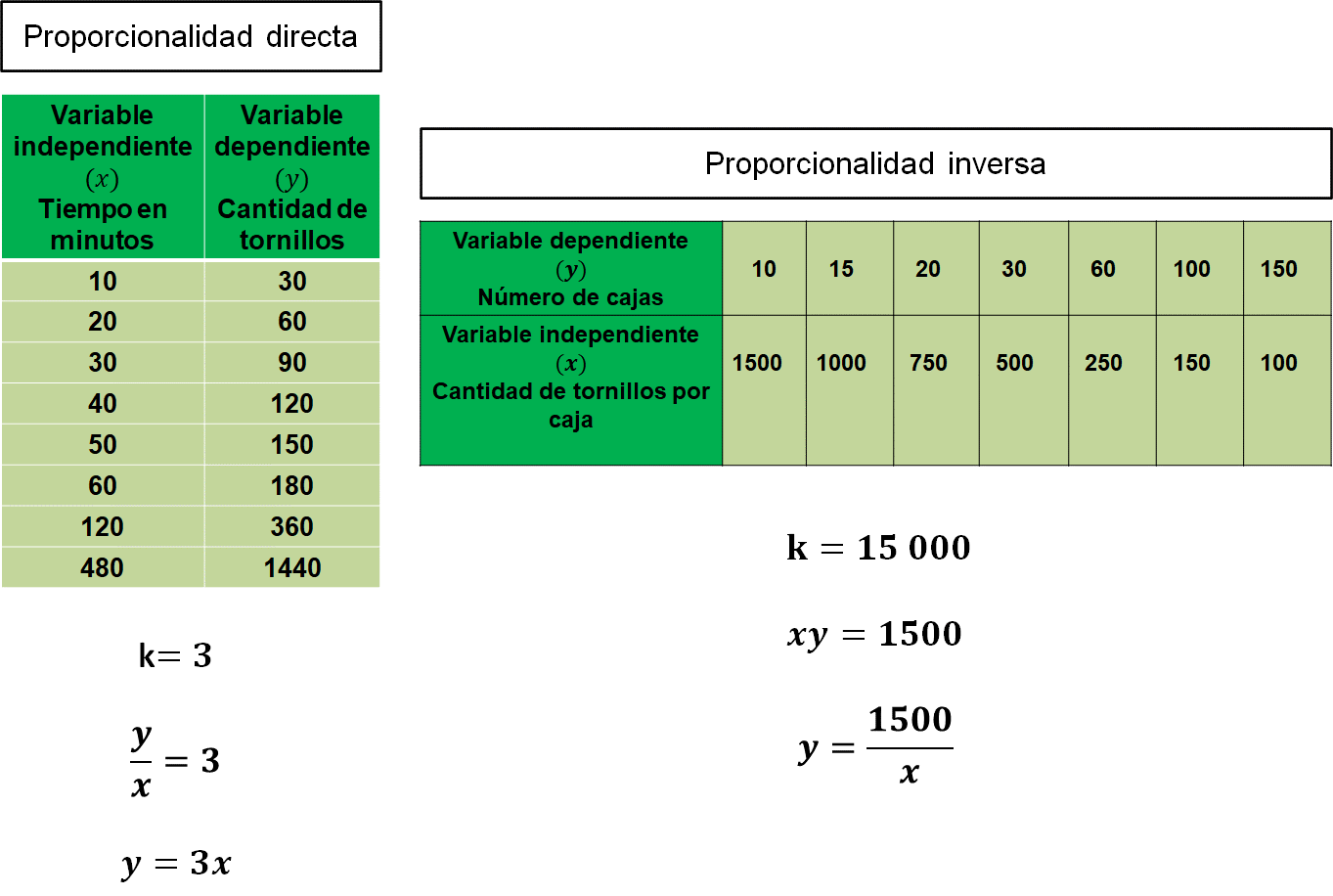
Observa que aquí se presentan las tablas y las expresiones algebraicas obtenidas para la situación de la producción de tornillos que corresponde a una relación de proporcionalidad directa; y a la colocación de los tornillos en cajas con diferente cantidad de ellos, donde se obtuvo una relación de proporcionalidad inversa.
Presta atención a las tablas y las expresiones algebraicas; reflexiona:
¿Qué semejanzas tienen?
¿Qué diferencias tienen?
Una semejanza es que ambas relaciones tienen una constante. Una diferencia es que, en la relación de proporcionalidad directa, la constante es el cociente de dos valores correspondientes en la tabla, “y” entre “x”; y en la relación de proporcionalidad inversa, la constante es el producto de dos valores correspondientes en la tabla, “x” por “y”
¿Qué otras afirmaciones puedes hacer con respecto a estas relaciones?
Regístralas y continúa.
Ahora, traza las gráficas de estas situaciones. Para ello, elabora un par de sistemas coordenados, como los que se muestran a continuación.

En uno traza la situación de proporcionalidad directa, es decir, sobre la producción de tornillos; en el otro sistema traza la situación de proporcionalidad inversa, es decir, la de empaquetar 15000 tornillos en cajas, cada una con la misma cantidad de tornillos.
Considera que debes ubicar en el eje “x” los valores de la variable independiente, el tiempo en minutos en el caso de la producción de tornillos; y la cantidad de tornillos por caja en el caso del empacado de los tornillos. En el eje “y” se deben ubicar la cantidad de tornillos producidos en la primera situación; y en el segundo caso, el número de cajas.
¿Ya tienes tus gráficas? Ahora, analiza esas gráficas. Seguramente obtuviste gráficas como las que se muestran.
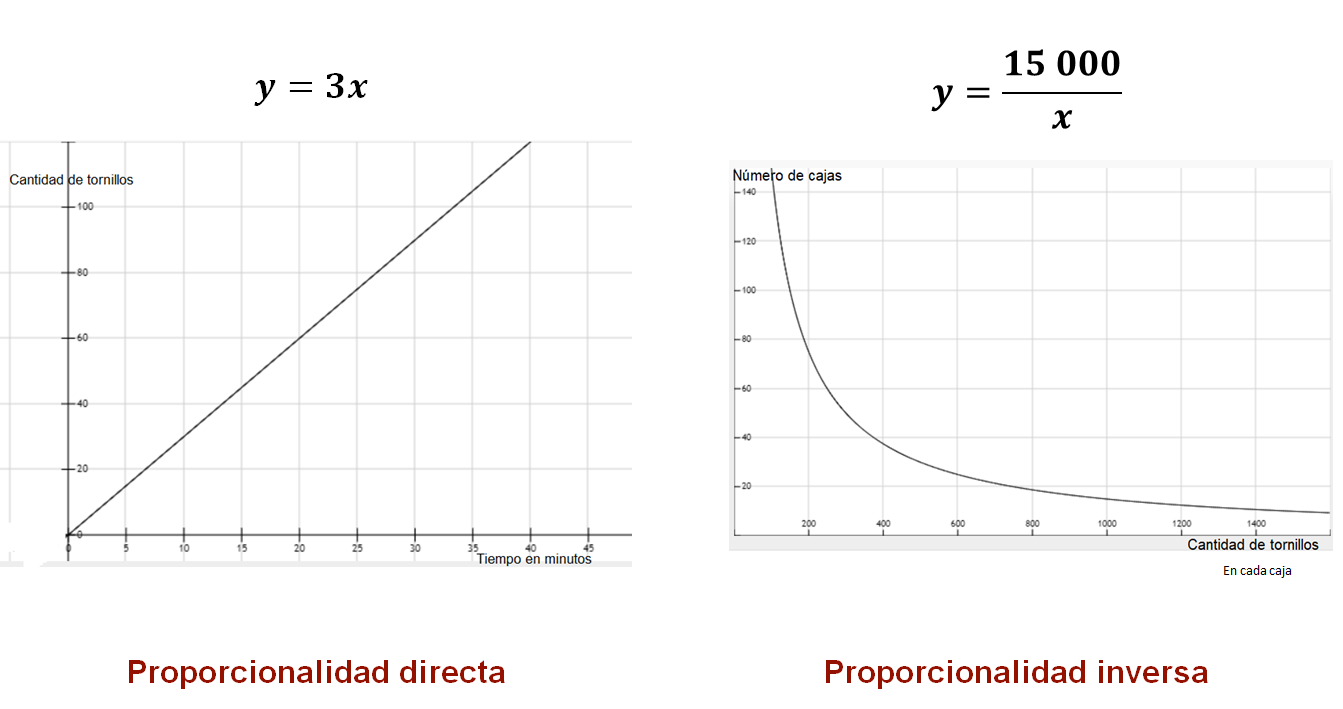
¿Qué diferencias notas entre ellas?
Algo que distingue a las gráficas de relaciones de proporcionalidad directa es que son líneas rectas que pasan por el origen del sistema coordenado. Por otro lado, la gráfica de una relación de proporcionalidad inversa es una línea curva llamada hipérbola.
A continuación, analiza la siguiente situación y determina el tipo de relación proporcional.
Situación-problema: remodelación para pintar una casa
Una empresa de remodelación requiere hacer el presupuesto para pintar una casa. Saben que 3 pintores tardan 12 días en hacer el trabajo, todos trabajando a ritmo constante.
El dueño de la empresa debe entregar la mejor oferta de acuerdo con los intereses del cliente. Por lo tanto, decide hacer el presupuesto para conocer cuánto tiempo se tardarán 2, 6 y 9 pintores en hacer el mismo trabajo, esto a ritmo constante.
¿Cuánto tiempo tardan 2, 6 y 9 pintores en hacer el mismo trabajo?
Contesta la siguiente pregunta: ¿se trata de una situación que representa una relación proporcional directa o inversa? Justifica tu respuesta.
Para contestar la pregunta anterior es posible realizar una tabla de valores para organizar la información y determinar los datos faltantes.
De acuerdo con la información que proporciona el problema, se sabe que existe una relación del número de pintores y el tiempo que tardan en realizar el trabajo.
En la relación que se acaba de mencionar, la variable dependiente son los días, porque estos valores están en función del número de pintores que realicen el trabajo si todos trabajan al mismo ritmo y su trabajo es constante cada día. De esta manera, la variable independiente son los pintores.

¿Ya lo resolviste? Considera que es necesario anotar y justificar los procedimientos.
Ahora, verifica tus resultados, ¿qué hiciste para completar la tabla? Si aumenta el número de trabajadores al doble, ¿el tiempo empleado se reduce a la mitad?
En este caso, si trabajan más pintores al mismo ritmo, los días que tardarán en realizar el trabajo serán menos y de manera proporcional, por lo tanto, se trata de una variación de proporcionalidad inversa.
La constante de proporcionalidad en este caso es “k”, que es igual a “x” por “y”

Con los datos que se mencionaron en el problema se tiene que la constante de proporcionalidad es el producto de 3 por 12, así, la constante de proporcionalidad es 36

Para determinar el número de días que tardarán los pintores en realizar el trabajo, se puede utilizar la expresión algebraica que ya se había mencionado:
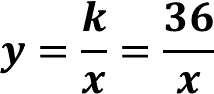
Realizando las operaciones, se obtiene que 2 pintores tardarán 18 días; si el trabajo lo realizan 6 pintores, tardarán 6 días, y finalmente, si trabajan 9 pintores, el trabajo se realizará en 4 días.
Con esto se puede dar solución al problema. Esta situación se trata de una relación de proporcionalidad inversa. Observa cómo quedo la tabla:
A continuación, analiza otra situación
Situación-problema: rectángulo
El área de un rectángulo es de doscientos cuarenta centímetros cuadrados; determina la medida del largo y ancho de este rectángulo.
¿Cuántos rectángulos diferentes cumplen con tener doscientos cuarenta centímetros cuadrados de área?
Contesta en tu cuaderno: ¿esta situación presenta una relación de proporción directa o inversa? Justifica tu respuesta.
Con base en la fórmula para calcular el área del rectángulo, piensa en dos números que al multiplicarse den como resultado doscientos cuarenta. De esta manera se tiene que los valores de “x” y de “y” que se corresponden, se deben multiplicar para obtener 240.
Esto hace que se tenga la igualdad:

Por lo tanto, es una relación de proporcionalidad inversa. Observa qué valores se tendrían en la tabla.

Si se utiliza la expresión algebraica obtenida para esta situación, se divide la constante “k” entre cada uno de los valores que se tienen para “x” y se determina el valor correspondiente de “y”
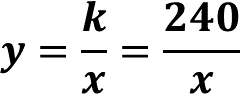
Por ejemplo, cuando la base “x” mide 2 centímetros, la altura “y” es igual a 240 entre 2 que es igual a 120. De la misma manera se puede calcular cada valor de “y” que le corresponde a cada valor de “x”
Por lo tanto, se obtiene que al rectángulo de 4 centímetros de base le corresponden 60 centímetros de altura; al de 6 centímetros de base le corresponden 40 centímetros de altura; para el rectángulo de 10 centímetros de base son 24 centímetros de altura; a 16 centímetros de base le corresponden 15 centímetros de altura; para el rectángulo de 24 centímetros de base se obtienen 10 centímetros de altura, y para el de 40 centímetros de base se tienen 6 centímetros de altura.
La tabla queda de la siguiente manera:
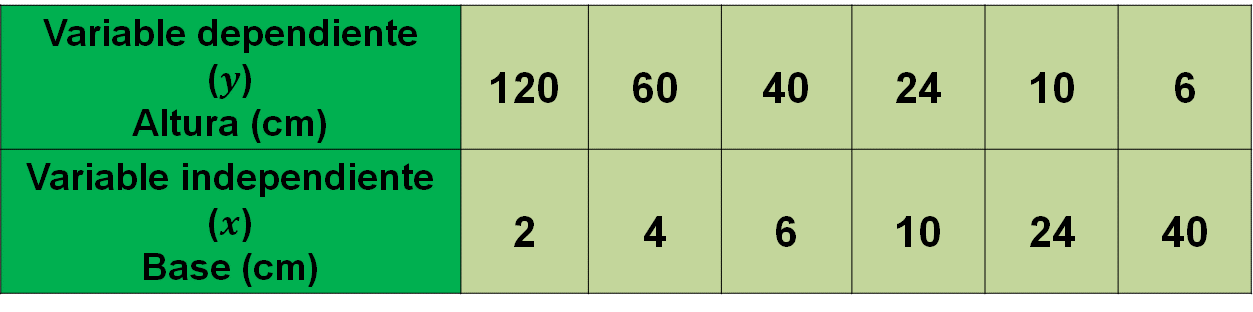
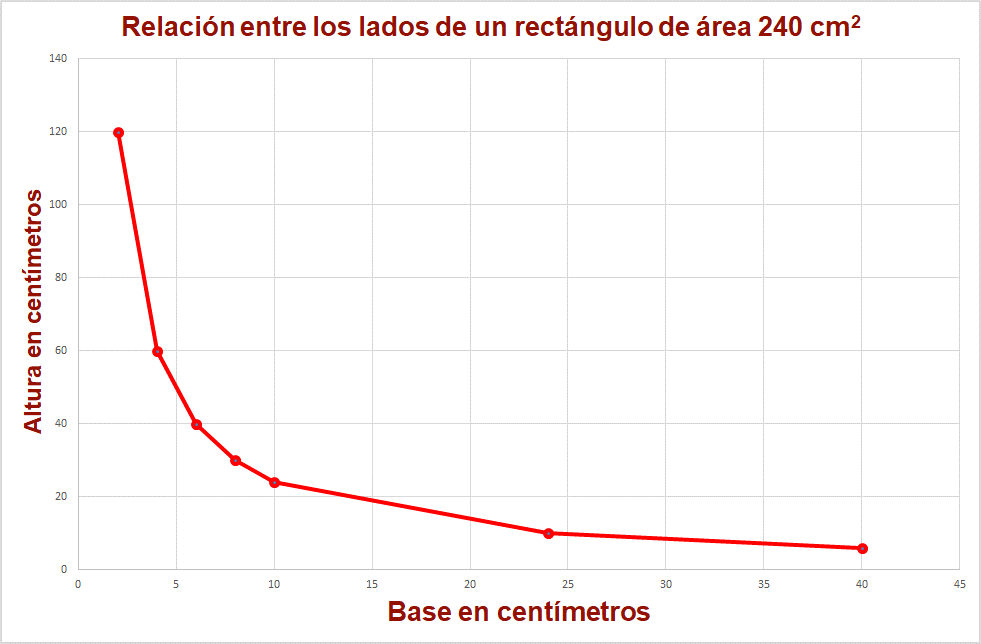
Analiza los valores obtenidos en la tabla: cuando la medida de la base aumenta, la medida de la altura disminuye.
Si la medida de la base aumenta al triple, por ejemplo, de 2 a 6 centímetros, la medida de la altura disminuye a la tercera parte, de 120 a 40 centímetros.
Entonces, por la forma de la gráfica, que es una hipérbola, y la manera como cambian los valores en la tabla, se puede afirmar que esta situación presenta una relación de proporción inversa.
Con esto has finalizado la sesión que se refiere al tema de variación proporcional directa y variación proporcional inversa.
Recuerda que este es un material de apoyo, y para complementar lo estudiado, puedes consultar otras fuentes, como tu libro de texto de Matemáticas de segundo grado.
El Reto de Hoy:
Resuelve algunos de los problemas o ejercicios sobre proporcionalidad directa e inversa de tu libro de texto de Matemáticas.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Los acrósticos y sus características
Aprendizaje esperado: Crea textos poéticos con formas gráficas.
Énfasis: Identificar características de acrósticos.
¿Qué vamos a aprender?
Continuarás con el estudio de los textos poéticos con distintas formas graficas. En esta sesión, te enfocarás en las características de los acrósticos e identificarás los mensajes ocultos dentro de estas manifestaciones poéticas.
¿Qué hacemos?
Para iniciar, lee el siguiente texto.
Aurora
"Alondras cantan, y ya
Un ansia de amanecer
Remece la noche ida
Oro y plata y rosicler
Respóndeme, ¿quién será?
Aurora, quién ha de ser".
Alfonso Reyes.
¿Qué es lo primero que identificas en este poema?
Observa nuevamente el texto, pero esta vez no lo leas como si fuera cualquier otro poema, presta atención a la primera letra de cada verso.
El inicio de cada verso forma la palabra Aurora, como el título del poema, pero no es ninguna casualidad, así son los acrósticos. La palabra acróstico proviene de dos raíces griegas, “ákros” que significa extremo, y “stíkhos” que significa surco, línea o verso.
Para comprender mejor esta palabra, analiza su significado:
Acróstico:
Composición poética constituida por versos, cuyas letras iniciales, medias o finales forman un vocablo o una frase.
Entonces los acrósticos son poemas que forman frases o palabras con las letras iniciales de sus versos, como en el ejemplo de “Aurora”, pero también puede ser en las letras medias o finales.
Existen varios tipos de acrósticos, como los dobles, en los que el efecto se repite en las letras iniciales y en las medias. Observa el siguiente ejemplo:

Las flechas rojas en esta ilustración indican dónde se encuentran los acrósticos dobles, es decir, al inicio y en medio de los versos. También existen acrósticos en los finales de los versos. Observa:

O bien, los acrósticos cruzados, en los que se puede leer una expresión al sesgo, desde el ángulo superior izquierdo al inferior derecho y a la inversa.
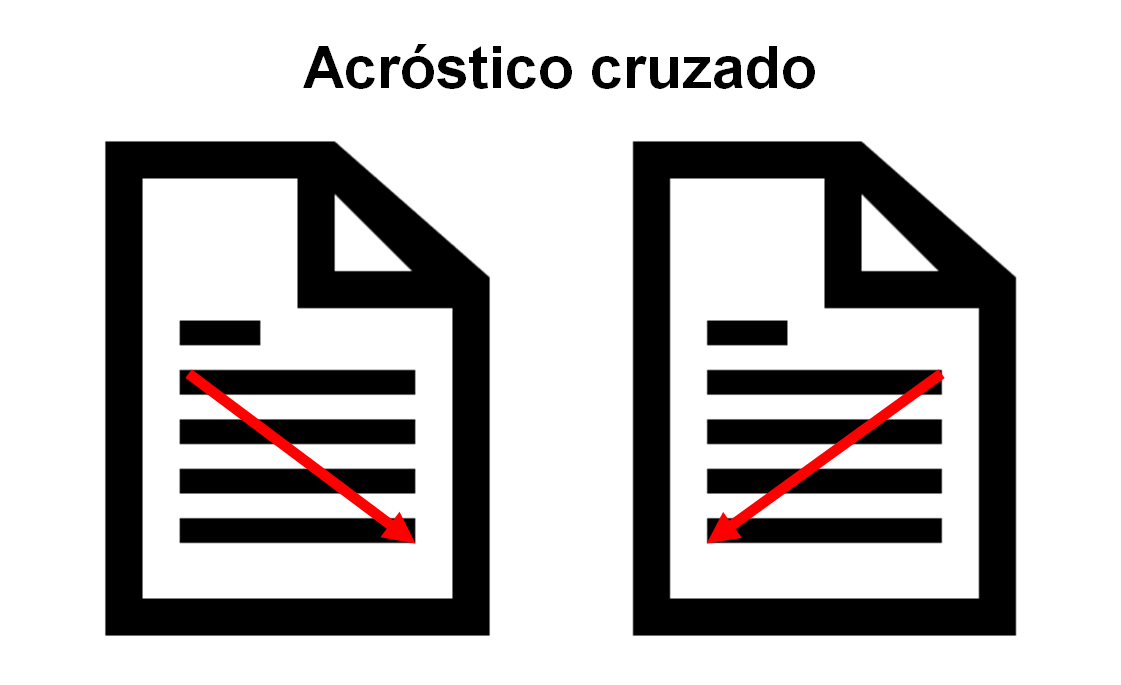
Al existir varios tipos de acrósticos, se sabe que, la palabra “escondida”, la que se genera con las letras de otras palabras, puede ir al inicio, en medio, al final o en diagonal del texto.
Los acrósticos son formas poéticas muy antiguas en el español. Por ejemplo, estas composiciones poéticas estuvieron en boga en la Europa de la Edad Media y en la España del Siglo de Oro, como un juego de ingenio.
Inclusive se han encontrado acrósticos más antiguos, un ejemplo es “El acróstico o laberinto del rey Silo”, de la iglesia de Santianes de Pravia en España; se encontró en una lápida fundacional de la misma época del rey Silo. La lápida original fue destruida en 1662 por un tal Fernando de Salas, y sólo se conserva un fragmento, pero gracias a éste se pudo reconstruir. Dicha reconstrucción se puede ver hoy en día en la iglesia.
La losa original era una piedra caliza con unas dimensiones de 53 cm de largo por 42 cm de ancho, y un espesor de 12 cm, formada por 19 columnas y 15 filas, con 285 letras grabadas con la frase «SILO PRINCEPS FECIT», que significa “Lo hizo el príncipe Silo”, partiendo de la “S” central, la combinación de las letras de columnas y filas. Este ejemplo data de los años 774-783
Desde entonces, el uso de los acrósticos está vigente, ya sea como parte de un diálogo de una obra teatral, dentro de un cuento, una novela, una carta de amor o un poema solitario.
Existieron muchos usos del acróstico y seguirán, pues es una manifestación que comúnmente se emplea para halagar o expresar imágenes literarias a partir de una palabra, por ejemplo, amor, paz, el nombre de un país, el de una persona amada y varios ejemplos más.
Las y los autores de los acrósticos en ocasiones generan estos mensajes escondidos sólo para quienes leen con más cuidado. Es decir, a pesar de conocer muy bien a un autor, se pueden encontrar sorpresas; tal vez descubras en un futuro algunos acrósticos si eres observadora u observador. Por ejemplo, en la obra de teatro “La Celestina”, de Fernando de Rojas, el autor escribió un acróstico que al leer las letras iniciales de cada verso dicen:
“El bachiller Fernando de Rojas acabó la Comedia de Calisto y Melibea y fue nascido en la Puebla de Montalbán.”
Una especie de mensaje secreto para quien se tome el trabajo de leer con cuidado. Recuerda que los acrósticos son manifestaciones poéticas y que un poema está conformado por versos. Ahora, analiza algunos otros aspectos.

El verso es cada línea de un poema y puede tener rima y métrica, que es la cierta cantidad de sílabas en cada línea que conforman un patrón.
Se les llama versos regulares cuando tienen rima y métrica; si no la tienen, se les denomina versos libres.
Lo más común es encontrar acrósticos conformados a partir de nombres propios y cuyos versos describen los atributos o las características de una persona o lugar, o expresan los sentimientos o aspectos que evoca el lugar o la persona.
Para profundizar en lo anterior, analiza algunos acrósticos que te ayudarán a comprender las características de estos singulares textos. El primer ejemplo es un acróstico de sor Juana Inés de la Cruz, que lo escribió para su maestro Martín de Olivas.
Soneto a Martín de Olivas
“Máquinas primas de su ingenio agudo
A Arquímedes, artífice famoso,
Raro renombre dieron de ingenioso:
¡Tanto en la fan y tanto el arte pudo!
Invención rara, que en el mármol rudo
No sin arte grabó, maravilloso,
De su mano, su nombre prodigioso,
Entretejido en flores el escudo.
¡Oh! Así permita el Cielo que se entregue
Lince tal mi atención en invitarte,
I en el mar de la ciencia así se anegue
Vajel, que ―al discurrir por alcanzarte―
Alcance que el que a ver la hechura llegue,
Sepa tu nombre del primor del arte".
Sor Juana Inés de la Cruz,
Soneto Martín de Olivas,
¿Qué te pareció?, ¿encontraste el mensaje escondido?
Vajel, es un término que significa embarcación y se escribe con b. Pero no es un error en este caso, “bajel” está escrito con “v” por una licencia poética para formar el acróstico.
Las licencias poéticas, son permisos que se toman los autores para hacer un uso distinto de las palabras y normas de la lengua dentro de sus poemas. Son recursos que se usan, por ejemplo, para ajustar la rima y métrica de los versos; también permiten usar las diferentes grafías que corresponden a un mismo sonido distintivo, como cuando escribe bajel con "v", cambiando su escritura convencional. Y hay otras que autorizan, incluso, a crear términos o palabras nuevas.
El mensaje oculto es el nombre del maestro de sor Juan Inés de la Cruz, Martín de Olivas; ahora puedes entender por qué sor Juana cambió la escritura de la letra "i" por la "y", así como la "v" por la "b" de bajel, para que coincidiera al leerse el apellido de la persona a quien fue dedicado este poema.
En el mundo de la poesía es muy común observar estas situaciones, sólo debes recordar que son licencias poéticas para que los autores puedan ajustar sus versos.
Continúa con el siguiente acróstico. Con este ejemplo, analizarás cómo se interpretan los acrósticos para las descripciones de atributos; recuerda que en muchos poemas se describe un objeto o se desarrolla un concepto, y todos los versos y las ideas que se exponen, giran en torno de este objeto o concepto.
Una característica de la mayoría de los acrósticos, como habrás visto con el ejemplo de sor Juana, es que se hace una descripción o se halaga a la persona que va dirigido; no sólo se forma su nombre, sino que se mencionan los atributos o características de la persona en cuestión.
El siguiente acróstico es “Aurora”, de Alfonso Reyes. Este ejemplo ya lo conoces. Léelo nuevamente y busca qué características de las que se han mencionado están presentes en el poema.
Aurora
"Alondras cantan, y ya
Un ansia de amanecer
Remece la noche ida
Oro y plata y rosicler
Respóndeme, ¿quién será?
Aurora, quién ha de ser".
Alfonso Reyes.
Aurora, en Guadalupe, Ricardo.
La primera característica es la que ya se había mencionado: que se forma una palabra con las letras iniciales de los primeros versos y se puede leer de forma vertical.
Ahora, ¿qué crees que busca comunicar Alfonso Reyes en estos versos?
Relaciona el nombre de Aurora con amanecer, remece y rosicler. Analiza el significado de las palabras para establecer el sentido del poema.
Remecer: Mover reiteradamente de un lado a otro.
Rosicler: El rosa claro de la aurora.
Por lo tanto, está describiendo ese momento en que la noche ya se va y se empieza a anunciar el amanecer, o sea la aurora.
Analiza el siguiente ejemplo con la misma consigna, ¿cuál es la palabra escondida y qué quiere comunicar el autor? Lee con atención “Acróstico”, de Francisco J. Briz Hidalgo.
Acróstico
“Aplícase a las
Composiciones poéticas,
Rimadas,
O de versos
Sueltos y de cualquier
Tamaño, en las que las letras
Iniciales, medianas o finales de los versos
Componen una palabra
una frase”.
Briz Hidalgo, Francisco J.
“Acróstico”
La palabra escondida es “acróstico”, y justamente usa el poema para explicar qué es un acróstico. El autor generó la exploración del acróstico utilizando la explicación de lo que es.
Por lo general, los acrósticos son composiciones que definen los atributos o las cualidades del concepto del que hablan. No obstante, lo que los hace poemas y no simples descripciones es la posibilidad de emplear recursos poéticos para evocar el objeto. Por ejemplo, en Aurora, en su segundo verso dice: “un ansia de amanecer”
Se refiere a la aurora, pero no usa lenguaje literal para describirla. En este caso, emplea una metáfora, pues la aurora es ese momento justo antes de amanecer; el autor interpreta esto como una ansiedad porque amanezca.
Antes de finalizar, recapitula sobre las características de los acrósticos:
- Las letras iniciales, medias o finales de cada verso forman una palabra que se lee de forma vertical.
- Pueden tener métrica regular o ser de versos libres.
- La palabra formada con las letras iniciales de los versos corresponde al tema del poema.
- Se forman nombres de personas, cosas o situaciones con letras intermedias de cada verso.
- Describe atributos del objeto o la persona nombrada.
Ahora, cada que leas, presta mucha atención porque tal vez haya un acróstico por ahí, esperando a ser descubierto por unos ojos hábiles, dispuestos a revelar los mensajes secretos del autor en cuestión.
El Reto de Hoy:
Lee el siguiente acróstico y busca los cuatro nombres que se encuentran en él. Recuerda que los acrósticos no sólo se forman con las iniciales del verso, pueden estar escondidas en cualquier sitio, a veces los poetas acomodan a su gusto las reglas ortográficas y la gramática para que queden bien sus versos.
“Feroz sin consuelo y sañuda dama
Remedia el trabajo a nadie creedero
A quien le siguió martirio tan fiero
No seas león o reyna pues t´ama […]”
Castillo, Hernando,
del “Cancionero general”, 1511.
Después, escribe tu propio acróstico con los nombres de tus amigos o de tu familia. Verás que te resultará muy interesante.
Y no olvides escribir en tu cuaderno las cinco características de los acrósticos.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
El universo en expansión
Aprendizaje esperado: Identifica algunos aspectos sobre la evolución del universo.
Énfasis: Reflexionar sobre la teoría del big bang y el universo en expansión.
¿Qué vamos a aprender?
En esta sesión, conocerás diversas investigaciones sobre cómo se originó el universo. Analizarás la teoría del big bang, la expansión del universo y qué sucedió con la radiación cósmica de fondo.
¿Qué hacemos?
Escribe en tu cuaderno las siguientes preguntas, y trata de dar una respuesta breve. De ser necesario compleméntalas con la información que conocerás a lo largo de esta sesión.
- ¿Sabes de qué manera se originó el universo?
- ¿Cuáles son las dos ideas que sostienen la teoría del big bang?
- ¿A qué se refiere la expansión del universo?
- ¿Qué sucedió con la radiación cósmica de fondo?
Antes de empezar con el tema, observa el siguiente video del minuto 6:31 al 8:04, que te dará un panorama general sobre la teoría del big bang.
- El Universo: origen, evolución y estructura. Segunda parte.
https://www.youtube.com/watch?v=cC-7u8CjWpg&feature=emb_logo
En el video se menciona que la edad del universo es de 13,700 millones de años, sin embargo, la teoría del big bang fue propuesta en 1927, es decir, hace poco menos de 100 años. ¿Cómo fue que los científicos llegaron a esa conclusión si el universo se creó hace muchísimo tiempo atrás?
Para dar respuesta a la pregunta anterior, primero debes conocer sobre George Lemaitre, un astrónomo y sacerdote originario de Bélgica quien propuso la teoría del big bang, se basó en dos ideas que dan soporte a dicha teoría: la expansión del universo y la radiación cósmica de fondo.
Para el sacerdote belga Georges Lemaitre, la historia del universo se divide en tres periodos: el primero es llamado la explosión del átomo primitivo, la cual dice que, hace 5,000 millones de años existía un núcleo de materia hiperdensa e inestable que explotó bajo la forma de una super radiactividad. Esta explosión se propagó durante mil millones de años y los astrónomos perciben sus efectos en los rayos cósmicos y las emisiones X.
Después viene el periodo de equilibrio o el universo estático de Einstein. Éste afirma que, finalizada la explosión, se establece un equilibrio entre las fuerzas de repulsión cósmicas en el origen del acontecimiento y las fuerzas de gravitación. Es durante esta fase de equilibrio que dura 2 mil millones de años, cuando se forman los nudos y dan nacimiento a las estrellas y galaxias.
Finalmente, siguen los periodos de expansión, iniciados hace 2 mil millones de años, que demostrarían que el universo se encuentra en expansión a una velocidad de 170 kilómetros por segundo de manera indefinida.
Sobre la expansión del universo, según la teoría del big bang, éste tiene unos 13,800 millones de años. Lo que se sabe, es que tuvo un pasado muy caliente y denso, y ahora se está expandiendo.
Gracias a todas las evidencias observacionales que apoyan la existencia del big bang. A finales de los años 20 del siglo pasado, el astrónomo Edwin Hubble se dio cuenta de que todas las galaxias se están alejando de nosotros y que, no solo se alejaban, sino que cuanto más lejos estaban, más rápido era ese alejamiento. Hubble se apoyó de sus observaciones de los espectros luminosos de las galaxias, sugiriendo que éstas se alejan entre sí, ya que el cambio en la longitud de la onda de luz se desplazaba hacia la parte del espectro con longitudes de onda más largas, a este fenómeno se le conoce también como corrimiento al rojo. Llegando así a la conclusión de que el Universo estaba en expansión.
Para ejemplificar el fenómeno de la expansión del universo, si está en tus posibilidades, realiza el siguiente experimento.
Experimento: expansión del universo
Los materiales que necesitarás son:
- 1 globo de color claro.
- 1 regla.
- Tijeras.
- 20 cm de hilo o estambre.
- Papel.
- Lápiz.
- Plumón.
Procedimiento:
- Lo primero que tienes que hacer es dibujar puntitos a lo largo de todo el globo. De esta manera simularás las galaxias.
- Después, elije dos puntos, los que quieras, y márcalos encerrándolos en un círculo. Una vez identificados, mide la distancia entre ellos y anótala en tu cuaderno.
- Ahora es momento de utilizar tus pulmones para inflar el globo, tendrás 10 segundos para ello y al finalizar lo amarras.
- Con ayuda del hilo ubica la distancia entre los dos puntos que elegiste al principio y corta el hilo.
- Finalmente, mide el tramo del hilo que cortaste y compara tu resultado con la medida inicial.
Como podrás darte cuenta, la distancia entre los puntos aumentó después de que inflaste el globo. Los puntos dibujados en el globo representan las galaxias y el globo representa el espacio conformado por el universo. Las mediciones de la distancia representan las observaciones de expansión a través del corrimiento en rojo de las ondas de luz.
Después de este análisis, continúa con el tema.
Otro de los pilares clásicos para aceptar el big bang es la radiación de fondo cósmico de microondas, que es una radiación que se produjo cuando el universo tenía unos 380,000 años (equivalente a un bebé de un día, en la escala temporal humana). Hubo un momento en el que la temperatura descendió lo suficiente como para que se formaran átomos neutros y los fotones pudieran propagarse libremente. La radiación cósmica de fondo es un tipo de radiación electromagnética que llenó todo el universo.
La radiación de fondo de microondas se detectó en 1964 por los radioastrónomos estadounidenses Arno Penzias y Robert Wilson; este gran descubrimiento se dio por mera casualidad.
Arno Penzias y Robert Wilson eran los encargados de calibrar la gran antena de Holmdel, que era usada para comunicación vía satélite, llevaban semanas intentando ponerla en funcionamiento, pero había un ruido de fondo que hacía imposible el trabajo. Probaron todo tipo de medidas para tratar de eliminar aquellas interferencias, orientaron la antena en todas direcciones, probaron de día y de noche, revisaron el sistema eléctrico, forraron con cinta aislante las juntas y remaches de la antena, limpiaron enchufes, hasta pensaron que todo era culpa de los nidos de las palomas que había. Y cuando ya no se les ocurría qué más hacer, desmontaron todos los instrumentos de la antena y los volvieron a montar desde cero. El ruido no desaparecía.
Después de reconstruir la antena en varias ocasiones, el origen cósmico era ya la última esperanza de Penzias y Wilson, aunque de eso no tenían ni idea. Se comunicaron con un equipo científico de la Universidad de Princeton dirigido por Robert Dicke para explicarle el problema con la antena por si él les podía ayudar a eliminar aquel incesante ruido. El físico de Princeton se dio cuenta inmediatamente de lo que habían encontrado los jóvenes Penzias y Wilson. Dicke colgó el teléfono y les dijo a sus colegas de laboratorio: “Bueno, muchachos, se nos acaban de adelantar”, según cuenta Bill Bryson en su obra, Una breve historia de casi todo.
En ese entonces, había dos teorías competidoras, por un lado, estaba el big bang y por otro lado estaba la teoría del estado estacionario que decía que el universo era básicamente el mismo en cualquier momento y lugar. La detección del fondo de microondas fue la confirmación del big bang. De hecho, el nombre lo acuñó el astrónomo inglés Fred Hoyle, defensor de la teoría del estado estacionario, en una entrevista en la BBC, posiblemente de forma despectiva pero el nombre cuajó.
El fondo de microondas es una radiación homogénea sobre todo en el cielo, pero con pequeñas diferencias de temperatura de aproximadamente una parte en cien mil. Estas pequeñas diferencias son muy importantes. Ahora se observa que el universo no es homogéneo porque hay galaxias y cúmulos de galaxias. Para que todo eso se haya formado por inestabilidad gravitatoria, tuvieron que existir semillas para su origen y pequeñas diferencias en la densidad de materia. Si esas pequeñas semillas existían en el universo temprano, eso debía reflejarse en el fondo de microondas. Y eso se vio con el satélite Cobe por primera vez en los años noventa del siglo pasado.
En la ciudad de Ginebra Suiza, la Organización Europea para la Investigación Nuclear desarrolló un acelerador de partículas, llamado Colisionador de Hadrones, que permite a los investigadores recrear las condiciones extremas de temperatura y densidad que había cuando ocurrió la Gran Explosión.
Esto quiere decir que, con el Gran Colisionador de Hadrones se puede explicar todo lo referente al origen del universo a partir del big bang.
Como puedes darte cuenta, para estudiar el origen del universo, existen diferentes estrategias que los científicos implementan para comprender lo que se observa hoy en día
Por lo tanto, se podría decir que, gracias a todas estas investigaciones, se puede conocer la historia del Universo, desde el big bang, hasta lo que se conoce actualmente. Al respecto se pueden identificar dos eras, la era de la radiación y la era de la materia.
La era de la radiación comprende desde la gran explosión hasta la de fondo. Y la era de la materia desde la radiación cósmica de fondo, hasta el presente.
En la era de la radiación se pueden identificar las siguientes fases:
Inflación: con la que da inicio la expansión del universo.
La formación de protones: en la que el espacio está ocupado principalmente por radiación electromagnética, protones y neutrones.
La formación de núcleos: en la que los neutrones y los protones empiezan a formar núcleos atómicos, pero debido a la alta temperatura, esta unión era tan débil que se rompía.
Radiación cósmica de fondo: donde los núcleos empiezan a captar electrones, formando los primeros átomos de hidrogeno y helio, pues la temperatura ya había disminuido lo suficiente para permitir que los enlaces de neutrones y protones ya no se rompieran. Lo cual permitió el paso libre de luz.
Por ello, antes de la formación de los átomos todo era obscuro. Esto era porque los electrones no podían unirse a los núcleos de protones y neutrones, y al estar libres en el espacio dispersaban la luz. Entonces, es a partir de este momento que se empieza a formar la materia. Y para que esto sucediera, tuvieron que pasar 380,000 millones de años. A partir de ahí, inicia la era de la materia, en la que se empiezan a formar las primeras estrellas, debido a que los átomos se aglutinan por acción de la gravedad. Y el universo comienza a tener luz.
Las investigaciones sobre el universo no se detienen y en 1998 los científicos Saul Perlmutter, Brian Schmidt y Adam Ries, descubrieron que el universo seguía creciendo cada vez a mayor velocidad, para ellos ese descubrimiento fue una gran sorpresa, pues estudios anteriores apuntaban a que la gravedad iba a detener la expansión. Para explicar esta aceleración, se maneja el concepto de energía oscura.
Existen diversos proyectos que han permitido a los científicos establecer o comprobar las bases para el planteamiento de las teorías acerca del big bang.
El primero de ellos es el Observatorio Espacial Planck, de la Agencia Espacial Europea, lanzado en mayo del 2009. Este observatorio es una máquina del tiempo, pues mira al pasado, al principio de los tiempos, cerca del big bang, a lo que ocurrió hace unos 13,700 millones de años. Planck analiza con una precisión no lograda hasta el momento, los remanentes de la radiación que llenó el universo inmediatamente tras el big bang, una radiación observada hoy en día como el fondo cósmico de microondas.
Estos resultados ayudarán a los astrónomos a decidir qué teorías del nacimiento y evolución del universo son correctas. Pero primero, Planck debe detectar y comprender la emisión del fondo cósmico que se encuentra entre nosotros y la primera luz del universo.
Planck observa en nueve bandas del espectro electromagnético, desde un centímetro a un tercio de milímetro, lo que corresponde al rango de la longitud de onda que va de las microondas al infrarrojo muy lejano. Los detectores de Planck se enfrían a temperaturas cercanas al cero absoluto ya que, de otro modo, su propia emisión de calor alteraría las medidas.
Con ello se complementó la información que obtuvo la Sonda de Anisotropía de Microondas de Willkinson (WMAP, por sus siglas en inglés) diseñado por la NASA.
La WMAP es una sonda de la NASA cuya misión es estudiar el cielo y medir las diferencias de temperatura que se observan en la radiación de fondo de microondas, un remanente del big bang. Fue lanzada en junio del 2001 y usa radiómetros diferenciales de microondas que miden las diferencias de temperatura entre dos puntos cualquiera del cielo
Otro proyecto es, el Gran Colisionador de Hadrones, que es un dispositivo acelerador de partículas con el cual se pueden recrear las condiciones extremas del universo temprano al hacer chocar iones pesados a muy altas energías acelerándolos a velocidades cercanas a la de la luz. A este proyecto se le conoce con el nombre de ALICE, por sus siglas en inglés.
Existen aún más proyectos, por ejemplo, el proyecto Big BOSS que tiene como finalidad encontrar la respuesta a algunas de las interrogantes acerca de la energía oscura y la expansión del universo. El instrumento principal de este experimento cuenta con cinco mil fibras ópticas conectadas a espectrógrafos de resoluciones de muy buena calidad sincronizados al telescopio Mayal.
Un dato relevante es que, tanto el proyecto ALICE como el Big BOSS tienen la participación de científicos mexicanos. Y algo más que debes recordar es que, las investigaciones sobre el universo se encuentran en constante actualización, por eso es importante mantenerte informada e informado a través de medios confiables.
Has finalizado esta sesión. Si deseas saber más del tema, puedes consultar tu libro de texto de Física.
El Reto de Hoy:
Reúnete con tu familia para reflexionar y dar respuesta a la siguiente pregunta: ¿cuál fue el origen de la gran explosión?
A partir de la información que aquí se presentó y con alguna otra que obtengas de fuentes de información confiable, amplía o corrige tus respuestas del inicio:
- ¿Sabes de qué manera se originó el universo?
- ¿Cuáles son las dos ideas que sostienen la teoría del big bang?
- ¿A qué se refiere la expansión del universo?
- ¿Qué sucedió con la radiación cósmica de fondo?
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Negociar para solucionar los conflictos
Aprendizaje esperado: Analiza el conflicto y opta por la forma más conveniente para lograr objetivos personales sin dañar al otro.
Énfasis: Reconocer en la negociación y la cooperación alternativas de solución pacífica de los conflictos.
¿Qué vamos a aprender?
En esta sesión, conocerás sobre la importancia de la negociación en los principales grupos sociales y cómo el diálogo debe estar presente para desarrollar estrategias asertivas en la resolución de conflictos.
¿Qué hacemos?
A lo largo de la sesión, anota por lo menos cinco ideas generales sobre este tema, así como todo lo que consideres relevante, ya que te servirá de insumo para la elaboración del reto de hoy.
De acuerdo con el Diccionario de la Lengua Española, el conflicto es, entre otras cosas, un combate, un problema o la materia de discusión. También puede significar: desavenencia, dificultad o rencilla. Algo muy importante es reconocer que la transformación del conflicto tiene como vías de negociación el diálogo y el debate inteligente.
Para iniciar, es necesario saber qué es la negociación en la solución de conflictos. Para ello, observa el siguiente esquema:

En la imagen anterior, aparecen algunos elementos para la transformación de los conflictos, esto te puede ayudar a profundizar en la definición. Se puede lograr dicha transformación mediante tres procesos en los cuales todas y todos los participantes colaboran y asimilan diversas experiencias que los enriquecen. Los tres procesos son: la prevención, la mediación y la negociación.
La prevención ocurre antes de que suceda el conflicto, tomando las medidas necesarias para que la situación no crezca. Se refiere a la actuación que se debe tener para evitar que una diferencia se convierta en conflicto. Es decir, se puede buscar una solución a las diferencias o problemas, lo cual estaría implicando asumir algunos cambios en nuestro actuar, para encontrar una solución.
Mientras que la negociación implica reconocer en el otro sus necesidades e intereses para llegar a un acuerdo, respetando la dignidad de ambas partes. Se tiene que identificar qué originó la diferencia o problema, poner las necesidades de los involucrados por encima de las opiniones propias para resolver el problema.
Finalmente, la mediación se presenta cuando las partes en conflicto no han podido negociar, se necesita de una tercera persona que favorezca el diálogo entre las partes involucradas y que ayude a atender la situación conflictiva para encontrar una solución que beneficie a ambas partes. La persona que actúe como mediador o mediadora debe buscar que la solución no afecte los intereses de las partes involucradas, aunque tendrá que convencerles de que, si fuera necesario, tendrán que ceder en algunos aspectos de sus intereses para encontrar una solución.
Es importante señalar que, quien ocupa el papel del mediador o mediadora debe revisar el proceso, observar cómo fue creciendo el conflicto y deteriorándose la relación entre las personas.
Las tres vías que pueden transformar el conflicto implican la aplicación de diferentes valores como el respeto, la empatía y la tolerancia.
A continuación, observa el siguiente video del minuto 1:06 al 2:44, para entender qué es un conflicto y cómo el diálogo puede ayudar a resolver las diferencias que se tienen con las personas que nos rodean.
- El diálogo y la solución de conflictos.
https://www.youtube.com/watch?v=fsdRq04hfvE.
El conflicto es inherente a la vida cotidiana, no se puede ver como algo ajeno y mucho menos sería sano evadirlo. Si bien habrá conflictos desagradables o inconvenientes, lo importante es aprovechar las situaciones conflictivas y transformarlas en oportunidades de aprendizaje y así, conocernos más a nosotras o nosotros mismos y a las demás personas.
Una de las habilidades importantes para hacer frente a los conflictos es el diálogo, el cual es una herramienta eficaz para resolver las diferencias que se presentan en la cotidianidad.
Pero ¿por qué el diálogo se convierte en una herramienta para solucionar los conflictos? Porque cuando se lleva a cabo un diálogo genuino, existirá siempre la apertura a las ideas de las y los demás, respetando a la otra parte, sus puntos de vista y argumentos, sin el objetivo de querer vencer o ganar.
El diálogo, como estrategia de negociación, buscará que ambas partes puedan ser escuchadas, atendiendo a sus necesidades. Esto quiere decir que, un requisito indispensable para dialogar es aprender a escuchar, sin tratar de imponer nuestra voluntad. Es decir, implica aceptar que las personas en conflicto puedan externar sus argumentos para identificar lo que originó el conflicto, ser receptivas a los argumentos que presentan las partes en conflicto y poder encontrar puntos de coincidencia que permitan llegar a acuerdos.
Ahora, observa el siguiente video del minuto 1:31 al 3:09, en el cual se explica la importancia del conflicto como medio de aprendizaje.
- La provención de los conflictos.
https://www.youtube.com/watch?v=mejtHUw_eo0
El conflicto puede aparecer en diferentes contextos, ya sea en la casa, la escuela, o en el vecindario. Cuando no se utilizan adecuadamente las habilidades para resolver conflictos de manera pacífica, se pueden desencadenar actos de violencia.
La provención, a diferencia de la prevención, permite reconocer en el conflicto una herramienta de crecimiento personal, para enfrentar los conflictos de manera no violenta.
Es evidente que la comunicación cobra especial importancia en todo proceso de regulación de conflictos. Por este motivo, es importante detenerse un instante en este punto, para conocer algunas de las técnicas comunicativas que ayudarán a desarrollar esta habilidad.
La escucha activa es una habilidad del ser humano en el proceso de la comunicación, que implica: comprender lo que la otra persona está diciendo y cómo se siente respecto a ello. Además de no interrumpir a la persona que habla, permanecer neutral y no adoptar posturas de uno u otro lado. Asimismo, mostrar comprensión y aceptación mediante comportamientos no verbales
En el proceso de escucha activa es importante cuidar el tono de voz al hablar, evitando en todo momento gritar o levantar la voz, mantener una postura de apertura. Para ello, se debe evitar utilizar las manos en forma de agresión, además de cuidar las expresiones faciales y gesticulares.
Mostrar interés por lo que dice la otra persona, no sólo evita situaciones de agresión, sino también contribuye a la solución, pues se muestra interés por encontrar alternativas para solucionar las diferencias. En el contexto escolar es muy común que ocurran diferentes tipos de conflictos. Por ejemplo, al organizarse en equipos para trabajar algún proyecto, los diferentes puntos de vista de cada una de las y los integrantes pueden generar enfrentamientos verbales.
Cuando no existe una adecuada práctica de los valores, como la tolerancia o la empatía, se pueden generar conflictos en los entornos escolares. Pero, no sólo en la escuela, también en la casa. Ahora que estás pasando más tiempo con tu familia, habrás notado que los conflictos pueden solucionarse de mejor manera cuando se dialoga entre todas y todos.
Para contar con más información al respecto, observa el siguiente vídeo del minuto 0:39 al 4:20, donde se presenta un ejemplo de la actuación de una mediadora ante un conflicto.
- El sentido de la mediación de los conflictos.
https://www.youtube.com/watch?v=nMimgPuUYD8
Del video anterior, seguramente encontraste similitud con los conflictos que has vivido en tu escuela, donde la intervención de un mediador o mediadora ha contribuido a encontrar una solución al conflicto.
Es importante mencionar que, un mediador o mediadora, puede ser una persona de la familia, quien establece solución a las diferencias, buscando que esa solución dé respuesta a las necesidades de las y los involucrados; en la escuela, puede ser una o un docente, directivo o un compañero o compañera que muestre habilidades para mediar entre las partes en conflicto; así como un amigo o amiga de la colonia o comunidad, quien favorece la búsqueda de acuerdos por consenso.
Después de haber analizado el video, se puede decir que la mediación es un punto de partida importante dentro de la negociación, ya que el mediador o la mediadora intervienen de manera neutral, sin favorecer a ninguna de las partes.
Ahora, analiza qué otros recursos se tienen para poder solucionar los conflictos a los que te enfrentas día a día.
Es necesario resaltar que, siempre, debes buscar que la solución de los conflictos sea pacífica, por lo cual, te centrarás en los recursos de negociación, colaboración/cooperación y mediación.
Como ya se mencionó, la negociación busca separar los elementos que conforman al conflicto: las personas, el proceso de disputa y el problema en sí, para ser tratado de manera efectiva y eficaz, involucrando el proceso de comunicación asertiva.
La colaboración/cooperación, tiene el objetivo de buscar soluciones que satisfagan a todas las partes involucradas.
Por último, la mediación, es utilizada como herramienta cuando se han agotado las posibilidades de resolver un conflicto entre los involucrados, es entonces cuando una tercera persona interfiere para su resolución.
Ahora, reflexiona en lo siguiente: ¿cuántos de estos recursos has utilizado?
Seguramente has recurrido a cada uno de ellos en diferentes contextos y situaciones, lo importante es que reconozcas los elementos de solución y puedas integrar nuevas herramientas para solucionar los conflictos.
En esta sesión, se explicó qué es un conflicto, destacando que es parte inherente a las relaciones humanas; que existen estrategias de negociación, para la resolución pacífica de las diferencias y que apoyan de manera fundamental la construcción de una nueva sociedad.
También estudiaste el tema de la escucha activa como elemento principal del uso correcto de los recursos para la resolución, como: la negociación, colaboración/cooperación y mediación.
Has concluido esta sesión. Consulta tu libro de texto para conocer más del tema y retomar los aprendizajes que favorezcan la construcción de una Cultura de Paz.
El Reto de Hoy:
Elabora un mapa mental con los conceptos principales de la sesión, no olvides utilizar las cinco ideas que anotaste.
Después, recuerda un conflicto que hayas tenido en la familia o la escuela y describe cómo te sentiste ante éste, cuáles fueron los recursos que se emplearon para buscar una solución y cuál fue la solución que se estableció. Pueden complementar la actividad agregando otras ideas y escribir las acciones que puedas hacer para solucionar conflictos de la mejor manera.
Finalmente, dialoga con tus familiares sobre la importancia de aprender a resolver los conflictos de manera pacífica, lo cual es necesario para dejar a un lado las actitudes y acciones violentas.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Importancia de la gestión técnica
Aprendizaje esperado: Planifica y organiza las acciones técnicas según las necesidades y oportunidades indicadas en el diagnóstico.
Énfasis: Reconocer el papel de la gestión técnica en la solución de problemas técnicos en procesos productivos.
¿Qué vamos a aprender?
En esta sesión, conocerás qué un proceso de producción, su clasificación y analizarás algunos ejemplos. Asimismo, profundizarás en la gestión técnica, su importancia e identificarás algunas técnicas para solucionar problemas que pueden surgir en el proceso productivo.
¿Qué hacemos?
Inicia con la siguiente pregunta:
¿Sabes qué son los procesos productivos?
Los procesos productivos son una serie de procedimientos que realizan las empresas, fábricas o personas para generar productos o servicios. Éstos se clasifican en:
Proyecto: es aquel producto específico y personalizado que se elabora para satisfacer las necesidades de un consumidor en particular, este proceso debe estar muy controlado. Pueden ser productos como una casa o edificio, un avión, un barco, una pintura, una escultura, una prótesis, productos médicos o también pueden ser servicios, como la organización de una boda.
Producción por lotes: es cuando se elaboran pequeñas cantidades de un producto con las mismas características; se usan plantillas y se adaptan máquinas para realizar el trabajo. Cuando se termina de producir el lote o número de piezas requeridas, se cambia a otro producto con rasgos diferentes. Este tipo de proceso es recurrente en la industria de alimentos y farmacéutica.
Producción en masa: este sistema se utiliza para producir grandes cantidades de un producto. Los procesos son continuos, tienen un orden y el trabajo humano que interviene es considerable. La maquinaria que se emplea para ese tipo de trabajo es particular, así como la capacitación de sus operadores. Un ejemplo donde se ocupa este modelo de producción es en la elaboración de bolígrafos, teléfonos inteligentes y automóviles.
Producción continua: es en la que el producto pasa por una serie de procesos constantes, requiere de una alta especialización en automatización y puede producir las 24 horas del día. Algunos ejemplos que se pueden mencionar son: textiles, papel y acero.
Para realizar estos procesos de producción se debe llevar a cabo una serie de pasos y acciones, en donde la administración juega un papel importante, pues es necesario seleccionar el tipo de acciones a desarrollar, los medios técnicos adecuados y los materiales y tipo de energía que se utilizará. Todos estos elementos están relacionados con la gestión técnica.
La gestión técnica tiene como propósito organizar todos los recursos disponibles, por ejemplo:
- Las personas: las cuales planifican, organizan y controlan los procesos técnicos; administran los recursos materiales y financieros y ejecutan órdenes. Entre ellas se encuentran los directivos, contadores, almacenistas, operadores, electricistas, analistas, ingenieros, choferes, vendedores, etcétera.
- Los recursos: diferentes clases de máquinas, herramientas, instrumentos, tipos de energía, insumos y costos.
- Los espacios de trabajo: localización de la empresa, distribución de las áreas de trabajo para los empleados y la maquinaria.
- Los tiempos de realización.
En pocas palabras, la gestión técnica es administrar todo lo que rodea la producción de un producto o servicio. Y las fases de la gestión técnica son:
- Planeación.
- Organización.
- Ejecución.
- Control.
- Evaluación.
Para ejemplificar lo anterior, toma como referencia una pirámide de 14 vasos. Puedes realizar una con algunos vasos que tengas en casa. El proceso es el siguiente:
- Producto: pirámide de vasos.
- Número de fases del proceso: seis.
- Material: vasos.
- Recurso humano: la persona que lo realiza.
- Proceso de producción: por proyecto, ya que es a petición de una persona y es una sola unidad, una pirámide.
- Ingeniería: otra persona encargada.
- Errores: falta un vaso para completar la pirámide.
Para este producto (construcción de una pirámide) se requiere de una serie de pasos. En un proceso perfecto no debería de existir ningún error, pero en este caso sí, así que identifica qué pasó.
Para ello, analiza cada proceso por separado:
Proceso uno: se acomodan cuatro vasos para que sean la base. Si se analiza, el tipo de material es el correcto; la cantidad de material es suficiente; el recurso humano es ideal, ya que se logra realizar la base de esta sin contratiempos.
Proceso dos: después se colocan tres vasos en la parte superior. Analizando, es similar al paso uno, el material y el recurso humano son adecuados.
Proceso tres: posteriormente, se colocan dos vasos y al final uno.
Proceso cuatro: se identifica que sobran cuatro vasos. Si se analiza, el tipo de material es correcto, también el recurso humano, pero el número de piezas es mayor. Por lo tanto, se señala que existe un error en este cuadro, el cual es el número de piezas sobrantes.
Proceso cinco: se agrega un vaso a cada nivel de la pirámide. En este caso, se soluciona el problema del sobrante de piezas, añadiéndolas a la pirámide.
Proceso seis: se identifica que falta una pieza. Analizando una vez más qué sucedió, el recurso humano es correcto, el tipo de material es correcto, el número de piezas es incorrecto; segundo error encontrado, se señala en el cuadro.
En dos de las seis fases hay errores. Por lo tanto, se descarta el tipo de material y el recurso humano capacitado para el trabajo, el error está en la falta de material.
Ahora, debes encontrar dónde está la falla para poder solucionarla. De acuerdo con los análisis que se realizaron, se puede observar que el responsable es ingeniería, el área que se encarga de la planeación de los recursos, es decir, que éstos sean los adecuados y en la cantidad exacta. En este ejemplo, no se contó con el material exacto para terminar la pirámide.
Uno de los procesos productivos en el que se debe llevar a cabo una gestión técnica muy rigurosa es el ensamblado de un automóvil, ya que en la misma intervienen no sólo la planta principal, sino también una serie de empresas que proveen una variedad de insumos, que son de suma importancia para terminar el automóvil. En algunas ocasiones, los proveedores de autopartes se instalan cerca de las plantas para proveerlas de los recursos necesarios y así evitar retrasos.
Algunas de las etapas más importantes en el ensamble son:
- Recepción y clasificación de piezas. Las piezas que se ocupan para el armado de un automóvil son manufacturadas por diferentes empresas especializadas cada una en su ramo.
- Corte de piezas metálicas. El corte de piezas grandes de metal servirá para hacer el armazón.
- Ensamblado del chasis y carrocería. En esta área tiene mayor injerencia el departamento de soldadura y lo realizan maquinarias especializadas o robots.
- Pintura. El siguiente paso es pintarlo, lo cual se realiza en un horno especializado.
- Ensamble de piezas mecánicas. En esta etapa también se ocupa el proceso de soldadura, pero acompañado de otras actividades, como el montaje de piezas mecánicas, por ejemplo: el motor, suspensiones, cableado, transmisión, etcétera.
- Terminación de excedentes. En este proceso se viste al automóvil: luces, llantas y parachoques.
- Acabados de interiores. En esta fase del proceso los operadores instalan alfombrado, asientos, volante, cinturones de seguridad, manijas, por mencionar algunos.
- Verificación. Antes de abandonar la línea de montaje cada parte del vehículo recibe una inspección final.
- Pruebas. Esta es la última fase del proyecto, la cual consiste en un banco de pruebas: eléctricas, mecánicas, prueba de lluvia, aceleración y frenado, entre otras.
En promedio un automóvil tarda 20 horas en ser ensamblado, pero en las cadenas de montaje se puede decir que se produce una unidad por minuto. Este es un ejemplo claro de un proceso de producción, donde se involucra una gestión técnica muy especializada.
Cabe mencionar que, la mayoría de los automóviles se ensamblan en línea y, como lo dice su nombre, van sobre una línea de ensamblaje donde se realiza un proceso tras otro; no se puede avanzar al siguiente si no se termina el anterior.
La falta de una pieza ya sea por la ausencia de entrega por parte del proveedor o porque está defectuosa, rota o no cumple con las especificaciones requeridas, retrasa el ensamble del automóvil y por lo consiguiente, el terminarlo a tiempo.
De aquí la importancia de la gestión técnica, que será la encargada de evitar este tipo de problemas; además, puede entrar en cualquier parte del proceso, siempre y cuando se sigan los pasos, los cuáles son: planeación, organización, ejecución, control y evaluación.
Un paro en la línea de producción de un automóvil genera la pérdida de tiempo y ganancias millonarias, tanto para las armadoras como para los proveedores de los componentes. El papel de la gestión técnica en este caso es prever la falta de piezas durante el ensamble, que estén justo en el momento y en el lugar adecuado para que el producto esté en el tiempo programado.
Algunas de las técnicas japonesas que usan las armadoras para una gestión adecuada son:
Justo a tiempo: es un sistema de organización, el cual se basa en eliminar todo aquello que no aporte valor al producto o servicio realizado; es decir, este sistema preverá que no falten piezas.
Kaizen: refiere a la mejora continua que realizan los empleados en los procesos de producción.
Kanban: es un sistema que controla el avance del trabajo de manera armónica, a través de tarjetas de información en las que se indica la cantidad y el tiempo en que se requiere.
Estas tres herramientas de gestión no sólo las adoptan las armadoras de los automóviles, sino también los proveedores de piezas.
En algunos contratos que se realizan entre las armadoras y empresas, estas técnicas son una condicionante, ya que, si no se entrega a tiempo y en forma, se verán penalizados con multas elevadas.
La gestión técnica coordina todos los recursos disponibles: humanos, materiales y de tiempo, para producir un bien o un servicio y, para que estos se produzcan de manera adecuada, se debe de seguir una serie de pasos ordenados, como la planeación, organización, ejecución, el control y la evaluación.
Has finalizado esta sesión, donde aprendiste que un proceso de producción es el conjunto de operaciones que generan un bien o un servicio, por ejemplo: una mesa, un automóvil, un edificio, una pluma, entre otros.
El Reto de Hoy:
Elabora una infografía de la gestión técnica y su importancia en el proceso de producción. Recuerda que una infografía es una serie de imágenes, gráficos y texto que son explicativos y resumen un tema; si tienes oportunidad compártela con tu familia.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario