Aprende en Casa III SEP: 25 de febrero TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 25 de febrero de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Jueves 25 de febrero, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Proporcionalidad inversa y arquitectura maya
Aprendizaje esperado: Analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.
Énfasis: Analizar y comparar situaciones de proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica.
¿Qué vamos a aprender?
Hoy se construirá geométricamente la curva que describe una proporcionalidad inversa.
¿Qué hacemos?
Para iniciar la sesión, reflexiona, ¿a quién no le gusta visitar alguna zona arqueológica?
¡En verdad eres muy afortunado!, ya que en el país se cuenta con una gran variedad de ruinas como Teotihuacan, Monte Albán, Uxmal, Tulum, Tajín, por sólo mencionar algunas que hoy puedes disfrutar en su infinita belleza y en todas ellas impresionan sus grandes construcciones.
En esta sesión vas a estudiar el vínculo entre las matemáticas y, en particular, la arquitectura maya. Seguramente te preguntarás: ¿de verdad las matemáticas tienen alguna relación con los mayas?
Los mayas tenían conocimientos de astronomía, matemáticas y agricultura, por mencionar algunos. Pero desde la perspectiva de las matemáticas uno de sus principales logros fue la invención de una representación matemática del cero, así como estudios de astronomía y de arquitectura.

¡Vaya que sí debes sentirte orgulloso de tus raíces!
Ahora, hay que analizar un poco la arquitectura maya. ¿Sabías que la cascabel yucateca, la serpiente endémica del sureste de México y parte de Centroamérica, era considerada un animal sagrado?
En la piel de esta serpiente los mayas encontraron una figura en forma de rombo llamada canamayté, la cual inspiró diseños arquitectónicos.

Así, inspirados por el ingenio de los mayas, verás aplicaciones del concepto de proporcionalidad inversa en la construcción, y así mismo, una representación geométrica de ella.
Ahora, verás cómo dar sentido y significado a la geometría de una proporción inversa. Para ello revisa la siguiente situación.
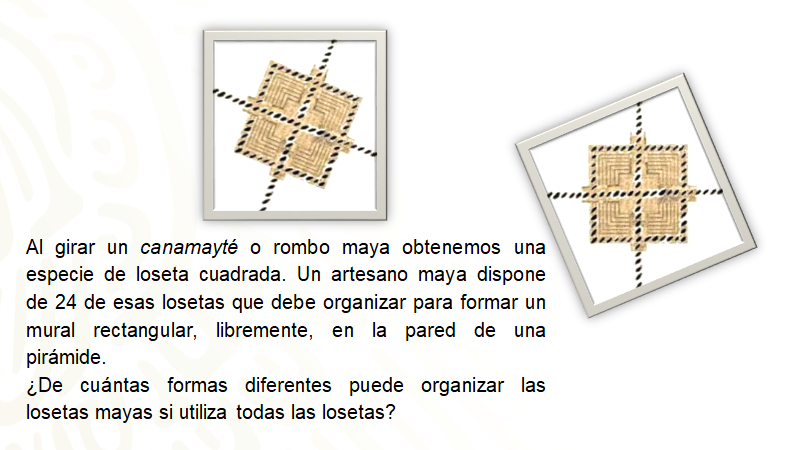
Como ya se tienen 24 losetas, una forma de organizar las losetas puede ser 4 columnas de 6 losetas de altura cada una.
Otras formas de acomodar pueden ser 8 columnas con 3 losetas de altura cada una, o una, que tal vez no es la más común, colocar todas las losetas una seguida de otra, lo cual daría un mural de 24 columnas con una loseta de altura cada una, lo cual daría un mosaico muy largo. Otro arreglo menos extenso serían 12 columnas con 2 losetas de altura cada una.
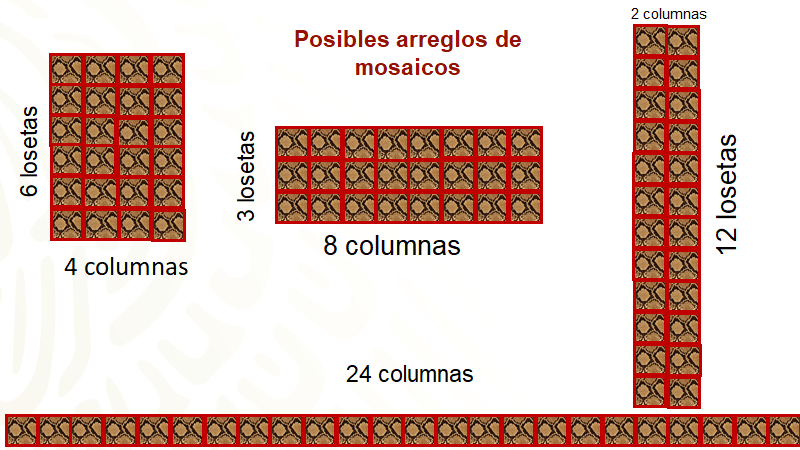
Las distintas formas de los mosaicos pueden tener un comportamiento entre las magnitudes de la base y altura de un rectángulo. Así es; si analizas en todos los posibles arreglos, hay algo que permanece constante, el número de las losetas que son 24, la superficie o área que abarca cada mural es la misma, por lo cual se observa que cuando el número de columnas aumenta, el número de losetas por columna disminuye en la misma proporción, es decir, dichas magnitudes están en proporción inversa.
Ya que se están construyendo mosaicos mayas que son agradables visualmente, observa que una proporción inversa no se queda atrás. Se te invita a que analices visualmente una proporción inversa, pues has trabajado tablas donde se ordenan los datos.
En este caso se hace un análisis del concepto de una proporción inversa utilizando aritmética, pero en las matemáticas existen distintas ramas, entre ellas, la geometría, por ejemplo, que ayudan a desarrollar un concepto desde otra perspectiva. Observa como:
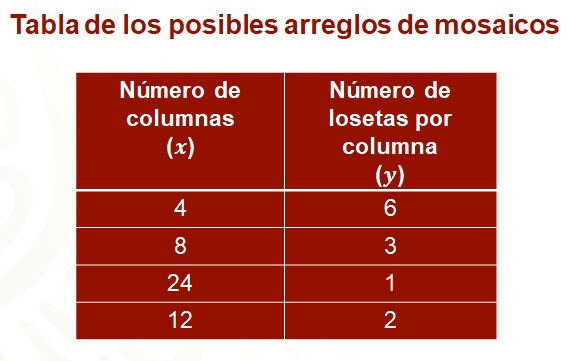
Para ello se realiza un arreglo tabular donde en la primera columna se coloca el número “x” de columnas que forman el mosaico y en la segunda columna el número “y” de losetas en cada columna.
Así, a partir de la propuesta inicial, en el primer renglón de la tabla se colocan 4 columnas con 6 losetas cada columna; en una segunda propuesta se tienen 8 columnas con 3 losetas cada una; en el tercer mosaico demasiado largo que corresponde al tercer renglón de la tabla se tienen 24 columnas con una loseta en cada columna, y en el último renglón, un mosaico con 12 columnas y 2 mosaicos por cada una.
Asimismo, se corrobora que se está en una proporción inversa, comparando los datos en el primer y último renglón, ahí se nota que mientras el número de columnas se triplica, el número de losetas por columna disminuye a la tercera parte, y de manera análoga con el segundo y tercer renglón.

Ahora, se hará uso de los datos en la tabla para el análisis geométrico de una proporción inversa, de, su arquitectura.
Se van a trazar dos segmentos de rectas perpendiculares entre sí, que llaman ejes de coordenadas, obteniendo así un eje horizontal donde se ubicará la variable “x”, que es el total de columnas en cada mosaico, es decir, los datos de la primera columna de la tabla, mientras que en el eje vertical se ubica la variable “y”, que representa el número de losetas en cada columna del mosaico correspondiente, que son los datos de la segunda columna de la tabla. Para simplificar la representación es conveniente elegir una escala en cada uno de los ejes, de donde por la forma que se encuentran representados los datos, se puede elegir una escala de 4 en 4 para ir haciendo marcas a la misma distancia en el eje horizontal y, por otro lado, la escala será de 2 en 2 para el eje vertical.
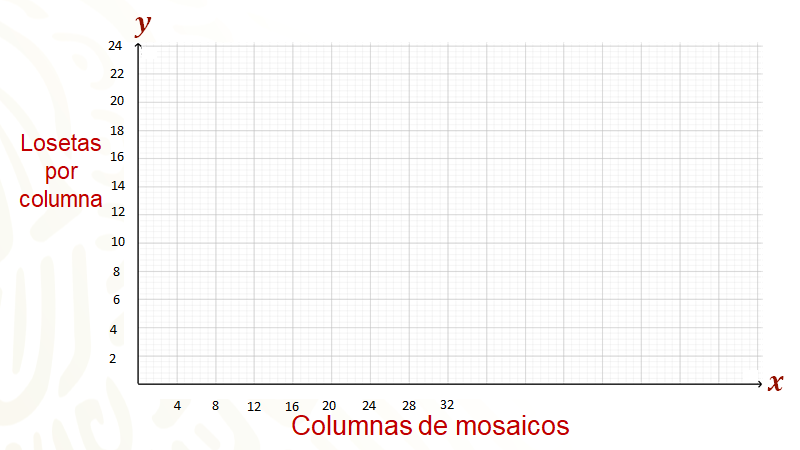
Con los datos del primer renglón se tiene que “x” es igual a 4 y “y” es igual a 6, formando la pareja ordenada “cuatro coma seis”; trazando rectas paralelas a los ejes por los puntos marcados en los ejes, se busca su punto de intersección identificando dicho punto “P” con la pareja formada.
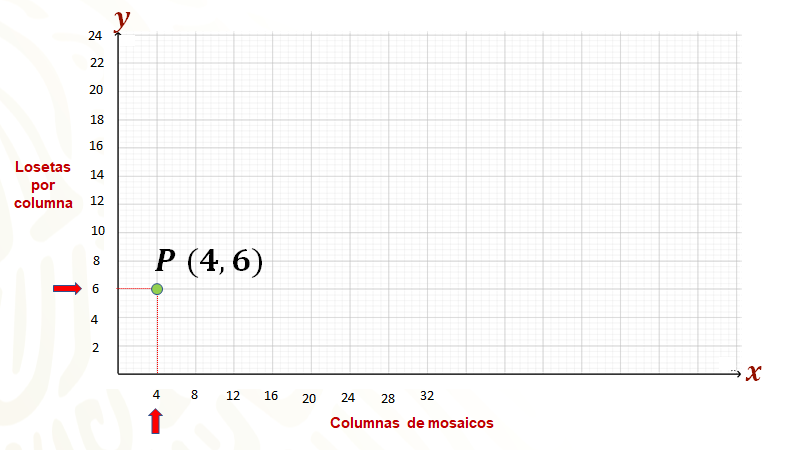
Se procede de la misma manera con el resto de los datos en la tabla, para así ir ubicando puntos que van formando una representación geométrica de la proporción inversa de la tabla que se construyó.
Ahora se localiza primero el “8” en el eje horizontal, que por la escala se ubica en la segunda marca, de la misma manera, pero en el eje vertical se ubica “3” que por la escala se encuentra a la mitad de entre la segunda y tercera marca del eje donde se está trabajando; con ello, se forma la pareja “8 coma 3”. Ahora se trazan rectas paralelas a los ejes para encontrar su punto de intersección, al cual se le llamará el punto “Q”.
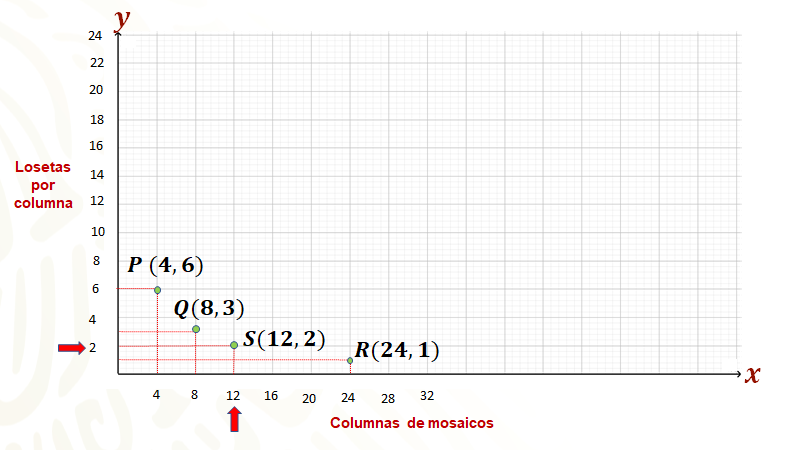
Procediendo de manera análoga, se ubica el resto de los puntos, a los cuales se les llamará “R” y “S” en los ejes de coordenadas. Si observas, hay puntos que están más arriba del eje horizontal que otros, inclusive hay un hueco entre el punto “R” y “S”; lo que puedes hacer es calcular más puntos en la tabla dando valores a “x”, determinando el valor faltante en la proporción inversa, y procediendo después a formar las parejas ordenadas correspondientes para ubicarlas en el plano. Observa.

Para ello, se van a dar los valores de 16 y 18 para “x” en la primera columna para obtener el valor correspondiente de “y” en la segunda columna.
Así, para el valor de “x” igual a 16, que es el doble de 8; en la segunda columna se tiene que el valor de “y” correspondiente es la mitad de “3” es decir, tres medios o 1.5, con lo cual se tiene el punto “T”, con coordenadas “16 coma tres medios”, que bajo las condiciones del problema, corresponde a un mosaico con 16 columnas cada una con una y media loseta de altura.
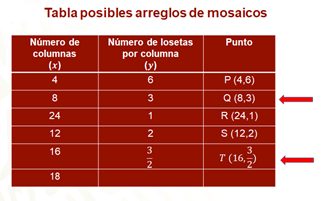
Para el valor de “x” igual a 18 se observa que el procedimiento puede complejizarse respecto al anterior, pero puedes recordar la propiedad que cumplen las variables de una proporción inversa, donde los productos de las magnitudes en cada renglón son constantes para tener que, 18 por “y”, es igual a 4 por 6.
De donde 18 por “y” es igual a 24, dividiendo de ambos lados en la igualdad anterior por 18, se tiene que “y” es igual a 24 sobre 18.
Simplificando la fracción, se tiene que “y” es cuatro tercios o un entero un tercio. Para tener el punto con coordenadas “U”, 18 coma cuatro tercios o un entero un tercio, y se coloca en la tabla.

Ahora, representando los nuevos puntos en la gráfica, se tiene que. puedes visualizar la representación geométrica de una proporción inversa, se ve cómo los puntos van bajando al eje horizontal.

Inclusive si vas considerando cada vez más valores para “x” de manera continua, sin dejar huecos, se van obteniendo más y más puntos que satisfacen las condiciones del problema, que, al ubicarse en el plano, se va observando el trazo de una curva continua que va uniendo todos los puntos, llamada hipérbola, que va a ser la representación geométrica de la proporción inversa.
La cual, por cierto, modela el fenómeno de una curva que va bajando hacia el eje horizontal conforme se va alejando del punto de intersección de los ejes que es el origen, cuyas coordenadas son “cero, coma cero”.
Ahora, se te invita a que reflexiones sobre la siguiente pregunta: ¿qué pasa conforme se acercas al cero?
Para responder la pregunta, se va a considerar una tabla ahora con valores de "x" próximos a cero, a partir del primer renglón que corresponde a un mosaico de 4 columnas con 6 losetas cada una, y recordando que en una proporción inversa, conforme una variable disminuye, la otra aumenta en la misma proporción, se tiene que, para cuando “x” vale 2, es decir, la mitad de 4, entonces el valor de “y” es el doble de 6, que es 12, por ello, en el penúltimo renglón se tiene el punto “(2,12)”; siguiendo con esa idea, para el siguiente renglón la mitad de 2 es ahora 1, que es el nuevo valor para “x”, y así sucesivamente se obtienen valores de “x” cercanos a “cero”, calculando las mitades del renglón inmediato anterior obteniendo así un medio, que es la mitad de 1, y un cuarto que es la mitad de un medio en la primera columna, por estar en proporción inversa con “y” se puede completar la segunda columna obteniendo el doble del valor en el renglón inmediato anterior, con lo cual, el doble de 12 es 24 y así sucesivamente.
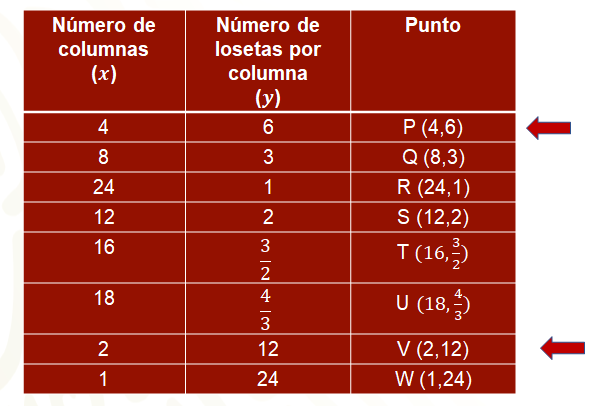
Ahora, formando las parejas correspondientes se obtienen los puntos de la tercera columna. que al representarlos en el plano con ejes de coordenadas, junto con el resto de los puntos, se tiene la siguiente configuración de puntos, que al unirlos con una curva continua, se obtiene una mejor idea de la hipérbola que representa la proporción de los mosaicos mayas, donde puedes observar que, conforme te aproximas a cero con valores en el eje horizontal tanto como quieras, con los valores de “y” te vas aproximando más y más al eje vertical, además de crecer la curva tanto como sea necesario.
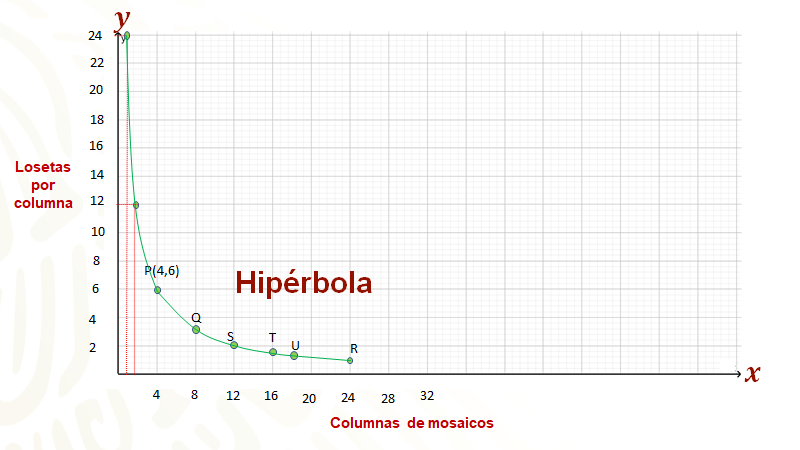
Es momento de hacer un alto en el desarrollo del tema, para puntualizar lo estudiado hasta aquí. Se verán los pasos para trazar la gráfica que representa una proporción inversa.

Ahora, se revisará una última situación.
Actualmente, con la construcción de un tren en el sureste del país, se busca tender un drenaje entre dos zonas arqueológicas mayas, se necesitan 6 000 tubos de 2.40 metros de largo.
Hay que determinar una manera gráfica de la relación existente entre el número de tubos “T” y la longitud “L” de cada uno de ellos.

Observa que conforme los tubos aumentan de tamaño, el número de tubos van a disminuir en la misma proporción, ya que la distancia entre ambas zonas arqueológicas no va a cambiar, por lo que se trata de graficar una proporción inversa entre las variables “T” y “L”.
Hay que considerar una tabla donde se encuentran tres columnas una para el número de tubos en la obra “T”, una segunda columna para la longitud correspondiente del tubo “L” y una última para ir formando las parejas ordenadas que pueden ayudarán a trazar la gráfica.
En el primer renglón se colocan 6 000 tubos a los que les corresponde 2.4 metros en la segunda columna, formando la pareja (6 000, 2.4).
Ahora, se proponen los demás valores para que sea accesible graficar; por ejemplo, se consideraron los siguientes valores de “T” en la primera columna: “3 000” tubos la mitad de “6 000”, “2 000” tubos la tercera parte de “6 000”, ”1 000” tubos la sexta parte de “6000”, “4 000” el doble de “2 000” y así hasta “8 000”, que es el doble de “4 000”; en la segunda columna se colocan las longitudes “L” correspondientes de los tubos para luego escribir en la última columna los puntos.

Para calcular las longitudes de los tubos, como las variables están en proporción inversa, entonces disminuyen y aumentan en la misma proporción; así, los datos para completar la tabla se obtienen usando esa condición, así, se tiene que en el segundo renglón el valor de “L” es 4.8, que es el doble de 2.4; para el tercer renglón, su valor es 7.2, que es el triple de 2.4; en el cuarto renglón, 14.4, que es el doble de 7.2; en el quinto renglón es 3.6, que es la mitad de 7.2; en el sexto renglón es 1.8, que es la mitad de 3.6.
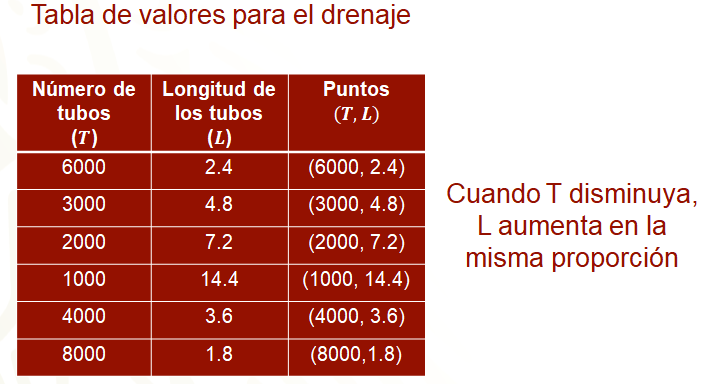
Como te diste cuenta, completar los datos de la tabla sabiendo que las variables están en proporción inversa fue relativamente fácil. Se precisa, que en una relación de proporcionalidad inversa la disminución de una cantidad implica el aumento de la otra, siempre en la misma proporción.
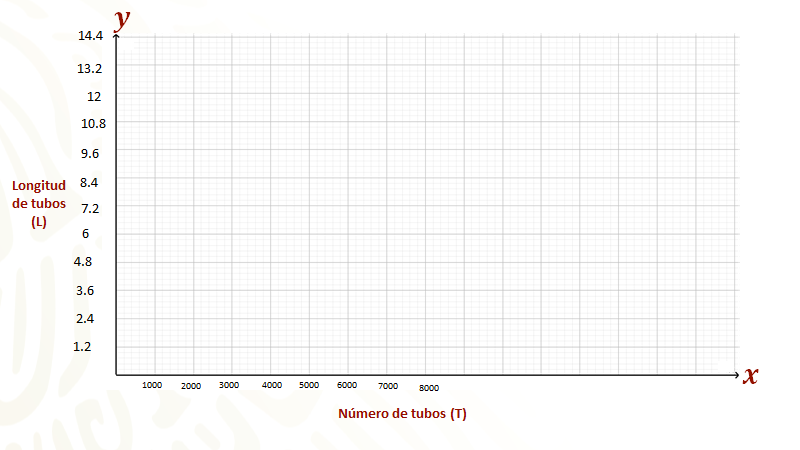
Ahora, se procede a realizar la gráfica ubicando primero las variables sobre los ejes de coordenadas, en el eje horizontal se ubica la variable “T” de la primera columna y en el eje vertical, la variable “L” de la segunda columna.
Después se procede a ubicar los puntos de la tercera columna, recordando que hay que buscar la intersección de las rectas paralelas a los ejes. Resultando un arreglo de los puntos como el que se puede ver en la siguiente gráfica.
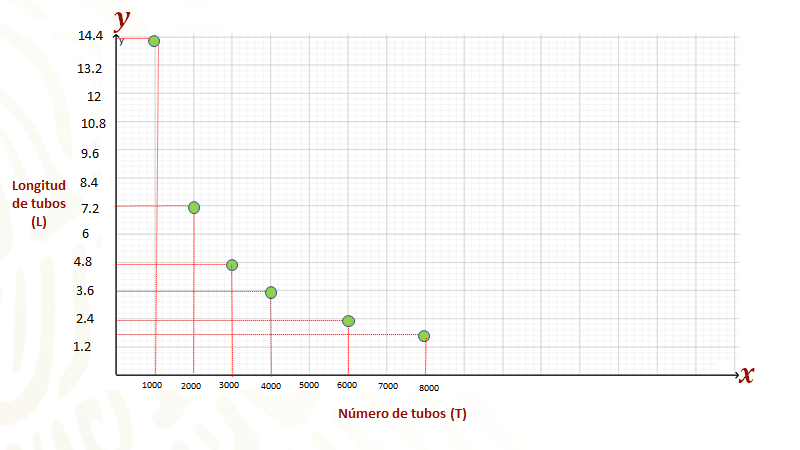
Al final se unen los puntos con una curva continua, para finalmente obtener la curva que representa la relación entre las variables “T” y “L” que son inversamente proporcionales.
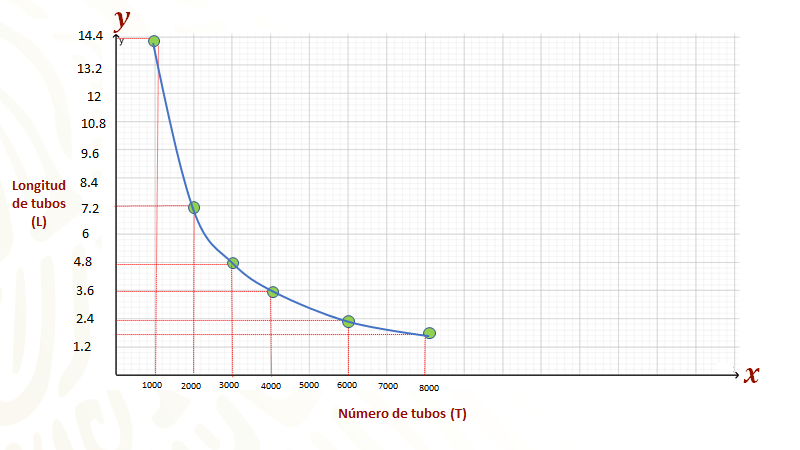
Se espera que hayas dado sentido y significado a la representación geométrica de la proporcionalidad inversa.
Una consideración que se tiene que tomar en cuenta es que al igual que en la proporcionalidad directa, en los casos de proporcionalidad inversa también se puede hallar una constante que te ayude a calcular algún valor faltante, ya sea de “x” o de “y”.
En este caso se llama constante de proporcionalidad inversa, ya que las variables son inversamente proporcionales, y se puede calcular de la siguiente manera.
Se van a utilizar los datos de las losetas mayas, que es una situación que ya se resolvió al inicio de la sesión.
En la situación se contaba con 24 losetas y se plantearon las siguientes maneras de agruparlas:
- 24 columnas por 1 loseta de alto.
- 12 columnas por 2 losetas de alto.
- 8 columnas por 3 losetas de alto.
- 4 columnas por 6 losetas de alto.
Primero se llamará “x” a los valores correspondientes a las columnas y “y” a los valores que correspondan al alto de losetas.
Si analizas los datos puedes percatarte de que el producto de “x” con su correspondiente valor de “y” es siempre el mismo, 24. Este valor representa la constante de proporcionalidad inversa y se llamará “k”, y puede ayudarte a calcular el número de columnas si conoces el número de losetas y viceversa.
La fórmula que relaciona a la constante de proporcionalidad inversa con las variables, tanto independiente como dependiente, es la siguiente: “x” por “y” igual a “k” o “y" es igual a "k" entre "x”, lo cual es la representación algebraica de una proporción inversa.
Para esta situación y con esta expresión algebraica es posible calcular cualquier combinación de losetas que se requiera, siempre y cuando no sean mayores a 24, por el planteamiento del problema, aunque observa que la expresión algebraica puede ya extenderse a otros valores, dejando de depender del problema y poder ya tener independencia para su estudio más adelante.
Has concluido el tema del día de hoy. Se te recuerda que debes elaborar tus notas, considerando las ideas más importantes del tema de hoy, anota tus dudas y posibles dificultades, para que de ser posible las puedas revisar con tu profesora o profesor de esta asignatura.
Se propone el siguiente reto:
Dadas dos magnitudes “x” y “y” que son inversamente proporcionales con constante de proporcionalidad negativa “k” igual a menos uno. Se te invita a realizar una tabla donde se calculen distintos valores de “x” y “y” que satisfagan dicha proporción, y que elabores la representación gráfica de la proporción a partir de las parejas de puntos en el paso anterior en el plano cartesiano.
Finalmente, describe el comportamiento de la curva analizando la variación de “y” respecto a la variación de “x” para valores próximos y lejanos al cero.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Al derecho y al revés, un poema es
Aprendizaje esperado: Crea textos poéticos con formas gráficas.
Énfasis: Identificar características de palíndromos y otros textos poéticos con diversas formas gráficas.
¿Qué vamos a aprender?
Identificarás características de palíndromos y otros textos poéticos con diversas formas gráficas.
¿Qué hacemos?
Hasta este momento, seguramente has leído y analizado poemas tradicionales, ¿no es así? esos que expresan sentimientos y emociones por medio de las palabras y sonidos.
Pero, si conoces, la poesía contemporánea, sabrás que en ella se busca, en sí, expresar sentimientos o emociones con las palabras, pero en ciertos momentos llega a hacerlo a través de imágenes o figuras.
Por ejemplo, ¿alguna vez has tenido la curiosidad de leer un texto al revés?
Tal vez sí, pero habrás encontrado, que el texto no tiene sentido.
Pero, observa el siguiente ejemplo, para ver qué es lo que sucede.
|
“La ruta nos aportó otro paso natural”
|
Fíjate, que pasa si lees de derecha a izquierda la oración.
Como te darás cuenta se lee lo mismo que si leyeras de izquierda a derecha. ¡Es como magia, pues dice lo mismo!
Pero no es magia, se les conoce como palíndromos y son una forma de jugar con las palabras y explorar su potencial ilimitado. Consiste en crear frases que se lean igual en los dos sentidos, es decir, de izquierda a derecha o de derecha a izquierda, como ya viste.
Para que tengas una mejor idea, revisa la definición de palíndromo, según el Diccionario de la Lengua Española.
|
“Palíndromo. Palabra o frase cuyas letras están dispuestas de tal manera que resulta la misma, leída de izquierda a derecha que de derecha a izquierda.”
|
Es como lo que pasa con la palabra “radar”, porque da igual que se lea empezando por delante que por detrás, el resultado es siempre el mismo.
La palabra palíndromo proviene del origen griego y viene de la construcción palin dromein, es decir, volver atrás, recorrer a la inversa.
Los palíndromos no son sólo palabras, sino frases. Si, por ejemplo, escribes en tu cuaderno “Anita lava la tina”, verás que se lee de la misma manera sin importar por dónde empieces.
Pero ¿existen palíndromos de autores conocidos?
La respuesta es sí, destacan los escritos por los argentinos Julio Cortázar, Jorge Luis Borges y los del cubano Guillermo Cabrera Infante. Cortázar incluye el palíndromo "Atar a la rata" en su cuento “Satarsa”, parte del libro de relatos Deshoras; de hecho, todo el cuento gira alrededor de esta frase.
Otro dato interesante, es que el palíndromo más largo del mundo lo escribió el escritor francés Georges Perec en 1969, y es una novela de 1 300 palabras que se puede leer tanto de izquierda a derecha como de derecha a izquierda.
¿Mil trescientas palabras? Suena como algo imposible, sin embargo, existe.
Revisa otros ejemplos un poco más cortos.
|
Palíndromo |
Autor |
|
“Etna da luz azul a Dante” |
Juan José Arreola.
|
|
“Amanecí de malas, Alá. Me dicen: ¡ama!” |
Rubén Bonifaz Nuño.
|
|
“Ave azul: al alba habla la luz a Eva” |
Adam Rubalcava.
|
Entonces, aunque no le pongas los acentos, ¿las palabras tendrán la misma intención?
Así es, pues una de las características de este juego poético es la sonoridad y no tanto los aspectos ortográficos.
Por esta importancia que se le da a la sonoridad, en los palíndromos sucede algo similar que en los acrósticos: se permite el uso no convencional de mayúsculas, así como la ausencia de tildes o el uso libre de signos de puntuación, principalmente cuando se hace la lectura de derecha a izquierda.
Observa el siguiente ejemplo, y analiza: ¿cómo inicia cada versión, la original y la que se reescribió? ¿Cómo termina cada una?
|
Versión original
|
Reescritura en sentido inverso
|
|
A ti mi ánimo, mina, imita.
|
Atimi anim omina im it a.
|
Pudiste observar que la frase en versión original de lado izquierdo y del lado derecho es la misma frase, pero se escribió de derecha a izquierda, es decir, empezando por la última letra.
Para repasar un poco, se te recuerda que un palíndromo debe cumplir con lo siguiente:
- El texto se lee igual de izquierda a derecha que de derecha a izquierda.
- Las letras que se emplean deben ser iguales para formar las mismas palabras en ambos sentidos.
Por ejemplo, “amo la paloma” se lee igual en ambos sentidos y tiene las mismas palabras, por consiguiente, es un palíndromo.
Pero ¿cómo podrías formar un palíndromo?
Revisa algunos pasos.
- Puedes partir por una simple palabra, por ejemplo, “miel”.
- La invierten y dice “leim”, que a simple vista no significa nada.
Si separan la expresión, queda así.
|
lei m
|
- Ahora ya tienes un efecto espejo, a partir de la “m” completa con el resto de las letras.
- El resultado es: leí miel. Donde el eje central del palíndromo fue la “m”.
A continuación, numeras letra por letra el ejemplo anterior en ambos sentidos.
Ahora que conoces qué es un palíndromo y cómo se forma, se te invita a que escribas algunos; puedes formarlos con una sola palabra o varias, revisa que se puedan leer de izquierda a derecha y viceversa, y verifica que no sobre ni falte ninguna letra.
Pero ¿a poco los palíndromos son la única forma gráfica para jugar con el lenguaje poético?
No, de ninguna manera. Existen también los video poemas, el quebrantahuesos, el poema diamante o el haiku, por mencionar aquellos de los que se hablará en esta sesión.
Ahora, revisa el siguiente video para que te quede más claro.
- #ComunidadContigo: Tutorial de Videopoesía.
https://www.youtube.com/watch?v=b_7I11NIt0k
Habrás visto aquí una breve explicación de qué es un video poema y algunos pasos para elaborar uno.
Para continuar la reflexión, responde las siguientes preguntas.
- ¿Qué elementos visuales destacan en el video poema?
- ¿Hay movimiento y sonido?
Los elementos visuales que destacan son las imágenes y los colores. Y sí hay movimientos cuando la mujer gira las flores y cuando muerde el durazno. Del video se rescata el dato importante de que el primer video poema fue realizado por Tom Konyves, un poeta canadiense.
Ese es un dato importante; qué te parece si conoces más sobre el video poema.
Videopoema.
También conocido como video poesía, es un género que se compone de imágenes, sonidos y palabras que interactúan entre sí, dando lugar a diferentes y originales creaciones artísticas.
Para complementar la definición, Tom Konyves dice que la principal función del video poema es demostrar el proceso de pensamiento y la simultaneidad de la experiencia expresada en palabras visibles o sonoras, cuyo significado se mezcla con la imagen y el sonido, sin estar ilustrado por ellos.
Entonces, ¿la video poesía busca la unión de la imagen con el sonido?
Así es. Aprovecha el uso de las nuevas tecnologías y el auge de las plataformas de video, ya que busca crear una nueva forma de emitir sentimientos.
Conoce las características del video poema.
- Pueden ser poemas publicados o inéditos.
- La música es una melodía de fondo con o sin letra.
- La imagen es el video en movimiento que refleja lo que dice una persona recitando o en un escenario.
- La duración es de dos a tres minutos. Hay algunas excepciones, pero no deben durar menos de un minuto y medio.
- El efecto que se usa es el juego de velocidad de imágenes, movimiento o tonalidad de luz.
Como observaste, el video poema requiere del poema escrito y los sonidos, la música y las imágenes, así como de la armonización de esos aspectos. La imagen puede consistir simplemente en colores, o en danza, expresión corporal, tomas cotidianas o realizadas para el video poema.
Entonces, si quieres pasar del poema al lenguaje corporal, ¿es válido?
La respuesta es sí, porque así tú le estás dando una significación; recuerda que el cuerpo también puede comunicar y a esto se le conoce como comunicación no verbal. Si tu cuerpo se mueve a la velocidad de la música de fondo, provocará una reacción en el espectador.
Otra duda es: ¿la música debe ir forzosamente?
No es necesario, pues va a depender de lo que quieras decir. Es como en el video que viste hace un momento, donde el autor sólo usa las imágenes y el silencio también provoca un sentimiento, el cual puede ser de ausencia, tranquilidad o melancolía.
¿Es necesario que cuentes con una cámara profesional?
No, ya que hasta con la cámara del dispositivo móvil o de la computadora puedes grabarlo. La calidad de la cámara no influirá, ya que se puede editar para resaltar ciertos aspectos en la imagen, hasta puede ser parte del concepto que estés manejando.
Eso te puede parecer fascinante, pues puedes enlazar varios aspectos para crear, una obra de arte visual.
Ahora bien, sabías que hay otras formas de crear poesía, por ejemplo, con recortes de letras de periódicos y revistas o incluso imágenes. ¿Sabes cómo se llama esa corriente?
Se les conoce como quebrantahuesos. Uno de los más famosos se le debe al poeta chileno Nicanor Parra, quien ideó y le dio nombre al concepto. Observa uno de ellos.

Como puedes observar, este quebrantahuesos está construido por una serie de recortes, los cuales están acomodados en forma de noticias relevantes que remiten a la primera plana de un periódico; en cada una de estas aparentes noticias construye títulos y frases satíricas, es decir, de burla hacia una situación relevante en ese momento.
También puedes observar, cómo se juega con el acomodo del tamaño y forma de las letras.
Es impresionante cómo utiliza oraciones, palabras e imágenes rescatadas del periódico para inventar nuevas noticias. Así es y lo que buscaba Parra es que todos tuvieran acceso a otra manera de ver la poesía. Pero, ahora lee la definición formal del quebrantahuesos para ampliar tu conocimiento.
Quebrantahuesos
Mensaje o anuncios que se forman recortando distintas letras de diferentes diarios o revistas, luego se pegan en una hoja formando palabras irónicas o humorísticas.
Tiene como principal característica que se organiza de forma libre o abusando del sentido común, es decir, en un collage de palabras, como se ve en este extracto de quebrantahuesos.

Entonces es una manera fácil de crear un poema, pues se necesitan sólo recortes, tijeras, pegamento y una cartulina y pueden presentarse en murales. Pueden usarse revistas, periódicos u otros materiales con elementos que se puedan recortar.
Seguramente se te habrán ocurrido muchos temas para tratar en un poema así, ¿por qué no lo intentas?
Pero, todavía faltan algunas formas poéticas que revisar y para comenzar a familiarizarte con la siguiente, se te pide que observes la siguiente imagen con detenimiento.

¿Qué características identificas? ¿Qué forma tiene? ¿Cuántos versos lo conforman?
A esta corriente poética visual se le conoce como poema diamante, y esto te resultará lógico por la forma en que están acomodados los versos. Pero observa más detalladamente en qué consiste. Pon atención.
Poema diamante.
Consta de siete versos. El primer verso tiene un sustantivo; el segundo, dos adjetivos que describen al sustantivo; el tercero, tres verbos; el cuarto, cuatro sustantivos: dos relacionados con el primer verso y dos con el séptimo. El sexto tiene dos adjetivos que describen el séptimo verso. Y el séptimo se forma por un sustantivo opuesto al del primer verso.

Se escucha como una estructura complicada; pero cuando la llevas a la práctica es sencilla, lo principal es elegir el sustantivo y su opuesto.
Así es, sólo hay que elegir los sustantivos. Por ejemplo, amor-soledad, agua-fuego, amigo-enemigo, piedra-planta.
Observa un ejemplo.

Como ves, el poema cumple con las características requeridas. Así es más fácil crear el poema y practicar los sustantivos, adjetivos y verbos.
Así es, y también puedes jugar con los colores y tipografía para formar tu poema diamante.
Pon lo aprendido en práctica. Realiza una actividad.
- Los quebrantahuesos son…
- Los video poemas se caracterizan por...
- Los poemas diamante se componen de...
Ahora ve respuestas.
- Los quebrantahuesos son recortes de periódicos o revistas que se acomodan de manera libre.
- Los video poemas se caracterizan por tener imágenes, movimiento, sonidos y una duración determinada.
- Los poemas diamante se componen de siete versos y usan sustantivos, adjetivos y verbos.
No olvides que estas características te sirven para identificar la estructura de los poemas visuales y, con ello, crear los propios.
Ahora conoce un último poema visual, los haikus. Éstos se caracterizan por comunicar ideas e imágenes con un mínimo de palabras y tienen una gran fuerza expresiva, pues en general hacen referencia a elementos de la naturaleza.
¿Sabías qué los haikus son originarios de Japón y se conforman por tres versos que se someten a reglas de medida, pero no de rima?
¿Quiénes fueron los principales poetas japoneses que escribieron haikus?
Los más reconocidos son Matsuo Bashô, Yosa Buson, Kobayashi Issa y Masaoka Shiki, aunque es un género que se sigue practicando hoy en día. El más famoso de ellos es Matsuo Bashô, quien capta en palabras el momento en el que el hombre se liga con la naturaleza.
Uno de los libros más famosos que contiene un haiku de Bashô, es el de la rana.
Revisa el poema original.

Como pudiste observar, el haiku es breve y está constituido por diecisiete sílabas, organizadas en el esquema 5/7/5, preferentemente, y sin rima. Con esta forma poética de sencillez y austeridad, se busca mostrar la sutileza, el instante y la emoción de un momento lleno de significado.
Entonces una de sus características es la economía de las palabras. Así es. Hay dos escritores mexicanos que sintieron fascinación por los haikús y que tradujeron poemas de Bashô: José Emilio Pacheco y Octavio Paz. Revisa la traducción de la rana, de Octavio Paz, aunque no cumple por completo con la métrica ideal.

Como puedes observar, la traducción transmite una imagen muy precisa de lo que podría hacer una rana.
Pero ¿cómo puedes hacer para ajustar la medida métrica de un verso?
Haciendo uso de la sinalefa, la cual es la unión de dos vocales, la del final de la palabra y la del inicio de la otra, como en “vie-joes-tan-que”. Con ésta puedes disminuir una sílaba.
Ahora que te queda más claro, ya puedes hacer tu propio haikú.
Además de las traducciones, hay varios poetas mexicanos que han escrito haikús, y entre ellos destaca el poeta Juan José Tablada. Lee uno de sus haikús.

Aquí la imagen que crea, ya lo habrás visto, es la del color de los sapos, porque dice que, en la penumbra, los sapos parecen pedazos de barro o de lodo, que saltan de repente.
Ahora, ¿puedes observar la métrica? Revísala.

Sí cumple la regla de la métrica de 5, 7 y 5.
Se espera que tengas la misma respuesta y no olvides que los haikus, en general, se refieren a la naturaleza, las estaciones del año y lo que rodea a ambos.
Ahora, que te parece si se recuperan las distintas formas gráficas de los poemas que se trabajaron durante la sesión.
- Los palíndromos se leen de igual forma de izquierda a derecha y de derecha a izquierda, como “atar a la rata”.
- Los video poemas contienen imágenes, texto y música en un video.
- Quebrantahuesos conllevan: recortes de revistas y periódicos que crean nuevos contenidos de naturaleza burlona o satírica.
- Poema diamante; está compuesto de siete líneas, a partir de un sustantivo y su opuesto.
- Haikús, son escritos derivados de la tradición japonesa, con tres versos de cinco, siete y cinco sílabas, respectivamente.
El Reto del Hoy:
En tu libro de texto de Lengua Materna 2 podrás encontrar más ejemplos de otros poemas visuales al igual que ligas electrónicas con materiales audiovisuales que te serán de ayuda.
También puedes ver, las clases de artes visuales, te serán de gran ayuda para que te surjan ideas gráficas para usar el espacio y así crear poemas visuales.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Comunicación eficaz para establecer acuerdos
Aprendizaje esperado: Analiza el conflicto y opta por la forma más conveniente para lograr objetivos personales sin dañar al otro.
Énfasis: Reconocer que la comunicación asertiva es una forma de lograr objetivos personales sin dañar a los otros.
¿Qué vamos a aprender?
A lo largo de esta sesión, podrás reconocer en la comunicación asertiva una forma eficaz para llegar a acuerdos y lograr tus objetivos personales sin dañar a las y los demás.
¿Qué hacemos?
¿Alguna vez has tenido un conflicto con otra persona y te ha costado mucho trabajo ponerte de acuerdo con ella para resolverlo?
Es muy común sentir frustración cuando se tiene un desacuerdo con otra persona y ésta no te permite expresarlo y limita las posibilidades de intercambiar puntos de vista y exponer tu descontento. Todas las personas quieren ser escuchadas y que las tomen en cuenta.
¿Te gustaría saber qué otros sentimientos y sensaciones experimentan las personas cuando tienen un conflicto y quieren que ser escuchadas?
Se te invita para que, pongas atención a algunos testimonios de la sección “La voz de la juventud”.
“Cuando comparto algo con otra persona, que para mí es importante, quiero que me ponga atención y sea respetuosa. Me molesta mucho que lo tomen a broma o no le den la misma importancia que yo.” Abril Camila |
|
|
“Cuando tengo un descuerdo con una persona, para mí es muy importante que me escuche, porque de esa manera yo le puedo explicar mi punto de vista, yo quiero que me comprenda. Si no me deja hablar no le podría expresar lo que siento o pienso respecto al problema.” Daniel. |
|
|
“Cuando he tenido un conflicto con alguien creo que lo más importante para mí ha sido enfocarme en que la otra persona me entienda. Quiero que entienda lo que pienso y siento, trato de ser muy clara con lo que digo, pero me ha pasado que no llegamos a ningún acuerdo, porque no siempre me quieren dejar hablar, eso me causa enojo y tristeza.” Liliana |
|
|
“Para podernos comunicar con una persona con la que tenemos un conflicto, creo que lo más importante es que ambos pongamos de nuestra parte, que los dos estemos dispuestos a resolverlo. Eso lo puedo notar si me prestan atención cuando yo estoy hablando y explicando mi opinión. Si eso no sucede, dejo que la persona se calme y después vuelvo a intentar hablar con ella.” Daana. |
|
|
“Cuando nos comunicamos con una persona con la que hemos tenido un desacuerdo, creo que nos debemos esforzar en comprender y captar lo que dice, pero también lo que hace. Si hace caras o se mueve de alguna forma, o si hace algún ruido mientras estoy hablando. A veces se necesita escuchar con el corazón, o sea tratar de entender los sentimiento o emociones.” Fátima |
Después de leer y escuchar los testimonios de las chicas y chicos, te puedes dar cuenta de que no eres el/la único(a) que se siente de esa forma cuando no te escuchan. Incluso, quizás te hayas podido identificar con estas situaciones.
Saber escuchar a las personas y exigir que te escuchen es parte importante de una aproximación asertiva durante un conflicto, pues se previene una reacción violenta o pasiva que no va a ayudar a resolver el problema.
Como pudiste darte cuenta, las y los adolescentes comentaron sobre observar las expresiones faciales y corporales de la persona con la que estás hablando ¿Esto sirve para saber si la otra persona te está entendiendo?
Así es, se llama retroalimentación no verbal. Cuando las personas se comunican, además de recibir el mensaje que la o el interlocutor está compartiendo con ellas, también pueden prestar atención a su lenguaje no verbal, pues les va a brindar más información sobre su estado de ánimo o la intención de su discurso, así como su reacción ante lo que están compartiendo con él o ella.
De esta forma sabrán si expresan claramente su mensaje, si les están poniendo atención o si la persona con la que están hablando también está siendo clara o directa. Estos elementos son muy importantes cuando se busca ser asertiva o asertivo en la comunicación.
Ahora, se te invita a prestar atención al siguiente fragmento audiovisual que te habla, precisamente, sobre qué cualidades debes trabajar si quieres expresarte de forma asertiva.
- “Expresión de sentimientos y asertividad”
https://www.youtube.com/watch?v=duxYDN0HJig
Revisa del 1:47 al 2:08.
En el video, pudiste reconocer que para resolver un conflicto debes ser más claro(a) y preciso(a) en los argumentos que compartas, debes ser congruente con lo que sientes y piensas para que tu discurso sea coherente y, sobre todo, no debes omitir nada que pueda ayudar a que la otra persona entienda tu perspectiva.
Un primer paso para la comunicación asertiva es asegurarte de compartir la información completa y necesaria para entablar un diálogo que te lleve al establecimiento de acuerdos que den solución a tu conflicto.
Pero eso no siempre es fácil. ¿Habrá alguna forma en la que puedas aprender a ser más asertivo(a) a la hora de comunicarte?
Hay algunos pasos que puedes seguir para transformar, día a día, tu actitud en asertiva, para hacer frente a situaciones de comunicación que te pueden causar problemas al encarar un conflicto.
¿Qué te parece si escuchas los consejos que la profesora Tamara Islas tiene para ti respecto a este tema? Observa el siguiente video y escucha el audio.
- “Video 1_Introducción”
- Audio 6. “Tamara_decálogo”.
|
Decálogo para la comunicación asertiva
|
|
|
|
|
|
|
|
|
|
|
|
|
- Video 2_Cierre.
Los consejos y el decálogo de la comunicación asertiva que se te proporcionaron en los recursos audiovisuales son muy útiles, pues no sólo te ayudan a tomar una postura asertiva sobre lo que sientes y piensas, sino que también te hacen consciente de que todas y todos los involucrados comparten la responsabilidad de llegar a una solución para los conflictos ¿No te parece?
Saber expresar tus opiniones y sentimientos es sólo una parte de la comunicación asertiva. También es importante que pongas en práctica la escucha activa y la empatía.
¿Has escuchado hablar de ellas?
La escucha activa implica poner especial atención a lo que la otra persona te dice y cómo lo dice; mientras que la empatía te permite ponerte en sus zapatos y tratar de comprender o aceptar sus puntos de vista, mientras la escuchas.
¿Qué consideras, qué es más importante, saber comunicarse o saber escuchar?
Las dos habilidades son igual de importantes, pero muchas veces cuesta más trabajo aprender a escuchar, e incluso, a veces se te puede olvidar cuando estas discutiendo con alguien.
¿A ti qué te resulta más fácil, aprender a ser un buen comunicador o aprender a saber escuchar?
Ahora que ya sabes cómo comunicarte asertivamente, se repasarán algunas ideas sobre cómo aprender a escuchar activamente.
La escucha activa requiere prestar atención y tener concentración en las palabras e ideas para entender mejor el mensaje. También se pide observar el lenguaje no verbal, como los gestos, ademanes o movimientos que la otra persona hace mientras está hablando. Incluso, su postura te puede advertir si está tranquilo o a la defensiva.
La distancia corporal entre quien habla y quien escucha, así como el contacto visual que establezcan deja ver si existe confianza para hablar abiertamente del tema o se está emplean evasivas. Cuando se escucha a alguien es importante no interrumpir, dejar que la otra persona termine sus argumentos, aún si no se esté de acuerdo.
Sin embargo, se puede pedir amablemente la palabra si se considera que no se comprende algo, puedes solicitar aclaraciones o ampliaciones de la información. También resulta útil resumir lo que has entendido para corroborar que lo has hecho bien.
Un factor fundamental en este ejercicio es evitar, a toda costa, el prejuicio o la predisposición ante lo que vas a escuchar. Debes mantener la mente abierta a los alegatos de tu contraparte. Y, aunque pareciera ser el paso más difícil, no debes comenzar a pensar en cómo formular tu respuesta sino hasta que se haya concluido, pues eso evitará que dejes pasar puntos importantes al concentrarte en no olvidar lo que quieres decir.
Es importante evitar las distracciones externas o internas, lo cual facilitará concentrarte en comprender los puntos de vista ajenos y, quizá, hasta te des cuenta de que hay algo de razón en ellos.
Si te esfuerzas en mejorar tu escucha se reducen la escalada de conflictos por malas interpretaciones, te das la oportunidad de aprender de los conocimientos y percepciones de las otras y otros y, también, amplias tu marco de referencia, en cuanto a cultura e intereses.
No debes olvidar que tu objetivo primordial es establecer acuerdos o lograr una resolución favorable para ambas partes, por lo que hay otro factor que debes tener presente todo el tiempo ¿Sabes cuál es?
La empatía, que no sólo requiere que escuches con la mente abierta y trates de entender cómo y por qué se siente de tal o cual manera una persona; sino que también te pide aprender a diferenciar entre el estado emocional de la persona durante la charla y los motivos que la han llevado a actuar de tal manera y a entablar un conflicto contigo.
Es decir, que no sólo debes atender a cómo se siente al dialogar contigo, sino que también debes tomar en cuenta sus sentimientos y formas de pensar de forma general. Cuál es su ideología, su contexto, la forma en que este conflicto le afecta y las posibles causas de su forma de actuar.
Es por ello que la escucha activa y la empatía se relacionan íntimamente. En ambos casos se requiere escuchar con atención, interpretar las señales no verbales, mostrar comprensión y ofrecer apoyo, en caso de que sea necesario.
Cuando muestras empatía, contribuyes en la búsqueda de una solución del tipo ganar-ganar, aun cuando alguna o ambas partes tengan que ceder un poco para hacerlo.
Si practicas la empatía de forma regular, te vuelves más consciente del respeto e incluso, aporta beneficios al desarrollo de tus capacidades de liderazgo, negociación y colaboración, muy útiles en este tipo de situaciones.
Después de escuchar sobre la comunicación asertiva, la escucha activa y la empatía, quizás te preguntes, si habrás desarrollado estas habilidades de forma suficiente.
Se propone que realices un test para identificar qué tan asertivo(a) eres en la forma en que resuelves tus conflictos. Prepara tu libreta o algunas hojas blancas, divide el espacio en tres columnas como se muestra a continuación y copia las siguientes oraciones.
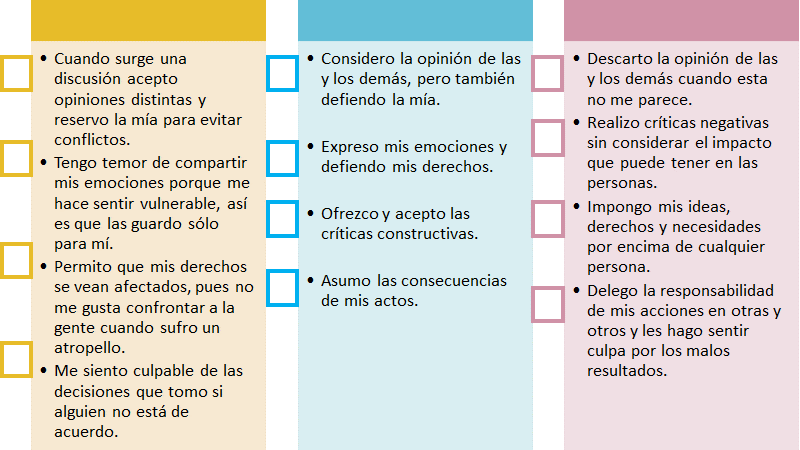
Lee las oraciones, reflexiona sobre ellas y coloca una marca dentro del cuadro de aquellas con las que te identifiques más. Una vez que hayas terminado, identifica en qué columna tuviste mayor puntaje, pasiva, asertiva o violenta.
No te preocupes, si tuviste más puntajes en las columnas de pasiva o violeta, pues puedes comenzar a poner en práctica lo que has aprendido para desarrollar tu asertividad.
Ahora se te invita a que escuches y leas algunas ideas que brindan las y los adolescentes en la sección “La voz de la juventud” para perfeccionar sus habilidades.
“Si alguien comparte conmigo cómo se siente yo debo escuchar con atención, observar sus gestos faciales o sus expresiones corporales y así tratar de comprender mejor lo que está experimentando.” Daniel |
|
|
“Es importante que nos comprometamos a entender lo que nos dicen o lo que la otra persona siente respecto al problema que tenemos.” Fátima. |
|
|
“Si quiero resolver un desacuerdo con alguien, voy a prestar atención a lo que me diga, preguntarle si no lo estoy entendiendo o si no me queda claro a qué se refiere con lo que me dijo, me comprometo a entender todos sus puntos de vista.” Liliana. |
|
|
“Creo que una de las cosas más importantes que debo hacer cuando alguien me está explicando algo, es poner mucha atención y tratar de comprender sus motivos.” Abril Camila. |
|
|
|
Audio 11. “Daana_receptor” “Para resolver un conflicto voy a ser respetuosa de la otra persona y voy a ofrecer la atención que quiero que me presten a mí cuando me toque hablar. Así habrá confianza, respeto y tolerancia.”
|
¿Qué opinas sobre las respuestas que brindaron las y los adolescentes?
Tal vez, debas tomarlas en cuenta, para mejorar en defender tus puntos de vista de forma que también se tome en cuenta tu opinión.
Todas las personas deben perfeccionar sus habilidades para la resolución de conflictos. Quizás, al inicio te cueste trabajo hacer valer tus ideas o no adelantarte a imponer tus puntos de vista, pero lo más importante es que no dejes ningún conflicto sin resolver. Pues, tal vez serían más grandes o provocarían otras situaciones igual de complicadas.
Revisa el siguiente fragmento audiovisual que lo explica a mayor profundidad.
- La provención de los conflictos.
https://www.youtube.com/watch?v=mejtHUw_eo0
Revisa del tiempo 2:02 al 2:29.
Después de haber revisado el video, y ver lo que se menciona sobre la violencia, puedes reafirmar tu idea de que es mejor resolver los conflictos de manera rápida y oportuna. Existen diferentes formas de abordar un diálogo para poder resolver un conflicto.
En algunas ocasiones, serás capaz de negociar y llegar a un acuerdo, en otras, quizá necesites de un tercero que medie para regular la conversación. En ambos casos es importante no olvidar tener una perspectiva asertiva sobre el problema.
Ahora se hará un recuento de lo que revisaste en esta sesión.
Recordaste lo importante que es establecer una comunicación eficaz cuando se quiere resolver un conflicto. Estableciste las características de la comunicación asertiva para evitar malos entendidos.
También te diste cuenta de que escuchar a la otra persona y concentraste en comprender sus puntos de vista es igual de importante que lograr que te escuchen y te entiendan.
En ambos casos el mensaje debe ser claro, coherente y completo, acompañarse de lenguaje no verbal que reafirme la intención, para brindar información adicional y expresar mejor las ideas o sentimientos.
No puedes olvidar que, durante un proceso de resolución de conflicto, la empatía es necesaria, pues contribuye al entendimiento entre partes y te predispone a querer arreglar las cosas.
El Reto de Hoy:
Consulta tu libro de texto e identifica que otras conductas favorecen la asertividad y la empatía. Recuerda ejercitar la escucha activa todos los días al platicar con tu familia.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
La contribución de México al desarrollo de la cosmología
Aprendizaje esperado: Identifica algunos aspectos sobre la evolución del universo.
Énfasis: Conocer algunas aportaciones de científicos mexicanos al desarrollo de la cosmología.
¿Qué vamos a aprender?
Si recuerdas, anteriormente se habló sobre la teoría del Big Bang y el Universo en expansión, y se mencionaron algunos proyectos en los que han participado científicos mexicanos.
En la sesión del día de hoy, se complementará esa información ya que conocerás: algunas de las aportaciones al desarrollo de la cosmología por científicos mexicanos.
¿Qué hacemos?
Esta sesión inicia con la siguiente pregunta: ¿qué sabes sobre la Cosmología?
Como recordarás es la ciencia que se encarga de estudiar el universo, desde su origen, composición y evolución. Se te invita a analizar la información que se presentará a continuación para que amplíes tu conocimiento.
Pero, antes escribe en tu cuaderno las siguientes preguntas y trata de dar una respuesta breve.
Las preguntas son:
- ¿Qué es la cosmología?
- ¿Cuáles fueron las primeras aportaciones de las civilizaciones mexicanas a la cosmología?
- ¿Quién es el Cosmólogo mexicano más reconocido?
Responde las preguntas con las que te sientas más seguro y, a partir de la información que se presentará a continuación, responde las demás.
Como se mencionó anteriormente, la cosmología es la ciencia que se encarga de explicar la composición, evolución y propiedades del universo. Y es así como gracias a esta ciencia sabes cómo fue el universo en el pasado, como es ahora y como será en el futuro.
Para llegar a obtener esos datos, se cuenta con científicos e investigadores, entre ellos algunos mexicanos, que realizan numerosos estudios muy interesantes. Para conocer cuáles fueron esas aportaciones mexicanas a la cosmología se revisará un poco historia.
¿Tienes alguna idea sobre las primeras aportaciones de las civilizaciones mexicanas a la cosmología?
Las civilizaciones mesoamericanas como la maya, azteca o tolteca aportaron algún conocimiento, pues utilizaban el sol, la luna y las estrellas para establecer ciclos en sus actividades, como por ejemplo en la agricultura.
Como se menciona para algunas civilizaciones mesoamericanas el sol es el eje rector del tiempo. Ahora, observa el siguiente video con el que tendrás una idea más clara sobre este tema.
- La física en México.
https://www.youtube.com/watch?v=qc8xAeeqJv8&feature=emb_logo
Revisa del 2:33 al 4:19
Como viste en el video, las culturas mesoamericanas, han aportado elementos a la cosmología, ya que sus observaciones les permitieron conocer el comportamiento de elementos del universo como el sol, con el que marcaban sus tiempos.
En Mesoamérica se diseñaron dos calendarios, uno de 365 días el cual estaba inspirado en los movimientos del sol, y que se denominaba civil o agrícola y otro de 260 días, en el cual las semanas tenían 13 días.
La cosmología ha sido parte importante en la vida de los seres humanos desde hace mucho tiempo. Incluso actividades económicas como la agricultura hoy en día siguen tomando las ideas de esas civilizaciones.
Así como fue evolucionando la vida del ser humano, el conocimiento del universo también fue más estudiado. En el transcurso de los siglos XVI y XVII, la física se hizo presente entre los científicos quienes trataban de entender y explicar algunos fenómenos naturales.
En ese tiempo Fray Alonso de la Veracruz realiza una obra titulada: La Física Speculatio, en la cual se planteaban ideas sobre la física elemental y astronomía, publicada en la Ciudad de México en 1556.
Más tarde el Fraile Diego Rodríguez, quien fuera el primer catedrático de la Real y Pontificia Universidad de México, escribe un libro explicando sus ideas sobre cometas, haciendo énfasis en su origen y composición. Además, desmiente que tengan efectos malos.
Posteriormente, Carlos de Sigüenza y Góngora, en 1690 desarrolla y publica la obra: Libra Astronómica y Filosófica, en la que explica las observaciones que hizo acerca de un cometa que entre 1680 y 1681 fue visto en gran parte del planeta, mencionando también que, los cometas no causaban daños. Ese libro es considerado como el primer libro científico moderno publicado en la entonces Nueva España.
Años más tarde, Andrés Guevara Basoazabal, publicó en 1786 su obra titulada: Pasatiempos de Cosmología, en la cual se manifiesta a favor de la teoría heliocéntrica de Nicolas Copérnico, que dice que los planetas giran alrededor del sol.
En esa obra, Andrés Guevara explicó tres ideas importantes para el: la idea general del universo, la edad del mundo y la figura y extensión del universo. A partir de todos sus estudios y observaciones, él define al universo de la siguiente manera: Vastísima extensión material que encierra todo el complejo de cuerpos que por todas partes se difunden desde la tierra hasta los últimos confines.
Con esta idea, identifica las diferencias que existen entre universo y sistema solar y propone que la vía láctea es solo una parte de todo lo que integra el cosmos.
A partir de esas observaciones el define que: En el cosmos hay muchos cuerpos luminosos, algunos con tamaños mayores al sol del sistema solar y que existía la posibilidad de que cada uno de esos soles era un sistema compuesto por planetas, cometas y lunas.
Con esto plantea la posibilidad de que existan otros planetas en otros sistemas solares que pudieran tener condiciones ideales para la vida.
Estas son algunas de las aportaciones por las cuales Andrés Guevara Basoazabal es considerado como el primer cosmólogo mexicano, precursor de la astronomía moderna.
Continuando con un poco de historia de la cosmología mexicana, en el siglo XIX surge el interés por determinar la posición de los astros y la medición del tiempo.
Uno de los acontecimientos más significativos de ese siglo surge en 1874, Francisco Díaz Covarrubias, organiza una expedición mexicana para viajar a Japón a observar el tránsito de Venus por el Sol. El grupo de investigadores estuvo conformado por Francisco Jiménez, Agustín Barroso, Manuel Fernández Leal y Francisco Bulnes.
La importancia de este fenómeno en el siglo XIX fue que si se observaba de manera muy precisa se podría determinar la distancia entre la tierra y el sol.
Gracias a esas observaciones, pudieron predecir que este fenómeno se presentaría nuevamente en el año 2004 siendo el 8 de junio de ese año cuando se pudo visualizar nuevamente, posteriormente se observó en la República Mexicana el 05 de junio. Observa el siguiente video, para conocer más sobre este tema.
- La física en México.
https://www.youtube.com/watch?v=qc8xAeeqJv8&feature=emb_logo
Revisa del 6:55 al 7:53.
Como pudiste observar en el video, la contribución de científicos mexicanos para el desarrollo de la cosmología desde tiempos muy antiguos ha sido muy importante para el planteamiento de teorías sobre el Universo.
No solo en la historia, sino también en la actualidad siguen estando presentes algunos investigadores y científicos mexicanos en proyectos sobre el estudio del universo, que han ayudado a profundizar más sobre el tema o a plantear nuevas teorías.
Ahora, se hablará de algunos proyectos que, a pesar de ser internacionales. En su equipo profesional cuentan con científicos mexicanos y que además en la actualidad se están desarrollando.
Primero se revisará el proyecto ALICE, ¿recuerdas algo sobre este proyecto?
El proyecto ALICE tiene que ver con el gran colisionador de hadrones. Como recordarás, el gran colisionador de hadrones es un dispositivo que, a través de campos electromagnéticos acelera iones a velocidades cercanas a las de la luz. Como finalidad del Colisionador, se hacen chocar iones con lo que se logra recrear las condiciones a partir de las cuales se originó la gran explosión o Big Bang.
El colisionador de hadrones es una maquina subterránea ubicada a 100 metros bajo tierra que tiene una circunferencia de 27 kilómetros de longitud, que fue diseñado en la Organización Europea de la Investigación Nuclear (CERN por sus siglas en inglés) en la ciudad de Ginebra, Suiza.
Pero ¿qué es el Proyecto ALICE?
El proyecto ALICE es un conjunto de experimentos que tienen como finalidad controlar las reacciones del gran colisionador de hadrones y con ello reproducir los primeros instantes del universo.
¿En qué consiste la participación de los científicos mexicanos en este importante proyecto?
La participación de México y sus investigadores se centra en el desarrollo de dos de los dieciséis dispositivos que conforman al gran colisionador de hadrones: uno es el detector de partículas subatómicas, llamado V0A y el otro es el detector de rayos cósmicos. Para ello, se contó con el gran apoyo del Consejo Nacional de Ciencia y Tecnología de este país.
Tal vez, no imaginabas que este gran desarrollo tecnológico tuviera parte del ingenio de científicos mexicanos para lograr comprender mejor el origen del universo.
Ahora, conocerás algunos aspectos sobre estos dos dispositivos.
El detector de rayos cósmicos (ACORDE, por sus siglas en inglés), es uno de los dispositivos que forman parte del gran colisionador de hadrones y tiene como finalidad detectar los rayos cósmicos de energías muy altas que desde el universo llegan al planeta tierra. Está ubicado a 50 metros de profundidad y las capas de la tierra que están sobre él, le sirven como filtro para que únicamente se puedan captar aquellos rayos de energías altas.

Por su parte, el dispositivo V0A, es un detector de partículas subatómicas, que se encarga de medir cuantas partículas se producen en cada uno de los choques que se provocan en el gran colisionador de hadrones, que se asemeja al dispositivo mostrado a continuación.

Estos dispositivos fueron diseñados por un grupo de investigadores del Centro de Investigación y de Estudios Avanzados que pertenece al Instituto Politécnico Nacional; del Instituto de Ciencias Nucleares de la Universidad Nacional Autónoma de México y de la Benemérita Universidad de Puebla.
¿Recuerdas algo sobre el término energía oscura?
Se le llama energía oscura, porque es una forma de energía que se encuentra en todo el universo y que se cree que está acelerando la expansión del universo debido a la presión que ejerce.
Ahora, se hará referencia acerca del experimento BIGBOSS, el cual tiene como finalidad ayudar a la comunidad científica a encontrar explicaciones sobre la llamada energía oscura, para ello se basan en las oscilaciones acústicas bariónicas y la teoría del corrimiento al rojo.
En este proyecto tienen participación científicos mexicanos que forman parte del Instituto Nacional de Investigaciones Nucleares
Como puedes darte cuenta, México ha aportado importantes datos y herramientas para el desarrollo de la cosmología, con la finalidad de mejorar y ampliar el conocimiento que se tiene sobre el universo, su origen, sus componentes y su evolución.
Se te recomienda que visites la página del Instituto de Astronomía de la Universidad Nacional Autónoma de México, para que indagues más sobre aquellos trabajos de científicos mexicanos que contribuyen al desarrollo de la Cosmología. No olvides apoyarte de tu libro de texto para profundizar en el tema.
Has concluido el tema del día de hoy.
El Reto de Hoy:
Se te invita a reunirte con tu familia para que reflexionen acerca de las interrogantes que se plantearon al inicio de la sesión, las cuales fueron:
- ¿Qué es la cosmología?
- ¿Cuáles fueron las primeras aportaciones de las civilizaciones mexicanas a la cosmología?
- ¿Quién es el Cosmólogo mexicano más reconocido?
A partir de la información que aquí se presentó y con otra que obtengas de fuentes de información confiables amplía, corrige o responde las preguntas de manera correcta.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario