Aprende en Casa III SEP: 22 de febrero TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 22 de febrero de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Lunes 22 de febrero, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en Casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Proporcionalidad directa III
Aprendizaje esperado: Analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.
Énfasis: Analizar y comparar situaciones de proporcionalidad directa a partir de sus representaciones tabular, gráfica y algebraica.
¿Qué vamos a aprender?
Continuarás con el estudio de proporcionalidad directa. En esta sesión, analizarás situaciones para la resolución de problemas a partir de sus representaciones algebraica, tabular y gráfica.
¿Qué hacemos?
Reflexiona sobre los siguientes planteamientos:
- ¿Es posible identificar en una fórmula de física, si las variables están relacionadas a través de la variación directa?
- ¿Qué condiciones deben de cumplirse para que una expresión algebraica modele una situación de proporcionalidad directa?
- ¿Cómo es la gráfica de una relación de proporcionalidad directa?
Registra tus reflexiones. A través de diversas situaciones y problemas, construirás las respuestas a éstas y otras preguntas.
Para iniciar con el tema de esta sesión, considera lo siguiente: ¿qué pesa más, un kilogramo de algodón o un kilogramo de plomo?, ¿cuál ocupa más espacio?
1 kilogramo de algodón pesa lo mismo que 1 kilogramo de plomo, pero dependiendo del material, puede ser una misma cantidad de masa. Por ejemplo, 1 kilogramo de algodón puede ocupar más espacio que 1 kilogramo de plomo si no se comprime, o menos espacio si está comprimido.
Ahora, analiza:
¿Qué ocupará más espacio, un centímetro cúbico de corcho o un centímetro cúbico de plomo?, ¿cuál pesará más?
Responde las preguntas anteriores y justifica tus respuestas.
Un centímetro cúbico de corcho ocupa la misma cantidad de espacio que un centímetro cúbico de plomo. Sin embargo, un centímetro cúbico de plomo tiene una masa mayor; por lo tanto, el plomo pesa más. Pero ¿por qué sucede esto?
La cantidad de masa de un material que cabe en una unidad de volumen se llama densidad. La densidad del plomo es de:

Esto significa que la masa de un centímetro cúbico de plomo es 11.3 gramos.
Por otro lado, la densidad del aluminio es de:

Y la del agua:
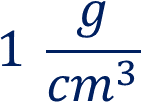
Ahora, presta atención a la siguiente información, pues te servirá para resolver las situaciones-problema que se presentarán más adelante.
Si “m” representa la masa y “v” el volumen, la expresión algebraica de la densidad "D" es la siguiente:

Reflexiona en torno a las siguientes preguntas:
¿Qué pasa con la densidad si el volumen aumenta y la masa permanece igual?
¿Qué pasa con el volumen si la masa aumenta y la densidad es la misma?
Registra tus ideas. Conforme avances en la sesión podrás fortalecerlas o modificarlas.
Ahora, toma como referencia lo anterior y analiza la siguiente situación de proporcionalidad directa, a partir de sus representaciones algebraica, tabular y gráfica.
Relación masa-volumen
Completa la siguiente tabla de datos que permite relacionar la masa y el volumen para distintas cantidades de aluminio.

Primero, calcula la masa que hay en un centímetro cúbico. Para ello, considera el valor de la densidad del aluminio, que tomará el valor de la constante de proporcionalidad “k”, y éste es igual a:

La expresión para calcular la segunda magnitud en una proporcionalidad directa “y”, es igual a la constante de proporcionalidad “k”, por su correspondiente de la primera magnitud “x”; por lo tanto, si se necesita encontrar la masa de un centímetro cúbico de aluminio, se puede recurrir a la siguiente fórmula:
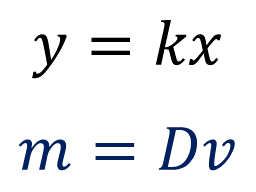
Sustituyendo los datos en la fórmula se tiene que:
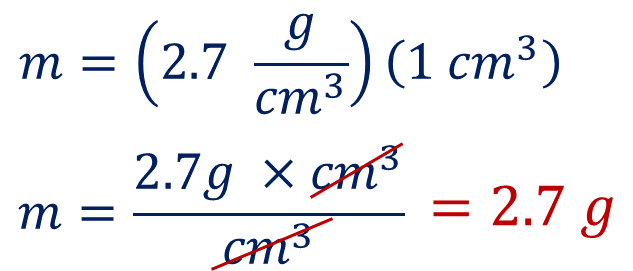
Por lo tanto, se obtienen 2.7 gramos.
Ahora, determina el volumen que ocupa una masa de 13.5 gramos.

¿Qué piensas que se necesita realizar para determinar el volumen que ocupa una masa de 13.5 gramos?, ¿qué dato o datos de los que ya se tienen se deben considerar para este cálculo?
Para calcular el volumen que hay en una masa de 13.5 gramos, utilizarás el valor de la densidad del aluminio, que tomará el valor de la constante de proporcionalidad “k”, es decir:

La expresión para calcular la primera magnitud en una proporcionalidad directa “x” es igual a la segunda magnitud “y” entre la constante de proporcionalidad “k”; por lo tanto, si se quiere encontrar el volumen de una masa de 13.5 gramos de aluminio, se puede utilizar la siguiente fórmula:
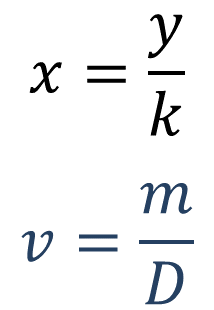
Sustituyendo los datos en la fórmula se tiene que:
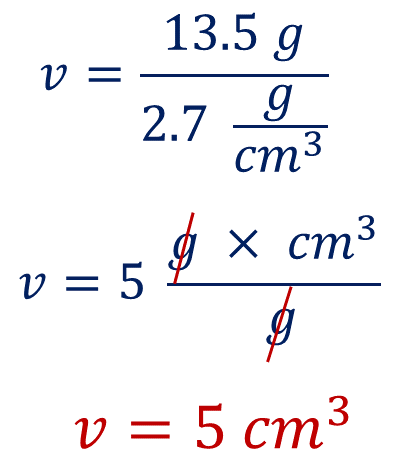
Por lo tanto, 13.5 gramos de masa ocupan 5 centímetros cúbicos.
Continúa con la masa que hay en 10 centímetros cúbicos.

¿Ya pensaste en alguna forma de hacerlo?, ¿cómo ocuparías la densidad del aluminio para realizar el cálculo que se necesita?
Para calcular la masa que hay en 10 centímetros cúbicos, lo primero que necesitas hacer es tomar el valor de la densidad del aluminio como el valor de la constante de proporcionalidad “k”, que es igual a:

Para calcular la segunda magnitud en una proporcionalidad directa, “y” es igual a la constante de proporcionalidad “k” por su correspondiente de la primera magnitud “x”; por lo tanto, si se quiere encontrar la masa de 10 centímetros cúbicos de aluminio, se puede utilizar la siguiente fórmula:
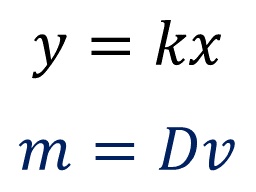
Sustituyendo los datos en la fórmula se tiene que:

Obteniendo 27 gramos, que corresponden a la masa que hay en 10 centímetros cúbicos de aluminio.
Finalmente, en la tabla falta el dato del volumen que corresponde a una masa de 32.4 gramos de aluminio.

Con lo trabajado hasta el momento, contesta lo siguiente: ¿qué se puede hacer para calcular ese dato?
Para calcular el volumen que hay en una masa de 32.4 gramos, usarás el valor de la densidad del aluminio, que tomará el valor de la constante de proporcionalidad “k” y que es igual a:

La expresión para calcular la primera magnitud en una proporcionalidad directa “x” es igual a la segunda magnitud “y” entre la constante de proporcionalidad “k”; por lo tanto, si se quiere encontrar el volumen de una masa de 32.4 gramos de aluminio, se utiliza la siguiente fórmula:

Sustituyendo los datos en la fórmula se tiene que
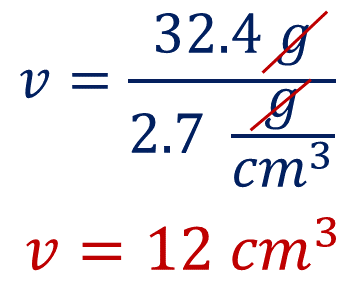
Obteniendo 12 centímetros cúbicos. Esto permite afirmar que una masa de 32.4 gramos de aluminio tiene un volumen de 12 centímetros cúbicos.
Has completado la tabla con una relación entre masa y volumen para distintas cantidades de aluminio. Ahora encuentra los puntos coordenados o coordenadas en una tabulación y represéntalas de forma gráfica.
En la tabla, cada punto coordenado se nombra utilizando letras mayúsculas y colocando dentro de un paréntesis los valores ordenados de “x” y de “y”. Por lo tanto, en la primera columna se anotan los valores de “x” que representan el volumen en centímetros cúbicos del aluminio; en la segunda columna se registran los valores de “y”, es decir, la masa del aluminio, y en la tercera columna, los puntos coordenados o coordenadas que están definidos como:
Punto "A" (1, 2.7)
Punto "B" (5, 13.5)
Punto "C" (10, 27)
Punto "D" (12, 32.4)
Con la información anterior, la tabla queda de la siguiente manera:

Ahora, traza la gráfica de la relación masa-volumen. En el eje horizontal se representa el volumen en centímetros cúbicos; en el eje vertical se representa la masa en gramos. Entonces, se ubican las coordenadas “x” y “y” que se obtuvieron en la tabulación.
Ubica el punto "A" (1, 2.7); la coordenada "B" (5, 13.5); la coordenada "C" (10, 27); y finalmente, la coordenada "D" (12, 32.4)
Ya que están ubicados los puntos, traza una línea que pase sobre los puntos identificados con su correspondiente letra mayúscula, como se muestra en la siguiente imagen.
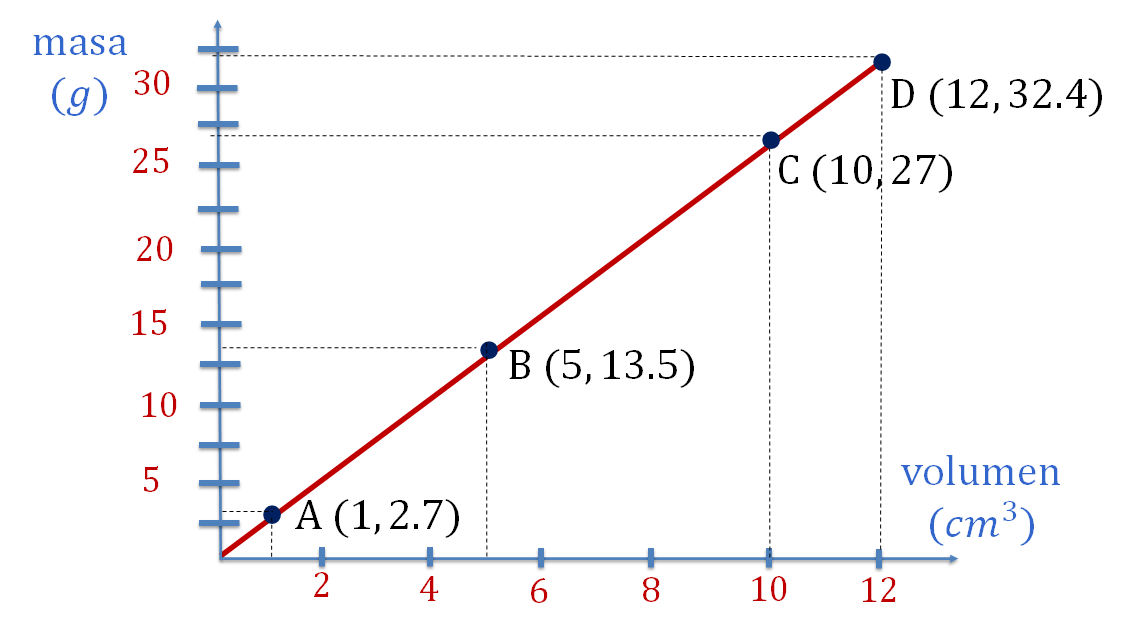
Ya tienes la representación gráfica de la relación masa-volumen.
De esta manera, se puede confirmar que los datos del planteamiento se relacionan a través de una proporcionalidad directa, porque las dos magnitudes son directamente proporcionales. Es decir, cuando una de ellas aumenta, la otra también y lo hace en la misma proporción, o si una disminuye, la otra también en la misma proporción.
Al observar la gráfica, las coordenadas "A" y "B" tienen una proporción directa, el valor de “x” en la coordenada "A" es igual a 1 y en la coordenada "B" es igual a 5, hubo un aumento de 5 veces; esta proporción se ve reflejada en el valor de “y”, donde en la coordenada "A" es igual a 2.7 y aumenta cinco veces en la coordenada "B", que es igual a 13.5
Para reforzar lo aprendido hasta el momento, analiza la siguiente situación-problema.
Relación tiempo-radio
Si se lanza una piedra a un estanque:
- ¿Qué sucede?
- ¿Alguna vez has arrojado una piedra el agua?
- ¿Qué se forma?
Cuando se lanza una piedra a un estanque se forman círculos concéntricos en la superficie del agua. El radio (r) del círculo mayor está dado por (r = 0.6 t), donde “t” es el tiempo transcurrido, en segundos, a partir de que la piedra se lanza y hasta que toca el agua. La expresión resultó después de experimentar varias veces el lanzamiento.

- ¿Esta situación corresponde a una relación de proporcionalidad directa?
- ¿Cuál es el radio del círculo mayor si la piedra tarda en chocar 4, 6 y 10 segundos en el agua?
Para contestar lo anterior, utilizarás la siguiente expresión o fórmula:
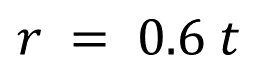
Donde:
r: representa el radio del círculo que se forma cuando la piedra choca en el agua, medido en centímetros.
t: el tiempo en segundos, que transcurre desde que la piedra se lanza, hasta chocar con el agua.
Sustituyendo los datos, se obtienen los siguientes valores:
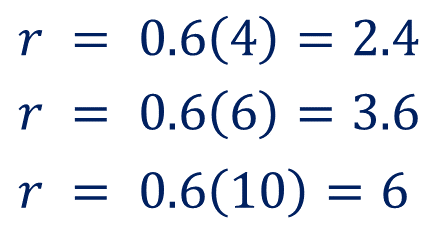
Esto quiere decir que cuando la piedra tarda 4 segundos en chocar con el agua, forma un círculo con radio igual a 2.4 cm; cuando tarda seis segundos forma un círculo con radio igual a 3.6 cm. Y cuando la piedra choca con el agua después de 10 segundos, forma un círculo con un radio igual a 6 centímetros.
Continúa ahora con la gráfica de esta situación.
En la tabla de la relación tiempo-radio, a cada punto se le nombrará utilizando letras mayúsculas y colocando dentro de un paréntesis los valores ordenados de “x” y de “y”. Recuerda que siempre el primer valor será el de las abscisas o de las “x”, y el segundo valor será el de las ordenadas o de las “y”
Por lo tanto, en la primera columna se anotan los valores de “t”, que representa el tiempo que transcurre desde que se lanza la piedra y hasta que choca con el agua, sus unidades están dadas en segundos. En la segunda columna se registran los valores de “r”, que corresponden al radio del círculo que se forma cuando la piedra choca en el agua, medido en centímetros. Por último, en la tercera columna se colocan los puntos coordenados o coordenadas que están definidos como:
Punto "A" (4, 2.4)
Punto "B" (6, 3.6)
Punto "C" (10, 6)
Con esta información, la tabla queda de la siguiente manera:
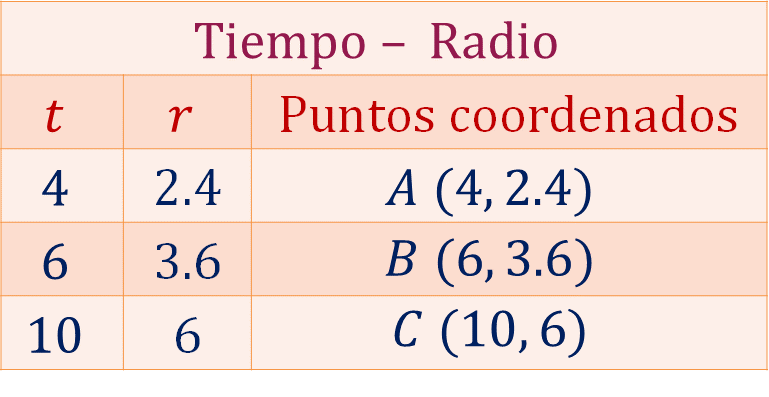
Ahora, traza la gráfica radio-tiempo. En el eje horizontal se encuentra el tiempo en segundos, en el eje vertical se tiene al radio en centímetros.
Ubica las coordenadas (x, y) que se obtuvieron de la tabla. Inicia con el punto "A" (4, 2.4); sigue con el punto "B" (6, 3.6); finalmente, ubica el punto "C" (10, 6).
Ya que están ubicadas las coordenadas, traza una línea que pase sobre los puntos identificados con su correspondiente letra mayúscula, como se muestra en la siguiente imagen.

Ya tienes la representación gráfica de una proporción directa tiempo-radio.
Reflexiona: ¿qué se debe observar en la gráfica para afirmar que esta es una situación de proporcionalidad directa?
Ahora, continúa con otra situación.
Relación pesos mexicanos-dólares
Analiza la siguiente gráfica que muestra la relación que existe entre los pesos mexicanos y los dólares.

La gráfica de la relación pesos-dólares, muestra en el eje horizontal o eje de las abscisas a los dólares, en el eje vertical o eje de las ordenadas a los pesos; por lo tanto, un punto coordenado o una coordenada es representada con un valor del eje “x” dólares y otro del eje “y” pesos. Piensa si esta situación es de proporcionalidad directa e identifica en la gráfica lo que te permita realizar tu afirmación.
- La primera coordenada mostrada en la gráfica es el punto "A" (40, 820).
- La segunda coordenada ubicada en la gráfica es el punto "B" (100, 2050).
Ya ubicados las coordenadas, traza una línea que pase sobre los puntos identificados, como se muestra en la siguiente imagen.
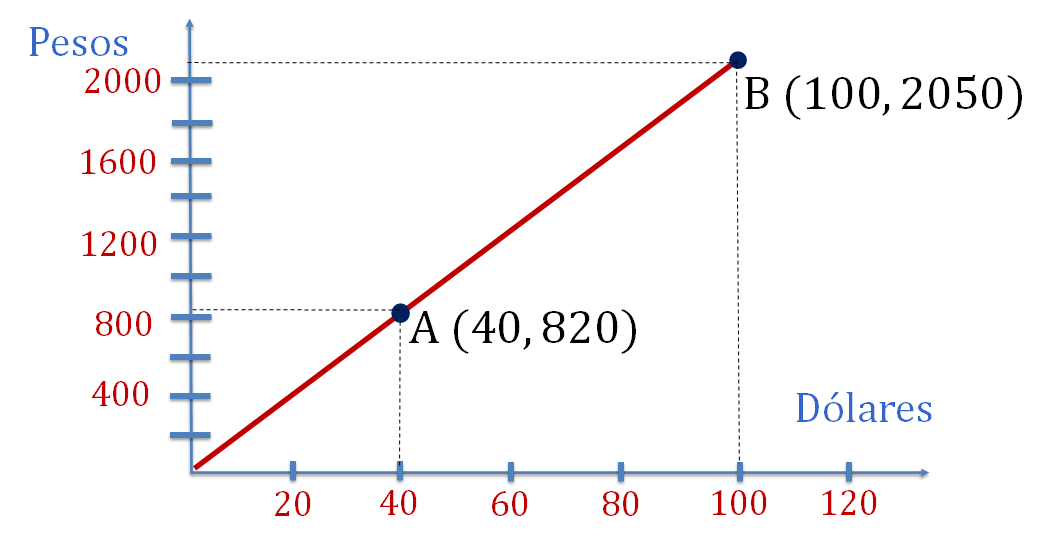
Ya tienes la representación gráfica de una proporción pesos-dólares.
Ahora, analiza las siguientes preguntas:
¿Qué datos se pueden obtener a partir de esta gráfica, viendo sus características?, ¿puedes decir si corresponde a una situación de proporción directa?, ¿sería posible encontrar una expresión que modele esta situación?
Al realizar la división de la ordenada entre la abscisa con cualquiera de las dos parejas de valores (coordenadas), se obtiene un valor. ¿Qué representa el cociente obtenido?
Como lo has estudiado, si se divide un número de la segunda magnitud “y” entre su correspondiente en la primera magnitud “x”, se obtiene la constante de proporcionalidad, en este caso, el costo de un dólar.
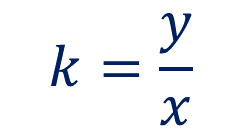
Tomando en cuenta las dos coordenadas, lo primero que harás será completar una tabla de la siguiente forma: coordenada "A" (40, 820), el primer valor de la coordenada representa los dólares y el segundo valor su equivalencia en pesos, por lo tanto, cuarenta dólares equivalen a ochocientos veinte pesos.
Para la coordenada "B" (100, 2050), el primer valor de la coordenada representa los dólares y el segundo valor su equivalencia en pesos, por lo tanto, cien dólares equivalen a dos mil cincuenta pesos.

La constante de proporcionalidad se calcula dividiendo el número de la segunda magnitud, “y”, entre su correspondiente en la primera magnitud, “x”.
Empieza con la sustitución de los valores de la primera fila

Por lo tanto “k” es igual a 20.5
Continúa con la segunda fila

Se obtiene el valor: “k” igual a 20.5.
De este modo, se puede afirmar que los valores de la gráfica representan un problema de proporcionalidad directa ya que al dividir cada número de la segunda magnitud “y” entre su correspondiente en la primera magnitud “x”, se obtiene el mismo número, es decir, los cocientes son constantes.
Reflexiona:
¿Cuál es la expresión algebraica o fórmula que permite convertir los dólares a pesos mexicanos?
Al tomar en cuenta la constante de proporcionalidad que se obtuvo en el inciso anterior, “k” es igual a 20.5 y recordando que en las sesiones anteriores se estableció la expresión para calcular la segunda magnitud en una proporcionalidad directa como:

Se puede afirmar que la expresión algebraica que corresponde a esta situación es:
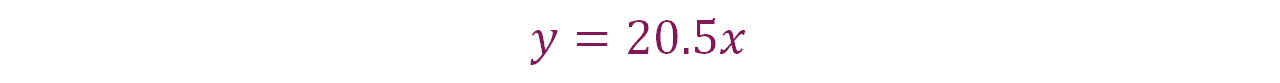
Donde:
y: es la cantidad en pesos.
x: la cantidad en dólares.
Después de haber obtenido la expresión algebraica para convertir los dólares americanos a pesos mexicanos, ¿cuántos pesos mexicanos equivalen a trescientos veinte dólares americanos?
Tomando en cuenta la expresión algebraica, “y” es igual a 20.5 por el valor de la primera magnitud, se puede calcular la equivalencia de los trescientos veinte dólares a pesos mexicanos.
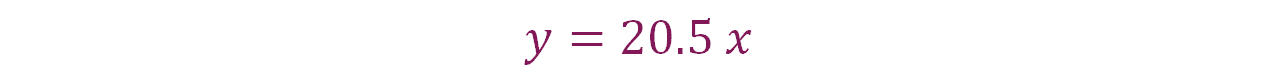
Sustituye los datos:
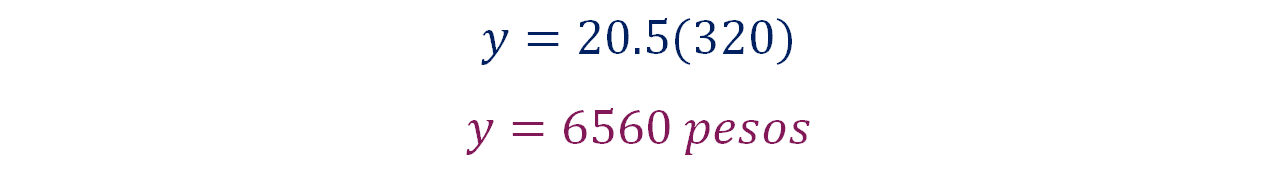
Por lo tanto, se obtiene que “y” es igual a 6,560 pesos.
Entonces, ¿esta situación es de proporcionalidad directa?
La relación pesos mexicanos y dólares americanos, están relacionados a través de la proporcionalidad directa.
Has finalizado. En esta sesión, analizaste situaciones de proporcionalidad directa, a partir de sus representaciones algebraica, tabular y gráfica para la resolución de problemas. Ejemplo de ello fueron: a mayor volumen, mayor masa, el radio de un círculo después de que choca una piedra en el agua y la conversión de dólares a pesos mexicanos.
El Reto de Hoy:
Resuelve algunos de los problemas o ejercicios sobre proporcionalidad directa de tu libro de texto de Matemáticas, de segundo grado.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Juguemos con las palabras haciendo poesía
Aprendizaje esperado: Crea textos poéticos con formas gráficas.
Énfasis: Generar interpretaciones de textos poéticos con distintas formas gráficas.
¿Qué vamos a aprender?
En esta sesión, conocerás cómo crear interpretaciones de textos poéticos con distintas formas graficas. Para ello, analizarás, examinarás y comprenderás detalladamente la interpretación de un poema, utilizando diversas estrategias.
¿Qué hacemos?
Reflexiona en la siguiente información.
¿Sabías que los poemas se basan principalmente en imágenes? Escribir un poema es como pintar con palabras.
Para escribir un poema no necesitas usar palabras complicadas. Se trata de hablar de tus sentimientos a partir de la creatividad con la que puedas usar las palabras que conoces.
Por ejemplo, un plato parece un simple y aburrido objeto, pero si lo observas con más detenimiento, lo puedes transformar en algo diferente: en una moneda, en el Sol, en la rueda de una carreta o en la salida de un túnel.
Ahora, si se agrega otro elemento, por ejemplo, un tubo de metal debajo del plato: ¿qué es lo que ves?
Podrían ser algunas imágenes como la rendija de la alcancía por la que va a entrar la moneda, el horizonte que se extiende debajo del Sol poniente, el camino sobre el que gira la rueda de la carreta o el tren que se aproxima a gran velocidad hacia la salida del túnel.
El mundo está lleno de objetos y escenas que se pueden transformar con la imaginación. Ahora, para dar el toque final, realiza lo siguiente:
Traza un círculo en tu cuaderno, puedes usar un plato pequeño para que te salga bien, y escribe las siguientes palabras alrededor del círculo:
“Destella y brilla, anuncia la vida y verá nuestro fin”.
Después, borra el círculo y sólo quedarán las palabras que describen poéticamente al Sol.
Este es un poema-dibujo y recibe el nombre de caligrama. En esta sesión, aprenderás a interpretar varios tipos de poemas de ésta y otras clases.
La poesía es una de las manifestaciones literarias más bellas y antiguas. Desde la primaria en algún momento has leído poemas. ¿Recuerdas alguno?, ¿cómo eran?
Seguramente has aprendido que algunos están escritos en verso, son melódicos y cuentan con rimas. Pero hay muchas formas de hacer poesía; ¿qué pasaría si jugaras con esas formas?
Para responder lo anterior, debes tener en cuenta que el arte es una manera en que el ser humano satisface su necesidad de expresarse y que puede cambiar y transformarse con el tiempo, influida por el contexto. Eso sucede con la poesía figurativa, concreta o visual, es decir, aquella que al escribirse recurre a nuevas formas. Observa un ejemplo de esto:

Al momento de interpretar un texto, no olvides hacer las siguientes preguntas:
- ¿Observas la forma que tiene?
- ¿Cuál es el sentimiento que predomina en los versos?
- ¿Qué características tiene el hablante lírico, es decir, la voz ficticia que se expresa en el poema?
Durante el siglo XX, muchos artistas buscaron nuevas maneras de plasmar sus emociones. En la actualidad se pueden encontrar e interpretar muchos de los poemas originales que cambiaron el panorama cultural del siglo pasado. Pero ¿qué significa “interpretar”?
Interpretar:
Del latín interpretatio, es la acción y efecto de interpretar. Se refiere a explicar o declarar el sentido de algo, traducir de una lengua a otra, expresar o concebir la realidad de un modo personal, ejecutar o representar una obra artística.
Por lo tanto, interpretar es explicar, a partir de la perspectiva personal, algún suceso, obra de arte o acto comunicativo. En este caso, se buscará explicar el sentido de algunos poemas y desentrañar su significado profundo, es decir, descubrirás las emociones e ideas que esos poemas buscan transmitir.
Antes de profundizar en el tema, analiza la definición de poesía.
Poesía:
La poesía es un género literario que se caracteriza por ser la más depurada manifestación, por medio de la palabra, de los sentimientos, emociones y reflexiones que puede expresar el ser humano en torno a la belleza, el amor, la vida o la muerte. Como tal, puede estar compuesta tanto en verso como en prosa.
En la poesía se utiliza un lenguaje figurado y el escritor puede apoyarse de figuras literarias interpretadas por el lector. Para tener un mayor conocimiento sobre éstas, observa el siguiente video del minuto 2:25 al 3:54.
- Lenguaje literal y figurado en la poesía.
https://youtu.be/uuPD36vkxPE
Un ejemplo de una metáfora puede ser “La flor de la vida”, que hace referencia a la juventud. Y ejemplo de la comparación puede ser: “Sus ojos son como dos luceros”.
Ahora, para poder interpretar los textos poéticos, tienes que saber en qué consisten. Observa la siguiente imagen que menciona su función.
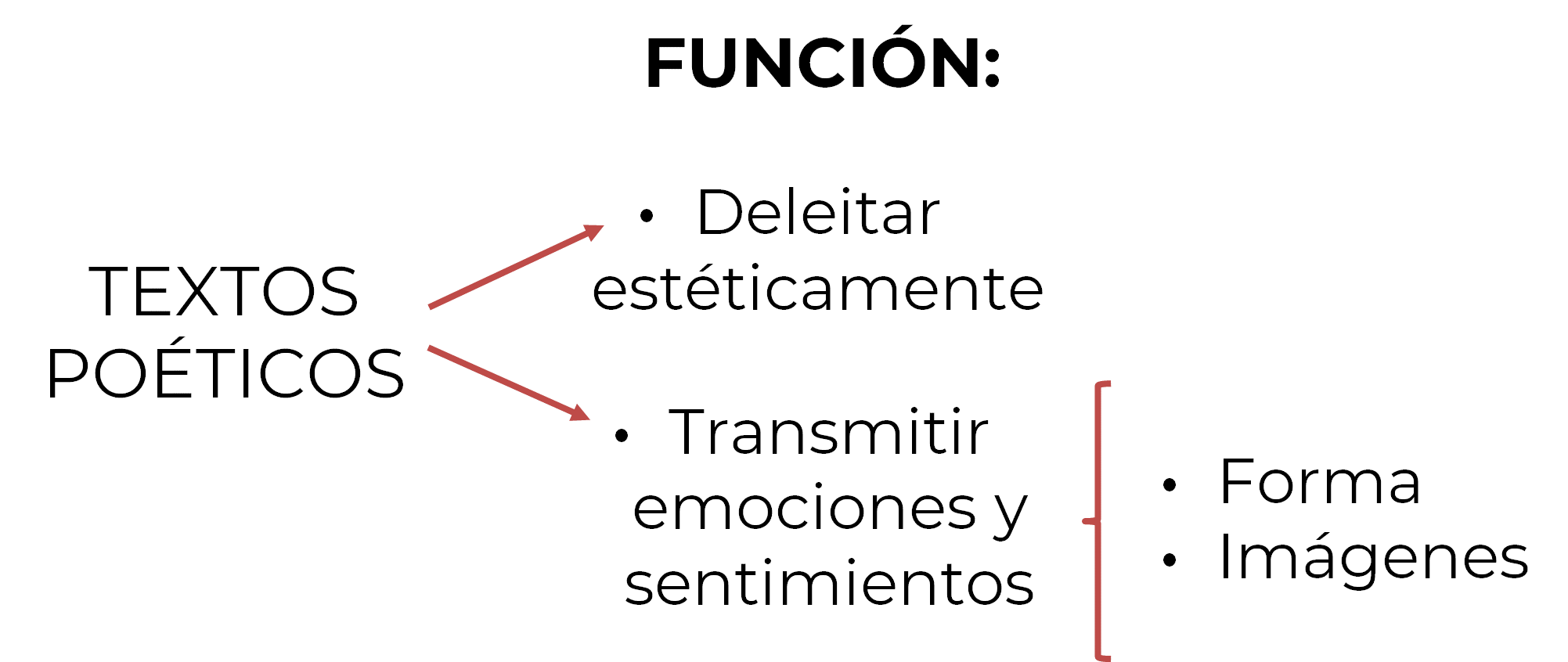
Los textos poéticos tienen la función de deleitar estéticamente y transmitir sentimientos y emociones. Todo esto se logra a partir de la forma en la que se presentan las palabras y de las imágenes que éstas evocan en la mente.
Entonces, cuando se analiza la forma de un poema, se tiene que considerar lo que dice y cómo lo dice. Por ejemplo, la forma considera la sonoridad, el ritmo y el verso, al que no todos los poemas recurren.
Un poema en el que la sonoridad es muy importante es, “En el silencio, sólo se escuchaba un susurro de abejas que sonaba”, la repetición de la letra “s” simula el zumbido de las abejas. Además, tiene ritmo y verso. El poema es de Garcilaso de la Vega.
Continúa con los poemas gráficos. Para ello, presta atención a la siguiente información.
Texto poético gráfico:
Es aquel que utiliza recursos estilísticos para transmitir emociones y sentimientos respetando el estilo del autor.
Ahora, observa las siguientes imágenes:
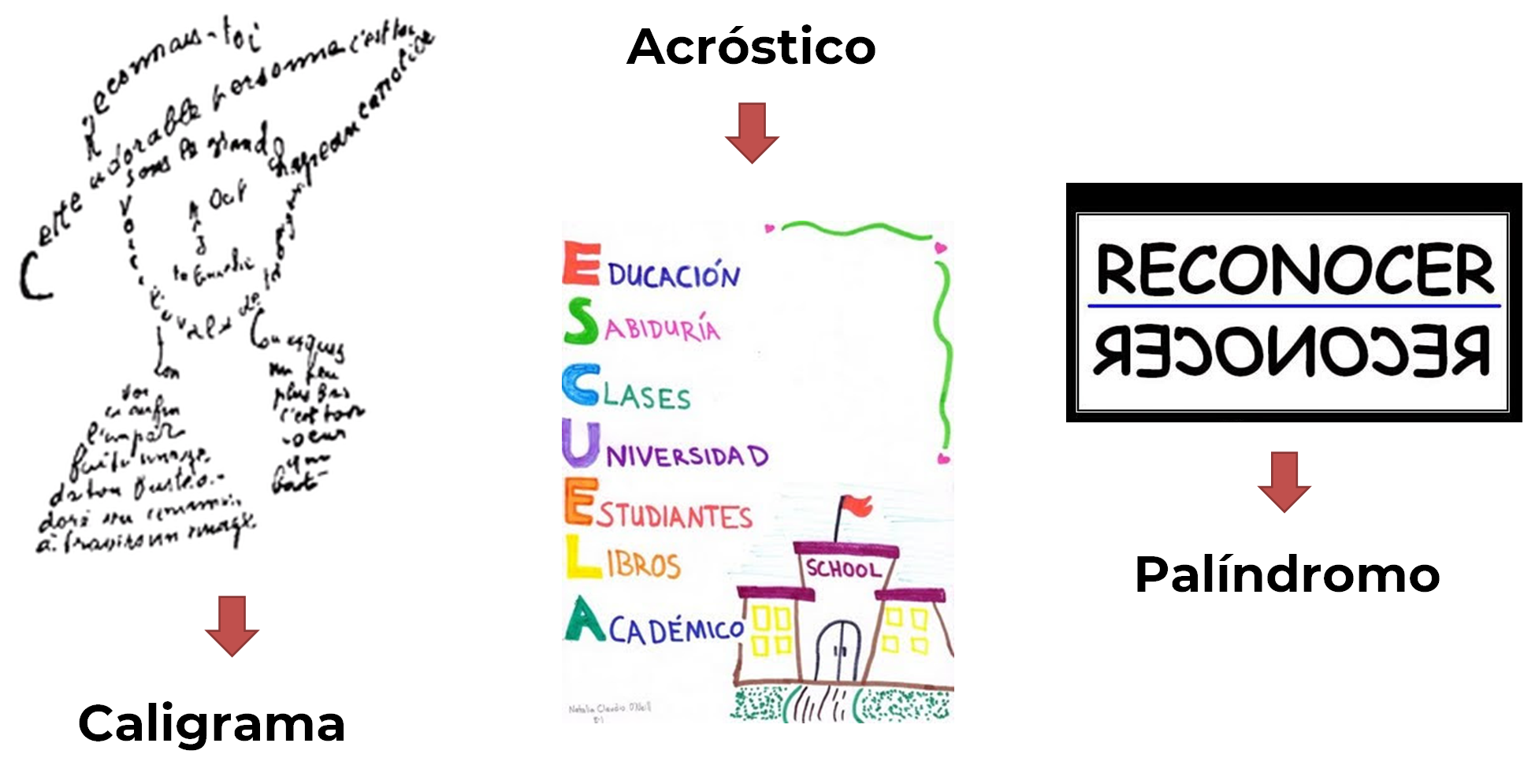
Estos son tres textos poéticos y cada uno tiene una forma diferente, y se les conoce como caligramas, acrósticos y palíndromos.
Los caligramas formaron parte de un movimiento literario llamado “vanguardismo”. La poesía vanguardista aporta una mayor libertad de creación al romper con las normas de escritura establecidas. Los poetas imprimieron en la poesía una reflexión del entorno social ante un mundo que cambiaba vertiginosamente. No sólo utilizaban el significado de las palabras y los recursos poéticos, también otorgaron importancia a la parte gráfica del poema.
Una de las corrientes vanguardistas es la poesía concreta y ésta es importante para la interpretación de los poemas. Observa la siguiente imagen.

La imagen es un ejemplo de poesía concreta y es un género de la poesía. Surge a mediados del siglo XX y se diferencia de la poesía tradicional, ya que no solamente busca que las palabras suenen en rima poética, sino que se formen figuras con ellas o se distribuyan de alguna forma sobre la hoja en donde se escriben; de esta forma, el autor de la poesía concreta añade más elementos visuales para que el lector pueda apreciar la obra que se encuentra ante sus ojos.
La principal característica de esta poesía es la creación de figuras utilizando las palabras para lograrlo. La repetición y los tipos de letra enriquecen la obra, ya que las palabras, sin su ubicación espacial, carecen de sentido o no dan el impacto que el poeta quiere causar.
Para profundizar en lo anterior, analiza los tipos de poesía concreta.
Visual:
Es una disposición de texto y elementos visuales que puede incluir símbolos e imágenes.
Háptica:
Combina la tipografía con las formas artísticas tridimensionales, como la escultura, para crear una obra que puede ser tocada, vista y leída.
Ahora, observa el siguiente video en el que aparecen algunos poemas visuales.
- Video. Palíndromo, acróstico y caligrama.
El caligrama es una disposición tipográfica que esboza figuras alusivas al tema tratado y fue utilizado por poetas vanguardistas, como Guillaume Apollinaire, José Juan Tablada u Octavio Paz; estos últimos, mexicanos.
Guillaume Apollinaire, poeta francés, tuvo una influencia decisiva en la formación de las vanguardias de principios de siglo XX. Leer los caligramas de Apollinaire por primera vez es semejante a presenciar el vuelo de miles de libélulas sobre el bosque.
Otro texto poético es el acróstico. Es una composición poética constituida por versos cuyas letras iniciales, medias o finales forman un vocablo o frase y fue utilizada en el siglo XV por el autor Alfonso Reyes Ochoa, quien fue un poeta, ensayista, narrador, traductor, humanista, diplomático y pensador mexicano. Se le conoce también como el Regiomontano Universal.
Y, por último, el palíndromo, es una frase cuyas letras están dispuestas de tal manera que resulta ser la misma al leerse de izquierda a derecha que de derecha a izquierda, donde destaca el autor Juan José Arreola. Hablar de Arreola es hablar de un mundo de referencias literarias universales; es evocar la pasión por el lenguaje en su máxima posibilidad expresiva.
Ya conociste algunos poetas y con los ejemplos que observaste en el video, a simple vista sólo se ven palabras, sin embargo, para entender el sentido del poema, debes descubrir la imagen que se revela a partir de la disposición de los vocablos.
A continuación, interpreta algunos de los caligramas de Apollinaire que aparecieron en el video anterior. Retoma el caligrama que le dedicó a Lou, la mujer de la que estaba enamorado. Para interpretarlo debes tomar en cuenta cuatro elementos principales:
- La distribución de las palabras.
- La imagen que esas palabras componen.
- El sentimiento que el poeta está tratando de transmitir.
- El significado metafórico que se desprende de la unión de las palabras y la imagen.
Recuerda que todos los poemas revelan el estado de ánimo del poeta, sus emociones y su forma de percibir el tema sobre el que está hablando.
Ahora, interpreta parte por parte el caligrama de Apollinaire en el que aparece una mujer con un sombrero.
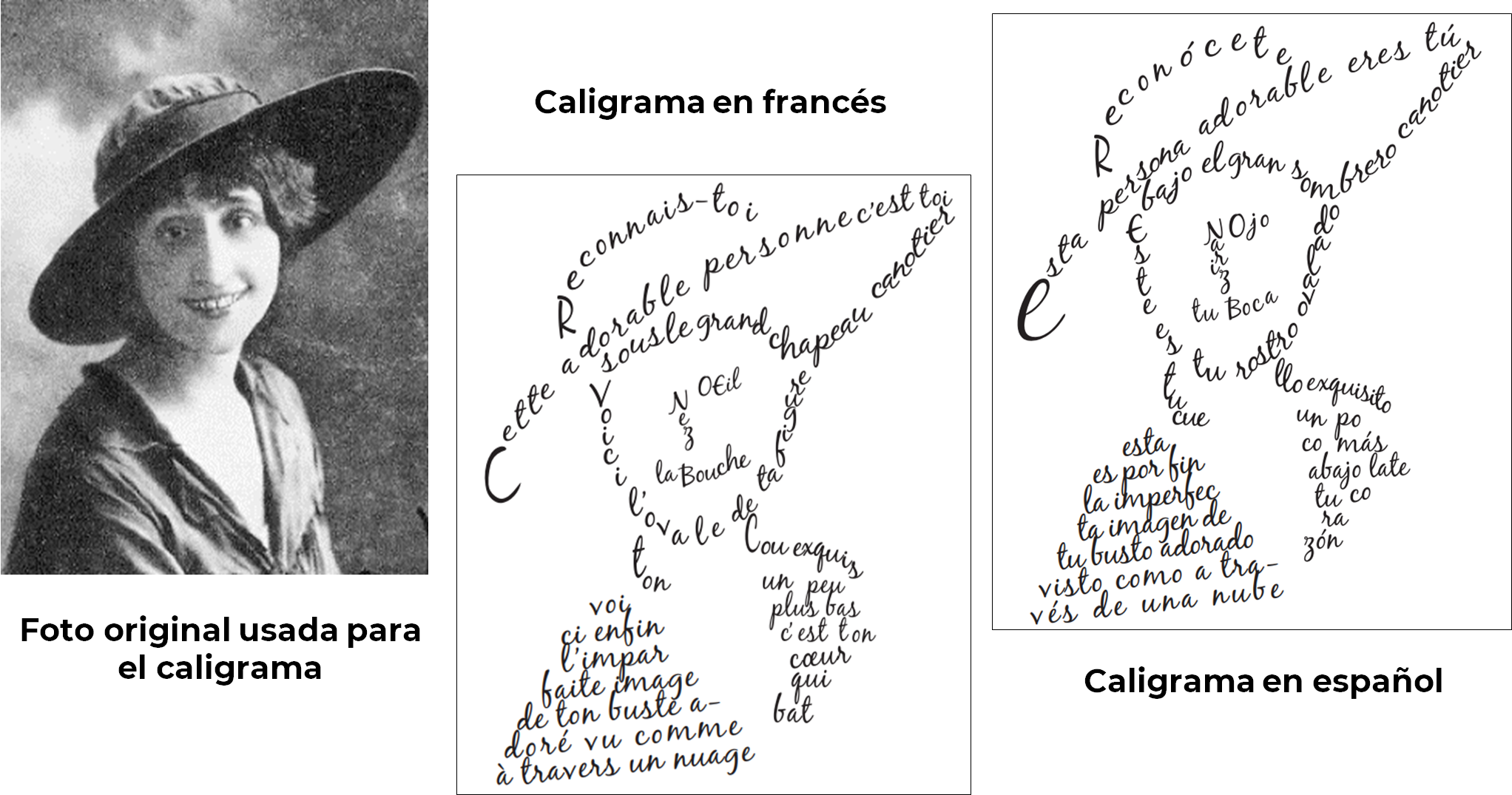
De izquierda a derecha se pueden ver tres imágenes, la primera es una foto; es con la que se basa el poeta para realizar su caligrama. La segunda imagen es la distribución de las palabras en francés; se puede notar que éstas delinean las partes del rostro, el sombrero y parte de la blusa. La distribución de las palabras y la imagen están íntimamente ligadas. Y la tercera imagen, es la traducción del caligrama.
Es importante saber que, muchas veces, al traducir un poema, el reto es grande, pues hay palabras o juegos de palabras que no existen de un idioma a otro, por lo que se requiere de ingenio y no perder la esencia del poema.
Lo que dice el poema en español, es lo siguiente:
“Reconócete esta persona adorable eres tú
Bajo el gran sombrero canotier
Ojo
Nariz
Tu boca
Este es tu rostro ovalado
Esta es por fin la imperfecta imagen de tu busto adorado visto como a través de una nube
Tu cuello exquisito
Un poco más abajo late tu corazón”.
Al escribir ese caligrama, Apollinaire quería garantizarle a Lou (la mujer de la foto) que, cada vez que pensaba en ella, la imagen de su rostro aparecía en su mente y esa remembranza despertaba en él las emociones que expresó.
Lo más interesante es que cada parte del caligrama o gran parte de él dibuja, y a la par se lee. Observa los aspectos resaltados en la siguiente imagen.

Es así como puedes observar que, por ejemplo, las palabras “ojo, nariz y tu boca” forman efectivamente esos aspectos de la cara; lo mismo pasa con “tu cuello” o cuando escribe “tu corazón”.
Ahora, analiza e interpreta otro caligrama, el del corazón.

La flecha está conformada por letras mayúsculas y minúsculas. El centro de la flecha está esbozado con mayúsculas y los detalles, las plumas y la punta, con minúsculas. En el corazón quedan reunidos el poeta y Lou, pues al inicio del trazo que delinea el corazón, aparece él y ella lo hace al final. En la flecha sólo aparece Lou, quien atravesó el corazón del poeta.
Metafóricamente, se pueden apreciar las dos facetas del amor: la felicidad y el sufrimiento. El amor es agridulce.
Finalmente, analiza un poema del cubano Guillermo Cabrera Infante, que se incluye en el libro Tres tristes tigres; presta atención.

Para que lo puedas interpretar debes tomar en cuenta los siguientes elementos:
- La distribución de las palabras.
- La imagen que esas palabras componen.
- El sentimiento que el poeta está tratando de transmitir.
- El significado metafórico que se desprende de la unión de las palabras y la imagen.
Recuerda analizar, es decir, examinar y comprender detalladamente el poema. La interpretación de un poema se trata de reconocer el sentido de éste y los recursos empleados para lograr ese sentido.
Has finalizado esta sesión. Refuerza este contenido buscando en tu libro de texto; puedes consultar nuevamente el aprendizaje esperado y el propósito, así como explorar las actividades referentes al tema atendido durante la sesión.
El Reto de Hoy:
Crea un poema visual. Para ello, deberás seleccionar algunas palabras y acomodarlas cómo consideres necesario. Por ejemplo, “Yo dono rosas, oro no doy”. Éste se lee igual al derecho y al revés, por lo que es un palíndromo.
No te preocupes si tu poema no se puede leer igual al derecho y al revés. No necesitas palabras muy elaboradas. Puedes realizar este ejercicio con palabras que tú conozcas o sacarlas al azar de un libro, realizar un caligrama, un acróstico o un palíndromo.
Anótalas en cuadrados pequeños de papel, saca algunas de ellas, acomódalas sobre una hoja y destapa tu imaginación para crear un poema. Puedes empezar por elegir las palabras para después acomodarlas y crear la imagen; o por el contrario, puedes iniciar eligiendo la imagen y después acomodar las palabras para realizar un caligrama. Deja que tu imaginación poética vuele y la pluma transite libremente.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Entre rastros y huellas
Aprendizaje esperado: Representa acontecimientos importantes vinculados a la historia de su comunidad mediante distintas formas expresivas.
Énfasis: Resignificar lugares de su entorno a partir de vivencias trascendentales que acontecieron allí para buscar maneras de cuidarlos y difundir su importancia.
¿Qué vamos a aprender?
En esta sesión, manifestarás a través del arte los acontecimientos más importantes de tu comunidad. Para ello, explorarás los lugares, objetos y prácticas culturales que han estado presentes a lo largo de la historia, esto con el fin de aprender y buscar la manera de cuidarlos.
¿Qué hacemos?
Inicia con las siguientes preguntas:
- ¿Cuáles son los lugares más importantes de tu comunidad y por qué lo son?
- ¿Qué sucesos han marcado a tu comunidad?
Probablemente te encuentres, al igual que todos, un poco aislada o asilado debido a las medidas preventivas que se deben de tomar. Pero seguramente sabes qué ha pasado en tu comunidad, cuáles son los lugares más reconocidos o qué es lo que la hace especial. Además, puedes preguntarle a alguien de tu familia que sea mayor y que lleve mucho más tiempo que tú habitando en la comunidad.
Ahora, busca un mapa de la República Mexicana que tengas en casa, para que señales estas huellas que desde tus antepasados se han quedado en nuestro país. ¿Sabes cuántas huellas habrá en nuestro país de lugares y sucesos legendarios que conforman nuestra identidad?
Si no cuentas con un mapa, puedes buscarlo en algún libro de geografía, historia o por internet. Si esto tampoco es una opción, no te preocupes, recurre a tu memoria y dibuja uno, recordando el contorno. Siempre puedes pedir la ayuda de algún familiar para recordarlo mejor.
Este mapa te servirá de referente para averiguar las huellas o rastros que ha dejado tu familia en este territorio e indagar si, en un momento dado, se entrelazaron estas huellas entre las huellas de alguien más. Para ello, averigua con tus familiares y pregúntales de donde son tus antepasados.
Después realizar el recorrido y de encontrar los lugares en los que han estado tus antepasados, responde las siguientes preguntas:
¿Qué lugares del país conoces?
¿De dónde es tu familia?
¿Cómo representarías ese lugar?
¿Cuáles son los platillos típicos?
México es un país maravilloso para vivir, pues literalmente puedes encontrar por todo su territorio gente que viene de distintas partes del mundo. Si analizas nuestra historia nacional, el mestizaje nos ha acompañado desde el principio del tiempo, por parte de nuestros pueblos originarios y con muchas otras naciones que han cruzado sus caminos con nuestro país.
Estas relaciones han generado intercambios culturales entre los pueblos y le dan a México una gran diversidad cultural. Todas las manifestaciones son igual de importantes, por eso es esencial el diálogo y el respeto mutuo.
A continuación, realiza los enlaces en tu mapa de dónde vienes, donde has estado y en dónde estás ahora con los materiales que tengas en casa, puede ser con chinches de colores, marcadores adhesivos, colores, plumones, etc.
Indaga sobre: ¿cuáles son las huellas y los rastros de tus historias familiares? Si conseguiste un mapa o lo dibujaste, señala esas huellas; si no es de un lugar a otro, dibuja tu entidad o comunidad para ver esas conexiones y seguir tus huellas. Incluso, a la distancia, podrías ver si en algún momento de tu historia familiar, te has encontrado con las huellas de algún compañero.
Asimismo, toma en cuenta cada lugar que hayas señalado en donde exista un baile típico, su música, festivales, carnavales, riquezas socioculturales, entre otras. Y para resaltar la riqueza cultural, podrías puntualizar con otro color en dónde nacieron tus artistas favoritos, pues ellos influyen en la historia de tu comunidad, y por lo tanto, en tu historia de vida. Indaga tus artistas y señálalos en tu mapa o cuaderno
Después de realizar lo anterior, fíjate cómo hasta el simple hecho de poner estas marcas de colores están formando una imagen interesante. Ahora, une esas marcas y observa qué formas o figuras pudieran representar estas uniones de huellas, conectándolo por manifestaciones artísticas.
Esta actividad te mostrará muchas cosas que enlazan a tu familia con las artes. Tus huellas se quedan, no sólo en los lugares, sino también al hacer conexiones con situaciones artísticas, como una canción, una pintura, un baile, entre otras.
El Reto de Hoy:
Realiza la actividad de esta sesión, si te es posible, pide a tus familiares que te acompañen mientras la realizas y reflexionen sobre sus huellas al andar y qué rastros han dejado en su historia.
Después, contesta la siguiente pregunta:
¿Cuáles son tus lugares entrañables, tus objetos cargados de valor histórico, las personas y las maneras de hacer ciertas actividades?
Comparte tus exploraciones con tus profesoras y profesores, para compartir tus rastros y huellas.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
¿Cómo se mide el universo?
Aprendizaje esperado: Identifica algunos aspectos sobre la evolución del universo.
Énfasis: Conocer y reflexionar sobre los diferentes métodos con los que se miden las distancias en el universo.
¿Qué vamos a aprender?
En esta sesión, revisarás algunas aportaciones acerca de cómo se mide el universo y las estrellas, analizarás diferentes métodos y reconocerás algunos aspectos sobre la evolución del universo.
¿Qué hacemos?
Antes de profundizar en el tema, analiza la siguiente información.
Es parte de la naturaleza el inferir acerca de lo que hay más allá, cuando somos pequeños el único mundo que conocemos es nuestra casa, después nuestro barrio y nuestra ciudad, quizá luego otras ciudades y hasta otros países. Después nos damos cuenta de que también existen otros planetas además de la Tierra. También de que en las noches se pueden ver las estrellas y todo esto hace que nos preguntemos acerca de ¿qué tan grande es el universo?
En la antigüedad, se llegó a tener la idea de que el universo sólo era la Tierra, y quizá les llegó a parecer un lugar enorme al no contar con medios de transporte que los ayudaran a desplazarse grandes distancias. Aristóteles planteo que la Tierra era el centro del universo, y que estaba rodeada por la Luna, el Sol, los planetas y una esfera negra con perforaciones, mejor conocidas como estrellas, mismas que permitían ver un fuego que estaba oculto.
A los relatos narrados a través de una leyenda, se les conoce como cosmogonías, que sin duda alguna son explicaciones fantásticas del origen del universo; sin embargo, además del origen del todo, existen factores que son de interés para la humanidad, como realizar expediciones espaciales, que permiten abandonar la atmósfera para alcanzar el espacio exterior.
Reflexiona en lo siguiente:
¿Sabes cómo se realizan los viajes al espacio?, ¿en qué consisten? ¿cómo llego el hombre a la Luna?, ¿cómo se miden estas distancias?
En el universo, sobre todo en el planeta Tierra se puede medir la distancia, la masa, el volumen, la densidad y la temperatura.
El planeta Tierra tiene sus propias unidades de medida, como los ejemplos que se acaban de mencionar, sin embargo, en el universo también se mide el brillo de los astros, la declinación, la longitud de onda y algunas otras magnitudes.
Quien intento medir el universo en primera instancia fue Arquímedes de Siracusa. Él quiso calcular cuántos granos de arena cabían en el cosmos, a partir de esa idea, le fue necesario medir el cosmos, a través del modelo de Aristarco de Samos, quien fue la primero que colocó al Sol y no a la Tierra al centro del universo, es decir, el modelo heliocéntrico del sistema Solar.
Arquímedes, se seguía imaginando que la orilla del universo era una esfera con las estrellas fijas, ya que no tenía los instrumentos para detectar que se mueven diferentes velocidades. Así que, usando ángulos y cálculos matemáticos, llego a la conclusión de que el universo debía medir unos 100 billones de estadios o 19 billones de kilómetros, o como mencionan los científicos 2 años luz, por ejemplo, la estrella más cercana al Sol, “Próxima centauri”, se encuentra a mayor distancia, aproximadamente a 4.2 años luz.
Los años luz son la distancia en el espacio a la que se encuentra un objeto, o en este caso, una estrella con respecto a la Tierra o lugar en el universo.
Para comprender el tamaño del universo, comienza por algo más familiar, la Tierra, su diámetro es de aproximadamente 12,000 kilómetros. A su vez, la Tierra forma parte del sistema solar que aproximadamente mide 4,500 millones de kilómetros. El sistema solar forma parte de la galaxia que se llama vía láctea, que resulta ser 10,000 veces mayor y mide 500 billones de kilómetros en su parte más larga, aproximadamente 50 años luz, de hecho, en 1920 los astrónomos consideraban que las estrellas estaban contenidas en la vía láctea, pero con los estudios del universo y los avances tecnológicos, descubrieron que existían otras galaxias. En la década de los 90´s el telescopio Hubble logro fotografiar una imagen, en la que cada mancha brillante es una galaxia que contiene sus propias estrellas y planetas, por otra parte, la vía láctea donde esta nuestro sistema solar es tal y como se percibe en la siguiente imagen.

Por lo tanto, somos demasiado pequeños, casi como si fuéramos un átomo, representado a través de una galaxia. Sin embargo, la vía láctea forma parte de una familia llamada el grupo local, que en él contiene unas 50 galaxias y se calcula que su diámetro es de 10 millones de años luz y aún éste pertenece al inmenso cúmulo de Virgo.
Entonces el universo es más grande de lo que podríamos imaginar y nosotros representamos una pequeñísima parte, pero ¿por qué se mide en años luz?
Para entender esta unidad de medida sólo es necesario realizar la siguiente afirmación: un año tiene 365, dicho de otro modo, el año es una unidad de tiempo. En algún momento has escuchado acerca de los años luz, para saber cuántos días tiene un año luz, te sorprenderá saber que el año luz no se emplea para medir tiempo, se utiliza para medir distancias, así como se utilizan unidades específicas para medir cosas pequeñas, el año luz se utiliza para medir distancias astronómicas. Por otra parte, la velocidad de la luz es exageradamente rápida, por ejemplo, un fotón de luz recorre una distancia de 300 millones de metros en un segundo, si se pudiera medir la velocidad con la que sale la luz de un láser, obtendrías un valor de 300 millones sobre segundo, entonces si un fotón de luz viajara durante un año, recorre 9 billones 460 mil 730 millones 473 mil kilómetros, esta cantidad es lo equivalente a un año luz.
Son distancias muy grandes para recorrer que, si se pensará recorrer esa distancia a la velocidad promedio de un automóvil, tardarías muchos años en recorrerla.
Ahora que ya comienzas a dimensionar las distancias en el universo, existen variaciones de distancia, como lo son la hora luz, el minuto luz y el segundo luz, este último, es la distancia que recorre la luz durante un segundo, por ejemplo, la Tierra está a poco más de 384 mil kilómetros de la Luna; la luz reflejada de la Luna tarda poco más de un segundo en llegar a la Tierra, entonces se dice que la Luna está a 1.3 segundos luz de la Tierra, a la luz del Sol le toma 8.3 minutos en llegar a la Tierra y se dice que la vía láctea tiene un diámetro de 100 mil años luz, estas medidas son aproximaciones.
Existen diferentes maneras de medir en el universo, una de ellas es el brillo de los astros o magnitud estelar, por ejemplo, los antiguos astrónomos griegos llamaban estrellas de primer tamaño o primera magnitud a las estrellas más brillantes que aparecían después de la puesta del Sol y las últimas que desaparecían tras el amanecer o la salida del Sol, la escala de magnitudes se considera de la magnitud 1 a la magnitud 6. Donde la magnitud 6 es la estrella más débil a simple vista y la magnitud 1 corresponde a la estrella más brillante.
Entonces de acuerdo con la magnitud estelar, se podría decir que la estrella que más brilla es porque está ubicada más cerca de la Tierra, pero esto puede ser relativo, ya que en realidad depende de la cercanía y el tamaño, a mayor brillo, una estrella se aleja y tiene un corrimiento hacia una tonalidad roja, por ejemplo, una estrella de neutrones, por sus características brillantes debido a la radiación propia, puede estar muy lejana y brillar, aunque esté muriendo.
El brillo de una estrella no siempre depende de la distancia a la que se encuentre con respecto a la Tierra, entonces como se podría saber ¿a qué distancia se encuentran los astros?
Medir estas distancias astronómicas parece imposible y así lo fue durante mucho tiempo; por ejemplo, si en una noche clara te pones a mirar hacia el cielo, te parecerá que todos esos puntos de luz se encuentran a la misma distancia, como si se tratara de una bóveda, si repites esta observación durante muchos días seguidos, notarás que algunos de esos puntos cambian su posición relativa a otras estrellas. Los antiguos astrónomos u observadores del cielo se dieron cuenta de ello y a las estrellas inquietas les dieron el nombre de planetas, que significa “errantes”.
Todo se basa en la observación, es por esta razón que imaginaban que la Tierra se encontraba en el centro del universo, con la Luna, el Sol y las estrellas girando a su alrededor y el resto de las estrellas se encontraban todas a la misma distancia. Ahora, ya se sabe que esto no es de esa manera y las estrellas se encuentran a distancias diferentes, pero ¿cómo logran los científicos o astrónomos determinar estas distancias?
Se utilizan dos técnicas: la primera se llama paralaje, este método es muy parecido a la manera en que se distinguen distancias cercanas en la Tierra, esto es gracias a que tenemos dos ojos. Para comprender este concepto, realiza el siguiente ejercicio.
Ejercicio: paralaje
Paralaje es el cambio de movimiento de vista del observador, para entender cómo funciona, estira un poco tu brazo hacia adelante y levanta tu dedo pulgar hacia arriba, ahora mira tú pulgar alternando tus ojos, primero con tu ojo derecho cerrado y después con tu ojo izquierdo cerrado, repite este ejercicio algunas veces más, incrementando la velocidad de apertura y cierre de tus ojos.
Ahora acerca un poco más tu dedo con respecto a la distancia de tu rostro, y repite la acción de abrir y cerrar los ojos algunas veces más.
¿Qué lograste observar?
Cuando cierras un ojo y abres el otro, tu dedo aparenta moverse de un lado a otro en contraste a los objetos más lejanos al fondo, esto mismo ocurre con la estrella de la cual quieres conocer su distancia, se verá en diferente posición dependiendo de, si la ves cuando la Tierra está en un punto de su órbita, por ejemplo, en verano, o en otro punto de la misma órbita, quizá en invierno.
Entonces, la forma en que se puede saber la distancia que existe entre una estrella con respecto a la Tierra, depende de realizar la observación en dos de las diferentes estaciones del año para conocer con exactitud su distancia. Esto ocurre cuando se observa que la Luna se ve en ocasiones más cercana a la Tierra y en otras aparenta estar mucho más lejana, cambiando también su tamaño por la posición relativa.
La distancia entre la Tierra, el Sol y la observación da el ángulo para calcular la distancia de la estrella y se utiliza una operación de trigonometría.
Sin embargo, existen estrellas en las que sus ángulos son demasiado pequeños o no se pueden distinguir, incluso es muy difícil de medir y esto dificulta o imposibilita conocer la distancia a la que se encuentra la estrella. Esto es lo que limita esta técnica “paralaje”, para ello existe otra alternativa.
En la ciencia existen diferentes alternativas para realizar cálculos, que cuando un método se ve limitado, existe otro con mayor amplitud que permitirá realizarlo; por ejemplo, el sistema de paralaje sólo funciona con estrellas que están a menos de 400 años luz de distancia. Para estrellas que están más lejos la técnica que se utiliza es la relación entre el color y brillo de las estrellas.
Estudiando las estrellas cercanas, sobre todo algunas con características muy peculiares conocidas como candelas estándar, se determina que, a cierto color de estrella, le corresponde cierto brillo o magnitud absoluta, vista a una distancia de 10 parsecs. El cálculo de la distancia se realiza con cálculos más avanzados como lo es la ley de la inversa del cuadrado que dice que, la intensidad es inversamente proporcional al cuadrado de la distancia, es decir, mientras mayor sea el brillo de la estrella, se encuentra más lejos.
Las unidades de medida, como el metro y el kilómetro, quedan demasiado pequeñas en astronomía. Es por eso que, se utilizan otras unidades de distancia como los años luz y las unidades astronómicas, mejor conocidas como UA, que son de las unidades más comunes y presentes en los cálculos astronómicos que representan la distancia media entre la Tierra y el Sol; y el pársec que está relacionada con mediciones de distancia hechas en segundo de arco.
Un pársec es la distancia a la que estaría un astro si el ángulo que forma con una unidad astronómica es de un segundo de arco, por su parte, un segundo de arco es un grado dividido entre 3,600, por tanto, un pársec equivale a 3.26 años luz.
El mirar en la lejanía del universo, significa mirar el pasado, los objetos lejanos permiten entender que hablar del universo, es prácticamente hablar del infinito. Pero aún existe un dato que es un referente para conocer distancias a las que se encuentran las estrellas lejanas, para ello, es necesario saber la distancia a la que está el Sol de la Tierra. ¿Cómo es que se logra medir la distancia del Sol a la Tierra?
Para responder esta pregunta, es necesario saber que, el primer astro del que se calculó la distancia fue la Luna, en el siglo II antes de nuestra era. Eratóstenes ya había calculado aproximadamente el diámetro de la Tierra, poco después Hiparco de Nicea al observar un eclipse Lunar y viendo cuanto se tardaba la Luna en atravesar la sombra de la Tierra, calculó que la Tierra era tres veces y media más grande que la Luna. Gracias a Eratóstenes ya se sabía la medida más aproximada de la Tierra, unos 12,700 kilómetros, de acuerdo con el sistema métrico, esto facilitó calcular el diámetro de la Luna, dando un total aproximado de 3,628 kilómetros.
Otro de los estudios más relevantes de Hiparco, fue que sostuvo una moneda frente a él, hasta que la moneda se veía del mismo tamaño que la Luna, midió la moneda, posteriormente midió la distancia entre la moneda y su ojo y determinó que la distancia era 108 veces el diámetro de la moneda. Por lo tanto, la distancia a la Luna debería de tener la misma proporción, 108 veces el diámetro de la Luna, dando como resultado 391, 878 kilómetros, muy cercano a las medidas actuales 384,400 kilómetros.
Por lo tanto, la forma en la que se toman las medidas en el universo es la misma que utilizo Hiparco para conocer las distancias, el paralaje, que se ocupa para las estrellas más cercanas.
La diferencia es que, ellos utilizaban los estadios como unidad de medida. Eso puede explicar la variación que existe entre la distancia que calculo a la Luna y el registro actual.
Retomando la pregunta anterior, quien realizó el primer cálculo de la distancia, de la Tierra al Sol, fue Aristarco de Samos, dedujo que cuando se veía exactamente media Luna desde su pueblo, significaba que una línea imaginaria que conectaba la Tierra con la Luna debía estar un ángulo recto con la línea que iba de la Luna al Sol. Sin embargo, él no realizó bien las medidas y supuso que el ángulo era de 87°, de tal modo que, su cálculo resultó erróneo para determinar la distancia entre la Tierra y el Sol, resultando en una distancia 20 veces mayor a la distancia que hay entre la Tierra y la Luna. Sin embargo, por mucho tiempo, nadie logro mejorar este cálculo, hoy en día se conoce que la distancia no es de 20 veces, si no de 400 veces la distancia de la Tierra a la Luna.
En esta sesión, aprendiste acerca de cómo se mide el universo además de las unidades de medida. El universo es infinitamente grande, resulta maravilloso descubrir lo que yace en él. La próxima ocasión que tengas la oportunidad de mirar las estrellas recordaras que para saber la distancia que tiene cada una, fue necesario conocer la distancia que existe del Sol a la Tierra.
Recuerda consultar tu libro de texto, así como investigar y resolver las preguntas que se realizaron a lo largo de esta sesión, para que puedas conocer más y resolver las dudas que pudieron surgir.
El Reto de Hoy:
Elabora una infografía que te permita recordar cómo se mide el universo, así como las y los científicos que contribuyeron al logro de esta gran travesía.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Imperio mexica e Imperio español
Aprendizaje esperado: Reconoce hechos ocurridos en Europa y América antes y durante los viajes de exploración. También estudia la relación entre la defensa de la religión cristiana y el proceso de conquista española.
Énfasis: Conocer las características del Imperio español y las del Imperio mexica.
¿Qué vamos a aprender?
En sesiones anteriores, estudiaste las culturas del Posclásico que se desarrollaron en la región de Mesoamérica, incluyendo al Imperio mexica. Durante el siglo XVI todas ellas tuvieron que hacer frente a la llegada de una entidad política ajena al mundo mesoamericano: el Imperio español. En esta sesión, comenzarás por conocer esa nueva entidad política y la compararás con el Imperio mexica.
¿Qué hacemos?
Inicia con el siguiente fragmento del libro “Historia general de las cosas de Nueva España”, escrito en el siglo XVI por el misionero franciscano Fray Bernardino de Sahagún y que, entre otras cosas, cuenta sobre la llegada de unos barcos extraños a las costas del territorio mexica:
La primera vez que parecieron navíos en la costa desta Nueva España, los capitanes de Motecuzoma, que se llamaban calpixques, que estaban cerca de la costa, luego fueron a ver que era aquello que venía, que nunca habían visto navíos, uno de los cuales fue el calpixque de Cuestecatl, que se llamaba Pinotl, llevo consigo otros calpixques […] fueron a ver qué cosa era aquello, y llevaron algunas mantas ricas, que solo Motecuzoma las usaba, ningún otro tenía licencia de usarlas.
Entraron en unas canoas y fueron a los navíos. Dijeron entre sí, “estamos aquí en guarda desta costa, conviene que sepamos de cierto, que es esto para que llevemos la nueva cierta a Motecuzoma”. Entraron luego en las canoas y comenzaron a remar hacia los navíos y como llegaron junto a los navíos y vieron a los españoles, besaron todas las proas de las canoas, en señal de adoración. Pensaron que era el dios Quetzalcóatl que volvía al cual estaban y están esperando según parece en la historia de este dios.
Más adelante, el libro narra el regreso de los calpixques ante Moctezuma:
…los indios se volvieron a tierra, y luego se partieron para México donde llegaron en un día y una noche, a dar la nueva a Motecuzoma de lo que habían visto, y trajéronle las cuentas que les habían dado los españoles y dijéronles de esta manera: “señor nuestro, dignos somos de muerte, oye lo que hemos visto y lo que hemos hecho”.
Tú nos pusiste en guarda de la orilla de la mar, hemos visto unos dioses dentro en la mar y fuimos a recibirlos, y dímosles varias mantas ricas y veis aquí estas cuentas dadlas a Motecuzoma para que nos conozca, y dijéronle todo lo que había pasado cuando estuvieron con ellos en la mar en los navíos...”. A lo que respondió el gobernante: “…venís cansados y fatigados, idos a descansar, yo he recibido esto en secreto, y os mando que no digáis nada de lo que ha pasado.
Historia general de las cosas de Nueva España
Fray Bernardino de Sahagún
Ahora, responde las siguientes preguntas:
¿Qué crees que llamó más la atención de los españoles sobre las nuevas tierras?
¿Cómo reaccionaron las poblaciones nativas ante el arribo de los españoles?
Como pudiste notar en el texto, para los mexicas los españoles eran unos desconocidos que llegaron a irrumpir su realidad. Y lo mismo puede decirse de los españoles, quienes ignoraban la existencia de la sociedad mexica. En esta sesión, conocerás al Imperio español y, por otro lado, al Imperio mexica, con la intención de poder compararlos en el momento de su encuentro. Empieza con el Imperio español.
Los expedicionarios que llegaron a las costas de la actual península de Yucatán y que continuaron su camino hasta las costas del estado de Veracruz y el centro de México eran parte del naciente Imperio español, y ¿qué era el Imperio español? La lectura de la intitulación de un documento del 11 de abril de 1498 puede servir como una pista. En él se puede leer:
“Don Fernando e donna Isabel, por la gracia de Dios rey de Castilla, de León, de Aragón, de Sicilia, de Granada, de Corcega, de Murcia, de Jahen, de los Algarbes, de Algecira, de Gibraltar, de las islas de Canaria, conde de Barcelona e sennores de Vizcaya e de Molina, duques de Athenas e de Neopatria, condes de Ruysellón e de Cerdania, marqueses de Oristán e de Gociano”.
Esta fórmula, que se repite más o menos igual en la mayoría de los documentos que hacían los reyes, sirve para comprender de que el Imperio español fue una entidad política que estaba compuesta por un conjunto de reinos y territorios, que fue fundada en la península Ibérica en el año de 1474, a raíz del matrimonio de los reyes católicos que selló la unión de los reinos de Castilla y Aragón, y marcó el comienzo de un periodo de gran expansión que llevaría al Imperio español en un siglo a dominar territorios en América, Asia, África y Europa.
De este Imperio, te enfocarás principalmente en el reino de Castilla, principal protagonista en la caída de Tenochtitlan.
Este reino se hallaba, a finales del siglo XV y principios del siglo XVI, saliendo del largo proceso de la Reconquista y en medio de una intensa carrera por encontrar tierras para conquistar y nuevas rutas comerciales con las cuales acceder a productos del lejano oriente, como la pimienta, la seda o la canela, sin tener que recurrir a intermediarios como los turcos o las ciudades italianas. Ambas situaciones cambiaron de manera dramática en el año de 1492, cuando tuvieron lugar dos eventos que dieron un impulso fuerte a la posición española, en particular la castellana.
El primero ocurrió en enero de dicho año, momento en que las tropas dirigidas por los reyes católicos lograron conquistar el reino de Granada, último reino musulmán en la península Ibérica, poniendo fin al largo proceso de la Reconquista, durante el cual, Castilla incrementó de manera sostenida su tamaño a costa de los reinos musulmanes que se hallaban en esa región desde el siglo VIII.
En los territorios conquistados por los cristianos durante la Reconquista, las poblaciones derrotadas debían convertirse a la religión de los conquistadores y aceptar las nuevas autoridades nombradas por el monarca castellano, debiendo perder su cultura o enfrentar la expulsión del reino.
Esta cercanía con entidades políticas musulmanas provocó en el reino de Castilla que, el Estado y la sociedad se estructuraran en torno a la guerra como una forma muy eficaz de ampliar su territorio. Para justificar tal forma de actuar, se aseguraba de que los mahometanos se encontraban ocupando territorio anteriormente cristiano y, por tanto, era una misión divina recuperar esos territorios para la fe católica.
El segundo gran acontecimiento sucedió meses después, en octubre de 1492, cuando Cristóbal Colón llegó por primera vez al continente americano, ayudado por varios avances técnicos y científicos. Su logro inauguró un periodo de rápida expansión territorial para el reino de Castilla y por extensión del Imperio español, que lo llevaría a conquistar y colonizar gran parte del continente americano.
La sociedad española estaba organizada a partir de jerarquías y estamentos fuertemente definidos. A la cabeza del Imperio se encontraba el rey, que llegaba a serlo por herencia. Su función era impartir justicia a todos sus súbditos, otorgar beneficios a quienes lo merecieran y cuidar el bienestar cristiano del Imperio. Debajo, se ubicaba el estamento noble, sus miembros estaban exentos de pagar contribuciones a la Corona. Este grupo se dividía en dos. Por un lado, estaban los políticamente importantes miembros de la alta nobleza y por el otro lado estaba la media y baja nobleza.
En la parte baja de la sociedad se encontrarían los llamados pecheros y los plebeyos, es decir, todos aquellos que debían trabajar para ganarse su subsistencia y, además, pagar contribuciones a la Corona, a las autoridades municipales o al dueño de las tierras donde trabajaran y vivieran (fuera laico o religioso). Aquí se podrían encontrar a los pequeños comerciantes, artesanos o campesinos. Si bien la pertenencia a estos estamentos dependía de la familia en la que se naciera, en ciertos casos era posible, aunque un tanto difícil, que un individuo cambiara de estamento y llegara a la nobleza.
Para lograrlo había que juntar una gran fortuna (principalmente por las armas o por el comercio) y conseguir que el rey, o en su defecto, un noble importante, diera ciertos privilegios. En este contexto, la actividad militar enfocada en la conquista de nuevos territorios se convirtió en la forma más común de adquirir estatus social y riquezas.
La economía del Imperio dependía de cada uno de los reinos; sin embargo, en general la tenencia de tierras y la agricultura seguían teniendo un papel fundamental como productores de riqueza. Junto a esta actividad, cada vez se volvió más importante el comercio, actividad principalmente desarrollada en centros urbanos como Sevilla o Barcelona. Por ambas razones, la conquista de nuevos territorios y el acceso a nuevos productos era algo fundamental para el Imperio español.
Un elemento central en la vida de la sociedad española de aquel tiempo lo era, sin duda, la religión cristiana, la cual estaba presente en todos los aspectos de la vida diaria, la política o el pensamiento, sobre la cual profundizarás en la siguiente sesión.
Del otro lado del océano Atlántico se encontraba el Imperio mexica, del que has estudiado en sesiones anteriores.
Fundada por el pueblo mexica en el año 1325, Tenochtitlan había logrado expandir su imperio de manera considerable hasta abarcar un territorio que llegaba de la región del Soconusco en el sur, a las costas de Guerrero y de Veracruz, así como a la zona de Tula y la colindancia con Michoacán. Por otro lado, se sabe que las redes de comercio e influencia Mexica llegaban a lugares tan apartados como el actual Nuevo México, en Estados Unidos, u Honduras, en América Central.
Para lograr esta impresionante expansión, los mexicas, como se les llamaba a los habitantes de Mexico-Tenochtitlan, se apoyaron en otras dos naciones nahuas que se hallaban en la cuenca del Lago de Texcoco: los altepeme de Texcoco y los de Tacuba, con quienes habían formado la llamada Triple Alianza en el año de 1430.
Si bien los mexicas y sus aliados lograron conquistar varios pueblos, el control que ejercían sobre ellos era fundamentalmente económico. En lugar de que controlaran al gobierno del pueblo conquistado, impusieran sus dioses y borraron la identidad local, en la mayoría de los casos, los mexicas sólo obligaban a los pueblos vencidos a entregar una cantidad determinada de tributos y prisioneros, así como a dar apoyo logístico y militar en ciertas campañas bélicas mexicas.
Es importante tener esto presente, puesto que el Imperio mexica en realidad era una red de poblaciones diversas y con un alto grado de autonomía política que únicamente estaban sometidas a los tributos y requerimientos del Huey Tlatoani de Tenochtitlan.
A pesar del poder de los ejércitos mexicas, existían en Mesoamérica varios pueblos que resistieron y no fueron sometidos, como los purépechas, en lo que ahora es la región de Michoacán, algunas poblaciones mixtecas, de lo que podría ser la zona actual de Oaxaca y Guerrero o los tlaxcaltecas.
Observa el siguiente video para profundizar en la importancia política, económica y social que tenía la guerra para el Imperio mexica.
- Guerra y tributo.
https://www.youtube.com/watch?app=desktop&v=f401gMAP_vA
La sociedad mexica estaba estructurada a partir de una división central, por un lado, se encontraban los nobles o pipiltin y, por otro lado, los macehualtin o plebeyos.
A la cabeza se hallaba el Huey Tlatoani, un cihuacoatl o consejero real, y los tetecutin, que serían los funcionarios nobles. Los hijos de estos últimos eran los pipiltin, todos ellos estaban integrados en el gobierno, donde cumplían diversas funciones, ya fuera que tuvieran algún puesto en el palacio real tenochca, se encontraran adscritos a algún tecpan o palacio de la ciudad como jueces, fungieran como sacerdotes en los templos principales o estuvieran encargados de recaudar tributos en las regiones del Imperio. Todos ellos gozaban de privilegios económicos, políticos y sociales, entre ellos, usar ciertos peinados o determinadas prendas de vestir.
Por el otro lado, los macehualtin estaban encargados de producir y de entregar una porción de sus productos en forma de tributo a los nobles, fueran estos nobles de su propio altépetl o de uno conquistado.
En esta sociedad la comunidad local era la base de la identidad; uno era quien era por su familia y, por su barrio o calpulli. En este sentido, no existía el individuo libre como se entiende actualmente, sino que su función era cumplir los roles que por su origen social y de nacimiento, tenía ya determinados.
En este mundo las diferencias entre estratos estaban muy marcadas y era mal vista la gente que intentaba salirse del esquema y romper con las tradiciones. El único medio de ascenso era el servicio a la sociedad y al gobernante mexica, a través de la guerra, la religión o el comercio.
Para los habitantes del Imperio mexica la vida representaba una constante repetición de ciclos regidos por las fuerzas sobrenaturales, dentro de los cuales se insertaba la vida de las personas. Todo estaba mediado por rituales que marcaban en todo momento el día a día y buscaban influir en los dioses y el destino del mundo. Debido a esto, en Mesoamérica la religión se encontraba en todos lados e influía todo, fenómeno que, guardando ciertas salvedades, era similar en el mundo de los castellanos.
En 1517 y 1518, ante la llegada de Francisco Hernández de Córdoba y Juan de Grijalva, frente a frente, se encontraron los representantes de dos Imperios. Lo que pasaría tras ese primer encuentro, cambiaría de manera radical el destino de ambas entidades políticas; para comprender este proceso resulta fundamental conocer las concepciones del mundo que tenía cada uno, aspectos que se seguirán profundizando en las siguientes sesiones.
Ahora, observa el siguiente video sobre las diferencias en la alimentación del Imperio mexica y del Imperio español.
- La dieta mesoamericana.
https://www.youtube.com/watch?v=5IcAlF05f9k
Has finalizado esta sesión. Si deseas saber más al respecto, puedes consultar tu libro de texto de Historia.
El Reto de Hoy:
Con la información que estudiaste sobre el Imperio mexica y el Imperio español, elabora un cuadro comparativo en el que, primero escribirás las características políticas, económicas y sociales de cada uno; y, posteriormente, con diferente color señalarás los aspectos en que eran similares y diferentes. Para resolver este reto, puedes apoyarte en las notas de las sesiones anteriores, así como en la información de tu libro de texto.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario