Aprende en Casa III SEP: 18 de febrero TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 18 de febrero de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Jueves 18 de febrero, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Proporcionalidad Directa II
Aprendizaje esperado: Analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.
Énfasis: Analizar y comparar situaciones de variación lineal y de proporcionalidad directa a partir de sus representaciones tabular, gráfica y algebraica.
¿Qué vamos a aprender?
Durante el desarrollo de la sesión analizarás y compararás situaciones de proporcionalidad directa y de variación lineal a partir de sus representaciones algebraica, tabular y gráfica, con el objetivo de resolver algunos problemas.
¿Qué hacemos?
La sesión se iniciará con la siguiente situación hipotética:
Un grupo de albañiles necesita preparar una mezcla para una construcción. Dicha mezcla debe tener las mismas características de consistencia y homogeneidad para evitar que la construcción se caiga. El ingeniero les indica que por cada cuatro botes de arena que utilicen para la mezcla, deben usar seis de grava.
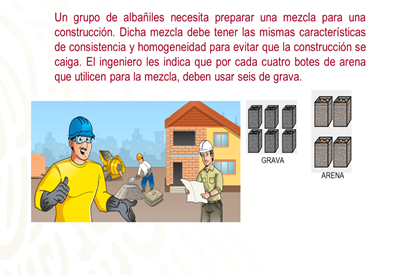
Ahora, se resolverá el primer problema.
¿Cuántos botes de grava son necesarios para preparar la mezcla cuando se usan quince botes de arena?
En el problema, el ingeniero indica que por cada cuatro botes de arena que utilicen para la mezcla, se deben usar seis de grava.
Para responder la pregunta se organizan los datos como se observa en la siguiente tabla, en la columna de la izquierda se registra la cantidad de botes de arena que se necesitan, y que en la relación establecida por el ingeniero son cuatro, y en la columna de la derecha los botes de grava, que son seis.

Dado que la pregunta indica que el número de botes de arena a utilizar es quince, se registra ese dato en la columna izquierda. Como se desconoce el número de botes de grava, entonces se le asigna una literal, en este caso “ye”. Esto permite visualizar la relación de proporcionalidad entre las cantidades.
Se debe aclarar que la proporcionalidad es una relación de tipo multiplicativo en la que a una variable independiente se le aplica el factor de proporcionalidad para encontrar el valor de la variable dependiente, es decir, “ye” es igual a “ka” por “equis”.

Desde el punto de vista algebraico, las cantidades que forman una pareja de la relación, es decir, las variables, se pueden reescribir como un cociente. Algebraicamente, si “ye” es igual a “ka” por “equis”, entonces “ka” es igual a “ye” sobre “equis”.
En la tabla elaborada para resolver el problema, la columna de la izquierda representa los botes de arena, esas cantidades se consideran parte de la variable independiente, por lo que se representan con “equis”.
La columna de la derecha representa los botes de grava, es la variable dependiente y, por lo tanto, se representa con “ye”.
En una relación de proporcionalidad se puede calcular la razón si las variables se relacionan como cociente.
De esa forma, la primera relación de cantidades, cuatro y seis, generan la razón seis sobre cuatro. Para encontrar el valor que resuelve el problema se establece la misma relación entre “ye” y quince, por lo que conforman la razón “ye” sobre quince.
Dado que se está buscando el dato que permita conservar la proporcionalidad, las razones deben ser iguales. Entonces se establece la siguiente proporción: seis sobre cuatro es igual a “ye” sobre quince.
Para resolver se puede manipular algebraicamente, es decir, para encontrar el valor faltante se lleva a cabo el despeje de “ye”.
En primer lugar, se resuelve la división. Se encuentra la representación numérica de la razón. Seis sobre cuatro es igual a uno punto cinco, lo que es igual a “ye” sobre quince. Se aplica la propiedad de la igualdad multiplicando ambos miembros de la ecuación por quince.
Ahora, se tiene que el producto de uno punto cinco por quince es igual al producto de “ye” sobre quince, multiplicado por quince. Se realiza la multiplicación del segundo término, con lo que la igualdad ahora es uno punto cinco por quince es igual a “ye”.
Con esto, se resuelve el primer problema. “Ye” es igual a uno punto cinco por quince, lo que es igual a veintidós punto cinco. Es decir, si se usan quince botes de arena se necesitan veintidós punto cinco botes de grava para conservar la homogeneidad de la mezcla.

Ahora se revisará un segundo problema.
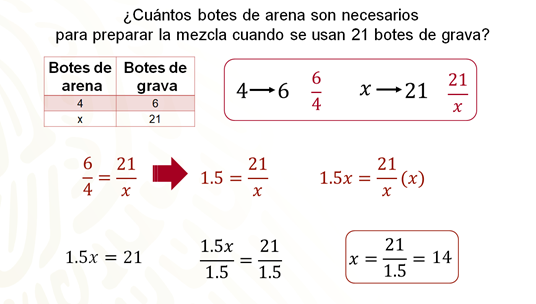
¿Cuántos botes de arena son necesarios para preparar la mezcla, si se usan 21 botes de grava?
Para responder la pregunta se organizan los datos iniciales del problema, del lado izquierdo los botes de arena, que son cuatro, del lado derecho los botes de grava, que son seis.
Se coloca la “equis” en el lugar que corresponde al número de botes de arena, ya que es el dato que se desconoce. El número veintiuno, que son los botes de grava a utilizar, se coloca en la fila correspondiente.
Con lo que ya se revisó se puede proceder de manera similar, nota que ahora el valor desconocido es “equis”. Se establece la relación algebraica y se tiene que cuatro y seis generan la razón seis sobre cuatro, por otra parte, equis y veintiuno componen la razón veintiuno sobre equis.
Por lo tanto, se tiene la proporción seis sobre cuatro es igual a veintiuno sobre equis.
Para despejar equis se obtiene el valor de seis sobre cuatro, que es uno punto cinco. Con esto se obtiene que uno punto cinco es igual a veintiuno sobre “equis”.
Ahora se multiplican ambos miembros de la ecuación por equis, respetando la propiedad de la igualdad. Así, se tiene que uno punto cinco “equis” es igual al producto de veintiuno sobre “equis” por “equis”. Se resuelve la multiplicación, con lo que la igualdad ahora es uno punto cinco equis es igual a veintiuno.
Entonces, para despejar “equis” se dividen ambos miembros de la ecuación entre el coeficiente de “equis” que es uno punto cinco. Entonces se tiene, uno punto cinco “equis” entre uno punto cinco es igual a veintiuno entre uno punto cinco. Al resolver las divisiones, la expresión que resulta es “equis” es igual a catorce.
Entonces, ¡cuando se usan veintiún botes de grava se deben utilizar catorce botes de arena!
Con lo explicado queda claro que el problema se puede resolver desde una perspectiva algebraica. Sin embargo, las relaciones de proporcionalidad directa tienen diferentes representaciones que permiten resolver problemas de diversas maneras. Es importante que aprendas a identificar las representaciones de este tipo de relación en un registro tabular y en el plano cartesiano.
Ya se tiene el trabajo muy avanzado para poder construir estas representaciones a partir del problema de los botes de grava y arena. De acuerdo con lo revisado sabes que: “equis” es la cantidad de botes de arena, y es la variable independiente; “ye” es la cantidad de botes de grava y es la variable dependiente; “ka” es el cociente de “ye” sobre “equis” y es la constante de proporcionalidad.
Durante la resolución de los problemas se encontró que “ka” es igual a uno punto cinco; por lo tanto, la expresión algebraica que define la relación de proporcionalidad es “ye” es igual a uno punto cinco “equis”.

A partir de la representación algebraica se pueden obtener infinidad de parejas de cantidades que mantienen la relación de proporcionalidad, basta con asignar valores a la variable independiente y llenar una tabla. Pero, por ahora, se aprovecharán los valores que se tienen para continuar. Esos valores pueden ser interpretados como pares ordenados, es decir, coordenadas que se pueden ubicar en el plano cartesiano. De ahí se obtiene la representación gráfica.
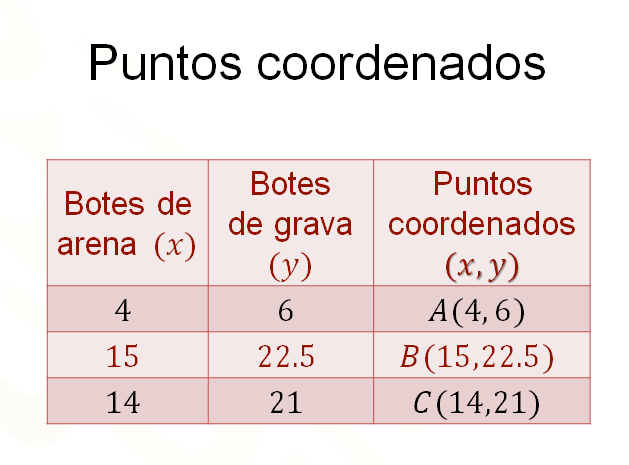
En la siguiente tabla se presenta la organización de los datos obtenidos. Cada punto se nombrará utilizando letras mayúsculas y colocando dentro de un paréntesis los valores de “equis” y de “ye”. Recuerda que siempre el primer valor será el de las abscisas o de las “equis”, y luego el segundo valor será el de las ordenadas o de las “ye”.
Por lo tanto, en la primera columna se tienen los valores de “equis” o botes de arena, en la segunda columna se tienen los valores de “y” o botes de grava y la tercera columna las coordenadas que son: “A” cuatro coma seis, “be” quince coma veintidós punto cinco y “ce” catorce coma veintiuno.
Ahora se puede construir la gráfica. En el eje “equis”, o de las abscisas, se representa la cantidad de botes de arena. En el eje “ye”, o de las ordenadas, los botes de grava. Después se ubican los puntos coordenados (“equis”, “ye”) que se obtuvieron en la tabla:
Por 4 botes de arena son 6 botes de grava.
Por 15 botes de arena son 22.5 botes de grava.
Por 14 botes de arena son 21 botes de grava.
Ya que cada punto está ubicado, se traza una línea que pase sobre los puntos identificados con su correspondiente letra mayúscula, como se muestra a continuación.

Observa en la siguiente recta que representa la relación de proporcionalidad directa que cuando aumenta la cantidad de botes de arena también aumenta la cantidad de botes de grava.
Además, todos los puntos que forman parte de la recta, ¡son parejas de cantidades que mantienen la proporción!
Por otra parte, la gráfica es una línea recta, entonces puede extenderse en sus extremos. Al realizarlo se puede observar que la recta pasa por el origen del plano cartesiano.

¡Esa es una característica particular de este tipo de relaciones!
Es muy importante que reflexiones con respecto a lo que se acaba de exponer.
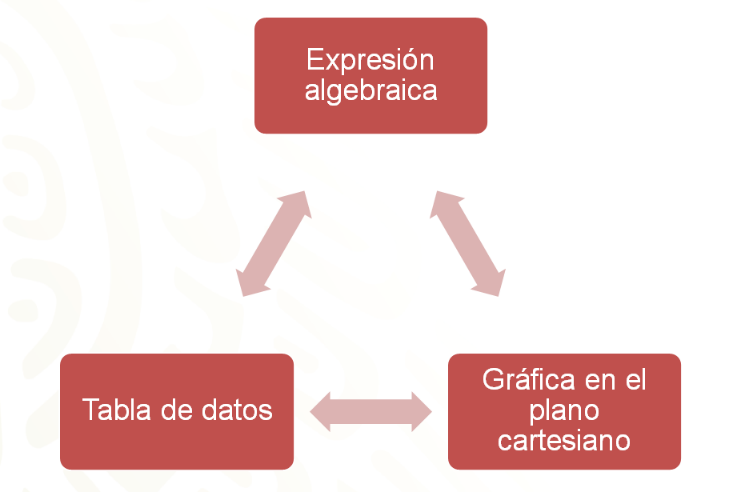
Las relaciones de proporcionalidad tienen tres representaciones que están íntimamente ligadas, con tener una sola de ellas se pueden definir las otras dos, en caso de ser necesario.
Como ya se expuso, si se tiene la expresión algebraica se pueden obtener los pares ordenados para construir la gráfica; si se tiene la gráfica, basta con identificar los puntos que forman parte de la recta para poder llenar una tabla que posteriormente se puede analizar para determinar la expresión algebraica. ¡Lo mismo ocurre si sólo se cuenta con una tabla con cantidades proporcionales se pueden obtener las otras dos expresiones!
Con este tipo de pensamiento matemático bien desarrollado serás capaz de identificar relaciones de proporcionalidad y resolver diversos problemas. Por ejemplo, cuando se busca adquirir algunos productos, se analizan las ofertas para comparar los costos y decidir dónde hacer una mejor compra.
Ahora reflexiona en torno al siguiente problema.
Existe un modelo de negocio que consiste en la renta de equipos de cómputo para empresas. La empresa “MicroChip” ofrece un paquete en el que por cada computadora se pagan cuatrocientos pesos mensuales, mientras que la empresa “MegaBits” solicita un pago inicial de mil doscientos pesos y un pago mensual de trescientos pesos por equipo.

¿Cuál de las empresas conviene contratar y por qué?
Tomando como base este problema, se desarrollarán las tres representaciones de las que se ha estado hablando y se determinarán cuál de las empresas utiliza una relación de proporcionalidad directa en su oferta.
Para comenzar se organizará la información para poder responder a la pregunta.
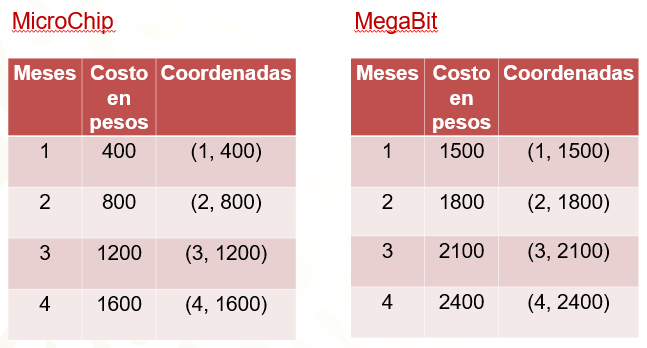
La empresa “MicroChips” pide cuatrocientos pesos mensuales, por lo que se puede hacer una tabla que relacione los meses de servicio con el costo. Por un mes se deben pagar cuatrocientos pesos; por dos meses ochocientos pesos; por tres meses son mil doscientos pesos y por cuatro meses mil seiscientos pesos.
Se hará lo mismo con la oferta de la empresa “MegaBits”. Aquí se debe considerar que hay un pago inicial, fijo, y luego el costo mensual. Por el primer mes se pagan mil doscientos pesos de pago inicial más los trescientos pesos, un total de mil quinientos pesos. Por el segundo mes se pagan mil ochocientos pesos; por el tercero dos mil cien pesos, y por el cuarto mes dos mil cuatrocientos pesos.
Con ese análisis, ¿puedes identificar la empresa que utiliza una relación proporcional en su oferta? En ambos casos parece que mientras uno de los datos crece el otro también lo hace. Esto parece indicar que ambas expresiones son proporcionales.

Sin embargo, se puede elaborar la gráfica con los datos ordenados para revisar si se genera una gráfica de proporcionalidad o no.
En el caso de “MicroChips” a uno le corresponde cuatrocientos; a dos, ochocientos; a tres, mil doscientos y a cuatro, mil seiscientos. Observa en la tabla que aparece abajo, cómo quedan relacionadas esas parejas en la tercera columna, son puntos que se pueden ubicar en el plano cartesiano.
Para “MegaBits” a uno le corresponde mil quinientos pesos, ya que el costo inicial es de mil doscientos, más la renta mensual de trescientos. A dos meses le corresponden mil ochocientos pesos; a tres, dos mil cien pesos y a cuatro, dos mil cuatrocientos.
Para poder comparar ambos conjuntos de datos se trazan las gráficas en el mismo plano cartesiano. ¿Qué observas?
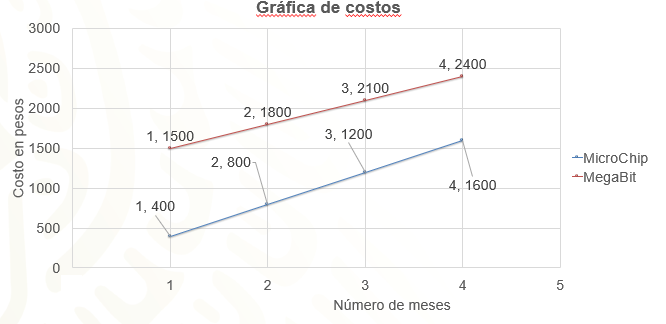
En los dos casos se generan líneas rectas y se puede identificar que mientras una cantidad crece, la otra también. ¿Será posible que ambas expresiones sean de proporcionalidad?
Se te invita a que registres tus argumentos. Más adelante podrás validarlos o refutarlos.
Hace falta revisar las expresiones algebraicas que modelan cada situación, en el caso de “MicroChips” se observa que las cantidades se relacionan multiplicativamente entre sí, ya que el costo depende del número de meses multiplicado por cuatrocientos pesos, que es la constante de proporcionalidad. Por lo tanto, para “MicroChip” su oferta queda definida por “ye” igual a cuatrocientos por “equis”.
En el caso de “MegaBits”, la relación no es tan sencilla. Se tiene un costo mensual de trescientos pesos, pero un pago inicial de mil doscientos pesos. Esta relación queda definida por la multiplicación de los meses de servicio por trescientos, más mil doscientos, es decir, “ye” es igual a trescientos por “equis” más mil doscientos.
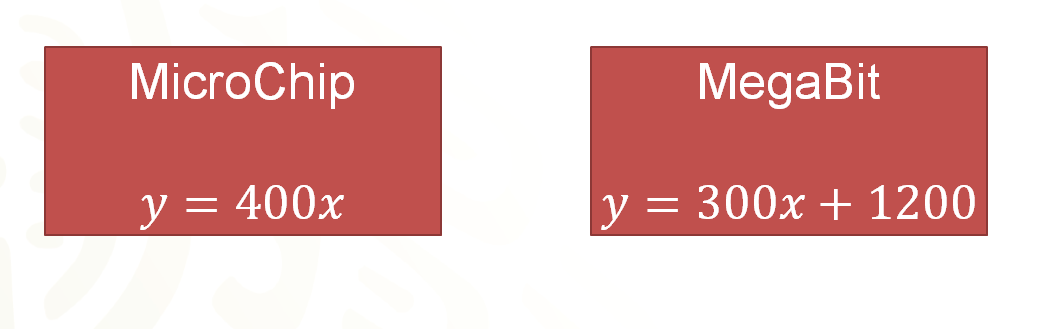
¡Por fin una diferencia clara entre las ofertas! La empresa “MicroChip” es la que tiene una relación de proporcionalidad en su oferta, ya que su expresión algebraica es de la forma “ye” es igual a “ka” por “equis”. En el otro caso, aparece un sumando, por lo que se trata de una expresión de variación lineal que no es directamente proporcional.
Regresando a la gráfica, los comportamientos de las ofertas se pueden comparar mejor si se extienden las rectas. Observa que cuando se extiende la recta de la empresa “MicroChip” pasa por el origen. ¡Eso ocurre con las gráficas asociadas a relaciones de proporcionalidad!
La otra recta corta en mil doscientos a la recta “ye” y no en el origen. Ésta es otra diferencia fundamental entre estas relaciones, por lo tanto, se comprueba que es una relación de variación lineal que no es directamente proporcional.
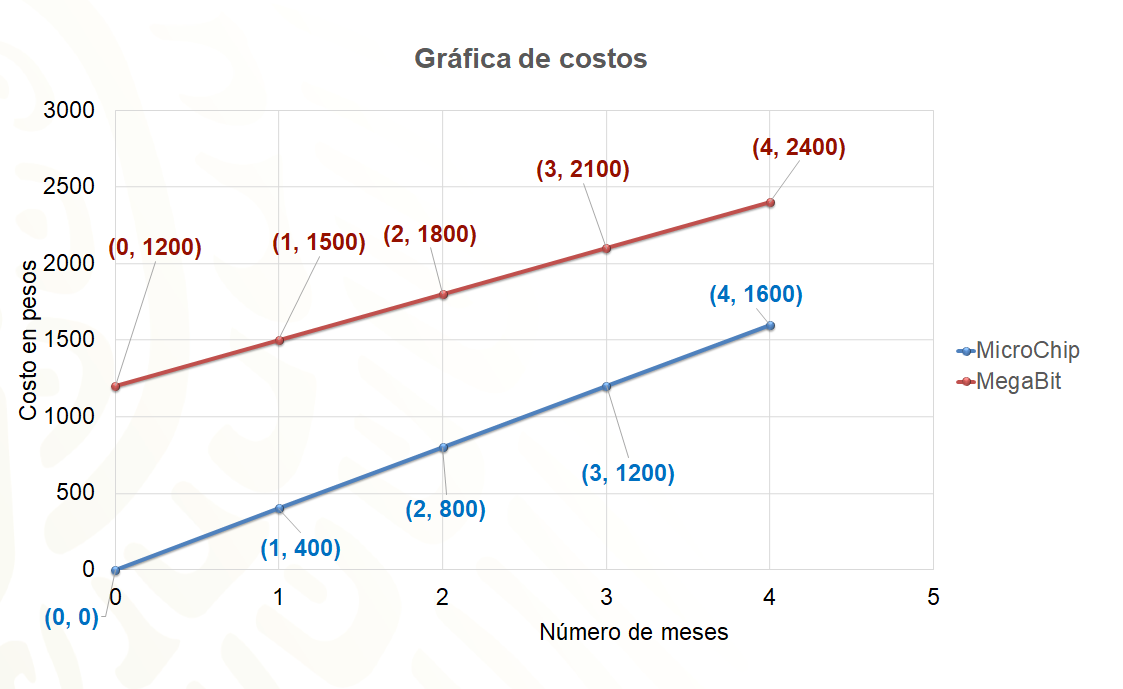
Pero, todavía no se contesta la pregunta. ¿Cuál de las empresas conviene contratar y por qué?
La manera más directa de observar las relaciones para compararlas es en la siguiente gráfica. Todo parece indicar que, si se necesita un servicio a corto plazo, conviene contratar a la empresa “MicroChip”. Pero si se está pensando en una empresa a largo plazo, conviene más la empresa “MegaBits”.

Es interesante analizar el punto en el que se cortan las dos rectas. Ese punto indica que, en un plazo de doce meses, ambas empresas están cobrando lo mismo por sus servicios.
Ahora se analizará una última situación.
Se tienen dos listas de precios de un mismo artículo en dos locales. Sólo en uno de ellos se pueden adquirir los artículos por mayoreo. En el otro no, la venta es al menudeo.
En La Jicarita el costo de diez artículos es de ochocientos pesos y el costo de treinta es de dos mil cuatrocientos pesos.
En El Surtidor el costo de veinte artículos es de mil quinientos pesos y el costo de cuarenta artículos es de dos mil ochocientos pesos. Es decir, a mayor cantidad de artículos, la tienda da un descuento.
¿En cuál de ellas hay una relación de proporcionalidad directa?

Fíjate que, en ambos locales, entre más artículos se compran, mayor es la suma total que se paga; pero como sabes, ésta no es una característica suficiente para determinar que hay una relación de proporcionalidad directa.
Al analizar los datos del registro tabular, en el local La Jicarita, se identifica que por diez artículos se pagan ochocientos pesos y por treinta artículos se pagan dos mil cuatrocientos pesos, es decir, por treinta artículos se paga el triple, en relación con la compra de diez artículos. La constante de proporcionalidad es ochenta, porque siempre que se multiplique la cantidad de piezas por ochenta se obtendrá el precio total. La expresión algebraica que modela la relación entre las piezas de datos adquiridos y su costo es: ye igual a ochenta equis.
Y en el caso del local El Surtidor, la relación entre la adquisición de veinte artículos por mil quinientos pesos y cuarenta artículos por dos mil ochocientos pesos no es proporcional, pues cuarenta es el doble de veinte, pero dos mil ochocientos no es el doble de mil quinientos. En este caso no hay una constante debido a que los datos no están relacionados proporcionalmente. La relación entre los datos obedece a otro tipo de variación. Observa las gráficas para corroborarlo.
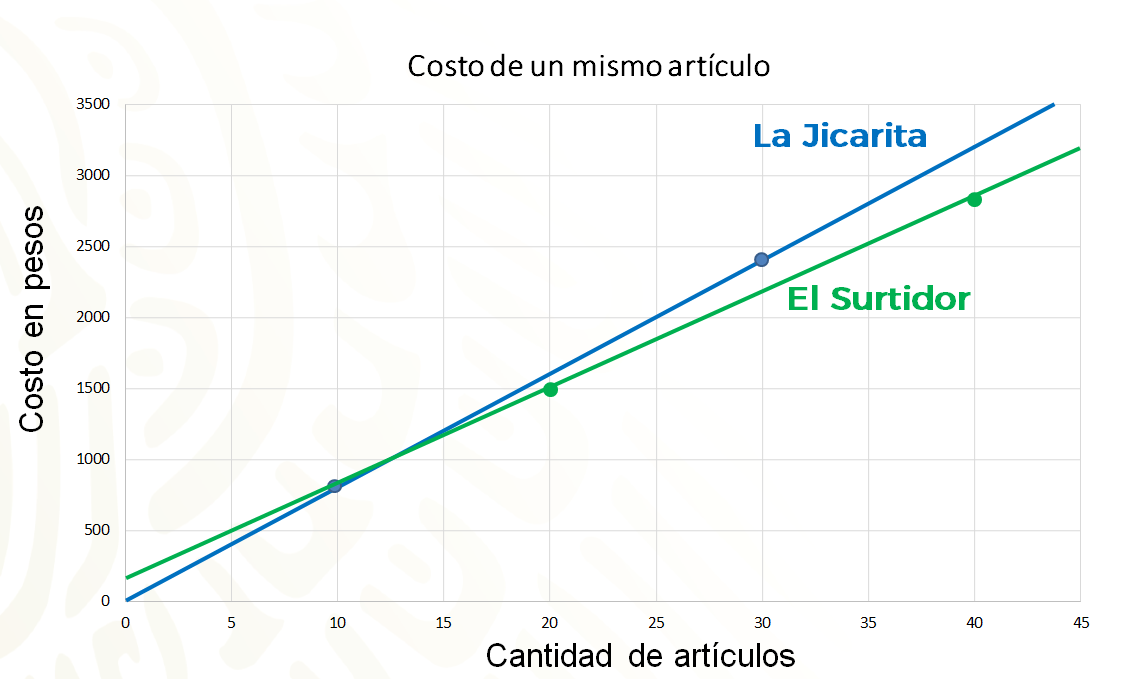
Al comparar las gráficas, efectivamente, los costos de acuerdo con la adquisición de los artículos en La Jicarita están en una relación de proporcionalidad directa, mientras que los del Surtidor no, ya que se ofrece un descuento a mayor cantidad de compra de artículos.
Haciendo un recuento de lo revisado el día hoy, se puede decir, que los problemas han quedado resueltos. Además, revisaste algunas características de las relaciones de proporcionalidad directa y de sus diferentes representaciones.
La representación algebraica debe tener la forma “ye” igual al producto de “ka” por “equis”, sin complemento aditivo.
La representación gráfica debe ser una línea recta que pasa por el origen.
Las tablas están conformadas por pares de cantidades que, relacionadas en forma de cociente, resulten con el mismo valor.
Con estas pistas te será sencillo reconocer una relación de proporcionalidad directa y no confundirla con una relación de variación lineal que no es de proporcionalidad directa.
En esta sesión analizaste situaciones de proporcionalidad directa a partir de representaciones algebraica, tabular y gráfica para la resolución de problemas. También se compararon situaciones que te permitieron establecer las diferencias entre las relaciones de proporcionalidad directa con las relaciones de variación lineal que no son proporcionales.
Has concluido el tema del día de hoy. Se espera que la información revisada en esta sesión, te permitan reflexionar para continuar con la construcción de tu pensamiento matemático.
Se te invita a poner a prueba lo aprendido hasta ahora, resolviendo algunas de las actividades de proporcionalidad directa contenidas en tu libro de texto de Matemáticas. Además, trata de relacionar estos fenómenos matemáticos con situaciones de tu vida cotidiana.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Comentarios de campaña
Aprendizaje esperado: Analiza el contenido de campañas oficiales.
Énfasis: Escribir comentarios sobre campañas oficiales.
¿Qué vamos a aprender?
Reflexionarás sobre la importancia de las campañas y acerca de los aspectos que las definen, por eso revisarás los elementos y herramientas que se utilizan en éstas para persuadir, crear conciencia o invitar a participar activamente en alguna acción social.
¿Qué hacemos?
En esta sesión revisarás los comentarios que se pueden hacer acerca de las campañas oficiales. Para empezar, lee la siguiente situación:
Cerca de la casa de Esteban, una constructora quiere derribar un árbol que tiene muchos años. Algunos vecinos y Esteban iniciaron una pequeña campaña local. Colocaron una “caja de opiniones” para que los demás habitantes de la zona expresaran su parecer. Al abrir la caja encontraron los siguientes comentarios.
Un vecino escribió: “qué feo, muy muy feo esto de la talada del árbol viejo. Ese árbol es aire puro, le tocó ‘ver’ la Revolución y es de un tipo muy raro”.
La idea de que el árbol fue testigo de la Revolución es interesante, pero para que la opinión de este vecino tenga mayor contundencia podría modificarse un poco la redacción.
¿Cómo retocarías esa opinión para convertirla en un comentario más formal?
¿Qué te parece si se agrega lo siguiente?
“Además, ciertos árboles pertenecen a especies vegetales que están en peligro de extinción, y el valor histórico de muchos ejemplares antiguos es incalculable.”
¿Anotaste tu frase?
La próxima vez, lo ideal será que estés preparado o preparada para anotar tus ideas. Aquí te puedes dar cuenta de la importancia de la escritura, la cual ha permitido a la humanidad dejar memoria de innumerables ideas y pensamientos.
Después de haber revisado la situación anterior, Te puedes dar cuenta de que casi todas las personas ejercitan la escritura cotidianamente y de muy diversas maneras. A veces lo hacen informalmente, como cuando anotan recordatorios en papeles sueltos o redactan textos en las redes sociales.
También se puede escribir formalmente, como cuando se redacta alguna carta, ensayo, reseña y, por supuesto, comentarios. Como te puedes dar cuenta, siempre se escribe con propósitos distintos.
¿Imaginas algún propósito que pudieran tener las y los alumnos al momento de redactar un escrito?
Un escrito puede tener muchísimos propósitos, pero todo depende del destinatario y de la situación. Por ejemplo, ahora se leerá un mensaje que mando un alumno llamado David a uno sus amigos acerca de la “caja de opiniones”, la situación planteada al inicio de la sesión, y dice así:
“Misión cumplida. La caja ya está a la vista de todo el vecindario. ¿Puedes colocar unas marcas en el piso para que todos respeten la sana distancia al momento de acercarse para dejar su comentario?”
Aquí, como verás el propósito del mensaje era doble: quería avisarle a su amigo que ya estaba instalada la caja y solicitar a la vez su ayuda.
Ahora que ya viste que un mensaje escrito puede tener una gran variedad de propósitos, que te parece regresar al objetivo central de esta sesión, que es redactar comentarios acerca de las campañas oficiales.
¿Qué te parece revisar una campaña oficial para después realizar un comentario?
Precisamente se mostrará una campaña que habla sobre el cambio climático y sus consecuencias. Para ello observa el siguiente video.
- Campaña océanos - cambio climático. Secretaría del Medio Ambiente.
Como pudiste ver en el video, esta campaña, difundida por la Secretaría del Medio Ambiente, se refiere a una problemática ambiental que todas las personas, de distintas maneras, pueden ayudar a detener. Además, permite dar tú opinión sobre esa problemática.
Ahora se revisará la opinión de una alumna sobre esta campaña.
|
“Creo que debemos hacer consciencia de todo el daño que los seres humanos le hemos hecho al planeta y tomar acciones para que este problema ya no avance más. Yo creo que la principal preocupación de los jóvenes es saber qué futuro nos espera”.
Alumna de la Secundaria Técnica #49 “José Vasconcelos”
|
Ésta, efectivamente, es una opinión, pero cuando se escribe, se deben estructurar las ideas de manera rigurosa y sustentar el punto de vista con argumentos sólidos.
Pero, ¿cuál es la diferencia entre una opinión y un comentario?
El comentario es un texto que permite argumentar para darle peso a las ideas y opiniones. Para ser más precisos, revisa la siguiente definición:
|
“Un comentario de textos es un escrito de tipo expositivo, pero con cierto acento crítico, en el que alguien hace referencia a un texto leído y con el que dialoga para establecer de manera explícita sus ideas y opiniones.” |
Con la definición ya podrás entender mejor el concepto, y sabrás que al redactar un comentario debes ahondar en tu opinión, en lugar de decir que “está bonito o está feo”.
Además, no debes olvidar que existen diversos tipos de comentarios. En esta sesión se revisará, específicamente, el comentario crítico sobre una campaña oficial.
Tal vez tengas algunas dudas hasta este momento, como en el caso de algunos de tus compañeros, por ello observa el siguiente video en donde un especialista en ciencias de la comunicación y producción visual llamado Ferrer Arturo González Lima, actualmente Jefe de la Delegación de RTV Veracruz, Boca del Río, dará respuesta a sus inquietudes.
- ANEXO_02_VIDEO_ESPECIALISTA.
Después de haber visto el video, ahora conoces cómo se puede organizar la información en un comentario, los aspectos que debes tomar en cuenta y algunos motivos por los cuales es importante que, como alumna o alumno, observes y analices campañas oficiales.
Pero, ¿existe algún secreto para que puedas escribir comentarios impecables?
La respuesta es que no existen secretos, pero sí estrategias de redacción y herramientas lingüísticas.
De acuerdo con el especialista Ferrer Arturo González Lima, se retomarán los elementos que debe contener tu comentario. Lo primero a lo que debes poner atención es a la estructura general que deberá tener.
|
Estructura del comentario |
|
|
La estructura general del comentario debe llevar un título que refiera al tipo de campaña que se presenta, una introducción, un desarrollo y una conclusión. Ésta sólo es la estructura general. Pero, hay que revisar cada uno de los elementos para entender claramente su uso y significado.
Se iniciará con el título.
Éste es un elemento importante que te guiará para saber de qué vas a hablar y ubicarte de manera inmediata en el tipo de campaña que se está analizando.
Puedes revisar tu libro de texto para ver el ejemplo que se sugiere en relación al título de un comentario, pero antes revisa la campaña sobre la cual hay que basar el comentario que se realizará. Para ello, observa la siguiente imagen.

¿Qué título se te ocurre para hacer un comentario de esta campaña?
Recuerda que tiene que ser claro, breve y hacer referencia a la campaña que se está comentando.
El título podría ser “Comentario sobre la campaña de salud Muévete” o “Comentario sobre una campaña de salud”. Esos títulos pueden funcionar.
Ahora revisarás si te es posible en tu libro de texto, Telesecundaria, Español, Segundo Grado. Volumen I, en la página 63 todas las partes de la campaña que analizarás en el desarrollo de este tema, para ello la dirección electrónica es:
https://conaliteg.sep.gob.mx/20/T2ESA.htm?#page/163
En este primer momento revisarás lo relacionado con el título de la campaña.

Como puedes ver, el título que se muestra es: Comentario sobre la campaña: “Chécate, mídete, muévete”.
A partir de ese título es fácil deducir sobre qué campaña hablará el comentario. El siguiente aspecto sería la introducción.
La introducción es un elemento esencial para la redacción de varios textos y, en especial, de tu comentario. Revisa cuáles son esos elementos que te conviene considerar al redactar.
|
|
|
|
Elementos de la Introducción: |
|
|
|
|
La introducción puede explicar algunos aspectos, como el tipo de campaña, las razones por las que se eligió, así como algunas de sus características generales.
En este caso, si revisas con atención los detalles de la campaña detectarás que se centra en la salud, razón por la cual resulta interesante y prioritario hablar sobre ella, ya que se enfoca en aspectos que la mayor parte de la población puede atender cotidianamente en el ámbito doméstico.
Revisa el ejemplo que te muestra el libro de texto y logra identificar los aspectos para la introducción de tu comentario.

https://conaliteg.sep.gob.mx/20/T2ESA.htm?#page/163
- Audio 01.
Como puedes ver, este primer párrafo de la introducción resalta el tipo de campaña, pues menciona que la promoción de la salud pública es su objetivo central; además, expresa que uno de sus propósitos es crear conciencia en la sociedad para cambiar hábitos.
Así se logra entender una de las razones por las que se eligió la campaña. También hacia el final se menciona que una meta particular de la campaña es evitar la obesidad y el sobrepeso.
Ahora revisa cuáles son los elementos que puede tener el desarrollo dentro del comentario.
|
|
|
|
Desarrollo: |
|
|
|
|
Es decir, tienes que analizar los aspectos formales de la campaña para dar tu opinión al respecto de esos elementos.
Antes de redactar tu comentario, tienes que describir de manera clara las imágenes, palabras y estrategias persuasivas que conforman la campaña oficial.
Ahora, revisarás los distintos aspectos que debes considerar en el desarrollo de tu comentario. Ve cómo podrías describir la estrategia de campaña. Para ello, observa el ejemplo que te muestra tu libro de texto.

https://conaliteg.sep.gob.mx/20/T2ESA.htm?#page/163
- Audio 02.
En este caso, al hablar sobre la estrategia central de la campaña se muestran situaciones cotidianas con las que la mayor parte de la población se puede sentir identificada.
Además, conforme al primer elemento del desarrollo del comentario, puedes mencionar que la estrategia que utiliza la campaña: “Chécate, mídete, muévete”, se basa en el uso de diversos medios de comunicación para alcanzar a un público general y que, a partir de ciertos recursos persuasivos, busca prevenir los problemas de salud.
El siguiente apecto a considerar en el desarrollo del comentario sería la referencia a los mensajes utilizados.

https://conaliteg.sep.gob.mx/20/T2ESA.htm?#page/163
- Audio 03.
Si puedes ver, el lema tiene una intención, además utiliza la rima como un recurso para conferirle ritmo y musicalidad.
Eso permite que el público en general se apropie del mensaje. Además, el texto menciona que esta misma campaña se encuentra en un medio audiovisual, lo que amplía su recepción.
Finalmente, en el desarrollo de tu comentario tienes que dar tu opinión sobre la campaña que estas comentando. Revisa el siguiente ejemplo, en tu libro de texto.

https://conaliteg.sep.gob.mx/20/T2ESA.htm?#page/163
- Audio 04.
De este modo, el desarrollo cumple con los tres aspectos señalados que tiene que abordar: la estrategia, las referencias al mensaje y la última, no menos importante, la opinión.
Cuando elaboras el desarrollo de tu comentario no debes perder de vista esos tres elementos. Ahora hay que revisar qué aspectos debe de tener la última parte de tu comentario: la conclusión.
|
Conclusión: |
|
|
En la conclusión se explica el efecto de la campaña en sus destinatarios y, nuevamente, se cierra con una opinión general sobre la campaña oficial comentada.
No se trata de una síntesis de lo que se había dicho con anterioridad, Revisa el siguiente ejemplo de este tipo de texto para que observes la manera en que lo puedes realizar.

https://conaliteg.sep.gob.mx/20/T2ESA.htm?#page/163
- Audio 05.
Si observaste con atención te habrás dado cuenta que inicia con la opinión genera y cierra explicando la importancia de la campaña, así como la necesidad de seguir generando conciencia.
Ahora se realizará una actividad que te podría ayudar a tener más ideas para crear tu propio comentario. Para ello, se retomará la campaña de los océanos y la contaminación.
Se te pide que tomes nota de los elementos que pueden ayudarte a crear tu comentario. Observa el siguiente video que habla de la campaña.
- Campaña océanos - contaminación. Secretaría del Medio Ambiente.
Como pudiste observar, la campaña muestra el lema: “Por nuestros mares, sin plástico esta bien”. Además, utiliza una serie de recursos, como la música, imágenes impactantes y resalta la importancia de cuidar los océanos.
Ahora se te invita a que elabores un comentario. Para ello, se se señalarán aspectos que no debes olvidar.
Primero recuerda los tres aspectos que conviene incluir en el párrafo de introducción. Observa como puedes organizar tus ideas.
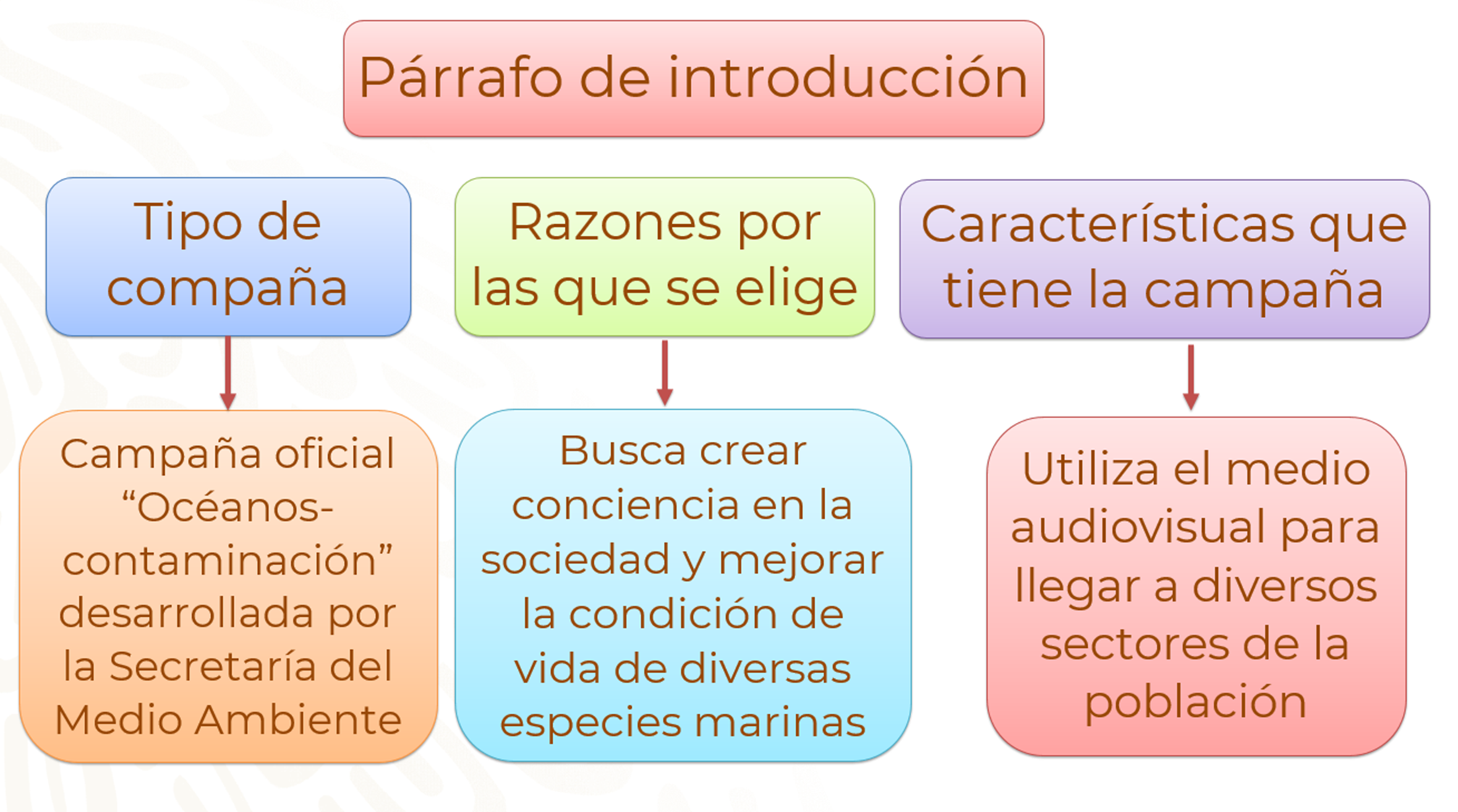
Después debes redactar esos datos en un párrafo. Pero observa que pasaría si no cuidas tu redacción y revisas lo que escribes.
|
Campaña oficial “Océanos-contaminación”, desarrollada por la Secretaría del Medio Ambiente. Busca crear conciencia en la sociedad y mejorar la condición de vida de diversas especies marinas. Utiliza el medio audiovisual para llegar a diversos sectores de la población.
|
Si te das cuenta, aunque el párrafo se logra comprender un poco, no se puede leer de manera fluida y las ideas están algo divididas.
Así es, al párrafo le hace falta coherencia, Ésta se puede lograr utilizando algunos nexos o signos de puntuación, Ve como quedaría el párrafo en una segunda versión.
|
La campaña oficial “Océanos-contaminación”, desarrollada por la Secretaría del Medio Ambiente, utiliza el medio audiovisual para llegar a diversos sectores de la población y crear conciencia, de esa manera busca mejorar la condición de vida de las diversas especies marinas.
|
Ahora se puede comprender con más claridad, Se espera que te sirva para que puedas seguir redactando tu comentario.
Recuerda que el aprendizaje esperado fue: analiza el contenido de campañas oficiales y el propósito fue: escribir comentarios sobre campañas oficiales.
Se espera que encuentres en la escritura de tu comentario una oportunidad para dar tu opinión, observar con detalle las problemáticas que se presenten; así como para mejorar tu redacción.
Con estos nuevos conocimientos ahora puedes realizar tu propio comentario acerca de una campaña oficial. Además, puedes buscar en tu libro de texto de Lengua Materna de segundo grado algunos otros ejemplos para reforzar lo aprendido.
También podrías investigar o revisar algunas otras campañas oficiales que sean de tu interés.
Has concluido el tema del día de hoy.
El Reto del Hoy:
Elabora tu comentario que se te pidió sobre la campaña océanos-contaminación, retomando los elemento que ya revisaste.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Actitudes ante el conflicto
Aprendizaje esperado: Analiza el conflicto optando por la forma más conveniente para lograr objetivos personales sin dañar al otro.
Énfasis: Analizas formas para enfrentar un conflicto.
¿Qué vamos a aprender?
Conocerás las formas para enfrentar un conflicto, para ello, se describirán las implicaciones de cada una de ellas y se darán algunos ejemplos de situaciones de la vida cotidiana; también se destacarán las ideas y actitudes que facilitan la solución pacífica.
¿Qué hacemos?
Recodarás que los conflictos forman parte de la vida, de la convivencia, de las interacciones sociales y, por tanto, son inherentes a las relaciones humanas. Aunque generalmente se asocian con situaciones negativas, la forma en la que se resuelven puede ser una oportunidad de aprendizaje y transformación.
Es decir, si aprendes a solucionarlos de forma constructiva, el crecimiento personal es invaluable; de otra forma, generarán violencia o daño a la integridad de los involucrados. Por lo tanto, necesitas aprender a construir relaciones de sana convivencia, solidarias y afectivas en las que, quienes integren un grupo, sientan seguridad, tengan reconocimiento y sean escuchadas y escuchados; es decir, que generen un ambiente en el que prevalezca el aprecio y el respeto.
Para ilustrar a lo que se hace referencia cuando se habla de conflictos y comiences a visualizar soluciones, sería interesante que escuches a Astrid, ella comparte la forma en cómo observa los conflictos en sus espacios de interacción, en el siguiente video.
- FCYE_B1_PG2_SEM23_VIDEOS 1_Astrid.
Astrid habla de elementos muy importantes en torno a los conflictos. Recuerda que es frecuente que surjan, ya que todas las personas son diferentes y tienen valores, intereses y necesidades propias que han adquirido en la familia y comunidad; aprendizajes culturales a los cuales recurren para dar respuesta a las situaciones que se les presentan, las cuales, en algunas ocasiones, pasan a ser un problema cuando no hay disposición de diálogo, comunicación, cooperación y apertura para solucionar las diferencias, lo que en muchas ocasiones deriva en situaciones de violencia entre las personas.
Además, suelen agravarse cuando existen dificultades para expresar lo que se piensa y siente, cuando se usan palabras o cometen acciones que lastiman a las personas, no sólo físicamente sino también en su dignidad, haciéndolas sentir inferiores. Es decir, cuando no aplican el asertividad.
En tu caso:
- ¿Qué conflictos observas en tu interacción con las y los demás?
- ¿Qué formas de resolver conflictos empleas?
- ¿Tienes disposición para promover relaciones solidarias y libres de violencia?
Antes de reconocer que existen formas diferentes para solucionar conflictos es necesario saber cómo identificarlos. Observa el siguiente video:
- Los elementos del conflicto.
https://www.youtube.com/watch?v=BTemeXm9klI
Revisa del tiempo 1:05 al 1:30.
Como observaste en el video, una forma de identificar un conflicto es detectando las diferencias entre la “verdad” de quienes participan, lo que es fundamental para saber que efectivamente ¡es un conflicto!, y buscar las acciones que ayuden a vislumbrar alternativas para su solución. Que permita, a las partes involucradas, hacerles frente sin violencia, es decir, lograr una convivencia pacífica en la que prevalezca el diálogo y la consideración de las necesidades.
Una vez que se detecta el conflicto es importante saber que existen formas de enfrentarlo. Para entenderlas observa en el siguiente video, al especialista Ricardo Ayllón, psicólogo experto en el tema de Conflicto y Cultura de Paz, quien te dará claridad sobre las formas que existen para resolver los conflictos y el cuidado de las personas involucradas.
- FCE2_B1_PG2_SEM23_VIDEOS 2_Ricardo.
Como pudiste ver en el video, el especialista habla de la importancia de entender que cuando los conflictos se evaden se compite o se somete a la otra persona, la convivencia se deteriora, lesionando la dignidad y se generan situaciones de injusticia.
Por lo tanto, se deben buscar alternativas pacíficas de cooperación y negociación a corto, mediano y largo plazo, para tener efectos favorables, lo que implica aprender a ponerse en el lugar de las y los demás, entender su punto de vista y respetar sus ideas. Esto se relaciona con la escucha activa y el deseo de buscar reconciliación como parte de un colectivo que cuida sus relaciones humanas.
Ahora observa el siguiente video en el que se habla puntualmente lo que puedes hacer para resolver conflictos.
- Los elementos del conflicto.
https://www.youtube.com/watch?v=BTemeXm9klI
Revisa del tiempo 3:32 al 4:15.
Como pudiste observar, tanto lo que dice el especialista, como lo que escuchaste en el video, confirma que poner al servicio de las personas tu educación, experiencias, creencias, actitudes, hábitos, valores, intereses y habilidades personales determinan el tipo de comportamientos que se emplearán como respuesta ante las tensiones que surgen al entrar en contacto con las diferencias, y que existen formas constructivas que permiten a las partes involucradas lograr sus objetivos sin lastimar a nadie.
Ahora se te invita a escuchar en voz de las y los jóvenes de la sección La voz de la juventud, los siguientes casos, donde te dan ejemplos de conflictos y su resolución.
Sobre las alternativas de las que habla el especialista, se te invita a desarrollar tu juicio crítico y preguntarte conforme escuches los casos: ¿qué harías tú? y ¿cómo podrías aplicar los pasos sugeridos anteriormente?
- Audio 1.
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202102/202102-RSC-JPOeM0iCyY-5.AUDIO1.mp3
|
A Mario no le gusta que Adrián obtenga mejores notas que él. A pesar de no entender algunos temas y de que Adrián le ofrece apoyo para estudiar juntos, Mario decide que es mejor esconderle a Adrián sus pertenencias al momento de hacer un examen, ya que de esa manera afectará su rendimiento y tendrá ventaja para avanzar en las preguntas. ¡Mario considera que siempre debe ser el mejor! |
Sin duda, Mario está decidiendo resolver el conflicto que tiene con Adrián mediante la competición, lo que seguramente le traerá mayores conflictos. Tú en casa, ¿consideras que la forma en que Mario está resolviendo su conflicto es adecuada?
Revisa el siguiente caso:
- Audio 2.
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202102/202102-RSC-TPOBq3q8ht-6.Audio23.mp3
|
Pablo le pide a Camila que sea su novia, pero ella le contesta que le dé un tiempo para pensar, ya que necesita conocerlo más antes de tomar una decisión.
La respuesta le molesta mucho a Pablo porque quiere que Camila ya sea su novia. Al ver la reacción de Pablo, Camila le dice que sí será su novia, con tal de que no se enoje.
|
Cómo pudiste observar, Camila está resolviendo el conflicto de propuesta de noviazgo mediante la sumisión, lo que no es adecuado, ya que está cediendo ante una manifestación de presión que seguramente derivará a la larga en mayor violencia por parte de Pablo.
Observa ahora el siguiente caso.
- Audio 3.
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202102/202102-RSC-0fwIAtKMo1-7.Audio3.mp3
|
Lucía quiere formar parte del equipo de futbol de su escuela. Habla con sus padres, pero no le dan permiso de inscribirse porque tuvo muy bajas calificaciones en el trimestre.
Ellos piensan que si su hija ingresa al equipo de futbol su situación académica empeorará.
Lucía siente mucha tristeza por la negativa de sus padres y a pesar de que desea realmente pertenecer al equipo de futbol, corre a su cuarto y muy enojada les dice a sus papás que no le importa y que no hablará más del asunto.
|
¿Tú qué harías?, ¿hablarías nuevamente de tus necesidades?, ¿te comprometerías a mejorar tus notas? o ¿resolverías con evasión, como lo hizo Lucía? ¿Verdad que lo mejor es que expongas nuevamente a tus padres tus necesidades y te comprometas a no descuidar tus estudios?
Presta atención al siguiente caso.
- Audio 4.
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202102/202102-RSC-ADAt3BoJnX-8.Audio4.mp3
|
Saúl siente que no tolera más el resguardo en casa, se enoja mucho y dice que la COVID ¡no existe!
Sus familiares hablan con él, le dicen que para ellos él es muy importante y que debe cuidarse. Así que, respira profundamente y decide seguir las medidas de cuidado estando en casa, ya que finalmente tiene mucho que estudiar y no quiere retrasarse en sus aprendizajes.
|
Como te puedes dar cuenta, Saúl, a pesar del cansancio que tiene por el resguardo en casa, de manera responsable decide aplicar la cooperación ante la situación de salud que se vive actualmente y contribuir con la parte de su responsabilidad para el cuidado de todos.
Observa un último caso.
- Audio 5.
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202102/202102-RSC-70DOm7kvkI-9.Audio5.mp3
|
Ana y Lucía están haciendo un cartel sobre el uso que las y los adolescentes dan a las redes sociales.
Ana piensa que es una forma de tener muchas amigas y amigos, que eso la hace feliz y que es lo que deberían hacer todas y todos.
Por su parte, Lucía considera que es un riesgo aceptar la amistad de personas desconocidas en una red social y que es mejor hacer amistades con personas conocidas.
Al darse cuenta de las dos posturas, discuten cuál puede ser la mejor y consideran la posibilidad de que su trabajo refleje los dos puntos de vista, pero recalcando el riesgo que implica hacer contacto con extraños en redes sociales.
|
Como te diste cuenta, escuchando y planteando ambas posturas se puede establecer un proceso de negociación y llegar a acuerdos entre ambas partes, como lo hicieron Ana y Lucía. Sin duda, la negociación y la cooperación son las mejores estrategias de solución.
Seguramente tú en casa pudiste imaginar otras opciones de solución ante los conflictos planteados, se trata de que te des cuenta de que hay opciones y estrategias que pueden emplearse sin usar violencia. Ya que seguramente te enfrentas a conflictos similares y es necesario que aprendas a actuar de forma ética, trazando planes personales de actuación, coherentes y responsables.
Para confirmar que sí es posible resolver los conflictos pacíficamente, se te invita a escuchar a Alvar, un adolescente que habla de la importancia de asumir actitudes que facilitan la solución de conflictos de forma pacífica.
- FCE2_B1_PG2_SEM23_VIDEOS 3_Alvar.
Como observaste, Alvar comparte que es posible solucionar los conflictos siguiendo algunos pasos. Y es que sí, debes saber que hay estrategias para lograr los objetivos personales que privilegian el diálogo.
Observa el siguiente esquema.

- Emplear la escucha activa, que significa disponerse emocional y físicamente para dialogar.
- Aplicar la empatía, que es entender el punto de vista de la otra persona poniéndose en su lugar.
- Establecer comunicación asertiva, que significa: expresar las opiniones y los sentimientos de manera clara, con un tono de voz adecuado y en el momento oportuno.
- Establecer acuerdos, es decir, buscar alternativas realistas en su solución, que sean aplicables a corto y mediano plazo.
Ahora se hará una recapitulación de lo trabajado en esta sesión:
La competición, sumisión y evasión son formas de darle solución a los conflictos, pero la cooperación y negociación son las mejores alternativas para hacerlo.
Privilegiar el diálogo por medio de la escucha activa, la empatía y la comunicación asertiva, permite llegar a acuerdos y lograr los objetivos personales sin dañar a otras y otros.
Es necesario desarrollar comportamientos, así como generar emociones y pensamientos que te lleven a mantener y fomentar competencias sociales de solidaridad, negociación y cooperación que influirán en la resolución pacífica de conflictos.
Has concluido el tema del día de hoy. Se te invita a que consultes tu libro de texto para informarte más del tema. Y recuerda que, ante un conflicto, es necesario tomarse un tiempo antes de hablar o actuar, realizar ejercicios de respiración, aplicar la empatía, la escucha activa y regular el tono de voz para comunicar las ideas de manera tranquila y asertiva
El Reto de Hoy:
Elabora una tabla y escribe el caso, así como las soluciones posibles, según las alternativas que has revisado. Observa la siguiente imagen.

El reto consiste en llenar tu cuadro, respondiendo las alternativas de competición, sumisión, evasión, cooperación y negociación que tienes para resolver el conflicto. Al final, señala la mejor alternativa para darle solución por medio del diálogo y sin violencia.
Para la solución recuerda que, de ti dependerá ser partícipe de una situación de violencia digital o detenerla. Así que deberás considerar todas las alternativas que tengas para no ser cómplice y evitar dañar la dignidad de tu compañera, ya que puede verse seriamente afectada y tú podrías contribuir en un delito que tendría consecuencias legales para tu persona, así que debes considerar que tu actuación sea éticamente correcta.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Leyendas del origen del universo
Aprendizaje esperado: Identifica algunos aspectos sobre la evolución del universo
Énfasis: Reflexionar sobre cómo algunas culturas antiguas explicaban el universo y su origen.
¿Qué vamos a aprender?
Hoy conocerás sobre distintas leyendas que explican el origen del universo.
Verás que resulta bastante interesante, sobre todo porque cada civilización tiene su propia versión acerca de cómo fue creado el universo.
¿Qué hacemos?
La mayoría, si no es que todas las civilizaciones, han desarrollado su propia mitología, en la cual han plasmado la forma en la que pensaban se creó el universo. La creación de todo lo que observas es algo que ha despertado la curiosidad del ser humano desde tiempos muy antiguos.
Muchos pensadores han formulado teorías en las cuales refieren que el universo es infinito, incluso se han aventurado a realizar especulaciones acerca de sus orígenes, cómo era en sus inicios, cómo ha cambiado, e incluso, si tendrá un fin o no.
Cada cultura tiene una leyenda o narración que trata de explicar o dar su propia respuesta al origen y evolución del universo. Con la aparición de las ciencias, en especial de la física, muchos científicos han intentado resolver estas mismas dudas. Ahora, se acompañan por las observaciones que se realizan en complejos telescopios, que se encuentran tanto en el planeta como fuera de él. Como verás la física ha contribuido al desarrollo de teorías que permitan explicar el origen del universo.
Ahora, anota y contesta las siguientes preguntas:
- ¿Conoces alguna leyenda que explique el origen del universo? Escribe un pequeño relato de ella.
- ¿Conoces alguna teoría que explique el origen del universo?, ¿en qué consiste?
- ¿Cómo consideras que se formó el universo?, ¿piensas que siempre ha existido?
Estas preguntas se irán resolviendo a lo largo de la sesión.
La evolución del universo, la aparición de la vida y particularmente del ser humano ha sido un asunto que las diferentes culturas han abordado a lo largo de la historia. El gran dilema del universo es parte de lo que puedes observar en una noche despejada.
Las culturas prehispánicas que habitaron el país tienen mitologías muy interesantes sobre el origen y evolución del universo. Muestra de ello es la cultura maya que, al igual que otros pueblos, creían en la existencia de un universo con características muy peculiares.
Pensaban que el universo se había formado en siete cielos planos superpuestos y de otros tantos niveles subterráneos donde habitaban los dioses. Su duda principal era cómo había surgido y como se había originado la vida, esto se encuentra narrado en el libro sagrado llamado Popol Vuh.
En las líneas del Popol Vuh se explica el origen del hombre y se describe el mundo que habitaba. Desde su descubrimiento ha sido traducido e interpretado un sinfín de veces. Es considerada como una de las mayores obras para el entendimiento de la cultura maya y de sus costumbres y creencias.
Los mayas tenían su propia interpretación del origen del universo, y el texto más importante de esta cultura por su contenido histórico y mitológico, el cual narra el desarrollo de su pueblo. Se tiene la creencia de que es una especie de versión mitológica sobre la creación del universo y la función del hombre en él. Describe la creación del hombre y de los fenómenos que suceden en la naturaleza, así como el comienzo de la civilización.
Por su contenido literario, el Popol Vuh ha sido comparado con otras obras muy importantes, como La Odisea, que es un poema griego, y con el Ramayana, un texto sagrado hindú. El Popol Vuh es una declaración universal sobre el papel del hombre en la naturaleza.
El contenido del libro sagrado habla acerca del conocimiento que fue transmitido a los humanos y el motivo de su creación, ya que los dioses querían que unos seres les rindieran culto. Narra que los humanos fueron creados a partir del maíz, luego, de que las divinidades fallaron en varias ocasiones al intentar hacerlos con lodo. También surgieron las aves y los animales de 4 patas.
Además, el Popol Vuh habla sobre el origen de las constelaciones, de lo avanzada que era la cultura maya en la agricultura y escritura, por mencionar algunas de las actividades que dominaban a la perfección.
Ahora, entenderás como los mayas veían el universo, además de tener grandes conocimientos de astronomía. Sin duda el Popol Vuh es un magnifico relato histórico y literario.
Pero también existen otras culturas que han descrito la creación del universo. Para saber más al respecto, observa el siguiente video.
- Leyendas del origen del universo.
https://www.youtube.com/watch?v=QN-sCRhvYTU
¿Te diste cuenta de que las cosmogonías son una forma de explicar el origen del universo?
Así es, resultan ser unas narraciones fantásticas las cosmogonías planteadas por los egipcios, mayas y aztecas, entre otros.
Pero, ¿no te gustaría conocer algunas diferentes?, por ejemplo, ¿cuál era la perspectiva de la cultura griega ante la creación del universo?
Al igual que los mayas con el Popol Vuh, dentro de la cultura griega existía la teogonía, una obra del siglo XIII antes de esta era. Es atribuida al poeta épico Hesíodo; es la versión más famosa de los griegos acerca del mito de la creación, aunque cabe señalar que no es la más antigua.
Como verás cada cultura puede tener sus propios escritos que narran el origen del universo, los cuales son diferentes entre sí, pero tratan de dar una explicación contundente acerca de cómo surgió todo.
Los griegos en la teogonía explican el surgimiento del cosmos físico, las divinidades, además de la jerarquía de dioses que terminaría gobernando su mundo.
Quizás durante mucho tiempo has escuchado acerca de los filósofos griegos, sin embargo, te puede resultar interesante también conocer su cosmogonía.
Pues bien, según su mitología, en primer lugar, existió el caos, una palabra que literalmente significa o simboliza el vacío producido en una abertura, pero era mucho más que un simple vacío. Era considerado como el elemento esencial del universo, oscuro y sombrío con cierto toque de temor o tristeza.
El caos también es descrito como una entidad sólida, que, con la creación de otras entidades del universo, quedaría relegado y solo, en el fondo de las profundidades conocidas. Esta interpretación es muy interesante, aunque podría ser incluso algo escalofriante. Sin embargo, el caos, según los griegos, fue la primera entidad en engendrar descendencia por su propia cuenta y sin intervención de nadie más.
Dio a luz a un hijo, Erebo, que es la personificación de la oscuridad subterránea, y a su hermana Nyx, que es el nombre de la negra noche. Ambos debían engendrar una descendencia de hijos y nietos con personificaciones oscuras y negativas. Sin embargo, de forma controversial, no logró esa encomienda, ya que dio a luz a Hemera, conocida como el día, y Eter, la luz.
Casi todas las cosmogonías antiguas atribuían los fenómenos naturales a entidades fantásticas. En este caso, tanto la oscuridad como la luz recaían en un par de deidades. Del mismo modo, en otras civilizaciones, fenómenos como la lluvia, truenos, vientos, entre otros, han sido relacionados con entidades divinas.
Sin embargo, con el paso del tiempo, se ha dado el alejado de las explicaciones místicas y, ayudados por la ciencia, se han podido encontrar explicaciones satisfactorias que no implican la participación de algún dios o hecho mágico.
La cosmogonía griega también explicaba la creación del mundo. Decía que, posterior a la existencia de caos, surgieron tres seres primordiales más, que serían las bases para la dinámica del cosmos.
Gea, conocida como la madre Tierra, de amplio seno en el que nacería y caminaría toda la naturaleza y civilización, representa a este planeta. El siguiente sería Tártaro, que es la personificación tenebrosa de las regiones más profundas de la Tierra. Después se crea Eros, el amor y la personificación del deseo; sin embargo, este último no tiene mayor relevancia o trascendencia como sus antecesores, pero sería el responsable de la procreación en la Tierra, es decir, el medio por el cual se da la vida.
Dicho de otro modo, Gea representa la fuente de toda la materia, incluyendo las características del universo físico que surgirían después, además de las divinidades que perciben todas las fuerzas de la naturaleza, así como los dioses y las diosas.
Gea engendra a dos varones quienes serían el medio para llevar acabo la creación de una larga estirpe con individuos de características distintas.
El primogénito de Gea fue Urano, que personifica al cielo, creado a imagen y semejanza de Gea, para cubrirla por todos lados. Después crearía las montañas y a Ponto, la personificación del mar y de la furia de sus olas. Gea y Urano formarían a la familia divina de la que nacerían todas las divinidades. Gea también sería la responsable de crear a las divinidades marinas y criaturas acuáticas.
Algunas veces has escuchado acerca de los dioses griegos, pero no de la creación del universo. ¿Entonces los titanes son parte de otro relato o tienen relación con la cosmogonía de los griegos?
El origen de los titanes se da de la unión entre Gea y Urano, y tenían como objetivo la gobernabilidad de la Tierra; en total fueron doce, el más destacado fue Cronos, que era la personificación del tiempo.
Es muy interesante la cosmogonía griega. De hecho, si te pones a pensar, puede tener algún parecido con la teoría del Big Bang, claro que con las debidas proporciones.
Como ya se mencionó a lo largo de esta sesión, en la Antigüedad surgieron diversas ideas de cómo era el universo y de su creación, que generalmente es atribuida a un Dios supremo, el cual, además, lo dotaba de movimiento. Siempre se involucraba a uno o más seres supremos responsables no sólo de la creación, sino de mantener el estado de las cosas en el universo.
Los seres humanos siempre han sentido la necesidad de encontrar la explicación a los fenómenos que observan a su alrededor.
Las primeras explicaciones fueron de carácter divino, pero eso no dejó conformes a todos. Por ejemplo, Tales de Mileto, comúnmente conocido como el padre de la ciencia griega y la matemática, se realizaba cuestionamientos sobre el universo, que no estaban basados en los dioses o los demonios, por ello se le considera como el precursor que dio paso de los mitos al mundo de la razón.
Utilizando los archivos astronómicos de los babilonios y de los egipcios pudo predecir con exactitud un eclipse solar en el siglo VI antes de esta era. Aunque, por otra parte, creía que la Tierra era plana y que flotaba como agua sobre un tronco.
Es un poco contradictorio pensar que pudo predecir un fenómeno tan raro como un eclipse, pero que tenía una idea sobre la forma de la Tierra, que estaba equivocada.
Aunque se tiene entendido, que desde la antigua Grecia se sabía que la Tierra era una esfera. Esta idea se le atribuye a Aristóteles, que creía que la Tierra era, en efecto, una esfera, aunque la localizaba en el centro del universo y postulaba que el Sol, la Luna, los planetas y todas las estrellas fijas giraban alrededor de ella.
Sus ideas fueron ampliamente aceptadas por los griegos de la época, sin embargo, apareció una excepción a esta idea originada por Aristarco, uno de los primeros creyentes del heliocentrismo.
Sin duda alguna, las cosmogonías enseñan mucho de las civilizaciones que las crearon, y muestran sus creencias y los fenómenos que eran importantes para ellos.
La observación de los astros ha sido parte fundamental de la humanidad, principalmente para ayudar a establecer periodos de siembra y recolección de cultivos, así como establecer fechas.
Sin embargo, la ciencia tuvo que romper con los dogmas tradicionales para poder encontrar respuestas a las preguntas fundamentales sobre el origen, dinámica y futuro del universo.
Quien revolucionó la percepción de la teoría del origen del universo fue Galileo a través de sus contribuciones al método experimental; con él nació una nueva manera de hacer ciencia, al observar los fenómenos, elaborar hipótesis, deducir y contrastar hechos, no como lo hacían los antiguos griegos, quienes no experimentaban y sólo discutían ideas. Como consecuencia de esta nueva manera de generar conocimiento, se desarrollan diversos instrumentos científicos y tecnológicos.
De este modo, a través de la evidencia surgieron nuevas hipótesis y teorías que tratan de explicar el origen y futuro del universo.
Las cosmogonías resultan interesantes, ya que cada cultura tiene una explicación propia para el origen del universo. Tan sólo en el país existen por lo menos dos perspectivas del origen: de los mayas y los aztecas.
Has concluido el tema del día de hoy.
El Reto de Hoy:
Revisa tus respuestas que escribiste a las preguntas que se hicieron al inicio de la sesión. De ser necesario, complementa o corrige tus respuestas.
Si no recuerdas las preguntas, éstas son:
- ¿Conoces alguna leyenda que explique el origen del universo? Escribe un pequeño relato de ella.
- ¿Conoces alguna teoría que explique el origen del universo?, ¿en qué consiste?
- ¿Cómo consideras que se formó el universo?, ¿piensas que siempre ha existido?
Recuerda consultar tu libro de texto o fuentes confiables de información para que puedas conocer más y resolver las dudas que pudieron surgir.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario