Aprende en Casa III SEP: 24 de febrero TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 24 de febrero de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Miércoles 24 de febrero, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Un subibaja matemático: proporcionalidad inversa
Aprendizaje esperado: Analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.
Énfasis: Analizar situaciones de proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica.
¿Qué vamos a aprender?
En esta sesión, profundizarás en la proporcionalidad inversa e identificarás sus principales características. Para ello, analizarás y resolverás problemas que se modelan con este tipo de variación a partir de sus representaciones algebraica, tabular y gráfica.
¿Qué hacemos?
Antes de comenzar, reflexiona en lo siguiente, ya que te servirá para la resolución de los problemas que se presentarán en esta sesión.
Si tuvieras que describir el movimiento de un carrito de juguete en línea recta, ¿qué aspectos considerarías?
Una descripción sencilla del movimiento del carrito sería que, en la velocidad interviene la distancia y el tiempo, por ejemplo.
Para profundizar en ello, considera algunos aspectos de la física. La velocidad media de un objeto es la razón o cociente de la distancia recorrida por el objeto entre el tiempo transcurrido. En lenguaje algebraico se dice que “v” es igual a “d” entre “t”
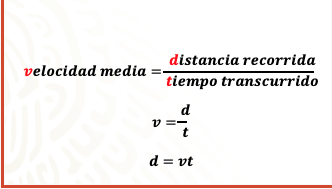
En donde despejando a “d”, se tiene que es igual a “v” por “t”.

Pero ¿por qué despeja “d”? En este caso, la distancia está fija, mientras que la velocidad y el tiempo del carrito son variables. Para comprender esta relación, analiza la siguiente situación.
Situación-problema: carrito de juguete
Antonio juega con su carrito de juguete, lo lanza 4 veces hacía una pared que se ubica a “10 m” de distancia. La hermana de Antonio utiliza un cronómetro para registrar en una tabla el tiempo (t) que el carrito tarda en llegar a la pared en cada lanzamiento.
Obteniendo en el primer lanzamiento 5 segundos; en el segundo lanzamiento, 10 segundos; en el tercer lanzamiento, 3 segundos, y en el cuarto lanzamiento, 6 segundos.
¿Cuál es la velocidad (v) del objeto para cada tiempo (t)?

Al observar los datos de la tabla, se puede deducir que el carrito lleva velocidades distintas al recorrer la misma distancia.
Analiza el comportamiento de las variables tiempo (t) y velocidad (v) involucradas. Para ello, considera las siguientes preguntas:
- ¿Cuál es la velocidad (v) del objeto para cada tiempo (t)?
- ¿Cómo se comporta la velocidad (v) del carrito respecto al tiempo (t)?
- ¿Qué relación existe entre el tiempo (t) y la velocidad (v) correspondiente?
Ahora, analiza los datos calculando las velocidades correspondientes organizando el tiempo de menor a mayor.
Utiliza la fórmula: d = v t Sustituyendo el valor de “d” igual a 10 metros, se tiene que:
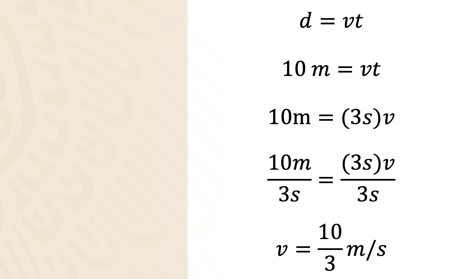
Ahora sustituye a “t” por 3 segundos, que es el menor tiempo que se obtuvo y realiza las operaciones correspondientes:

Por lo tanto, para calcular la velocidad correspondiente, los 10 metros se dividen entre el tiempo en segundos que tardó el carrito en el lanzamiento.
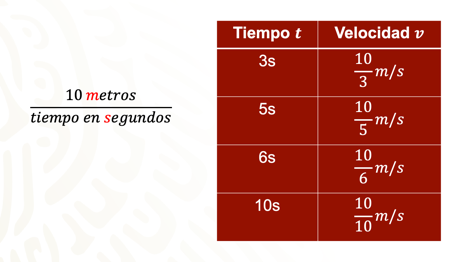
Con lo cual se puede completar el primer renglón de la siguiente tabla. En la primera columna están ordenados, de menor a mayor, los tiempos de cada lanzamiento.

De la misma manera que se realizó para el primer renglón, se pueden obtener el resto de las velocidades que faltan en la segunda columna, obteniendo 10 entre 5 metros sobre segundo en el segundo renglón, 10 entre 6 metros sobre segundo en el tercer renglón, y 10 entre 10 metros sobre segundo en el último lanzamiento. Con esto la tabla queda de la siguiente manera:
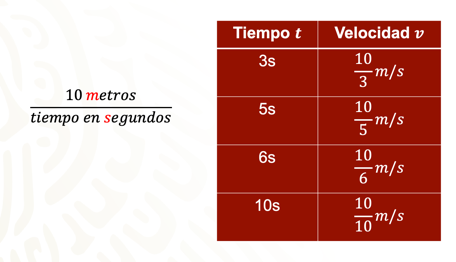
Ahora, analiza los datos obtenidos.
Observa el segundo y cuarto renglón, se tiene que el tiempo aumenta al doble mientras la velocidad media disminuye a la mitad.
El doble de 3 segundos es 6 segundos, por otro lado, la mitad de “10 tercios de metros sobre segundo”, es “10 sextos de metros sobre segundo”.
Pero ¿qué pasa con la velocidad si el tiempo aumenta al triple?
El tiempo dado es: t = 9 segundos, y se sabe que la velocidad se obtiene con la siguiente fórmula:

Sustituyendo el tiempo se obtiene la velocidad, 10 sobre 9 metros por segundo.

Observa que: 10 novenos es igual a un tercio por 10 tercios de metros sobre segundo. Es decir, la velocidad disminuye una tercera parte mientras el tiempo aumenta al triple.

Por lo tanto, se puede decir que conforme el tiempo aumenta, la velocidad disminuye en la misma proporción. Además, el producto entre el tiempo (t) y la velocidad (v) es igual a 10, la cual se llama constante de proporcionalidad inversa.
Pero ¿qué pasa con el tiempo si la velocidad aumenta al triple?
Piensa que la velocidad (v) es de 4 metros por segundo. Utilizando la fórmula: d = v t Entonces se tiene que:

Realizando las operaciones correspondientes, se tiene que “t” es igual a cinco medios que es igual a 2.5 segundos.


Comparando con la velocidad 1 m/s del penúltimo renglón, se identifica que una velocidad de 4 m/s es el cuádruple o 4 veces, mientras que el tiempo 2.5 segundos que se obtiene es la cuarta parte de 10 segundos.
A partir de los casos anteriores se puede decir que las variables “t” y “v” son inversamente proporcionales.
Continúa con otra situación de este tipo.
En la geometría también se presentan situaciones de proporcionalidad inversa, específicamente en el cálculo de áreas. Analiza el siguiente problema agrario.
Situación-problema: agrario
Un campesino ejidal quiere cercar un terreno rectangular de 120 metros cuadrados de superficie donde piensa cosechar maíz para cuidarlo del maíz transgénico
¿Cuáles son las dimensiones del terreno?
Para que puedes responder, apóyate de lo que ya sabes, es decir, el área de un rectángulo es igual a su base por su altura. Observa algunas posibles opciones de terrenos rectangulares:
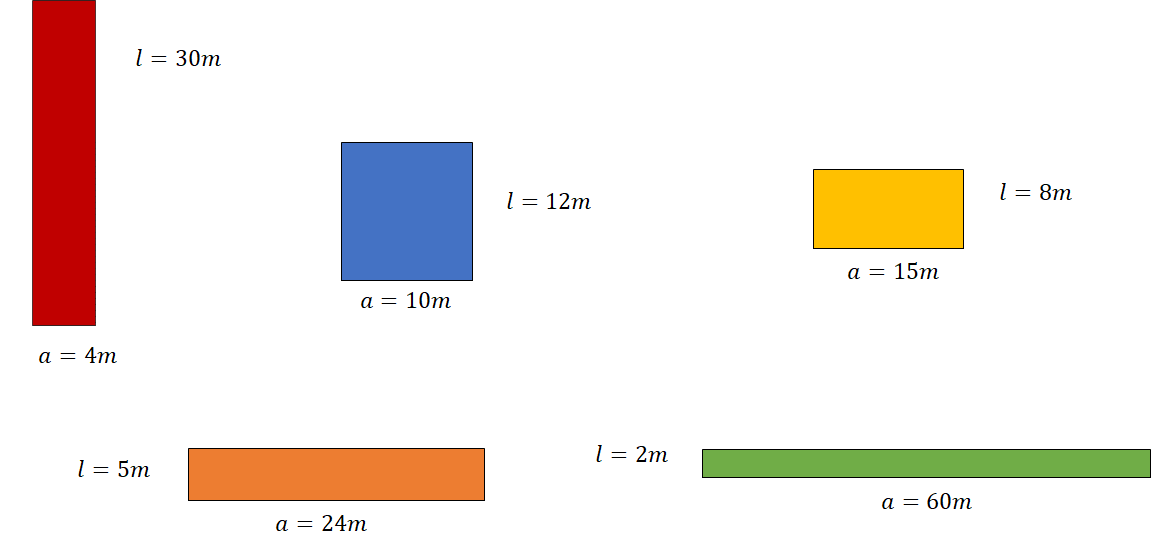
El terreno rojo tiene 4 metros de base y 30 metros de altura, mientras que el terreno azul mide 10 metros de base y 12 metros de altura, y así sucesivamente, sin olvidar que todos deben tener 120 metros cuadrados de área.
Considera que hay terrenos de distintos tamaños, unos más alargados, otros más anchos, algunos con forma de cuadrado, pero la clave está en que se pueda ordenar la información para identificar relaciones que a simple vista no son fáciles de percibir.
Para poder analizar mejor el comportamiento de las dimensiones de los rectángulos, organízalos como se muestra en el siguiente esquema.
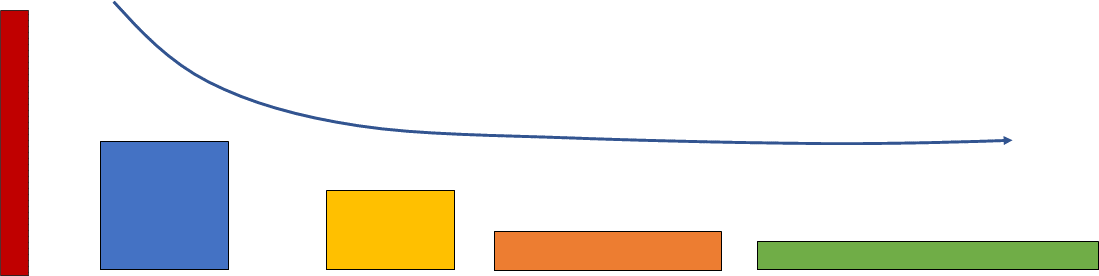
Ahora, se puede observar que las alturas de los rectángulos van disminuyendo conforme las bases aumentan, pero la pregunta clave es: ¿las alturas disminuyen mientras las bases aumentan en la misma proporción?
Para responder esta pregunta, elabora una tabla de datos con 4 columnas: en la primera colocarás el color del rectángulo; en la segunda, la longitud de las bases “b”; en la tercera columna, la longitud las alturas “a”; y al final el producto de ambas para confirmar que el rectángulo con dichas dimensiones tiene 120 metros cuadrados de superficie.
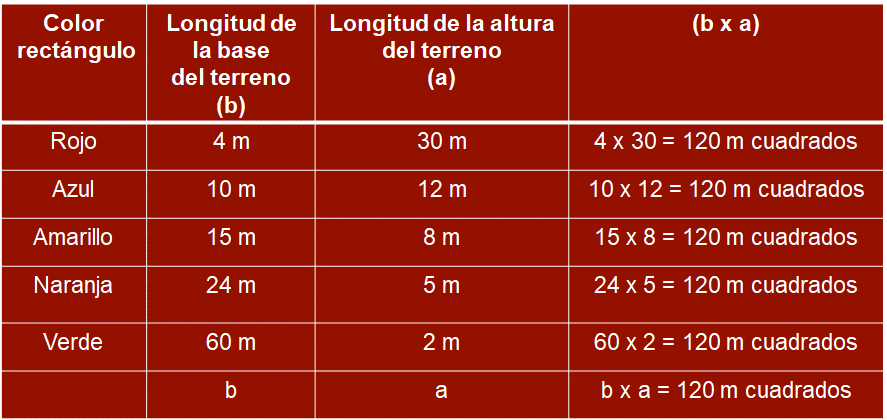
Los datos de cada rectángulo se ordenaron de manera creciente respecto a la base del terreno. El rectángulo rojo su base mide 4 metros y su altura es de 30 metros, mientras que en el rectángulo azul su base mide 10 metros y su altura es de 12 metros, y así sucesivamente hasta completar la tabla con los datos que se tienen. ¿Qué observas?
Existe un comportamiento similar de variación entre las magnitudes de la base y la altura de los rectángulos; por ejemplo, en el rectángulo rojo su base es la sexta parte de la base del rectángulo naranja, mientras que la altura del rectángulo rojo es seis veces la altura del rectángulo naranja.
Un comportamiento similar se tiene con las dimensiones del rectángulo amarillo y el rectángulo verde, mientras que la base del rectángulo amarillo es la cuarta parte de la base del rectángulo verde, la altura del rectángulo amarillo es cuatro veces la altura del verde.
Por ello, se puede decir que la base del terreno aumenta y la altura del terreno disminuye en la misma proporción, con constante de proporcionalidad igual a 120. Entonces, las magnitudes “b” y “a” son inversamente proporcionales.
Es momento de recapitular lo discutido hasta el momento.
Dos magnitudes “a” y “b” en proporción inversa:
- Su producto es constante “a” por “b” es igual a “k”
- Cuando una de ellas aumenta, la otra magnitud disminuye en la misma proporción.
- “k” es la constante de proporcionalidad.
Con ello, se puede plantear un problema inverso, es decir, partir de dos magnitudes que son inversamente proporcionales para calcular datos faltantes.
En los problemas anteriores lo que has hecho es partir de datos para inferir si la relación entre ellos es una proporción inversa. Ahora, la idea es aplicar lo discutido para encontrar valores faltantes en una relación de proporcionalidad inversa para ayudar en la toma de decisiones.
Analiza el siguiente problema.
Situación-problema: alimento de vacas
Un productor lechero tiene pasto y alimento procesado para mantener a 162 vacas durante 4 meses, pero sabe que habrá desabasto alimenticio en los próximos meses.
¿Cuántas vacas se podrán mantener en la finca durante 12 meses con el mismo alimento, si suponemos que todas las vacas comen la misma cantidad de alimentos?
Observa que la cantidad de alimento será la misma, es constante, lo que va a aumentar es el tiempo, entonces es de esperar que el número de vacas que se pueden alimentar sea menor, suponiendo que las condiciones son las mismas siempre. Por lo tanto, el tiempo “t” y el número de vacas “v” será inversamente proporcional.
Para iniciar con la resolución de este problema, elabora una tabla con los siguientes datos: una columna para el tiempo y otra para el número de vacas; en donde para el tiempo de 4 meses corresponden 162 vacas y para el tiempo de 12 meses corresponde un valor faltante de vacas “v” que se debe calcular.

Por las características de una proporción inversa, se sabe que los productos de los elementos en cada renglón son iguales a la constante de proporción. Entonces:
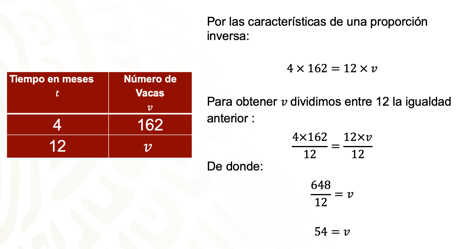
Para obtener “v”, se divide entre 12 la igualdad anterior:

Realizando la división de 648 entre 12 se tiene que 54 es igual a “v”. Es decir, el número de vacas que podrá alimentar el granjero son 54

Con dicho dato el granjero ya tomará una decisión sobre si va a tener que vender algunas de sus vacas o trasladarlas a otra granja, lo que mejor le convenga.
¿Ya identificaste cómo las proporciones inversas pudieron ayudar a tomar decisiones? Las matemáticas pueden llegar a ser divertidas e interesantes, aunque hay que tener cuidado sobre cuándo concluir que dos variables o magnitudes son inversamente proporcionales.
Analiza la siguiente situación.
Situación-problema: terreno rectangular
El campesino ejidal ahora quiere cercar un terreno rectangular con 120 metros de malla. ¿Cuáles pueden ser las dimensiones del terreno?
Para resolver este problema, primero trabajarás con el perímetro del rectángulo, ya que se quiere cercar el terreno, a diferencia del problema anterior donde el campesino tenía un problema referente al área.
Observa algunos posibles tamaños del rectángulo que el campesino puede cercar.
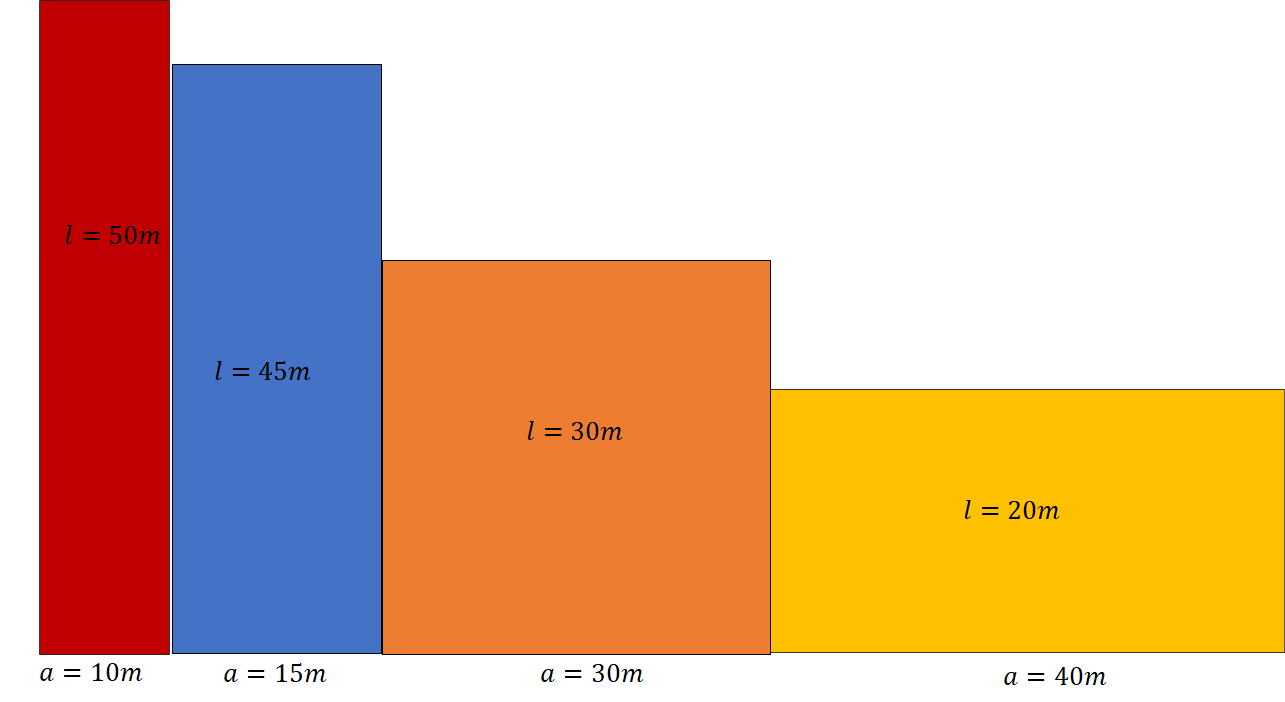
Una opción puede ser el rectángulo rojo de 10 metros de ancho y 50 metros de largo, como cada lado se repite en la figura, se tiene que su perímetro es igual a dos veces 10 más dos veces 50, lo cual da 120 metros. Otra opción puede ser el rectángulo azul que mide 15 metros de ancho y 45 metros de largo, también el rectángulo naranja de ancho y largo iguales a 30 metros, y el rectángulo amarillo 40 metros de ancho y 20 metros de largo. A primera vista se puede pensar que es un problema de variables inversamente proporcionales.
Ahora, elabora una tabla donde organices los datos de las posibles opciones para el ancho “a” y el largo “l” del terreno: en la primera columna colocarás el color del rectángulo; en la segunda columna, la longitud de su ancho; en la tercera columna, la longitud de su largo; y al final se calcula el perímetro para verificar que se obtienen los 120 metros de malla.
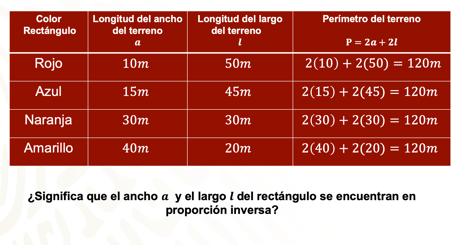
En el primer renglón, para el rectángulo rojo su ancho “a” es de 10 metros, mientras que su largo “l” es de 50 metros. Se realizan las operaciones correspondientes y se verifica que el resultado es 120 metros. Y así sucesivamente para el resto de los rectángulos.
Ahora, observa con detenimiento la tabla. Se nota que el ancho y el largo del rectángulo se comportan de tal manera que conforme uno aumenta el otro disminuye, ¿significa que el ancho “a” y el largo “l” del rectángulo se encuentran en proporción inversa?
Recuerda que una condición que deben satisfacer “a” y “l” consiste en que, su producto en cada renglón debe ser constante para reconocer la constante de proporcionalidad.
Para comprobarlo, elabora una tabla como la siguiente, donde en la última columna se encuentran los productos correspondientes a cada renglón:

Analizando, los productos “a” por “l” de esta tabla no son constantes. Por ello las variables “a” y “l” no son inversamente proporcionales.
A primera vista uno podría suponer que las magnitudes de los lados del rectángulo en este caso también eran inversamente proporcionales, ya que tienen el comportamiento de un subibaja, mientras una aumenta, la otra disminuye.
Por ello, debes analizar el comportamiento de las variables, ya que la condición de que sus productos sean constantes no se satisface. Aunque una de las variables aumenta y la otra disminuye, no lo hacen en la misma proporción, ya que, si observas el segundo y tercer renglón, el ancho “a” del rectángulo aumenta al doble, mientras que el largo “l” no disminuye a la mitad, es decir, “a” aumenta y “l” disminuye, pero no en la misma proporción. Entonces, se puede decir que, el ancho “a” y el largo “l” del rectángulo no son inversamente proporcionales.
Aunque el comportamiento de dos variables o magnitudes sea que una crece mientras la otra decrece, eso no es suficiente para decir que dos variables son inversamente proporcionales.
Las características que debe cumplir una proporción inversa siempre deben verificar que los productos, entre ellas las variables, sean igual a una constante o, en otras palabras, mientras una variable crece, la otra decrece en la misma proporción y viceversa.
Has finalizado esta sesión. Recuerda que este es un material de apoyo y puedes consultar otras fuentes para complementar lo que aprendas aquí, como tu libro de texto de Matemáticas.
El Reto de Hoy:
Analiza y responde las siguientes preguntas.
En una proporción inversa:
¿Existen cantidades inversamente proporcionales cuya constante de proporcionalidad pueda ser negativa?
¿Qué signos deben tener las cantidades consideradas para que su constante de proporcionalidad sea una constante negativa?
Reflexiona y considera algún caso práctico donde se opere con cantidades con signos distintos.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
La poesía también se pinta
Aprendizaje esperado: Crea textos poéticos con formas gráficas.
Énfasis: Identificar características de caligramas.
¿Qué vamos a aprender?
Continuarás con el estudio de los textos poéticos con distintas formas graficas. En esta sesión, estudiarás las características de los caligramas, conocerás algunos de sus autores más representativos y revisarás sus aportaciones.
¿Qué hacemos?
Analiza la siguiente información, que te servirá para comenzar a profundizar en el tema de esta sesión.
Para escribir un poema, no necesariamente tienes que hacerlo de manera tradicional, puedes crear dibujos con palabras. A este tipo de poema se le llama caligrama. El tamaño de las letras, la puntuación y la distribución de las palabras te ayudarán a crear una imagen que reforzará los sentimientos que deseas transmitir.
Seguramente en tu vida has leído textos poéticos, y te has dado cuenta de que éstos ayudan a ver cosas que antes no percibías, que despiertan ciertos sentimientos que antes no habías experimentado y favorecen el desarrollo de tu sentido del humor e imaginación.
La palabra poesía proviene del griego poíÄ“sis, que significa “hacer o realizar algo”, es decir, mediante un poema se puede dar forma a las reflexiones, emociones y preocupaciones personales.
La poesía tiene muchas formas y características; puede hablar de temas como el amor, la tristeza, la soledad, el universo, la naturaleza, entre otros.
Los poemas no sólo pueden escribirse en verso, también existe algo que se denomina prosa poética, la cual se organiza en párrafos o en formas gráficas diversas, mediante estas estructuras es posible conjugar formas y contenidos. Para comprender lo anterior, observa la siguiente imagen.

Reflexiona en lo siguiente:
¿Qué forma logras distinguir?
¿De qué te imaginas que trata?
La imagen anterior, es un claro ejemplo de caligrama, y tiene la forma de un pájaro. Ahora, lee con atención si en efecto habla acerca de ello.
"Un pájaro que trina musical y breve, como una ocarina en un almendro florido de nieve".
José Juan Tablada
Este caligrama es del escritor mexicano José Juan Tablada, a quien también se le atribuye la introducción del haiku en la literatura mexicana.
Los caligramas son poemas en los que la tipografía y la disposición de las palabras forman figuras o imágenes relacionadas con el contenido y el sentido del texto. Por esta razón, a los caligramas también se les llama poesía visual o poesía concreta.
En el ejemplo anterior, Tablada se inspiró en la imagen de un pájaro postrado en una rama de almendro. El poema se compone por frases breves, e incluso tiene una rima, trina/ocarina; es decir, compara el trino del ave con el sonido de la ocarina, que es parecido al de un silbato.
Muchos expertos sitúan el nacimiento de la poesía visual en las creaciones del poeta Simmias de Rodas, que vivió en Grecia alrededor del año 300 a.C. Sus obras estaban diseñadas para escribirse encima de objetos, que después se obsequiaban.
La siguiente obra, titulada “El hacha”, es una de las obras atribuidas a él. Los versos de este poema forman dos semicírculos alrededor de un eje central. Los versos impares se sitúan a la derecha del eje, y los pares a la izquierda. Se debe comenzar la lectura por la línea superior derecha hasta completar el círculo.

De este autor, sólo se conservan tres piezas: “las alas”, “el huevo” y “el hacha”.
Como puedes observar, en los caligramas se hace uso del lenguaje figurado, a fin de lograr que su contenido sea más expresivo. Es por lo que se suelen encontrar comparaciones, semejanzas, entre otros recursos.
A continuación, observa el siguiente video para conocer un poco más acerca de la poesía concreta.
- Libro poema.
https://www.youtube.com/watch?v=NYmHao1qPTU
En la mayoría de los casos, las letras, antes de ser eso, eran más figuraciones o acercamientos a un objeto. Uno de los máximos exponentes de esta estructura vanguardista fue el francés Guillaume Apollinaire, quien introdujo los caligramas en el panorama artístico de inicios del siglo XX, pero ya desde la Antigüedad existían, como lo viste con Simmias de Rodas, pero es partir de Apollinaire que autores de otros países siguieron su ejemplo y exploraron la poesía visual.
Apollinaire popularizó esta figura poética a comienzos del siglo XX, en un intento por innovar la creación literaria que le trajo reconocimiento internacional. En 1918, publicó una colección de poemas titulada “Calligrammes, Poèmes de la paix et de la guerre” (1913-1916), que incluía diversos poemas que representaban visualmente varias situaciones.
Trataba de que la literatura no fuera opacada por el nacimiento del cine. Algunos caligramas son divertidos y otros son dedicados a amigos, a la guerra, al amor y otras cuestiones. Cada caligrama se proponía liberar a los lectores de la poesía tradicional.
Él le dio el nombre al caligrama, ya que es una contracción de las palabras caligrafía e ideograma. Asimismo, desarrolló una forma de expresión que llamaba "el acto de escribir con belleza".
Los caligramas hacen convivir a la poesía con el dibujo. Esa unión da pie a una variación sintáctica, distributiva, tipográfica y de lectura. Además, promueve nuevas interpretaciones y significaciones, y sobre todo, propone una crítica lúdica de la guerra a partir de la palabra y la imagen.
Observa el siguiente caligrama “La mandolina, el clavel y el bambú” para conocer más acerca de su obra.
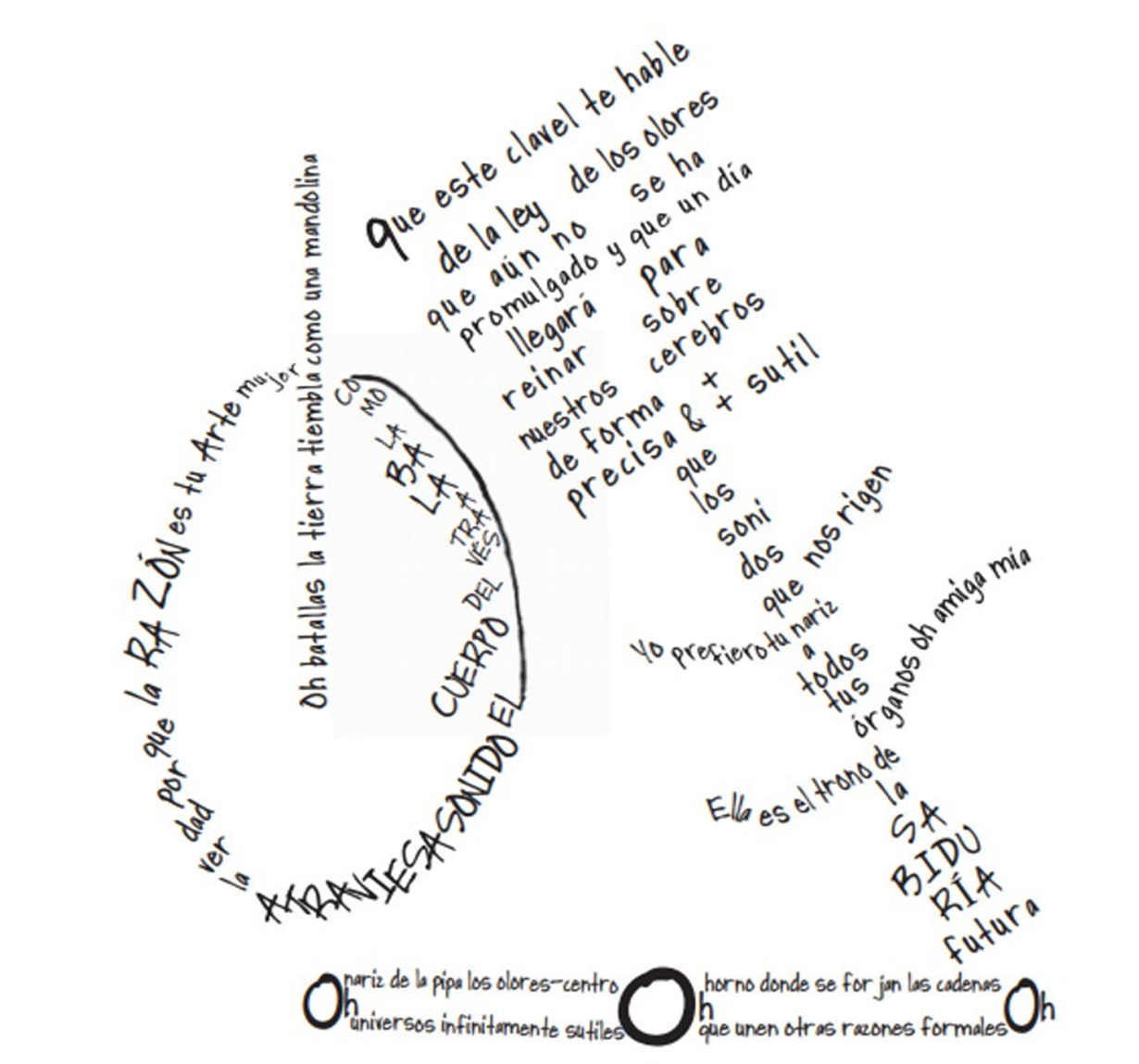
Ahora, lee con atención lo que dice en él:
"Oh batallas la tierra tiembla como una mandolina, como la bala a través del cuerpo, el sonido atraviesa la verdad porque la razón es tu arte mujer…
… que este clavel te hable de la ley, de los olores que aún no se ha promulgado y que un día llegará para reinar sobre nuestros cerebros de forma más precisa y sutil que los sonidos que nos rigen…
… yo prefiero tu nariz a todos tus órganos amiga mía. Ella es el trono de la sabiduría futura. Oh nariz de la pipa los olores centro, oh universos infinitamente sutiles. Oh horno donde se forjan cadenas que nutren otras razones formales."
¿Qué pudiste observar en el caligrama anterior? ¿En qué se diferencia con los poemas convencionales?
El texto va en diferentes direcciones, además, se observan las formas de un clavel y una mandolina. Para entender los nombres que reciben estas características, presta atención a lo siguiente:
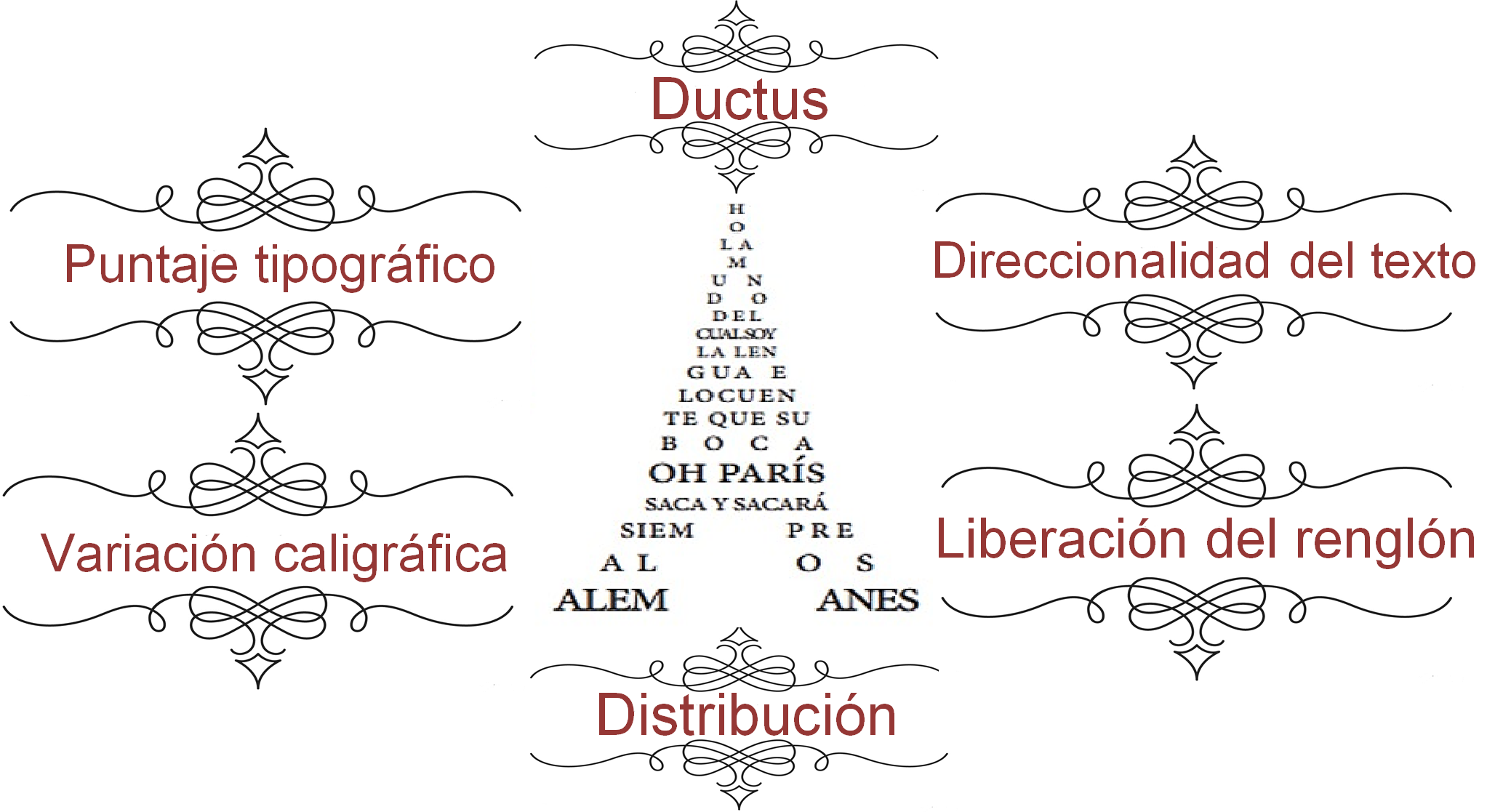
Al juego sintáctico de Apollinaire se agrega:
- El contraste de puntaje tipográfico para resaltar tamaños, es decir, jugar con el tamaño de las letras.
- La variación caligráfica no sólo depende de redondas o itálicas.
- También la distribución de las imágenes trazadas, que pueden ser dependientes o independientes.
- El ductus: cuando una misma letra o palabra se emplea para dos versos.
- La direccionalidad del texto: cuando se lee hacia arriba, en espiral, de derecha a izquierda o hacia cualquier otra dirección.
- Así como la liberación del renglón: cuando las letras o sílabas salpican el poema y la lectura comienza donde lo decide el lector.
Ahora que ya conoces estas características, puedes identificar que en el caligrama de “La mandolina, el clavel y el bambú” se incluyen los elementos anteriores, ya que se utilizan diferentes tamaños de letras, se forman tres figuras con ayuda de los versos y no hay un punto en específico para iniciar la lectura.
Otro ejemplo es el poema “Océano-carta”. En él, Apollinaire aborda los conocimientos de México que pudo tener. Lo más bello es la forma en la que explota la disposición de una tarjeta postal. Además, emplea dibujos, en este caso, líneas onduladas. Si deseas saber más sobre este poema, puedes buscar las imágenes y analizarlas.
En los caligramas la rima tiende a desaparecer, ya que como se mencionó anteriormente, no existe un orden lineal que pueda evidenciarse. También cuentan con juegos de palabras que incorporan la sátira o humor en los escritos.
Dos movimientos que aprovecharon mucho la libertad creativa que les brindaban los caligramas fueron “el creacionismo”, pues los poetas proclamaron absoluta libertad para crear, alejados de las formas convencionales; y “el cubismo”, que intentaba reflejar a través de la imagen, ángulos nunca vistos de la realidad.
La obra del poeta argentino Oliverio Girondo, es una de las más singulares y menos conocidas de la poesía hispanoamericana del siglo XX, lo que le convierte en una figura de culto. Su poesía se traslada de lector a lector como una secreta confidencia; constantemente se descubre su nombre en las antologías más insospechadas, escondido como un poeta furtivo.
Ha llegado el momento de realizar una actividad, la cual consiste en un juego que les gustaba a los surrealistas, ellos fueron los artistas que revolucionaron la forma del ver el arte en el ajetreado siglo XX.
Actividad: caligrama
Toma un libro, una revista o cualquier otro papel impreso. Después, cierra los ojos y señala con tu dedo cualquier página para elegir una palabra.
Posteriormente, anótala en tu cuaderno. Vas a repetir varias veces el mismo procedimiento hasta contar con las palabras suficientes.
Ya que tengas las palabras seleccionadas, vas a usar como motivo visual la palabra que elegiste al inicio. Es decir, dibujarás con palabras tu motivo visual.
Antes de realizar esta actividad, analiza el siguiente poema de Oliverio Girondo, “Yo no sé nada”, a través del siguiente video, para que te algunas ideas y desarrolles tu propio caligrama.
- Video. Caligrama “Yo no sé nada”.
“Yo no sé nada” toma la figura del espantapájaros, protagonista del libro. El juego figurativo arranca con la declaración de ignorancia general en la cabeza, llena de paja, del espantapájaros. El cuerpo, una serie de preguntas, dudas y casi afirmaciones de un poeta que forma parte de una vanguardia estética que rompe deliberadamente con lo anterior. Una juventud de entreguerras que toma un mundo partido y lo deforma hasta que se pierde y emerge como en otro mundo. Finalmente, en las piernas, el cantar de las ranas que suben y bajan y buscan allí y buscan acá para recuperar el sentido.
Para que te sientas más segura o seguro, puedes elegir un poema que ya exista y transcribirlo, pero de forma que con él puedas crear una imagen. Otra opción puede ser dibujar siluetas sencillas, como el viento, las olas, una hoja de un árbol o una letra, de modo que seas capaz de plasmar lo que sientes al pensar en estos objetos.
Cabe señalar que, no todos los autores se adaptaron a las reglas de esa vanguardia. Por ejemplo, el chileno Vicente Huidobro no aplicó los cambios de Apollinaire, sino que se basó en la forma original del caligrama, es decir, la de los griegos, a pesar de su conexión con el movimiento.
Para Huidobro: "El poema creacionista se compone de imágenes creadas, de situaciones creadas, de conceptos creados; no escatima ningún recurso de la poesía tradicional, salvo que en él dichos elementos son íntegramente inventados, sin preocuparse en absoluto de la realidad ni de la veracidad anterior al acto de creación". Observa el siguiente ejemplo:

La armonía a la que se refiere el título no va dirigida al texto, pues aunque habla de una princesa japonesa y su belleza, se preocupa más por la composición geométrica del signo. Se puede decir que, su única intención era la de hacer una figura geométrica y equilibrada a través de las palabras.
El caligrama, si lo piensas, es una estrategia poética que ayuda a enviar mensajes y a romper estructuras. Además, evoca sentimientos, emociones, sensaciones y provoca en el lector una percepción espacial.
Con esto, has concluido la sesión. Recuerda que puedes leer más ejemplos en tu libro de texto de Lengua Materna 2, así como visitar el sitio de la Nueva Escuela Mexicana para ampliar tus conocimientos sobre el tema.
El Reto de Hoy:
Revisa el siguiente poema de Tablada y analízalo. Después, contesta las siguientes preguntas:
- ¿Qué figuras se forman a través de las palabras?
- ¿Qué versos le podrían agregar a este caligrama?
- ¿Qué figuras formarían?

Finalmente, integra esos versos a la composición y comparte tus resultados con tus familiares.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Acordar para solucionar
Aprendizaje esperado: Analiza el conflicto y opta por la forma más conveniente para lograr objetivos personales sin dañar al otro.
Énfasis: Valorar la mediación como alternativa para solucionar los conflictos.
¿Qué vamos a aprender?
En esta sesión, conocerás algunos aspectos que te permitirán reflexionar sobre tus ideas, conductas y acciones de la vida cotidiana. Además, comprenderás la importancia de dialogar y tomar acuerdos para resolver los conflictos, como la mediación y la negociación.
¿Qué hacemos?
Analiza la siguiente información.
Somos seres libres, lo que significa que tenemos la capacidad de decidir sobre lo que hacemos. Pero, nuestra libertad termina donde comienza la de otros, esto quiere decir que, algunas veces nuestros deseos pueden afectar la libertad de los demás.
Por ejemplo: eres libre de elegir una silla en la mesa, pero no puedes elegir un asiento donde alguien más se encuentra desde antes, pues esto implicaría que quien está ocupando ese lugar, estaría obligado a quitarse, entonces ella o él no tendría la capacidad de elegir libremente un lugar para sentarse. Tu libertad, entonces, se limita cuando se encuentra con la de las demás personas y esto pasa en todo momento.
Además de la libertad, otros principios de la democracia y de la Cultura de Paz son: la igualdad, la equidad y la justicia. Por lo tanto, sólo cuando todas y todos somos igualmente libres, hay justicia y viceversa; así que es necesario que prevalezcan todos estos principios juntos para evitar la violencia y vivir en paz.
La convivencia entre las personas implica una serie de retos para vivir en paz y en el pleno respeto a los derechos de todas y todos.
Tenemos derecho a pensar, hablar y hacer ciertas actividades, mientras que, al mismo tiempo, estamos obligados a abstenernos de pensar, decir y hacer otras tantas porque pueden afectar a otras y otros.
Cuando nuestras acciones, aun siendo un derecho, afectan los derechos de las y los demás, es entonces, cuando surgen los conflictos. Recuerda que el conflicto es la imposibilidad de que dos personas puedan ejercer su derecho o libertad sin tomar en cuenta a los demás. Generalmente surgen estos desacuerdos por los siguientes motivos.
Por escasez: esto es, cuando dos personas desean una misma cosa que no se puede o no se quiere dividir o compartir. Por ejemplo, una silla, un billete, un dulce, etc.
Por abuso: es cuando alguien hace valer su derecho por la fuerza.
Por engaño: es cuando alguien miente para hacer su voluntad. También se llama fraude.
Por mala comunicación: esto es, cuando no hay un conflicto real, pero alguien cree, por ignorancia, falta de información o un malentendido, que ha sido afectado por la acción de otra u otras personas.
Como podrás darte cuenta, los conflictos son parte de lo cotidiano y no siempre se pueden evitar. Por lo tanto, debes entender que, como dijo la periodista Dorothy Thompson:
"La paz no es la ausencia de conflictos, sino la presencia de opciones creativas para afrontarlos; alternativas a las respuestas pasivas o agresivas, opciones para evitar la violencia".
A continuación, escucha el testimonio de Yaretzi, alumna de secundaria, que cuenta sobre su experiencia y la forma en que ella pudo encontrar una solución a un conflicto.
- Video. Solución a un conflicto, testimonio 1.
¿Has coincidido con Yaretzi y María en la forma de solucionar los conflictos?
Para poder llegar a resolver un conflicto, es necesario analizar la situación para conocer sus partes y las funciones de cada una de ellas. Los elementos del conflicto son los siguientes.
Las partes: es cada una de las posiciones confrontadas, puede ser una persona en cada parte, o un grupo de personas.
Objeto de la discordia: representa a menudo un bien escaso o una situación donde alguien salió afectado.
Mediador: es una persona que no pertenece ni tiene un interés o simpatía especial por alguna de las partes que contribuye al diálogo.
Una vez que se identificaron los elementos, debes buscar las condiciones mínimas para establecer un diálogo entre las partes. Estas son, entre otras.
- Que las partes estén tranquilas y tengan voluntad de hablar y escuchar.
- Que se tenga la seguridad de que se ha renunciado a toda forma de violencia (mentiras, burlas o ironías, insultos, gritos, amenazas o agresiones físicas)
- Que todos respeten las normas del diálogo, sin descalificaciones ni engaños.
La importancia del diálogo es imprescindible. Cuando una persona se reúsa a contestar una solicitud o propuesta o a expresar sus deseos y puntos de vista sin motivo que lo justifique, la posibilidad de llegar a acuerdos se desvanece y los conflictos no pueden ser superados.
La palabra y el lenguaje, es lo que nos distingue de los animales y del estado de naturaleza donde se impone la ley del más fuerte y no la justicia, es por eso que, nunca podemos renunciar ni evadir tanto los conflictos como ese proceso de sanación social que es el diálogo.
Observa el siguiente video del minuto 1:50 al 3:00, que profundiza en lo anterior. Presta mucha atención.
- El diálogo y la solución de conflictos.
https://www.youtube.com/watch?v=fsdRq04hfvE
Sólo la palabra y el diálogo pueden conducir al entendimiento mutuo que es necesario para superar un conflicto. Debes recordar que la propia palabra “diálogo” etimológicamente hace referencia a un medio o método para entenderse unas personas con otras, a través del intercambio de argumentos que lleven a ponerse de acuerdo.
Un conflicto no pasa de su inicio a su resolución inmediatamente, sino que es necesario que se resuelva a través del intercambio respetuoso de demandas y puntos de vista entre las partes. Es así como surge la figura del mediador o mediadora, como aquella persona que ayuda a las partes a establecer el diálogo y llegar a un acuerdo.
Observa el siguiente video del minuto 1:08 al 1:50, que explica más sobre esta labor de la mediación.
- La mediación en la solución de conflictos.
https://www.youtube.com/watch?v=-lsifcMK9oQ.
La mediación requiere que la persona que funja como mediadora o mediador, sea neutral en el conflicto y tenga la confianza de ambas partes. Pero no sólo eso, sino que su papel debe ser siempre el de buscar que quienes están en conflicto encuentren por ellos mismos las condiciones que les satisfagan.
El mediador o la mediadora debe siempre proceder bajo los principios de la cultura de paz y evitar cualquier posibilidad de acción violenta entre las partes. Debe promover la búsqueda de coincidencias por sobre las diferencias, que son las que han causado el conflicto.
La persona mediadora debe estar a una cierta distancia del conflicto, pues si alguna decisión o acción le afecta de cualquier forma, dejará de ser neutral y no podrá cumplir sus funciones debidamente.
Es importante señalar que quien media no debe actuar como una autoridad que decida o imponga sus ideas o soluciones a las partes, pues esta no es su función, sino precisamente evitar que una autoridad imponga a alguna de las partes responsabilidades o penas. El mediador o mediadora no es un policía ni un juez en ningún caso.
Para apoyar la información anterior, observa con atención el siguiente video del minuto 1:51 al 3:20
- La mediación en la solución de conflictos.
https://www.youtube.com/watch?v=-lsifcMK9oQ
Como pudiste apreciar en el video, es necesario llegar a una solución que les convenga a ambas partes en conflicto. De esto se trata la negociación, no es imponer las necesidades de una persona sobre la otra, sino de llegar a un acuerdo donde ninguna de las dos partes se vea afectada, por el contrario, que ambos ganen y tengan la seguridad y la tranquilidad de que lo que se propone es algo justo.
El filósofo Aristóteles definía la justicia como el momento de la negociación en que finalmente ninguna de las dos partes tiene pérdidas ni ganancias. Sin embargo, en el caso de los conflictos, se deben ver bajo la óptica de la dialéctica del filósofo Friedrich Hegel, donde dos partes opuestas no se anulan, sino que se superan llegando a un nivel más alto de entendimiento.
Es por eso que, más que solucionar los conflictos o deshacerlos, se debe decir que se superaron, pues al llegar a un acuerdo, no se queda como antes, sino con una mejor posición y relación con los demás. Es la misma razón por la cual no se deben de evadir, sino de aprovecharlos para llegar a nuevos acuerdos con los otros.
Un acuerdo es el momento donde las dos partes en conflicto coinciden en cumplir con ciertas demandas o solicitudes de la parte contraria, comprometiéndose igualmente a cumplir con lo solicitado para poder lograr finalmente, lo que en un principio no se podía tener o hacer.
La persona mediadora, frecuentemente tiene la función de testigo de que las partes han alcanzado un acuerdo y ha cumplido su misión.
Lo más importante es que haya verdadera satisfacción en quienes tienen el acuerdo, pues ésta es la mejor garantía de que cumplirán con lo que se han comprometido. Si alguna de las partes no queda a gusto o de algún modo es injusto lo que se ha acordado, el conflicto volverá a surgir e incluso podría profundizarse, agravarse o generar más desacuerdos en el futuro.
Los conflictos en la historia que se han resuelto por medios pacíficos han permitido que se tenga cada vez un mejor entendimiento entre los países, a través de las negociaciones internacionales. Los acuerdos alcanzados se ven reflejados en los diferentes documentos que constituyen el derecho internacional. Y es sólo este diálogo entre naciones y grupos sociales el que ha permitido acercarnos verdaderamente a la paz.
La mediación en el ámbito internacional, frecuentemente la hacen las organizaciones internacionales como la Organización de las Naciones Unidas u otros países que fungen como mediadores neutrales, cuando surgen conflictos entre dos países.
A continuación, observa el siguiente video del minuto 3:20 al 4:20, que habla de lo que significa la negociación en todos los niveles.
- La mediación en la solución de conflictos.
https://www.youtube.com/watch?v=-lsifcMK9oQ
Antes de finalizar, recapitula. En esta sesión, reflexionaste sobre las circunstancias principales que pueden provocar un conflicto como la escasez, abuso, engaño o mala comunicación. Analizaste el papel fundamental de la mediación, de la mediadora o mediador y sus funciones en la búsqueda de acuerdos entre las partes de un conflicto. Finalmente, identificaste la importancia de la negociación para poder superar las diferencias y aprovecharlas para llegar a niveles superiores de entendimiento entre las personas.
Con esto, has concluido. Consulta tu libro de texto de Formación cívica y ética, para saber más acerca de las alternativas que tienes para solucionar los conflictos que se van presentando en la vida cotidiana.
El Reto de Hoy:
Dialoga con tus familiares, amigas y amigos acerca de las diversas formas en que pueden encontrar soluciones a conflictos que surjan en la familia, entre las amistades y la comunidad, y piensa en quién podría fungir como mediador o mediadora en caso necesario.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Guerras religiosas
Aprendizaje esperado: Reconoce hechos ocurridos en Europa y América antes y durante los viajes de exploración. También estudia la relación entre la defensa de la religión cristiana y el proceso de conquista española.
Énfasis: Reconocer el papel de la religión en la guerra de la península ibérica y las creencias religiosas y bélicas de los mexicas.
¿Qué vamos a aprender?
Estudiarás los hechos ocurridos durante el proceso de la conquista. En esta sesión, profundizarás en sus religiones y cómo estas creencias influyeron en ambas culturas, reconociendo su papel en la guerra.
¿Qué hacemos?
Para iniciar, lee el siguiente fragmento del libro “Historia General de las Indias”, escrito por el cronista Francisco López de Gómara en el siglo XVI, en específico la dedicatoria que hizo el autor al rey de España, Carlos I.
Muy soberano Señor: La mayor cosa después de la creación del mundo, sacando la encarnación y muerte del que lo creó, es el descubrimiento de Indias; y así las llaman Nuevo Mundo. Y no tanto te dicen nuevo por ser nuevamente hallado, cuanto por ser grandísimo y casi tan grande como el viejo, que contiene a Europa, África y Asia.
También se puede llamar nuevo por ser todas sus cosas diferentísimas de las del nuestro. Los animales en general, aunque son pocos en especie, son de otra manera; los peces del agua, las aves del aire, los árboles, frutas, hierbas y grano de la tierra, que no es pequeña consideración del Creador, siendo los elementos una misma cosa allá y acá.
Empero los hombres son como nosotros, fuera del color […] Mas no tienen letras, ni moneda, ni bestias de carga; cosas principalísimas para la policía y vivienda del hombre; que ir desnudos, siendo la tierra caliente y falta de lana y lino, no es novedad. Y como no conocen al verdadero Dios y Señor, están en grandísimos pecados de idolatría, sacrificios de hombres vivos, comida de carne humana, habla con el diablo, sodomía, muchedumbre de mujeres y otros así.
Aunque todos los indios que son vuestros subjetos son ya cristianos por la misericordia y bondad de Dios, y por la vuestra merced y de vuestros padres y abuelos, que habéis procurado su conversión y cristiandad. El trabajo y peligro vuestros españoles lo toman alegremente, así en predicar y convertir como en descubrir y conquistar […]
Comenzaron las conquistas de los indios acabadas la de moros, porque siempre guerreasen españoles contra infieles; otorgó la conquista y conversión el papa […] Justo es, pues, que vuestra majestad favorezca la conquista y los conquistadores, mirando mucho por los conquistados. Y también es razón que todos ayuden y ennoblezcan las Indias, unos con santa predicación, otros con buenos consejos, otros con provechosas granjerías, otros con loables costumbres y policía.
Francisco López de Gómara
Historia General de las Indias
Este texto aporta mucha información, sin embargo, te centrarás en lo que dice sobre la guerra y la religión, por ejemplo: “comenzaron las conquistas de los indios acabadas la de moros, porque siempre guerreasen españoles contra infieles”. Con esta frase se hace innegable que guerra y religión están estrechamente relacionadas para el autor.
Ahora, reflexiona en las siguientes preguntas:
¿Cuál era esa relación para los soldados españoles del siglo XVI?
¿Cuál para los mexicas?
Si bien las sociedades española y mexica del siglo XVI tenían muchas diferencias, había algo en lo que se parecían mucho y es en el papel fundamental de la religión como elemento cohesionador de la sociedad y pilar central de su forma de ver el mundo, incluyendo aspectos como la guerra.
Los españoles, como la mayoría de los habitantes del Occidente europeo de principios del siglo XVI, eran cristianos católicos. Esta religión era monoteísta, lo cual significa que creían y rendían culto a un solo dios.
El cristianismo, como su nombre lo indica, gira en torno a las enseñanzas y mensajes de Jesucristo, quien se creía que era hijo de Dios y que había venido a la tierra a salvar a los hombres del pecado original por medio de su propia muerte. Gracias a su sacrificio los hombres habían quedado libres de pecado y en posibilidades de alcanzar el cielo, siempre y cuando mantuvieran una forma recta de vivir.
Por mandato de Jesús, esta noticia la debían transmitir los cristianos a todo el mundo, por lo cual, desde muy temprano, miembros de esta religión comenzaron a propagar y llevar su noticia a todos los lugares del mundo, con la creencia de que sólo convirtiéndose a la religión cristiana y uniéndose a su iglesia, los humanos alcanzarían la salvación eterna.
Por tanto, era la misión de los cristianos transmitir y convertir a la mayor cantidad de personas. Y esta misión aplicaba por igual a sacerdotes que a reyes, por lo que, con el paso de los años, figuras políticas como el emperador Carlomagno o el rey Recaredo, comenzaron a buscar la conversión de sus súbditos al cristianismo, aún por la fuerza de las armas. Quien se resistiera a ello era considerado como un infiel.
Esta relación de las armas con la religión cristiana se vio fortalecida en el año de 1095, cuando el papa de aquel entonces, Urbano II, convocó a los soldados cristianos a una cruzada contra los musulmanes para recuperar la ciudad donde Jesús había muerto, Jerusalén, que había sido conquistada por los musulmanes años antes.
Esta guerra fue declarada “una guerra santa”, en tanto que su objetivo era defender los sitios sagrados del cristianismo, y a la población que ahí vivía, del dominio de los musulmanes, quienes eran vistos como infieles y enemigos de la religión cristiana. El papa incluso señaló que, esta empresa era algo que Dios deseaba y, por lo tanto, quien participara en ella vería sus pecados perdonados.
Esta idea de guerra santa y de cruzada, nombre que venía de las cruces en la ropa de los participantes, viajaría a España, donde los reyes de Castilla y Aragón la empezaron a utilizar para avanzar en el proceso de la Reconquista.
Como se mencionó en la sesión anterior, la Reconquista fue un proceso de varios siglos durante los cuales los reinos cristianos de la península ibérica fueron conquistando poco a poco los territorios de los reinos musulmanes.
Esta lucha inevitablemente se vio influida por el tema religioso. Los ejércitos cristianos eran acompañados por sacerdotes, quienes daban su bendición y absolvían los pecados de los soldados. En batalla, los soldados creían en tener la protección de Dios, de los santos, en especial Santiago Matamoros, y de la virgen, a quienes incluso creían llegar a ver en medio del combate apoyándolos. Y muchos creían que, al haber tomado parte en la batalla, Dios les perdonaría sus pecados.
Pero no sólo eso, una vez que conquistaban las ciudades musulmanas, procedían a convertir las mezquitas, lugares de culto de los creyentes de Mahoma, en iglesias cristianas, como fue el caso de la mezquita de Córdoba o la de Sevilla.
Por otro lado, a la población musulmana que era derrotada se le daba la oportunidad de convertirse al cristianismo o de ser expulsada del reino, como pasó tras la conquista del reino de Granada. Y es que, para los soldados cristianos, combatir a los musulmanes y conquistar sus territorios, era una misión que Dios les había encomendado, puesto que, sólo así se podía extender la religión cristiana y su mensaje redentor. Pelear contra los infieles significaba ser un buen cristiano.
Esta era la idea que tenían los soldados españoles que llegaron a América. Más allá de las riquezas que podrían conseguir, los hombres creían que su misión era extender el cristianismo a estas tierras, por lo que debían convertir a los indígenas que aquí vivían, sólo así salvarían sus almas.
Como señala el historiador Antonio Rubial García en un texto sobre la religiosidad de los conquistadores españoles:
“Una clara muestra de la fuerte presencia entre los españoles de las creencias religiosas y de su manifestación en actos externos fue la obsesión que tenía Hernán Cortés por derribar “ídolos” en los adoratorios indígenas por considerarlos representaciones demoníacas y suplantarlos con cruces. Su firme convicción de cumplir con un mandato divino y tener un mesiánico destino lo llevaba a ver la conversión de los nativos a la fe cristiana como una justificación suficiente para pensar que el oro obtenido era un premio merecido por esta labor”.
Para los españoles existía una relación muy fuerte entre la religión y la guerra. Sin embargo, no eran los únicos, los mexicas también las relacionaban, aunque de manera diferente.
A continuación, observa el siguiente video sobre el mito de la creación del Quinto Sol y Xipe Totec.
- La creación del Quinto Sol y Xipe Totec.
https://www.youtube.com/watch?v=Qv7ntN6H2DI&t=258s
Este mito alrededor de la creación del Sol y la Luna fue uno de los varios relatos que servían para que los mexicas dieran una explicación al mundo que les rodeaba y la forma en que éste funcionaba.
Los mexicas, al igual que las otras culturas de Mesoamérica, eran politeístas, es decir, contaban con una gran cantidad de dioses, por ejemplo, Quetzalcóatl, Huitzilopochtli, Tezcatlipoca, Mictlantecuhtli, entre otros. Cada uno de ellos representaba uno de los distintos fenómenos de la naturaleza o de la vida de los hombres.
Para ellos, estos dioses tenían el poder de mantener o afectar las fuerzas que representaban, por lo que era el deber de los seres humanos mantenerlos contentos y vivos, a manera de pago por el hecho de mantener con vida a la humanidad. Por ejemplo, el caso del Sol, el cual se creía que si no era alimentado podía desaparecer.
Sin embargo, a los dioses, pensaban los mexicas en aquel entonces, sólo se les podía ofrecer lo más valioso que existiera, y si bien recursos como el maíz podían ser ofrendados, en realidad sólo había una cosa que los dioses realmente valoraban, la misma vida humana; por lo tanto, era a través de los sacrificios humanos que se podía retribuir a las divinidades y así mantener el mundo funcionando.
El pueblo mexica, que se creía como el pueblo elegido por Huitzilopochtli para cumplir el papel de los cinco mimixcoas, que en el mito fueron elegidos por el Sol para mantenerlo, debían de obtener los alimentos de los dioses, para lo cual necesitaban conseguir gente para sacrificar.
El mito de la caza de los mimixcoas se tradujo en términos prácticos, en la obtención de víctimas para el sacrificio por medio de la guerra. Y es que era durante la guerra que los mexicas podían atrapar a presas que se convirtieran en las víctimas que serían sacrificadas durante las múltiples celebraciones y fiestas religiosas en honor a los dioses. Está relación de la guerra, y los cautivos, estaba tan desarrollada que lingüísticamente algunas de las palabras relacionadas con la caza también estaban relacionadas con aspectos de la guerra.
De esta forma, la guerra se convirtió en un asunto sagrado que estaba sancionada por la deidad tutelar de los mexicas, Huitzilopochtli. El carácter de sacralidad que envolvía esta actividad también es evidente en la idea de que los soldados muertos en batalla o sacrificados tras ser capturados, pasarían a acompañar al dios en su marcha por el cielo.
Conseguir cautivos para los sacrificios se volvió tan importante para los mexicas que decidieron inventar un tipo especial de combate dedicado específicamente para este fin, las conocidas como guerras floridas o xochiyaoyotl.
Eran enfrentamientos pactados con antelación con otros pueblos, en los que la finalidad no era obtener tributo o extender el dominio político del Imperio mexica, sino simplemente conseguir cautivos que posteriormente serían sacrificados. Durante estas guerras, los mexicas podían llevar a cabo su misión de capturar a los “mimixcoas”.
A pesar del significado claramente religioso de estas guerras, detrás también existía un objetivo político. La obtención de muchos prisioneros de guerra por parte de los mexicas para sus rituales y sacrificios servía como una forma de demostrar el poderío político y militar de Tenochtitlan sobre las otras entidades mesoamericanas, así como el poderío de Huitzilopochtli, pero sin que esto implicara eliminar o sustituir a los dioses de los otros pueblos.
Además, la existencia de estas guerras servía para legitimar la posición de los soldados en la sociedad mexica y la participación en estas guerras era uno de los pocos espacios donde se podía obtener un ascenso social.
Es importante señalar que, esta actitud no fue exclusiva de los mexicas, también los tlaxcaltecas, los purépechas y otros pueblos recurrían a los sacrificios humanos de los prisioneros de guerra como una forma de congraciarse con las deidades.
Finalmente, como has visto, españoles y mexicas tenían en común la concepción de una misión en la tierra que les había sido dada por sus deidades, aunque ciertamente esa misión era muy diferente tanto para unos, como para otros. Estas dos concepciones tan distintas de ver la guerra se encontrarían en 1519.
El Reto de Hoy:
Imagina que eres un mexica o un español del siglo XVI, y te encuentras en las rutas de exploración o la llegada de los españoles a Mesoamérica. Ahora, le tienes que explicar al otro ¿por qué peleas en una guerra? o ¿cuál es tu concepción de guerra?
Ya que tengas la respuesta, escribe un diálogo o párrafo donde expongas o argumentes tu explicación, recuerda hacerlo en primera persona. Te puede ayudar señalar las diferencias o similitudes entre ambas concepciones.
Para resolver este reto, no dudes en consultar tu libro de texto, así como en los retos de las sesiones anteriores.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Los procedimientos de la gestión técnica
Aprendizaje esperado: Planifica y organiza las acciones técnicas según las necesidades y oportunidades indicadas en el diagnóstico.
Énfasis: Identificar los procedimientos básicos de la gestión técnica.
¿Qué vamos a aprender?
Retomarás el concepto de la gestión técnica e identificarás sus procesos básicos en los sistemas de producción. En esta sesión, estudiarás dos de ellos, la planeación y la organización.
¿Qué hacemos?
Observa el siguiente mapa conceptual.
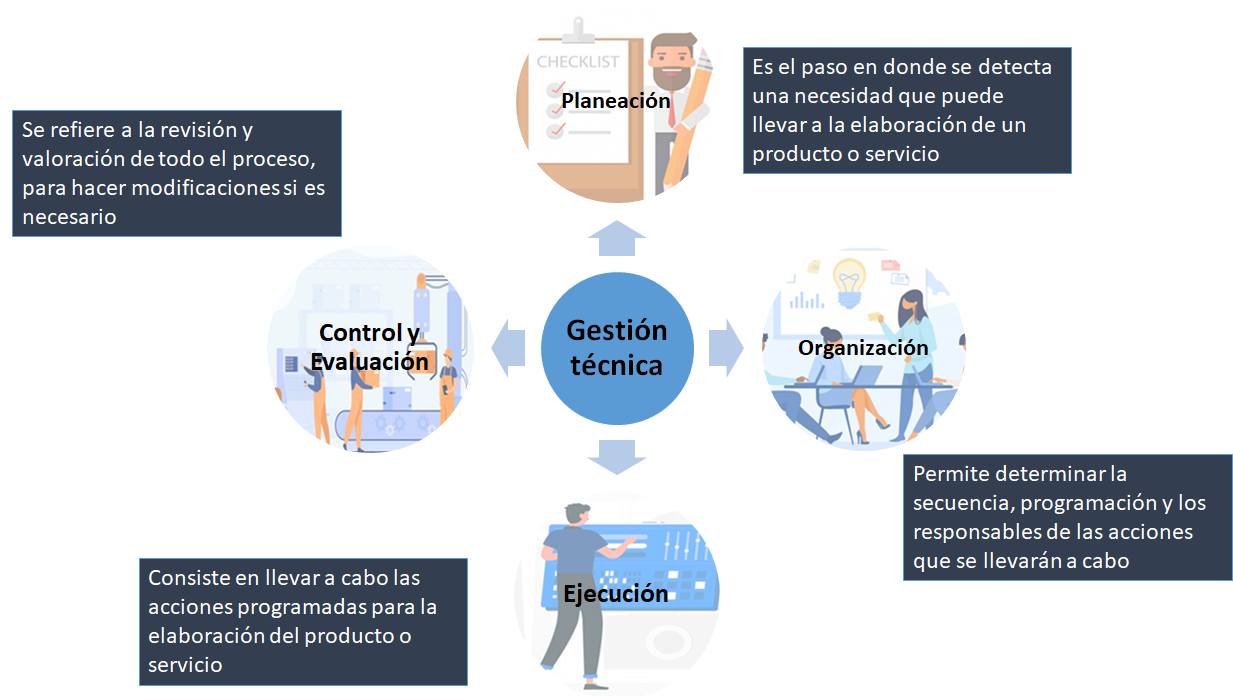
Ahora, analiza el siguiente concepto que ya estudiaste anteriormente.
La gestión técnica es el término utilizado para describir el conjunto de técnicas relacionadas con la administración, como la planeación, organización, dirección y control de las operaciones. Sin darnos cuenta, la gestión la aplicamos en la vida diaria cuando llevamos a cabo un proceso para obtener un producto, por ejemplo, una gelatina o un pastel.
Después de retomar esta información, continuarás con los procesos básicos de la gestión técnica en los sistemas de producción. En el mapa conceptual, la gestión técnica tiene varias fases, las cuales se articulan para generar un producto o servicio. Cada una tiene su propia complejidad, en esta sesión te centrarás en la planeación y la organización.
Inicia con la planeación, ésta responde principalmente a dos preguntas:
¿Qué se quiere hacer?
¿Qué se va a hacer?
Para responder a estas preguntas, se debe tener bien identificada la necesidad que se quiere satisfacer, definir el problema a resolver, además de haber elegido la alternativa de solución que se le dará.
Esta etapa es muy importante porque se toman las decisiones de acuerdo con lo que se quiere lograr, se identifican los recursos necesarios como los medios técnicos, insumos y el número de personas que intervienen en el proceso. Por ello, se dice que la planeación tiene como meta la eficiencia y entre sus principios está la factibilidad, la precisión y la flexibilidad.
Por otro lado, la organización responde a la siguiente pregunta:
¿Cómo se va a hacer?
En esta fase se definen las funciones y las responsabilidades de todas las personas que intervienen en el proceso de elaboración de un producto o servicio. Así, cada una se dedica a la realización de tareas específicas, se evita que varias personas hagan lo mismo y se alcanza el objetivo planteado desde el inicio.
Esto se puede ver en la vida cotidiana. Por ejemplo, ¿cuántas veces has realizado actividades con el propósito de obtener algo que deseabas?
Primero, es necesario identificar qué necesidad se quiere satisfacer. Si por alguna razón, no se puede satisfacer esa necesidad, entonces se está ante un problema que se debe identificar claramente.
Pero no basta con identificarlo, pues ahora se tienen que buscar alternativas para solucionarlo. Esto requiere de una investigación y a partir de ella, poder encontrar varias. Entre todas ellas, se debe elegir la más adecuada considerando su costo, el tiempo para desarrollarla y sus implicaciones en la naturaleza y la sociedad.
Por lo tanto, estas fases de la gestión técnica normalmente las utilizamos todas las personas, pero no las llamamos con ese nombre. Para comprenderlo mejor, realiza lo siguiente:
Imagina que desarrollarás un proyecto sobre el emprendimiento de un negocio de gelatinas:
- ¿Cuál sería el primer paso de este proceso?
- ¿Cuántas personas intervendrán en el proceso de producción?
- ¿Cómo te beneficiaría determinar qué recursos requieres para alcanzar la meta?
Si la meta es producir el máximo de gelatinas y obtener la mayor cantidad de ganancias, en el proceso de producción se debe considerar que puede haber riesgos, tanto para quien las elabora como para quien las consume.
Entonces, lo primero que tendrías que hacer es conocer el proceso técnico para generar gelatinas, porque sin eso no podrías avanzar en las fases de la gestión técnica.
Quizá se podría pensar que es un proceso sencillo, pero vale la pena recordarlo con el siguiente video. Observa con atención y piensa en los medios técnicos e insumos que se requieren.
- Video. Elaboración de gelatinas.
Ahora que ya conoces el proceso para hacer gelatina, observa el siguiente video con las preguntas clave en una planeación y contéstalas en tu cuaderno. Recuerda que tienes que planear para llevar a cabo el proyecto de emprendimiento.
- Video. Planeación.
Después de observar y contestar las preguntas del video anterior, comenzarás a planear, pues de esta manera tendrás una visión panorámica de la solución como un todo integrado por diferentes partes.
Ya con la planeación lista, se puede comenzar a organizar, y así determinar la secuencia en que se realizará cada una de las acciones que integran el proceso productivo. Por ejemplo, ¿cuáles serían las acciones necesarias para producir las gelatinas?
Además, tienes que pensar ¿quiénes intervendrán en el proceso? y ¿qué hará cada persona? Si se determina esto, todas las personas trabajarán de forma eficaz para alcanzar la meta, y se coordinarán agrupando todas las actividades necesarias para obtener una buena relación y funcionamiento.
Para comprender lo anterior, observa otro video con algunas preguntas clave para iniciar con la organización. Recuerda anotar tus respuestas en tu cuaderno, considerando el mismo proyecto.
- Video. Organización.
Ya se tiene una idea de la planeación y organización para el emprendimiento. Sin embargo, no se está exento de los problemas o riesgos que puedan presentarse.
A veces cuando se planea y organiza, se cree que todo va a salir excelente y no se consideran los factores que pueden influir en el logro de la meta. Por ello, se debe tomar en cuenta que puede haber problemas en los procesos productivos.
Por ejemplo, puede pasar que soliciten un pedido de emergencia de 30 gelatinas para una fiesta. Por lo tanto, se deben hacer en un mismo día y no se puede detener la producción para evitar atrasos.
Otro ejemplo sería que, en la planeación está elaborar 30 gelatinas por día, pero ocurren imprevistos como la falta de energía, el gas se ha terminado, el proveedor de gas pasará hasta el siguiente día. También puede suceder que no haya luz eléctrica y, por lo tanto, el refrigerador donde se mantienen las gelatinas no enfríe. Esto implicaría nuevamente detener la producción, pero no se puede detener.
Para este tipo de problemas, siempre se puede tener “un as bajo la manga”. Por lo que es necesario estar preparada y preparado para ello. De acuerdo con lo anterior: ¿cuántas y cuáles soluciones considerarías?
Para conocer algunas de ellas, observa en el siguiente video.
- Video. Alternativas de solución.
Desde la planeación, ¿qué medidas consideras que se deben tomar en cuenta para evitar estos contratiempos? Reflexiona y comenta tus opiniones con tu maestra o maestro de Tecnología.
Además de estos riesgos, es necesario considerar los que tienen que ver con la seguridad e higiene de las personas que intervienen en los procesos productivos. Éstos no se deben perder de vista para evitar enfermedades y accidentes laborales.
La prevención de riesgos, que están presentes en la planeación, permite alcanzar altos niveles de productividad y hace más eficiente la gestión total de los procesos técnicos.
Considera que, en todo proceso donde las personas tienen que entrar en contacto con maquinaria, fuentes de energía, como el gas o la luz eléctrica, materias primas, productos en proceso y terminados, existen situaciones de riesgo.
Es aquí donde entra la gestión técnica, que permitirá llevar a cabo un proceso técnico exitoso, administrando de manera adecuada todos los elementos involucrados y estableciendo un objetivo a alcanzar, las acciones que permitirán lograrlo considerando siempre los posibles riesgos.
Por ejemplo, en el proyecto de emprendimiento de gelatinas, se pueden correr riesgos desde que se calienta el agua hasta que se abre el refrigerador para sacarlas cuando ya están listas. Por eso es necesario conocer muy bien y respetar los procedimientos para manipular los medios técnicos y los insumos.
Una vez iniciado el proceso de producción, la gestión se enfoca en evaluar los resultados de las etapas, corregir los errores que se presentan durante la ejecución de cada una y coordinar a las personas durante todo el proyecto.
Ahora, recapitula los puntos más importantes que estudiaste en esta sesión.
La planeación y la organización son parte de la gestión técnica y son necesarias para generar cualquier producto o servicio que satisfaga una necesidad. Además, la planeación abarca todo lo relacionado con la previsión de los insumos o materiales, herramientas, máquinas e instrumentos y los recursos humanos que necesitará el sistema técnico para su operación, incluyendo los procedimientos que se seguirán para la transformación de los insumos.
Es muy importante que en la planeación se consideren los posibles riesgos, ya que éstos pueden impedir la operación completa del proceso técnico. Y muy de la mano de la planeación va la organización, en la cual se deben considerar a las personas que intervendrán, sus tareas específicas y los tiempos a los que deberán apegarse durante el proceso de producción.
La gestión técnica también se aplica en la vida cotidiana. Para identificar sus fases, observa el siguiente video.
- Video. Proyecto aplicando la gestión técnica.
Con el ejemplo que acabas de ver, podrás darte cuenta de que la gestión técnica es parte de la vida cotidiana. Con esto, has finalizado la sesión.
El Reto de Hoy:
Realiza un cuadro sinóptico sobre los procesos básicos en los sistemas de producción. En esta sesión, incluirás los procesos de planeación y organización. Finalmente, comparte la información que aprendiste con tu familia.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario