Aprende en Casa III SEP: 8 de febrero TAREAS y ACTIVIDADES de 2° de secundaria

¿Cuáles fueron los temas del día?

A continuación dejamos los temas vistos el 8 de febrero de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Lunes 8 de febrero, así como las dudas que se plantearon.

La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en Casa III:

https://aprendeencasa.sep.gob.mx/#

Compra en Amazon

Sucesiones I

Aprendizaje esperado: Verifica algebraicamente la equivalencia de expresiones de primer grado, formuladas a partir de sucesiones.

Énfasis: Explicar la equivalencia de las distintas expresiones algebraicas cuando representan la regla de una misma sucesión.

¿Qué vamos a aprender?

En esta sesión, las actividades están centradas en verificar la equivalencia de expresiones algebraicas a través de la construcción y el análisis de sucesiones numéricas.

Este tema de estudio no es nuevo, pues ya has trabajado con sucesiones de figuras geométricas y numéricas. Además, en tu trayectoria escolar aprendiste a encontrar otros términos de sucesiones mediante la regla que las genera, la describiste con tus propias palabras y, posteriormente, a través de una expresión algebraica. Por lo tanto, reconocerás que existen diversas sucesiones de figuras y que éstas se pueden organizar numéricamente para analizar su comportamiento y así, deducir el número de elementos de acuerdo con el número de posición.

¿Qué hacemos?

En la siguiente imagen se muestran tres arreglos formados por cuadrados. El punto de partida fundamental para comenzar el análisis de una sucesión de figuras es determinar que cada arreglo de la sucesión es un término de esta y esos términos se pueden representar utilizando números. Es decir, el primer arreglo será el término 1 de la sucesión, a continuación, el segundo será el término 2 y así, sucesivamente.

 

 

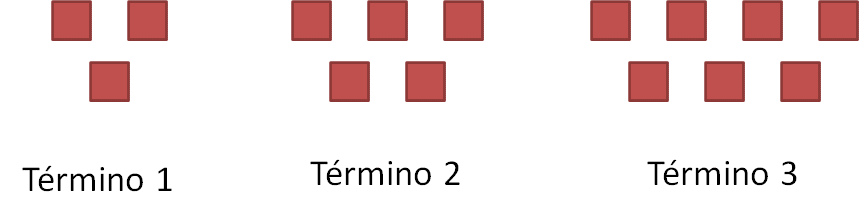
Una vez representada la sucesión de figuras usando números, se pueden hacer observaciones respecto a la manera como se va construyendo el siguiente término. Incluso se pueden dibujar los siguientes términos. Además, los elementos gráficos de la sucesión se pueden analizar numéricamente, convirtiéndolos en una sucesión numérica.

 

 

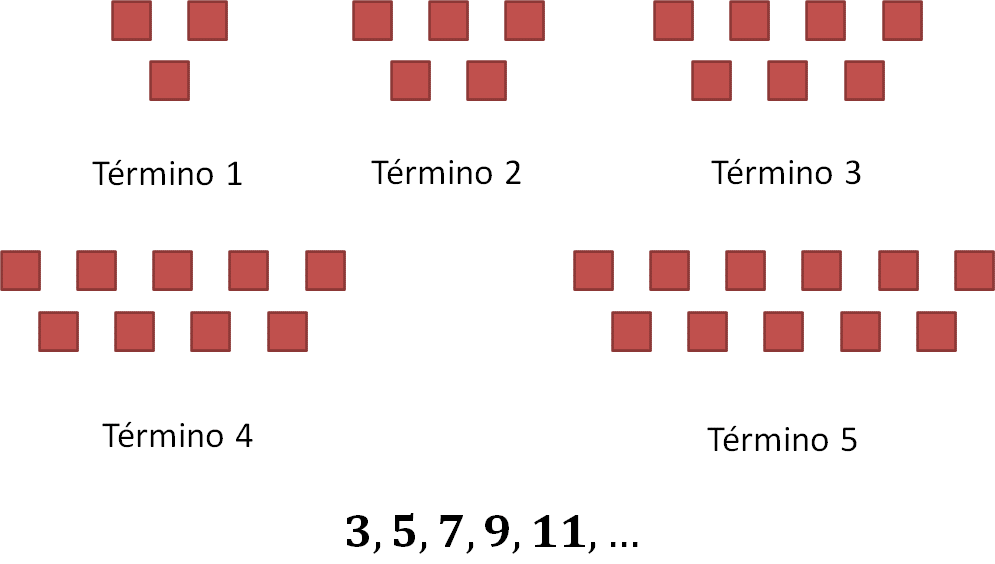
Ahora, escribe con tus propias palabras qué entiendes por sucesión numérica. Después analiza la siguiente definición.

Una sucesión es un conjunto de números ordenados a través de la regla que los origina. Los elementos que forman una sucesión numérica se llaman términos. Los términos que constituyen una sucesión pueden calcularse a través de una regla o patrón que puede describirse por medio de una expresión algebraica o regla general. Los puntos suspensivos, significan que la sucesión continúa, es decir, que no tiene fin.

 

 

A continuación, analiza cómo tres alumnos de secundaria explican lo que saben acerca de las sucesiones. Esto, al trabajar con la sucesión de figuras que se usó de ejemplo. Algunos de ellos visualizaron cada término de la sucesión como un conjunto, al cual se agrega cierta cantidad de cuadrados de figura en figura.

Alumno 1:

 

El alumno 1, identificó que la sucesión de figuras va aumentando de dos en dos, pero eso no fue suficiente para que pudiera definir el comportamiento de la sucesión con una expresión algebraica.

 

 

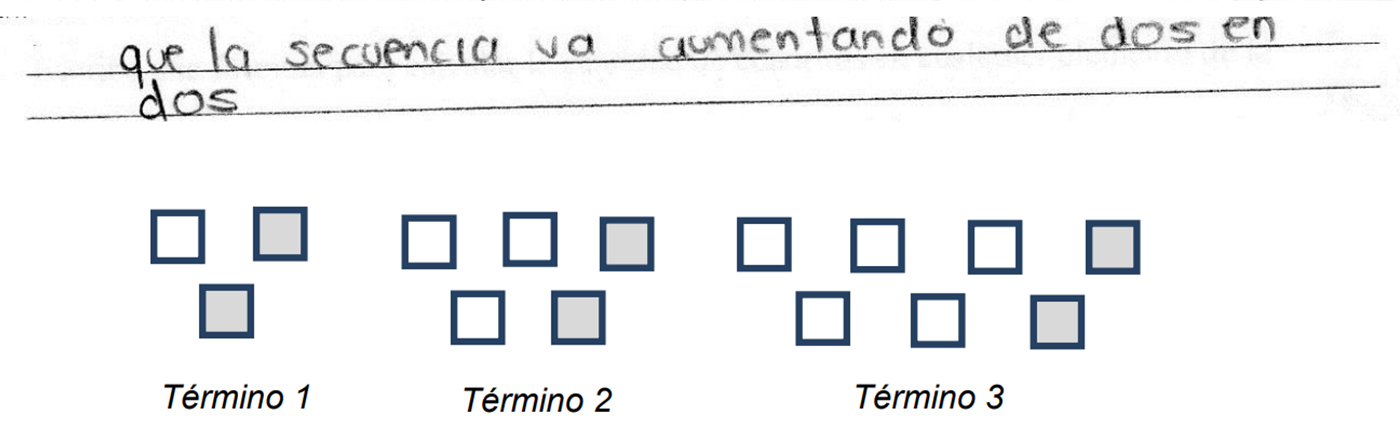
Aunque cabe aclarar que identificar el comportamiento de la sucesión es un primer paso muy importante.

Alumna 2:

La alumna 2, a partir de la visualización, consigue expresar las relaciones entre las figuras y es capaz de explicar y dar razón de los crecimientos y la relación de éstos con la posición que ocupan los elementos de la secuencia.

Ella relaciona la cantidad de los elementos presentes en cada arreglo con el número de término que le corresponde, lo que facilita la construcción de la expresión que genera la sucesión. La expresión general la plantea en función del número de término o de posición, al que habitualmente se le asigna la literal “n”

 

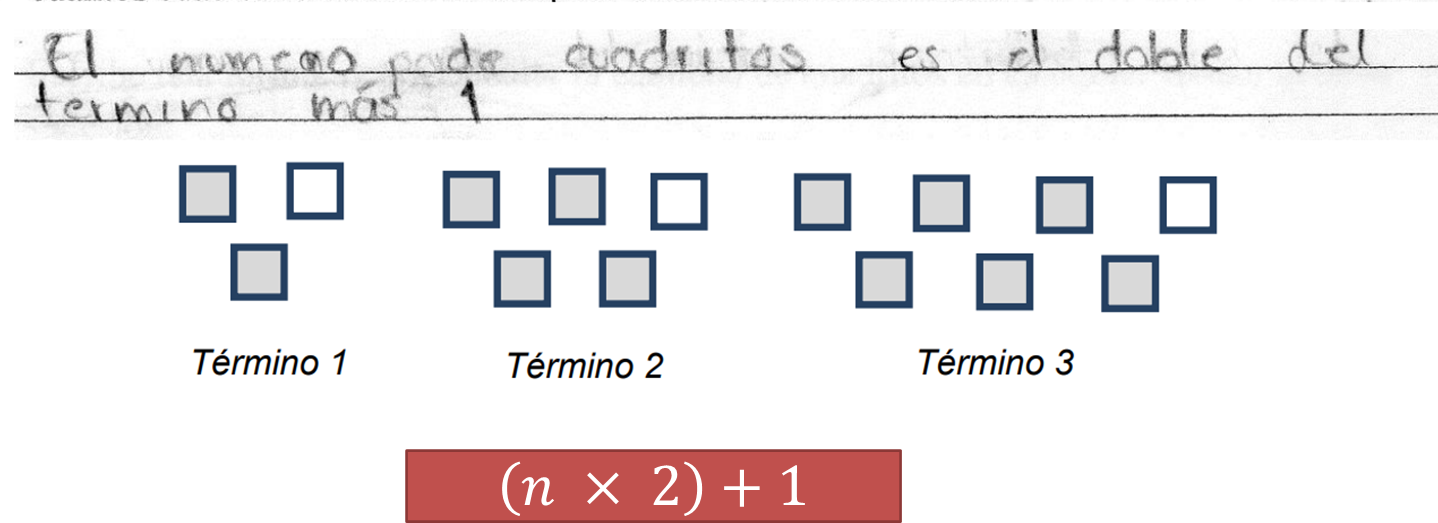
En este caso, la alumna indica que la expresión general de la sucesión es (n x 2) + 1, y es capaz de explicarla: “n” es el término, entonces si el término es uno, se multiplicará por dos, más el uno que siempre va a ser constante.

Después, ella lleva su razonamiento al siguiente caso, es decir, en lugar de “n” coloca 2 y comprueba que obtiene el número de elementos del segundo término, que son 5.

Pero ¿esta expresión algebraica funciona para cualquier término de la sucesión? Compruébalo con el quinto término.

Si “n” toma el valor de cinco, entonces en lugar de “n” por dos más uno, se coloca (5 x 2) + 1, el resultado es once y efectivamente, el quinto término de la sucesión tiene once elementos.

 

 

Alumno 3:

 

El alumno 3 descompuso la secuencia en filas, y cada fila en subelementos que forman subfiguras, cuya cantidad depende de la posición que ocupa cada elemento dentro de la secuencia.

Él escribe: “Los cuadros de abajo son el número de la posición y arriba son el número de la posición más uno”. Esto permitió al estudiante organizar de manera adecuada la relación existente entre los elementos de la figura y lo llevó a generalizar con una expresión algebraica.

 

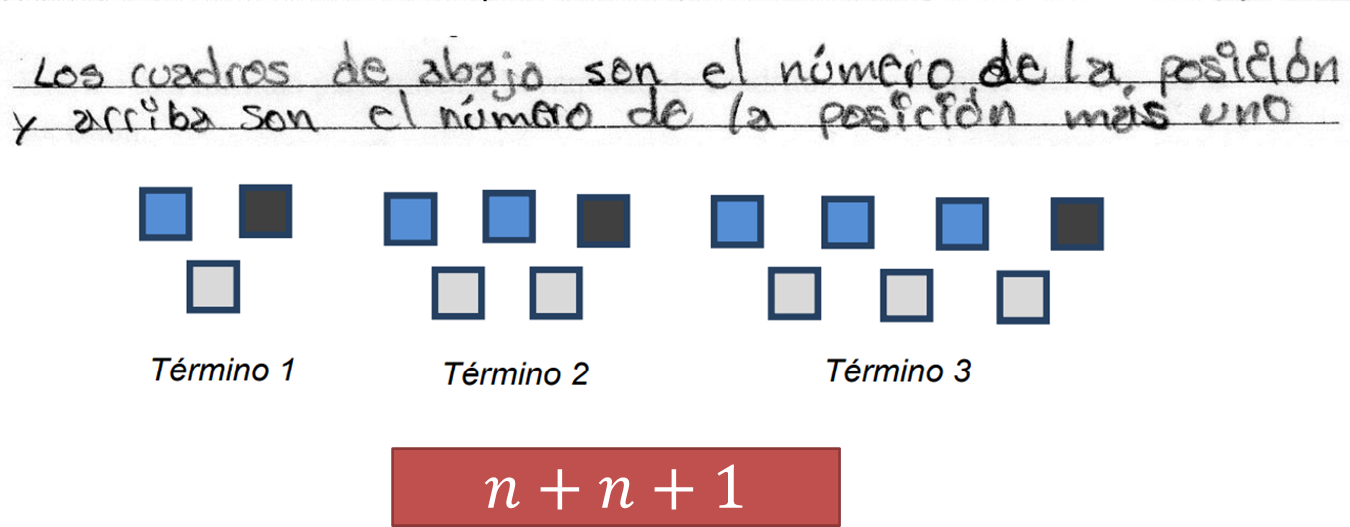
En este caso, el número de la posición se representa con “n” y, por lo tanto, el número de elementos que contiene la posición se puede encontrar con (n + n + 1). El primer término “n” representa el número que se asigna “a la posición” del término, y el término “n” más uno se refiere a “el número de la posición más uno”.

Así, se puede observar cómo es que los estudiantes pudieron conectar lo que vieron, con lo que escribieron con los símbolos algebraicos.

Analiza lo siguiente:

 

Esta última expresión es diferente a la que plantea la alumna 2. ¿Alguien está mal?

 

Para conocer lo anterior, revisa lo que plantea cada alumno y reflexiona al respecto.

 

La alumna 2 encuentra la expresión (n x 2 + 1), mientras que el alumno 3 plantea (n + n + 1). Si se cambia la variable “n” por el número diez ¿qué ocurre en cada caso?

 

 

Al resolver, empleando la jerarquía de operaciones, ambas expresiones llevan al mismo resultado. Por lo tanto, ambas son correctas.

Esto muestra que las dos formas son equivalentes, es decir, son dos expresiones algebraicas diferentes que formulan la misma situación. Entonces, es posible tener respuestas diferentes para la misma situación.

Cuando dos o más expresiones algebraicas generan la misma sucesión numérica se dice que las expresiones algebraicas son equivalentes, es decir, tienen el mismo valor.

A continuación, analiza el siguiente ejemplo.

 

2b = b + b

 

¿Qué piensas que pasaría si se cambia la letra “b” por el número 1? Toma un momento para reflexionar y después, observa qué sucede.

 

Al sustituir la letra “b” por el número 1, se obtiene la siguiente igualdad:

 

2 (1) = 1 + 1

 

Si se resuelven las operaciones, se obtiene que 2 es igual a 2. ¿Qué piensas que significa eso?, ¿pasará lo mismo si en lugar del número 1 se usa el número 2, el 3, el 8, o cualquier otro número?

 

Toma un momento para pensar y reflexionar, después, escribe una breve conclusión en tu cuaderno.

 

Ahora, el valor de la letra “b” será 8. Sustituye los valores en la igualdad.

 

2b = b + b

 

2 (8) = 8 + 8

 

16 = 16

 

Se obtiene que 16 es igual a 16.

De lo anterior se puede deducir que lo mismo pasará si se sustituye la letra “b” por cualquier número. Cuando sucede esto, se comprueba que las expresiones algebraicas son equivalentes.

Piensa en la siguiente cuestión:

¿Qué se puede hacer para encontrar una expresión equivalente a otra?

Para dar respuesta a la pregunta anterior, trabaja con la siguiente sucesión numérica que está parcialmente formada por los números:

3, 6, 9, 12, 15…

 

Los puntos suspensivos indican que la sucesión no tiene fin, es decir, es infinita.

 

Ahora, encuentra la manera de saber cuál es la regla que genera una sucesión.

 

¿Conoces algún procedimiento para encontrar la regla general de una sucesión numérica? Describe tu procedimiento en tu cuaderno.

 

Para encontrar la regla general de una sucesión, se identifica la diferencia entre un término y su consecutivo. Asimismo, se observa si la diferencia es constante entre los demás términos.

¿Ya sabes cuál es la diferencia entre los términos de la sucesión anterior?

Como puedes notar, la sucesión numérica aumenta de tres en tres. Entonces, para escribir la regla general de esa sucesión, se anota el número 3, porque ya sabes que aumenta de tres en tres. Se relaciona con el número de término, es decir, con el número de posición. Como ese número es variable, se le asigna una literal, generalmente la letra “n”.

De tal manera, que la regla que genera la sucesión numérica es (3n). El 3 porque la sucesión va aumentando de tres en tres y la “n” para representar cualquier término de la sucesión.

 

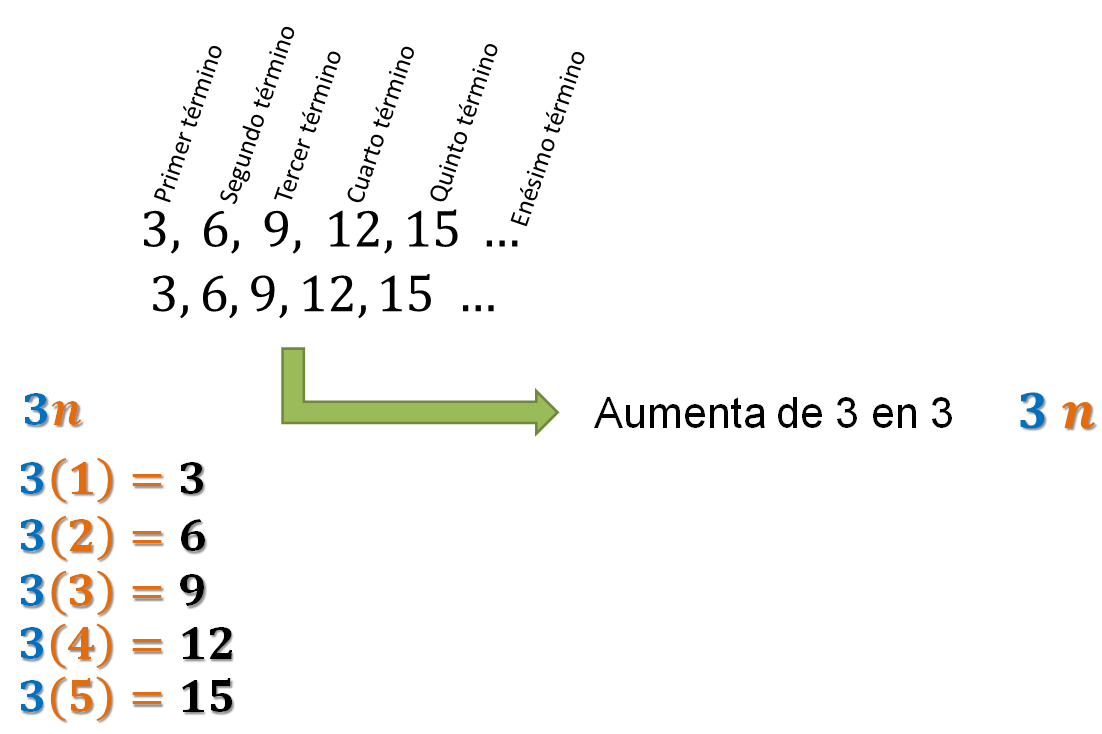
Un método para encontrar expresiones algebraicas equivalentes a otra, consiste en descomponer una expresión algebraica en sus partes.

Ahora, debemos preguntarte:

¿Cómo puedes descomponer 3n en partes?

Para descomponer una expresión algebraica es muy importante saber leerlas y entender su significado. Si sabes eso, también puedes saber las partes de las que se compone cualquier expresión algebraica.

¿Cuál es el significado de 3n? 3n significa tres veces el valor de “n”. Entonces, ¿de cuántas partes se forma 3n? Piénsalo un momento.

La expresión algebraica 3n se forma de tres partes y sus partes son tres letras “n”. Ahora, debes pensar una forma diferente de unir esas partes, ¿tienes alguna idea de cómo hacerlo?

Se pueden unir esas letras a través de signos que indiquen una operación, en este caso, puede ser por medio de una suma, ya que, si se suma “n”, más “n”, más “n”, se tiene 3n; y con eso, ya se ha descompuesto la expresión algebraica; pero también existe otra expresión algebraica equivalente a 3n, que es 2n más “n”.

 

 

Ahora, encuentra por lo menos dos expresiones algebraicas equivalentes a:

 

6n + 4

 

Primero, observa cuáles son las partes que la forman. Si se separan todos los elementos queda de la siguiente forma:

 

n + n + n + n + n + n + 4

 

Incluso ese cuatro puede separarse en 1 + 1 + 1 +1

Con los elementos separados, ¿puedes escribir por lo menos dos expresiones equivalentes? Coméntalas y compáralas a distancia con tus compañeras y compañeros.

Ahora, analiza las siguientes expresiones y comprueba si son equivalentes:

 

2 (3n + 2)

 

2n + 2n + 2n + 4

 

Reflexiona:

 

¿Se parecen estas expresiones algebraicas a las que escribiste?

¿Cómo puedes comprobar que estas expresiones algebraicas son equivalentes?

 

Comprueba que las expresiones algebraicas anteriores son equivalentes a 6n + 4. Después, comprueba que las expresiones algebraicas que propusiste también sean equivalentes.

Una de las formas para comprobar la equivalencia de expresiones algebraicas consiste en resolver las operaciones algebraicas indicadas; otra es construir la sucesión numérica que representan. En esta sesión, construirás sucesiones numéricas para realizar las comprobaciones.

Primero construye la sucesión numérica que genera 6n + 4 Lo harás para los primeros 5 términos.

Lo que debes hacer es sustituir el valor de “n” por 1, pues como recordarás, “n” representa el valor del término que se está buscando, en este caso, representa el primer término de la sucesión. Por lo tanto, se tiene que:

6n + 4

 

6(1) + 4 = 10

 

Entonces se puede decir que cuando “n” vale 1, el término es 10

Ahora, calcula el segundo término. “n” vale 2 porque se está buscando el segundo término de la sucesión, Realiza los caculos:

 

6n + 4

 

6(2) + 4 = 16

 

Entonces podemos decir que cuando n vale 2, el término es 16

 

Para el tercer término “n” vale 3; entonces se tiene que:

 

6n + 4

 

6(3) + 4 = 22

 

Por lo tanto, se puede decir que cuando “n” vale 3, el término es 22

 

Para el cuarto término, “n” vale 4; entonces se tiene que:

 

6n + 4

 

6(4) + 4 = 28

 

Por lo tanto, se puede decir que cuando “n” vale 4, el término es 28

 

Para el quinto término, “n” vale 5; entonces se tiene que:

 

6n + 4

 

6(5) + 4 = 34

 

Por lo tanto, se puede decir que cuando “n” vale 5, el término es 34

 

Ya has terminado de calcular los primeros 5 términos de la sucesión. Eso quiere decir que la sucesión que genera la regla 6n + 4, está formada por los términos 10, 16, 22, 28 y 34. Observa como quedaron los resultados de esta expresión:

 

 

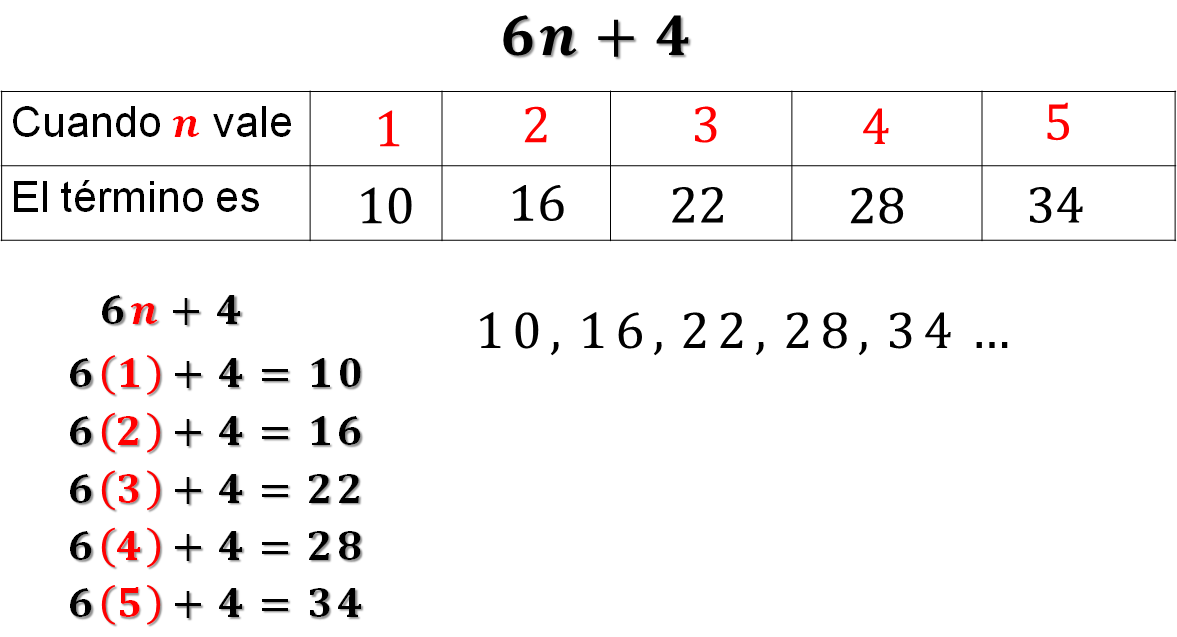
Al final se le agregan puntos suspensivos, ya que la sucesión continúa y no tiene fin.

 

Ahora ya sabes cuáles son los primeros términos de la sucesión. Para comprobar que las expresiones algebraicas que se escribieron son equivalentes a 6n + 4, sustituye “n” en las expresiones anteriores, por los números del uno al cinco. Si los resultados son idénticos, entonces la expresión algebraica es equivalente a 6n + 4.

 

Comienza con la expresión: 2 (3n + 2)

 

Se sabe que, para el primer término “n” vale 1. Sustituye y resuelve las operaciones paso a paso.

 

2 (3n + 2)

 

2 [3(1) + 2] = 2 [3 + 2] = 2 [5] = 10

 

Esto quiere decir que cuando “n” vale 1, el término es 10.

 

Para el segundo término “n” vale 2. Realiza la sustitución y resuelve las operaciones.

 

2 (3n + 2)

 

2 [3(2) + 2] = 2 [6 + 2] = 2 [8] = 16

 

Esto quiere decir que cuando “n” vale 2, el término es 16

 

Para el tercer término “n” vale 3

 

2 (3n + 2)

 

2 [3(3) + 2] = 2 [9 + 2] = 2 [11] = 22

 

Esto quiere decir que cuando “n” vale 3, el término es 22

 

Para el cuarto término “n” vale 4

 

2 (3n + 2)

 

2 [3(4) + 2] = 2 [12 + 2] = 2 [14] = 28

 

Esto quiere decir que cuando “n” vale 4, el término es 28

 

Para el quinto término “n” vale 5

 

2 (3n + 2)

 

2 [3(5) + 2] = 2 [15 + 2] = 2 [17] = 34

 

Esto quiere decir que cuando “n” vale 5, el término es 34

 

Ya has terminado de calcular los primeros 5 términos de la sucesión. Esto quiere decir que la sucesión que genera la regla “2 (3n + 2)”, está formada por los términos 10, 16, 22, 28 y 34. Observa como quedaron los resultados:

 

 

Como puedes observar, los términos de esta sucesión son idénticos a la sucesión anterior. Esto significa que ambas expresiones algebraicas son equivalentes.

 

Continua con la siguiente expresión: 2n + 2n + 2n + 4

 

Comprueba que esta expresión es equivalente a las dos expresiones algebraicas anteriores. Ya conoces el procedimiento para sustituir y resolver operaciones, así que esta vez te apoyaremos en el cálculo mental para avanzar más rápido.

 

Para “n” en el primer término se tiene que:

 

2n + 2n + 2n + 4

 

2(1) + 2(1) + 2(1) + 4 = 2 + 2 + 2 + 4 = 10

 

Para “n” en el segundo término se tiene que:

 

2n + 2n + 2n + 4

 

2(2) + 2(2) + 2(2) + 4 = 4 + 4 + 4 + 4 = 16

 

Para el tercer término se tiene que:

 

2n + 2n + 2n + 4

 

2(3) + 2(3) + 2(3) + 4 = 6 + 6 + 6 + 4 = 22

 

Para el cuarto término se tiene que: 2

 

2n + 2n + 2n + 4

 

2(4) + 2(4) + 2(4) + 4 = 8 + 8 + 8 + 4 = 28

 

En el quinto término se tiene que:

 

2n + 2n + 2n + 4

 

2(5) + 2(5) + 2(5) + 4 = 10 + 10 + 10 + 4 = 34

 

Al calcular los primeros 5 términos de la sucesión que genera la regla (2n + 2n + 2n + 4), se encuentra que está formada por los términos 10, 16, 22, 28 y 34. Observa como quedaron los resultados:

 

 

Los términos de esta sucesión son idénticos a los términos de las dos sucesiones anteriores. Entonces, las tres expresiones algebraicas son equivalentes.

 

Para finalizar, compara las siguientes expresiones. Sustituye el valor de “n” para comprobar si son equivalentes o no.

 

Expresión algebraica 1: 3 (n + 1)

 

Expresión algebraica 2: 5n + 1

 

Expresión algebraica 3: 3n + 3

 

En la primera expresión, sustituye “n” por 1 y 2:

 

3 (n + 1)

 

3 (1 + 1) = 3 (2) = 6

 

3 (2 + 1) = 3 (3) = 9

 

Al resolver, se obtiene el valor de 6 y 9, respectivamente.

 

En la segunda, también sustituye “n” por 1 y 2

 

5n + 1

 

5 (1) + 1 = 5 + 1 = 6

 

5 (2) + 1 = 10 + 1 = 11

 

Y en la tercera, sustituye de la misma manera a “n” por 1 y 2:

 

3n + 3

 

3 (1) + 3 = 3 + 3 = 6

 

3 (2) + 3 = 6 + 3 = 9

 

Cómo puedes observar, sí sólo se calcula el primer término de la sucesión en las expresiones algebraicas “3 (n + 1)”, “5n + 1” y “3n + 3”, parece que las expresiones son equivalentes, ya que, en los tres casos, se obtiene el mismo resultado.

 

Sin embargo, si se hace el cálculo con el segundo término de cada sucesión, puedes identificar que las tres expresiones algebraicas no son equivalentes entre sí.

 

¿Ya observaste que el valor del segundo término de la segunda expresión algebraica fue diferente? ¿Qué significa eso?

 

Esto significa que, solamente la primera y la tercera son equivalentes.

 

Por lo tanto, se puede concluir que: no basta con calcular un solo término para comprobar si dos o más expresiones algebraicas que generan una sucesión son equivalentes.

 

Con estos ejemplos aprendiste que se pueden identificar diferentes reglas que generan la misma sucesión numérica y a verificar su equivalencia con otras expresiones. Aunque sólo lo hiciste con la construcción de las secuencias numéricas que generan.

 

Hemos llegado al final de la sesión. Recuerda que este es un material de apoyo. Para complementar lo estudiado puedes consultar otras fuentes, como tu libro de texto de matemáticas de segundo grado.

 

 

El Reto de Hoy:

 

Escribe expresiones equivalentes de los ejemplos que se mencionaron en esta sesión. Además, resuelve los ejercicios de tu libro de texto de Matemáticas, correspondientes a este tema. Finalmente, coméntalas y compáralas a distancia con tus compañeras y compañeros.

 

 

¡Buen trabajo!

 

Gracias por tu esfuerzo.

Aprendizaje esperado: Verifica algebraicamente la equivalencia de expresiones de primer grado, formuladas a partir de sucesiones.

 

Énfasis: Explicar la equivalencia de las distintas expresiones algebraicas cuando representan la regla de una misma sucesión.

 

 

¿Qué vamos a aprender?

 

En esta sesión, las actividades están centradas en verificar la equivalencia de expresiones algebraicas a través de la construcción y el análisis de sucesiones numéricas.

 

Este tema de estudio no es nuevo, pues ya has trabajado con sucesiones de figuras geométricas y numéricas. Además, en tu trayectoria escolar aprendiste a encontrar otros términos de sucesiones mediante la regla que las genera, la describiste con tus propias palabras y, posteriormente, a través de una expresión algebraica. Por lo tanto, reconocerás que existen diversas sucesiones de figuras y que éstas se pueden organizar numéricamente para analizar su comportamiento y así, deducir el número de elementos de acuerdo con el número de posición.

 

 

¿Qué hacemos?

 

En la siguiente imagen se muestran tres arreglos formados por cuadrados. El punto de partida fundamental para comenzar el análisis de una sucesión de figuras es determinar que cada arreglo de la sucesión es un término de esta y esos términos se pueden representar utilizando números. Es decir, el primer arreglo será el término 1 de la sucesión, a continuación, el segundo será el término 2 y así, sucesivamente.

 

 

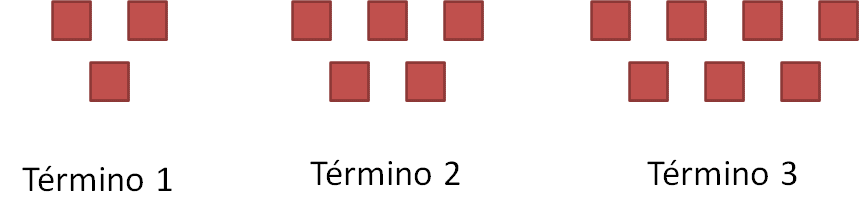
Una vez representada la sucesión de figuras usando números, se pueden hacer observaciones respecto a la manera como se va construyendo el siguiente término. Incluso se pueden dibujar los siguientes términos. Además, los elementos gráficos de la sucesión se pueden analizar numéricamente, convirtiéndolos en una sucesión numérica.

 

 

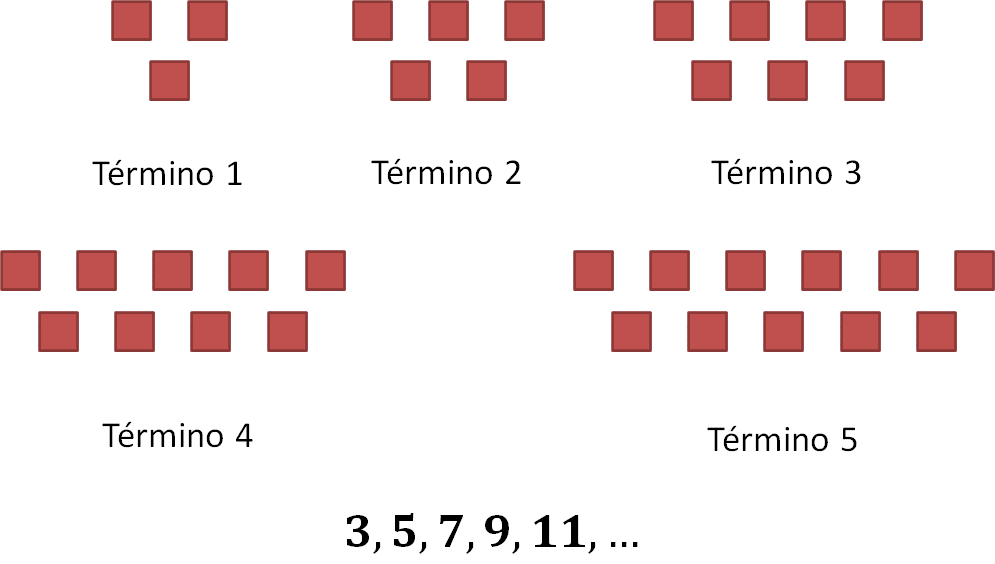
Ahora, escribe con tus propias palabras qué entiendes por sucesión numérica. Después analiza la siguiente definición.

 

Una sucesión es un conjunto de números ordenados a través de la regla que los origina. Los elementos que forman una sucesión numérica se llaman términos. Los términos que constituyen una sucesión pueden calcularse a través de una regla o patrón que puede describirse por medio de una expresión algebraica o regla general. Los puntos suspensivos, significan que la sucesión continúa, es decir, que no tiene fin.

 

 

A continuación, analiza cómo tres alumnos de secundaria explican lo que saben acerca de las sucesiones. Esto, al trabajar con la sucesión de figuras que se usó de ejemplo. Algunos de ellos visualizaron cada término de la sucesión como un conjunto, al cual se agrega cierta cantidad de cuadrados de figura en figura.

 

Alumno 1:

 

El alumno 1, identificó que la sucesión de figuras va aumentando de dos en dos, pero eso no fue suficiente para que pudiera definir el comportamiento de la sucesión con una expresión algebraica.

 

 

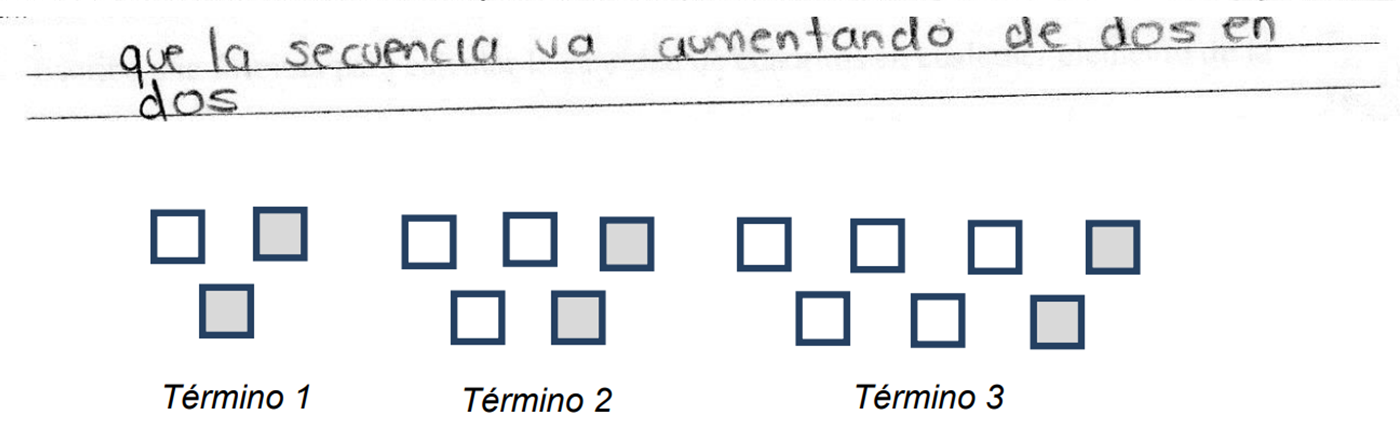
Aunque cabe aclarar que identificar el comportamiento de la sucesión es un primer paso muy importante.

 

Alumna 2:

 

La alumna 2, a partir de la visualización, consigue expresar las relaciones entre las figuras y es capaz de explicar y dar razón de los crecimientos y la relación de éstos con la posición que ocupan los elementos de la secuencia.

 

Ella relaciona la cantidad de los elementos presentes en cada arreglo con el número de término que le corresponde, lo que facilita la construcción de la expresión que genera la sucesión. La expresión general la plantea en función del número de término o de posición, al que habitualmente se le asigna la literal “n”

 

 

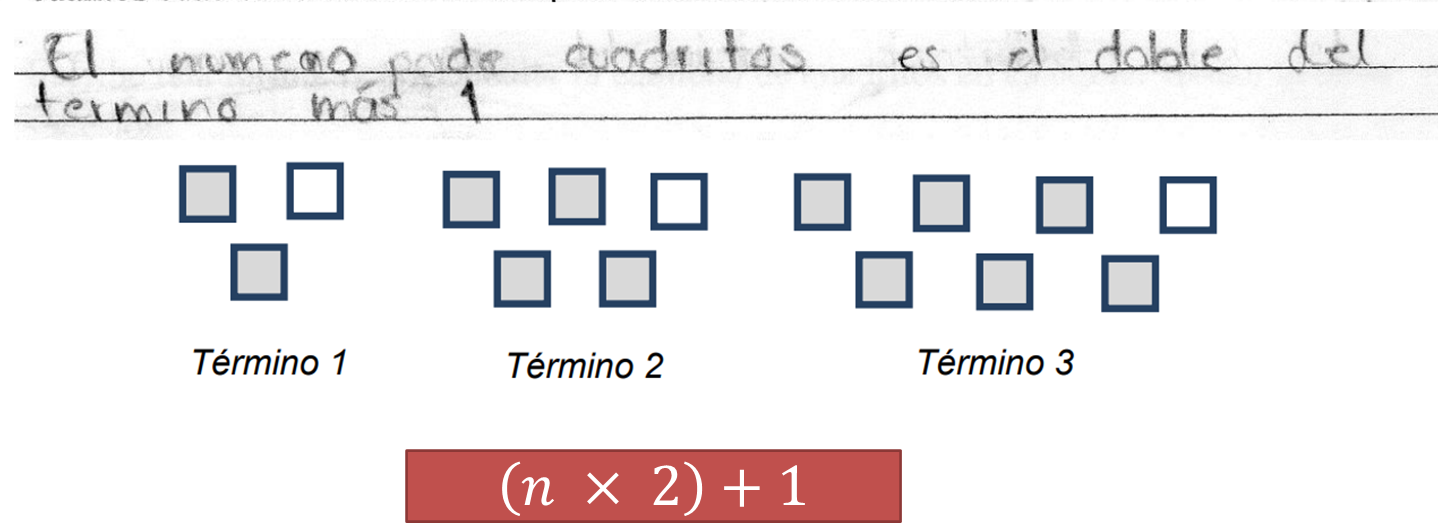
En este caso, la alumna indica que la expresión general de la sucesión es (n x 2) + 1, y es capaz de explicarla: “n” es el término, entonces si el término es uno, se multiplicará por dos, más el uno que siempre va a ser constante.

 

Después, ella lleva su razonamiento al siguiente caso, es decir, en lugar de “n” coloca 2 y comprueba que obtiene el número de elementos del segundo término, que son 5.

 

Pero ¿esta expresión algebraica funciona para cualquier término de la sucesión? Compruébalo con el quinto término.

 

Si “n” toma el valor de cinco, entonces en lugar de “n” por dos más uno, se coloca (5 x 2) + 1, el resultado es once y efectivamente, el quinto término de la sucesión tiene once elementos.

 

 

Alumno 3:

 

El alumno 3 descompuso la secuencia en filas, y cada fila en subelementos que forman subfiguras, cuya cantidad depende de la posición que ocupa cada elemento dentro de la secuencia.

 

Él escribe: “Los cuadros de abajo son el número de la posición y arriba son el número de la posición más uno”. Esto permitió al estudiante organizar de manera adecuada la relación existente entre los elementos de la figura y lo llevó a generalizar con una expresión algebraica.

 

 

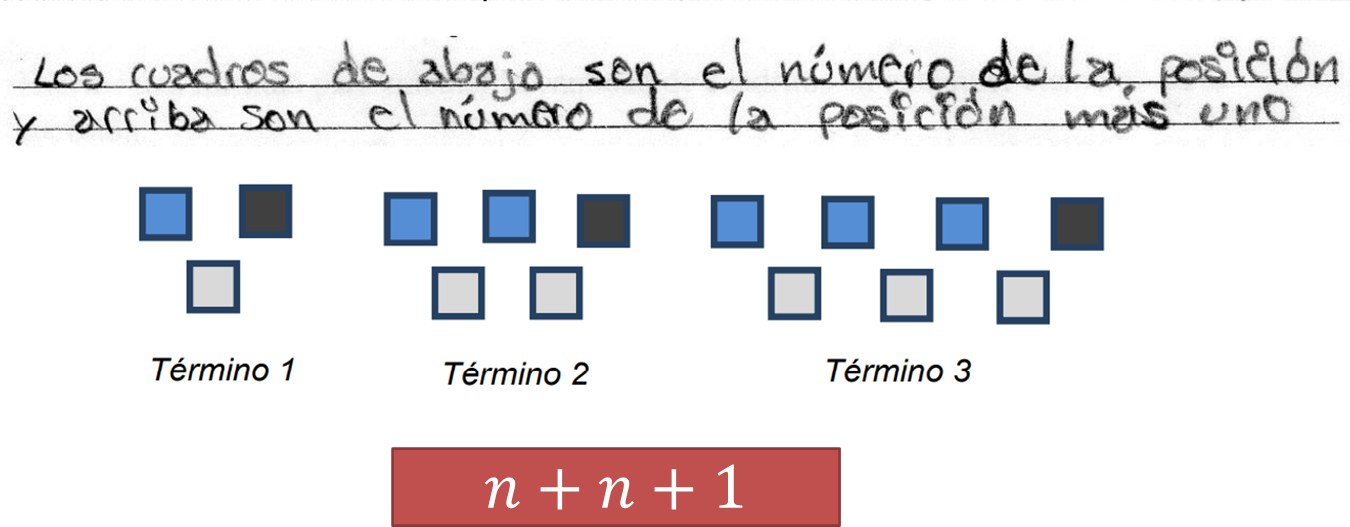
En este caso, el número de la posición se representa con “n” y, por lo tanto, el número de elementos que contiene la posición se puede encontrar con (n + n + 1). El primer término “n” representa el número que se asigna “a la posición” del término, y el término “n” más uno se refiere a “el número de la posición más uno”.

 

Así, se puede observar cómo es que los estudiantes pudieron conectar lo que vieron, con lo que escribieron con los símbolos algebraicos.

 

Analiza lo siguiente:

 

Esta última expresión es diferente a la que plantea la alumna 2. ¿Alguien está mal?

 

Para conocer lo anterior, revisa lo que plantea cada alumno y reflexiona al respecto.

 

La alumna 2 encuentra la expresión (n x 2 + 1), mientras que el alumno 3 plantea (n + n + 1). Si se cambia la variable “n” por el número diez ¿qué ocurre en cada caso?

 

 

Al resolver, empleando la jerarquía de operaciones, ambas expresiones llevan al mismo resultado. Por lo tanto, ambas son correctas.

 

Esto muestra que las dos formas son equivalentes, es decir, son dos expresiones algebraicas diferentes que formulan la misma situación. Entonces, es posible tener respuestas diferentes para la misma situación.

 

Cuando dos o más expresiones algebraicas generan la misma sucesión numérica se dice que las expresiones algebraicas son equivalentes, es decir, tienen el mismo valor.

 

A continuación, analiza el siguiente ejemplo.

 

2b = b + b

 

¿Qué piensas que pasaría si se cambia la letra “b” por el número 1? Toma un momento para reflexionar y después, observa qué sucede.

 

Al sustituir la letra “b” por el número 1, se obtiene la siguiente igualdad:

 

2 (1) = 1 + 1

 

Si se resuelven las operaciones, se obtiene que 2 es igual a 2. ¿Qué piensas que significa eso?, ¿pasará lo mismo si en lugar del número 1 se usa el número 2, el 3, el 8, o cualquier otro número?

Toma un momento para pensar y reflexionar, después, escribe una breve conclusión en tu cuaderno.

Ahora, el valor de la letra “b” será 8. Sustituye los valores en la igualdad.

 

2b = b + b

 

2 (8) = 8 + 8

 

16 = 16

 

Se obtiene que 16 es igual a 16.

De lo anterior se puede deducir que lo mismo pasará si se sustituye la letra “b” por cualquier número. Cuando sucede esto, se comprueba que las expresiones algebraicas son equivalentes.

Piensa en la siguiente cuestión:

¿Qué se puede hacer para encontrar una expresión equivalente a otra?

Para dar respuesta a la pregunta anterior, trabaja con la siguiente sucesión numérica que está parcialmente formada por los números:

 

3, 6, 9, 12, 15…

 

Los puntos suspensivos indican que la sucesión no tiene fin, es decir, es infinita.

 

Ahora, encuentra la manera de saber cuál es la regla que genera una sucesión.

 

¿Conoces algún procedimiento para encontrar la regla general de una sucesión numérica? Describe tu procedimiento en tu cuaderno.

Para encontrar la regla general de una sucesión, se identifica la diferencia entre un término y su consecutivo. Asimismo, se observa si la diferencia es constante entre los demás términos.

¿Ya sabes cuál es la diferencia entre los términos de la sucesión anterior?

Como puedes notar, la sucesión numérica aumenta de tres en tres. Entonces, para escribir la regla general de esa sucesión, se anota el número 3, porque ya sabes que aumenta de tres en tres. Se relaciona con el número de término, es decir, con el número de posición. Como ese número es variable, se le asigna una literal, generalmente la letra “n”.

De tal manera, que la regla que genera la sucesión numérica es (3n). El 3 porque la sucesión va aumentando de tres en tres y la “n” para representar cualquier término de la sucesión.

 

 

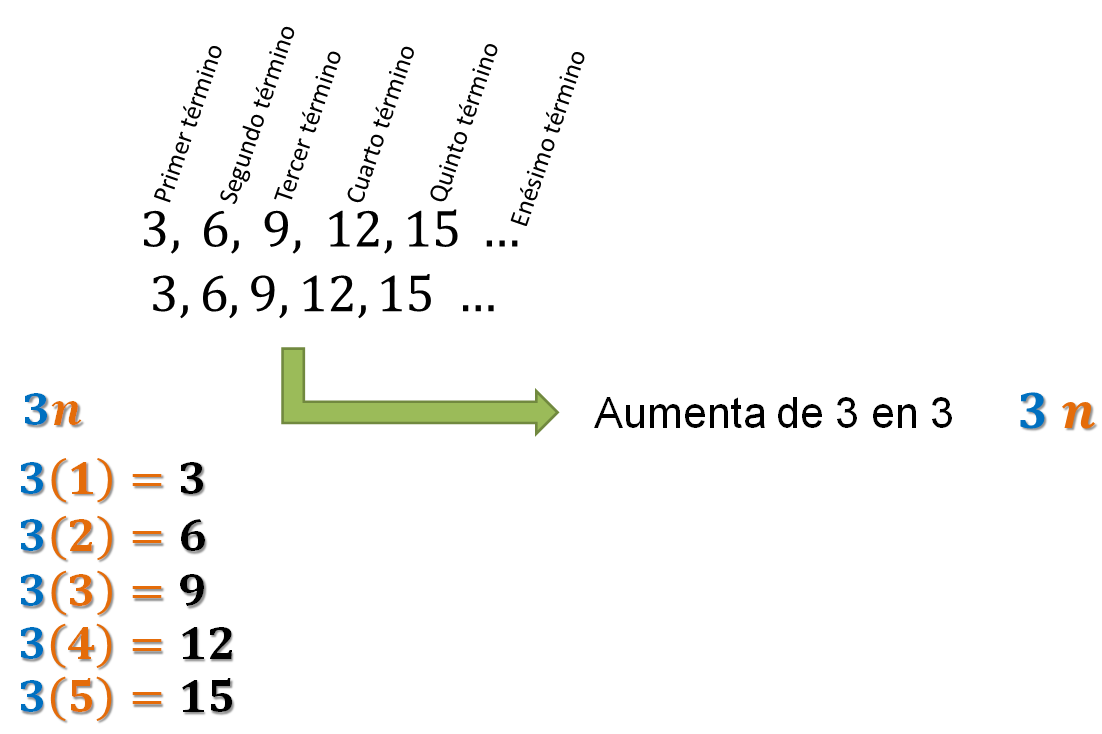
Un método para encontrar expresiones algebraicas equivalentes a otra, consiste en descomponer una expresión algebraica en sus partes.

Ahora, debemos preguntarte:

 

¿Cómo puedes descomponer 3n en partes?

 

Para descomponer una expresión algebraica es muy importante saber leerlas y entender su significado. Si sabes eso, también puedes saber las partes de las que se compone cualquier expresión algebraica.

¿Cuál es el significado de 3n? 3n significa tres veces el valor de “n”. Entonces, ¿de cuántas partes se forma 3n? Piénsalo un momento.

La expresión algebraica 3n se forma de tres partes y sus partes son tres letras “n”. Ahora, debes pensar una forma diferente de unir esas partes, ¿tienes alguna idea de cómo hacerlo?

Se pueden unir esas letras a través de signos que indiquen una operación, en este caso, puede ser por medio de una suma, ya que, si se suma “n”, más “n”, más “n”, se tiene 3n; y con eso, ya se ha descompuesto la expresión algebraica; pero también existe otra expresión algebraica equivalente a 3n, que es 2n más “n”.

 

 

Ahora, encuentra por lo menos dos expresiones algebraicas equivalentes a:

 

6n + 4

 

Primero, observa cuáles son las partes que la forman. Si se separan todos los elementos queda de la siguiente forma:

 

n + n + n + n + n + n + 4

 

Incluso ese cuatro puede separarse en 1 + 1 + 1 +1

Con los elementos separados, ¿puedes escribir por lo menos dos expresiones equivalentes? Coméntalas y compáralas a distancia con tus compañeras y compañeros.

Ahora, analiza las siguientes expresiones y comprueba si son equivalentes:

 

2 (3n + 2)

 

2n + 2n + 2n + 4

 

Reflexiona:

 

¿Se parecen estas expresiones algebraicas a las que escribiste?

¿Cómo puedes comprobar que estas expresiones algebraicas son equivalentes?

 

Comprueba que las expresiones algebraicas anteriores son equivalentes a 6n + 4. Después, comprueba que las expresiones algebraicas que propusiste también sean equivalentes.

Una de las formas para comprobar la equivalencia de expresiones algebraicas consiste en resolver las operaciones algebraicas indicadas; otra es construir la sucesión numérica que representan. En esta sesión, construirás sucesiones numéricas para realizar las comprobaciones.

Primero construye la sucesión numérica que genera 6n + 4 Lo harás para los primeros 5 términos.

Lo que debes hacer es sustituir el valor de “n” por 1, pues como recordarás, “n” representa el valor del término que se está buscando, en este caso, representa el primer término de la sucesión. Por lo tanto, se tiene que:

 

6n + 4

 

6(1) + 4 = 10

 

Entonces se puede decir que cuando “n” vale 1, el término es 10

Ahora, calcula el segundo término. “n” vale 2 porque se está buscando el segundo término de la sucesión, Realiza los caculos:

 

6n + 4

 

6(2) + 4 = 16

 

Entonces podemos decir que cuando n vale 2, el término es 16

Para el tercer término “n” vale 3; entonces se tiene que:

 

6n + 4

 

6(3) + 4 = 22

 

Por lo tanto, se puede decir que cuando “n” vale 3, el término es 22

Para el cuarto término, “n” vale 4; entonces se tiene que:

 

6n + 4

 

6(4) + 4 = 28

 

Por lo tanto, se puede decir que cuando “n” vale 4, el término es 28

 

Para el quinto término, “n” vale 5; entonces se tiene que:

 

6n + 4

 

6(5) + 4 = 34

 

Por lo tanto, se puede decir que cuando “n” vale 5, el término es 34

Ya has terminado de calcular los primeros 5 términos de la sucesión. Eso quiere decir que la sucesión que genera la regla 6n + 4, está formada por los términos 10, 16, 22, 28 y 34. Observa como quedaron los resultados de esta expresión:

 

 

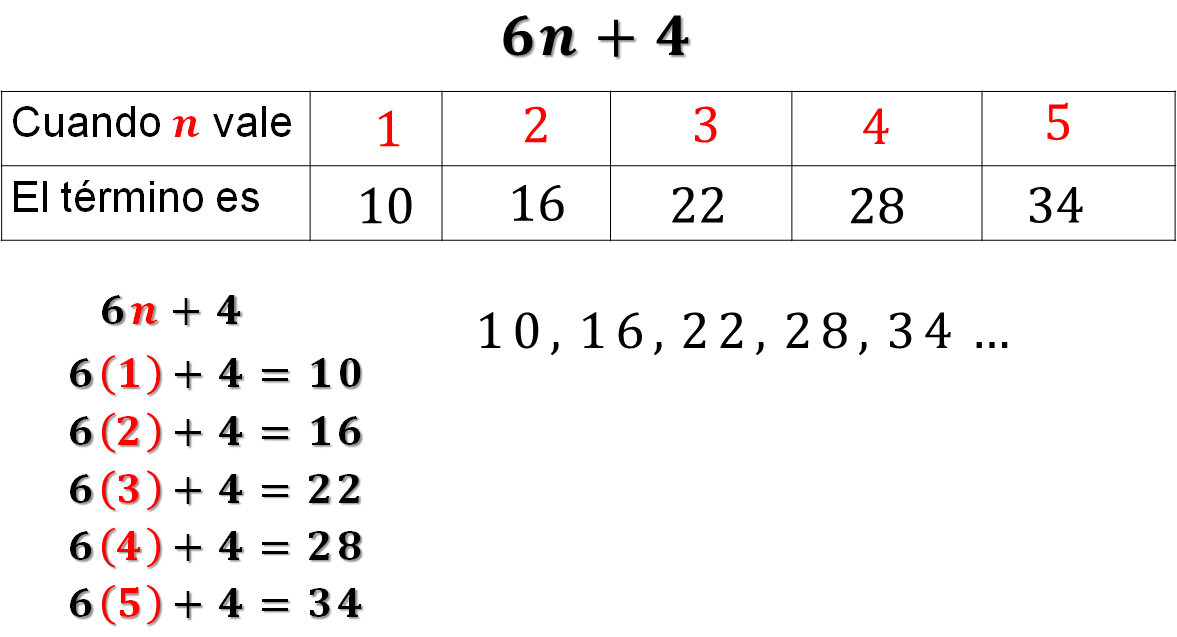
Al final se le agregan puntos suspensivos, ya que la sucesión continúa y no tiene fin.

Ahora ya sabes cuáles son los primeros términos de la sucesión. Para comprobar que las expresiones algebraicas que se escribieron son equivalentes a 6n + 4, sustituye “n” en las expresiones anteriores, por los números del uno al cinco. Si los resultados son idénticos, entonces la expresión algebraica es equivalente a 6n + 4.

Comienza con la expresión: 2 (3n + 2)

Se sabe que, para el primer término “n” vale 1. Sustituye y resuelve las operaciones paso a paso.

 

2 (3n + 2)

 

2 [3(1) + 2] = 2 [3 + 2] = 2 [5] = 10

 

Esto quiere decir que cuando “n” vale 1, el término es 10.

Para el segundo término “n” vale 2. Realiza la sustitución y resuelve las operaciones.

 

2 (3n + 2)

 

2 [3(2) + 2] = 2 [6 + 2] = 2 [8] = 16

 

Esto quiere decir que cuando “n” vale 2, el término es 16

Para el tercer término “n” vale 3

 

2 (3n + 2)

 

2 [3(3) + 2] = 2 [9 + 2] = 2 [11] = 22

 

Esto quiere decir que cuando “n” vale 3, el término es 22

Para el cuarto término “n” vale 4

 

2 (3n + 2)

 

2 [3(4) + 2] = 2 [12 + 2] = 2 [14] = 28

 

Esto quiere decir que cuando “n” vale 4, el término es 28

Para el quinto término “n” vale 5

 

2 (3n + 2)

 

2 [3(5) + 2] = 2 [15 + 2] = 2 [17] = 34

 

Esto quiere decir que cuando “n” vale 5, el término es 34

Ya has terminado de calcular los primeros 5 términos de la sucesión. Esto quiere decir que la sucesión que genera la regla “2 (3n + 2)”, está formada por los términos 10, 16, 22, 28 y 34. Observa como quedaron los resultados:

 

 

Como puedes observar, los términos de esta sucesión son idénticos a la sucesión anterior. Esto significa que ambas expresiones algebraicas son equivalentes.

Continua con la siguiente expresión: 2n + 2n + 2n + 4

Comprueba que esta expresión es equivalente a las dos expresiones algebraicas anteriores. Ya conoces el procedimiento para sustituir y resolver operaciones, así que esta vez te apoyaremos en el cálculo mental para avanzar más rápido.

Para “n” en el primer término se tiene que:

 

2n + 2n + 2n + 4

 

2(1) + 2(1) + 2(1) + 4 = 2 + 2 + 2 + 4 = 10

 

Para “n” en el segundo término se tiene que:

 

2n + 2n + 2n + 4

 

2(2) + 2(2) + 2(2) + 4 = 4 + 4 + 4 + 4 = 16

 

Para el tercer término se tiene que:

 

2n + 2n + 2n + 4

 

2(3) + 2(3) + 2(3) + 4 = 6 + 6 + 6 + 4 = 22

 

Para el cuarto término se tiene que: 2

 

2n + 2n + 2n + 4

 

2(4) + 2(4) + 2(4) + 4 = 8 + 8 + 8 + 4 = 28

 

En el quinto término se tiene que:

 

2n + 2n + 2n + 4

 

2(5) + 2(5) + 2(5) + 4 = 10 + 10 + 10 + 4 = 34

 

Al calcular los primeros 5 términos de la sucesión que genera la regla (2n + 2n + 2n + 4), se encuentra que está formada por los términos 10, 16, 22, 28 y 34. Observa como quedaron los resultados:

 

 

Los términos de esta sucesión son idénticos a los términos de las dos sucesiones anteriores. Entonces, las tres expresiones algebraicas son equivalentes.

Para finalizar, compara las siguientes expresiones. Sustituye el valor de “n” para comprobar si son equivalentes o no.

 

Expresión algebraica 1: 3 (n + 1)

 

Expresión algebraica 2: 5n + 1

 

Expresión algebraica 3: 3n + 3

 

En la primera expresión, sustituye “n” por 1 y 2:

 

3 (n + 1)

 

3 (1 + 1) = 3 (2) = 6

 

3 (2 + 1) = 3 (3) = 9

 

Al resolver, se obtiene el valor de 6 y 9, respectivamente.

En la segunda, también sustituye “n” por 1 y 2

 

5n + 1

 

5 (1) + 1 = 5 + 1 = 6

 

5 (2) + 1 = 10 + 1 = 11

 

Y en la tercera, sustituye de la misma manera a “n” por 1 y 2:

 

3n + 3

 

3 (1) + 3 = 3 + 3 = 6

 

3 (2) + 3 = 6 + 3 = 9

 

Cómo puedes observar, sí sólo se calcula el primer término de la sucesión en las expresiones algebraicas “3 (n + 1)”, “5n + 1” y “3n + 3”, parece que las expresiones son equivalentes, ya que, en los tres casos, se obtiene el mismo resultado.

Sin embargo, si se hace el cálculo con el segundo término de cada sucesión, puedes identificar que las tres expresiones algebraicas no son equivalentes entre sí.

¿Ya observaste que el valor del segundo término de la segunda expresión algebraica fue diferente? ¿Qué significa eso?

Esto significa que, solamente la primera y la tercera son equivalentes.

Por lo tanto, se puede concluir que: no basta con calcular un solo término para comprobar si dos o más expresiones algebraicas que generan una sucesión son equivalentes.

Con estos ejemplos aprendiste que se pueden identificar diferentes reglas que generan la misma sucesión numérica y a verificar su equivalencia con otras expresiones. Aunque sólo lo hiciste con la construcción de las secuencias numéricas que generan.

Hemos llegado al final de la sesión. Recuerda que este es un material de apoyo. Para complementar lo estudiado puedes consultar otras fuentes, como tu libro de texto de matemáticas de segundo grado.

El Reto de Hoy:

Escribe expresiones equivalentes de los ejemplos que se mencionaron en esta sesión. Además, resuelve los ejercicios de tu libro de texto de Matemáticas, correspondientes a este tema. Finalmente, coméntalas y compáralas a distancia con tus compañeras y compañeros.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

Compra en Amazon

Éste es un mensaje oficial

Aprendizaje esperado: Analiza el contenido de campañas oficiales.

Énfasis: Explorar campañas oficiales.

¿Qué vamos a aprender?

En esta sesión, iniciarás con el estudio de campañas oficiales. Para ello, conocerás qué es una campaña oficial o pública, qué la hace distinta de otro tipo de campañas, qué situaciones aborda, quiénes las promueven, cuáles son sus características y cómo se presentan. Esto te permitirá identificar cómo influyen las campañas oficiales en la vida cotidiana y de qué manera podemos, como ciudadanos, realizar acciones en pro de la resolución de problemas que afectan a la población.

¿Qué hacemos?

Para comenzar con esta sesión, reflexiona en lo siguiente.

Es probable que recuerdes haber visto en tu comunidad campañas de vacunación, para cuidar el medio ambiente, para prevenir accidentes o enfermedades, entre otras.

¿En qué lugares recuerdas haber visto estas campañas?

Las campañas se difunden a través de diversos medios de comunicación y en distintos formatos. Antes de comparar las campañas oficiales o públicas con otras, como las políticas, publicitarias, de divulgación científica y cultural o ciudadana, explora el mundo de las campañas.

De acuerdo con el Diccionario de la Lengua Española, la palabra “campaña” proviene del latín tardío “campania”, que se deriva del latín campus, “llanura”. Este término se relaciona con las campañas militares, a través de las cuales los romanos iban consiguiendo territorios. Los soldados colocaban sus tiendas en terrenos abiertos y buscaban conseguir objetivos estratégicos. Uno de los significados actuales de la palabra “campaña”, se refiere a un conjunto de actos o esfuerzos de índole diversa que se aplican para conseguir un fin determinado.

Las campañas se conforman por acciones y mensajes que se transmiten por diversos medios para llegar a una población o audiencia determinada. Existen diferentes tipos de campañas de acuerdo con quien las organiza, el objetivo que persiguen y, sobre todo, la población a la cual desean llegar.

A continuación, identifica algunos tipos de campañas.

Las campañas políticas son organizadas por grupos políticos y una de sus funciones es generar simpatía para ganar militantes o adeptos.

Las campañas publicitarias son emitidas por empresas y tienen como finalidad posicionar alguna marca, producto, o servicio de tal forma que aumente sus ventas y genere más ganancias económicas.

Las campañas oficiales o públicas las promueven las instituciones gubernamentales y pretenden concientizar a diversos sectores de la población para que lleven a cabo acciones en beneficio propio y de la comunidad.

Las campañas de divulgación científica y cultural son organizadas por cualquier grupo o institución interesada en la difusión del conocimiento o cultura, como escuelas o universidades.

Las campañas ciudadanas regularmente las emiten organizaciones no gubernamentales o movimientos civiles.

Las campañas oficiales, de divulgación científica y cultural, y las ciudadanas, se les denominan “campañas de acción social” por pretender el bien público. Por ejemplo, campañas relacionadas con la prevención de adicciones o la reducción de desechos no reciclables, en las se advierte de esos problemas a la población y se invita a las personas a adoptar una conducta que beneficie a todos.

Ahora, profundiza en qué son las campañas oficiales o públicas.

Campaña oficial:

Consiste en una estrategia de difusión de información; que tiene como finalidad sensibilizar o persuadir al público receptor, para modificar actitudes y comportamientos encaminados a prevenir o resolver problemas sociales.

Las campañas oficiales también conocidas como campañas públicas son estrategias para difundir información, y éstas sensibilizan al público para modificar su actitud o comportamiento y así resolver o prevenir problemas sociales.

¿Sabes qué tipos de problemas sociales se manejan en las campañas oficiales?

 

Para dar respuesta a esta pregunta, realiza la siguiente actividad.

Observa con atención el siguiente cartel e identifica lo siguiente:

¿Qué situación aborda?

¿Quién lo difunde?

¿Alude a algún problema social?, ¿cuál?

 

 

Recuerda que atrás de cada campaña pública existe un problema que nos atañe a todos. La Secretaría de Medio Ambiente y Recursos Naturales (SEMARNAT) lanzó la campaña “Protección de los océanos, mares y costas de México”, con el propósito de que la sociedad en general tome conciencia de la importancia de cuidar y proteger nuestros recursos marinos de las amenazas que actualmente enfrentan: contaminación por plásticos de un solo uso, cambio climático y tráfico de especies.

Lograste identificar ¿qué situación aborda?, ¿quién la promueve?, ¿a qué problema social alude?, y ¿cuál?

En este caso se aborda un problema relacionado con el medio ambiente, con esta campaña se pretende informar a la población sobre las afectaciones que las personas hemos causado a los océanos. Asimismo, se busca exhortar a un cambio de hábitos de consumo para detener la contaminación por plásticos de un solo uso. También se invita a la sociedad a tomar acciones para enfrentar los efectos del cambio climático y denunciar el saqueo de especies marinas, muchas de ellas endémicas. Quien difunde la campaña es SEMARNAT.

Reflexiona:

¿Cómo podemos sumarnos como ciudadanos a esa campaña?

Podríamos empezar por no contaminar los mares, si estamos en la playa, debemos tirar la basura en los lugares destinados para ello.

A continuación, observa otra campaña más y descubre la problemática social que pretende abordar.

1. México siempre será tu casa.

https://www.cndh.org.mx/video/mexico-siempre-sera-tu-casa

 

La campaña oficial “México siempre será tu casa” promovida por la Comisión Nacional de Derechos Humanos, CNDH, pretende orientar a las personas migrantes, en este caso repatriadas, y mostrarles que deben hacer valer sus derechos. Por lo tanto, atiende a un problema de derechos humanos.

Todos como ciudadanos debemos estar informados de las acciones de la Comisión Nacional de Derechos Humanos en materia de migrantes, para cuando se observe que alguien requiere información poderlos orientar.

Ahora, observa otra campaña oficial y descubre qué problema aborda, recuerda identificar quién promueve la campaña y a quién consideras que va dirigida.

2. Campaña Nacional contra las adicciones COVID 19 y Salud Mental.

https://www.youtube.com/watch?v=dDWhIFMYy70&feature=emb_logo

 

Esta campaña “Juntos por la Paz” que promueve la Comisión Nacional contra las adicciones, CONADIC, se aborda un problema social relacionado con la salud. La campaña se dirige a toda la población en general. La salud es muy importante y debemos sumarnos todos a las acciones del Sector Salud para contribuir a una sociedad saludable.

Como puedes observar, usualmente los problemas sociales que se manejan en las campañas oficiales se relacionan con: tabaquismo, desnutrición, consumo de sustancias ilícitas, contaminación del medio ambiente, violación de derechos humanos, entre otros. Problemas de importancia para la sociedad en general.

Escucha ahora qué campañas oficiales conocen algunas y algunos adolescentes y qué problemas sociales se abordan.

3. Video. Estudiantes, campañas oficiales.

https://drive.google.com/file/d/1iz92ox9dhZRh93banHoPtLGbXyC_zxcm/view?usp=sharing

 

Después de conocer la definición y las clases de campañas que existen, además de haber revisado los componentes de aquellas que son conocidas como oficiales o públicas, explorarás las campañas a través de sus objetivos y características.

Observa el video de la campaña oficial “Estereotipos y prejuicios”, promovida por el Consejo Nacional para Prevenir la Discriminación, CONAPRED.

 

4. Estereotipos y prejuicios, CONAPRED.

https://www.youtube.com/watch?v=uQf1rb6pbFQ&feature=youtu.be

 

Ahora, reflexiona a través de los siguientes cuestionamientos:

¿Cuál es el objetivo de esta campaña?

¿Qué actitudes invita a poner en práctica?

El objetivo de esta campaña es sensibilizar al público sobre los efectos negativos que conlleva relacionarnos a partir de prejuicios y estereotipos con quienes nos rodean. La discriminación derivada de estas actitudes niega a las personas el goce de sus derechos. Asimismo, invita a poner en práctica actitudes no discriminatorias, valores asociados al respeto y al reconocimiento de los otros.

El objetivo de las campañas oficiales es definir ideas y persuadir a la audiencia para que modifique su forma de pensar o actuar. La palabra persuadir, significa conseguir con razones y argumentos que una persona actúe o piense de un modo determinado.  Dentro de las campañas oficiales, se pretende convencer a las personas y audiencia a que deben modificar su forma de pensar o actuar en beneficio de sí mismo y de la comunidad.

Es por lo que en la campaña que acabas de observar, trata de convencer de establecer relaciones alejadas de los prejuicios y estereotipos. Si se practica el respeto y se reconoce la diversidad, se puede disminuir la discriminación, exclusión y las violencias.

Otro de los objetivos de las campañas oficiales es llegar a la mayor cantidad de individuos posibles, para así, conseguir un cambio de mentalidad hacia un asunto que el grupo considere negativo o problemático. Por ello, la campaña “Estereotipos y prejuicios” se ha difundido por redes sociales, radio, televisión, canales de internet en formato de audio, video y carteles.

Ahora, explora las campañas oficiales a través de sus características. Observa con atención el siguiente cartel que pertenece a la campaña oficial “Cuenta hasta 10 y saca la bandera de la paz”.

 

 

Características de las campañas oficiales:

 

1. Tener una audiencia definida y adaptarse a sus valores.
2. Expresar un mensaje claro, que no deje lugar a dudas sobre la problemática que se desea solucionar.

 

Se debe entender como “audiencia definida” al grupo social hacia el cual se quiere enfocar el mensaje. Las estrategias de difusión dependen mucho de las características particulares que definan a ese sector poblacional.

 

Después de observar el cartel anterior, responde lo siguiente:

 

¿A quiénes va dirigida la campaña “Cuenta hasta 10 y saca la bandera de la paz”?

 

La campaña “Cuenta hasta 10 y saca la bandera de la paz” va dirigida a toda la población y tiene la finalidad de prevenir la violencia intrafamiliar y el maltrato hacia las mujeres.

La segunda característica es que la campaña social tenga un mensaje claro, esto quiere decir, que no debe tener dificultad para entenderse y no debe generar dudas en el espectador.

Reflexiona:

¿Qué pasaría si en la campaña “¿Cuenta hasta 10 y saca la bandera de la paz”, no tuviera un mensaje claro?

No se entendería lo que está tratando de decir y en vez de generar un cambio, no se le daría importancia a esta campaña.

Continúa con otras características de las campañas oficiales.

3. Presentar propuestas de solución y estas pueden ser evidentes.
4. Emplear recursos que permitan que el mensaje se quede en la mente de la audiencia.

Por ejemplo, para lograr lo anterior se puede usar la música, las figuras retoricas, imágenes, entre otros.

A continuación, observa la siguiente cápsula del minuto 0:54 al 3:12 e identifica los beneficios que trae consigo la participación ciudadana en corresponsabilidad con las autoridades.

5. Para fortalecer el Estado de derecho y la convivencia democrática.

https://www.youtube.com/watch?v=3IP9KNIq0jw

 

Las campañas oficiales brindan la posibilidad de participar con las autoridades en la disminución de algunos problemas que se enfrentan. En la actualidad, se presentan diferentes retos en materia de salud, en temas del medioambiente, equidad de género, seguridad pública, y es necesario que los ciudadanos nos involucremos.

También es importante que, por medio de las campañas oficiales, se sensibilice y concientice a la sociedad sobre estos problemas. Todos podemos convertirnos en agentes de cambio.

Recuerda, que las campañas oficiales son una estrategia para difundir información sobre las diferentes problemáticas que existen en la comunidad, región o país.

Has finalizado la sesión. Para complementar lo visto, en tu libro de Lengua Materna 2 podrás encontrar ejemplos de campañas oficiales. También puedes consultar tu libro de Formación Cívica y Ética para conocer más sobre los problemas sociales, la participación ciudadana y la corresponsabilidad.

El Reto de Hoy:

Observa el siguiente video y contesta las preguntas.

¡Evita quemaduras! La prevención es vital.

https://youtu.be/blC6fYOipGY

 

1. ¿A qué tipo de campaña pertenece?

 

1. Campaña oficial o social
2. Campaña política
3. Campaña publicitaria

 

 

2. ¿Cuál es el objetivo de esta campaña?

 

1. Cuidar el medioambiente
2. Prevenir accidentes
3. Cuidar la salud

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

Compra en Amazon

Pero ¿Qué ha pasado aquí?

Aprendizaje esperado: Representa acontecimientos importantes vinculados a la historia de su comunidad mediante distintas formas expresivas.

Énfasis: Reconocer elementos que han modificado aspectos del paisaje de la comunidad para representarlos mediante las artes.

¿Qué vamos a aprender?

En esta sesión, conocerás cómo representar aspectos del paisaje de tu comunidad mediante las artes. Para ello, explorarás e imaginarás todo tu alrededor y describirás cómo es el paisaje de tu localidad.

¿Qué hacemos?

Para iniciar, reflexiona en las siguientes preguntas:

 

¿Has observado cambios en el paisaje de tu comunidad?, ¿cómo han sido?

¿Reconoces los elementos que se han modificado recientemente en estos paisajes?, ¿cuáles podrías mencionar?

 

Tal vez te encuentres, al igual que todos, un poco aislada o aislado debido a las medidas preventivas que debemos de tomar. Pero probablemente puedas tener una ventana cerca que te brinde un panorama. Acercarte a esa ventana y observa el exterior. Presta mucha atención.

 

¿Qué ves por la ventana?

Escribe todo lo que veas en tu cuaderno. Asimismo, menciona los cambios que identifiques de unos años a este momento.

 

Por ejemplo, podría ser una calle llena de autos, donde vayan en una misma dirección. Sin embargo, esa calle antes pudo haber sido en ambos sentidos y apenas hace unos días cambiaron la dirección. O quizá, construirán algo porque se ven señalamientos anaranjados que cortan la circulación vehicular, ya que se puede ver una maquinaria grande.

También podría ser que veas por tu ventana montañas, árboles y animales, una zona preciosa llena de colores verdes, donde muchas personas hacen sus labores del día: alimentan a sus animales, como vacas, gallinas, cerditos; pero a lo lejos se nota cómo construyen también algo.

Intenta describir cada aspecto que identifiques: cómo es el paisaje de tu localidad y cómo era antes. Si no tienes ventanas, construye una con tu imaginación. Incluso puedes dibujar una en el aire, frente a ti. Ahora puedes ver, con el poder de tu imaginación, el recuerdo de tu entorno y, de esta manera, puedes describirlo.

¿Qué elementos reconoces que han modificado tu comunidad?

 

Para inspirarte, realiza un ejercicio de memoria.

¿Recuerdas si en tu comunidad existen esculturas, quioscos, parques o fuentes?

¿Hay murales, mercados, plazas, monumentos o música característica de tu localidad, quizá de alguna festividad o de algún momento especial?

¿Conoces los colores, formas, texturas, sonidos u olores de tu localidad?

Por ejemplo, podría ser que existe un mercado que antes era de un color específico y ahora tiene otros colores y formas, donde hay murmullos y gritos, olor a frutas, a verduras, a madera y a plantas. Incluso puedes imaginar que vas caminando ahí en este momento.

Puedes recordar también otros elementos, como un kiosko, una iglesia, un jardín o una plaza donde venden helados y comida típica.

¿Qué recuerdas?

Ahora con ayuda de tu imaginación responde las siguientes preguntas:

Si tu comunidad fuera un platillo, ¿a qué sabría?

¿A qué olería tu comunidad si fuera un perfume?

Anota en tu cuaderno las respuestas de estas interrogantes o, si lo deseas, dibújalas. Recuerda que, en artes, la libertad de expresión es latente.

Ya que observaste todos los elementos característicos de tu comunidad con detenimiento:

¿Qué te provocan estos elementos?

Seguramente existen dentro de tu comunidad lugares que te gustan o te atraen, ya sea por sus formas, tamaños, colores, texturas o por lo que se realiza en ese sitio.

No obstante, también puede haber algunos elementos que no te agraden mucho, pero debes reconocer que tienen un sello y distinción. De acuerdo con lo anterior, reflexiona:

¿Por qué crees que están ahí estos elementos?

¿Cómo te imaginas que era tu comunidad hace 50 años o hace 100 años?

Gracias a tus clases de historia, conoces los acontecimientos que han ocurrido en tu comunidad. Y si no es así, seguramente alguna familiar tuyo te habrá narrado de forma cotidiana cómo se han transformado los espacios que habitas.

Ahora, responde lo siguiente:

 

A ti, ¿cuáles historias te han contado tus familiares, sobre la transformación de tu comunidad?

¿Qué imágenes has visto de antaño de tu localidad?

Anota todo lo que recuerdes. Y si te es posible, pregúntales a tus familiares. Será un buen pretexto para hacer una llamada telefónica o videollamada y conversar sobre las historias de los cambios de tu comunidad.

El arte de la conversación generará un grato recuerdo que llevarás contigo, pues debes de recordar que todos somos parte fundamental de una localidad. Y a través de la transmisión de las historias a otras generaciones, también se crea la identidad de la localidad.

Después de haber realizado lo anterior, dibuja cómo se encuentra tu localidad hoy en día y realiza un comparativo con lo que tus familiares te narraron. Haz un antes y un después de tu localidad. De tal manera que un dibujo salga de lo que imagines con la narración y el otro dibujo busque representar lo que percibes de ese mismo lugar en la actualidad. Recuerda compartirlo con tus profesores. No olvides estar en contacto con ellos, es muy importante.

A continuación, a modo de ejemplo, observa el siguiente video que comparte un alumno de segundo grado y analiza cómo elaboró la actividad.

1. Video. Transformación de mi comunidad.

https://youtu.be/yS19vbz-36g

 

¿Qué te pareció la historia? Es muy importante conocer sobre otras localidades y sus modificaciones. Muchas veces, se conocen personas que atesoran historias de cambios sobre un mismo lugar, ¿conoces alguna?

Para finalizar, realiza la siguiente actividad.

 

Juega a viajar en taxi.

 

Pide ayuda a tus familiares y cuenten las historias que conocen sobre los aspectos que modifican los espacios. Busquen entre las cosas que estén a su alrededor.

 

Por ejemplo, cómo era un lugar antes, qué historia se cuenta de ese lugar, qué se destaca de tu comunidad, qué lugar recomendarías visitar, qué elementos han cambiado o ya no existen, qué se ha construido últimamente. En fin, las posibilidades son infinitas. Juega con tu familia y diviértanse a través de las artes.

Has llegado al final de tu destino. Recuerda que puedes transformar a través de las artes lugares, respetando y cuidando el medio ambiente, el entorno visual, social y cultural, para la mejora de tu comunidad. Puedes iniciar no tirando basura, no desperdiciando los recursos naturales y siendo amigable con el medio ambiente. Pequeñas acciones hacen grandes cambios.

El Reto de Hoy:

Recopila las historias de tus abuelos, tíos o padres, que indiquen la transformación que han sufrido los espacios de tu comunidad y recuerda observar a través de la ventana y dibujar en tu cuaderno los cambios que ha sufrido tu comunidad a través de la propia percepción y las narraciones de tus familiares.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

Compra en Amazon

Energía solar y energía eólica

Aprendizaje esperado: Describe el funcionamiento básico de las fuentes renovables de energía y valora sus beneficios.

Énfasis: Reflexionar sobre los beneficios y desventajas de la energía solar y la energía eólica.

¿Qué vamos a aprender?

En esta sesión, conocerás acerca de la energía solar y la energía eólica, para que puedes reflexionar sobre los beneficios y desventajas de estos tipos de energía, así como su importancia en la vida cotidiana

¿Qué hacemos?

Para comenzar con el tema, recuerda qué es la electricidad.

La electricidad es una de las formas de energía más usada en las actividades diarias, tanto en ciudades como en poblaciones pequeñas. Esta se genera utilizando fuentes renovables y no renovables de energía.

Las fuentes renovables de energía son aquellas que son inagotables o prácticamente inagotables. Además, reducen el impacto medioambiental, ya que, una vez que entran en funcionamiento, no originan emisiones contaminantes, ni gases de efecto invernadero.

Pero ¿qué tipos de energías renovables se usan para producir electricidad? 

Los tipos de energías renovables que existen son los siguientes:

Solar, que se obtiene a partir de la radiación del Sol.

Eólica, que se consigue del movimiento del viento.

Geotérmica, que se obtiene al aprovechar el calor interno de la Tierra.

Hidráulica o hidroeléctrica, que usa el movimiento del agua en ríos o en corrientes de agua dulce.

Biomasa y biogás, que se extrae de la materia orgánica.

Undimotriz, que se genera a partir del oleaje del mar.

Existe un número bastante elevado de alternativas para generar energía de manera renovable y, además, limpia. Primero analizarás la energía solar para conocer sus ventajas y desventajas.

El Sol es una fuente de energía primaria fundamental para el planeta en todos los sentidos. La energía solar no sólo ha permitido la proliferación de distintas formas de vida en el planeta, sino que se puede aprovechar para realizar diversas actividades.

Hay tres formas básicas de utilizar la luz solar. La primera es el aprovechamiento directo de la iluminación, esto permite sustituir la electricidad o la quema de gas en una casa, por lo que se debe tratar de aprovechar al máximo la luz del Sol.

Incluso hay unos dispositivos llamados tubos de luz, que son canales que dejan pasar la luz del Sol a través del techo para que ilumine el interior de una casa y así no se dependa tanto de la energía eléctrica. El problema es que, si la casa ya está construida, puede resultar muy difícil o costoso hacer las adecuaciones necesarias.

También en algunas comunidades han desarrollado alternativas a estos sistemas, donde colocan botellas de plástico llenas de agua en sus techos. Éstas dejan pasar la luz del Sol y permiten iluminar dentro de una casa sin usar energía eléctrica.

La segunda forma de aprovecharla es concentrando su radiación en un punto para aumentar la temperatura de un cuerpo o sustancia. Aquí se habla de energía fototérmica. En este caso, hay gran variedad de aplicaciones. Se puede utilizar para elevar la temperatura de un fluido, esto se hace con colectores solares

Existen tres tipos de colectores solares.

El de placa plana, que es una caja con una tapa que deja pasar la radiación solar, y dentro de la caja puede haber una tubería por la que circula agua o aire.

 

El colector de tubos de vacío está conformado por una serie de tubos de vidrio, donde cada tubo tiene una doble capa, en otras palabras, es un tubo dentro de otro. En el tubo interior circula agua, que es calentada por la radiación solar.

En ambos casos, si el fluido que se calienta es agua, ésta puede ser colectada en un recipiente aislado térmicamente, lo que permite conservarla a una temperatura elevada por mucho tiempo.

Si lo que se calienta es aire, éste puede servir para la proporcionar calefacción en una casa.

El último tipo es un colector de concentración. Éstos suelen ser espejos en forma de parábola, que hacen que la energía del Sol se concentre en un tubo llamado receptor. Este tubo contiene un fluido, que es el que almacena el calor. Con los colectores de concentración se llegan a alcanzar temperaturas de hasta 400 grados Celsius, por lo que algunas veces se utilizan incluso para generar energía eléctrica.

Este tipo de plantas generadoras se llaman centrales solares de torre. Constan de una superficie llena con espejos, que reflejan la radiación solar y la concentran en un receptor, usualmente colocado sobre una torre. Los espejos tienen la capacidad de moverse para poder estar siempre orientados con el Sol. El receptor aloja agua, la cual se transforma en vapor por las altas temperaturas y mueve unas turbinas para generar la energía eléctrica.

También se pueden utilizar colectores de energía solar para realizar algunas actividades. Por ejemplo, construir un horno solar tan sólo con cajas de cartón, papel aluminio y un trozo de vidrio o plástico. Su uso reduce el consumo de otro tipo de energías contaminantes como el gas, el petróleo o la leña.

La energía que irradia el Sol también puede ser aprovechada y transformada a través de celdas fotovoltaicas. Las celdas fotovoltaicas son dispositivos que convierten la luz solar en energía eléctrica. Se fabrican con silicio, y en algunos casos con arseniuro de galio. Una celda solar no genera mucha energía, así que se colocan en grandes conjuntos que se conocen como paneles solares.

Los paneles pueden estar constituidos por 36 celdas solares o más, dependiendo del tamaño o de la potencia eléctrica que se quiera alcanzar.

Dependiendo de cómo se almacene la energía generada por un sistema de paneles solares, éstos se clasifican en sistemas aislados y sistemas interconectados.

En los sistemas aislados la energía eléctrica generada se guarda en una o en varias baterías. En estos casos la energía almacenada se puede utilizar cuando no se cuente con la luz del Sol, ya sea en días nublados o simplemente en la noche.

Actualmente, en varios lugares de México, el alumbrado público funciona con este tipo de sistemas. Esto presenta la ventaja de poder utilizarse en zonas donde no se cuente con infraestructura de cableado eléctrico.

La segunda forma de aprovechar la energía eléctrica generada por paneles fotovoltaicos es en los sistemas interconectados. Éstos reciben su nombre debido que están conectados a la red eléctrica, y tienen la característica de que la energía producida se puede transferir a la red eléctrica local.

En México, la Comisión Federal de Electricidad da la opción de adquirir un medidor bidireccional. Si en tu casa tuvieras paneles solares que en determinadas horas del día produjeran más energía que la que se consume, podrías transferir el excedente de electricidad a la red eléctrica, lo que generaría un saldo a favor de kilowatts.

Los medidores bidireccionales contabilizan la energía entregada y se la restan al consumo que se hace cuando los paneles no producen la energía suficiente, como ocurriría en la noche. Esto hace que el importe a pagar cada bimestre sea menor al que se tendría que pagar si no se contara con los paneles solares. Además, no se tiene que adquirir un banco de baterías, que puede ser muy costoso.

Además, si se aprovecha al máximo la luz del Sol en las actividades, se ahorraría más electricidad y se ayudaría a disminuir las emisiones contaminantes. Recuerda que muchas centrales termoeléctricas siguen utilizando combustibles fósiles, y su quema produce grandes cantidades de gases de efecto invernadero.

Por otra parte, la energía solar es prácticamente inagotable y no produce contaminación acústica, ya que se genera de forma silenciosa.

Pero ¿por qué si estas tecnologías son tan buenas, no las tenemos en nuestras casas?

El principal impedimento es económico. Estos sistemas que transforman la radiación solar en otro tipo de energía pueden ser muy costosos. Los colectores térmicos para calentar el agua se han popularizado en los últimos años y tienen precios relativamente altos.

Esto mismo ha pasado con los paneles fotovoltaicos, pero éstos tienen costos aún más elevados, ya que su proceso de fabricación es complejo y requiere materiales muy específicos.

Además, la producción de los paneles usa químicos tóxicos. Esto hace que la disposición y reciclaje de las celdas que ya no se utilicen sea complicado.

También dependen de la cantidad de radiación solar que llegue, que varía en función de qué tan nublado esté el día o de los niveles de contaminación del aire.

Otra ventaja es su amplia disponibilidad, ya que incluso en lugares remotos, que pueden ser de difícil acceso para obtener energía de otras fuentes, siempre es posible contar con la energía solar. Sin embargo, si se desea obtener un suministro que abastezca un gran número de casas, se necesitan implementar plantas generadoras, que utilizan grandes superficies.

México tiene 50 parques fotovoltaicos de gran escala, lo que genera una potencia eléctrica de alrededor de 4,549 mega watts. Incluso se tiene el parque solar más grande de América Latina, la Planta Solar Villanueva, en Coahuila, con una superficie de 2,400 hectáreas.

Ahora, profundizarás en la energía eólica, que proporciona energía sin necesidad de recurrir a la combustión.

La humanidad se ha valido de ella desde civilizaciones muy antiguas. Algunos de los usos que se le han dado incluyen:

• La propulsión de barcos de vela.
• Moler granos y semillas en los molinos de viento.
• Bombeo de agua a través de las bombas eólicas.

 

También se han implementado dispositivos para transformar la energía del viento en energía eléctrica a través de los aerogeneradores. Para entender mejor cómo funcionan, observa el siguiente video.

 

• Energías limpias.

https://www.youtube.com/watch?v=ZOFGmcrANUQ

 

La energía eólica es una de las que más ha crecido en los últimos años debido a las ventajas que presenta. Entre éstas, se puede encontrar que un aerogenerador compensa en menos de un año la energía consumida para su fabricación, y tiene una vida útil de más de 30 años. Cada aerogenerador puede producir la energía eléctrica suficiente para cubrir el consumo de unos 2,000 hogares.

Si bien los aerogeneradores deben ser colocados en lugares abiertos, donde el viento circule libremente, la superficie que ocupan es mínima.

Los parques eólicos son perfectamente compatibles con las actividades agrícolas y ganaderas, que pueden desarrollarse en el mismo espacio. Además, también se pueden establecer parques eólicos marinos, ubicados en aguas que no tengan una profundidad mayor a 60 metros y estén alejados de las costas, rutas e instalaciones marítimas.

Se tiene la creencia de que los aerogeneradores son muy ruidosos, pero si te colocarás directo debajo de uno, el sonido que se escucharía tendría una intensidad comparable a la de una aspiradora funcionando. Pero a una distancia de unos 400 metros, lo que escucharías sería el equivalente al sonido que hace un refrigerador, es decir, casi imperceptible.

Sin embargo, se llevan a cabo estudios sobre la contaminación acústica de los aerogeneradores de los parques eólicos marinos, ya que se han detectado altos niveles de sonido emitido en bajas frecuencias, lo que puede afectar a especies que sean sensibles a éstas. Además, las ondas de sonido en el agua se pueden propagar por grandes distancias.

Una desventaja que presenta este tipo de generación de energía eléctrica es que no se pueden colocar parques eólicos en cualquier lugar, independientemente de si se tiene el espacio o no. Esto se debe a que se requiere una corriente más o menos constante de viento, que tenga una velocidad mayor a los 3 metros por segundo, pero que no supere los 24 metros por segundo.

También se deben hacer estudios de impacto ambiental, ya que algunos animales, como insectos, aves y murciélagos llegan a morir al estrellarse contra las aspas de los generadores. Por eso, se deben estudiar las rutas que siguen las especies endémicas de cada zona, así como las migratorias.

Otra desventaja es que se tienen que disponer sistemas de almacenaje de energía, como baterías, que son costosas y generan residuos altamente contaminantes.

En México, sólo nueve estados son productores de energía eólica, aunque el potencial del país es alto.

El laboratorio nacional de energías renovables de Estados Unidos estima que nuestro país puede llegar a producir valores superiores a los 40,000 mega watts. Por lo tanto, si se explotara todo el potencial eólico de México, sería capaz de satisfacer una gran parte de su demanda energética.

Un ejemplo a seguir en este rubro es China, que ostenta el título de los mayores productores de energía eólica en el mundo, pues genera 37% de la producción mundial. Además, ha trazado un plan para generar, de forma eólica, toda la energía eléctrica que consume su población para el año 2030.

México aún está muy lejos de esas cifras. Tan sólo en el año 2019 se produjeron 3,500 mega watts de energía, que es suficiente para cubrir las necesidades anuales de 3 millones de viviendas. Tan sólo entre 1% y 2% de la energía eléctrica que se consume en México, se produce con este método.

El estado que más contribuye con este tipo de energía es Oaxaca. El istmo de Tehuantepec tiene una potencia de viento que excede los 1,200 watts por metro cuadrado entre los meses de octubre y febrero, con una velocidad promedio de 8 metros por segundo.

En el municipio de Juchitán de Zaragoza, en Oaxaca, se encuentra el parque eólico llamado Energía Eólica del Sur, que tiene 132 aerogeneradores, con una potencia total de 396 mega watts, y es considerado el más grande de América Latina.

En el municipio de General Bravo, en Nuevo León, se encuentra el complejo integrado por los parques eólicos Ventika, y Ventika 2. Éstos tienen una potencia total de 252 mega watts. Este parque es el segundo más grande de México.

Has concluido esta sesión. Si deseas profundizar en el tema o resolver tus dudas, revisa tu libro de texto o recurre a fuentes de información confiable.

El Reto de Hoy:

Reflexiona sobre estas alternativas limpias y renovables de energía eléctrica. Después, anota en tu cuaderno las siguientes preguntas, analízalas y responde con base en lo aprendido.

 

1. ¿Por qué es importante generar energía eléctrica a partir de la energía solar y la energía eólica?
2. ¿Cuáles son las ventajas de utilizar la energía solar y la energía eólica?
3. Escribe cuando menos tres ventajas de cada tipo de energía.
4. ¿Qué desventajas presenta el aprovechamiento de la energía solar y eólica?
5. Escribe cuando menos tres desventajas de cada tipo de energía.
6. ¿Por qué el clima puede ser un inconveniente para la energía solar?

Finalmente, reúnete con tu familia y comenten sobre la importancia de utilizar la energía solar y eólica en la vida cotidiana.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

Compra en Amazon

El poderío mexica

Aprendizaje esperado: Identifica la historia del pueblo mexica, así como sus principales características, costumbres, creencias y organización; también conoce cómo los mexicas lograron dominar gran parte de Mesoamérica.

 

Énfasis: Conocer las primeras conquistas más allá de la cuenca, la organización política, los calpulli, los barrios y la economía mexica.

¿Qué vamos a aprender?

Continuarás con el estudio de la cultura mexica. En esta sesión, conocerás sus aspectos políticos y económicos, sus expansiones militares y sus primeras conquistas más allá de la cuenca.

¿Qué hacemos?

Para hacer una recapitulación de la sesión anterior, lee algunos fragmentos del texto de Miguel León-Portilla, titulado “Los antiguos mexicanos a través de sus crónicas y cantares”, donde el historiador reconstruye, a través de fuentes primarias, la historia mítica de la fundación de Mexico-Tenochtitlan.

El texto comienza con Huitzilopochtli diciéndoles a los mexicas:

“—Yo os iré sirviendo de guía, yo os mostraré el camino. Enseguida, los aztecas comenzaron a venir hacia acá […]

 

Y cuando vinieron los mexicas, ciertamente andaban sin rumbo, vinieron a ser los últimos. Al venir, cuando fueron siguiendo su camino, ya no fueron recibidos en ninguna parte. Por todas partes eran reprendidos. Nadie conocía su rostro. Por todas partes les decían: —¿Quiénes sois vosotros? ¿De dónde venís?

 

Así, en ninguna parte pudieron establecerse, sólo eran arrojados, por todas partes eran perseguidos. Vinieron a pasar a Coatepec, a Tollan, a Ichpuchco, a Ecatepec […]

 

Establecidos momentáneamente en Chapultepec, comenzaron pronto a ser hostilizados por la gente de Azcapotzalco […] refugiándose en la región sur del lago, en las inmediaciones del señorío de Culhuacán. [De allí] los enviaron a la región pedregosa de Tizapán […] con el propósito de que las víboras ponzoñosas, que abundaban en esa región, acabaran pronto con ese pueblo de rostro desconocido, los indeseables aztecas.

 

En vez de morir picados por las víboras, los aztecas les dieron muerte y las convirtieron en su alimento. [Tiempo después] Huitzilopochtli ordenó que fueran a pedir al nuevo rey de Culhuacán, Achitómetl, le cediera a su hija doncella, para convertirla en su diosa Yaocíhuatl, “la mujer guerrera” […]. El dios de la guerra ordenó que la joven culhuacana fuera sacrificada de inmediato. Con su piel se atavió luego un sacerdote que debía simbolizar a Yaocíhuatl, la mujer guerrera.

 

Se horrorizó grandemente el señor de Culhuacán […] persiguieron a los aztecas, los arrojaron al agua.

 

Llegaron entonces allá donde se yergue el nopal. Cerca de las piedras vieron con alegría cómo se erguía un águila sobre aquel nopal. Allí estaba comiendo algo, lo desgarraba al comer. Cuando el águila vio a los aztecas, inclinó su cabeza. De lejos estuvieron mirando al águila, su nido de variadas plumas preciosas […].

 

Establecidos ya los aztecas en Mexico-Tenochtitlan, eligieron allí a su primer señor o tlatoani, de nombre Acamapichtli […], las persecuciones continuaron. Procedían esta vez de los tepanecas de Azcapotzalco, en cuyos límites quedaba comprendido el islote de Mexico-Tenochtitlan”.

 

Los antiguos mexicanos a través de sus crónicas y cantares

Miguel León-Portilla

 

Tras establecerse en el lago de Texcoco y haber fundado la ciudad de Mexico-Tenochtitlan en 1325, vivieron bajo el yugo de Azcapotzalco hasta 1428, la ciudad que en ese momento tenía la hegemonía sobre la mayoría de los pueblos del centro del valle de México.

Durante este periodo, gobernaron los tlatoanis mexicas Acamapichtli, Huitzilíhuitl y Chimalpopoca. Cuando este último gobernaba, en Azcapotzalco tuvo lugar una disputa por la sucesión en el trono de la ciudad, alcanzando el poder Maxtla, quien tenía una animadversión hacia los mexicas. Debido a que éstos se opusieron al nuevo gobernante, Chimalpopoca fue asesinado, aunque algunas fuentes afirman que se suicidó.

Estos acontecimientos desencadenaron un enorme descontento entre la población mexica. A Chimalpopoca lo sucedió en el poder Itzcóatl, quien estableció una alianza con Nezahualcóyotl, gobernante de Texcoco, quien estaba refugiado en el valle de Puebla tras ser perseguido por las tropas de Maxtla. Esta alianza entre mexicas y texcocanos logró la caída definitiva de Azcapotzalco y el inicio de la hegemonía mexica.

Durante los acontecimientos que propiciaron la liberación de los mexicas, con Itzcóatl al frente, ocurrió algo que definió la organización política de esta civilización.

Al saberse las intenciones de Maxtla de atacar Tenochtitlan, Itzcóatl y Tlacaelel (Cihuacóatl o sumo sacerdote de Tenochtitlan) convencieron al pueblo de ir a la guerra.

Tras el triunfo de los mexicas, el tlatoani Itzcóatl consolidó el poder de los gobernantes guerreros por encima de la mayoría de la población de Tenochtitlan. Además, ocurrió un acontecimiento, muy interesante de estudiar, que relata Fray Bernardino de Sahagún, la quema de códices:

Porque se guardaba la historia, pero ardió cuando gobernaba Itzcóatl en México. Se hizo concierto entre los señores mexicas. Dijeron: “No es conveniente que todo mundo conozca la tinta negra, los colores. El portable, el cargable se pervertirá, y con esto se colocará lo oculto sobre la tierra; porque se inventaron muchas mentiras”.

Esto puede interpretarse como el momento en que la élite de Tenochtitlan, conformada por los tlatoanis y sus descendientes, se afianzó en el poder tras reescribir la historia y subordinar a los calpullis.

Los calpullis (o barrios) eran un conjunto de linajes o familias que compartían un mismo espacio, el cual incluía tierras que trabajaban de manera conjunta para su usufructo, así como el culto a alguna deidad en común entre los miembros del calpulli. El calpulli tenía plena autonomía en la manera en que se asignaban las tareas a sus miembros, así como la organización en tiempos de guerra o de migración. En resumen, el calpulli era una unidad administrativa, social, económica y cultural que, en conjunto con otros calpullis, tomaban decisiones para una población mayor.

Tras el éxito de los mexicas contra los tepanecas en el año 1434, formaron una alianza en conjunción con las ciudades de Texcoco y Tlacopan, llamada Excan Tlatoloyan o Triple Alianza, la última de estas organizaciones en Mesoamérica. A partir de esto, comenzó a expandirse el dominio de los mexicas y sus aliados por gran parte de Mesoamérica.

Ahora, presta atención a los siguientes videos que abordarán dos aspectos relevantes del poderío mexica: la guerra y los tributos.

1. Guerra y tributo.

https://www.youtube.com/watch?v=f401gMAP_vA

 

2. Un mosaico de reinos.

https://www.youtube.com/watch?v=sp6Q213V8E4

 

Como pudiste apreciar a través de los videos, la expansión de la Triple Alianza, encabezada por los mexicas, conquistó gran parte del centro de Mesoamérica, e incluso otras regiones.

Esta expansión permitió la diversificación de la economía. Por un lado, en el mismo valle de México se producían productos de consumo local como el maíz, el frijol o la calabaza, para lo cual fueron muy importantes las chinampas.

También fueron importantes las conquistas de los valles de Tenango y de Oaxaca, pues aportaron productos importantes como la grana cochinilla, y permitieron el comercio con diversas regiones de Mesoamérica.

Al extender su dominio en distintas regiones, numerosos productos estuvieron disponibles para los miembros de la Triple Alianza, ya fuera como tributo o como artículos de intercambio: cacao y plumas de quetzal de la región de Soconusco; obsidiana de la región de Hidalgo; caracoles, conchas y peces provenientes de ambas costas de Mesoamérica; entre otros numerosos productos, los cuales podían encontrarse en el famoso mercado de Tlatelolco.

Pero esta imponente economía no se logró de la noche a la mañana. Tras el gobierno de Itzcóatl, lo sucedió su sobrino Moctezuma Ilhuicamina, quien llevó a cabo las primeras grandes conquistas fuera del Valle de México entre los años de 1440 y 1469. Bajo su mandato, fueron sometidas numerosas poblaciones en lo que serían los  estados de Guerrero, Hidalgo, Puebla, Oaxaca y Veracruz.

Durante los años de 1450 y 1455 tuvieron lugar una serie de sequías que afectaron profundamente a la población, debido a esto, Moctezuma emprendió lo que se conoce como guerras Florales o Floridas, una serie de enfrentamientos armados con pueblos como Calixtlahuaca o Tlaxcala, que no tenían el objetivo de conquistarlos, sino de adquirir prisioneros de guerra para ser sacrificados en pro del cese de las sequías y la abundancia de las lluvias y las cosechas. A su vez, Moctezuma impulsó una serie de cambios en Tenochtitlan muy importantes.

Por un lado, con ayuda de Nezahualcóyotl, se construyeron importantes acueductos que suministraron de agua potable a la ciudad; asimismo, se construyeron los centros donde se impartía educación: el calmécac y el telpochcalli.

En el aspecto político, se abrió la posibilidad de que, a través del desempeño en la guerra, las personas pudieran ascender a la nobleza mexica, que gozaba de diferentes privilegios como la exención del pago de tributos.

De esta manera quedó consolidada la organización política de los mexicas. En la cima del poder se encontraba el tlatoani o aquel que tiene la palabra. Él se encargaba de tomar las decisiones más importantes acerca de cómo hacer la guerra, aunque en muchas ocasiones debía consultar a un consejo conformado por los pipiltin o la nobleza, y por los otros gobernantes de la Triple Alianza.

Por debajo del tlatoani estaba el cihuacóatl o mujer serpiente. Se trataba de un sacerdote militar que fungía como principal asesor del tlatoani y como principal sacerdote. El más famoso de todos los cihuacóatl fue Tlacaelel, quien asesoró a los tlatoanis Itzcóatl, Moctezuma y Axayácatl.

Prácticamente estas personas eran quienes decidían y administraban todo lo relativo a la política. Ellos se encargaban de nombrar jueces y otros funcionarios que se encargarían de solucionar conflictos, imponer castigos, cobrar tributos, organizar fiestas, entre otras funciones.

A Moctezuma lo siguió Axayácatl, quien logró el sometimiento de Tlatelolco, ciudad aledaña a Tenochtitlan, que se había separado de ella años atrás y que sería cede del mercado más grande de su época.

Durante los 12 años que duró su gobierno, sufrió varias derrotas ante el Imperio tarasco de Michoacán, al que nunca logró conquistar. Su sucesor, Tizoc, gobernó sólo del 1481 al 1486.

Tras éste, fue electo tlatoani Ahuízotl, en cuya coronación se afirma que fueron sacrificados hasta 80,000 prisioneros huastecos. Sin duda, la cifra es grande, pero habla de la gran expansión que tenía para ese entonces el Imperio Mexica, extendiéndose de costa a costa, alcanzando la región del Soconusco en la actual Guatemala.

El último de los gobernantes mexicas antes de la llegada de los españoles fue Moctezuma Xocoyotzin o Moctezuma II, quien realizó una serie de importantes reformas.

En primer lugar, excluyó de la nobleza a aquellas personas que habían logrado ascender socialmente por medio de la guerra, restringiendo este poder sólo a los descendientes directos de los tlatoanis. Esto lo alejó del resto de la población y comenzó a mostrarse a sí mismo como un hombre-dios, al cual debían veneración como si fuera un dios, pues ni siquiera lo podían ver a la cara.

En cuanto a la Triple Alianza, comenzó a imponer las decisiones de Tenochtitlan por encima del mutuo acuerdo con Tlacopan y Texcoco, además de que buscó con mayor insistencia la conquista de Tlaxcala.

A Moctezuma II le tocó vivir la invasión de los españoles a Mesoamérica, para ese momento los mexicas eran, sin duda, los habitantes de la ciudad más poderosa, la Gran Tenochtitlan, que asombraría a los invasores europeos.

Aunque no se sabe qué habría pasado de no haberse dado el contacto con los europeos, es posible pensar en que la expansión de los mexicas había llegado hasta su máximo posible.

A continuación, observa el siguiente video y conoce un poco más sobre el mandato de Moctezuma II.

 

3. Moctezuma II: Auge.

https://www.youtube.com/watch?v=uIXC3KMS1xQ

 

A lo largo de esta sesión, estudiaste aspectos políticos y económicos de los mexicas.

En primer lugar, aprendiste que las expansiones militares de los mexicas los llevaron al control de gran parte del centro de Mesoamérica, dominando parte de las costas del océano Pacífico hasta el golfo de México, en el océano Atlántico, incluso la región de Soconusco, que entonces abarcaba hasta lo que hoy es Costa Rica, el país de Centro América.

Esto permitió que la riqueza de Tenochtitlan creciera gracias a los numerosos productos que se tributaban o comerciaban, entre ellos, productos alimenticios hasta objetos decorativos.

Durante la expansión mexica ocurrieron también grandes transformaciones políticas. Los calpullis, las formas de organización local, fueron subordinados ante el poder central impuesto por los tlatoanis que encabezaban un gobierno completamente militar-religioso, convirtiendo así la guerra en parte importante de la vida cotidiana.

A pesar de la imposición de la Triple Alianza, varios señoríos no pudieron ser conquistados por los mexicas, como los tarascos, también conocidos como purépechas, en el actual Michoacán, o los tlaxcaltecas, en el actual estado colindante con la ciudad de México.

Has finalizado esta sesión. No olvides que puedes consultar tu libro de texto y, si tienes la posibilidad, discute con tus compañeras y compañeros las respuestas a las últimas interrogantes.

El Reto de Hoy:

Elabora un esquema de la cultura mexica, mismo que completarás también en la siguiente sesión.

En tu cuaderno u hojas blancas, traza un cuadro con cuatro columnas; en el encabezado coloca los cuatro ámbitos de estudio de la historia: político, económico, social y cultural. Con la información de esta sesión, puedes llenar las primeras dos columnas.

 

Cultura mexica
Político	Económico	Social	Cultural

Finalmente, reflexiona en lo siguiente:

¿Cómo crees que influyó la expansión militar y los tributos que cobraban los mexicas a otros pueblos ante la llegada de los españoles?

¿Consideras que el Imperio mexica habría logrado sobrevivir o expandirse aún más de no haber llegado los españoles?

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

Compra en Amazon