Aprende en Casa III SEP: 18 de enero TAREAS y ACTIVIDADES de 2° de secundaria

¿Cuáles fueron los temas del día?

A continuación dejamos los temas vistos el 18 de enero de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Lunes 18 de enero, así como las dudas que se plantearon.

La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en Casa III:

https://aprendeencasa.sep.gob.mx/#

El factor inverso en figuras a escala

Aprendizaje esperado: Resuelve problemas de proporcionalidad directa e inversa y de reparto proporcional.

Énfasis: Identificar el factor inverso en figuras a escala.

¿Qué vamos a aprender?

Continuarás con el estudio de la proporcionalidad a través de diferentes planteamientos. En esta sesión, analizarás diversos problemas donde deberás obtener el factor inverso de proporcionalidad en el ámbito de las figuras a escala.

¿Qué hacemos?

Los materiales que necesitarás para esta sesión son:

• Tu cuaderno de Matemáticas u hojas blancas.
• Un lápiz o una pluma.
• Una goma.
• Juego de geometría.
• Y calculadora.

 

Para iniciar, reflexiona sobre la siguiente situación.

 

Planteamiento 1, factores de escala

 

En una clase de dibujo, el maestro les pidió a las alumnas y alumnos que encontraran los factores de escala que hacen posible pasar de la figura 1 a la figura 2, de la figura 2 a la figura 3 y al revés. La siguiente imagen muestra las tres figuras mencionadas.

 

 

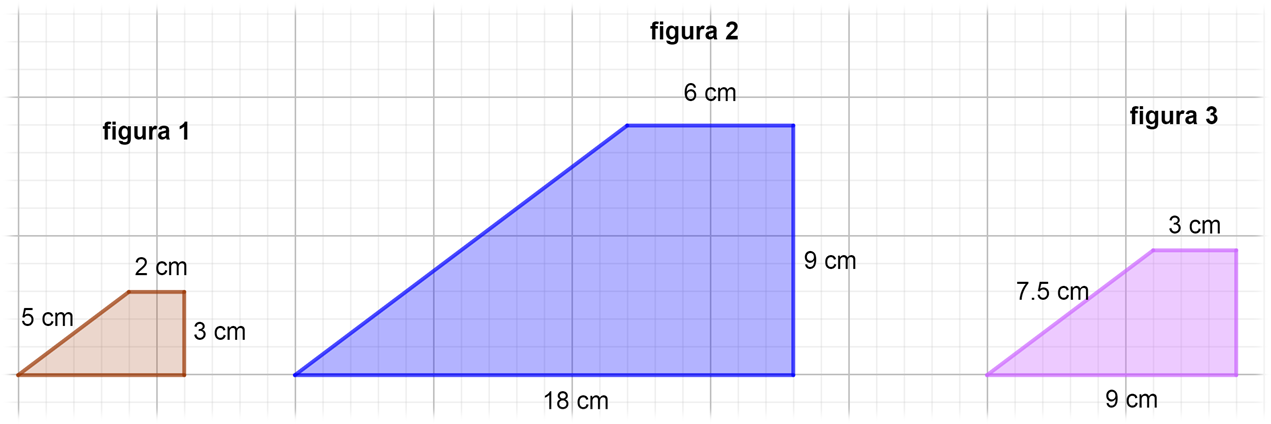
Se trata de una familia de cuadriláteros. Analízalos considerando las siguientes interrogantes:

 

• ¿En qué son parecidos y en qué son diferentes?
• ¿Qué relación se puede establecer entre las medidas de los lados homólogos?
• Y en este contexto, ¿qué significa pasar de una figura a otra?

 

Para responder las interrogantes anteriores, primero analiza qué es el factor de escala. De esta manera, tendrás argumentos para validar o refutar tus ideas.

El factor de escala es el número por el que se multiplica, de ahí su nombre factor, la medida del lado de una figura 1, para obtener la medida de su lado correspondiente —u homólogo—, en una figura 2, o figura a escala.

Los elementos de una multiplicación son los factores. Y en este caso específico, para conocer la medida del lado correspondiente de la figura uno a la figura dos, considera lo siguiente.

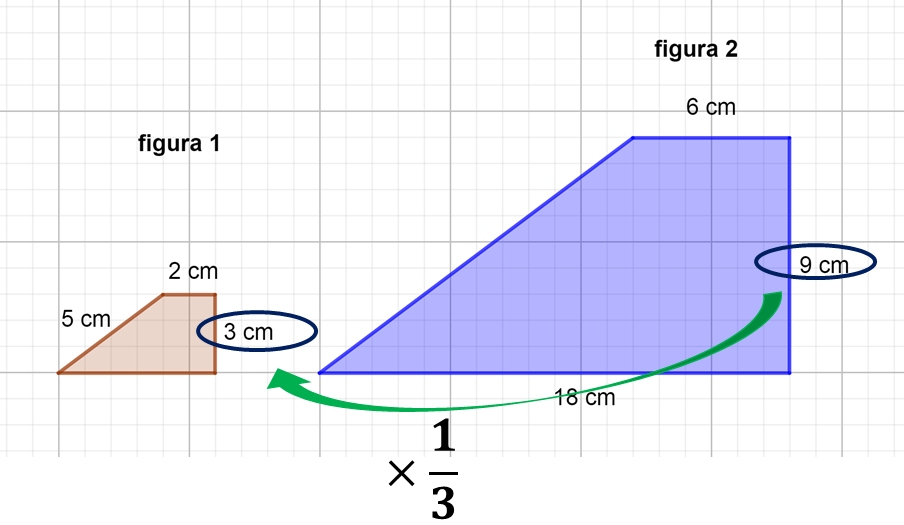
Factor de escala de la figura 1 a la figura 2:

El lado que mide dos centímetros de la figura 1 es correspondiente con el lado que mide 6 centímetros de la figura 2, y el lado de 3 centímetros con el de 9 centímetros.

 

 

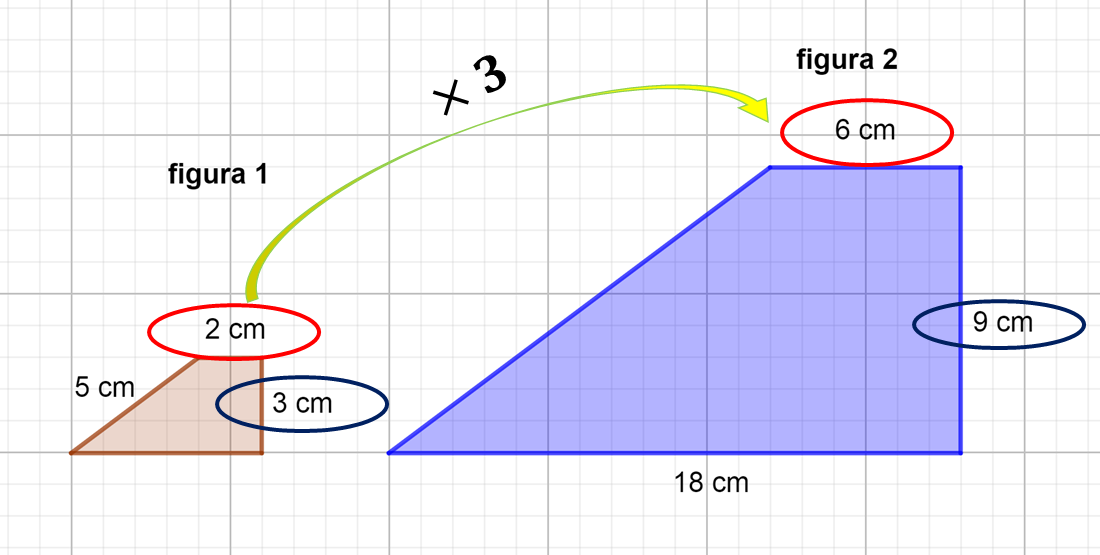
Por lo tanto, el factor de escala es 3, y como son figuras a escala, es el mismo factor que se usa para determinar la medida de todos los lados correspondientes entre la figura 1 y la figura 2. Por ello se llama factor de escala.

Ahora analiza lo qué sucede entre la figura 2 y la figura 3.

Factor de escala de la figura 3 a la figura 3:

Como puedes observar, el lado de 6 centímetros de la figura 2, es correspondiente al lado que mide 3 centímetros en la figura 3. 

 

 

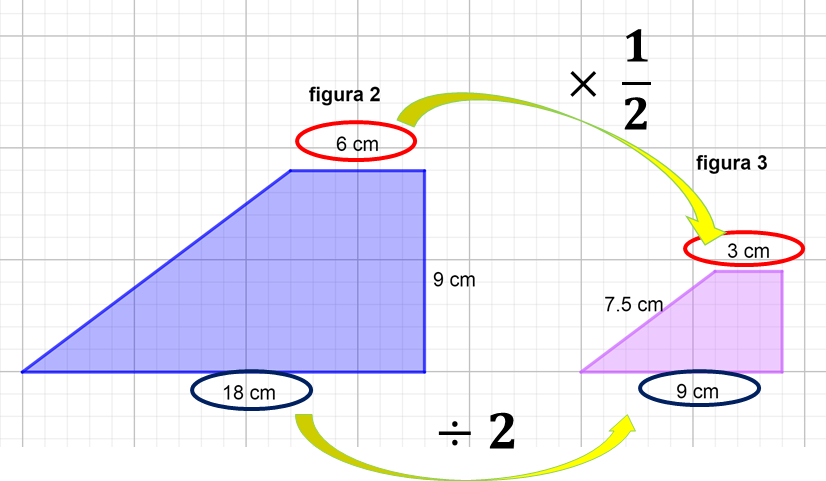
Por lo tanto, el factor de escala es un medio, lo que significa, multiplicar la medida del lado de la figura 2 por un medio, o bien dividir entre dos la medida de los lados de la figura 2, para obtener la medida de los lados de la figura 3.

Reflexiona: ¿cuál es el factor que permite pasar de la figura 2 a la figura 1?

El factor de escala para pasar de la figura 1 a la figura 2, es tres, es decir, se multiplica por tres la medida de algunos lados de la figura 1 para obtener la medida de sus lados homólogos de la figura 2.

Antes de continuar, considera las características de las figuras semejantes, como lo son la familia de cuadriláteros que estás examinando:

“A los lados que se corresponden se les llaman lados homólogos, es decir, son los lados que ocupan el mismo lugar en otra u otras figuras”.

Ahora, debes encontrar el factor que hace que ese proceso de escala se revierta, y esto lo lograrás conociendo el factor inverso, y retomando el planteamiento inicial.

¿Qué es el factor inverso?

 

Registra tus ideas o conceptos. A lo largo de la sesión podrás confirmarlos o resignificarlos.

 

El factor inverso de un número es aquel que, al multiplicarse por dicho número, tiene como producto la unidad.

En este caso, el factor inverso de 3, es un tercio, ya que 3 por 1/3 es igual a 1.

 

 

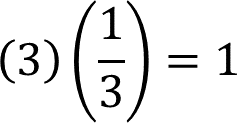
Ahora comprueba que 1/3 es el factor inverso que al multiplicar la medida del lado de 9 centímetros de la figura 2 es igual a tres.

 

 

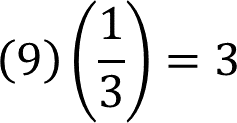
Entonces, tres es la medida del lado correspondiente u homólogo de la figura 1.

 

 

El factor inverso de un número también es conocido como recíproco, dos números son recíprocos si al multiplicarse uno por el otro, el producto es igual a uno.

De esta manera, el segundo factor de escala, el cual permite pasar de la figura dos a la figura tres, es un medio y su recíproco es dos, y el resultado de multiplicarse entre ellos es igual a uno.

 

 

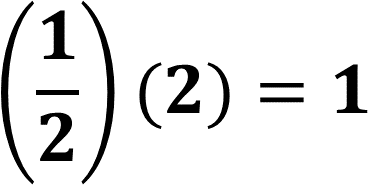
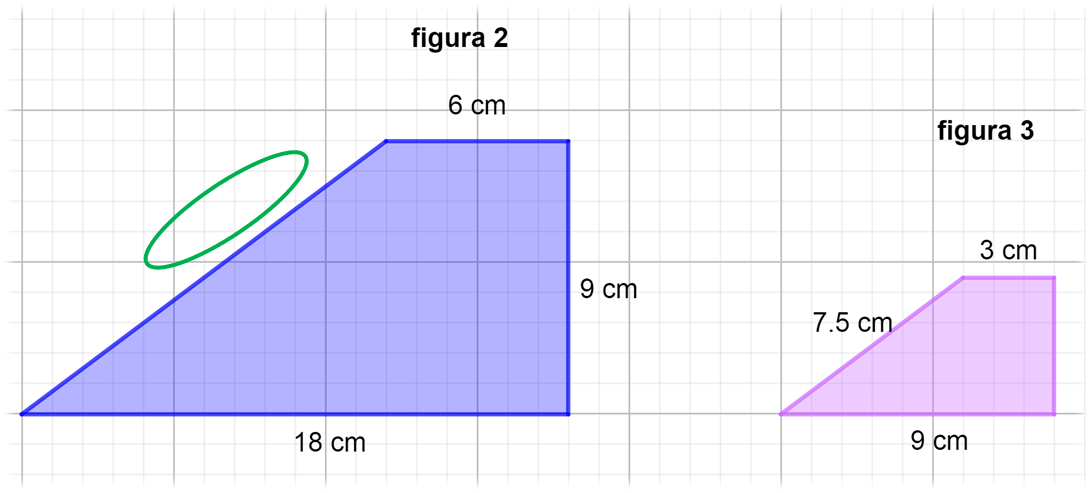
Ahora, analiza la siguiente imagen y realiza lo siguiente:

 

Aplicando los factores inversos respectivos, encuentra la medida faltante de la figura 2 a partir de la figura 3. Considera utilizar el factor inverso o recíproco del factor de escala.

 

 

Registra tu resultado. Posteriormente, podrás corroborar o ajustar tu respuesta. Es importante que trates de realizar las actividades, pues ello te permitirá acceder al conocimiento matemático y entender mejor el desarrollo de la sesión.

 

El factor de escala es un medio, por lo tanto, debes multiplicar la medida de la figura 3, (7.5), por el factor inverso del factor de escala, es decir, por dos.

 

¿Cuánto mide el valor del lado faltante de la figura 2?

 

 

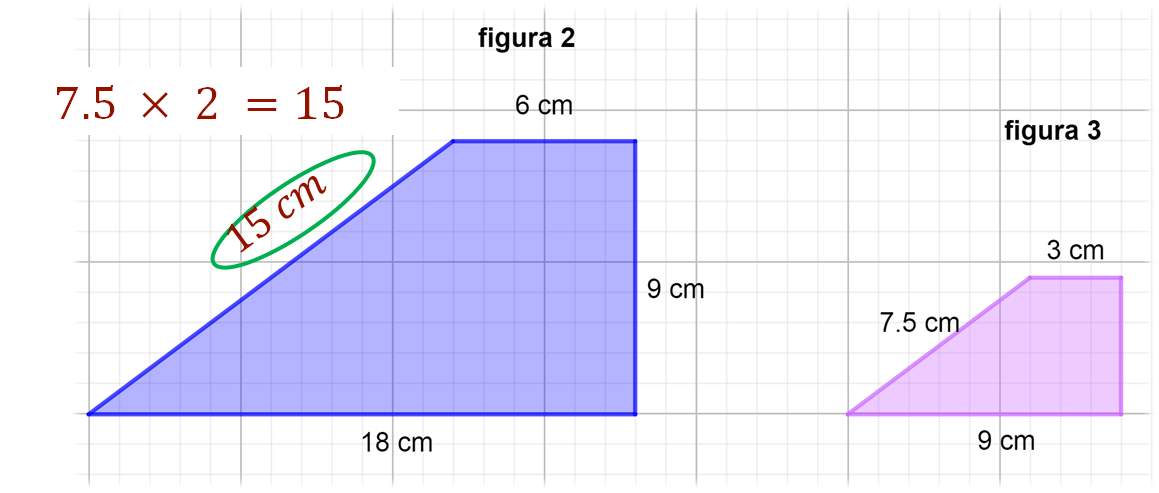
Mide 15 centímetros.

Ahora resuelve lo que falta para concluir el desafío.

Calcula la medida del lado faltante de la figura 1, desde la figura 3. Para ello considera que para pasar de la figura 1 a la figura 2 el factor de escala es (tres) y para ir de la figura 2 a la 3, el factor de escala es (un medio).

 

 

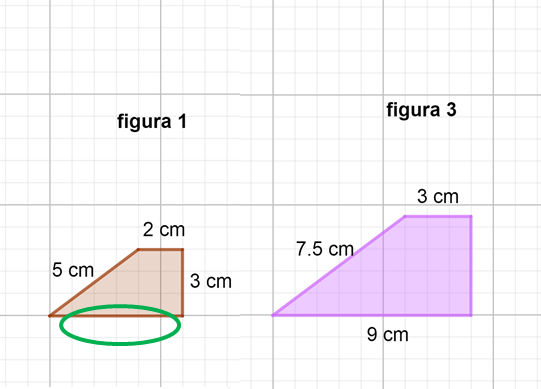
Como la intención es pasar de la figura 3 a la 1, debes utilizar los factores inversos.

En este caso, el factor inverso (dos), para ir de la figura 3 a la 2, y el factor inverso (un tercio) para pasar de la figura 2 a la 1, por lo tanto, multiplica ambos factores para encontrar el nuevo factor inverso que te ayudará a pasar desde la figura 3 a la 1, en este caso:

 

 

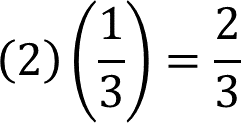
Ahora debes multiplicar la medida de 9 centímetros del lado inferior de la figura 3 por el factor inverso, (dos tercios).

 

 

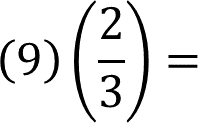
Para multiplicar un entero por una fracción, debes colocar al entero, uno como denominador, y posteriormente realizar la multiplicación de numeradores y denominadores, de la siguiente manera:

 

 

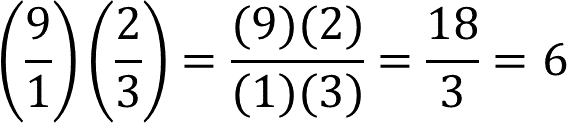
Se obtiene como resultado 6, que es la medida del lado faltante de la figura 1.

 

Ahora, analiza el siguiente planteamiento.

 

Planteamiento 2

 

Observa la siguiente imagen. Del lado izquierdo se encuentra un dibujo con sus respectivas acotaciones, y del lado derecho, la medida en centímetros de cada uno de sus lados.

 

 

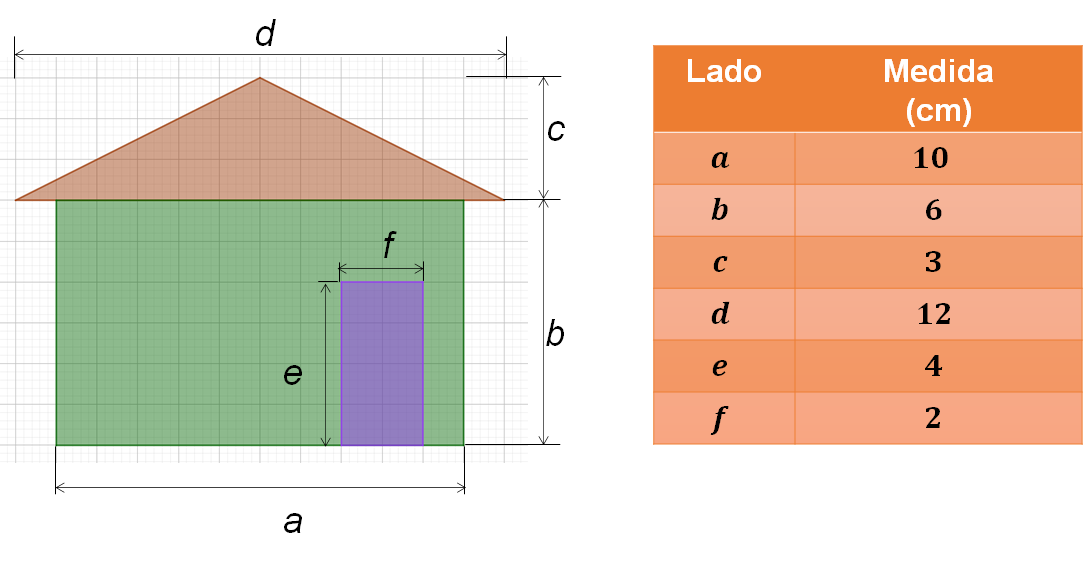
Determina la longitud de cada lado cuando se le aplica un factor de escala dado. Para el primer caso, considera el factor de escala, tres medios.

 

 

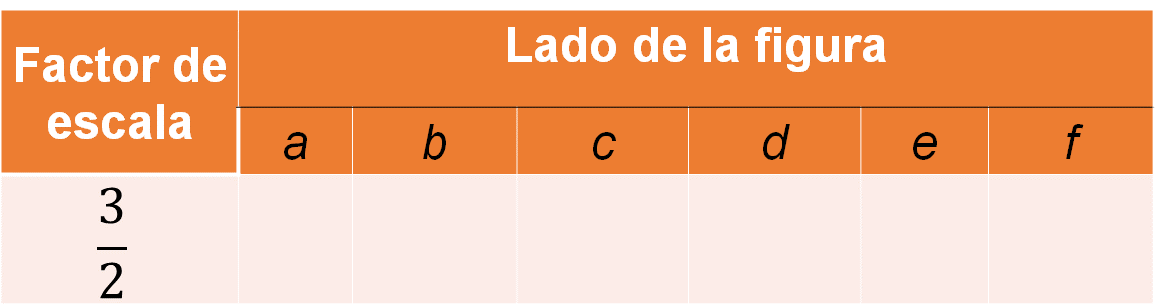
Para obtener la longitud de cada lado debes multiplicar cada uno de ellos por el factor de escala proporcionado, de esta manera, tienes lo siguiente:

 

La medida del lado que es igual a 10 centímetros se multiplica por el factor de escala tres medios, como se indica a continuación:

 

 

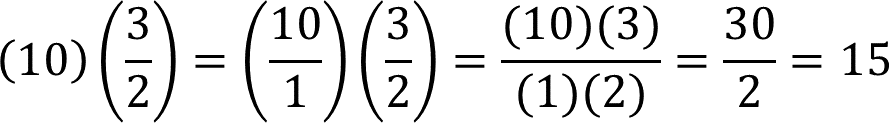
Por lo tanto, la medida del lado “a”, afectada por el factor de escala tres medios, es igual al 15 cm.

Siguiendo el mismo procedimiento, obtendrás la medida de los lados “b” y “c”.

Para b, establece la multiplicación 6 por tres medios:

 

 

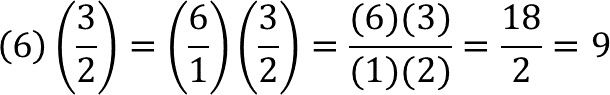
El lado “b” en la figura a escala es igual a 9 centímetros.

 

Continúa ahora con el lado “c”. Al realizar la multiplicación de la medida del lado “c” que es igual a tres, por el factor de escala tres medios, obtienes:

 

 

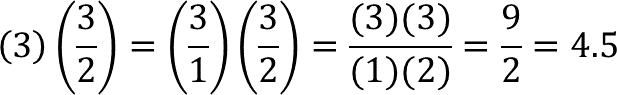
El lado “c” en la figura a escala es igual a 4.5 centímetros.

 

Ahora, encuentra las medidas de los lados faltantes, aplica el procedimiento planteado. Cuando termines, verifica tus resultados.

Al aplicar el factor de escala 3/2 a las medidas de los lados, tienes que:

 

 

Todas las medidas son proporcionales a las medidas del dibujo original, por ello, son dibujos a escala o figuras semejantes. Es importante hacer los cálculos y seguir el procedimiento, pero es más relevante comprender las relaciones y significados entre los números y las operaciones que se emplean en la resolución de los planteamientos.

Un procedimiento mecanizado es útil, pero comprenderlo es una herramienta poderosa para activar tu creatividad y tu pensamiento matemático.

A continuación, pon tus conocimientos en práctica con el siguiente planteamiento.

 

Planteamiento 3

 

Considera la siguiente figura con sus respectivas acotaciones. La tabla de la derecha proporciona algunas medidas de sus lados, en centímetros.

 

La figura tiene 7 lados: a, b, c, d, e, f, g.

 

 

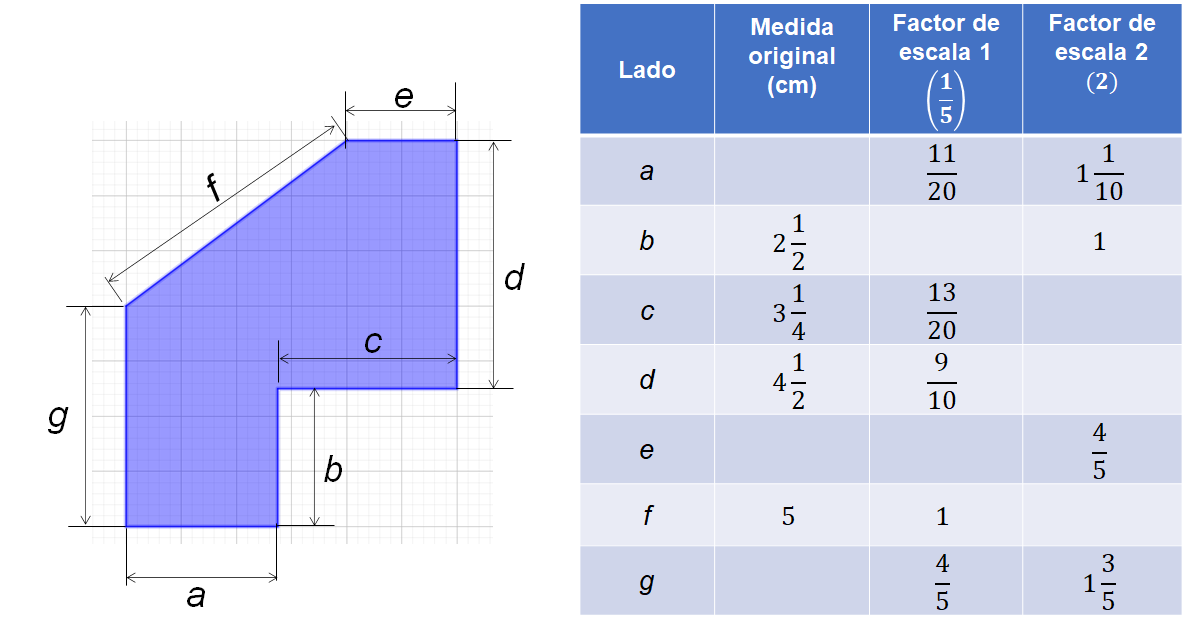
Encuentra las medidas faltantes utilizando, ya sea los factores de escala o los factores inversos de los mismos.

 

Inicia calculando la medida del lado “a”.

 

Lado “a”:

 

Para determinar su medida original, cuentas con la medida afectada por los factores de escala 1 y 2. Una manera es, tomar como punto de partida la medida afectada por el primer factor de escala; es decir, un quinto.

Para obtener la medida original que ha sido afectada por un factor de escala, debes multiplicar la medida que tienes por el factor inverso del factor de escala, por lo tanto, del factor de escala “un quinto”, obtienes su recíproco o factor inverso que es 5.

Multiplica la medida 11 veinteavos por 5:

 

 

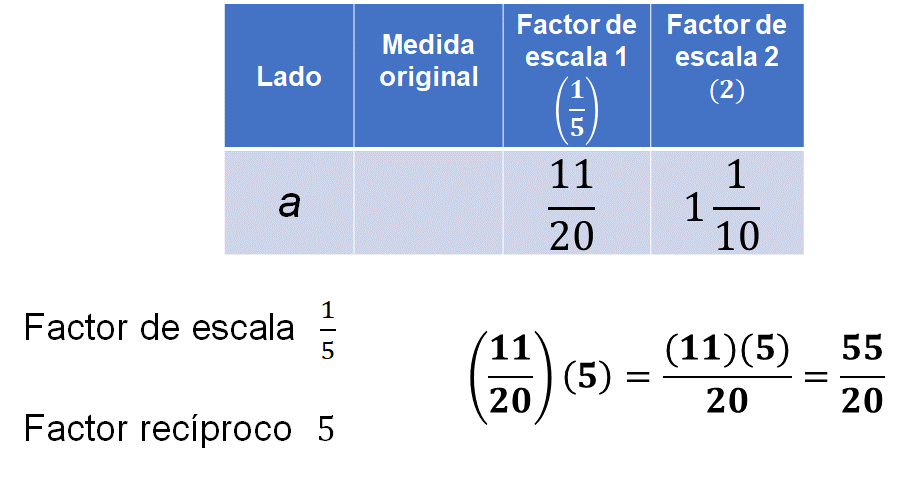
El producto es igual a cincuenta y cinco veinteavos, pero debes reducirlos a su mínima expresión, o bien, plantearlo como el resultado del cociente, en este caso, al reducir la fracción cincuenta y cinco veinteavos, tienes que es igual a once cuartos, que se puede representar como dos enteros y tres cuartos.

 

 

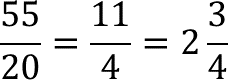
¿Qué significa este número en el contexto del problema?

 

Considera que, una vez que calculas un resultado, éste debe de tener sentido y significado en el contexto del planteamiento. En este caso, la fracción dos enteros y tres cuartos significa que la medida original del lado “a” mide 2 centímetros y 3/4 de centímetro; o 2.75 centímetros, si se expresa en su equivalente, en forma decimal.

 

Lado “b”:

 

Ahora, identifica lo que sucede con el lado “b”, del cual hace falta la medida afectada por el primer factor de escala, entonces multiplicarás la medida original por el factor de escala un quinto.

 

Para multiplicar un número mixto, es recomendable representarlo en su equivalente como fracción impropia, en este caso, cinco medios.

 

Multiplicando cinco medios por el factor de escala un quinto, tienes que el producto es igual a cinco décimos.

 

 

Al hacer la reducción de la fracción, se obtiene un medio.

 

 

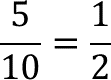
Es decir, un medio de centímetro o 0.5 centímetros en su forma decimal, que es la medida del lado “b”, al ser afectada por el factor de escala 1.

 

Lado “c”:

 

Considera ahora el lado “c”, del cual no conoces la medida afectada por el factor de escala dos.

 

Debes multiplicar la medida afectada del factor de escala 1 por el factor de escala 2, teniendo entonces:

 

 

Al hacer la reducción de la fracción:

 

 

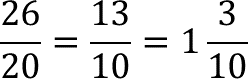
Obtienes como resultado un entero tres décimos, que en el contexto del problema significa que el lado “c” mide 1.3 centímetros.

 

Lado “d”:

 

En el lado “d” sucede lo mismo que en lado “c”, por lo que tienes que multiplicar la medida afectada del factor de escala uno, por el factor de escala 2.

 

 

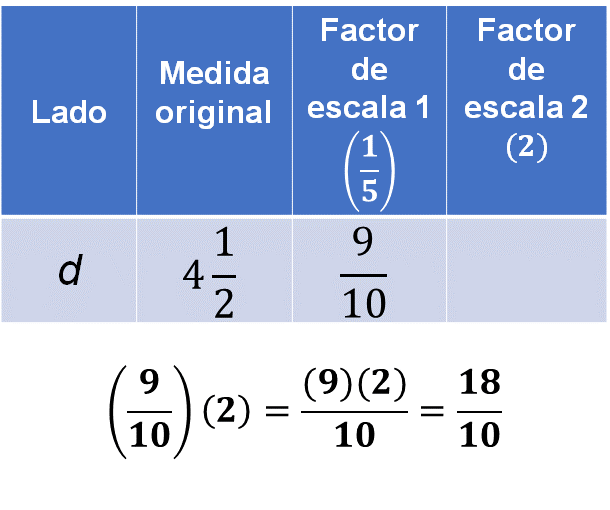
Al hacer la reducción de la fracción:

 

 

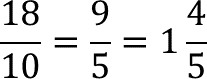
Es decir, el lado “d” mide 1 centímetro y 4/5 de centímetro, que es igual a 1.8 centímetros.

 

Lado e:

 

En el caso del lado “e”, se identifica que sólo se cuenta con la medida afectada por ambos factores de escala. Inicia reconociendo el recíproco del factor de escala, un medio.

 

Ahora, multiplica la medida cuatro quintos por el factor recíproco un medio.

 

 

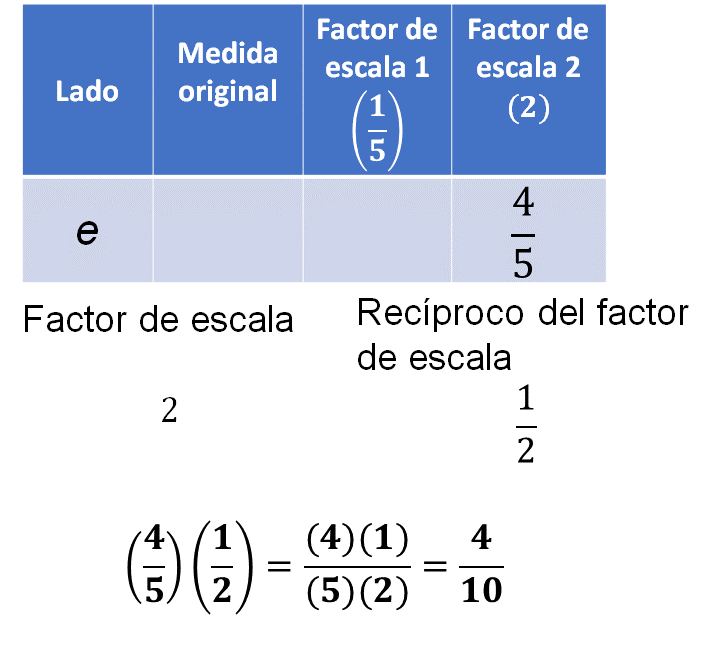
Reduce la fracción:

 

 

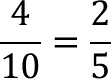
Obtienes dos quintos, que es la medida afectada por factor de escala 1.

 

Ahora, observa que la medida faltante es la original. Para obtenerla debes multiplicar la medida dos quintos por el recíproco del factor de escala. El recíproco del factor de escala un quinto es, cinco.

 

Realizando la multiplicación de dos quintos por cinco, se obtiene como producto diez quintos, que es equivalente a 2, es decir, 2 cm es la medida original del lado e.

 

 

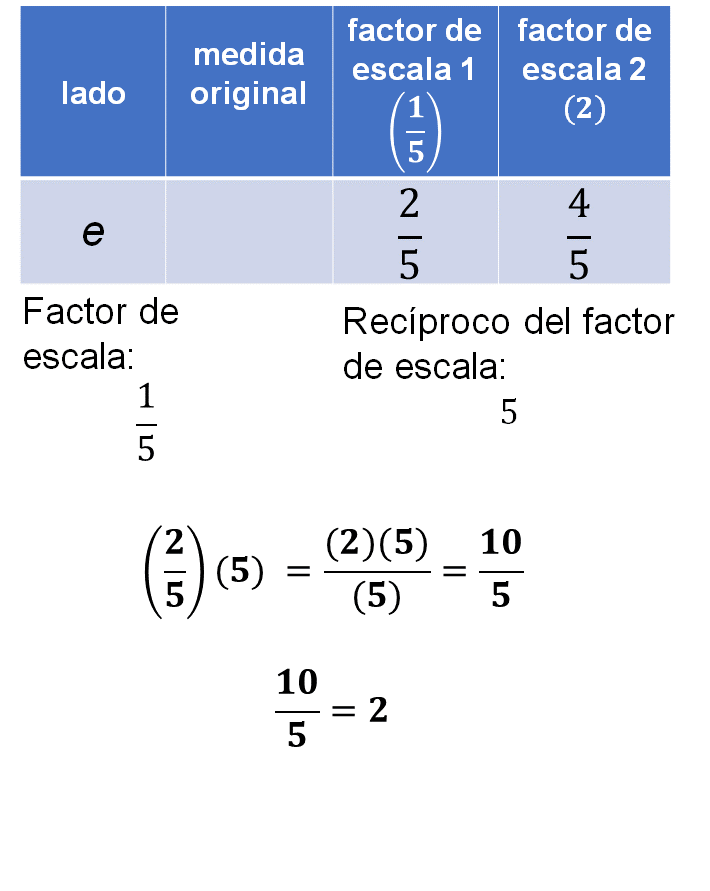
Antes de continuar, realiza una revisión de lo visto hasta ahora con el planteamiento 3.

 

La tabla o registro tabular concentra de manera organizada las medidas de la figura que se han obtenido al aplicar el factor de escala 1 o 2, según cada caso.

 

Se obtuvieron las medidas de los lados a, b, c, d, y e. En este caso, al hacer un análisis de los términos, la palabra factor da la idea del procedimiento a seguir, que es una multiplicación, donde los factores son la medida del dato conocido y el valor del factor de escala correspondiente.

 

Observa como va la tabla hasta el momento y verifica tus resultados:

 

 

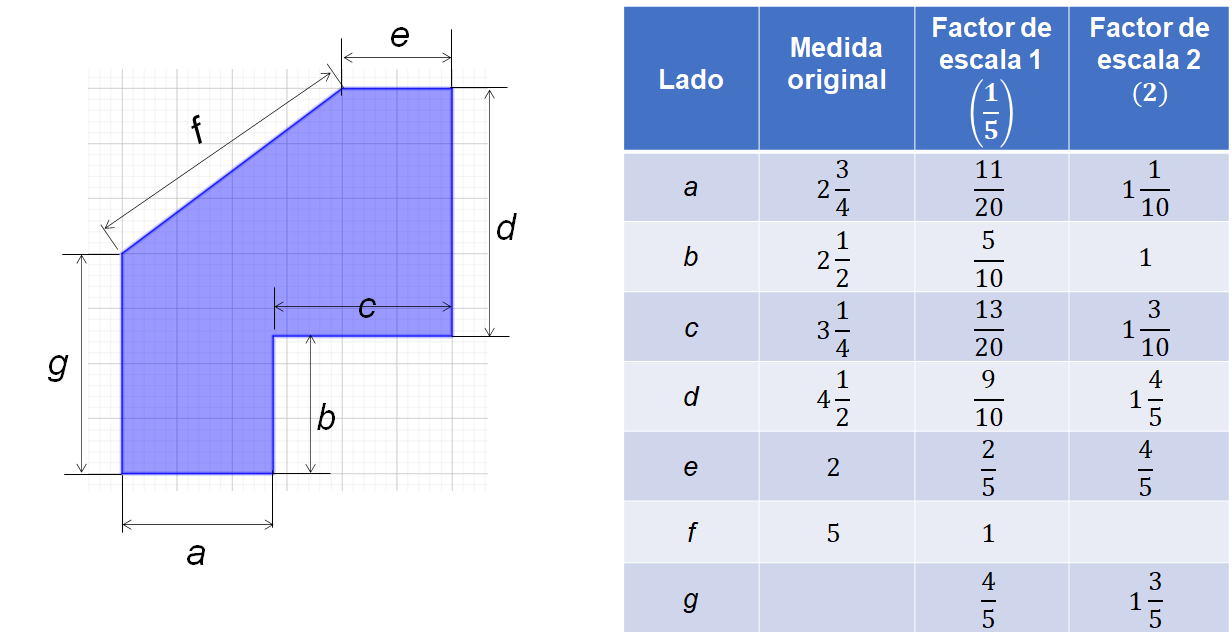
Continúa con los lados que faltan.

 

Lado “f”:

 

El lado “f” se obtiene multiplicando uno por el factor de escala 2, en este caso, uno por dos, es igual a dos.

 

 

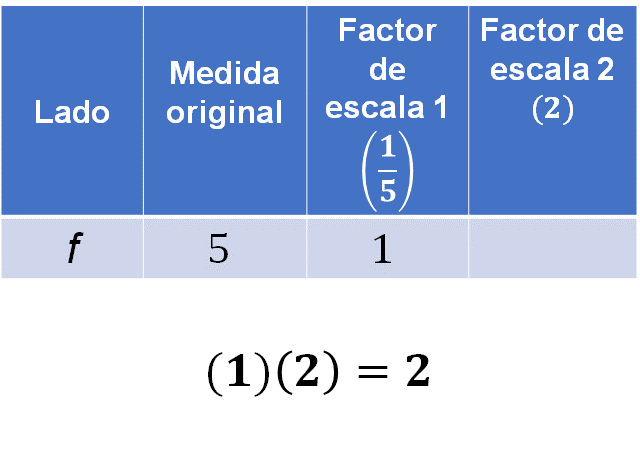
Por lo tanto, la medida faltante del lado “f” es igual a dos centímetros.

Lado “g”:

Dado que has analizado el procedimiento y has buscado la manera de dar sentido y significado al factor de escala y al factor inverso, al operar, sabes que el lado “g” tiene un valor de 4 cm.

 

 

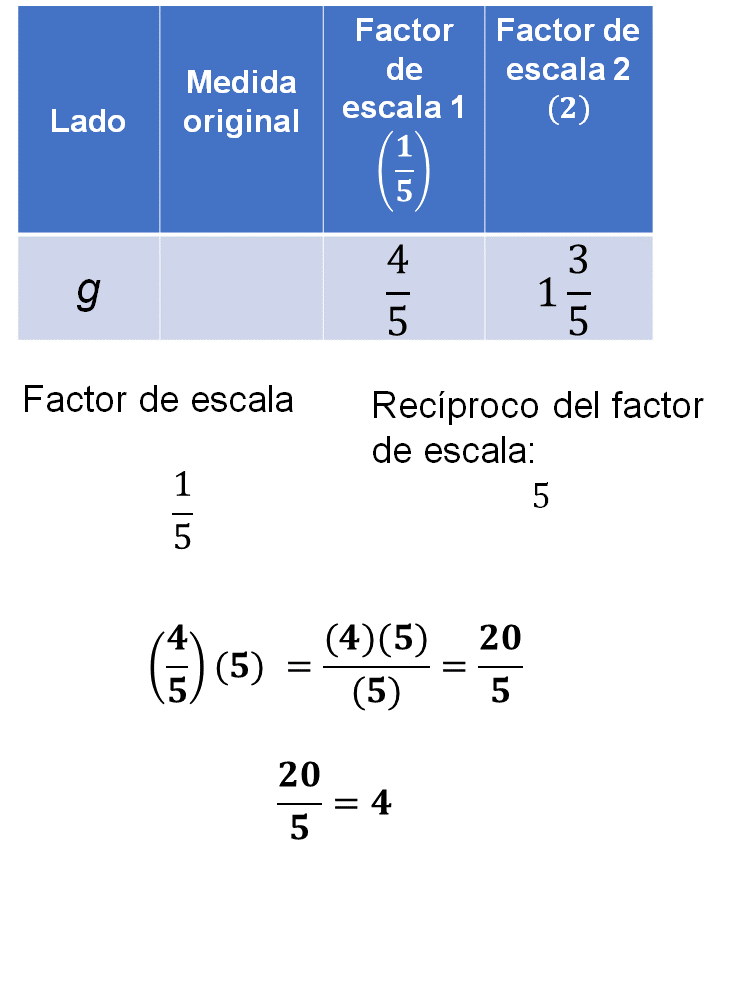
Antes de finalizar la sesión, recapitula acerca de los conceptos aplicados en la resolución de los planteamientos.

Factor inverso de un número:

Es aquél que, al multiplicarse por dicho número, es igual a la unidad.

 

 

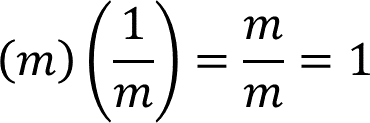
El factor inverso también se conoce como: recíproco.

Multiplicación de fracciones:

Debes multiplicar numerador por numerador y denominador por denominador. Por ejemplo:

 

 

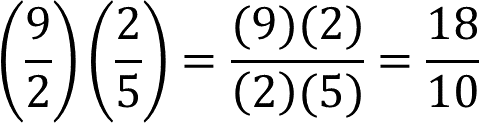
Finalmente, reducir el producto a su mínima expresión. Por ejemplo:

 

 

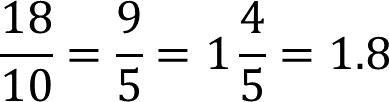
Has concluido. Elabora tus notas, considerando las ideas más importantes del tema que has estudiado, sobre todo, anota tus dudas y posibles dificultades.

Recuerda que éste es un material de apoyo y puedes consultar otras fuentes para complementar lo que aprendas aquí.

El Reto de Hoy:

Consulta tu libro de texto de Matemáticas y realiza los ejercicios relacionados con los temas que aprendiste en esta sesión, es decir, el factor inverso en figuras a escala.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

Ilustrando la ficción

Aprendizaje esperado: Transforma narraciones en historietas.

Énfasis: Distinguir usos de recursos gráficos en historietas para contar una historia.

¿Qué vamos a aprender?

Conocerás los recursos gráficos que deben utilizarse para adaptar un texto narrativo a una historieta.

Éstos son un conjunto de estrategias visuales y signos gráficos que son a la vez creativos y convencionales, por ejemplo: para simbolizar la duda se usa un signo de interrogación, un signo de pesos para expresar la avaricia, corazones rotos para las decepciones amorosas y el engrosamiento de las letras junto con formas creativas para simbolizar tristeza, sorpresa, enojo, entre otros.

Todos estos son elementos gráficos, significativos que pueden ser comprendidos por el lector.

¿Qué hacemos?

Comenzarás con una historia conocida que, de leyenda, se convirtió a texto narrativo y de ahí se transformó en una historieta, el clásico cuento de “Caperucita Roja”. Observa con atención:

 

 

 

 

Esta narración transformada en historieta utiliza recursos gráficos. Para lograrlo, primero tienes que echar a volar tu imaginación y divertirte con ello.

Una de las características más importantes de la historieta, es la brevedad de sus mensajes; el relato se sintetiza en unas pocas viñetas, con frases cortas y estrategias discursivas e icónicas que contienen una pluralidad de significados.

Por otra parte, el uso del espacio gráfico constituye un desafío para la interpretación y la producción de estos textos ya que, a partir de normas generales, el autor propone soluciones originales y asegura que se comprenda la narración; incluso un acomodo gráfico o el modo en que se ilustra una viñeta; utilizando diversas perspectivas, puede comunicar ciertos mensajes.

Relatar historias es una actividad inherente al ser humano. Desde hace miles de años, los humanos empezaron a reunirse y comenzaron a comunicar vivencias, conocimientos, valores y creencias. Por ejemplo, en tiempos primitivos, una representación de estas historias se hacía a través de las pinturas rupestres. Desde entonces, el dibujo gráfico o imagen es un elemento imprescindible en el proceso comunicativo; y en las historietas, no es la excepción. 

Ahora, conocerás qué otros recursos gráficos existen y cómo los puedes utilizar en la historieta para contar una historia. Para ello, observa los siguientes materiales que elaboró la alumna Karin:

 

 

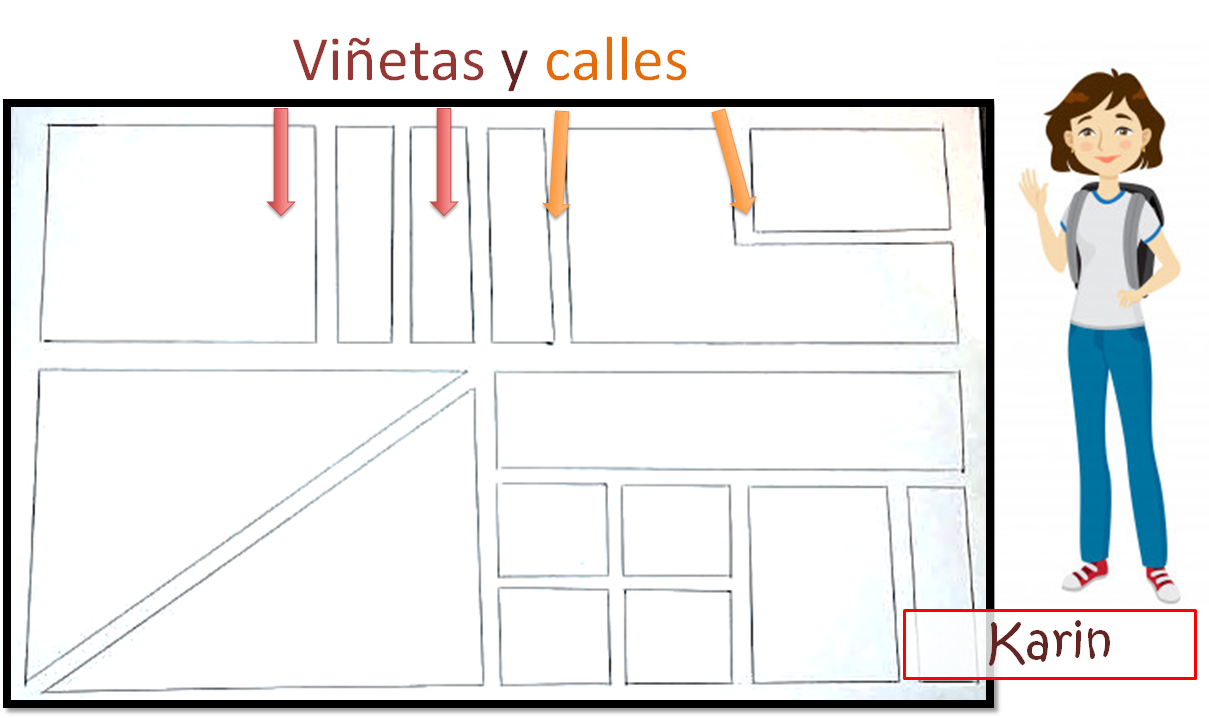
Como puedes observar, las viñetas son recuadros en los que se ilustra lo que sucede en la historia y siguen un orden; por lo general se leen de izquierda a derecha y de arriba hacia abajo. Cada una, es un momento preciso de la historia y conforme pasa de una viñeta a otra, avanza la acción y la narración.

Las viñetas forman la historieta, que es un conjunto de elementos y texto que tienen como objetivo narrar una historia. Éstas son de distintas formas, aunque las clásicas son rectangulares, pero pueden presentarse en cuadrados, círculos, triángulos, o la forma que más convenga.

Además, entre cada viñeta hay una separación que se hace llamar “calle” y estos espacios de división son importantes ya que marcan el paso del tiempo y crean un efecto de lo que sucede entre una imagen y otra.

Como cada viñeta representa una situación, es importante sintetizar la historia, ya que, de lo contrario, se realizaría la ilustración de un texto y ése no es el fin que se persigue.

Observa las siguientes imágenes para profundizar más acerca de las historietas:

 

 

Los globos o bocadillos contienen los diálogos o conversaciones de los personajes de la historia. Por lo general, el orden de la lectura es de izquierda a derecha y de arriba abajo; el globo o bocadillo consta de un rabillo, cola o delta, que señala al personaje que está hablando. Si el rabillo señala fuera del recuadro es un personaje que esta fuera o lejos.

En este tipo de texto narrativo, los dibujos son los encargados de representar la historia, y éstos van acompañados de los globos o bocadillos para intercambiar sus pensamientos.

A continuación, observa qué diseño de globos son los más usuales.

 

 

En la imagen anterior, puedes observar las clásicas formas, con leves variaciones de los globos o bocadillos:

 

• En el diálogo o narración normal, puedes observar rectángulos, círculos o quizá otra forma, pero su característica es que no tiene bordes salientes.

 

• En los diálogos donde se habla bajo o se murmura, se puntea el globo con líneas.

 

• Cuando se quiere mostrar grito, enojo u emoción, se usan globos con picos o salientes.

 

• En cambio, cuando es un pensamiento o se está soñando pueden usarse los globos con forma de nube.

 

• Para mostrar cómo se quiebra la voz, se tiene miedo o se está a punto de llorar, se pueden usar los globos como si se estuvieran derritiendo.

 

• Y, para mostrar el movimiento o que la voz tiembla por correr o brincar, se le agregan, a los globos, líneas por fuera que simulan ese movimiento.

 

Las formas de los globos pueden dar carácter y emoción al texto, lo que provoca que casi se escuche a los personajes, aunque sólo estén dibujados.

La comunicación gráfica, es un recurso fundamental en la creación de una historieta. Otro recurso es el uso de mayúsculas, que puede significar que se está gritando, por ejemplo. Observa lo siguiente:

 

 

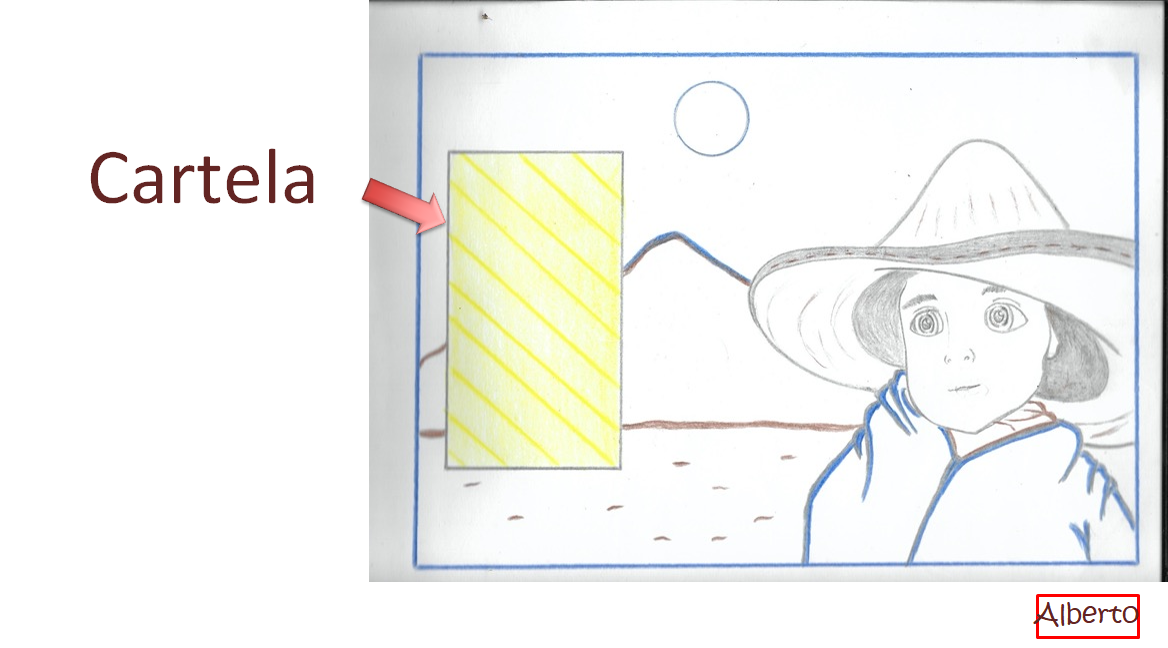
El cartel, cartela o cartucho son recuadros que están dentro de la viñeta y explican el contexto de lo que sucede; se usan cuando los dibujos y los diálogos no son suficientes para comprender la historia o un momento específico de ella.

Las cartelas suelen aparecer en la primera viñeta, a modo de introducción y, en ocasiones, también en la última, como conclusión y para encerrar la palabra "Fin"; y es un recurso que puede utilizarse cuando hay un narrador.

Éste, como los otros recursos gráficos, permiten identificarlos dentro de la secuencia gráfica de la historia. Analiza otros aspectos:

 

 

Otra estrategia son las onomatopeyas, que son palabras o grupos de letras que se usan para representar los sonidos o ruidos que se escuchan en la historia; para la intensidad del sonido o ruido se juega con el tamaño de éstas. También es la figura retórica que consiste en una repetición o aliteración de sonidos lingüísticos que imitan los sonidos con algún elemento de la realidad.

Las onomatopeyas son utilizadas en las historietas como efectos de sonido. Hay que notar que cada idioma tiene las suyas y, a pesar de que surgen a partir de la imitación de los mismos sonidos, las diferencias pueden ser considerables.

Por ejemplo, la onomatopeya del ladrido de un perro en español es “guau”, y en inglés es “woof”. El pollito que dice “pío”, en inglés es “tweet”.

Observa más recursos gráficos para contar historias, como las líneas cinéticas o de movimiento.

 

 

Éstas son líneas que salen del cuerpo del personaje, aparato u objeto y se utilizan para dar la idea o efecto de movimiento; por ejemplo, cuando el sombrero se vuela por aire o para representar el temblor del cuerpo, entre otros.

Por simple que parezca, este elemento comunica detalles importantes. Las líneas cinéticas son los símbolos gráficos que dotan de dinamismo y énfasis a la narración de manera que el lector pueda seguir con la vista lo que está sucediendo sin necesidad de leer ninguna frase. También indican la trayectoria que siguen los elementos móviles de cada viñeta. Con este recurso gráfico y sin palabras, se transmite un mensaje claro al lector.

Continúa con más recursos gráficos:

 

 

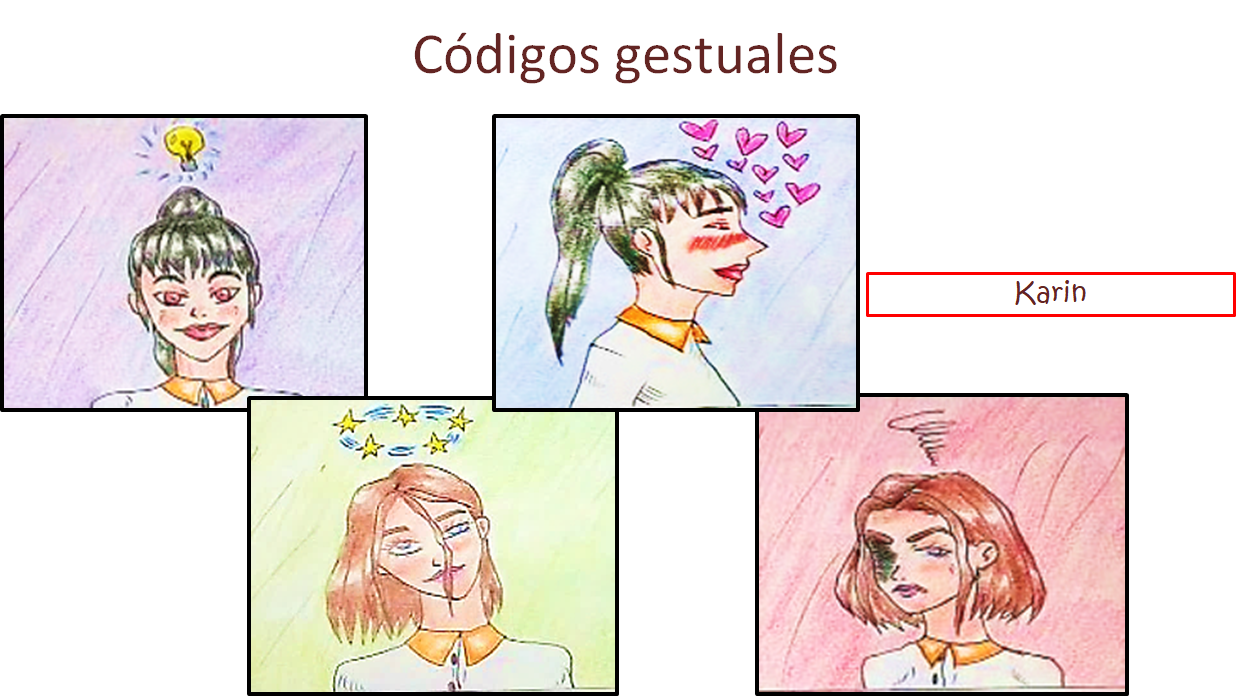
Este recurso se basa en los gestos y en algunas características físicas de los personajes, que tienen el propósito de expresar algo. Por ejemplo: las cejas altas, expresan sorpresa; las cejas fruncidas, enojo; los ojos grandes, asombro.

Sin embargo, esto depende del plano que se utilice en la historieta. Por ejemplo, un plano detalle, consigue que la mirada se centre en algo específico, mientras que un plano general lejano, lo hace sobre todo un escenario.

La expresión de los personajes a través del rostro o de la posición del cuerpo es muy diversa y compleja. Esto es la expresividad estética y depende, en gran medida, de la capacidad creadora del dibujante.

Además, mediante los gestos del personaje, se puede conocer su manera de pensar, de hablar, así como su ideología; pues sus gestos complementan la información que se ofrece en el texto.

También hay historietas que no requieren del lenguaje escrito, sino que, a través de las viñetas, con códigos gestuales, y otros recursos gráficos, muestran procesos, situaciones o actitudes que dan la oportunidad de descubrir más a fondo detalles que hablan por sí solos.

Para descubrir más sobre las historietas, observa el siguiente video.

 

1. ¿Con qué propósitos se usa la historieta hoy en día?

Ahora, para profundizar más en el tema, observa el siguiente video, y escucha con atención al investigador, humorista gráfico, articulista, caricaturista e historietista mexicano Rubén Eduardo Soto Díaz. Quien, de la mano de las imágenes del creador visual veracruzano César Augusto Bautista Esparza, explicará con mayor detalle la función de los recursos gráficos en la historieta, la dirección u orden que deben de llevar entre las calles las viñetas y la connotación de los diferentes tipos de letra en la viñeta.

 

2. Video. Función de los Recursos Gráficos.

Un dato curioso de Rubén Eduardo Soto Díaz, mejor conocido como Soto, es que fundó el Museo de la Caricatura y la Historieta, único de su género en nuestro país; conocido por sus siglas MUCAHI.

Ahora, realiza la siguiente actividad que te ayudará a organizar una historia para luego convertirla en historieta.

 

Toma como base el cuento de Caperucita roja y elabora de un cuadro como el siguiente. Dentro del cuadro, puedes organizar la información de tu texto narrativo de la siguiente manera:

 

Título: “Caperucita Roja”.

Apartado 1. Lo que se cuenta en la historieta.

 

 

En las columnas 1 y 2 colocarás las preguntas con su respectiva respuesta, según se muestra en el cuadro anterior.

 

Después de terminar este primer cuadro ya tienes una idea de cómo comenzarás a realizar los bocetos de cada personaje.

Como se mencionó anteriormente, una historieta se puede definir como un conjunto de texto y elementos gráficos que tienen como objetivo narrar una historia o idea. De forma general, los personajes son parte de esos elementos icónicos.

Continúa con el análisis. Observa el siguiente ejemplo:

 

 

Al culminar esta actividad, ya podrás identificar los recursos gráficos para definir en qué momento los debes emplear para comunicar mejor el mensaje de una historieta.

Para finalizar, observa el siguiente video sobre lo que Soto y Bautista tienen que decir acerca de la “voz en off”.

 

3. Video. Voz en off.

Ahora ya sabes que es la voz en off, cómo se utiliza en la historieta y cómo darle vida a un personaje. Crear historietas es una cuestión de creatividad, pero también de aprender bien el oficio.

Has concluido la sesión, donde conociste cómo repartir el texto narrativo en la historieta y qué marcas gráficas pueden apoyar el sentido comunicativo que se desea transmitir al lector.

Recuerda que para ampliar o conocer más sobre el tema puedes revisar tu libro de texto para ahondar en la información o complementarla.

El Reto de Hoy:

Realiza en tu cuaderno una historieta basada en un texto narrativo que conozcas o de tu propia inventiva. Recuerda hacer uso de los diferentes recursos gráficos que aprendiste de manera creativa.

En el transcurso de la transformación de tu texto narrativo a historieta, es vital analizar los fragmentos del original que se mantendrán y que representarás con imágenes.

Al adaptar la narración, descubrirás que es necesario resumir o sintetizar la historia original y un elemento que te ayudará a separar la narración son las viñetas.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

Tú, yo, nosotros: comunidad

Aprendizaje esperado: Reflexiona acerca de cómo las experiencias con el arte conectan a un individuo con otro, le permiten conformar grupos de interés y establecer lazos de identidad en su comunidad.

Énfasis: Realizar producciones, prácticas o ejercicios artísticos interdisciplinarios que permitan la conexión entre sus participantes a partir de sus intereses.

¿Qué vamos a aprender?

Analizarás e identificarás cómo las actividades artísticas pueden conectarte con otras personas para lograr establecer lazos de comunicación e identidad a partir de tus intereses, sentimientos y emociones. Asimismo, conocerás el significado de estos conceptos y cómo expresarlos.

¿Qué hacemos?

Para abordar el tema de esta sesión, será indispensable que primero reflexiones sobre cómo te sientes y qué emociones tienes, que tal vez están “atoradas”, es decir, que no se dejan expresar.

Para lograrlo, busca un “gritadero”, es decir, encuentra un lugar en donde puedas cerrar tus ojos, respirar profundo y pensar en todo aquello que no te deja estar bien contigo mismo y en donde puedas gritar. Después, puedes regalarte un apapacho y compartirlo con alguien más, de esta manera, seguramente encontrarás que otros se identifican contigo, ya que a veces tienes las mismas emociones, pero no sabes cómo expresarlas.

Antes de comenzar con la actividad, profundiza en sus definiciones.

La Real Academia Española define como “emoción” a:

 

“La alteración del ánimo intensa y pasajera, agradable o penosa, que va acompañada de cierta conmoción somática”.

 

Y como sentimiento, se refiere a:

 

“Hecho o efecto de sentir o sentirse”, es un estado de ánimo causado por alguna circunstancia o situación.

 

Y, ¿sabes qué es un apapacho?

 

La palabra apapachar viene del náhuatl “pachoa”, y significa “acurrucarse”, “dar cariño y protección”. Con el paso del tiempo, se duplicó la sílaba “pa” y de “pachoa” pasó a “papachoa”, hasta llegar a ser “apapacho”.

 

Es por ello que, en esta sesión la actividad estará dirigida para dar un gran “apapacho” y extenderlo con las personas que te rodean en casa: tu familia.

Los seres humanos “sentimos y nos emocionamos”, y muchas veces necesitamos liberar esa energía -sin lastimar a nadie-, así que se podría decir que el espacio del “¡gritadero!” te puede servir para liberar el cúmulo de tensiones por el encierro, las tareas y los deberes en casa. Es decir, dar una “caricia escandalosa a tu alma”. Apapacharte, enamorarte de ti mismo, como cuando sientes “mariposas”.

 

¿Alguna vez has sentido mariposas en el estómago?

 

Observa el siguiente video y escuca lo que dicen algunas y algunos estudiantes sobre haber sentido mariposas, ¿en dónde?, ¿cómo y cuándo? O, dicho de otra forma, ¿cómo se sienten, qué emociones han tenido recientemente?

 

1. ¿Cómo estoy? ¿Cómo me siento?

Es muy importante que te expreses en donde te sientas cómodo, en confianza, tal vez con tus amigos, o con un amigo o amiga en particular en quien confíes mucho, o con tu familia o realizando alguna actividad.

Por ejemplo, en el “gritadero”: tu espacio para la liberación de energía.

Es por eso que ahora tendrás que encontrar un lugar de tu casa para que hagas tu “gritadero”. No olvides explicarle la actividad a tu familia, de lo contrario los puedes espantar al escuchar tus gritos por sorpresa.

 

Una vez que le comentes a tus familiares la actividad y hayas encontrado el lugar indicado, haz un grito liberador.

 

A la cuenta de tres, grita ¡1..., 2..., 3!

 

Recuerda que es un espacio de confianza en donde nadie te va a juzgar.

Después de tu grito liberador, realiza lo siguiente:

 

Respira-exhala, respira-exhala, respira y, grita otra vez lo más que puedas.

 

Ahora, ve recuperando tu respiración y tu calma.

Puedes gritar, llorar, reír, expresar tus emociones y, cuando termines, reflexiona sobre lo que ocurrió y contesta las siguientes preguntas:

 

• ¿Cómo me siento?
• ¿Qué emociones he tenido recientemente?
• ¿He sentido mariposas?
• ¿En qué parte del cuerpo?

 

Estas respuestas te servirán para hacer una radiografía de tus emociones. Es decir, una imagen de ti mismo, en donde plasmes en qué parte de tu cuerpo están ubicados tus sentimientos, tus sentipensamientos y tus sentiemociones. Para ello, realiza lo siguiente:

 

A través de un dibujo, traza la silueta de tu cuerpo y distingue con los colores que desees, en dónde se ubican estos sentimientos y emociones, así como aquellas zonas en donde sientes mariposas. Si lo deseas, puedes darle cierto valor a los colores que escojas, por ejemplo: rojo para el enojo, verde para la paz, azul para la melancolía.

 

Recuerda hacer uso de tu imaginación y creatividad, los elementos artísticos que no pueden faltar.

 

Para darte más ideas, observa el siguiente video sobre lo que hicieron algunas y algunos estudiantes al respecto.

 

2. Radiografía de mis emociones.

A partir de la radiografía que elaboraste, identifica aquello que “te hace falta”, y de la carencia que identifiques ¡hazte un regalo! El cual se lo entregarás a la persona más importante de tu vida; aquella que te acompañará por el resto de sus días; por la que realmente debes sentir “maripositas en tu pancita”, la que tiene que hacerte sentir orgullosa u orgulloso cada vez que la miras en el espejo: “tú mismo”. Te harás un regalo para ti.

No un regalo material y costoso que pudieras desear para satisfacer alguna necesidad, sino uno que “apapache tu corazón, tu alma, tu ser emotivo”.

El valor de este regalo estará en el hecho de haber sido realizado por ti. Lo elaborarás tomando en cuenta algún lenguaje de las artes, como: un poema, una canción, un dibujo, una escultura, un cuento; o empleando los elementos de las artes (líneas, colores, formas, sonidos, movimiento), o inventando algo novedoso, incluso un nuevo juego, por mencionar algunos.

Observa en el siguiente video algunos ejemplos.

 

3. Los regalos.

Maravillosos regalos o, mejor dicho, maravillosas caricias al corazón que se han dedicado estos estudiantes.

Observa el siguiente ejemplo sobre estos maravillosos regalos:

 

“Hoy, me regalo una caricia,

Que ilumine una sonrisa

Que te quiero compartir.

A veces vivo de prisa

Sin voltear a los detalles

Como el canto de las aves

En el amanecer”.

 

“¡Regalos, regalos!

¡Un regalito, será apachito!

Regalote, ¡será un apachote!”

 

“Mi familia son los de casa:

sus abrazos me cobijan

Me abrazan hoy

en una alegre canción,

haciendo de este fandango

algarabía de multicolor”.

 

“Y me regalo una caricia,

Que ilumine una sonrisa

Que te quiero

Compartir”.

 

Después de apreciar estos regalos, reflexiona:

 

¿Será que el arte, nos puede ayudar a expresar lo que sentimos y lo que pensamos?

 

A continuación, a través de siguiente video, observa algunas reflexiones.

 

4. Reflexiones.

Finalmente, analiza en la siguiente pregunta:

 

¿Será que puedes identificarte con los demás por las emociones y sentimientos que tienes?

 

Has llegado al final de esta sesión. Recuerda también darte un apapacho, una caricia para tu alma, y extiende ese amoroso apapacho con tu comunidad: tu familia.

El Reto de Hoy:

Elabora un regalo a través del lenguaje de las artes, que esté basado en tu imaginación y creatividad; luego entrégalo a tu familia. También puedes invitar a tus familiares a que hagan el suyo, y cuando estén juntos, hagan un intercambio de regalos que acarician el alma, y así propicien “un momento especial”.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

Galileo Galilei

Aprendizaje esperado: Analiza cambios en la historia, relativos a la tecnología en diversas actividades humanas (medición, transporte, industria y telecomunicaciones), para valorar su impacto en la vida cotidiana.

Énfasis: Reconocer las aportaciones de Galileo Galilei a la ciencia.

¿Qué vamos a aprender?

Conocerás sobre la vida de uno de los más grandes científicos de todos los tiempos, un famoso astrónomo, matemático, ingeniero, que cambió el rumbo de la humanidad y contribuyó al desarrollo de la ciencia, tal como la conocemos, el padre de la ciencia, mejor conocido como Galileo Galilei.

¿Qué hacemos?

Analiza la siguiente información.

Galileo Galilei fue el mayor de siete hermanos, nació el 15 de febrero de 1564, en la Toscana. Tuvo una infancia llena de música, su padre fue el famoso compositor Vincenzo Galilei y gracias a él, Galileo se interesó en la física y las matemáticas desde muy joven.

Su madre fue Giulia Ammannati, ella era artesana. Debido a que en su familia eran muchos hermanos, su madre no podía cuidar de todos, por eso, cuando Galileo cumplió los 10 años, quedo al cuidado de Jacobo Borghini, quien se encargó de que recibiera una buena educación en un convento de Florencia.

Galileo estudió ahí hasta casi los quince años, pero su papá aprovechó que tuvo una infección en los ojos para sacarlo de esa escuela y un par de años después, lo inscribió en la Universidad de Padua para que estudiara medicina. No obstante, al poco tiempo de entrar a la universidad, Galileo se dio cuenta de que le gustaban más las matemáticas y la física. Leer a filósofos y matemáticos griegos como Euclides, Pitágoras, Platón y Arquímedes le hicieron perder todo el interés en la medicina e interesarse totalmente en las matemáticas y la física.

Cuando cumplió 25 años, se convirtió en catedrático de matemáticas en la Universidad de Pisa. En esa época realizó muchos experimentos, uno de ellos fue tirar dos piezas diferentes, una de plomo y una de madera, desde una ventana bastante alta al mismo tiempo y con la misma fuerza. La bola de plomo cayó junto con la bola de madera. Realizó el experimento no una, sino muchas veces, y siempre con el mismo resultado. Esto iba totalmente en contra de lo que Aristóteles había dicho, y se había mantenido como cierto por más de 1500 años.

Este experimento se ha repetido millones de veces, con diferentes materiales livianos y pesados. Muchos detractores de las ideas de Galileo sobre la caída de los cuerpos ponían de ejemplo una pluma y un martillo de acero. En este particular caso, si se deja caer una pluma, será evidente que el aire evita que la pluma caiga en línea recta, por lo que llegará al suelo mucho después que el martillo. Una posible solución para comprobar que una pluma y un martillo caen al mismo tiempo, si es que caen desde la misma altura, sería colocarlos en una habitación sin aire. Lo que no resultaría fácil y sería muy costoso.

Afortunadamente, en 1971 el astronauta David Scott realizó una versión del experimento en la Luna durante la misión del Apolo 15, dejando caer una pluma y un martillo de sus manos. Debido a la falta de atmósfera lunar, no había ninguna resistencia en la pluma, la cual tocó el suelo al mismo tiempo que el martillo.

En Pisa sólo estuvo hasta 1591, después se fue a la Universidad de Padua donde trabajó por casi 18 años hasta 1610. En la Universidad de Padua lo nombraron profesor de geometría, mecánica y astronomía. Y dado que la inquisición no intervenía en las decisiones de la universidad, se sentía en casi total libertad para poder expresar sus ideas. Mientras estaba ahí, falleció su papá y tuvo que hacerse cargo del resto de su familia, por lo que tuvo que empezar a dar clases particulares.

En esa época conoció a Marina Gamba, con ella tuvo tres hijos: Virginia, Livia y Vicenzo. En 1604, descubrió la ley del movimiento uniformemente acelerado; observó una nova aparecer y desaparecer en el cielo; demostró que los proyectiles siguen trayectorias parabólicas; construyó su primer termoscopio, un aparato que permite medir cualitativamente los cambios en la temperatura; y por último estudió el comportamiento de los imanes.

En mayo de 1609, uno de sus antiguos alumnos le envió una carta contándole sobre la existencia de un telescopio que permitía ver los objetos lejanos. Este aparato lo había fabricado Hans Lippershey en Holanda. Con este telescopio, se podían ver estrellas que eran invisibles a simple vista. Tiempo después, Galileo mejoró el diseño del telescopio y logró que aumentara 6 veces el tamaño de los objetos que se observaban, lo que era el doble que lograba el diseño original. Además de que la imagen no se veía de cabeza, pues le colocó una lente divergente en el ocular. El construir este telescopio le trajo mucha fama, además de una modesta fortuna que le ayudó con algunos problemas económicos que tenía.

Con el telescopio, Galileo vio que, al igual que nuestro planeta, los satélites naturales son cuerpos rocosos llenos de irregularidades en su superficie y no una esfera impecable hecha de éter, como se sostenía en aquel entonces. Esas observaciones pusieron en entredicho las tesis aristotélicas tradicionales sobre la perfección del mundo celeste, que residía en la completa esfericidad de los astros.

También pudo observar que Saturno tenía unos apéndices extraños, parecidos a dos asas. Medio siglo después, el matemático, físico y astrónomo holandés Christiaan Huygens descubrió que esas asas eran en realidad sus anillos.

Asimismo, descubrió que Júpiter estaba rodeado de lunas y constituían un sistema parecido a lo que debería ser el sistema solar. Para ello, observó lo que en un principio pensaba que eran estrellas cercanas al planeta que formaban una línea que lo atravesaba, estos cuerpos celestes nunca abandonaban la vecindad de Júpiter, cambiando su posición respecto a las otras “estrellas” y al planeta. Galileo determinó que lo que había estado observando no eran estrellas, sino satélites planetarios y publicó sus conclusiones en su obra titulada Siderius Nuncius, en marzo del mismo año. Galileo llamó originalmente a las lunas de Júpiter “Planetas Medicianos”, en honor de la familia Medici, y se refirió a ellas con los números I, II, III y IV. Ese sistema se emplearía durante dos siglos, hasta que se adoptó la denominación dada por el astrónomo alemán Simon Marius: Io, Calisto, Europa y Ganímedes.

Las observaciones sobre los satélites de Júpiter y constatar que Venus pasa por fases similares a las de la Luna terrestre, confirmaron la validez del sistema heliocéntrico de Copérnico, que defendía que la Tierra no es el centro del sistema solar.

Un año después de publicar su libro Siderius Nuncius, el que se convertiría en el Papa Urbano VIII, lo recibió para que le diera a conocer sus descubrimientos astronómicos y finalmente el colegio romano confirmó que sus observaciones eran correctas.

Otro descubrimiento que refutaba la perfección de los cielos fue la observación de manchas en el Sol. A principios de 1613, Galileo realizó observaciones y pudo concluir que el Sol tenía manchas. Al comienzo, realizó sus observaciones viendo directamente al Sol, aprovechando cuando las nubes se interponían al disco solar, o en las mañanas o atardeceres, cuando la intensidad de la luminosidad solar se hacía soportable a la vista. Tristemente esta práctica terminó por dejarlo totalmente ciego.

Antes de perder la vista por completo, pudo seguir observando las maravillas del sistema solar y plasmar sus descubrimientos en obras que cambiaron la historia.

Su obra llamada “Diálogos” sobre los dos máximos sistemas del mundo, le tomó seis años escribirlo. Decidió escribirlo en italiano en lugar de latín, como era la costumbre para publicar libros científicos en esa época.

En este libro el diálogo se desarrolla en Venecia durante cuatro jornadas entre tres interlocutores:

 

• Salviati, defensor del sistema copernicano. Quien representa la propia visión de Galileo. Llamado “el académico” en honor a la pertenencia de Galileo a la Accademia dei Lincei, el nombre proviene del apellido de uno de sus amigos: Filipo Salviati.

 

• Simplicio, quien aboga por el sistema de Ptolomeo y Aristóteles. Es una amalgama de dos académicos de visión conservadora y rivales de Galileo. El nombre del personaje proviene del filósofo homónimo del siglo VI, férreo defensor de los fundamentos aristotélicos.

 

• Sagredo, representa la visión neutral de quien busca la verdad sin aferrarse a dogma alguno. Es nombrado en honor al amigo de Galileo, Giovanni Francesco Sagredo.

 

Después de muchas dificultades, el libro apareció publicado a principios de 1632, pero para agosto de ese año fue confiscado por la Inquisición, y el primero de octubre lo citaron a comparecer en Roma.

Dos días antes de su cumpleaños número 69, llegó a Roma a declarar. Estuvo en calidad de prisionero, pero lo mantuvieron en las habitaciones del fiscal, no en la cárcel. Hizo una declaración en la que tuvo que decir que en su libro de “Diálogo” reconoce el copernicanismo, aunque esa no era la intención de su obra. Después de confesar, tuvo que pedir clemencia por escrito y finalmente declaró que no tenía ni había tenido la intención de apoyar la teoría de Copérnico y se puso en las manos de la Inquisición.

A pesar de todo lo que hizo, lo encontraron “vehementemente sospechoso de herejía”, que constituía una categoría específica de crimen, e incluía prisión formal, la prohibición de su libro, además de algunas “saludables penitencias”.

A Galileo se le condena a prisión perpetua y se le conmina a jurar que abandonará las ideas copernicanas. El papa Urbano VIII intercede por Galileo y logra cambiar su sentencia en prisión por un arresto domiciliario de por vida. Se le permitió vivir en su villa de Arcetri, cerca de Florencia, próximo al convento donde residían sus hijas: la hermana María Celeste y la hermana Arcángela. Allí siguió trabajando en el problema del movimiento, cuyo estudio había iniciado en Pisa medio siglo antes.

Giuseppe Baretti, un escritor y crítico de la ilustración italiana, afirmó que después de la abjuración Galileo dijo la famosa frase “Eppur si muove”. “Y, sin embargo, se mueve”, pero según es poco probable que Galileo pronunciara esa famosa frase en ese momento, ya que no se encontraba en situación de libertad y sin duda era desafiante hacerlo ante el tribunal de cardenales de la Inquisición.

El texto de la sentencia fue difundido por doquier, la noticia llegó hasta Alemania y Bélgica. Muchos científicos de la época, entre ellos René Descartes, pensaron que Galileo era la víctima de una confabulación de los jesuitas.

Galileo permaneció confinado en su casa de Florencia desde diciembre de 1633 hasta 1638. Allí recibió algunas visitas, lo que le permitió que alguna de sus obras en curso de redacción pudiera cruzar la frontera. Estos libros aparecieron en Estrasburgo y en París en traducción latina.

El último libro que escribiría Galileo sería “Discursos sobre dos nuevas ciencias”; en él establece los fundamentos de la mecánica y marca así el fin de la física aristotélica. Terminó este libro justo antes de perder la vista en el ojo derecho el 4 de julio de 1637.

En enero de 1638, Galileo perdió definitivamente la vista. Por aquel entonces, Dino Peri había recibido la autorización para vivir en casa de Galileo y asistirlo junto con el padre Ambrogetti, que tomará nota de la sexta y última parte de los “Discursos”. Esta parte no apareció hasta 1718.

Galileo, recibió la autorización para instalarse cerca del mar, en su casa de San Giorgio. Permaneció allí hasta su muerte, rodeado de sus discípulos, trabajando en la astronomía y otras ciencias.

Unos días más tarde, el 8 de enero de 1642, Galileo murió en Arcetri a la edad de 77 años. Ahora, sus restos descansan en un mausoleo construido en su honor dentro de la iglesia de la Santa Cruz de Florencia, Italia.

Por todo lo anterior, la importancia de Galileo Galilei, sus descubrimientos y sus aportes se siguen sintiendo hasta nuestros días. Porque fue quien nos enseñó a ver las cosas desde otra perspectiva. Como lo dice una de sus frases más célebres: “Donde los sentidos nos fallan, la razón debe intervenir”. Y él lo hizo de tal manera que el mundo ya no fue el mismo.

El Reto de Hoy:

Reflexiona acerca de las circunstancias que rodearon la vida de este gran personaje y elabora un cuadro con las más importantes aportaciones de Galileo Galilei.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

Preclásico

Aprendizaje esperado: Recuerda que la cultura olmeca es representativa del periodo Preclásico, así como sus principales características: actividades económicas, políticas, sociales y culturales.

Énfasis: Revisar e integrar los principales rasgos del periodo Preclásico de Mesoamérica, así como algunos de sus centros regionales y su importancia en el posterior desarrollo de las culturas mesoamericanas.

¿Qué vamos a aprender?

Repasarás las características generales del periodo Preclásico, centrándote en su ubicación temporal y espacial, así como en el legado brindado por las civilizaciones de este periodo al desarrollo mesoamericano.

¿Qué hacemos?

Para iniciar, lee el siguiente fragmento del texto “Preclásico (2500 a.C.-200 d.C.)”, del arqueólogo Enrique Vela, que se puede consultar en la revista Arqueología Mexicana, edición especial número 34.

 

Preclásico (2500 a.C. - 200 d.C.)

 

Con este nombre se conoce al periodo en el que se consolidan varios de los rasgos que serían característicos de las culturas mesoamericanas hasta la conquista española. Con frecuencia se ve este periodo como uno en el que no se habían alcanzado los grados de complejidad de las sociedades de los periodos posteriores, aunque no es así. El Preclásico es una época plena de logros y con una notable variedad en cuanto a expresiones culturales.

 

En el Preclásico temprano (2500-1200 a. n. e.) se dieron cambios fundamentales en la vida de los grupos humanos y que tendrían repercusiones en prácticamente todos los ámbitos. Entre esos cambios están la adopción de la agricultura como medio de subsistencia principal y el establecimiento de aldeas. Seguirían después prácticas como la fabricación de cerámica y el desarrollo de rasgos asociados a la organización social, la que paulatinamente sería cada vez más compleja. Esta creciente complejidad alcanzaría altos niveles en el Preclásico medio (1200-400 a. n. e.), principalmente con la cultura olmeca.

 

En ese entonces cristalizan las tendencias en curso durante los más de mil años de la época previa. La estratificación social, el gobierno legitimado por ritos públicos y la cosmovisión, entre otros aspectos, adquieren las características esenciales que se encontrarán entre las sociedades mesoamericanas en adelante.

 

Tras la decadencia de la cultura olmeca, en el Preclásico tardío (400 a. n. e.-200 d. n. e.), gran parte de Mesoamérica vivió una dinámica en la que nuevamente se consolidan procesos en curso desde el periodo anterior, como la escritura, el calendario y ritos como el del Juego de Pelota. Los rasgos más distintivos de este periodo son un notable crecimiento poblacional y el surgimiento de asentamientos de gran tamaño, muchos de ellos con construcciones monumentales, alrededor de los cuales se conforman sistemas regionales que les aseguraban el mantenimiento de sus crecientes poblaciones.

 

Preclásico (2500 a.C. - 200 d.C.)

Revista Arqueología Mexicana, edición especial número 34

Enrique Vela

 

Seguramente, con la lectura anterior, habrás recordado los tres periodos que conformaron el Preclásico. Por lo tanto, para iniciar esta sesión es necesario reconocer cuáles son.

Los tres periodos del Preclásico son:

 

1. El Preclásico temprano: del 2500 al 1200 a.n.e. y duró 1,300 años.
2. El Preclásico medio: del 1200 al 400 a.n.e., con una duración de 800 años.
3. El Preclásico tardío: del 400 a.n.e. al 200 d.n.e., el cual duró un total de 600 años.

El periodo Preclásico temprano se caracteriza por la aparición de las primeras aldeas agrícolas, en donde las sociedades eran igualitarias y vivían en no más de 20 chozas. El principal cultivo era el maíz, frijol chile y calabaza. Hacia el 1500 a.n.e. surgen las primeras aldeas olmecas en San Lorenzo, actual estado de Veracruz.

En el Preclásico medio las sociedades aldeanas comienzan a ordenarse por jerarquías sociales, así como la especialización del trabajo, sobre todo en la zona olmeca y en la cuenca de México. Un rasgo del Preclásico medio es la implementación de sistemas de riego para no depender absolutamente de la agricultura temporal. El Preclásico medio es el periodo de esplendor de los olmecas, y su gran capital, La Venta, en Tabasco.

Finalmente, el Preclásico tardío es la etapa en la que ya existe una fuerte jerarquización social, así como pequeños centros urbanos que dominan a aldeas más pequeñas a su alrededor. En esta etapa se distinguen los centros ceremoniales en donde se encuentra un gran basamento de estructura rectangular o circular que funciona como el centro religioso, cívico y político de una región como lo fue Cuicuilco en la cuenca de México.

Para profundizar y conocer más de los primeros centros urbanos, observa el siguiente video.

 

1. Primeros centros urbanos mesoamericanos.

Después de la información anterior, es momento de ubicar las principales culturas del Preclásico que habitaron el área cultural de Mesoamérica. Para ello, prepara tus conocimientos adquiridos, y si te es posible, utiliza un mapa de la República Mexicana. De no contar con uno a la mano, puedes dibujarlo en tu cuaderno.

En primer lugar, recuerda que Mesoamérica cuenta con seis regiones, ¿sabes cuáles son?

En Mesoamérica se localiza hacia el sureste la región maya; en el sur, la región de Oaxaca; en la costa del Pacífico, la región de Occidente; en la frontera con Aridoamérica se encuentra la región Norte; en el centro, la región del Altiplano Central; y finalmente, la región de Costa del Golfo.

Esta última región abarca los estados de Veracruz y parte de Tabasco, y la cultura principal que se desarrolló en ella durante el periodo Preclásico fueron los olmecas, quienes tenían como principales sitios dentro de esta región, San Lorenzo, Tres Zapotes y, como gran capital, la ciudad de La Venta.

Uno de los elementos más característicos de la cultura olmeca es, la elaboración de enormes esculturas denominadas “cabezas colosales olmecas”.

Esta civilización tuvo una enorme influencia en otras regiones de Mesoamérica, por lo que no sólo se encuentran rasgos de esta cultura en la costa del golfo.

Ahora ubica la región del Altiplano Central. La civilización que se estableció durante el Preclásico en el actual municipio de Naucalpan fue la cultura tlatilca, la cual recibió influencia de la cultura olmeca, representada en su cerámica hallada en los más de 200 entierros excavados por cuatro temporadas de investigación arqueológica. Recuerda que Tlatilco era una aldea donde se acostumbraba a enterrar a sus muertos debajo de sus casas.

 

Reflexiona:

 

¿Habrá existido otro sitio del Preclásico en el Altiplano Central que haya tenido influencia olmeca?

¿Recuerdas el principal sitio olmeca localizado en el actual estado de Morelos?

 

Su nombre es Chalcatzingo, donde se pueden admirar hasta el día de hoy sus impresionantes relieves esculpidos en los abrigos rocosos del sitio, así como la construcción de un centro ceremonial asociado a la montaña sagrada de este lugar.

Finalmente, otro sitio olmeca importante, ubicado en la región de Occidente, particularmente en el estado de Guerrero, es el sitio de Teopantecuanitlán, asentamiento olmeca donde se pueden observar restos de esculturas representando a animales míticos como el jaguar y el monstruo de la tierra.

El periodo Preclásico temprano marca el inicio del surgimiento de la cultura olmeca en San Lorenzo; sin embargo, fue el periodo Preclásico medio donde la influencia olmeca se extendió en la costa del golfo y otras partes de Mesoamérica hasta su fin, hacia el 400 antes de nuestra era.

Tras finalizar la influencia olmeca y, con ella, el final del Preclásico medio, se desarrollaría un sitio que ejercería un control político y comercial en la región de la cuenca de México en el Preclásico tardío, la cual se caracterizó por la construcción de un basamento de grandes dimensiones de forma circular, Cuicuilco, sitio donde se nota una mayor complejidad social que las culturas vistas anteriormente. Cuicuilco destacó por su gran pirámide circular, así como por su sistema agrícola consistente en chinampas, el Juego de Pelota y el culto al dios viejo del fuego Huehuetéotl.

Hacia el 200 de nuestra era, esta ciudad quedó sepultada por la lava del volcán Xitle. Durante esta época surgirían diversos asentamientos en otras regiones de Mesoamérica que tendrían su máximo esplendor en el periodo Clásico, no obstante, surgieron desde el Preclásico. Son las ciudades de Teotihuacan en el Altiplano Central, la ciudad de Monte Albán en Oaxaca y algunas ciudades mayas como El Mirador, en Guatemala.

Has ubicado los principales sitios del Preclásico, ahora recuerda algunas de sus características principales con el siguiente video.

 

2. Preclásico. Olmeca. Cuarta entrega.

Hasta el momento has ubicado temporal y espacialmente el periodo Preclásico, pero ¿qué legado dejaron las civilizaciones del Preclásico en el desarrollo de las demás culturas mesoamericanas del Clásico y Posclásico?

Para conocer el legado de las civilizaciones del Preclásico, realizarás la construcción del siguiente mapa mental, del cual tomarás como base siete ideas principales:

 

 

1. Asentamientos del Preclásico, San Lorenzo, La Venta y Tres Zapotes dentro del área nuclear olmeca, y Teopantecuanitlán y Chalcatzingo, en Guerrero y Morelos, respectivamente. También están los asentamientos de Tlaltilco y Cuicuilco, así como el inicio de asentamientos en otras regiones que tendrían su máximo esplendor en el periodo Clásico, como Teotihuacan y Monte Albán, de los zapotecas.

 

2. Juego de Pelota, el cual se trata de un juego ritual donde se representaba la lucha de las fuerzas del Universo y culminaba en el sacrificio humano.

 

3. Agricultura, en donde se utilizaron diversas tecnologías y técnicas como la unión de canales de riego, el almacenaje de agua, las presas, y el uso de la coa, chinampa, tala y quema. Los cultivos básicos fueron el maíz, frijol, chile y calabaza.

 

4. Comercio, el cual se basó en el trueque o intercambio comercial. Se formaron rutas de comercio que conectaron los primeros centros urbanos de la época y se distribuía cerámica fina y objetos de lítica como la obsidiana.

 

5. Cosmovisión, donde se marcan los principios de la religión mesoamericana; fueron el jaguar, el monstruo de la tierra y el dios viejo del fuego Huehuetéotl las principales deidades.

 

6. Escritura, la cual, en la época prehispánica se representaba en códices, vasijas y en estelas de piedra; el bloque de Cascajal es la muestra de escritura más antigua de Mesoamérica hasta el momento.

 

7. Calendarios, los cuales fueron producto de la observación de los astros. Destaca el calendario solar de 365 días, de 18 meses, de 20 días más 5 días adicionales, y el calendario ritual de 260 días, resultado de la combinación de 20 signos con 13 numerales. 

Has finalizado la sesión, donde retomaste la división del Preclásico en temprano, medio y tardío, ubicaste las principales culturas del Preclásico; la olmeca es una de las más representativas. En el Preclásico tardío, una de las culturas más representativas fue la cuicuilca; además, se asentaron civilizaciones que tendrían su mayor esplendor en el periodo Clásico, como la teotihuacana, zapoteca y maya. También retomaste el legado de las culturas del Preclásico a las de los periodos siguientes.

Si deseas saber más del tema, puedes consultar tu libro de texto de segundo grado, de Historia.

El Reto de Hoy:

Continúa recabando información para la realización de tu infografía. Si tu cultura a elegir fue una del Preclásico, la información de hoy te servirá mucho.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.