Aprende en Casa III SEP: 25 de enero TAREAS y ACTIVIDADES de 1° de secundaria
A continuación dejamos los temas vistos el 25 de enero de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 1° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Lunes 25 de enero, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en Casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Pongamos en orden las ideas
Aprendizaje esperado: Elabora fichas temáticas con fines de estudio.
Énfasis: Comprender y usar apoyos gráficos.
¿Qué vamos a aprender?
En esta sesión, tendrás la oportunidad de revisar tus conocimientos y vincularlos de la mejor manera, específicamente, trabajarás el aprendizaje esperado: “Elabora fichas temáticas con fines de estudio”, y te centrarás en “Comprender y usar apoyos gráficos”, con el objetivo de realizar fichas de estudio que conserven y organicen la información central de cualquier tema que estudies a lo largo de tu vida, ya sea de la clase de Lengua Materna o de otras áreas del conocimiento.
Es muy importante que prestes mucha atención a la información y pongas en orden las ideas con la ayuda de los apoyos gráficos.
Te sugerimos que tengas listos tus materiales escolares: cuaderno de notas y un bolígrafo o lápiz para que puedas registrar los conceptos o ideas claves, así como aquellos ejemplos que te ayuden a comprender mejor el contenido estudiado.
También puedes apoyarte en el libro de texto de Lengua Materna para cumplir los retos propuestos durante la sesión, con la finalidad de que conozcas qué tipos de apoyos gráficos existen e identifiques cuáles son las características que los conforman. Así podrás elaborarlos con gran facilidad.
¿Qué hacemos?
Comienza con la siguiente pregunta:
¿De qué manera podrías contar brevemente tu historia de vida, colocando las fechas y acontecimientos más importantes de forma cronológica?
Si recuerdas las lecturas de Historia, seguramente habrás podido observar que con frecuencia los sucesos más relevantes ocurridos durante un cierto periodo se presentan de manera concreta y secuencial en una línea de tiempo. Este ejemplo, la línea de tiempo, es un ejemplo de apoyo gráfico.
Un apoyo gráfico es una herramienta que se utiliza para mostrar datos de manera abreviada, con una interpretación fácil, que permite comparar información, ordenar en categorías, representar datos numéricos o lugares específicos en un espacio geográfico y señalar las partes de un objeto o las fases de un proceso. Los cuadros sinópticos, mapas mentales, conceptuales, tablas, gráficas, diagramas o líneas del tiempo forman parte de algunos ejemplos que conforman los diversos apoyos gráficos que existen.
Para conocer más sobre el tema y saber qué son los apoyos gráficos, qué tipos de organizadores existen y para qué se utilizan, observa la siguiente cápsula del minuto 1:22 al 4:41 .
- ¿Cómo leer y construir apoyos gráficos?
https://www.youtube.com/watch?v=GCsX8h-dfpg
Como pudiste observar, las fichas de trabajo son un recurso que permite registrar la información más importante de un tema de forma ordenada. En ocasiones, la información y datos recopilados se pueden presentar mediante una imagen o esquema, con palabras clave que permiten estructurar y sintetizar la información de manera visual, facilitando la comprensión, el análisis y la memoria del texto, al tiempo que se brinda una idea clara del contenido. A estas imágenes y esquemas se les conoce genéricamente como apoyos gráficos.
Sin duda, existe una amplia variedad de apoyos gráficos, compuestos por ideas o conceptos claves e imágenes o dibujos que explican el contenido, resumen la información y facilitan la comprensión del texto.
Para poder elaborar y utilizar los diferentes apoyos gráficos que existen, es necesario conocer los elementos y características que conforman cada uno. Así que a continuación revisarás los 5 organizadores gráficos más comunes.
En tu cuaderno elabora un cuadro comparativo como el que se presenta en la siguiente imagen:

En la primera columna enlista el nombre de los gráficos que se mencionen durante la sesión, seguido de cinco características específicas para cada recurso y finalmente, en la tercera sección, ejemplifica el diagrama con una imagen o dibujo.
Aprenderás sobre los cinco organizadores gráficos más frecuentes.
Número 5: Gráfica de barras
Un diagrama de barras, también conocido como gráfico de barras o columnas, es un elemento que sirve para representar y comparar con un solo golpe de vista un conjunto de datos o valores por categorías mediante recursos visuales. Las barras pueden orientarse horizontal y verticalmente, sin embargo, la altura de cada una será proporcional al número de datos o valores que represente.
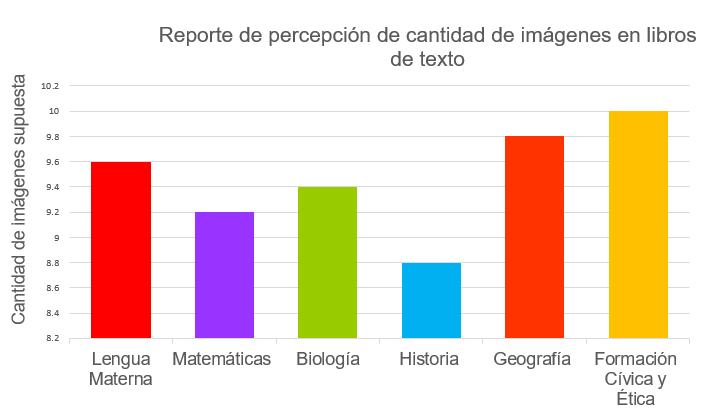
Por ejemplo: en esta gráfica se consideran los datos sobre la percepción de la cantidad de imágenes en los libros de texto. Si graficas la percepción sobre la cantidad de imágenes por página, podrás colocar los números obtenidos de forma vertical y las asignaturas de forma horizontal; diferenciándolas por colores, tal como se muestra en el ejemplo. El tamaño de las barras dependerá de los datos, en este caso, de la cantidad de imágenes percibida en los materiales de cada asignatura.
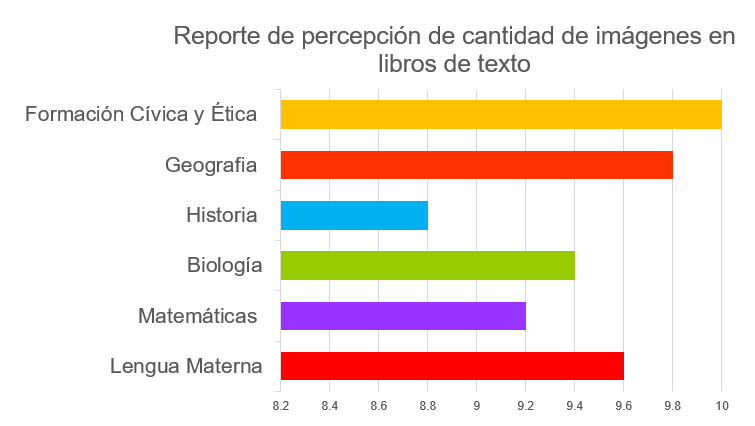
Otra forma de ordenar los datos es orientar las barras de manera vertical. En este ejemplo, los elementos aparecen de forma inversa, es decir, de manera vertical se enlistan todas las asignaturas mientras que de manera horizontal se coloca la cantidad de imágenes percibidas.
En ambos casos puedes agregar leyendas, componentes usados para identificar con mayor claridad los distintos elementos que conforman un gráfico, tales como colores o formas. Para este ejemplo se utilizan colores diferentes para representar cada asignatura.
Numero 4: Cuadro Sinóptico
El cuadro sinóptico es una estrategia que permite organizar y clasificar el contenido de un texto de manera sencilla para expresar visualmente las ideas principales de una temática y sus múltiples relaciones, partiendo del concepto general y dirigiéndolo hacia datos particulares, utilizando llaves para conectar la secuencia de la información, a través de una estructura lógica.
Sirve para contrastar los contenidos, anotando las semejanzas y diferencias, entre una o varias variables de un mismo tema. Pueden utilizarse como estrategias de enseñanza para organizar las ideas que aprendas durante tus clases.
Para elaborar un cuadro sinóptico de manera fácil, puedes dividir el contenido en subtemas y describir estos dentro de subdivisiones o llaves; así los conceptos o palabras claves que utilices estarán clasificados y descritos brevemente, facilitando la comprensión y memorización del tema.
Por ejemplo: si elaboras un cuadro sinóptico de los diferentes deportes que existen, primero puedes colocar el tema central, “deportes”, después puedes agregar dos categorías: los deportes individuales y los deportes que se practican en equipo; posteriormente, en esas categorías puedes anotar las clasificaciones que existen de manera individual y grupal. Finalmente, en cada clasificación, puedes escribir los tipos de deportes que pueden practicarse en las diferentes clasificaciones asignadas:
Por ejemplo, en los deportes individuales encuentras los atléticos como “natación” o los de combate como “boxeo”; mientras que en los deportes de equipo encuentras aquellos que se juegan con pelota como “futbol”, “basquetbol” o “futbol americano”.
Numero 3: Línea del tiempo
Si deseas ordenar cronológicamente procesos o acontecimientos que han ocurrido a lo largo de un período específico como años, lustros, décadas, siglos o milenios, entonces puedes hacer uso del apoyo gráfico denominado línea del tiempo.
Esta herramienta permite comprender cómo se relacionan los hechos, cuál fue su duración y en qué momento se produjeron; observando con claridad la relación temporal que existió entre ellos.
Su elaboración es sencilla, pero requiere que se siga una serie de pasos:
1. Primero debes seleccionar un tema y determinar la fecha inicial y final que representarás.
2. Después debes elegir el periodo que deseas representar. Es importante que utilices una misma medida de tiempo en todo el gráfico.
Por ejemplo: si vas a elaborar una representación de los hechos más importantes de este siglo, la línea del tiempo puede estar dividida en años.
3. Al concluir, debes ubicar los acontecimientos más relevantes en orden cronológico y trazar una línea recta para comenzar a escribir la información en forma de diagrama; las palabras o ideas clave deben ser breves, concretas y suficientes para facilitar su comprensión.
Si la línea recta se traza de forma horizontal los acontecimientos deberán escribirse de izquierda a derecha; si se realiza de forma vertical escribirás de arriba hacia abajo.
También puedes agregar imágenes o dibujos que representen y complementen los datos expuestos; es recomendable utilizar diferentes tipos de líneas o colores para distinguir cada periodo o acontecimiento histórico y ubicar con mayor facilidad los datos en el tiempo.
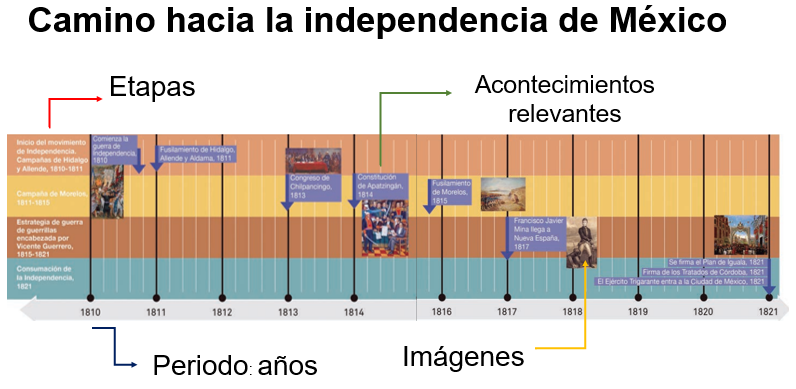
La imagen anterior es un ejemplo de línea de tiempo. En ella, puedes observar el camino hacia la independencia de México, dividido en etapas que se encuentran ubicadas con diferentes colores y utilizando como referencia temporal los años. Puedes ver que a lo largo de la línea se localizan los acontecimientos más relevantes que ocurrieron en cada fase, y está ilustrado con fotografías que complementan y ejemplifican la información expuesta.
Numero 2: Mapa Conceptual
Para crear una sinopsis gráfica de un tema en específico, puedes hacer uso de los mapas conceptuales. El mapa conceptual es un recurso que establece ideas de manera descendente, escritas de forma jerárquica dentro de figuras geométricas como óvalos o recuadros, que se conectan entre sí a través de líneas y palabras de enlace.
Esta técnica obliga a relacionar con el tema y jugar con los conceptos, pues debes organizar y resumir la información de manera correcta, situando el tema central y los términos conceptuales en los recuadros, relacionándolos con palabras de enlace para formar una proposición a través de líneas que logren la unión de dicha idea.
Los elementos que caracterizan este tipo de diagramas son la “jerarquización”, que permite ordenar en grado de importancia los conceptos; la “síntesis”, que incluye únicamente lo más importante del texto; el “impacto visual”, que muestra las relaciones entre las ideas principales de un modo simple y vistoso; las “proporciones”, que permiten identificar fácilmente los conceptos más o menos importantes, con letras de diferentes tamaños escritas en mayúsculas o minúsculas, y el “uso de conectores”, que hará que la interpretación de la información sea adecuada.
Para poder elaborar un mapa conceptual debes “seleccionar” un tema y los conceptos relacionados con dicho texto para enlistarlos, sin repetir términos, “agrupar” los conceptos que se relacionan y “ordenar” las ideas en grado de importancia, partiendo de las generales y finalizando en las específicas. Después, debes “representar” los conceptos en el diagrama y “conectarlos” para comprobar si el tema es comprensible.
Numero 1: Mapa Mental
El mapa mental es un diagrama que sirve para representar información a través de una palabra clave o idea central de forma lógica y creativa, haciendo uso de dibujos, imágenes, palabras clave, signos, símbolos, códigos y colores que transmiten información específica de un tema en particular o de la ramificación de varios temas relacionados con un punto central.
Su elaboración genera apuntes visuales que permiten sintetizar los conocimientos, transmitir el pensamiento y generar el aprendizaje.
Para entender mejor la estructura del mapa mental, imagina el plano de una ciudad: el centro representa la idea principal; las principales avenidas que llevan al centro representan los pensamientos clave del proceso mental; las calles menores representan los pensamientos secundarios y las imágenes, anuncios o nombres de establecimientos ejemplifican ideas especialmente importantes.
Un mapa mental se obtiene y se desarrolla alrededor de una palabra, frase o texto, situado en el centro, seguido de ideas, palabras y conceptos, mediante líneas que se trazan alrededor del título en el sentido de las manecillas del reloj.
Cabe también hacer mención a otros, que son comunes, como las tablas, cuadros comparativos, mapas o diagramas.
Hacer uso de uno u otro organizador depende de la información que quieras presentar y las relaciones que se establecen entre los conceptos. Por ejemplo, ¿podrías hacer una gráfica con la información de los diversos deportes? Probablemente no, ya que no cuentas con cifras. Para representar el desarrollo del periodo conocido como la Paz Armada, ¿qué organizador utilizarías?
Es importante elegir el organizador que mejor presente la información y la relación que se establece entre los conceptos, en función de las fuentes que consultes para la elaboración de tus fichas temáticas.
Retoma el apoyo gráfico que se mencionó como número uno de la lista, y elabora un mapa mental con la información que acabas de aprender.
Te recomendamos realizar la actividad en tu cuaderno; de esta manera podrás sintetizar la información que aprendiste durante la clase y repasar el tema las veces que lo consideres necesario.
Para comenzar debes escribir el tema central de tu mapa: “apoyos gráficos”:
Y realizar la primera ramificación donde escribirás “gráfica de barras” desprendiendo algunos otros conceptos como: datos, categorías, recursos visuales, leyendas para identificar distintos elementos con colores o formas y barras horizontales y verticales; además, incluirás dos imágenes que ejemplifiquen este apoyo gráfico.
En la segunda ramificación colocarás el “cuadro sinóptico” para desglosar conceptos como contenido organizado, semejanzas y diferencias, estructura lógica, ideas clave: generales y particulares, múltiples relaciones, subdivisiones y llaves.
En la tercera ramificación anotaras “línea del tiempo” y subramas que contengan la cronología de procesos o acontecimientos, periodos donde señales los meses, años, lustros, décadas, siglos o milenios, y funciones de las cuales se desprenden comprender hechos, relación temporal y duración de los sucesos. También agregarás una subdivisión que indique la elaboración: seleccionar el tema, determinar la fecha inicial y final, periodo en que se dividirá, ubicación de acontecimientos, orden cronológico y orientación de la línea: horizontal con una escritura de izquierda a derecha o vertical para anotar los datos de arriba hacia abajo; e imágenes o colores que representen y diferencien la información. Para concluir esta ramificación agregarás ilustraciones que muestren distintos ejemplos de líneas del tiempo.
La penúltima ramificación corresponderá al “mapa conceptual” y de esta línea desglosarás otras para colocar sinopsis gráfica, ideas descendentes y jerarquización, síntesis, impacto visual, palabras escritas en óvalos o recuadros, proporciones de letras con mayúsculas o minúsculas y uso de conectores con líneas y palabras de enlace. Además, agregarás los pasos para su elaboración en subdivisiones que contengan las palabras: seleccionar tema y conceptos principales, agrupar ideas, ordenar generales y específicas, representar los conceptos y conectarlos.
Por último, añadirás una ramificación que explique las características del mapa mental, desprendiendo conceptos como: idea central, palabras clave, dibujos, signos, símbolos y códigos de forma lógica y creativa, y ramificaciones en sentido de las manecillas del reloj, con temas relacionados y asociación de ideas. Podrás terminar el diagrama con dibujos que representen la información expuesta.
Al completar todas las ramificaciones y apoyos gráficos que se mencionaron en la lista, tu mapa mental estará terminado. No olvides añadir creatividad a tu trabajo a fin de que adquiera una presentación adecuada y útil para repasar el contenido de la sesión.
Puedes consultar en tu libro de texto los contenidos relacionados con el aprendizaje esperado: “Elabora fichas temáticas con fines de estudio”, y realizar las actividades propuestas para poder afianzar sus conocimientos.
Recuerda que colocar estos apoyos gráficos en tus fichas temáticas te permitirá identificar y distinguir las ideas principales de las secundarias, así como establecer relaciones entre los conceptos. Por ejemplo, puedes utilizar las tablas para comparar datos, los cuadros sinópticos para ordenar información en categorías, las gráficas para representar datos numéricos, y los diagramas para señalar las partes de un objeto o las fases de un proceso.
El Reto de Hoy:
Observa la siguiente ficha de trabajo realizada por un compañero de secundaria y posteriormente analizarás qué tipo de información presenta y qué organizador gráfico podrías usar.

Responde las siguientes preguntas:
¿La ficha presenta información sobre un proceso? ¿Expone datos numéricos? ¿Aborda un periodo? ¿Ordena información en conceptos?
El texto indica que las células se dividen en unicelulares y pluricelulares y ofrece algunas características y ejemplos. Por lo tanto, un mapa conceptual en este caso ayudaría a presentar la información.
Además, sería bueno que añadieras colores diferentes para cada categoría, recuerda que así podrás distinguir los sucesos y visualizar fácilmente la información.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
La representación más adecuada
Aprendizaje esperado: Convierte fracciones decimales a notación decimal y viceversa. Aproxima algunas fracciones usando la notación decimal. Ordena fracciones y números decimales.
Énfasis: Identificar la representación más adecuada al ordenar los números decimales y fraccionarios.
¿Qué vamos a aprender?
En esta lección podrás identificar la representación más adecuada al ordenar números decimales y fraccionarios, a partir de situaciones que combinen ambas representaciones numéricas.
Para esta lección necesitarás:
â— Cuaderno o papel para tomar notas.
â— Lápiz, goma y sacapuntas.
â— Libro de texto de Matemáticas para primer grado.
Una pregunta frecuente es, qué representación es más conveniente utilizar, fracciones o sus equivalencias en número decimal. Una de las respuestas más comunes es el uso de una u otra dependiendo del planteamiento, y a veces es mejor utilizar números decimales, pero no siempre. Piensa, ¿qué representación es más conveniente usar: fracciones o números decimales?
¿Qué hacemos?
En ocasiones puede ser útil usar decimales y en otras fracciones, pero, ¿cómo saber cuándo es más conveniente usar uno u otro tipo de representación numérica?
Utilizando diversos ejemplos, se responderá a la pregunta, sin embargo, se considera que exista más de una respuesta. Observa el primer ejemplo.
Ejemplo, granola artesanal
Una empresa familiar se dedica a elaborar distintos tipos de granola de manera artesanal, para ampliar sus ventas, crearon una nueva receta y necesitan considerar las cantidades de ingredientes que involucra para nombrar al producto según el ingrediente predominante. A partir de la receta se deben ordenar los ingredientes de mayor a menor o de menor a mayor, es indistinto, lo importante será identificar al mayor para determinar cuál es el ingrediente principal y así nombrar su nuevo producto.
La receta incluye los siguientes ingredientes para la elaboración de un paquete de granola:
- Una y media tazas de amaranto.
- Una y un tercio de tazas de avena.
- Tres cuartos de taza de pasas.
- 25% (0.25) tazas de almendra troceada.
- Dos tercios de taza de cacahuate troceado.
- 50% (0.5) tazas de coco seco rallado.
Con base en esta situación, para comparar y ordenar las cantidades pueden usarse fracciones o números decimales.
¿Cuál representación consideras que es la más adecuada? ¿Por qué?
Se considera que, tanto los números decimales como las fracciones representan la misma cantidad de cada ingrediente, pero es más común la medición por tazas en las recetas que usan fracciones y por el tipo de números decimales y fracciones que se presentan.
Para el ejemplo, necesitamos ordenar las cantidades de los ingredientes para conocer el predominante y así elegir el nombre del producto. Sin embargo, tanto los números decimales cómo números fraccionarios pueden ser útiles.
La consideración más importante en esta situación es que hay fracciones como 1 1/3 o 2/3 que no tiene una fracción decimal equivalente, por lo tanto, no se pueden representar como un número decimal finito, y éstas son justo algunas de las medidas en fracciones involucradas en la receta, por lo tanto, no puedes expresar todas las medidas en números decimales exactos, es decir, 1 1/3 en notación decimal es 1.33... …infinito y 2/3 es 0.66… infinito, por lo tanto, dos tercios no es equivalente a 1.33… sino que 2/3 es aproximadamente 1.33... …
Con base en esta observación, en este planteamiento es más conveniente utilizar fracciones como la representación más adecuada para comparar las cantidades. Aunque la notación decimal también permite comparar las medidas, porque no quieres obtener cantidades exactas, pero existen casos en los que si se requiere dicha medida, por eso, en casos como este, se opta por la representación como fracción.
Ya has definido la representación más adecuada, ahora corresponde obtener las fracciones equivalentes de los números decimales 0.25 y 0.5, para después ordenar las cantidades de los ingredientes y hallar el ingrediente predominante que corresponde a la fracción mayor.
En primera instancia, hay que establecer la fracción equivalente a 0.25 Como este número se lee: veinticinco centésimos, es posible determinar que la fracción equivalente es veinticinco cienavos que puede simplificarse como cinco veinteavos, misma que puede simplificarse como un cuarto. Para comprobarlo, si se divide 1 entre 4 efectivamente, encontrarás un cociente igual a 0.25, o bien veinticinco centésimos.
Como cero punto cinco es igual a 5 décimos que es igual a un medio. De manera que 0.5 es equivalente también a un medio. Finalmente, corresponde ordenar las fracciones de mayor a menor.
Las cantidades expresadas como números mixtos o fracciones quedan de la siguiente manera:
- Una y media tazas de amaranto.
- Una y un tercio de taza de avena.
- Tres cuartos de taza de pasas.
- Un cuarto de taza de almendra troceada.
- Dos tercios de taza de cacahuate troceado.
- Media taza de coco seco rallado.
Para comparar y ordenar las medidas, se recurre a la recta numérica. En este caso usa 3 rectas numéricas, con la misma escala del 0 al 2, una seccionada en tercios, otra en cuartos y otra en medios. Así es posible ubicar todas las medidas involucradas, como se muestran a continuación.
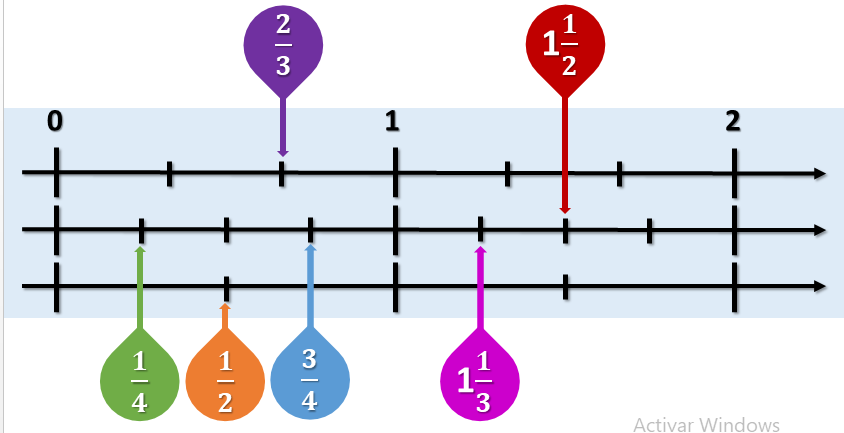
- Un entero y un medio
- Un entero y un tercio
- Tres cuartos
- Un cuarto
- Dos tercios
- Un medio
Para determinar cuál es la fracción mayor, puedes ordenarlas de mayor a menor o de menor a mayor, es indistinto. En este caso lo harás de menor a mayor:
- Un cuarto
- Un medio
- Dos tercios
- Tres cuartos
- Un entero y un tercio
- Un entero y un medio
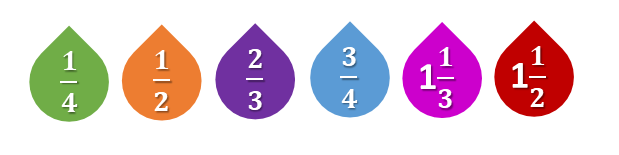
Cómo puedes observar, el número mayor es uno y medio y el menor es un cuarto. Amaranto es el ingrediente que predomina en la receta.
A continuación, analiza el siguiente ejemplo para que te sea más fácil poder identificar más elementos que permitan determinar qué representación es la más adecuada al comparar fracciones y decimales.
Revisa el siguiente ejemplo.
Ejemplo, fertilizantes
En un laboratorio de Biología se realizan pruebas para la creación de fertilizantes orgánicos en beneficio de cultivos alimentarios. Para este ejemplo, se considera que se rociaron 5 plantas con distintos fertilizantes, para determinar su posible efecto en el crecimiento de las plantas, ya que se cultivaron en las mismas condiciones y la diferencia radica en el fertilizante utilizado en cada una durante su cultivo.
Después de aplicar de manera constante el fertilizante durante 30 días a las cinco plantas, dos laboratoristas se encargaron de medir su altura.
Los laboratoristas reportaron las siguientes alturas:
El laboratorista 1, reportó que la altura de la planta 1 fue de tres cuartos de metro mientras que la altura de la planta 2 fue de dieciocho veinticincoavos de metro. Por otro lado, el laboratorista 2, reportó que la altura de la planta 3 fue de 0.73 metros, la altura de la planta 4 fue de 0.77 metros y que la altura de la planta 5 fue de 0.69 metros.
Para organizar el informe global y poder comparar el crecimiento de las plantas, se tienen que ordenar las medidas de mayor a menor altura. Piensa ¿cuál de las plantas alcanzó mayor altura?, ¿cuál menos?, ¿cuál representación sería la más adecuada para comparar las alturas?
Recuerda que es importante considerar los beneficios de ambas representaciones, para determinar cuál es la más adecuada para comparar y ordenar las alturas obtenidas, ya sea que se elija representar los resultados como fracciones o como números decimales, se tendrán que obtener equivalencias, ya que se encuentran representaciones combinadas.
Es importante saber que cuando las fracciones no tienen un denominador común, podrían requerirse más cálculos para ordenarlas, primero se tendría que buscar un común denominador en todas las fracciones y después, convertirlas a su equivalente con dicho denominador. Además, en este caso, al comparar números decimales que se encuentran en un rango cercano, existe mayor facilidad para ordenar de mayor a menor. Aunque un criterio que se podría considerar es verificar si las fracciones involucradas tiene una fracción decimal equivalente. Si fuera el caso, comparar fracciones decimales podría ser una buena opción también.
Estos criterios sin duda te resultarán muy útiles para decidir que tipo de números usar
Reflexiona: ¿Cuál es el proceso que seguirás para ordenar las medidas como números decimales? Compara tu respuesta con los pasos que seguirás a continuación.
Antes de ordenar las medidas, realiza las equivalencias. Primero usa la representación decimal, debido a:
1. La cercanía del rango en el que se encuentran los números.
2. Que hay menos operaciones que realizar, es decir, el proceso es más corto, ya que hay menos fracciones que número decimales.
Entonces, primero debes obtener las equivalencias de las alturas de las plantas 1 y 2 que corresponden a las fracciones tres cuartos y dieciocho veinticincoavos, respectivamente, número decimal. Para ello, se divide el numerador entre el denominador para cada fracción. La equivalencia decimal de la fracción tres cuartos: 3 entre 4 es igual a 0.75. Enseguida, procedes a encontrar la equivalencia decimal de la fracción dieciocho veinticincoavos: 18 entre 25 es igual a 0.72.
Ahora sí, puedes ordenar las alturas de las plantas que se encuentran representadas en números decimales.
La forma de hacerlo es comparar cifra con cifra cada uno de los números. En este caso, primero compara la posición de los décimos y luego la de los centésimos, por lo que encuentras el siguiente orden de mayor a menor, en las alturas de las plantas:
Primero, la planta 4 con 0.77metros de altura, luego la planta 1 con 0.75 metros de altura, enseguida la planta 3 con 0.73metros de altura, luego la planta 2 con 0.72metros de altura y finalmente, la planta 5 con 0.69metros de altura.

Usar como representación a los números decimales para las alturas de las plantas es una buena opción. Ahora observa el mismo procedimiento, pero usando fracciones.
Lo primero que debes hacer es obtener las fracciones decimales equivalente a 3/4 y 18/25. Al dividir 10 entre 4, el resultado no es exacto, ya que 10 entre 4 es igual a 2.5 y como 10 es menor al denominador 25, por ello, se divide entre 100.
Divide 100 entre 4, cuyo resultado es igual a 25. Después, se multiplica a 3 y a 4 por 25 para obtener la fracción decimal equivalente.
Ahora, divide 100 entre 25 que es igual a 4, y el numerador y el denominador de 18/25 los multiplicas por 4, al resolver las operaciones, la fracción decimal equivalente es 72/100.

Ahora únicamente tienes que convertir los números decimales a fracción decimal, es decir, que para la planta 3 que mide 0.73 m, su medida equivalente como fracción decimal es 73 sobre 100, 73 centésimos, la planta 4, 77 centésimos y la planta 5, 69 centésimos.
Ya que tienes las medidas como fracciones decimales, las ordenas, como a continuación se muestra
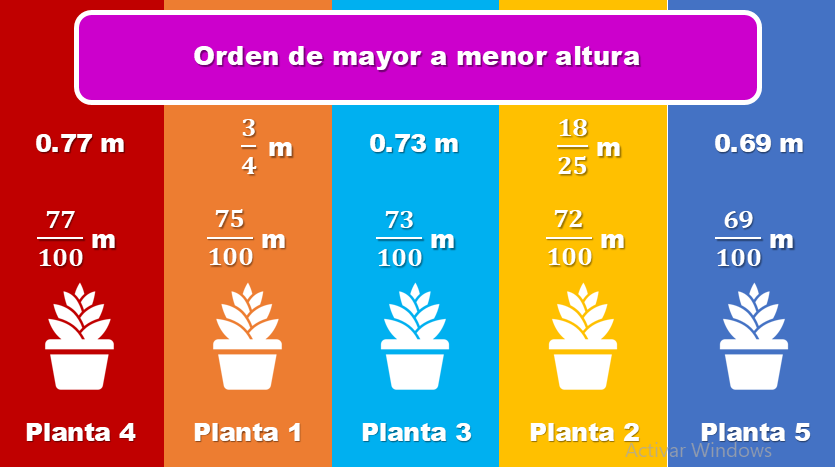
Se corrobora que la planta con mayor altura es la 4, con 77 centésimos de metro y la de menor altura es la 5, con 69 centésimos de metro.
En los ejemplos anteriores observaste que para ordenar cantidades que involucran fracciones y decimales, es posible trabajar con la fracción o su expansión decimal, según sea el caso, ahora qué sucede si tienes que operar con dichas cantidades, es decir, que las utilizarás para realizar un cálculo.
Observa la siguiente capsula del segundo. 0:45 al 01:30.
- Una vuelta y media
Como pudiste observar, en esa situación se debe multiplicar la medida de la pista, es decir 360 metros por cada una de las fracciones registradas en cada recorrido diario, puede ser una forma más eficiente de operar con números decimales.
Ahora analiza el siguiente caso:
El lunes corrió 1 1/4 el martes 1 1/2, el jueves 2 3/8, el viernes 3 3/5 y el sábado 5 1/5.
- El número mixto 1 1⁄4 es equivalente al número decimal 1.25.
- El número mixto 1 1/2 es equivalente a 1.5.
- El número mixto 2 3/8 es equivalente a 2.375.
- El número mixto 3 3/5 es igual al número decimal 3.6.
- Y el número mixto 5 1/5 es equivalente a 5.6.
En este caso todos los números mixtos, pudieron representarse como un decimal finito ya que su expansión decimal fue exacta y se tiene la libertad de decidir si se trabaja con fracciones o con decimales ya que en cualquiera de los casos se llegará al mismo resultado. Piensa ¿con qué tipo de números prefieres operar?
El Reto de Hoy:
Calcula la distancia recorrida para cada día de la semana
Los días que corrió fueron: lunes, martes, jueves viernes y sábado. En la siguiente columna multiplica el número de vueltas por la medida de la pista que es de 360 metros, así: 1.25 por 360, 1.5 por 360, 2.375 por 360, 3.6 por 360 y 5.6 por 360.
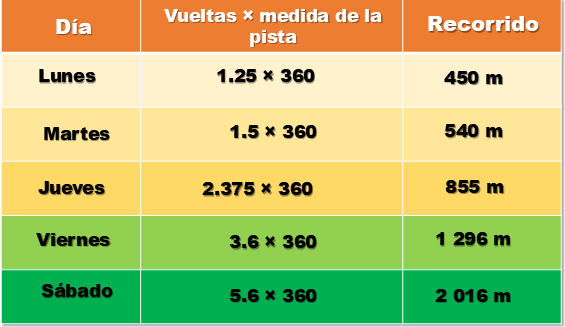
En la última columna se observan las respuestas que representan los recorridos en metros: el lunes fueron 450 metros; el martes, 540 metros; el jueves, 855 metros; viernes, 1 296 metros y sábado, 2 016 metros
En conclusión; existe una representación adecuada dependiendo de la situación y que a partir de tus conocimientos y pericia matemática puedes encontrarla. Así decidirás si usas a los números decimales o los fraccionarios.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
1° Secundaria 25 de enero
Aprendizaje esperado: Identifica a la célula como la unidad estructural de los seres vivos.
Énfasis: Relacionar tipos de células con tejidos vegetales.
¿Qué vamos a aprender?
En esta sesión te encaminarás específicamente en relacionar tipos de células con tejidos vegetales
Recuerda que en casa observarás cómo desarrollar un proyecto con base en la propuesta que se estará presentando durante las sesiones.
Te sugerimos que tengas listos tus materiales escolares: tu cuaderno de notas, un bolígrafo o lápiz y colores, no olvides tu “abecedario biológico”, ya que te apoyará para comprender el tema, pues aprenderás conceptos que has estudiado anteriormente.
Reflexiona sobre la siguiente pregunta: ¿alguna vez te has preguntado de qué están hechas las plantas?
Las plantas tienen características diferentes a los animales, lo cual está estrechamente relacionado con su estructura y composición.
Y con lo que aprenderás en esta sesión podrás reconocer de qué están hechas y cómo están organizadas.
En las sesiones anteriores, identificaste que los seres vivos tenemos varios niveles de organización ¿Recuerdas cuáles son?
Son las siguientes:
Átomos, moléculas, células, tejidos, órganos, sistemas y organismo, además podrás identificar esos niveles en ciertos animales y como ejemplo al ser humano. Pero en las plantas también puedes reconocer esta organización.
Recapitulando un poco, recuerda que la célula es la parte anatómica, estructural y funcional de un ser vivo, misma que al agruparse con células similares forman “tejidos”, que desarrollan una función específica dentro del organismo.
Así mismo, te enfocarás en conocer tipos de células que forman a este reino y sus principales tejidos.
¿Qué hacemos?
Es importante conocer que las células que constituyen a las plantas son del tipo eucarionte vegetal, son unas estructuras que parecen pequeños ladrillos y están uno junto de otro, como se muestra en la siguiente imagen.
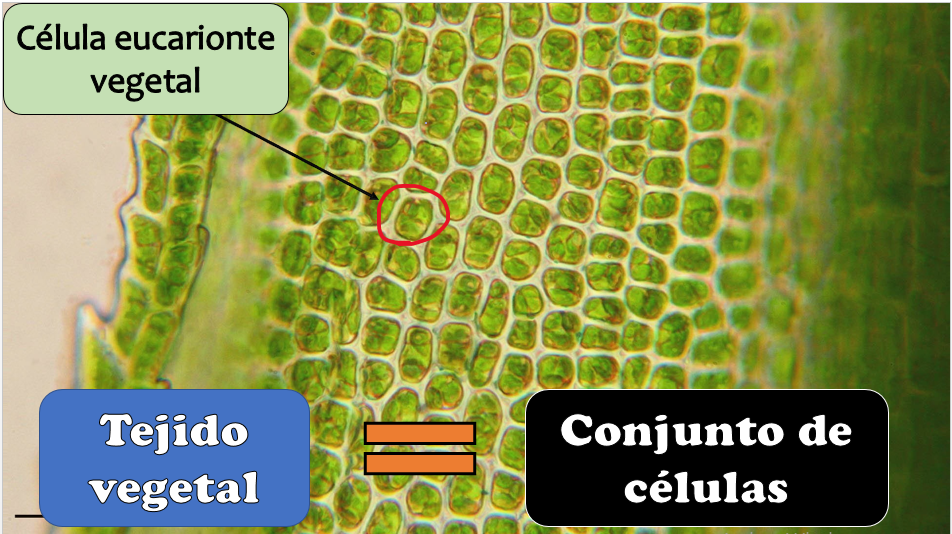
Como puedes ver, tiene muchas células ya que es un organismo pluricelular, pero principalmente las plantas están compuestas por dos tipos de células:
Las células meristemáticas y las células diferenciadas.
En el caso de las células meristemáticas o células de crecimiento, se encuentran ubicadas en toda la planta y son capaces de realizar una división celular constante, lo que permite que la planta crezca durante toda su vida, como lo muestra el siguiente ejemplo

Esta muestra es de la raíz de una cebolla. En ella se puede apreciar cómo están dividiéndose las células.
Por otra parte, las células diferenciadas, son aquellas que tienen una función especializada dentro de la planta, como lo muestra imagen.

Las hojas, como la del ejemplo anterior, una vez que han alcanzado el máximo crecimiento, su función se transforma, es entonces cuando se dice que la hoja ha “madurado”.
Los tejidos vegetativos corresponden a un conjunto de células vivas que se encargan de realizar todos los procesos de desarrollo, los cuales incluye a la fotosíntesis, la respiración, el almacenamiento de diversas sustancias; así como también las fases de crecimiento y de reparación para reemplazar células muertas. Y en las plantas se presentan tres sistemas de tejidos.
Sistema de tejido dérmico, que cubre la superficie externa del cuerpo de la planta; el sistema de tejido fundamenta que permite la realización de funciones importantes como la fotosíntesis; y el sistema de tejido vascular, que transporta los líquidos a todo el cuerpo de la planta.
El sistema de tejido dérmico cubre el cuerpo de la planta, el cual le otorga protección, por ejemplo, de una invasión de microorganismo que pueda provocarle alguna enfermedad; a su vez regula su temperatura, con la finalidad de reducir la evaporación.
Las plantas tienen dos tipos de tejido dérmico: y el que se conocerás en esta sesión es el llamado epidérmico:
Este tejido forma la epidermis, que es la capa celular más exterior que cubre hojas, tallos y raíces de todas las plantas, es decir, es el conjunto de células que se encuentran alrededor como lo pueden observar en la imagen que está en pantalla.
También el tejido epidérmico cubre flores, semillas y frutos. Y las partes que sobresalen del suelo cuentan con unas células epidérmicas comprimidas y delgadas que están recubiertas por una “cutícula” cerosa resistente al agua que secretan este tipo de células.
Ahora imagina, que tienes una planta, con un plástico cubriendo la planta actuando como cutícula, esta se vuelve impermeable al momento de querer regarla, esto es similar a nivel microscópico, el tejido epidérmico da protección logrando que tanto el agua como microorganismos externos no la invadan, cabe resaltar, que esta cutícula solo se encuentra en hojas y tallos, ya que, si se encontrara en las raíces de una planta, esta evitaría que se absorbiera agua y minerales.
A continuación, aprenderás sobre el tejido fundamental.
Ahora analiza la siguiente pregunta: ¿Por qué se llamará tejido fundamental?
Se llama así porque en las células de este sistema de tejidos se realizan la mayoría de las funciones esenciales de la planta, es decir, los principales tejidos, entre los que se encuentra al parénquima, que es el tejido fundamental más abundante, ya que constituye la mayor parte del cuerpo de una planta. Es un tejido vegetal que consta de células poco especializadas, susceptibles de diferenciación.
Observa la siguiente imagen:

Las células del parénquima están conformadas por paredes delgadas, y están vivas en la madurez. Por lo general, llevan a cabo la mayoría de las actividades metabólicas de la planta, como son la fotosíntesis, la secreción de hormonas y el almacenamiento del alimento.
Un ejemplo de células parenquimatosas lo puedes ver en las papas, semillas, frutas y raíces de almacenamiento como las zanahorias o jícamas, que están repletas de estas células, que guardan diversos tipos de carbohidratos
Otro tejido que también es parte del sistema fundamental es el esclerénquima que está compuesto por células con paredes celulares gruesas y endurecidas. Estas células sostienen y fortalecen el cuerpo de la planta y mueren después de que se especializan.
Un ejemplo lo encuentras en las cáscaras de nuez, la cubierta exterior de la semilla del durazno y en la cáscara de una pera, la cual le da su textura granulosa. Así mismo, forman un importante componente de la madera.
Y el último sistema de tejidos, el vascular, su función es principalmente el transporte de agua y nutrimentos, el sistema de tejido vascular de las plantas tiene una función similar a la de los vasos sanguíneos en los animales; pues transportan sustancias por todo el cuerpo.
Para transportar sustancias cuenta con dos conductos llamados, xilema (constituido por células alargadas denominadas vasos y traqueidas) y floema (constituido de manera general por células largas y delgadas denominadas células cribosas).
Si te es posible, podrías realizar el siguiente experimento:
Materiales: Ten a la mano dos vasos, colorante vegetal azul y verde, agua, 2 servilletas de papel, dos hojas de papel, y un gotero.
- Primero identifica los colores, el azul será para representar el agua y minerales que serán transportados por el xilema y el verde para reconocer los nutrientes producidos por la planta y que serán transportados a través del floema.
- Realiza una figura en papel con forma de una planta, y en una servilleta de papel haz la misma figura de la planta y ahora las unes.
- Ahora agregas en un vaso 1/3 de agua, posteriormente colocas cuatro gotas de colorante azul.
- Tomas la silueta de la planta y la sumerges en el agua.
Observa que el líquido contenido en el vaso empieza a fluir hacia arriba, a través de la servilleta, desde la raíz hacia todas las partes de la planta.
Algo semejante sucede en el xilema, ya que estas células absorben el agua y los minerales que están disueltos en ella, desde las raíces y los transportan a las partes más altas de una planta, con dirección hacia arriba. Cabe destacar que en el xilema el líquido se mueve en una sola dirección.
Ahora para el segundo modelo nos concentraremos en las hojas, agrega 1/3 de agua en nuestro segundo vaso y las cuatro gotas de colorante verde, lo disuelves y tomas un poco de esta disolución con el gotero.
El líquido representa los azucares (carbohidratos) elaborados en las hojas gracias a la fotosíntesis. Dichos nutrientes se encuentran disueltos en el agua y son el alimento de la planta, los cuales deben moverse a otras partes para nutrir las estructuras no fotosintéticas (como las raíces y las flores) o almacenarse en las células de la corteza de las raíces y los tallos. Como lo podemos observar en nuestro modelo.
El floema transporta carbohidratos y otras moléculas orgánicas, como aminoácidos, proteínas y hormonas a todo el cuerpo de la planta. Por lo que estos líquidos se pueden mover desde las hojas hacia arriba y hacia abajo de la planta, según sea requerido por el organismo.
Es interesante ver como la planta utiliza su sistema vascular para distribuir lo que obtiene desde sus raíces y lo que produce desde las hojas.
Observa la siguiente imagen:

Es el sistema vascular del maíz visto en el microscopio, si observas con atención, el xilema contiene dos tipos de células conductoras; tienen un diámetro mucho mayor y casi siempre tienen extremos redondeados. Mientras que por el otro lado el floema incluye elementos unidos extremo con extremo, donde se unen grandes poros revestidos con membranas y permiten que el líquido se mueva entre ellos.
El Reto de Hoy:
Necesitarás la imagen de una planta donde se observen las hojas, el tallo y la raíz, una cartulina, lápiz, goma, sacapuntas, colores, y marcadores.
Coloca la imagen en la cartulina, la puedes dibujar, tomando como modelo alguna que encuentren en tu libro de texto o que tengan en el jardín o en alguna maceta.
Ahora con base en la información vertida durante la sesión, señala dónde se ubica cada tipo de sistema de tejido, utiliza un color distinto para cada uno de los tres tipos.
También puedes agregar un dibujo o imagen de cómo se vería si esa parte se observara bajo el microscopio.
Al finalizar compártelo con tus familiares, maestra o maestro y tus compañeras y compañeros.
Ahora, trabaja en el desarrollo del proyecto, anteriormente identificaste las fases principales que tienen los proyectos.
Planeación, desarrollo, comunicación y evaluación. Mismas que recorrerás al construir tu proyecto.
El tema es: Estructura y función celular.
Y la problemática que tratarás de resolver es: ¿Cómo representar estructuras básicas de la célula, explicar sus funciones e identificarlas como características comunes de los seres vivos?
Tenlo a la mano porque es la que guiará todo tu proyecto.
El día de hoy continuarás con la fase llamada “Planeación”, donde determinaremos las acciones a realizar y los tiempos destinados a cada una.
Todo esto es muy importante ya que el objetivo del proyecto científico demostrativo será:
Construir un modelo de célula que permita representar sus estructuras básicas, explicar sus funciones e identificarlas como características comunes de los seres vivos, y se sugirió implementar un cronograma y conociste un ejemplo claro de cómo llenarlo para que todo quede organizado.
Cabe resaltar que este proyecto lo iras desarrollando a lo largo de tres aprendizajes esperados, mismos que te permitirán profundizar en el conocimiento sobre el tema y te darán un mayor sustento científico que enriquecerá tu proyecto.
A continuación, construirás el cronograma que guiará tu proyecto.
Observa la tabla que utilizarás para el cronograma.

En la primera fila se encuentran los días marcados para el proyecto y en la primera columna se describen cada una de las cuatro fases que anteriormente se mencionaron.
Ahora, dentro del cronograma anotarás las acciones a desarrollar y el tiempo que esto te tomará.
Inicia con la fase 1: “Planeación”:
En primer lugar, selecciona el tema a desarrollar y la problemática a resolver. Esto lo definiste en la sesión anterior.
Posteriormente organiza las actividades y definimos los tiempos para cada una. Que es lo que estás haciendo en este momento, con tu cronograma, por tanto, lo asignas en el día 2.
En el desarrollo, incluirás las actividades seleccionadas para dar respuesta al problema, iniciando por la búsqueda, análisis y selección de la información. En las siguientes sesiones estarás presentando varios datos que será la base para tu proyecto, pero también puedes recurrir a diversas fuentes como libros, revistas especializadas, internet, entre otras. Para estas acciones destinarás del día 3 al 10.
Asimismo, recuerda que vas a construir un modelo de la célula que permita representar estructuras básicas, explicar sus funciones e identificarlas como características comunes de los seres vivos; por ello también es importante que definas una estrategia para reunir el material que vas a utilizar y cómo lo vas a construir.
Posteriormente se presentará un ejemplo sobre su construcción y los materiales requeridos.
Una vez que tengas la información, es importante que la analices y resaltes los aspectos más importantes que te ayuden a comprender la estructura y función celular. Y en el día 10 elaborarás un informe en donde se describan el tema, la problemática que elegimos, la información sintetizada y los resultados y conclusiones a las que llegaste.
Con respecto a la fase 3 “Comunicación”:
Una característica importante en la ciencia es la divulgación de sus hallazgos ya que es la forma de compartirlos a la sociedad. Por ello, después se realizará una sesión específica para presentar el modelo culminado, analizar los resultados y conclusiones entorno a tu problemática.
Asimismo, se brindará un tiempo para la cuarta y última fase que es la “Evaluación”. Los proyectos son también oportunidades para aprender sobre el trabajo personal y el trabajo en equipo. Con estos aprendizajes podrás realizar mejores proyectos.
Es importante mencionar que este cronograma puede tener ajustes en las fechas dependiendo de las situaciones que se presenten, así que no te preocupes si alguna acción te lleva un poco de más tiempo.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
El crecimiento de la población
Aprendizaje esperado: Argumenta implicaciones ambientales, sociales y económicas del crecimiento, la composición y la distribución de la población en el mundo.
Énfasis: Identificar la tendencia del crecimiento de la población a nivel mundial.
¿Qué vamos a aprender?
En esta sesión identificarás las tendencias del crecimiento de la población.
Para ello conocerás el significado y las características de la tasa de crecimiento de la población a nivel mundial.
También reconocerás los factores que inciden en dicha tasa de crecimiento, así como las proyecciones que se tienen a futuro.
Ten listos tus materiales escolares: tu cuaderno de notas, un bolígrafo o lápiz y tu libro de texto de Geografía, de igual forma, te sugerimos tomar notas; recuerda colocar el título, la fecha y anotar las ideas que consideres más importantes.
¿Qué hacemos?
Para comenzar con la sesión, reflexiona en la siguiente pregunta:
¿Sabes cuál es la ciencia que se encarga del estudio de la población?
Recuerda que la demografía es la rama de la geografía que se ocupa de estudiar la estructura, evolución, características y tamaño de las poblaciones humanas, cabe aclarar que las poblaciones humanas se definen como los grupos de personas que viven en un lugar, comunidad o territorio, y que comparten un idioma, costumbres y tradiciones, además, en nuestro país las tendencias de crecimiento poblacional han cambiado con el paso del tiempo.
En el pasado, las familias eran más numerosas que en la actualidad, por ejemplo, en la década de 1940, las familias se conformaban por 8, 10 o hasta 12 hermanos, en 1970 el número de hermanos descendió entre 6 y 9 por familia, mientras que en la actualidad la mayoría de las familias mexicanas se componen de 1 hijo o 2 hermanos por familia.
Se sabe esto gracias a los datos que se obtienen de los censos y conteos de población, los cuales se llevan a cabo en México y a nivel mundial, el crecimiento de la población se identifica a partir de la natalidad y de la mortalidad.
La natalidad se define como el número de nacimientos registrados en un lugar o país en un periodo determinado, mientras que la mortalidad se refiere al número de defunciones registradas en un lugar o país en un periodo de tiempo determinado.
Analiza, en la siguiente pregunta: ¿cómo sabes cuánto aumentó o disminuyó la población humana?
La tasa de crecimiento poblacional es un indicador demográfico expresado en porcentaje, que te permite conocer el aumento o la disminución de la población de un lugar o país en un periodo de tiempo determinado, para obtener la tasa de crecimiento de la población, necesitas conocer la población inicial y la población final de un lugar o país en un periodo de tiempo determinado.
La tasa de crecimiento de la población la puedes obtener a través de la siguiente fórmula.
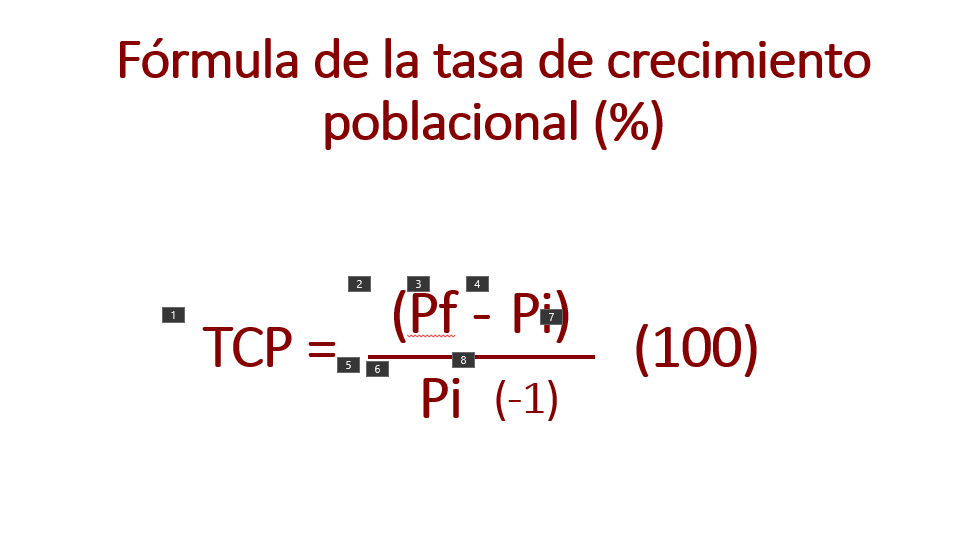
La tasa de crecimiento de la población (TCP) es igual (=) a la población final (Pf), menos la población inicial (Pi), entre (/), la población inicial (Pi) por cien (100).
Recuerda multiplicar por menos uno (-1) el denominador de la población inicial en caso de que la diferencia entre población final e inicial sea negativa; esto es, en caso de que haya un decremento de la población.
Para comprenderlo mejor, realiza el siguiente ejercicio:
Toma como ejemplo la tasa de crecimiento de la población en China desde el año 2000 hasta 2010.
El año 2010 representa la población final, mientras que el año 2000, la población inicial.
Luego divide el resultado de esa diferencia entre la población inicial, que es nuevamente el año 2000, y multiplica por (-1) cuando la diferencia sea negativa; esto es, cuando haya un decremento de la población.
Esto, con la finalidad de obtener un número relativo que pueda ser multiplicado por cien (100) para obtener la tasa de crecimiento de la población.
Ahora sustituye la población total China en el año 2010 era de 1,338,000,000 de habitantes, mientras que en el año 2000 era de 1 263 000 000 de habitantes. Después resta y el resultado que es 75,000,000 entre 1,263,000,000, lo que es igual a 0.059. Como es un número positivo, indica un crecimiento de la población y, por lo tanto, no es necesario que lo multipliques por (-1).
Pero sí debes multiplicarlo por cien, 0.059 (100), para saber en qué proporción creció la población China, lo que da como resultado (=) 5.9%.
Se concluye que la población China creció desde 2000 hasta 2010 en aproximadamente 6% con respecto a su población total.
Realiza cinco ejercicios como el anterior: elige los cinco países que más te gustaría visitar; encuentra las tasas de crecimiento de la población y compártelas con tus familiares.
Para conocer el crecimiento de la población tienes que hacer uso de habilidades matemáticas, esto implica sumas, restas, multiplicaciones y divisiones.
Para complementar el tema observa el siguiente video del minuto 1:15 al 2:53:
- Cómo es y dónde está la población
https://www.youtube.com/watch?v=mw5SEFdlKwA
En el video se mencionó que tanto la natalidad como la mortalidad te ayudan a conocer el crecimiento de la población, esto es, si restas la población que fallece a la cantidad de personas que nacieron, se puede saber cuánta población aumentó o disminuyó en un país.
A esto se le conoce como crecimiento natural de la población, año. En el mundo nacen al año 19 personas por cada 1 000 habitantes, pero pierden la vida 8 personas por cada 1 000 habitantes, eso significa que se suman 11 personas por cada 1 000 habitantes, lo que significa que hay un crecimiento natural positivo.
Sin embargo, en caso contrario, cuando fallecen más personas de las que nacen, el número será negativo, lo que indica un decremento, esto suele pasar en situaciones de guerra, de manera natural o por envejecimiento demográfico, como en el caso de algunos países europeos.
Un ejemplo de esto último es Italia, donde la tasa de natalidad es de 8 pero la de mortalidad es de 11 por cada 1 000 habitantes. Es decir, Italia pierde 3 personas por cada 1,000 habitantes por año, por lo tanto, su población está decreciendo.
Observa la siguiente imagen:
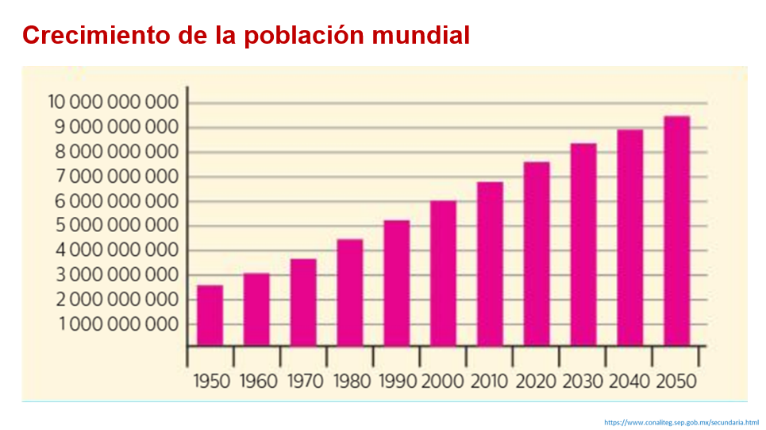
En la imagen anterior, se puede observar que el crecimiento de la población mundial ha sido constante a través de los años, en 1950 la población era de 2,557 millones de habitantes; para 1990 había crecido lo doble; para el año 2010 la población creció aún más, alcanzando los 6,863 millones de personas, en octubre de 2011, la población aumentó a 7,000 millones; a mediados de 2015, la población se incrementó a 7,300; hoy en día, la población asciende a 7,700 millones de habitantes y se estima que para 2050 la población rebase los 9,000 millones de habitantes.
Por otro lado, la población mundial mantuvo un crecimiento moderado hasta mediados del siglo XVIII, sin embargo, a partir de la Revolución Industrial, creció de manera acelerada, ya que durante esta época se hicieron descubrimientos y avances en la ciencia y medicina que permitieron prolongar la esperanza de vida de la población y, por lo tanto, aumentó la población.
La esperanza de vida se refiere al número de años que viven las personas, en promedio, dependiendo del contexto geográfico y socioeconómico en el que se desarrollan. Esto significa que la esperanza de vida varía de acuerdo con las condiciones socioeconómicas de los países.
Por ejemplo, en los países africanos la esperanza de vida es de 60 años; en Asia es de 72; en Latinoamérica y el Caribe es de 75; en Europa, de 77; en América del Norte, de 79, y en Australia y Oceanía, de 82 años en promedio.
Un factor que interviene en el crecimiento de la población y que varía en cada región del mundo es la fecundidad, la fecundidad se refiere al número de hijos que tienen las mujeres en edad fértil, en promedio.
Algunos de los países con mayor fecundidad en el mundo son Nigeria, República Democrática del Congo, Tanzania y Uganda en África, y Afganistán e India en Asia, los países con menor tasa de fecundidad se ubican en Europa y América del Norte.
Otro factor del crecimiento de la población es la migración, la cual implica un crecimiento social y se refiere al desplazamiento de la población de un lugar a otro con la finalidad de mejorar las condiciones de vida.
La influencia de la migración en el aumento de la población ocurre primero en los países desarrollados, es decir, en los países “receptores” de la migración, como Estados Unidos de América en este continente; Alemania, Francia e Inglaterra en Europa, y Japón en Asia.
De acuerdo con datos del Fondo de Población de las Naciones Unidas (UNFPA, por sus siglas en inglés), se observan altas tasas de crecimiento social o migración de la población hacia la mayoría de los países desarrollados, mientras que en los países subdesarrollados la tendencia es contraria, por otro lado, en Asia la población crece rápidamente; se dice que sólo este continente aportó y aportará unos 900 millones de personas entre 2015 y 2050, caso contrario es el de los países europeos, en cuyo territorio se prevé que la población disminuya notablemente.
Lee la siguiente noticia:
La población mundial sigue en aumento, aunque sea cada vez más vieja
17 de junio de 2019, Nueva York
“En 2018, por primera vez en la historia, las personas de 65 años y más, a nivel mundial, superaron en número a los niños menores de cinco años. Sin embargo, para 2050 la población de África subsahariana podría duplicarse y la India superaría a China como el país más poblado, llegando el planeta a los 9 000 millones de habitantes en ese año.
La población mundial aumentará en 2 000 millones de personas para el año 2050, pero sólo nueve países representarán más de la mitad del crecimiento proyectado para entonces, asegura un nuevo informe de las Naciones Unidas”
Para concluir, da respuesta a las siguientes preguntas y realiza la actividad:
- Se refiere al promedio de años que se espera viva una persona dependiendo del lugar o país en donde nace.
- Según las proyecciones del crecimiento poblacional, ¿cuál será el país más poblado del mundo para el año 2050?
- ¿Cuál es la operación matemática que realizas para saber el crecimiento de la población?
- Menciona tres países con una tasa de fecundidad alta. Es un país que se localiza en África
El Reto de Hoy:
Realiza un árbol genealógico de tu familia, desde ti hasta tus abuelos.
Busca fotografías de tus abuelos y de tus padres, coloca los hijos que correspondan hasta llegar a ti
Una vez diseñado tu árbol genealógico, contesta las siguientes preguntas.
1. ¿Ha aumentado o disminuido el número de hijos por familia?
2. ¿Cuáles crees que han sido las causas?
3. ¿Esta tendencia influye en la cantidad de población que hay en el mundo?, ¿por qué?
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Veo, siento, escucho... el arte en todas pArtes
Aprendizaje esperado: Reflexiona acerca de cómo la contemplación de una obra o manifestación artística puede modificar su percepción del mundo y de sí mismo, y registra sus reflexiones.
Énfasis: Descubrir cómo nuestras sensopercepciones influyen en la contemplación de las obras o manifestaciones artísticas y en nuestra manera de representar el mundo que nos rodea.
¿Qué vamos a aprender?
En esta sesión explorarás el modo de representar el mundo, con posibilidades de apreciación artística, para modificar tu entorno a partir de las sensaciones que éstas producen.
Descubrirás la relación que existe entre lo que se siente y se percibe al apreciar una obra de arte y la forma en que representan el mundo los artistas.
También explorarás el modo de representar el mundo, de darle forma, color, olor y sonido a lo que crees que es “el mundo”, surge de ti mismos, de lo que eres, sientes y percibes.
Para que notes o descubras cómo es que representan al mundo, cómo lo conciben, es importante recordar lo aprendido hasta hoy; Ten a la mano libreta y lápiz o bolígrafo para tomar apuntes. Anota la fecha para llevar un mejor registro.
¿Qué hacemos?
Para comenzar la sesión observa la siguiente imagen:

Se llama cuera e identifica al estado de Tamaulipas, con adornos de cuero y barbas en las mangas, pecho y espalda y se reconoce como el vestuario de gala del estado de Tamaulipas.
Se sabe que el vestuario tiene relación con la flora y la fauna de Tamaulipas, la relación que tienen las “barbitas” con la flora y fauna del estado de Tamaulipas, es basicamente para protegerse de las ramas y espinas que hay en la region fría y seca de Tula.
Y bien la cuera antes se llamaba cotón, en la actualidad, hoy luce con grecas blancas o adornos florales que representan a la fauna y flora que se encuentra en el lugar
La cuera, lo llevan varios cantantes de musica norteña mexicana y huapango, por eso se le conoce a la cuera como parte de la vestimenta en la música popular, y con ella tambien se baila polka, redova y chotis
Adicionalmente, varias canciones hacen referencia al "cuerudo", es decir, al vaquero que utiliza la cuera porque su origen está entre los vaqueros de un clima seco y frío.
Reflexióna las siguientes preguntas:
El escuchar y ver elementos culturales de una región ¿qué les hace sentir? ¿Qué pasa por su mente mientras lo hacen?
Ahora, conocerás un poco del estado de Chiapas.
El traje típico de Chiapas describe la riqueza de la flora local y sus colores contrastan con la negrura de la selva, de ahí que el tul donde se hace el bordado sea negro.
México tiene 32 estados y cada uno de ellos es rico en cultura, conocer a detalle cada uno de ellos te da identidad como mexicano y modifica la percepción del mundo que te rodea porque te permite reconocer las múltiples formas de representar el mundo en lo cotidiano.
Existe una frase: “maderas que cantan”, refiere a un instrumento típico de Chiapas, la marimba, es el modo en que las personas materializan su identidad por la riqueza de la región: es un instrumento hecho de madera que se golpea, o percute con unas baquetas
Por ese motivo a la marimba se le clasifica en los instrumentos de percusión.
A la marimba de le considerada que tiene la distribución de un piano, pero a diferencia de éste, la marimba se percute, es decir se golpea con las baquetas.
Además la música de marimba de Chiapas tiene relación con la fauna del lugar y algunas de sus piezas musicales llevan por nombre el de algunos animales, por ejemplo: el jabalí, el alcaraván y el gallito.
Chiapas es rico en fauna; y uno de los animales más espectaculares de esa región es el jaguar, está plasmado en varias obras prehispánicas, y algunos vestuarios típicos hacen referencia a él.
A continuación tratande identificar los sonidos que hay a tu alrededor, afina el oído y por 3 minutos registra todo aquello que escuchan. Al terminar de escucharlo, describe cada sonido y qué te hace sentir eso que oyes.
Por ultimo, conocerás un poco del Estado de México.
En el Estado de México se puede apreciar un majestuoso volcán. Cuenta con un grupo indígena llamado mazahuas y entre sus platillos tradicionales está el chorizo verde.
En el Estado de México solamente 25 familias mazahuas se dedican a la elaboración de las máscaras que se elaboran en Temascalcingo llamadas “Viejos de Corpus”, algunas miden entre tres y cinco metros de altura.
La máscara está elaborada en madera con texturas de ixtle y es ritual porque le da sentido a la relación que hay entre la danza y la naturaleza, entre la persona que la porta y su pensamiento mágico-natural representado en la danza, en las texturas y los materiales.
Las máscaras son talladas en maguey, tronco de palma o árbol de colorín, usan zacate de ixtle y se asocian a las tradiciones para la buena cosecha.
Asi mismo, se reliza una danza con más de 100 años de historia que le da identidad a la región por la manera en que representan el mundo, a través de tus sentidos, puedes acercarte a las manifestaciones artísticas de comunidades o lugares de tu país, puedes percibir elementos artísticos como la música, la danza, la vestimenta, el color, la forma o la textura.
Como has visto, cada estado de la república tiene una riqueza cultural y artística que te permite percibir distintas formas de expresión que influyen en uno mismo.
La danza, la música, la comida, la creación de objetos como las máscaras, la vestimenta son representaciones artísticas que expresan formas de vida con tus emociones, tradiciones, sensaciones y sentimientos hacia tu manera de concebir el mundo o cosmovisión, como en estos tres elementos que estados que se abordaron en la sesión de hoy.
El Reto de Hoy:
Intenta representar tu visón del mundo, utilizando materiales que tengas a la mano, eso que percibes alrededor, represéntalo con los elementos del arte, recuerda tus tradiciones, tu cultura, aquellos valores que has ido heredando de generación en generación.
Ahora bien, escucha atento de tu entorno por al menos 3 minutos, observa todo lo que te rodea detenidamente, mira con atención las formas, los colores, cierra los ojos, huele tu entorno, acaricia las texturas y dejate llevar por ellas. Se sabe que al estar en casa tu percepción del entorno puede cambiar, pero no por ello dejas de sensopercibirlo.
Desde donde te encuentres, trata de realizar una creación artística donde representes lo que sientes y percibes del entorno que te rodea. Hoy conocise tres ejemplos, puedes utilizar los materiales que te sean más fáciles de conseguir y con esos tres elementos plasma lo que quieras comunicar.
Toma en cuenta tu cosmovisión, es decir tu manera de comprender el mundo, la cual puede ser antes de la pandemia y durante ésta, recuerda que hay arte en todas partes y puedes usar los elementos de la naturaleza como piedras, hojas, tierra, así como hojas de colores, gises, estambres, su cabello o lo que se les ocurra.
También considera tus emociones actuales, preguntate ¿qué te hace sentir lo que ves y percibes? Tal vez quieras hablar del distanciamiento social o tal vez del color y la textura del sol o cómo se siente su calor.
Recuerda que puedes realizar cualquier obra artística para representar esas sensaciones y sentimientos con el uso de tu cuerpo, el movimiento, el sonido, el color, las formas o las texturas.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario