Aprende en Casa III SEP: 21 de enero TAREAS y ACTIVIDADES de 3° de secundaria
A continuación dejamos los temas vistos el 21 de enero de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 3° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Jueves 21 de enero, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Pocas letras que dicen mucho
Aprendizaje esperado: Verifica que la información que reporta sea completa y pertinente en relación con lo que se solicita.
Énfasis: Identificar abreviaturas comunes en formularios.
¿Qué vamos a aprender?
Las actividades que trabajarás están encaminadas a conocer qué son las abreviaturas, cómo se presentan en los textos, así como su función y características.
Es necesario que pongas atención, ya que para el reto que se te planteará más adelante deberás aplicar lo aprendido y reforzar tus conocimientos.
Antes de iniciar ten a la mano tu cuaderno de apuntes, un bolígrafo o lápiz y tu libro de texto.
No olvides que debes tomar notas y, en la medida de lo posible, registrar las dudas que se te presenten, anota la información que consideres clave, así como aquellos ejemplos que te ayuden a comprender mejor el contenido estudiado.
Lee con atención:
“Hace unos días fui al puesto de periódicos para comprar una revista de divulgación científica, ya que me gusta e interesa leer sobre ciencia y tecnología.
Revisé algunas que tenían de muestra y una en particular llamó mi atención, así que la compré y la llevé a casa.
Cuando me decidí a leerla, me encontré con un artículo que me pareció muy interesante y sinceramente me quedaron ganas de saber más acerca del tema.
Afortunadamente, al final venía una dirección electrónica de acceso a otros sitios electrónicos para que los lectores interesados, como yo, continuaran conociendo más y visitando otros sitios en internet con información relacionada.
Así que desde mi computadora ingresé a la página web y me encontré con una base de datos para generar un perfil de acceso, pero al dar clic me solicitaban algunos datos que por el tipo de escritura no lograba entender bien; así que me di a la tarea de investigar sobre aquellas formas que allí aparecían y adivinen qué fue lo que encontré. Nada más y nada menos que con abreviaturas situadas en un formulario.
Por lo anterior, es importante utilizarlas como ejemplo para que puedas entender y comprender lo que aprenderás en esta sesión.
¿Qué hacemos?
Inicia con la definición de que es una abreviatura. De acuerdo con el Diccionario de la Lengua Española, una abreviatura es una representación gráfica reducida de una palabra o de un grupo de palabras, obtenida mediante un procedimiento en el cual se suprimen letras finales o centrales y terminan generalmente con un punto.
En pocas palabras, puedes decir que una abreviatura es un conjunto de letras que representan a una palabra.
Para que quede un poco más claro, observa el ejemplo que se mencionaba anteriormente:
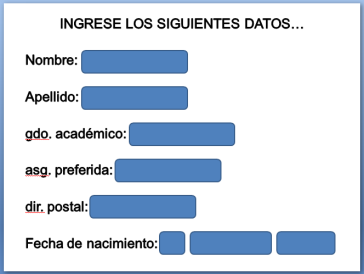
Cómo puedes observar en el ejemplo las abreviaturas son aquellas que suprimen a la palabra y esto se hace para no colocar la palabra completa y ahorrar un poco de espacio.
¿Pero qué significan esas abreviaturas?
Observa que:
-gdo. significa grado
-asg. significa asignatura
-dir. significa dirección
Y así como estas abreviaturas puedes encontrar muchas más dependiendo del texto o uso que les quieras dar.
Las palabras que se pueden abreviar, en muchos casos, pueden ser los nombres de las ciudades o estados de la República Mexicana, por ejemplo, en las aerolíneas y empresas dedicadas al turismo se usa la forma abreviada, para México, se usa MEX; para Guadalajara, GDL, para Chihuahua, CHIH; para Chiapas, CHIS, y así con varios estados más.
Las formas de tratamiento que se encuentran en ciertos formularios constituyen otro ejemplo clásico: por ejemplo sr., por señor; sra., para señora; dr., en vez de doctor; mtra, para maestra; ing., para ingeniera o ingeniero.
También pueden encontrarse: D.G, por diseñador gráfico; Arq. Arquitecto; QFB, químico farmacéutico biólogo; C.P., contador público.
Pero, una abreviatura es sólo una más de los tipos de abreviaciones que existen en el español, ya que existen muchas más.
Por ejemplo, tienes las siglas que también son de uso muy frecuente para ahorrar espacio, tiempo o simplemente para no ser repetitivos a la hora de escribir.
Como cuando dices, quiero ir a tramitar mi credencial para votar, así que voy a sacar una cita en el INE.
O cuando algún familiar te ve enfermo, te dice: “es importante que acudas al IMSS o al ISSSTE para que atiendan tu malestar”.
O también podría ser cuando dices que alguien estudió en la UNAM, en la UAM, la UAZ o la UAT y no mencionas su nombre completo, sino que dices sólo sus siglas.
Efectivamente, es por ello que debes tener claro qué es una abreviatura y una sigla, para que cuando te encuentres con ambas abreviaciones de palabras no las confundas, porque cada una tiene sus características.
Las siglas son abreviaciones de palabras formadas por la primera letra de las palabras a las que representa, no llevan punto y por lo general se escriben en mayúsculas y con ello se pueden diferenciar de una abreviatura.
Por ejemplo, has escuchado o visto en comerciales de televisión, en folletos o alguna otra propaganda algunos servicios sociales que ofrece el gobierno del país y que se refieren a ellos sólo con letras, por ejemplo:
IMSS
INE
SEP
CNDH
Entre otras, donde cada letra que se utiliza compone una palabra.

Cómo puedes ver, las letras que se utilizan como siglas para los servicios sociales están subrayadas.
FGR, que significa Fiscalía General de la República.
La letra “F” es de Fiscalía, la “G” de General y la “R” que significa República.
Lo mismo sucede con las siguientes como:
CJEF, que significa Consejería Jurídica del Ejecutivo Federal, y observas lo mismo que en la anterior, donde las siglas se crean tomando la primera letra de cada palabra.
Lo que también sucede con: SE, donde su significado es Secretaría de Economía.
Y, por último, SCT, que significa Secretaría de Comunicaciones y Transportes.
Un aspecto muy importante es que no todas coinciden de manera lineal, es decir, no es una generalidad que cada letra corresponda a una palabra y en otros casos las siglas de ciertos organismos internacionales, por lo que generalmente se hace la aclaración.
Otro punto a considerar es que las siglas no utilizan punto al final de cada una y en las abreviaturas, sí. Esta es una diferencia que hay entre ambas.
Ahora bien, ya observaste la diferencia entre las abreviaturas y las siglas.
Con los ejemplos que analizaste, puedes ver que son muy distintas y además que se utilizan con diferente propósito.
Una abreviatura se utiliza como una forma de resumir una palabra, evitando muchas veces tener que escribir de más, ahorrándonos tiempo y así generar una mejor fluidez. Esta es parte de su importancia.
Lo mismo sucede por cuestiones de espacio: es decir, en los formularios, particularmente aquellos que requieren mucha información, encontrarás múltiples palabras abreviadas para dar más espacio a las respuestas. Considera que los formularios largos gastan papel, si son impresos, o espacio de almacenamiento virtual, si son digitales, por lo que es importante ahorrar espacio.
Observa el siguiente ejemplo:

Se observan desde el principio siglas y abreviaturas.
En la parte de arriba verás ID, que remite a identificación, mientras que el NIP es el Número de Identificación Personal.
Y la parte de datos personales está llena de abreviaturas.
Este formato tiene dos páginas, pero sólo se muestra una parte de la primera página. Como te imaginarás, es importante ahorrar espacio. Además, las abreviaturas permiten ordenar y categorizar la información en rubros que faciliten su llenado y la sistematización de los datos que hace a partir de ella.
Puedes darte cuenta en la parte de la dirección que en una misma línea están las abreviaturas Col., para colonia; Mun., para municipio y C. P., para código postal.
Todos esos datos son parte de la dirección y se puede ver rápidamente, lo cual evita que olvides alguno. Si estuvieran en líneas separadas sería más fácil que se te olvidara llenarlo.
Y para las personas que capturan esta información en una base de datos pueden detectar fácilmente si hay omisiones o errores; o bien, si el formato está bien llenado.
En este formulario aparecen otras abreviaturas que no son tan habituales, pero que puedes entender por contexto, como la A. para abreviar apellido.
Se pueden inventar abreviaturas con la condición de que sean claras y que no se confundan con otras. Aunque ya conocerás que hay algunas que pueden ser ambiguas.
Puedes observar “No., Ext., e Int.”. Seguramente sabes que significan número exterior e interior, pero puede causar confusión, ¿qué pasa si tu casa no tiene número interior? Ya que ahí dice “Int.”.
En esos casos, sólo se anota el número exterior. El número interior es para las personas que viven en edificios de departamentos, condominios horizontales, privadas y semejantes. Y recuerda que si donde vives no tiene número oficial asignado, se anota la abreviatura S/N: sin número, aun cuando el formato te pide que no abrevies.
En las abreviaturas: DD, MM y las cuatro A en la fecha de nacimiento, están duplicando la D y la M para indicar que escribas el día y el mes a dos posiciones; es decir, si naciste el 5 de julio, escribirás 05/07 y no 5/7. Por su parte, el año lo escribirás a cuatro dígitos.
Analiza detenidamente el caso de las siglas. Como ya se mencionó, se utilizan para referirse de una forma abreviada a los organismos, las instituciones, las empresas, los objetos, los sistemas o algunas asociaciones, etcétera
Observa el siguiente ejemplo:

Puedes observar que es una lista de instituciones o empresas que se encuentran en nuestro país, tienen diferentes funciones, pero siguen las mismas normas para convertir esos nombres largos en siglas.
Analiza ahora algunos ejemplos de abreviaturas y de siglas para identificar sus usos y diferencias de manera gráfica.
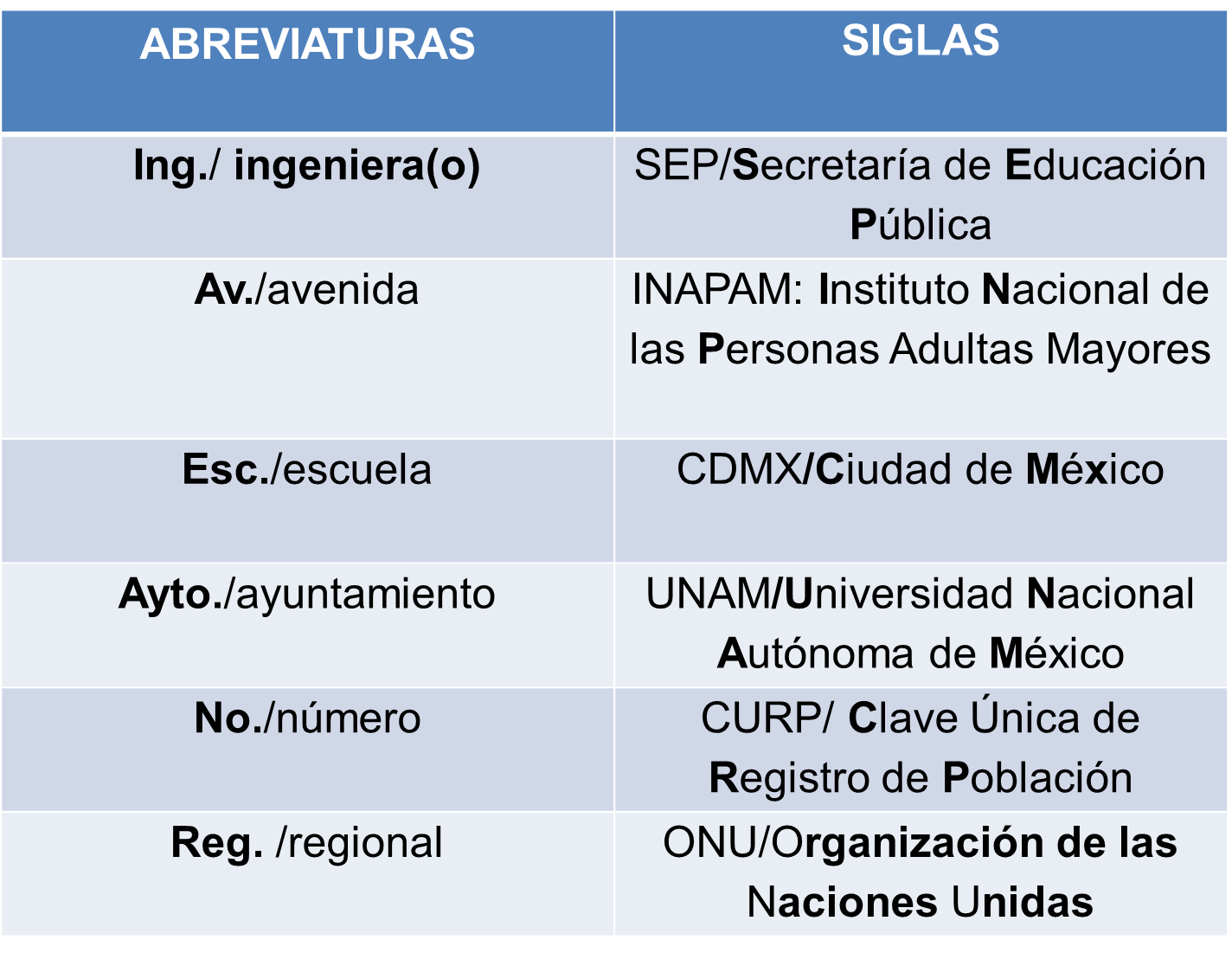
En la columna izquierda puedes notar las que son abreviaturas y, utilizan más de una letra para así formar la reducción de la palabra, también observas que manejan un punto final.
En la columna derecha están las siglas que, a diferencia de las abreviaturas sólo se utilizan las primeras letras de cada palabra, tal como lo notan las letras tomadas para elaborar la sigla de color diferente a las demás.
Profundiza en las abreviaturas. ¿Sabías que es difícil llevar un conteo de cuántas abreviaturas existen, porque cada vez se agregan más y más en nuestra lengua?
El Diccionario de la Lengua Española consigna aproximadamente 300 abreviaturas.
Otro punto importante sobre las abreviaturas tiene que ver con las convenciones que existen para usarlas de forma adecuada.
Trabaja con los siguientes ejemplos y con la norma que se mencionará para cada abreviatura:
1.- Deben finalizar en punto:

2.- Llevan tilde si conservan la vocal que tenía tilde en la palabra de origen.

3.- Se usan mayúsculas si se refieren a tratamientos de personas, o al comienzo de escritura, o después de punto, o cuando la palabra a la que se refiere empieza por mayúscula (nombre propio), o algunas abreviaturas especiales.

4.- Para formar el plural, se les añade la letra “s” al final, salvo si la abreviatura tiene sólo la primera letra de la palabra. En tal caso, se duplica dicha letra.

Si prestas atención a estas normas, será más sencillo identificar una abreviatura en cualquier texto que leas.
Revisa algunas de ellas, que puedes encontrar en los formularios, por ejemplo, cada ciclo escolar: al momento de inscribirte te piden como requisito llenar una solicitud de reinscripción y en ella aparecen varias abreviaturas y siglas, algunas de ellas son:
Fec. Nac., que significa: Fecha de Nacimiento.
Otro caso es cuando te piden especificar tu sexo, ya sea con una “M” de masculino o una “F” de femenino.
O cuando piden tu número de teléfono o celular y se abrevia Núm. tel. / Núm. cel.
Otra abreviatura sería la de tu dirección, que la encuentras como “Dir.”.
Hasta aquí has aprendido el concepto de abreviatura, sus características, su función y las diferencias que tienen con las siglas.
Ahora realizarás un breve juego, para saber cuántos significados conoces con sólo ver algunas abreviaturas.
Observa las abreviaturas, y di cuál es la palabra a la que se refiere.
Te sugerimos que escribas en tu cuaderno de apuntes las abreviaturas y su significado.
La abreviatura “gral.”.
La respuesta es general.
Correcto. La verás en instituciones como Hosp. Gral., es decir Hospital General.
La abreviatura que sigue es “sig.”.
Su significado es “siguiente”.
Muy frecuente en los formularios de varias páginas.
Tercer ejercicio y tienes las abreviaturas “Dr.” y “Dra.”.
Es doctor y doctora.
Cuarta y última abreviatura “cap.”.
¿Cuál crees que sea su significado?
Podría decir que es capitán o capítulo.
Esta es una abreviatura que se comparte con el grado de un militar que es “capitán” y ambas respuestas pueden ser válidas, sin embargo, cuando forma parte de un documento, el contexto es el que te dará la respuesta, es decir, si se refiere a un significado o al otro.
Lo más probable es que un formulario remita a Capitán, por lo que la verás escrita en mayúscula, como Cap.
Por último, que es “admón”.
Su significado es “administración”.
Continua entonces, para hacer uso de las abreviaturas basta sólo con conocerlas y saber su significado, si en algún momento te encuentras con algunas que desconozcas será necesario recurrir y hacer uso de un diccionario impreso o digital.
Has aprendido qué es una abreviatura, que las puedes encontrar en casi cualquier texto, sobre todo en formularios o solicitudes para ahorrar espacio, también conociste las normas que deben tener.
También aprendiste que no sólo existen las abreviaturas, como técnica de abreviación, sino que también existen las siglas y aunque sirven para lo mismo se especializan en otros organismos.
Para ampliar la información sobre esta sesión, consulta en tu libro de texto el aprendizaje esperado: “verifica que la información que reporta sea completa y pertinente en relación con lo que se solicita.”, y recuerda realizar las actividades que se sugieren en tu libro de texto para reafirmar tus conocimientos.
También puedes exponer tus dudas a tus maestras y maestros en su momento.
El Reto de Hoy:
Revisa diferentes formularios que tengas en casa, después identifica las abreviaturas que contengan y busca su significado si es que no lo sabes, ya sea en el diccionario o en algún medio digital. Realiza un ejercicio en familia, algo así como el juego de “Basta”. Escribe una lista de abreviaturas y pide a algún familiar que te escriba el significado y acuerda un tiempo específico para que respondan.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Leyes de cancelación
Aprendizaje esperado: Resuelve problemas que implican el uso de ecuaciones de segundo grado.
Énfasis: Usar las leyes de cancelación al resolver ecuaciones.
¿Qué vamos a aprender?
Analizarás las leyes de cancelación en términos aritméticos y algebraicos.
Los materiales que vas a utilizar es tu cuaderno de apuntes, bolígrafo, lápiz y goma.
En Matemáticas, al simplificar expresiones numéricas o algebraicas, se usan leyes y propiedades que aplican a ciertas operaciones.
Al resolver algunos problemas, posiblemente has aplicado estas leyes sin darte cuenta. Cada una de ellas tiene su nombre y propiedades.
- Las propiedades del elemento neutro,
- Las leyes asociativas, conmutativas, y
- Las leyes de cancelación.
La propiedad del elemento neutro se aplica para la suma y resta, así como para la multiplicación y división.
¿Son diferentes para cada operación?
No propiamente, el elemento neutro de una operación es el número que, operado con cualquier otro número, no altera al número original, es decir, en el caso de la suma o resta, el número cero es el que no cambia el resultado al realizar la operación.
¿Qué hacemos?
Observa algunos casos numéricos y algebraicos para que quede clara la propiedad.
Por ejemplo:

En el caso de la multiplicación y la división, no se puede considerar al cero como elemento neutro, ya que, si partes del mismo principio que debe ser un número que no altere o modifique al original al momento de realizar la operación de multiplicación o división, este número ahora debe ser el uno.
Entonces, todo número o término multiplicado o dividido por uno permanece igual. Observa los siguientes ejemplos:
Si se multiplica: 459.58 por 1, el resultado es 459.58.
Tres décimos por 1, son tres décimos.
Si se divide 459.1 entre 1, el resultado es 459.1
Tres décimos entre 1, se obtiene tres décimos
5x^2 entre 1 es igual a 5x^2
Entonces existen dos elementos neutros, uno aditivo para la suma y resta, que es cero, y otro multiplicativo para la multiplicación y división, que es uno.
Continua con las leyes asociativa y conmutativa.
Pero ¿qué diferencia hay entre las leyes asociativa y conmutativa?
Se diferencian una de la otra en que la ley asociativa permite agrupar o asociar los sumandos o factores y se obtiene el mismo resultado y, en el caso de la ley conmutativa, se intercambian de lugar los sumandos o factores sin cambiar el resultado.
La ley asociativa se aplica en la suma o multiplicación, al agrupar o reagrupar los números, ya sean sumandos o factores, con paréntesis, por ejemplo:

Si se agrupan (12 + 56) + 44, es igual a sumar 68 + 44 con resultado 112.
Al cambiar la agrupación, se tiene 12 + (56 + 44), el resultado es 12 + 100, es decir, 112.
En el caso de la multiplicación, 4 por 10 por 5, se agrupan en 4 por 10 por 5, se tiene 40 por 5 y el resultado es 200.
Otra forma de agrupar es multiplicar 4 por la agrupación (10 por 5), que es igual a 4 por 50 y el resultado es igual a 200.
Es decir, los números se pueden agrupar o reagrupar, así como las personas pueden asociarse con otras personas en grupos diferentes.
Es importante resaltar que para la resta y división no se puede aplicar la ley asociativa, en estas operaciones sí importa cómo se agrupen las cantidades al realizar la operación.
La ley conmutativa sólo se puede aplicar en la suma y la multiplicación. Se cambia el orden de los sumandos o en la multiplicación los factores, ambos con el mismo resultado. Por ejemplo:
Si se divide 15 entre 3, su resultado es 5. Si se divide 3 entre 15, el resultado es 1/5.
Se muestran los siguientes ejemplos:
1. Se quiere sumar 28.48 + 100.12, el resultado es: 128.60. La ley conmutativa permite expresar la suma como 100.12 + 28.48 con el mismo resultado 128.60

2. Al multiplicar tres quintos por dos séptimos, el producto es seis treintaicincoavos. Se aplica la ley conmutativa al cambiar el orden de los factores: dos séptimos por tres quintos, cuyo resultado no se altera y es seis treintaicincoavos.

3. Con tres o más factores ocurre exactamente igual, por ejemplo: se multiplica 4x^2 por 10x^3 por 11x.
Al multiplicar 4x^2 por 11x y, el resultado 44x^3 se multiplica por 10x^3, dando 440x^6.
O bien, se multiplica 10x^3 por 11x y, el resultado 110x^4 se multiplica por 4x^2, se obtiene 440x^6.

Al aplicar la ley conmutativa y cambiar el orden de los sumandos y/o factores, no se altera la suma y/o producto. Lo cual facilita resolver las operaciones. No es posible aplicar esta ley en la resta o división, pues, al invertir el orden de las operaciones, cambia el resultado.
Un ejemplo de la ley conmutativa en la vida diaria es: invertir el orden de los pies al colocar los calcetines, es decir, no importa si primero se coloca el derecho o primero el izquierdo.
Pero si se intercambia el colocar primero los zapatos y luego los calcetines, en ese caso es importante el orden.
Ahora, analiza la ley de cancelación, primero para la suma y resta.
En una expresión numérica o algebraica se encuentra el mismo número o término realizando la misma operación de suma o resta en ambos lados de la igualdad, entonces se puede cancelar.
Para que esta ley de cancelación quede más clara, se muestran algunos ejemplos:
Los valores numéricos se representan con literales:

“a” más “x” es igual a “b” más “x”.
El término “x” está en ambos lados de la igualdad, aplicando la misma operación de suma.
Entonces, se cancela el término “x” en ambos lados de la igualdad y el resultado es “a” igual a “b”.
En el caso de la resta, es igual.
“a” menos “x” igual a “b” menos “x”, se cancela el término “x” en ambos lados de la igualdad, el resultado es “a” igual a “b”.
Esta ley de cancelación ayuda a simplificar procedimientos. Observa los dos casos.
Se tiene la siguiente igualdad:
(15 por 2) + 9 = 18 +12 + 9

En ambos miembros de la igualdad, el número 9 está sumando, se aplica la ley de cancelación para eliminar el número 9, se obtiene 15 por 2 = 18 + 12.
Las operaciones de cada miembro, 15 por 2 es 30 y 18 más 12 es 30.
30 igual a 30. Se mantiene la igualdad.
¿Ocurre lo mismo si son términos algebraicos? Para responder se analiza la siguiente igualdad.
10n + 14n – 35m + 8 = 4 por 2 – 35m + 24n

Se observa que en ambos miembros de la igualdad se resta 35m. Se aplica la ley de cancelación y se elimina 35m en ambos términos, el resultado es: 10n + 14n + 8 = 4 por 2 + 24n
Se opera en ambos miembros:
En el primer miembro se suman 10n + 14n, por ser términos semejantes, se obtiene 24n y el número 8 se escribe igual.
En el segundo miembro se realiza el producto de 4 por 2, se obtiene 8 y se repite 24n.
Al final, se tiene: 24n + 8 = 8 + 24n.
En el resultado anterior se observa que no está escrito de la misma forma en la igualdad, se aplica la ley conmutativa y representan lo mismo.
En la siguiente ecuación lineal se puede observar lo útil que es la ley de cancelación.
“x” más 2 por “x” menos 5 igual a, 2x menos 10 más 4

Al operar, se escribe la “x” más el resultado de multiplicar 2 por “x” menos 5.
Dos por “x” es 2x, dos por 5 negativo es 10 negativo. En el segundo miembro, se escribe igual 2x menos 10 más 4.
No se agrupan los términos porque se repiten en ambos miembros de la igualdad.
Se aplica la ley de cancelación para eliminar de ambos lados de la igualdad los términos “2x menos 10”, el resultado es “x” igual a 4. Este resultado es la solución de la ecuación.
Una ecuación que aparentemente se observa larga y compleja, se puede resolver de una forma rápida al aplicar la ley de cancelación.
Falta la ley de cancelación para multiplicación y división. ¿Cómo se puede aplicar?
En este caso, para aplicar la ley de cancelación en la multiplicación, se puede eliminar un número o término que esté multiplicando en ambos lados de la igualdad y que se trate del mismo número o término.
Este número o término se debe considerar que sea diferente de cero para poder aplicar la cancelación.
El siguiente ejemplo precisa esta condición.
Se tiene la siguiente igualdad:

“a” por “x” es igual a “b por “x”. El término “x” al multiplicar en ambos lados de la igualdad, se cancela siempre y cuando “x” sea diferente de cero.
El resultado es “a” igual a “b”.
Para aclarar esta situación, se presenta un ejemplo numérico.
En la igualdad, 20 por 7 es igual a 2 por 2 por 5 por 7, en ambos lados está multiplicando el 7 positivo, se aplica la ley y se cancela, el resultado es 20 es igual a 2 por 2 por 5, al realizar las operaciones se obtiene 20 es igual a 20. Se mantiene la igualdad.

En la igualdad 40 por 0 es igual a 2 por 5 por 0, el resultado es cero en ambos lados. Porque 40 por cero es cero, e igual a dos por cinco por cero igual a cero.
Si se aplica la ley de cancelación al número 0, se altera la igualdad porque 40 no es igual a dos por cinco y el resultado es 40 es desigual a 10.
Al no cumplirse la igualdad, es la razón por la cual no es posible eliminar el cero cuando está multiplicando en ambos lados de la igualdad.
Esta consideración sólo es para el cero en el caso de la multiplicación, pero ¿qué ocurre con la división?
En el caso de la división, cuando en una igualdad ambos lados son divididos por la misma cantidad, se puede eliminar de ambos lados.
Se debe cuidar que el divisor afecte a todo el miembro de la igualdad. Se muestra un ejemplo:
“a” entre “x” igual a “b” entre “x”, tiene el mismo divisor, es “x”, que afecta a todo el miembro en ambos lados. Se elimina la “x”.

Para poder eliminar la “x”, debe ser diferente de cero. En caso contrario, genera una indefinición, es decir, el resultado es “a” igual a “b”.
En la ley de cancelación, tanto para la multiplicación como para la división, el número o término por eliminar no debe ser cero.
Observa un ejemplo numérico para la división, se tienen las siguientes igualdades.
La igualdad 15 más 10 entre 5 es igual a 5^2 entre 5. El resultado en ambos lados es 25.

El 5 como divisor en ambos lados, permite aplicar la ley de cancelación: en el primer miembro quedan 15 + 10 y en el segundo miembro 5 al cuadrado.
Al realizar operaciones 25 es igual a 25. La igualdad se mantiene.
Otro caso es 24 entre 2 es igual a 5 por 4 entre 2 más 2, en ambos lados, el resultado es 12.
La diferencia con la igualdad anterior es que el divisor 2 no afecta a todo el miembro de la igualdad, si se aplica la ley de cancelación para eliminar el divisor 2, el resultado es:
24 es igual a 5 por 4 más 2. Al realizar operaciones, se obtiene 24 es igual a 20 más 2, es decir, 24 es desigual a 22.
En este último ejemplo, no se cumple la ley de cancelación y se altera la igualdad porque el divisor no afecta a todo el lado de la igualdad.
En situaciones algebraicas, es posible aplicar esta ley de cancelación
Realiza el siguiente ejercicio en donde se aplique lo analizado en una ecuación lineal.
Inicia con una ecuación lineal.
5 multiplica a 2x más 3 más 4x, que es igual a 10 x más 39.

Se realiza la multiplicación para eliminar paréntesis, se obtiene 10x más 15 más 4x igual a 10x más 39.
Se aplica la ley de cancelación con 10x en ambos lados de la igualdad, se tiene 15 más 4x es igual a 39.
Se resta 15 en ambos miembros de la igualdad para eliminarlo del primer miembro, se tiene 4x es igual a 39 menos 15.
Por último, se divide entre 4 ambos lados de la igualdad, se elimina el 4 del primer miembro, se obtiene “x” es igual a 24 entre 4, el valor de “x” es igual a 6.
La ley de cancelación se aplica en diversos problemas.
Ahora realiza otro ejercicio:
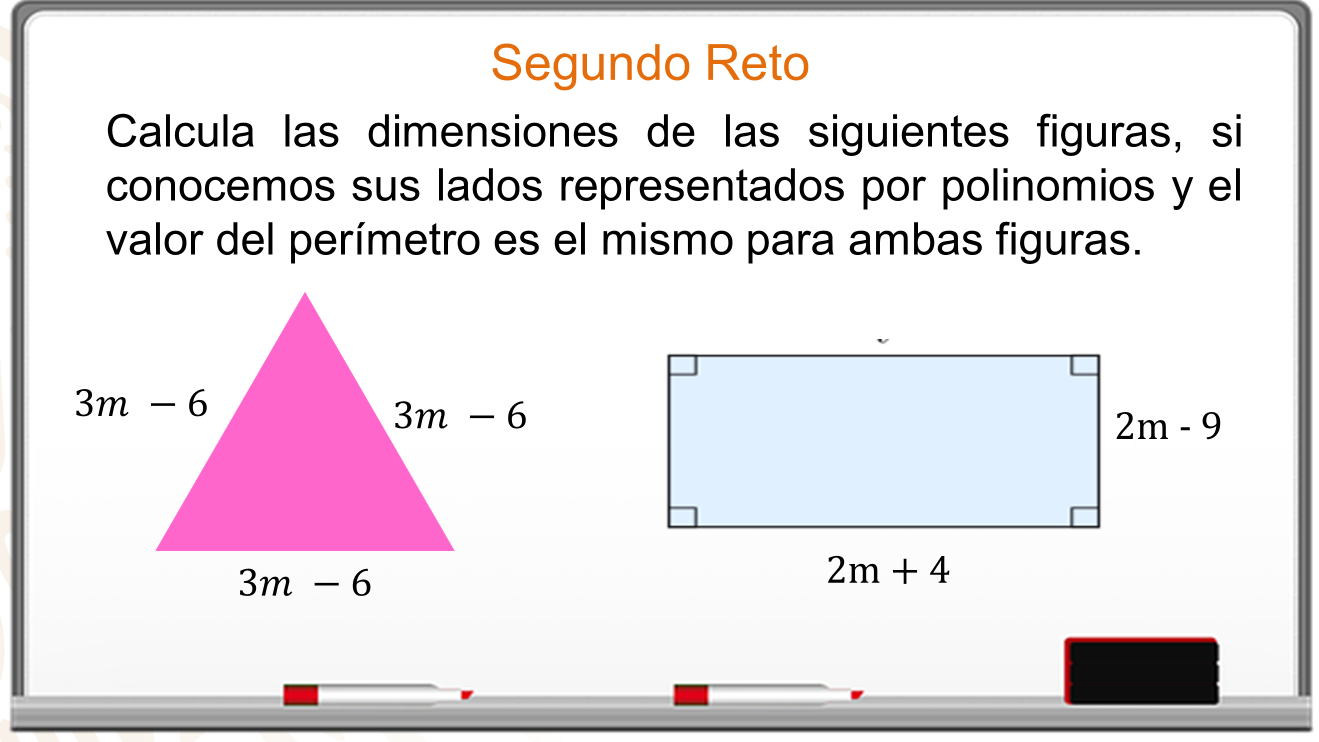
El perímetro es la suma de todos sus lados y en ambas figuras es el mismo, entonces, se igualan las expresiones.
El perímetro del triángulo es 3 por 3m menos 6, que es igual al perímetro del rectángulo, 2 por 2 m más 4, más 2 por 2 m menos 9.
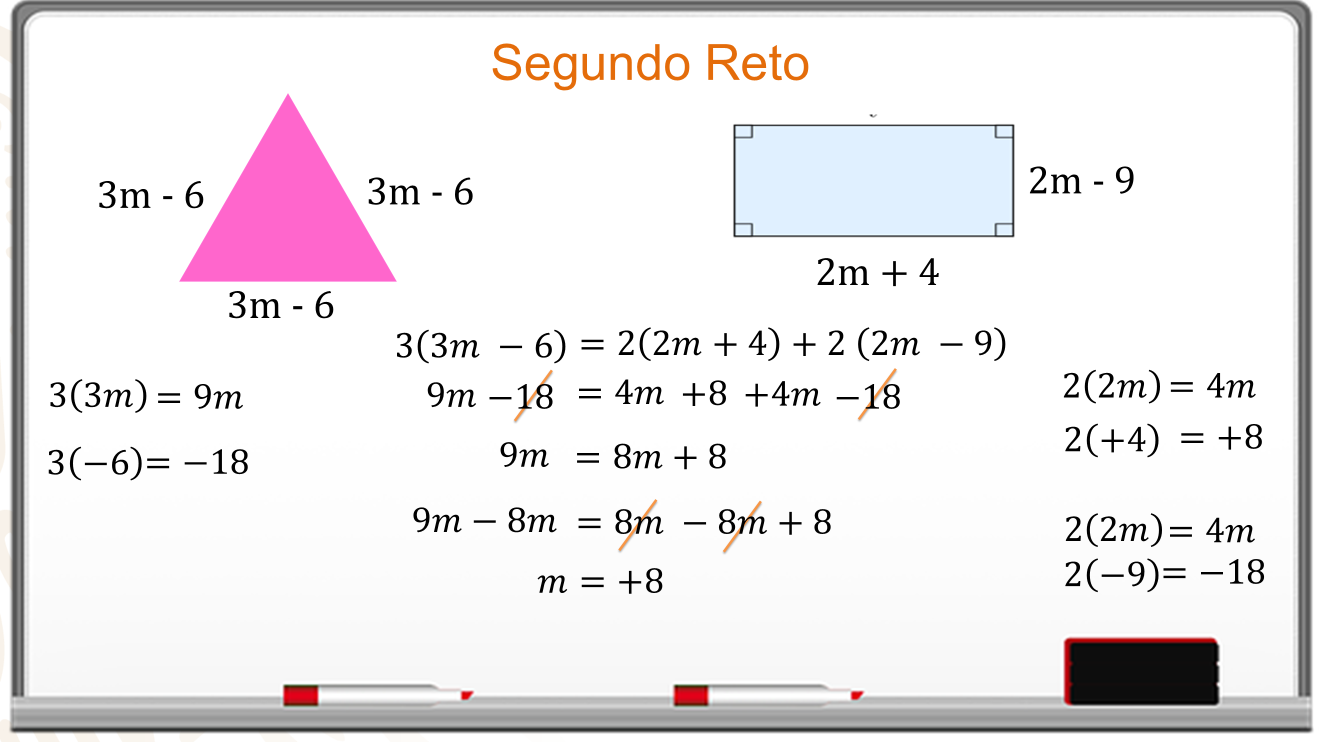
Se realizan los productos y queda:
9 m menos 18 es igual a 4 m más 8, más 4 m menos 18.
Se reducen términos semejantes y se aplica la ley de cancelación para eliminar el 18 de ambos lados, el resultado es: 9 m es igual a 8m más 8.
En ambos lados de la igualdad se resta 8m.
En el primer miembro se reducen los términos semejantes. En el segundo término se cancelan los términos 8 m.
El valor de “m” es 8.
Pero, no se ha resuelto el problema con el cálculo anterior, porque se solicitan las dimensiones de las figuras.
Sólo se sustituye el valor de “m” en las expresiones proporcionadas como medida de los lados de cada figura.
El lado del triángulo es 3 m menos 6, se sustituye el valor de “m”.
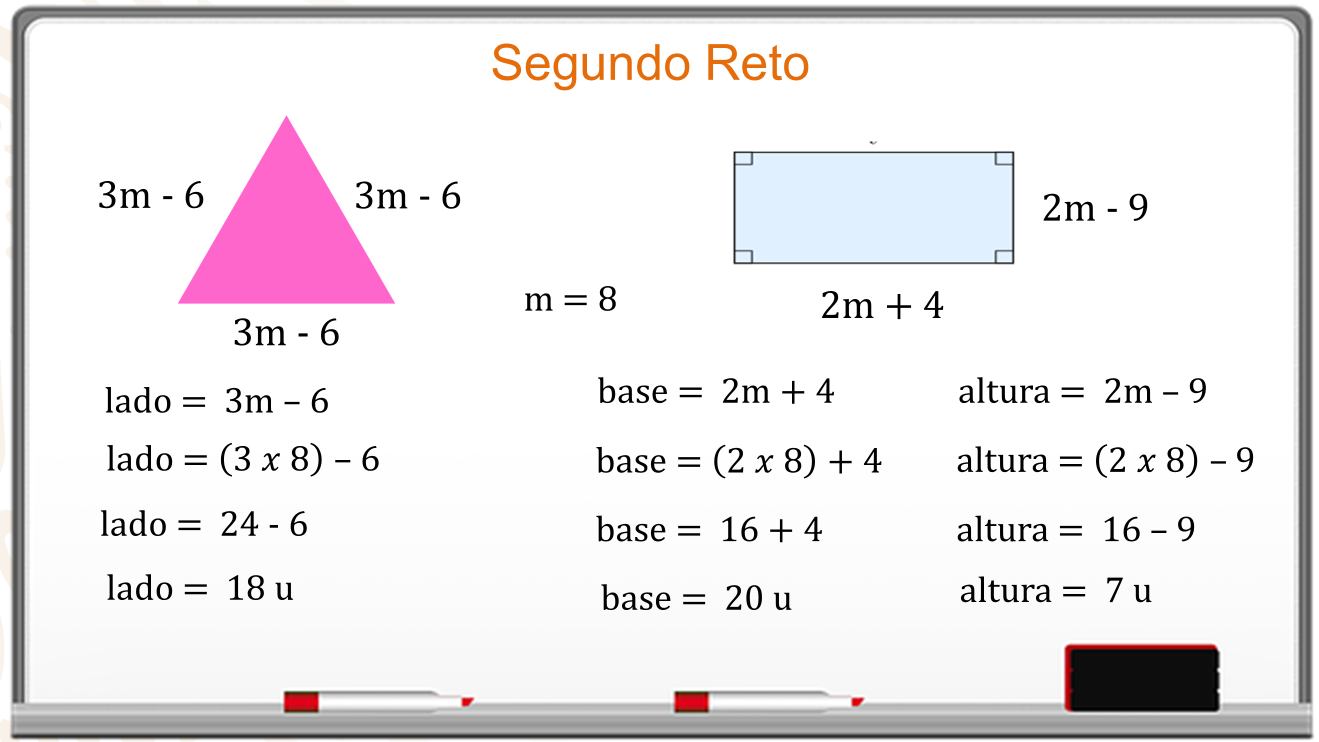
La operación es 3 por 8 menos 6 igual a 24 menos 6 y la medida del lado es de 18 unidades.
El rectángulo tiene como base igual a 2 m más 4, se sustituye el valor es de “m”, es 2 por 8 más 4, igual a 16 más 4. La medida de la base es 20 unidades.
La altura del rectángulo es 2 m menos 9, se sustituye 2 por 8 menos 9, igual a 16 menos 9. La medida de la altura es 7 unidades.
Por último, se comprueba que las dos figuras tienen el mismo perímetro.
Para calcular el perímetro del triángulo se multiplica 3 por la medida del lado que es 18. El perímetro es de 54 unidades.
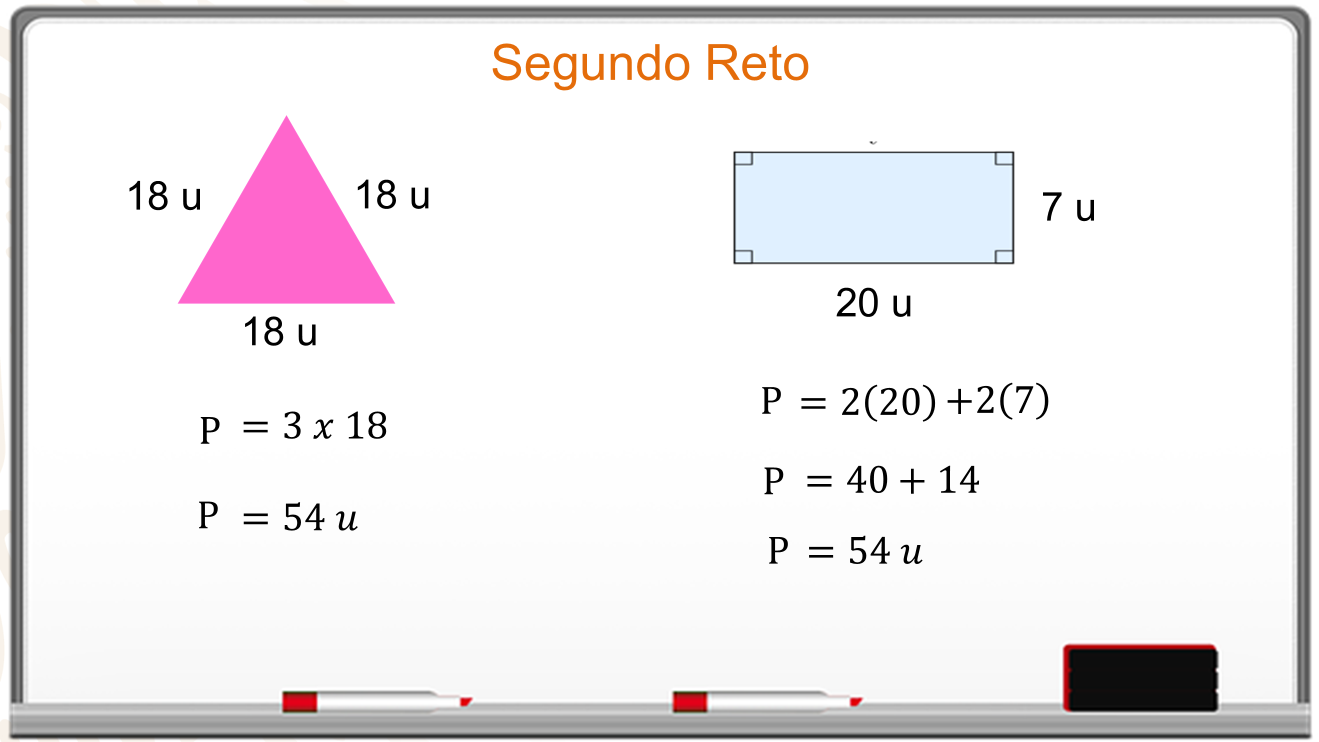
En el caso del rectángulo, su perímetro se obtiene al multiplicar 2 por 20 más 2 por 7. Se hacen las operaciones, 40 más 14 y el perímetro del rectángulo es igual a 54.
Los dos perímetros son iguales.
Las propiedades y leyes facilitan los procedimientos numéricos y algebraicos.
En la ley de cancelación, para todas las operaciones, se deben de considerar dos aspectos:
Para eliminar un número o término, debe de estar en lados contrarios de la igualdad y realizar la misma operación.
Para eliminar un número o término en el mismo lado de la igualdad, la operación del número o término debe de ser inversa para poderla eliminar.
Una reflexión del matemático alemán George Cantor dice: “La esencia de las matemáticas está en su libertad”, en casa, al resolver los problemas y ejercicios aprovecha esa libertad de las matemáticas en tus procedimientos.
El Reto de Hoy:
Para saber más del tema, busca en tu libro de texto todo lo relacionado y resuelve los ejercicios que ahí se proponen.
Así, podrás enriquecer tu conocimiento y tomar notas en tu cuaderno.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Desigualdad y marginación en el mundo
Aprendizaje esperado: Formula compromisos ante desafíos derivados de su pertenencia a la humanidad.
Énfasis: Reconocer los diferentes problemas que enfrentan las personas, ocasionados por la desigualdad y la marginación.
¿Qué vamos aprender?
Reconocerás los diferentes problemas que enfrentan las personas y grupos sociales originados por la desigualdad y la marginación.
Necesitarás tu cuaderno de notas, hojas de colores, lápiz o pluma.
Como habrás escuchado en noticieros, leído en periódicos o noticias de Internet, la desigualdad en el mundo es un problema que afecta a muchas personas. Puedes imaginar que entre los problemas que se enfrentan están el hambre y la mala alimentación, la falta de servicios, las carencias educativas, entre otros. Pero, ¿qué otros problemas son motivados por la desigualdad?
Observarás que hay diferentes problemas motivados por la desigualdad. La desigualdad socioeconómica, por ejemplo, refiere a los contrastes que se presentan entre un grupo minoritario de personas que concentran la mayor parte de la riqueza, respecto a las personas que viven en situación de pobreza y no logran cubrir sus necesidades más elementales.
¿Qué hacemos?
Es importante recordar que existe un marco legal internacional y nacional que garantiza que las personas puedan tener acceso al ejercicio a los derechos humanos.
Has estudiado, en sesiones previas, que la Declaración Universal de los Derechos Humanos, en su artículo primero, reconoce la igualdad de las personas.
Este documento también señala, en su artículo 25°, que: “Toda persona tiene derecho a un nivel de vida adecuado que le asegure, así como a su familia, la salud y el bienestar, y en especial la alimentación, el vestido, la vivienda, la asistencia médica y los servicios sociales necesarios”. Condiciones que el Estado debe proporcionar a su población, mediante políticas, programas e Instituciones.
Cómo has estudiado también, en el artículo primero de la Constitución Política de los Estados Unidos Mexicanos se prohíbe toda discriminación motivada por origen étnico o nacional, género, edad, discapacidades, condición social, condiciones de salud, religión, opiniones, preferencias sexuales, estado civil o cualquiera otra que atente contra la dignidad humana y tenga por objeto anular o menoscabar los derechos y libertades de las personas.
Para consolidar este derecho, en el artículo 4° se menciona que:
“…los niños y las niñas tienen derecho a la satisfacción de sus necesidades de alimentación, salud, educación y sano esparcimiento para su desarrollo integral.”
Corresponde a los padres satisfacer dichas necesidades y al Estado brindar oportunidades para un trabajo digno y bien remunerado que permita ganar lo suficiente para contar con los recursos económicos adecuados.
Estos artículos contribuyen a garantizar el derecho a la igualdad que implica, entre otras cosas, generar políticas públicas para cubrir las necesidades básicas, acordes al contexto histórico y cultural de cada sociedad.
Todas y todos tenemos necesidades básicas que se deben satisfacer para poder vivir y desarrollarse plenamente. La satisfacción de necesidades se relaciona de manera directa con las condiciones y recursos que se tienen para cubrirlas, tanto de manera personal como a través de las políticas e Instituciones que el Estado designe para coadyuvar en el bienestar de su población.
¿Pero si todas y todos tenemos derecho a la alimentación, vestido, vivienda, salud, educación, sano esparcimiento y servicios sociales, por qué observas a tantas personas, en diferentes partes del mundo, de todas las edades, que no pueden satisfacer esas necesidades?
Porque la satisfacción de necesidades de la población depende de la política pública que impulse el Estado, de la generación de empleos, el desarrollo económico y la distribución equitativa de la riqueza. Las condiciones sociales y la satisfacción de las necesidades básicas, así como el entorno de seguridad que cada país les brinda a sus habitantes es responsabilidad del Estado.
El programa de Naciones Unidas para el Desarrollo estableció el Índice de Desarrollo Humano, IDH, un indicador que mide el nivel de desarrollo de cada país, que permite saber las condiciones de vida que se tienen en cada Nación.
Observa el siguiente video del inicio al minuto 3:11, para saber qué es el Índice de Desarrollo Humano y cómo se mide.
- Desigualdad mundial
https://www.youtube.com/watch?v=CcO9kHHrABw
Puedes rescatar que el IDH considera la esperanza de vida, escolaridad promedio y el producto interno bruto per cápita, es decir, por persona. Aunque debes destacar también que son datos de 2016, cuando consulten información recuerda preguntarse si es la más actualizada.
En el Informe sobre Desarrollo Humano 2019, Australia, por ejemplo, está en el lugar 6° del ranking mundial, Uruguay en el lugar 57 y México en el lugar 76.
Pero, si México está en el lugar 76 de 188 y se coloca en un nivel de desarrollo alto ¿por qué se parece más a los países que muestran un índice de desarrollo bajo?
Hay algunos puntos que es necesario aclarar. El Índice de Desarrollo Humano se obtiene del promedio estadístico de diferentes datos; por ejemplo, el promedio de vida en nuestro país es de 75.1 años, eso no quiere decir que todas o todos vivan 75 años.
Recuerda que el promedio se obtiene sumando las edades de toda la población y dividiéndola entre el número total de personas consideradas para ese dato. Por lo que algunas personas viven 2 años, otras 30, 70, 80 o 95. Lo mismo sucede con los ingresos y años de estudio.
Esto quiere decir, que no todos tienen un índice de desarrollo medio alto, y México es un país de grandes contrastes, por ejemplo:
De acuerdo con datos de CONEVAL, hacia 2015 uno de los municipios más pobres de nuestro país era Santos Reyes Yucuná, Oaxaca. El 44.20% de la población tenía rezago educativo. El 62.1% tenía carencia de acceso a servicios de salud.
Por su parte, entre los municipios con mayor Índice de Desarrollo Humano de nuestro país, está San Pedro Garza García, Nuevo León. En el municipio habitan personas con altos ingresos, puedes encontrar casas muy grandes, centros comerciales de lujo y un nivel de vida parecido al de países europeos.
A través del Informe sobre Desarrollo Humano 2019, puedes notar que existen condiciones favorables y desfavorables al desarrollo humano de las personas, uno de los problemas que dificultan avanzar hacia mejores niveles de desarrollo es la pobreza que, no sólo afecta a la economía de los países, sino, sobre todo, afecta el bienestar y la calidad de vida de las personas, porque se les dificulta cubrir sus necesidades básicas y no les permite alcanzar niveles de bienestar que fortalezcan la dignidad humana.
Cómo puedes notar, en el ámbito nacional, en algunas regiones y entidades del país, existen desequilibrios y desigualdades que afectan la dignidad de las personas y su calidad de vida.
Seguramente recordarás que en historia aprendiste que, desde la época de la conquista y la colonia en nuestro país, hay una gran desigualdad social porque la riqueza y las propiedades están concentradas en una pequeña parte de la población. Además, desde entonces, un sector de la población ha vivido discriminación por su color de piel, origen, grupo étnico, lengua, costumbres o tradiciones, lo que ha venido generando un desarrollo desigual en estos sectores de la población. En la actualidad, uno de los principales problemas que se generan por la desigualdad social es la pobreza.
Pero hay diferentes formas de pobreza. Hay personas que no tienen ingresos suficientes para satisfacer sus necesidades alimentarias, esto se conoce como pobreza extrema. Otras personas pueden satisfacer sus necesidades de alimentación, pero no cuentan con educación o servicios de salud, a esto se le conoce como pobreza de capacidades. Una forma más de la pobreza es aquella en que las personas no cuentan con el ingreso suficiente para satisfacer las necesidades de vivienda, vestido y transporte. A esto se conoce como pobreza patrimonial.
La satisfacción de necesidades básicas, además de asegurar la vida de los individuos, permite, en la medida en que estas se cumplan, cierto grado de bienestar que le garantiza a la población gozar de los derechos humanos y un desarrollo pleno. La desigualdad social genera pobreza, marginación y migración.
La pobreza limita las oportunidades de vivir mejor y, por lo tanto, de tener una vida digna, porque no permite el bienestar de las personas al no cumplirse con:
- Alimentación óptima
- Un medio ambiente sano y libre de contaminación
- Una vivienda adecuada, salubre y que brinde resguardo adecuado
- Servicios que favorezcan una higiene personal y la prevención de enfermedades
- Lugares para un sano esparcimiento, descansar y divertirse
- Un trabajo digno y bien remunerado
La desigualdad social propicia la marginación al discriminar o excluir a las personas por su color de piel, tradiciones culturales, formas de vida, pertenencia a un grupo étnico, situación económica, preferencia sexual, creencias religiosas o ideología.
Marginar a las personas, por la razón que sea, es no ser tolerante, no respetar su integridad y dignidad humana, lo que limita la convivencia y la interacción social, excluyéndolas de los beneficios de gozar de los derechos sociales y oportunidades económicas de una comunidad.
Las consecuencias de la marginación son fácilmente observables como:
- Desventaja socioeconómica por el aislamiento
- Bienes y servicios fundamentales inasequibles
- Carencia de oportunidades sociales, económicas y culturales
- Vulnerabilidad social, de salud y de educación
- Hacinamiento que limita la privacidad y el bienestar por no contar con espacios adecuados para la realización de actividades cotidianas
Al no reconocer a las y los que son distintos a nosotras y nosotros no se dan condiciones para la inclusión. La desigualdad social también contribuye a la migración; observa el siguiente video del inicio al 3:46, que te explica qué es, sus causas y consecuencias.
- Jóvenes migrantes
https://www.youtube.com/watch?v=pp4qDtNDy3U
Aunque, aparentemente, la migración también tiene consecuencias positivas como mejorar la calidad de vida personal y de la familia, además de la reactivación de la economía de las comunidades de origen. Sin embargo, es innegable que puede darse la fragmentación familiar, porque uno de los padres o ambos, dejan a los hijos para poder ganar dinero y satisfacer sus necesidades básicas, viviendo separados, incluso años, no teniendo la oportunidad de vivir como una familia unida, que crece y se apoya mutuamente.
Si bien es cierto que una de las libertades es el derecho al libre tránsito, el desplazarse a otro lugar para tener mejores condiciones de vida, obedece a que en la comunidad de origen no hay oportunidades de trabajo, lo cual puede no ser justo, pero se convierte en una necesidad.
Vivir en una comunidad extraña implica adaptarse a situaciones y condiciones que no siempre se entienden o nos agradan, también requiere, en ocasiones, dejar de practicar el propio idioma, costumbres y tradiciones, adoptando un nuevo estilo de vida con el que no siempre se está de acuerdo o, incluso, puede ser desagradable porque genera exclusión; por ejemplo, al sufrir rechazo o discriminación por ser diferente o el ser explotado al no recibir un pago justo por el trabajo desempeñado.
Las pequeñas comunidades que son abandonadas porque las y los jóvenes buscan en otro lugar mejores condiciones de vida, limitan su desarrollo, y aun cuando pueden mejorar económicamente por el dinero enviado por las personas que emigraron, se convierten en lugares no productivos, con pocas o nulas posibilidades de desarrollo. ¿tú que crees que pueda hacerse para reducir la desigualdad social?
Puedes pensar que debe haber organizaciones internacionales y gubernamentales que favorezcan ciertas condiciones para reducir la desigualdad social, porque no es algo que pueda resolverse sólo a nivel individual.
Las acciones que pueden ayudar a reducir la desigualdad pueden ser: Internacionales, nacionales e individuales.
Internacionalmente, líderes mundiales pertenecientes a las Naciones Unidas establecieron en septiembre del 2015, 17 Objetivos para el Desarrollo Sostenible (ODS), con los que se busca proteger al planeta, asegurar la paz, prosperidad y justicia para todas y todos, poniendo especial énfasis en la erradicación de la pobreza.
El primer de los ODS es: “Erradicar la pobreza en todas sus formas en todo el mundo”, centrando su atención en los grupos más vulnerables por conflictos bélicos, desastres naturales, marginados socialmente favoreciendo su acceso a programas de apoyo, recursos y servicios básicos.
El Consejo Nacional de Evaluación de la Política de Desarrollo Social (CONEVAL) es un organismo público que evalúa programas y políticas sociales del Gobierno Federal, proporcionando información sobre las condiciones de pobreza que se viven en el país, para generar políticas públicas y programas que favorezcan la inclusión social y garanticen el cumplimiento de los derechos económicos y sociales.
Dicho organismo plantea que, para superar la desigualdad social y la pobreza, debe haber acciones de política pública enfocadas a los grupos vulnerables que propicien:
- Empleos bien remunerados y con prestaciones básicas, como servicios de salud
- Asistencia escolar y cobertura universal de la educación básica
- Condiciones mínimas de habitabilidad de las viviendas
- Acceso a una adecuada cantidad, calidad y variedad en la alimentación
Si bien la pobreza es un problema que requiere la intervención de organismos nacionales e internacionales, cada una y uno de nosotros puede contribuir a mejorar la problemática que se deriva de esta situación, con acciones que, por mínimas que sean, ayuden a grupos vulnerables, por ejemplo:
- Consumir productos artesanales y locales, a un precio justo, que brinden a sus productoras y productores una retribución adecuada
- Participar con organizaciones que recolectan productos para hacer donaciones a aquellas personas que más lo necesitan
- Allegarnos de información que permita tomar mejores decisiones de vida, cuidando el bienestar personal y de la comunidad
- Participar en la toma de decisiones de la localidad
- Tratar con dignidad a todas las personas, independientemente de su condición social, preferencia sexual, condición étnica o género
La pandemia que se está viviendo actualmente ha tenido efectos adversos en los grupos marginados.
El Programa de las Naciones Unidas para el Desarrollo informó recientemente que las consecuencias por las medidas de confinamiento, adoptadas por los gobiernos de todo el mundo ante la pandemia por COVID-19, especialmente en Latinoamérica, son:
- Drástica caída de ingresos en todos los sectores de la población
- Disminución en la accesibilidad de servicios de salud y medicamentos
- Incremento de la violencia doméstica por el aumento del uso de alcohol, drogas y por el hacinamiento
- Acceso limitado a la educación en línea
- Riesgo de deserción escolar
Lamentablemente, ante este panorama, y aun cuando de momento no se tienen datos concretos, se estima que los niveles de pobreza en Latinoamérica volverán a ser como hace 10 años, presentándose un retroceso respecto a los avances logrados antes de la pandemia. Es importante que todas y todos colaboremos en la mejora de las condiciones de vida de la población, por ello es necesario seguir las indicaciones de distanciamiento social, pues en tanto haya menos contagios, las personas podrán preocuparse por satisfacer otras necesidades.
Podrías hacer caso a Martin Luther King cuando expresó, en su discurso titulado Yo tengo un sueño:
“[…] Yo tengo un sueño de que un día esta nación se elevará y vivirá el verdadero significado de su credo: 'Creemos que estas verdades son evidentes: que todos los hombres son creados iguales'.
Yo tengo el sueño de que un día en las coloradas colinas de Georgia los hijos de los ex esclavos y los hijos de los ex propietarios de esclavos serán capaces de sentarse juntos en la mesa de la hermandad.
[…] Yo tengo el sueño de que mis cuatro hijos pequeños vivirán un día en una nación donde no serán juzgados por el color de su piel, sino por el contenido de su carácter. ¡Yo tengo un sueño hoy!”
Podrías compartir el sueño de lograr la igualdad entre las personas.
Pon a prueba tus conocimientos.
Elabora un organizador gráfico sobre la desigualdad social considerando causas, consecuencias y retos.
Para el organizador gráfico elabora 4 triángulos de diferente color, colócalos de la siguiente manera:
En cada triángulo coloca las palabras:
Desigualdad social
Causas
Consecuencias
Retos
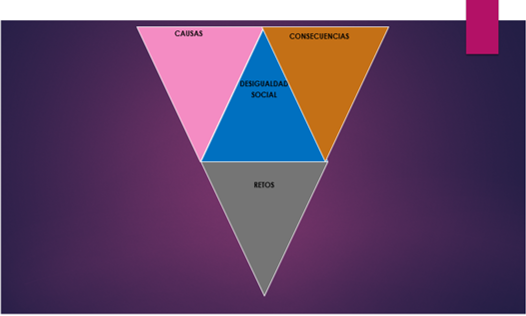
Un ejemplo de lo que se pondría poner en el triángulo de desigualdad social es la definición del concepto diciendo que es una situación derivada del desarrollo económico y condiciones sociales que coloca a grupos en desventaja para la satisfacción de sus necesidades.
En el triángulo de causas puedes escribir: “La riqueza y propiedades están concentradas en una pequeña parte de la población”.
Termina el organizador gráfico con los conceptos que faltan. Plasma en cada apartado tus propias ideas.
El Reto de Hoy:
Recuerda que para seguir aprendiendo puedes consultar tu libro de texto de Formación Cívica y Ética. También puedes consultar medios de comunicación impresa y digital para saber cuáles acciones han realizado personas, grupos o naciones para ayudar a disminuir la desigualdad y la marginación en el mundo y en México.
Puedes escribir un poema, hacer una canción o un cartel sobre tus sueños, en relación con la igualdad entre las personas, así podrás compartir lo que aprendiste en esta sesión con tu familia, conocidas y conocidos.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Semana de la ciencia VII
Aprendizaje esperado: Selecciona hechos y conocimientos para planear la explicación de fenómenos químicos que respondan a interrogantes o resolver situaciones problemáticas referentes a la transformación de los materiales.
Énfasis: Explicar fenómenos químicos que respondan a interrogantes o resolver situaciones problemáticas referentes a la transformación de los materiales, mediante el desarrollo de conocimientos, habilidades y actitudes.
¿Qué vamos aprender?
¿Sabes cómo se representan los elementos y compuestos?
Te invitamos a conocer más acerca de la representación de elementos y compuestos.
¿Sabes cuál es la importancia de la correcta escritura de una fórmula química?
En una fórmula encuentras los símbolos de los elementos que integran una sustancia y un número muy importante, como subíndice, el cual te permite conocer la cantidad de átomos que integran al elemento, compuesto o la proporción entre ellos. Gracias a estos números, puedes diferenciar una sustancia de otra cuando están compuestas por los mismos elementos y, por lo tanto, identificar las propiedades que tienen.
Por ejemplo, si hablas de elementos, te encuentras con el oxígeno, el símbolo es O, pero al ser un gas debe escribirse O2, porque las moléculas están formadas de dos átomos de oxígeno, por lo que se identifica como oxígeno molecular (O2).
Cuando la luz ultravioleta del Sol rompe la molécula de oxígeno, da como resultado dos átomos de oxígeno, los cuales son muy inestables, por lo que se unen a una molécula de oxígeno formando el ozono, que tiene la fórmula O3, pues está formada por tres átomos de oxígeno.
¿Qué hacemos?
Ahora puedes identificar la importancia de escribir de forma correcta la fórmula química de una sustancia, el oxígeno molecular (O2) tiene propiedades diferentes al ozono (O3). Observa la simulación.
- Simulación
Las diferencias son que el oxígeno molecular (O2) no tiene olor, ni color, es imprescindible para la mayoría de los seres vivos. En cambio, el ozono (O3), tiene color azul, un olor muy intenso e incluso puede ser perjudicial para la salud.
Ahora observa dos ejemplos con compuestos que tienen los mismos elementos, pero diferente cantidad de átomos. El monóxido de carbono (CO) y el dióxido de carbono (CO2). Observa la simulación.
- Simulación
Cuando la combustión de carbono se completa, requiere la presencia de oxígeno suficiente; el resultado es principalmente dióxido de carbono. Lo que ocurre cuando hay limitada disponibilidad de aire, sólo la mitad del oxígeno se agrega al carbono y, por lo tanto, se forma el monóxido de carbono.
La mayor parte del CO2 liberado a la atmósfera proviene de fuentes naturales, entre ellas se cuentan los océanos, la respiración vegetal y animal (incluida la humana), la descomposición de materia orgánica, incendios forestales y erupciones volcánicas. Si bien la menor cantidad de generación de CO2 es causada por la actividad humana, 87% de todas las emisiones producidas por los seres humanos deriva de la quema de combustibles fósiles, como el carbón, gas natural y petróleo.
¿Reconociste la importancia de los subíndices en una fórmula química? Si se modifican estos números, estarás hablando de sustancias diferentes con propiedades distintas; el monóxido de carbono está formado por un átomo de carbono y un átomo de oxígeno, y el dióxido de carbono está constituido por un átomo de carbono y dos átomos de oxígeno.
Otro ejemplo es el del agua y el peróxido de hidrógeno, conocido comúnmente como agua oxigenada. Observa la fórmula del agua (H2O). El agua está formada por dos átomos de hidrógeno y un átomo de oxígeno.
El peróxido de hidrógeno o agua oxigenada está constituido por dos átomos de hidrógeno y dos átomos de oxígeno (H2O2).
Observa la simulación:
- Simulación
Pues bien, al tener el peróxido de hidrógeno un átomo más de oxígeno que el agua, éste presenta propiedades diferentes; a simple vista se ven iguales, son traslúcidas, pero si agregas un poco de óxido de manganeso, observarás una diferencia notable. Esto se debe a que presenta propiedades diferentes a las que tiene el agua.
El peróxido de hidrógeno es un líquido transparente, con una temperatura de ebullición de 150 grados Celsius y es completamente miscible con el agua; sin embargo, se puede separar completamente por destilación, ya que su temperatura de ebullición es más alta que la del agua.
El agua es un líquido transparente, incoloro, insípido e inodoro; puede encontrarse en diferentes estados de agregación, como niebla, rocío, nieve, hielo, vapor, entre otros. El agua pasa al estado gaseoso cuando se calienta a más de 100 grados Celsius.
Es posible separar los elementos que forman al agua por medio de una electrólisis. Imagina lo que sucede al acercar una pajilla de madera encendida a las burbujas que se obtienen.
Recuerda, la importancia de colocar el subíndice correcto en una fórmula química es que te permite identificar de qué sustancia se trata, así como sus propiedades y el número de átomos que integra el compuesto.
Ahora analiza, ¿cuál es la importancia de la participación de las mujeres en la ciencia?
Desde el surgimiento de la ciencia, a las mujeres no se les permitió participar en las actividades científicas. Las primeras tuvieron que luchar contra los prejuicios de la familia. Sus padres fueron sus principales opositores, y cuando algunas lograron superar este obstáculo, se enfrentaron a la oposición de los científicos y de la sociedad en general.
Aún hoy, cuando uno pensaría que las mujeres ya pueden dedicarse a la ciencia sin problemas sociales o de género, siguen siendo pocas las científicas en las universidades.
De acuerdo con el Centro de Investigaciones y Estudios de Género, en 2015 la licenciatura en la que menos mujeres estaban inscritas fue la de Ingeniería Mecánica y Eléctrica, pues por cada 100 estudiantes había 9 alumnas. En los posgrados de Físico-Matemáticas hubo 30 mujeres por cada cien hombres. En el caso de las carreras no científicas, la licenciatura en pedagogía tenía 480 mujeres por cada 100 hombres.
Sin embargo, el nivel de participación de la mujer en las carreras científicas no se relaciona con la capacidad, pues el promedio de las calificaciones en el bachillerato fue de 8.0 para las mujeres y 7.5 para los hombres.
Por otra parte, de acuerdo con la Organización de las Naciones Unidas, para la educación, la ciencia y la cultura, uno de cada cinco países ha alcanzado la paridad de género, mientras que en nuestro país sólo 33% de los científicos son mujeres.
Pero el papel de la mujer a lo largo de la historia ha sido fundamental para el desarrollo de la ciencia, desde Hipatia de Alejandría, hasta las galardonadas con el premio Nobel de Química este año, la francesa Emmanuelle Charpentier y la estadounidense Jennifer Doudna, quienes desarrollaron “un método para la edición de genes” que podría ayudar a combatir enfermedades como el cáncer. Las mujeres han tenido un papel muy importante en el desarrollo científico de la humanidad, aunque no siempre ha quedado registro.
En esta sesión se hace mención de algunas de esas mujeres que, con su trabajo, perseverancia, dedicación, rompiendo estereotipos y luchando contra la desigualdad de género, lograron trascender en la historia.
La primera es Hipatia de Alejandría, quien fue la primera mujer en realizar una contribución sustancial al desarrollo de las matemáticas, una verdadera precursora y hasta una mártir como mujer de ciencias; su imagen se considera un símbolo de la defensa de las ciencias.

La segunda mujer es Marie-Anne Pierrette Paulze, 1758-1836, conocida como Marie Lavoisier, esposa del científico Antoine Lavoisier, y es considerada como “la madre de la química moderna”.
Asistía a Lavoisier en el laboratorio durante el día, anotando observaciones en el libro de notas y dibujando diagramas de sus diseños experimentales.
Debido a su dominio del inglés, latín y francés, realizó traducciones de varios trabajos sobre la teoría del flogisto para que su esposo los leyera; probablemente el más importante sea el “Ensayo sobre Flogisto”, de Richard Kirwan, en el que además introdujo notas puntualizando los errores químicos del trabajo.
Continua ahora con una mujer que, sin duda, fue una de las químicas más importantes de la historia, Maria Salomea Sklodowska-Curie, mejor conocida como Marie Curie, quien es reconocida fundamentalmente por su trabajo de toda la vida sobre la radioactividad, pero también por el hecho de haberse abierto paso en la comunidad científica, completamente dominada por hombres que no veían con buenos ojos que una mujer se dedicara a la ciencia, ya que era “cosa de hombres”.
Marie Curie sentó las bases para nuestra comprensión de la física y la química y nos abrió caminos en oncología, tecnología, medicina y física nuclear, por nombrar algunos.
Nació el 7 de noviembre de 1867 en Varsovia, Polonia; fue una estudiante brillante, pero enfrentó barreras como mujer que le impedían seguir sus estudios superiores, así que estudió en una pequeña universidad que brindaba estudios clandestinos a la juventud polaca. Ahorrando dinero y trabajando como institutriz y tutora, finalmente pudo mudarse a París para estudiar en la prestigiada Sorbona; ahí obtuvo el título en física y en matemáticas.
En el año 1903 recibió, junto con su esposo Pierre Curie y Henri Bequerel, el Premio Nobel de Física, convirtiéndose así en la primera mujer en recibir tal condecoración.
Fue la primera mujer en las Conferencias de Solvay, una serie de congresos con los científicos más importantes de la época, donde participó al lado de figuras como Einstein y Schrödinger.
Sus investigaciones en el campo de la radiación la llevaron a descubrir dos nuevos elementos: el radio (Ra) y el polonio (Po). Ella lo nombró así en honor a su país natal, Polonia, por lo que recibió un segundo Premio Nobel, esta vez de Química, en 1911, convirtiéndose así en la primera persona en recibir dos Premios Nobel en categorías distintas.
Se convirtió en la primera catedrática en la Sorbona de París en Francia. El 4 de julio de 1934, Marie Curie murió a causa de anemia aplásica, causada por la exposición prolongada a la radiación, al manipular material radiactivo sin el equipo recomendado y por guardar tubos de ensayo con radio en los bolsillos. Sus posesiones terminaron gravemente contaminadas. Los efectos nocivos de la radiación no se conocían en ese momento. Su investigación terminó matando a la polaca nacionalizada francesa.
Su hija mayor Irène Curie-Joliot, también dedicó su vida a la ciencia, y al igual que su madre, consiguió un Premio Nobel de Química por sus investigaciones. Recibió el premio en 1935 junto con su marido “por sus trabajos en la síntesis de nuevos elementos radiactivos”.
A pesar de que han transcurrido más de 100 años, gran parte de los objetos personales de Curie, incluyendo la ropa, muebles, libros y las notas de laboratorio siguen contaminados por la radiación. Estos objetos, considerados como tesoros nacionales y científicos, se almacenan en cajas forradas con plomo en la Biblioteca Nacional de Francia en París y requieren un equipo especial para aquellos investigadores que quieran consultar sus notas.
Tampoco el cuerpo de Marie Curie se libró de la radiación. Fue colocado en un ataúd forrado con aproximadamente una pulgada de plomo.
En una sesión anterior, se expuso el caso de Rosalind Franklin, una científica que realizó investigaciones sobre la estructura de ADN, cuyo invaluable aporte fue robado por dos científicos hombres, James Watson y Francis Crick. Ellos se llevaron el reconocimiento por el trabajo de Franklin, quien murió en 1958, a sus 38 años, sin ser debidamente reconocida por la comunidad científica.
Desde la primera edición en 1901 de los Premios Nobel, tan sólo 54 mujeres han sido galardonadas en alguna de las cinco categorías, frente a los 869 hombres; es decir, únicamente 5.8% de mujeres científicas han sido reconocidas en esta ceremonia.
La participación de las mujeres en el desarrollo de la ciencia en nuestro país no es de menor importancia, sólo por mencionar algunos nombres, contamos con científicas destacadas como Helia Bravo Hollis y sus trabajos sobre las cactáceas, o la doctora Julieta Fierro, destacada astrónoma y divulgadora de la ciencia, pero este será tema para una sesión posterior.
Lee la siguiente entrevista al maestro en ciencias con especialidad en Toxicología del Centro de Investigación y Estudios Avanzados, CINVESTAV, del IPN, M. en C. Ramsés Enrique Santacruz Márquez quién hablará sobre un tema muy interesante: las nanopartículas, sus usos y sus potenciales peligros.
- ¿Por qué eligió estudiar esa carrera?
Respuesta: Yo soy químico en alimentos y elegí esa carrera porque me llamaba la atención entender cómo se procesan los alimentos para preservarlos más tiempo, hacerlos más nutritivos, etcétera, principalmente me interesaba entender qué procesos suceden en nuestro cuerpo para que los nutrientes de los alimentos se absorban y proporcionen energía.
- ¿Cuál es su libro preferido?
Soy fan de los cuentos de Gabriel García Márquez. Me gusta mucho “Alguien desordena estas rosas” y “El rastro de tu sangre en la nieve”, por ejemplo. Así que mi libro favorito es la colección de cuentos de este autor.
- ¿Qué hace los días en que no se levanta con ánimo?, ¿tiene algún lema, alguna frase que le motive?
En general, cuando me siento así, procuro darme un tiempo para mí, me permito sentirme desanimado por un momento, pero me pongo la meta de activarme y trabajar a una hora determinada.
- ¿Tiene algún ídolo a quien seguir, algún referente en su vida profesional?
Admiro a las personas que se ponen metas y las cumplen, pero también a quienes saben ponerle límites al trabajo y separarlo del hogar o de otras actividades. Me parece muy sano poder hacer esto y busco lograr que mis días sean así.
- La importancia de la armonía en la relación familiar es algo que se tiene muy presente en este tiempo de pandemia. Se ha dedicado a evaluar el efecto de algunas nanopartículas usadas en alimentos y cosméticos, sobre la función reproductiva femenina. ¿Podría, hablarnos más sobre esto, no sin antes explicarnos qué son las nanopartículas? ¿a qué se refiere ese término?
Bueno, esas preguntas son muy interesantes. Primero veamos qué son las nanopartículas y por qué son importantes.
El termino nanopartícula se emplea para referirse a todas aquellas partículas con un tamaño muy pequeño. Se ha establecido que las nanopartículas son materiales que tienen un tamaño menor a los 100 nm, es decir, pueden ser más pequeñas que el diámetro de un cabello humano.
Ese tamaño tan pequeño les proporciona características fisicoquímicas muy interesantes. Debido a esto, son ampliamente utilizadas, ya que contribuyen a la creación de materiales más durables, resistentes, duraderos, livianos, mejores conductores eléctricos, entre muchas otras características.
Algunas nanopartículas son usadas en la industria de los cosméticos, en textiles y en algunos productos de uso cotidiano y alimentos. Por ejemplo, las nanopartículas de dióxido de titanio se encuentran en algunos cosméticos, ya que contribuyen en la función de los mismos. Estas mismas nanopartículas también se pueden encontrar en algunos alimentos como aditivo alimentario. Otras nanopartículas se pueden emplear en la medicina como herramientas terapéuticas y de diagnóstico.
En particular, estudié los efectos de las nanopartículas de dióxido de titanio y óxido de zinc sobre algunas funciones del ovario, como la producción de hormonas. Usando un modelo de exposición in vitro, es decir, con exposición directa de las nanopartículas en las células en cultivo, observamos que éstas pueden afectar distintos parámetros funcionales y de calidad del ovario, y que esto podría traducirse en otro tipo de alteraciones. Ojo, no estoy diciendo que hacen daño o que no usen productos que las contengan. Lo que digo es que la ciencia debe ir conociendo cada vez más de qué manera estos materiales, relativamente nuevos y cuyos efectos aún no se conocen bien, pueden interactuar con el cuerpo y si modifican o alteran algunas funciones. Aunque estos hallazgos son importantes en el área, se deben realizar aún más estudios para determinar los niveles de exposición a estas nanopartículas y sus efectos en otros modelos.
- ¿De qué color son las nanopartículas? y ¿cuáles son los potenciales riesgos para nuestra salud o el ambiente por el uso de ellas?
Las nanopartículas pueden variar en su color, tamaño y otros debido a su composición. Es decir, el elemento o material del que están hechas influye en el color. Las nanopartículas de dióxido de titanio y de óxido de zinc, por ejemplo, se ven como un polvo blanco. Por otro lado, las nanopartículas de hierro se pueden ver de color oscuro.
Si existe un riesgo potencial a nuestra salud y la del ambiente por el uso de productos que contienen nanopartículas, bueno, este es un tema que está en debate actualmente. Sin embargo, sabiendo que son ampliamente usadas, es importante que se realicen estudios que ayuden a garantizar que no resulten dañinas a nuestro organismo ni al de otros animales en el ambiente, ya que muchas nanopartículas pueden depositarse en suelos o en agua y permanecer ahí por un tiempo.
Nuestro más sincero agradecimiento para el maestro, por darse el tiempo de motivar a seguir haciendo ciencia. Si te interesara hacerle alguna pregunta sobre el tema, le puedes escribir al correo rsantacruzm@cinvestav.mx.
Es imposible adentrarse en el bello y maravilloso mundo del conocimiento y no darte cuenta de que desconoces mucho más de lo que creías saber; sin embargo, eso, en lugar de ser frustrante, es una invitación a continuar con la investigación.
Cómo pudiste darse cuenta, en esta sesión se trataron conocimientos que ya adquiriste en sesiones anteriores, como la representación de elementos y compuestos, así como la participación de las mujeres en la ciencia y la importancia de la investigación científica.
El Reto de Hoy:
Comparte con tu familia lo que más te gustó de esta sesión.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario