Aprende en Casa III SEP: 9 de marzo TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 9 de marzo de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Martes 9 de marzo, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Resolver problemas de cálculo de perímetro y área de polígonos regulares
Aprendizaje esperado: Calcula el perímetro y el área de polígonos regulares y del círculo a partir de diferentes datos.
Énfasis: Calcular el perímetro y el área de polígonos regulares.
¿Qué vamos a aprender?
En esta sesión, resolverás diferentes situaciones con la finalidad de dar sentido y significado al cálculo del perímetro y área de polígonos regulares.
¿Qué hacemos?
Inicia con la siguiente información sobre qué es un polígono regular.
Un polígono es una figura plana cerrada, formada por tres o más lados rectos. Un polígono es regular si tiene sus lados y sus ángulos iguales entre sí. La palabra polígono es un término de origen griego cuyo significado es: polys (muchos) y gonos (ángulos).
A continuación, revisa la siguiente situación.
Situación: marcos de madera
Carlos construyó los siguientes marcos de madera para colocar espejos en ellos, a solicitud de un cliente. Calcula la cantidad de metros de madera que necesitó Carlos para hacer los marcos.
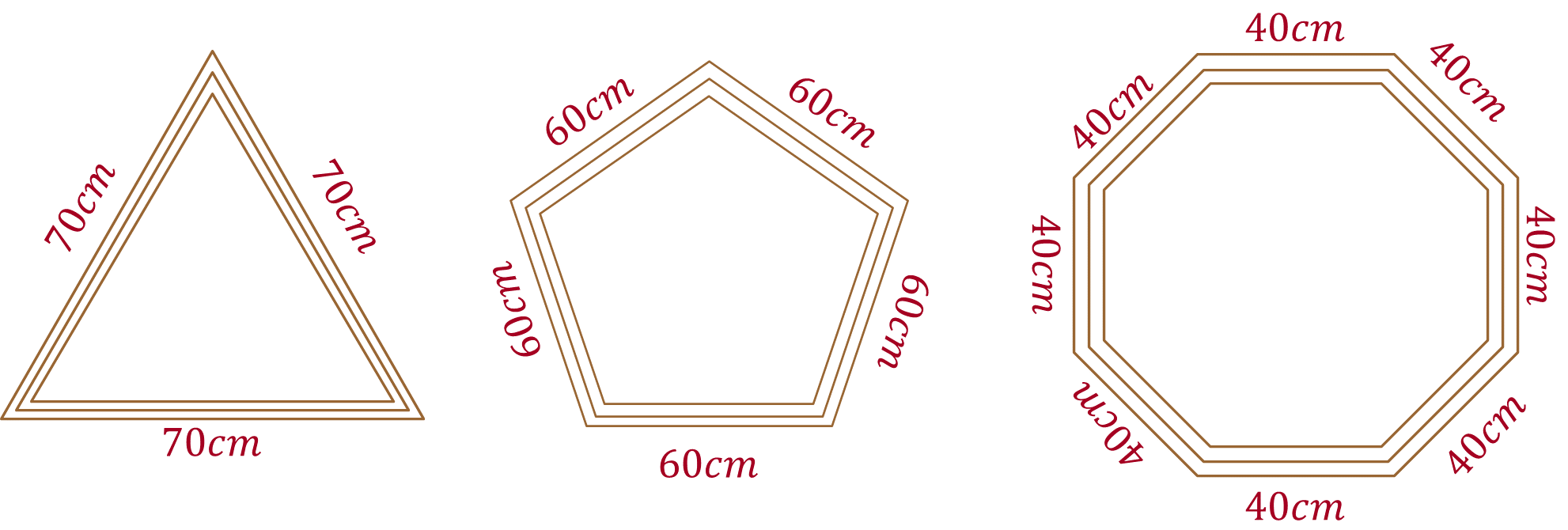
Ahora, analiza las siguientes preguntas y respóndelas:
- ¿Qué tienen en común los tres marcos?
- ¿Qué forma geométrica tienen los marcos?
- ¿Qué se debe hacer para calcular la cantidad de metros de madera necesaria para construir los marcos?
- ¿El procedimiento es el mismo o cambia según la forma del marco?
- Si el marco tiene forma de polígono regular de “n” lados, ¿cómo se determina su perímetro?
- ¿Qué fórmula permite calcular el perímetro de cualquier polígono regular?
- ¿Qué hacer para calcular cuántos metros cuadrados de espejo se requiere para cada marco?
Primera pregunta: ¿qué tienen en común los tres marcos? De acuerdo con los datos, lo que tienen en común los marcos es que los lados de cada figura son iguales, y si sus ángulos interiores también son iguales, entonces son polígonos regulares.
Segunda pregunta: ¿qué forma geométrica tienen los marcos? El primer marco tiene forma triangular, ya que tiene tres lados. El segundo marco tiene forma pentagonal, ya que es de cinco lados. Y el tercer marco tiene forma octagonal, ya que tiene ocho lados.
Tercera pregunta: ¿qué se debe hacer para calcular la cantidad de metros de madera? Toma un momento para pensar en dos formas de calcular la cantidad de madera necesaria para que Carlos elabore estos tres marcos. Regístralos en tu cuaderno.
El perímetro es la línea o conjunto de líneas que forman el contorno de una superficie o una figura, es decir, el marco representa el perímetro de cada figura.
Como el marco representa el perímetro del triángulo, entonces una manera de calcular su perímetro es sumar las medidas de sus lados. De esta manera, se tiene la siguiente suma:
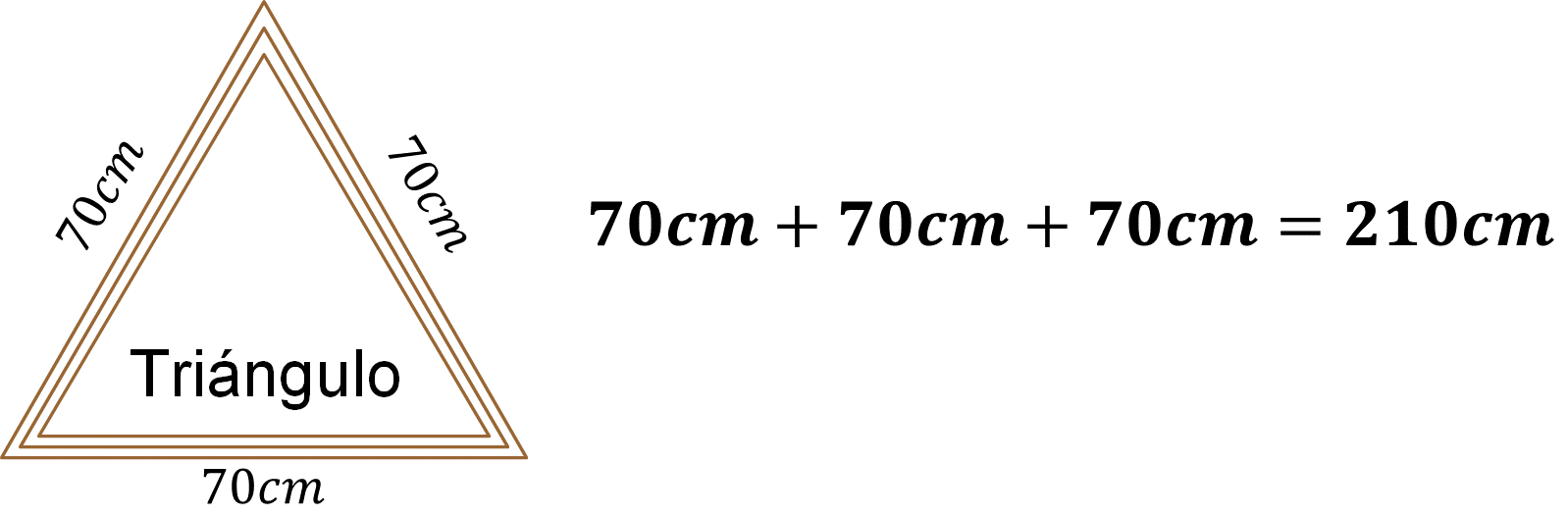
Se puede afirmar que el perímetro del marco triangular es de 210 centímetros. ¿Qué representa este valor en el contexto del problema?
Representa la cantidad de madera que se utilizó para realizar el marco triangular, es decir, 210 centímetros. Continúa con el cálculo del perímetro de los otros marcos.
Para el marco pentagonal se realiza la siguiente suma:
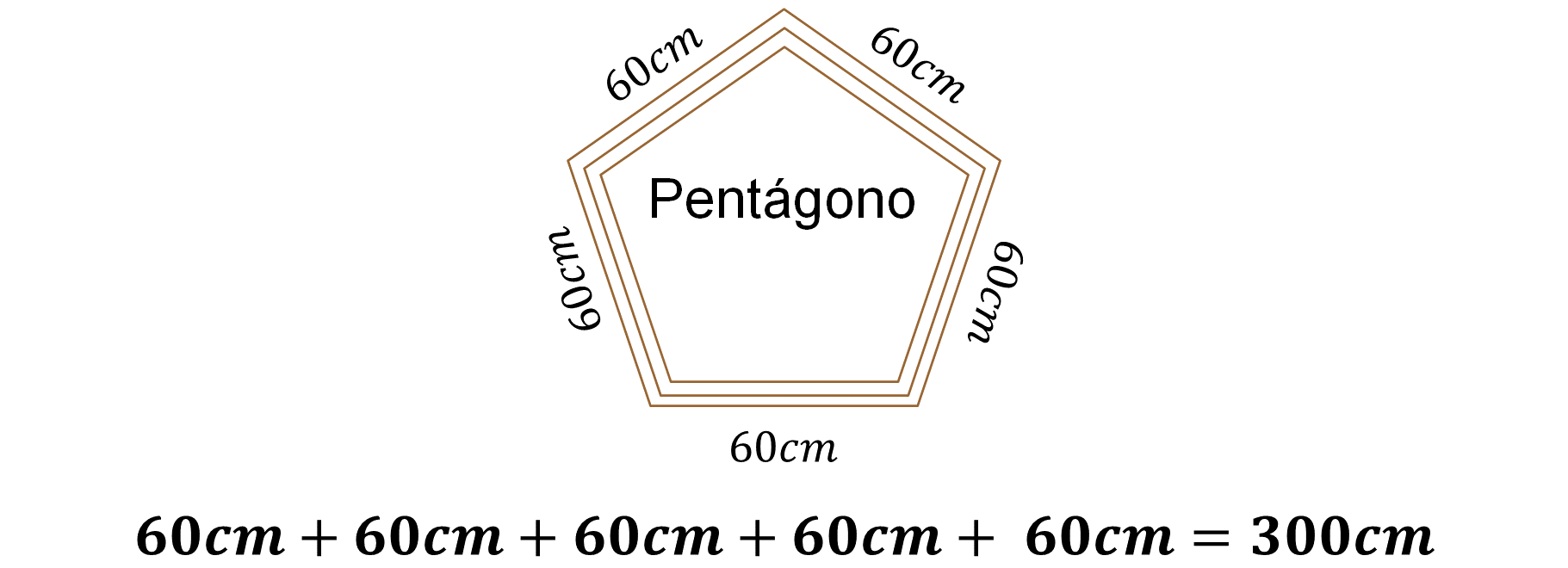
Por lo tanto, el perímetro del marco pentagonal es de 300 centímetros ¿Qué representa este valor en el contexto del problema? Representa la cantidad de madera necesaria para construir el marco pentagonal. Continúa con el marco octagonal.
Una manera de calcular el perímetro del marco octagonal es sumar la medida de sus lados:
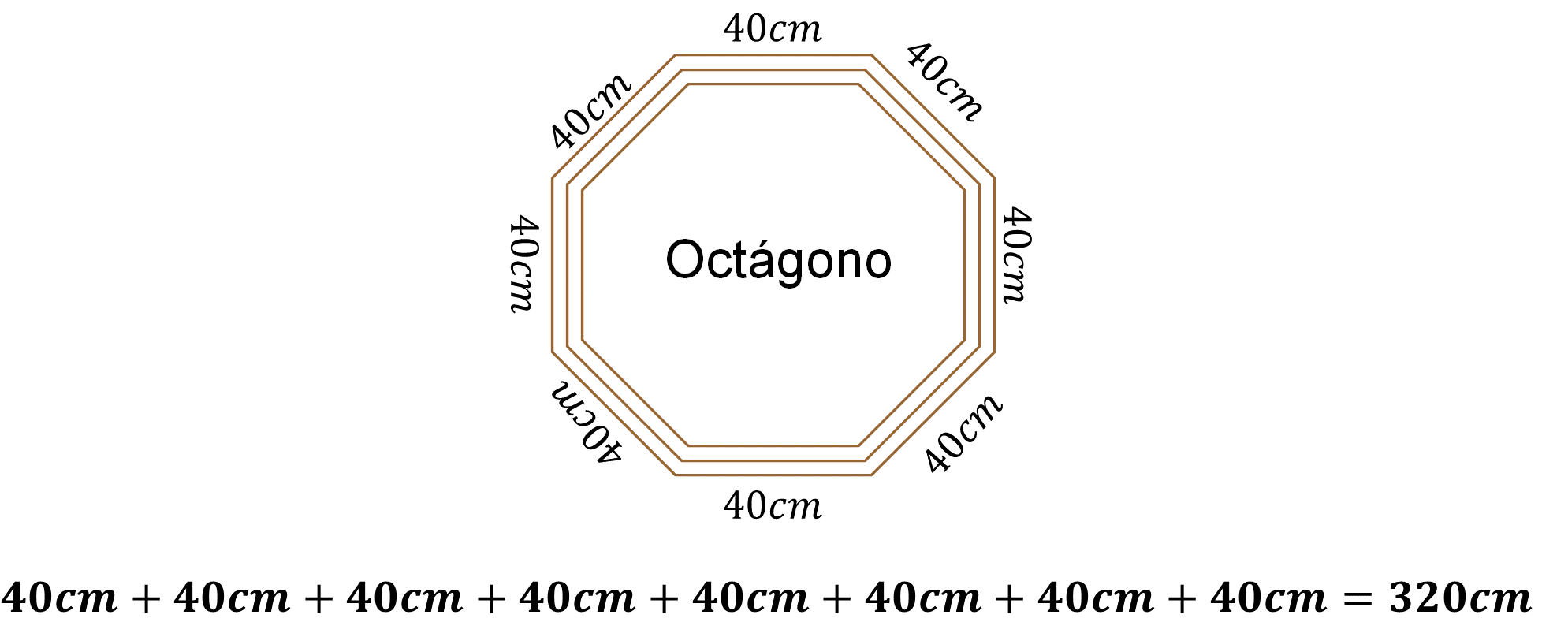
¿De qué otra manera se podría calcular el perímetro de este octágono regular? ¿Qué representa la medida del perímetro del octágono en la situación que se está trabajando? Representa la cantidad de madera que se utilizó para construir el marco octagonal, es decir, 320 centímetros.
Ahora retoma la quinta y sexta pregunta: si el polígono es regular de “n” lados, ¿cómo se determina su perímetro?, ¿qué fórmula permite calcular el perímetro de cualquier polígono regular?
Considera que el perímetro es la medida del contorno de la figura y se mide en unidades lineales. Para el contexto del problema, los marcos de madera representan el perímetro, si los marcos tienen forma de polígonos regulares ¿cómo se determina su perímetro?
Hasta el momento, has calculado el perímetro de los polígonos regulares con la suma de las medidas de sus lados, que son iguales. Sin embargo, también puedes calcular el perímetro mediante una multiplicación, donde los factores son la cantidad de sus lados y la medida de sus lados. Para verificar esto, resuelve el marco triangular mediante este proceso.
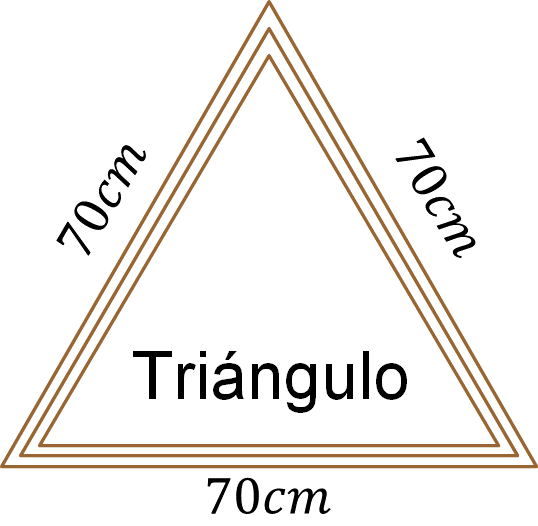
Como es un polígono regular, se trata de un triángulo equilátero, ya que sus tres lados son iguales. Multiplica 3, que es su cantidad de lados, por la medida de uno de sus lados, es decir, 70 centímetros, y se obtiene como producto: 210 centímetros.
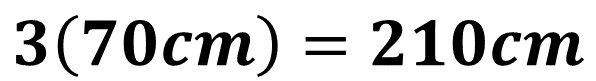
Ahora, aplica la multiplicación para el pentágono y el octágono.
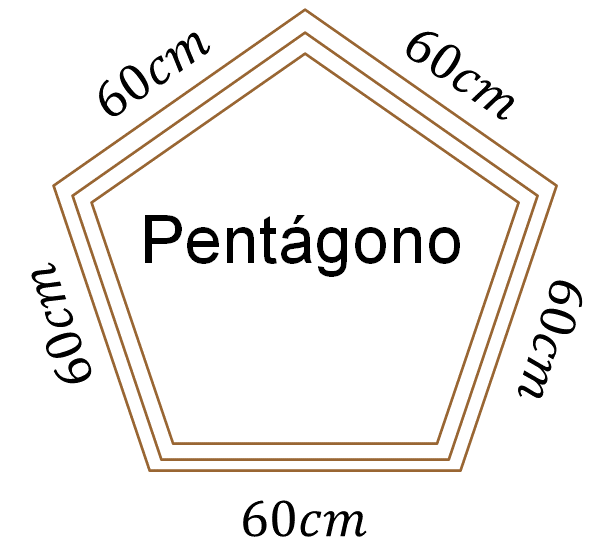
Este es un polígono regular, es decir, un pentágono equilátero porque todos sus lados son iguales. Si multiplicas 5, que es el número de sus lados, por la medida de uno de sus lados, es decir, 60 centímetros, obtienes 300 centímetros.
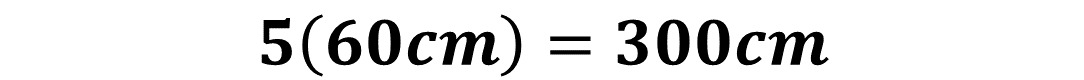
¿Este resultado es igual al obtenido con la suma de las medidas de sus lados? Se obtiene el mismo resultado cuando se sumó 5 veces la medida de uno de sus lados que cuando se multiplicó 5 por la medida de uno de sus lados.
Continúa con el marco octagonal.
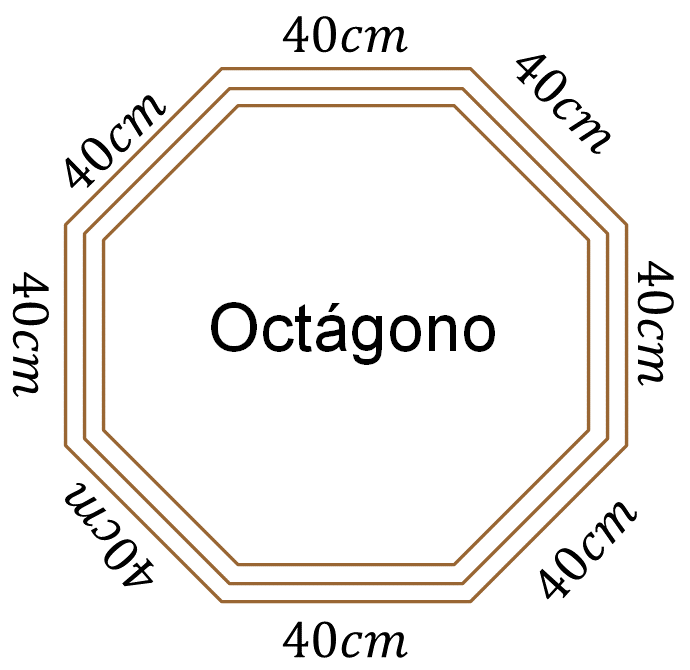
Ya que todos sus lados son iguales, multiplica 8, que es el número de lados por la medida de uno de sus lados, es decir, 40 centímetros, lo que arroja un producto de 320 centímetros.
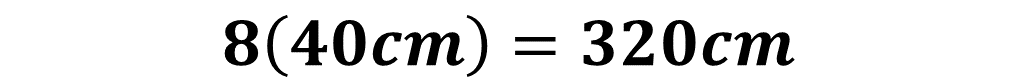
Toma un momento para pensar sobre las siguientes preguntas:
- ¿Qué podría hacer Carlos para calcular la cantidad de madera necesaria para hacer un marco en forma de un hexágono regular y para determinar la cantidad de madera necesaria para un marco de decágono regular?
- ¿Habrá alguna fórmula para calcular el perímetro de cualquier polígono regular?
Responde la pregunta: ¿qué fórmula permite calcular el perímetro de cualquier polígono regular?
Como un polígono regular tiene todos sus lados de la misma medida, el perímetro será el producto del número de lados del polígono (n) por la longitud de uno de ellos (l); por lo tanto, la fórmula para calcular el perímetro de polígonos regulares queda definida como:
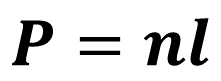
Donde:
P: perímetro
n: es el número de lados.
l: la longitud de un lado.
Ahora calcula la cantidad de madera que necesitó Carlos para hacer los marcos. Para ello, suma la medida del perímetro de cada marco, que en ambos procedimientos fue el mismo, es decir, 210 centímetros del perímetro del triángulo más 300 centímetros del perímetro del pentágono más 320 centímetros del perímetro del octágono, que es igual a 830 centímetros.
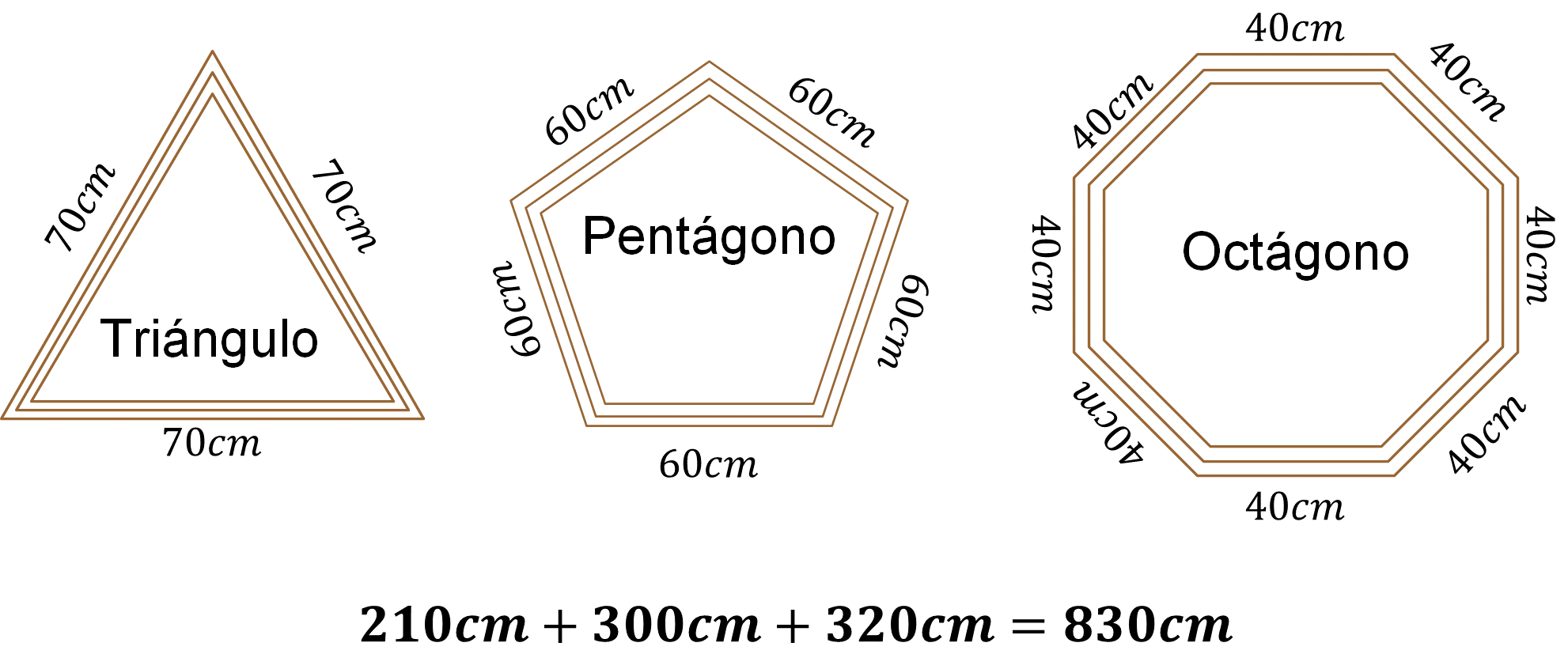
De esta manera, se puede afirmar que Carlos utilizó 830 centímetros de madera para la elaboración de los tres marcos, pero la situación problema pregunta: ¿cuántos metros de madera necesitó Carlos para hacer los marcos?
1 metro es igual a 100 centímetros y la cantidad total de madera que se utilizó para los marcos es de 830 centímetros, por lo que necesita determinar su equivalente en metros.
Una manera de hacerlo es establecer una tabla de variación proporcional directa, de donde se puede establecer que “x” es el cociente de 830 entre 100, que es igual a 8.30 metros.

Ahora realiza la conversión del perímetro de cada figura de centímetros a metros, ¿cómo realizarías estas conversiones?
Al convertir el perímetro de cada figura de centímetros a metros, se tiene que el perímetro del triángulo es de 2.1 metros, el del pentágono es 3 metros y el del octágono 3.2 metros. La suma de estas cantidades es 8.3 metros.
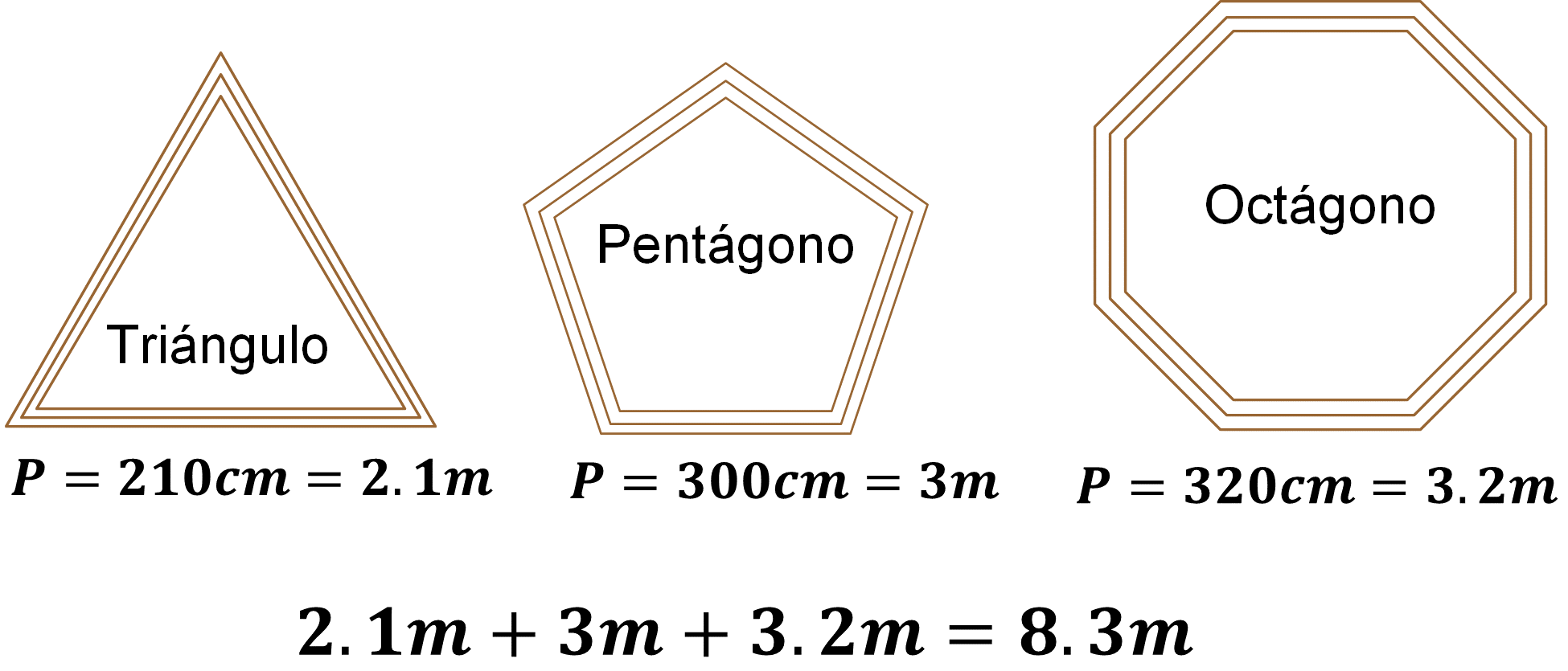
Entonces, la cantidad de madera que necesitó Carlos para construir los marcos fue de 8.30 metros.
Ahora analiza el segundo procedimiento para calcular el perímetro de los marcos, ¿fue el mismo o cambió según la forma del marco? El procedimiento para calcular el perímetro en cada marco es el mismo, ¿por qué?
Porque los tres marcos representan polígonos regulares, por lo tanto, la formula es la siguiente:
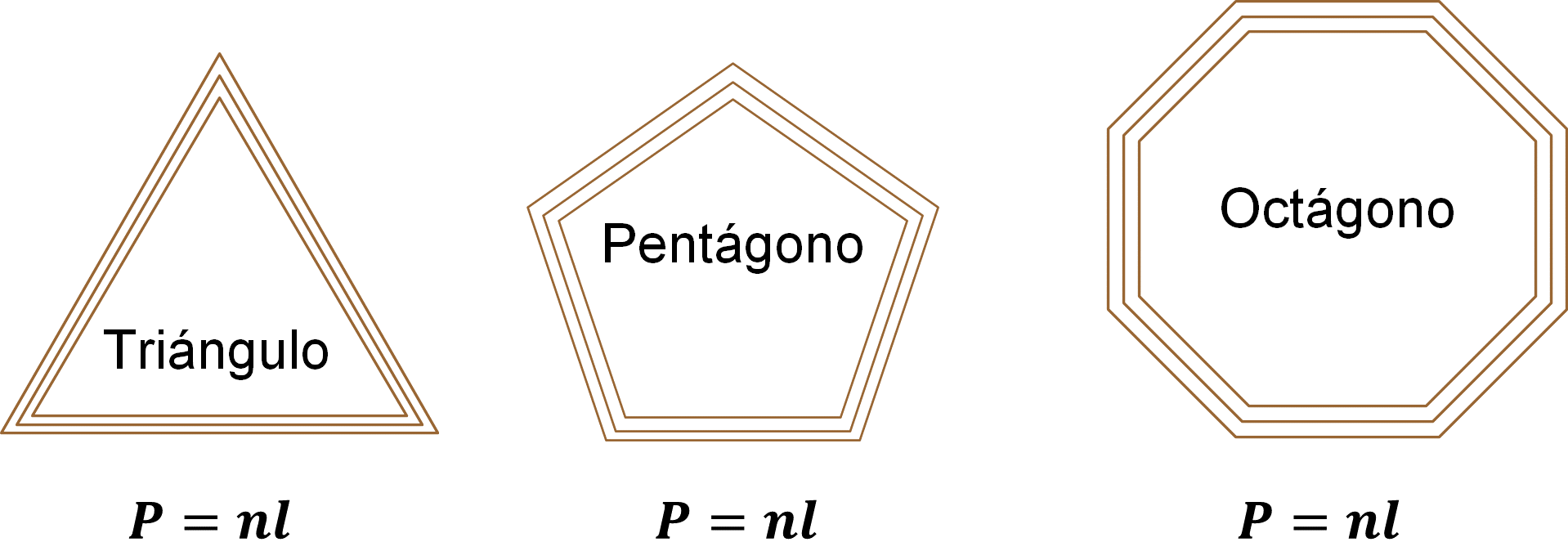
Donde:
P: perímetro
n: es el número de lados.
l: la longitud de un lado.
De acuerdo con esto, esta fórmula se puede aplicar para calcular el perímetro de cualquier polígono regular.
Ahora recuerda que se dijo que esos marcos serían utilizados para colocar espejos. Retoma el problema, pero ahora para calcular la medida de la superficie o área de los espejos que colocará Carlos en cada marco.
Los lados del triángulo miden 0.7 metros y su altura 0.6052 metros. A partir de la fórmula: área igual a base por altura entre 2, sustituye valores:
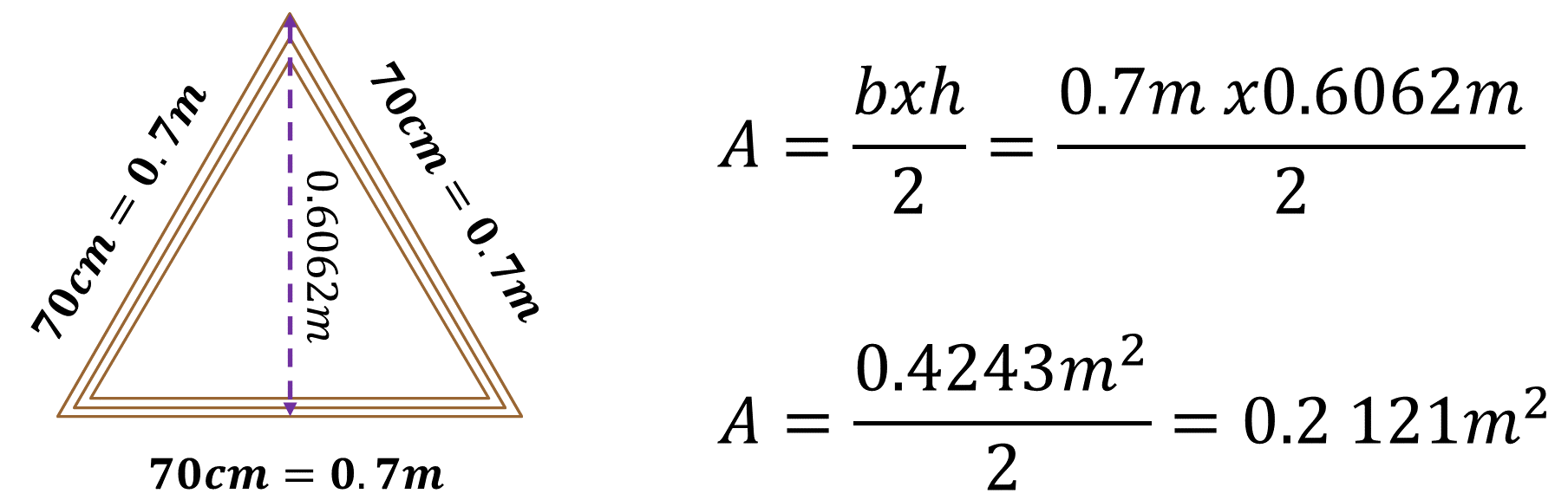
Se obtiene 0.2121 metros cuadrados. ¿Qué significa este valor en el contexto del problema? Es el área que ocupa el espejo en el marco triangular.
Ahora, responde la siguiente pregunta: ¿hay alguna fórmula, como en el caso del triángulo, que permita calcular el área del pentágono y el octágono cuando estos polígonos son regulares? Explica tu respuesta.
Carlos afirma que sí hay una fórmula para calcular el área del pentágono y octágono. Observa lo que hizo Carlos.
Él nombró los vértices del marco octagonal con las letras: A, B, C, D, E, F, G y H. Posteriormente, trazó cuatro diagonales en el octágono:
- Del vértice A al vértice E.
- Del vértice B al vértice F.
- Del vértice C al vértice G.
- Y del vértice D al vértice H.
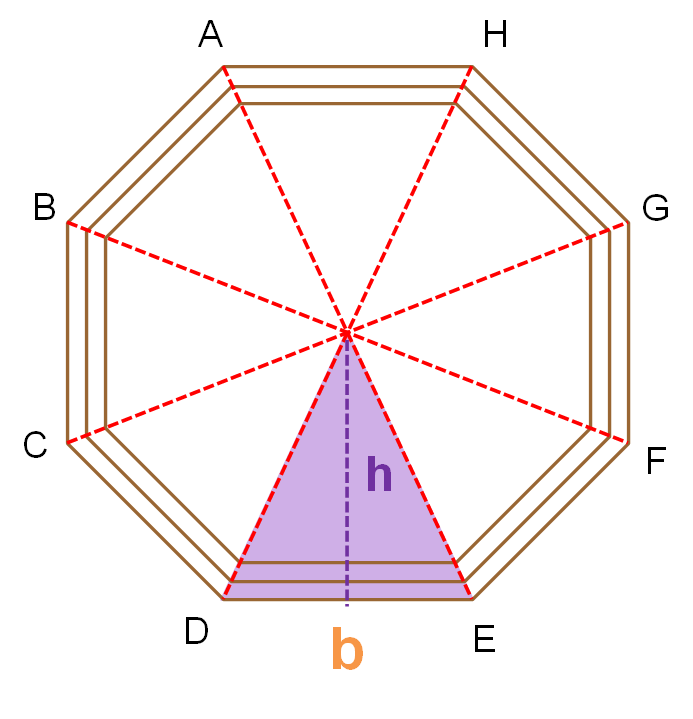
Se ha dividido el octágono en ocho triángulos congruentes, tantos como lados tiene el octágono. Después, Carlos analizó uno de los triángulos identificando sus elementos. La base, que es de 40 centímetros es igual a 0.4 metros y midió la altura obteniendo 27.5 centímetros igual a 0.275 metros.
Posteriormente, Carlos usó la fórmula:
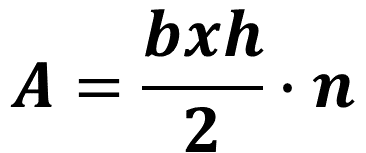
Donde:
b: es la base de los triángulos (40cm, 0.4m).
h: es la altura de los triángulos (27.5, 0.275m).
n: es la cantidad de triángulos formados dentro del octágono (8).
Después, Carlos resolvió las operaciones aritméticas. Sustituyendo valores:
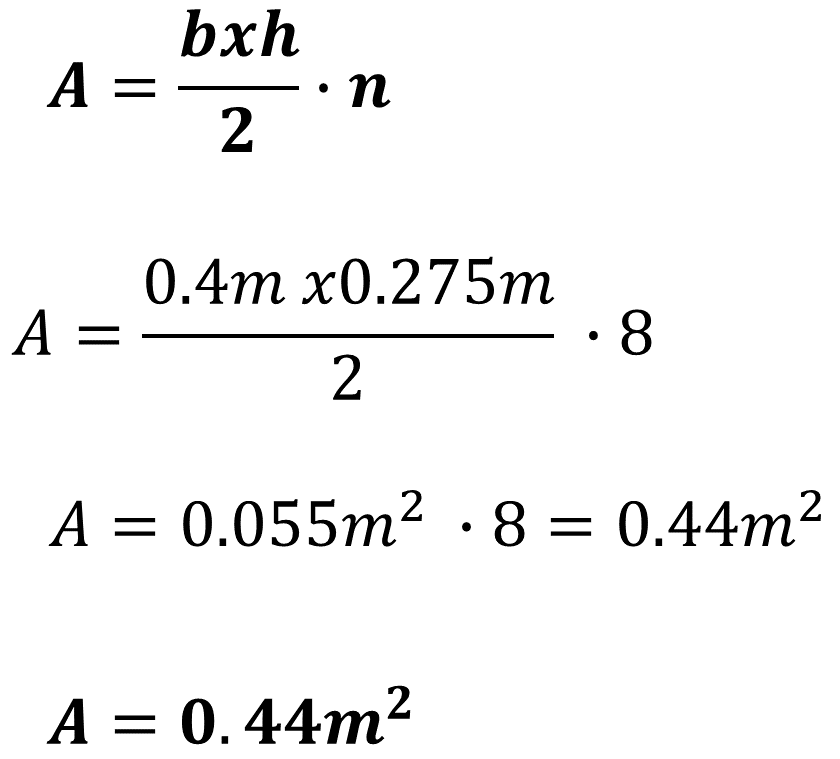
Área es igual a 0.44 metros cuadrados.
¿Qué significa esta medida en el contexto del problema? Es la medida de la superficie o área del espejo que colocará en el marco octagonal.
En conclusión, Carlos identificó que para calcular el área de un polígono regular se puede calcular el área de uno de los triángulos que se forman en su interior, y después multiplicar ese resultado por el número de triángulos, que es igual al número de lados del polígono.
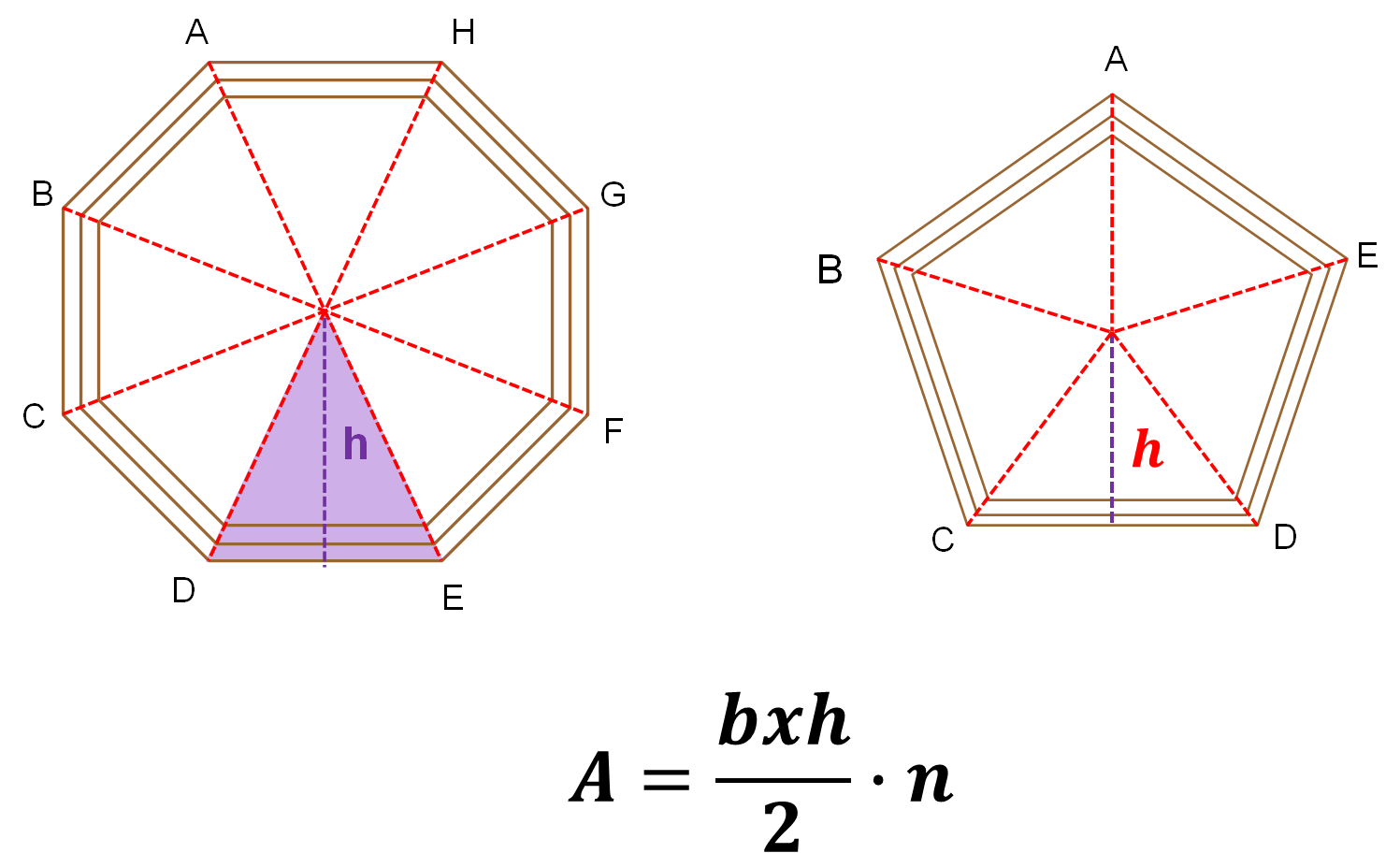
Este procedimiento se puede aplicar para calcular el área de cualquier polígono regular. Toma un momento y piensa si existe otra manera de calcular el área de un polígono regular.
Ahora analiza lo que hizo Carlos para calcular el área del pentágono.
De igual manera que con el octágono, dividió el pentágono en cinco triángulos congruentes. Luego, los unió y marcó con líneas punteadas como se muestra en la siguiente imagen.
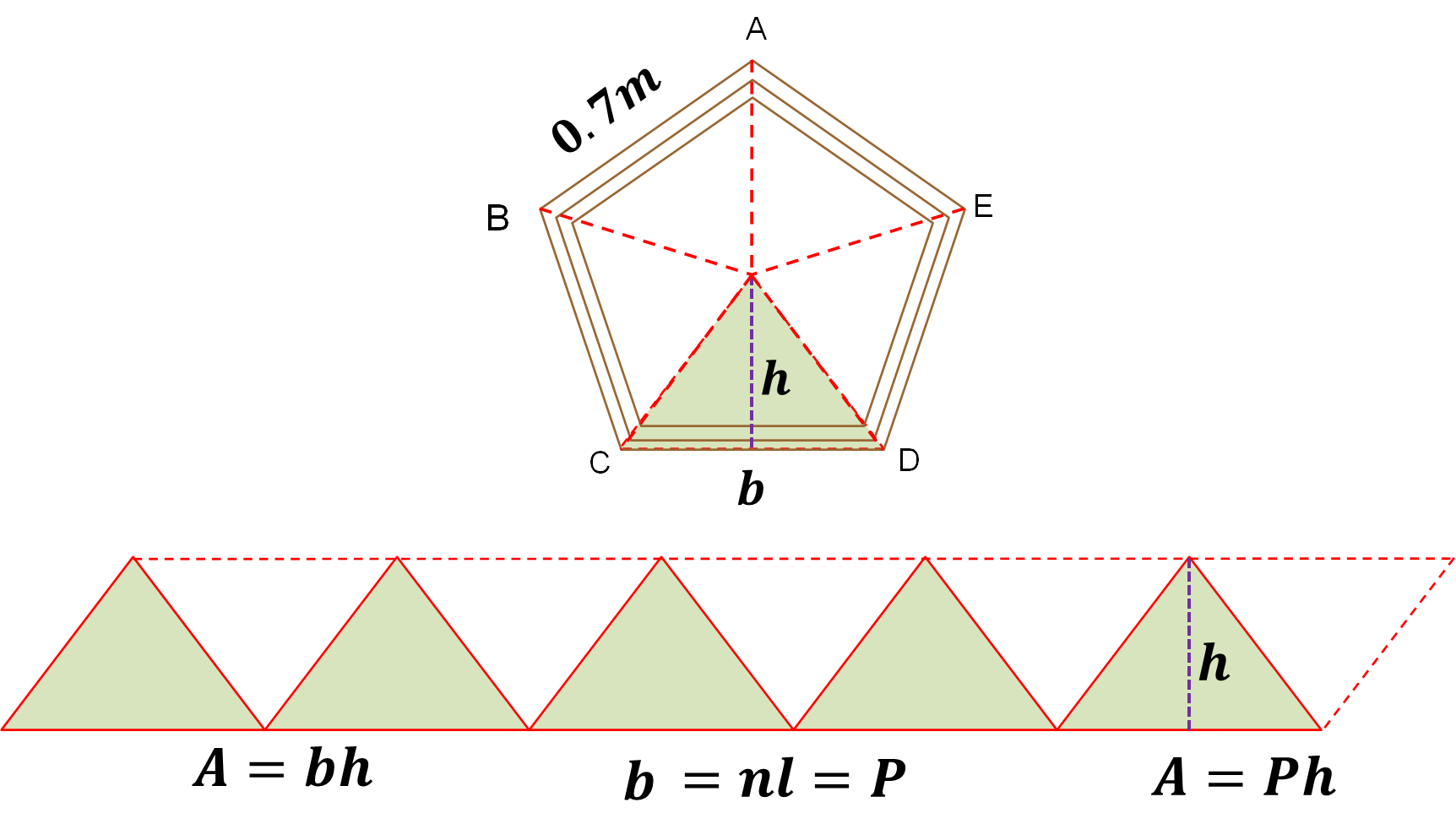
¿Qué figura formó? Él formó un romboide. La fórmula que permite calcular el área del romboide es:
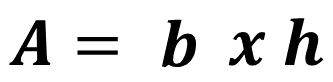
Donde:
b: es la base del romboide. Pero se observa que la base del romboide es igual a “n” por “l”, donde:
n: es el número de lados del pentágono.
l: es la longitud de uno de los lados del pentágono.
Por lo tanto, “n” por “l” es igual al perímetro del pentágono en este caso, y de los polígonos regulares, en general.
h: es la altura de los triángulos, pero en los polígonos regulares se nombra como a: que es la apotema del polígono. La apotema es el segmento que une el centro del polígono con el punto medio de uno de sus lados.
De lo anterior, Carlos concluye que el área del pentágono es la mitad del área del romboide que formó con la mitad de los triángulos del pentágono.
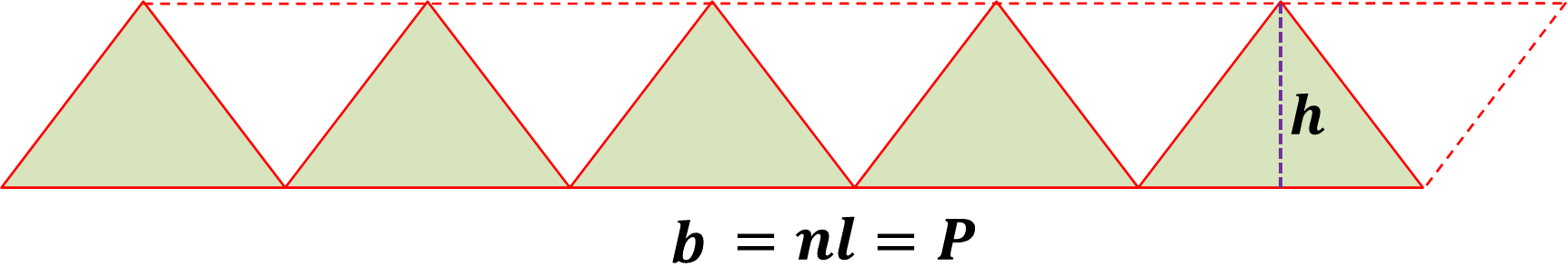
Al sustituir en la fórmula para calcular el área del romboide, la base del romboide por el perímetro del pentágono y la altura del romboide por la apotema del pentágono, se tiene que el área del pentágono es igual a perímetro por apotema. Como el área del pentágono es la mitad del área del romboide, entonces, la fórmula para calcular el área del pentágono es la siguiente:
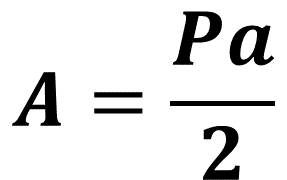
De esta manera, Carlos establece que la fórmula para calcular el área de cualquier polígono regular es área igual a perímetro por apotema entre 2.
Usa esta fórmula para calcular la cantidad de espejo necesario para los marcos que hizo Carlos. Inicia con el pentágono.
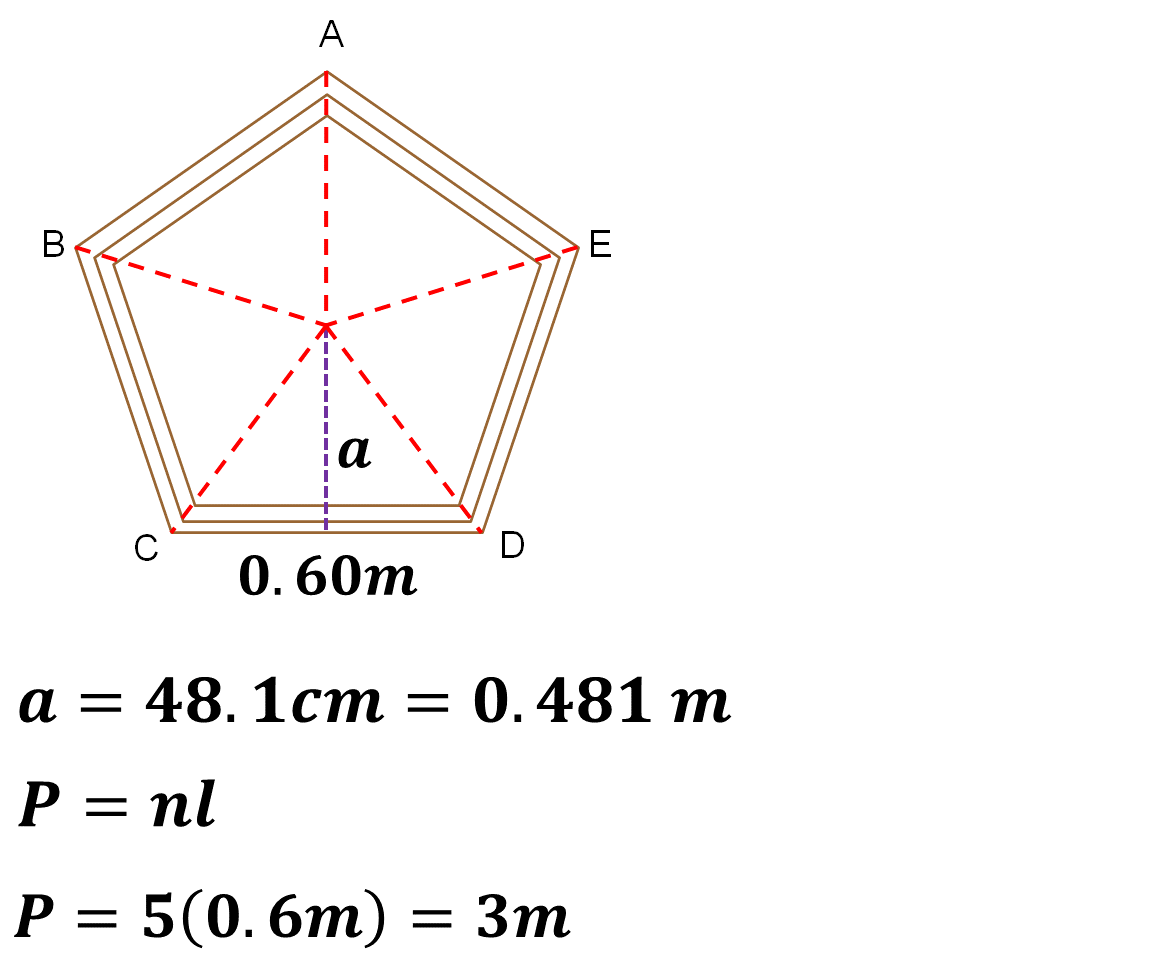
Carlos midió la longitud de la apotema y encontró que mide 0.481 m.
Ya sabes que el perímetro del pentágono es de 3 metros. Utiliza la fórmula y sustituye los valores:
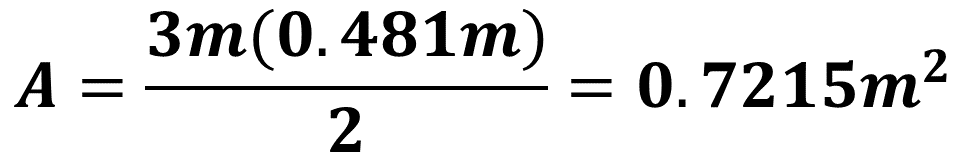
Lo que resulta igual a 0.7215 metros cuadrados, que es área que ocupará el espejo que se colocará en el marco pentagonal.
Toma un tiempo y, con lo realizado hasta el momento, calcula el área total que ocuparán los espejos.
Ya que tengas los resultados, verifícalos y suma cada área obtenida.
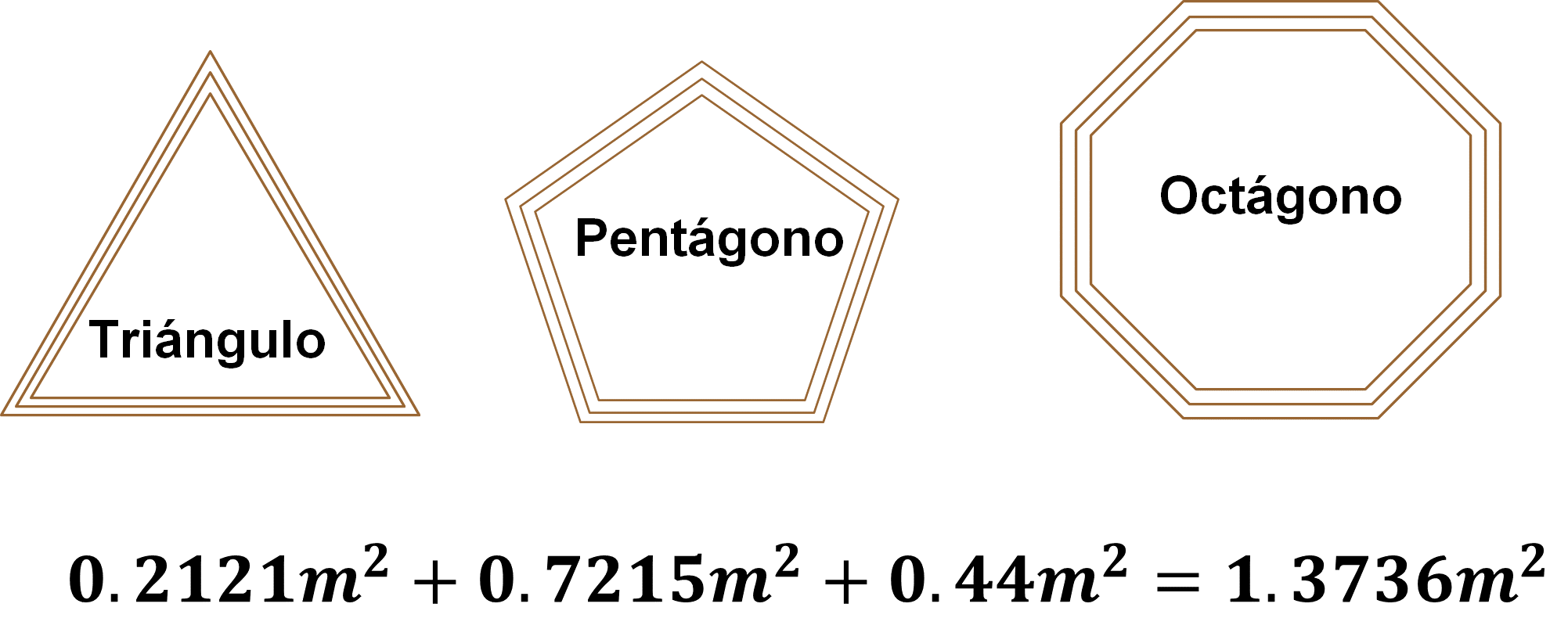
Lo que resulta igual a 1.3736 metros cuadrados. Entonces, la cantidad de vidrio que requiere para los marcos es de 1.3736 metros cuadrados.
Reflexiona sobre lo visto hasta el momento y contesta: ¿qué parte de lo trabajado te resultó más fácil?, ¿en qué parte tuviste mayores dificultades?
No olvides anotar tus respuestas a las preguntas anteriores para aclararlas con tus compañeras y compañeros, así como con tus profesoras y profesores, cuando tengas comunicación con ellos. Es importante que anotes las operaciones y trates de resolverlas con el conocimiento que vayas adquiriendo.
Aplica lo aprendido resolviendo el siguiente problema.
Problema: cuadrado
¿Cuál es el área del siguiente cuadrado?

¿Recuerdas la fórmula para calcular el área de un cuadrado? La fórmula es: área igual a lado por lado.
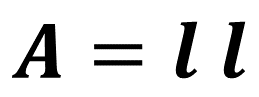
En el caso del cuadrado que se presenta, y de acuerdo con la fórmula anterior, el área es el producto de 5 centímetros por 5 centímetros. Entonces, el área de este cuadrado es de 25 centímetros cuadrados.
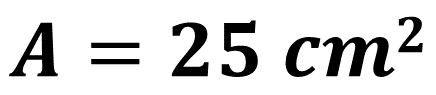
Ahora, reflexiona en la siguiente pregunta: ¿el cuadrado es un polígono regular?
Recuerden que al principio de la sesión se comentó que un polígono regular es aquél que tiene todos sus lados iguales y también iguales todos sus ángulos. ¿Cumple el cuadrado con estas condiciones?
El cuadrado tiene sus cuatro lados de la misma medida y sus cuatro ángulos son rectos. Por ello, se trata de un polígono regular.
Entonces, ¿se puede aplicar la fórmula: área igual a perímetro por apotema entre 2 para calcular el área del cuadrado?, ¿qué piensas al respecto?
Aplica esta fórmula para comprobarlo. Para ello, necesitas conocer la medida de la apotema. Recuerda que la apotema es el segmento que une el centro del polígono con el punto medio de uno de sus lados. Entonces, la apotema de este cuadrado mide 2.5 centímetros.
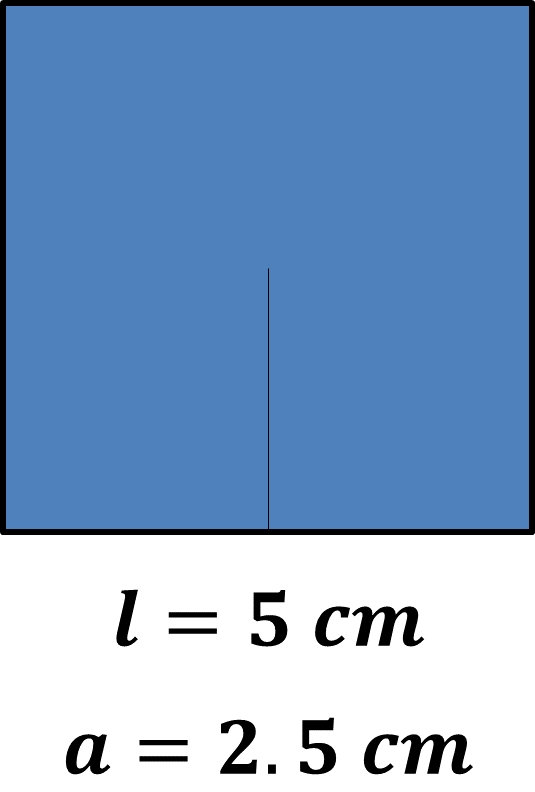
Ya cuentas con la medida de la apotema, ahora aplica la fórmula y sustituye:
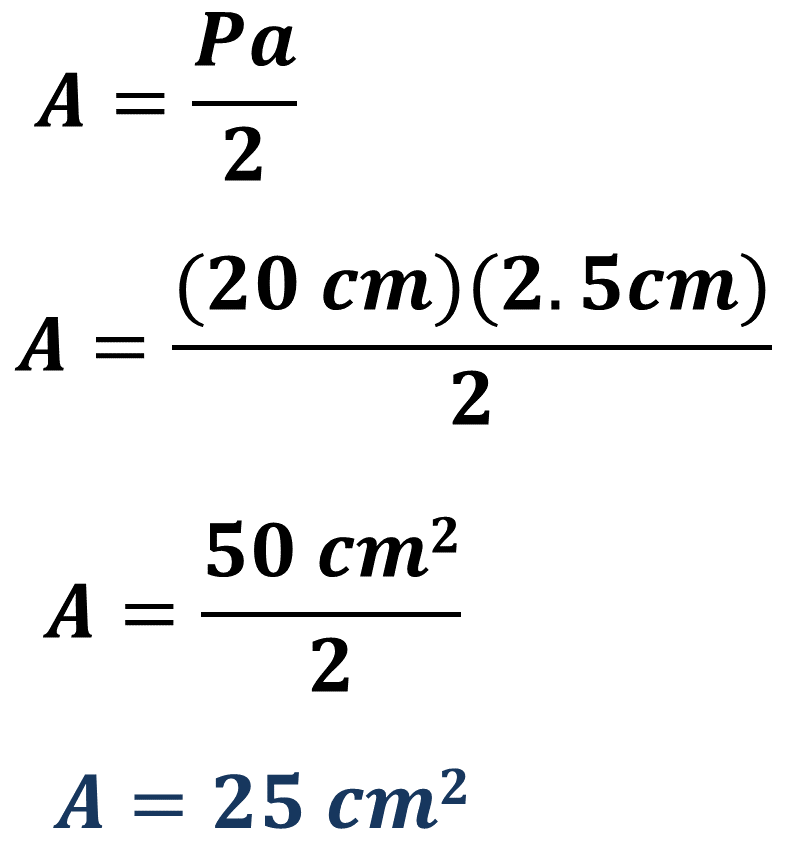
Al resolver las operaciones, el área de este cuadrado es de 25 centímetros cuadrados. El mismo resultado que se obtuvo con la otra fórmula.
Con esto has finalizado la sesión. Es importante que tengas presente que las actividades que se realizaron corresponden a un material de apoyo, y puedes fortalecer lo aprendido resolviendo las actividades del libro de texto de Matemáticas de segundo grado.
El Reto de Hoy:
Calcula el área del siguiente triángulo equilátero que mide 6 centímetros de cada lado.
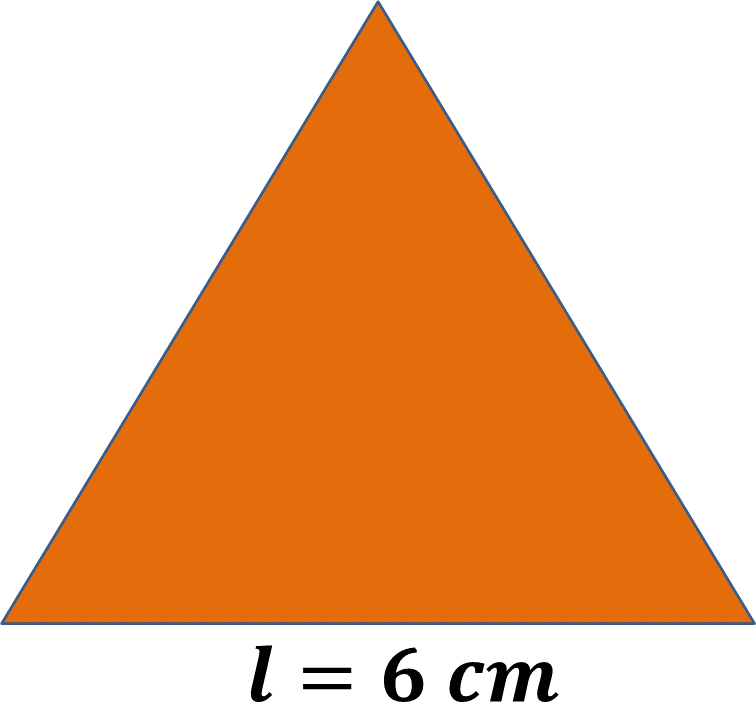
Usa las dos fórmulas para calcular el área, la del triángulo y la de los polígonos regulares. Recuerda trazar el triángulo con esa medida en sus tres lados y toma las medidas necesarias para realizar los cálculos.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Recovecos literarios
Aprendizaje esperado: Crea textos poéticos con formas gráficas.
Énfasis: Explorar diversos formatos y soportes de antologías para compartir poemas.
¿Qué vamos a aprender?
En esta sesión, conocerás diferentes formas para realizar y presentar antologías sobre la poesía. Esto con la finalidad de identificar y explorar, además del mensaje que se transmite, el uso de diversos formatos y soportes como un medio de comunicación y visualizar la creatividad de los creadores de estas formas literarias.
¿Qué hacemos?
Un caligrama es un medio de expresión gráfica que puede representarle al lector una serie de ideas, sentimientos, emociones o sensaciones; por lo tanto, en esta sesión, utilizarás esta estrategia literaria para echar a volar tu imaginación y creatividad para explorar diversos formatos y soportes de antologías para compartir poemas.
A lo largo de tu vida, probablemente hayas visto muros con poemas o frases que van acompañados de dibujos o también el llamado grafiti. Observa las siguientes imágenes tomadas afuera de una estación del metro en la Ciudad de México.

Las imágenes muestran pensamientos de superación pintadas en muros, son coloridas y con diferentes tipos de letras. Pero ¿qué pasaría si estos lugares tuvieran varios poemas con diferentes formas gráficas?, ¿sería una antología?
Seguramente has escuchado sobre las antologías, ya sea de cuentos o poemas y, en tu vida académica, has tenido que elaborar una. ¿Recuerdas alguna antología que te haya gustado mucho?
La antología es una colección constituida por fragmentos de obras literarias, musicales, científicas, entre otras, las cuales pueden ser de uno o varios autores, y éstas son escogidas en función de un criterio o temática. Para profundizar en ello, analiza su definición.
Antología: colección de piezas escogidas de literatura, música, etc.
Diccionario de la lengua española
En el contexto literario, la antología es una compilación de obras ya sea de un mismo autor o de varios. Observa el siguiente video del minuto 1:58 al 2:47, que brinda más información al respecto.
- Paisaje de poemas.
La antología es una colección de textos literarios y está conformada por el título, descripción de la antología y comentario sobre los autores.
Es importante tener en cuenta las características principales de la antología, ya que éstas deben tener una base común, es decir, que traten sobre un género o tema específico. Reúne diferentes fuentes de información, como hechos históricos, noticias o datos que complementan la compilación. Mantiene un mismo formato, es decir, tiene una misma presentación que destaca la selección cuidadosa de la información a utilizar.
La antología debe realizarse de manera detallada, ya que le puede ser de ayuda a alguien más. No olvides que la forma tradicional o convencional de elaborar una antología es en forma de libro, ya sea elaborada a mano o en computadora.
A continuación, retoma el video “Paisajes de poemas” y observa del minuto 1:17 al 1:54, para conocer las opiniones de algunas y algunos alumnos de secundaria.
- Paisaje de poemas.
Para elaborar una antología de poemas hay que pensar primero en el tema, de ahí comenzará la búsqueda por los diferentes poemas que lo aborden y se tendrá el material para ir armando esta compilación de una manera creativa.
Realizar una antología no sólo es recopilar textos, el tema habla mucho de la persona que realiza la compilación, muestra sus intereses, anhelos y emociones; por lo que, para romper con lo tradicional, se propone elaborar un trabajo más didáctico, creativo, artístico y visual, con el que seguramente cambiará tu concepto respecto a la poesía.
El arte de expresarse no tiene límites, un pensamiento, un poema o un acróstico pueden estar presentes en la vida diaria y tal vez no habías puesto atención.
Observa el siguiente poema titulado “autoreflejo”, el cual escribió la alumna Carla y lo transcribió a un espejo, pues el tema lo relaciona con el objeto en cuestión.

La alumna decidió representar su poema en un espejo, pues el texto que es de su autoría le recuerda día con día que mirar lo físico no es lo importante para ella, sino la belleza interior de los demás. Ella eligió este objeto porque está presente en su entorno y porque se relaciona con la temática desarrollada.
Siguiendo con la misma línea, esta alumna realiza sus escritos o pensamientos y busca lugares o materiales comunes en su vida cotidiana. Observa otro ejemplo, el cual plasma en uno de sus cuadernos de clase.

En este caso, la alumna pone su pensamiento en la portada de uno de sus cuadernos de clase, se observa que lo decoró y en él se ve reflejado su sentir, su uso práctico es que cada vez que ella trabaje con este material recordará su mensaje. Indudablemente, los cuadernos son objetos inherentes a la vida académica, por lo tanto, el acercamiento a estos pensamientos estarán al alcance en todo momento.
Los textos poéticos pueden representarse de diversas formas, si cuentas con cuadernos que ya no usas, puedes reciclarlos y crear un espacio muy propio en el cual representes tus pensamientos, es decir, tu propia antología. Incluso, podrías plasmar poesía en un jarrón, en una taza o en tu pared, pues cada vez que veas estos objetos, observarías tus obras.
Esta manera de representar la poesía en sus diversas formas es una opción para hacer una antología visual, no se requiere encuadernarla y dejarla olvidada para consultarla de vez en cuando. Si buscas maneras creativas de representarla, estarás creando nuevas perspectivas para que tú y los demás tengan un acercamiento a la poesía.
Retomando la idea de la pared, ésta es una propuesta de la alumna Iridia, ella realizó su escrito en el muro de su habitación. Observa con atención.

La alumna escribió un poema de un dragón, el cual pintó en la pared de su recámara, alrededor de la figura puso los versos en los cuales utilizó una estrofa con versos pareados (dos versos), una con terceto (tres versos) y una con cuarteto (cuatro versos). Como puedes observar, su trabajo quedó plasmado para que los demás lo puedan observar.
Esta es otra manera creativa de exponer los poemas a los demás, de mostrarles a través de las formas visuales que la poesía tiene algo que decir y no sólo de una forma tradicional.
En diversas áreas se pueden exponer obras artísticas, como las presentadas hasta el momento, y crear así una exposición permanente; recuerda siempre pedir autorización a los mayores para colocar tus trabajos.
Existen muchas formas de expresar los poemas, observa otra manera en la que puede quedar plasmado un acróstico, la misma alumna Iridia hizo lo siguiente.

En la playera, ella escribió lo siguiente sobre la vida:
“Vivo feliz mi vida
Ilusionada por lo vivido
Doy lo mejor que tengo
A pesar de mi juventud”.
En este ejemplo, se puede ver el proceso de cómo acomodó los versos y luego los detalles que le agregó a la camiseta.
Ahora, observa la siguiente imagen.

En esta imagen, se puede observar que la alumna realizó un caligrama con forma de flor-corazón, y le puso las letras con recortes de periódico, además lo enmarcó, su creación dice lo siguiente:
Mi cora…
“Es medio alocado
mi corazón apasionado.
Con su latir me deslumbró,
en un momento inesperado.
Siempre tan humano,
aunque para otros no lo será.
Eres mi gran cora…
y mi gran regalo”.
Estos son otros formatos muy creativos en los que se pueden visualizar textos literarios, la alumna representa su sentir y, además, lo plasma en un objeto práctico para que quien lo vea entienda el mensaje de trasfondo. En el caso de la playera, expondrá su mensaje cada vez que se la ponga, escogió un objeto muy personal para mostrar su creatividad; y en el caso del cuadro, es una forma de exponer dentro de su casa la libertad expresiva que posee. Con estos objetos ella reconoce un entorno libre donde puede seguir creando poesía.
El diseño lo puede proponer cada persona, sólo es cuestión de seleccionar el texto, el objeto o el lugar donde quedará plasmado el trabajo, la creatividad hablará por sí sola.
A continuación, observa cómo representa la alumna Melanie Michelle un poema de creación propia, el cual se titula “Canto nórdico melodioso”.
- Video. Poema “Canto nórdico melodioso”.
Indudablemente, la creatividad para expresar arte de diversas maneras y en diversos objetos o lugares existe, sólo es cuestión de decidir qué hacer y dónde, para poner manos a la obra como lo hizo la alumna Michelle, pues ella, con materiales que tenía en casa, hizo su trabajo, el cual exhibirá en la sala de su casa.
Ya que has revisado diversas formas de representar la poesía, ha llegado el momento de crear. Para ello, plasma un poema utilizando una cartulina, hojas de árbol secas, colores, pegamento y mucha creatividad.
Si no cuentas con estos materiales, puedes aprovechar los que tengas en casa o a tu alrededor, y con ellos hacer obras de arte visual. Recuerda que se trata de presentar una antología poética de manera diferente a la tradicional. No olvides que estás jugando y experimentando con las formas gráficas para escribir un poema. Entonces, manos a la obra.
Primero, debes tener elaborado el poema. En este caso, trabajarás con un haiku sobre el otoño, escrito por Mariana. El cual dice así:
“El viento fuerte
tirando las hojas
mostrando el otoño”.
Como este haiku habla de hojas, dibujarás un árbol en una cartulina o un material más duro, debes tener en cuenta que el tamaño del árbol y sus brazos dependerán de las hojas que logres recoger.
Dentro de cada una de las hojas, dibujarás las letras del haiku y luego puedes jugar y acomodarlas en el árbol que has dibujado, el punto es que estén de tal manera acomodadas que se lea con facilidad el poema.
Puedes pintar tu cartulina y hacer la forma del árbol con distintos materiales o sólo dibujarlo, también puedes pintar tus hojas o dejarlas al natural y sólo dibujar las letras. Sólo recuerda que las hojas deberán estar completamente secas. Echa a volar tu imaginación e incluso puedes recortar las hojas simuladas de materiales que tengas a la mano.
Esta forma de presentar un poema muestra cómo se puede jugar con los colores y tamaños de las letras y las hojas, lo cual le da una presentación diferente.
Como observaste con las otras formas de presentar poemas, la creatividad y el ingenio no tiene límite, puedes crear una antología fuera del papel y trasladarlo a varios objetos de una forma creativa y original.
Ahora, escucha al poeta Oscar de Pablo, quien da algunos consejos para realizar una antología. Observa el video del minuto 3:46 al 6:18.
- Paisaje de poemas.
Después de escuchar los consejos del poeta Oscar de Pablo, ya cuentas con diversas herramientas para salir de lo convencional y realizar una antología, jugar con la imaginación y con los elementos y materiales con los que se cuenten al momento de realizarla. Ten en cuenta que la poesía es un universo de palabras que misteriosamente hablan de un todo, de una manera interesante y que, si a esto se le agrega un toque de creatividad, el gusto por ella será mayor.
Has finalizado la sesión. Para reforzar tus conocimientos, cuentas con la ayuda de tu libro de Lengua Materna 2.
También puedes buscar en libros de poesía que tengas en casa, en fuentes confiables de páginas de internet o preguntar a tus familiares y conocidos sobre el tema.
El Reto de Hoy:
Escoge o escribe algunos poemas para realizar tu propia antología. Elige los materiales que tengas a la mano y ponle tu toque personal. Con tu imaginación y creatividad lograrás trabajos únicos y expresivos.
Una vez que hayas terminado tu trabajo, compártelo con tus amigas, amigos y familiares, y pídeles una opinión sobre tu antología o invítalos a realizar la actividad. Recuerda que siempre se puede mejorar con las opiniones y el apoyo de los demás.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Tycho Brahe: un astrónomo fuera de este mundo
Aprendizaje esperado: Analiza la gravitación y su papel en la explicación del movimiento de los planetas y en la caída de los cuerpos (atracción) en la superficie terrestre.
Énfasis: Conocer y reflexionar sobre las aportaciones de Tycho Brahe y el estudio del sistema solar.
¿Qué vamos a aprender?
Estudiarás sobre los avances tecnológicos que disfrutamos en la actualidad, como el telescopio, los satélites y muchos aparatos más, gracias a las aportaciones de grandes científicos. En esta sesión, conocerás sobre el estudio y las aportaciones del astrónomo Tycho Brahe.
¿Qué hacemos?
Antes de iniciar, responde las siguientes preguntas para que, al finalizar la sesión, revises tus respuestas y compruebes si tu forma de pensar con respecto a la formación del universo es la misma después de haber analizado la información que se presentará aquí.
- ¿De qué manera están relacionados los conocimientos de los filósofos y científicos de la Antigüedad con nuestra vida cotidiana?
- ¿Crees que exista una diferencia en la forma de percibir y observar los fenómenos naturales que sucedían en la Antigüedad con la de la vida actual?
- ¿Consideras que los estudios de los antiguos científicos sobre el sistema solar son relevantes para conocer y entender el universo en nuestros días?
En sesiones anteriores, analizaste cómo grandes filósofos y científicos como Aristóteles, Ptolomeo, Nicolás Copérnico, Johannes Kepler, Galileo Galilei, Isaac Newton y muchos científicos más, como en este caso, Tycho Brahe, han aportado grandes conocimientos derivados de sus observaciones sobre las estrellas, planetas y sobre cómo está formado el sistema solar y el universo en general.
Estas teorías han permitido a la humanidad evolucionar en sus conocimientos, diseñar equipos e instrumentos que, con el tiempo, ayudaron a tener grandes avances tecnológicos. Gracias a esto, se logró conocer lugares nunca vistos por los científicos de esa época que sólo usaban sus sentidos.
Los conocimientos de estos grandes científicos estaban tan limitados por las prohibiciones de la Iglesia, los prejuicios de la sociedad, la falta de tecnologías para sus investigaciones y las supersticiones por lo desconocido, que lo único que podían usar era su imaginación.
En esa época, estaba prohibido expresar las ideas o investigar sobre algún fenómeno de la naturaleza que no estuviera relacionado con Dios. Quien se atreviera a hablar sobre cualquier cosa científica, le acusaban de brujería o herejía; en la mayoría de las veces, si alguien inventaba un instrumento o descubría algo, preferían mantenerlo en secreto. Una superstición es una creencia que no tiene explicación racional.
Si la Iglesia se enteraba de algún descubrimiento científico, los acusaban de brujería ante la Santa Inquisición, la cual los torturaba o los mataba. Sólo si un rey o una persona con mucho poder los protegía, podían desarrollar el pensamiento científico, como sucedió en muchos casos, pero existieron muchos filósofos o científicos que no contaban con el apoyo de ningún rey y fueron perseguidos, por ejemplo, el filósofo Platón, Kepler o Galileo Galilei.
Las supersticiones o prejuicios eran un obstáculo para que se pudiera desarrollar la ciencia, por ejemplo, durante un eclipse solar, si se obscurecía durante el día, pensaban que era un mal presagio, que Dios los castigaba con la obscuridad, y nadie salía de su casa por miedo a que les pasara algo, sin saber que era un fenómeno natural.
El temor y la ignorancia de la gente impedían su desarrollo intelectual, eran su propio enemigo. Desde la época de Aristóteles se sabía de la existencia de este fenómeno astronómico, pero fue tal el impacto que generó en Tycho Brahe cuando lo vio, que se dedicó a investigar sobre él, descubriendo que se repetía cada cierto tiempo y que recibía el nombre de eclipse, por lo que, desde ese momento, Tycho Brahe se enamoró de la astronomía.
Los conocimientos de los científicos de esa época fueron adquiridos aplicando al máximo sus sentidos; sólo con sus habilidades naturales y paciencia pudieron desarrollar su capacidad de observación para la reflexión, el análisis y, en algunos casos, la reproducción de los fenómenos naturales.
Ahora podemos llamarlos grandes pensadores y científicos, pero ellos no contaban con ningún instrumento para observar el cosmos, hasta 1609, cuando se inventó el telescopio. Pero ¿quién era Tycho Brahe?
Tycho Brahe nació en 1546, en el antiguo reino de Dinamarca, ahora Suecia. A la edad de dos años, sus padres lo dejaron al cuidado de su tío Joergen Brahe, quien le proporcionó estudios y una educación muy estricta. Al cumplir 13 años, fue enviado a la Universidad de Leipzig, en Copenhague, para continuar con la carrera de Leyes y Filosofía, ya que su tío pretendía que continuara su carrera al servicio del rey como su consejero.
En el año 1560, cuando se produjo un eclipse de Sol, Tycho Brahe se impresionó tanto que decidió investigar sobre el fenómeno, enamorándose de la astronomía.
Con la ayuda de algunos maestros de astronomía en la Universidad, aprendió a identificar las estrellas de los planetas. Le enseñaron a medir las angulaciones y a elaborar tablas astronómicas. Con estos aprendizajes pudo observar que, durante la conjunción entre Júpiter y Saturno, se incurría en un error en las predicciones astronómicas, lo que lo llevó a diseñar nuevas cartas de previsiones; consideraba que éstas necesitaban medidas sistemáticas de observación; también se opuso a las teorías de Aristóteles con respecto a su teoría geocéntrica.
Las cartas astronómicas son aquellos escritos en donde se describían las coordenadas, el color, la posición y la temporada del año en la que se podían observar las estrellas, como en la siguiente imagen.
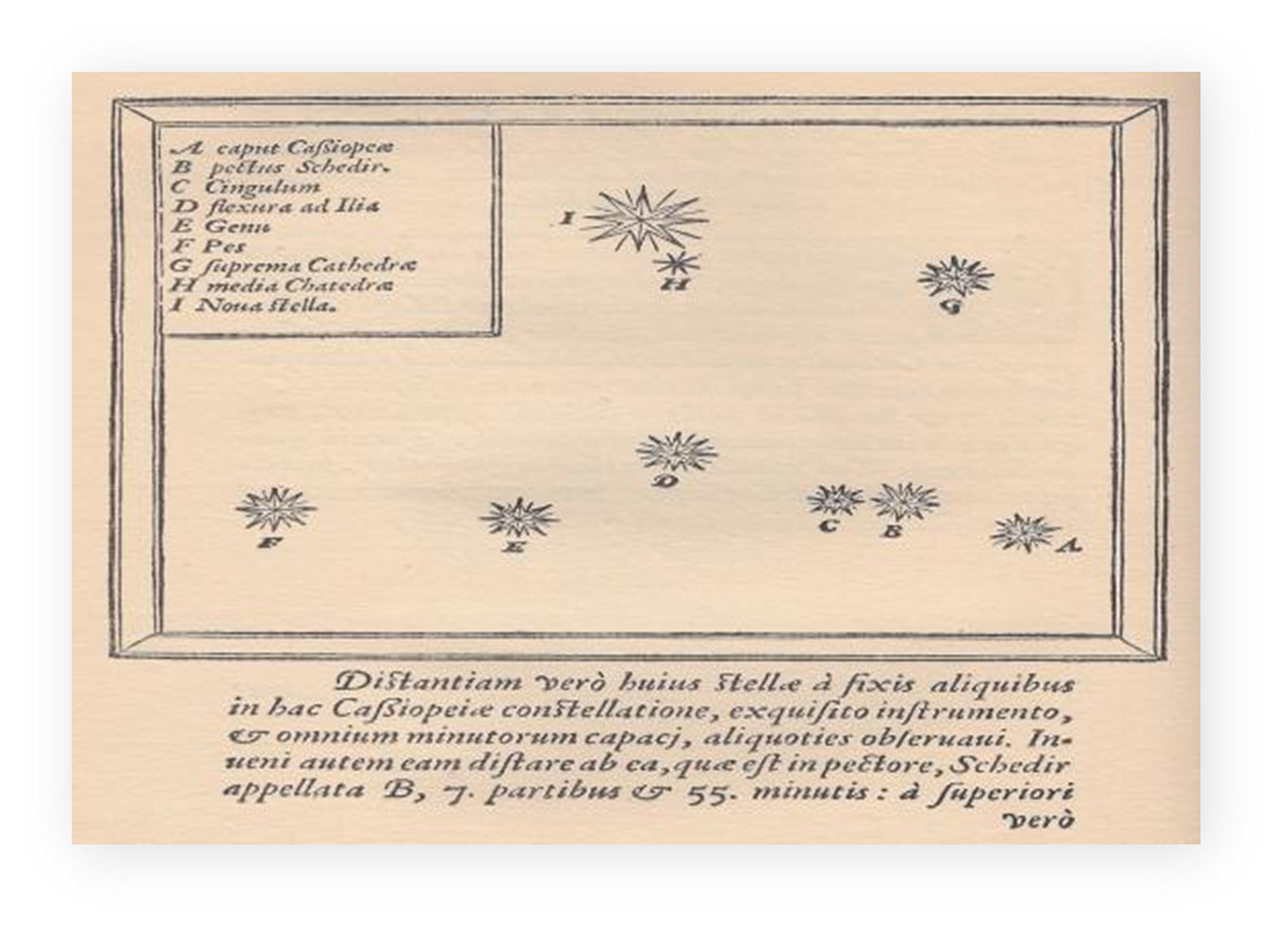
La teoría geocéntrica afirmaba que el Sol, los planetas y las estrellas giraban en torno a la Tierra. La teoría geoheliocéntrica, que proponía Tycho Brahe, afirmaba que la Luna y el Sol giraban en torno a la Tierra, mientras que Marte, Mercurio, Venus, Júpiter y Saturno giraban alrededor del Sol.
En 1572, mientras Brahe observaba el cielo, apareció una estrella que jamás había visto. Esta estrella era una nova, a la cual observó durante un año. Con esta observación pudo contradecir la idea vigente de que las estrellas eran fijas; estas ideas eran inmutables. Esta supernova ahora lleva su nombre.
En 1573 publicó un escrito que llevaba por nombre “De Nova Stella”, el cual alcanzó una gran popularidad. El rey Federico II lo nombró matemático de la Corte hasta que en 1588 falleció, lo que supuso la pérdida de los privilegios que tenía como astrónomo, por lo que tuvo que abandonar la isla de Hven.
Para el año de 1599 fue acogido en Praga por el rey Rodolfo II, quien lo convirtió en el matemático imperial. Por esa época conoció al famoso astrónomo Johannes Kepler, a quien tomo como discípulo y, aunque no se llevaban bien, con el tiempo tuvieron una fructífera colaboración.
El 13 de octubre de 1601 fue invitado a un banquete en la Corte del barón Rosenberg, su protector. En aquella época se consideraba de mala educación levantarse de la mesa antes de que los demás comensales terminaran de comer y antes de que se levantara el anfitrión, por lo que aguanto tanto que le provocó una infección en la vejiga que le impidió orinar con normalidad. Tras 11 días de dolorosa agonía, su vida llegó a su fin, pero antes de morir, le obsequio sus escritos a Johannes Kepler, le pidió que no los dejará en el olvido y que la clave de estos estudios era Marte y debía seguir observándolo. En su agonía le repitió a Kepler: “Non Frustra vixisse vidcor”, que significa: “no he vivido en vano.”
Johannes Kepler estaba tan agradecido con Tycho Brahe, que nunca olvidó su promesa de estudiar, analizar y descifrar los misterios que Tycho había descrito en sus manuscritos, y cuando postuló las leyes del movimiento de los planetas, le dio crédito a Tycho Brahe.
Tycho Brahe fue una de las grandes mentes de la Edad Media que hicieron posible el avance científico en la investigación y misterios del sistema solar y el universo.
La observación de las estrellas era una cualidad que caracterizaba a este científico, ya que tenía una habilidad y paciencia para distinguir y clasificar lo que observaba en el cielo, sobre todo, de noche.
Tycho Brahe inició con lo que se conoce como “la nueva astronomía”. El legado de Tycho Brahe a la astronomía es enorme, gracias a él se llegó a investigar con mayor profundidad el universo y se pusieron en duda muchas teorías de épocas pasadas. Tycho Brahe es considerado uno de los más importantes astrónomos, fue fuente de inspiración para muchos otros, como Kepler, a quien pidió que terminara su obra.
Johannes Kepler llegó a decir antes de su muerte:
“Confieso que cuando Tycho Brahe murió, rápidamente me aproveché de la ausencia o falta de circunscripción de sus herederos tomando las observaciones conmigo, quizá, usurpándolas, gracias a esos datos, pude deducir las órbitas planetarias, por eso ahora reconozco el valor que se merece Tycho Brahe”.
Así Kepler pudo formular sus tres leyes del movimiento de los planetas en su órbita alrededor del Sol.
Gracias a esos gigantes del conocimiento, nosotros podemos disfrutar de las comodidades y tecnologías actuales; aunque no lo creas, muchos de los avances tecnológicos y científicos de esta época se basan es esas teorías.
El uso de los telescopios espaciales como Hubble, la sonda Viking o el satélite artificial Sputnik y muchos aparatos más, se debe, en gran parte, a estos trabajos y observaciones que a muchos científicos les dañaron los ojos sin saberlo, ya que de tanto observar los astros durante el día y la noche, perdieron la vista, parcial o totalmente, como Galileo Galilei, dejando un gran legado a la astronomía y al estudio del universo.
Aunque Brahe pasó a la historia por sus observaciones del cielo nocturno, este astrónomo también dedicaba parte de su tiempo a hacer experimentos alquímicos. Desafortunadamente no ha llegado mucha información sobre sus experimentos hasta nuestros días, porque procuraba reservarla para sus mecenas, y su laboratorio fue destruido después de su muerte, pero se sabe que su trabajo alquímico estaba inspirado en la obra de Paracelso y orientado hacia la vertiente «medicinal» de esta actividad.
Teniendo en cuenta que la actividad alquímica de la época solía involucrar el uso de mercurio o plomo y que otras mentes brillantes de la época aficionadas a la alquimia, como Isaac Newton, sucumbieron a los efectos neurotóxicos de estos metales, cualquiera hubiera dicho que el comportamiento estrafalario de Brahe podría ser un resultado de su exposición constante a este elemento. Pero, no, nada más lejos de la realidad.
En el 2016, el cuerpo de Brahe se exhumó y se analizaron químicamente muestras de pelo y huesos de sus restos. La concentración de mercurio, plomo y arsénico que exhibía el cuerpo del astrónomo no era elevada en comparación con la del resto de la población de la época, lo que indica que no fue expuesto a una cantidad elevada de estos elementos debido a su actividad alquímica. El cuerpo sí que presentaba niveles altos de hierro y manganeso, pero estos elementos se debieron depositar sobre él, después de que falleciera, a través del agua que se filtraba en su tumba.
El mismo análisis arrojó un resultado sorprendente: el cuerpo de Brahe contenía niveles de oro entre 21 y 97 veces superiores a los de un ser humano moderno.
Los propios autores del estudio indican que no están seguros de cuál era la fuente de oro a la que estaba expuesto Brahe, pero especulan que, dada su condición de noble, podría haber entrado en contacto a menudo con este metal a través de una cubertería hecha de oro o de platos chapados en él. Además, también señalan que el astrónomo podría haber consumido pan de oro con regularidad o que ingiriera algún brebaje a base de oro, ya que, en esa época, a este valioso metal se le atribuían propiedades medicinales.
Sea cual sea el caso y teniendo en cuenta que conociste sobre Tycho Brahe, un cadáver enriquecido con oro simplemente pasará a ser un dato curioso más de una larga lista de datos excéntricos que rodean la interesante figura de este astrónomo.
Tycho Brahe vivió con el lema "Non viduri sed esse"; traducido al español dice: "Aunque no lo podamos ver, no significa que no está ahí". Con esto, has concluido la sesión. No olvides comentar con tu familia acerca de los científicos de otras épocas y sus aportaciones para mejorar nuestra vida en la actualidad.
El Reto de Hoy:
Revisa las preguntas que se presentaron al inicio de esta sesión y compleméntalas con lo que aprendiste o con información que encuentres en fuentes o en sitios de internet confiables.
- ¿De qué manera están relacionados los conocimientos de los filósofos y científicos de la Antigüedad con nuestra vida cotidiana?
- ¿Crees que exista una diferencia en la forma de percibir y observar los fenómenos naturales que sucedían en la Antigüedad con la de la vida actual?
- ¿Consideras que los estudios de los antiguos científicos sobre el sistema solar son relevantes para conocer y entender el universo en nuestros días?
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
La cultura de paz y no violencia: estrategias ante la violencia
Aprendizaje esperado: Promueve la postura no violenta ante los conflictos como un estilo de vida en las relaciones interpersonales y en la lucha social y política.
Énfasis: Reconocer los tipos de violencia y las implicaciones de la cultura de paz y no violencia para erradicarlos.
¿Qué vamos a aprender?
Reflexionarás sobre aspectos que te permitirán reconocer qué es la violencia, los tipos de violencia que existen, cómo identificarlos y algunas sugerencias para fomentar la postura de la cultura de paz y no violencia ante situaciones o hechos violentos.
¿Qué hacemos?
Antes de iniciar, no olvides anotar por lo menos cinco ideas generales sobre el tema de esta sesión, así como todo lo que consideres relevante, ya que servirá de insumo para la elaboración del reto al final.
Seguramente has escuchado infinidad de veces la palabra violencia en las noticias, en la calle, en la colonia, inclusive en la escuela, pero ¿es fácil identificar un hecho, acto o comportamiento violento? Para poder responder esta primera pregunta de forma reflexiva e informada, presta atención en lo siguiente.
La violencia se define como una manifestación extrema de abuso de poder, teniendo varias maneras de expresarse y sus causas son múltiples. Se distinguen tres grandes tipos de violencia: directa, estructural y grupal. Para conocer más de ellas, observa el siguiente video del minuto 1:19 al 3:31.
- Las violencias en la convivencia cotidiana.
https://www.youtube.com/watch?v=T_X1xAO9SmQ&t=60s
Se puede tener una primera conclusión al argumentar que las violencias directa, estructural y cultural están de alguna manera vinculadas y unas permiten que las otras existan o surjan.
La violencia directa se materializa en hechos que van en contra de las necesidades básicas, como golpes, insultos, acoso y represión; sus consecuencias afectan el desarrollo y derechos de todas las personas.
La pobreza, el desempleo y la falta de acceso a la educación son algunos ejemplos del tipo de violencia estructural que está en las raíces de la violencia directa.
La violencia de tipo cultural o simbólica se trata de un poder sutil, instalado en usos, costumbres y expresiones cotidianas, como el lenguaje, formas de pensar, religiones o estereotipos, por ejemplo, en expresiones como “los niños no lloran”, “corres como niña”, etc.
En la siguiente imagen se puede observar el triángulo de la violencia, que Galtung dividió horizontalmente en dos planos: arriba colocó la violencia directa, que está en el plano de lo visible, y en la base, del lado derecho, colocó la violencia estructural y del lado izquierdo la violencia cultural, ambas están en el plano de lo invisible.
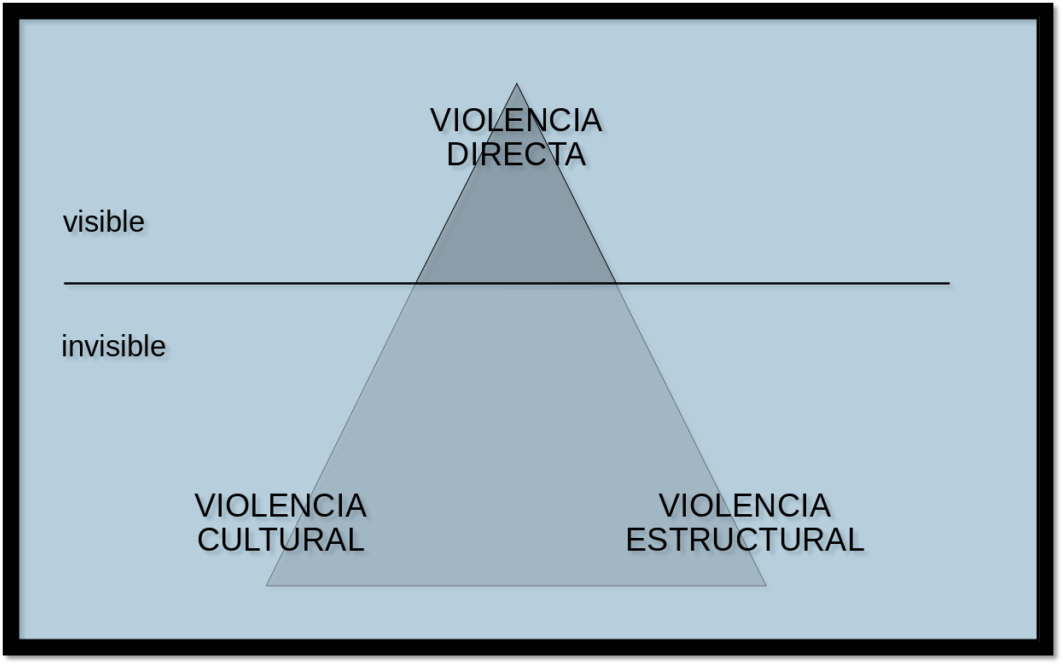
Después de haber visto el video y la imagen de la pirámide de Galtung, se pueden identificar los tres tipos de violencia: directa, estructural y cultural.
Ahora, reflexiona en las siguientes preguntas: ¿qué sucede si no puedo reconocer la violencia en la vida cotidiana?, ¿qué se puede hacer para lograr identificar los actos o manifestaciones de violencia?, ¿cómo prevenir y atender la violencia si escapa al reconocimiento oportuno?
Para responder estas preguntas, se necesita información como la que has reflexionado. Además, debes sensibilizarte y concientizarte para identificar en la convivencia diaria cualquier acto o manifestación de violencia.
Sin embargo, no siempre es sencillo pues hay formas de actuar que pueden ser tan comunes que se toman casi como normales y dejan de verse como violencia. En la casa, con las amigas y los amigos y en la escuela, establecemos formas de convivencia que tienen como referencia actitudes violentas y que se han ido naturalizando en las relaciones que establecemos.
Por eso es importante que te des un espacio para reflexionar sobre lo que has vivido y preguntarte: ¿dirías que en tu escuela y en tu localidad hay paz?, ¿por qué?
Piensa un poco en las respuestas y considera:
- Si alguna vez has recibido violencia.
- Si has hecho algo cuando la vives.
- Si no has hecho algo.
- Si lo has comentado con alguien.
- Si has ejercido violencia.
- Cuando observas que alguien más es víctima de violencia, ¿qué haces?
Al identificar en qué posición te has encontrado, también reflexiona y valora qué tipo de ambiente has ayudado a construir para evitar situaciones de violencia, ya sea en tu casa, escuela, comunidad, espacio recreativo u otro.
Para reflexionar un poco más sobre el tema, observa el siguiente video del minuto 1:10 al 3:53.
- Reconocimiento y valoración de los conflictos.
https://www.youtube.com/watch?v=78xODu81594
El conflicto se puede resolver de forma pacífica o violenta y, por lo tanto, es muy importante reconocer la presencia de la violencia en la vida cotidiana, para ello, debes reflexionar sobre las implicaciones de ésta en la vida de las personas.
Para una mejor comprensión, observa la explicación del siguiente recuadro, titulado “La violencia afecta a todos”.

¿Alguna de esas frases te suena conocida? Cada una de esas cinco personas representa una forma de violencia y, es de suma importancia reconocerla, ya que sólo de esa manera podremos construir condiciones de justicia y paz.
En los relatos que presentan las personas, se manifiestan la violencia directa, la estructural, la cultural y la simbólica, de acuerdo con lo mencionado por Galtung.
Cuando se habla de justicia, se refiere a lograr que todas las personas tengan aquello que necesitan y merecen para vivir plenamente y con dignidad. Existe ahí, donde las personas se reconocen como iguales en derechos, se evitan y castigan los abusos y se procura el bienestar tanto personal como colectivo.
Por otro lado, de acuerdo con Lederach, existe más de una forma de concebir la paz. Históricamente, expresa un ideal y una ilusión humana muy deseada y buscada, siendo ésta sinónimo de felicidad, tranquilidad y serenidad. Por su parte, Alba retoma el concepto anterior y distingue dos conceptos de paz: negativa y positiva.
¿Alguna vez pensaste que existía la paz negativa? Analiza a qué se refiere en el siguiente esquema:
|
Paz negativa |
|
|
La paz como armonía interior |
Se relaciona con la ausencia de conflictos y problemas, es decir, la paz si no se tienen o se evitan los conflictos. |
|
La paz como ausencia de guerra |
Se define como la ausencia de conflictos bélicos. La paz se impone mediante las armas y la guerra contra quienes no aceptan el orden establecido por un gobierno o dictadura militar. |
|
Paz positiva |
|
|
La paz como presencia de justicia |
Se define por la presencia de la justicia social y el bienestar, por la satisfacción de las necesidades básicas de todas las personas y grupos sociales, tanto en el sentido espiritual y material. La paz es un proceso, algo que hay que construir. |
La paz es un tema extenso para explicar en la historia de la humanidad, pero simple en su práctica, por ello, es importante abordar el siguiente punto. Presta atención en las siguientes recomendaciones para identificar la violencia desde la cultura de paz y no violencia.
Primero, debes saber a qué se refiere la cultura de paz. La Organización de las Naciones Unidas la define como una serie de valores, actitudes y comportamientos que rechazan la violencia y resuelven los conflictos mediante el diálogo y la negociación entre las personas, los grupos y las naciones, basada en el respeto a los derechos humanos.
En 1999, la Organización de las Naciones Unidas para la Educación, la Ciencia y la Cultura (Unesco) definió algunos de estos elementos e invitó a todas las personas y las naciones a trabajar sobre ellos como retos del nuevo siglo. Observa cuáles son:
- Respetar la vida: implica poner fin a la violencia y actuar para que esto suceda.
- Respetar todos los derechos humanos y las libertades de las personas y los pueblos.
- Comprometerse a enfrentar pacíficamente los conflictos.
- Velar porque se proteja el medio ambiente.
- Respetar el derecho de las personas y los pueblos a desarrollarse. Por ejemplo, superar la pobreza.
- Asegurar que exista igualdad de derechos y oportunidades entre mujeres y hombres.
- Cuidar que se respete el derecho de todos a expresarse, opinar e informarse con libertad.
- Comprometerse con valores como la justicia, la solidaridad, la cooperación y el respeto a la diversidad.
- Respetar el derecho que tienen las naciones a decidir su destino, sin que otros quieran intervenir.
La construcción de una cultura de paz es un tema de interés mundial y es imperante poner de nuestra parte para que juntas y juntos podamos lograrlo. Recuerda que no existen esfuerzos pequeños, pues todo suma, y al comenzar con nosotras y nosotros mismos en el lugar en donde vivimos, se mirará con mayor posibilidad de alcanzar estos objetivos.
Todo lo que has aprendido hasta este momento, tiene el propósito de que puedas encontrar acciones que favorezcan una cultura de paz y no violencia ante situaciones o hechos violentos.
Antes de finalizar, recapitula. En esta sesión se explicó qué es la violencia, cuáles son los tipos de violencia que existen, así como cuáles son las consecuencias de no reconocer la violencia en la vida cotidiana.
De igual forma, abordaste el tema de las implicaciones de la violencia en la vida de las personas, para poder conocer las recomendaciones e identificar la violencia desde la cultura de paz y no violencia.
Por último, a través de un ejercicio, conociste algunas formas para reconocer tu postura dentro de la cultura de paz y no violencia en situaciones o hechos violentos.
Has finalizado esta sesión. Consulta tu libro de texto para saber más del tema y retomar los aprendizajes que favorezcan la construcción de una cultura de paz.
Recuerda que es continuo el aprendizaje y las decisiones, en las que se necesita poner límites y elegir aquellas acciones y comportamientos que favorezcan la justicia y contribuyan a una cultura de paz.
El Reto de Hoy:
Con base en tu experiencia, completa los siguientes cuadros.
El cuadro 1 señala lo siguiente:
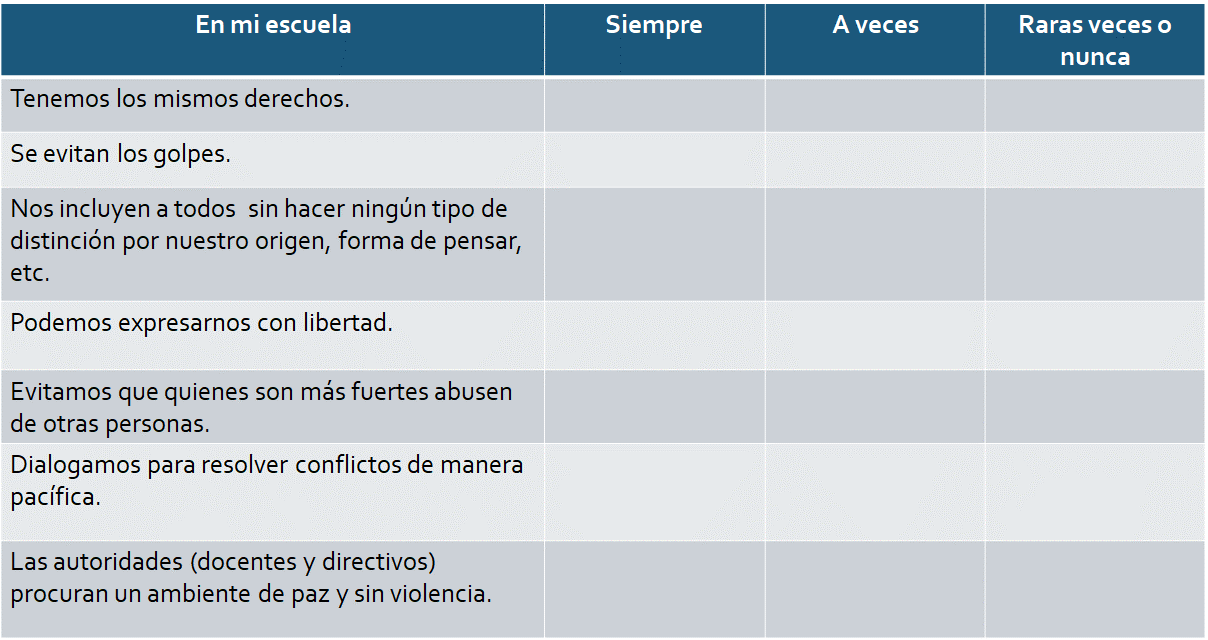
En el cuadro 2 se señala que:
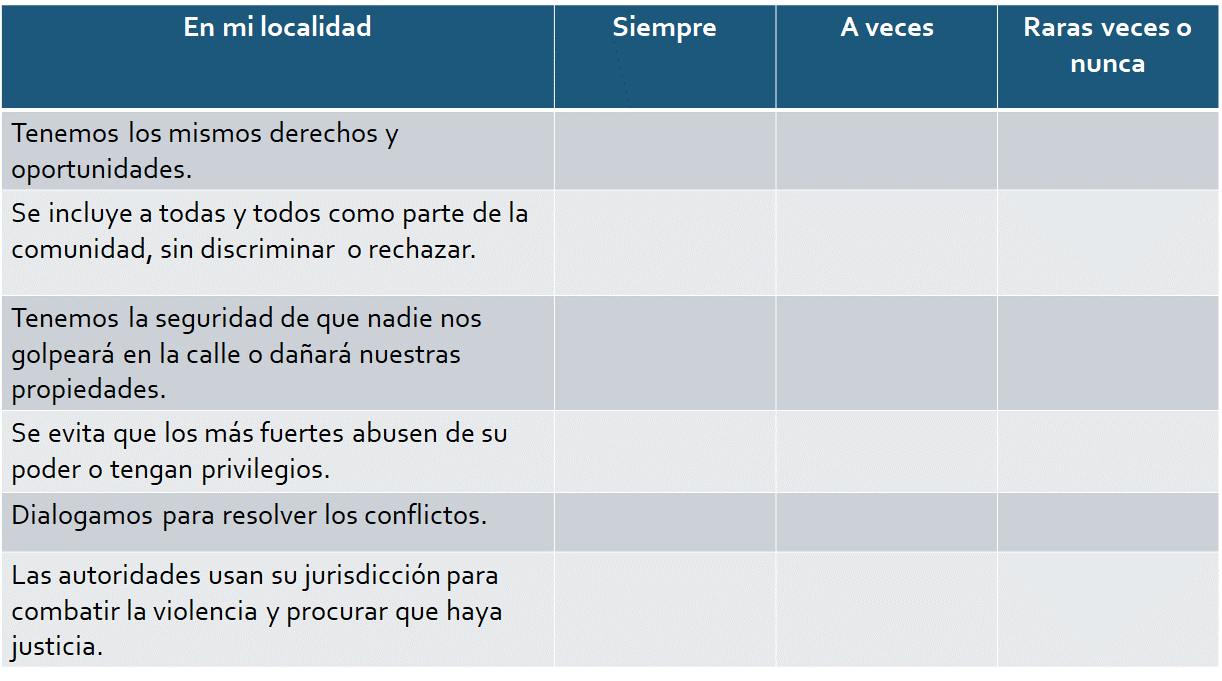
Al finalizar, elabora una reflexión de un párrafo en el que incluyas algunos de los conceptos de esta sesión. Además, dialoga con tus familiares sobre la importancia de aprender a reconocer la violencia en el entorno y realizar acciones contundentes para que ese ciclo llegue a su fin.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
El diagnóstico comunitario
Aprendizaje esperado: Planifica y organiza las acciones técnicas según las necesidades y oportunidades indicadas en el diagnóstico.
Énfasis: Identificar las características de las técnicas utilizadas para hacer el diagnóstico de las necesidades de la comunidad y la pertinencia de su uso.
¿Qué vamos a aprender?
En esta sesión, profundizarás en el diagnóstico comunitario, el cual te permitirá identificar las necesidades, no solo de una persona o un grupo familiar, sino de una comunidad en particular. Para ello, conocerás las características de las técnicas utilizadas en este tipo de diagnósticos y la pertinencia de su uso.
¿Qué hacemos?
Analiza la siguiente información.
Los seres humanos tenemos necesidades básicas que son imprescindibles para vivir, como dormir, comer, entre otras; y también existen las necesidades secundarias que permiten mejorar la calidad de vida, y muchas de ellas se pueden satisfacer a través de algún producto o servicio.
Por ello, el diagnóstico es el primer paso de la planeación, pues no se debe generar ningún producto, servicio o proceso sin antes realizar un diagnóstico.
Para poder saber qué pasa en una comunidad o qué necesidades tiene, se puede utilizar el diagnóstico comunitario. Por lo regular comienza cuando en la vida cotidiana se identifica la existencia de alguna necesidad que no está satisfecha. Estas necesidades insatisfechas pueden ser las mismas que otras personas tienen y, por lo tanto, se comparten.
Al realizar un diagnóstico comunitario, se puede identificar si esto es así, para luego distinguir el problema y buscar soluciones. Para hacerlo, se requiere obtener información sobre esas necesidades, y no lo hace una sola persona, sino que la comunidad puede participar en todo el proceso; es decir, se intercambian puntos de vista sobre las necesidades que tienen y experimentan, y así pueden organizarse para recabar la información que se requiere.
Entonces, se realiza un diagnóstico comunitario para conocer más sobre las necesidades que se tienen. El paso número uno es recabar la información que se necesita a través de algunas técnicas como:
- La encuesta.
- La entrevista.
- Y la observación.
La encuesta es una técnica que permite obtener información de muchas personas de manera más rápida que otras técnicas. Consiste en hacer sólo algunas preguntas, normalmente por escrito, aunque también se puede hacer oralmente.
Esta técnica es utilizada por organizaciones y empresas para poder saber sobre los gustos de las personas. Por eso se dice que la información es poder, ya que, por medio de ella, se pueden tomar decisiones.
Para tener una idea más clara de la forma en que se puede obtener información, observa el siguiente video del minuto 7:20 al 9:56.
- Video. Encuesta.
A través de una encuesta se puede conocer cómo piensan las personas, cuáles son sus gustos o necesidades, y con base en los datos que se obtienen, poder alcanzar el éxito en la solución de necesidades.
No obstante, todavía hay otros pasos que se tienen que seguir y, para obtener más información en menor tiempo, se puede trabajar en equipo.
Observa el siguiente video del minuto 9:57 a 10:41 para saber más al respecto.
- Video. Comunidad.
Hoy en día, debido a la contingencia, hacer encuestas de persona a persona sería complicado, otra manera de realizarlo es por medio del teléfono.
También se puede recurrir a otros medios para realizarla, como páginas web, redes sociales, correos electrónicos o mensajes de texto. Incluso se puede usar el teléfono de casa y pensar, en conjunto, otras alternativas para lograrlo.
Otra herramienta para recabar información es la entrevista, que en algunos aspectos es parecida a la encuesta porque también se requiere de preguntas y de contacto con varias personas; ésta también es de manera directa, de persona a persona; o indirecta, utilizando medios que permitan realizarla a distancia.
La diferencia es que la entrevista da la oportunidad de profundizar más en la información porque es posible hacerles más preguntas a las personas con las que se habla. Incluso, si ellas autorizan, se puede grabar lo que comparten y volverlo a escuchar para no perder detalle de la información.
A continuación, observa el siguiente video para conocer más sobre la entrevista.
- Video. Si de preguntar se trata.
https://www.youtube.com/watch?v=PXU_vl1V8ZA
Es muy importante investigar previamente para poder realizar las preguntas adecuadas al entrevistado, pues de ello depende que se obtenga toda la información. Aplicar la entrevista apropiada puede ayudar a suscitar cambios favorables en la comunidad.
Observa la siguiente cápsula del minuto 5:51 a 6:33
- Video. Si de preguntar se trata. ¿Sabías que?
https://www.youtube.com/watch?v=PXU_vl1V8ZA
Hasta el momento conoces dos técnicas que se pueden complementar muy bien con otra más, la observación. A través del sentido de la vista, se puede adquirir información de forma rápida. Además, es una herramienta esencial al momento de realizar la investigación.
Cabe mencionar que, por la vía de la contemplación es como se ha podido analizar gran parte de los conocimientos científicos.
Para llevar a cabo la observación, se debe tener la certeza de algunas situaciones que se pudieran observar con atención y registrar en algún cuaderno. De esta manera, se puede entender mejor cuál es la necesidad insatisfecha de la comunidad.
La observación se puede obtener a partir de lo que se observa, se siente y se escucha; es decir, no sólo lo que percibes con los ojos, también lo que aprecias con tus sentidos del tacto, oído, olfato y gusto.
La observación permite registrar algunas conductas o situaciones que a veces pasan desapercibidas para los demás, pero si se presta atención, todos los datos que se recaben serán importantes para el propósito. Con esto, ya tienes tres técnicas que puedes utilizar en el diagnóstico de necesidades.
Antes de usar cualquiera de las tres, debes conversar con las personas de tu comunidad que participarán en el diagnóstico, para acordar y tener claridad en la información que desean obtener para saber qué, cuándo, con qué y dónde se realizará, para tener conocimiento de lo que está pasando en la comunidad, así como quiénes harán la observación y qué instrumentos van a utilizar.
Teniendo claridad en estos puntos, se puede decidir cuáles son las técnicas más apropiadas y si se pueden realizar para registrar lo que se observa en la comunidad.
Has finalizado esta sesión. Comparte lo que aprendiste sobre el diagnóstico comunitario con tu familia y con tu maestra o maestro de Tecnología, para comenzar a plantear la forma en cómo harás tu propio diagnóstico comunitario.
El Reto de Hoy:
Reflexiona y contesta las siguientes preguntas:
- ¿Qué necesidades tiene tu comunidad?
- ¿Cómo harías un diagnóstico de necesidades comunitario?
Además, realiza un cuadro sinóptico sobre las técnicas utilizadas para hacer el diagnóstico de las necesidades.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario