Aprende en Casa III SEP: 16 de marzo TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 16 de marzo de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Martes 16 de marzo, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Perímetro y área de polígonos regulares y del círculo
Aprendizaje esperado: Calcula el perímetro y el área de polígonos regulares y del círculo a partir de diferentes datos.
Énfasis: Resolver problemas que impliquen el cálculo del perímetro y el área de polígonos regulares y del círculo.
¿Qué vamos a aprender?
En esta sesión, reflexionarás en la forma de proceder para resolver problemas que impliquen el cálculo del perímetro y el área de polígonos regulares, así como del círculo. Para ello, profundizarás en las fórmulas que se pueden utilizar para calcular esas dimensiones.
¿Qué hacemos?
Inicia con la siguiente información sobre el perímetro y el área.
¿Qué es el perímetro? El perímetro es la longitud del contorno de una figura geométrica.
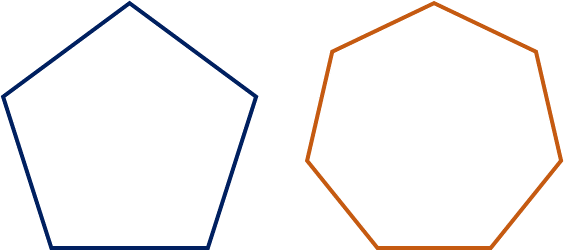
En el caso de los polígonos regulares, está definida por la suma de sus lados y, como sus lados tienen la misma medida, se puede establecer una expresión matemática de la siguiente manera: perímetro igual al número de lados del polígono, multiplicado por la medida del lado.
Entonces, si se trata de un hexágono regular, queda de la siguiente manera:
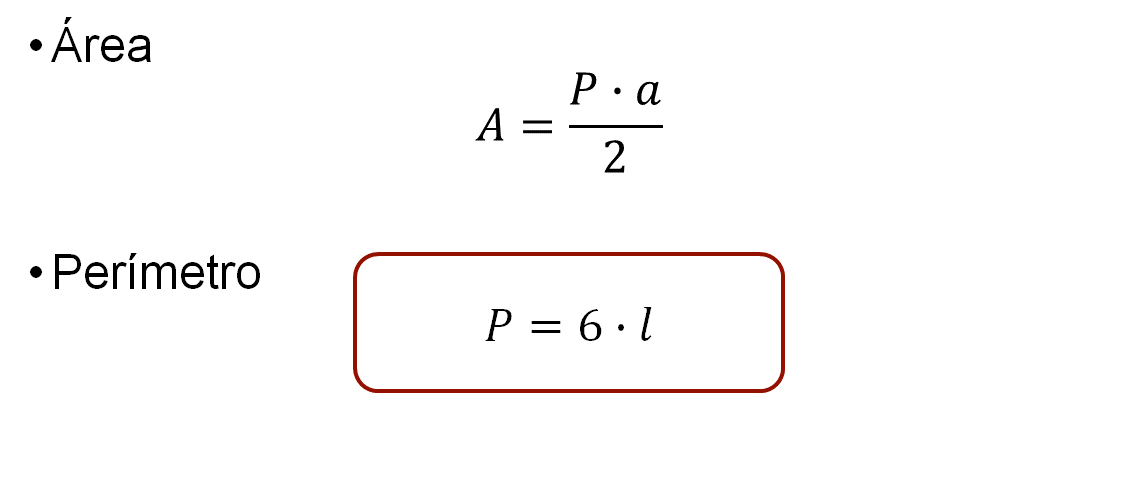
Donde:
l: es la medida de un lado del hexágono.
¿Qué es el área? Área es la medida de la superficie delimitada por el contorno de una figura geométrica.

Para determinar su valor, se pueden utilizar las fórmulas ya establecidas. Para el caso de los polígonos regulares, la fórmula es: área igual al producto del semi perímetro por apotema. Dicho de otra manera, área igual al producto del perímetro por apotema dividido entre dos.
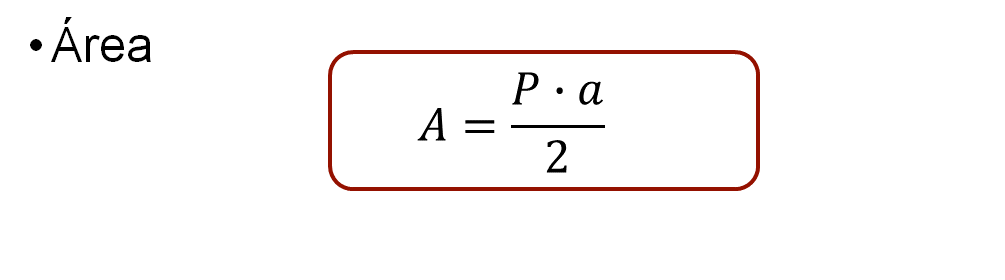
Observa el siguiente video del minuto 3:39 al 4:08, para profundizar al respecto.
- El área de polígonos.
https://www.youtube.com/watch?v=6HIADlG1mQc
La base del paralelogramo es igual a la mitad del perímetro, es por ello que, en la fórmula del área aparece el divisor dos, y se entiende que la apotema se refiere a la altura de los triángulos centrales en que se divide el polígono.
Conocer las fórmulas es importante porque ayuda a realizar el cálculo de una figura de manera más rápida que usando otras estrategias, como el conteo de unidades cuadradas. Otra ventaja de las fórmulas es que se pueden aplicar en la resolución de problemas, en los que se debe centrar más la atención en las estrategias de resolución que en el cálculo mismo del área.
Resuelve la siguiente situación.
Problema 1
En un jardín de niños se tiene una zona de juegos en forma de octágono regular de 4 metros de lado. Para mejorar las condiciones, le pondrán alfombra y la delimitarán con un cerco.
¿Cuántos metros cuadrados de alfombra deben colocar?
¿Cuál es la longitud del cerco?

Para realizar este trabajo cuentan con un presupuesto de 16,000 pesos. En ese jardín de niños se contactaron con un proveedor, quien les dio la cotización de 110 pesos por metro cuadrado de alfombra y 200 pesos por metro lineal de cerco. Los integrantes del comité se preguntan si es suficiente el presupuesto que tienen.
Reflexiona: ¿piensas que el presupuesto es suficiente?, ¿por qué? Registra tus respuestas en tu cuaderno.
Una manera de iniciar para dar respuesta a las interrogantes es observar el planteamiento y determinar cuáles son los datos y cuáles son las incógnitas del problema.
En este caso, se conoce la forma de la zona de juegos, que es un octágono regular; también se sabe la medida de la longitud del lado: 4 metros. Además se conoce el presupuesto con el que cuentan: 16,000 pesos.
Como incógnitas, es decir, lo que se desea conocer son el valor del área de la alfombra, el perímetro de la zona de juegos, así como determinar si el presupuesto es suficiente.
Es importante analizar los datos para determinar si con ellos es posible dar solución al problema. Una forma de hacer este análisis es considerar las fórmulas para calcular el área y el perímetro del octágono regular.
Para calcular el área del octágono del problema, que es un polígono regular, la fórmula es área igual al producto del perímetro por apotema, dividido entre dos.
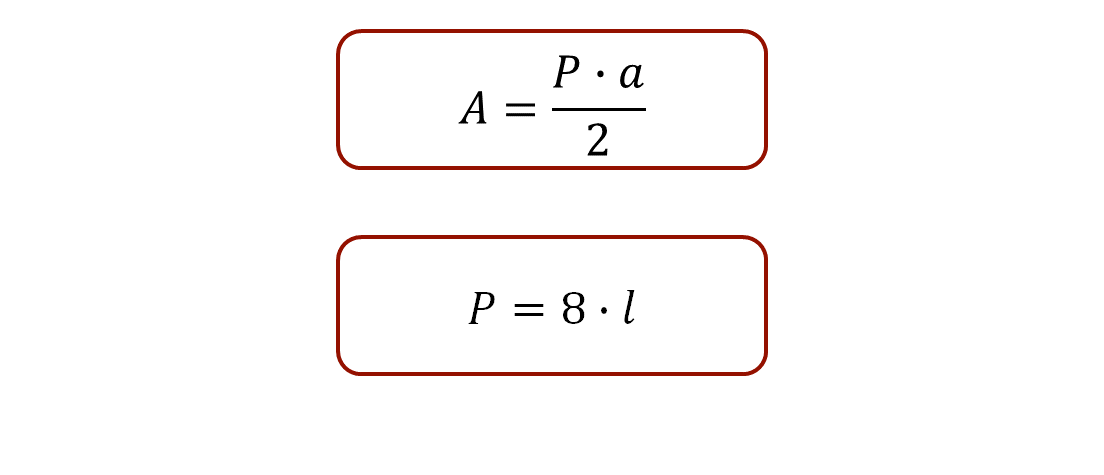
Para el perímetro del octágono regular, la fórmula establece que el perímetro es igual al producto de ocho por el valor de la medida del lado.
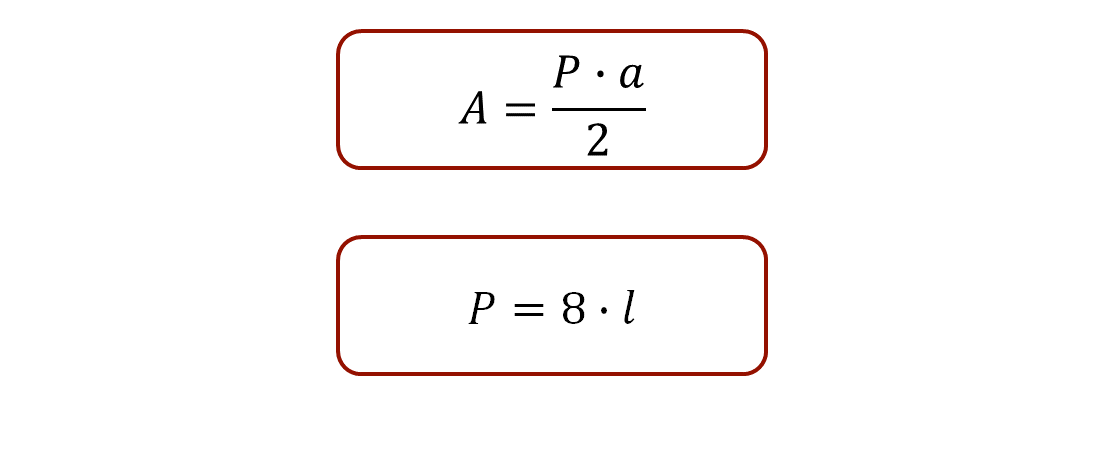
Registra en tu cuaderno el perímetro y el área de este octágono.
Con los datos que se tienen es posible calcular el perímetro, que es la medida de la longitud del cerco. Entonces, se sustituye en la fórmula del perímetro el valor de la medida del lado, 4 metros.
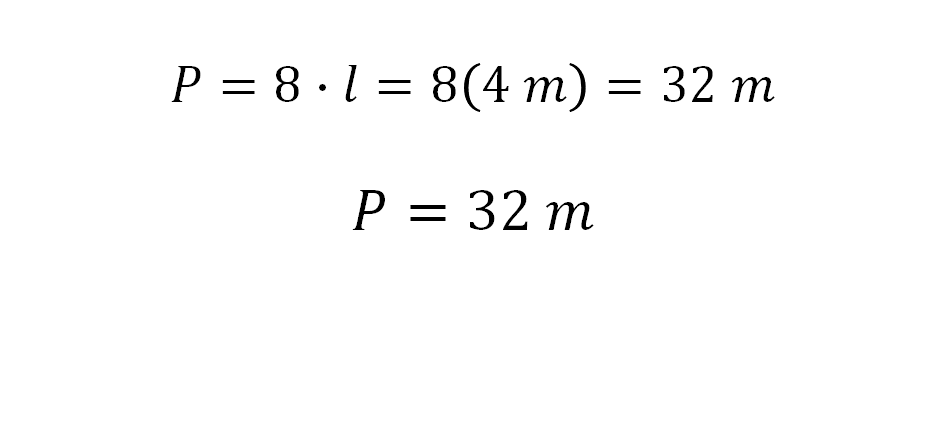
Al hacer el cálculo, se obtienen 32 metros de perímetro, es decir, la longitud del cerco a colocar en el jardín debe de ser de 32 metros.
Para el caso del área, la aplicación de la fórmula requiere conocer la medida de la apotema. Una manera de obtenerla es medir la distancia del centro del octágono al punto medio de cualquiera de los lados. Existen otras formas de calcularla, dos de ellas las trabajarás en tercer grado de secundaria.
Al hacer la medición mencionada, se obtienen 4.828 metros como medida de la apotema.
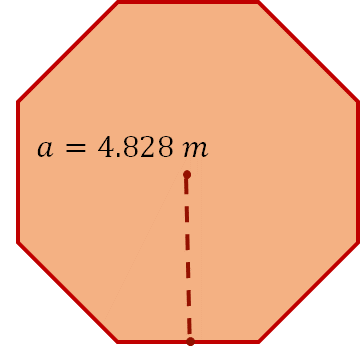
Ahora que conoces la medida de la apotema, es posible proceder al cálculo del área del octágono utilizando la fórmula correspondiente.
Al sustituir los valores, se tiene lo siguiente:
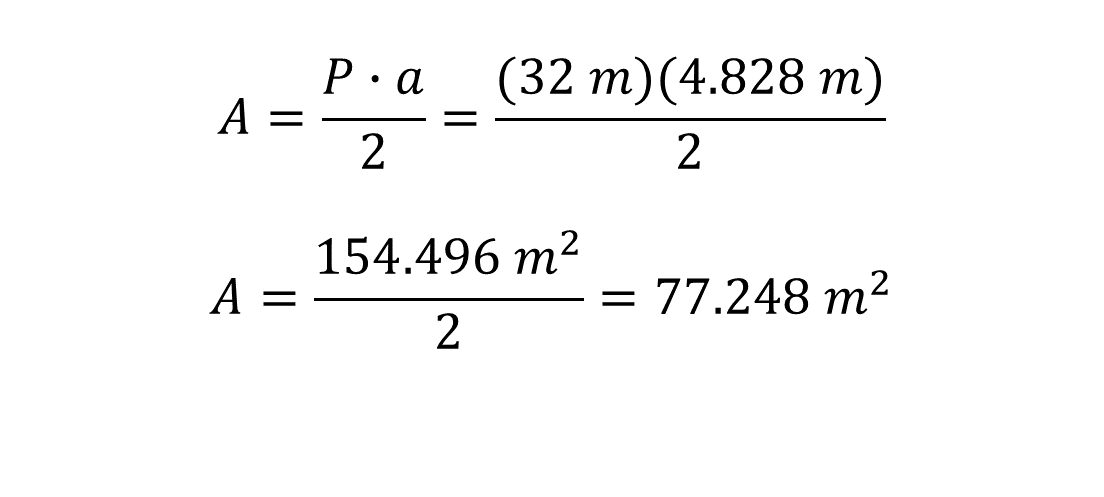
Se obtiene 77.248 metros cuadrados. Por lo tanto, la cantidad de alfombra necesaria para el trabajo es de aproximadamente 78 metros cuadrados.
Entonces, ¿qué se puede hacer para continuar con la resolución del problema? Una manera de continuar es hacer el cálculo del costo, tanto de la alfombra como del cerco. Para ello, puedes multiplicar los valores calculados para el área y el perímetro por los costos unitarios respectivos.
En el caso de la alfombra, se multiplican 78 metros cuadrados por 110 pesos por metro cuadrado.
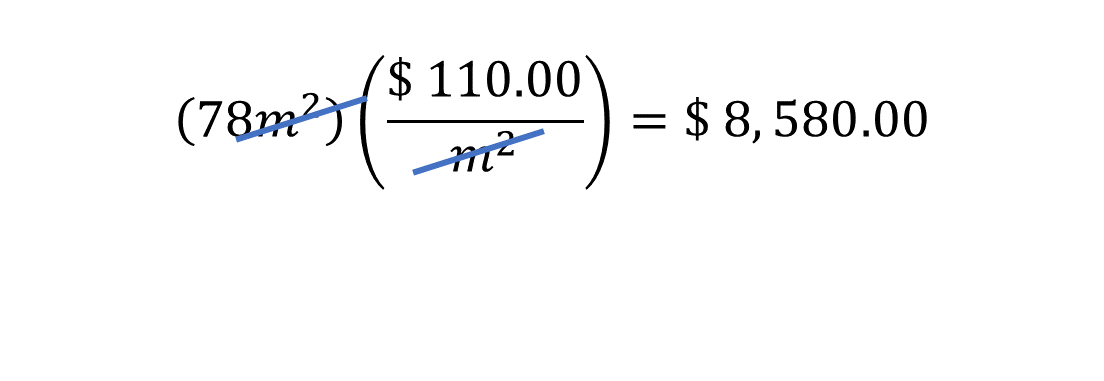
Por lo tanto, el costo de alfombrar la zona de juegos es de 8,580 pesos.
Para saber el costo de colocar el cerco en la zona de juegos, se puede multiplicar la longitud del perímetro por 200 pesos, que es el costo de cada metro lineal de cerco. Entonces, se puede multiplicar 32 metros, que es la medida del perímetro, por 200 pesos por metro.
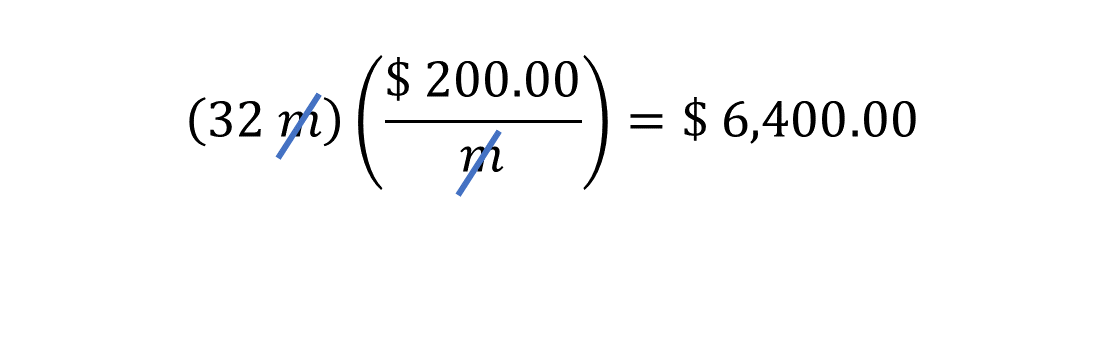
Por lo que el costo del cerco es de 6,400 pesos.
Sumando ambos costos resultan 14,980 pesos, ¿recuerdas de cuánto es el presupuesto asignado? El presupuesto es de 16,000 pesos.
Entonces, al comparar el costo con el presupuesto con que cuenta el comité de la escuela, se puede afirmar que sí es suficiente para realizar este trabajo de mejoras en ese jardín de niños.
Como puedes darte cuenta, conocer y aplicar las fórmulas y procedimientos matemáticos adecuadamente es una manera eficiente para el planteamiento y resolución de problemas en la vida cotidiana.
A continuación, observa el siguiente video del minuto 0:44 al 2:29, para continuar con el tema.
- El área del círculo.
https://www.youtube.com/watch?v=myqZP3Qhxp0
Como pudiste observar, en la aplicación de las fórmulas para obtener el área y el perímetro del círculo, se debe recurrir al número “pi”, que es una constante, y al cual se le asigna el valor de 3.14.
¿Te has preguntado sobre el origen de este número tan misterioso? Para descubrirlo, observa el siguiente video del minuto 0:44 al 2:36 y del minuto 4:11 al 4:45.
- Conocer el número “pi”.
https://www.youtube.com/watch?v=498dAwpvlKM
Ahora ya puedes darle más sentido a la aplicación del número “pi” en las fórmulas para calcular el perímetro y el área de la circunferencia.
Resuelve el siguiente problema.
Problema 2
En una fábrica de láminas decorativas utilizan como base hojas de lámina de 244 centímetros de largo por 122 centímetros de ancho.
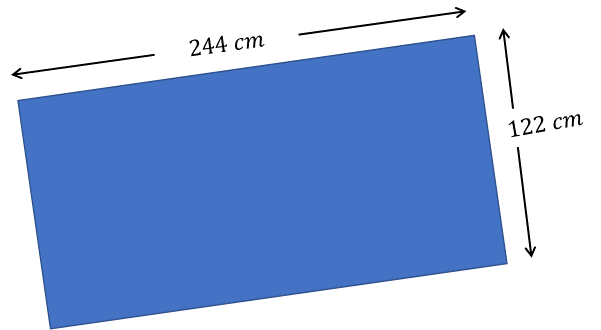
El patrón del decorado es el siguiente: recortes de figuras de flor formadas por 4 semicírculos de 10 centímetros de diámetro que se repiten en la hoja de lámina 32 veces.
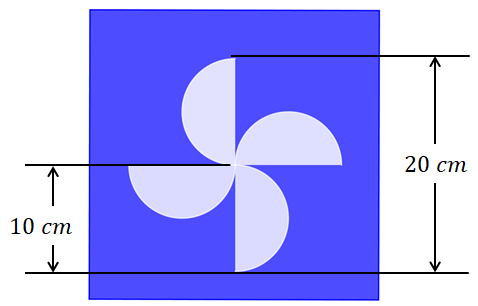
La lámina utilizada es calibre 18. Por información del proveedor, se sabe que su masa es de 9.67 kilogramos por metro cuadrado. La empresa requiere saber ¿cuál es el peso de la lámina después de realizar el recorte de las 32 figuras?
¿Qué harías para resolver el problema? Anota tus estrategias en tu cuaderno y realiza una estimación del peso de la lámina después de ser recortada.
Una manera de dar respuesta al problema es identificar los datos y las incógnitas de este. Los datos son:
- Medidas de la placa, 244 centímetros por 122 centímetros.
- Medidas de los semicírculos que se cortan en cada patrón, 10 centímetros de diámetro.
- Masa de la lámina, 9.67 kilogramos por metro cuadrado.
Las incógnitas del problema son:
- Área de la lámina antes de los cortes.
- Masa de la lámina antes de los cortes.
- Área y peso de las secciones cortadas.
- Masa de la lámina después de realizar los recortes.
Ahora que ya se identificaron los datos e incógnitas del problema, se pueden establecer las fórmulas que permitirán dar una solución. Por ello, se requiere de las fórmulas para calcular el área de un rectángulo y el área del círculo.
Para el rectángulo: área es igual al producto del largo por el ancho.
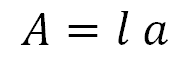
Y para el círculo: área igual a pi por el valor del radio al cuadrado.
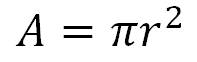
Ahora, calcula el área de la hoja de lámina antes de realizar los cortes, el largo es de 244 centímetros y el ancho es de 122 centímetros.
A = l (a) = 244 (122) = 29,768
Al calcular el producto, el resultado es un área de 29,768 centímetros cuadrados.
La masa de la lámina está en función del área de esta; sin embargo, con el resultado que se obtuvo para el área de la lámina no es posible determinarlo, ya que se obtienen centímetros cuadrados y se debe expresar en metros cuadrados, como se enuncia en el problema. Para ello, realiza una conversión de unidades de área.
Un metro cuadrado es equivalente a diez mil centímetros cuadrados; utilizando esta equivalencia, se puede convertir el área en metros cuadrados.
Para calcular el área en metros cuadrados se multiplican 29,768 centímetros cuadrados por el factor de conversión, un metro cuadrado sobre 10,000 centímetros cuadrados.
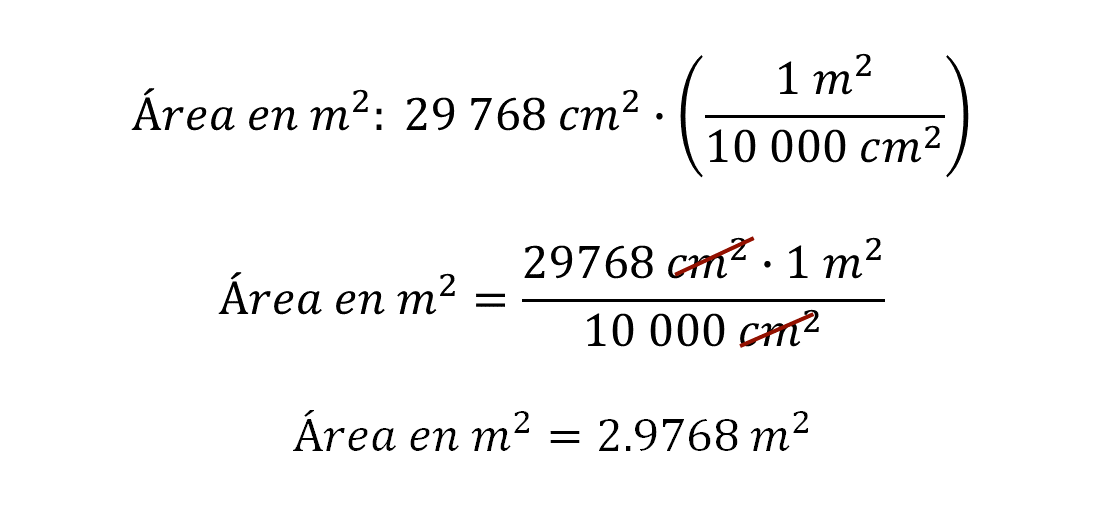
Al calcular el producto y el cociente, nota que el divisor es una potencia de diez, por lo que en el dividendo se puede recorrer el punto decimal hacia la izquierda tantas veces como ceros aparezcan en esa potencia, en este caso, cuatro. En cuanto a las unidades, se pueden reducir los centímetros cuadrados que aparecen, tanto en el numerador como en el denominador, y se tiene el resultado en metros cuadrados. Por lo tanto, el área es igual a 2.9768 metros cuadrados.
Es momento de determinar el peso de la lámina antes de realizar los cortes. Para ello, se debe multiplicar el área de la lámina por el peso de la misma por metro cuadrado. En este caso, 2.9768 metros cuadrados por 9.67 kilogramos por metro cuadrado.
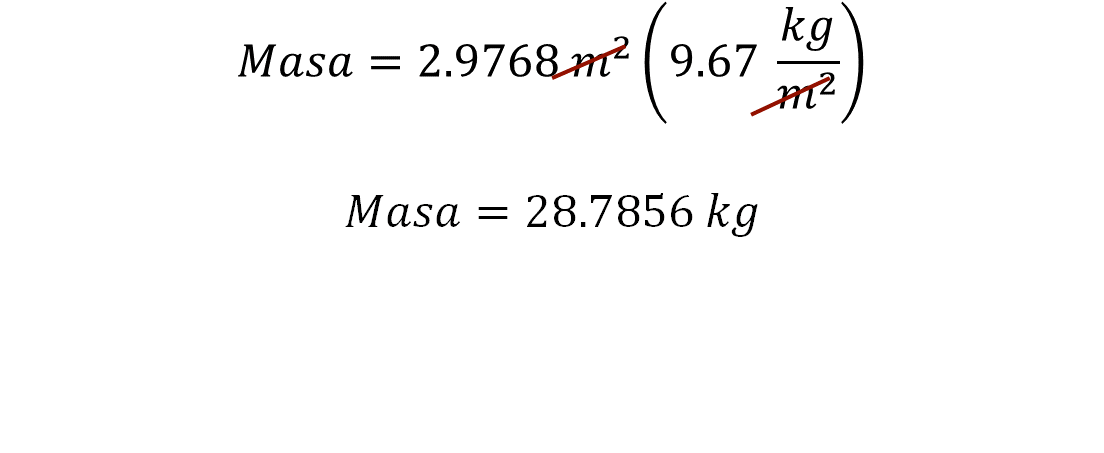
Al calcular el producto, el resultado es 28.7856 kilogramos. Por lo que la hoja de lámina antes de cortar las piezas pesa 28.7856 kilogramos.
Para determinar la masa del material que se retira, se puede calcular el área de los cortes realizados para cada figura. Esos cortes corresponden al área de dos círculos de diez centímetros de diámetro, ya que cada corte es de cuatro semicírculos.
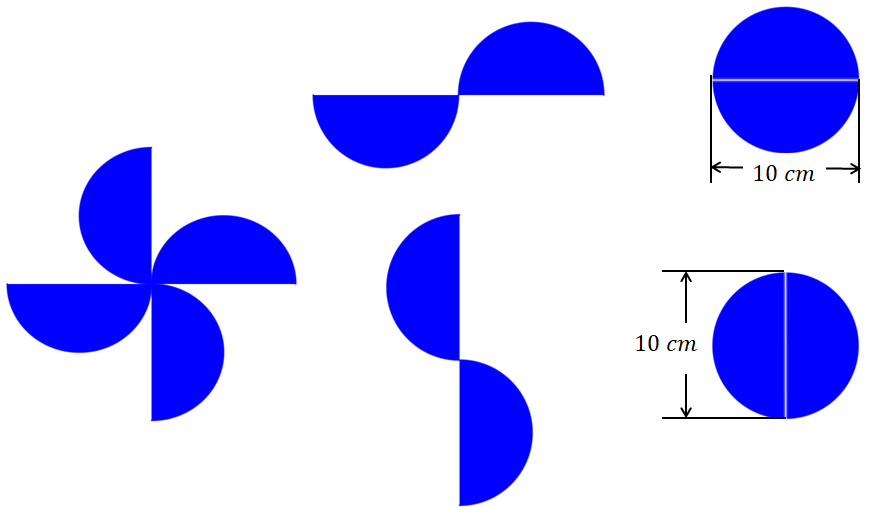
Las figuras muestran la descomposición de los cortes para formar dos círculos de 10 centímetros de diámetro. Ten presente que, para calcular el área del círculo, la fórmula es la siguiente:
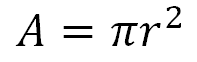
Se conoce el valor del diámetro y para obtener el radio se divide por dos la medida del diámetro. En este caso, 10 centímetros entre 2 es igual a 5 centímetros.
El radio del círculo es de cinco centímetros. Sustituyendo los valores de pi y del radio en la fórmula, se tiene que:
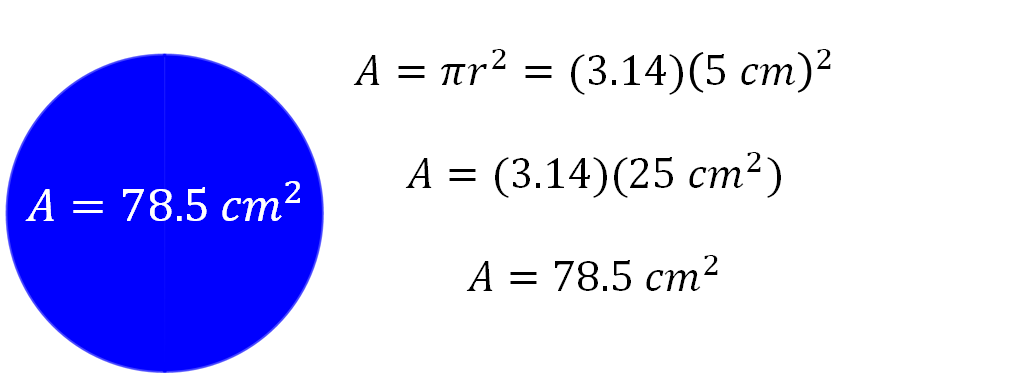
El producto es 78.5 centímetros, que corresponden al área de cada círculo.
Recuerda que cada corte equivale a dos círculos como el anterior, por lo que el área de cada corte es de 157 centímetros cuadrados.
A (corte) = 2 (78.5) = 157 centímetros cuadrados
Como dato inicial se realizaron 32 figuras en la hoja de lámina, por lo que, para obtener el área total retirada, se multiplica 32 por el área anterior.
A (retirada) = 32 (157) = 5024 centímetros cuadrados
Por lo tanto, el producto es 5,024 centímetros cuadrados.
Ahora se puede determinar la masa del área de la lámina retirada. Para lograrlo se expresa en metros cuadrados. Usando el factor de conversión anotado y calculando las operaciones, se tiene que 5,024 centímetros cuadrados es equivalente a 0.5024 metros cuadrados.
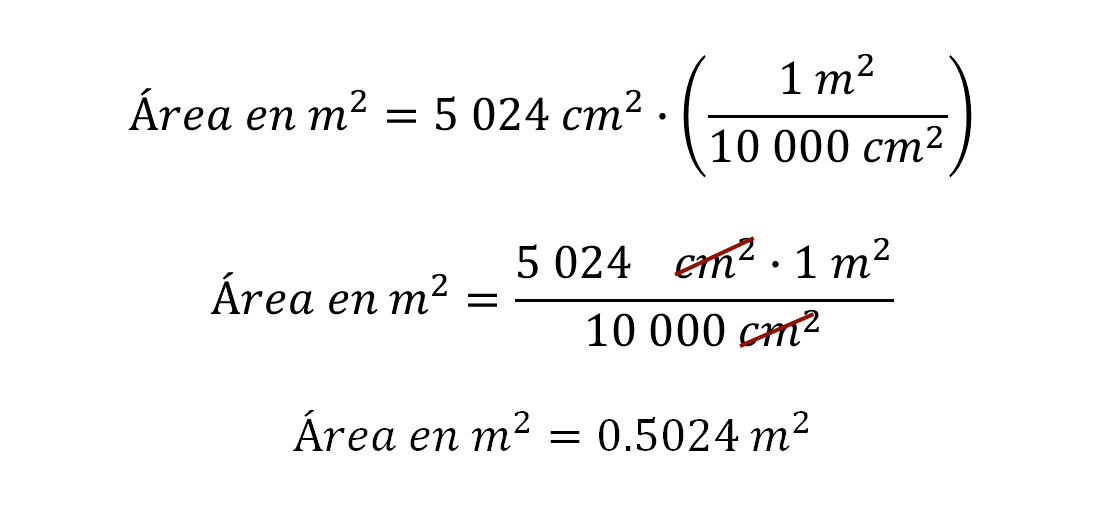
Para calcular la masa de la lámina retirada, se multiplica 0.5024 metros cuadrados por 9.67 kilogramos por metro cuadrado.
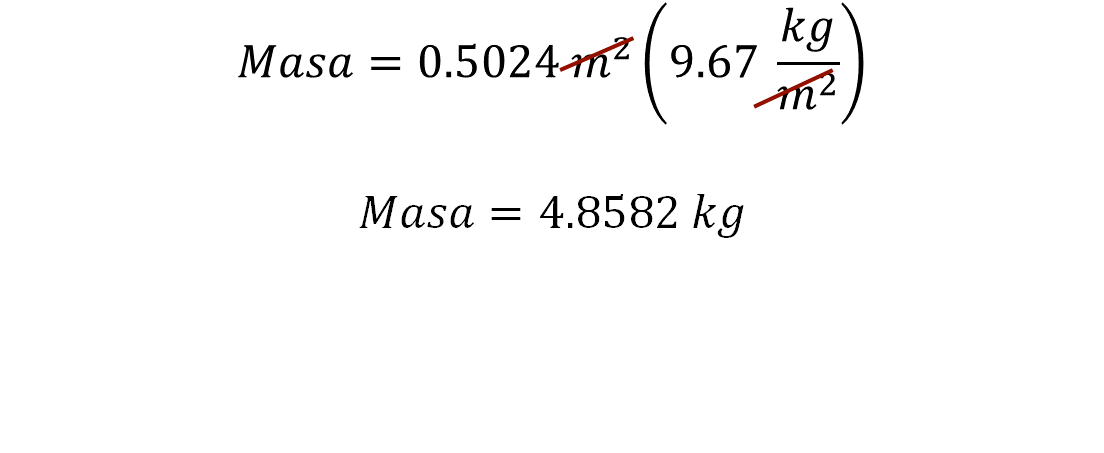
El resultado permite afirmar que se retiraron 4.8582 kilogramos de lámina.
En este momento ya es posible responder la pregunta inicial del problema: ¿cuál es la masa de la lámina después de realizar el recorte de las 32 figuras?
¿Cómo calcularías esa masa? Se puede calcular restando a la masa de la lámina antes de los recortes, la masa de la lámina retirada, esto es, la masa de la lámina decorada es igual a 28.7856 kilogramos menos 4.8582 kilogramos.
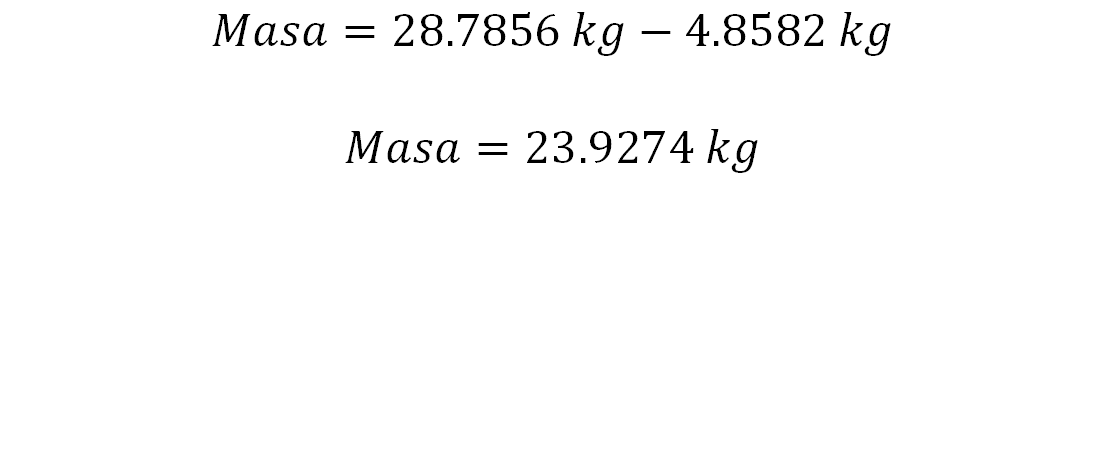
De esta manera, se concluye que la masa de la lámina decorada es de 23.9274 kilogramos.
Para continuar aplicando las fórmulas del área y el perímetro, resuelve el siguiente problema.
Problema 3
La figura representa el desarrollo plano de un cilindro, en ella se muestran algunas de sus dimensiones.
Calcula el área y el perímetro del desarrollo plano.
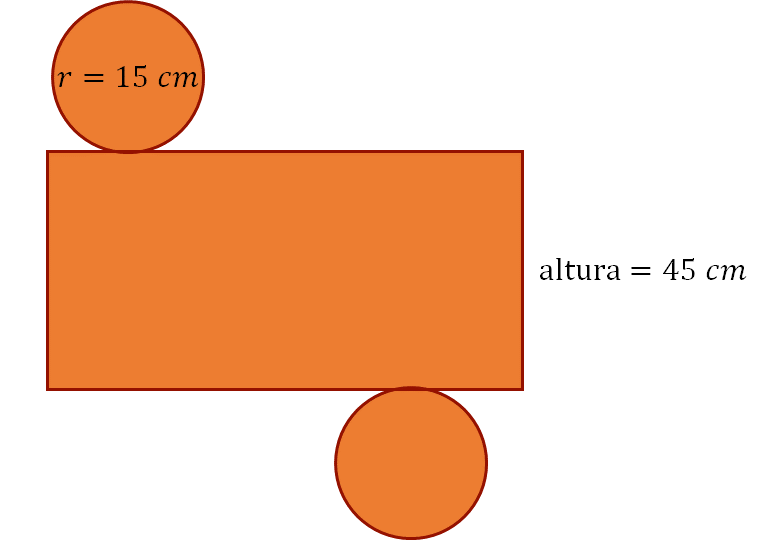
¿Qué harías para resolver el problema?, ¿qué datos se necesitan? Primero, identifica los datos e incógnitas del problema.
Se conoce el radio de la circunferencia igual a 15 centímetros, el alto del rectángulo mide 45 centímetros y las fórmulas para calcular el área y el perímetro de las figuras que se presentan, que en este caso son medidas que se deben calcular.
- Perímetro de la circunferencia es igual al doble producto de pi por el radio.
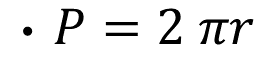
- Perímetro del rectángulo es igual a sumar el doble del largo y el doble del ancho.
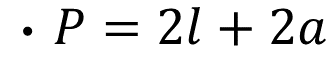
- Área del círculo es igual al producto de pi por el cuadrado del radio.
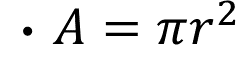
- Área del rectángulo es igual al producto del largo por el ancho.
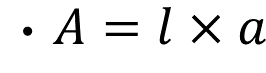
En las fórmulas del rectángulo aparece el valor del largo “l”, que en este caso, es igual al perímetro de la circunferencia, pues es la parte del rectángulo que se enrolla para lograr formar el cilindro.
En la fórmula uno, perímetro igual al doble producto de pi por el radio, se sustituye la medida del radio, que es de 15 centímetros, y se obtiene 94.2 centímetros.
P = 2 (3.14) 15 = 94.2
Igualando este valor con el largo del rectángulo ya es posible calcular su perímetro. Usa la segunda fórmula para calcular el perímetro del rectángulo. Perímetro es igual a la suma del doble del largo más el doble del ancho, que en este problema representa la altura del cilindro. Por lo tanto, sustituyendo ambos valores y resolviendo las operaciones:
P = 2l + 2a = 2(94.2) + 2(45) = 188.4 + 90 = 278.4
El perímetro del rectángulo es igual a 278.4 centímetros.
El desarrollo plano está compuesto por dos círculos y un rectángulo, por lo tanto, para determinar el valor del perímetro, se suman dos veces el perímetro de la circunferencia más el perímetro del rectángulo:
P (total) = 2 (94.2) + 278.4 = 466.8
Da como resultado 466.8 centímetros.
Para calcular las áreas del desarrollo plano, una manera es iniciar con el círculo. Al sustituir la medida del radio, 15 centímetros en la fórmula y resolviendo las operaciones, el área es igual a 706.5 centímetros cuadrados.
Área del círculo = 3.14 (15) al cuadrado = 3.14 (225) = 706.5
Como en el desarrollo plano hay 2 círculos, se puede multiplicar este valor por dos. El resultado es 1,413 centímetros cuadrados.
Para el área del rectángulo se multiplica el valor del largo 94.2 centímetros por el ancho, 45 centímetros; el producto es igual a 4,239 centímetros cuadrados.
Área del rectángulo = 94.2 (45) = 4239
El área del desarrollo plano es entonces igual a la suma de 1,413 centímetros cuadrados más 4,239 centímetros cuadrados, por lo que el área del desarrollo plano es igual a 5,652 centímetros cuadrados. Con esto has resuelto el problema planteado que solicitó calcular el perímetro y el área del desarrollo plano.
Recuerda la importancia de hacer anotaciones de los aspectos que consideres importantes, así como también de las dudas que puedan presentarse.
Has finalizado la sesión. No olvides que este es un material de apoyo y puedes consultar otras fuentes para complementar lo que aprendas aquí.
El Reto de Hoy:
Resuelve algunos de los problemas o ejercicios sobre el perímetro y área de polígonos regulares y del círculo, de tu libro de texto de Matemáticas de segundo grado.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
A resumir se ha dicho
Aprendizaje esperado: Elabora resúmenes que integren la información de varias fuentes.
Énfasis: Seleccionar textos para resumir.
¿Qué vamos a aprender?
En esta sesión, aprenderás a escoger, definir y esquematizar la información esencial de varias fuentes sobre un tema para hacer un resumen. Esto con la finalidad de que los documentos aporten al escrito una visión más amplia del tema.
¿Qué hacemos?
Reflexiona en lo siguiente:
¿Alguna vez te has preguntado por qué en una situación cotidiana de pronto sucede un acontecimiento que te hace cuestionarte ese suceso?
Observa el siguiente video sobre lo que se cuestiona Ulises, alumno de secundaria.
- Video. Ulises.
El gas helio es lo que permite que los globos se mantengan suspendidos, y es algo muy común en festejos y tradiciones; sin embargo, ¿sólo para eso servirá el helio?
Para descubrir más sobre ello, primero debes cuestionarte: ¿qué es el helio y cuáles son los usos que se le dan?
Una técnica de estudio para recabar la información es el resumen, pues permite copiar las ideas principales de uno o varios textos, reduciendo la información original sin perder lo sustancial. También se debe identificar el tipo de fuente de información que se utilizara.
Lee el siguiente texto para entenderlo.
La paradoja del helio
“Con el paso del tiempo y el desarrollo tecnológico surgieron muchos usos para el helio. Posiblemente el más importante en la actualidad aprovecha una característica única del helio. Bajo presiones atmosféricas todos los elementos de la Tabla Periódica, menos el helio, se solidifican a temperaturas lo suficientemente bajas. Pero el helio es siempre líquido. Esta propiedad lo hace ideal para usarlo como refrigerante y mantener las cosas a muy bajas temperaturas.”
Luis. F. Rodríguez (17 de septiembre de 2019).
“La paradoja del helio”.
Este extracto de artículo de opinión se titula “La paradoja del helio”, y señala que ha habido muchos usos del helio y que bajo la presión de la atmósfera todos los elementos de la tabla periódica se solidifican, pero el helio no, es decir, permanece líquido y eso lo hace ideal como refrigerante.
Este texto es una fuente de información primaria. Las fuentes primarias contienen información original, el tema que contienen no ha sido nunca tratado, la información se ha mantenido intacta, es decir, no ha sido interpretada o analizada por un investigador o institución, y pueden ser generales o especializadas.
Este tipo de fuente de información se encuentra en tesis doctorales, libros, actas de congresos, revistas, normas, artículos periodísticos o patentes.
Ahora, lee un extracto de fuente de información secundaria.
La materia a muy bajas temperaturas
“Se encontró que por debajo de las temperaturas de 2.18 K, conocido como el punto lambda, por la forma que adquiere la gráfica de la capacidad calorífica contra la temperatura, la temperatura de toda la masa de helio se hace homogénea, aun cuando se le comunique calor a una porción de ella. Este resultado implica que la conductividad calorífica del helio a esta temperatura es muy elevaba. Para explicar este fenómeno, el físico ruso Piotr Kapitsa supuso que el helio en estas condiciones era un superfluido, lo que significa que el liquido se mueve con una facilidad extraordinaria.”
Morones Ibarra, J. R. (2008).
“La materia a muy bajas temperaturas”,
en Ingenierías, Vol. XI. Núm. 38.
Este texto de investigación, publicado en una revista especializada y titulado “La materia a muy bajas temperaturas”, refiere en lo subrayado que a partir de cierta temperatura la masa del helio se hace homogénea, y quien escribe el artículo retoma lo que supuso el físico ruso Piotr Kapitsa, quien señaló que el helio era un superfluido.
Este texto es una fuente de información secundaria porque cita a otra persona. Para comprenderlo mejor, analiza la definición de las fuentes secundarias
Fuentes secundarias: son una ampliación de los resultados concretos que aportan las fuentes primarias. Es decir, se genera un contenido a partir de la extracción de información de un recurso primario.
Esto significa que se usan cuando alguien necesita información pero, al no localizarla en una fuente primaria, entonces acude a otra fuente que cita lo que hizo o dijo otra persona. Entre ellas se encuentran antologías, artículos de revista, reseñas, biografías, resúmenes de trabajos científicos, reportajes, entre otros.
Ahora, continúa con las fuentes terciarias. Observa el siguiente ejemplo.

Lo que se observa en esta imagen es la bibliografía o referencias de un artículo de investigación titulado “El origen de los elementos químicos”; este tipo de información generalmente se localiza al final de muchas fuentes terciarias.
Esto significa que casi cualquier fuente, si da referencias, podría ser una fuente de información terciaria. Para profundizar al respecto, analiza qué es y qué otros aspectos componen las fuentes terciarias.
Fuentes terciarias: contienen información de fuentes primarias y secundarias y su función es remitirlas. Cumplen las funciones de compilar, organizar, recoger y depurar las fuentes primarias y secundarias.
Estas fuentes son utilizadas para buscar datos o para obtener una idea general de algún tema y pueden ser bibliografías, almanaques, directorios, catálogos de biblioteca, directorios, listas de lecturas, entre otros. La referencia de otros documentos o nombres, títulos de revistas y otras publicaciones.
Los tipos de fuentes de información usan diferentes medios para ser encontrados, estos pueden ser impresos o digitales.
Las fuentes primarias, secundarias y terciarias en su formato impreso o textual contemplan información que se presenta en forma de texto como libros, periódicos, revistas, entre otros.
Los dispositivos digitales, como los celulares, son un medio por el cual se puede obtener información proveniente de las tres fuentes: primarias, secundarias y terciarias.
Ahora, ya que sabes de dónde extraer la información, seleccionarla pertinentemente será el siguiente paso. Escucha con atención lo que la profesora María de Jesús Cerón Rivero dice al respecto.
- Video. Especialista.
Como se mencionó, la finalidad principal de una estrategia de búsqueda es encontrar información de calidad en el menor tiempo posible. Por ello es necesario el desarrollo de habilidades que permitan valorar, conocer los recursos y desarrollar habilidades que logren cumplir con la formación. Observa el siguiente video sobre cómo seleccionar materiales de lectura.
- Cómo seleccionar materiales de lectura de acuerdo con su pertinencia.
Lo anterior te servirá para seleccionar y buscar los textos para hacer un resumen. Observa en la siguiente imagen algunos aspectos acerca de las pautas para seleccionar información.

La pertinencia es un criterio subjetivo, pues el usuario evalúa si el texto es o no adecuado, es decir, pertinente de acuerdo con su necesidad. Un documento pertinente sirve a las necesidades individuales de información, las cuales deben ser precisadas, como el título, subtítulo, el autor, las palabras clave y la fecha de publicación, que permiten evaluar rápidamente la pertinencia.
Además, hay que cuestionarse: ¿están relacionadas con mi tema de investigación?, ¿el ámbito de estudio del autor está relacionado con algún aspecto de mi tema?
Es importante recurrir al resumen, la tabla de materias, la introducción y la conclusión que aportan información de los aspectos tratados y el enfoque del análisis.
A continuación, observa el siguiente video sobre Ulises, alumno de secundaria, y su proceso de selección de la información.
- Video. Profesora-estudiante.
Como puedes observar, Ulises recurrió a su maestra de Ciencias para resolver su duda, esta es una fuente verbal secundaria porque ella estudia estos procesos y cuenta con los conocimientos para responder de primera mano su duda.
Para ampliar lo anterior, observa la siguiente información de un portal educativo.
Usos del helio
“…el helio se prefiere al hidrógeno para producir la ascensión de los globos aerostáticos y en los globos sonda que se envían a la atmósfera con fines científicos y que pueden alcanzar alturas de hasta 30 km […]
En cirugía, se utilizan cabezas de helio ionizado en el tratamiento de tumores de los ojos, estabilizando o provocando la remisión de los mismos […]
Otro uso común del helio es como aire artificial, mezclado con oxígeno, para los buzos […]. En personas con asma y otros problemas respiratorios también suelen utilizarse mezclas de oxígeno y helio, ya que su menor densidad y mayor fluidez facilitan la respiración.”
Como puedes observar, las palabras que resaltan sobre los usos del helio son: se prefiere, se utilizan, uso común y suelen utilizarse, que se refieren al uso de la lectura de barrido, es decir, se buscan palabras clave según lo que se esté buscando.
En este caso, puedes utilizar un lápiz o tu mano para guiar la lectura. El objetivo es que tus ojos “alcancen” las palabras. Ahora retoma el texto y presta atención a las palabras subrayadas.
Usos del helio
“…el helio se prefiere al hidrógeno para producir la ascensión de los globos aerostáticos y en los globos sonda que se envían a la atmósfera con fines científicos y que pueden alcanzar alturas de hasta 30 km […]
En cirugía, se utilizan cabezas de helio ionizado en el tratamiento de tumores de los ojos, estabilizando o provocando la remisión de los mismos […]
Otro uso común del helio es como aire artificial, mezclado con oxígeno, para los buzos […]. En personas con asma y otros problemas respiratorios también suelen utilizarse mezclas de oxígeno y helio, ya que su menor densidad y mayor fluidez facilitan la respiración.”
Como lo que se busca, son los usos, estas oraciones muestran la “lectura de exploración”. Este proceso viene después de la técnica de barrido.
Para comprenderlo mejor, observa cómo lo hizo Ulises.
- Video. Estudiante 2.
Lo que descubrió Ulises es que el helio pertenece a los elementos que no son metales. Y, al verlo en la tabla periódica, puede retomar esa información para seguir buscando.
No olvides que, si realizas una búsqueda en internet debes verificar la información, esto se localiza observando el final de la dirección electrónica, pues si tiene las letras: “.gob”, “.org” o “.edu” suelen ser confiables.
En internet, también puedes entrar a sitios de instituciones públicas o privadas, universidades, organismos internacionales, agencias de noticias o revistas especializadas. Observa la siguiente información al respecto.
Helio
“El helio tiene muchos importantes usos. Su bajo punto de ebullición lo hace útil en las investigaciones científicas que implican bajas temperaturas. Dado que el helio es liviano, la gente lo usa para hacer flotar dirigibles y globos meteorológicos en el aire.
Uno de los usos más importantes del helio es que mantiene fríos los escáneres de imágenes de resonancia magnética, que son los aparatos que permiten observar el interior del cuerpo humano [...].
Los buceadores respiran una mezcla de helio y oxígeno bajo el agua. El helio ayuda a impedir que los buzos se intoxiquen por inhalar demasiado oxígeno…”
Britannica Escola (2021)
“Helio”, en Usos.
En este caso es un texto de internet, pero es de una enciclopedia escolar en la que se habla del helio. De sus apartados, se seleccionó el de “usos”, y como puedes observar en el primer subrayado, se señala que “su bajo punto de ebullición lo hace útil en las investigaciones científicas que implican bajas temperaturas”, y luego enlista algunos usos.
Al momento de seleccionar los textos para resumir, debes cuidar que la información sea comprensible y buscar las palabras que no entiendas, de otra manera, podrías resumir información que no comprendes.
Por otro lado, al obtener pocos resultados, es conveniente adicionar términos que contribuyan a obtener más información relevante.
Con toda la información recabada hasta el momento ya se puede elaborar un resumen. Sólo falta el último paso a seguir. Con los resultados obtenidos se debe organizar, administrar y usar la información, y esto se logra haciendo las anotaciones en el cuaderno, sin olvidar que se debe mencionar la referencia bibliográfica.
La referencia bibliográfica es la ubicación de la información y es útil para verificar la información en referencias impresas, o bien el URL, que es la dirección electrónica de donde se extrajo.
No olvides seguir estos pasos fundamentales en el proceso de búsqueda de información. También puedes realizar un trabajo colaborativo, y con apoyo de tus docentes, pues sus opiniones e información favorecerán la elaboración del resumen de manera clara y precisa; una característica del resumen es hablar de lo esencial.
Has concluido esta sesión. Si deseas ampliar o conocer más sobre del tema, puedes consultar tu libro de Lengua Materna 2 o buscar en libros y bibliotecas digitales.
El Reto de Hoy:
Ahora que has descubierto la manera adecuada para seleccionar información, realiza lo siguiente: comienza por plantear un tema sobre el que quieras saber más. Después, selecciona una fuente, por ejemplo:
- Un libro sobre el tema publicado por una editorial que suele publicar textos serios y fundamentados.
- Una revista científica publicada por una universidad.
- Una página de internet en la que habitualmente buscan muchas personas información de cualquier tipo.
Además de estos, ¿en dónde más buscarías y qué criterios utilizarías para seleccionar textos para resumir?
Con las herramientas que aprendiste en esta sesión, realiza una lista de fuentes y compárala con tus pares para reforzar tu propia lista.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Galileo: cómo caen las cosas
Aprendizaje esperado: Analiza la gravitación y su papel en la explicación del movimiento de los planetas y la caída de los cuerpos (atracción) en la superficie terrestre.
Énfasis: Conocer y reflexionar sobre las aportaciones de Galileo y las primeras ideas acerca de la gravedad.
¿Qué vamos a aprender?
Estudiarás sobre el origen de la gravedad y el movimiento de los cuerpos. En esta sesión, conocerás sobre las aportaciones de Galileo y las primeras ideas sobre la gravedad.
¿Qué hacemos?
Analiza la siguiente información. Al término de la sesión, si es necesario, puedes consultar otras fuentes confiables de información con las que profundices más sobre lo que aquí aprendas.
Reflexiona en lo siguiente:
¿De dónde surgió la gravedad que nos tiene fijos en la superficie del planeta y evita que salgamos disparados hacia el espacio?
¿Qué es lo que hace que los cuerpos caigan?
Estos cuestionamientos acerca del origen de la gravedad no son nuevos, ya que desde la antigua Grecia se tenían explicaciones acerca del movimiento de los cuerpos, antes de que Newton y Galileo Galilei lo hicieran.
En el año 55 a. C., el poeta y filósofo romano Lucrecio explicó que: la velocidad de los objetos en caída se reduce sólo mediante la resistencia hidrodinámica o aerodinámica y que los cuerpos livianos caen más lentamente, por este motivo todos los cuerpos deben caer a la misma velocidad en el vacío.
La opinión del filósofo griego Aristóteles acerca de que los cuerpos pesados deben caer al suelo más rápidamente que los livianos es porque se hunden en el agua mientras que los más livianos se elevan.
Fue Galileo, el principal científico de principios del siglo XVII, quien dio crédito a la idea de Copérnico, la cual planteaba tener un planeta Tierra en movimiento. Aunque no fue el primero en señalar los problemas en las ideas de Aristóteles, sí fue el primero en refutarla contundentemente mediante la observación y la experimentación, donde demostró que el experimento es la mejor prueba del conocimiento.
Galileo demolió con facilidad la hipótesis de Aristóteles acerca de la caída de los cuerpos, al dejar caer objetos de varios pesos desde lo alto de la Torre Inclinada de Pisa y comparó las caídas. Al contrario de la aseveración de Aristóteles, Galileo encontró que una piedra con el doble del peso que otra no caía con el doble de rapidez.
Aunque Galileo usó los conceptos de inercia y de aceleración y fue quien midió primero la aceleración de objetos que caen, no pudo explicar por qué los objetos de diversas masas caen con aceleraciones iguales.
La masa parece no tener nada que ver en el experimento, no importa de qué materiales se componen los objetos que se dejan caer, ya que la gravedad los acelera exactamente igual, o como se dice normalmente: el objeto está en caída libre.
Derivado de lo expuesto hasta ahora Galileo Galilei presentó su principio que dice:
“Si se dejan caer dos cuerpos desde la misma altura, al mismo tiempo e independientemente de su composición, su masa y su forma, ambos tocarán el suelo al mismo instante en el vacío” (sin la presencia de aire).
La forma en la que actúa la gravedad no depende de la naturaleza de los cuerpos, entonces ¿qué rodea a estos cuerpos cuando caen al vacío? La respuesta es: nada, sólo espacio. Y ¿qué características se le pueden asociar al espacio?, sólo características geométricas. La gravedad se debe relacionar de alguna manera con la geometría del espacio, es decir, con su curvatura.
Se sabe que los objetos caen a causa de la fuerza de gravedad y cuando lo hacen están libres de toda restricción sin fricción del aire ni de cualquier otro tipo y caen bajo la influencia de la gravedad.
En el caso de los objetos en caída libre se hace uso de la letra “g” para representar a la gravedad que se produce sobre los cuerpos, y que se encuentra cerca de la superficie de la Tierra, la cual tendrá una aceleración constante de: g = 9.8 m/s2. Así que, al hablar de caída libre se refiere, por el momento, a un movimiento rectilíneo vertical de un cuerpo al que no se le imprime ninguna velocidad y que se acelera de manera constante como consecuencia de su peso. Como en el caso de una persona al caminar, los pies tienden a caer por la fuerza de gravedad que se presenta en ese instante, en caída libre.
Pero qué pasa si una persona da un salto, ¿crees que permanece en el espacio flotando? El resultado es que tiende a caer, y esto es por la gravedad que está presente en ese instante, cae en caída libre con un movimiento rectilíneo vertical.
Esto quiere decir que todos los objetos por estar sujetos a un campo gravitacional, que es una región del espacio donde actúa la fuerza de gravedad, caen.
Para saber más del tema, observa el siguiente video del minuto 1:23 al 5:25.
- ¿Cómo caen los cuerpos?
A Galileo se le llama con frecuencia el padre de la ciencia moderna, ya que fue el instrumento para descubrir ante el mundo que la experimentación es el método más válido para conocer los hechos de la naturaleza, como podrás ver a continuación, con el clavado de Paola Espinosa.
- Clavado de Paola Espinosa.
https://www.youtube.com/watch?v=BRhoWtjzoYE
Lo que acabas de observar es debido a las contribuciones que realizó Galileo a la Ciencia.
Reflexiona en lo siguiente: imagina que un hombre y una mujer se lanzan en paracaídas desde la misma altura y al mismo tiempo, el hombre pesa el doble que la mujer y sus paracaídas son del mismo tamaño y se abren desde el principio. ¿Quién llega primero al suelo, el hombre pesado o la mujer ligera?
La respuesta es: la persona que cae con mayor rapidez llega primero al suelo, es decir, la persona que tiene la mayor rapidez terminal. Al principio se creería que, como los paracaídas son iguales, la rapidez terminal de los dos sería igual y que, en consecuencia, los dos llegarían juntos. Sin embargo, eso no sucede porque también la resistencia del aire depende de la rapidez. Una mayor rapidez equivale a una mayor fuerza de impacto en el aire.
La mujer llegará a su rapidez terminal cuando la resistencia del aire contra su paracaídas sea igual a su peso. Cuando eso sucede, la resistencia del aire contra el paracaídas del hombre no habrá igualado a su peso todavía, debe caer con mayor rapidez que ella para que la resistencia del aire coincida con su peso mayor. La velocidad terminal es mayor para la persona más pesada y como resultado llega primero al suelo.
Lo mismo sucede con los toboganes que se encuentran en las albercas, ahí también está presente el principio de la caída de los cuerpos de Galileo, al igual que en los deportes, como salto con garrocha y carreras de velocidad, entre otros.
Para seguir ampliando el tema, observa el siguiente video del minuto 5:28 al 9:14.
- ¿Cómo caen los cuerpos?
Con esta información, has concluido. Si deseas profundizar en el tema o resolver algunas dudas, revisa tu libro de texto o recurre a fuentes de información confiable.
El Reto de Hoy:
Analiza y contesta las siguientes preguntas con tu familia:
- ¿De dónde surgió la gravedad que nos tiene fijos en la superficie del planeta y evita que salgamos disparados hacia el espacio?
- ¿Qué es lo que hace que los cuerpos caigan?
- ¿Qué dice el principio de Galileo?
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
La convivencia pacífica: una forma de aprender a estar juntos
Aprendizaje esperado: Promueve la postura no violenta ante los conflictos como un estilo de vida en las relaciones interpersonales y en la lucha social y política.
Énfasis: Identificar la convivencia pacífica como una forma de aprender a estar juntos y adaptarla a su estilo de vida en las relaciones interpersonales.
¿Qué vamos a aprender?
En esta sesión, comprenderás qué es la convivencia pacífica y cómo adaptarla a tu estilo de vida en las relaciones interpersonales. Asimismo, reflexionarás en la postura no violenta ante conflictos personales, sociales y políticos, y profundizarás en el dialogo como una herramienta primordial para la resolución de estos.
¿Qué hacemos?
Para iniciar, escucha con atención la siguiente problemática que comparte una alumna de secundaria sobre una situación de conflicto que se hizo presente en la comunidad donde vive.
- Audio. Problemática.
“En la calle donde vivo se armó tremendo problema: los vecinos de la esquina se han agarrado a gritos. El señor Mauro alega que Sofía y Juan son unos desobligados porque sus dos perros siempre están ladrando y haciendo mucho ruido.
“Ustedes no les hacen caso, ¡pobres animales!”, se alcanzó a escuchar que decía don Mauro muy molesto. “Mis perros hacen mucho ruido porque les gusta jugar, ladran porque se buscan uno al otro y también porque hay muchos perros vagabundos que se acercan a la casa”, le contestó Sofía, tratando de no alterarse.
Pero todo se puso muy mal cuando don Mauro amenazó con llamar a la perrera para que se llevaran a Tino y Tommy porque, según él, los perros son los causantes de que haya excremento en las jardineras de los vecinos y que algunas plantas se hayan maltratado.
Aunque Juan intentó explicarle a don Mauro que eso no era cierto, pues los perros sólo salen con correa y él o Sofía recogen sus heces, don Mauro insistió en que, aunque ellos no fueran directamente, era su culpa porque atraían a otros perros de la calle.
El pleito se puso mucho peor cuando más vecinos intervinieron. Por un lado, unos apoyaban a Juan y Sofía y, por el otro, otros vecinos se unieron a don Mauro declarando que los espacios comunales deben ser respetados y que la pareja debía reparar todos los daños ocasionados o atenerse a las consecuencias.”
¿Qué opinas respecto al problema que cuenta esta adolescente?, ¿tendrá razón don Mauro en dejar caer toda la responsabilidad en Sofía y Juan?
Existen algunas situaciones que no están bajo el control de ninguno de los vecinos, pero aun así pueden llegar a generar descontento. ¿De quién sería entonces la responsabilidad de darle una solución a este tipo de problemáticas?
La responsabilidad es de toda la comunidad, pues de alguna forma está afectando a todo el vecindario, ya sea por el ruido, las plantas que fueron maltratadas, los riesgos sanitarios que implican las heces al aire libre o, en el caso de Juan y Sofía, que están siendo directamente acusados. Entonces, ¿por qué crees que se hacen presentes estos tipos de conflictos?
En ocasiones, aquellos temas que tienen que ver con espacios compartidos o áreas comunes en las cuales no hay un titular o encargado, son un poco más difíciles de sobrellevar, pues cuesta más trabajo ponerse de acuerdo y no todos quieren tomar responsabilidad.
Compartir es parte de aprender a convivir y establecer relaciones sociales, por lo que hay ciertos valores y ciertas actitudes que se deben dominar. Con relación a este punto, la alumna Natalia Martínez señala algunos ejemplos. Presta atención al siguiente video.
- Video. Natalia.
Por lo tanto, en todos los espacios donde se socializa, se debe procurar que las diferencias no se conviertan en una problemática, sino en una oportunidad para convivir. Y para lograrlo, se debe fomentar día a día la convivencia pacífica en las relaciones interpersonales.
Para conocer más sobre la convivencia pacífica, escucha la siguiente explicación que la alumna Victoria Sánchez menciona al respecto.
- Video. Victoria.
La convivencia pacífica se refiere a la forma en cómo se establecen las interacciones con la gente que nos rodea, la cual debe ser guiada por valores como el respeto y la tolerancia, y debe encaminarse al logro del desarrollo colectivo.
Para comprender más a fondo este término, es importante entenderlo como un estado de relaciones humanas, cuya dinámica se basa en el fomento y ejercicio de tres principios éticos: la inclusión, la democracia y la cultura de paz, los cuales, a su vez, tienen implicaciones específicas que favorecen diversas dimensiones de la interacción.
Según la doctora Alelí Chaparro Caso-López y colaboradores, la inclusión favorece el reconocimiento de la dignidad de todas las personas. Lejos de ver su género, etnia, religión, cultura, grupo social o capacidades como un criterio para segregarlos, existe una valoración de sus particularidades como algo positivo.
En la convivencia se hace presente la pluralidad, se destaca la importancia del reconocimiento de logros, esfuerzos y capacidades, el cuidado a las necesidades de otros, el trabajo colaborativo, así como el sentido de pertenencia.
En cuanto a la democracia, la convivencia se enriquece con la participación y corresponsabilidad en la generación y seguimiento de los acuerdos que regulan la vida en común, así como el manejo de las diferencias y conflictos.
Finalmente, la convivencia pacífica se refiere a la capacidad de establecer interacciones humanas basadas en el aprecio, el respeto y la tolerancia, la prevención y atención de conductas de riesgo, el cuidado de los espacios y bienes colectivos, la reparación del daño y la reinserción comunitaria.
A propósito de este último punto, Johan Galtung, sociólogo y matemático noruego, propone que una idea creativa puede transformar un conflicto en acciones para construir la paz. Parte de la convivencia pacífica implica accionar para resolver las desavenencias que se puedan tener en nuestro día a día.
Para saber cómo lograrlo, observa el siguiente video del minuto 3:03 al 3:33.
- Las violencias en la convivencia cotidiana.
https://www.youtube.com/watch?v=T_X1xAO9SmQ
La convivencia pacífica no sólo busca prevenir los conflictos, sino que también requiere que los problemas que se han hecho presentes se solucionen, las relaciones interpersonales se restauren, se limen asperezas y, sobre todo, que los daños causados sean reparados.
Reflexiona en lo siguiente: ¿qué otras acciones se pueden hacer para fomentar la cultura de paz en las relaciones cotidianas?
La convivencia pacífica es una tarea personal y colectiva. Las acciones globales, por ejemplo, los gobiernos y las sociedades deben involucrarse en la misma medida, ya que es una tarea conjunta.
Algunas de las acciones que el gobierno y la sociedad deben trabajar juntos se enfocan en la educación, ya que la Declaración Universal de los Derechos Humanos establece lo siguiente:
“Debe tener como objeto fortalecer la personalidad humana y fomentar el respeto a las libertades fundamentales y a los derechos humanos, favoreciendo la comprensión, la amistad y la tolerancia, no sólo entre las naciones, sino también entre los grupos étnicos y religiosos; esto promoverá el mantenimiento de la paz”.
Declaración Universal de los Derechos Humanos (ONU, 1948).
Por lo tanto, se podría decir que un buen clima afectivo y emocional en las escuelas y los espacios en los que se desarrollan niñas, niños y adolescentes es determinante para el desarrollo de los seres humanos y el fomento de la convivencia pacífica, y un factor muy importante que se debe tener en cuenta es que cada individuo posee características, cualidades, capacidades e intereses que lo hacen único y que no deben convertirse en un impedimento para poder integrarse a las dinámicas de convivencia.
Lamentablemente, la discriminación y la violación a los derechos humanos siguen siendo un obstáculo para que todas las personas que integran una sociedad, sobre todo una tan diversa como la nuestra, coexistan de manera pacífica y armónica.
Con el fin de salvaguardar una convivencia pacífica, se deben eliminar dos tipos de comportamientos nocivos: los prejuicios y las intransigencias, ya que dificultan las relaciones entre los individuos y sociedad, en contraposición deben promoverse la comunicación, solidaridad, cooperación, colectividad y el trabajo colaborativo.
La convivencia pacífica no sólo nos aleja del conflicto, sino que también nos acerca al desarrollo de nuestro máximo potencial por medio de la interdependencia. Se puede entender como una gran red de relaciones, en la que todo lo que le ocurre a una de sus partes, afecta a las y los demás, por lo que se deben fomentar las acciones positivas para obtener beneficios colectivos.
Esto se puede lograr por medio de ciertos valores y actitudes como:
El respeto. La base de las interacciones debe ser el reconocimiento de la dignidad de las personas, sin prejuicios ni discriminaciones, entender que pueden tener pensamientos y opiniones distintos a los nuestros y que quizá se sienta el deseo de discutir o combatir estas opiniones, pero siempre respetando a la persona.
La afabilidad. Es decir, ser amables y atentos en el trato con otras personas. Ésta pronto se convertirá en una actitud positiva en la relación con las y los demás, ya que un ambiente de cordialidad facilitará el flujo de la misma.
La inteligencia. Es importante saber escuchar e intentar conocer a las personas con las que se coincide cotidianamente para poder conducirse con pertinencia y pericia en las interacciones. Una persona socialmente inteligente sabe estar y comportarse con personas muy diversas, social y culturalmente.
Estos aspectos pueden ayudar no sólo cuando se tiene un problema, también se pueden integrar a la interacción diaria que se establece con las diferentes personas con las que se convive, ya que orientan sobre cómo aprender a convivir de forma armónica en los diferentes espacios.
A continuación, escucha la opinión de dos alumnas de secundaria en la sección “La voz de la juventud”.
- Video. Sofía Xanat.
- Video. Karol Monserrat
El saber escuchar y entablar un diálogo permite resolver los conflictos que se hacen presentes en las relaciones interpersonales. El diálogo es una herramienta que brinda grandes beneficios.
Observa siguiente video del minuto 1:51 al 2:42, que habla más sobre el papel del diálogo en las relaciones humanas.
- El diálogo y la solución de conflictos.
https://www.youtube.com/watch?v=fsdRq04hfvE
Antes de finalizar, recapitula. En esta sesión comprendiste que la convivencia pacífica se refiere a la dinámica en la interacción social que se desarrolla dentro de valores como el respeto, la cordialidad y el entendimiento.
La convivencia pacífica no sólo busca evitar el conflicto, sino que las personas trabajen en conjunto para desarrollarse plenamente y aprender las unas de las otras. De igual forma, aquellos problemas que se lleguen a presentar deben ser resueltos y los daños reparados para que la armonía perpetúe en las relaciones.
El diálogo es una herramienta primordial para la afabilidad y la resolución de conflictos, pues al escuchar y ponernos en los zapatos de los demás logramos el entendimiento mutuo.
Has concluido. Para más información sobre el tema, consulta tu libro de texto e identifica qué otras acciones personales y colectivas enriquecen la convivencia pacífica. Practica lo aprendido para mejorar tu interacción con la gente que te rodea, sobre todo ahora que las condiciones de convivencia se han visto afectadas por la pandemia.
Si está en tus posibilidades, recurre a algunos otros libros que tengas disponibles, o bien, consulta sitios electrónicos confiables que te den más información relacionada con el tema.
El Reto de Hoy:
En tu libreta o en hojas blancas, narra una experiencia que hayas vivido o presenciado en la que el diálogo haya servido para prevenir o frenar un enfrentamiento violento, teniendo como consecuencia el mejoramiento de la convivencia entre las personas implicadas. Los ejemplos que escuchaste en esta sesión podrán ayudarte en la redacción de tu propia historia.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
El informe de diagnóstico
Aprendizaje esperado: Planifica y organiza las acciones técnicas según las necesidades y oportunidades indicadas en el diagnóstico.
Énfasis: Identificar las características del informe de diagnóstico y los elementos de éste que se deben considerar para decidir el proceso o producto técnico a desarrollar.
¿Qué vamos a aprender?
En esta sesión, conocerás cómo elaborar un informe técnico, para ello, identificarás sus características y los elementos de éste para decidir el proceso o producto técnico a desarrollar. Asimismo, analizarás el documento en que se presenta este informe y algunos ejemplos.
¿Qué hacemos?
Inicia con los siguientes conceptos.
Informe técnico: es un documento donde se exponen los resultados, en el que se analizan, las posibles soluciones a un problema, o situación de una empresa, aportando ideas, recomendaciones y conclusiones y va dirigido a un grupo calificado.
Producto técnico: es un objeto que surge después de un proceso de fabricación, transformando materia prima, también puede ser un servicio, ambos satisfacen una necesidad o un interés.
En sesiones anteriores, estudiaste lo que es un diagnóstico comunitario, así como los instrumentos que permiten recabar información sobre ciertas necesidades.
En el informe técnico, se menciona con claridad, la necesidad que dio origen al diagnóstico, los medios e instrumentos que se utilizaron para la obtención de información (observación, entrevista, etc.), los participantes (que pueden ser un grupo de personas o la comunidad) y el tiempo requerido en las etapas.
Los resultados del diagnóstico están determinados por toda la información relevante que se obtiene, sobre la situación que causa la necesidad; como son las condiciones sociales, económicas, culturales y naturales; así también, las características técnicas, es decir, los sistemas y procesos técnicos relacionados directamente con la necesidad que se detecta.
La información, ayuda para poder plantear el problema técnico y para definir de qué manera se buscarán soluciones. Las propuestas pueden venir de la comunidad, sobre todo si se trata de un diagnóstico comunitario.
Pero el informe técnico, también presenta resultados de otros tipos de diagnóstico, como aquellos que buscan identificar necesidades y problemas en los procesos técnicos, en los talleres artesanales, empresas o servicios. Su finalidad, siempre va a ser presentar información, para tomar decisiones; está dirigido a personal calificado, que puede evaluar y proponer cambios técnicos en los procesos, productos o servicios.
Revisa algunos ejemplos en los que los diagnósticos y sus respectivos informes técnicos aportan información relevante.

Como ya conoces, las actividades económicas se dividen en tres sectores. El primario, que refiere a la obtención de la materia prima derivada de los recursos naturales; el sector secundario, en el que se transforma la materia prima; y el terciario, que es de servicios.
En cada uno de estos sectores, la planeación y organización de sus procesos, parten de un diagnóstico que se hace de manera periódica, y que arroja resultados e información, con la finalidad de identificar si está funcionando el sistema de acuerdo con lo planeado y de ser necesario corregir a tiempo el proceso.
Para ello, el informe técnico proporciona información específica sobre los procesos, productos o servicios para que, en un tiempo determinado, personal especializado, realice los cambios necesarios. Debe ser de manera periódica, ya que tanto las necesidades de la sociedad, como los procesos, van cambiando.
Para comprender mejor esta fase del diagnóstico, analízalo con la escuela. La educación se ubica en el sector terciario. El servicio que aporta es la enseñanza, para ello requiere de instituciones que crean espacios físicos y virtuales, donde se forma y transforma a la población de todas las edades de una sociedad.
No revisarás cómo funcionan las escuelas, sólo analizarás una actividad que se lleva a cabo dentro de éstas, la evaluación diagnóstica. Para ello, reflexiona en las siguientes preguntas, a manera de cuestionario.
- ¿Cuándo se realiza la evaluación diagnóstica? Cada ciclo escolar inicia con reuniones preparativas con el personal de la institución, para elaborar el plan de trabajo.
- ¿A quiénes se aplica? A las alumnas y alumnos, esta primera etapa consiste en la presentación y aplicación de la evaluación diagnóstica, sobre los conocimientos, habilidades y aptitudes adquiridas con anterioridad.
- ¿Qué instrumentos se utilizan para recabar la información? En algunos casos, se recurre a entrevistas con la o el docente, que tuvo al grupo en el ciclo escolar anterior, se realiza en caso de que el grupo siga con los mismos integrantes.
Se aplican instrumentos, como es el cuestionario de preguntas cerradas y el de preguntas abiertas, así como el de opción múltiple. Que arrojan datos precisos sobre el conocimiento de los aprendizajes de cada uno de los miembros del grupo.
En el caso de Tecnología, se valora a partir de un diagnóstico práctico, y teórico, así como la verificación sobre su forma de aprendizaje, con el propósito de indagar sobre las habilidades y conocimientos sobre los procesos técnicos.
- ¿Qué se hace con la información? Los resultados obtenidos, se presentan en un informe técnico; el cual ofrece un panorama de las estrategias que se deben implementar, para alcanzar los aprendizajes programados.
La maestra o maestro, los analiza y organiza, para después planear y aplicar acciones pedagógicas por medio de un documento escrito que, puede incluir gráficos y tablas.
- ¿A quién se le entrega el informe técnico? A las autoridades educativas del plantel y a los profesores de las materias, para que en conjunto lleguen a acuerdos, sobre cómo se va a proceder para trabajar con las alumnas y los alumnos de cada grado, durante el ciclo escolar.
Al final de cada periodo, se realiza una reunión para evaluar las estrategias que se aplicaron al inicio del ciclo y, se modifican las que no hayan obtenido resultados.
Los informes técnicos, se presentan ante un grupo de personas que está directamente involucrado con los procesos, y que tiene la facultad de realizar acciones, para la resolución de las necesidades y problemas.
Como puedes observar, no eres ajena o ajeno a esto, ahora ya tienes más claro por qué son tan importantes las evaluaciones que se realizan al inicio de cada año escolar.
Es muy importante para las instituciones, proporcionar un buen servicio a la comunidad y, aunque no se vea a simple vista, siempre se está en competencia con instituciones del mismo nivel, esto se cumple, con pruebas que se aplican a profesores y alumnos, arrojando información para evaluar y diagnosticar a las instituciones y la educación en México.
Algunas características del documento en que se presenta el informe técnico son:
- Hoja tamaño A4, con margen de 2.54 cm, todas las páginas van numeradas.
- El título va en el encabezado, para ubicarlo fácilmente.
- El resumen se coloca al comienzo del informe. Se dirige a los posibles lectores, dándoles la bienvenida con una breve idea de lo que hay en el informe, sin abarcar los resultados, ni las conclusiones.
- Índice, están contenidos todos los nombres de las secciones y en qué página se puede consultar de manera organizada.
- La introducción es la presentación del tema del informe a desarrollar, se explica el motivo y beneficiarios.
- Cuerpo del informe es la más importante, pues es donde se colocan los gráficos, imágenes o tablas facilitando la comprensión.
- Se explica el objetivo del estudio, las propuestas, los procesos utilizados para la recolección de datos, comparación con otros informes afines y los resultados obtenidos del proceso de evaluación.
- Conclusiones, son las respuestas a la problemática o situación del estudio.
- Referencias y bibliografía, son las fuentes consultadas en la adquisición de información para el informe técnico.
Pero antes de todo hubo una sección de planeación y revisión, también conviene hacer un borrador, con el fin de no cometer errores.
Para continuar, analiza otro ejemplo de los informes técnicos, pero esta vez en el sector secundario de la economía. Observa el siguiente video.
- Video. Tipos de casas.
En la construcción, existen empresas dedicadas exclusivamente a la construcción de viviendas como: departamentos, casas dúplex, plurifamiliar, residencial, unifamiliar, adosada e interés social.
Tienen la responsabilidad de seguir los lineamientos, normas, reglas y leyes de cada localidad, ciudad o país, respetando las características del ambiente, impacto ambiental, estructura del suelo y necesidades de la comunidad.
Al aprobar todos estos aspectos, se inicia la obra; la supervisión se realiza desde el comienzo del proyecto y en cada una de las etapas constructivas, hasta su entrega.
Al finalizar la obra, se entrega un informe con los siguientes datos:
- Título, incluye el nombre de la empresa.
- Índice.
- Descripción, etapas de la elaboración del informe.
- Desarrollo metodológico, que es donde se describen las especificaciones técnicas o siglas.
Para este caso, el informe técnico de la obra o construcción, la recopilación de datos incluye:
- Los materiales utilizados, tipo y marca.
- Los muros, trabes, columnas, espacios arquitectónicos, etc.
- Especificaciones técnicas.
- Fecha de inicio y final de la obra.
- Se incluyen los resultados en las hojas de revisión y de datos.
- Se anexan los lineamientos, manuales técnicos y otros documentos que fueron consultados.
Por ello, cada una de las tareas que se llevan a cabo en el desarrollo de la obra, las realiza personal especializado, como arquitectos, ingenieros, maestros de obra, y demás personal experimentado.
Los informes técnicos son importantes en cada uno de los campos tecnológicos, con el fin de mejorar o cambiar los procesos, para poder satisfacer necesidades actuales y las que vayan surgiendo.
Ayudan también para identificar lo que sigue funcionando con el transcurso del tiempo y lo que se mejora dentro de cada proceso, para obtener un producto técnico de calidad.
Ahora, continua con las siguientes preguntas para ahondar más en el tema.
La palabra globalización:
¿A qué se refiere?
¿Por qué es importante en los países industrializados?
Se refiere a la integración de los países del mundo en cuestión económica, política, tecnológica, social y cultural, expandiendo la comercialización a todos los países, así como la fabricación de los productos en países con mano de obra barata.
Seguro te preguntarás:
¿Qué relación hay entre la globalización y el tema de esta sesión?
¿Por qué se menciona?
Un aspecto de la globalización es la tecnología, lo que implica procesos técnicos que cubren ciertas necesidades, no solo a nivel local, también internacional.
Seguramente, te has dado cuenta de que existen varios productos elaborados en otras naciones y continentes; para que un productor pueda ofrecer sus productos en el mercado internacional, tiene que hacer cambios técnicos en los procesos productivos.
Para identificar claramente qué debe mejorar o innovar, se recurre a los informes técnicos. Según lo que arroje el informe, se puede identificar qué parte del proceso se puede mejorar para cubrir los requerimientos de los mercados propios de la empresa, así como los locales e incluso internacionales.
Como se mencionó anteriormente, cada informe es muy particular, pues depende de la necesidad a satisfacer y de las metas o logros que se quieren cubrir.
El Reto de Hoy:
Retoma tus notas de las sesiones anteriores y realiza la observación de tus actividades en casa, pueden ser las tuyas o de toda la familia, y elabora un informe de cómo mejorar esas actividades para tener más tiempo libre o para obtener mejores resultados. Escribe en tu cuaderno tus observaciones y coméntalas con tus familiares.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario