Aprende en Casa III SEP: 1 de marzo TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 1 de marzo de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Lunes 1 de marzo, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en Casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Variación lineal y proporcionalidad inversa
Aprendizaje esperado: Analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.
Énfasis: Analizar y comparar situaciones de variación lineal y proporcionalidad inversa.
¿Qué vamos a aprender?
En esta sesión, estudiarás el tema de la variación lineal, comparándola con la variación proporcional directa y la variación proporcional inversa. Para ello, analizarás y resolverás situaciones a partir de sus representaciones tabular, gráfica y algebraica.
¿Qué hacemos?
Analiza la información de la siguiente situación y anota en tu cuaderno tus dudas y hallazgos.
¿Has escuchado en alguna ocasión que la temperatura en alguna ciudad es de 80 grados Fahrenheit?, ¿esto es posible?
Si es posible, se debe analizar la relación entre los grados Fahrenheit y los grados Celsius, se trata de una relación de variación lineal que está dada por la siguiente fórmula:
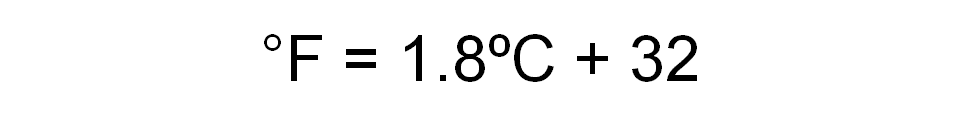
Donde:
°F: es la temperatura en grados Fahrenheit.
°C: representa la temperatura en grados Celsius.
Pero ¿qué significa que se trate de una relación de variación lineal?, ¿es una variación de proporcionalidad directa como lo has estudiado?
Para comprender la variación lineal, revisa la siguiente situación.
Situación-problema: grados Fahrenheit
En un día soleado en el puerto de Veracruz, anunciaron que nos encontrábamos a 80 grados Fahrenheit.
¿Qué significa esto?, ¿estaba haciendo “mucho calor”?
Para contestar la pregunta: ¿qué es una variación lineal? Comienza por recuperar qué características tiene este tipo de variación.
Características de la variación proporcional directa:
- Su gráfica es una línea recta.
- Cuando la variable independiente aumenta, también aumenta la variable dependiente, siempre en la misma proporción.
- Existe una constante (k) de proporcionalidad.
- La recta que la representa pasa por el origen del plano cartesiano.
Para verificar sí la relación entre los grados Fahrenheit y los grados Celsius cumplen con las características mencionadas. Realiza la siguiente tabla.
|
Características |
Si o No |
|
Su gráfica es una línea recta. |
|
|
Cuando la variable “x” aumenta, también aumenta la variable “y”, siempre en la misma proporción. |
|
|
Existe una constante de proporcionalidad “k”. |
|
|
La recta que la representa pasa por el origen del plano cartesiano. |
|
En la columna de la derecha deberás escribir Sí o No según corresponda. Si cumple con todas esas propiedades, entonces se trata de una relación de proporcionalidad directa.
Para apoyar el llenado de la tabla es importante conocer la gráfica que relaciona las variables: grados Celsius y grados Fahrenheit.
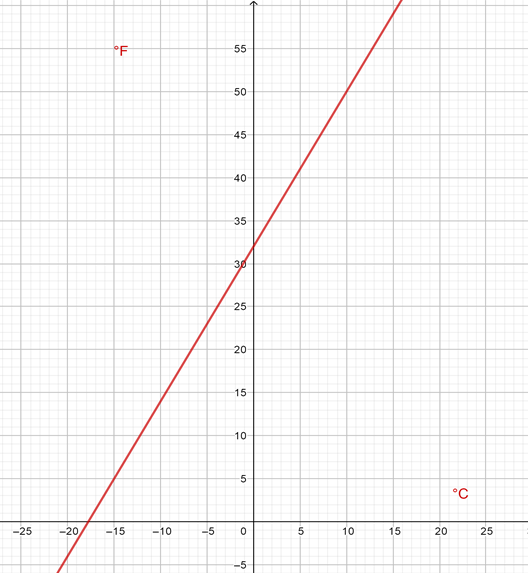
En la gráfica, en el eje “x” se representan las cantidades de grados Celsius y en el eje “y” se encuentran las cantidades en grados Fahrenheit.
Como puedes observar, la gráfica sí es una recta, pero no pasa por el origen. Así que, ya puedes completar las dos celdas correspondientes de tu tabla con la palabra No. Con esto es suficiente para determinar que no se trata de una relación de proporcionalidad directa.
También se observa que si las cantidades correspondientes a los grados Celsius aumentan: diez, veinte, treinta, cuarenta, etc., también lo hacen las de los grados Fahrenheit: 20, 40, 60, 70, etc. Pero no lo hacen en la misma proporción. Por lo tanto, se escribe No en la celda correspondiente de la tabla.
Falta verificar una característica más: ¿Existe constante de proporcionalidad entre las variables?, ¿cómo puedes saberlo?
Se sabe que la constante de proporcionalidad se simboliza con la letra “k” y es el cociente que se obtiene de la división de la primera variable “y” entre la variable “x”. El número que se obtiene es constante, esto quiere decir que, aunque cambien las cantidades de las variables “x” y “y”, el cociente no cambia.
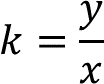
Verifica si existe o no constante de proporcionalidad, para ello, usa la fórmula. La variable “x” corresponde a los grados Celsius y la variable “y”, corresponde a los grados Fahrenheit.
Por ejemplo, para saber cuántos grados Fahrenheit corresponden a 5 grados Celsius, se sustituye en la fórmula el número 5 en la variable grados Celsius y se realiza las operaciones correspondientes:
Fórmula: °F = 1.8°C + 32
Sustituyendo 5°C: °F = 1.8 (5) + 32
Realizando operaciones: °F = 9 + 32 = 41
Coordenadas: (5, 41)
Entonces: 5°C = 41°F
Por lo tanto, a 5 grados Celsius le corresponden 41 grados Fahrenheit. Así, se determina la primera coordenada: 5 corresponde a “x” y 41 corresponde a “y”. Ahora, calcula dos coordenadas más con 10 y con 15 grados Celsius.
Una vez que ya tengas tus resultados verifícalos. Seguramente las coordenadas que obtuviste son:
Coordenadas:
(10, 50)
(15, 59)
(5, 41)
Es decir, que a 10 grados Celsius le corresponden 50 grados Fahrenheit, y que a 15 grados Celsius le corresponden 59 grados Fahrenheit. Y ya conocías la coordenada (5, 41).
Ahora, verifica si existe constante de proporcionalidad en la relación entre grados Celsius y Fahrenheit. Para hacerlo, se dividen los valores de la variable “y” entre los de la variable “x”, es decir, los grados Fahrenheit entre los grados Celsius con las tres coordenadas que se conocen.
Divisiones:
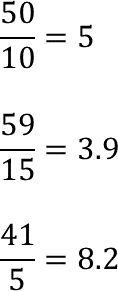
Observa que los resultados de las divisiones no son iguales, por lo tanto, no existe constante de proporcionalidad.
En resumen, la característica que comparte la variación lineal con la variación proporcional directa es: su grafica es una línea recta.
Si en una variación lineal los valores de la variable “x” crecen, también crecen los de “y”. En una variación de proporcionalidad directa hay una condición: el aumento o disminución entre los valores siempre es en la misma proporción, además, la gráfica que la representa pasa por el origen del plano cartesiano.
A continuación, estudiarás otras propiedades de la variación lineal donde se relacionan dos variables, a través de otros ejemplos.
Las expresiones algebraicas que caracterizan este tipo de variación tienen la forma:
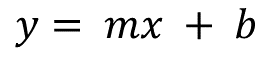
Como en el problema de los grados Celsius y Fahrenheit, donde las variables “x” y “y”, se sustituyen por grados Celsius y grados Fahrenheit, pero también donde el parámetro “m” corresponde al número 1.8 y la “b” corresponde a 32.
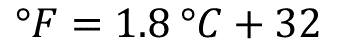
Para una mejor comprensión del tema de variación lineal, analiza los siguientes ejemplos, que tienen la misma forma general y todos representan una variación lineal.
Primer ejemplo:
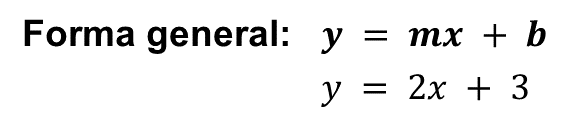
Donde:
m = 2
b = 3
Segundo ejemplo:
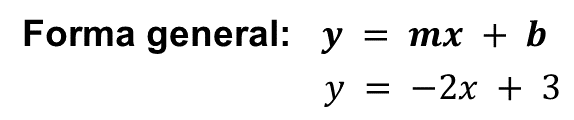
Donde:
m = -2
b = 3
Tercer ejemplo:
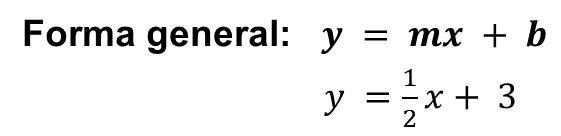
Donde:
m = un medio
b = 3
¿Sabes por qué en todos los ejemplos, “b” es igual a 3? “b” puede ser cualquier número real, en este caso, los ejemplos presentan al parámetro (b = 3), esto para observar lo siguiente.
Es importante recuperar que al parámetro “m” se le conoce como pendiente de la recta y al parámetro “b” se le llama ordenada al origen.
Observa las tres ecuaciones representadas en estos ejes de coordenadas.
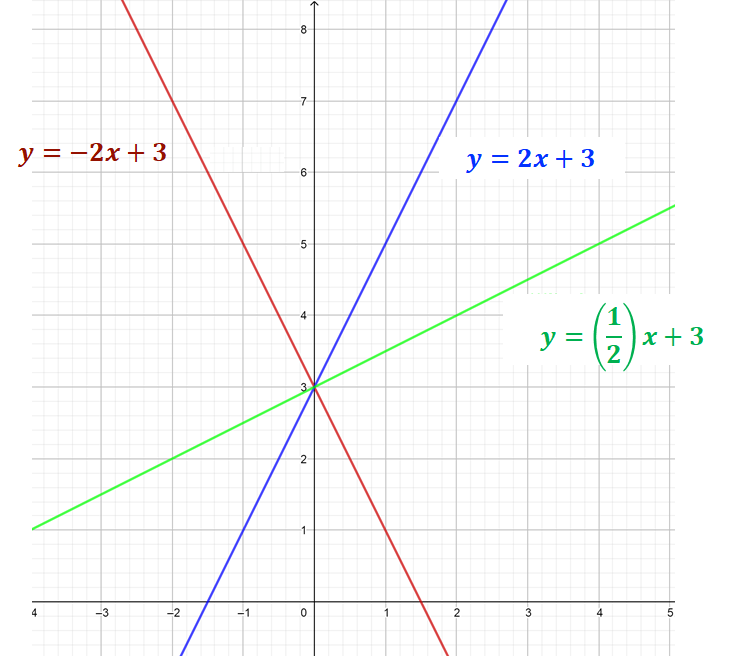
Todas tienen diferentes pendientes, pero la misma ordenada al origen. Las pendientes son: -2, 2 y un medio, respectivamente. Mientras la ordenada al origen en todas es tres. La pendiente de una recta se relaciona con el ángulo de inclinación de la recta. Como puedes observar, unas rectas están más inclinadas que otras. Y todas coinciden en el punto (0,3), que es donde cruzan al eje de las “y”, lo que se llama ordenada al origen, representado por el parámetro “b”.
Después de esta información, analiza los siguientes ejemplos relacionados con la inclinación de la recta, para aclarar a qué se refiere la pendiente de una recta. Observa las siguientes imágenes:

La imagen de la izquierda representa una señal de tránsito indicando que se aproxima una pendiente en la carretera. La de la derecha representa la pendiente que existe en un tramo de carretera.
¿Entonces, si una carretera está plana significa que no tiene pendiente? Efectivamente, también se puede decir que la pendiente de esa carretera es cero.
Si observas las siguientes gráficas de las rectas “A” y “B”, notarás que tienen diferentes pendientes.
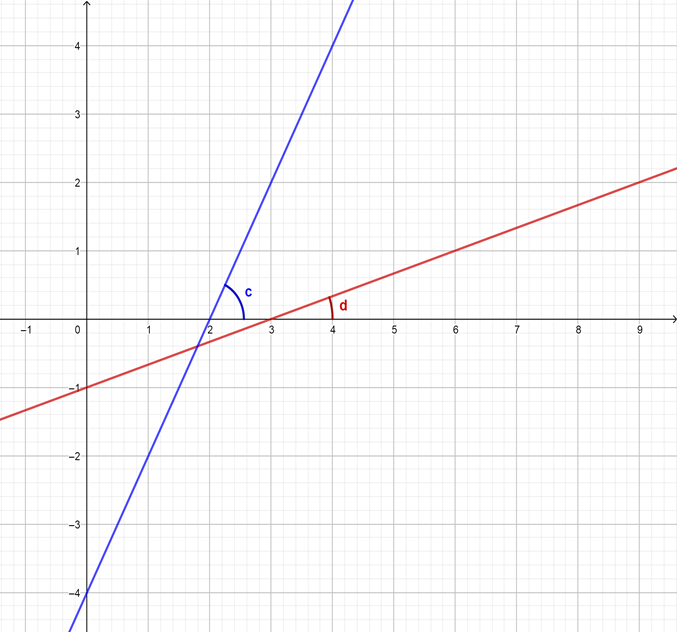
La recta “A” está más inclinada que la recta “B”, es decir, tienen diferente ángulo de inclinación. Observa el ángulo de inclinación que forma cada una de las rectas con el eje de las abscisas o eje “x”.
Por ejemplo, la recta A forma un ángulo con el eje “x”, que se identifica con la letra “c”, este ángulo se llama ángulo de inclinación. ¿Cuál es el ángulo inclinación de la recta B?
Seguramente pensaste en el ángulo representado con la letra “d”, Observa que es mayor el ángulo “c” que el ángulo “d”, por lo tanto, la recta A tiene mayor pendiente que la recta B.
Retoma las gráficas de las tres rectas para concluir el análisis de la pendiente.
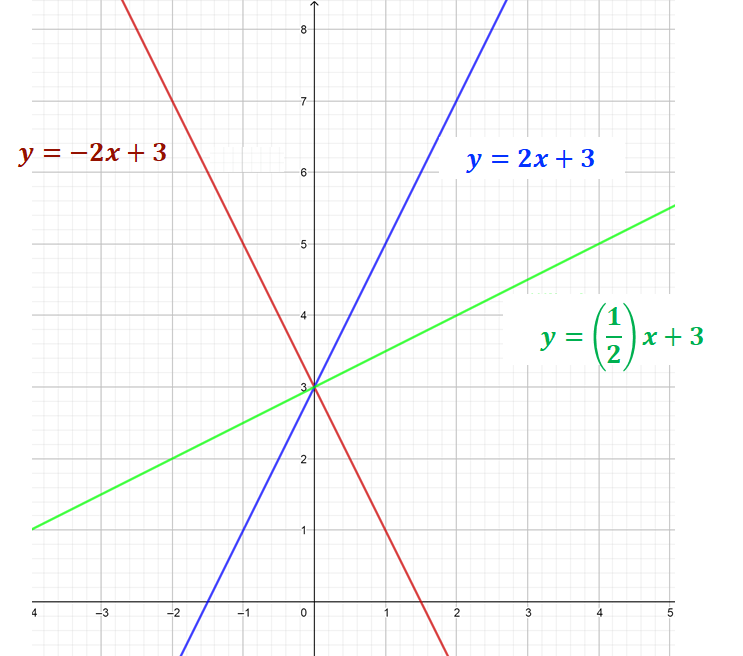
Las pendientes son (m = -2), (m = 2) y (m = 1/2). Analiza primero las dos pendientes positivas, es decir, con “m” igual a 2 y “m” igual a un medio.
Como 2 es mayor que un medio, la recta y = 2x + 3, tiene mayor pendiente que la recta y = 1/2x + 3. Pero ¿qué ocurre con la pendiente negativa de la gráfica de la ecuación y = -2x + 3?
Observa que la recta y = -2x + 3, es completamente simétrica a la recta y = 2x + 3, es decir, si se piensa en el eje “y” como espejo, la recta con pendiente negativa refleja a la recta con pendiente positiva. Esto sucede porque los valores de “m” en esas rectas también son simétricos.
Para que no haya duda respecto a la pendiente negativa, compara otro par de rectas, una con pendiente positiva y otra con pendiente negativa.
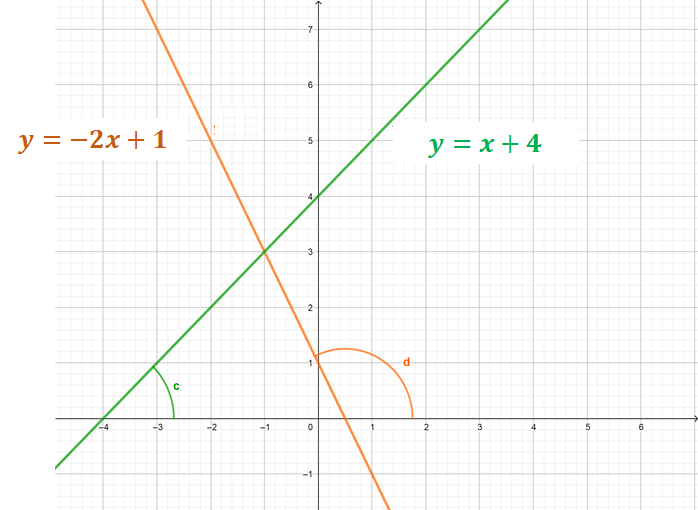
Estas rectas no son simétricas, la recta y = x + 4 tiene pendiente 1 y la recta y = -2x + 1 tiene pendiente negativa.

Observa que la recta con pendiente positiva se inclina hacia la derecha con respecto al eje “y” y la recta con pendiente negativa se inclina hacia la izquierda. También puedes notar que el ángulo “c” de la recta con pendiente positiva, es agudo, es decir, menor a 90 grados, en cambio el ángulo “d”, de la recta con pendiente negativa es un ángulo obtuso, es decir, un ángulo mayor a 90 grados pero menor a 180 grados.
Ahora, reflexiona en lo siguiente: ¿qué sucede si la recta tiene un ángulo de inclinación de cero grados? La recta sería paralela al eje “x”, como la recta A de la siguiente imagen. Tiene una pendiente de valor cero.
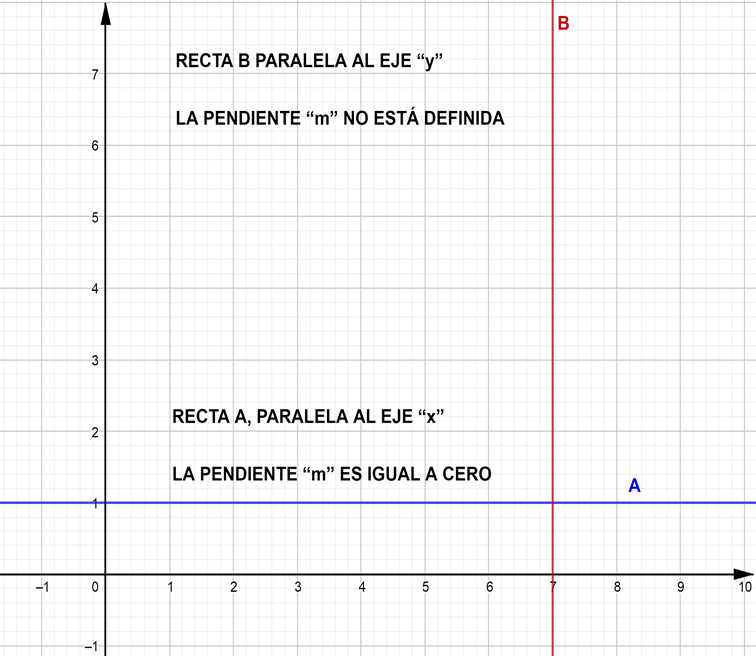
Si la recta es completamente vertical, es decir, si es paralela al eje “y”, como la recta B, ¿cuál es su pendiente? En este caso la recta no está definida, significa que la pendiente no existe para una recta así.
Ya conoces el significado de pendiente de la recta “m”, un concepto muy importante en las Matemáticas avanzadas, al igual que el concepto de Ordenada al origen.
En la forma general de la variación lineal (y = m x + b), a la “b” se le conoce como ordenada al origen.
En los siguientes ejemplos, las ordenadas al origen (b) son: 4, 8 y -6, respectivamente.
Ejemplo 1: y = 5x + 4
Ejemplo 2: y = -3x + 8
Ejemplo 3: 7x - 6
Ahora, retoma las gráficas de las tres y observa que en todas, la ordenada al origen, es decir, la letra “b” es igual a 3.
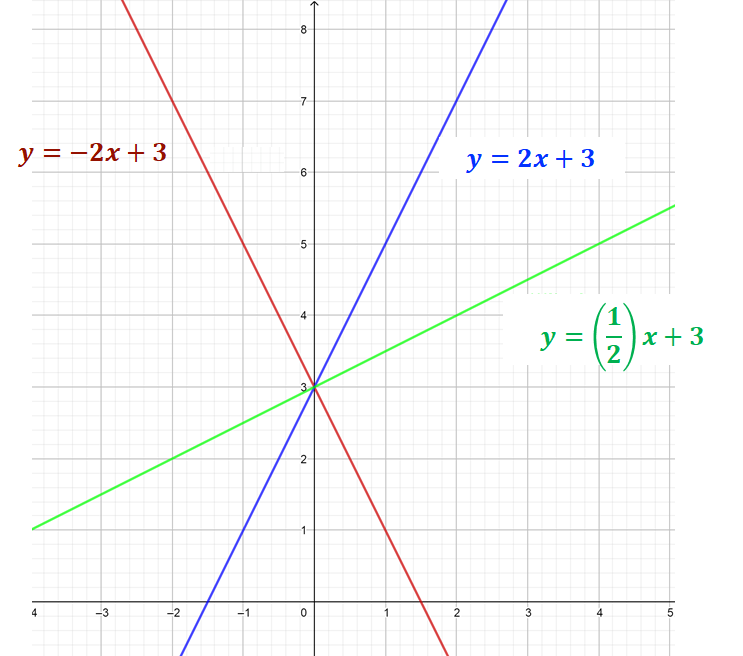
Puedes identificar que las tres rectas pasan por el mismo punto al cortar al eje de las “y”. ¿Cuál es ese punto? Seguramente ya sabes que es tres. Ahora reflexiona: ¿cuáles son las coordenadas de ese punto?
Las coordenadas son: (0, 3). Las tres rectas comparten esta coordenada, y significa que cuando la variable “x” es cero, la variable “y” será tres.
Entonces:
¿Por qué punto del eje de las “y”, pasará la recta: y = 9x - 5?
¿Cuál son las coordenadas de ese punto?
La recta (y = 9x – 5), cruza al eje “y” en el punto -5. Las coordenadas de ese punto son (0, -5). Traza la gráfica para comprobarlo.
Ahora, reflexiona en la siguiente cuestión:
¿Qué sucede con la recta cuando el parámetro “b” vale cero?
Para saber qué sucede analiza el siguiente ejemplo:
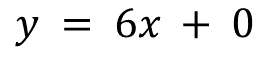
En este caso, como cero es neutro aditivo, la variación lineal estaría representada por la ecuación:
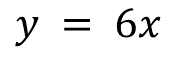
Si “b” es igual a cero, indica una variación proporcional. Se sabe que la constante “k” en una variación proporcional, se calcula dividiendo los valores de la variable “y” entre los valores correspondientes de la variable “x”. En forma general:
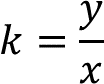
En la forma general de la constante “k”. Despeja la variable “y”.
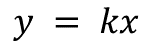
Por lo tanto, se puede ver que el ejemplo (y = 6x) tiene la misma forma que la ecuación general, esto significa que es una variación proporcional donde la constante “k” es 6.
A continuación, asigna valores a las variables “x” y “y”, y divide para comprobar que el valor que se calcule siempre es seis.
Se ha comparado la variación lineal de la forma (y = m x + b) con la variación proporcional directa, pero ¿qué sucede con la variación proporcional inversa?, ¿tienen alguna característica en común? Estas variables no comparten ninguna característica en común, pero si se pueden decir las características principales de la variación proporcional inversa. Para ello, analiza la siguiente situación.
Situación-problema: cajas de naranjas
Para empacar una cosecha de naranjas se requieren 3,000 cajas, colocando 20 kilogramos de naranjas en cada caja. ¿Cuántas cajas se necesitan si ahora se quieren colocar solamente 15 kilos, 10 kilos y 5 kilos en cada caja?
En una variación inversa, cuando una de las magnitudes crece, la otra disminuye; por ello, entre más kilos de naranja se coloquen en una caja, disminuirá la cantidad de cajas que se necesiten.
“x” será el número de kilogramos y “y” la cantidad de cajas que se necesitan.

Observa en la siguiente tabla que, mientras las cantidades de “x” disminuyen las cantidades de “y” aumentan. Así, para cajas con 20 kilos se requieren 3,000 cajas, para cajas con 15 kilos se requieren 4,000 cajas, y así sucesivamente.
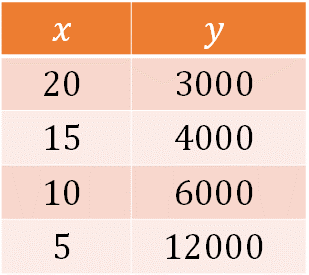
En una variación proporcional inversa: Si la variable “x” aumenta, entonces disminuye la variable “y”, y si la variable “x” disminuye, aumenta la variable “y” de manera proporcional. Por ejemplo, si la cantidad de cajas disminuye a la mitad, la cantidad de naranjas aumenta al doble.
En la tabla anterior, se puede observar que si la cantidad de kilos por caja (15 por ejemplo) disminuye a la tercera parte, es decir a 5 kilos, la cantidad de cajas (4,000 para 15 kilos) aumenta al triple (12,000 para 5 kilos por caja).
En la variación proporcional inversa también existe una constante de proporcionalidad. Observa lo que sucede si se multiplican las cantidades de la variable “x” por las cantidades correspondientes de la variable “y”.
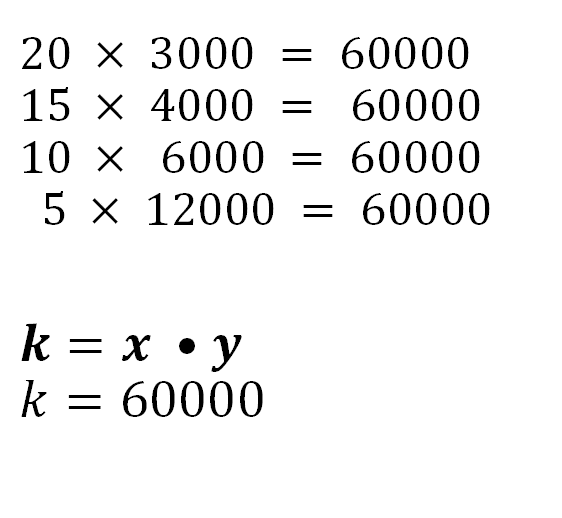
El resultado es 60 mil, un número constante. En toda variación proporcional inversa al multiplicar las cantidades correspondientes de “x” y “y” el resultado representa a la constante de proporcionalidad simbolizada con la letra “k”, por lo tanto, “k” es igual a “x” por “y”.
En la variación lineal, sea o no proporcional, la gráfica es una línea recta. Como puedes observar, la gráfica de la variación proporcional inversa es una curva llamada hipérbola.
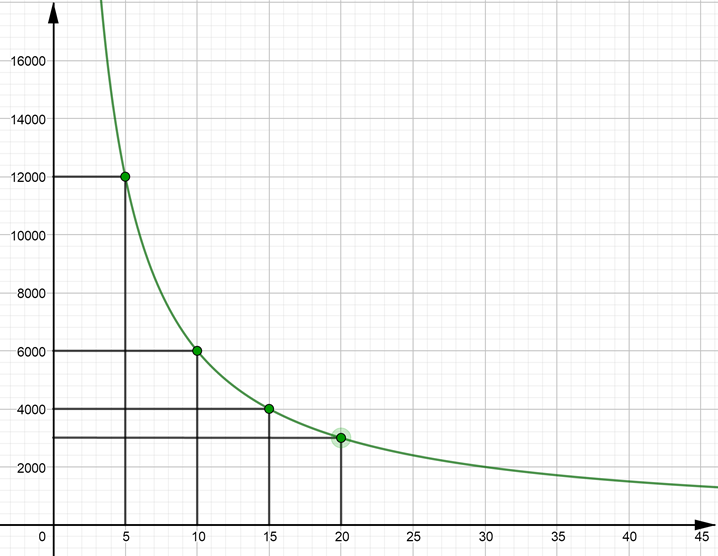
Observa cómo la curva se acerca a los ejes, pero no los llega a tocar, esto es independiente de los valores que le asignen a la variable “x”. Puedes comprobarlo asignando los valores que desees a la variable “x” para obtener los de “y”.
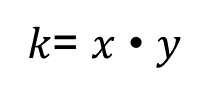
Al despejar “y” de la ecuación, se obtiene “y” igual a “k” entre “x”. En el problema, “k” es igual 60 mil, por lo tanto, “y” es igual 60 mil entre “x”.
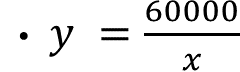
Usando esta fórmula puedes obtener los valores de “y” y comprobar que la curva nunca toca los ejes “x” y “y”. Utilicen esta misma fórmula y calcula el número de cajas que se necesitarán si cada caja contuviera 25, 30 y 35 kilos de naranjas.
Retoma la situación de los grados Fahrenheit y grados Celsius. Las coordenadas por la que pasa la recta son (0, 32), porque el parámetro “b” en esta ecuación es igual a 32. Pero ¿qué significa esto en el problema planteado inicialmente?
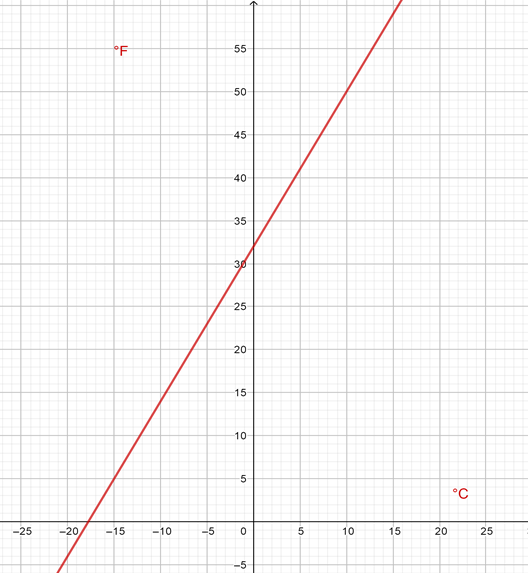
Significa que cuando en algún un lugar la temperatura está a cero grados Celsius, la temperatura en ese lugar es de 32 grados Fahrenheit. Esto se puede comprobar si se sustituye en la fórmula cero grados Celsius, lo multiplicas por 1.8 y sumas 32, el resultado será 32.
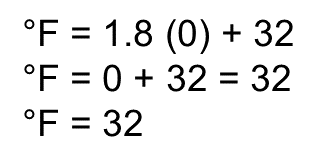
Entonces, cuando la temperatura en el puerto de Veracruz está a 80 grados Fahrenheit: ¿cuántos grados Celsius son?, ¿es posible utilizar la misma fórmula?
Sí es posible utilizar esta fórmula, sólo habrá que despejar los grados Celsius. Presta atención al procedimiento:
Primero, aplica la propiedad uniforme, restando 32 en cada lado de la igualdad. Haciendo operaciones, grados Fahrenheit menos treinta y dos es igual a uno punto ocho grados Celsius más cero, ya que treinta y dos menos treinta y dos es igual a cero.
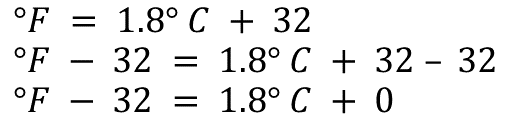
Aplicando el neutro aditivo, grados Fahrenheit menos treinta y dos es igual a uno punto ocho grados Celsius.
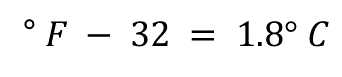
Después, se divide uno punto ocho de cada lado de la igualdad. Haciendo operaciones, grados Fahrenheit menos treinta y dos, todo esto entre uno punto ocho es igual a grados Celsius.
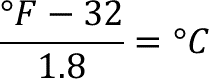
Finalmente, se aplica la propiedad simétrica de la igualdad que permite intercambiar los lados de la igualdad sin alterarla.
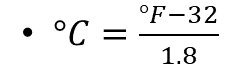
Todavía falta sustituir los 80 grados Fahrenheit en la fórmula y hacer las operaciones para saber cuánto calor hacía ese día en Veracruz.
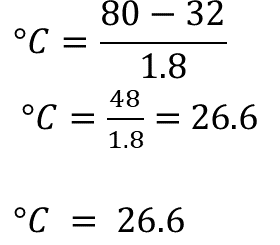
La temperatura fue de casi 27 grados Celsius, es decir, hacía calor en Veracruz, pero no demasiado.
Durante la sesión se ha estudiado el tema de la variación lineal, comparándola con la variación proporcional directa y la variación proporcional inversa.
Es importante que elabores tus notas, considerando las ideas más importantes de la sesión, resuelve las actividades planteadas y, sobre todo, anota tus dudas y posibles dificultades.
Recuerda que éste es un material de apoyo y puedes consultar otras fuentes, aparte de tu libro de texto, para complementar lo que aprendas aquí.
El Reto de Hoy:
Completa la siguiente tabla para distinguir las características más importantes de cada una de estas variaciones. Escribe un tache donde corresponda.
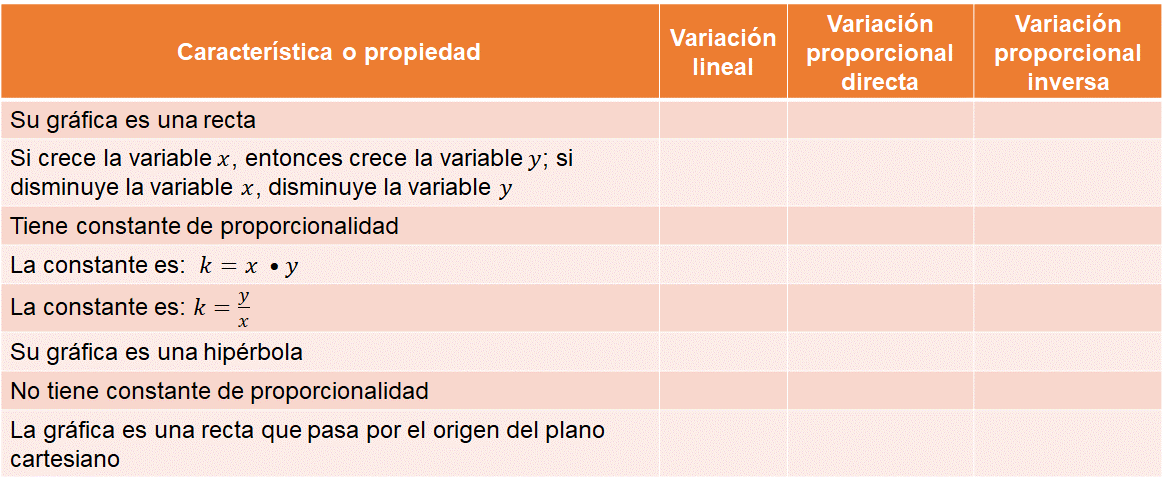
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Explorando las formas de un poema
Aprendizaje esperado: Crea textos poéticos con formas gráficas.
Énfasis: Considerar formas gráficas como indicios de contenido.
¿Qué vamos a aprender?
En esta sesión, conocerás las formas gráficas que tienen los poemas, esta relación te permitirá comprender que los poemas visuales no sólo brindan significado a través de lo que éste dice; también su forma gráfica adquiere expresividad, lo que posibilita tener muchas otras formas de representar el contenido.
¿Qué hacemos?
Reflexiona en la siguiente información.
La vida, si miras a tu alrededor, se compone de formas, ya sean naturales como una nube o una montaña, o creadas por la mano de los humanos como una casa o una carretera; y éstas pueden ser palpables, sólo observables e imaginarias, pero cualquiera de estas formas se pueden representar, por ejemplo, en un poema de forma gráfica.
Para profundizar en ello, observa las siguientes imágenes.
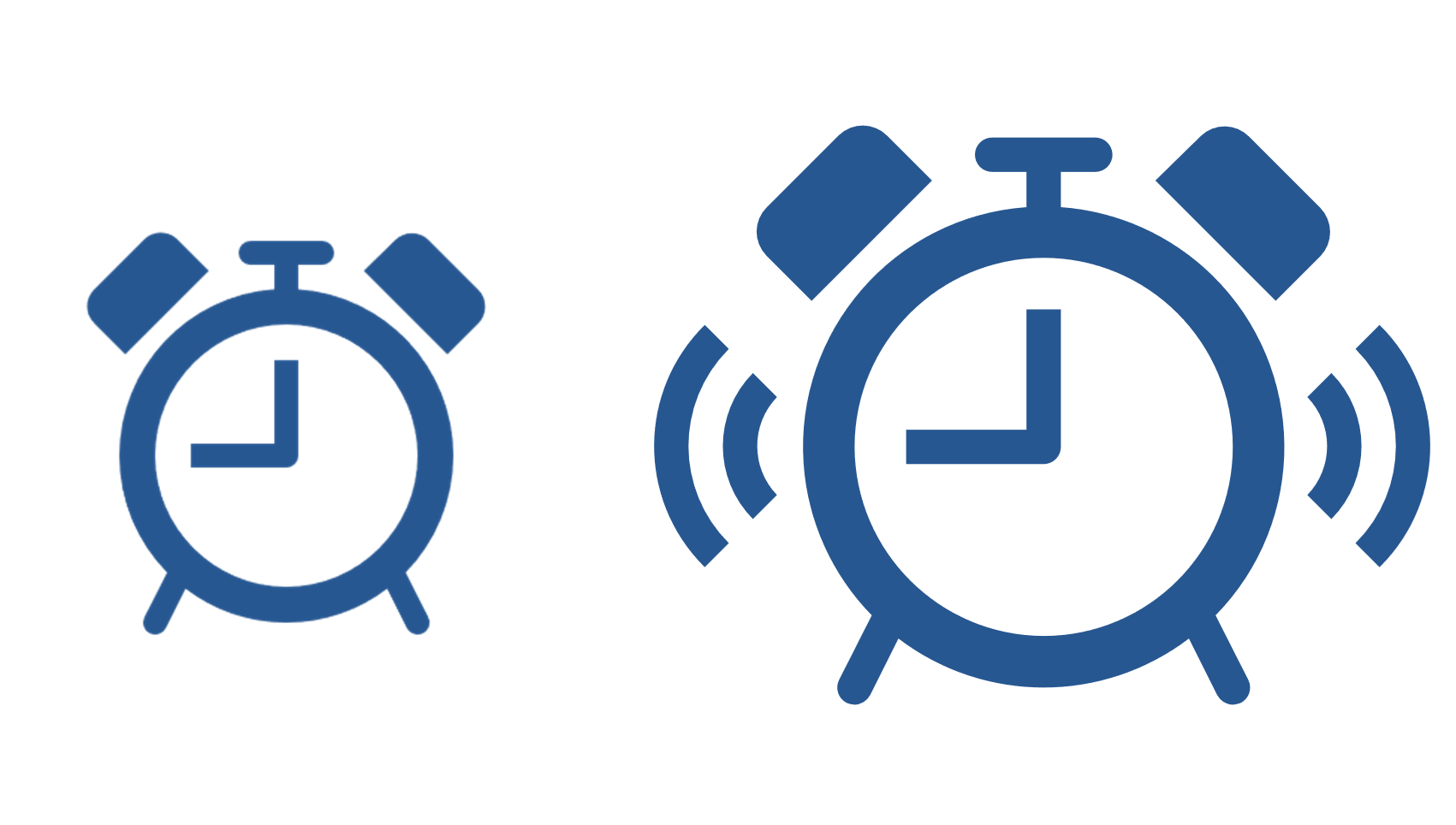
De las imágenes anteriores, se podría intuir que es un reloj despertador y un reloj despertador sonando, pero ¿cómo sabes que está sonando? Si lo piensas un poco, te darás cuenta de que existen algunos aspectos que hacen inferirlo.
En la segunda imagen, el reloj tiene unas líneas curvas a los costados, esas marcas gráficas señalan movimiento y hacen pensar que está sonando, es decir, permiten crear nuevos significados.
La poesía visual o concreta utiliza formas que pueden ser comunes o reconocibles para llamar la atención del lector. Es decir, todos pueden comprender el mensaje de la poesía desde su forma.
Para comprenderlo, imagina los números del uno al nueve. Piensa: ¿cómo los dibujarías? Observa con atención.

Ahora, contesta las siguientes preguntas sobre este texto intitulado “Cuento” del poeta español Felipe Boso:
¿Se te dificultó la lectura?
¿Qué aspectos de forma se te hicieron llamativos?
Te puedes dar cuenta de que la forma de los números y las palabras no interfirieron en la lectura ni en la apreciación, es decir, dos aspectos distintos se lograron relacionar.
Ahora, ya tienes una noción de lo que es la forma. Observa el siguiente video para tenerlo más claro.
- La forma.
Reflexiona en lo siguiente:
¿Has visto poemas que se sirvan de formas figurativas o abstractas?
¿Qué forma te imaginas que podría tener algún poema que te guste o que hayas leído en la forma convencional? Es decir, de izquierda a derecha y de arriba hacia abajo.
Esto significa que las formas abstractas, requieren más esfuerzo y detalle para apreciarlas. Además, cada autor decide utilizar las formas figurativas para expresar su relación entre contenido e imagen, y otros prefieren las formas abstractas para que el lector llegue a sus propias interpretaciones.
De alguna manera la forma predispone a tener algunas pistas sobre el contenido que se puede encontrar, aunque no fuera en nuestro idioma. Es decir, la distribución de los poemas, la disposición de las estrofas, el espacio, la puntuación y la tipografía, ayudan al lector a tener una noción del contenido del poema.
Por ejemplo, observa el siguiente caligrama.
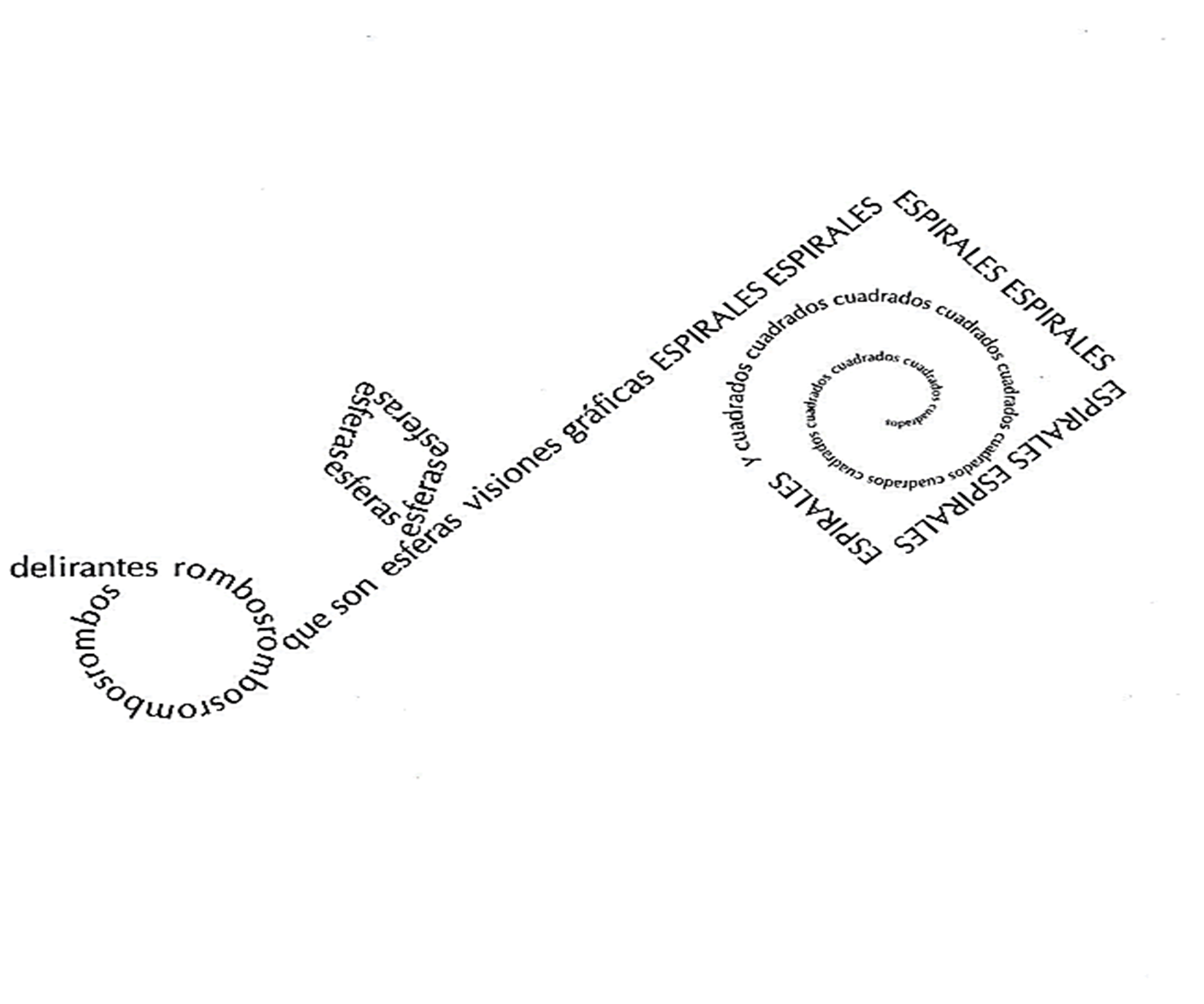
En este caligrama la forma se asemeja a una flor. Sin embargo, las palabras expresan más sentidos geométricos; se puede asumir que la forma de la flor es un pretexto para hablar de las formas geométricas o viceversa. Por eso el poema dice: delirantes rombos, rombos, rombos. Y, en el apartado que simboliza a la flor dice: espirales, espirales, espirales y cuadrados, cuadrados; y con la palabra “rombo” se representa una hoja. Mientras que la flor comienza con un cuadrado y después forma una espiral.
De alguna manera, la imagen podría predisponer sobre el contenido, pero al encontrarse con el texto original, será posible que nazca más curiosidad para adentrarse a la lectura de estos poemas, porque en la poesía visual la forma gráfica y el contenido forman nuevas perspectivas, así como imágenes que generan distintas emociones.
A continuación, observa los siguientes poemas del catalán Joan Brossa.
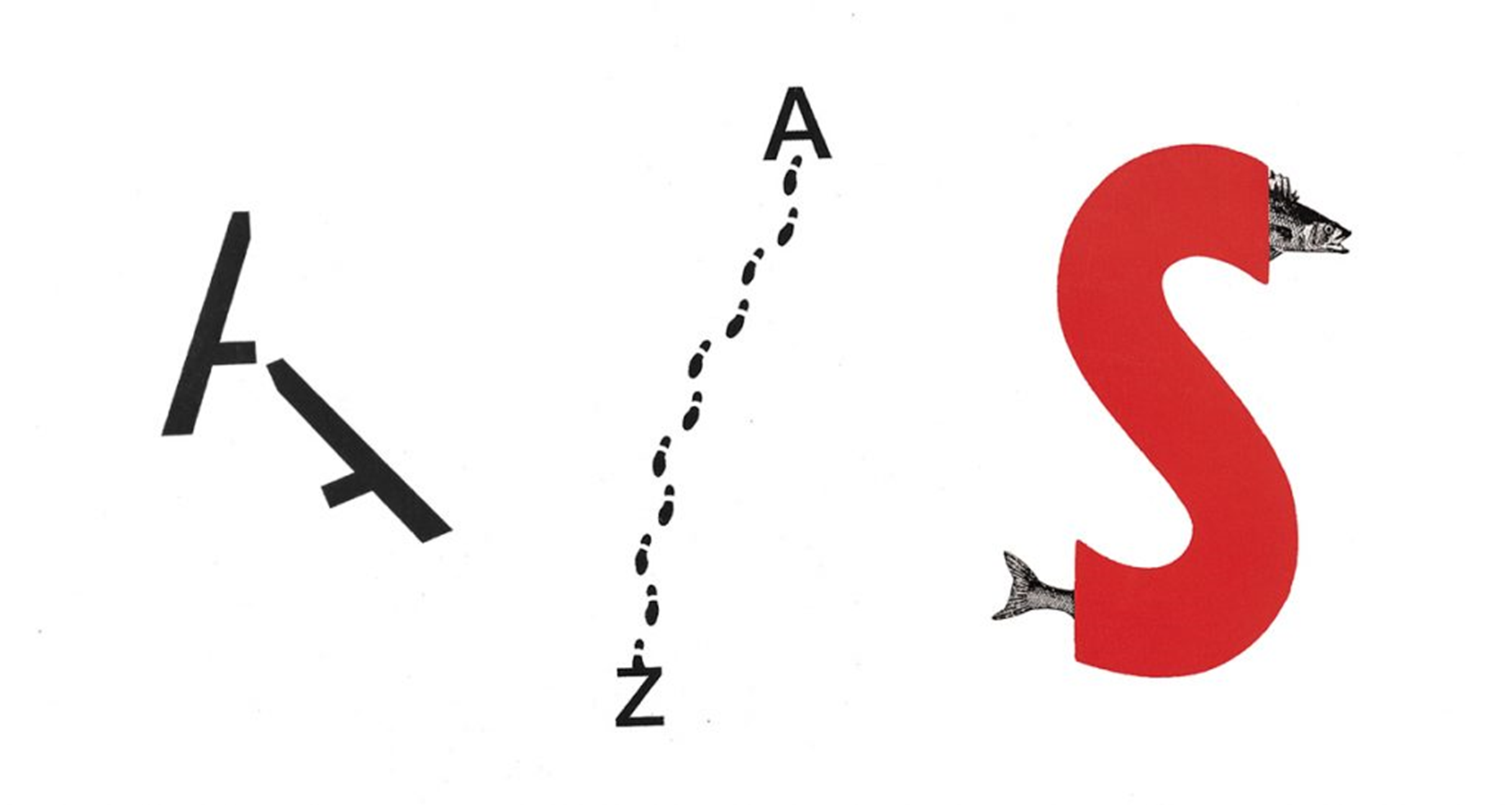
En estos tres poemas puedes encontrar otros aspectos que van más allá de la forma. Aunque es inevitable observar que son letras y muestran una relación muy estrecha entre la forma y el contenido.
La poesía visual busca crear una experiencia donde se encuentren lo estético, las formas, el signo, los significados y los soportes a través de los cuales se transmite.
La estética tiene varios campos de estudio, pero en este caso se refiere a la manera en que se relaciona lo que se percibe y la apreciación que se tiene con la imagen. Por ejemplo, en la tercera imagen del poeta Brossa, ¿qué percibes?
La poesía visual busca que las palabras se parezcan a las cosas, incluso busca que los objetos se transformen en poesía. Es decir, que las palabras tengan esa cercanía con lo que se dice y se ve.
Las formas gráficas de la poesía buscan ser, de alguna manera, palabra y objeto. Dar a conocer a través de esta expresión emociones, significados y otras maneras de comprender lo que se dice.
Para conocer cómo esa forma gráfica tiene relación, observa la siguiente imagen sobre la distribución de las letras y la proporción que tienen.

Reflexiona:
¿Qué es lo que puedes ver en este poema del chileno Nicanor Parra?
¿Qué forman las primeras cuatro figuras?
Se pueden observar formas hechas que, además, forman la palabra “todo”, lo que hace más interesante la figura, pues utiliza recursos gráficos.
Las y los poetas se valen de algunos recursos gráficos como el ícono y el símbolo, por lo que se marca una diferencia entre estas dos posibilidades de expresión. Se pueden utilizar algunos de estos recursos gráficos para construir el poema.
Ahora, observa y describe lo que ves en la siguiente imagen.

En esta imagen, se puede observar una jirafa, pero del otro lado está un poema visual que dice también, “jirafa”. Por lo tanto, si se dice que está imagen tiene una relación icónica, ¿qué se podría entender por ícono?
Para dar respuesta a esta cuestión, analiza qué es el ícono.
Ícono: los íconos son signos que mantienen una relación o semejanza con el objeto representado.
Como en la imagen que observaste donde una forma se parece a la otra. El cuello largo de la jirafa se representa con la “i” larga y hay una semejanza evidente.
Otro recurso gráfico para la poesía es el símbolo. Éste es un recurso que se puede utilizar para construir un poema. Para ahondar en este concepto, describe la siguiente imagen que se presenta.

Una imagen que te puede resultar conocida es la primera y se le conoce como la paloma de la paz y, la segunda figura, se utiliza para referirse a la “paz”, ambas imágenes son símbolos.
Un símbolo es una manera de representar algo con una forma convencional, es decir, aceptada por los demás. Asimismo, es una fácil darle significado a algo que, además de nombrarlo, se puede representar de forma sencilla. Por eso se dice que es una forma simbólica de representar algo.
Para comprender lo anterior, analiza su definición.
Símbolo: es un elemento u objeto material que, por convención o asociación, se considera representativo de una entidad o idea.
Por lo tanto, a la poesía le sucede algo igual, las palabras y su organización también pueden simbolizarse.
Lee el siguiente poema del poeta mexicano Raúl Renán.

Ahora, responde las siguientes preguntas:
¿Cómo lo leíste?, ¿de arriba hacia abajo como se lee en la forma convencional o de abajo hacia arriba?
¿Por qué crees que al final del poema hay un pez que, al parecer, nada hacia arriba?
Este poema, es difícil leerlo de la manera convencional, es decir, de arriba hacia abajo, pero si se lee de abajo hacia arriba, entonces se tiene lo siguiente:
“Salto de limo al corazón,
del río
donde la cumbre acogerá
mi vida en desove”.
Un pez que nada a contracorriente es el salmón y lo hace para depositar sus huevecillos, así que la fuerza que debe emplear requiere un esfuerzo mayor y corre enorme peligro porque en ese camino lo esperan fieras y humanos que lo quieren cazar.
Entonces, ¿qué parece que asemeja la forma del poema y su lectura? Asemeja a ese río que debe nadar hacia arriba el salmón. Estas formas gráficas y de contenido pueden tener diversas posibilidades de expresión.
A continuación, observa el siguiente video y agudiza tu vista y oído con el poema “Dentro de ti está el secreto”. Analiza de qué trata y cómo se representa.
- Intervenciones poéticas: Dentro de ti está el secreto.
¿Observaste cómo se relacionan las imágenes con ciertas palabras?
Esto muestra que las formas gráficas permiten ver los indicios del contenido, incluso puedes no leer un poema completo, sino una palabra y una forma que, juntos, tengan un significado más amplio.
Todos tenemos distintas maneras de expresar nuestras ideas. Por ello, puedes explorar esas formas gráficas que tengan relación con el contenido desde distintas posibilidades.
Con todo lo anterior, puedes comprender ahora que las formas gráficas dicen más que sólo las líneas y curvas.
Observa la siguiente imagen, pero antes piensa qué juegos de palabras o formas te vienen a la mente con la palabra “Universo”. Analiza lo que hizo el poeta surcoreano Yong-Tae Min con esa palabra.

En la parte superior se puede observar que son tres palabras al inicio, al centro y al final. Una de ellas está en el centro del círculo que contrasta el blanco con el negro.
Ahora reflexiona: ¿Tendrá una parte simbólica o icónica?
Cuenta con una parte simbólica porque que refiere al Ying y el Yang, es decir, al equilibrio. Y además hace un juego entre la dualidad: la Luna y el Sol, es decir, el complemento que forman un verso. También es importante recuperar cómo es la distribución de la palabra universo y las otras posibilidades de crear nuevas palabras como: “undiverso”, “lun-ver-sol” y “un verso”.
En la exploración de las formas gráficas, tienes una oportunidad para crear y desarrollar tu imaginación. Busca más maneras y posibilidades de plantear formas en los poemas.
Has finalizado esta sesión. Con estos nuevos conocimientos ahora puedes realizar diversos tipos de poemas visuales y tener tus propias creaciones. Además, puedes buscar en tu libro de texto de Lengua Materna de segundo grado algunos otros ejemplos para reforzar lo aprendido. También podrías investigar o revisar algunas otras formas gráficas que sean de tu interés.
El Reto de Hoy:
Observa detenidamente las siguientes palabras compuestas e imágenes, y piensa cómo podrías considerarlas para crear un poema visual o concreto.
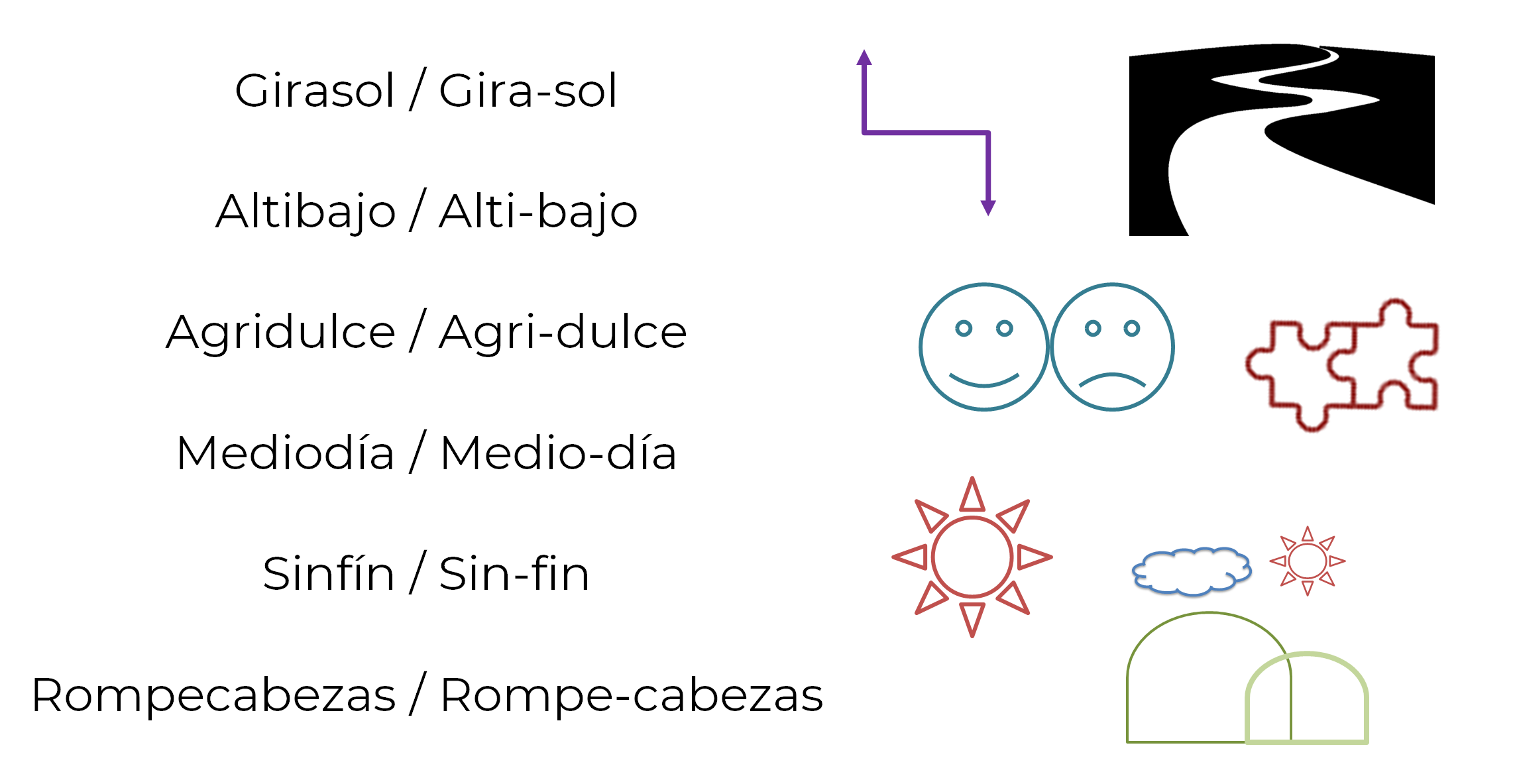
Imagina qué podrías hacer con las palabras y la forma, incluso, puedes pensar en otras formas para aplicar cualquiera de estas palabras. Para darte una idea, observa lo que hizo una alumna con una de las palabras.

Puedes hacer el mismo reto con otros poemas, ya sea de tu autoría o de otros; como te puedes dar cuenta, tienes enormes posibilidades al momento de considerar las formas gráficas en tus creaciones o al momento de observar un poema visual o concreto.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Habito mis hábitos y ayudo en mi entorno
Aprendizaje esperado: Representa acontecimientos importantes vinculados a la historia de su comunidad mediante distintas formas expresivas.
Énfasis: Plasmar sus hábitos por medio de los elementos del arte para comprender su manera de habitar una comunidad e impulsar prácticas a favor del medio ambiente.
¿Qué vamos a aprender?
En esta sesión, reflexionarás sobre los hábitos para comprender cómo todo está conectado entre sí, tus acciones con el mundo que te rodea.
El arte, permite conectar el mundo interior con el exterior, por medio de las experiencias artísticas y las producciones que se realizan para representarlo, mientras que en la naturaleza todo un ecosistema funciona a partir de los elementos que lo conforman y si alguno se rompe, se contamina o se daña, todo el conjunto tiende a desaparecer. Por ello, explorarás estas conexiones entre el arte, la naturaleza y las acciones para comprender mejor esa interacción.
¿Qué hacemos?
Los materiales que necesitaras para esta sesión son cosas u objetos que te sean significativos, tal vez un juguete o un objeto especial, también requerirás estambre, tierra, piedras, plantas pequeñas, agua, una maceta, así como un lápiz y tu cuaderno. Si no cuentas con alguno de estos materiales, puedes utilizar papel y telas. Recuerda siempre prender tus sentidos, tu mente y tu corazón.
Un hábito es una acción constante que se tiene o se repite frecuentemente. Existen hábitos individuales y colectivos. Los hay de muchos tipos: de higiene, mentales, físicos, afectivos, entre otros.
Existen hábitos que ya están ahí plasmados socialmente y que se han ido formando sin que seamos conscientes, pero lo interesante es que se pueden transformar cuando no son positivos y construir nuevos, como lo harás ahora por medio del arte.
Lo primero será reflexionar si las cosas que haces cotidianamente, es decir, tus hábitos, causan un impacto positivo o negativo en tu familia, en tu comunidad y al medio ambiente. Algunos hábitos impactan directamente, mientras que otros van más allá de tu persona, tu casa o, incluso, tu comunidad.
Después de esta información, reflexiona al respecto:
¿Qué hábitos tienes?
¿Has generado nuevos hábitos últimamente?
Por ejemplo, puedes tener el hábito de regar plantas, o de decirle todas las mañanas a tu familia que los quieres. Un hábito que puede impactar mucho en la comunidad es sembrar y cuidar plantas y árboles, por ello, la propuesta de esta sesión es generar un pequeño ecosistema, una especie de micro jardín, para valorar tus acciones y su impacto en la naturaleza y en el medio ambiente.
Para esto, deberás elegir pequeñas plantas, piedritas, y decidir cómo acomodarlos en un espacio reducido. A este hábitat creado por los seres humanos para reproducir las condiciones de la naturaleza se le conoce como terrario.
Recuerda que puedes transformar tus hábitos y aquí el reto será que, además de construir el terrario, formes el hábito de cuidarlo y regarlo para mantenerlo vivo, darle amor, hablarle, observar sus formas y registrarlo en tu bitácora. Como en los libros de botánica, que muestran la morfología de las plantas.
Las plantas son esenciales para nuestra existencia, la vida no sería posible sin ellas. Este pequeño ecosistema te servirá perfectamente para reflexionar sobre los cuidados que has tenido contigo y con los demás durante este periodo de contingencia sanitaria, ya que todo lo que recibe amor crece y perdura.
La naturaleza y el arte siempre han estado ligados, el reino vegetal se instala en las prácticas artísticas desde las representaciones primitivas de la flora y la fauna, las bitácoras de viaje de los ecologistas de siglos pasados, como Humboldt, el Art Nouveau y su belleza florista, los jardines japoneses y la integración con la arquitectura, y el Land Art o Arte de la Tierra y su carácter temporal. Observa las siguientes imágenes al respecto.

Existen muchos libros de botánica o bitácoras de viaje que muestran distintos tipos de plantas y sus usos, así como su ubicación geográfica. Algunas plantas son medicinales y se han usado en la medicina tradicional mexicana.
Para construir tu terrario, puedes hacerlo simbólico para que represente el ecosistema y lo que hay dentro de ti. Para ello, analiza la siguiente información.
El perfeccionamiento de técnicas para la obtención de alimentos generó una revolución causada por la domesticación de plantas. Los nómadas desarrollaron las técnicas de los primeros cultivos, dando con el paso del tiempo el inicio del sedentarismo agrícola.
Los pobladores del México antiguo tenían un gran amor por las flores, tanto así que existía una festividad cuya única actividad era gozar de las flores, ofreciéndolas a los amigos.
Los xochimanque eran “los oficiales de las flores” y realizaban ramilletes hechos con singularidad.
El mundo de la flora impresionó tanto a los europeos a su llegada a la Nueva España, que muchos cronistas describieron los bellos jardines, adornos del vestuario y arreglos florales.
Ligando lo anterior, realiza la siguiente actividad. Esta actividad generará una emoción positiva, evocando imágenes o pensamientos apacibles.
La realización de un terrario
Pero… ¿qué es un terrario? Un terrario es un espacio cerrado y controlado que pretende reproducir las características del ambiente en el que habitan ciertos seres vivos, al complementarlo con otros elementos se puede dejar volar la imaginación y recrear espacios o traer a la memoria un momento agradable.
Los materiales que podrías ocupar son:
- Recipiente (vidrio, maceta, tronco, etc.)
- Cactáceas
- Crasuláceas
- Musgo
- Tezontle
- Tierra
- Elementos decorativos
Las cactáceas y crasuláceas son un tipo de plantas que no requieren de mucho riego porque viven en zonas áridas; tienen adaptaciones anatómicas, como tallos fotosintéticos, que almacenan agua u hojas gruesas. En el caso del musgo va a permitir que el terrario conserve humedad y requiera menos riego.
Para realizarlo se hace una mezcla de 50 % tierra, 50 % tezontle; se van acomodando las plantas de manera vistosa y, por último, se agregan los elementos decorativos. El riego se realiza 1 vez por semana y el terrario se debe de colocar en la resolana (que no le dé el sol directo, en caso de usar recipiente de vidrio).
Las pequeñas acciones pueden generar grandes cambios. Con esto, generarás una conexión con tu hábitat creativo, del cual formas parte; tanto las plantas del terrario como tus recuerdos significativos requieren hábitos de cuidado.
Ahora, recrea tu terrario simbólico para que representes el “tejido social” en un espacio más grande, por ejemplo, tu recámara, tu casa o el patio. Para ello, pensarás en espacios, palabras o acciones que te conecten e interconecten como ser vivo habitando este mundo.
Este tejido que armarás es una metáfora del tejido social del que formas parte. Lo conformas con acciones diarias o hábitos que benefician tu entorno. Es muy importante que día con día refuerces estos hábitos para que tu tejido social no se desmorone.
A continuación, revisa los hábitos que benefician el entorno de algunas alumnas, a través del siguiente video.
- Hábitos de alumnas.
Es interesante cómo el entorno ideal cambia de acuerdo con la perspectiva de cada uno, en el video anterior existe una coincidencia, un medio ambiente más limpio.
Cada uno contribuye, aunque sea un poco, en el ambiente, ya sea de manera positiva o negativa. Pero si las acciones son mayormente positivas, se generará un impacto muy grande en el contexto y en el planeta.
Acciones como tirar basura en la calle, fumar o incluso escuchar música a un volumen demasiado fuerte son “malos hábitos” que afectan al entorno. A manera de reflexión, piensa en las acciones positivas y negativas que realizas, tratando de reafirmar las primeras y corregir las segundas. Puedes lograr mejor esta reflexión al construir tu terrario simbólico.
Recuerda que no hay acciones pequeñas y entre más granitos de arena positivos existan, la playa será más habitable. Observa el siguiente video sobre los trabajos de algunas y algunos alumnos de secundaria.
- Trabajos de alumnos.
Con la información de esta sesión, comprenderás cómo tus hábitos se quedan y se construyen dentro de tus comunidades y, además, puedes hacer de ellos conexiones con situaciones artísticas.
Reflexiona a lo largo de tu vida sobre tus hábitos y cómo se modifican positivamente con un toque artístico.
El Reto de Hoy:
Realiza las actividades que se presentaron en esta sesión, y si te es posible, construye tu propio ecosistema, siguiendo la idea del terrario. Lo importante es que reflexiones que eres parte de la naturaleza y que estás plenamente conectada o conectado contigo, con otras personas y con el hábitat.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
El Sol
Aprendizaje esperado: Describe las características y dinámica del sistema solar.
Énfasis: Conocer las características de nuestro sol según el tipo de estrella al que pertenece.
¿Qué vamos a aprender?
En esta sesión, identificarás las principales características del Sol, entre ellas, su estructura y cómo intervienen en su funcionamiento. Asimismo, conocerás lo que ha indagado la ciencia acerca de esta estrella, que hace posible la existencia del Sistema Solar, además de ser un astro de gran importancia para los seres vivos.
¿Qué hacemos?
Inicia con la siguiente cuestión:
¿Qué conoces acerca del Sol?
Hay mucho que conocer sobre el astro rey, ya que la investigación científica está en permanente búsqueda de mejores explicaciones acerca de cómo es y de los fenómenos que en él ocurren, entre ellos, la actividad solar que puede afectar el funcionamiento de aparatos de comunicación en nuestro planeta.
Anota las siguientes preguntas y contéstalas conforme avances en la sesión:
- ¿De qué está hecho el Sol?
- ¿Cómo se genera la luz y el calor que irradia el Sol?
- ¿Cuál es el tamaño del Sol, comparado con el de otras estrellas?
- ¿Qué edad tiene el Sol?
- ¿Cuánto tiempo más durará?
El Sol es una de las millones de estrellas que forman parte de la Vía Láctea. Una estrella se puede describir como un cuerpo celeste que emite luz, ya que es una masa de materia gaseosa incandescente.
Para comenzar a profundizar en el tema, observa el siguiente video del minuto 1:53 al 3:14, acerca de las estrellas.
- Galaxias, estrellas y otros cuerpos.
Como todas las estrellas, el Sol está compuesto principalmente por los elementos químicos hidrógeno y helio; que representan respectivamente, casi el 75% y el 24% de la masa del Sol. También hay otros elementos como el oxígeno, el carbono, el neón y el hierro que en conjunto representan menos del 2% de la masa de este astro.
En el año de 1925, la astrónoma y astrofísica inglesa Cecilia Payne, en su tesis de doctorado, propuso que las estrellas están compuestas principalmente por hidrógeno. Como toda teoría nueva, sin duda causó conflicto ya que en ese momento se pensaba que las estrellas tenían una composición química similar a la de la Tierra.
Incluso Henry Norris Russell, quien era un astrónomo famoso en ese entonces, le sugirió eliminar esa idea de su tesis. Sin embargo, años más tarde, con la evidencia de nuevos experimentos, el mismo Russell y la comunidad científica aceptaron las conclusiones que la astrónoma Cecilia Payne expuso acerca de que el Sol está constituido por el 75% de hidrógeno y el 24% de helio.
Por lo tanto, se puede considerar que los elementos que forman al Sol están presentes en la Tierra y en los demás planetas, aunque en diferentes proporciones, ya que forman parte del Sistema Solar y tienen un origen común.
El Sol ha sido de gran interés para el ser humano desde la antigüedad, al grado que lo consideraban un dios e hicieron construcciones para venerarlo y estudiarlo.
Un ejemplo de ello es la cosmovisión de los mexicas, en la que el Sol simbolizaba la vida y su lucha contra la muerte. Los mexicas creían que cada día el astro transitaba por el mundo de los vivos hasta el atardecer, cuando moría y recorría el inframundo, al tiempo que fertilizaba la tierra. Para nuevamente aparecer por el Este en el amanecer y renacer triunfante llenando de alegría y esperanza a esa civilización.
Los mayas también observaron y registraron fenómenos relacionados con este astro, entre ellos, el ciclo anual, los equinoccios y los solsticios, simbolizándolos en templos ceremoniales como en Chichén Itzá.
Por ejemplo, en Chichén Itzá hay una pirámide con una escalinata de 91 escalones que, junto con los de su plataforma, suman 365 que representan los días del año. Pero esto no es lo más asombroso, ya que, en el equinoccio de primavera, la luz que incide en la escalinata proyecta una sombra que simula una serpiente, como una representación del descenso de su dios Kukulkán. Esto es una muestra del conocimiento que los mayas tenían acerca de los astros que observaban en la bóveda celeste.
Desde la perspectiva científica, con su avance y el de la tecnología se han obtenido evidencias y construido explicaciones acerca del movimiento del Sol, tanto del que efectúa sobre su eje, como el de su desplazamiento a través de la Vía Láctea, acompañado con los planetas del Sistema Solar que giran a su alrededor.
En cuanto al tamaño de esta estrella, desde hace cientos de años, se ha tratado de indagar la dimensión de los astros.
Tres siglos antes de nuestra era, el sabio griego Eratóstenes propuso una forma de medir la circunferencia de la Tierra, a partir de las relaciones de los ángulos de un triángulo, el cual formó con la sombra proyectada con dos postes, cada uno en ciudades alejadas. Este método lo retomó el matemático y astrónomo griego Aristarco de Samos para deducir mediciones de la Luna y el Sol, entre ellas su distancia a la Tierra.
Eratóstenes tuvo un error mínimo en la medición de la circunferencia de la Tierra, comparado con el dato aceptado por la ciencia actual. Por su parte, Aristarco calculó que el Sol era 19 veces más grande que la Luna y se encontraba 19 veces más lejos; actualmente se sabe que es 400 veces más grande y está 400 veces más lejos. No tuvo la misma precisión que Eratóstenes, posiblemente por no contar con los instrumentos adecuados, aunque matemáticamente el procedimiento que utilizó era correcto.
La astronomía de este sabio en la antigua Grecia marcó un precedente en el estudio del Sol, pues además lo consideró como una estrella que estaba en el centro de los demás astros, conocimientos que no eran aceptados en la época y fueron retomados muchos siglos después.
Hoy en día, se sabe que el diámetro del Sol es de casi 1,400,000 kilómetros, gracias a las mediciones realizadas del 2003 al 2006, mediante el telescopio solar a bordo del Observatorio Solar y Hemisférico, conocido como SOHO por sus siglas en inglés, de la NASA.
También se ha identificado que el Sol es una estrella de tamaño medio y de color casi blanco. Asimismo, los astrónomos la han clasificado como una estrella enana amarilla, por sus características, entre ellas el tamaño, color, masa, luminosidad y la temperatura de su superficie.
En el Sol se han identificado varias capas en las que ocurre la generación de energía y su transferencia por diferentes mecanismos:
- El núcleo.
- La zona radiante.
- La zona convectiva.
- La fotosfera.
- La cromosfera.
- La corona.
El núcleo es la región más interna del Sol y ocupa una quinta parte del total de la estrella. En esta zona ocurre la gigantesca explosión atómica debido a las reacciones nucleares de millones de toneladas de hidrógeno; produciendo la energía que tarda un millón de años en viajar a la superficie debido a la enorme fuerza de gravedad que allí prevalece. En esta capa, se estima una temperatura de 15 millones de grados Celsius.
La zona radiante está compuesta de plasma, es decir, de gases como helio e hidrógeno ionizados. La energía obtenida en el núcleo se transporta por radiación hacia las capas de afuera, lo cual disminuye considerablemente la temperatura de esta región.
La zona convectiva, se trata de una región donde se producen constantes movimientos de los gases que circulan ascendiendo y descendiendo, con lo que la energía es transportada. Así, el fluido solar se calienta de manera desigual, originando corrientes como una marea interior. Por lo tanto, en esta zona como su nombre lo indica, la energía se transfiere por convección.
La fotosfera es la región del Sol donde se emite la luz visible. Se puede considerar como la superficie de la estrella, que no es de material sólido, sino de plasma con una temperatura de alrededor de 6,000° Celsius. En ella se observan las manchas solares con intensa actividad magnética, además de que se presentan llamaradas o erupciones de gran magnitud que generan ráfagas las cuales pueden llegar a la Tierra y producir las auroras boreales, así como afectar el funcionamiento de dispositivos electromagnéticos que se utilizan en las naves espaciales, en las comunicaciones y en la navegación. Se podría decir que la fotosfera es la que irradia luz y calor al espacio.
La cromosfera es la capa externa de la fotosfera. Comparada con las anteriores, es una capa fina, casi transparente. Además de que solo se puede ver durante un eclipse de sol, de color rojizo anaranjado. Un eclipse solar es el fenómeno astronómico que se produce cuando la Luna oculta al Sol visto desde la Tierra. Es importante aclarar que no hay que ver directamente al Sol porque su luz daña la visión.
Finalmente, la corona solar se conoce así porque son varias capas tenues de la atmósfera externa del Sol, en las que la temperatura es mayor que en las capas interiores, lo cual es un misterio para los científicos. Es una zona poco densa, presenta intensos campos magnéticos y emite gran cantidad de radiación de rayos X. La corona solar también se aprecia durante un eclipse solar.
Para comprender cómo es que el Sol emite luz y calor, se podría comparar con una vela, porque ambos tienen combustible para liberar energía por un tiempo determinado. Luego se agota. El combustible del Sol es el hidrógeno; en el interior de la estrella se transforma la materia en energía: cuando los millones de toneladas de átomos de hidrógeno se fusionan formando átomos de helio, liberando calor en este proceso.
El Sol tiene una edad de cuatro mil millones y medio de años, aproximadamente. Este dato es útil para determinar cuándo morirá el Sol, ya que se calcula que durante el tiempo que lleva activo ha consumido la mitad del hidrógeno de su núcleo y se estima que puede vivir alrededor de 10 mil millones de años. Esto quiere decir que está a la mitad de su vida y falta muchísimo tiempo para que el Sol muera.
El Sol, como todas las estrellas, tiene un ciclo de vida. Para ahondar en ello, observa el siguiente video del minuto 3:15 al 4:53.
- Galaxias, estrellas y otros cuerpos.
A pesar de lo que se sabe hasta la fecha, hay muchos fenómenos que ocurren en el Sol que intrigan a los científicos, entre ellos, la aparición y desaparición de las manchas solares de manera cíclica cada 11 años.
El Sol encierra muchos misterios y los científicos continúan investigando y buscando explicaciones al respecto. El estudio del Sol y el aprovechamiento óptimo de su energía son indispensables para la existencia de la vida y la conservación de nuestro planeta.
Has finalizado esta sesión. Si deseas saber más del tema, puedes consultar tu libro de texto de Física.
El Reto de Hoy:
Con todo lo que has aprendido en esta sesión, retoma las preguntas planteadas al inicio y respóndelas o compleméntalas. Después, realiza un mapa mental sobre el Sol.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Llegaron los extraños
Aprendizaje esperado: Conoce los principales acontecimientos del proceso de Conquista de México-Tenochtitlan y analiza algunos de los factores que lo determinaron.
Énfasis: Conocer los eventos que ocurrieron en Mesoamérica con la llegada de los españoles y las primeras alianzas. Además, identificar las condiciones de vida en el valle de Puebla-Tlaxcala.
¿Qué vamos a aprender?
En esta sesión, profundizarás en el proceso de avance de los españoles en Mesoamérica, desde su desembarco en Veracruz hasta la llegada a la Ciudad de México-Tenochtitlan. Asimismo, conocerás los eventos que ocurrieron durante este proceso y cómo fue su paso por el valle central de México.
¿Qué hacemos?
Para iniciar con el tema, lee el siguiente texto retomado del libro "Visión de los vencidos", de Miguel León Portilla, que narra cuál fue la postura de Moctezuma II ante le llegada de los españoles.
Primeras noticias de la llegada de los españoles
De acuerdo con el testimonio de Alvarado Tezozómoc en su "Crónica Mexicana", perturbado Motecuhzoma por los varios presagios […], hizo llamar a sabios y hechiceros con objeto de interrogarlos. Quería averiguar si había señales de próximas guerras, de desastres imprevistos o de cualquier otra forma de desgracia. Los nigrománticos en realidad no pudieron dar respuesta. Pero en cambio, por ese tiempo vino un macehual (hombre del pueblo) de Mictlancuauhtla, que nadie lo envió, ni principal ninguno, sino sólo de su autoridad. Luego que llegó a México, se fue derecho al palacio de Motecuhzoma y díjole: señor y rey nuestro, perdóname mi atrevimiento. Yo soy natural de Mictlancuauhtla; llegué a las orillas de la mar grande, y vide andar en medio de la mar una sierra o cerro grande, que andaba de una parte a otra y no llega a las orillas, y esto jamás lo hemos visto, y como guardadores que somos de las orillas de la mar, estamos al cuidado. Dijo Motecuhzoma: sea norabuena, descansad. Y este indio que vino con esta nueva no tenía orejas, que era desorejado, tampoco tenía dedos en los pies, que los tenía cortados. Díjole Motecuhzoma a Petlacálcatl, llevad a éste y ponedle en la cárcel del tablón, y mirad por él. Hizo llamar a un teuctlamacazqui (sacerdote) y díjole: id a Cuetlaxtlan, y decidle al que guarda el pueblo, que si es verdad que andan por la gran mar no se qué, ni lo que es que lo vayan a ver, y que qué es lo que guarda o encierra la mar del cielo, y esto sea con toda brevedad y presteza […]
Volviéronse con toda la brevedad posible a la gran Ciudad de México–Tenochtitlan a dar la razón de lo que habían ido a ver. Llegados a México, fuéronse derechos al palacio de Motecuhzoma, a quien hablaron con la reverencia y humildad debida. Dijéronle: señor y rey nuestro, es verdad que han venido no sé qué gentes, y han llegado a las orillas de la gran mar, las cuales andaban pescando con cañas y otros con una red que echaban. Hasta ya tarde estuvieron pescando, y luego entraron en una canoa pequeña y llegaron hasta las dos torres muy grandes y subían dentro, y las gentes serían como quince personas, con unos como sacos colorados, otros de azul, otros de pardo y de verde, y una color mugrienta como nuestro ychtilmatle, tan feo; otros encarnado, y en las cabezas traían puestos unos paños colorados, y eran bonetes de grana, otros muy grandes y redondos a manera de comales pequeños, que deben de ser guardasol (que son sombreros) y las carnes de ellos muy blancas, más que nuestras carnes, excepto que todos los más tienen barba larga y el cabello hasta la oreja les da. Motecuhzoma estaba cabizbajo, que no habló cosa ninguna.
Visión de los vencidos
Miguel León Portilla
Ahora, contesta las siguientes preguntas:
- ¿Qué llamó más tu atención de la lectura anterior?
- ¿Te fijaste en las palabras que utilizan los indígenas para explicar cómo vestían los españoles?
- ¿Crees que Moctezuma haya estado preocupado por esa extraña llegada?
A continuación, observa el siguiente video que habla sobre la figura de Marina y los conquistadores. Con él, podrás ahondar más sobre el papel que jugaron los diversos protagonistas del proceso de conquista. Presta atención y escribe en tu cuaderno quiénes son los protagonistas de esta historia.
- Los conquistadores.
https://www.youtube.com/watch?v=X_mdngs-mWQ
Es importante destacar, como señala el investigador Federico Navarrete, que la historia de los pueblos mesoamericanos no acabó con el proceso de Conquista, y es interesante saber qué pasó con los pueblos originarios después de la colonización; por ejemplo, con los aliados tlaxcaltecas o los mayas en el sureste mexicano. Hay mucho que conocer sobre el mundo indígena en el México antiguo y en la actualidad.
Observa con atención las siguientes imágenes y reflexiona: ¿puedes darte una idea del periodo que se abordará en esta sesión?, ¿quiénes imaginas que serán los protagonistas de esta historia?

En esta sesión conocerás sobre la ruta que siguió Hernán Cortés para llegar a la Ciudad de México-Tenochtitlan. Pero ¿cómo era Mesoamérica antes de la llegada de los españoles? El territorio de lo que hoy es México, no era una nación como se conoce ahora. El territorio estaba conformado por una gran diversidad de pueblos y señoríos.
Para la llegada de los españoles, las relaciones políticas estaban determinadas por cuestiones económicas, principalmente a través del pago de tributos a los pueblos más poderosos, como fue el caso del Imperio mexica, quienes además tenían un gran poder militar, el cual no dudaban en usar contra los pueblos que no aceptaran pagar el tributo impuesto.
Por esta razón, cuando llegaron los conquistadores, los pueblos indígenas aunque estaban acostumbrados a pagar tributo y aceptar a diferentes dinastías reinantes, no estaban contentos ya con el Imperio mexica.
Este descontento y falta de unión política en los diferentes pueblos, les permitió a los extranjeros construir fuertes alianzas entre grupos opositores a los tenochcas, no sin algún enfrentamiento previo en la mayoría de las ocasiones. Tal es el caso de los tlaxcaltecas.
El 18 de febrero de 1519, Hernán Cortés partió de Cuba en un viaje de expedición hacia México. Contó con el apoyo de Pedro de Alvarado, Cristóbal de Olid, Diego de Ordaz y Antón de Alaminos. Al llegar a Cozumel, se le unió Jerónimo de Aguilar, quien había naufragado unos años antes y por eso conocía la lengua maya.
De ahí partieron hacia el actual río Grijalva, donde tuvieron una batalla con indígenas chontales. Una vez concertada la paz, el cacique de Centla les otorgó 20 mujeres, entre las cuales, se encontraba Malintzin o Marina. El asignar mujeres para el vencedor tenía en el fondo una vieja práctica de concertar alianzas por vía matrimonial.
Para abril de 1519, Hernán Cortés desembarcó en las costas de la isla de San Juan de Ulúa, y para aprovechar el marco legal que lo designara como capitán, fundó la Villa Rica de la Vera Cruz. Al mismo tiempo, se alió con el señorío de Cempoala, que era un estado totonaco que pagaba tributo a la Triple Alianza de México-Texcoco y Tacuba.
Para el investigador Luis Barjau, fue este grupo de cempoaltecas con el que Cortés entabló la primera alianza con los reinos indígenas.
De agosto a noviembre de 1519, Hernán Cortés partió rumbo a la ciudad de Tenochtitlan con aproximadamente 400 hombres más los aliados indígenas. Muchos de los lugares que Cortés visitaría, entablarían alianzas con el conquistador debido a que se encontraban sometidos bajo el mismo sistema tributario que los cempoaltecas.
El camino por el que llegarían a la ciudad de Tenochtitlan sería una antigua ruta de comercio. El numeroso ejército indígena, junto con el ejército español y su armamento, lograrían vencer al poderoso Moctezuma II Xocoyotzin.
Cuando los españoles llegaron a tierras tlaxcaltecas, no fueron bien recibidos y les hicieron la guerra, sobre todo, al ver que venían en colaboración con tributarios del Imperio mexica, los totonacas. Después de tres intentos de detenerlos por la fuerza, el jefe de Tizatlán, Xiconténcatl, animó a los tlaxcaltecas a aceptar hablar con los españoles. Al ver que los españoles podrían ser recibidos por el tlatoani Moctezuma y después de varias derrotas sufridas, decidieron recibirlos en Tlaxcala.
El 23 de septiembre de 1519, Cortés entró a la ciudad de Tlaxcala, donde le informaron de la situación que vivían bajo el dominio del imperio de Moctezuma II. Los tlaxcaltecas dirigieron a los españoles hacia Cholula por ser éstos, aliados de los mexicas.
El 18 de octubre, Cortés cometió una primera masacre y sometió a los cholultecas. Cholula era una gran ciudad y un importante centro de comercio para la región.
Una versión sobre cómo ocurrió la masacre para someterlos dice que mandó a reunir a los principales de Cholula y cerró las entradas del lugar, cometiendo así una matanza como respuesta a una posible emboscada. Otras versiones mencionan que la matanza se dio durante una celebración al dios Quetzalcóatl, pues Cholula era un importante recinto de adoración a dicha deidad mesoamericana.
La matanza en Cholula significó una advertencia para los mexicas. Una vez controlada la ciudad, los españoles avanzaron hacia Tenochtitlan. Ante los ojos de los españoles se presentaba la majestuosa Ciudad de México-Tenochtitlan. El 8 de noviembre de 1519 fueron recibidos en el palacio de Axayácatl.
A continuación, lee el siguiente fragmento de las Cartas de Relación de Hernán Cortés, que describe cuál fue su primera impresión de la ciudad.
“Esta gran ciudad de Temixtitan está fundada en esta laguna salada, y desde la tierra firme hasta el cuerpo de la dicha ciudad, por cualquiera parte que quisieren entrar a ella, hay dos leguas. Tiene cuatro entradas, todas de calzada hecha a mano, tan ancha como dos lanzas jinetas. Es tan grande la ciudad como Sevilla y Córdoba. Son las calles de ella, digo las principales, muy anchas y muy derechas, y algunas de éstas y todas las demás son la mitad de tierra y por la otra mitad es agua, por la cual andan en sus canoas, y todas las calles de trecho a trecho están abiertas por donde atraviesa el agua de las unas a las otras, y en todas estas aberturas, que algunas son muy anchas, hay sus puentes de muy anchas y muy grandes vigas, juntas y recias y bien labradas, y tales, que por muchas de ellas pueden pasar diez de a caballo juntos a la par. Y viendo que si los naturales de esta ciudad quisiesen hacer alguna traición, tenían para ello mucho aparejo, por ser la dicha ciudad edificada de la manera que digo, y quitadas los puentes de las entradas y salidas, nos podrían dejar morir de hambre sin que pudiésemos salir a la tierra”.
El fragmento de Hernán Cortés sobre la descripción de la Ciudad de México- Tenochtitlan refleja asombro. Del mismo modo que los indígenas, puedes darte cuenta cómo para describir a Tenochtitlan, Cortés la compara con ciudades españolas como Sevilla y Córdoba.
Por otra parte, la importancia de las alianzas fue decisiva en el proceso de Conquista. Desde la primera alianza con los cempoaltecas hasta 1524 o 1525, se concertaron otras alianzas tlaxcaltecas, Huexotzingo, Tepexi, Tehuacan, Coxcatlan, Tamazulapan, Zacatalán, los señoríos totonacos serranos, entre otros. Pero hubo otras alianzas que se concertaron por medio de la guerra, Tepeaca, Tecamachalco, Itzocan, Xalapa, entro otros.
Derivado de algunas alianzas como la española-tlaxcalteca, Tlaxcala fue considerada con privilegios dentro de la organización política de la Nueva España. Por ejemplo, la organización indígena tradicional fue respetada.
El Cabildo, máxima autoridad durante el Virreinato, fue compuesto por indígenas tlaxcaltecas. Se creó el cargo de gobernador indio y gobernador español, ambos sujetos a la decisión del cabildo.
Tlaxcala fue una población realenga, es decir, que dependía directamente del rey y en cualquier momento podían apelar a éste sin que mediara alguna otra autoridad novohispana. Esto le otorgó una gran autonomía como pueblo tlaxcalteca.
Para finalizar, observa el siguiente video que traza en un mapa virtual la ruta seguida por Cortés. Presta mucha atención.
- La ruta de Hernán Cortes.
https://www.youtube.com/watch?v=Db7lHUWWwgk
El 8 de noviembre de 1519 se llevaría a cabo la primera entrevista entre Moctezuma y Hernán Cortés en la calzada de Iztapalapa. Malinzti tradujo la conversación entre estos dos hombres de mundos diferentes. Mientras Cortés fue alojado en el palacio de Axayácatl, Moctezuma sería tratado cada vez más como rehén dentro de su propia ciudad.
Has concluido esta sesión. Para saber más del tema, puedes consultar tu libro de texto de Historia, Bloque 2.
El Reto de Hoy:
Elabora un diario del día 8 de noviembre de 1519, el día que Cortés llegó a México-Tenochtitlan. Desde el punto de vista de un indígena tenochca, relata tu primera impresión al ver a esos hombres barbados. Con la ayuda de tu libro de texto y tus apuntes, así como con el relato que se presentó al inicio, imagina que acabas de ver por primera vez a aquellos extraños. ¿Qué te llama la atención de ellos? Describe qué llevan puesto y cómo hablan. Usa tu imaginación histórica.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario