Aprende en Casa 2 SEP: 03 de noviembre TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 03 de noviembre de clases virtuales mediante el programa Aprende en Casa 2, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa 2, compartimos los temas y actividades que se abordaron este Martes 03 de noviembre, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa 2:
https://aprendeencasa.sep.gob.mx/#

Propiedades de los polígonos regulares
Aprendizaje esperado: Deduce y usa las relaciones entre los ángulos de polígonos en la construcción de polígonos regulares.
Énfasis: Desarrollar el razonamiento deductivo al examinar las propiedades de los polígonos regulares.
¿Qué vamos a aprender?
Continuarás con el estudio de las figuras geométricas. En esta sesión, conocerás cómo resolver problemas que implican obtener el número de diagonales que pueden trazarse desde un vértice, el número de diagonales en total y la suma de los ángulos interiores en polígonos regulares.
¿Qué hacemos?
Analiza la siguiente situación:
Problema 1
Alma tiene una casa en el interior de un terreno cuadrado, como se muestra en la siguiente figura:
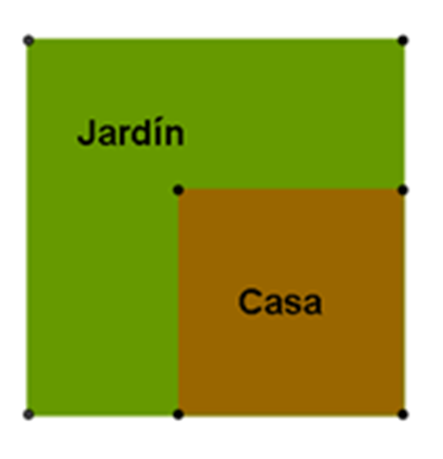
- ¿Qué polígonos puedes encontrar en la imagen?
- ¿Qué forma tienen la casa y el jardín?
Ella tiene dudas acerca del tipo de figuras que conforman su terreno. Su hijo pequeño le ha dicho que su jardín tiene forma rectangular y que su casa está construida sobre un terreno que tiene forma cuadrada, pero su hija, que está en la secundaria, no está de acuerdo, expresando que el jardín no tiene forma de un rectángulo, aunque tenga forma irregular.
Para salir de dudas, determina quién tiene la razón. Analiza:
¿Qué polígonos puedes encontrar en la imagen?
Para contestar esta pregunta, reflexiona un poco acerca de la forma que tienen los terrenos sobre la casa y el jardín:
¿Qué forma tienen la casa y el jardín?
Si se separa la casa y el jardín, puedes identificar dos polígonos diferentes.
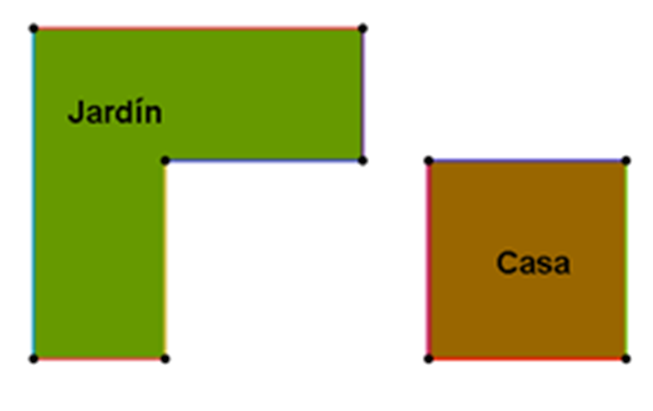
Analiza primero el terreno sobre el que está construida la casa.
¿Cuántos lados tiene el terreno sobre el que está construida la casa?
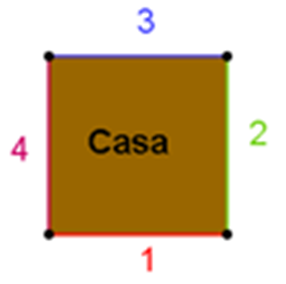
Al contar el número de lados, te puedes percatar de que son cuatro los lados del terreno sobre el que está construida la casa, entonces, es un cuadrilátero. Ahora, para determinar qué tipo de cuadrilátero es, necesitamos saber cuáles son las medidas de sus lados y de sus ángulos.
¿Cuáles son las medidas de sus lados entre sí?, ¿iguales o diferentes?
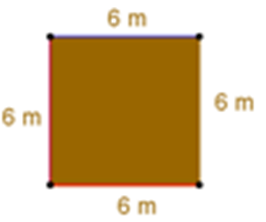
El primer lado mide 6 metros; el segundo, el tercero y el cuarto lado también miden 6 metros.
Como puedes observar, todos los lados tienen la misma medida, miden 6 metros, pero ¿esto quiere decir que se trata de un cuadrado? ¿Cómo puedes saberlo?
Para determinarlo, puedes recurrir a la medida de sus ángulos interiores.
Observa en el cuadrilátero ¿Cuál es la medida de sus ángulos interiores?
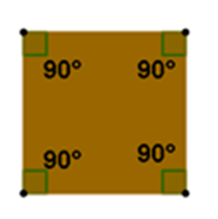
En el primer vértice, su ángulo mide 90 grados, el siguiente ángulo también es de 90 grados, en el tercer vértice su ángulo mide 90 grados y el cuarto ángulo es de 90 grados.
Entonces, como la medida de todos los ángulos interiores de este cuadrilátero es de 90°, puedes concluir que la casa de Alma está construida sobre un terreno cuadrado que representa un polígono regular.
De acuerdo con lo anterior, reflexiona en lo siguiente:
¿Cómo deben ser los ángulos interiores de un polígono para que éste sea regular?
¿Cómo deben ser los lados de un polígono para que éste sea regular?
Para poder dar respuesta a las preguntas anteriores sobre la casa de Alma, analiza lo siguiente y conoce más sobre los polígonos:
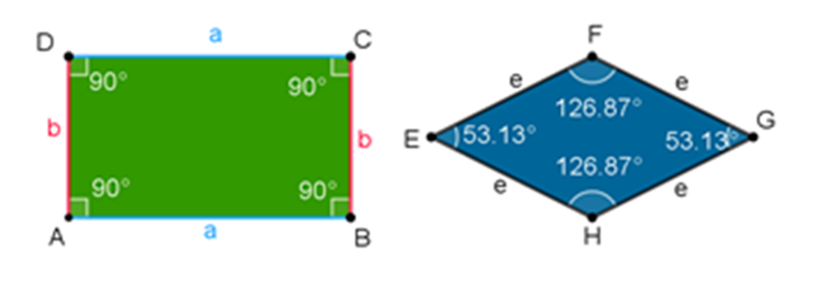
¿Por qué estos polígonos no son regulares?
El rectángulo no es regular porque, aunque sus ángulos interiores miden 90 grados, los lados no tienen la misma medida.
El rombo tampoco es regular porque, aunque la medida de sus lados es igual, la de sus ángulos interiores no lo es.
Regresando al problema inicial, ¿identifica qué tipo de polígono tiene el jardín de Alma?
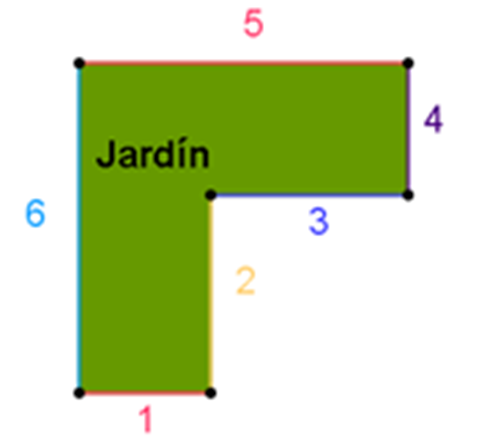
Por tener seis lados, el jardín es un hexágono, ¿y qué tipo de polígono es, regular o irregular?
Al analizar los lados, puedes observar sin necesidad de medirlos, que su longitud es diferente, por lo tanto, se trata de un polígono irregular.
Has analizado que, para que un polígono sea regular, es necesario que se cumplan a la vez las dos condiciones:
- Que la longitud de todos sus lados sea igual.
- Que la medida de todos los ángulos interiores sea igual.
Ahora analiza las diagonales que pueden trazarse desde un vértice y las diagonales totales que tienen los polígonos regulares.
Para esto, resuelve la siguiente situación.
Problema 2
En el parque hay tres diferentes áreas para juegos infantiles en forma de pentágonos regulares seccionados, como se muestra en la siguiente figura.
Identifica en cuál de ellos se utilizan las diagonales.
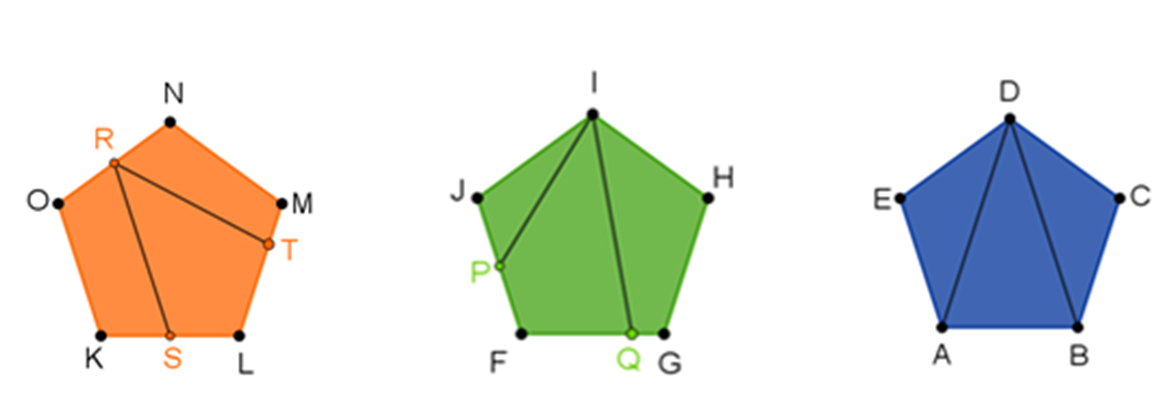
Después de haber leído el problema, analiza el primer polígono.
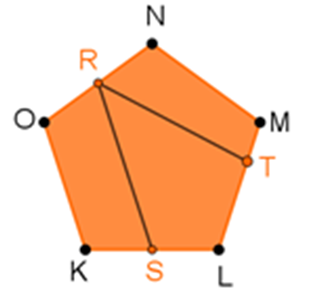
¿Cómo es que está seccionado este polígono?
Primero identifica los puntos que se encuentran marcados en el polígono.
- Los vértices del polígono son los puntos K, L, M, N y O.
- R es el punto medio del lado (NO).
- S es el punto medio del lado (KL).
- T es un punto que pertenece al lado (LM).
Este polígono está seccionado por dos segmentos de recta, el primero es el segmento “RS” y el segundo es el segmento “RT”.
El origen de la palabra diagonal hace alusión a los vértices de un polígono, por lo tanto, los segmentos RS y RT no pasan por los vértices, entonces no son sus diagonales.
Analiza el segundo polígono, ¿está seccionado por sus diagonales?
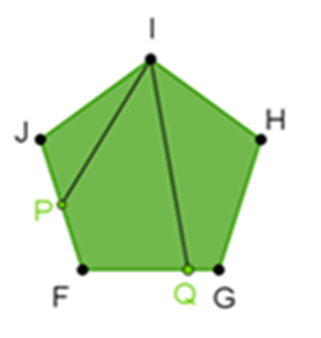
- Los vértices del polígono son los puntos F, G, H, I y J.
- P es el punto medio del segmento (JF).
- Q es un punto que pertenece al segmento (FG).
- Los segmentos con los que está seccionado el pentágono son “IP” e “IQ”.
Reflexiona sobre la siguiente pregunta:
¿Los segmentos que dividen el polígono pasan por dos vértices?
El segmento “IP” y el segmento “IQ” pasan por un solo vértice, esto quiere decir que esos segmentos no son sus diagonales.
Analiza el tercer pentágono y determina si está dividido por sus diagonales.
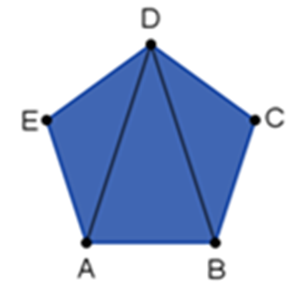
Los vértices del polígono son los puntos A, B, C, D y E.
¿Cuáles son los segmentos que dividen el pentágono?
Los segmentos que dividen al pentágono son (DA) y (DB).
¿Estos segmentos van de un vértice a otro vértice?
Estos segmentos pasan por dos vértices y dividen el polígono, entonces puedes concluir que los segmentos (DA) y (DB) son las dos diagonales del vértice D.
¿Todos los segmentos que van de vértice a vértice son diagonales?
Observa el pentágono, los segmentos “DE” y “DC” no son diagonales, ya que forman parte de los lados del pentágono. Entonces, las diagonales son segmentos de recta trazados de un vértice a otro vértice, no contiguos o no consecutivos.
A continuación, presta atención al siguiente problema.
Problema 3
¿Cuántas diagonales pasan por un vértice en cualquier polígono regular?
Analiza cuántas diagonales se pueden trazar desde un solo vértice en un cuadrado, un pentágono y un hexágono.
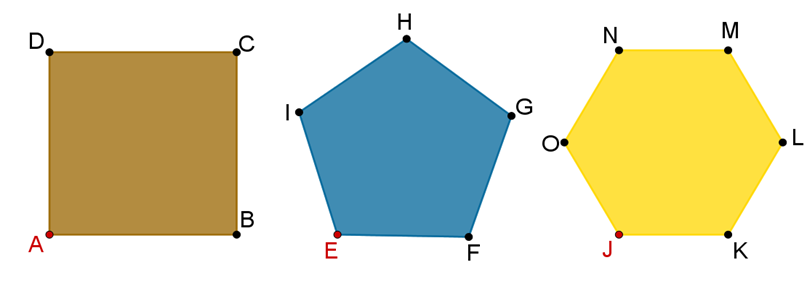
Los cuatro vértices del cuadrado son A, B, C y D, ahora considera el vértice A y traza todas sus diagonales.
¿Cuántas diagonales se pueden trazar?
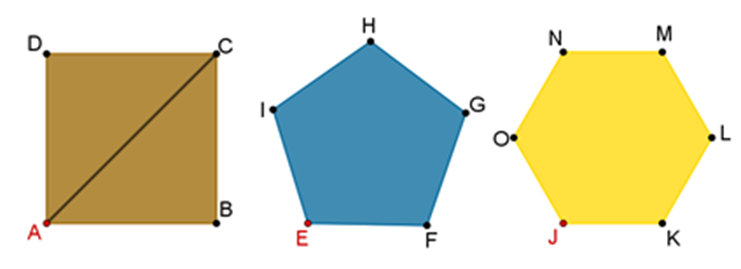
En el cuadrado, sólo se puede trazar una sola diagonal partiendo del vértice A, correspondiente al segmento (AC).
Ahora, traza las diagonales que sean posibles desde el vértice E en el pentágono.
¿Cuántas diagonales se pueden trazar desde el vértice E?
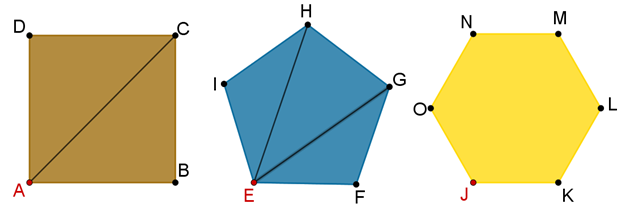
En el pentágono se pueden trazar dos diagonales, correspondientes a los segmentos (EH) y (EG).
¿Cuántas diagonales consideras que se pueden trazar en el hexágono desde el vértice “J”? y ¿cuáles son?
Traza las diagonales en el hexágono desde el vértice “J”.
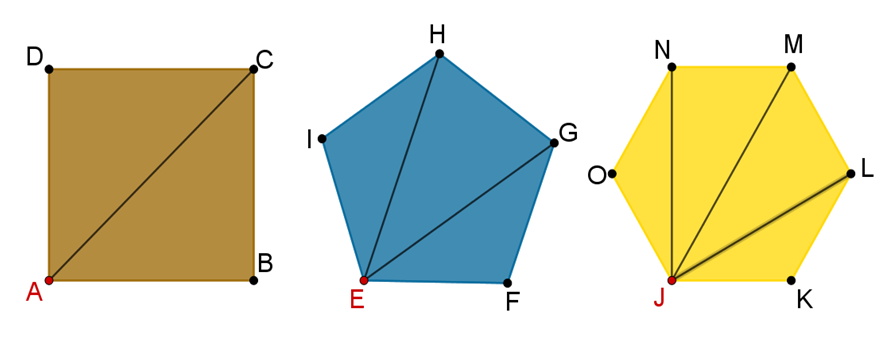
Las diagonales son 3, (JN), (JM) y (JL).
Da seguimiento a las preguntas anotándolas en tu cuaderno. Traza las figuras y usa colores para diferenciar las diagonales.
¿Cuántas diagonales se pueden trazar desde un vértice para cualquier polígono regular de “n” lados?
Para responder esta pregunta, elabora una tabla, ésta te ayudará a encontrar un patrón y te permitirá hallar el número de diagonales que se pueden trazar desde un solo vértice, aplicable a cualquier polígono regular.
En la primera columna anotarás el nombre del polígono regular; en la segunda, el número de vértices que tiene cada polígono, y en la tercera, el número de diagonales que se pueden trazar desde un vértice.
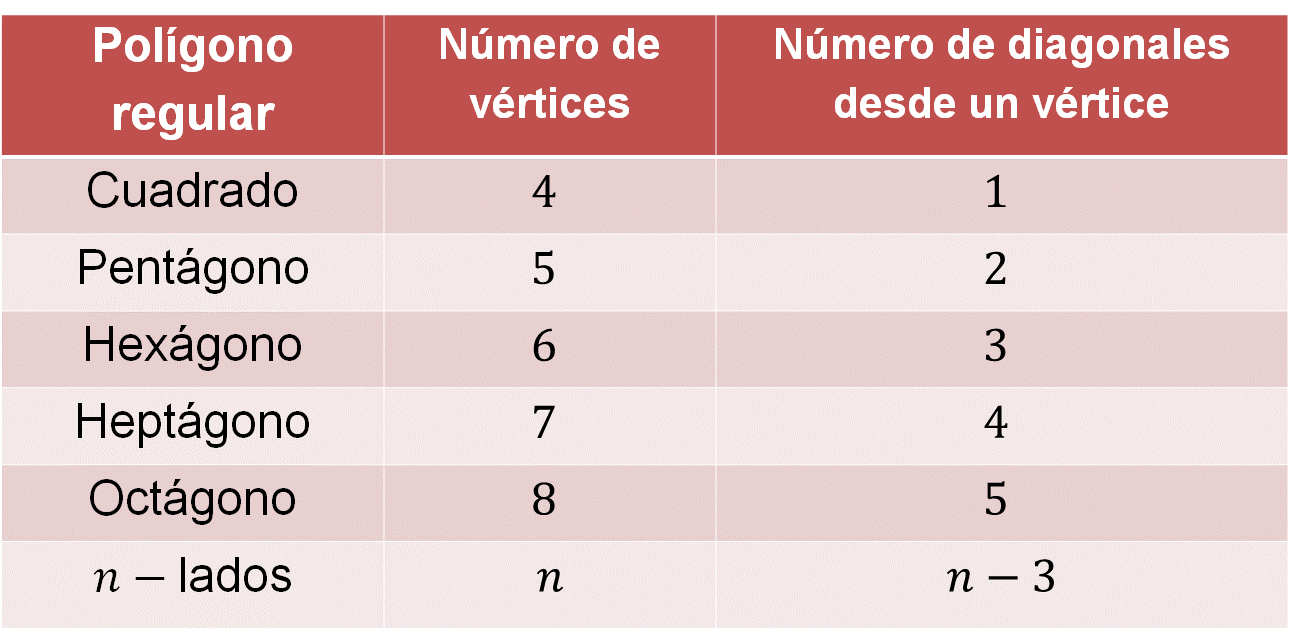
Al trazarse las diagonales desde un vértice y al no poderse trazar con los dos vértices contiguos, debes considerar tres vértices menos para encontrar el número de diagonales que se pueden trazar desde un solo vértice.
Por lo tanto, para cualquier polígono regular de “n” lados, tendrás:
n - 3 diagonales que pueden trazarse desde un vértice
Has aprendido a identificar los polígonos regulares, y a encontrar el número de diagonales que pueden trazarse desde un vértice en un polígono regular.
Ahora, examina todas las diagonales que se pueden trazar.
En tu cuaderno bosqueja un cuadrado, un pentágono y un hexágono, y traza todas las diagonales que te sean posibles en todos los vértices.
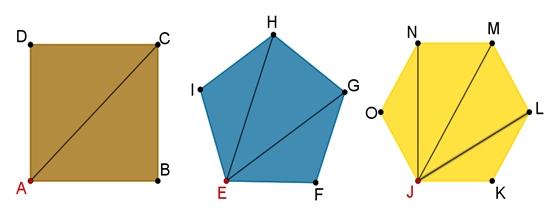
Ya que tengas todos tus trazos de las tres figuras, compáralos; seguramente tus trazos son parecidos a los que se presentarán a continuación:
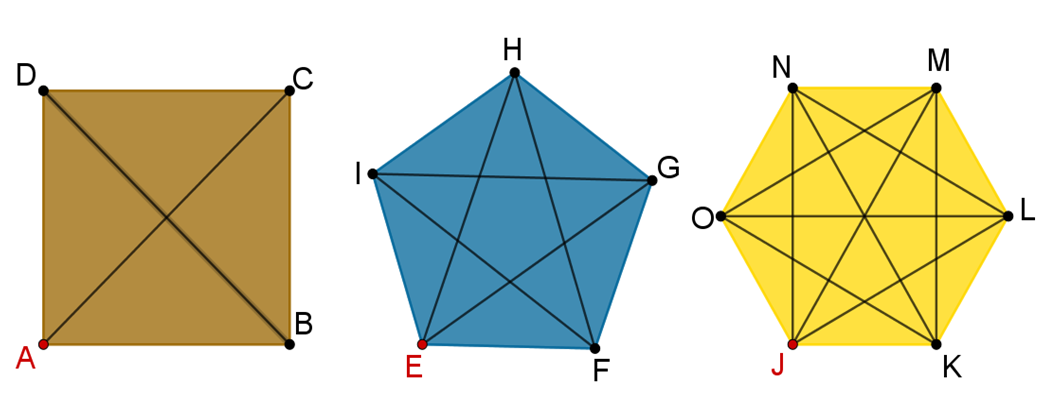
Te habrás dado cuenta de que, al trazar todas las diagonales de todos los vértices, las diagonales se repitieron. Por ejemplo, en el cuadrado, la diagonal que se trazaron desde “A” hasta “C” es la misma que se trazó de “C” hasta “A”, y esto mismo ocurre para todas las diagonales.
Ahora remarca de diferente color cada una de las diagonales para cada polígono sin repetirlas, para así poder contabilizar el número de diagonales totales. Observa el ejemplo:
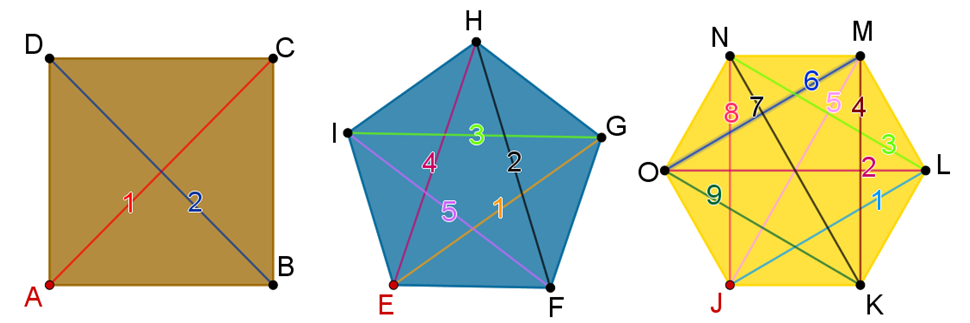
¿Cuántas diagonales tiene el cuadrado?
Para el cuadrado se tienen: dos diagonales totales.
Ahora cuenta cuántas diagonales totales tiene el pentágono:
Son cinco las diagonales totales del pentágono.
Finalmente, realiza lo mismo con el hexágono:
Son nueve las diagonales totales que tiene el hexágono.
Recapitulando, para el cuadrado se tienen dos diagonales totales, para el pentágono son cinco y para el hexágono son nueve.
¿Cómo puedes obtener el número de diagonales totales de cualquier polígono sin realizar los trazos y el conteo?
Analiza a detalle la información que has obtenido.
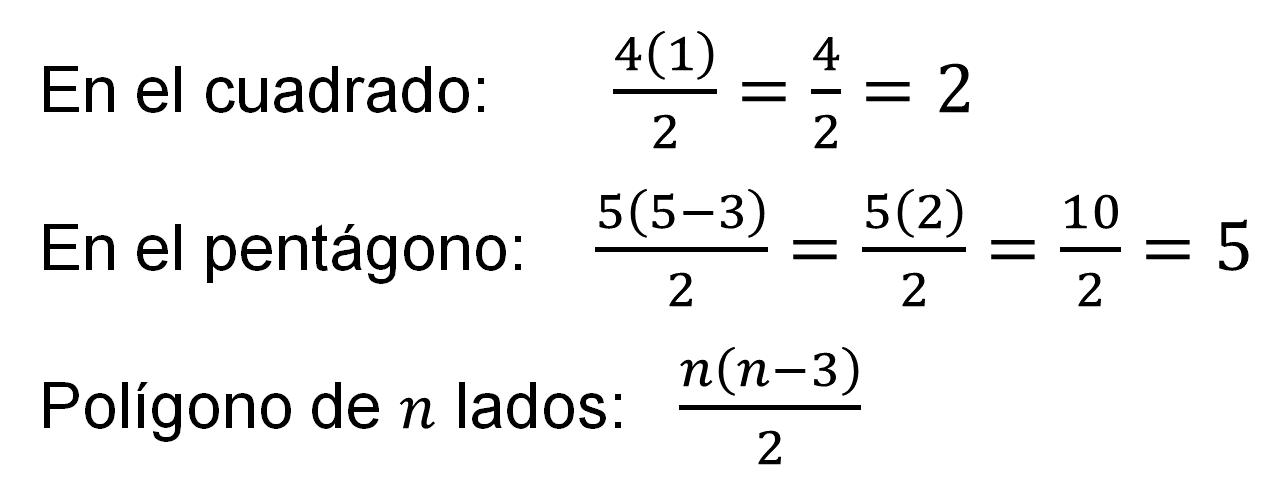
En el cuadrado, si se trazan las diagonales de todos los vértices, que son 4, a cada vértice se le podría trazar (1) diagonal, de forma que se podrían considerar 4 diagonales totales, sin embargo, se repiten el doble de diagonales; para evitar repetirlas, se dividen entre dos, por ello aparecen sólo dos.
En el pentágono, si se trazan todas las diagonales desde cada vértice, se deben multiplicar el número de vértices (5), por el número de diagonales que se pueden trazar desde cada vértice (5 - 3), es decir, 5(2) que son 10. Pero aquí se están considerando el doble de las diagonales porque éstas se duplican, y para no duplicarlas, tienes que dividir entre dos el producto, esto es: 10/2, igual a 5.
Generalizando, para un polígono regular de “n” lados. Si para un vértice se pueden trazar “n - 3” diagonales, para “n” vértices serán “n (n – 3)” diagonales, pero no se ha considerado que las diagonales se duplican y para no duplicarlas tienes que dividir entre dos este producto, quedando la expresión:
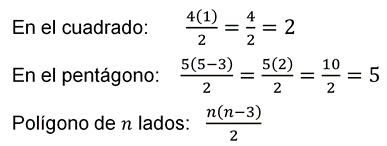
Para corroborar que la generalización es correcta, puedes realizar una sustitución numérica y verificar que se cumple para los polígonos que has analizado.
A continuación, realiza la comprobación.
Para un cuadrado que tiene cuatro vértices, “n” es igual a cuatro, y al sustituirlo en la generalización se tiene que el número total de diagonales es igual a “n”, por lo tanto:

Realiza la siguiente actividad:
Corrobora en tu cuaderno los polígonos regulares de 5 y 6 lados al sustituir “n” igual a cinco y “n” igual a seis, respectivamente.
Como ésta es una generalización, ahora puedes calcular el número de diagonales totales que tiene un icoságono regular, que es un polígono de veinte lados. Realízalo.
Hasta este momento has aprendido a identificar los polígonos regulares, a encontrar el número de diagonales que pueden trazarse desde uno de sus vértices y a encontrar el número de sus diagonales totales.
Ahora, explorarás diferentes polígonos para obtener la suma de los ángulos interiores en un polígono regular.
Analiza los siguientes polígonos regulares:
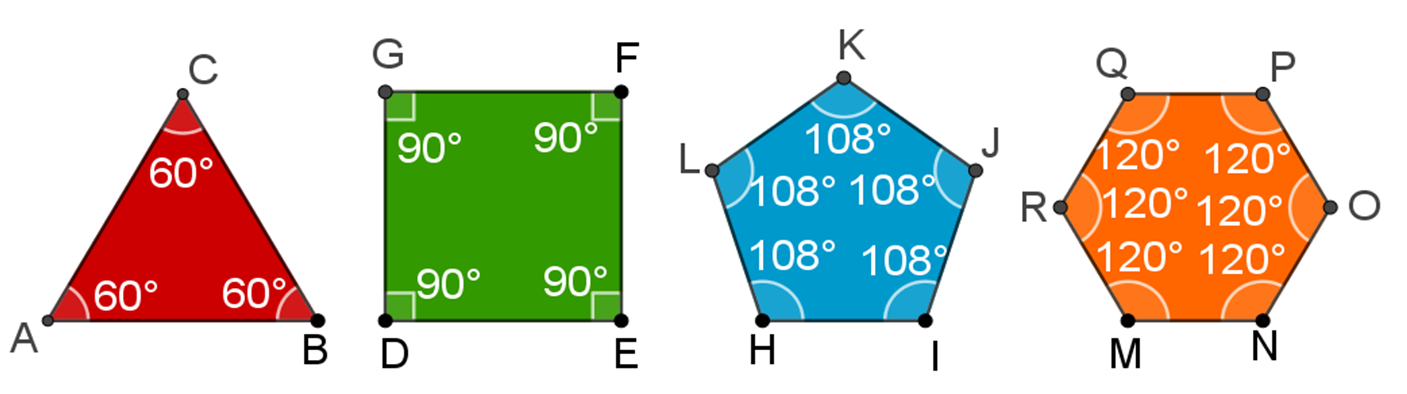
Recuerda que, para que sean polígonos regulares, la longitud de todos sus lados es igual y, además, todos sus ángulos interiores también son iguales.
Comienza con el triángulo equilátero:
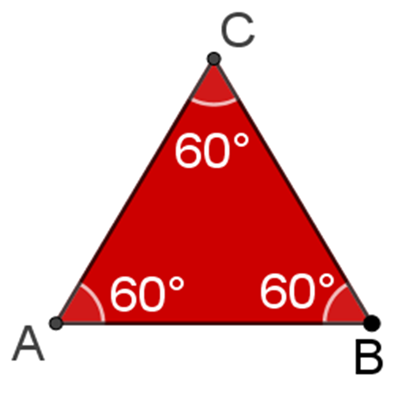
Este triángulo tiene tres lados y tres vértices, y además mide 60 grados en cada uno de sus ángulos interiores.
¿Cómo puedes encontrar la suma de sus ángulos interiores?
Se puede obtener de dos formas: sumando 60 grados 3 veces o multiplicando tres por sesenta grados, es decir, 180 grados.
60° + 60° + 60° = 3 (60°) = 180°
Continúa con el cuadrado:
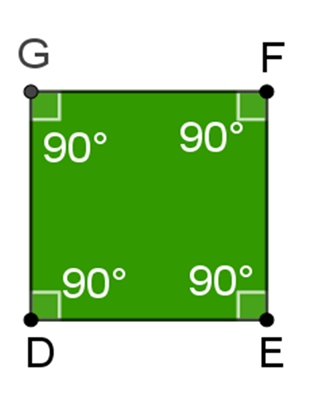
Este polígono tiene cuatro lados y cada uno de sus ángulos interiores mide 90 grados, entonces la suma de sus ángulos interiores se obtiene multiplicando 4 por 90 grados, igual a 360 grados.
4 (90°) = 360°
Ahora con el pentágono:
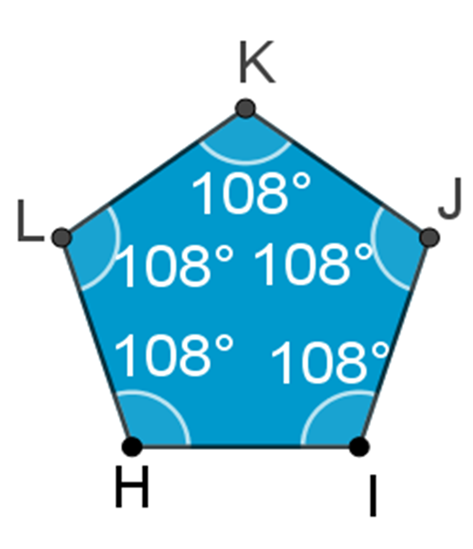
Como tiene cinco ángulos interiores y cada ángulo interior tiene una amplitud de 108 grados, entonces la suma de los ángulos interiores corresponde al producto de 5 por 108 grados, es decir, 540 grados.
5 (180°) = 540°
Finalmente, con el hexágono.
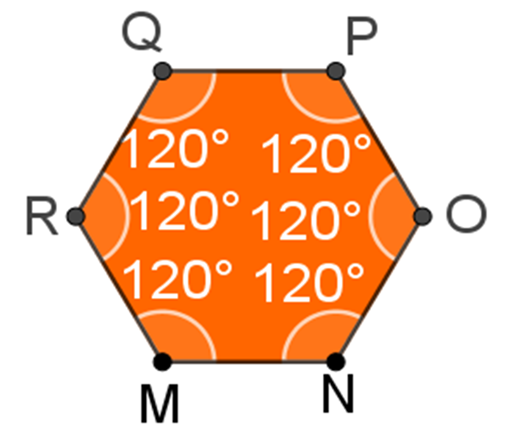
El hexágono, es un polígono de seis lados con seis vértices, y cada ángulo interior mide 120 grados, entonces la suma de sus ángulos interiores es 6 por 120 grados, o la multiplicación de 6 por 120 grados, es igual a 720 grados.
6 (120°) = 720°
Recapitulando:
La suma de los ángulos interiores de:
- un triángulo equilátero es: 3(60°) = 180°
- un cuadrado es: 4(90°) = 360°
- un pentágono regular es: 5(108°) = 540°
- un hexágono regular es: 6(120°) = 720°
Generalizando, se tiene que la suma de los ángulos interiores de un polígono regular es el producto del número de lados o vértices por la amplitud de uno de sus ángulos interiores.
A continuación, analiza los polígonos y traza en uno solo de sus vértices todas las diagonales posibles.
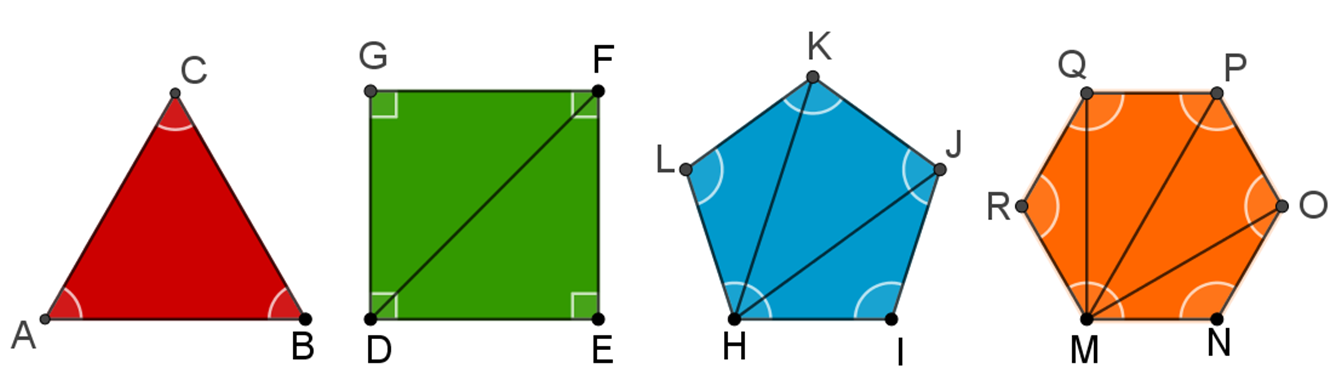
En el triángulo no se tienen diagonales, por lo tanto, el número de diagonales es cero, en el cuadrado el número de diagonales es 1, en el pentágono es 2, en el hexágono hay 3 y así sucesivamente.
Examina cuántos triángulos se pueden formar en un cuadrado al seccionarlo por medio de su diagonal.
¿Cuántos triángulos se forman en un cuadrado?
Dos triángulos.
Si se sabe que la suma de los ángulos interiores de un triángulo es de 180 grados, en un cuadrado que está conformado por dos triángulos, ¿cuánto medirá la suma de sus ángulos interiores?
Si en un triángulo la suma de los ángulos interiores es de 180 grados, la de un cuadrado conformado por dos triángulos será el doble de 180 grados, esto es, dos por 180 grados, es decir, 360 grados.
Analiza el pentágono.
Al trazar las diagonales que pasan por uno solo de sus vértices, ¿cuántos triángulos se forman?
Se forman tres triángulos
Por lo tanto, ¿cómo puedes obtener la suma de los ángulos interiores de un pentágono?
Como el número de triángulos que se forman al trazar las diagonales desde un vértice son tres, entonces la suma de los ángulos interiores del pentágono regular se obtiene al multiplicar 3 por 180 grados, que es igual a 540 grados.
Para el hexágono.
La suma de los ángulos interiores es 4 por 180 grados, que es igual a 720 grados.
Generalizando, se tiene que la suma de los ángulos interiores de un polígono regular se obtiene al multiplicar el número de triángulos que se forman al trazar desde un solo vértice todas sus diagonales por 180 grados.
¿Cómo puedes relacionar el número de triángulos que se pueden formar con el número de lados o vértices?
Organiza tu información en la siguiente tabla.
En la primera columna anotarás el polígono; en la segunda, el número de lados; en la tercera, el número de triángulos, y en la cuarta columna, la suma de los ángulos interiores del polígono regular.
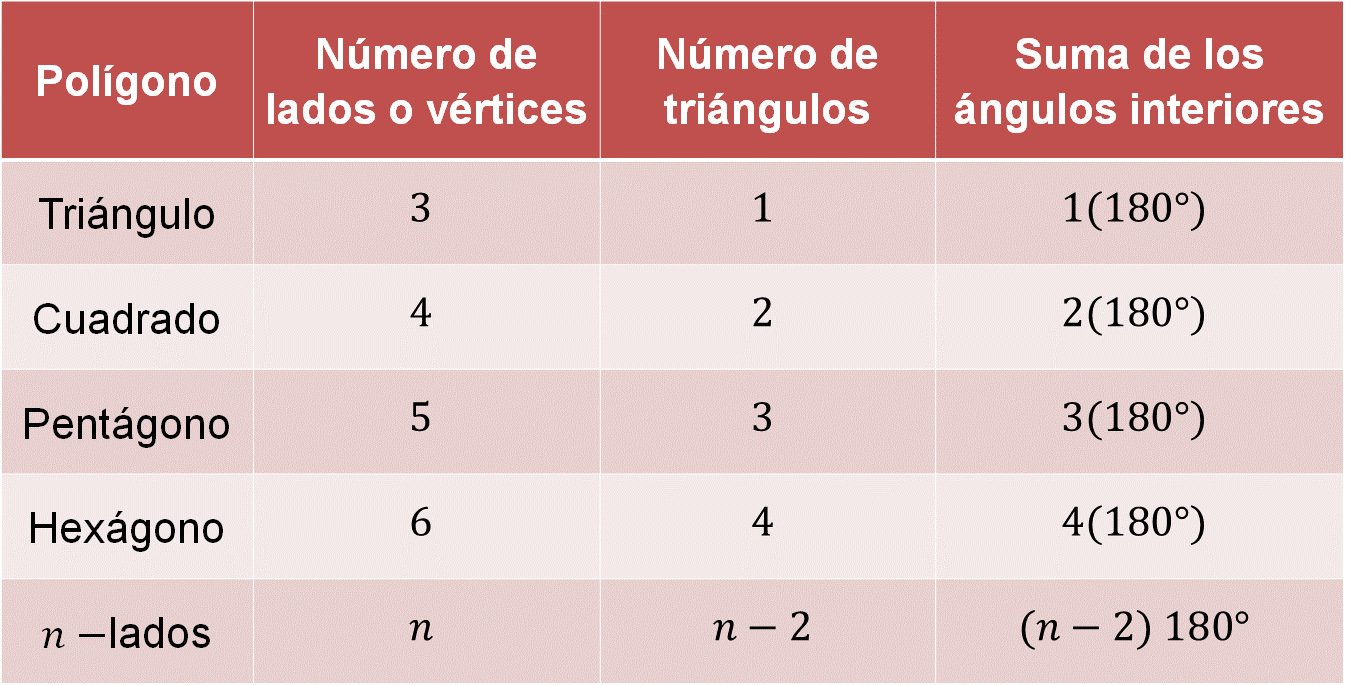
Para un triángulo con 3 lados, el número de triángulos es 1 y la suma de los ángulos interiores es 1 por 180 grados.
En un cuadrado el número de lados es 4, el número de triángulos es 2 y la suma de los ángulos interiores es 2 por 180 grados, y así sucesivamente.
Observamos que, para un polígono de “n” lados, el número de triángulos que se pueden formar es el número de lados menos dos, y la suma de los ángulos interiores de un polígono es el número de triángulos que se pueden trazar desde un vértice que es “n - 2” por 180 grados.
El Reto de Hoy:
Traza un decágono regular y las diagonales de todos sus vértices en tu cuaderno. Corrobora que el número de diagonales totales coincidan con el obtenido por medio de la generalización.
Finalmente, utilizando la generalización, responde cuánto debe medir el ángulo interior para el polígono y confírmalo midiendo uno de los ángulos interiores del polígono que trazaste.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Historias de leyenda
Aprendizaje esperado: Recopila leyendas populares para representarlas en escena.
Énfasis: Recopilar leyendas para leer.
¿Qué vamos a aprender?
Profundizarás en las leyendas populares y sus características. Para ello, te acercarás a la literatura oral y leerás algunas de ellas.
La literatura oral es algo vivo que crece con el ser humano, reactiva la memoria colectiva, forma parte del patrimonio intangible de la humanidad y es un pequeño gran tesoro que depende de la voluntad de todos para su permanencia en el tiempo.
Desde la antigüedad, el ser humano ha tratado de dar una explicación a los diversos fenómenos que ocurren a su alrededor. De igual forma, ha contado su historia y ha conservado la de sus antepasados con el fin de preservar la memoria histórica y los acontecimientos más importantes de su paso por el planeta.
En el género de la narrativa se encuentra la leyenda, expresión que se ha utilizado en diversas épocas y civilizaciones.
Ésta es, junto con el cuento y el mito, de los primeros subgéneros que utilizaron la mayoría de los pueblos para expresar su ideología, testificar acontecimientos o explicar sucesos.
En consecuencia, las leyendas son altamente valoradas, porque forman parte de la cultura de una población, pero también porque en su contenido está plasmada la cosmovisión, la historia, las creencias, los conocimientos geográficos, históricos, la organización política, económica y social de una época, y un lugar en particular.
¿Qué hacemos?
Analiza qué es una leyenda, según Arnold van Gennep:
Las leyendas son relatos que hablan de personajes y sucesos que alcanzan resonancia en una comunidad. Se transmiten de generación en generación, mayormente de manera oral.
Es una narración que “indica el lugar con precisión, los personajes son individuos determinados, y tienen sus actos un fundamento que parece histórico y son de cualidad heroica”.
La leyenda, según Arnold van Gennep.
Los mitos y las leyendas forman parte de la tradición oral, es decir, de la identidad cultural de una comunidad.
Éstos forman parte de la cultura de un pueblo, y a través de estos textos se transmiten visiones del mundo, creencias y valores que se transforman en el eterno proceso de creación y de recreación permanente de la cultura popular. Además, ambos retoman elementos fantásticos o sobrenaturales, es decir, sería improbable que sucedieran así.
Para conocer la diferencia entre una leyenda y un mito, observa el siguiente cuadro:

Los mitos son la primera forma narrativa creada por la humanidad, la cual cuenta una historia sagrada, pues a través de ellos se intenta explicar el origen de las cosas, del mundo, de la vida, y es por esa razón que los personajes más recurrentes son divinidades.
Además, se tienen diferentes versiones según la cultura que los exprese y los narre. Por ejemplo, para los griegos, las estaciones surgen a partir del rapto de Perséfone, y para los babilonios, éstas se explican a partir del mito de Tamuz.
En el caso de las leyendas, éstas nacen de un elemento real, al cual se le agregan elementos imaginarios o sobrenaturales, o personajes muertos. Y tienen un valor histórico por su contenido y por su antigüedad.
Narrar relatos de la tradición oral es una práctica que ha acompañado a la humanidad; en todos los tiempos y lugares la gente se ha reunido a contar historias sobre experiencias paranormales o inexplicables, creando en los oyentes miedo, curiosidad, identidad, sentido de pertenencia, entre otros.
En algunos pueblos, las leyendas, igual que los mitos, han servido como elementos de cohesión y permiten conocer el funcionamiento de sus cultos. Las leyendas tienen un significado profundo dentro de la comunidad en la que se insertan. Suelen tener elementos sobrenaturales, aunque no siempre son de terror.
Cuando un hecho real, interesante o extraordinario es narrado a lo largo del tiempo, es común que se le agreguen nuevos datos, exageraciones o elementos de tipo sobrenatural o simbólicos.
A continuación, escucha el siguiente relato de “La leyenda del fantasma de la monja”, del estado de Guanajuato.
- La leyenda del fantasma de la monja.
En México tenemos una gran diversidad de leyendas, y eso hace que tengamos una infinidad de versiones de ellas.
En un principio fueron transmitidas de manera oral y solamente con el tiempo han ido cambiando.
Ahora, realiza la siguiente actividad de la leyenda que acabas de escuchar.
Responde las siguientes preguntas en tu cuaderno:
- ¿Qué historia relata la leyenda?
- ¿En qué época está ambientada?
- ¿Quiénes son los personajes?
- ¿Qué elementos reales encontraste en esta historia?
“La leyenda del fantasma de la monja” habla de la historia de María de Ávila, quien se enamoró de un hombre que sólo tenía un interés monetario y social en ella, pero su inmenso amor por él fue su perdición.
Los corazones rotos pueden dar lugar a terribles y escalofriantes leyendas.
Las leyendas, al ser textos narrativos, permiten observar un planteamiento que ayuda a ubicar la época, además de un desarrollo, un clímax y un desenlace. Además, es común encontrar leyendas con variaciones o adaptaciones propias de cada región, como el caso de “La llorona”.
La función de la leyenda es transmitir una historia basada en una creencia popular, arraigada en un lugar; con ella se busca explicar o darle sentido a algún suceso extraño que resulta difícil de entender. Además, ofrece información acerca de la cultura y la diversidad lingüística del lugar con el que se relaciona.
Las leyendas son consideradas textos breves debido a que desarrollan un solo motivo; es decir, únicamente narran un acontecimiento. Del mismo modo, no suelen abundar en detalles y descripciones.
Generalmente, la narración combina la tercera y la primera persona; sin embargo, cuando la creencia o el tema central está arraigado en la comunidad y es conocido por todos, se tiende a narrar únicamente la anécdota relacionada.
Algunas leyendas narran acerca de los nombres alternos que se les otorgan a calles, barrios o lugares, tales como el Callejón del Beso, la Calle del Mono Prieto, el Callejón de la Condesa, tal y como ocurre en la leyenda de “La curva del charro negro”. Lee con atención y conoce esta leyenda:
La curva del charro negro
Hubo un tiempo en que corrió el rumor de que en el pueblo de Jiquipilco se aparecía por las noches un Charro negro. Dicen que salía de una curva del camino y que llegaba hasta el centro del pueblo, después entraba a la Presidencia haciendo mucho escándalo, aventando los papeles que encontraba para regresarse, después, por donde había venido.
Un señor, que vivía cerca de la Presidencia y que siempre lo oía, decidió esperarlo para ver quién era. Una noche se escondió cerca de la puerta de la Presidencia, llevaba una espada en la mano.
Esperó a que el Charro entrara y cuando lo vio salir le encajó la espada. Y dicen que el señor recordaba perfectamente cómo se la había encajado pero que después ya no supo más de él porque cayó desmayado. Dicen que, desde entonces, ya no vieron jamás al Charro negro.
Y también, desde entonces, a esa curva la llaman la “Curva del Charro negro”.
Esta leyenda menciona el lugar en el que ocurren los hechos. Sin embargo, no menciona una época en específico.
Leyendas como la que acabas de escuchar, reciben el nombre de leyendas toponímicas, pues narran el origen nominal de un lugar.
Ahora, responde lo siguiente:
¿En qué otros lugares has escuchado una versión del charro negro? Pregunta a tus familiares si ellos conocen alguna otra versión.
¿En tu comunidad hay alguna calle que reciba el nombre a partir de una leyenda?
La narración de una leyenda es sencilla o simple en el sentido de que, generalmente, se cuenta lo que le sucede a un personaje. En la medida en que una leyenda narra acontecimientos ocurridos en la misma comunidad en que se cuenta, quien narra suele hacer uso de un lenguaje coloquial y, con frecuencia, pleno de regionalismos y términos locales.
En algunos lugares, como Guanajuato, se cree que existe una ciudad que conserva oculta las riquezas del pasado, pero para acceder a ellas es necesario romper algún tipo de hechizo. Esta historia, unida a los referentes reales, se combina con la fantasía y el simbolismo en leyendas que perduran como un referente cultural de esta localidad.
La enunciación de las leyendas no requiere de un espacio ni de un auditorio específico; puede ser contada a un receptor o a un público más amplio y de cualquier edad. Se transmite con el afán de conservar ciertos valores y conocimientos acerca de la propia comunidad, ya sea de su historia o su vida cotidiana.
Para el folclorista español Vicente García de Diego, la leyenda: “es una narración tradicional fantástica, en esencia, admirativa, generalmente puntualizada en personas, época y lugar determinados”, y como tal, tiene ciertas características, como son:
- Las leyendas explican algún hecho con elementos sobrenaturales, a través de ellas se busca dar una explicación a estos sucesos.
- Cambian con el paso del tiempo, pues se agregan detalles a la narración.
- Contaminación: tiene elementos de una leyenda en otra.
- Personificación: se pueden encontrar nombres concretos, es decir, con apellidos.
- Localización y deslocalización: algunas sugieren lugares concretos, ambas son frecuentes en leyendas hagiográficas.
- Elementos fantásticos: se puede saber de criaturas o sucesos inexistentes.
Las leyendas narran sucesos reales o irreales, sin comprobar. En su estructura es frecuente la combinación de elementos reales y falsos.
Precisamente la característica principal de las leyendas es la fusión de elementos reales e imaginarios para crear una historia y, con ello, tratar de explicar ciertos sucesos.
Escucha el siguiente audio, donde conocerás la leyenda de “La confesión”, perteneciente a la Ciudad de México. Trata de identificar los elementos reales e imaginarios que se narran.
¿Qué te está pareciendo la historia?
¿Lograste ubicar los lugares y la situación paranormal?
Continúa escuchando la historia…
En la mayoría de las comunidades hay una historia que contar y que dejará a más de uno pensando.
Ahora, realiza la siguiente actividad.
Lee los siguientes fragmentos de la historia que acabas de escuchar e identifica los hechos reales y los hechos imaginarios.
¿A dónde corresponde cada uno?
- Don Agustín era un sacerdote.
- Encontró a dos hombres que le pidieron confesar a una moribunda.
- La mujer le confesó los pecados más horribles que el cura hubiera oído.
- El sacerdote no encontró a los hombres que lo llevaron.
- El padre no dejaba de decir: “¡Confesé a una muerta!”. Se había vuelto loco.
En los hechos que se presentan como verosímiles o creíbles, se tiene don Agustín era un sacerdote al que acudieron dos hombres para pedirle que confesara a una moribunda y que éste fue para que ella le confesara sus pecados.
Los hechos sobrenaturales ocurren cuando el sacerdote no encontró a los hombres que lo llevaron, y el hecho de haber confesado a una muerta.
En la leyenda, estos dos elementos se entrelazan para crear una historia.
El mundo de las leyendas es infinito, desde los sucesos que intentan explicar hasta las diferentes versiones que puedes encontrar.
Al caminar por las calles de la Ciudad de México puedes encontrarte con sitios que, se dice, fueron escenarios de curiosos y muy peculiares hechos, en especial en el Centro Histórico, justo donde nace la leyenda de “La mujer herrada”. Lee y conoce esta historia:
La mujer herrada
Se dice que alrededor del año 1600, un solitario clérigo vivía en la calle llamada Puerta Falsa de Santo Domingo, lo que hoy se conoce como República de Perú. Dada su soledad, el hombre optó por buscar una mujer con quien vivir, a pesar de que nadie veía su acción con buenos ojos, en especial su compadre, un herrero que vivía a unas calles de distancia y era profundamente religioso.
El herrero solía insistirle al clérigo que alejara a dicha mujer de su vida y volviera a encauzar su vocación, sin embargo, el religioso se resistía a dejarla.
Una noche, el herrero escuchó fuertes golpes en su puerta y se apresuró a ver quién podía acudir a su taller tan tarde. Al abrir se encontró con dos hombres que llevaban amarrada a una mula. Le comentaron que el clérigo los había mandado a verlo para que herrara a la mula cuanto antes, pues apenas llegara la mañana debía salir de viaje.
El herrero se apresuró a ponerle las herraduras a la mula y, una vez que estuvo lista, los mensajeros se la llevaron dándole fuertes golpes.
¿Quieres saber en qué termina la historia?
Investiga en libros, en Internet e incluso con tus familiares, posiblemente alguno de ellos conozca esta leyenda.
Las leyendas no tienen una versión definitiva, pues es posible que las vuelvas a escuchar en lugares y épocas diferentes, y con variaciones.
La leyenda ofrece la posibilidad de alimentar las dudas y contradicciones que se encuentran en el hombre en los límites de la ficción y de la realidad, y te acercan a las costumbres y tradiciones de determinados lugares.
Recuerda que lo asombroso de las leyendas es que existen tantas versiones que al final tú podrías construir una propia.
Revisa tu libro de texto para ampliar tu conocimiento.
El Reto de Hoy:
Pregunta a tus familiares si conocen alguna otra leyenda e identifica los hechos reales y los hechos imaginarios. También puedes escuchar los audios de leyendas que encontrarás en la Fonoteca Nacional, o a observar los videos que ofrecen el Instituto Nacional de Antropología e Historia, INAH, o el Instituto Nacional de Lenguas Indígenas.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

¡A que te congelo!
Aprendizaje esperado: Explica los estados y cambios de estado de agregación de la materia, con base en el modelo de partículas.
Énfasis: Identificar los cambios de estados de agregación de la materia.
¿Qué vamos a aprender?
Realizarás un recorrido científico y tecnológico en el que conocerás y analizarás, de forma práctica, los cambios de estado de agregación y las propiedades de la materia. Asimismo, profundizarás en el modelo de partículas.
¿Qué hacemos?
Para comenzar, anota las siguientes preguntas e intenta responderlas:
- ¿Por qué la materia cambia de estado de agregación?
- ¿Cómo se produce la nieve en los volcanes o la escarcha de hielo en los jardines?
Ya que respondiste las preguntas, observa el siguiente video.
- Calor y temperatura.
En el video se habló de estados de agregación de la materia: sólido, líquido y gaseoso.
El plasma, a pesar de ser el estado de agregación más abundante en el universo, es difícil de reproducir, ya que se requieren condiciones muy específicas, como grandes temperaturas o corrientes eléctricas.
A continuación, realiza el siguiente experimento para observar los cambios de algunos estados de agregación. Recuerda registrar tus observaciones, elaborar dibujos y anotar el o los cambios de estado que se produjeron en cada caso.
Si deseas reproducir este experimento, recuerda usar tu bata y realízalo en compañía de un adulto.
Experimento 1.
Este experimento es para demostrar el cambio de estado de fusión y de solidificación.
El material que se necesita es:
- Trozo de vela
- Cristalizador
- Lámpara de alcohol
En casa, puedes utilizar una cuchara de metal grande en lugar del cristalizador y la flama de la estufa para sustituir el mechero.
Procedimiento:
- Primero toma un trozo de vela y colócala en el cristalizador (cuchara de metal). Ahora, con ayuda de la lámpara de alcohol (estufa), calienta el pedazo de vela.
- Observa qué sucede.
Al calentar la vela, aumenta la energía cinética de sus partículas, por lo que comienzan a separarse. Llega un punto en el cual la separación debilita la fuerza de cohesión, entonces la materia pasa del estado sólido al estado líquido, es decir, ocurre la fusión del sólido.
Después, al enfriarse, la vela va cediendo calor a la atmósfera, esto hace que la energía cinética de sus partículas disminuya, por lo que los espacios intermoleculares también lo hacen hasta que la fuerza de cohesión vuelve a ser significativa. Esto produce que la vela pase del estado líquido al estado sólido y es cuando ocurre la solidificación.
En nuestra vida cotidiana utilizamos la solidificación cuando hacemos hielo. Se extrae tanto calor a las partículas del agua, que se solidifica.
Realiza el siguiente experimento para observar la solidificación instantánea del agua. No olvides hacerlo en presencia de un adulto.
Experimento 2.
Este experimento es para demostrar el cambio de estado de solidificación.
El material que necesitaras es:
- Una botella de agua de 1/2 litro,
- un recipiente donde quepa la botella,
- cubos de hielo,
- agua,
- sal y
- un plato de cristal.
Procedimiento:
- Introduce la botella dentro del recipiente.
- Cubre con hielo hasta la mitad del recipiente y agrega medio vaso de agua.
- Agrega 4 cucharadas de sal sobre los hielos.
- Vas a poner más hielo hasta cubrir toda la botella y agrega otras 4 cucharadas de sal sobre los hielos.
- Deja reposar el recipiente durante 40 min.
(Si cuentas con un congelador en casa, puedes poner la botella en él durante una hora. Y así no tienes que preparar el recipiente con hielos y sal).
- Transcurrido el tiempo, retira la botella del recipiente o del congelador, con mucho cuidado y no la agites.
- Después, colocar tres hielos sobre el plato.
- Finalmente, vierte despacio el agua sobre los hielos, recuerda no agitar la botella.
- Observa atentamente lo que sucede.
Observarás que el agua se está hace hielo mientras cae.
¿Por qué pasa eso?
Para que la sal se pueda disolver en el agua, necesita energía, esa energía la obtiene en forma de calor, que extrae de lo que la rodea.
En este caso, la sal que se está disolviendo en los hielos absorbe el calor de la botella con agua, sin llegar al punto de congelación. Al dejar durante un tiempo prolongado la botella dentro de los hielos, la temperatura del agua puede estar entre -2 y -4 grados Celsius.
Cuando vertimos el agua sobre los cubos de hielo, la temperatura y la presión cambian rápidamente haciendo que ésta se congele, pasando del estado líquido al estado sólido. A este fenómeno se le llama sobrefusión o súper enfriamiento.
Realiza otro experimento, no olvides tener cuidado y hacerlo en compañía de un adulto.
Experimento 3.
Este experimento es para demostrar la evaporación y la condensación.
Los materiales que necesitas son:
- Agua,
- vaso de precipitados de 250 ml,
- lámpara de alcohol,
- soporte universal,
- vidrio de reloj y
- hielos.
En casa, puedes sustituir el vaso de precipitados y el vidrio de reloj, con un sartén con tapa. Y en lugar del mechero, puedes usar la flama de la estufa.
Procedimiento:
- Agrega un poco de agua dentro del vaso de precipitados (sartén).
- Luego lo sometes a calentamiento sobre el soporte universal, con ayuda de una lámpara de alcohol (estufa).
- Espera unos minutos a que hierva.
- Ya que esté hirviendo el agua, tapa el vaso de precipitados con el vidrio de reloj (tapa del sartén), colocando dos cubitos de hielo sobre él.
- Retira del fuego y espera unos minutos para ver lo que sucede.
Observarás que se forman gotitas de agua en el vidrio de reloj (tapa).
En este experimento se producen dos cambios de estado.
Como se está calentando el agua, aumenta la energía cinética de sus partículas. Al alcanzar la temperatura de ebullición, las moléculas tienen tanta energía cinética, que la fuerza de cohesión que sentían ya no las puede mantener juntas y se separan pasando al estado gaseoso. Esto hace que se evapore el agua.
Cuando se coloca el vidrio de reloj con hielos sobre el vaso de precipitados, sucede el proceso contrario. Las partículas del gas ceden energía a las del vidrio de reloj porque está a menor temperatura. Pierden tanta energía que la fuerza de cohesión entre las partículas hace que se sientan ligadas de nuevo y vuelven al estado líquido.
A este fenómeno se le llama condensación.
Este fenómeno lo puedes observar cuando te bañas: el agua sale tan caliente que una parte se evapora. Este vapor de agua, al tocar la superficie de las paredes y techo, se enfría formando gotitas de agua.
Otro ejemplo es cuando exhalas tu aliento sobre un espejo, puedes observar cómo se forman microgotas sobre la superficie de éste.
Continúa con la sublimación y la deposición, a través de los siguientes experimentos y recuerda nuevamente hacerlo en compañía de un adulto.
Experimento 4.
El material que necesitarás es:
- Hielo seco
- 1 globo
Procedimiento:
- Ponte guantes e introduce un trozo de hielo seco dentro de un globo.
- Lo anudas y déjalo reposar unos minutos para observar lo que sucede.
Observarás que el globo se infla un poco. Después, al romper el globo para ver qué queda adentro, te darás cuenta de que no tiene líquido.
El hielo seco no está formado por agua, se produce con gas de dióxido de carbono a bajas temperaturas.
Cuando entra en contacto con la atmósfera, absorbe calor del aire, incrementando su temperatura y sublimándose. Es por lo que no hay agua en el globo, pues el hielo seco se transformó en gas de dióxido de carbono.
Continúa con el siguiente experimento.
Experimento 5.
El material que necesitarás es:
- Una lata sin la tapa superior
- 6 cubos de hielo
- 2 cucharadas de sal
Procedimiento:
- Agrega los cubos de hielo dentro de la lata de aluminio y dispersa la sal sobre ellos.
- Después, agita la lata con movimientos circulares, observa que la lata por fuera está seca.
- Espera unos minutos y presta atención a lo qué sucede en la parte externa.
Como pudiste observar al principio, el recipiente estaba seco, al agregar los hielos y la sal, la temperatura de los hielos y la lata disminuyó aproximadamente hasta –4 grados Celsius.
Esto hizo que la temperatura del vapor de agua que se encuentra en el aire también bajara hasta congelarse, por eso puedes ver que en la parte de afuera del recipiente se formó hielo, es decir, el vapor de agua hizo una sublimación inversa o deposición.
Esto mismo pasa en las mañanas muy frías, cuando encuentras escarcha en las plantas, es porque el vapor de agua ha realizado una sublimación inversa.
Consulta tu libro de texto o fuentes de información confiables, si quieres conocer más acerca del tema que revisaste.
El Reto de Hoy:
Invita a tu familia a que observen la elaboración de los experimentos y comparte a que se deben estos cambios de estados de agregación de la materia.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Mis ámbitos de participación como adolescente
Aprendizaje esperado: Analiza críticamente información para tomar decisiones autónomas relativas a su vida como adolescente (sexualidad, salud, adicciones, educación, participación).
Énfasis: Indagar respecto a las formas de participación y ámbitos en que puede involucrarse como adolescente.
¿Qué vamos a aprender?
Describirás y destacarás tu participación en los ámbitos en los que puedes intervenir; por ejemplo, en eventos culturales, políticos, sociales y deportivos en tu comunidad. También analizarás algunos casos de adolescentes que han desarrollado actividades en pro de su entorno.
¿Qué hacemos?
Reflexiona en el siguiente caso:
Un alumno, llamado Fernando, se preguntaba qué podía hacer, debido a que en su colonia había poco alumbrado y esto, en los últimos meses, había derivado en mayor inseguridad, así como en situaciones de violencia.
Él quería saber cómo podía contribuir a generar espacios de convivencia donde las familias que viven en la colonia se sintieran seguras y pudieran salir a la calle sin temor alguno.
Tiempo después, logró obtener información sobre cómo las y los adolescentes tienen diversos mecanismos de intervención para apoyar a su comunidad. Así que visitó su alcaldía para preguntar qué podía hacer y de qué manera podía solicitar el apoyo del gobierno local, para promover una participación conjunta.
Al día siguiente, investigó todo el procedimiento para solicitar el apoyo de sus autoridades, e incluso, asistió a una audiencia pública con su alcaldesa para que, en compañía de sus padres, hicieran su solicitud por escrito y darle seguimiento a esta problemática.
En nuestro país todas las personas deben gozar de seguridad y cuidado de su integridad, tal y como lo indican las leyes.
Así fue como Fernando, con el apoyo de sus padres, ejerció el derecho plasmado en el artículo 8º de la Constitución Política de los Estados Unidos Mexicanos, el cual señala que:
“… Los funcionarios y empleados públicos respetarán el ejercicio del derecho de petición, siempre que éste se formule por escrito, de manera pacífica y respetuosa…”
Todas y todos tenemos derecho a participar para mejorar la convivencia en nuestro entorno. Destaquemos que fue posible que Fernando formulara la solicitud ante la autoridad, gracias al apoyo de sus padres, ya que aún no cumple la mayoría de edad; pero no por eso su participación y opinión pierden importancia.
Observa el siguiente video donde, al igual que Fernando, otras personas, orientadas por sus profesoras y profesores, ganaron un premio a nivel internacional, participando e impulsando actividades a favor de su comunidad escolar.
- Acciones organizadas.
La participación de las y los adolescentes en la resolución de problemas que viven en sus comunidades puede marcar la diferencia, no sólo en su comunidad, sino en el mundo, poniendo el nombre de México en alto. Significa formar parte a favor de una acción colectiva para promover cambios. El ejemplo que viste te puede dar una idea de cómo organizarte; el proyecto del grupo que participó buscaba resolver la escasez de agua en la comunidad, a través del uso de agua de lluvia, lo que los llevó a buscar formas de ahorro de energía que se multiplicaron en su comunidad.
Las y los adolescentes también son capaces de participar en su comunidad para dar respuesta a las problemáticas que se viven.
A continuación, observa el siguiente esquema sobre los ámbitos de participación de las y los adolescentes.
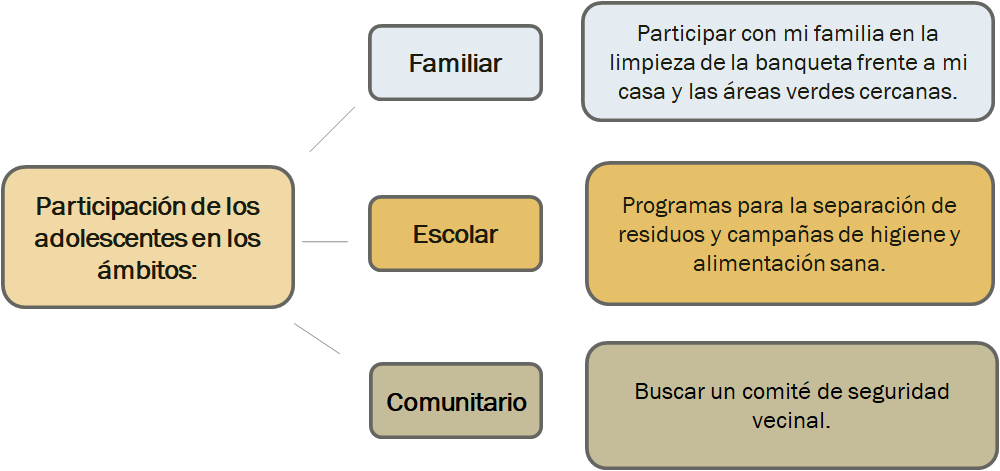
Los ámbitos en los cuales puedes participar son el familiar, en donde su desarrollo personal inicia. Ahí adquieres tus primeros conocimientos y valores, por ejemplo, en las labores del hogar, en el cuidado de los integrantes de la familia, en las compras, entre otras actividades.
En el ámbito escolar convives con otras y otros adolescentes y tienen problemáticas en común, por ejemplo: el cuidado de los salones de clase, de los espacios donde conviven, la prevención de situaciones de violencia, la solución de diferencias por medio del diálogo, entre otras actividades.
Y el ámbito comunitario, en donde la responsabilidad social es de suma importancia. Ejemplo de ello es el cuidado de las áreas verdes y del agua, entre otras cosas.
Involucrarse en estos ámbitos genera sentido de pertenencia. La familia es el núcleo del cual se desprenderán acciones primarias; en el ámbito escolar reconocerás que las necesidades de otros también pueden ser las tuyas, pasando a la participación con la comunidad en beneficio de las demás personas.
Para participar de forma activa, es importante que conozcas que en la Ley General de los Derechos de Niñas, Niños y Adolescentes se establece que tienes derecho a buscar, recibir y difundir información e ideas de todo tipo y por cualquier medio, siempre que no dañe los derechos y la vida privada de las y los demás.
En el artículo 13 de la Ley General de Educación, se menciona que la educación que se brinde fomentará una educación que promueva la responsabilidad ciudadana y la participación activa en la transformación de la sociedad, para mejorar sus espacios de convivencia, el respeto y cuidado del medio ambiente, así como el respeto a la diferencia entre las personas con las que se convive. Como podrás notar, la participación en los ámbitos de convivencia es un derecho que tienes garantizado.
Retomando los ejemplos que hasta el momento has visto, también puedes participar y comprometerte para buscar solución a los problemas de tu entorno. Para ello, deberás organizarte con los miembros de tu comunidad.
Considera los siguientes ejemplos de acciones y buenas prácticas que puedes llevar a cabo:
- Separación de la basura en orgánica e inorgánica.
- Recolección de basura en ríos, lagos y mares.
- Ahorro de agua y energía tanto en las zonas urbanas y rurales.
- Campaña de respeto a los peatones.
- Limpieza de calles, parques y zonas públicas.
Acércate a las autoridades correspondientes para participar en más actividades de acción organizada.
En las escuelas, los docentes y directivos generalmente están abiertos a que tú, como adolescente, puedas participar y opinar para garantizar tu derecho establecido en el Artículo 71º de la Ley General de los Derechos de Niñas, Niños y Adolescentes, que dice:
“Niñas, niños y adolescentes tienen derecho a ser escuchados y tomados en cuenta en asuntos de su interés conforme a su edad, desarrollo evolutivo, cognoscitivo y madurez”.
Participar en asuntos que conciernen a la comunidad involucra a todas y todos los que conformamos un espacio social, así que tu opinión es importante, por lo que puedes y debes actuar, decididamente, en tu entorno.
La participación no es algo que se realice de manera espontánea para que tu actuar tenga impacto en los espacios de convivencia.
De acuerdo con tu experiencia y capacidades, considera que cada vez son más los ámbitos en los que puedes participar y, para que tu actuar contribuya a mejorar la convivencia en los espacios donde participas, tendrá que ser de manera organizada, estableciendo acuerdos con las personas con las que convives y considerando el diálogo como un recurso que permite establecer acuerdos.
A continuación, escucha las entrevistas de tres estudiantes de secundaria, quienes respondieron preguntas relacionadas con su participación en su familia, la escuela y en su comunidad. Son Ximena, Naomi y Juan Carlos quienes brindan su opinión sobre la intervención de los adolescentes en sus ámbitos de participación.
- Video. ¿De qué manera participas, como adolescente, en tu familia?
- Video. ¿Cómo has participado en tu escuela?
- Video. ¿De qué manera has participado en tu comunidad?
La participación de las y los adolescentes está presente en diversos ámbitos, como el familiar, escolar o comunitario.
Ximena destaca la organización que existe en su casa para la realización de las actividades del hogar, así como la importancia del diálogo para tomar acuerdos.
Nahomi deja ver cómo en la escuela a la que asiste, existe una planeación de actividades en las cuales ella participa, como la canasta de lectura y los juegos de mesa.
En cuanto a Juan Carlos, destaca la importancia de planear actividades para dar respuesta a una problemática que se vive en la comunidad, para ello fue necesario establecer alianzas con los comerciantes y así lograr que su colonia se vea más limpia y agradable.
Existen diferentes formas de participación de las y los adolescentes, en los diversos ámbitos en que se desenvuelven: familiar, escolar y comunitario.
Reflexiona sobre las situaciones que vives en el día a día, en la interacción con tu entorno.
Ahora, escucha al maestro Héctor Osnaya Murcia, director de un plantel educativo de nivel secundaria, quien comparte información sobre las formas de participación en el ámbito escolar de las y los adolescentes.
- Video. Formas de participación en el ámbito escolar.
De acuerdo con lo mencionado por el director, en la secundaria existe una planeación para favorecer la participación de las y los adolescentes; ello implica que las autoridades motiven y contribuyan a generar espacios de participación de las y los adolescentes en los que, además de atender asuntos relacionados con el cuidado de la escuela, se establezcan mecanismos de representación como la Asociación de Alumnos, quienes participan en la organización de las actividades. Este sería un ejemplo de cómo se favorece la participación de las y los adolescentes en los asuntos de la escuela.
Atendiendo a las palabras del director, se te invita a participar en las actividades escolares, de manera activa, generando un cambio personal y colectivo en otros ámbitos de tu comunidad y el país.
Cuidar y preservar los espacios donde convivimos es responsabilidad de todas y todos, por ello debe ser una prioridad. Recuerda que no tenemos futuro sin pasado y tú puedes marcar la diferencia. Siendo adolescentes, es posible participar para mejorar el entorno, por ello no olvides imaginar, analizar y crear en beneficio de tus entornos.
Ahora observa el siguiente video, en el que podrás conocer actividades que desarrollan alumnas y alumnos enfocados al arte y la cultura, mismas en las que puedes participar y compartir en tus ámbitos sociales para que estas buenas prácticas sean replicadas en otras escuelas, fomentando así el interés de tu comunidad escolar.
- Video. Actividades enfocadas al arte y la cultura.
El arte puede mostrar hechos históricos pasados o presentes, pero también nos muestra la cultura y diversidad de nuestro país, generando con ello un interés social y la participación de las y los adolescentes.
Como adolescente debes participar en los actos cívicos, así como en las votaciones para la Asociación de alumnas y alumnos y jefes de grupo escolar, tomando decisiones colectivas que, además de permitirte visitar lugares históricos, contribuyan a que tu opinión sea tomada en cuenta para la realización de actividades deportivas, el cuidado de la salud, la protección y cuidado de las áreas comunes de la escuela, la promoción de actividades culturales y acciones para el cuidado de la naturaleza, entre otras.
Recuerda involucrar a todas las personas que están a tu alrededor.
Todas las actividades que desempeñes en estos ámbitos deberán estar encaminadas a un bien específico, logrando tus metas individuales y colectivas.
Las problemáticas que existen en tu entorno tienen solución; si aún no logras definir qué hacer para contribuir en resolver las situaciones o problemas, toma en cuenta que puedes apoyarte en tus padres o profesoras y profesores para que te asesoren y orienten.
No olvides que los grandes cambios inician con pequeñas acciones.
Un aspecto que tiene que destacarse es que existen mecanismos que garantizan que la voz de las y los adolescentes sea escuchada y tomada en cuenta. Como se presenta a continuación:
- La Constitución Política de los Estados Unidos Mexicanos, de la cual emanan los principios de toda ley secundaria.
- Ley General de los Derechos de Niñas, Niños y Adolescentes, misma que destaca sus derechos y ámbitos de participación mencionados con anterioridad.
- Y los derechos humanos de niñas y niños, respaldados por la Comisión Nacional de los Derechos Humanos.
Además de ello, tienes la posibilidad de actuar en varios ámbitos, como el escolar, el familiar y el comunitario.
Seguramente, en tu entorno existen diferentes problemáticas, identifícalas y actúa.
Recuerda que la mejor práctica es poner el ejemplo, ayudando a las demás personas.
No olviden que, como adolescentes, sus opiniones y participación también son importantes y tienen derecho a la orientación de sus padres, de su familia y sus profesoras y profesores.
Consulta tu libro de texto para complementar el tema visto en esta sesión.
El Reto de Hoy:
Elabora un mapa mental donde identifiques una problemática que existe en la escuela o la comunidad, donde tu participación sea activa y determina tres posibles soluciones viables.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Factores sociales y sistemas técnicos
Aprendizaje esperado: Emplea de manera articulada diferentes clases de técnicas para mejorar procesos y crear productos técnicos.
Énfasis: Relacionar los sistemas o productos técnicos con las necesidades de los grupos que los crean.
¿Qué vamos a aprender?
Indagarás cómo los factores sociales interactúan con los sistemas técnicos e identificarás las técnicas que se desarrollan según el contexto en el que se aplican. Además, profundizarás en el uso de las máquinas y herramientas en nuestra vida cotidiana.
¿Qué hacemos?
Observa el siguiente video y responde la pregunta:
¿Reconoces estas máquinas y herramientas?
- Video. Herramientas y maquinas.
De las máquinas y herramientas que observaste en el video anterior, aunque todas sirven para moler, no muelen las mismas cosas ni lo hacen de la misma forma. Algunas son de uso doméstico y otras de uso comercial o industrial, dependiendo de las necesidades que se tengan. Pueden servir para triturar o moler, aunque también dependen de la cantidad y del lugar donde se encuentren.
Por ejemplo, quienes viven en una comunidad donde no cuentan con el servicio de energía eléctrica, no pueden utilizar la licuadora, utilizan el molcajete.
El ser humano ha modificado las técnicas que emplea, no sólo para satisfacer sus necesidades, sino también para hacerlo de manera más rápida, agradable y confortable.
Desde la Antigüedad hasta nuestros días, el ser humano ha buscado siempre la forma de satisfacer sus necesidades. Son tantas y tan variadas que se han clasificado en diferentes tipos, en necesidades primarias y las secundarias.
Las necesidades primarias son aquéllas de las que depende la supervivencia, como respirar, alimentarse, beber agua, dormir, abrigarse.
Y las necesidades secundarias son las que proporcionan mayor bienestar a las personas, pero que no son indispensables para sobrevivir, como poseer un automóvil, tener éxito, ser aceptado por los demás, viajar, entre otras. Estas necesidades varían de una sociedad a otra y de una época a otra.
El ser humano ha creado diferentes técnicas para satisfacer sus necesidades empleando conocimientos, habilidades, destrezas, inteligencia y el uso de medios técnicos, como las máquinas y las herramientas.
Si alguna de esas necesidades no está satisfecha, se busca la forma de poder satisfacerla y se convierte en un estímulo para producir alguna técnica o producto que cumpla con las expectativas que se tienen al respecto; en otras palabras, se fomenta el desarrollo de técnicas.
Por esto, las técnicas siguen cambiando y se mejoran continuamente.
Por ejemplo, las clases presenciales en la escuela y las clases a distancia, ya que la educación también se ha ido adaptando a las necesidades de nuestra vida.
Para comprender la relación entre la tecnología y la sociedad, primero deberás conocer qué es cultura y qué es sociedad, para saber cómo éstas interactúan.
La sociedad se refiere a un grupo de individuos unidos entre sí por un conjunto de relaciones que se establecen con la finalidad de construir cierto tipo de pertenencia, adaptación, participación, comportamiento, autoridad y otros, es decir, tienen un fin común, originalmente surgido por la necesidad de protección y alimentación.
Al paso del tiempo, estas sociedades cambiaron y se volvieron más complejas, transformando sus necesidades hasta convertirse como en las que hoy conocemos.
Observa con atención la siguiente imagen donde se muestra la sociedad griega de la antigüedad y anota en tu cuaderno las diferencias que encuentres con la sociedad actual.
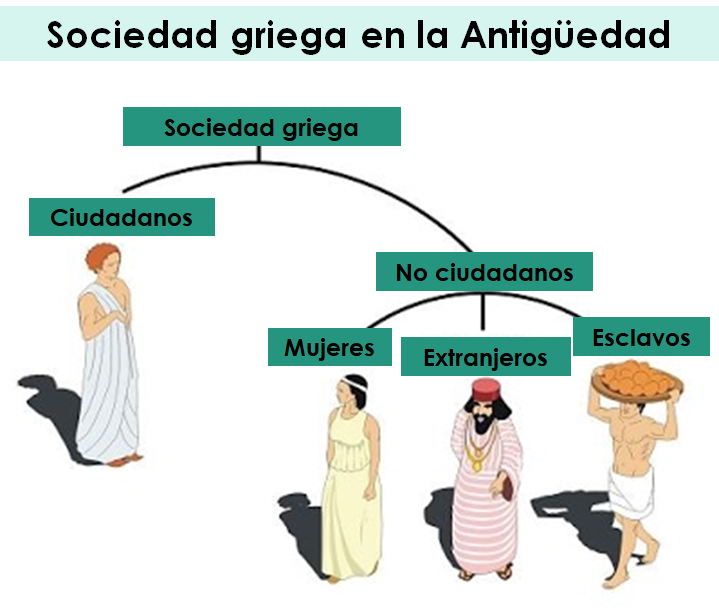
Ahora vamos a indagar en la cultura, presta atención:
La cultura es el conjunto de rasgos distintivos, materiales, intelectuales y afectivos que caracterizan una sociedad o grupo social incluyendo modos de vida, ceremonias, arte, invenciones, tecnología, sistemas de valores, derechos, tradiciones y creencias.
A través de la cultura se expresa el ser humano, toma conciencia de sí mismo, cuestiona sus creaciones, busca nuevos significados y crea obras que trascienden e influyen la vida de otras generaciones.
En tu comunidad puedes reconocer la cultura en las formas y materiales de las construcciones o cómo visten las personas, también en las maneras que tienen para saludarse y las creencias que practican, entre muchas otras. De hecho, todo es expresión de la cultura.
Las sociedades han creado diversas técnicas para satisfacer sus necesidades en diversos contextos, como las técnicas de escritura o las técnicas de construcción, por ejemplo, las empleadas por las culturas mesoamericanas en las pirámides.
Las técnicas de cultivo en chinampas, utilizadas por la cultura mexica, han sido tan efectivas que, a pesar del paso del tiempo, aún se continúan practicando en algunos lugares, como en Xochimilco, en la Ciudad de México. Para que logres entender mejor de estas técnicas, observa el siguiente video.
- Video. Las chinampas.
Otra muestra de cómo se relaciona la sociedad con la tecnología, la puedes ver en el énfasis del campo, en la preparación y conservación de alimentos.
La población mundial consume alimentos todos los días para sobrevivir, y a veces no se pueden consumir de manera inmediata, por ello se desarrollaron distintos sistemas técnicos para conservar los alimentos mediante el frío, el calor y la deshidratación; cada uno de esos sistemas desarrolló técnicas específicas según el lugar y la necesidad. Cada creación técnica tiene una función en la sociedad.
¿Qué es un sistema técnico y cómo se relaciona con las necesidades de los seres humanos?
Un sistema es un conjunto de elementos que funcionan de manera organizada e interrelacionada para un propósito.
Dentro de éstos se encuentran los sistemas naturales y los sistemas elaborados por el ser humano, a los cuales se les conoce como sistemas técnicos.
Los sistemas técnicos, están conformados por la interrelación de los materiales, los medios técnicos, las acciones y, por supuesto, por las personas que aportan sus saberes y son las que realizan las acciones.
Una representación de lo anterior se puede observar en el caso de la fabricación de conservas alimenticias como las mermeladas, dulces cristalizados y jaleas; pasan por una serie de procesos, desde la selección de las semillas, el cultivo, su transformación y su comercialización. Cada uno de estos procesos es, a su vez, un sistema técnico y juntos conforman un gran sistema, en este caso, de la producción de dulces.
Observa el siguiente video donde se muestra el proceso artesanal de la producción de amaranto.
- Video. Proceso artesanal de amaranto.
En el video se utilizan materias primas que pasan por distintos procesos; cada proceso es un sistema técnico porque en él intervienen de manera interrelacionada los insumos, los medios técnicos, las acciones y las personas que elaboran.
Es a través de los sistemas técnicos que los materiales son transformados para crear productos o servicios.
A continuación, observen con atención el siguiente gráfico donde se muestra la estructura de un sistema técnico. Anótalo en tu cuaderno, ya que lo necesitarás para completar el reto.
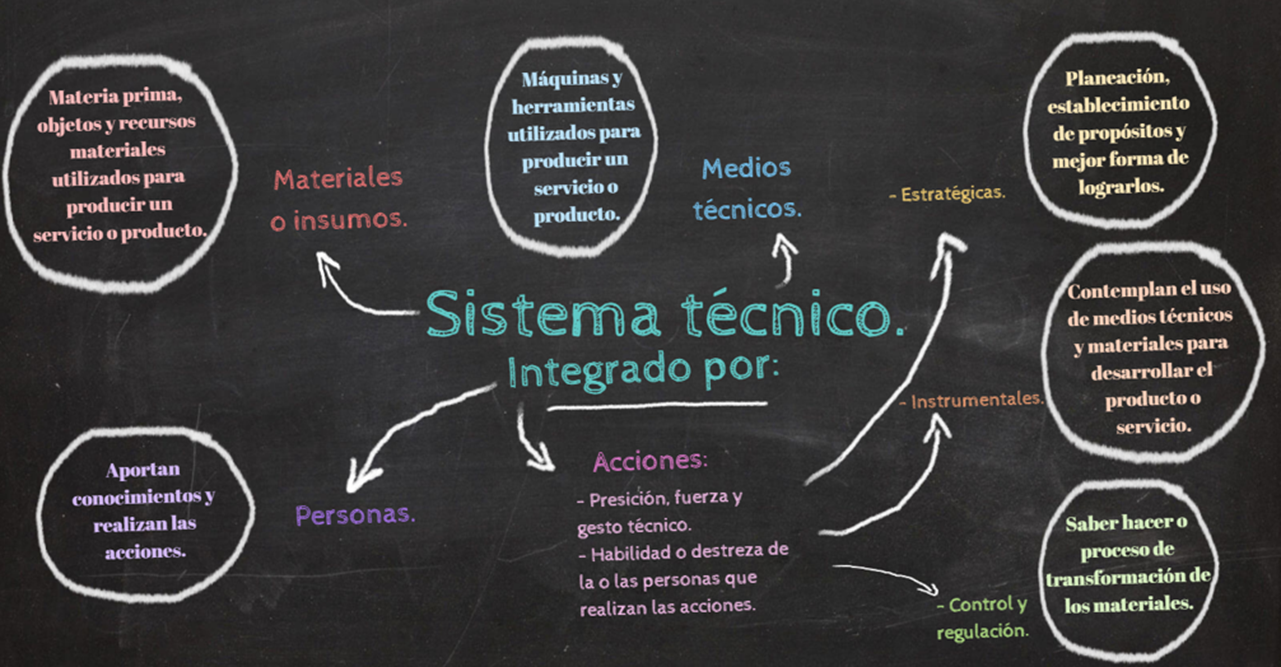
La actividad económica ha influido en los procesos de producción, ya que de éstos dependen los medios técnicos que se utilizarán. En el video observaste una producción artesanal del amaranto, en donde el tipo de herramientas que se utilizan son manuales, mientras que en los procesos fabriles se utilizan máquinas.
Las actividades económicas se organizan en tres sectores: primario, secundario y terciario, los cuales generan bienes y servicios que demanda la población.
En el primario se clasifican las actividades que utilizan los recursos de la naturaleza sin transformarlos, como la caza, la pesca, la agricultura, entre otros.
El secundario transforma los recursos naturales para producir artículos diversos, como vehículos, ropa y calzado, entre otras creaciones técnicas.
Y el sector terciario proporciona servicios, algunos de ellos son comercio, educación, medicina, turismo y transporte.
En cada uno de estos sectores se utilizan máquinas, herramientas e instrumentos para realizar las actividades.
Hoy el avance tecnológico está originando rápidos cambios en los modos de producir los bienes y prestar los servicios. La incorporación de la electrónica y la robótica a la fabricación de los diversos productos, procesos y servicios permite elaborar productos en cantidades mayores en poco tiempo, con lo que se satisface la demanda de millones de personas en el mundo.
El Reto de Hoy:
Con todo lo que acabas de aprender, contesta lo siguiente:
¿Crees que los sistemas técnicos tienen relación con los sistemas de producción?, ¿por qué?
Describe brevemente cuáles son las necesidades e intereses sociales que satisface tu énfasis de campo.
Finalmente, con el video de la producción del amaranto o de las chinampas, identifica cada proceso y los medios técnicos que se utilizan.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Aprende en casa II SEGUNDO DE SECUNDARIA 03 DE NOVIEMBRE










Publicar un Comentario