Aprende en Casa 2 SEP: 29 de septiembre TAREAS y ACTIVIDADES de 3° de secundaria
A continuación dejamos los temas vistos el 29 de septiembre de clases virtuales mediante el programa Aprende en Casa 2, para los alumnos de 3° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa 2, compartimos los temas y actividades que se abordaron este Martes 29 de septiembre, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa 2:
https://aprendeencasa.sep.gob.mx/#

Movimientos literarios en la poesía
Aprendizaje esperado: Reconoce el contexto histórico y social de la poesía dentro de un movimiento literario.
Énfasis: Seleccionar poemas de un movimiento literario.
¿Qué vamos a aprender?
El propósito es que conozcas las características de algunos de los distintos movimientos literarios para que puedas identificar el contexto histórico-social que influyen en un poeta cuando escriben su obra.
Anota lo que consideres más importante, o la información que no sabías. No intentes escribir todo como si fuese un dictado, mejor trata de anotar palabras clave para formar un organizador gráfico o haz una lista de ideas principales.
¿Alguna vez has leído un poema que no trate de amor o de la naturaleza? ¿De qué podría hablar entonces?
En la poesía los temas son muy variados y esto se debe a que existen diversas corrientes o movimientos literarios. Lee un poema de este tipo, titulado “¡Alarma!”

El poema que acabas de leer es un poema estridentista. Es decir, pertenece al movimiento literario conocido como estridentismo.
El estridentismo es uno de los distintos movimientos literarios que conforman la literatura universal. Algunos movimientos literarios se construyen con base en ciertos principios o reglas, que asientan lo que se quiere decir o transmitir a través de los poemas. Y estos principios se escriben en un documento que se conoce como manifiesto.
El estridentismo pertenece a este tipo de movimientos. Lee un fragmento del “Manifiesto Estridentista” para conocer un poco más acerca de las características de este movimiento.

Este texto fue escrito hace muchos años, por lo que utiliza un lenguaje que podría ser complicado.
El estridentismo es un movimiento artístico perteneciente al vanguardismo. En México surge casi a la par de la Revolución Mexicana, a principios del siglo XX.

Esto quiere decir que los estridentistas veían la vida como algo que acontece, que sucede como lo hace la lluvia, por ejemplo, que es difícil de predecir, pues a veces parece que será una tormenta enorme y sólo cae una lluvia ligera.
El estridentismo surge en nuestro país en un contexto en el que se buscaba un sentido de identidad nacional, había una búsqueda de lo mexicano. Se planteaba una lucha entre imitar o adoptar los estilos de vida de otras sociedades como la europea y lo que tendría que ser el estilo propiamente mexicano.
Así que, hay una relación entre lo que estaba pasando en el país, que luchaba para definirse, y lo que pasaba por la poesía. En los dos casos, se quiere definir lo que es ser mexicano, lo que caracteriza al país.
Por eso se dice que el contexto histórico-social influye en la poesía. Además de la importancia de definir lo mexicano, el estridentismo apuesta por “ser” con los cambios y las transformaciones, por apreciar no sólo la naturaleza misma (árboles, plantas, animales) sino también lo que el ser humano ha creado para transformarla, por eso dice:
"Para hacer una obra de arte […] es preciso crear, y no copiar. ‘Nosotros buscamos la verdad en la realidad pensada, y no en la realidad aparente.’ En este instante asistimos al espectáculo de nosotros mismos. […] Es necesario exaltar, en todos los tonos estridentes de nuestro diapasón propagandista, la belleza actualista de las máquinas, de los puentes recientemente extendidos sobre las vertientes por músculos de acero, el humo de las fábricas, las emociones cubistas de los grandes trasatlánticos con humeantes chimeneas de rojo y negro, anclados horoscópicamente […] junto a los muelles efervescentes y congestionados, el régimen industrialista de las grandes ciudades palpitantes, las blusas azules de los obreros explosivos en esta hora emocionante y conmovida; toda esta belleza del siglo, […] tan ampliamente dignificada y comprometida por todos los artistas de vanguardia."

No sólo el estridentismo reflexionaba sobre la vida cotidiana, en general, esta es una característica de todos los movimientos de vanguardia: ser críticos de lo cotidiano, de la vida común de la sociedad. A los estridentistas les asombraba que la gente conviviera con máquinas o fábricas y que no se sorprendieran por ello. En este sentido, la poesía de vanguardia rompe con los estereotipos de "lo bello" de la poesía clásica.
Sí, no es común que los poemas hablen de fábricas o de obreros, generalmente hablan del amor, o de la belleza del ser amado.
Finalmente, el manifiesto nos dice:

El estridentista piensa que describir, recordar o visualizar las emociones es algo artificial, es algo que el ser humano construye, como construye una máquina. Lo natural es que las emociones sucedan como el día y la noche, como la lluvia o el viento.
En otras palabras, el estridentismo rechaza la idea de que las emociones puedan ser manipuladas o que exista la distinción entre buenos y malos sentimientos, así como cosas bonitas y feas porque todo lo que sucede es digno de admiración.
¿Por eso da la impresión de que las palabras salen, como si no pudieran pararse? ¿Por eso los poemas no son como otros, que todos los versos miden lo mismo y están ordenados por estrofas? Sí, también esto tiene que ver en la forma de los poemas.
¿Qué hacemos?
Ya conoces algunas características del movimiento estridentista y analizaste un poema perteneciente a esta corriente literaria, observa el siguiente vídeo sobre los movimientos literarios, no olvides anotar la información que consideres más relevante o aquella que es nueva para ti.
Generación del 27
Bloque 1. Secuencia 3
En el video se mencionan tres movimientos literarios, y eso te ayuda a entender de qué se habla cuando se refieren a los movimientos literarios.
Pero, ¿qué es un movimiento literario? Recupera la información sobre las características de los tres movimientos mencionados en el video.
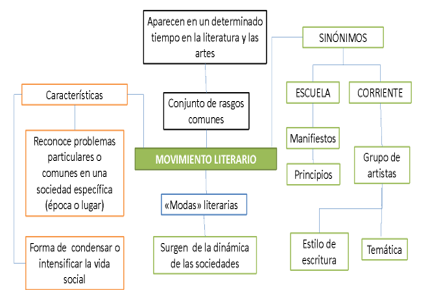
Un movimiento literario es un conjunto de rasgos comunes que aparecen en las artes y en la literatura en un tiempo determinado.
Otros nombres con los que se puede identificar a un movimiento literario son "Escuela" o "Corriente" literaria. Sin embargo, existe una sutil diferencia entre una y otra. Se llama "escuela literaria" cuando existen principios o reglas que la definen y que están plasmados por escrito en textos denominados "manifiestos" como en el caso del estridentismo.
Cuando no existen estas reglas o principios, pero hay un grupo de artistas que comparten ciertos rasgos en sus obras como la temática o el estilo de escritura, se habla de una "corriente literaria".
Puedes comparar los movimientos literarios con la moda. Los objetos de moda responden a iniciativas comerciales o mercantiles dónde se promueve que la mayoría de la gente quiera tener esos objetos para que "todos" estén en sintonía. Pero los movimientos literarios suceden al revés, pues surgen de la sintonía que se da en la mayoría de las personas en una sociedad determinada de acuerdo con la cultura vigente en esa época.
Los movimientos artísticos surgen de la sociedad, de lo que está viviendo y pensando, de tal manera que los temas de la poesía y el arte surgen de las preocupaciones de la sociedad. Por eso el entrevistado que aparece en el video identifica como principales características de un movimiento literario, primero, que éste reconoce los problemas comunes en una sociedad de un tiempo y lugar determinados, y segundo, que es una forma de condensar o intensificar el estilo de vida de esa sociedad.
Entonces un movimiento literario se refiere a la relación que se establece entre grupos de artistas, en este caso escritores, que se identifican porque comparten características comunes. Además, surgen en determinadas épocas, por lo que sus obras se relacionan con los cambios sociales, políticos y religiosos de la época.
Las características principales son que comparten una temática, es decir, abordan problemas particulares o generales que afectan a la sociedad y la forma de crear sus obras.
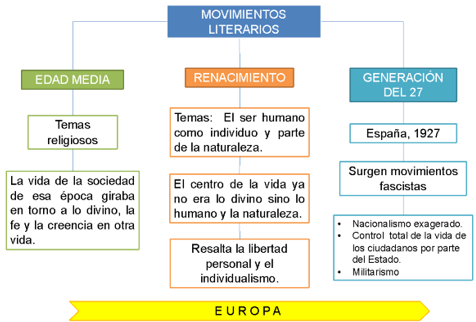
En la época medieval, la poesía abordaba temas principalmente religiosos, porque en esa época el centro del conocimiento y de la vida de las personas era lo divino, pues creían en la existencia de un ser supremo que debían conocer en una vida después de la muerte, y vivían preparándose para ese momento.
En el Renacimiento, esta visión cambia y ahora el centro del conocimiento es el ser humano y su relación con el mundo que lo rodea, por eso, los temas que aborda el movimiento renacentista tienen que ver con los sentimientos y emociones humanas, y con la forma en que hombres y mujeres vivían en esa época. Tanto el Medioevo como el Renacimiento surgen y se desarrollan en Europa.
Más recientemente, puedes mencionar como ejemplo de movimiento literario a la Generación de 1927. Este movimiento se da en España en el año de 1927, con motivo del homenaje a Luis de Góngora, un poeta que vivió en el siglo XVII y formó parte muy importante de lo que se conoce como el Siglo de Oro español, porque se considera que en esta época se produjo poesía y literatura de gran calidad.
La conmemoración de tres siglos del fallecimiento de Luis de Góngora en 1927 propició una revolución en la poesía española y por eso a quienes participaron de esta reflexión profunda en torno a la poesía española, se les conoce como Generación del 27.
La generación del 27 es una corriente literaria que se da a la par de los movimientos fascistas. Estos movimientos se caracterizaron por promover, por un lado, un nacionalismo exagerado y, por el otro, el militarismo. En esa época el gobierno pretendía ejercer un control total sobre la vida de sus ciudadanos.
Los escritores pertenecientes a esta corriente literaria criticaban y estaban en contra de los movimientos fascistas, por lo que la mayoría de ellos fueron encarcelados. Es decir, que la poesía, lo que sucede en el mundo y en la sociedad están muy unidos.
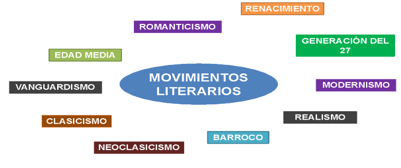
A lo largo de la historia de la literatura y de las sociedades, han existido distintas escuelas y corrientes literarias. En el caso de la lengua española podrías ordenar cronológicamente las escuelas y corrientes de la siguiente manera: la Antigüedad clásica, el Medioevo, el Renacimiento, el Barroco, el Neoclasicismo, el Romanticismo, el Realismo, el modernismo, el vanguardismo y generación del 27.
Para cada sociedad las corrientes podrán ser distintas, o tendrán un matiz especial, de acuerdo con lo que esté pasando en ese momento.
Ya has aprendido cuáles son las características de un movimiento literario; también, has conocido cuatro ejemplos de corrientes literarias (la edad media o medioevo, el renacimiento, el vanguardismo (al cual pertenece el estridentismo) y la generación del 27.
Para reforzar lo que has aprendido, trata de identificar las características de un movimiento literario a partir de un poema.
En este caso, retoma el poema que leíste al inicio, se llamaba Alarma. Recupera algunas de las características del estridentismo.

Podrías empezar diciendo que habla de las banderas negras de las fábricas y la ira roja de las calderas.
Mientras se habla de las corrientes y los movimientos, se piensa que algunos tienen los mismos nombres que etapas de la historia. El medioevo o el renacimiento, por ejemplo, son etapas que se estudian también en historia, y eso hace que no sean desconocidos por completo, porque coinciden con etapas históricas que has estudiado en las clases de historia universal.
Esto se debe a que la literatura refleja los movimientos sociales que han modificado y modificarán la historia del mundo.
El Reto de Hoy:
Para finalizar te retamos a que investigues las características de los otros movimientos que se mencionan, y que las anotes en tu cuaderno como una tabla comparativa o un organizador gráfico.
También, te retamos a que busques un poema que llame tu atención, y a que primero que nada lo leas y lo disfrutes, y después, con calma, identifiques el movimiento literario al que pertenece.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Aplicación de los criterios de semejanza de triángulos
Aprendizaje esperado: Resuelve problemas de congruencia y semejanza que implican utilizar estas propiedades en triángulos o en cualquier figura.
Énfasis: Aplicar los criterios de semejanza de triángulos.
¿Qué vamos a aprender?
Resuelve problemas de congruencia y semejanza que implican utilizar estas propiedades en triángulos o en cualquier figura.
Anteriormente aprendiste sobre congruencia y semejanza de figuras, especialmente de triángulos y cuadriláteros, pero… ¿dónde puedes utilizarlos en tu día a día?
Conocerás uno de los tres criterios de congruencia de triángulos, el que se conoce como Ángulo-Ángulo haciendo un énfasis en la relación de proporcionalidad de sus lados.
Comenzarás con un repaso del tema proporcionalidad, que te brindará información importante antes de entrar al contenido central.
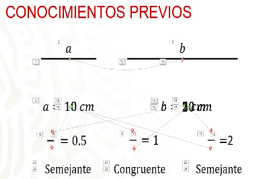
Consideras un segmento de recta al cual denominarás segmento “a” y tiene una longitud de 10 centímetros, y de él mismo, desprendes otro segmento al cual llamarás segmento “b”, y que al copiar del segmento “a” como consecuencia mide también 10 cm de longitud, ambos segmentos son congruentes entre sí ya que tienen la misma forma y tamaño. Comprueba esto matemáticamente hablando: si obtienes el cociente de la medida de ambos segmentos, es decir, 10 centímetros que mide el segmento “a” entre los 10 centímetros que mide el segmento “b” obtienes como cociente el número 1.
Con esto puedes determinar que el segmento “a” es congruente con el segmento “b”, ya que el cociente obtenido de la división de sus medidas te da como resultado 1. Ahora, si aumentas el tamaño del segmento “b” al doble, es decir, en lugar de medir 10 centímetros ahora mide 20 y si realizas el mismo proceso para obtener el cociente encontrarás que 20 entre 10 nos da como resultado 2, es decir que el segmento “a” es el doble del segmento “b” y, por lo tanto, son proporcionales entre sí, ya que tienen las mismas características, pero la medida de uno es el doble de la medida del otro porque el cociente obtenido es mayor a 1.
Ahora al segmento “b” lo reduces hasta llegar a 5 centímetros y realizas la misma operación matemática, encontrarás que 5 entre 10 nos da como resultado 0.5, es decir que el segmento “b” es la mitad del segmento “a” porque el valor obtenido es menor a uno, es decir el segmento resultante es más pequeño.
Estos valores que encuentras al dividir las medidas de los segmentos es el factor constante de proporcionalidad o razón de proporcionalidad.
Cuando el valor del factor de proporcionalidad da como resultado uno, nos indica que ambas líneas son congruentes, es decir que tienen las mismas características y la misma medida, pero si el valor es mayor te indica que las líneas son semejantes ya que tienen las mismas características, pero una es mayor que la otra, si el resultado del coeficiente de proporcionalidad es menor a uno, te indica que la línea comparada es más chica por lo tanto también son semejantes, ya que conservan la misma figura.
Te sugerimos anotar la idea principal de este repaso, ya que con esta información te será más fácil comprender la semejanza en figuras más complejas.

Puedes observar los valores de proporcionalidad obtenidos y podrás comprobar que: cuando el factor constante de proporcionalidad es igual a uno las medidas obtenidas son congruentes, ya que tienen el mismo tamaño. Pero cuando el factor de proporcionalidad es mayor a uno, debes comprender que la figura con la cual se comparó es mayor que la figura original, es decir, es más grande, por lo tanto, son semejantes.
Al contrario, si el factor de proporcionalidad disminuye la figura comparada es más pequeña que la original. Por lo tanto, también es semejante.
La idea es que hayas recordado el concepto de proporcionalidad y hayas anotado la idea principal.
Continúa ahora con figuras un poco más complejas: “Los triángulos”.
Como sabes, cada triángulo está formado por 3 segmentos de líneas rectas, los cuales, al cruzarse entre sí, forman diferentes ángulos, en este caso se refiere específicamente a los ángulos internos, los cuales son un dato más para que puedas comparar los triángulos entre ellos y puedas deducir si son congruentes, semejantes o de plano no se parecen en nada.
Tienes un triángulo al cual denominarás “ABC”, recuerda la nomenclatura para denominar un triángulo.
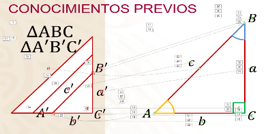
Así nombrarás a sus vértices “A”, “B” y “C”, además nombrarás también los segmentos que lo conforman con letras minúsculas para que las puedas distinguir segmento “a”, “b” y “c”.
Además, tienes también los 3 ángulos internos que forman parte de él, de amarillo tenemos el ángulo que se encuentra en el vértice A.
El ángulo formado por el vértice “B” y el ángulo formado por el vértice “C”. ¿Qué pasaría si copias este triángulo y además lo haces más pequeño?.
¿Cómo podrías comparar ambos triángulos? Primero, deberías buscar los vértices correspondientes, por ejemplo, el vértice “A” correspondería ahora con el vértice “A” prima.
Le colocas una comilla y le denominamos “prima”, ya que es el correspondiente con el vértice “A” del triángulo original, esto es una forma de que los identifiques para no confundirte.
Busca ahora el vértice correspondiente a “B”, de esta forma ya tienes dos vértices identificados, lo llamarás “B” prima, por lo tanto, solo queda el vértice “C”.
Ahora tienes un triángulo más pequeño que el original al que denominarás triángulo “A’B’C‘“. Ya has encontrado los 3 vértices, ahora debes encontrar los lados correspondientes entre ambos triángulos.
El lado “a“ lo denominarás ahora “a“ prima siguiendo el mismo procedimiento que hiciste con los vértices. El lado “b” con “b’” prima. Y el lado “c” con “c” prima.
Para finalizar, observa que los ángulos del triángulo “ABC” también tienen su ángulo correspondiente en el triángulo “A’B’C’”, observa el primero:
El ángulo formado en el vértice A corresponde con el ángulo formado en el vértice “A” prima y el ángulo del vértice “B“ con el vértice en “B“ prima y por supuesto el ángulo en el vértice “C“ y “C“ prima.
Con estos datos puedes comparar dos triángulos y descubrir si son congruentes, semejantes o de plano no tienen que ver uno con otro.
¿Qué hacemos?
Se enfatiza en los ángulos que los conforman, ya que ellos y la medida proporcional de los lados correspondientes te ayudarán a resolver algunos problemas de la vida diaria, como el que verás a continuación:
Lee el siguiente relato:
Cuando yo era adolescente era un poco inquieto, me gustaba correr y jugar, pero sobre todo probar cosas nuevas, así que un buen día en la casa encontré un bote de pintura en spray (bote de pintura), misma que mi papá había comprado para poder pintar el marco de una ventana, al tomarlo tuve la idea de pintar algo, pero dentro de la casa no encontré nada que se acomodara a mis gustos, quería que fuera algo grande y espectacular, así que salí al patio trasero… y al abrir la puerta… ¡Estaba ahí!, una gran barda pintada de color rojo que me invitaba a utilizar la pintura, no lo dudé y con calma destapé la pintura, la agité y la coloque en dirección a la barda ¡no lo pensé! y escribí una palabra que delataba al autor de los hechos: Jerry, como me decían mis amigos, lo disfruté tanto que lo remarqué hasta que se hicieron más grandes y negras las letras.
En la tarde cuando mi papá regresó de la fábrica donde laboraba recibió una gran sorpresa al asomarse al patio trasero y ver mi nombre pintado en la pared, se molestó tanto que levantó la voz para que yo acudiera a su encuentro, lo primero que me preguntó es que si yo había realizado tal acto de vandalismo en la pared, y al estar de pie frente a esa enorme pared roja y ver mi nombre pintado en ella no pude decir que no, mi padre muy molesto no me dijo nada, solo se metió a la casa y yo me quedé de frente a la pared viendo mi nombre con un gran remordimiento.
Más tarde fui a ver a mi padre y le pedí una disculpa, él me explicó que todos cometemos errores, lo importante era reconocerlos y después tratar de enmendarlos, por lo que decidí pintar la barda con mis propios métodos.
Como buen adolescente no tenía dinero para comprar la pintura que necesitaba para pintar la pared, así que antes que otra cosa me dirigí a la tienda de pinturas y le pregunté al encargado cuánta pintura requería para pintar una barda grande, este me preguntó: ¿Cuántos metros cuadrados mide la barda?

Yo le respondí que era muy alta y larga, sonrió y me dijo: “Ve a donde está la barda, mides el alto y el largo, lo que obtengas lo multiplicas para obtener el área, de esa forma sabes cuantos metros cuadrados de pintura necesitas”, y me mostró un bote de pintura y me dijo: “Esta es la pintura más barata que tengo y un litro te sirve para pintar 10 metros cuadrados, el litro te cuesta 80 pesos.
Regresé corriendo a la casa tratar de medir la barda. El largo lo medí exactamente 12 metros, pero el tratar de medir el alto fue imposible, ya que estaba realmente alta y en la casa no teníamos escalera, fui con mis vecinos y nadie me pudo prestar una, así que fui a recostarme en mi casa a tratar de pensar cómo medir el alto de la barda.

A la mañana siguiente, me asomé a la ventana de mi cuarto, que tiene vista al patio trasero, y observé con curiosidad que el sol brillaba fuertemente sobre la barda y que esta proyectaba una sombra sobre el patio,
Recordé entonces que la maestra de Matemáticas alguna vez nos puso problemas de sombras proyectadas en el piso o algo así, me fui corriendo a buscar mis cuadernos de tercero de secundaria y en los apuntes encontré unos ejercicios que nos puso en donde se podían obtener medidas de lugares inaccesibles solo con la luz del sol.

Traté de recordar lo que nos había explicado al ir leyendo los apuntes, pero no encontraba cómo lo había hecho, entonces recordé un problema que tenía un edificio y un poste que reflejaban la luz del sol en el piso y con esos datos podían obtener la altura del edificio sin tener que subirse ni arriesgarse a lastimarse en el intento.
La sombra que proyectaba la barda mediante los rayos del sol, la barda en sí y el suelo; formaban un triángulo, por lo que decidí poner en práctica lo que me había enseñado mi maestra, con mucha emoción fui a ver cómo estaba conformado el triángulo de forma física, llevé un metro para medir las distancias: 9.3 metros era la medida de la sombra del muro sobre el piso, pero algo me faltaba, no podía medir solo el lado de la sombra, algo más faltaba…
¡Algo más me faltaba!, ¡Contra qué lo compararía! Así que busque algo que pudiera mover y ponerlo como el poste del ejemplo del problema de la maestra, busque y busqué hasta que encontré un palo de escoba a la cual le retiré el cepillo, con gran disposición me lo llevé hacia la barda y descubrí que el sol ya había subido más por lo que la medida de la sombra ya no era la misma, me recordé: “El tiempo y el movimiento del planeta siguen su curso, lo tienes que hacer rápido, así que medí primero el palo de la escoba y encontré que exactamente tenía un metro y 19 centímetros, es decir 1.19 metros, pero algo me falta, regresé a mi cuaderno y vi que para que los triángulos fueran semejantes y poder calcular la medida de la barda los ángulos comprendidos entre el lado que es proporcional deben medir lo mismo.
Al medir el ángulo formado por la base del muro el suelo descubrí que medía exactamente 90°, por lo tanto, era un ángulo recto, así que el palo de la escoba debería formar un ángulo congruente con el formado por la pared y el suelo, así que desplacé el palo hacia la sombra que se formaba por la luz del sol sobre la pared haciendo que limitara exactamente con la coronilla superior y trate de formar un ángulo recto entre el palo de escoba y el suelo, como era demasiado trabajo tuve que pedir apoyo a mi hermano para que él lo sostuviera mientras yo tomaba las medidas necesarias.
Sólo me faltaba un ángulo más este ángulo era común a los dos triángulos que ya había formado. ¿Cuáles triángulos? El formado por la barda, el suelo y la sombra del sol y el formado por el palo de escoba, el suelo y la sombra del sol, procedí entonces a medir la base del triángulo mayor y me dio como resultado 8.41 metros después medí la base del triángulo menor y obtuve como resultado 1.75 metros. De esta forma ya había conseguido todas las medidas necesarias, ¿Qué me faltaba?
Realiza los cálculos: Sólo recuerda que el alto del palo de escoba era de 1.19 metros
Es importante obtener la proporcionalidad de los lados correspondientes de cada triángulo, en este caso de sus bases, entonces obtén el cociente de ellos, y divide 8.41 entre 1.75 y obtienes como resultado 4.8, que es el factor constante de proporcionalidad entre los lados correspondientes de ambos triángulos.
Como la altura del muro es el valor que desconoces, lo marcarás como una “x” para poder realizar las operaciones, así que tomas esta incógnita y la divides entre el valor del lado correspondiente del triángulo que es de 1.19 metros.
Y lo igualas a la constante de proporcionalidad que habías encontrado previamente, es decir 4.8. Ahora despejarás la incógnita, en este caso “x” para poder encontrar su valor, como la incógnita está dividiendo a 1.19 y deberás utilizar la operación contraria para poder despejar la “x”, lo que te lleva a multiplicar el segundo miembro de la ecuación por 1.19 y obtienes como resultado 5.71 que es en realidad la altura del muro que estás buscando.
Solo hace falta calcular la cantidad de pintura que va a necesitar y con ello calcular el costo de la travesura.
Si el largo de la barda era de 12 metros y su altura de 5.71, sólo debía multiplicar el largo de la barda por el alto, lo que da como resultado 68.52, pero como se está multiplicando metros por metros, la unidad resultante es metros cuadrados.
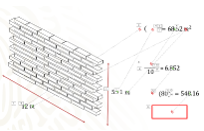
Ahora ya sabes que debe pintar 68.52 metros cuadrados, el vendedor de pinturas le dijo que un litro alcanzaba para 10 metros cuadrados, por lo que se divide 68.52 metros cuadrados entre 10 metros cuadrados que le indicaron para obtener cuántos botes de pintura requiere y ahora sabes que requiere 6.852 botes de pintura.
Pero cada bote cuesta 80 pesos, por lo que se requiere multiplicar para obtener el costo total de la pintura para poder pintar la pared que rayó. Requiere exactamente 548.16 pesos para comprar la pintura. El resultado final del problema es 548.16.
Pero como sabrás, no venden una fracción del bote, entonces se debe comprar completo, por lo tanto, son 7 botes de pintura a 80 pesos, me da en total 560 pesos sólo para la pintura, y eso sin contar el demás material como las brochas.
Todo esto porque no pensó antes de hacer las cosas y rayó una pared que no era suya.
Ahora un resumen de las cosas que realizó para tener claro que fue lo que se utilizó en cada caso.
Para poder medir distancias inaccesibles (como la del muro del problema) puedes utilizar la semejanza de triángulos, estos triángulos deben cumplir con ciertas características para que sean semejantes, en este caso se utilizó el criterio de semejanza ángulo-ángulo, es decir que los ángulos adyacentes a un lado proporcional sean iguales, aunque no es el único criterio ya que existen dos más.

Para eso compara dos triángulos que se obtienen del problema que se planteó, pero, debe quedar claro por qué los dos triángulos son semejantes, de esta forma podrías comprender mejor el corolario que indica que “si dos pares de ángulos correspondientes de dos triángulos son iguales, entonces los triángulos son semejantes”, para eso elimina algunas partes de la imagen que observaste con anterioridad y encontrarás que tienes dos triángulos, los cuales vas a separar para que los puedas contemplar mejor.
Para que puedas identificarlos bien, utilizarás lenguaje matemático, y nombrarás cada vértice de cada triángulo con literales, por ejemplo, del triángulo más grande empezarás por el primer vértice y le pondrás A.
Al segundo vértice le pondrás B y al tercero le pondrás C.
De tal forma que tienes el triángulo ABC y se escribe en lenguaje matemático como triángulo ABC.
De la misma forma, ahora al triángulo más pequeño lo nombrarás según los vértices que corresponden en el triángulo mayor, el vértice A correspondería con el vértice A’ en el triángulo menor. De la misma forma el vértice B con el B’ y por supuesto el vértice C con el C’. Por lo que el triángulo resultante se denominará triángulo A’B’C’.
La idea es demostrar que ambos triángulos son semejantes, lo que se representa matemáticamente con la tilde invertida, pero por ahora la eliminarás hasta comprobar que realmente son semejantes ambos triángulos.
Lo primero que harás es usar un transportador para medir el ángulo en B y observa que mide exactamente 90°. Mide ahora el ángulo correspondiente en B, es decir B’ y observa que también mide 90°, por lo tanto, el ángulo en B es igual al ángulo en B’.
Ahora mide el ángulo en C, coloca tu transportador y mide exactamente 34.17°.
Con el mismo transportador mide ahora el ángulo en C’ y observa que mide 34.17°, por lo tanto, los dos ángulos son iguales.
Ya comparaste dos ángulos correspondientes de cada triángulo y observaste que miden lo mismo, pero falta el tercer ángulo, es decir, el que se encuentra en el vértice A y en A’ pero ya no lo medirás, ahora utilizarás un teorema que ya es conocido, y es aquel que dice: “La suma de los ángulos interiores de un triángulo es igual a 180°”.
Si sumas el ángulo en A más el ángulo en B + el ángulo en C debe dar en total 180°.
Ahora reemplaza el valor del ángulo en B por el que ya tenías que es 90° y el del ángulo en C por 34.17°. Suma los valores y obtienes 124.17°. Despeja el ángulo en “A” restándole a ambos miembros de la ecuación 124.17 y obtienes como resultado la medida del ángulo en A el cual tiene un valor de 55.83°, en el caso del triángulo A’B’C’ los valores de los ángulos son los mismos, por lo que el valor del ángulo en A’ es igual al valor del ángulo en A. Por lo tanto, matemáticamente has encontrado que en ambos triángulos los ángulos correspondientes miden lo mismo, por lo que deduces que son semejantes.
Probablemente pensaste que la geometría es difícil, sin embargo, está presente en el día a día, todos utilizamos algo que se llama razonamiento deductivo, el cual permite inferir respuestas desde observaciones comunes, así como cuando ves que el cielo se nubla, podrías pensar que hay una probabilidad que llueva, de la misma manera a lo largo de la humanidad diferentes pensadores y filósofos han ido acrecentando el conocimiento matemático. Realiza la siguiente lectura, es de tu libro de matemáticas de segundo grado para que conozcas un ejemplo:
“Eratóstenes fue un matemático, astrónomo, geógrafo y poeta griego. Fue llamado a Egipto, en el año 236 a. C., para que se hiciera cargo de la biblioteca de Alejandría, donde aprendió que Siena (hoy Asuán, en Egipto) está situada prácticamente sobre el trópico de Cáncer, y por esto, el día del solsticio de verano, a mediodía, los objetos no proyectan sombra.
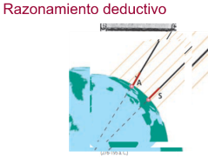
En Alejandría, en el solsticio de verano, Eratóstenes enterró una vara en el suelo y notó que, a pesar de ser mediodía, esta proyectaba sombra. Determinó, mediante un instrumento parecido al reloj solar, que el ángulo que se formaba entre la vara y los rayos del sol era de un cincuentavo de trescientos sesenta grados. Pensó que como el Sol se encuentra tan alejado de la Tierra sus rayos podían suponerse paralelos entre sí.”
“Eratóstenes mandó medir la distancia entre Siena (representado por una “S” y Alejandría (representada por una “A”), pero es probable que ya conociera ese dato. La distancia que utilizó para sus cálculos fue de 5 000 estadios. Esta distancia es la longitud del arco de circunferencia comprendido entre A y S.
Conociendo la medida del ángulo ACS y la longitud del arco AS, Eratóstenes pudo calcular la longitud de la circunferencia terrestre”
Sólo con la deducción matemática Eratóstenes pudo medir la distancia de la circunferencia de la tierra apoyado en la observación de fenómenos naturales que existían a su alrededor, en este caso de los rayos del sol, como lo hiciste en esta lección.
Te sugerimos que seas más observador con lo que ocurre a tu alrededor, analízalo y observa hasta dónde te conduce, te maravillarás de lo que puedes descubrir.
Para finalizar anota en tu cuaderno el criterio de semejanza de triángulos que trabajaste, lo conoces como el criterio ángulo-ángulo; en donde encuentras que: “Si dos pares de ángulos correspondientes de dos triángulos son iguales, entonces los triángulos son semejantes”. Si recuerdas este corolario te podrás ahorrar muchos cálculos en un futuro.

El Reto de Hoy:
Te recomendamos buscar en tu libro de texto de Matemáticas de tercer grado, problemas de semejanza de triángulos que utilicen el criterio ángulo-ángulo, los podrás encontrar en el Bloque I.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

¿Cuáles son los beneficios de separar mezclas en tu vida diaria?
Aprendizaje esperado: Deduce métodos de separación de mezclas con base en las propiedades físicas de sus componentes.
Énfasis: Deducir métodos de separación de mezclas y su aplicación en diferentes ámbitos.
¿Qué vamos aprender?
El propósito es deducir métodos de separación de mezclas y su aplicación en diferentes actividades humanas.
Con base en estos conocimientos, vas a proponer procedimientos de separación de mezclas en una situación de la vida cotidiana.
Antes de comenzar lee la cita de una frase de Marie Curie:

En tu cuaderno registra todas las dudas e inquietudes que surjan durante la sesión, así como las actividades y experimentos propuestos. Durante el desarrollo de las actividades experimentales ocuparás materiales de laboratorio y mencionarás sus nombres y el uso que tienen.
Para las actividades experimentales que realizarás en casa, ocuparás materiales de uso casero.
Si ya cuentas con tu libro de texto, puedes consultarlo para retroalimentar y saber más acerca de los métodos de separación de mezclas en tu vida cotidiana.
¿Sabías que en tu casa cuentas con un laboratorio?
A pesar de que estás en casa resguardado, no es un impedimento para entender la química, ya que cuentas con tu propio laboratorio y el lugar donde se encuentra es la cocina.
Si le solicitas a un adulto que te muestre todo lo que tiene, te darás cuenta que hay una gran variedad de sustancias, semillas, diferentes líquidos, especies o hierbas.
Puedes preparar, con mucho cuidado para evitar los accidentes, diversas mezclas en recipientes y observar sus propiedades, de manera similar a como se trabaja en un laboratorio.
Realizarás actividades experimentales sencillas, con la finalidad de que puedas deducir qué métodos de separación vas a emplear con base en las propiedades de los componentes de una mezcla.
Es interesante e inquietante reflexionar y analizar, cómo contribuyen los métodos de separación en diferentes actividades de la vida diaria.
Reflexiona acerca del tema y responde:
- ¿Cómo impacta un derrame de petróleo en el mar?
- ¿Cuál es el tratamiento que se realiza a las aguas residuales?
- ¿Cómo separarías una mezcla de alcohol y agua?
- ¿De qué manera puedes identificar los componentes de una mezcla?
En tu vida diaria has mezclado sustancias para analizar fenómenos, ahora harás lo contrario, separar los componentes de las mezclas.
Define algunos métodos de separación de mezclas.
Filtración
Este método se utiliza comúnmente en tu vida cotidiana, en donde separas dos componentes, un sólido de un líquido, utilizando un medio poroso para dicha separación de mezclas.
Debido a que en cada tipo de suspensión el tamaño del sólido es distinto, se fabrican materiales con diferentes tamaños de poro, en casa puedes tener coladeras de varios tipos, hay papel filtro con aberturas microscópicas de diversas medidas.
Si te encontraras en la escuela los pasos serían los siguientes: en un vaso de precipitado colocas 20 g de tierra, ahora agregas 70 ml de agua, acabas de formar una mezcla; en el embudo coloca un pedazo de papel filtro e introdúcelo al matraz Erlenmeyer, entonces toma la mezcla y deposítala sobre el papel filtro que tiene el embudo, observa que empieza la separación, el sólido se queda en el papel filtro y el agua comienza a caer en forma de goteo en el matraz Erlenmeyer.
Este método se utiliza en la preparación de la bebida de café, también en la preparación de agua de guayaba sin semillas, ¿en dónde más ocupas este método?
Destilación
Este método se basa en las diferencias de la temperatura de ebullición de los componentes de la mezcla, es decir, cuando los líquidos empiezan a hervir.
En este vaso de precipitado tengo 100 ml de agua y en este otro vaso 100 ml de alcohol, ambos se mezclan, y ahora ¿De qué manera los separarías?
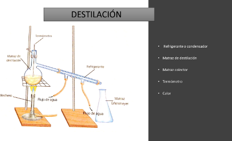
Ambos son líquidos e incoloros, no los puedes distinguir a simple vista, el punto de ebullición del alcohol etílico es de 78.4°C, y el del agua a nivel del mar es de 100°C, entonces para poder separar la mezcla se emplea lo siguiente:
Este método requiere de cierto equipo, si estuvieras en la escuela, el cual utiliza un refrigerante que hará que el vapor se enfríe y se condense, es necesario llevar la lectura de la temperatura de la mezcla con un termómetro de laboratorio, como el alcohol tiene una temperatura de ebullición menor a la del agua, será el primero en separarse de la mezcla, lo hará en forma de vapor por el refrigerante posteriormente se condensará, el alcohol saldrá del refrigerante y se recibirá en otro recipiente.
Este procedimiento es muy común en la industria y se usa en la refinación del petróleo, para obtener alcoholes, aceites, ácido láctico, bebidas alcohólicas como licores, aguardientes, cerveza, y sidra, por mencionar algunas.
Cromatografía
Es una palabra que proviene del griego croma/color y grafos/escribir –escritura a color– que técnicamente significa la separación física de compuestos coloridos como colorantes o pigmentos de un extracto o mezcla orgánica. ¿Te gustaría separar una mezcla por colores?
En la siguiente actividad experimental necesitarás un gis que es un medio poroso, la tinta de un plumón que es la mezcla, 20ml de agua en un vaso de precipitado que servirá como disolvente. Se marca el contorno del gis con el plumón, el gis se introduce, de tal manera que quede la marca en la parte inferior, pero sin que se sumerja en el agua.
Mientras el gis absorbe el agua, en otro recipiente que contiene 20 ml de alcohol se coloca un pedazo de papel filtro de 10 x 10 cm, le dibujas con el plumón un círculo de 2 cm de diámetro aproximadamente, con una tira de papel filtro de 2 cm de ancho por 5 cm que se coloca en medio del primer papel filtro, ahora lo introduces en donde tienes el alcohol que funciona como disolvente.
¿Qué te imaginas que ocurra en ambos casos? Identifica lo que está ocurriendo en el papel filtro.
Observa como los diferentes componentes que tiene la tinta, que es la mezcla, se separan. El método que estás utilizando es cromatografía en papel, que se basa en la absorción selectiva de distintos componentes de una mezcla.
Como puedes darte cuenta, la movilidad de los componentes depende de la afinidad química.
Examinemos nuevamente el gis, observa qué le ha ocurrido durante este tiempo.
¿Esperabas que ocurriera esto?
Este método se ocupa para detectar y cuantificar sacarina, benzoatos, cafeína, para determinar la cantidad de vitamina D en la leche en polvo y los cereales.
También se usa para caracterizar los aceites esenciales y los aromas empleados en saborizantes, aromatizantes, licores, perfumes, artículos de aseo y productos farmacéuticos.
En química, específicamente, en la forense se emplea para determinar y cuantificar el alcohol en la sangre. También para detectar trazas de drogas en la supervisión de terminales de aeropuertos como cocaína, anfetaminas o heroína.
¿Cómo separar una mezcla de arroz con sal?
Un panadero para preparar su masa necesita cernir la harina para separar los grumos. En otra situación, un albañil que desea un aplanado fino de una pared, debe tamizar o cribar la arena para quitar piedras grandes y de este modo obtener una arena más fina.
Si te es posible, en un recipiente deposita una mezcla de 20g de arroz con 30g de sal de mesa, ambos son sólidos, su tamaño es diferente, entonces para realizar la separación de esta mezcla necesitamos un colador como el que tienes en casa y otro recipiente que recibirá lo que logre pasar por los orificios de la malla del colador, la sal por ser de menor tamaño pasa por los agujeros del colador, en cambio el arroz queda retenido por su mayor tamaño.
Este procedimiento se conoce como tamizaje o cribado, es un método mecánico mediante el cual se separan partículas sólidas de diferentes tamaños, para ello se ocupa una malla llamada criba o tamiz, ésta permite pasar las sustancias que son más pequeñas que sus agujeros y retiene a las que son más grandes.
El uso del método del tamizaje se emplea en la elaboración de filtros de agua, en la minería para separación de rocas, separación de basura de aguas residuales, por mencionar algunos.
Comenta con un familiar dónde has empleado este método de separación.
¿Sabes cómo se obtiene la sal de mesa? Igual que muchas sustancias que hay en el laboratorio, está formada por pequeños cristales.
Este proceso consiste en la separación de dos o más sustancias, aprovechando su capacidad para formar cristales, por ejemplo, para separar una mezcla de agua y sal, se calienta el agua, conforme esta se evapora y disminuye su volumen, la concentración de la sal de la disolución, aumenta hasta que se forman cristales.
Para la obtención, se extrae del agua de mar de grandes extensiones de terreno que se inunda de ella, por la acción de los rayos del sol evaporan el agua y se forman los cristales de sal.
Este proceso también se emplea en la industria farmacéutica para obtener cristales de las sustancias activas que tienen un efecto curativo.
En algunas minas se han encontrado ciertos minerales que tardaron miles de años en cristalizar y forman estructuras impresionantes.

Esta explicación será de gran ayuda para desarrollar el proyecto del bloque.
¿Cómo separas los desechos metálicos?

Los automóviles cuando son desechados se trituran y por medio de un imán potente se extraen los materiales metálicos que pueden ser reciclados.
Si te es posible, haz una mezcla de fragmentos de cobre y hierro, ambos son metales, imagina que estás en un lugar donde llegan todos los desechos metálicos y para empezar a separar los metales empleas un imán.
¿Serán atraídos los metales? Acerca el imán, observa cómo es atraído el hierro mientras que el cobre no, debido a que este metal no es ferromagnético.
Si te es posible en una caja de Petri mezcla azúcar y limadura de hierro, mezcla bien y coloca la tapa, ¿cómo harías para separar los componentes de esta mezcla de sólidos?
Acerca el imán a la tapa de la caja Petri y examina cómo es atraída la limadura de hierro hacia el imán, con cuidado la retiras y la llevas a otro recipiente para recolectar la limadura de hierro.
Este método de separación de mezclas recibe el nombre de magnetización, consiste en atraer el metal ferromagnético por un imán.
Se utiliza en la industria metalúrgica, en algunos deshuesaderos y en lugares donde se separa la chatarra.

El siguiente método, la centrifugación, separa dos o más sustancias debido a las diferentes densidades, por medio de una centrífuga.
La fuerza centrífuga es una fuerza de inercia que aleja del eje de rotación a los cuerpos que giran respecto de este eje, los impulsa hacia afuera.
Este método tiene muchas aplicaciones industriales e incluso se emplea en lavadoras para centrifugar la ropa y quitar la mayor cantidad de agua posible.
También en el análisis de sangre, pues contiene suero con materiales disueltos y glóbulos rojos y blancos en suspensión, después de centrifugar en el fondo del tubo quedan glóbulos rojos que ocupan la mitad del volumen, sobre ellos queda una pequeña capa de glóbulos blancos y encima queda suero de color amarillo transparente, gracias a esta separación se puede analizar cada parte por separado.

El proceso de decantación se usa para separar dos sustancias aprovechando la diferencia de sus densidades. Si te es posible realiza una mezcla de arena en estado sólido y agua en estado líquido, para realizar la separación de la mezcla, la arena se hunde por acción de la gravedad hasta el fondo del recipiente que la contiene. Una vez separados en dos fases se vierte el agua en otro recipiente, separándolo de la arena.
En el hogar utilizas este método de manera muy cotidiana, cuando se sirven caldo y le quitan la grasa que está en la superficie o cuando preparan un rico espagueti, y separan la pasta del agua.

Ahora el embudo de separación, agrega 20 ml de agua y también 20 ml de aceite, estos líquidos no se disuelven entre sí debido a su diferencia de densidad. Para poder realizar la separación se abre la llave para dejar salir la fase más densa.
¿Qué hacemos?
Realizarás la siguiente actividad experimental en casa, recuerda que con la familia aprendes y refuerzas lo aprendido.
El propósito de esta actividad es diseñar en familia, y con materiales que tengan a la mano, un método de los que se abordaron en esta sesión para separar una mezcla.

Para llevar a cabo el desarrollo de la actividad experimental en familia y sea más divertido e interesante el intercambio de opiniones, pon a prueba un procedimiento de separación de mezclas con los materiales propuestos.
Aprovecha tu creatividad, conocimientos, ingenio y materiales que se te ocurra emplear.
Elabora un reporte de la actividad experimental en tu cuaderno, con ilustraciones de lo que hiciste. Plantea la conclusión con base en las evidencias.
Cuanto más diferentes son los materiales, más fácil resulta separarlos.
Al término de la actividad desecha lo que no pudiste separar, enjuaga y seca los materiales que ocupaste y colócalos en el lugar que corresponda.
Recuerda tener orden y limpieza en el espacio donde trabajaste, y de los utensilios.
Es momento de responder las preguntas que te plantearon al inicio:
- ¿Cuándo se derrama el petróleo en el mar que proceso ocupan para retirarlo?
- ¿Cuál es el tratamiento de las aguas residuales?
El método de decantación se emplea para el tratamiento de aguas residuales, para la potabilización del agua y para separar el petróleo del agua de mar.
Es muy impactante esta afectación a la naturaleza, pero el ser humano mediante un proceso de separación de mezclas ha intervenido para reducir el daño causado.
Ya cuentas con los conocimientos y métodos para separar diferentes mezclas en sus actividades diarias.
El Reto de Hoy:
Elabora un breve texto de lo que aprendiste y cómo puedes aplicar estos saberes en la vida cotidiana.
Recuerda que en tu libro de texto puedes consultar el tema, para aclarar cualquier duda.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Atrévete a soñar. Tu proyecto de vida
Aprendizaje esperado: Valora sus aspiraciones, potencialidades y capacidades personales (para el estudio, el trabajo y la recreación) y se plantea estrategias para desarrollarlas.
Énfasis: Identificar aspiraciones personales y cómo se relacionan con el estudio, el trabajo y la recreación.
¿Qué vamos aprender?
El reconocimiento de las aspiraciones y potencialidades personales que debes considerar para planear su proyecto de vida.
Identificarás elementos que te ayuden a responder a las preguntas: ¿Quién soy? ¿De dónde vengo? y ¿A dónde voy? ¿Para qué sirve un proyecto de vida y de dónde surge?
La idea es que te acerques a dar los primeros pasos que te ayudarán a identificar los elementos que tienes que considerar para construir tu proyecto de vida.
Necesitarás tu cuaderno, bolígrafo, colores, una cartulina u hojas blancas y revistas, si es que tienes a la mano. Si no las tienes, no te preocupes, lo que tengas a la mano es suficiente. Lo importante es tu creatividad. Te recomendamos tomar notas de lo que te parezca más relevante.
En ocasiones, vas por la vida sin pensar hacia dónde te diriges. Otras veces, sientes que no tienes aspiraciones en la vida o que no eres bueno para algo. Que estás perdido en el camino.
En ocasiones, vives el presente sin que te importe el futuro, o piensas en un futuro muy fantasioso e imposible de realizar.
¿Qué hacemos?
Observa el siguiente video que plantea una mirada sobre las aspiraciones en la vida.
¿Recuerdas que en primer grado en la materia de Geografía aprendiste el tema Índice de desarrollo humano? Recuérdalo con el siguiente video:
Sigue estudiando sigue tus sueños
Es muy importante tener un proyecto de vida
Es probable que hayas pensado acerca de lo que harás saliendo de la secundaria; por ejemplo, si seguirás estudiando o comenzarás a trabajar, o tal vez ambas cosas. La cuestión es, ¿qué deberás hacer para lograr lo que te propongas de ahora en adelante? ¿Cómo hacer, qué cosa?
La etapa que estás viviendo es muy importante porque tendrás que tomar decisiones que trazarán el camino de tu vida y van a influir en el desarrollo de sus potencialidades. Por ello, es crucial que, como un primer paso, reflexiones sobre cuáles son tus aspiraciones.
Posiblemente te has preguntado, cómo puedes diseñar tu plan de vida, y por dónde comenzar. Pero antes de que des una respuesta, qué te parece si primero retomas la siguiente frase que dice la estudiante en el video:
“Es fácil, si sabes lo que quieres.” Esto quiere decir que, para comenzar a diseñar un plan de vida, ¿es necesario “saber lo que se quiere”? ¿Qué significa esto?
En el Programa de televisión de Aprende en Casa entrevistarán a una especialista a la que le harán muchas preguntas como las siguientes:
- Pero, ¿qué pasa cuando una persona no sabe lo que quiere? ¿Qué debe de hacer en este caso?
- Entonces, como parte de ese primer paso para construir un futuro, es necesario conocerse así mismo. Por ejemplo, puedes preguntarte: ¿Quién soy y dónde estoy?
- ¿Qué necesitarían hacer las y los jóvenes para adentrarse en el camino del autoconocimiento?
Esto es importante, porque esto da pauta para saber qué quieres en un futuro próximo o distante, y evita que te pierdas, o que no tengas claro qué hacer.
Por ejemplo, en la imagen observas dos casos extremos con respecto a la mirada hacia el futuro: hay personas que no pueden pensar en el futuro porque no creen en ellas mismas y hay otras que proyectan un futuro inalcanzable.
Seguramente tienes diversas aspiraciones; sin embargo, es importante que tengas en cuenta tus capacidades.
Y continúan las preguntas a la especialista:
- ¿Puede comentar qué son las capacidades? y ¿qué tipo de capacidades es preciso que contemple en sí mismo una o un adolescente?
Entonces, quiere decir que las capacidades pueden aprovecharse para que las aspiraciones se concreten en algo real.
Ahora bien, para realizar un ejercicio de proyección, algunos aspectos comunes que se te recomiendan definir son: misión, visión, metas y sueños.
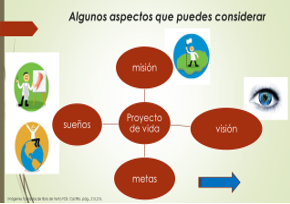
- ¿Cuáles de estos aspectos son cruciales en la adolescencia? ¿Por dónde tendrías que iniciar las y los jóvenes para hacer una proyección?
Se podría decir que los sueños, son el equivalente a las aspiraciones. Por ejemplo, se puede decir que uno de mis sueños es conocer diferentes países, incluso trabajar y vivir en otro país.
- Podría decirse que esto es una aspiración. ¿Es así, doctora?
- ¿Podríamos decir, entonces, que los sueños, son el equivalente a las aspiraciones?
Escribe en tu cuaderno, tres aspiraciones que tengas, para ello, usa frases cortas.
- Doctora ¿nos puede compartir dos ejemplos de aspiraciones?
Tú que estás en casa, ¿qué anotaste?
No te preocupes si consideras que son sueños o ideas que en este momento no son tangibles. Tus aspiraciones pueden llegar a convertirse en metas, hasta concretarlas en logros personales; lo importante es comenzar a visualizarlas.
- Doctora, ¿considera usted que podemos tener distintas aspiraciones? Es decir, ¿estas aspiraciones corresponden a distintos ámbitos de nuestra vida? ¿Van cambiando con el tiempo?
Por ejemplo, una aspiración relacionada con el trabajo. La especialista hizo referencia a aspiraciones relacionadas con la educación o la recreación según sea al caso.
Entonces, para que identifiques con qué ámbito se relacionan las aspiraciones que anotaste, te propongo que escribas delante de cada oración, “educación”, “trabajo”, “recreación”, según corresponda.
Es posible que las tres aspiraciones que hayas anotado tengan que ver con un sólo ámbito.
Si fuera el caso, escribe una aspiración relacionada con los otros ámbitos.
Qué te parece si presentas tu información en un organizador gráfico.
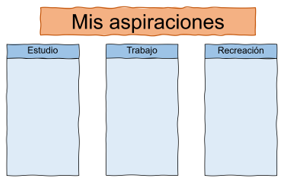
Este es un ejemplo de cómo podrías hacerlo, pero tú puedes hacer uso de tu creatividad para generar diseños distintos.
Te recomendamos que, en otro momento, vuelvas a leer lo que escribiste y modifiques lo que consideres necesario o redacta de manera que sean más precisas tus aspiraciones.
- ¿Puede dar alguna sugerencia más al respecto, doctora?
Finalmente, una vez que ya tienes claro cómo te ves ahora, qué capacidades y habilidades tienes, y, por otro lado, cuál es el ideal de tí mismo, es decir, cómo quieres verte en un futuro, ¿qué estrategias podrías plantearte para desarrollar esas capacidades?
Haz de tu vida un sueño, y de tu sueño una realidad, dice El Principito.
- ¿Qué tan importante es la automotivación y de qué forma los estudiantes pueden cultivarla?
El Reto de Hoy:
Para terminar, te sugerimos la siguiente actividad:
En una cartulina o el material que tengas a la mano, realiza un “collage”. Se trata de hacer una composición artística de manera libre.
Usa recortes de revistas o periódicos, pedazos de tela, dibujos, fotografías, pedazos de papel. Busca representar un mapa del momento en que estás y el camino para llegar a ese lugar a donde quieres llegar.
Para realizar la composición, te sugerimos tener en cuenta las siguientes preguntas.
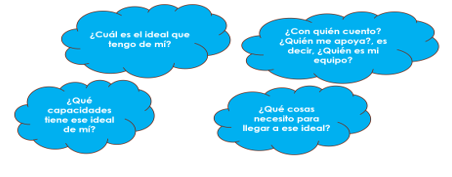
- ¿Cuál es el ideal que tienes de ti?
- ¿Qué habilidades y capacidades tiene ese ideal de mí mismo?
- ¿Con quién cuento?, ¿quién me apoya?, es decir, ¿quién es mi equipo?
- ¿Qué cosas necesito para llegar a ese ideal?
Es recomendable que te tomes el tiempo para realizar el ejercicio y que una vez terminado, lo cuelgues en algún lugar visible.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Las innovaciones y la organización técnica
Aprendizaje esperado: Identifica las características de un proceso de innovación a lo largo de la historia como parte del cambio técnico.
Énfasis: Analizar los cambios técnicos y de organización en su manipulación a partir de una innovación técnica.
¿Qué vamos aprender?
¿Recuerdas en qué aspectos es necesario basarse para hacer un análisis sistémico?
Es necesario revisar:
- los intereses.
- las necesidades.
- los ideales.
- y los valores que favorecen a la innovación
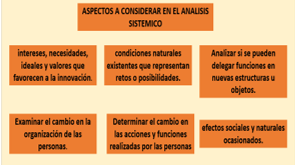
Valorar las condiciones naturales existentes que representan retos o posibilidades. Examinar el cambio en la organización de las personas que intervienen en los procesos técnicos.
Determinar el cambio en las acciones y funciones realizadas por las personas, así como los efectos sociales y naturales ocasionados. Y, analizar si se pueden delegar funciones en nuevas estructuras u objetos.
¿Qué hacemos?
Para profundizar en ello y ponerlo en práctica, observa el siguiente video:
De mediados del siglo XIX a principios del XX. Panorama del periodo.
Plataforma Aprende 2.0
Cómo pudiste observar, la vida cambia a través de un continuo desarrollo tecnológico, y a la inversa, el cambio social demanda innovaciones, y a la vez, estas innovaciones generan cambio social.
Este periodo de la industrialización se caracteriza por las nuevas fuentes de energía.
Si el vapor había constituido la principal fuente de energía durante la primera revolución industrial, durante la segunda se desarrolló el petróleo y este funcionó como combustible para motor de combustión interna.
Y la industria automotriz alcanza la madurez con Henry Ford en el primer tercio del siglo XX.
Después otra fuente de energía fue la electricidad, y su consecuencia fue la creación de la bombilla eléctrica para la iluminación.
Otra consecuencia de la revolución industrial fue la aparición de nuevos sectores de la producción como la industria textil, la siderúrgica, la química, e industrias alimentarias, entre otras.
Puedes darte cuenta del impacto que tuvo en los cambios técnicos que se dieron entre el siglo diecinueve y el siglo veinte.
Con el uso de las tecnologías cambia la forma de organización de las personas.
Aquí entra la organización técnica de los trabajos fabriles, en donde a diferencia de los procesos artesanales en donde por lo regular, todo el proceso es elaborado por una persona, en los trabajos fabriles intervienen varias, cada una se dedica a un proceso y, por lo regular, desconocen el siguiente paso; podría decirse que es aquí en donde inicia la especialización del trabajo.
Te preguntarás: ¿Qué es la especialización del trabajo?
Este concepto fue desarrollándose con la aparición de las labores artesanales, y la industrialización y la creación de modelos productivos en masa.
Adam Smith definió que la división del trabajo por medio de la aparición de profesionales más habilidosos conllevaba el alcance de mayores niveles de eficiencia y ahorro de recursos.
En esta parte es en donde se ve el sistema persona máquina.
¿Qué es el Sistema Persona máquina?
Sistema en el que las funciones de un operador humano (o grupo de operadores) y de una máquina están integradas como una sola entidad, controlada por el operador (o grupo de operadores), que interacciona con el entorno.
Cómo el ser humano interactúa con las máquinas. Observa el siguiente video para profundizar en el tema.
- La tecnología ¿Al alcance de todos?
Plataforma Aprende 2.0
No olvides registrar en tu cuaderno todas tus dudas, inquietudes y hallazgos, para después compartirlo con tu familia y amistades.
Con las innovaciones tecnológicas tu forma de vivir se modifica: adquieres estilos diferentes de acuerdo a los contextos en donde te encuentras, las actividades que realizas se vuelven más fáciles de hacer, se hacen en menos tiempo; sin embargo, las consecuencias a la naturaleza no son del todo favorables.
Debes ser responsable de lo que produces, consumes y desechas.
En pocas décadas se han modificado los hábitos de consumo, de producción, de información y comunicación.
La transformación que se produce con las innovaciones tecnológicas y que van surgiendo en tu vida diaria es sorprendente.
En el video te diste cuenta de cómo las sociedades con un acceso más restringido a las tecnologías, resuelven sus necesidades de diferente manera, a veces más compleja.
Uno de los ejemplos es el transporte: para ellos trasladarse de un punto a otro resulta más complicado y lento.
La comunicación se vuelve muy ineficiente, pues los mensajes tardan días o más en llegar a sus destinatarios, y la sociedad no está comunicada de las últimas noticias o temas relevantes.
Para reflexionar observa el siguiente video:
- ATRAPADOS EN LA TECNOLOGÍA
Plataforma Aprende 2.0
https://www.aprende.edu.mx/recursos-educativos-digitales/recursos/atrapados-tecnologia-1635.html
Aprovechando esta amplia información acerca de los cambios en los medios de comunicación, te sugerimos realices un análisis sistémico de la innovación del teléfono.
El primer aspecto a considerar son los intereses, necesidades, ideales y valores que favorecieron la innovación del teléfono.
Desde que Graham Bell realizara con éxito su primera prueba del teléfono, hoy en día ha resuelto la necesidad de comunicarse de manera eficiente con los demás, acortando distancias.
Lo anterior permitió que a medida que la sociedad tenía otras necesidades, el diseño y nuevos materiales fueron, y siguen innovando de forma paralela al teléfono.
El segundo aspecto a considerar son las condiciones naturales que representaron retos o posibilidades.
La creación del teléfono favoreció el desarrollo comercial y dio inicio a varias compañías para hacer llegar el teléfono a más usuarios, sin embargo; uno de los retos que tuvieron que enfrentar estas empresas y, que aún hoy se tienen algunas complicaciones, es llevar el teléfono a los poblados de difícil acceso por sus condiciones geográficas.
El tercer aspecto a considerar es la delegación de funciones en nuevas estructuras u objetos.
El teléfono simplifica nuestra vida, su objetivo es darnos bienestar y comodidad; no discrimina edad ni intereses, prácticamente se ha convertido en una extensión de nuestro cuerpo y ha permitido satisfacer nuestras necesidades como:
Jugar.
Entretenerse.
Informarse.
Comunicarse a través de mensajes, ya sea escritos o por audio.
El cuarto aspecto es el cambio en la organización de las personas.
Las organizaciones han cambiado, pues a medida que el teléfono fue innovando, permitió que la sociedad estuviera comunicada en tiempo real y con mayor facilidad, como lo observaste en el video; antes hasta fila había que hacer para ocupar los teléfonos públicos, y de cierta manera, la comunicación se retrasaba.
Además, tenías que invertir más tiempo y dinero para hacerlo. Hoy lo podemos hacer más rápido y a un menor costo, pues la gran mayoría de las personas tienen su propio teléfono, con la posibilidad de enviar mensajes de texto o el uso de otras aplicaciones de manera efectiva.
El quinto aspecto son las acciones y funciones realizadas por las personas.
Con el desarrollo del teléfono, el Internet y varias aplicaciones, hoy este aparato se vuelve indispensable para todos, ya que es nuestra principal forma de comunicarnos, a pesar de que el teléfono de casa lo usemos en mucha menor proporción que el móvil.
El último aspecto por considerar son los efectos sociales y naturales ocasionados. Es posible que en este aspecto encuentres algunos aspectos negativos. Quizá no sea útil generalizar, pero a veces parece que el uso del teléfono y el internet resulta excesivo. Esto, a la larga, podría modificar y entorpecer las formas en que te relacionas con las demás personas. Sin embargo, no se puede negar los múltiples y variados beneficios que estas tecnologías nos brindan.
Esto ha traído un impacto social y una nueva experiencia, ya que la tecnología invade la convivencia. Así que reflexiona en familia. Recuerda, todo en exceso es malo.
Y hablando de los impactos naturales, el equipo celular, al desecharlo de una forma inadecuada, genera a la atmosfera grandes emisiones contaminantes, por lo que es recomendable prolongar su vida útil.
Cuida tu teléfono y así cuidarás el medio ambiente.
El Reto de Hoy:
Ten presente que las innovaciones tecnológicas son aquellos aparatos de nuestra vida diaria que han cambiado con el tiempo para satisfacer de mejor manera tus necesidades.
Te sugerimos que con ayuda de tu familia realicen un análisis sistémico de la computadora, tal como lo hicimos con el teléfono.
Recuerda analizar todos sus aspectos:
- Antecedentes.
- Efectos en la organización del trabajo.
- Contexto natural, social y económico.
- Necesidades que satisfacen.
- Innovaciones que tú crees presentarán en el futuro.
¡Buen trabajo!
Gracias por tu esfuerzo.
Aprende en casa II 2DO Y 3RO DE SECUNDARIA 29 DE SEPTIEMBRE









Publicar un Comentario