Aprende en Casa 2 SEP: 29 de septiembre TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 29 de septiembre de clases virtuales mediante el programa Aprende en Casa 2, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa 2, compartimos los temas y actividades que se abordaron este Martes 29 de septiembre, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa 2:
https://aprendeencasa.sep.gob.mx/#

Relaciones de proporcionalidad y reparto proporcional
Aprendizaje esperado: Resuelve problemas de proporcionalidad directa e inversa y de reparto proporcional.
Énfasis: Identificar las diferencias entre una variación de proporcionalidad directa con las de constante aditiva y resolver problemas de reparto proporcional.
¿Qué vamos a aprender?
Comprenderás la diferencia entre una variación de proporcionalidad directa con las de constante aditiva y otro tipo de variación. Además, resolverás problemas de reparto proporcional.
¿Qué hacemos?
En la sesión anterior conociste las características de una relación de proporcionalidad directa, usando tablas de datos y la expresión algebraica correspondiente para resolver problemas.
Ahora, realiza lo siguiente. Reflexiona y responde:
¿Cómo puedes identificar si la relación entre dos variables representa una relación de proporcionalidad directa?
¿Qué piensas qué es un reparto proporcional?
Para dar respuesta a las preguntas anteriores. Inicia con el siguiente problema.

¿Qué se tiene que hacer para responder las preguntas anteriores?
¿Qué tipo de relación se establece entre los datos del problema?
¿Sabes cuánto pagarían en cada una de las opciones?
Para analizar que opción les conviene más, por el número de días de renta de un automóvil, los amigos decidieron realizar el siguiente registro, que muestra el costo por día de la renta de un automóvil, para ambas opciones.

Registra en tu cuaderno las diferencias que identificaste en la relación que se establece entre la cantidad de días de renta y el costo.
En la primera tabla, la relación que se establece entre los días de renta y el costo es una relación de proporcionalidad directa, cuya expresión general ya conoces

La tabla muestra la relación que se establece entre los días de renta y el costo del automóvil.
La expresión general, permite calcular el costo de la renta para x número de días.
y = 520x,
donde:
“x” representa el tiempo en días de renta.
“y” corresponde al costo total de la renta del automóvil.
“520” es la constante de proporcionalidad

Entonces, para conocer la cantidad que se paga por día de renta, se multiplica 520 por el número de días, en este caso, se quiere conocer lo que se paga por cinco días de renta, entonces, se multiplica 520 por 5.
En este problema, se observa que la constante es multiplicativa, por lo que, 2 600 pesos se pagarían en la opción 1,
¿Qué sucede con la relación entre las variables de la segunda tabla?
La segunda tabla representa una relación de variación lineal, también tiene una constante multiplicativa, pero tiene una constante aditiva, cuya regla general es:
y = kx + b,
Donde a y b son constantes.

Observa nuevamente la segunda tabla para responder a la otra pregunta del problema.

La tabla muestra la relación que se establece entre los días de renta y el costo del automóvil.
A la relación que se da entre los datos mostrados en la tabla se le llama “relación lineal” de la forma y = kx + b, como se explicó antes.
Para este caso, la expresión general que permite calcular el costo de la renta para x número de días es:
y = 400x + 420
donde:
“x”, representa el tiempo en días de renta.
“y”, corresponde al costo total de la renta del automóvil.
400, es la constante multiplicativa, (que se obtiene al calcular la diferencia entre valores consecutivos de “y”, por ejemplo, 1 620 – 1 220 = 400).
420, es la constante aditiva (que se obtiene al restarle al costo por un día de renta la constante multiplicativa, es decir, 820 – 400 = 420).
Entonces, para responder la pregunta:
¿Cuánto pagarían por la renta de automóvil por 5 días?
Se sustituye x por el valor de 5 en la expresión general y se realizan las operaciones correspondientes. De este modo, se tiene que:
y = 400 (5) + 420
y = 2 000 + 420
y = 2 420
Así puedes saber que el costo sería de 2 420 pesos por los cinco días de renta.

Ahora, resuelve el siguiente problema.
Karla sabe que la actividad física le permite mantenerse con buena salud y que además le ayuda a mejorar su sistema inmunitario, lo cual aumenta sus defensas para prevenir que su cuerpo adquiera posibles infecciones.
Karla considera que hacer ejercicio y aprovechar el tiempo que pasa en casa es muy importante; por lo que todas las mañanas, utiliza una caminadora eléctrica para realizar su rutina de entrenamiento.
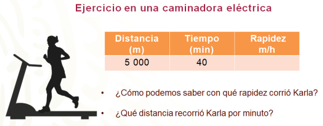
El día de hoy Karla recorrió sobre la banda de una caminadora, una distancia de 5 000 m, que es equivalente a 5 km, en 40 minutos.
¿Cómo puedes saber con qué rapidez (metros por hora) corrió Karla?
¿Qué distancia recorrió Karla por minuto?
Analiza la información con la que se cuenta.
En la relación distancia-tiempo del problema, considerando que la rapidez se mantiene constante:
¿Qué sucede con la distancia cuando aumenta el tiempo?
¿El problema representa una relación de proporcionalidad directa? ¿Por qué lo considerarías así?
La relación distancia-tiempo representa una relación de proporcionalidad directa cuando la rapidez es constante.
Para saber con qué rapidez corrió Karla, se pueden utilizar diferentes procedimientos. Para calcularlo, puedes usar una regla de tres simple o proporción:
Para resolver el problema, opera en kilómetros y minutos para facilitar los cálculos.
5000 m equivalen a 5 km y 1 hora es equivalente a 60 minutos.
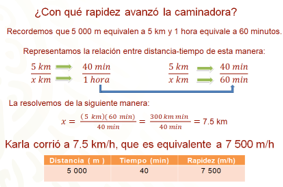
La relación entre distancia-tiempo se representa como se muestra en la imagen anterior; para encontrar el valor de equis, se multiplica cruzado y se divide entre el tercer valor, es decir, se multiplica 5 por 60 y se divide el resultado entre 40, 5 por 60 es igual a 300, y 300 entre 40 es igual a 7.5 km, es decir, a la misma rapidez. Karla hubiera recorrido 7.5 kilómetros en una hora.
Por lo tanto, Karla corrió sobre la banda de la caminadora a 7.5 km por hora, es decir, a 7 500 m por hora.
Para responder la segunda pregunta:
¿Qué distancia recorrió Karla, por minuto?
Karla corrió de manera constante 5 000 m en 40 minutos.
¿Cómo se puede saber la distancia que recorrió en un minuto?
Se divide la distancia que recorrió entre el tiempo, es decir, 5 000 entre 40 cuyo resultado es igual a 125.
De esta manera se conoce que Karla recorrió 125 m en un minuto; 250 m en 2 minutos y así sucesivamente.
La relación distancia-tiempo representa una relación de proporcionalidad directa cuando la rapidez es constante, entonces, el valor anterior, corresponde a la constante de proporcionalidad.
Ya que, a partir de este valor se puede saber la distancia que recorrió en x número de minutos, considerando que la rapidez se mantiene constante.
¿Cuál es la expresión algebraica que representa está relación?
La expresión algebraica de la relación distancia-tiempo, con la rapidez constante, en este caso es: y = 125x. Donde “x” representa el tiempo en minutos, “y” la distancia en metros, y, 125 la constante de proporcionalidad.
Ahora, reflexiona en la siguiente pregunta:
Si Karla recorre los mismos 5 000 m pero modifica la rapidez de la caminadora, ¿qué pasará con el tiempo del recorrido?
Ejercicio 1.
Imagina que Karla quiere saber cuánto tiempo tardará en correr los mismos 5 000 m o 5 km, si cambia la rapidez de la caminadora, como se muestra enseguida. Toma nota de la información e intenta completar los datos faltantes.

Considera los casos que aparecen en la imagen y resuélvelos.
El caso 1 muestra que la caminadora se mueve a 10 000 m/h; en el caso 2 lo hace a 6 000 m/h y en el caso 3, a 12 000 m/h.
Como puedes ver, la distancia es constante; la magnitud que varía es la rapidez, y lo que se quiere conocer es el tiempo en que Karla recorrería 5 000 m en cada caso.
Después de haber resuelto los casos, contesta las siguientes preguntas:
¿Qué sucederá con el tiempo cuando se incremente la rapidez?
¿Cómo puedes calcular el tiempo en cada caso?
¿Qué sucedió con el tiempo cuando la rapidez de la caminadora aumentó?
¿Y qué pasa con el tiempo del recorrido cuando la rapidez de la caminadora disminuye?
Al aumentar la rapidez, el tiempo no aumentó en la misma proporción, al contrario: disminuyó. Es decir, entre mayor rapidez, menor el tiempo del recorrido. Por esta razón, la relación rapidez-tiempo no representa una relación de proporcionalidad directa.
Ya se analizaron un par de relaciones entre dos variables que no corresponden a una relación de proporcionalidad directa.
A continuación, presta atención en el siguiente planteamiento.
Hilda hace galletas para vender. Una de las recetas que utiliza es la que aparece en la imagen.
La receta muestra que, para preparar 12 galletas, necesita:
El día de hoy Hilda recibió un pedido especial y tiene que hacer 180 galletas.
¿Qué cantidad de cada ingrediente se necesita para elaborar todas las galletas?
¿Qué tiene que hacer Hilda para calcular las cantidades?
Para calcular los ingredientes para las 180 galletas, se puede utilizar el valor unitario, de cada ingrediente. Es decir, la cantidad que se necesita de cada ingrediente para hacer una galleta y multiplicarla por 180. No obstante, este procedimiento no es conveniente porque no tiene sentido pensar en un sexto de huevo.
También, se podrían calcular los valores de la receta por medio de razones equivalentes, como en la siguiente imagen.
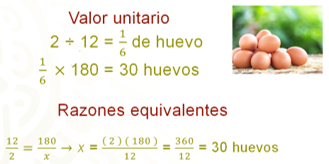
Aunque este procedimiento es correcto, resultaría largo y poco práctico, porque se repiten las operaciones con cada ingrediente.
¿Habrá un procedimiento que pueda ser más eficiente?
¿Cuál sería?
Analiza y resuelve mediante el siguiente procedimiento. Recuerda tomar nota del procedimiento y anotar las cantidades finales en tu cuaderno.

Ahora, sabes que para obtener la cantidad que necesita Hilda de cada ingrediente, basta con multiplicar las cantidades de la receta original por 15.
¿Pensaste en otra forma de resolver el problema?
Si fue así, anótalo en tu cuaderno y resuelve el problema.
Observa y verifica los resultados.
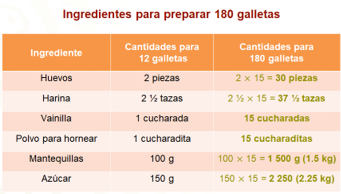
Al multiplicar por 15 cada ingrediente, se obtienen las cantidades que aparecen en la tabla.
Para 180 galletas se necesita:
30 piezas de huevo, 37 ½ tazas de harina, 15 cucharadas de vainilla, 15 cucharaditas de polvo para hornear, 1.5 kg de mantequilla y 2.25 kg de azúcar.
Ya conoces la cantidad de cada ingrediente que necesita Hilda para hacer las 180 galletas.
Ahora analiza la siguiente situación relacionada con la venta de galletas de Hilda.
Si Hilda quiere guardar las 180 galletas en paquetes con 20 piezas, ¿cuántos paquetes puede hacer?
¿Qué operación permite obtener la respuesta?

Realiza las operaciones necesarias y completa la tabla de datos.
A continuación, presta atención en otra situación relacionada con la venta de galletas de Hilda.

La situación se puede representar por medio de una tabla de datos y asignar literales a los valores que se deben encontrar. Se llamará “x” a las galletas que le corresponden a Edson, “y” a las que le corresponden a Carlo, y, “z” a las de Santiago.
Existen diferentes procedimientos para resolver este tipo de problemas, además de la regla de tres, se puede utilizar el cálculo de porcentajes.
Observa cómo se resuelve una situación de reparto proporcional con ambos procedimientos.
Se representa la situación por medio de razones equivalentes y se resuelve cada razón por separado, con el procedimiento que ya conoces de la regla de tres.
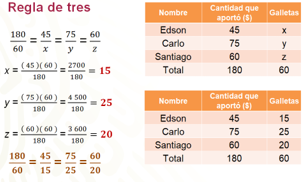
A Edson le tocan 15 galletas, a Carlo 25 galletas y a Santiago, 20 galletas.
El reparto fue de manera proporcional respecto al dinero que cada uno aportó; ya que las razones obtenidas son equivalentes.
Ahora, resuelve el mismo problema, pero esta vez por medio del cálculo de porcentajes.

Se calcula qué porcentaje de 180 pesos representa lo que aportó cada amigo y se multiplica por el total de galletas. Para obtener el porcentaje como número decimal, se divide 180 entre lo que cada uno aportó. Recuerda que la representación decimal de un porcentaje, por ejemplo 0.25, equivale a 25/100, que corresponde a veinticinco de cada 100, es decir, 25%.
Ahora, presta atención en un tercer procedimiento para este mismo caso. Que es mediante el cálculo del precio de cada galleta, es decir, mediante el valor unitario.
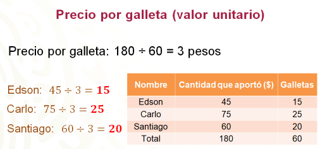
Para calcular el valor unitario o precio de cada galleta, se divide 180 entre 60. Ya que tienes el costo por galleta, se divide lo que cada uno aportó entre el precio por galleta, es decir, entre 3 pesos. Así se obtienen las galletas que le corresponden a cada uno.
En esta sesión, resolviste problemas de proporcionalidad directa, analizaste e identificaste situaciones que no corresponden a una relación de proporcionalidad directa y, finalmente, resolviste un problema de reparto proporcional, mediante distintos procedimientos.
El Reto de Hoy:
Reflexiona y responde las siguientes preguntas:
¿Cuál de los procedimientos te pareció el más eficiente?
¿En qué situación, de tu vida diaria, piensas que podrías realizar un reparto de manera proporcional?
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

¿Cuáles son los desafíos para ejercer las libertades fundamentales en mi país?
Aprendizaje esperado: Argumenta sobre la vigencia de las libertades fundamentales como garantías de todo ciudadano y reconoce sus desafíos.
Énfasis: Analizar los desafíos para el ejercicio de las libertades fundamentales en México.
¿Qué vamos a aprender?
Examinarás en cuáles son los desafíos que dificultan el ejercicio de las libertades fundamentales en el país. Lo anterior, con la finalidad de que reflexiones acerca de ellos y de qué podrías hacer para ejercerlas a pesar de esas circunstancias que las limitan.
Emplearás el pensamiento crítico, es decir, analizarás un problema o situación y comprenderás sus efectos, para luego pensar en opciones o alternativas.
¿Qué hacemos?
Inicia con la siguiente reflexión:
Seguramente has leído o escuchado acerca de las diversas situaciones o problemas que hay en el país. Puede que algunas de esas situaciones sean cercanas a ti o sepas de ellas; por ejemplo, la pobreza, la violencia, las actividades ilícitas como la trata de personas o el narcotráfico, la marginación, la discriminación, la desigualdad social o ciertas costumbres que atentan contra la dignidad de las personas, entre otras.
Es probable, que en la localidad o municipio donde se desenvuelven no existan esas situaciones, pero hay lugares del país donde los adolescentes se enfrentan a una o varias, de forma cotidiana, y se convierten en un obstáculo para el ejercicio de las libertades fundamentales.
Por tal razón, es necesario que los identifiques y reflexiones en torno a ello, para que, a lo largo de tu formación académica y como parte de tu participación ciudadana, propongan ideas y emprendan acciones que permitan difundir la importancia del ejercicio de las libertades fundamentales en tu entorno y así evitar que problemas como los que se mencionaron afecten tu ejercicio.
La reflexión anterior permite comprender lo importante que es analizar los desafíos que existen para el ejercicio de las libertades.
Las libertades fundamentales están reconocidas y garantizadas en la Carta Magna del país y en diversas leyes, por ejemplo, en la Ley General de Niñas, Niños y Adolescentes.
A continuación, realiza la siguiente actividad.
Anota tus respuestas o ideas sobre las siguientes preguntas:
¿Qué son las libertades fundamentales?
¿Por qué se les llama libertades fundamentales?
Puedes plasmarlas también en un organizador gráfico, como un cuadro sinóptico o un mapa mental o elaborar un collage. Se tan creativos como quieras.
Se llaman libertades fundamentales porque están reconocidas y garantizadas en el marco jurídico de los países, es decir, en las leyes. Esas libertades fundamentales se sustentan en la dignidad humana.
En nuestro país, la Constitución Política de los Estados Mexicanos, y varias leyes más, promueven y garantizan las libertades fundamentales; sin embargo, depende de todas las personas propiciar las condiciones para ejercerlas a plenitud.
Al hablar de libertades fundamentales, se hace referencia a las distintas expresiones de la libertad, que permiten a las personas manifestar su forma de pensar y desenvolverse, así como participar en la vida social, política y económica del país.
Libertades fundamentales.
La libertad de pensamiento, conciencia y religión se refiere a que las personas son libres de tener sus propias ideas o convicciones, así como participar de manera pública o privada en actos de culto, conforme a sus creencias.
La libertad de expresión faculta a las personas a manifestar sus ideas y difundir opiniones e información, a través de diferentes medios.
La libertad de asociación es el derecho de vincularse y reunirse pacíficamente para defender sus intereses o bien para participar en asuntos públicos.
La libertad de tránsito es el derecho a desplazarse libremente por el país.
Para que éstas sean respetadas, además de saber cuáles son, es importante reconocer que existen desafíos que pueden llegar a impedir el ejercicio de dichas libertades.
A continuación, observa el siguiente video en relación con algunos de los desafíos que existen en ciertos países. Reflexiona si en el país prevalecen las limitantes que se mencionan o si existen otras. Anota en tu cuaderno los desafíos que vayas identificando.
Desafíos de la libertad en la adolescencia.
En el video se mencionan casos donde el ejercicio de la libertad tiene restricciones porque así lo establecen las leyes o bien, por determinadas costumbres.
Algunos de los desafíos que se mencionan, fueron la falta de oportunidades, el embarazo temprano, el matrimonio a temprana edad o el trabajo infantil.

Por ejemplo, en las guerras, las personas enfrentan situaciones que les impiden incluso decidir sobre su propia existencia, como sucedió durante la Segunda Guerra Mundial, donde miles de personas fueron privadas de su libertad en los campos de concentración. Se trata de un desafío porque se deben tomar decisiones para superar los obstáculos, desde lo individual y lo colectivo.
En nuestro país, existen muchos desafíos que también afectan el ejercicio de las libertades.
¿Por qué se considera un desafío, por ejemplo, que a las mujeres no se les permita ir a la escuela en algunos países?
Se considera un desafío, porque es una situación que enfrentan las mujeres y las niñas para ejercer su derecho a la educación y las libertades que esto conlleva, como la libertad de pensamiento o la de expresión.
Los derechos y libertades al estar proclamadas en las leyes son inalienables y no se puede renunciar a ellas; pero, por desgracia muchas mujeres y niñas tienen que luchar o buscar las maneras de recibir educación, incluso de manera clandestina o a escondidas, para evitar ser castigadas.
Por lo tanto, las mujeres y las niñas deben enfrentar cotidianamente esa limitante, debido a la desigualdad de género que se refleja en políticas, costumbres o estereotipos que condicionan los derechos de las mujeres y las niñas, principalmente, promoviendo ideas que van en contra de su dignidad y que restringen sus libertades.
En México, por ejemplo, estaba arraigada la idea, e incluso aún persiste en diversas regiones del país, de que las mujeres no debían estudiar, ya que se consideraba que no era necesario para ellas, porque al casarse sería poco útil tener estudios, pues tendrían que dedicarse al cuidado del hogar y los hijos, mientras el esposo le aportaría lo necesario.
Esto también representa un desafío porque para las mujeres y las niñas de varios lugares de nuestro país, esa es una situación que les impide el acceso a la educación y ejercer a plenitud las libertades fundamentales, por lo tanto, muchas se esfuerzan por enfrentar esa limitante, ya sea migrando a otro lugar o cuestionando esas ideas, hasta tomar la decisión de estudiar sin el consentimiento o acuerdo de sus familiares. Ambos ejemplos hacen referencia a desafíos, porque representan un reto para las mujeres y niñas el poder ir a la escuela.
En el video anterior se habló de Malala, quien fue reconocida por sus acciones cuando era adolescente. Ella tuvo que decidir ir a la escuela a pesar de que en su país estaba prohibido, además generó un blog y se pronunció en favor de la educación para las niñas, lo que puso en riesgo su vida.
Las restricciones relacionadas con el acceso a la educación son uno de los grandes desafíos, porque limitan la libertad de pensamiento, por mencionar un ejemplo.
Sin embargo, en el video se mencionaron otros desafíos que afectan a la adolescencia en diversas partes del mundo, incluyendo México, tales como los matrimonios a temprana edad y los trabajos forzados.
Para facilitar que organices tus anotaciones respecto a los desafíos para ejercer las libertades fundamentales en México, en tu cuaderno, o en una hoja blanca, elabora un mapa mental como el siguiente o, si lo prefieres, puedes hacer un diagrama radial o un collage.
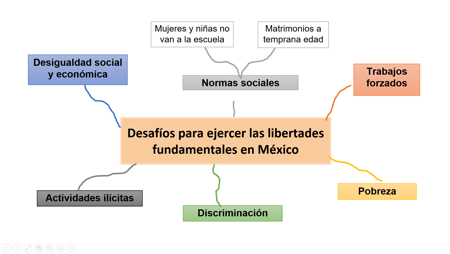
En el centro escribe el título de tu mapa mental: “Desafíos para ejercer las libertades en México”.
A partir de esa frase, traza algunas líneas con distintos colores. Pueden ser cinco o seis.
Al final de cada línea, anotarás los diferentes desafíos que prevalecen en México para ejercer las libertades fundamentales.
Por ejemplo, los desafíos que se han explicado hasta el momento.
Ahora, lee algunos textos sobre adolescentes dando su opinión en la sección Los jóvenes participan en línea.
Las opiniones de estos jóvenes muestran distintos desafíos a los que se están enfrentando diariamente. Ahora, responde las siguientes preguntas:
¿Ustedes qué opinan sobre lo que nos contaron?
¿Algunas de estas situaciones suceden en su día a día?
¿Qué otros desafíos consideran que existen en México, que limitan el ejercicio de las libertades fundamentales?
Cada uno de esos desafíos obstaculizan el ejercicio de las libertades fundamentales, por eso es necesario que las y los estudiantes los identifiquen y sepan de qué se tratan para tomar decisiones que les permitan afrontarlos, las libertades fundamentales están proclamadas en las leyes, pero hacerlas efectivas requiere de una cultura basada en el respeto al ejercicio de los derechos y las libertades.
Para complementar la información sobre uno de los desafíos que mencionó Tere, que está relacionado con normas sociales o incluso costumbres, en ciertas partes del país, lee el siguiente dato.
“En México, hasta el año 2019, muchas niñas y adolescentes eran obligadas a casarse con hombres mayores; a veces a cambio de dinero o bienes.”
Desafortunadamente, a pesar de que las leyes en nuestro país establecen que la edad mínima para contraer matrimonio es a los 18 años, esta situación sigue afectando, principalmente, a niñas y adolescentes, e incluso hay varones menores de edad que también son forzados a casarse. En ambos casos, esta situación limita el ejercicio de las libertades.
Además de los desafíos que comentaron los adolescentes, existen varios más, como la pobreza, la marginación, la desigualdad social y económica.
Por ejemplo, el Consejo Nacional de Evaluación de la Política de Desarrollo Social (CONEVAL), señala que…
“La pobreza es un fenómeno con diversas causas que comprende aspectos relacionados con las condiciones de vida que vulneran la dignidad de las personas, limitan sus derechos y las libertades fundamentales”.
Este fenómeno social, afecta a más de la mitad de la población en México y es un obstáculo para el ejercicio de las libertades, porque las personas no tienen las condiciones necesarias para cubrir sus necesidades básicas, tales como alimentación, salud, educación, empleos y otros.
En una situación de pobreza, las personas se ven obligadas a atender las carencias que enfrentan, por lo tanto, se ven limitados en el ejercicio de las libertades como la de expresión o asociación.
La pobreza también propicia que muchos niños y adolescentes tengan que trabajar, incluso exponiéndose a labores riesgosas o que implican largas jornadas, como sucede con quienes se emplean en las labores agrícolas.
Otro desafío, es la discriminación. En nuestro país, se discrimina a los grupos minoritarios como el caso de la población indígena o a las personas con alguna discapacidad.
La población indígena, ha sido segregada cuando se les discrimina por hablar su lengua, usar su vestimenta o bien por sus creencias.
Las personas con discapacidad han sido excluidas de diversos espacios, debido a que no se han promovido las condiciones necesarias para un trato igualitario, por ejemplo, la falta de infraestructura acorde a sus necesidades para desplazarse de un lugar a otro.
La proliferación de actividades ilícitas también constituye un desafío para el ejercicio de las libertades, ya que generan violencia e inseguridad.
Además, como lo comentó Emiliano, afectan la vida de las personas en sus comunidades. Una de esas actividades ilícitas es la trata de personas, que atenta contra niñas, niños, adolescentes y mujeres, quienes muchas veces son privados de sus derechos y libertades. Por otra parte, los grupos criminales reclutan a jóvenes, exponiéndolos, a ellos y a sus familias, a muchos riesgos e incluso la muerte.
Es indispensable estar informados e identificar los desafíos que se han mencionado, así como otros más, para tomar mejores decisiones y promover una cultura en favor del ejercicio de las libertades fundamentales.
Como se comentó al inicio, hay desafíos que se conocen de cerca y otros de los cuales probablemente leíste o te contaron; sin embargo, es necesario saber de qué se tratan, porque afectan a las personas más allá de tu comunidad.
Recapitulando, en esta sesión, se explicó que un desafío hace referencia a situaciones, obstáculos o limitantes que se presentan en la sociedad, en sus diferentes ámbitos.
También se mencionaron algunos de los desafíos a escala mundial, como la prohibición que tienen mujeres y niñas de asistir a las escuelas.
Analizaste algunas situaciones que obstaculizan el ejercicio de las libertades fundamentales en nuestro país, como determinadas normas sociales o leyes locales, la pobreza, la discriminación y las actividades ilícitas.
La finalidad es que tengas el conocimiento de esos desafíos y puedas informarte más. De ser posible, promover acciones en favor de una cultura que procure el respeto a los derechos y las libertades fundamentales.
El Reto de Hoy:
Dialoga con tus familiares acerca de otros desafíos que existen en el país para ejercer las libertades fundamentales y complementa tu mapa mental y tus anotaciones a partir de la información que se ha tratado en esta sesión y compártelo con tus familiares
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Siguiendo las leyes
Aprendizaje esperado: Identifica y describe la presencia de fuerzas en interacciones cotidianas (fricción, flotación, fuerzas en equilibrio).
Énfasis: Explicar movimientos en su entorno. Primera ley de Newton (inercia).
¿Qué vamos a aprender?
Comprenderás e identificarás la primera ley de Newton en cualquier caso, incluyendo situaciones de la vida cotidiana.
Seguramente has escuchado la palabra ley en algún momento de tu vida y no solo la has escuchado, también la has utilizado. Por ejemplo, cuando escuchas en las noticias que cambiaron algunas leyes o que alguien quebró alguna ley, o en los reglamentos de la escuela.
Ese en un claro ejemplo de que existen leyes que nos rigen, pero en la ciencia las leyes cubren otras características, por esa razón, en ciencia, una ley es una afirmación corroborada por hechos o experimentos y una de sus características es que se cumplirá en cualquier lugar o tiempo.
Entonces, en física, una ley debe estar comprobada con experimentos y el resultado siempre será el mismo.
¿Qué hacemos?
En esta sesión, profundizarás en las leyes del movimiento. Para ello, comenzarás recapitulando el tema de movimiento.
A los objetos en movimiento se les llama móviles. A los objetos que no se mueven, se les puede decir objetos en reposo, es decir, cuando los objetos tienen un cambio en su posición igual a cero, es decir no se mueven, se dice que se encuentran en estado de reposo.
Teniendo en cuenta estos conceptos de reposo, movimiento y ley, debes saber que las leyes del movimiento son tres:
- La primera ley de Newton, llamada también ley de inercia.
- La segunda ley de Newton, también llamada ley fundamental de la dinámica.
- La tercera ley de Newton, conocida como ley de acción y reacción.
Isaac Newton propuso estas leyes e inventó el dinamómetro, explicó el concepto de fuerza y gracias a sus leyes se le denominó a la unidad de medida de fuerza, el Newton abreviada con una N.
La inercia siempre está presente, en cualquier actividad que se realice. Una bicicleta, un auto o una pelota no se moverían si no es que se aplica una fuerza.
La inercia es una propiedad que tienen los objetos de permanecer en reposo o en movimiento con velocidad constante y en línea recta. La inercia depende de la cantidad de masa que tiene un objeto; por ejemplo, si un ferrocarril intenta detenerse abruptamente, tardará un tiempo en hacer alto total, comparado con algún objeto que tenga menor masa.
Todo comenzó con las ideas de Galileo y terminó con las aportaciones de Isaac Newton. Ellos fueron unos científicos muy reconocidos en su tiempo.
Para que comprendas por qué fueron tan importantes, lee su biografía, ya que los nombrarás frecuentemente en física.
Galileo Galilei.
Astrónomo, ingeniero, filósofo, matemático y físico italiano nacido en Pisa, Italia en 1564. Es reconocido por mejorar el telescopio y ser el primero en observar las manchas solares, los cráteres y montañas lunares, los satélites de Júpiter y los anillos de Saturno. Relacionó los fenómenos físicos con las matemáticas. Es considerado el padre de la ciencia moderna al considerar la experimentación como parte de la metodología científica.
Aunque se tiene registro de más aportaciones realizadas por Galileo, tal vez la más importante, fue que propuso que las cosas no podían explicarse solamente con la observación, sino que, necesitaban ser experimentadas y comprobadas, y eso dio pie a que los demás científicos comenzaran a comprobar con experimentos sus ideas y no sólo por la lógica. Por esa razón, se le considera como padre de la ciencia.
Isaac Newton.
Físico, teólogo, inventor, alquimista y matemático inglés nacido en 1643. Algunos de los aportes más importantes de este científico son:
- Las tres leyes del movimiento
- La ley de gravitación universal
- Desarrollo del cálculo matemático
- Adelantos en el mundo de la óptica, que incluyen el estudio de la descomposición de la luz blanca y la fabricación del primer telescopio reflector.
- La teoría corpuscular de la luz
- La teoría de mareas
Como puedes darte cuenta, Isaac Newton realizó grandes aportaciones al mundo de la física. Además de que la unidad de fuerza lleva su nombre: Newton.
En esta sesión, te enfocarás sólo en una de sus aportaciones: la primera ley de newton, también conocida como la “Ley de inercia”.
La Ley de inercia dice que: Todo cuerpo mantendrá su estado de reposo o movimiento rectilíneo uniforme, a menos que una fuerza externa actúe sobre él.
¿Qué quiere decir esto?
Si un objeto está en movimiento o en reposo, no podrá detenerse o moverse espontáneamente, necesita que una fuerza lo detenga o lo mueva. Recuerda que las fuerzas modifican el estado de movimiento de los objetos.
Por ejemplo, si se aplica una fuerza a un objeto que se encuentra en reposo, provocará un movimiento. Si el objeto se está moviendo y se le aplica una fuerza, se puede cambiar su dirección o frenarlo.
Debes tomar en cuenta que la fuerza siempre dependerá de la masa del objeto para poder ponerlo en movimiento o detenerlo, pero esto se verá con más detalles cuando profundices en la segunda ley.
Si está en tus posibilidades, realiza el siguiente experimento. Para que puedas comprobar la Ley de inercia.
Experimento 1.
Vas a necesitar los siguientes materiales:
- Un vaso o recipiente de plástico.
- Una tarjeta o un pedazo de cartón o cartulina.
- Una moneda.
- Un carrito.
- Una pelota.
Primero, coloca el frasco (vaso) en un estado de reposo, sobre él, la tarjeta, y sobre la tarjeta, la moneda.
Ahora, aplica una fuerza sobre la tarjeta y observa lo que pasa.
Todos los objetos que están en la mesa se encuentran en estado de reposo, pero al aplicar una fuerza a la tarjeta, ésta se mueve y la moneda cae al vaso. Recuerda que existe la aceleración de la gravedad que actuará sobre la moneda y por eso cae, pero si la gravedad no estuviera presente, la moneda se quedaría en el mismo lugar.
Experimento 2.
Fuerza que detiene algún objeto
Primero, toma el carrito y aplica una fuerza en éste para que avance, eventualmente la fuerza de fricción provoca que se detenga. La fuerza que apliqué y la fuerza de fricción son fuerzas externas.
La primera ley de Newton dice que todo cuerpo se mantendrá en un estado de reposo o movimiento rectilíneo uniforme, a menos que una fuerza externa lo cambie.
En el primer experimento, la fuerza externa que provocó el movimiento de la tarjeta fue tu mano.
Y en el segundo experimento, tu mano también fue la fuerza externa que provocó el cambio de reposo del carrito a movimiento, aunque al final, la fuerza de fricción del suelo provocó que se detuviera.
En conclusión, siempre son fuerzas externas las que provocan el cambio de movimiento a reposo o viceversa.
Esto pasa con todo lo que se mueve, por esa razón se considera una ley, pues no importa el objeto ni el lugar, tampoco el tiempo. Todo cuerpo mantendrá su estado de reposo o movimiento rectilíneo uniforme, a menos que una fuerza externa actué sobre él.
La primera ley de Newton también llamada Ley de inercia, es muy fácil comprenderla, aunque Newton debió de haber hecho muchos experimentos antes de llegar a esta conclusión, para poder proponerla como ley.
El Reto de Hoy:
Reto 1.
Realiza un mapa mental utilizando los conceptos principales, no olvides incluir ejemplos de la vida cotidiana, puedes incluir algunas ilustraciones.
Reto 2.
Reflexiona en la pregunta y realiza lo siguiente:
¿Has experimentado la primera ley de Newton llamada también Ley de inercia?
Piensa dónde podrías aplicar esta ley y utiliza esos ejemplos para completar tu mapa mental.
Recuerda que puedes utilizar tu libro de texto, y, si es posible consulta fuentes confiables de internet.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Otras voces para contar historias
Aprendizaje esperado: Selecciona, lee y comparte cuentos o novelas de la narrativa latinoamericana contemporánea.
Énfasis: Revisar voces y perspectivas en la narrativa latinoamericana.
¿Qué vamos a aprender?
Conocerás cómo contar historias, enfocándote en las diferentes voces y perspectivas existentes que puede tener una historia a partir del uso de un narrador con ciertas características. En esta sesión, leerás y compartirás nuevos fragmentos de cuentos o novelas de diversos autores latinoamericanos.
También, te acercarás a algunas obras literarias latinoamericanas y analizarás las voces narrativas que utilizan diferentes autores para expresar las situaciones y emociones que viven los personajes.
¿Qué hacemos?
Para comenzar, reflexiona en la siguiente pregunta:
¿Qué es un narrador?
El narrador, es la voz que cuenta la historia, es un tipo de personaje dentro de la misma que cuenta y relata los sucesos.
Primero debes comprender que narrar es una forma de explicar un hecho. Por ejemplo, el diccionario de la Real Academia de la Lengua lo define como:
“Narrar: contar, referir lo sucedido, de un hecho o una historia ficticios”
Es decir, cuando se narra algo, es cuando se cuenta una historia real o inventada.
Esta forma de contar ha existido desde las civilizaciones más antiguas, primero de manera oral y después, con la escritura, la necesidad de contar historias dio lugar a la literatura universal.
Y como ya conoces, la literatura latinoamericana es aquella creada por las autoras y autores nacidos en los países de América latina.
Seguramente, al leer un cuento o una novela, puedes reconocer casi de forma inmediata a la figura del narrador, que es el que cuenta la historia. Pero en otras ocasiones puede parecer extraño el modo en que se van relatando los hechos.
En la literatura latinoamericana, los autores exploraron otras maneras de contar, todo con el propósito de animar la curiosidad por la lectura, relacionarse con la trama y así seas cómplice de la historia.
Entonces, la autora, o autor no es precisamente el narrador de la obra, más bien, el narrador es una figura más dentro de los personajes de una historia.
A continuación, observa algunos ejemplos para ver cómo funciona la voz del narrador en la literatura.
Observa la siguiente imagen, donde puedes encontrar algunos personajes: un niño vestido de azul, y un conejo vestido de traje.

Imagina y responde lo siguiente:
¿Cómo se contaría la historia desde el punto de vista del conejo?
¿Cómo la contaría el niño?
Y en dado caso, ¿cómo podría ser contada por el hongo gigante?
Serían historias muy distintas, el niño de azul va pasando por ahí, mientras el hongo lleva toda una vida plantado a la orilla del camino.
Una misma escena podría contarse de distintas formas, y eso se logra por los distintos tipos de voces narrativas y perspectivas que se logran diferenciar.
Las autoras y autores, al enfrentarse a la hoja en blanco para escribir una historia, tienen varias decisiones que tomar, una de ellas, es decidir sobre el punto de vista que tendrá su historia. Es decir, desde que ángulo de observación contará los sucesos.
El ángulo de observación que decide el autor le da forma al texto y determina lo que el autor quiere contarle al lector o destinatario.
Es como cuando tú relatas un suceso, por ejemplo, el día en que ganaste una carrera en el parque a tu amiga o amigo, lo contarán desde el punto de vista en que fueron los que ganaron, pero si lo contara su amiga o amigo vencido, la historia sería diferente.
Los autores deciden la perspectiva que se dará a su historia según el punto de vista de lo que quieran contar.
Se podría decir que algunos tipos de perspectivas posibles son:

Observa algunos ejemplos donde se puede reconocer la perspectiva que los autores decidieron para contar una historia
“Hubo un tiempo en que yo pensaba mucho en los axolotl. Iba a verlos al acuario del jardín des Plates y me quedaba horas mirándolos, observando su inmovilidad, sus oscuros movimientos. Ahora soy un axolotl”.
Julio Cortázar
Este es el fragmento de un cuento de Julio Cortázar, aquí la voz narrativa es la del personaje cuando él ya se ha convertido en un axolotl. Desde ahí lo está contando.
Observa otro ejemplo:
“Era la última hormiga de la caravana, y no pudo seguir la ruta de sus compañeras. Un terrón de azúcar había resbalado desde lo alto, quebrándose en varios terroncitos. Uno de éstos le interceptaba el paso. Por un instante la hormiga quedó inmóvil sobre el papel color crema.”
La historia se cuenta desde una voz que observa a la hormiga, la cual se encuentra en una situación particular: Un terrón de azúcar le intercepta el paso.
Es curioso que, en ambos relatos, los personajes, no son humanos.
A continuación, observa el siguiente esquema, que te ayudará a organizar este nuevo aprendizaje.
En los cuadros de abajo del esquema, anotarás los títulos de los relatos que irás conociendo.
Ahora lee el siguiente extracto de Balún - Canán, de la autora mexicana Rosario Castellanos:
Balún – Canán
“No soy un grano de anís. Soy una niña y tengo siete años. Los cinco dedos de la mano derecha y dos de la izquierda. Y cuando me yergo puedo mirar de frente las rodillas de mis padres. Más arriba no. Me imagino que sigue creciendo como un gran árbol y que en su rama más alta está agazapado un tigre diminuto. Mi madre es diferente. Sobre su pelo –tan negro, tan espeso, tan crespo– pasan los pájaros y les gusta y se quedan. Me lo imagino nada más. Nunca lo he visto.”
Balún – Canán
(Fragmento)
Rosario Castellanos
La niña, es quien está contando la historia, desde su visión particular y bajo su propia perspectiva. Se puede imaginar a esta narradora protagonista, como una niña pequeña, ya que su mirada llega a la altura de las rodillas de sus padres.
La voz narradora protagonista, también se conoce como voz narrativa en primera persona.
Ahora, lee el siguiente fragmento de la obra “Crónica de una muerte anunciada”, del escritor colombiano Gabriel García Márquez.
En este fragmento, el narrador vuelve para contar la historia de lo que había sucedido en ese pueblo. Tal como el título de la novela lo dice, ésta es la crónica de un suceso reconstruido desde su forma literaria.
Con estos ejemplos puedes comprender mejor las voces narrativas. Para recapitular, observa el siguiente video sobre cómo funcionan las voces narrativas.
Tipos de narrador y voces narrativas.
Los relatos, cuentos y novelas son construcciones creativas, surgen de la imaginación de las autoras y autores. Siempre y cuando se piense en cómo es la mejor forma de compartir las historias con sus lectores o destinatarios, los creadores pueden explorar distintas formas de escribir una historia. En eso, como en otras cosas, radicará su talento.
Hay veces, en que, en una misma novela, se puede jugar con dos historias contadas por distintos tipos de narrador. Todo depende de cómo y para qué se elegirán los tipos de narradores.
Ahora, profundizarás en el narrador omnisciente, a partir de los siguientes ejemplos.
Lee un fragmento de la novela “Aura”, del autor mexicano Carlos Fuentes, que se presenta en el libro de texto de Telesecundaria, Segundo grado, Volumen 1.
https://libros.conaliteg.gob.mx/T2ESA.htm?#page/31
Ahora, contesta las siguientes preguntas:
¿En qué persona gramatical está hecha la narración (primera persona: yo / nosotros, nosotras, segunda persona: tú / ustedes, o tercera persona: él / ella / ellos / ellas)?
¿Qué impresión o sensación se busca transmitir al lector con el uso de esa persona gramatical?
Este tipo de narrador omnisciente que utiliza Carlos Fuentes en su novela Aura, permite saber todo lo que les pasa a los personajes tanto física como emocionalmente. Y también tiene la libertad de decir lo que sucede antes o después del relato.
Presta atención a cómo la perspectiva está modificada. El relato se plantea poniendo las acciones en segunda persona. El efecto que produce es la sensación de ser nosotros, los lectores, quienes están realizando la acción. Eso le causa al lector una sensación que lo involucra, sin duda, esto es lo que Fuentes quería que provocara.
Existen distintas maneras de contar una historia. Ya que has revisado estas voces narrativas, realiza la siguiente actividad.
Practica lo aprendido, intenta reescribir en tu cuaderno el fragmento anterior, parafraseando algunas cosas o como lo recuerdes, transformando la voz narrativa a primera persona.
Esta será una buena actividad para que practiques la escritura.
Finalmente, responde las siguientes preguntas:
¿Cómo cambian las versiones cuando cambia el narrador?
¿Cuál de los narradores nos resulta más sencillo utilizar?
¿Por qué?
La narrativa latinoamericana presenta distintas formas de ser contada. Algunas de estas formas permiten comprender la manera de sentir de otros e imaginar la realidad de ellos como si fuera tuya.
Ahora que estás en casa, puedes escribir tus propias historias, corregirlas, compartirlas con tus familiares y amigos, ya sea de manera escrita o que se las lean en voz alta.
Escribir historias, siempre es una buena manera de poner en juego la imaginación e invitar a otros a vivir nuevas experiencias.
Sigue explorando la gran variedad de lecturas e historias que existen. Buscando en bibliotecas, en Internet, con familiares, buscando lecturas que te atrapen y no puedas soltar. Leer es una muy buena manera de viajar y de conocer a otras personas.
El Reto de Hoy:
Reto 1.
Con la primera imagen, si tienes oportunidad de hacer el ejercicio con otras personas, busca que cada uno lo haga desde un personaje distinto, al compararlas, verás que todas las versiones son buenas, pero diferentes.
Reto 2.
Escribe un pequeño relato inspirado en una historia en primera persona, es decir, en voz de narrador protagónico.
Puedes realizar una práctica de escritura. Por ejemplo, contar una historia propia, pero desde los ojos de alguien de tu familia.
También podrías darle una voz protagonista a un insecto o un anfibio
Aquellos que tienen una mascota, podrían hacer el ejercicio de contar este día desde su perspectiva.
Usa las siguientes preguntas que te ayudarán a desarrollar tu historia:
¿Qué contarían ellos?
¿Cómo nos verán a nosotros los humanos?
¿Cuál sería su conflicto?
¿Cómo lo resolverían?
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

La técnica en la práctica social
Aprendizaje esperado: Compara las finalidades de las ciencias y de la tecnología para establecer sus diferencias.
Énfasis: Reconocer a la técnica como práctica social en la satisfacción de necesidades.
¿Qué vamos a aprender?
Profundizarás en las diferencias de las ciencias y la tecnología. Además, reflexionarás en la técnica como practica social, porque la técnica está en todo. En cada aspecto de tu vida, puedes notar la presencia e importancia de ella en el desarrollo y evolución de todo.
¿Qué hacemos?
Para entrar en materia, observa el siguiente video sobre el “Barro negro de Oaxaca”. Pon atención a las imágenes del video, centrándose en las técnicas que aparecen en él.
Barro negro de Oaxaca.
Ahora, reflexiona. Lee y escribe las siguientes preguntas e intenta darles varias respuestas. No le pongas límite a tu creatividad.

Sin duda el barro de Oaxaca es un tema más que interesante y útil. Además de una gran aportación cultural de nuestro país.
Para que te quede más claro, en una comunidad hay panaderías en donde la elaboración del pan aún es de manera artesanal. Esto quiere decir que el amasado es a mano, algunas de sus herramientas fueron fabricadas por ellos mismos, por ejemplo: el horno de leña, sus cortadoras; pero también existen otros negocios donde ya intervienen máquinas para el amasado, y sus hornos funcionan con gas, es decir, el proceso es industrializado.
Para que te quede más claro, observa el siguiente video.
Panaderías.
En tu comunidad, ¿conoces algún taller que fabrique productos de manera artesanal o industrial?
¿Identificaste algunas de las técnicas que utilizó el artesano?
Como te puedes dar cuenta, en la fabricación del barro y el pan, el fuego tiene una participación primordial. Este ha permitido a través de la historia de la humanidad la fabricación de una gran diversidad de utensilios y herramientas de diferentes materiales, como el vidrio, la cerámica y algunos metales blandos, principalmente el oro, la plata y el cobre; las cuales facilitaron las actividades cotidianas de la humanidad.
A continuación, observa las siguientes imágenes para que desde tu casa, logres identificar algunas características.
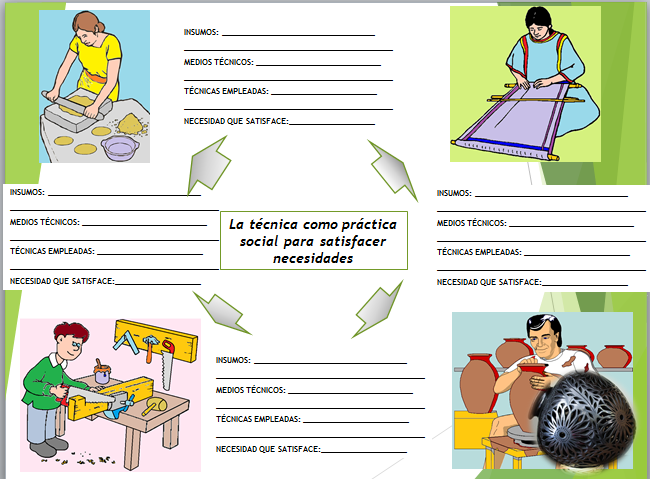
En el primer dibujo, hay a una mujer elaborando tortillas o tostadas de maíz, empleando como insumos: masa, del nixtamal, agua y leña.
Y como medios técnicos: un metate, un rodillo de piedra y un recipiente, que posiblemente fueron elaborados por ella misma. La técnica aplicada es artesanal, pues el amasado y el moldeado de las tortillas es a mano. Finalmente, la necesidad que satisface es la de alimentar a la familia.
En el siguiente ejemplo, se observa a una persona trabajando con un telar. Los insumos son las fibras que se convierten en hilos y los pigmentos que usan para dar color. El medio técnico es la máquina que se construye con madera, integrado con un pedal y un mecanismo que teje los hilos. La técnica aplicada es el movimiento de las manos y los pies, para que cada uno de los hilos sean hilados. Finalmente, la necesidad que satisface es la de vestir o cubrirse del frio.
En la siguiente imagen, hay a una persona elaborando muebles. Los insumos son la madera que utilizará para hacer muebles. Los medios técnicos que utilizará son martillo, escuadra, serrucho o sierra para cortar. La técnica es artesanal ya que utiliza cada una de las herramientas con sus manos. Y la necesidad que cubren los muebles es que nos servirán para estar cómodos, en el hogar, en la escuela o la oficina
Ahora es tu turno.
Observa y analiza el último dibujo, descríbelo en tu cuaderno:
- Los insumos
- Los medios técnicos utilizados.
- Las técnicas aplicadas.
- Y qué necesidades satisface.
Es muy clara la relación que existe entre la técnica y tu vida cotidiana.
Observa el siguiente video sobre la elaboración de tortillas.
Elaboración de tortillas.
La técnica en la práctica social ha presentado innovaciones, ejemplo de esto es la maquina tortilladora, inventada en 1904 por el mexicano Everardo Rodríguez Arce y su socio Luis Romero.
El nuevo aparato constaba de rodillos laminados y una transportadora que llegaba a un comal, pero curiosamente no producía tortillas redondas, sino cuadradas. Tres décadas más tarde el señor Fausto Celorrio inventó la primera máquina tortilladora automática, o sea, la primera que funcionaba por sí sola, sin la intervención de un operador.
Existen diversas maneras de tener producciones, con las máquinas, es posible la producción en serie, mayor producto con menor esfuerzo. Utilizando de la misma manera insumos, medios técnicos, en este caso máquinas, y con la finalidad de satisfacer diferentes necesidades.
Para reforzar la importancia de empleo de la técnica como práctica social, presta atención en otros ejemplos: en el siglo XIX, durante la Revolución Industrial, el uso del hierro favoreció la fabricación de máquinas, las que mejoraron los procesos productivos, hasta alcanzar el desarrollo tecnológico actual.
Las innovaciones tecnológicas han favorecido la creación de productos como las computadoras, los teléfonos celulares, la televisión satelital o simplificado procesos en los servicios para mejorarlos. Todo lo anterior forman parte de la vida diaria y contribuye a una mejor comunicación y calidad de vida.
La técnica es dinámica pues cambia y se adapta, además en ella se ponen en juego los saberes y experiencia de las personas en un contexto social, se va adecuando por particularidades económicas, culturales e históricas.
La técnica surge con el fin de resolver necesidades, las cuales varían según el entorno; por ejemplo, las técnicas agrícolas cambian según el tipo de tierra, la imprenta cambió sus instrumentos mecánicos por dispositivos eléctricos y electrónicos, con lo que fue posible reducir su tamaño para llegar a las oficinas y hogares, actualmente las conocemos como impresora.
Otra innovación muy clara es la forma de comunicarnos, que datan de la prehistoria, donde se utilizó lenguaje arcaico o pinturas y hoy la forma de comunicarnos nos da una gama muy amplia de opciones, desde una llamada telefónica hasta una video llamada
El Reto de Hoy:
Describe todas las técnicas de las que hacen uso en un día cotidiano. Por ejemplo: cómo se lavan las manos, los dientes, cuando ayudan con las labores del hogar, lavar los trastes o barrer, sus tareas y técnicas para estudiar.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Aprende en casa II SEGUNDO DE SECUNDARIA 29 DE SEPTIEMBRE









Publicar un Comentario