Aprende en Casa III SEP: 3 de junio TAREAS y ACTIVIDADES de 3° de secundaria
A continuación dejamos los temas vistos el 3 de junio de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 3° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Jueves 3 de junio, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Expresémonos en orden y con coherencia
Aprendizaje esperado: Jerarquiza las acciones de la autobiografía en un orden cronológico y coherente.
Énfasis: Revisar expresiones que jerarquizan información en autobiografías.
¿Qué vamos a aprender?
Esta sesión te permitirá profundizar en el conocimiento de las diversas expresiones que puedes utilizar en los textos orales y escritos, de tal manera que estas expresiones favorecen la organización del texto de manera coherente con la finalidad de que sea comprendido por quien lo lee.
Dicen que la mejor manera de aprender a escribir es leyendo, por eso en esta sesión te dedicarás a leer una autobiografía en la cual podrás identificar aquellas expresiones que organizan de manera lógica al texto.
Por eso, la sesión está centrada en revisar estas palabras o expresiones que el autor usa para establecer importancia a los eventos que narra en su autobiografía.
Los materiales que necesitarás para esta sesión son tu cuaderno, y lápiz o bolígrafo para tomar notas. También ten a la mano tu libro de texto.
No olvides que todo lo que aprendas es para fortalecer tu conocimiento, se te recomienda llevar un registro de las dudas, inquietudes o dificultades que surjan durante la sesión, pues muchas de éstas las podrás resolver al momento de consultar tu libro de texto y revisar tus apuntes.
¿Qué hacemos?
Lee el siguiente fragmento de la autobiografía de Charles Darwin.
Al principio de la etapa escolar, un chico tenía un ejemplar de Wondersofthe World, Las maravillas del mundo, que lo leía con frecuencia, y discutíamos con otros muchachos sobre la veracidad de algunos relatos; creo que este libro me inspiró el deseo de viajar por países remotos, que se cumplió finalmente con el viaje de Beagle.
Después durante mi vida escolar, me aficioné apasionadamente a la caza; no creo que nadie haya mostrado mayor entusiasmo por la causa más santa que yo por cazar pájaros.
La autobiografía es un texto que informa sobre los acontecimientos más relevantes de la vida de quién la escribe. Los acontecimientos suelen estar ordenados cronológicamente.
En el fragmento leído, encuentras esas expresiones que te ayudan a comprender cómo se fueron dando los hechos en esta etapa de la vida de Darwin.
Por supuesto, tiene que ver con el orden de la información, lo que el autor decidió que era lo más relevante y los sucesos que consideró menos importantes, pero necesarios de narrar.
En el caso del fragmento que leíste puedes observar que el autor de la autobiografía plantea como un suceso definitorio en su vida la etapa escolar a partir de las discusiones sobre la veracidad de los relatos que aparecían en la revista “Maravillas del mundo”, hecho que posteriormente lo llevó a aficionarse a la caza de pájaros.
Has escuchado hablar sobre una de las más grandes escritoras mexicanas del siglo XX. La gran Elena Garro, una de las poetas, narradoras y dramaturgas más prolíficas del país.
Elena Garro fue una mujer de gran valía para nuestro país, y mucho se ha escrito y hablado de su vida, ha habido muchos cronistas y personalidades que han hablado sobre ella, pero ella no escribió una autobiografía.
Así sabrías de primera mano muchos de los sucesos que marcaron su vida y su obra.
En la escritura para jerarquizar la información se utilizan distintas expresiones para distinguir el argumento o situación principal.
Esas expresiones también reciben el nombre de marcadores del discurso, conectores del discurso, operadores pragmáticos o partículas discursivas.
Existe una clasificación grande, Martín Zorraquino y J. Portolés, son lingüistas españoles, estos autores diferencian cinco grupos de marcadores discursivos, los cuales son:
- Estructuradores de la información
- Conectores
- Reformuladores
- Operadores argumentativos
- Marcadores conversacionales
Analiza la clasificación de Zorraquino y Portolésy para ello usarás la autobiografía de Darwin.
Estructuradores de la información: Éstos señalan la organización informativa de los discursos. En este grupo se distinguen:
- Los que introducen un nuevo comentario: pues, bien, pues bien, así las cosas, dicho esto, etc.
- Los que agrupan diversos miembros del discurso como partes de un único comentario, llamados ordenadores: en primer lugar, en segundo lugar, en un primer momento, antes de nada, por un lado, para empezar, a continuación, al principio, primero, después, luego, por último, finalmente, para terminar, etc.
- Y los digresores, que introducen un comentario lateral en relación al tópico principal del discurso: por cierto, a propósito, a todo esto, etc.
El texto que ocuparás es el fragmento de Charles Darwin, en éste podrás observar que marcadores usó el autor.

Al inicio se encuentra el primero que pertenece a los ordenadores; que es al principio. Más adelante encuentras otro marcado en color amarillo: después, que del mismo modo pertenece a los ordenadores.
El segundo grupo de marcadores pertenece a:
Conectores:
Vinculan un miembro del discurso con otro anterior, o con una suposición contextual. Se distinguen tres tipos:
- Los aditivos: incluso, además, en suma, también, incluso, es más, etc.
- Los consecutivos o ilativos: pues, entonces, luego, por ende, por eso, etc.
- Y los contra argumentativos: en cambio, ahora bien, por el contrario, aunque, sin embargo, no obstante, etc.
Ahora, lee un fragmento de la autobiografía de Rigoberta Menchú, activista guatemalteca y defensora de los derechos humanos. Trata de identificar los conectores que analizaste.
…me cuesta mucho todavía hablar castellano ya que no tuve colegio, no tuve escuela. No tuve oportunidad de salir de mi mundo, dedicarme a mí misma y hace tres años que empecé a aprender el español y a hablarlo; es difícil cuando se aprende únicamente de memoria y no aprendiendo en un libro. Entonces, sí, me cuesta un poco. Quisiera narrar desde cuando yo era niña o incluso desde cuando estaba en el seno de mi madre, pues, mi madre me contaba como nací…
Nuestra costumbre, no permite a una mujer soltera que vea un parto. Pero, sin embargo, ante la necesidad, vi cuando mi hermana se compuso y que no estaba nadie en casa. Eso cuando ya estábamos en plena persecución. Aunque no vi exactamente, estuve presente cuando nació su niño.
Como podrás darte cuenta, en estos dos párrafos encuentras seis conectores de los tres tipos; Aditivos, consecutivos y contra argumentativos como se muestra en las tablas.

Una recomendación es: primero, prestar mucha atención a los textos y segundo tener a la mano la lista de los conectores para identificarlos, y después, poco a poco, ya no habrá necesidad de usarla ya que la práctica te ayudará a comprender el uso de este tipo de expresiones que se usan en los textos autobiográficos y sobre todo permiten al lector reconocer los pasajes que el autor jerarquiza de acuerdo a la importancia en su vida.
El tercer grupo pertenece a:
Reformuladores:
Favorecen la comprensión de los textos como una mejor forma de lo que se expresó previamente. Según su función discursiva éstos son:
- Explicativos: es decir, o sea, esto es, en efecto, con esto quiero decir, en otras palabras, etc.
- De rectificación: mejor dicho, más bien, digo, etcétera.
- De distanciamiento: en cualquier caso, de todos modos, de todas formas, etc.
- Y recapitulativos: en suma, en conclusión, o tal, en fin, al fin y al cabo, en definitiva, etcétera.
Prosigue con la autobiografía de la ganadora del Nobel de la Paz en 1992 e identifica este grupo de marcadores.
Soy de San Miguel /Uspantán, Departamento El Quiché. El Quiché se ubica en elNoroccidente del país. Vivo en el Norte del Quiché, o sea cerca de Chajul.
Puedo decir que ahora es una aldea de cinco o seis caballerías cultivadas por los campesinos.
Inmediatamente cuando el niño nace se le amarran sus manitas, o sea, se le ponen rectas sus manitas y sus piecitos. Esto significa que sus manos son sagradas para el trabajo y que esas manos tienen que actuar donde tienen que actuar, o sea, nunca van a robar; el niño, nunca va a abusar de la naturaleza.
Como te has podido percatar, existen muchas costumbres y eso dependerá de la región. Todas ellas son respetables. ¿Lograste encontrar algunos reformuladores? Recuerda se trata de identificar algunos en las autobiografías y el sentido que le dan al texto.
En los párrafos anteriores que has leído encuentras los siguientes:
- O sea
- Puedo decir
- Esto significa que
Pertenecen a los reformuladores explicativos, en otras palabras, aclaran un hecho o situación.
Continua con el cuarto grupo:
Operadores argumentativos. Condicionan de alguna forma las posibilidades discursivas del segmento en el que se incluyen, pero sin relacionarlo con otro elemento anterior. Se diferencia entre:
- Operadores de refuerzo argumentativo: en realidad, de hecho, en el fondo, etc.
- Operadores de concreción: por ejemplo, en particular, concretamente, en concreto, etc.
Nuestros padres nos enseñan a ser responsables, como ellos son responsables. Por ejemplo, el hijo mayor tiene una responsabilidad en la casa. Las cosas que el padre no puede corregir, el hijo mayor las puede corregir.
Nosotros tenemos divididos los días en perros, en gatos, en toros, en pájaros. Cada día tiene un nahual. Si el niño nació el día miércoles, por
ejemplo, su nahual sería una ovejita. El nahual está determinado por el día del nacimiento.
[…] se empezó a educar a los niños a ser discretos. De hecho, son discretos, pero a recomendarles que no tienen que contar una sola palabra a otros niños fuera de la comunidad, de lo que hacen los padres, de lo que hace la comunidad.
Es interesante la vida de esta activista social, y la estás conociendo, a través de las sus vivencias la cultura, las costumbres del pueblo de Guatemala, pero además su texto proporciona ejemplos claros del uso de distintas expresiones que tienen diversas funciones, pero sobre todo que le dan coherencia al texto.
En la lectura encuentras:
- Por ejemplo, el hijo mayor tiene…
- Si el niño nació el día miércoles, por ejemplo, su nahual sería una ovejita.
Estos pertenecen a los marcadores de concreción. Y también pudiste identificar uno de refuerzo argumentativo:
- De hecho, son discretos, pero a recomendarles que…
De esta manera le dan fuerza al argumento.
Por último, tienes los:
Conversacionales.
Son los que aparecen con frecuencia en la conversación.
A este grupo pertenecen entre otros:
- claro
- desde luego
- por lo visto
- bueno
- bien
- vale
- hombre
- oye
- bueno
- eh
- este
Lee los últimos fragmentos de la autobiografía de Rigoberta Menchú y trata de identificar estos marcadores.
Claro, no estábamos con un territorio liberado, sino que de un rato al otro se temía al enemigo ya que el régimen siempre cuenta con maquinarias modernas, cuentan con armas modernas, entonces era posible que hubiera una masacre en mi aldea.
Cuando yo por primera vez señalé un error de un compañero ladino, me sentía la mujer más deshecha, claro; porque nunca en mi vida había criticado a un ladino. Y precisamente porque la humillación la he sentido en carne propia, porque me han tratado siempre de india. "Es que ella es indígena", decían como un insulto, desde luego, para mí criticar a un compañero ladino era como poner una máscara y hacer algo descaradamente. Sin embargo, mi crítica era constructiva. Era para corregir al compañero y después aceptar que el mismo compañero me critique a mí.
Ubica las palabras subrayadas. Cómo se mencionaba anteriormente, no siempre encontrarás los marcadores discursivos, en este caso solo encuentras tres y dos de ellos se repetían.
Lee los últimos fragmentos de la autobiografía de Rigoberta Menchú y realiza un ejercicio.
De esta manera pondrás en práctica los diferentes marcadores discursivos que has analizado.
Conforme sigues la lectura trata de identificar algunos de los marcadores que recuerdes.

¿Lograste identificar algunos?
Revisa el texto para que des cuenta cuanto pudiste identificar.
…la señora dijo: "Les traigo una sorpresa. Yo he matado un soldado", dice; "he matado un soldado". Y nadie creía. Claro, cómo era posible creer que la señora que en primer lugar era anciana, en segundo, ya ni veía y en tercer lugar, no tenía armas iguales a las armas del enemigo... Entonces la señora dijo: "Estoy contenta, no quiero morir, quiero vivir más. Yo maté a un soldado." Y nadie le creía. "Yo estoy diciendo la verdad", decía. "Si quieren les enseño las armas."
¿Pudiste identificar todos los elementos?
Analizaste una autobiografía y las expresiones que se utilizaron, también llamados como marcadores discursivos que te ayudaron a ordenar de lo más relevante a lo menos importante, además de otras palabras y frases que indicaban sucesión de hechos, es decir, qué acontecimientos sucedieron antes y cuáles después.
Es importante conocer cada uno de los marcadores del discurso y saberlos utilizar para que tu texto o autobiografía tenga sentido y orden.
El Reto de Hoy:
Indaga y realiza una tabla de la clasificación de los marcadores discursivos, y posteriormente, en tu libro de español o en internet imprime una autobiografía e identifica los marcadores que jerarquizan la información.
Recuerda siempre poner en práctica todo lo aprendido, puedes guiarte con tus notas, libros e incluso tener un diálogo con tus padres con respecto a lo aprendido en la sesión, de tal manera que el aprendizaje obtenido este siempre en movimiento y así afianzarlo.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Probabilidad
Aprendizaje esperado: Calcula la probabilidad de ocurrencia de dos eventos mutuamente excluyentes.
Énfasis: Conocer el desarrollo de la probabilidad.
¿Qué vamos a aprender?
Se te pide tener a la mano tu cuaderno, lápiz y goma.
¿Por qué es importante el estudio de la probabilidad?
La probabilidad permite construir modelos, desarrollar procedimientos para calcular y estimar las posibilidades de que ocurra un evento en situaciones donde interviene el azar o hay un grado de incertidumbre.
Su importancia es creciente en diversas áreas del conocimiento, por ejemplo: En ciencias básicas como la Física, la Química y la Biología, los modelos probabilísticos han favorecido a la comprensión de los fenómenos naturales.
No es entonces una exageración afirmar que conocer algunos elementos de probabilidad y estar familiarizados con el razonamiento probabilístico, es necesario tanto para el especialista como para el ciudadano informado.
Los conceptos de la Teoría Elemental de la probabilidad son ricos en resonancias intuitivas. En el cotidiano, se tiene que valorar y tomar decisiones en circunstancias donde hay incertidumbre o interviene el azar.
Debido a ello, se desarrollan ciertas intuiciones acerca de los fenómenos probabilísticos —y aunque estas intuiciones son con frecuencia inexactas o se apoyan en concepciones no siempre correctas—, proporcionan un comienzo para afinarlas y acercarse a formulaciones matemáticas más precisas.
El estudio de la probabilidad se presta para lograr un ambiente de estudio participativo. Puedes abordar algunos problemas por medio de la exploración empírica de situaciones aleatorias.
Asimismo, puedes formular hipótesis, contrastar tus expectativas con los resultados que se presentan experimentalmente, y producir y discutir tus propias explicaciones.
Estas explicaciones te ayudan al desarrollo de las nociones matemáticas.
¿Qué hacemos?
Pascal, Fermat y el Caballero de la Meré son pioneros en “Los inicios de la probabilidad”.

El origen del estudio de la probabilidad está asociado a los nombres de Blais Pascal y Pierre Fermat.
Al parecer, el Caballero de la Meré, un hombre culto aficionado a los juegos de azar, planteó ciertos problemas de juego a Pascal y éste a su vez, los discutió con Fermat por correspondencia en el año de 1654.
El siguiente problema fue conocido como el “Problema de los puntos” o “De la división de la apuesta”.
Dos personas compiten en un juego hasta completar un cierto número de puntos. Cada una tiene la misma oportunidad de hacer un punto; aquel que los complete primero se lleva la totalidad de la apuesta.
Pero si el juego tiene que interrumpirse antes de que algún jugador complete los puntos ¿Cómo se debe dividir la apuesta?
Por ejemplo, se tienen a dos personas: Llamémosles A y B, que juegan a los volados.
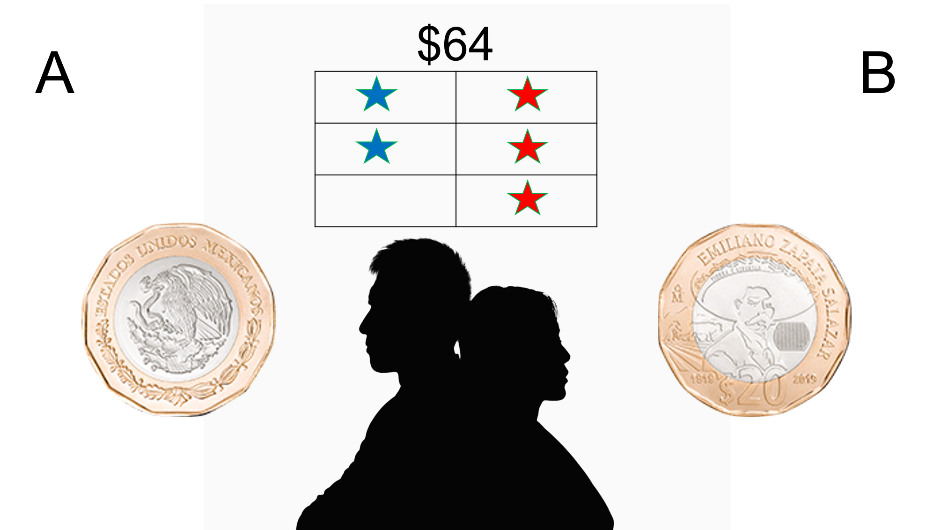
Si sale águila, “A” gana un punto; si sale sol, “B” gana un punto; juegan varios volados y el que complete primero tres puntos, gana una apuesta de 64 pesos.
Pero después de tres volados, cuando “A” lleva dos puntos y “B” lleva un punto, el juego se interrumpe.
Entonces ¿Cómo se debe dividir la apuesta?
Primero, se descarta la solución inmediata que argumenta “que se reparta mitad y mitad”, porque es probable que “A” protestará, ya que él lleva la ventaja y exigiría que se le compense con una mayor parte de la apuesta.
Tampoco es viable otra solución inmediata que sugiere repartir la apuesta en partes proporcionales a los puntos acumulados. Es decir: 2/3 de la apuesta para “A”, porque lleva 2 puntos y 1/3 de la apuesta para “B” porque lleva 1.

Esta es la “solución” que proponía el Caballero de la Meré, pero tanto Pascal como Fermat estuvieron de acuerdo en que no era correcta.
Antes, se debe considerar que dicha “solución” no depende del número de puntos que se necesitan acumular para ganar la apuesta.
En una carta a Fermat, fechada el 29 de julio de 1654, Pascal comenta el método que encontró para resolverlo: “Supongamos que se juega el siguiente punto, puede suceder alguna de dos cosas: Gana A o gana B. “
Si gana “A”, entonces se completan los 3 puntos, llevándose toda la apuesta. Pero si gana B, entonces tanto A como B se llevarían 2 puntos y la apuesta se divide en partes iguales, es decir, mitad y mitad.

Por este motivo, “A” razona así:
“Yo estoy seguro de obtener, por lo menos, la mitad de la apuesta, 32 pesos, porque aún si perdiera, el siguiente punto lo obtendría. Pero la otra mitad quizás me la lleve yo, o tú, o ambos con las mismas oportunidades. Entonces, divide esta mitad entre ambos y entrégame la mitad que ya tengo asegurada.”
Por ello, “A” reclama para sí tres cuartas partes de la apuesta:
1/2 más 1/4 igual a 3/4, es decir, 48 pesos y una cuarta parte para B, es decir, 16 pesos.

Por otra parte, la solución de Fermat es la siguiente: Se debe observar que, a lo más, en dos tiradas extras se decidiría el juego.
Supón que necesariamente se juegan esos dos puntos; se señala con “a” cuando el punto lo gana A y con “b” cuando lo gana B.

Todos los posibles desarrollos del juego son los siguientes: “aa”, “ab”, “ba”, “bb” y de éstos, en 3 casos ganaría A, contra un solo caso en el que ganaría B.
Por esto, la fracción de la apuesta que se debe llevar “A” es 3/4, es decir, 48 pesos y 16 pesos para B.
Realiza la primera actividad, desarrolla el problema de la división de la apuesta cuando “A” y “B” juegan a 4 puntos en una apuesta de 64 pesos, teniendo como situación que el juego se interrumpe cuando “A” lleva 3 puntos y “B” 1.
El cálculo de la probabilidad está basado en algunos conceptos fundamentales, mismos que se desarrollan a lo largo de tu educación secundaria.
Se identifican a continuación las diferencias entre un experimento aleatorio y uno determinista, que son parte de estas ideas fundamentales.
Observa el siguiente video del inicio al minuto 01:41.
- ¿Qué es el azar? ¿Qué es aleatorio?
https://www.youtube.com/watch?v=ViMZbNG5Klw
Analiza algunos procedimientos para registrar y visualizar datos, realizar conjeturas, verificar tendencias y otros requerimientos.
El uso de diagramas de árbol y arreglos rectangulares —así como de otras técnicas sencillas de conteo para enumerar casos—, son habilidades que se deben desarrollar.
Los diagramas de árbol, además de facilitar la enumeración de los resultados que pueden presentarse al realizar una experiencia aleatoria, proporcionan una imagen visual de los desarrollos posibles de la experiencia.
Para ello es importante que te acostumbres a escribir en cada rama las probabilidades, tal y como se muestra en el siguiente ejemplo.

Se tienen cinco canicas blancas y cinco negras en una caja.
Extraes al azar una canica de la caja y se deja de lado, para después extraer una segunda canica también al azar.
¿Cuáles son los posibles resultados?
Utilizando un diagrama de árbol, del punto de partida se tienen dos ramificaciones: 5 de las 10 canicas son blancas y 5 canicas son negras.
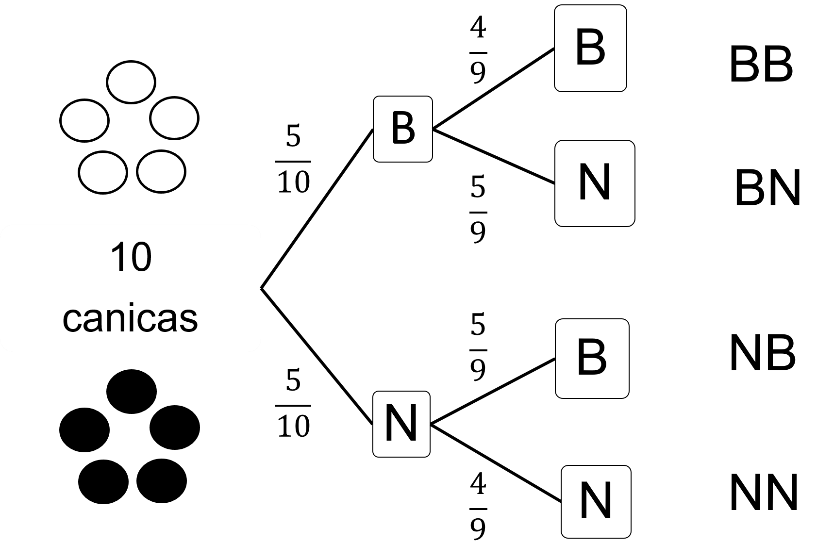
Después de extraer la primera canica y dejarla fuera de la caja, se extrae la segunda y las ramificaciones quedan de la siguiente manera.
Si la primera en salir fue blanca, 4 de las nueve restantes son blancas y 5 de las 9 restantes son negras.
Si la primera canica es negra, entonces 5 de las nueve restantes son blancas y 4 de las 9 restantes son negras.
Por ende, los resultados posibles después de las dos extracciones son:
Blanco, blanco.
Blanco, negro
Negro, blanco.
Negro, negro.
En otro ejemplo, se tiene que de una serie de 3 volados consecutivos hay 8 resultados posibles. Observa su representación:
Se comienza la ramificación con 1 de 2 resultados para “águila”, y 1 de 2 resultados para “sol”.

En el segundo lanzamiento se tiene de nueva cuenta 1 de 2 resultados para águila, y 1 de 2 para sol.
Y para el tercer lanzamiento se repiten los resultados anteriores.
De esta manera, el diagrama permite visualizar todos los resultados posibles después de terminado el experimento.
En este caso, se observa que son 8 posibilidades:
La primera posibilidad indica que puede salir 3 veces águila.
También se puede obtener águila, águila y sol
Águila, sol, águila.
Águila, sol, sol.
Sol, águila, águila.
Sol, águila, sol.
Sol, sol, águila.
Y Sol, sol, sol.
También existe otro tipo de situaciones en las que se pueden emplear las tablas de doble entrada.
Por ejemplo:
En el patio de la escuela se encuentran los alumnos del grupo “3ro A”.
Se quiere escoger un alumno al azar y ver a cuál taller pertenece.
Para hacer un análisis de probabilidad, la tabla de doble entrada queda de la siguiente forma:

El Grupo A tiene 15 alumnos en informática, 3 en el taller de dibujo, 22 en el taller de corte y confección, y 10 en conservación de alimentos.
Ya con la tabla realizada, se puede conocer cuál taller tiene la mayor probabilidad y cuál tiene la menor al escoger a un alumno al azar.
Para denotar el grado de incertidumbre respecto al taller, se pueden usar oraciones como: “Es muy probable […]” o “La mayor probabilidad la tiene […]”.
Para informática, se puede indicar que es “probable” seleccionar un alumno al azar; para dibujo es “muy poco probable”; para un alumno del taller de corte y confección es “muy probable”, y “poco probable” encontrarse con un alumno de conservación de alimentos.
“La escala de la probabilidad”.
Considera que se tiene una escala de 0 a 1, como en la figura siguiente, en la cual se asigna un número a algunas expresiones relacionadas con el azar.
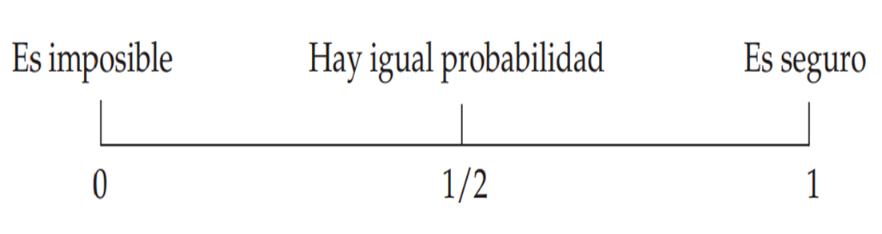
Pero ¿cómo se ubican en esta escala los términos que se ordenaron en el ejercicio anterior?
Una de las ideas fundamentales de la probabilidad en las nociones intuitivas acerca del azar, es que en el lenguaje cotidiano se expresan frases como: “Se espera que […]”, “Hay igual probabilidad…” o “Es bastante probable […]”, se normen dentro de una teoría matemática.
De tal manera, los eventos imposibles tengan probabilidad 0 y los eventos seguros probabilidad 1, de los que se asignan valores entre 0 y 1 ante las probabilidades de que sucedan.

Se tiene una bolsa opaca con 20 canicas, iguales en todos aspectos salvo en el color: 15 de ellas son blancas y 5 rojas. Si se agita la bolsa de tal manera que se mezclen bien las canicas y sin mirar adentro de la bolsa, se toma al azar una canica.
Entonces ¿cuál color de canica saldrá?
No se está seguro del color de la canica que saldrá, ya que el resultado depende del azar.
Y si se apuesta a favor de un color antes de sacar la canica, debe ser de manera racional y no confiando meramente en la suerte.
Así se debe determinar cuál de los dos colores tiene mayor probabilidad.
El anterior es un buen ejemplo del problema probabilístico.
Se tiene una experiencia aleatoria, en donde no se produce el mismo resultado cada vez que se repite en las mismas condiciones.
El problema consiste en determinar cuál de los eventos —“extraer una canica blanca” o bien “extraer una canica roja”— es más probable. En este caso la solución al problema es sencilla.
Son 15 canicas blancas contra 5 rojas; hay más posibilidades de escoger una canica blanca que de escoger una roja. Es decir, es mayor la probabilidad de escoger una canica blanca.
Dado que, en la bolsa, 15 de un total de 20 canicas son blancas, la probabilidad de sacar una canica blanca es de 3/4, 0.75 o 75%, según se exprese como una fracción, un decimal o en forma de porcentaje.

El problema anterior condujo finalmente a una consideración de la forma: Tal evento tiene “n” formas de ocurrir sobre un total de “N” posibilidades.
Este cociente, con algunas precisiones que se explican a continuación, se conoce como la “Fórmula clásica de la probabilidad”:
Si el que todos los eventos tienen condiciones iguales de ocurrencia.
Si se conoce el número total de resultados posibles “N”.
Y si se sabe el número de resultados favorables al evento que te interesa “n”.
Entonces, se puede ocupar la Fórmula Clásica de la probabilidad.

Se realiza esto para el ejemplo de escoger aleatoriamente a un alumno del Grupo “3ro A”, con relación a sus talleres, y se complementa la idea empírica ya formulada.
Primero se verifica si cumple con las condiciones: ¿Cualquier alumno tiene las mismas probabilidades de ser escogido?
Según el enunciado de la situación, todo el grupo está en el patio de la escuela y se puede seleccionar a cualquier alumno. Por lo tanto, todos los resultados son igualmente probables.
¿Cuál es el número total de resultados posibles?
Aunque no se tiene el dato de manera explícita, la suma de cada uno de los datos permite conocer el total de alumnos del grupo 3ro A.
Son 15 alumnos en informática, más 3 en el taller de dibujo, más 22 en el taller de corte y confección, y 10 más en conservación de alimentos para un total de 50 alumnos.

El número total de casos favorables al evento se encuentra en la tabla. Son 15 en informática, 3 de dibujo, 22 de corte y confección y 10 en conservación de alimentos.
Entonces, si todos los resultados son igualmente probables, la probabilidad se obtiene calculando el cociente:
Probabilidad de (A) es igual al número de casos favorables entre el número de total de casos.

Para la probabilidad de escoger al azar un alumno del taller de informática se tiene que:
La Probabilidad de (i) es igual a casos probables que son 15, entre el número total de casos, que son 50.
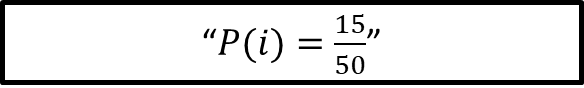
Se reduce la fracción a su mínima expresión para obtener la forma fraccionaria de la probabilidad, que es igual a 3 décimos.
Se hace la división de 3 entre 10 para obtener su forma decimal, o se multiplica por 100 para obtener su porcentaje, el 30%.

Para el resto de los talleres, el cálculo de la probabilidad clásica es:
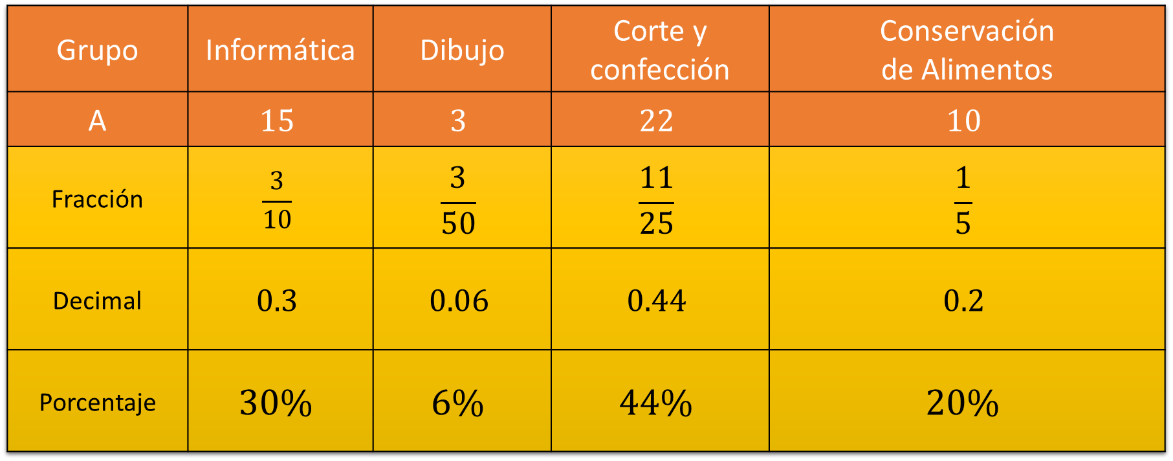
Dibujo son: 3 de 50, que es irreducible: 0.06 en su forma decimal que representa el 6% de las probabilidades.
Corte y confección, 22 de 50 y se reduce a 11 veinticincoavos: 0.44 en su forma decimal y representa el 44% de las probabilidades.
Conservación de alimentos con 10 alumnos de 50: Se reduce a 1/5 en forma de fracción, 0.2 en su forma decimal y representa el 20% de la probabilidad.
De este modo, ya se tiene la certeza matemática de los posibles resultados del experimento, y no solo una intuición del análisis de los datos.
Observa el siguiente video.
- Probabilidad frecuencial de un evento
https://www.youtube.com/watch?v=Ld7RcoVl6Dk

La idea de simular consiste en explorar el comportamiento de una experiencia aleatoria observando otra experiencia equivalente, pero más fácil de realizar o de estudiar.
La situación que consiste en extraer al azar una o más canicas de una bolsa en donde hay diversos colores, es uno de los modelos universales de la probabilidad.
Esto se debe porque a través de él se puede representar y resolver casi cualquier problema donde intervenga un número finito de resultados posibles.
También puede utilizarse para simular casi cualquier experiencia aleatoria con las mismas características.
Por ejemplo, analiza “El problema del agente de ventas”:
Un agente comercial sabe que cada vez que visita un cliente tiene 20% de probabilidades de hacer dos ventas; 50% de probabilidades de hacer sólo una y 30% de no hacer ninguna.
Un día tiene cita con cinco clientes: ¿Cuánto puede esperar ganar ese día si por cada venta que realiza gana $20?
Para simular la situación del ejemplo, se ponen dos canicas azules, cinco blancas y tres rojas en una bolsa. Después, se extrae una a una al azar, cinco canicas de la bolsa, devolviendo cada vez dentro de la bolsa la canica que se consiguió antes de la siguiente extracción.
Dependiendo de lo que salga, se puede decir:
Si sale azul, el agente hizo dos ventas y ganó $40.
Si sale blanca, sólo hizo una venta y ganó $20.
Si sale roja, no hizo ninguna venta y no ganó.
Llevando una estadística de lo que ocurre al repetir varias veces el experimento anterior, se llega a estimar con alta exactitud la cantidad que el agente puede esperar ganarse ese día.
Se conoce otro ejemplo que, aunque es posible realizar el experimento en la vida real, se facilita con la simulación.
Cinco personas desconocidas se suben al elevador de un edificio de 10 pisos.
¿Es grande o es pequeña la probabilidad de que dos personas bajen en un mismo piso?
Para simular esta situación, se meten en una bolsa 10 pelotas marcadas con los números del 1 al 10, que representan los 10 pisos del edificio. Después, se extraen cinco pelotas al azar, devolviendo una a la bolsa cuando se consigue otra pelota, antes de realizar la siguiente extracción.
Los resultados que se obtengan muestran en cuáles pisos bajaron las personas y permite comprobar si hubo dos que descendieron en el mismo piso.

En algunos de los ejemplos de cálculo de probabilidades hay un elemento muy interesante: En un momento dado, un razonamiento del estilo: “la probabilidad de que esto junto con esto otro suceda”.
Por ejemplo, supón que se arrojan simultáneamente un dado y una moneda del que se quiere calcular la probabilidad de obtener un cinco y un sol.

La probabilidad de obtener un cinco al arrojar un dado es 1/6, y la probabilidad de que salga sol en un volado es 1/2.
Entonces, la probabilidad de obtener un cinco y un sol al lanzar simultáneamente un dado y una moneda es igual a: 1/6 por 1/2 igual a 1/12.
En el diagrama de árbol del experimento se observa que al final son 12 resultados posibles, y solo 1 de ellos cumple con la condición de “cinco y Sol”.
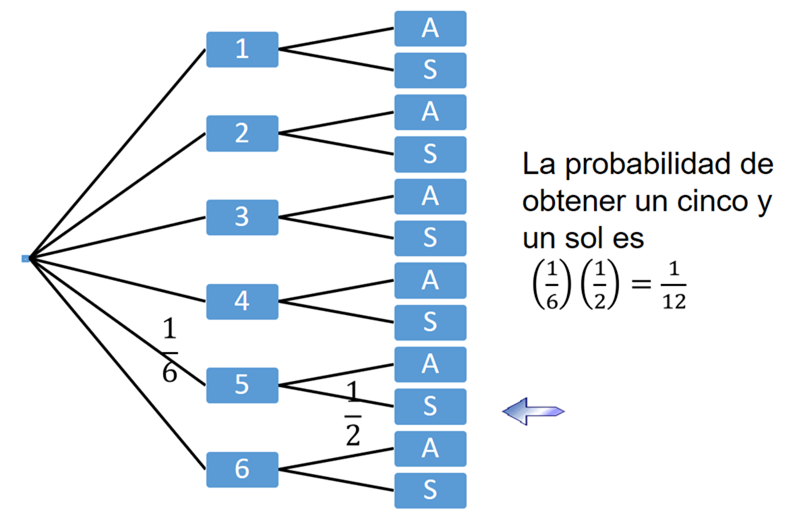
¿Qué significa la condición de que los eventos A y B sean independientes? Que la ocurrencia de cualquiera de ellos no afecta la probabilidad de ocurrir del otro.
Dicha condición da por sentado que satisface el ejemplo anterior: Si sale cinco al arrojar un dado, esto no afecta la probabilidad de obtener sol al realizar un volado y recíprocamente, el resultado en el dado no afecta el del volado.
Pierre Simón de Laplace, un gran matemático francés y pionero de la probabilidad, afirmaba que esta disciplina es, en el fondo, “sentido común reducido a cálculos”.
Esta idea puede interpretarse como un proceso en donde las primeras apreciaciones probabilistas se transforman en conceptos y enunciados cada vez más precisos, a los cuales será luego posible aplicarles el poder analítico de las matemáticas.
El Reto de Hoy:
Para resolver dudas o ejercitar lo aprendido, te puedes apoyar en tu libro de texto.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Las claves para exigir la rendición de cuentas
Aprendizaje esperado: Analiza la legitimidad de la autoridad y su desempeño con base en la rendición de cuentas, la transparencia y el acceso a la información pública.
Énfasis: Identificar conceptos clave en la exigencia de rendición de cuentas.
¿Qué vamos a aprender?
Como sabes, en nuestro país, las autoridades son electas por vías democráticas. Pero su legitimidad no sólo debe estar presente cuando acceden al cargo, mediante elecciones limpias, pues una vez que están en funciones deben respetar las leyes y actuar con honestidad. Su comportamiento se puede verificar mediante la transparencia, el acceso a la información pública y la rendición de cuentas.
Existen leyes que respaldan la rendición de cuentas. Esta es un ejercicio obligatorio de las autoridades públicas que consiste en informar a las y los ciudadanos cuáles han sido las acciones concretadas, a fin de que sean revisadas y se determine si responden al interés y bienestar de la población.
La obligación que tiene la autoridad de informar periódicamente es el derecho a la información que tiene la ciudadanía, establecido en el artículo 6° constitucional y que está garantizado en La ley General de Transparencia y Acceso a la Información Pública, donde se establecen los principios, bases y procedimientos para garantizar el derecho de acceso a la información en posesión de cualquier autoridad o persona que reciba y ejerza recursos públicos o realice actos de autoridad en las entidades federativas y municipios.
En esta ocasión, identificarás los “Conceptos claves en la exigencia de la rendición de cuentas de las autoridades”.
Podrás profundizar sobre estos conceptos, pero debes comenzar por conocer sobre la importancia de la rendición de cuentas.
Además de tu libro de texto, ten a la mano tu libreta de apuntes y un bolígrafo, pues seguramente anotarás ideas, inquietudes y reflexiones.
También se te sugiere dialogar con los miembros de tu familia acerca de lo que ha significado, para ellas y ellos, que su opinión sea tomada en cuenta por parte de las autoridades, para determinar qué obras públicas se tienen que realizar, así como el que la autoridad del país, entidad o municipio, rinda cuentas sobre su actuación.
¿Qué hacemos?
Cómo puedes observar, la rendición de cuentas es muy importante para la vida en una sociedad democrática, todas y todos tienen derecho a ejercerla.
Observa y escucha la siguiente cápsula para recordar algunas palabras claves que te ayudarán a comprender mejor el tema, toma nota:
- Resumen rendición de cuentas
Existen avances en materia legal para garantizar la rendición de cuentas. Cada vez hay más ciudadanas y ciudadanos que ejercen su derecho a conocer y evaluar las acciones de las autoridades, así lo demuestran las solicitudes de acceso a la información que diariamente recibe el INAI.
La rendición de cuentas te permite conocer la forma en que se gobierna con claridad. También es útil para que las y los ciudadanos puedan exigir o promover mejores formas de hacer obras públicas que atiendan las necesidades de la ciudanía y beneficien a la sociedad.
Asimismo, debes saber que, para ejercer este derecho, es conveniente que las y los gobernantes y servidores públicos tengan determinadas cualidades.
Sobre este punto, la maestra Caren Irán Navarro Valenzuela realizó un foro de discusión con un grupo de adolescentes, observa y escucha qué es lo que comentaron al respecto.
- La transparencia para legitimar la democracia
Reflexiona sobre los temas que se expusieron. Sobre todo, es importante conocer más sobre el derecho al acceso a la información.
La reflexión que realizan las alumnas y los alumnos en torno a la rendición de cuentas, su utilidad y qué se requiere para que la ciudadanía cuente con una rendición de cuentas efectiva.
Un primer aspecto que se tendría que destacar es que las y los adolescentes consideran que tienen derecho a estar enterados de lo que pasa en la sociedad. Asimismo, señalan que las y los adultos tienen una idea equivocada de ellos, pues mencionan que no les interesa lo relacionado con los temas políticos, que son apáticos e indiferentes a los asuntos públicos y a las acciones que llevan a cabo las y los gobernantes.
Asumen que esto es posible, pero la sociedad se tendría que preguntar el motivo por el cual algunas y algunos adolescentes actúan de esta manera. ¿Será que ello es ocasionado porque se sienten excluidas y excluidos de las decisiones públicas y que sus opiniones no son tomadas en cuenta por gobernantes, autoridades y sociedad en general?
Destacan la importancia de conocer las leyes, pues éstas garantizan sus derechos en general y, en específico, el derecho que tiene la ciudadanía a conocer cómo se gastan los recursos públicos y la actuación de las y los funcionarios de gobierno.
Resulta de gran interés abrir espacios de comunicación donde la voz de la juventud pueda ser escuchada.
Revisa con atención el siguiente caso.
Un presidente municipal contrató a una empresa para construir una escuela, un centro comunitario y dos espacios para deportes en una de las zonas más pobres del municipio, pero al terminarse su administración, la construcción del platel educativo solamente se quedó a medias y las demás obras no se cumplieron.
Las y los pobladores nunca recibieron explicaciones por parte de las autoridades. Además, se cree que la empresa encargada de las obras era de propiedad del cuñado del presidente municipal.
Un grupo de personas de la comunidad quieren saber:
- ¿Quiénes son los dueños de la empresa que se contrató y cuánto se les pagó?
- ¿Qué otras empresas presentaron ofertas para las obras y por cuánto dinero?
- ¿En qué tiempo debían entregar las obras?
- ¿Qué funcionarios firmaron los contratos?
- ¿Por qué no se han terminado las obras y qué sanciones tendrá la empresa por este motivo?
- ¿Cómo puedes ayudar a las y los habitantes de ese municipio para que puedan tener respuesta a las preguntas que realizan?
- ¿Crees que conocer estas cuentas es del interés de las personas que solicitan la información? ¿Por qué? ¿Crees que esta información debe darse a quienes la solicitan? ¿Por qué? ¿Qué podrían hacer las personas de la comunidad con esa información?
A partir de lo que se ha mencionado en programas anteriores y lo que has aprendido hasta el momento, debes recordar que existen leyes que garantizan nuestro derecho a solicitar información a nuestros gobernantes sobre las obras públicas que realizan durante su gestión.
Este es un derecho consagrado en nuestra Carta Magna, por lo cual, las ciudadanas y los ciudadanos del municipio al que se hace referencia, estarían ejerciendo su derecho a contar con información relacionada con las obras públicas que se estaban realizando y que no se concluyeron.
Como ya se ha mencionado, en un gobierno democrático es importante que la autoridad explique los actos y decisiones que lleva a cabo durante su gestión, pues ello le permite ganar legitimidad ante la sociedad.
Asimismo, la ciudadanía puede ejercer el derecho a demandar transparencia y acceso a la información pública sobre las obras que se realizan en su municipio, entidad o país.
Esta es una manera de participar en las decisiones públicas, pero esto se tiene que realizar a partir de las instituciones y mecanismos establecidos en las leyes, las cuales obligan a las instituciones a atender las peticiones ciudadanas.
De acuerdo a sus atribuciones, las autoridades y servidores públicos deben brindar a la ciudadanía la información que solicita, siempre y cuando no esté reservada por razones de seguridad y no se refiera a la vida privada de los gobernantes, autoridades o servidores públicos.
En este caso, es importante señalar que el artículo 6º de la Constitución Política de los Estados Unidos Mexicanos, indica que todas y todos tienen derecho a la información y para garantizarlo, se elaboró la Ley Federal de Transparencia y Acceso a la Información Gubernamental.
Producto de esta ley, en el año de 2002 se creó el instituto Nacional de Transparencia, Acceso a la Información y Protección de Datos Personales (INAI), que tiene una representación en cada una de las entidades federativas.
La ley obliga a todas las Instituciones de gobierno a publicar y actualizar en sus sitios web, información como:
- Nombre y cargo de todos sus funcionarios
- Sueldos
- Programas públicos
- Obras
- Servicios contratados
- Informes periódicos de sus actividades, y
- Responder a solicitudes de información, siempre que ésta no esté reservada por razones de seguridad y no refiera a la vida privada de las y los servidores públicos.
No se necesita justificar por qué se requiere información, pero se debe solicitar por escrito, ya sea que se llene la solicitud electrónica, se utilice un formato disponible en la página del INAI, o se redacte un texto libre con el nombre completo del solicitante, domicilio, correo electrónico (opcional) y la descripción de la información requerida.
La solicitud se envía a través de la página del INAI, por mensajería o se entrega personalmente en las oficinas de la dependencia correspondiente. La respuesta debe llegar en un plazo máximo de 20 días después de la fecha de entrega.
Una de las funciones que tiene el INAI es garantizar la protección de los datos personales de las y los ciudadanos, gobernantes, autoridades y servidores públicos.
Para conocer más al respecto, observa y escucha el siguiente vídeo, en el cual se describen los riesgos de compartir sus datos personales.
- Protección de datos personales
En una sociedad democrática, es importante que existan leyes e instituciones encargadas de proteger los datos personales, pues además de ser un derecho ciudadano, permite evitar situaciones que ponen en riesgo nuestra tranquilidad.
Realiza la siguiente actividad con el apoyo de tu familia:
1.-Entrevista a tus familiares o investiga en periódicos locales o nacionales, situaciones que se relacionen con los siguientes casos:
Un ejemplo de rendición de cuentas, en el cual, la autoridad informa y explica de manera transparente y honesta sus decisiones y su actuación, de modo que la comunidad tenga información objetiva, oportuna y completa.
Un caso en el cual se piden cuentas a una autoridad y su respuesta no es objetiva, transparente, ni completa por lo cual no satisface a la ciudadanía.
2.- Redacta cada uno de los casos, explicando ampliamente las situaciones.
Consultar tu libro de texto de Formación Cívica y Ética de tercer grado, para saber más sobre la transparencia y la rendición de cuentas. También puedes consultar el portal del INAI.
El Reto de Hoy:
Dirige a las y los servidores públicos de tu comunidad una carta en la que valores su desempeño y también sugiéreles un modo de actuación apegado a la legalidad y a los principios de transparencia, acceso a la información y rendición de cuentas.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
¿Cuáles son las regularidades de la tabla periódica?
Aprendizaje esperado: Identifica la información de la tabla periódica, y analiza sus regularidades y su importancia en la organización de los elementos químicos.
Énfasis: Explicar la valencia e identificar las regularidades de elementos químicos representativos como el radio atómico y la electronegatividad.
¿Qué vamos a aprender?
Lee la siguiente frase:
“Si una persona es perseverante, aunque sea dura de entendimiento, se hará inteligente; y aunque sea débil se transformará en fuerte”.
Leonardo Da Vinci.
Los materiales que utilizarás son tu cuaderno de Ciencias. Química, tu libro de texto, tabla periódica de los elementos, lápiz, colores y bolígrafo.
¿Qué hacemos?
En el mundo de los átomos existe una capacidad de combinación llamada valencia.
En química se le llama valencia a la capacidad de combinación de un átomo de determinado elemento. Según los modelos atómicos que se emplean hoy en día para explicar el comportamiento de la materia, los electrones en el átomo están acomodados en distintos niveles de energía.
A los electrones que se encuentran en el último nivel se les llama electrones de valencia, y son los responsables de los enlaces entre átomos para formar compuestos.
Como recordarás, el número atómico define el número de protones y en un átomo eléctricamente neutro es igual al número de electrones, es decir, que tienen igual número de cargas positivas y de cargas negativas.
Sin embargo, en una reacción química, al ceder o ganar electrones, pueden alterar su carga eléctrica; a los átomos con carga eléctrica se les denomina iones.
Cuando un átomo cede electrones, queda con exceso de protones, por lo que su carga eléctrica será positiva; a estos se les llama cationes.
Si un átomo acepta electrones, queda con exceso de cargas negativas y forma aniones.
Es importante saber qué elementos de la tabla periódica pueden ceder y aceptar electrones. En la fórmula química de un compuesto, como son sales binarias, primero se escribe el símbolo del elemento que cede electrones y que queda con carga positiva, y después se escribe el símbolo del elemento que acepta electrones y que queda con carga negativa.
Mendeléyev fue un científico ruso que postuló que los elementos tienen propiedades periódicas y los ordenó en la primera propuesta de la tabla periódica de los elementos.
Uno de los criterios que utilizó Mendeléyev para clasificar a los elementos, fue el tipo de compuestos que forman con el hidrógeno y el oxígeno. Por ejemplo, los elementos del grupo 1, hidrógeno, litio, sodio, potasio, rubidio, cesio y francio, a los que representarás con la letra R, forman óxidos con el oxígeno, cuyo símbolo es O, formando compuestos con fórmula R2O, la cual, significa que un átomo de oxígeno se combina con dos átomos de los elementos de ese grupo.
Si lo analizas permite obtener la valencia de los elementos involucrados.
Cabe mencionar que el subíndice 1 del oxígeno por convención, no se escribe, pero se muestra en los siguientes ejemplos para hacer explícita la valencia del elemento positivo.
Por ejemplo, toma al hidrógeno, que está en el grupo 1, recuerda que su símbolo es H. Al sustituir en la fórmula R2O, queda H2O, la fórmula del agua, también llamado óxido de hidrógeno.
Puedes encontrar con facilidad la valencia que tienen los elementos; observa, el hidrógeno tiene el subíndice 2, que corresponde a la valencia del oxígeno y éste tiene subíndice 1, que corresponde a la valencia del hidrógeno.
Es importante verificar que el compuesto debe de ser eléctricamente neutro, lo cual le da estabilidad a una sustancia.
Como en la fórmula primero se escribe el símbolo del elemento con carga positiva y después el símbolo del elemento con carga negativa, entonces los números de oxidación quedan de la siguiente manera.
Hidrógeno +1
Oxígeno -2.
Trabaja el ejemplo del siguiente elemento que es el litio, para formar el óxido de litio. Recuerda que la fórmula general es R2O, por lo tanto, sustituyes R y colocas el símbolo del litio Li, anotas el subíndice 2 y después el símbolo del oxígeno.
Por lo tanto, la fórmula es Li2O, la valencia del oxígeno se puede deducir por el subíndice del litio que es dos, asimismo, la valencia del litio se puede deducir por el subíndice del oxígeno que es 1.
Como primero se escribe el símbolo del elemento con carga positiva, el número de oxidación del litio es de +1, después se escribe el símbolo del oxígeno al tener carga negativa, su número de oxidación es de -2. Sin embargo, puede variar dependiendo de los compuestos que forme el oxígeno con otros elementos.
Ahora ya puedes obtener la fórmula y las valencias de los elementos del grupo 1. En el caso de los elementos del siguiente grupo de la tabla periódica. Si interaccionas químicamente el oxígeno con los elementos del grupo 2, la fórmula que puedes utilizar es RO, debido a que ambos tienen valencia 2 donde R puede ser berilio, magnesio, calcio, estroncio, bario o radio; el símbolo del oxígeno es O.
Ahora arma la del óxido de berilio. Considera la fórmula RO, sustituye R por el símbolo del berilio que es Be, enseguida se escribe el símbolo del oxígeno que es O, y la fórmula queda como BeO. La fórmula queda así porque, como ya se mencionó anteriormente, ambos elementos tienen valencia 2, y al ser iguales se pueden omitir los subíndices
Toma en cuenta cómo primero se escribe el símbolo del elemento con carga positiva y después el símbolo del elemento con carga negativa, el número de oxidación del berilio es +2 y el del oxígeno es de -2.
En la tabla periódica puedes encontrar muchos datos importantes. En esta ocasión te enfocarás en la valencia. Puedes encontrar este dato en la siguiente tabla.
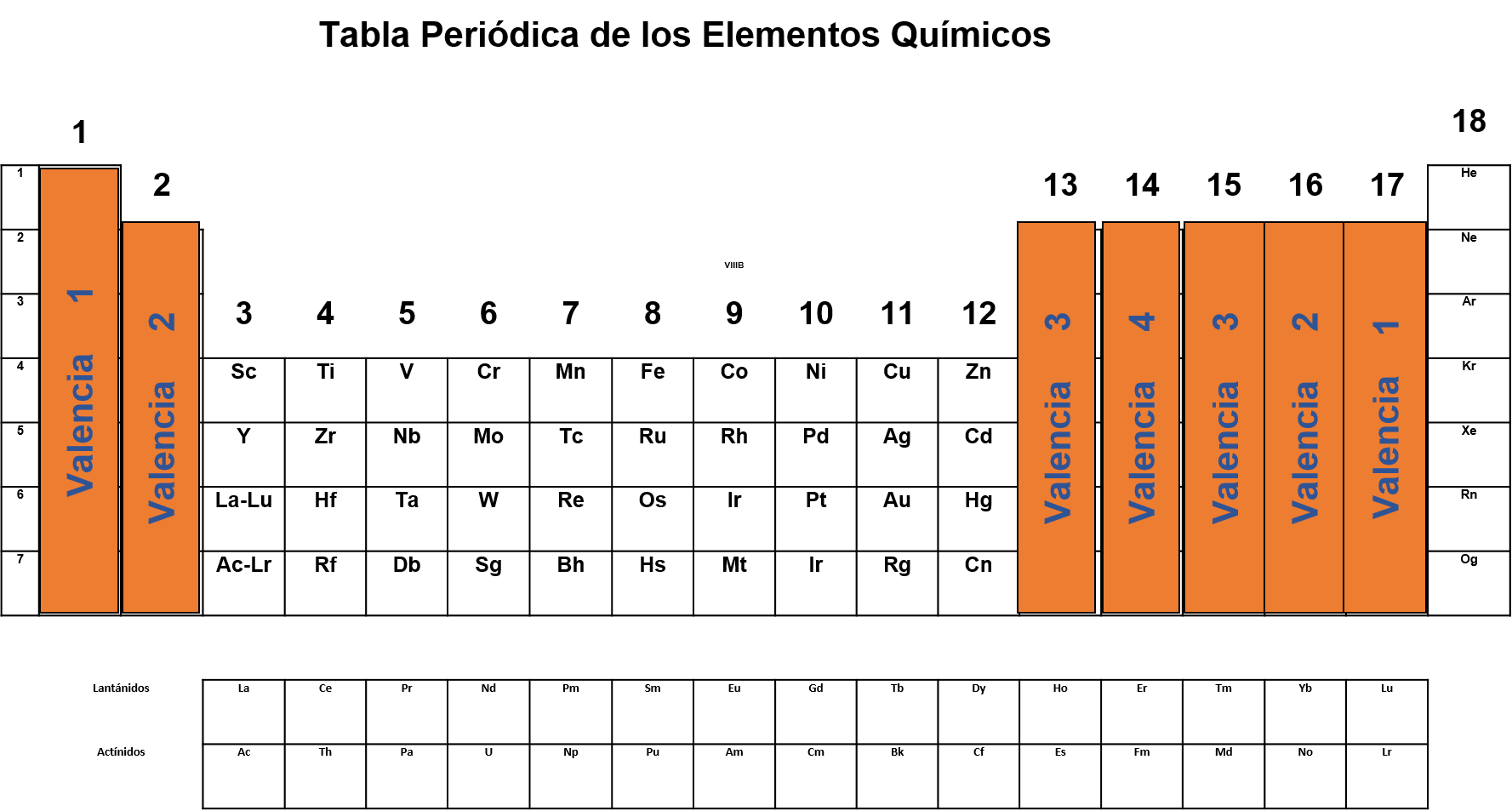
Cabe señalar que valencia y número de oxidación no son lo mismo, la carga que presenta un elemento en un compuesto químico representa su número de oxidación, el cual depende o está relacionado con la valencia. Para un halógeno le es más fácil ganar un electrón que perder 7, por lo que al formar compuestos tiene a ganar un electrón y por lo tanto a adquirir una carga 1- Es por eso que puedes considerar que la valencia, definida como la capacidad para combinarse de los halógenos, es de 1.
Cuando un metal interacciona químicamente con un halógeno se forma el halogenuro del metal, por ejemplo, el cloruro de sodio y el fluoruro de potasio, entre otros.
Diseña un juego de memorama, para lo cual necesitarás el siguiente material.
- 14 tarjetas de 10 centímetros de cada lado en cartulina color blanco
- 7 tarjetas de 10 centímetros de cada lado en cartulina color azul claro
- Marcadores de agua del color que desees
Primero coloca en siete tarjetas blancas a los halógenos con su símbolo, nombre y valencia; así como en otras siete su par, que será un metal que contendrá el nombre, símbolo y valencia de los elementos del grupo uno. Las tarjetas de color azul tendrán la formula y nombre del compuesto.
El juego comienza cuando uno de los jugadores destapa una tarjeta azul, la cual contiene el nombre y la fórmula del compuesto, después buscará en dos tarjetas blancas a los elementos indicados en la fórmula, las levantará y las enseñará a los jugadores. Si acierta se quedará con las tarjetas y ganará un par de tarjetas blancas.
Eventualmente el segundo jugador destapara una tarjeta azul, observará la fórmula y buscara en las tarjetas blancas a los elementos indicados en la fórmula. En caso de no coincidir con los elementos de la fórmula, volverá a voltear las tarjetas y continuará el juego hasta que los jugadores hayan completado con las tarjetas blancas las fórmulas indicadas en las tarjetas de color azul.
Puedes modificar el juego con algunas variantes colocando el oxígeno para formar óxidos, con el azufre, para formar sulfuros y en la medida que te familiarices con otros cationes y aniones.
Es importante mencionar que esta fórmula para conocer las valencias de los elementos químicos sólo es aplicable para aquellas fórmulas químicas que están formadas por dos elementos, es decir, compuestos binarios.
Se considerará la estructura de Lewis para explicar la valencia. Comenzarás con mencionar que los electrones que están en la órbita o nivel de energía más alejado del núcleo, son los que pueden representarse en la estructura de Lewis, ya que son los electrones de valencia los que intervienen en la formación de un compuesto.
Recuerda que los grupos de los elementos representativos tienen el siguiente número de electrones de valencia que se encuentran en la órbita o nivel de energía más alejado del núcleo.
Si quieres que el carbono interaccione químicamente con el hidrógeno para formar metano, cuya fórmula es CH4, considera la estructura de Lewis de cada elemento.
El carbono, al estar en el grupo catorce, tiene cuatro electrones de valencia representados con puntos; el hidrógeno, al estar en el grupo uno, tiene un electrón de valencia, representado con una “X”.
Entonces, el carbono para completar su última órbita o nivel de energía con ocho electrones puede aceptar cuatro electrones de valencia que, en este ejemplo, compartirá con cada uno de los electrones de los cuatro átomos de hidrógeno; de esta manera logra su estabilidad alcanzando la configuración del neón y cumple así la regla del octeto. Lo anterior sucede porque el carbono tiene una valencia de 4, por lo que puede formar la molécula de metano CH4.
Como el hidrógeno tiene valencia de uno, entonces su único electrón de valencia que se encuentre en la órbita o nivel de energía, tiende a compartirlo con otro electrón de átomos iguales o diferentes para lograr su estabilidad. En este caso, comparte con los átomos del carbono, los correspondientes electrones de valencia de manera que logra la configuración del helio con dos electrones de valencia en su nivel de energía.
Recuerda que los átomos eléctricamente neutros cuentan con varias propiedades periódicas, una de ellas es el radio atómico.
El radio atómico se define como la mitad de la distancia ente dos núcleos atómicos adyacentes de un elemento.
Realiza la siguiente actividad para organizar a estos elementos de mayor a menor radio atómico, serian aluminio, calcio y cesio
Primero debes conocer qué es el radio atómico. El radio atómico se define como la mitad de la distancia entre 2 núcleos atómicos adyacentes de un elemento.
Observa de qué modo esta propiedad periódica depende de las interacciones entre el núcleo y los electrones de un átomo.
Recuerda que la tabla periódica de los elementos consta de 118 elementos reconocidos por la
Para las siguientes actividades te enfocarás sólo en algunos de ellos. Observa la siguiente tabla, en la cual se muestran la mayoría de los elementos representativos, en particular, los grupos 1 y 2, así como los del 13 al 18, y los períodos del 1 al 6.

El radio atómico es una distancia, por lo tanto, tendrá unidades de longitud y como las distancias son tan pequeñas, empleas una unidad llamada picómetro (pm); esta es una unidad de longitud equivalente exactamente a la billonésima parte de un metro, que expresado en notación científica es de 1 x 10-12 m.
Por ejemplo, la bacteria del escherichia coli tiene una longitud de 2 x 10-3 picómetros.
Así como algunas bacterias son tan pequeñas, ¿cómo crees que son los tamaños de los radios atómicos de los elementos?
Analiza, el cesio tiene un radio atómico de 343 pm, el litio de 152 pm y el helio de 31
Observa qué le sucede al radio atómico de algunos elementos del segundo período al ir desplazándonos de izquierda a derecha.

Se tiene al litio en el grupo 1, período 2, con un radio de 152 pm.
Sigue con el berilio en el grupo 2, período 2, y un radio de 112 pm.
Ahora el boro, en el grupo 13, período 2, y un radio atómico de 85 pm.
¿Qué es lo que observas?
¿Qué sucede conforme te mueves a la derecha en el período? Disminuye el radio atómico.
Al aumentar el número de protones en el núcleo, también se agregan electrones para que el átomo sea eléctricamente neutro. En un mismo período los electrones se agregan en la misma capa, es decir, a la misma distancia del núcleo y, por lo tanto, al aumentar el número de protones en el núcleo aumenta la fuerza con la que el núcleo atrae a los electrones, ocasionando que disminuya el radio atómico.
Los radios atómicos de los elementos situados en el lado izquierdo de la tabla periódica son mayores que los radios atómicos de los elementos situados del lado derecho en un mismo período.
Ahora observa qué pasa con el radio atómico si se mueve del período 1 al período 6, dentro de un mismo grupo. Revisa el grupo 1.
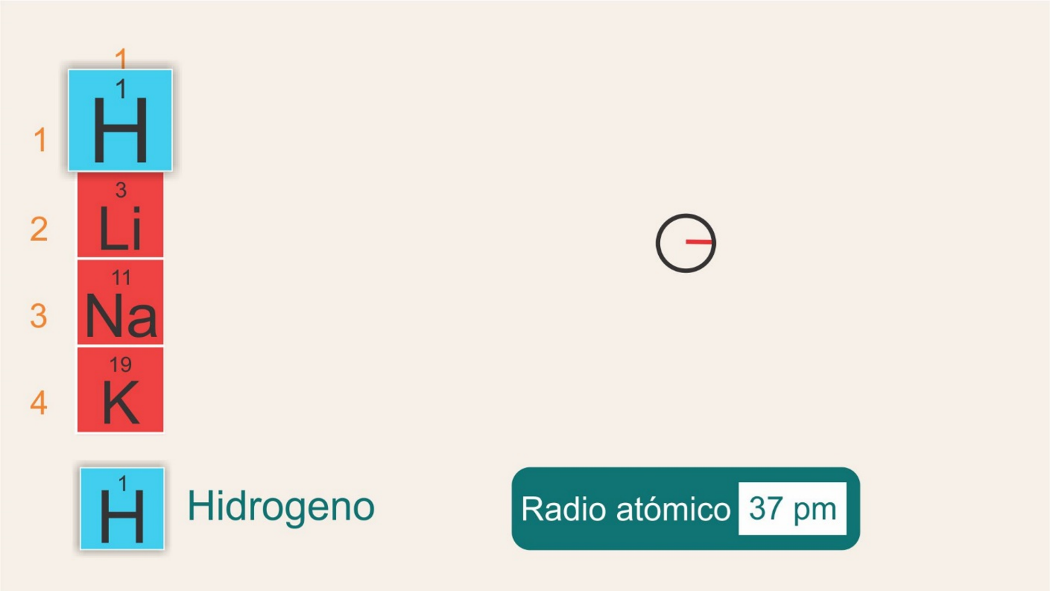
Tienes hidrógeno, situado en el grupo 1, período 1, con un radio de 37 pm.
Luego en el grupo 1, período 2, está el litio, con un radio atómico de 152 pm.
Después el sodio en el período 3, grupo 1, con un radio atómico de 186 pm.
¿Qué notas?
Que fue aumentando el radio atómico conforme ibas bajando de periodos dentro del mismo grupo.
En efecto, los radios atómicos de los elementos que se encuentran en la parte inferior de la tabla periódica normalmente son mayores a los radios de los elementos situados en la parte superior de la tabla.
Por eso el radio atómico es una de las propiedades periódicas de los elementos, ya que presenta cambios constantes y consistentes a lo largo de la tabla periódica. Esto lo pudiste observar en el aumento constante del radio al bajar en un mismo grupo y su disminución constante a lo largo de un mismo periodo.
Entonces, sólo por la posición de los elementos en la tabla periódica podrías saber qué elementos tienen mayor radio atómico. Por ejemplo, quedarían de mayor a menor radio atómico, el cesio, el calcio y el aluminio.
Imagínate el enlace entre átomos diferentes como una “lucha de tira y afloja” por los electrones de valencia. Para usar este modelo de reparto de electrones necesitas tener una forma de determinar la fuerza de atracción que ejerce cada átomo sobre los electrones compartidos, a la medida de esa fuerza se denomina electronegatividad.
La electronegatividad de un elemento se define como la capacidad relativa de un átomo para atraer electrones de otro átomo al enlazarse químicamente y formar un compuesto.
La electronegatividad es una propiedad periódica.
Observa la variación de la electronegatividad; ésta va aumentando de izquierda a derecha a lo largo de los períodos, y de abajo hacia arriba dentro de cada grupo.
Los valores de electronegatividad fueron asignados con base en una escala denominada “escala Pauling”.
Observa la siguiente tabla:
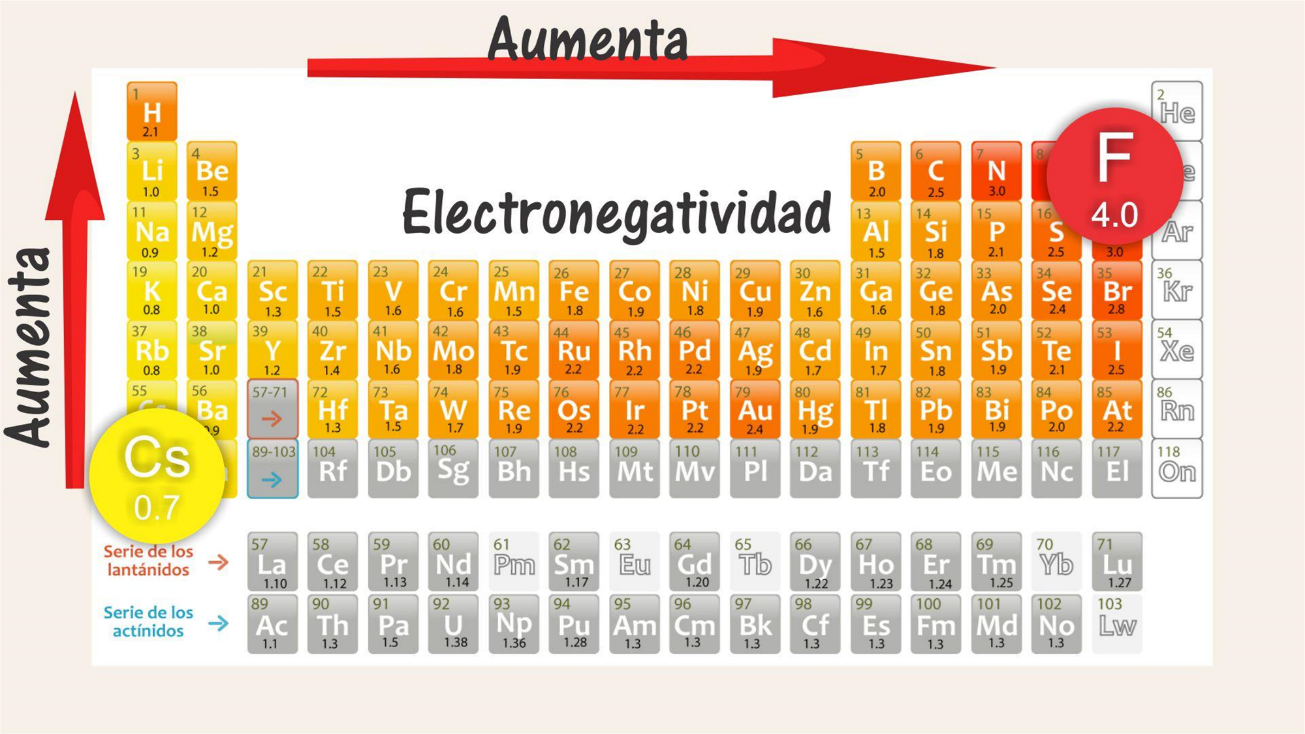
El elemento que presenta el valor más alto, es decir, mayor electronegatividad, es el flúor, que se localiza en el período 2, grupo 17, con 4 unidades Pauling; mientras que los valores más bajos, es decir, con menor electronegatividad, corresponden al cesio y al francio con 0.7 Pauling, cuyos elementos se localizan en el grupo 1, períodos 6 y 7 respectivamente.
¿Entonces quiere decir que la electronegatividad de los elementos en la tabla periódica va aumentando de izquierda a derecha y de abajo hacia arriba y por lo tanto disminuye de derecha a izquierda y de arriba hacia abajo?
Ordena de mayor a menor electronegatividad los siguientes elementos en la tabla periódica.
Los elementos son silicio, bario, oxígeno y galio.
Ubica cada elemento en la tabla periódica; observa que:
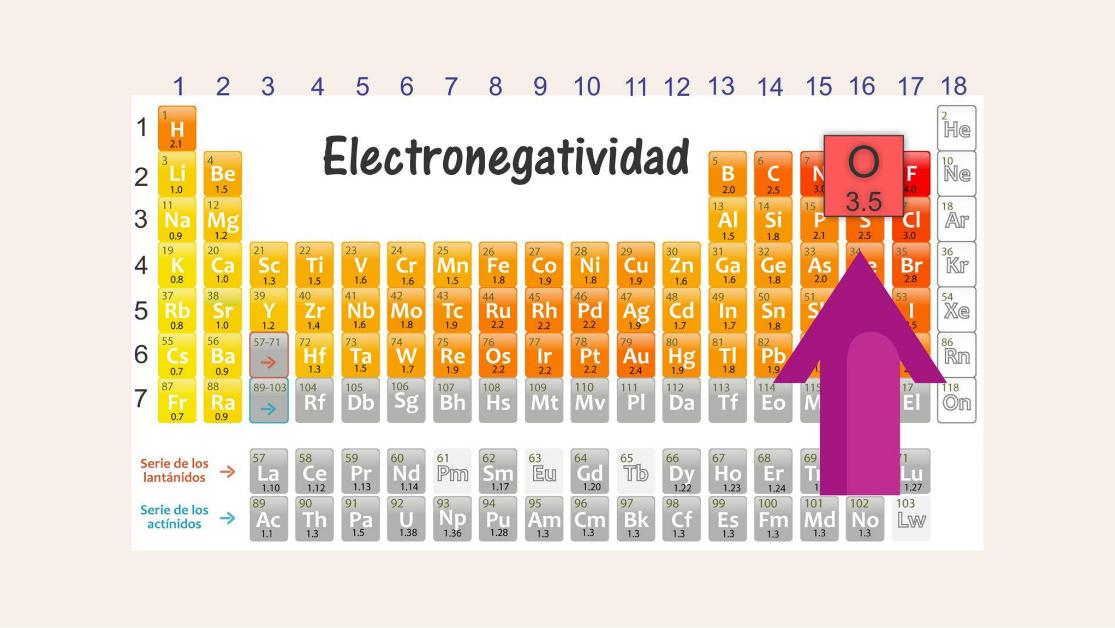
El
El siguiente elemento sería el galio, que ubicas en la tabla periódica, está en el grupo 13, periodo 4, y el de menor electronegatividad sería el bario, por estar en el grupo 2, período 6, y en la tabla de electronegatividad a la izquierda y abajo, disminuyendo su valor de la electronegatividad.
No es tan difícil saber cuáles elementos tienen menor o mayor electronegatividad, sólo es cuestión de recordar hacia qué dirección aumenta o disminuye observando la tabla periódica.
La electronegatividad varía en forma periódica, puedes predecir la diferencia de electronegatividad que existe entre los átomos enlazados observando la distancia que los separa en la tabla.
Recuerda que en la formación de compuestos las diferencias de electronegatividades te pueden indicar qué tipo de enlace químico se está formando, ya sea una covalente polar, covalente no polar o iónico.
Esto tiene una consecuencia en la formación de compuestos, por ejemplo, se forma un enlace iónico entre dos elementos cuando la diferencia de electronegatividad es mayor a 1.7 en la escala de Pauling; tal es el caso del cloruro de sodio, buscas en la escala de Pauling el valor de la electronegatividad de los elementos involucrados, para este caso el sodio y el cloro.
Observa que el cloro tiene un valor en la escala de Pauling de 3.0 y el sodio de 0.9, al restar estos valores obtienes un resultado de 2.1, por lo que el enlace que se forma es iónico.
Linus Pauling se interesó desde muy joven por la naturaleza del enlace químico, inspirado por los artículos de Langmuir y los trabajos de Lewis acerca del comportamiento de los electrones entre átomos. Trabajó en Europa con Sommerfeld y Bohr.
Escribió varios libros, entre ellos La naturaleza del enlace químico.
Se interesó en campos tan diversos como la determinación de la estructura de los cristales, de las proteínas y de los anticuerpos, así como la de la hemoglobina. Por otro lado, luchó para que no hubiera guerras y se opuso a la utilización de armas nucleares. Obtuvo el Premio Nobel de Química en 1954 y el de la Paz, en 1965. Puede considerarse como uno de los químicos más destacados del siglo XX.
En esta sesión recordaste que la valencia es el número de enlaces que un átomo de cualquier elemento puede formar al unirse con otros átomos. La valencia de un elemento es la capacidad de combinación de un átomo con otro similar o diferente.
La tabla periódica permite predecir las propiedades de los elementos con sólo observar su posición dentro de ella, así como realizar comparaciones entre las diferentes propiedades de los elementos.
Por ejemplo, el radio atómico, que aumenta en los períodos de arriba hacia abajo dentro de los grupos y disminuye de izquierda hacia la derecha dentro de los períodos.
La electronegatividad, que utiliza la escala Pauling de 0 a 4. En la tabla periódica puedes observar cómo aumenta de izquierda a derecha y de abajo hacia arriba.
Se te sugiere que observes la sesión del día jueves 29 de octubre para tener más referencias de estos temas. Anota en tu quimi-glosario las ideas clave.
El Reto de Hoy:
Para que puedas reafirmar lo aprendido en esta sesión, se te propone llenar la siguiente tabla. En ella colocarás la valencia, el radio atómico y la electronegatividad.
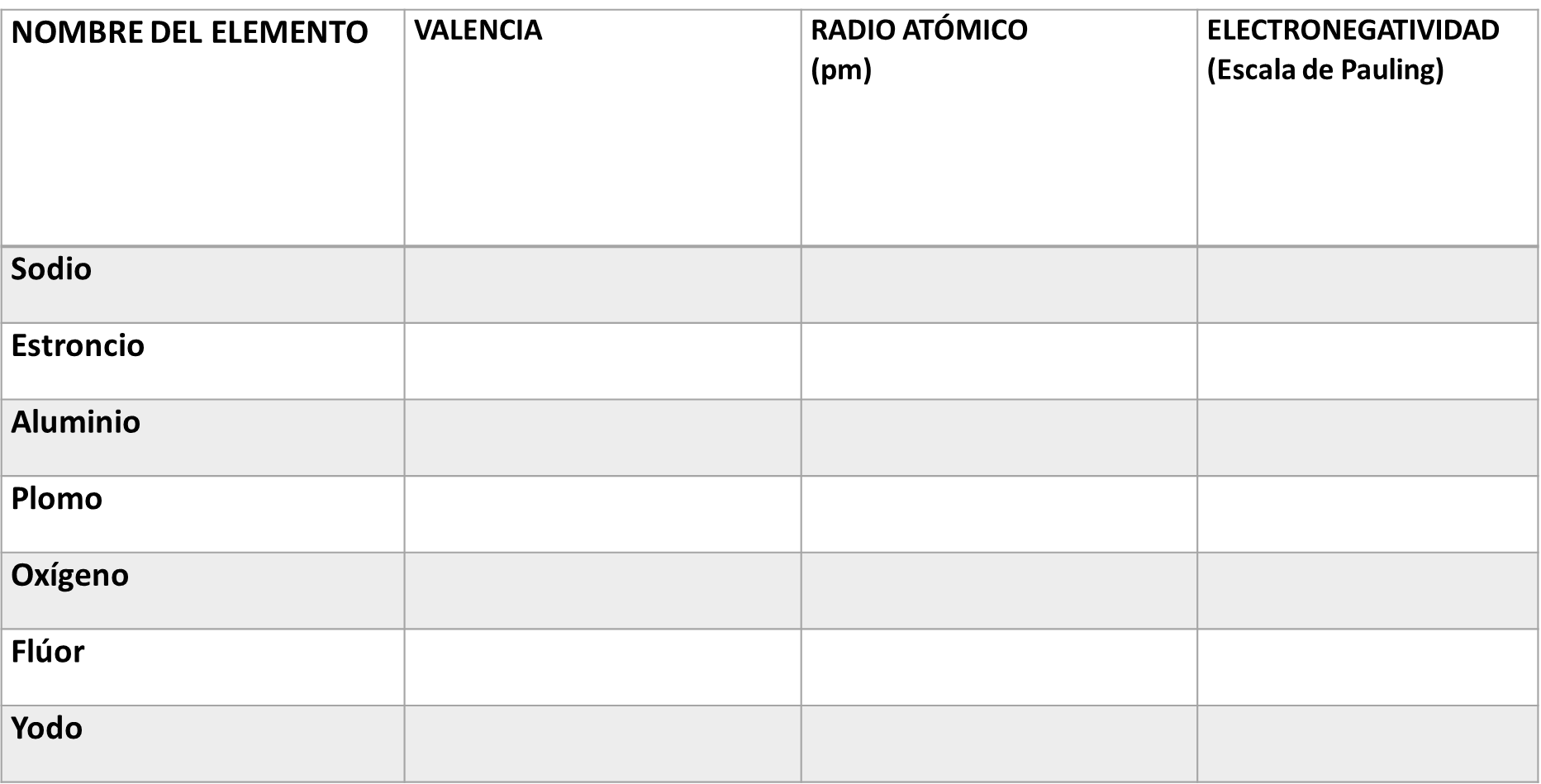
Resuelve el primer elemento químico, que es el sodio;
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon











Publicar un Comentario