Aprende en Casa III SEP: 3 de junio TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 3 de junio de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Jueves 3 de junio, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Volumen de cilindros
Aprendizaje esperado: Calcula el volumen de prismas y cilindros rectos.
Énfasis: Dar sentido y significado al cálculo del volumen de cilindros rectos.
¿Qué vamos a aprender?
En esta sesión resolverás problemas en los que se requiere aplicar la relación entre el volumen y la capacidad de cilindros rectos.
Ten a la mano tu cuaderno, lápiz o bolígrafo, goma y sacapuntas. Así como tu libro de texto. Para que tomes tus notas y escribas las inquietudes que vayan surgiendo.
¿Qué hacemos?
Para iniciar considera el siguiente problema.

Realiza los dibujos que representen los recipientes descritos en el problema. Toma en cuenta que los cilindros rectos están conformados por una superficie curva y dos bases circulares y paralelas. También considera que la distancia perpendicular entre las dos bases de un cilindro, corresponde a su altura.
Mientras dibujas, realiza una estimación de la cantidad de agua que le cabe a cada recipiente. Luego piensen en un procedimiento que los pueda conducir a verificar o corregir su estimación.

Toma un momento.
Ahora analiza detenidamente cada una de las siguientes opciones que se dan para resolver el problema y elije la que consideres más adecuada.

En la opción 1 se propone que la máxima cantidad de líquido que cabe en un recipiente, se relaciona directamente con la cantidad de espacio máximo que hay al interior del recipiente. Por lo tanto, se propone calcular el valor del volumen de los recipientes y el de mayor volumen será al que le quepa una mayor cantidad de agua.
En la opción 2 se propone que la máxima cantidad de líquido que cabe en un recipiente, se relaciona únicamente, y siempre, con la cantidad de área en la superficie del recipiente.
Por lo tanto, se sugiere calcular el área de la superficie curva de cada cilindro y de sus bases y sumar las áreas para calcular el área total de la superficie de cada cilindro. Al cilindro con mayor área será al que le quepa mayor cantidad de agua.
En la opción 3 se propone que la máxima cantidad de líquido que puede contener un recipiente se relaciona directamente con el ancho del mismo. Por lo tanto, se propone que al recipiente con 20 centímetros de diámetro, le cabe una mayor cantidad de líquido.
Anota en tu cuaderno la opción que consideres correcta y trata de justificarla.
Para llegar a un acuerdo, primero reflexiona sobre lo siguiente:
En el problema inicial de los recipientes, se pregunta por el recipiente al que le cabe más agua. ¿Con qué conceptos matemáticos se relaciona la cantidad de agua que cabe en un recipiente?

Considera un objeto cilíndrico sólido como una pila y un objeto cilíndrico hueco como un vaso. Primero señala el espacio que ocupa la pila. Para eso, puedes rodear la pila con una mano. Así estarás señalando el volumen externo de la pila.
Ahora señala el espacio en el vaso que puede ser ocupado por agua o cualquier otra sustancia u objeto. Para eso, puedes introducir una mano al vaso. Así, estarás señalando el volumen interno del vaso.
Al máximo espacio de un recipiente que puede ser ocupado por sustancias u objetos, sin sobrepasar sus límites, se le llama capacidad.
Con base en esto, ¿qué procedimiento se puede seguir para averiguar la cantidad de líquido que cabe en un recipiente?
Para averiguar la cantidad de líquido que cabe en un recipiente se puede medir su capacidad. Es decir, se puede medir el máximo espacio o volumen de los recipientes que puede ser ocupado por agua, sin sobrepasar sus límites.
En el caso del problema, se puede medir el máximo volumen de recipientes cilíndricos rectos que puede ser ocupado por agua. Pero ¿cómo se mide el volumen de un cilindro recto?
Para medir el volumen de un cilindro recto, puedes considerar lo que sabes sobre cómo medir el volumen de prismas rectos cuya base es un polígono regular. Sabes que puedes multiplicar el valor del área de la base de los prismas por el valor de su altura.
¿Cómo se relaciona el cálculo del volumen de un prisma con el cálculo del volumen un cilindro?
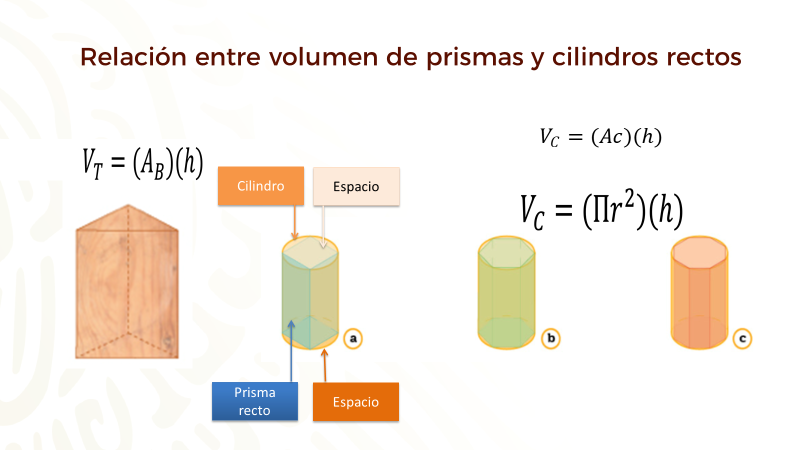
Considera los tres cuerpos que se muestran en la imagen. Observa que cada cuerpo está conformado por un cilindro, un prisma inscrito y un espacio entre el cilindro y el prisma inscrito.
Si observas las bases de estos cuerpos, también hay un espacio entre la superficie poligonal de las bases del prisma y la superficie circular de las bases del cilindro recto.
Conforme aumenta el número de lados de los polígonos de las bases de los prismas y las caras laterales aumentan, el espacio entre el cilindro recto y el prisma, disminuye, y el espacio entre la superficie poligonal de las bases del prisma y la superficie circular de las bases de los cilindros, también disminuye
Si se considera que esos espacios alcanzan ser nulos, entonces, el volumen del cilindro y el del prisma se calculan de la misma forma. Así se puede considerar que el volumen de un cilindro se calcula multiplicando el área de su base por el valor de su altura.
Como la base de un cilindro es un círculo, entonces el volumen de un cilindro se puede calcular multiplicando el valor de “pi”, por el valor del radio de la base circular al cuadrado, por el valor de la altura del cilindro.
Una vez, que te has acordado del procedimiento para calcular el volumen de un cilindro, se puede aplicar éste para resolver el problema inicial.
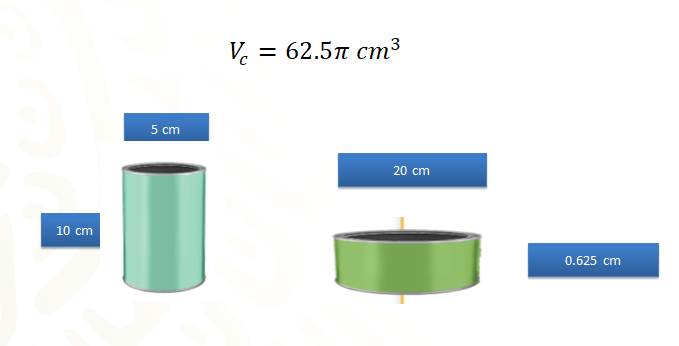
Considera el recipiente con forma de cilindro recto cuyo diámetro de la base mide 5 centímetros y cuya altura mide 10 centímetros.
Como la forma del recipiente es un cilindro, de acuerdo con lo visto anteriormente, su volumen se calcula multiplicando el valor de “pi” por el valor de su radio al cuadrado por el valor de su altura.
En el problema se menciona que el valor del diámetro del círculo de la base es de 5 centímetros.
Como el diámetro de un círculo mide el doble que su radio, entonces el valor del radio del círculo de la base, es de 2 punto 5 centímetros.
Por tanto, el valor del volumen del recipiente se calcula multiplicando el valor de “pi”, por 2 punto 5 centímetros al cuadrado, por 10 centímetros.
Al elevar 2 punto 5 al cuadrado, se obtiene 6 punto 25 centímetros cuadrados. Así, el valor del volumen del recipiente se calcula multiplicando el valor de “pi” por 6 punto 25 centímetros cuadrados por 10 centímetros.
Al multiplicar 6 punto 25 centímetros cuadrados por 10 centímetros se obtiene 62 punto 5 centímetros cúbicos.
Entonces, el valor del volumen del recipiente se puede expresar como “pi” por 62 punto 5 centímetros cúbicos.

Calcula el volumen del otro recipiente. El valor del diámetro de sus bases es de 20 centímetros y el valor de su altura es de cero punto 625 centímetros. De la medida del diámetro se puede desprender que el valor de su radio es de 10 centímetros.
Por tanto, el valor del volumen del recipiente se calcula multiplicando el valor de “pi”, por 10 centímetros al cuadrado, por cero punto 625 centímetros.
Al elevar 10 centímetros al cuadrado, se obtiene 100 centímetros cuadrados. Así, el valor del volumen del recipiente se calcula multiplicando el valor de “pi” por 100 centímetros cuadrados por cero punto 625 centímetros.
Al multiplicar 100 centímetros cuadrados por cero punto 625 centímetros se obtienen 62 punto 5 centímetros cúbicos. Entonces el valor del volumen de ese recipiente se puede expresar como “pi” por 62 punto 5 centímetros cúbicos.

De acuerdo con lo anterior, se obtuvo que, aunque los dos recipientes del problema tienen diferentes medidas en su altura y en el radio de su base, su volumen es el mismo, 62 punto 5 “pi” centímetros cúbicos.
¿Qué te parecen los resultados?
Por un lado, puedes observar que la capacidad o el volumen de los recipientes que puede ser ocupado por agua sin sobrepasar sus límites, se expresa en centímetros cúbicos. En la vida cotidiana se utiliza el litro, o sus múltiplos y submúltiplos, como unidades de capacidad.
Por otro lado, observa que la capacidad de ambos recipientes es la misma.
Comienza por la observación relacionada con la unidad de medida que se utilizó para medir la capacidad de los recipientes. Se utilizó el centímetro cúbico. Esto es, porque la capacidad hace referencia al espacio de un recipiente que puede ser ocupado por alguna sustancia u objeto sin sobrepasar sus límites, es decir, hace referencia al volumen interno y la unidad que se utiliza para medir el volumen es la cúbica (un cubo con ciertas medidas). Sin embargo, en la vida cotidiana cuando ese cubo es ocupado por agua, dependiendo del tamaño, se utiliza el litro o sus múltiplos y submúltiplos. Por ejemplo, si el espacio de un centímetro cúbico es ocupado por agua se puede llamar mililitro. Para ilustrar lo anterior, considera lo siguiente:
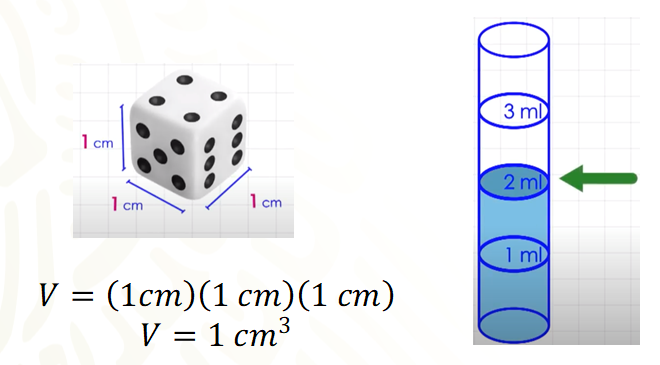
Por ejemplo, si el espacio de un centímetro cúbico es ocupado por agua se puede llamar mililitro. Para ilustrar lo anterior, considera lo siguiente: Considera un dado cuyas aristas miden un centímetro. Este dado ocupa un lugar. Para señalar el espacio que ocupa, se tiene que rodear el dado con la mano. Es decir, tiene un volumen externo.
Para medir ese espacio, se multiplica un centímetro por un centímetro por un centímetro. Por lo tanto, el volumen del cubo mide 1 centímetro cúbico.
Ahora considera que en un recipiente con agua se pinta una marca en el nivel que alcanza el agua ¿Qué pasa si el dado se mete al agua de tal forma que no toque las paredes? El nivel del agua sube. ¿Por qué?
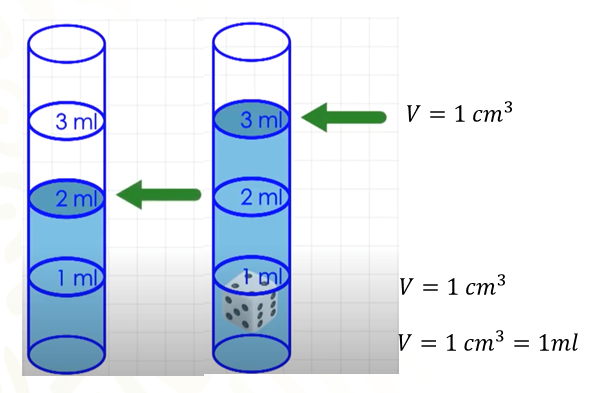
Para encontrar una explicación, considera que dos cuerpos no pueden ocupar un mismo lugar en el espacio. Por ejemplo, tú no puedes ocupar el mismo sitio que otra persona. Para ocupar el sitio de esa persona, ella tendría que moverse o desplazarse.
De forma similar, cuando se introduce el dado en el agua, el dado ocupa un lugar que antes era ocupado por el líquido. Específicamente, el dado ocupa un centímetro cúbico.
En tanto, el líquido se desplaza a un nuevo lugar, que ocupa un espacio igual al que ocupa el cubo. Es decir, un centímetro cúbico. Sin embargo, en la vida cotidiana se dice que el cubo, por ser sólido, ocupa un centímetro cúbico y el agua, por ser líquido, aunque ocupe el mismo espacio se dice que ocupa un mililitro. En otras palabras, un centímetro cúbico equivale a un mililitro.
Por tanto, si los recipientes del problema inicial tienen un volumen interno de 62 punto 5 “pi” centímetros cúbicos, se dice que su capacidad es de 62 punto 5 “pi” mililitros.
Si consideran el valor de “pi” como 3 punto 14 y lo multiplicas por 62 punto 5 mililitros obtienen 196 punto 25 mililitros.

Ahora bien, quizá también te sorprendió que los dos recipientes cilíndricos del problema inicial tengan la misma capacidad, a pesar de que el valor de su altura y la medida del radio de sus bases son distintas.
De aquí, se puede desprender la siguiente conclusión. Aunque las dimensiones de los recipientes sean distintas, su capacidad puede ser la misma.
Trata de plantear un problema en el que esta conclusión sea importante y que involucre recipientes o contenedores cilíndricos. Toma un momento para hacerlo.
Se puede plantear el siguiente problema.

Realiza una estimación y anótala en tu cuaderno.
Para averiguar si ambos recipientes tienen la misma capacidad, primero se puede calcular el volumen interno de cada recipiente. Toma en cuenta que cada recipiente tiene forma de cilindro recto.
Entonces, para calcular el volumen de cada recipiente cilíndrico se puede multiplicar el valor de “pi”, por la medida del radio de su base elevada al cuadrado, por la medida de su altura.
En el caso del recipiente cuyo radio de la base mide 2 punto 5 centímetros y cuya altura es de 15 centímetros, para calcular su volumen interno, se multiplica el valor de “pi” por 2 punto 5 centímetros por 15 centímetros. Al multiplicar ese resultado por pi, se obtiene 93.75.
Al elevar 2 punto 5 centímetros al cuadrado se obtiene 6 punto 25 centímetros cuadrados. Al multiplicar este resultado por 15 centímetros, se obtiene 93 punto 75 centímetros cúbicos. Al multiplicar ese resultado por “pi” se obtiene 93 punto 75 “pi” centímetros cúbicos.

En el caso del recipiente cilíndrico cuyo radio de la base mide un centímetro y cuya altura mide 93 punto 75 centímetros, para calcular su volumen interno, se multiplica el valor de “pi”, por un centímetro elevado al cuadrado, por 93 punto 75 centímetros.
Al elevar un centímetro al cuadrado, se obtiene un centímetro cuadrado. Al multiplicar este resultado por 93 punto 75 centímetros, se obtiene 93 punto 75 centímetros cúbicos. Al multiplicar ese resultado por “pi”, se obtiene 93.75 “pi” centímetros cúbicos.
De acuerdo con lo anterior, ambos recipientes tienen un volumen interno de 93 punto 75 centímetros cúbicos, pero como se acordó, un centímetro cúbico equivale a un mililitro. Por lo tanto, se puede decir que la capacidad de ambos recipientes es de 93 punto 75 pi mililitros.

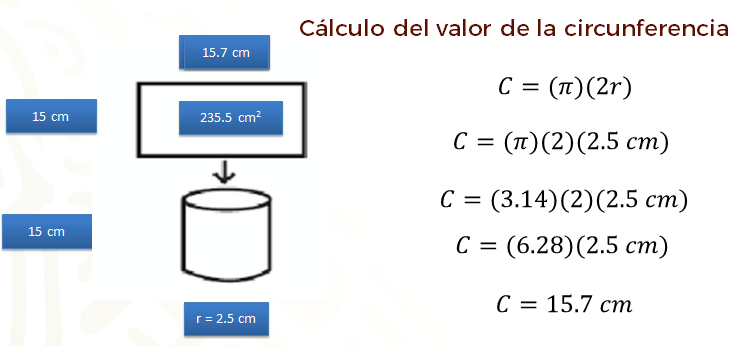
Ahora bien, para el recipiente cuyo radio de la base mide 2 punto 5 centímetros y cuya altura es de 15 centímetros, se puede calcular el material que se necesita, tomando en cuenta que el desarrollo plano del cilindro está conformado por un rectángulo y dos círculos.

Para averiguar las dimensiones del rectángulo que conforma la superficie curva de ese cilindro, considera que la circunferencia de una de las bases del cilindro corresponde al largo del rectángulo que conforma dicha superficie curva y que la altura del cilindro corresponde al ancho del rectángulo de esa superficie curva.
Por tanto, el ancho del rectángulo que conforma la superficie curva del cilindro mide 15 centímetros.
Para calcular la medida de la circunferencia de una de las bases del cilindro, se puede utilizar el hecho de que el valor de la longitud de la circunferencia equivale al valor de “pi” por 2 veces el valor del radio.
Así, la medida de la circunferencia es “pi” por dos veces 2 punto 5 centímetros. Si se considera el valor de “pi” como 3 punto 14, la medida de la circunferencia se puede expresar aproximadamente como 3 punto 14 por 2, por 2 punto 5 centímetros.
Al multiplicar 3 punto 14 por 2 se obtiene 6 punto 28; al multiplicar 6 punto 28 por 2 punto 5 centímetros se obtiene 15 punto 7 centímetros. Entonces, el largo del rectángulo que conforma la superficie curva del cilindro mide aproximadamente 15 punto 7 centímetros.
Por tanto, para construir el rectángulo que conforma la superficie curva del cilindro, se requiere una superficie de 15 centímetros por 15 punto 7 centímetros. Realizando operaciones, se concluye que la superficie del rectángulo mide 235 punto 5 centímetros cuadrados.
Para averiguar la cantidad de material que se requiere para construir una base del cilindro, se puede calcular su área. Para eso se puede utilizar la fórmula valor del área igual al valor de “pi” por el valor del radio al cuadrado.
Como el valor del radio es 2 punto 5 centímetros, y si se considera el valor de “pi” como 3 punto 14, el área del círculo se puede expresar como 3 punto 14 por 2 punto 5 centímetros al cuadrado.
Al elevar 2 punto 5 centímetros al cuadrado se obtiene 6 punto 25 centímetros cuadrados. Al multiplicar este valor por 3 punto 14, se obtiene 19 punto 625 centímetros cuadrados.
Para averiguar la cantidad de material que se requiere para elaborar los dos círculos que conforman las bases del cilindro se puede multiplicar esa cantidad por 2.
Al multiplicar 19 punto 625 centímetros cuadrados por 2 se obtiene 39 punto 25 centímetros cuadrados.

Para averiguar la cantidad de material que se requiere en la construcción de todo el cilindro, se puede sumar el área del rectángulo que conforma la superficie curva del cilindro y el área de los círculos que conforman las bases del cilindro.
Al sumar 235 punto 5 centímetros cuadrados, que corresponde al área del rectángulo que conforma la superficie curva del cilindro, más 39 punto 25 centímetros cuadrados, que corresponde al área de las bases circulares del cilindro, se obtiene 274 punto 75 centímetros cuadrados.
De modo que, para construir al cilindro, se requiere una superficie que mida 274 punto 75 centímetros cuadrados.

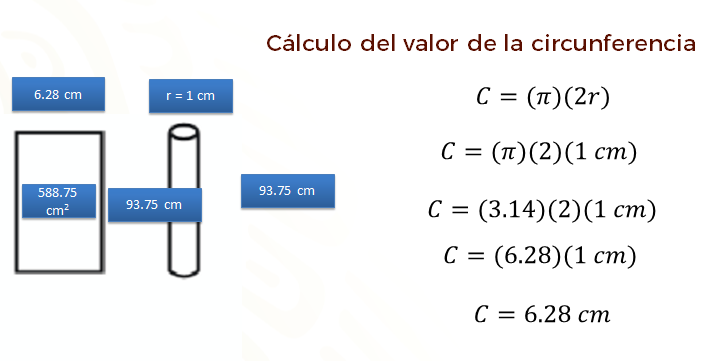
Se puede realizar un análisis similar para el caso del recipiente cilíndrico cuyo radio de la base mide 1 centímetro y cuya altura mide 93 punto 75 centímetros.
En ese caso, la circunferencia de una de las bases mide “pi” por 2 por un centímetro. Si se considera el valor de “pi” como 3 punto 14, se obtiene 3 punto 14 por 2, por un centímetro. Al multiplicar 3 punto 14 por 2 se obtiene 6 punto 28. Al multiplicar 6 punto 28 por 1 se obtiene 6 punto 28 centímetros.
Observa que esta es la medida del ancho del rectángulo que conforma la superficie curva del cilindro. El largo del rectángulo mide 93 punto 75 centímetros. Al multiplicar 6 punto 28 centímetros por 93 punto 75 centímetros, se tiene el total que se requiere para construir el cilindro pues se obtiene 588 punto 75 centímetros cuadrados, que es la medida de la superficie del rectángulo.
El área de uno de los círculos de la base es igual a “pi” por el valor del radio al cuadrado.
Al sustituir valores se obtiene que el área del círculo mide 3 punto 14 por un centímetro al cuadrado. Al elevar un centímetro al cuadrado se obtiene un centímetro cuadrado.
Al multiplicar un centímetro cuadrado por 3 punto 14 se obtiene 3 punto 14 centímetros cuadrados. Ésta es el área de una de las bases del cilindro. Al multiplicar por 2 esa cantidad, se obtiene que, para las dos bases, se requieren 6 punto 28 centímetros cuadrados.

Para calcular la cantidad de material total que se requiere en la construcción del cilindro, se suma 588 punto 75 centímetros cuadrados más 6 punto 28 centímetros cuadrados. Al sumar se obtiene 595 punto cero 3 centímetros cuadrados.

Para contestar las preguntas del problema, aunque ambos recipientes tengan una capacidad de 93 punto 75 pi mililitros, para uno se requiere aproximadamente 274 punto 75 centímetros cuadrados de material y para otro aproximadamente 595 punto cero 3 centímetros cuadrados de material.
Para gastar menos material en la construcción del cilindro, al dueño de la fábrica le conviene más el que tiene 2 punto 5 centímetros de radio en la base y 15 centímetros de altura.
En general, aunque un recipiente tenga mayor cantidad de área en su superficie, no siempre quiere decir que tenga una capacidad mayor.

Con lo revisado hasta ahora, puedes regresar a las opciones de respuesta que se dieron inicialmente y corregir o verificar tu elección.
De acuerdo con lo que se ha estudiado en esta sesión, la opción 2 que propone relacionar siempre la capacidad de un recipiente únicamente con el área de su superficie, es incorrecta porque, por ejemplo, se pueden construir recipientes cilíndricos con la misma capacidad, pero con distinta medida en sus superficies.
La opción 3 que propone relacionar siempre la capacidad de un recipiente únicamente con la medida del ancho de una de sus bases, tampoco es la más adecuada.
Puedes regresar a revisar las medidas de los recipientes y percatarte de que puedes construir recipientes con distintas medidas en el diámetro de tus bases, pero con la misma capacidad.
Como se ha visto en esta sesión, la capacidad se relaciona directamente con el volumen interno del recipiente, como se indica en la opción 1.

Con esto se responde la pregunta inicial y se concluye la sesión. En esta sesión, se vio que el valor del volumen de un cilindro recto es igual al valor de “pi” por el valor del radio de la base al cuadrado por el valor de la altura. También se analizó la relación entre el volumen y la capacidad de un recipiente con forma de cilindro.
Concluye los ejercicios que se desarrollaron a lo largo de la sesión, en caso de que aún te haya quedado alguno pendiente.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Ponga usted atención
Aprendizaje esperado: Participa en una mesa redonda sobre un tema específico.
Énfasis: Desarrollar estrategias de escucha activa y atenta.
¿Qué vamos a aprender?
Desarrollarás estrategias de escucha activa y atenta, esto es cultivar una serie de mecanismos para participar en un acto de comunicación de manera más involucrada.
Ten a la mano tu cuaderno, lápiz o bolígrafo para que puedas tomar notas. Así como tu libro de texto.
¿Qué hacemos?
Te ha pasado alguna vez que hablas con alguna persona y tienes la certeza de que te están poniendo atención y esa persona está haciendo un esfuerzo por entender lo que tú le estás diciendo.
Esto que se describe en el párrafo anterior, se llama escucha activa y atenta, y es precisamente lo que se revisará en la sesión del día de hoy, ya que es una práctica que no sólo hace sentir bien a quien habla y se siente escuchado; sino que permite a quien escucha ponerse en el lugar de su interlocutor y adquirir mayor conocimiento sobre el tema del que se trata.
Para entrar en materia, ¿qué te parece si revisas el siguiente video?
- Telesecundaria tercer grado. Bloque II Español 15.
Revisa del tiempo 01:11 al 01:58.
Después de haber observado el video, quizás ahora entiendas la diferencia que hay entre lo que es, que las personas te oigan y que las personas te escuchen.
Porque como ya revisaste, no son la misma cosa. A pesar de que los seres humanos, no todo el tiempo están poniendo atención ni procesando todo lo que oyen; imagínate, se volverían locos. Sin embargo, es posible desarrollar estrategias para elegir qué se quiere escuchar y hacerlo de mejor manera.
Poniéndolo en otros términos para que vaya quedando más claro. Así como oír es un acto físico, ajeno a tu voluntad, la escucha es un acto voluntario, algo que eliges hacer y a lo que dedicas tu atención y tu energía. Oír es pasivo, pero escuchar es activo, implica atención a lo que se dice y a cómo se dice; es decir, a la comunicación verbal y a la no verbal.
Eso ¿cómo es, lo de lo verbal y lo no verbal?
El lenguaje verbal es lo que se dice con palabras, el contenido de tu discurso, mientras que el lenguaje no verbal son todos esos gestos y movimientos que realizas tal vez sin darte cuenta y que le transmites a tu interlocutor que está muy interesado en lo que le dices o, por el contrario, que no te está poniendo atención o que, con lo que le dices, no captas su interés. Y que puede ser viceversa, que sea otra persona que te está hablando y tú puedes poner o no atención a lo que dice.
Por ejemplo, un compañero tuyo llamado Antonio, que estando en una mesa redonda, le tocó ver a compañeras o compañeros bostezando, eran como leones enjaulados.
Este es un tema muy importante, pues la escucha atenta no solamente puede llevarse a cabo entre dos personas, sino que está muy presente en toda tu vida escolar, constantemente se te pide que escuches las presentaciones u opiniones de quienes, por ejemplo, participan en una mesa redonda, y si no realizas una escucha atenta, es posible que no seas capaz de aprovechar completamente el conocimiento que te están transmitiendo.
Hay que recordar que en una mesa redonda intervienen varias personas con la finalidad de intercambiar ideas y opiniones en relación con un tema específico y en esta dinámica los integrantes tienen la misma oportunidad de argumentar sus puntos de vista. Así es, y por eso es importante escuchar activamente.
Cuando se escucha activamente, no se está únicamente sentado, con la mente divagando y sin concentrarte en lo que pasa a tu alrededor. Escuchar implica involucrar tu atención y tus sentidos, tomar la decisión consciente de poner atención y de procesar aquello que estas escuchando, ¿notas la diferencia?
No es lo mismo estar sentado pensando en el emparedado que te vas a comer en el recreo o en sí estará libre la cancha para jugar futbol, que tomando notas y contrastando lo que escuchas, por ejemplo, en una mesa redonda.
Ahora, revisa otra parte del video que observaste anteriormente, en donde se explica esto con mayor amplitud.
- Telesecundaria tercer grado. Bloque II Español 15.
Revisa del tiempo 01:58 al 03:40.
Es interesante lo que revisaste en el video, quizás nunca te habías puesto a pensar en todo lo que tienes que hacer para escuchar correctamente al otro. Tal vez pensabas que era algo que sucedía naturalmente, sin que tú tuvieras que hacer un mayor esfuerzo.
Ya te disté cuenta de que no es así y seguramente recordarás algún momento en que, al participar en una mesa redonda, pudiste darte cuenta de cuáles de tus compañeras y compañeros te estaban escuchando activamente y cuáles no.
La escucha activa es un acto de empatía, es decir, de identificarte con el otro y absorber lo que se te está queriendo transmitir. Y esto es válido, como ya viste, tanto para los diálogos entre dos amigos o conocidos, como para las actividades escolares.
Tal vez, ahora te arrepientas de todas las veces en que alguna de tus compañeras o compañeros, al participar en una mesa redonda, esperaban que el público participara y los demás compañeros, incluida o incluido tú, se quedaban en silencio.
Esto es muy importante, porque hay distintos tipos de silencio, y quien habla puede distinguirlos; no es lo mismo un silencio atento, señal de que tu interlocutor está procesando lo que le dices, que un silencio vacío, que indica que los oyentes no pusieron atención a lo que dijiste y, por lo tanto, no tienen nada que añadir.
Si escuchas con atención, serás capaz de tomar las ideas que se te están transmitiendo y tal vez ponerlas en duda o contrastarlas con algo más que tú sabes. Aunque tampoco es cosa de decirle a quien acaba de exponer “lo que dijiste no es cierto”.
Se insiste, de lo que se trata es de un acto de empatía y, por lo tanto, requiere que participes con respeto para no herir los sentimientos de quien está exponiendo sus ideas. Pues, no está bien descalificar o insultar, pero parte de la escucha activa también es hacer preguntas y cuestionar a quien expone algo que no te quedó claro o de lo cual tenías otra impresión.
Por ejemplo, Antonio dice que a él, le pasa que escucha de pronto algo con lo que no está de acuerdo y ya, automáticamente deja de poner atención.
Es muy frecuente que eso pase y te puedes perder la oportunidad de escuchar una opinión distinta, que puede cambiar o enriquecer la tuya, o de darte cuenta de que lo que sabías no era correcto.
Así que debes practicar y ejercitar la escucha activa. Como muchas otras cosas en la vida, ésta también es cuestión de práctica, pero también hay una serie de acciones que puedes realizar para ayudarte a participar activamente en una mesa redonda. Hay, por ejemplo, quien toma notas para obligarse a concentrarse en lo que se está diciendo, o quien pone atención a su postura, para no quedarse dormido o distraerse. Ahora revisa, otro fragmento que detalla más este tipo de estrategias, en el siguiente video.
- Telesecundaria tercer grado. Bloque II Español 15.
Revisa del tiempo 03:50 al 04:34.
¿Viste cuáles son las estrategias que puedes poner en práctica?
Así es, la primera es establecer contacto visual, pues resulta importante mirar a los ojos de la persona que habla; cuidar el lenguaje no verbal, inclinándote por ejemplo hacia enfrente en actitud de atención total, y sonreír en actitud de empatía al realizar preguntas referentes al tema, pues esto genera una mejor interacción.
Recuerda que éstas son estrategias que puedes seguir para ponerte en actitud de escucha atenta, pero cada persona debe encontrar las propias, y una forma de hacerlo es pensar qué actitud te gustaría a ti, que adopten tus interlocutores o tu público y actuar de esa forma.
Ahora, ¿qué te parece si se revisa lo que no debes hacer si quieres que tu interlocutor se sienta escuchado de manera activa y atenta?
Para realizar eficazmente una escucha activa, debes evitar las siguientes actitudes y acciones.
- Evita interrumpir a quien habla. La escucha activa implica un intercambio de ideas, y no se puede hablar de un intercambio cuando tú no escuchas al otro. Deja que quien está hablando termine su idea y sólo entonces expresa tu opinión o tu comentario.
- Evita distracciones. La mente no puede ocuparse de dos cosas al mismo tiempo; si estás poniendo atención a algo, ya sean las expresiones de un compañero, o tu celular o cualquier otra cosa, te será imposible realizar una escucha atenta de las palabras de quien está exponiendo o quien te está contando algo que le preocupa.
- No des por hecho que ya sabes lo que se te está diciendo. De la misma forma que no puedes pensar que tienes la solución a los problemas de alguien más, no debes dar por hecho que sabes todo lo que un expositor tiene que decirte. La escucha atenta está abierta al conocimiento nuevo, aún si éste pone en duda cosas que ya sabías.

Parte de la escucha atenta y activa también consiste en hacerle ver al expositor o al interlocutor que te interesa lo que dice.
No importa si es una plática entre amigos o una mesa redonda en el salón de clases, el principio es el mismo, debes concentrarte, llevar tu atención a quien habla y hacer lo posible por entender lo que escuchas y asimilarlo a tus conocimientos previos. Si tienes algo importante y constructivo que aportar, lo haces y si no, escuchas empáticamente y estas completamente presente, no a medias.
Ahora se revisarán algunas acciones y actitudes que debes procurar si quieres realizar una escucha atenta. Para que se lleve a cabo de una manera eficaz la escucha activa, debes tener en cuenta las siguientes técnicas y consejos.
- Mantener la mente abierta, pues esto te permitirá aceptar opiniones diversas y ser imparcial.
- Esperar turnos para poder hablar, pues esto permite analizar la idea que el otro está transmitiendo y dar tu opinión.
- Cuidar tu lenguaje corporal. Si estas cruzando los brazos, con la mirada lejos de quien está hablando, bostezando o mal sentado, no estás mandando la señal a tu mente de que debes poner atención, y harás sentir a tu interlocutor que no te interesa lo que dice.
- Sonríe, o asienta con la cabeza, ya que es una forma de manifestar apoyo a quien está hablando o exponiendo, de animarlo a seguir.

Como se mencionó, todo esto es cuestión de práctica, pero si preparas a tu cuerpo para poner atención, mirando a quien habla, irguiendo la postura y sin buscar distracciones, ayudarás a tu mente a estar presente y escuchar activamente, lo cual hará sentir bien a quienes te hablan y propiciará que entiendas mejor lo que escuchas.
Quizás en alguna ocasión. tú querías que alguna de tus compañeras o compañeros te hiciera caso y ella o él, ni siquiera te miraba. En este caso, si ella o él hubieran obligado a sus ojos a verte, su mente hubiera estado más receptiva para escuchar la inquietud que le estabas transmitiendo.
Entonces, ¿el cuerpo ayuda a la mente a estar atenta?
Desde luego. Ahora, para probar qué tanto has aprendido sobre el ejercicio de la escucha atenta, ¿qué te parece si se realiza una actividad?
No, para estar realmente lista o listo, es necesario que tú, prepares tu cuerpo y con ello, prepares tu mente.
Hay que ir paso por paso.
- Colócate bien sentada o sentado en tu silla, con la espalda pegada al respaldo, los hombros relajados y las manos sobre tus piernas o la mesa o sobre tu regazo.
- Mantén la mirada en el expositor (en este caso pide ayuda a un familiar que será quien te vaya leyendo la actividad).
- Trata de imaginar todo aquello que vas a escuchar. Si escuchas con atención, te será más sencillo llegar a la respuesta.
- Pide a un familiar tuyo que lea la imagen en la que aparece la actividad.
Esta actividad se llama el autobús. Escucha con atención.

¿Qué tal? ¿Tienes la respuesta?
Algunas de tus compañeras o compañeros al estarla haciendo, van contando cuántas personas se subían y cuántas se bajaban.
Por eso se trata de realizar una escucha atenta, de tal manera que al final del ejercicio puedes distinguir entre la información que te servirá y la que no.
Tal vez, en un primer momento, pensaste; ¿cómo voy a saber eso?, pero luego recordaste el primer enunciado, “imagina que conduces un autobús”. El número de calzado del conductor es el tuyo.
Ya viste que la escucha atenta, empática y constructiva, es una práctica que promueve el aprendizaje y propicia una correcta interacción en una mesa redonda. Puesto que la escucha atenta y activa sólo se desarrolla a través del ejercicio de las estrategias, procura poner en práctica lo que aprendiste en esta sesión.
Recuerda que puedes buscar en tu libro de texto de Lengua Materna de segundo grado, ejercicios que puedes realizar para reforzar lo aprendido.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Por una convivencia democrática escolar
Aprendizaje esperado: Valora la importancia de participar conjuntamente con la autoridad en asuntos que fortalecen el Estado de derecho y la convivencia democrática.
Énfasis: Participar en acciones que contribuyen a la convivencia democrática en el ámbito escolar.
¿Qué vamos a aprender?
En esta sesión reflexionarás sobre la participación que tú puedes tener para contribuir a gestionar espacios de convivencia escolar democrática en la escuela, en el salón de clases y en los diversos espacios en que te desenvuelves.
Los materiales que utilizarás son: un bolígrafo o lápiz, tu cuaderno u hojas, colores, y tu libro de texto.
Si cuentas con una discapacidad visual, se te pide que también prepares tus materiales como hojas leyer, punzón y regleta.
¿Qué hacemos?
Para iniciar revisa la siguiente ejemplificación en donde un compañero tuyo llamado Diego comenta que cuando tenía la oportunidad de asistir a clases presenciales, su profesora los ponía a él y sus compañeras y compañeros; en todo momento, a tomar decisiones, principalmente sobre actividades grupales o escolares. Por ejemplo, la elección de la jefa o jefe de grupo, hasta la manera de organizar los convivios escolares.
Como lo menciona Diego, esas acciones son parte importante de una vida democrática.
Es importante reconocer si en tu escuela, se fomenta una convivencia escolar pacífica. Para ello, se utilizarán las siguientes preguntas.
Recuerda si en tu escuela:
- ¿El trato entre las alumnas y los alumnos era respetuoso?
- ¿El trato entre docentes y alumnado era respetuoso?
- ¿Existía confianza con el grupo docente de la escuela?
- ¿Se atendían las conductas de riesgo en la escuela, por ejemplo: las adicciones y la violencia?
- ¿Se procuraba mantener limpios los espacios escolares, invitando al alumnado a su buen uso?
Diego, después de leer las preguntas menciona que las maestras y los maestros, siempre les pedían mantener limpio el salón, su banca y el patio de la escuela a la hora del receso.
También recuerda que con el profesor de Ciencias, hicieron un proyecto para arreglar el jardín de la escuela. Con la maestra de artes siempre hacían los adornos de la escuela, para las ceremonias los lunes.
Cuando había riñas, las prefectas y los prefectos regañaban a las personas involucradas, luego mandaban citar a las mamás y/o papás para que, en conjunto, se comprometieran a seguir el reglamento escolar, principalmente el punto de respetar a las compañeras y compañeros y brindarles un trato digno; con esto se comprometían a mejorar su conducta.
Después de leer lo que comenta Diego. Esas son acciones que fomentan una convivencia pacífica en las escuelas. La Organización de las Naciones Unidas para la Educación, la Ciencia y la Cultura, por sus siglas en inglés (UNESCO), propone una serie de acciones que contribuyen a hacer de la escuela un espacio de convivencia pacífica donde intervengan todas y todos los actores de la escuela: alumnado, docentes, directivos, familias y comunidad en general.
Para una mejor comprensión, revisa la explicación del siguiente esquema.
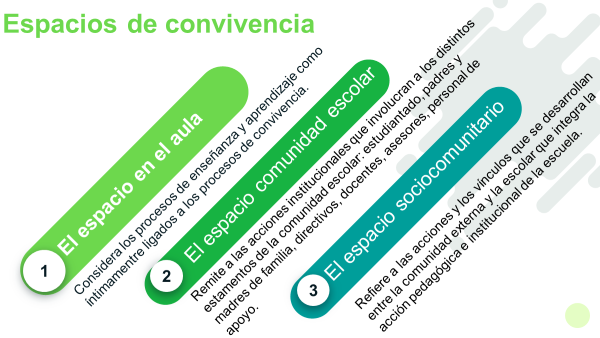
El espacio en el aula es el que considera los procesos de enseñanza y aprendizaje como íntimamente ligados a los procesos de convivencia.
El espacio de comunidad escolar es el que concierne a las acciones institucionales que involucran a los distintos estamentos de la comunidad escolar: estudiantado, padres y madres de familia, directivos, docentes, asesores y personal de apoyo.
El espacio sociocomunitario se refiere a las acciones y los vínculos que se desarrollan entre la comunidad externa y la escolar, que integra la acción pedagógica e institucional de la escuela.
Como te podrás dar cuenta, en cada momento de tu vida es imprescindible fomentar actitudes democráticas.
Entonces, en el aula se pueden seguir estrategias para fomentar las conductas democráticas, dirigidas por el profesorado, por ejemplo: para realizar el reglamento interno o para la organización de alguna actividad en concreto.
Y en la escuela, puede ser la participación de las familias en las juntas escolares o reuniones con diversos propósitos, por ejemplo, lo de escuela para padres y madres de familia. Quizás alguno de tus padres o tutores le ha tocado asistir a esas reuniones.
La participación de las familias en las actividades escolares es muy importante porque así están al pendiente de lo que sucede en la escuela, se involucran en el aprendizaje de sus hijas e hijos, además de que, a través del ejemplo las alumnas y los alumnos, pueden valorar la participación para la mejora de la escuela.
Quizás te haya surgido alguna duda con relación al espacio sociocomunitario. Ahora, revisarás un ejemplo de ello.
Es importante recordar que la escuela es parte de la comunidad, colonia o barrio en donde te encuentras, por eso mismo debe ser ejemplo de institución democrática y coadyuvar en el mejoramiento de la zona donde se ubica.
Para logarlo, es importante el liderazgo que tenga ante la comunidad, los puentes de comunicación y la corresponsabilidad que debe existir entre escuela y sociedad. Por ejemplo, las escuelas tienen sus mecanismos de seguridad para acceder a ellas; sin embargo, las maestras y maestros no pueden controlar totalmente la hora de la entrada porque hay un sinfín de situaciones que se deben cuidar, por ejemplo: dar el paso al alumnado al cruzar las calles o avenidas, hacer brigadas de vigilancia si necesitan pasar un puente, controlar qué se vende afuera de la escuela, entre otras cosas.
Por lo tanto, la escuela solicita el apoyo de la seguridad pública y de las familias para atender todas estas situaciones. Esto que se acaba de mencionar es un ejemplo de corresponsabilidad, esto es, que comparten la responsabilidad de las alumnas y los alumnos en el momento que ingresan a la escuela.
Para que comprendas mejor, lo que se acaba de explicar, revisa el siguiente video. No olvides realizar tus anotaciones de lo más relevante.
- Para fortalecer el Estado de derecho y la convivencia democrática.
https://www.youtube.com/watch?v=3IP9KNIq0jw
Revisa del tiempo 03:26 al 04:30.
¿Qué te pareció el vídeo?
Seguramente encontraste varias formas en las que puedes poner en práctica la democracia en la escuela.
Tal vez, te quedaste pensando en el caso de Pedro, porque es muy común que en la escuela se den episodios de violencia entre compañeros y compañeras; cuando esto sucede, regularmente hay alumnas o alumnos observando la situación. Esto es comunidad que es testigo de las agresiones y su reacción, frecuentemente, es quedarse calladas o callados por temor a sufrir de represalias que puedan enfrentar.
Sin embargo, este punto es importante, ya que debes recordar que callar te hace partícipe de la agresión, esto es, te hace cómplice por la inacción. Lo mejor es hacer lo que hizo Pedro, para contribuir a que no se siga reproduciendo la violencia escolar.
Es muy importante denunciar las agresiones ante las autoridades escolares y las familias, es parte de una vida democrática en la escuela, ya que con ello se fomentan valores como la justicia y el respeto.
Por otro lado, en el video también se menciona que en la familia está presente la democracia, ¿de qué manera se representa?
La vida democrática en casa se da cuando existe un trato igualitario y justo en las relaciones familiares, esto es sin privilegiar a unos en detrimento de otros, por ejemplo: una organización democrática familiar es cuando se reparten de manera equitativa las tareas domésticas entre todas y todos los integrantes o cuando se decide en conjunto lo que se hará un fin de semana.
Una compañera tuya llamada Emma menciona, que en su casa, su hermano mayor trabaja y casi siempre le toca lavar los trastes a ella, y no se le hace justo porque considera que tiene más deberes que él.
Hay que considerar que todas las familias son distintas, ya sea por el número de integrantes o por las personas que la componen. Lo importante es llegar a acuerdos, incluso tú, siendo menor de edad, puedes participar en el dialogo familiar, externar tus ideas y llegar a acuerdos, para ello puedes hacer uso de lo estudiado sobre el conflicto y las formas de resolverlo.
Un ejemplo para llegar a un acuerdo familiar en el caso de Emma sobre el trabajo doméstico, es dosificar los quehaceres. Quizás le toque lavar los trastes entre semana, pero el fin de semana puede tocarle esa responsabilidad a su hermano. Para que la convivencia familiar sea equitativa y democrática, se tiene que recordar que todas las personas que la integran son coparticipes y corresponsables del orden, limpieza y todas las actividades que se den en ella.
Ésa es una muy buena idea, así que Emma debe dialogar con su hermano, esperando llegar a un acuerdo.
Es probable que lo siguiente te brinde más elementos para la convivencia democrática. En nuestro país las normas y reglamentos están basados en la constitución política, lo cual garantiza el fomento de la igualdad, la seguridad y la inclusión de todas y todos, tanto en derechos como en obligaciones. Por eso, es importante observar las políticas públicas de nuestro país.
Revisa el siguiente video, para que conozcas un poco más sobre lo que se te mencionó.
- Para fortalecer el Estado de derecho y la convivencia democrática.
https://www.youtube.com/watch?v=3IP9KNIq0jw
Revisa del tiempo 01:05 al 03:11.
Como te pudiste dar cuenta, la vida democrática en el país está estrechamente ligada a la esfera personal. Así como se denuncian las injusticias de nuestro país y se lucha por un trato digno, equitativo y justo, debes fomentar en casa y en la escuela los valores que permitan una convivencia pacífica, respetando la dignidad de cada una de tus compañeras y compañeros, así como de los integrantes de tu grupo social y tu núcleo familiar.
Se puede decir que, hasta el momento, vivir en democracia no es fácil, ya que implica romper con esquemas, tradiciones y costumbres de las sociedades mexicanas.
Lo importante es que cada persona se asuma como ciudadana y ciudadano para aprender los valores democráticos y así cada quien pueda ser parte del cambio. En estos momentos de contingencia, en los que se pasa todo el tiempo con la familia, es un buen momento para poner en práctica los valores democráticos y convivir pacíficamente; sin duda, esto puede ser un precedente para cuando regreses a la escuela, ya que será importante retomar todo lo aprendido hasta el momento.
El respeto a las compañeras y compañeros debe ser parte de tus hábitos en el día a día y no sólo en momentos específicos.
Ahora, se realizará una recapitulación de lo aprendido en esta sesión.
Has analizado lo que es la convivencia escolar y la convivencia democrática, además revisaste ejemplos que te permitieron entender cómo fomentar la democracia dentro de la escuela.
Se resaltó la importancia de la participación de la comunidad escolar, desde los directivos hasta las familias.
Se te invita a que consultes tu libro de texto para informarte más del tema y retomar los aprendizajes que favorezcan la construcción de la convivencia democrática.
Dialoga con tus familiares sobre la importancia de la vida democrática en la familia y la escuela. De ser posible, compartan más ejemplos sobre el tema.
En el reto del día de hoy, se te pide que te concentres, dejes volar tu imaginación y traigas al presente tu mejor recuerdo de la escuela, el cual debe estar ligado con la vida democrática en el entorno escolar.
En una hoja blanca o en tu libreta deberás plasmarlo con un dibujo.
Para contar con elementos, en la elaboración de tu dibujo puedes utilizar una tabla en la que especifiques las acciones democráticas que pueden implementar las y los diferentes actores de la escuela, puedes guiarte con una tabla similar a la que se te presenta a continuación. Después de eso, te será más fácil realizar tu dibujo.
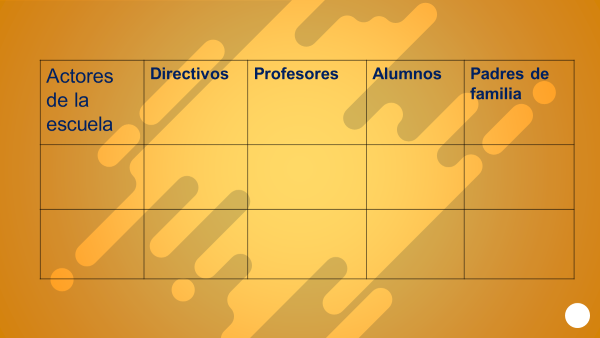
Puedes obtener apoyo de tu familia y/o docentes.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
La verdadera historia de la Tierra plana
Aprendizaje Esperado: Analiza cambios en la historia relativos a la tecnología en diversas actividades humanas (medición, transporte, industria, telecomunicaciones) para valorar su impacto en la vida cotidiana.
Énfasis: Discernir información científica de otros tipos por medio de la reflexión de los saberes adquiridos acerca de la Tierra y los planetas.
¿Qué vamos a aprender?
En esta sesión discernirás información científica de otros tipos, por medio de la reflexión de los saberes adquiridos acerca de las características de la Tierra y los demás planetas.
Ten a la mano tu cuaderno, lápiz o bolígrafo. Así como tu libro de texto.
Para el caso de los alumnos que cuenten con alguna discapacidad visual, preparen sus hojas leyer, regleta y punzón.
¿Qué vamos a hacer?
Para entrar en el tema contesta la siguiente pregunta: ¿qué forma tiene la Tierra?
Si recuerdas tus clases de Geografía, se decía que era “redonda y achatada por los polos” la figura que la representa se llama geoide.
Pero, ¿estás seguro(a) de ello?
Hace poco apareció un artículo en internet acerca de que existen algunas personas que no creen que la Tierra tenga la forma de geoide como se mencionaba arriba.
Pero, ¿cómo podría ser eso, si durante toda la vida escolar has aprendido que así es?
Lo mas sorprendente es que mucha gente estaba de acuerdo con esta teoría.
¿Qué te parece si se aprovecha este tema para hacer un repaso de cómo fueron evolucionando las ideas de la forma de la Tierra?
Es una buena propuesta y así podrás revisar argumentos que se contraponen a las ideas de los terraplanistas.
¿Qué es eso de terraplanistas?
Una persona que se hace llamar terraplanista piensa que la Tierra no tiene forma esférica, sino que es como un disco plano.
Algunas personas al escuchar la palabra se imaginan que son personas que no tienen estudios, pero es lo contrario. Estas personas también estudiaron el Sistema Solar y sus planetas en la escuela, pero que después consideraron que todo eso de "la bola", como le llaman al modelo geoide, es una gigantesca manipulación para mantener a las personas sometidas.
¿Sometidos a qué?
Es raro, eso suena a teoría de conspiración.
Así es. En esta sesión se hará un recuento de los descubrimientos, datos y evidencias que se han generado a lo largo de la historia y que sugieren que la Tierra no es plana.
Se comenzará por revisar un video, en el cual observarás algunas concepciones que tenían diferentes civilizaciones antiguas acerca del universo y de la Tierra.
- Leyendas del origen del universo.
Revisa del tiempo 00:39 al 05:01.
Como pudiste observar en el video, en la cosmovisión de los hindúes estaba planteada la consideración de que la Tierra era plana y que era cargada por cuatro elefantes.
Estas ideas fueron producto de la curiosidad y del ingenio de todas esas culturas, tienen un gran significado y valor por sí mismas. Se han ido modificando con el paso del tiempo para llegar a las nociones generalmente aceptadas y validadas por la ciencia que se tienen hoy en día.
Ahora se retomará a la civilización griega antes de Cristo. Si recuerdas a Tales de Mileto, él fue el primer filósofo a quién se le atribuye el comenzar a pensar en este tema.
En el siglo VI a. C., él proponía en su teoría que la Tierra era una isla que flotaba en el agua. Se piensa que probablemente le surgió esta idea al escuchar historias de la mitología mesopotámica que hablaban de un disco plano de piedra en medio de un gigante océano.
Pitágoras por otra parte aludía a una Tierra esférica, aunque basado en la teoría sobre la armonía de las esferas, donde todos los cuerpos celestes, incluida la Tierra, son reconocidos de forma esférica, aunque cierta su idea en ese momento no tenía mucho sustento e incluso algunos de sus discípulos discrepaban y mantuvieron una visión de la Tierra de forma plana.
También se puede mencionar a Platón, quién aseguraba que la Tierra era una esfera, aunque no ofreció ninguna justificación para esto.
Hay que destacar que todas estas concepciones de estos grandes filósofos sólo eran ideas y no estaban sustentadas con experimentos u observaciones directas.
Si recuerdas en algunas sesiones pasadas, se mencionó que la experimentación era mal vista en épocas antiguas.
Así es. Aristóteles es considerado el primer filósofo griego que contribuyó con argumentos observacionales que sustentaban la idea de una Tierra esférica.
¿Cómo cuáles observaciones hizo Aristóteles?
Por ejemplo, notó que algunas estrellas eran visibles en ciertos territorios, pero no en otros. También observó que la sombra proyectada por la Tierra sobre la luna durante un eclipse era redonda.
En general, Aristóteles desarrolló una visión en la cual destacaba la figura esférica como una forma divina, al ser simple y homogénea. Incorporó esta forma en su teoría acerca de cómo estaba conformado el universo; propuso que estaba constituido de esferas de diferente material como fuego, aire, agua y tierra.
El planteamiento de Aristóteles es interesante, la figura esférica fue retomada por varios filósofos posteriores a él para plantear sus ideas del universo.
Ahora se hablará de otro griego quién aportó muchas ideas y evidencias al entendimiento de este planeta y su forma, él es el astrónomo, matemático y geógrafo Eratóstenes, quien calculó la circunferencia de la Tierra utilizando su observación y la geometría.
La historia relata que un día Eratóstenes leyó en un libro de la biblioteca de Alejandría que, en la ciudad de Siena, situada a unos 800 kilómetros al sur de Alejandría, durante el mediodía del solsticio de verano los objetos no producían sombra y que en los fondos de los pozos se podía ver completamente al Sol. Eratóstenes trató de verificar si en Alejandría se daba este mismo resultado durante el solsticio de verano a mediodía y descubrió que no era así.
Lo que sí pudo observar, es que los objetos sí proyectaban una sombra. Esto era congruente con sus ideas acerca de que la Tierra no era plana, si así fuera, no hubiera observado diferencia en la sombra producida en ambos lugares.
Eratóstenes midió la sombra producida y con esto pudo calcular el ángulo de incidencia del Sol en Alejandría, mientras que sabía que, al no proyectarse sombra en Siena durante el mediodía del solsticio, los rayos del Sol eran completamente perpendiculares ahí.
Además, sabía la distancia entre ambas ciudades, con todo esto calculó que la circunferencia de la Tierra debería ser de 360,500 estadios, unidad de medida de longitud utilizada entonces y que ahora sería equivalente a unos 6,366 km, mientras que la medida de la circunferencia de la Tierra aceptada actualmente es de 6,371 km. Como verás si que calculó la circunferencia con bastante precisión.
Eratóstenes es muy famoso por ese descubrimiento, además de que fue capaz de calcular la inclinación del eje de rotación de la Tierra y creó el primer mapa del mundo.
Recuerda que Eratóstenes hizo todo esto entre el siglo 3 y el siglo 2 antes de nuestra era, con tecnología muy limitada, pero con un gran ingenio y observación.
Más adelante en el tiempo, a inicios de nuestra era, se encuentra a Ptolomeo, matemático, geógrafo y astrónomo griego cuyo modelo geocéntrico proponía que la Tierra estaba en el centro del universo, tenía forma esférica y que rotaba sobre su eje.
Fue difícil que en un inicio la iglesia aceptará esta teoría, ya que iba en contra de muchas de sus creencias.
Esto se debe a que la base de sus creencias es la biblia y en distintos fragmentos de este libro, se hace mención a que la tierra es plana. En consecuencia, no permitían la idea de una tierra esférica, pues no querían contradecir la palabra de dios, por esta razón fue muy difícil convencer a esta institución, la cual en ese entonces tenía un gran peso en todo el mundo.
Aunque la propuesta de la Tierra esférica era difícil de asimilar por la religión cristiana, el hecho de que la Tierra fuera el centro del universo si iba acorde con lo que consideraba, por lo que la teoría geocéntrica de Ptolomeo permaneció vigente por varios siglos.
Hasta que Nicolás Copérnico presentó su teoría heliocéntrica, la cual ponía al Sol en el centro del sistema solar y proponía que la Tierra presentaba movimiento de rotación y traslación alrededor del Sol.
El modelo heliocéntrico de Copérnico también fue muy condenado por la iglesia católica, incluso él y Galileo Galilei, otro científico de gran renombre que apoyaba la teoría heliocéntrica y brindó muchas evidencias que la sustentaban, fueron juzgados por la santa inquisición.
Sin embargo, poco a poco y gracias a muchos científicos y aficionados interesados en el tema, se fueron reuniendo cada vez más evidencias que apoyaban a esta teoría y que aportaban al reconocimiento de la forma verdadera de la Tierra.
Ahora se mencionarán otras evidencias que se han presentado.
Por ejemplo, al navegar en el mar, es posible ver sólo la parte superior de los objetos que se encuentran a lo lejos, como se ve en la siguiente imagen.

A medida que te acercas, ya se puede ver el objeto completo. Esta es una evidencia de la curvatura de la tierra, si fuera plana se vería todo el objeto sin importar la distancia.
Por otra parte, los fenómenos cósmicos como lluvias de estrellas y eclipses son observados en diferentes momentos en distintas regiones de la Tierra.
También se ha logrado medir variaciones en la gravedad de la Tierra en diferentes puntos de esta, lo cual habla acerca de que el planeta tiene una distribución desigual de su masa, por lo que se apoya la teoría de que la Tierra no es una esfera perfecta, sino que está achatada en los polos debido al movimiento de rotación.
Además, se ha podido ver directamente la Tierra mediante los satélites, la estación espacial, viajes a la Luna y sondas espaciales para corroborar en definitiva su forma desde el espacio.
Así es, los satélites fueron los primeros objetos fabricados por el hombre que lograron orbitar nuestro planeta. Ciertamente, gracias a los satélites se ha aprendido y se sigue aprendiendo mucho acerca de nuestro planeta.
Ahora, revisa el siguiente video, para conocer las diferentes funciones y reflexionar acerca de su importancia.
- Cómo funcionan los satélites
https://www.youtube.com/watch?v=UWHKSupEanw
Revisa del tiempo 01:10 al 02:57.
Como pudiste ver, los satélites cumplen diferentes funciones y gracias a ellos se cuenta con imágenes espectaculares de la Tierra.
¿Y a pesar de todas estas evidencias, sigue habiendo personas que piensan que la Tierra es plana?
Así parece. El movimiento terraplanista moderno comenzó en siglo XIX y tuvo su origen en la obra de un escritor inglés llamado Samuel Birley Rowbotham.
Quién, en uno de sus libros, planteaba que la Tierra era un disco plano en el que el polo norte se encontraba al centro de este y estaba rodeado por un muro de hielo. La inspiración que tuvo para este trabajo eran pasajes bíblicos.
Rowbotham y sus seguidores ganaron notoriedad y fueron confrontados por varios científicos de la época, aunque su fuerza fue disminuyendo y prácticamente desapareció al terminar la primera guerra mundial. En Estados Unidos, las ideas de Rowbotham fueron adoptadas y diseminadas desde finales del siglo XIX por un culto religioso, el cual estuvo involucrado en desvíos financieros y finalmente se desintegró en los años 40.
¿Y qué pasó después?, ¿cómo se ha mantenido esa postura hasta nuestros días?
En 1956, surgió la Sociedad Internacional de la Tierra plana.
Eso fue un año antes de que la Unión Soviética, ahora Rusia, lanzará al espacio a Sputnik, el primer satélite artificial. Incluso antes de las fotografías que mostró de la Tierra el Sputnik, ésta ya había sido fotografiada en la década de los cuarenta por un cohete.
A continuación, se te presenta la primera foto en la que se pudo apreciar a la Tierra, y puedes notar su curvatura.

Aún con todas estas fotografías y evidencias, la sociedad Internacional de la Tierra plana seguía incrédula y atribuían todo a un engaño perpetrado por diferentes gobiernos y organizaciones mundiales, aunque todo esto sin ningún sustento real.
¿Cómo una conspiración?
Así es, la popularidad del movimiento terraplanista ha ido variando con los años, últimamente se ha potenciado mucho debido al internet y a la facilidad que se tiene de compartir información de manera rápida y con un número grande de personas. Ellos siguen sosteniendo que la Tierra es plana, con el polo norte en el centro y la Antártida cubriendo toda la orilla.
Como conclusión se puede decir que todas las evidencias indican que la Tierra no es plana sino semejante a una esfera ligeramente achatada en los polos y abultada en el Ecuador además tiene una superficie irregular.
Y que gracias a las aportaciones de muchísimas personas a lo largo de los años se ha podido comprobar la forma de la Tierra por medio de la experimentación y la observación directa.
Se te recuerda, que no debes olvidar la importancia de investigar y analizar críticamente antes de creer todo lo que llega a tus sentidos.
Asimismo, debes leer y buscar en distintas fuentes de información, para tener varias perspectivas que te permitan ejercer un pensamiento crítico.
El Reto de Hoy:
Escribe en tu cuaderno y da respuesta a las siguientes preguntas:
- ¿Qué forma tiene la Tierra?
- ¿Qué ejemplo podrías dar donde se compruebe tu respuesta anterior?
- ¿Por qué es importante investigar antes de creer en toda la información que te llega?
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon










Publicar un Comentario