Aprende en Casa III SEP: 4 de junio TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 4 de junio de clases virtuales mediante el programa Aprende en Casa III, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa III, compartimos los temas y actividades que se abordaron este Viernes 4 de junio, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en Casa III:
https://aprendeencasa.sep.gob.mx/#

Compra en Amazon
Polígonos regulares I
Aprendizaje esperado: Deduce y usa las relaciones entre los ángulos de polígonos en la construcción de polígonos regulares.
Énfasis: Construir polígonos regulares con GeoGebra.
¿Qué vamos a aprender?
Analizarás la construcción de polígonos regulares a partir de diferentes datos.
¿Qué hacemos?
¿Alguna vez te has puesto a observar la naturaleza, un cuadro, una fotografía o una construcción? te han preguntado ¿qué tienen que ver todo esto con las matemáticas?

Seguramente lo que puedes notar es que son elementos geométricos, como una flor, una semilla, la piel de una serpiente, la fachada de un edificio, la forma de una pirámide.
Como habrás observado, en los ejemplos anteriores aparecen distintas formas geométricas dentro de las que destacan los polígonos regulares, es decir, que con ayuda de estas figuras puedes representar distintos objetos en la vida cotidiana; por ejemplo, en la estrella de mar y en la flor se observa un pentágono, o en las celdas del panal de abejas y en los mosaicos se pueden ver hexágonos. En esta sesión vas a trabajar cómo hacer esas construcciones geométricas, con las cuales la naturaleza, los arquitectos y artistas nos maravillan.
Por ello, necesitas recordar algunos conceptos, elementos y propiedades de los polígonos regulares que serán útiles en su construcción.
La palabra polígono proviene de la composición de dos palabras griegas, polys que significa mucho y gonos, que significa ángulos; así que un polígono es una figura geométrica de muchos ángulos, aunque en la práctica a los polígonos los identificamos más por sus lados.
Ahora que tienes claro el concepto de polígono recuerda algunos de sus elementos.
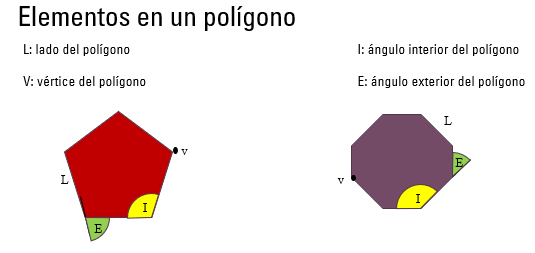
Un lado, “L”, de un polígono es un segmento que conforma el polígono.
Un vértice, “V”, es el punto de intersección de dos lados consecutivos.
Un ángulo interior, “I”, se forma por dos lados consecutivos y es interno al polígono. En las figuras se muestran con color amarillo.
Un ángulo exterior, “E”, se forma por un lado del polígono y la extensión del lado consecutivo, siendo externo al polígono. En las figuras se encuentran en color verde.
Los polígonos pueden tener distintas formas dependiendo del número y tamaño de sus lados, así como de sus ángulos interiores.
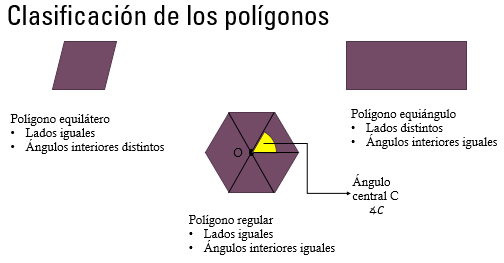
Un polígono es equilátero cuando todos sus lados son iguales, como el cuadrado o el triángulo equilátero. Mientras que un polígono es equiángulo cuando sus ángulos interiores son iguales, como el rectángulo y o el triángulo equilátero.
Puede haber polígonos con lados iguales y ángulos desiguales, como el rombo, y viceversa, con lados desiguales y ángulos iguales, como el rectángulo.
Cuando un polígono tiene sus lados y ángulos iguales decimos que es un polígono regular. En este tipo de polígonos, notamos sus ejes de simetría con los cuáles podemos obtener su centro “O”, que es la intersección de dos de sus ejes de simetría; asimismo se forma un ángulo “C” con dos segmentos que parten del centro “O” a los extremos de uno de los lados. Este ángulo es un ángulo central.
Por cierto, los polígonos regulares aparecen en nuestro entorno con mucha frecuencia, por ello, verás algunos métodos geométricos para su construcción.
Ahora que has recordado brevemente cómo se clasifican los polígonos, te vas a centrar en la construcción de polígonos regulares.
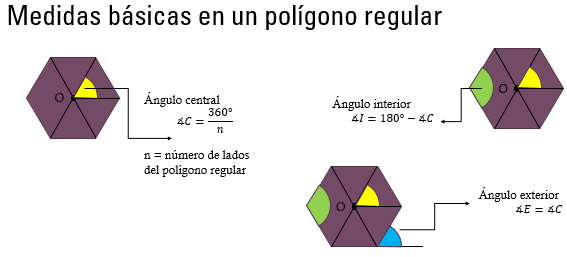
Para lo anterior, ten presentes algunas relaciones métricas para el cálculo del valor de los ángulos que los constituyen. De esta manera, tenemos que el valor del ángulo central “C” es igual a 360 grados entre “n”, siendo “n” el número de lados del polígono. La medida del ángulo interior “I” en un polígono regular es igual a 180 grados menos la medida del ángulo central “C” y la medida del ángulo exterior “E” es la misma que la del ángulo central “C” del polígono regular.
No olvides registrar los aspectos que consideres más relevantes para que los puedas utilizar en el transcurso de la sesión.
Ahora verás cómo puedes trazar polígonos regulares a partir de algunos de sus elementos; por ejemplo, si te piden simplemente trazar un pentágono regular o un hexágono regular, sin darte más información. Ello significa que en principio no se conoce el tamaño del lado “L” del polígono, pero recuerda el significado etimológico de la palabra, polígono significa varios ángulos, y ahí está la clave. Para las construcciones te vas a apoyar en sus ángulos, en particular en el ángulo central “C”. Aquí se nota la importancia de entender el significado de las palabras.
Para trazar un pentágono regular sin más información, puedes iniciar con el cálculo de la medida de ángulo central de esa figura.
Recuerda que en los polígonos regulares la medida del ángulo central “C” es igual a 360 grados entre “n”, en donde “n” es el número de lados. Como en un pentágono regular “n” vale 5, se sustituye este valor y se tiene que el ángulo central es igual a 360 grados entre 5, lo que resulta 72 grados, que es la medida del ángulo central de un pentágono regular.

Con ello vas a trazar un pentágono regular.
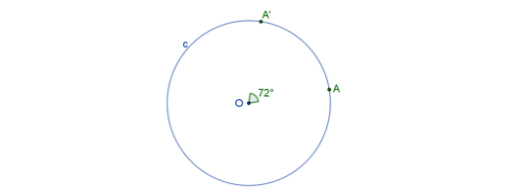
Primero, elige un punto arbitrario “O”. Con ayuda del compás, traza una circunferencia de cualquier radio o abertura que tenga como centro el punto “O”. Con el centro “O” de la circunferencia como vértice y con ayuda del transportador, mide un ángulo central “C” de amplitud 72 grados, marcando sobre la circunferencia las intersecciones “A” y “A” prima de los lados del ángulo.
Ahora ve trazando más ángulos centrales de amplitud “72 grados”, uno junto al otro, con la ayuda del transportador. Conforme se van trazando marca los puntos de las intersecciones de los lados de los ángulos centrales con la circunferencia. Llamamos a esos puntos de intersección, “A” prima, “A” doble prima, “A” triple prima y “B”. Estos puntos serán los vértices de la figura que debes trazar.

Posteriormente, se unen los puntos de intersección de manera consecutiva con segmentos de recta para ir formando los lados del polígono.
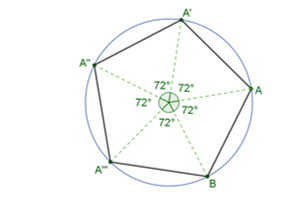
Para la construcción del hexágono regular procede de manera análoga. Primero vas a determinar el valor del ángulo central “C” que es igual a “360 grados entre “n”, donde “n” es el número de lados. Como en el hexágono “n” es igual a 6, se sustituye obteniendo 360 grados entre 6, lo que resulta 60 grados, que es la medida del ángulo central “C”.
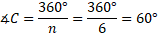
Con dicha amplitud del ángulo central vas a trazar tu hexágono regular. De nuevo, vuelve a elegir un punto “O”. Con ayuda de un compás, traza una circunferencia de cualquier radio o abertura, que tenga como centro el punto “O”. Luego, con ayuda del transportador, vas a trazar el ángulo central “C” de amplitud 60 grados, que tenga como vértice el centro de la circunferencia. Marca sobre la circunferencia los puntos de las intersecciones de los lados del ángulo con ella. Nombramos a esos puntos como “A” y “A” prima.
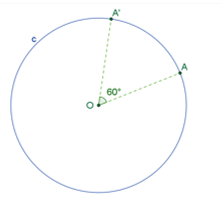
Ahora ve trazando más ángulos centrales de amplitud 60 grados, uno junto al otro con la ayuda del transportador. Conforme vas trazando estos ángulos, marca las intersecciones “A” doble prima, “A” triple prima, “B” y “B” prima. Estos puntos serán los vértices del hexágono que se desea construir.
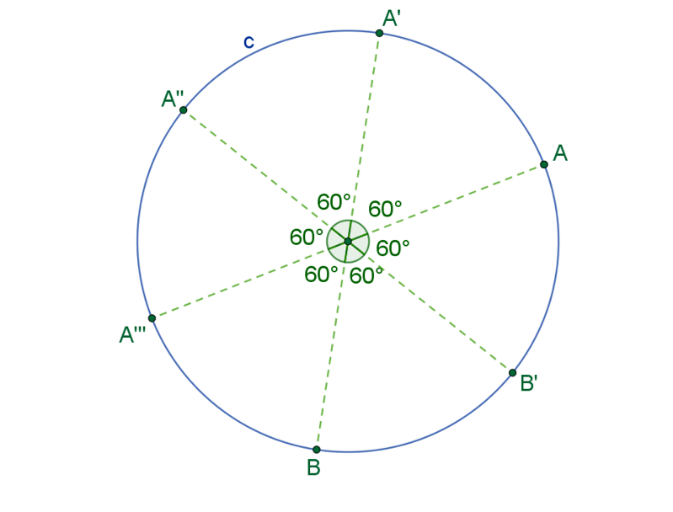
Posteriormente, ve uniendo los puntos que marcaste sobre la circunferencia, de manera consecutiva. Los segmentos de recta que unen esos puntos son los lados del hexágono regular.
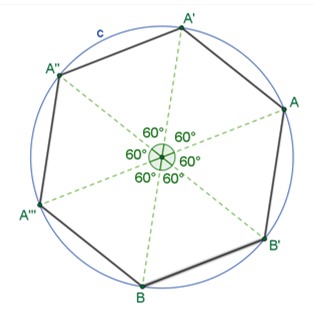
Ahora, vas a trazar polígonos regulares con otras condiciones. Anteriormente construiste los polígonos regulares a partir de conocer el número de sus lados. Ahora verás la manera de construir polígonos regulares conociendo la longitud de sus lados. Para las construcciones con esta condición, también usarás alguno de los ángulos existentes en los polígonos regulares. De esta manera, una construcción la harás usando el ángulo interior y para la otra, el ángulo exterior.
Analiza entonces otro método de construcción de polígonos regulares a partir de conocer la medida de sus lados usando su ángulo interior.
Volverás a construir un pentágono y un hexágono, ambos regulares.
Como viste al principio de la sesión, el valor o la amplitud del ángulo interior “I” en un polígono regular es igual a “180 grados menos el valor del ángulo central “C” de ese polígono. Para el caso del pentágono regular, sabes que el ángulo central “C” es igual a 72 grados, entonces sustituyendo ese valor en la expresión anterior, se tiene que el ángulo interior “I” en el pentágono regular es igual 180 grados menos 72 grados, por ello, el valor del ángulo interior “I” en un pentágono regular es igual a 108 grados.

Por otro lado, repitiendo el mismo procedimiento para el hexágono regular, se tiene que el ángulo central “C” del hexágono es igual a 60 grados, y sustituyendo en la expresión para calcular el ángulo interior “I” se tiene que el ángulo “I” es igual a 180 grados menos 60 grados. Por ello, el valor del ángulo interior “I” en un hexágono regular es igual a 120 grados.
Recuerda que esta construcción se hará conociendo la medida de los lados. Esta medida puede ser cualquiera que tu decidas o que te sea indicada; en este caso, la llamaremos “L”.
Una vez que tienes el valor del lado “L” y el valor del ángulo interior procede a la construcción del pentágono regular.
Primero, traza un segmento con la longitud dada para el lado “L” o lado “AB”. Con uno de los extremos del lado “L” como vértice y haciendo uso del transportador se traza un ángulo de amplitud igual a 108 grados; Este ángulo será un ángulo interior del pentágono regular. Luego, a partir del vértice y sobre el otro lado del ángulo, localiza el punto “A” prima que determina el segmento “BA” prima, de igual longitud que el lado “L”. Este segmento será el segundo lado del pentágono, y se llamara “L” prima.
Para la construcción del siguiente lado del pentágono regular se considera el extremo libre del lado “L” prima como vértice para trazar un nuevo ángulo de 108 grados, respetando la orientación hacía donde se quiere el interior del pentágono. Luego ubica el punto “A” doble prima sobre el nuevo lado de este ángulo de manera que se determine un segmento de igual medida a la del lado “L”. De esta manera se obtiene un nuevo lado del pentágono, al que llamaremos “L” doble prima.
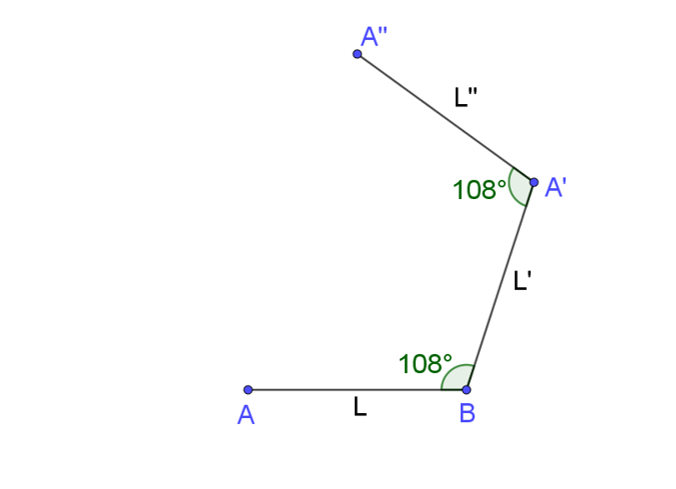
Procediendo de la misma manera para la construcción de los ángulos interiores y los lados de esta figura, ve construyendo los lados faltantes hasta completar el pentágono regular.
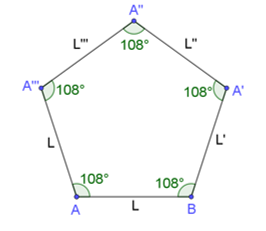
Ahora procede a la construcción del hexágono con lado “L” igual al del pentágono.
Puedes realizar los mismos pasos que para el pentágono regular, pero de acuerdo con las medidas correspondientes al hexágono regular. Si tienes la oportunidad de utilizar el software GeoGebra también puedes realizar los trazos con esta herramienta tecnológica.
Por un cálculo previo, sabes que el valor del ángulo interior para un hexágono regular es de 120 grados.
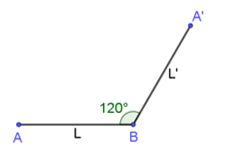
Primero traza un segmento con la longitud dada para el lado “L”, aquí llamado lado “AB”. Con uno de los extremos del lado “L” como vértice y haciendo uso del transportador, se traza un ángulo interior de amplitud igual a 120 grados; se hemos trazado el ángulo con vértice en “B”. Este ángulo será un ángulo interior del hexágono regular. Luego, a partir del vértice y sobre el otro lado del ángulo, localiza el punto “A” prima que determina el segmento “BA” prima, de igual longitud que el lado “L”. Este segmento será el segundo lado del hexágono, que llamaremos “L” prima.
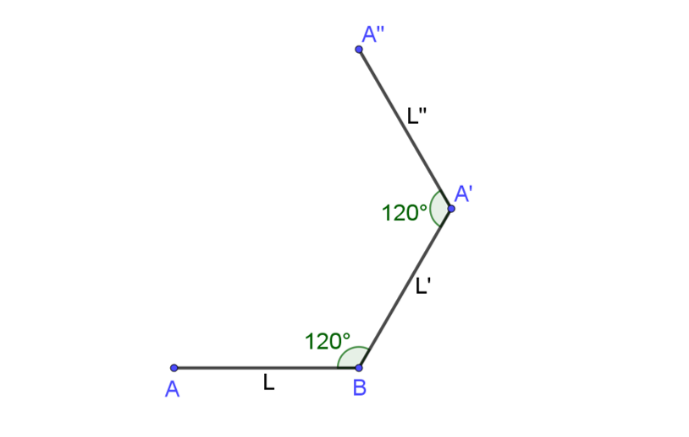
Para la construcción del siguiente lado del hexágono regular se considera el extremo libre del lado “L” prima como vértice para trazar un nuevo ángulo de 120 grados, respetando la orientación hacía donde quieres el interior del hexágono. Luego, ubica el punto “A” doble prima sobre el nuevo lado de este ángulo, de manera que se determine un segmento de igual medida a la del lado “L”. De esta manera se obtiene un nuevo lado del hexágono, al que llamaremos “L” doble prima.
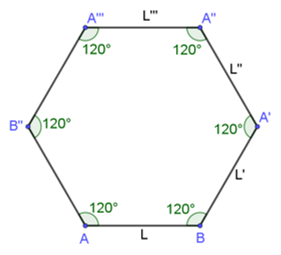
Procediendo de la misma manera para la construcción de los ángulos interiores y los lados de esta figura, ve construyendo los lados faltantes hasta completar el hexágono regular.
Hasta aquí llevas dos métodos para construir polígonos regulares. En el primero partiste del ángulo central “C”, y en el segundo usaste el ángulo interior “I”, una vez que la longitud del lado “L” del polígono está dada.
Ahora continua con otro método utilizando el otro ángulo asociado, es decir, el ángulo exterior.
Sabes por lo que viste al inicio de la sesión, que la amplitud del ángulo exterior “E” en un polígono regular es igual a la de su ángulo central “C”. A partir de lo anterior, puedes encontrar que para el pentágono regular, como su ángulo central “C” es igual a 72 grados, sustituyendo en la expresión anterior, se tiene que su ángulo exterior “E” es igual a 72 grados.

Por otro lado, para el hexágono regular su ángulo central tiene una amplitud de 60 grados, de donde el ángulo exterior “E” es igual también a 60 grados.
Estos trazos los puedes hacer con regla, compás y transportador o como en este caso, lo haremos con el uso de GeoGebra. Una manera de iniciar es trazar el lado “L” con la longitud dada, aquí representado por el segmento “AB”.
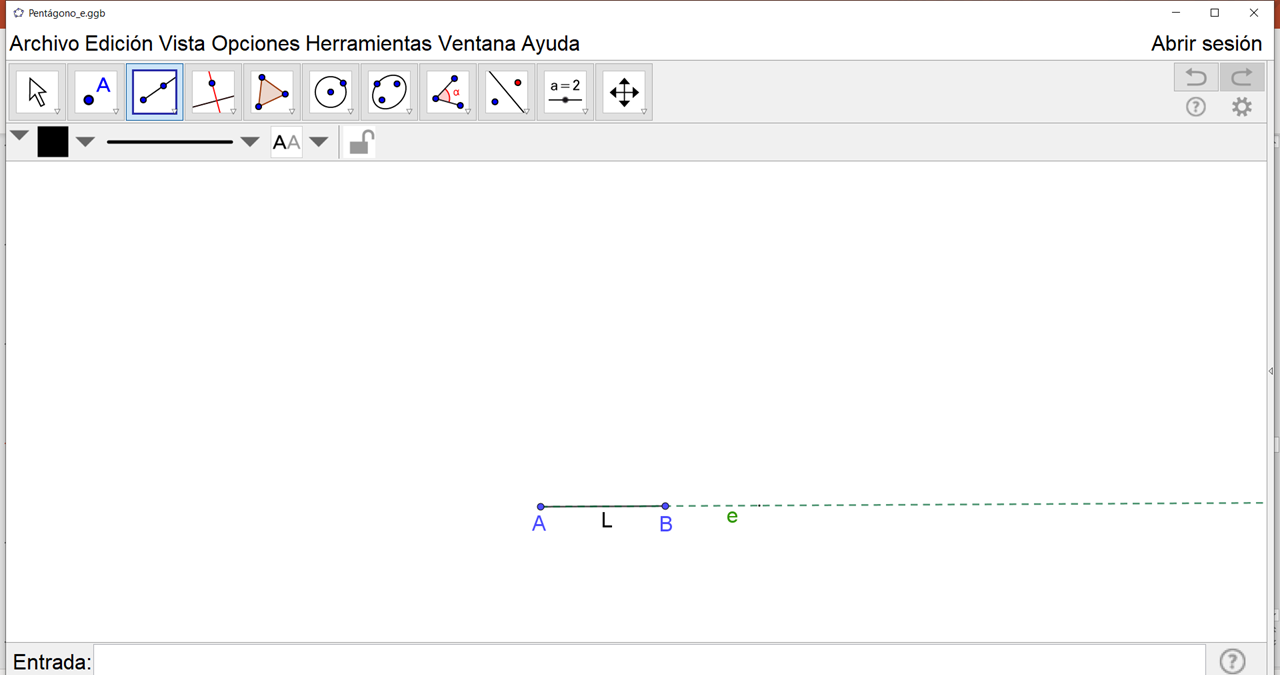
En la imagen se muestra con la flecha roja en la barra de herramientas, el ícono con el cual pueden trazar el segmento “AB”; para seleccionarlo, deben hacer clic con el botón izquierdo del ratón en él. Se procede al trazo.
Por uno de sus extremos, desde “A” hacia “B”, prolonga dicho lado con una línea “e” punteada o tenue. Para prolongarlo en GeoGebra traza una semirrecta seleccionándola de la barra de herramientas y procediendo al trazo.
Haciendo uso de un transportador mide el ángulo exterior “E” de amplitud igual a 72 grados, con vértice en “B” y cómo lado inicial la prolongación del segmento “AB”. Esto porque dicho ángulo debe ser externo al polígono y por ello hay que cuidar su orientación para ubicarlo en el exterior del polígono. Para trazarlo con GeoGebra se utiliza de la barra de herramientas el ícono ángulo dada su amplitud.

Sobre el lado final del ángulo trazado, se mide una longitud igual al lado “L” a partir del vértice “B”, con lo que se determina el segmento “B”, “C” prima. De esta manera se determina el segundo lado del pentágono regular, que llamaremos “L” prima.
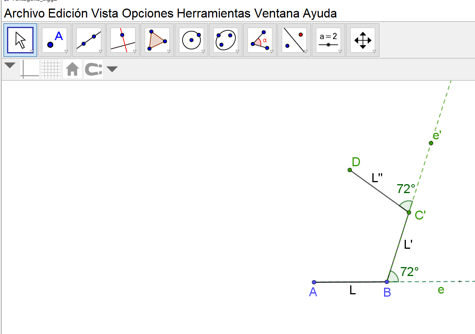
Una vez trazado el lado “L” prima, prolongamos este lado, lo que aquí se muestra con la línea punteada “e” prima. Nuevamente, tomando como lado inicial esta prolongación, haz uso de un transportador para trazar otro ángulo exterior de 72 grados y, repitiendo los pasos anteriores, construye otro lado del pentágono, que llamaremos “L” doble prima. En GeoGebra puedes utilizar de la barra de herramientas para prolongar el lado con el ícono de semirrecta y para medir el ángulo exterior usamos el ícono de ángulo dada su amplitud.
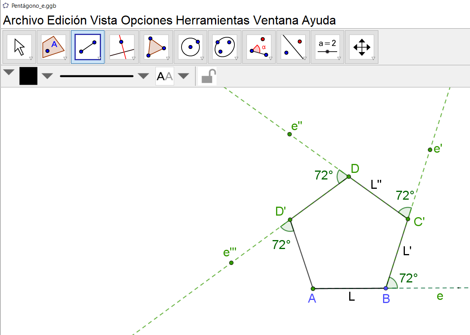
Para continuar con la construcción del resto de los lados del pentágono regular procede de manera análoga, es decir, extendiendo cada nuevo lado del pentágono regular y, sobre dicha extensión, se traza el ángulo exterior de 72 grados, y así vas trazando los lados faltantes.
Ahora realiza la construcción del hexágono regular usando este método de construcción a partir de la medida del ángulo exterior “E”. Como ya calculaste anteriormente, la medida de dicho ángulo es igual a 60 grados.
Puedes iniciar de la misma manera que la construcción anterior, es decir, traza el lado “L” pero ahora con una la longitud de 5 cm, aquí representado por el segmento “AB”. Por uno de sus extremos, “B”, prolonga dicho lado con una línea “e” punteada. Recuerda que si quieres usar GeoGebra, primero debes usar el ícono “segmento”, y para prolongar ese segmento puedes usar el ícono “semirrecta”.
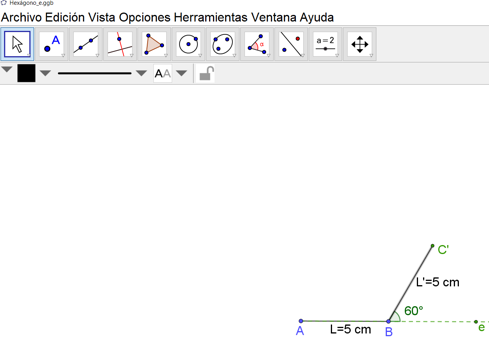
Luego, haciendo uso de un transportador medimos el ángulo exterior “E” de amplitud igual a 60 grados, con vértice en “B” y como lado inicial la prolongación del segmento “AB”. Esto porque dicho ángulo debe ser externo al polígono y por ello hay que cuidar su orientación para ubicarlo en el exterior del polígono.
Para trazarlo con GeoGebra, busca en la barra el icono de ángulo dada su amplitud y traza el ángulo exterior.
Sobre el lado final del ángulo trazado, se mide una longitud igual al lado “L” a partir del vértice “B”, con lo que se determina el segmento “B”, “C” prima. De esta manera, se determina el segundo lado del hexágono regular, que llamaremos “L” prima.

Una vez trazado el lado “L” prima, prolonga este lado, lo que aquí se muestra con la línea punteada “e” prima. Nuevamente, tomando como lado inicial esta prolongación, haz uso de un transportador para trazar otro ángulo exterior de 60 grados y, repitiendo los pasos anteriores, construye otro lado del hexágono, que llamaremos “L” doble prima.
Para continuar con la construcción del resto de los lados del hexágono regular procede de manera análoga, es decir, extendiendo cada nuevo lado del hexágono regular y, sobre dicha extensión, se traza el ángulo exterior de 60 grados, y así vas trazando los lados faltantes.

Ahora conoces algunos métodos para construir polígonos regulares. Unos son más accesibles que otros, dependiendo de los datos que te den, pero todos tienen algo en común, se apoyan en algún tipo de ángulos de los polígonos. Además de la medida de lados, cuando ésa es una condición de la construcción.
Así que cuando tengas que trazar un polígono regular, el método que decidas va a depender de los datos que te proporcionen y de las herramientas tecnológicas con las que cuentes.
Así ha llegado al final de esta sesión, recuerda que éste es un material de apoyo y que puedes consultar otras fuentes para complementar lo que aprendas aquí, como tu libro de texto.
El Reto de Hoy:
El reto de hoy es que contestes las siguientes preguntas.
Los métodos de construcción de polígonos regulares que has estudiado en esta sesión, ¿se pueden aplicar para construir cualquier polígono, independientemente de su número de lados?
¿Cualquier polígono regular se puede construir usando sólo regla y compás?, ¿por qué?
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Ellos dicen que...
Aprendizaje esperado: Participa en una mesa redonda sobre un tema específico.
Énfasis: Formular comentarios sobre puntos de vista ajenos.
¿Qué vamos a aprender?
Durante esta sesión profundizarás sobre el aprendizaje esperado “Participa en una mesa redonda sobre un tema específico”, con el propósito de formular comentarios sobre puntos de vista ajenos.
Recuerda que una mesa redonda es un tipo de conversación formal que reúne a especialistas para que dialoguen acerca de un tema de interés general. De este modo, el público obtiene información actualizada y confiable, además de formarse un punto de vista a partir de las opiniones y los argumentos de los ponentes.
¿Qué hacemos?
Entre los objetivos de la mesa redonda está el presentar un tema y así desarrollar opiniones y puntos de vista que nos ayuden tanto a conocer más sobre estos, como a tomar mejores decisiones en torno a lo que se está discutiendo. Y en realidad, siempre estamos escuchando opiniones de los demás, y en ese aspecto, muchos han realizado sus propios comentarios acerca de lo que esas personas dicen; pero ¿qué sucede cuando se les complica plantear el comentario o lo hicieron, pero no de la forma correcta?
Antes de continuar observa el siguiente video que te va a recordar un elemento esencial para construir mejores comentarios.
- La polémica está por doquier
https://www.youtube.com/watch?v=9-LIpMOqLSM
En esta sesión vas a ver qué otros aspectos se usan para la construcción de comentarios a partir de las opiniones de otros, para que, en una mesa redonda, realices comentarios más propositivos, que sobre todo que fomenten el diálogo.
¿Qué otros elementos crees que son esenciales en la construcción para hacer un comentario?
Además de argumentar, también es necesario saber escuchar y tener conocimiento del tema. Con estos ingredientes puedes comenzar.

Observa al siguiente video para saber lo que algunos alumnos tienen que decir acerca de este tema.
- VIDEO_01_ENTREVISTAS ALUMNOS.
Con lo que nos acabas de ver, ya vas teniendo más ingredientes para elaborar mejores comentarios.
Antes de continuar, es importante definir algunos conceptos fundamentales, las definiciones de: comentario y punto de vista.
Para ayudarte un poco, observa el siguiente video de una mesa redonda sobre el tema grupos juveniles, en el cual dos panelistas expresan su punto de vista, a partir de algunas estrategias discursivas. Y al final del video un participante expresa un comentario sobre estos puntos de vista.
- Una mesa redonda.
En lo dicho por los panelistas. Estos manifiestan su punto de vista, es decir, una opinión, en la cual emiten un juicio sobre el tema, basados en un conocimiento sobre éste y utilizando algunas estrategias de argumentación.
En cuanto al participante, éste expresa su comentario para exteriorizar un juicio acerca del tema. Sin embargo, a pesar de que se percibe que tiene conocimiento sobre el tema, pudo haber construido de mejor forma su comentario.

La Academia de la Lengua Española define comentario como.
“Juicio, parecer, mención o consideración que se hace oralmente o por escrito, acerca de alguien o algo”
Se puede decir que la función del comentario es servir como opinión, observación, argumento o juicio sobre un tema en particular; el comentario puede buscar una respuesta o una aclaración.
Y no hay una definición como tal sobre el punto de vista, pero la podríamos definir como el lugar desde el cual una persona observa una situación. Podríamos decir que es la forma de considerar un asunto de manera particular, y a partir de sus creencias, ideología o su estado de ánimo, expone una opinión.

Con lo anterior podemos concluir que tanto en el comentario, como en el punto de vista, se emite un juicio que se sustenta en el conocimiento amplio del tema.
Y como en esta ocasión te estas enfocando en los comentarios, entonces vas aprovechar estas similitudes para ver cómo se construyen los comentarios a partir de un punto de vista.
Dentro de una mesa redonda surgen comentarios a partir de lo que dijo un ponente, muchas veces estas participaciones vienen de su punto de vista y es ahí donde debes tener capacidad de escucha, pues hay que detectar qué de aquello que se dice se está argumentado y qué viene de su manera particular de ver la situación.
No siempre tienes que estar de acuerdo. De ahí la necesidad y la importancia de saber formular comentarios con respeto. Estos no deben hacerse con la intención de producir una polémica que cause conflictos, es decir, sólo por causar molestia a alguien.
El comentario debe ser propositivo para que se agreguen más elementos que puedan contribuir tanto ampliar el conocimiento del tema, como a fomentar un diálogo que propicie tomar acuerdos con un mejor análisis de la situación, en caso de que se requiera.

Analiza algunas frases que podrías usar para realizar tus comentarios.

Como observas, las frases en color vino, son el preludio o la entrada, y las marcadas en anaranjado son el argumento del comentario.
Esto significa que, para formular comentarios sobre puntos de vista ajenos, también debes retomar lo que han sido y luego llegar a tu propia conclusión.
Para profundizar en esto. Vas a utilizar otro ejemplo.
“Le dije a mi hermana, que por nada del mundo iba a permitir que ella decidiera lo que todos íbamos a comer de ahora en adelante, pues la variedad de proteínas es esencial en la alimentación de todos en casa”.
Ahora vas a analizarlo. ¿Qué crees que se debió hacer antes de decir el comentario? El argumento planteado, ¿estuvo correctamente fundamentado?
Saber escuchar permite hacer un análisis objetivo de lo que se está exponiendo, pues es la herramienta que nos ayuda a empatizar o no con el comentario de alguien más. Para las mesas redondas se necesita una capacidad de escucha activa.
La escucha activa consiste en una forma de comunicación que demuestra al hablante que el oyente le ha entendido. Para emplearla hay algunas recomendaciones como: Mirar a los ojos al hablante, no estar pensando en qué se le va a responder antes de que éste termine de hablar y hacerle preguntas abiertas para poder conocer un poco más de lo que nos está diciendo.
En este ejemplo, primero se debió haber escuchado con mucha atención lo que la otra persona tenía que decir sobre el tema, antes de reaccionar y soltar un comentario sin fundamentos.
También hay que agregar los siguientes aspectos.
- Capacidad para escuchar y poner atención
- Tener amplio conocimiento del tema
- Mostrar respeto ante las opiniones de los demás
- Habilidad para rebatir mediante razones y argumentos
- Habilidad para analizar de manera objetiva los puntos de vista de los demás
- Habilidad para pensar clara y rápidamente
Rebatir significa rechazar una idea, pero se tiene que hacer con diplomacia y respeto usando razones y argumentos válidos, como podrían ser el uso de datos duros y actuales para así fundamentar el rechazo a ese punto de vista sin perjudicar a quien lo emitió y con la intención de fomentar el diálogo entre ambas partes.
Ahora tienes más elementos con los que puedes modificar tus comentarios. Así, el día que participes en una mesa redonda, puedas formular comentarios válidos y propositivos.
Recuerda que, para apoyarte y reforzar el conocimiento de lo trabajado, cuentas con el apoyo de tu libro de Lengua Materna 2. También puedes buscar en libros que tengas en casa o en fuentes confiables de páginas de internet para reforzar tus conocimientos.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
Recorrer el mundo con los pies descalzos
Aprendizaje esperado: Reelabora obras o manifestaciones del arte, por medio de otros lenguajes artísticos, para reinterpretar su significado en una producción interdisciplinaria original que presenta ante el público.
Énfasis: Recrear el significado de las obras y manifestaciones elegidas al reacomodar los elementos del arte presentes en ellas y darles una nueva intencionalidad.
¿Qué vamos a aprender?
En esta sesión vas a reelaborar obras de arte por medio de otros lenguajes artísticos, para reinterpretar su significado a través de una producción interdisciplinaria original que se presente ante un público.
¿Qué hacemos?
Una de las primeras acciones que deberás hacer, es elegir un tema. ¿De qué te gustaría que tratara la pieza artística que elegirás?
Una vez elegido el tema, podrás buscar la obra que te inspire para hablar de ello.
Aunque también puede ser al revés, primero puedes elegir la obra que te interese y después el tema. Lo importante es que lo decidas.
Una idea interesante es sacar de contexto las cosas para ver la reacción de las personas. Por ejemplo, imagínate llegar a pedir empleo “con los pies descalzos”. O ir al banco en tutú. Para romper la rutina y salir de lo cotidiano.
¿Has oído hablar del “flashmob”?
Para conocer al respecto, le la siguiente cita textual:
El Flashmob, respuestas artísticas hoy
María del Pilar Chauca García
“La aparición en el siglo XXI de prácticas artísticas tales como el Flashmob confirma la necesidad actual del género humano de colaboración y reivindicación social al margen de la institución…”
“Un flashmob, traducido literalmente del inglés como “multitud instantánea”, flash-destello, mob-multitud, consiste en una acción colectiva, convocada por un soporte digital como el móvil o Internet, que tiene lugar en un espacio público. En origen, su duración era corta y su naturaleza espontánea, sin embargo, el filón que algunas marcas le han visto los han convertido en acciones coreografiadas en manos de campañas publicitarias. Con todo, su intención sigue siendo la de realizar algo inusual que incomode o llame la atención del espectador.”
Recuerado de: https://revistes.ub.edu/index.php/REGAC/article/view/regac2015.1.13/19243
¿Consideras que esta expresión artística pueda funcionar para sacudir la vida cotidiana?
Ahora tienes dos situaciones que resolver.
1. El elegir un tema y la pieza artística, y
2. Cómo hacer un flashmob desde casa.
Imagina que estás esperando a que mamá o papá lleguen y, cuando lo hagan, los sorprendes con una expresión como la que hoy te proponemos.
Sería como el ritual del protagonista en la novela de “El Principito”, de Saint-Exupéry, cuando le pregunta al zorro “–¿Qué es un rito?”, y el zorro le responde “–Es lo que hace que un día sea diferente”. ¿Para ti, en estos días, qué haría que tu día fuese diferente?
Escoge un tema con el cual te sientas cómoda o cómodo, te sientas libre y en donde su sentipensar esté presente.
El tema podría ser la amistad, la fraternidad, la alegría, el llevarse bien con el otro. El recordar los momentos felices con tus amigas y amigos.
Ya tengas el tema, tendrás que elegir la pieza artística con la que vas a trabajar y resignificar.
Son infinidad de temáticas que podrás abordar, pero lo importante es que partas de tu interés personal, porque si no te atrae lo suficiente el tema, no le pondrás la pasión que se necesita a ese flashmob.
Para resignificar, puedes inventar tu propia versión de la canción que te guste y agregarle algunos movimientos coreográficos. Déjate llevar por la inspiración. Conviértete en danzante.
El Reto de Hoy:
Realiza tu propia expresión en casa y sorprende a tus familiares. ¡Sácalos de contexto! ¡Sacúdelos! ¡Y también considera la posibilidad de sorprender a toda tu escuela!
Puedes trabajar el ejercicio de manera individual y presentarlo a tus familiares. O puedes tomar el riesgo de hacer un trabajo conjunto con todo tu grupo. Para ello, organícense con su docente y juntos preparen la canción junto a la coreografía, para que al final, de manera individual, puedan grabar su presentación.
Un responsable voluntario será el encargado de compilar todos los materiales y de editarlos. Verás que será un maravilloso regalo a ti misma o ti mismo.
Y al compartir ese regalo con su escuela, harás que todos vivan un día diferente, lleno de recuerdos de amistad, fraternidad y alegría. Y quien sabe, en una de esas se hace viral.
Recuerda que sólo necesitas partir de un tema y de una pieza artística, y de tu locura, como el recorrer el mundo con los pies descalzos.
No olvides que arte también es una forma de crear momentos memorables que van definiendo nuestra vida.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
La física y el arte
Aprendizaje esperado: Analiza cambios en la historia relativos a la tecnología en diversas actividades humanas (medición, transporte, industria, telecomunicaciones) para valorar su impacto en la vida cotidiana.
Énfasis: Reflexionar sobre las contribuciones de la física al mundo del arte.
¿Qué vamos a aprender?
Reflexionarás sobre las contribuciones y relación entre la física y el arte.
¿Qué hacemos?
Ambas disciplinas, la física y el arte, son desarrolladas por la humanidad; la física busca comprender los fenómenos naturales que ocurren en cada rincón de nuestro universo y el arte puede ser empleado para conocerse a si mismo, retratar la naturaleza y expresar las emociones y conductas humanas. Ambas requieren creatividad para desarrollarse, sólo que lo hacen por diferentes caminos, la física, por el camino de la ciencia, es decir, la comprobación experimental y el modelamiento con las matemáticas y el arte por el camino de la expresión libre.
Por otra parte, el arte se beneficia del conocimiento desarrollado por la física y otras disciplinas científicas y tecnológicas para sus procesos, e incluso la física ha encontrado inspiración en el arte.
Podríamos decir que ambas disciplinas interpretan nuestro entorno desde dos perspectivas distintas, pero además pueden colaborar entre sí. Ambos son procesos desarrollados por los seres humanos y ningún proceso creativo es independiente de los demás.
En todas las sesiones que has tenido de física, se han tratado de relacionar los contenidos teóricos con la vida diaria, por ejemplo ¿Alguna vez te has puesto a pensar en la relación que tiene la música con la física?
Aparentemente no tiene ninguna relación, pero si lo analizas verás que tienen una gran conexión. Comienza entonces la sesión revisando la relación existente entre la música y la física.
Recuerda que la música es un sonido o conjunto de sonidos y estos son una manifestación de energía. Para poder crear un sonido, es necesario interactuar con la materia. Esto se puede hacer de diferentes formas, por ejemplo, golpeando unos tambores o rasgando las cuerdas de una guitarra. El sonido se transmite después por medio de ondas.
Las ondas sonoras son ondas de tipo mecánico, a diferencia de las ondas electromagnéticas, las ondas mecánicas necesitan un medio material por el cual propagarse, este puede ser el aire, aunque también lo pueden hacer a través de otros materiales o sustancias, como objetos sólidos y el agua.
Por eso podemos escuchar sonidos aun estando en el agua o a través de una pared. Pero, debajo del agua, por ejemplo, se pueden escuchar sonidos, pero no de la misma manera como cuando se está fuera de ella. Esto sucede porque el sonido se propaga en los medios a diferente velocidad. Debes tener presente que los materiales están conformados de átomos y moléculas y que estos están más juntos o separados dependiendo de su estado de agregación. En gases como el aire, las partículas están más alejadas las unas de las otras, y eso produce que las ondas no viajen tan rápido a través del gas. En cambio, en los sólidos las partículas están muy cerca y el sonido viaja mucho más rápido.
Como otras ondas, están caracterizadas por tener una cierta amplitud, la cual se relaciona con su volumen, y una frecuencia que se relaciona con su tono, como verás más adelante.
Para entender ¿cuál es la diferencia entre sonido y ruido? realiza la siguiente actividad.
Primero vas a aplaudir aleatoriamente e identificar si se trata de ruido o sonido.
Ahora vas a volver a aplaudir, pero marcando tiempos, es decir, darás tres aplausos y descasas dos tiempos, tres aplausos y dos tiempos.
¿Qué notaste en ambos momentos?
Pues en el primer momento no había un tiempo, ni un ritmo. En el segundo momento, sí había un ritmo.
Cuando los sonidos no tienen un ritmo, pueden ser catalogados como ruido. Aquí puedes observar otra característica en común entre la física y el arte, algunos de los sonidos en la música tienen simetría y otros no, y estos pueden ser utilizados en diferentes situaciones para enfatizar alguna emoción o para transmitir tranquilidad.
Puedes distinguir perfectamente en la vida cotidiana el ruido. Por ejemplo, los gritos en un estadio suenan muy diferente a comparación de cuando todas y todos los aficionados entonan el himno del equipo. Puedes identificar cuando un instrumento musical está afinado o cuando no lo está, aún sin tener mucho entrenamiento musical.
La voz humana constituye un instrumento maravilloso de matices y frecuencias donde la laringe y la boca logran modificar los sonidos que de ella emanan. La voz humana es muy interesante. Observa el siguiente video acerca de esta.
- ¿Cómo es mi voz?
https://www.youtube.com/watch?v=guqhdYqI8Pc
La intensidad del sonido está relacionada con la amplitud de la onda sonora, si la amplitud de la onda es grande, lo que se producirá es un sonido con volumen alto, mientras que, si la onda tiene una amplitud pequeña, el sonido que percibiremos será de un volumen menor.
Nos es muy sencillo distinguir sonidos con volumen alto y con volumen bajo. Incluso, los podemos percibir con otras partes de nuestro cuerpo, no sólo con los oídos.
Recuerda que los sonidos son vibraciones y que esas vibraciones se transmiten de la bocina al aire que las rodea y después a nuestros cuerpos. A mayor volumen, mayor energía, es por esto por lo que sentimos también las vibraciones producidas por las ondas sonoras en nuestros cuerpos, en especial en el pecho que es muy sensible.
Otra característica es la duración, esto es es el tiempo durante el cual se mantiene un sonido.
Escucha el siguiente sonido.
- sonido_001.mp3
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202105/202105-RSC-dbIMb7pwMb-sonido_001.mp3
Ahora éste otro.
- sonido_002.mp3
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202105/202105-RSC-nBtGApjWmn-sonido_002.mp3
Nota que el primer sonido tuvo una duración corta y el segundo una duración más larga. Al escuchar la música que crea un conjunto de instrumentos o una orquesta, podemos identificar que algunos de ellos tienen una duración corta, como el sonido producido por un triángulo, y otros de duración larga, como el de un tambor. Juntos forman la melodía que apreciamos.
Otra cualidad es el tono, este está asociado con la frecuencia de la onda sonora y mediante este podemos clasificar a los sonidos como agudos y graves.
Escucha el siguiente sonido.
- sonido_003.mp3
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202105/202105-RSC-By7kaeZvPP-sonido_003.mp3
Y ahora escucha el segundo.
- sonido_004.mp3
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202105/202105-RSC-WFUykct2bx-sonido_004.mp3
¿Cuál sonido corresponde a un tono agudo y cuál a uno grave?
Los sonidos agudos son como chillantes, hasta nos pueden lastimar los oídos, mientras que los sonidos graves son sonidos profundos. Así que, el primer sonido tuvo un tono grave y el segundo un tono agudo.
Escucha ahora cuatro instrumentos musicales para tratar de identificar si se tratan de sonidos graves o agudos.
- sonido_005.mp3
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202105/202105-RSC-dmZWfxTmgX-sonido_005.mp3
- sonido_006.mp3
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202105/202105-RSC-G8Zlkf5bbS-sonido_006.mp3
- sonido_007.mp3
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202105/202105-RSC-scZNd13FBX-sonido_007.mp3
- sonido_008.mp3
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202105/202105-RSC-hxYyrwY2IE-sonido_008.mp3
El primer sonido fue grave, el segundo agudo, el tercero agudo y el cuarto grave
Finalmente, el timbre. ¿Pueden existir dos sonidos del mismo volumen, que sean de duración corta y que ambos sean agudos?
Escucha los siguientes sonidos.
- sonido_009.mp3
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202105/202105-RSC-cgJtDZml6M-sonido_009.mp3
- sonido_0010.mp3
https://aprendeencasa.sep.gob.mx/multimedia/RSC/Audio/202105/202105-RSC-QBToE4ZM65-sonido_010.mp3
¿Fueron iguales estos sonidos?
Ambos tuvieron la misma duración, mismo volumen y son agudos, pero sonaron distinto. A esto se refiere la cualidad de timbre. El timbre es el sonido particular que tienen los objetos, dados diferentes factores como su composición y resonancia. Cada instrumento musical tiene un timbre distinto, así como cada persona tiene su particular timbre de voz. El primer sonido fue producido por un triángulo y el segundo por una flauta.
Entonces la intensidad, duración, tono y timbre son las cualidades de los sonidos.
De ahora en adelante cada que escuches una canción trata de identificar estas cualidades de las cuales se compone el sonido.
Ahora ya sabes cómo la física interviene en el mundo de la música, pero también interviene en las obras de arte como las pinturas, de hecho, uno de los principales temas en los que se relacionan es en cuanto a la luz y el color.
Recuerda que la luz son ondas que forman parte del espectro electromagnético, en donde todas las ondas que lo conforman tienen diferentes frecuencias o longitudes de onda. En particular la luz visible, es un rango de ondas electromagnéticas que podemos detectar a través de nuestros ojos y cerebro.
También debes recordar que la luz blanca se descompone en luces de colores, y eso lo comprobó Isaac Newton. Él utilizó un prisma de vidrio para observar la descomposición de la luz blanca en diferentes colores.

Esto también lo puedes observar en un arcoíris o simplemente al observar luz a través de gotas de agua, ya que estas también refractan la luz, es decir, el material cambia la dirección de las ondas del espectro de manera diferencial y las desvía, haciendo que percibas que la luz se descompone. A ese fenómeno se le conoce como refracción de la luz.
Ahora piensa en objetos opacos. ¿recuerdas los fenómenos de reflexión y absorción de la luz? Entender este par de fenómenos es esencial para conocer cómo vemos los objetos que nos rodean.
La luz llega a los objetos y una parte de esta es absorbida, mientras que otra es reflejada. La luz que reflejan los objetos y que llega a nuestros ojos es el color que percibimos.
Por ejemplo, el color de una manzana, si es roja, entonces eso significa que las ondas correspondientes al color rojo son las reflejadas por la manzana, mientras que todas las demás son absorbidas.
Estos principios son esenciales para entender por qué en una pintura apreciamos unos colores y no otros. Todo tiene que ver con los pigmentos y su composición. Observa el siguiente video para aprender más acerca de los colores en las pinturas.
- Abanico de colores
https://www.youtube.com/watch?v=9J7uCzdUkLs
La apreciación de los colores depende de los procesos del sistema visual humano., donde la luz, al pasar a través del cristalino y la pupila, llega a las células receptoras que tenemos en la retina. Ahí los fotones de luz son transformados en impulsos nerviosos que son transmitidos a nuestro cerebro. Es este último el que los interpreta y recompone en una imagen.
Por eso, hay que personas perciben los colores de forma diferente, pues tienen una condición llamada daltonismo. Existe la teoría de que el pintor Vincent Van Gogh era daltónico, y ese era el motivo por el cual elegía tonalidades muy peculiares para plasmar sus obras.

Además, las y los pintores experimentan con diferentes pigmentos de colores para poder expresar de una mejor manera sus sentimientos, y lo que buscan comunicar al espectador.
Además de la luz y el color utilizados en su elaboración, también se emplea la física en el estudio de las obras de arte. Por ejemplo, se utilizan diversos tipos de microscopios para observar las fibras y pigmentos de las pinturas para analizarlas, conservarlas o poder restaurarlas posteriormente.
Incluso los restauradores utilizan técnicas de cromatografía para conocer la composición exacta de los pigmentos y los lienzos, con el objetivo de elaborar los mejores protocolos de tratamiento para que se preserven por mucho más tiempo.
La técnica de la radiografía en las pinturas permite observar los bocetos originales de la obra, lo que está debajo de la pintura, directamente sobre el lienzo.

Con esta información se puede verificar la autenticidad de las obras o ayudar en la investigación histórica sobre la obra de arte o del artista.
El Reto de Hoy:
Elije tres canciones que te gusten y trata de identificar las cualidades del sonido, escribe tus observaciones en el cuaderno.
Además, reflexiona acerca de cómo piensas que se relaciona la física con otras artes como la danza, la escultura o el cine. Conversa con tu familia acerca de esto y elije una disciplina del arte para investigar más.
No olvides consultar fuentes de información confiables o libros especializados, para resolver tus dudas y profundizar más en este tema.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Compra en Amazon
La ciencia, el arte y la educación con las reformas borbónicas
Aprendizaje esperado: Conoce los principales rasgos de la cultura y la sociedad novohispanas en el siglo XVIII y cómo se transformaron por efecto de las reformas borbónicas.
Énfasis: Identificar la modernización de la educación, el papel de los franciscanos y agustinos, y las nuevas instituciones educativas, científicas y artísticas.
¿Qué vamos a aprender?
El propósito de la sesión de hoy es: identificar la modernización de la educación, el papel de los franciscanos y agustinos, las nuevas instituciones educativas, científicas y artísticas.
¿Qué hacemos?
Relacionado con el tema de hoy, lee la siguiente carta escrita por el filósofo y científico José Antonio Alzate en la Ciudad de México durante el siglo XVIII. La carta se encuentra en el tercer tomo de la obra Historia de la ciencia en México, realizada por el historiador de la ciencia Elías Trabulse. Dice así:
El excelentísimo don Antonio de Ulloa, uno de nuestros mayores sabios y promovedores de la literatura española, navegando de Veracruz para Cádiz, observó en 24 de junio de 1778 un eclipse total de Sol, al que acompañaba un raro fenómeno, cual era haber registrado en el disco obscurecido de la Luna un punto luminoso. Dicho señor publicó la observación, y propuso a los sabios la explicación de un efecto tan raro: procuró probar que era un taladro formado en el cuerpo lunar por donde la luz del Sol se comunicaba a la Tierra.

José Antonio Alzate
La observación pasmó a los físicos por ser una novedad no esperada; más el padre Beccaria, insigne físico de la Academia de Turín, intentó defraudar el mérito a dicho señor excelentísimo queriendo lograr la prioridad de tiempo, y publicó […] una observación que, como propia, dictaba en su cátedra, y era haber observado lo mismo en el eclipse total de Luna de 11 de octubre de 1772.
Pero en los opúsculos escogidos que se imprimieron en Milán, página 166 ya advierte […] confió la observación a su sobrino y sobrina, los que le advirtieron haber observado al tiempo del eclipse total en el disco de la Luna un punto luminoso, todo esto con el intento, como dije, de debilitar el mérito de la observación de nuestro sabio. Mas si un físico italiano intentó defraudar el mérito del descubrimiento a un astrónomo español, ¿no podré decir al padre Beccaria, aunque no me reconozca por astrónomo, sino por aficionado, que en México se imprimió observación anterior a la suya, y no menos que con la anticipación de más de tres años?

Eclipse de Luna de 12 de diciembre de 1769, observado en la imperial ciudad de México.
En el cuaderno que publiqué con este título: Eclipse de Luna de 12 de diciembre de 1769, observado en la imperial ciudad de México, y dedicado al Rey nuestro Señor por D. José Antonio de Alzate y Ramírez, impreso en México por el Licenciado don José de Jaureguí, calle de San Bernardo, año de 1770, se leen estas expresiones: Los fenómenos que observé en el eclipse son, primero: que no se observó ninguna luz en la parte obscurecida de la Luna ni con el telescopio, ni a simple vista […] La observación de este eclipse pasó a Europa, se hizo mención de ella en las Memorias de la Academia de las Ciencias de Paris, y en el Diario de los Sabios. ¿Cómo, pues, intenta el padre Beccaria dar su observación en 1772 como la primera que se haya ejecutado sobre el particular?

El siglo XVIII se caracterizó en varios países de Europa por el creciente desarrollo de la corriente de la Ilustración y del método científico entre los pensadores y científicos. Este impulso, como pudieron apreciar en la carta, también alcanzó a la Nueva España, gracias a la llegada de estas ideas que venían tanto en las mentes de diversos personajes provenientes de España, como en libros, algunos llegados a estas tierras de manera ilegal.

Ilustración “Siglo de las Luces”
Este desarrollo de las ciencias y de las artes, en un inicio estuvo fundado en la labor de ciertas órdenes religiosas, con los jesuitas a la cabeza, sin embargo, a partir de la década de 1780 desde la Corona española se decidió promover la fundación de nuevas instituciones dedicadas a la educación y modernización de la enseñanza, con la finalidad última de mejorar el conocimiento que existía sobre la Nueva España y así poder hacer más eficiente su control.
¿Cuáles fueron las instituciones que se fundaron en la Nueva España? Y ¿cómo se desarrolló esta aparente modernización de la enseñanza, la ciencia y el arte en la Nueva España? Estas serán dos preguntas que se buscara responder durante la sesión.
Como recordarás, en sesiones anteriores estudiaste que la llegada de los borbones al trono español significó la introducción de una serie de cambios y modificaciones en todos los territorios dominados por la monarquía hispánica, incluyendo la Nueva España. Y uno de los cambios más importantes en relación a la educación y la ciencia fue, sin lugar a dudas, la polémica expulsión de la Compañía de Jesús que tuvo lugar en el año de 1767.

Expulsión de la Compañía de Jesús, 1767.
La razón de este cambio fue que los religiosos jesuitas habían adoptado un papel central en todo lo referente a la educación en la Nueva España, especialmente durante el siglo XVIII, a tal grado que con la expulsión de la orden los colegios novohispanos perdieron un total de 454 individuos que se desempeñaban, entre otras cosas, como profesores de primeras letras, gramática latina, retórica, filosofía o teología. La expulsión también significó que en 21 ciudades y villas de la Nueva España se cerraran todos los colegios jesuitas dedicados a la enseñanza, los cuales fueron expropiados por el gobierno real.
El impacto fue sin duda muy duro, sobre todo en el ámbito de la educación para seglares, es decir, las personas que no pertenecían al clero, toda vez que las escuelas de las otras órdenes religiosas estaban dirigidas principalmente a novicios o seminaristas, por lo que de un momento a otro un sector de la población, principalmente el criollo, se quedó sin alternativas para continuar con sus estudios.

Además de la pérdida de los espacios educativos, la expulsión de los jesuitas implicó el freno a los cambios que algunos miembros de esa orden, habían intentado implementar en sus formas de enseñanza. Maestros como Francisco Xavier Clavijero habían empezado a limitar el uso del método escolástico para remplazarlo por el método científico experimental que, entre otras cosas, les permitió difundir algunas de las ideas de los científicos más importantes de esa época como Isaac Newton, Rene Descartes, Francis Bacon o Benjamin Franklin.

Francisco Xavier Clavijero
Fue gracias a sus esfuerzos que a mediados del siglo XVIII en Nueva España comenzó a tomar forma un tímido movimiento de “ilustración católica”, dentro del cual destacó gente como Antonio de Alzate, autor de la carta que leíste al principio de la sesión.
Frente a la situación de vacío creado por la intempestiva salida de los jesuitas del reino de la Nueva España, se tomaron diversas acciones.
Por un lado, los franciscanos y agustinos, tenían seminarios y colegios especialmente dirigidos a novicios y religiosos, lograron abrir sus cursos para que los laicos pudieran ingresar en ellos. Para lograrlo la Real y Pontificia Universidad de México tuvo que validar dichos cursos.

Por otro lado, los colegios jesuitas de las ciudades de Puebla, Guanajuato, Querétaro y México reabrieron ahora bajo el control y financiamiento del gobierno, sin embargo, muchas de las propiedades jesuitas que aportaban dinero para mantener los colegios fueron vendidas por el gobierno y los recursos obtenidos de esas ventas enviados a España, con lo que la educación novohispana se descapitalizó.

Templo de San Francisco Javier y antiguo Colegio Jesuita de San Francisco Javier, actual Museo Nacional del Virreinato, Tepotzotlán, Estado de México.
Pero si con la expulsión de los jesuitas la Corona española había afectado el ámbito educativo en la Nueva España, a partir de la década de 1780 la situación cambió radicalmente, puesto que en esos años desde Madrid se decidió apoyar algunas propuestas novohispanas para crear tres instituciones que tendrían un papel muy importante en el desarrollo de la educación, la ciencia y las artes en la Nueva España.
La primera de ellas fue la Academia de las Nobles Artes de San Carlos, la cual fue propuesta por el director de grabado de la Casa de Moneda de México cuyo proyecto estaba inspirado en la Academia de San Fernando de Madrid y tenía por objetivo la creación de una escuela donde se enseñarán las bellas artes .

Academia de San Fernando de Madrid, España.
La propuesta fue aceptada por Carlos III en 1784 y, al año siguiente, fue inaugurada en la Ciudad de México, ofreciendo cursos de arquitectura, dibujo, grabado, matemáticas y escultura.
Sin embargo, su creación no estuvo libre de polémica, debido a la preferencia que se le dio a los profesores de origen español. Esto causó que en 1788 el director de la Academia solicitará que 3 de sus 4 maestros fueran cambiados. También causó conflicto en varios alumnos la predilección de la institución por instaurar el estilo neoclásico y rechazar la corriente barroca, tan desarrollada en Nueva España.
Estas quejas provocaron que la planta docente cambiara y con eso se diera la llegada de nuevos profesores venidos de España que lograron levantar el nivel académico de la Academia, convirtiéndola en una de las escuelas de bellas artes más importantes del continente. Artistas españoles de la talla de Manuel Tolsá o Rafael Ximeno y Planes se ocuparon de las cátedras de escultura y pintura respectivamente, con lo que se le dio un impulso definitivo al desarrollo del estilo neoclásico en Nueva España.

Retrato de Manuel Tolsá por Rafael Ximeno y Planes.
En el mismo año de 1788 otra institución dedicada a la educación y la ciencia apareció en el ámbito novohispano: el Jardín Botánico. Esta institución también se inspiró en su homónima de Madrid y fue fundada en 1788 bajo la dirección de dos científicos españoles, Martín de Sessé y Vicente Cervantes.
Si bien esta institución también tuvo problemas relacionados con la aparente discriminación a los criollos, el jardín siguió con sus actividades como una institución interesada en el carácter práctico de la botánica, generando una importante colección de especímenes vegetales y siendo un espacio en el que se impartían cátedras. El Jardín Botánico también sirvió como plataforma desde la cual Vicente Cervantes introdujo en Nueva España conocimientos científicos novedosos en los campos de la biología o la química, como lo fue el sistema de taxonomía creado por Carlos Linneo, al cual se opuso férreamente el pensador novohispano Antonio de Alzate, sin mucho éxito.
Otra de las instituciones en aparecer en Nueva España fue el Colegio de Minería. Este tuvo su origen en la propuesta de dos criollos, Joaquín Velázquez de León y Juan Lucas de Lassaga, de crear un tribunal de minería y un “seminario metálico”.

Edificio del Colegio de Minería, estilo neoclásico.
La idea recibió la aprobación de Carlos III quien, para disgusto de los criollos, nombró como director al español Fausto de Elhúyar. A pesar de las quejas de los novohispanos, Elhúyar se mantuvo en su puesto. El colegio abrió sus puertas en el año de 1792 con maestros traídos de Europa, entre los cursos que se impartían había clases de mineralogía, latín, calculo integral y química. Con el tiempo, el colegio llegó a dar becas para que algunos estudiantes continuaran sus estudios en Europa y entre sus logros se puede señalar la traducción del trabajo clásico de Lavoisier, Tratado elemental de química en 1797 o el descubrimiento en 1801 de un nuevo elemento químico: el vanadio.

Real Seminario de Minas
Para construir la sede del colegio de Minas se eligió ni más ni menos que al arquitecto Manuel Tolsá cuyo edificio pervive hasta nuestros días. Observa el siguiente video para conocer más de la institución y su edificio sede.
- Manuel Tolsá. Palacio de Minería
https://www.youtube.com/watch?v=DOBuAffZ3AU&t=170s
El Real Seminario de Minas o colegio de Minas, junto con el Jardín Botánico y la Academia de San Carlos alcanzaron su mayor desarrollo a principios del siglo XIX, de tal forma que Alexander von Humboldt en esos años escribió: “Ninguna ciudad del Nuevo Continente sin exceptuar las de los Estados Unidos, presenta establecimientos científicos tan grandes y sólidos como la capital de México. Citaré sólo la Escuela de Minas […] el jardín Botánico y la Academia de pintura y escultura conocida con el nombre de Academia de Nobles Artes”. Pero el desarrollo de las ciencias y el arte no se redujó a estas tres instituciones. Además, se llevaron a cabo numerosas tentativas para difundir el conocimiento científico, las cuales contaron con el apoyo del gobierno real.

Alexander von Humboldt
En este respecto tendríamos que nombrar la aparición de la Gaceta y del Diario de México, las primeras publicaciones periódicas en la Nueva España. La inclusión de temáticas y discusiones científicas en ellas abrió este tipo de conocimientos a un mayor público del que antes conocía sobre ellos.

También se promovió la realización de varias expediciones tanto con fines geográficos, como botánicos e incluso médicos, como fue el caso de la expedición encabezada por el médico Francisco de Balmis a principios del siglo XIX el cual buscó difundir la técnica de la vacunación contra la viruela entre la población novohispana.

Sin embargo, la expedición más importante realizada en aquella época fue sin duda la llevada a cabo por el barón de Humboldt, que, aunque era una empresa personal, fue apoyada por la Corona durante el tiempo que el aristócrata alemán permaneció en la Nueva España, dándole todas las facilidades para que pudiera conocer lo más posible de los territorios americanos.

Por último, es importante señalar que el gobierno virreinal también dio un empuje decidido e importante a la educación elemental, toda vez que favoreció el surgimiento de algunas escuelas de primeras letras gratuitas, tanto en el ámbito urbano español como en los pueblos indígenas, con lo que buscó llenar el vacío provocado por la expulsión de los jesuitas.
Para recapitular lo estudiando en esta sesión observa el siguiente video.
- Reformas modernizadoras
https://www.youtube.com/watch?v=Yx6B7Jxm9jw
A finales del siglo XVIII y principios del siglo XIX, la educación, la ciencia y el arte se encontraban en una fase de desarrollo, gracias en parte al apoyo decidido de la monarquía española, la cual, siguiendo los preceptos del absolutismo ilustrado, vio en el apoyo a estos ámbitos una oportunidad para controlar y desarrollar más sus territorios ultramarinos.
Tras la expulsión de los jesuitas fue a través de la participación de otras órdenes religiosas, apoyos a expediciones científicas, creación de escuelas de primeras letras y del desarrollo de tres nuevas instituciones educativas y científicas, que Carlos III buscó favorecer el desarrollo científico y artístico de la Nueva España.
El Reto de Hoy:
Responde ¿qué repercusiones tuvieron las Reformas Borbónicas en la ciencia, el arte y la educación novohispana? Y presenta tu trabajo en formato de infografía. Seguro encontrarás gran variedad de pinturas y litografías de la época que te permitirán ilustrarlo.
Para resolver el reto no dudes en recurrir a tu Libro de Texto.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Compra en Amazon










Publicar un Comentario