Aprende en Casa 2 SEP: 30 de octubre TAREAS y ACTIVIDADES de 3° de secundaria

¿Cuáles fueron los temas del día?

A continuación dejamos los temas vistos el 30 de octubre de clases virtuales mediante el programa Aprende en Casa 2, para los alumnos de 3° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa 2, compartimos los temas y actividades que se abordaron este Viernes 30 de octubre, así como las dudas que se plantearon.

La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa 2:

https://aprendeencasa.sep.gob.mx/#

Revisando tu puntuación y ortografía en informes

Aprendizaje esperado: Describe el impacto de los anuncios publicitarios en la sociedad mediante un texto.

Énfasis: Revisar puntuación y ortografía de informes.

¿Qué vamos a aprender?

Trabajar con tu ortografía y redacción es muy importante. Si no las practicas, te puedes encontrar con dificultades al comunicarte de manera escrita. Analizarás los aspectos fundamentales para el uso de la ortografía al revisar informes.

Recuerda que todo lo que revisas es para reforzar tu conocimiento, así que te recomiendo llevar un registro de las dudas, inquietudes o dificultades que se te presenten. Cuando te surjan dudas, revisa los apuntes que tomas o las explicaciones del libro de texto, te ayudara a resolverlas.

¿Qué hacemos?

La ortografía y la puntuación te ayudan a expresar tus ideas de una manera más clara. Sin estas herramientas sería más complicado que alguien entendiera lo que escribes. Hasta podría generarse malos entendidos.

Saber usar la ortografía te ayuda a reducir las ambigüedades. Es la base de una comunicación efectiva.

La escritura es una de las formas más utilizadas para comunicarte, por tal motivo, es importante reflexionar acerca del uso adecuado de la puntuación y la ortografía.

Observa el siguiente ejemplo de un texto sin puntuación adecuada:

 

Delicioso pan relleno de muerto venga a probarlo

 

¿Qué entendiste en este anuncio publicitario? ¿Cómo lo interpretas?

La verdad es que, aunque se puede comprender, suena incoherente. Hasta parecería que el pan está relleno de un muerto.

Requiere un esfuerzo extra por parte del lector. Este anuncio, sin puntuación, provocaría risa y, tal vez, hasta miedo.

Observa el mismo anuncio, pero utilizando signos de puntuación y modificando un poco su sintaxis.

 

Delicioso pan de muerto, relleno. Venga a probarlo.

 

Ahora se puede leer más claramente.

¿Y qué tal si agregas unos signos de exclamación y cambias un poco el orden de este anuncio publicitario?

 

Pan de muerto relleno. ¡Delicioso!, venga a probarlo.

 

¿Qué te parece el cambio?, ¿se entiende mejor la información?

Esa persona incluso podría tener más ventas de sus productos con un anuncio mejor redactado.

En la actualidad, la escritura ha ganado terreno en todos los ámbitos. Un gran número de personas hacen uso de ésta, ya sea para dejar un mensaje, llenar un formulario, escribir una carta, hacer una petición y hasta redactar un texto académico o informe.

Lo mejor es que te preocupes porque todo lo que escribas pueda cumplir su cometido, que es comunicarte efectivamente.

Y, para eso, es necesario prestar mucha atención a la puntación y la ortografía.

Revisa algunos elementos que te ayudarán a reconocer la importancia de la ortografía en tus textos.

Presta atención a lo que te compartirán los personajes María Moliner y Miguel de Cervantes Saavedra.

¿Sabías que María Moliner fue lexicógrafa y autora del Diccionario de uso del español?

Y, por otro lado, Miguel de Cervantes Saavedra fue un novelista y dramaturgo español.

Escucha a dichos personajes en el siguiente video del minuto 3:52 al 5:11:

 

1. La importancia de revisar la ortografía

Reforzar tu ortografía y observar tu puntuación es fundamental. Te recomendamos contar con un diccionario al momento de realizar tu informe u otro tipo de texto.

Es una gran estrategia. Teniéndolo a la mano, podrás conocer el significado de todas las palabras que vas usar, además de corroborar la manera correcta de escribir aquéllas con las que tengas dudas.

Con el apoyo del diccionario, podrás redactar textos con mayor seguridad.

Además de la ortografía, la puntuación también tiene una importancia fundamental en la construcción de los textos, pues permite:

 

• Jerarquizar las ideas.
• Dar estructura al escrito.
• Destacar ideas principales.
• Evitar ambigüedades.
• Hacer comprensibles las oraciones.

 

Por ejemplo, usar los dos puntos. Éstos indican una pausa que te ayuda a notar la relación entre lo que se dice y el texto que le sigue, o bien a preparar una numeración explicativa.

Un ejemplo aplicado en una numeración de elementos puede ser el siguiente.

Algunos medios de comunicación explorados en este informe fueron:

 

• Televisión
• Teléfono
• Redes sociales
• Correo electrónico

 

Entre otros. ¿Te diste cuenta de cómo, antes del listado, el autor utilizó los dos puntos? También, al elaborar un informe, puedes emplearlos para hacer referencia a un texto o a un autor.

Los anuncios en los medios de comunicación, en ocasiones provocan que las personas compren cosas que no necesitan, como lo explica el autor en su libro:

 

“Los medios de comunicación tienen estrategias para convencer al consumidor de que compre productos que no son de uso indispensable.”

 

Con los signos, consigues una mejor explicación y ejemplos más claros de aquello que buscas describir. En este ejemplo puedes identificar el uso de las comillas.

Las comillas, en este caso, hacen referencia a una cita de autor. Gracias a ellas marcas que esta idea no te pertenece, sino a alguien más; en este caso, indica que la oración fue escrita en un libro.

Es muy útil saber cómo las comillas y los dos puntos te ayudan a estructurar mejor tus ideas al escribir. También está el punto y seguido, que se usa al final de una oración que no depende de otra para entenderse.

Un ejemplo es el tomado de las conclusiones de un informe.

Es importante aprender cómo obtener información acerca de los productos comerciales. Los mensajes no necesariamente están ofreciendo el producto; muchas veces lo que venden es una imagen.

En la primera oración se explica una idea sobre la importancia de obtener información de los productos. Pero en la segunda se habla de cómo los mensajes publicitarios no venden un producto, sino una imagen. Aunque ambas oraciones se complementan, éstas se pueden separar y siguen siendo comprensibles. Para esto sirve el punto y seguido.

El punto y aparte, por su lado, ayuda a separar párrafos completos. Es decir, separa grupos de ideas que se interrelacionan.

El punto y seguido separa ideas que se complementan y que son más cercanas entre sí. Mientras que el punto y aparte separa grandes bloques que giran en torno a una idea central. Esos bloques, que visualmente puedes distinguir en un escrito, se llaman párrafos.

Aprenderás ahora, el uso de la coma. Ésta se utiliza para separar oraciones subordinadas, es decir, oraciones que se encuentran juntas, y que se complementan una con otra. Una de esas oraciones depende de la otra, ya que, sin la oración principal, tiene un sentido incompleto. Las comas también se utilizan para separar diversos elementos de una serie o enumeración.

Dependiendo del medio por el que se difunden los mensajes publicitarios, éstos se conforman de elementos como imagen, sonido y principalmente de palabras.

Las comas, en este caso, te ayudan a comprender mejor la oración, y separan adecuadamente las oraciones para que no hubiera errores de percepción al leerla. Otro elemento de la ortografía importante es el uso de las mayúsculas.

Repasa su uso, se utilizan mayúsculas:

 

• Al principio de un escrito.
• En el nombre de calles, avenidas, monumentos.
• Cuando se escriben nombres propios.
• Después de cualquier punto.
• Y también en los nombres de épocas, acontecimientos y movimientos sociales. 

 

Continúa ahora con el punto y coma. Este signo ortográfico representa una separación de ideas mayor que la marcada por la coma, pero menor a la que se señala en el punto. Se escribe antes de los conectores de oraciones, como:

 

• Pero
• Mas
• Aunque
• Por lo tanto
• Es decir

 

El punto y coma también se utiliza para separar oraciones independientes que se complementan entre sí, formando parte de una misma idea.

Cuando eliges algún producto lo haces dependiendo de tus gustos; aunque también puedes estar haciendo dicha elección tomando en cuenta si el producto beneficia o perjudica tu salud. La ortografía es fundamental para escribir cualquier informe. Un informe es un escrito que tiene como objetivo comunicar, de manera detallada, algo que se está realizando, puede ser una investigación, un hecho o un evento.

Debe tener un lenguaje claro, concreto y objetivo para que cualquiera que lo lea lo pueda entender sin complicaciones. Escucha a la maestra especialista que te hablará al respecto, a través del siguiente video de minuto 8:14 al 10:24

 

2. ¿Cómo te lo explico? Informes y experimentos

No olvides estos consejos para la redacción de un informe claro y efectivo. El lenguaje debe de ser preciso y claro, además, puedes usar “tecnicismos”, es decir, palabras técnicas relacionadas con el tema.

Entre las características a tomar en cuenta, se encuentra la elaboración de una carátula, incluir los antecedentes, mencionar a aquellas personas que han hablado del tema, los propósitos, los pasos que utilizaste al elaborar tu trabajo, la descripción, pueden ser gráficos o esquemas, el análisis de lo que encontraste, así como las conclusiones y la bibliografía. Además, debes contar con una adecuada ortografía y puntuación.

Complementa la información y repasa algunos elementos que te pueden ayudar al elaborar un informe.

1. Tener claro el tema del que tratará tu texto. Esto es importante para tener claras las ideas, como la información que vas a escribir.

2. Organiza la información en subtemas, categorías, conceptos o preguntas. Si tu informe gira en torno al impacto que tiene la publicidad en la sociedad, ¿cuáles piensas que podrían ser algunos ejemplos? Podrían ser las cualidades y funciones de la publicidad. O la forma en que sus características influyen en ti para comprar algún producto. Incluso las estrategias que puedes usar para ser mejor consumidor.

Hay mucha información que puedes integrar, lo importante es tenerla clara para no desviarte del tema central.

3. Detalla y explica a profundidad la información recabada en tu texto. Anota en tus descripciones los ejemplos que hayas encontrado, y textos de especialistas sobre el tema. Así el lector tendrá más clara la idea que quieres trasmitir.

4. Utiliza recursos lingüísticos como:

 

• Adjetivos calificativos
• Adjetivos explicativos
• Figuras literarias

 

Recuerda anexar a tu texto una introducción y una conclusión.

En la introducción puedes explicar brevemente de qué tratará tu texto y los subtemas por abordar. Mientras que en la conclusión puedes realizar un breve resumen del tema y explicar las ideas más importantes. No olvides que tu descripción deberá ser técnica.

Es decir, tendrás que definir y explicar el tema dando referencias, utilizando descripciones detalladas, lenguaje objetivo y planteando diferentes opiniones acerca del mismo. Con estos elementos y tienes más herramientas para realizar tus informes.

Observa la entrevista acerca de la cultura del consumidor en el país y las técnicas que tiene la publicidad, del inicio al minuto 3:41

 

3. Los recursos de la publicidad

En la entrevista te presentan preguntas que puedes ocupar en tu redacción. La información que observaste puede servirte para que en tu informe puedas describir con detalle la manera en que los medios influyen en la toma de decisiones.

Pero este video sólo es una fuente de información que se te presentó como ejemplo. Puedes explorar otros videos, textos o publicaciones que sean realizados por investigadores, expertos o instituciones educativas. Lo importante es ahondar en el tema para dominarlo de la mejor manera posible.

En resumen, los informes se caracterizan por ser:

 

• Concisos
• Claros
• Objetivos

 

También te puedes apoyar usando imágenes y gráficos que muestren visualmente tus ejemplos.

Realiza la siguiente actividad, te ayudará a comprender un poco mejor. Pon atención a las preguntas y ejercicios. En caso de ser necesario, consulta tus apuntes o palabras clave para ayudarte a recordar.

¿Qué estrategias te pueden ayudar a mejorar tu ortografía?

 

1. Aprenderte de memoria las reglas ortográficas.
2. Busca videos sobre cómo escribir un texto.
3. Utiliza el diccionario y consulta las palabras que no conoces.

 

No puedes mejorar tu ortografía si no la practicas. Y usar el diccionario te ayuda a familiarizarte con las convenciones ortográficas.

Por supuesto que ver videos y tratar de recordar las reglas es útil, pero la mejor forma de afianzar las reglas ortográficas es practicándolas.

Te recomiendo revisar el texto mientras lo escribes, pero también al finalizarlo. Hacer más de una revisión evitará que se te escape algún error.

Además, no olvides que algo fundamental para refinar tu ortografía es la lectura. Fomentar este hábito te proporcionará elementos para ensanchar tus horizontes.

¿Para qué sirven los signos de puntuación?

 

1. Jerarquizar las ideas.
2. Destacar ideas principales.
3. Evitar ambigüedades.
4. Todas las anteriores.

 

¿Cuál es tu respuesta?

En esta sesión has visto que los signos de puntuación te ayudan a organizar tus ideas, a destacar lo más importante y evitar escribir ideas que son poco claras. Si te das cuenta, los signos de puntuación parecen muy sencillos, pero su uso correcto es de vital importancia para los textos. Entre mejor las domines, tendrás un texto más claro y efectivo.

Lee el siguiente ejemplo e intenta señalar cuál es el signo de puntuación faltante.

Los productos o servicios que se promocionan son

 

1. Ofertas.
2. Promesas vinculadas a la percepción emocional.
3. Promesas relacionadas al éxito social.

 

¿Te percataste cuál signo falta?

Antes del listado de productos o servicios que se promocionan, tendrían que existir dos puntos que dieran pie a los ejemplos.

Los mensajes publicitarios no necesariamente están ofreciendo el producto muchas veces lo que venden es una imagen

Lo que falta es una coma después de la palabra producto. También falta otro signo. Es el punto final para indicar que la idea o párrafo está terminando.

De manera que el texto, con un correcto uso de la puntuación, quedaría de la siguiente manera:

Afinar la puntuación y ortografía es importante, pero también es un proceso gradual. Así que no te preocupes si al inicio te cuesta o se te escapan algunos aspectos. La práctica hace al maestro. Lo importante es el interés por aprender.

¿Qué puedes corregir del siguiente texto?

propósito: diferenciar entre la información presentada en los mensajes publicitarios y la realidad,

Los signos de puntuación son fundamentales. El texto no sólo se ve raro, además es un poco complicado leerlo.

¿Qué le arreglarías?

Agrega mayúsculas. Al iniciar el párrafo deben incluirse, igual que después de los dos puntos.

También sustituye la coma del final del texto por un punto, ya que no se está haciendo una enumeración, sino que se está cerrando una idea.

Quedaría de la siguiente manera: Propósito: Diferenciar entre la información presentada en los mensajes publicitarios y la realidad.

A veces puede parecer que esas modificaciones son mínimas, pero también son importantes, porque son parte de tus recursos de expresión.

Sin duda, la ortografía y puntuación son herramientas fundamentales para comunicarte de manera escrita. Ya sea para hacer tus informes, o bien para comunicarte con amigos o familiares. Cada vez utilizas más los mensajes de texto con la gente cercana y quieres que todo aquello que intentas decirles siempre quede claro.

La buena escritura es una práctica fundamental que, mientras más prácticas, mejor podrás emplearla, ya sea en tu vida académica o el ámbito personal.

No sería agradable generar malos entendidos porque usaste mal algún signo de puntuación, como en el ejemplo del pan de muerto.

Recuerda que puedes preguntar tus dudas a tus maestros, o bien hacer llegar tus inquietudes o sugerencias a través del correo electrónico: aprende_en_casa@sep.gob.mx.

El Reto de Hoy:

Redacta el informe de un experimento o sobre alguna actividad que hayas realizado.

Recuerda revisar la ortografía y puntuación durante la redacción y al terminar, solicita a un integrante de tu familia que lo lea y te dé su opinión, identificando si te faltó algún signo de puntuación u ortografía.

Recuerda prestar atención a los elementos que has trabajado mientras redactas cada escrito, así como cuando los concluyas.

No olvides que para que mejores tu puntuación y ortografía, puedes apoyarte en el diccionario. Pero, sobre todo, hay que fomentar el hábito de la lectura.

Te sugerimos que continúes aprendiendo; es tiempo de buscar, investigar, y leer.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

Completar el trinomio cuadrado perfecto

Aprendizaje esperado: Resuelve problemas que implican el uso de ecuaciones de segundo grado

Énfasis: Resolver problemas cuadráticos usando factorización.

¿Qué vamos a aprender?

En esta sesión estudiarás un caso especial de resolución de ecuaciones de segundo grado mediante el método de factorización, pero completando cuadrados.

No olvides registrar tus dudas, inquietudes y anotaciones respecto a esta lección. Podrás apoyarte en tu libro de texto para consolidar los aprendizajes.

Estudiarás ecuaciones de segundo grado que no tienen en su primer miembro trinomios cuadrados perfectos.

¿Qué hacemos?

Inicia con una situación que aparece propuesta en el libro de texto:

 

Luis es un profesor de tercer grado de secundaria, él les propuso a sus alumnos como un reto resolver, integrados en equipos, una situación que puede ser modelada y resuelta mediante una ecuación de segundo grado de la forma: equis cuadrada más be equis más ce igual a cero, donde a debe ser siempre diferente de cero; y en este caso a es igual a uno o bien diferente de uno, pero no es un número cuadrado.

 

Después de analizar la información de la situación, una de sus alumnas llamada Roxana propuso a sus compañeros de equipo que la situación se podía modelar con la ecuación: equis cuadrada menos cuatro equis más tres igual con cero, el profesor les indicó resolver la ecuación utilizando el método de factorización, con la condición de transformar el trinomio de segundo grado escrito en el primer miembro como un trinomio cuadrado perfecto; por lo que Eduardo, otro de los alumnos integrantes del equipo, les mencionó que sí era posible lograr lo que el profesor Luis les indicaba.

 

Mariana, otra de sus compañeras de equipo, preguntó a Eduardo: ¿y por qué afirmas eso? Eduardo les dijo: miren vamos a analizar con cuidado la ecuación propuesta por Roxana y se darán cuenta que es cierto que no se tiene un trinomio cuadrado perfecto en el primer miembro de la ecuación, cuya factorización sería un producto de binomios semejantes, o bien, expresarlo como un binomio al cuadrado.

 

Eduardo les dijo: recuerden que el profesor Luis ya explicó antes, que para que se tenga un trinomio cuadrado perfecto se deben cumplir tres requisitos:

 

El primero es que el polinomio tenga tres términos, el segundo es que dos de los términos sean cuadrados, y el tercero es que el tercer término sea igual al doble del producto de las raíces de los dos términos cuadrados.

 

Observemos que en la ecuación: equis cuadrada menos cuatro equis más tres igual a cero, se tiene en el primer miembro, un término cuadrático “a equis cuadrada”, al cual se le puede extraer la raíz cuadrada; un término lineal o de primer grado, “be equis”; y un término numérico, “ce”, por lo que no se puede factorizar como un trinomio cuadrado perfecto debido a que no está completo.

 

 

¿Cómo explicó Eduardo a sus compañeros la manera en que se puede proceder para completar un trinomio y que sea cuadrado perfecto?

 

Eduardo les dijo: ¡en realidad, compañeros, el procedimiento es muy sencillo! pongan mucha atención, se requieren realizar algunas operaciones vinculadas con los términos algebraicos, es decir, con el término cuadrático y con el término lineal o de primer grado, veamos cómo:

 

Para completar el trinomio: equis cuadrada menos cuatro equis más tres, en la ecuación donde el segundo miembro es cero, operaremos con el binomio equis cuadrada menos cuatro equis, lo escribimos en el siguiente renglón el término cuadrático y el término de primer grado dejando espacio para escribir otros dos términos y luego más tres igual a cero.

 

 

Obtenemos la mitad del coeficiente del término de primer grado: cuatro entre dos es igual a dos, dicho valor ahora se eleva al cuadrado y el valor obtenido se anota sumando como tercer término para completar el trinomio cuadrado perfecto, pero como sumamos cuatro también restamos cuatro, lo que significa que hemos sumado cero para no afectar el equilibrio de la igualdad, quedando: Equis cuadrada menos cuatro equis más cuatro menos cuatro más tres igual a cero.

 

¿Pudiste descubrir el trinomio cuadrado perfecto? La respuesta es equis cuadrada menos cuatro equis más cuatro. Y además es equivalente a tener un binomio al cuadrado.

Recuerda que se identifican los dos términos cuadrados del trinomio y le extraes la raíz cuadrada, preparas un paréntesis en el cual a continuación anotas las raíces separadas del signo que tenga el otro término que es equivalente con el doble del producto de las dos raíces obtenidas, sólo falta agregar el exponente dos al binomio.

 

En este caso el trinomio equis cuadrada menos cuatro más cuatro es equivalente con el binomio equis más dos al cuadrado.

 

Después de tener el binomio al cuadrado ahora escribe menos cuatro más tres igual a cero.

A continuación, se reducen los términos numéricos, quedando el binomio equis más dos al cuadrado menos uno igual a cero.

A partir de aquí, puedes continuar resolviendo la ecuación recurriendo a la factorización de la diferencia de cuadrados que se tiene en el primer miembro de la ecuación para determinar los valores de las raíces de equis.

Recuerda que, para factorizar la diferencia de cuadrados escrita en el primer miembro de la ecuación, extraes la raíz cuadrada del primer término cuadrado, es decir, el binomio equis más dos elevado al cuadrado, la raíz cuadrada es el binomio equis más dos, también extraes la raíz cuadrada de 1, la cual es uno.

 

 

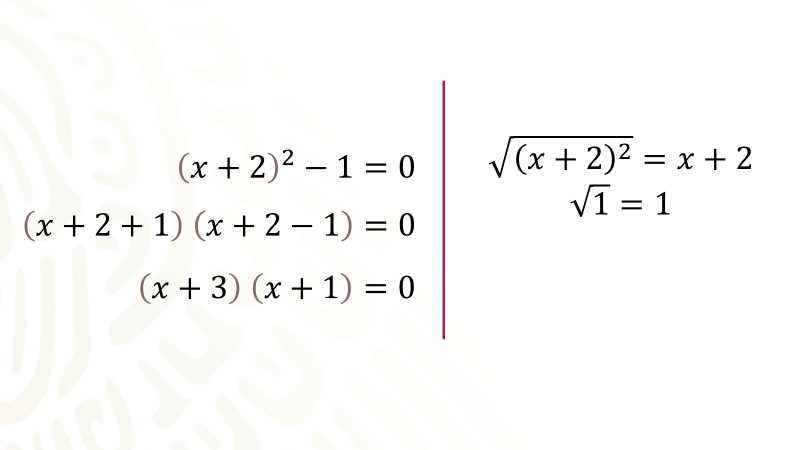
Para continuar preparas un par de paréntesis para expresar el producto de dos binomios conjugados, que son la factorización de la diferencia de cuadrados sin olvidar igualar a cero, recuerda que estas resolviendo una ecuación.

Para formar dichos binomios conjugados escribe como primer término en los dos factores, la primera raíz, equis más dos; luego escribes como segundo término la segunda raíz, que es uno, en el primer factor escribes el signo de más entre los dos términos y en el segundo factor escribes el signo de menos entre los dos términos.

En el primer factor queda equis más dos más uno y en el segundo factor queda equis más dos menos uno, continúas reduciendo términos numéricos, obteniendo un producto de dos binomios conjugados igual con cero.

Ahora la respuesta a la interrogante ¿cuál es el valor numérico de las raíces o soluciones de la ecuación de segundo grado propuesta?

Para eso, utilizarás la propiedad del producto cero, la cual, simplemente establece que si ab = 0, a por be es igual acero, entonces puede suceder que:

 

• Que el factor “a” sea igual a cero.
• Que el factor “b” sea igual a cero.

 

También puede suceder que ambos factores sean igual a cero. Lo anterior significa que debes igualar cada factor binomio a cero, lo que dará origen a dos ecuaciones de primer grado muy sencillas de resolver. Tienes entonces el binomio equis más tres igual a cero y el binomio equis más uno igual a cero.

Después de resolver la ecuación de primer grado, equis más tres igual con cero, obtienes el valor de la primera raíz que es equis igual a tres negativo.

Si ahora resuelves la ecuación de primer grado, equis más uno igual con cero, obtienes el valor de la segunda raíz que es equis igual a uno negativo.

Has resuelto la ecuación de segundo grado propuesta utilizando el método de factorización y un procedimiento especial conocido como “completar el trinomio cuadrado perfecto”.

Para entender este nuevo procedimiento especial de completar un trinomio cuadrado perfecto utilizado para resolver ecuaciones de segundo grado mediante factorización, observa el siguiente ejemplo:

Te proponemos resolver la ecuación

 

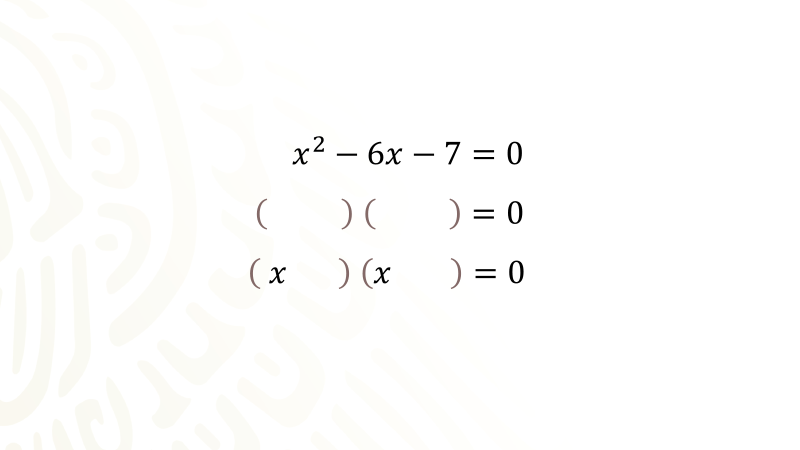
Cómo puedes observar esta ecuación tiene la forma “a equis cuadrada más be equis más ce igual a cero” donde en el término cuadrático “a es igual a uno”, el término de primer grado es seis equis negativo y el término numérico es siete negativo; esta ecuación la resolverás factorizándola utilizando el procedimiento de transformar el trinomio que se encuentra en el primer miembro de la ecuación como un trinomio cuadrado perfecto, es importante hacer algunas precisiones para favorecer que se entienda de mejor manera el procedimiento propuesto por Eduardo en la situación anterior.

El trinomio que se encuentra en el primer miembro de la ecuación dada se puede factorizar con un procedimiento que ya conoces, sin embargo, lo interesante de las matemáticas es que puede haber varios procedimientos para resolver determinadas situaciones, en este caso, estas estudiando ¿cómo completar un trinomio para que sea cuadrado perfecto?

Para dar sentido al uso de este nuevo procedimiento primero recuerda el procedimiento que ya conoces con la finalidad de que puedas verificar que los valores obtenidos de las raíces de las ecuaciones son los mismos que se obtienen con el nuevo procedimiento.

Tienes la ecuación:

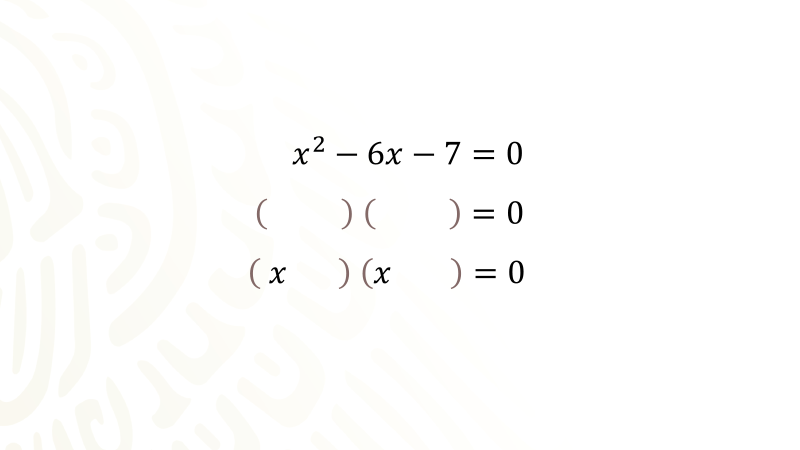
Preparas un par de paréntesis para formar un producto de binomios igualados con cero. El siguiente paso es extraer la raíz cuadrada del término cuadrático, en este trinomio la raíz cuadrada de equis cuadrada es equis, la escribes como primer término en cada binomio:

Ahora, necesitas determinar dos números considerando sus respectivos signos (positivo o negativo) que al mismo tiempo multiplicados den como resultado el valor del término numérico, es decir, siete con signo negativo y que sumados den como resultado seis con signo negativo.

 

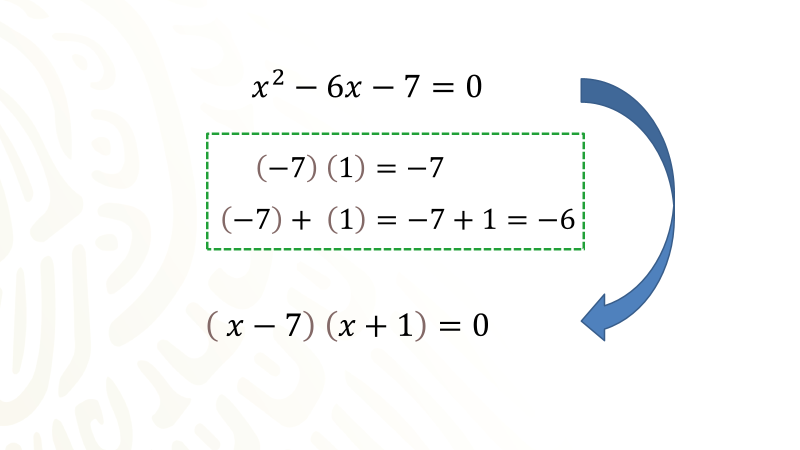
Recuerda que para determinar dichos números puedes apoyarte en la factorización del término numérico, en este caso, necesitas dos números que al multiplicarlos el producto sea un siete negativo, por lo que, uno de los números será positivo y el otro número será negativo, de las opciones posibles, elegirás la que también cumpla con que dichos números sumados den como resultado seis negativo, esto último nos indica que en realidad se restan los valores absolutos de dos números donde el de mayor valor es negativo.

Entonces al multiplicar siete con signo negativo por uno con signo positivo obtienes como resultado siete con signo negativo.

Por otra parte, al sumar el número siete negativo más el número uno positivo da como resultado seis negativo.

Anota como segundo término del primer factor binomio al siete negativo y como segundo término del segundo factor binomio al uno positivo, quedando, el indicado el producto del binomio equis menos siete por el binomio equis más uno igual a cero.

Cómo puedes observar se tiene la forma factorizada de la ecuación dada, sin embargo no se tiene en el primer miembro un producto indicado de binomios semejantes que también se puede expresar como un binomio al cuadrado que a su vez es equivalente con un Trinomio Cuadrado Perfecto, lo cual, permite afirmar que no se puede construir de manera geométrica, un cuadrado perfecto ya que las dimensiones de los lados no son valores iguales, lo que requiere es utilizar el procedimiento para completar el trinomio cuadrado perfecto.

Retoma la ecuación dada en su forma general: equis cuadrada menos seis equis menos siete igual a cero, escribes en el siguiente renglón el término cuadrático y el término de primer grado dejando espacio para escribir otros dos términos y luego menos siete igual a cero.

Obtienes la mitad del coeficiente del término de primer grado, seis entre dos es igual a tres, dicho valor ahora se eleva al cuadrado y se anota sumando como tercer término para completar el trinomio cuadrado perfecto, pero como sumas nueve también restas nueve, lo que significa que has sumado cero para no afectar el equilibrio de la igualdad, quedando: Equis cuadrada menos seis equis más nueve menos nueve menos siete igual a cero.

Tienes ahora el Trinomio Cuadrado Perfecto: Equis cuadrada menos seis equis más nueve. Y además es equivalente con un binomio al cuadrado, ahora escribes dicho binomio menos nueve menos siete igual a cero.

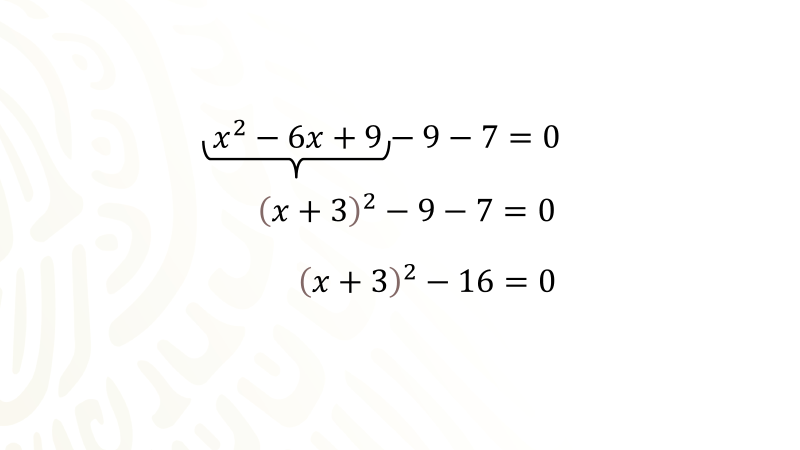
A continuación, se reducen los términos numéricos, quedando el binomio equis más tres al cuadrado menos dieciséis igual a cero.

A partir de ahí, puedes continuar resolviendo la ecuación ya sea recurriendo a la factorización de la diferencia de cuadrados que se tiene en el primer miembro de la ecuación o bien despejando la incógnita para determinar los valores de las raíces de equis.

En esta ocasión, factorizarás la diferencia de cuadrados escrita en el primer miembro de la ecuación, extraes la raíz cuadrada del primer término cuadrado, es decir, el binomio equis más tres elevado al cuadrado, la raíz cuadrada es el binomio equis más tres, también extraes la raíz cuadrada de dieciséis, la cual es cuatro.

Ahora prepara un par de paréntesis para expresar el producto de dos binomios conjugados, que son la factorización de la diferencia de cuadrados sin olvidar igualar a cero, recuerda que estas resolviendo una ecuación.

Para formar dichos binomios conjugados escribes como primer término en los dos factores, la primera raíz, equis más tres; luego escribes como segundo término la segunda raíz, que es cuatro, en el primer factor escribes el signo de más entre los dos términos y en el segundo factor escribes el signo de menos entre los dos términos.

En el primer factor queda equis más tres más cuatro y en el segundo factor queda equis más tres menos cuatro, continúa reduciendo términos numéricos, obteniendo un producto de dos binomios conjugados igual con cero.

Pero, este producto de binomios igualados con cero ya lo habías obtenido cuando se utilizó el primer procedimiento, esa era la finalidad, que te dieras cuenta que aprender otros procedimientos es muy útil y más al estudiar matemáticas.

Todavía falta determinar ¿cuál es el valor numérico de las raíces o soluciones de la ecuación de segundo grado propuesta?

Para eso, vas a utilizar la propiedad del producto cero, que explicas al resolver el primer ejemplo, la cual puedes resumir así: un producto de factores es cero si y sólo si uno o más de los factores es cero. Esta propiedad es particularmente útil cuando resuelven ecuaciones cuadráticas

 

 

Lo anterior significa que debes igualar cada factor binomio a cero, lo que dará origen a dos ecuaciones de primer grado muy sencillas de resolver. Tienes entonces el binomio equis más siete igual a cero y el binomio equis menos uno igual a cero

Después de resolver la ecuación de primer grado, equis más siete igual con cero, obtienes el valor de la primera raíz que es, equis igual a siete negativo. Si ahora, resuelves la ecuación de primer grado, equis menos uno igual con cero, obtienes el valor de la segunda raíz que es, equis igual a uno.

Has resuelto la ecuación de segundo grado propuesta utilizando el método de factorización y un procedimiento especial conocido como “completar el trinomio cuadrado perfecto”.

Sin embargo, debes hacer notar lo siguiente:

 

Como resultado del procedimiento utilizado para transformar la ecuación dada a otra donde se completó el trinomio como cuadrado perfecto, se realizó con base en considerar que el binomio equis cuadrada menos seis equis en la ecuación equis cuadrada menos seis equis menos siete igual a cero es equivalente con la expresión formada por el binomio equis más tres al cuadrado menos nueve en la ecuación obtenida que es equis cuadrada más tres al cuadrado menos nueve menos siete igual a cero.

Entonces es necesario preguntarse ¿Cómo verificar de manera geométrica la equivalencia de ambas expresiones? ¿Y cómo se puede verificar la equivalencia de las expresiones profesora?

Moldea las expresiones de la equivalencia propuesta para verificar si es verdadera.

Primero factoriza el binomio escrito en el primer miembro de la igualdad, equis cuadrada menos seis equis, queda factorizado como equis que multiplica al binomio equis más seis.

 

 

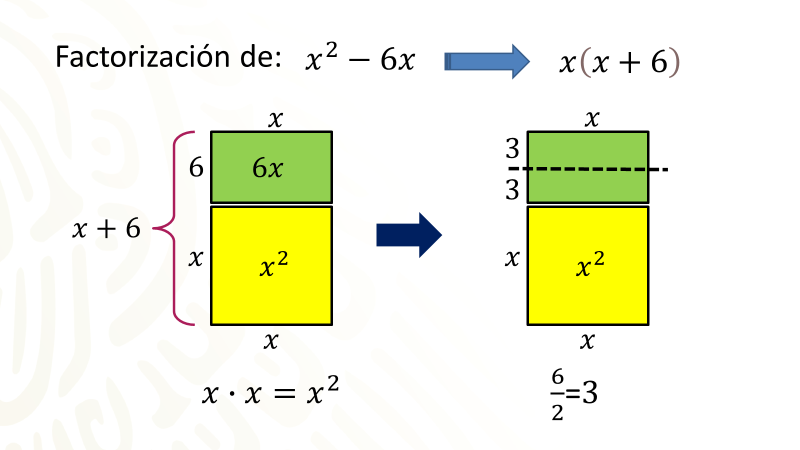
Ahora dibuja un modelo geométrico, tienes equis cuadrada, es decir, puedes dibujar un cuadrado cuyos lados miden equis, luego sabes que la factorización indica que uno de los lados mide equis y el otro lado mide equis más seis, el procedimiento algebraico indica que se divida entre dos el coeficiente del término de primer grado, esto es, dividir seis entre dos, obteniendo como cociente tres. En el modelo geométrico se divide con una línea punteada la longitud seis en dos partes iguales.

 

 

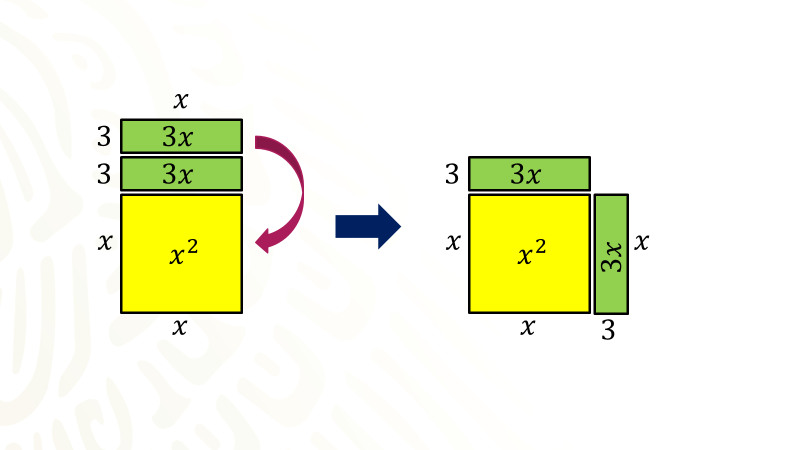
Se tienen dos rectángulos cuyos lados miden tres por equis; ahora traslada uno de los rectángulos para ponerlo a un lado del cuadrado en posición vertical, como puedes observar se tiene un cuadrado incompleto, ahora tienes la representación de la expresión algebraica equis cuadrada menos seis equis.

 

 

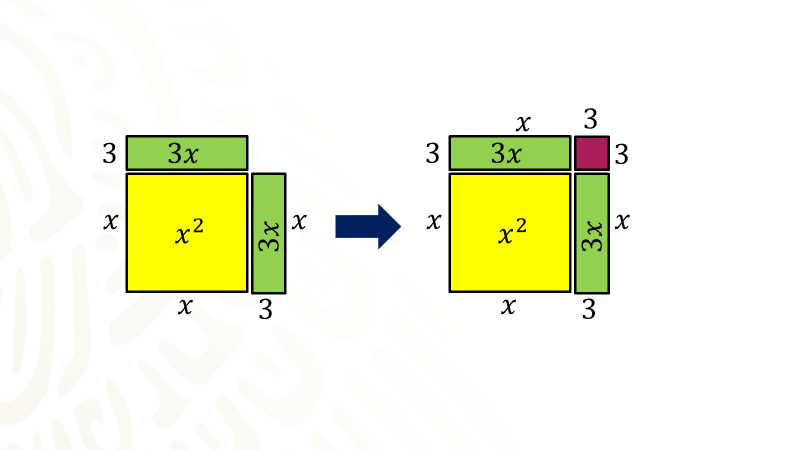
Trabaja con la interpretación de la expresión escrita en el segundo miembro de la igualdad que es el binomio equis más tres al cuadrado menos nueve, como puedes observar el cuadrado, cada lado ahora mide equis más tres, sin embargo es un cuadrado incompleto, en el procedimiento algebraico al dividir seis entre dos, se obtuvo tres como cociente, dicho valor se elevó al cuadrado obteniendo nueve, el cual se sumó para completar el trinomio y fuera un cuadrado perfecto, como se muestra en el modelo.

 

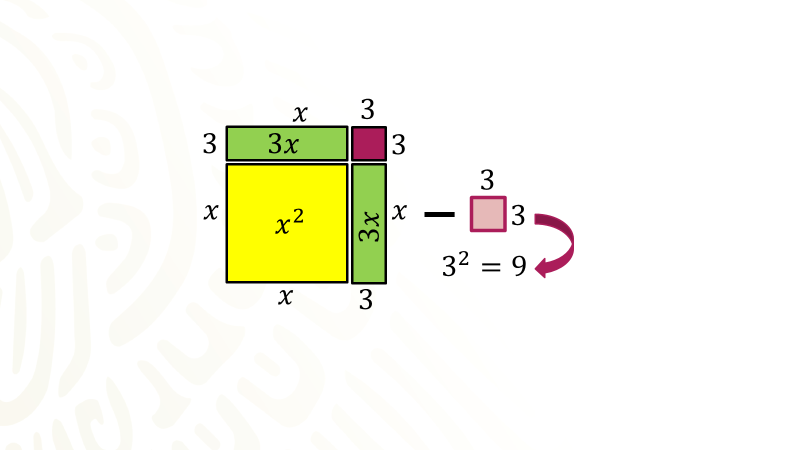
Pero recuerda que no sólo se suma el nueve también se resta nueve para evitar romper el equilibrio de la ecuación, dado que nueve menos nueve es cero, el modelo obtenido representa la expresión formada por el binomio equis más tres al cuadrado menos nueve.

De esta manera has verificado de manera geométrica que la expresión seis equis cuadrada más seis equis si es equivalente con la expresión formada por el binomio equis más tres al cuadrado menos nueve dando sentido al procedimiento de completar un trinomio como cuadrado perfecto.

Resuelve ahora una ecuación de segundo grado donde el coeficiente del término cuadrado no es igual a uno, la ecuación es:

 

Es recomendable, que de ser posible siempre trata de simplificar las expresiones matemáticas, en este caso, los números que forman parte de los tres términos del trinomio que se encuentra en el primer miembro de la ecuación son múltiplos de dos y por lo tanto son divisibles entre dos.

Antes de simplificar la ecuación dada, les recomiendo ordenar los términos del primer miembro de la ecuación de tal manera que en la primera posición este escrito el término cuadrático, en la segunda posición este escrito el término de primer grado y en la tercera posición este escrito el término numérico, después el trinomio es igualado con cero.

Para continuar divide entre dos negativo ambos miembros de la ecuación y con ello cada término que forma los dos miembros de la misma.

 

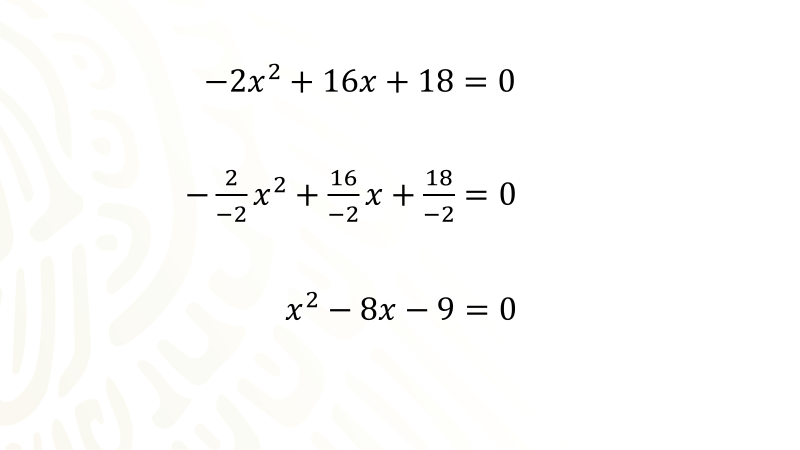
La intención es que el término cuadrático se transforme en positivo. Dos equis cuadrada negativo entre dos negativo se obtiene equis cuadrada; luego al dividir dieciséis equis entre dos negativo se obtiene ocho equis negativo, y al dividir dieciocho entre dos negativo se obtiene nueve negativo, finalmente al dividir cero ente dos negativo se obtiene cero. La ecuación equis cuadrada menos ocho equis menos nueve igual a cero que se obtuvo es equivalente a la primera.

Comienza completando el trinomio equis cuadrada menos ocho equis menos nueve en la ecuación donde el segundo miembro es cero, operarás con el binomio equis cuadrada menos ocho equis, escribe en el siguiente renglón el término cuadrático y el término de primer grado dejando espacio para escribir otros dos términos y luego menos nueve igual a cero.

 

 

Para continuar con el procedimiento, obtienes la mitad del coeficiente del término de primer grado, cuatro entre dos es igual a dos, dicho valor ahora se eleva al cuadrado y el valor obtenido se anota sumando como tercer término para completar el trinomio cuadrado perfecto, pero como sumas dieciséis también restas dieciséis, lo que significa que has sumado cero para no afectar el equilibrio de la igualdad, quedando: Equis cuadrada menos ocho equis más dieciséis menos dieciséis menos nueve igual a cero.

El Trinomio Cuadrado Perfecto es: Equis cuadrada menos ocho equis más dieciséis. Y además es equivalente a tener un binomio al cuadrado, en este caso el trinomio equis cuadrada menos ocho equis más dieciséis es equivalente con el Binomio equis menos cuatro al cuadrado

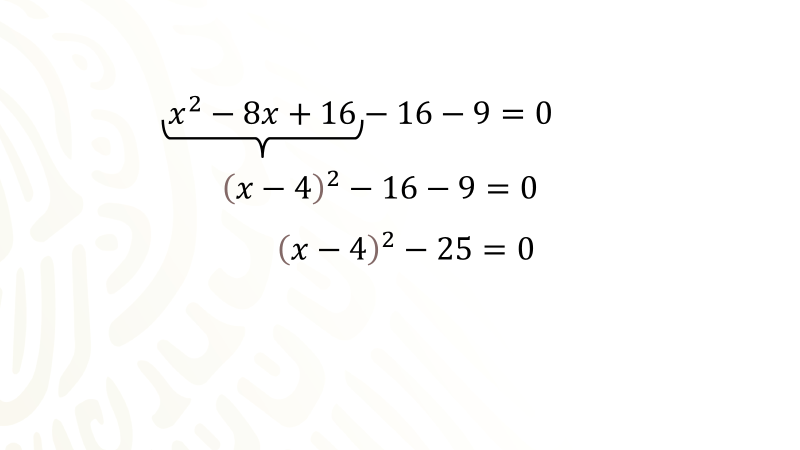
Después de tener el binomio al cuadrado ahora escribe menos dieciséis, menos nueve igual a cero. A continuación, se reducen los términos numéricos, quedando el binomio equis más cuatro al cuadrado menos veinticinco igual a cero.

A partir de aquí, puedes continuar resolviendo la ecuación recurriendo a la factorización de la diferencia de cuadrados que se tiene en el primer miembro de la ecuación para determinar los valores de las raíces de equis.

Es importante tener presente que, para factorizar la diferencia de cuadrados escrita en el primer miembro de la ecuación, extraes la raíz cuadrada del primer término cuadrado, es decir, el binomio equis más dos elevado al cuadrado; la raíz cuadrada es el binomio equis más dos, también extraes la raíz cuadrada de 1, la cual es uno.

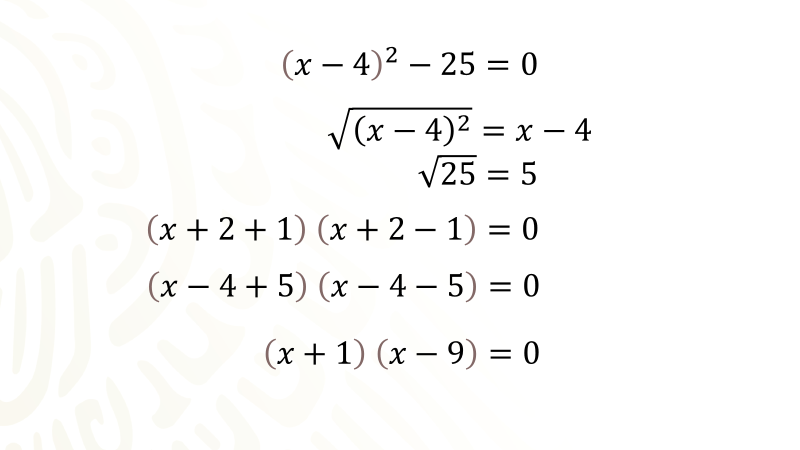
Para continuar preparas un par de paréntesis para expresar el producto de dos binomios conjugados, que son la factorización de la diferencia de cuadrados sin olvidar igualar a cero, recuerda que estas resolviendo una ecuación.

Para formar dichos binomios conjugados escribes, como primer término en los dos factores, la primera raíz, equis menos cuatro; luego escribes como segundo término la segunda raíz, que es cinco, en el primer factor escribes el signo de más entre los dos términos y en el segundo factor escribes el signo de menos entre los dos términos.

En el primer factor queda equis menos cuatro más cinco y en el segundo factor queda equis menos cuatro menos cinco, continúa reduciendo términos numéricos, obteniendo un producto de dos binomios conjugados igual con cero.

Pero, ¿cuál es el valor numérico de las raíces o soluciones de la ecuación de segundo grado propuesta? Para eso, utilizarás la propiedad del producto cero, que ya conoces, entonces igualas cada factor binomio a cero, lo que dará origen a dos ecuaciones de primer grado muy sencillas de resolver. Tienes entonces el binomio equis más uno igual a cero y el binomio equis menos nueve igual a cero.

Después de resolver la ecuación de primer grado, equis más uno igual con cero, obtienes el valor de la primera raíz que es, equis igual a nueve negativo.

Si ahora resuelves la ecuación de primer grado, equis menos nueve igual con cero, obtienes el valor de la segunda raíz que es equis igual a uno. Pero, ¿cómo puedes saber si los valores obtenidos como raíces de la ecuación de segundo grado dada la hacen verdadera?

Recuerda que para verificar si los valores obtenidos como raíces de la ecuación de segundo grado dada la hacen verdadera, es necesario sustituir dichos valores en la ecuación, por ejemplo: al sustituir el valor de equis igual a uno negativo en la ecuación original que es dos equis cuadrada negativo más dieciséis equis más dieciocho igual a cero, después de realizar las operaciones queda de la siguiente manera:

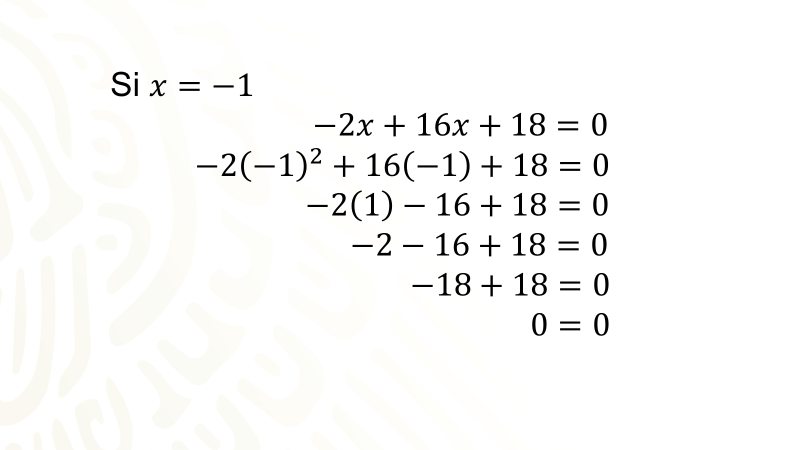
El Reto de Hoy:

Te sugerimos efectuar la verificación utilizando la ecuación original o la ecuación equivalente obtenida para cuando equis es igual a nueve. Consulta tu libro de texto de Matemáticas de tercer grado, ahí encontrarás otras actividades que te ayudarán a profundizar en este tema.

Es de mucha utilidad que pongas en práctica todo lo aprendido en la clase. Y un gran apoyo, es tu libro de texto.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

Herbolaria tradicional

Aprendizaje esperado: Investiga las transformaciones de la cultura y de la vida cotidiana a lo largo del tiempo y valora su importancia.

Énfasis: Identificar la importancia de las haciendas y las condiciones de vida de los peones.

¿Qué vamos aprender?

Como has visto en sesiones pasadas, el proceso de conquista y colonización de nuestro territorio supuso el triunfo de los europeos sobre los naturales, los indígenas, pero también supuso el origen de una nueva cultura con elementos americanos, europeos, africanos y asiáticos.

Los europeos, al ser el grupo dominante en Nueva España, destruyeron infinidad de códices que resguardaban importante información del conocimiento indígena, derrumbaron templos o adoratorios, prohibieron la religión de los pueblos originarios, e impusieron de manera violenta, en muchos casos, el cristianismo. Muchos conocimientos indígenas se perdieron, pero otros lograron permanecer.

La medicina prehispánica, que se fundamentó principalmente en la herbolaria, fue un conocimiento que al principio no fue aceptado por los conquistadores por considerarlo íntimamente ligado a la religión de los naturales. Sin embargo, de manera clandestina los curanderos tradicionales ejercieron su labor terapéutica.

Toda invasión y conquista supone resistencia,  y el conocimiento de la herbolaria siendo un saber indígena tan valioso  quedó arraigado, se reconoce y sigue vigente.

Te recomendamos que tengas a la mano una libreta y una pluma o un lápiz para que hagas tus anotaciones, también puedes utilizar tu libro de texto para que consultes imágenes o el tema en particular.

 

 

¿Qué hacemos?

 

Observa la primera parte de un video donde se entrevistó a la abuelita Amalia Salas Casales originaria de Xochimilco:

 

1. Entrevista a Amalia Salas. parte 1

La abuelita Amalia menciona que la herbolaria es el conocimiento de hierbas y plantas.

Seguramente conoces alguna de ellas, tal vez cuando te duele el estómago o cuando tienes cierto malestar, un familiar u otra persona cercana a ti te prepara una infusión y, desde luego, cuando comes algún platillo casero o de la región donde vives es aderezado por alguna hierba.

Por lo anterior, surgen las siguientes preguntas: ¿Qué hierbas son originarias del México Antiguo? ¿Para qué se usaron y se siguen usando?

Los pueblos prehispánicos eran excelentes observadores de la naturaleza, en especial de las plantas. Muchos se especializaron en ese estudio encontrando propiedades curativas en las hierbas. Sin embargo, los antiguos indígenas ligaron las enfermedades y su sanación a su religión, por lo que los españoles prohibieron su práctica.

De este modo, los curanderos tradicionales ejercían su labor terapéutica desde la clandestinidad, escondidos,  e incluso llegaron a cambiar el nombre a las hierbas para darles un toque cristiano y así despistar a los españoles: por ejemplo, al peyote le nombraron Rosa de María, la hierba de ololiuhqui se bautizó como Nuestro Señor y el yauhtli como Hierba de Santa María. Estas hierbas se utilizaban en rituales especiales para tener contacto con los dioses.

Pero no todas las hierbas son para sanar sino también para comer, tenemos el caso de los quelites, los nopales o el epazote que se utilizan para sazonar la comida. Otro tipo de hierba comestible es el huauzontle que puede ir capeado con huevo y relleno con queso; cuando el huauzontle se seca se vuelve amaranto, por vieja costumbre le ponen miel  surgiendo la famosa “alegría”.

Como puedes darte cuenta, la herbolaria es el conocimiento empírico de plantas y hierbas que pueden servir para comer y sanar algunos malestares. Su estudio es muy antiguo y es herencia de nuestros antepasados indígenas los cuales cuidaban de ellas en jardines especiales.

Los jardines, para los indígenas, representaron un espacio de recreación, de  cuidado de la salud y un  lugar donde podían aliviar el hambre. No en balde Bernal Díaz del Castillo quedó maravillado por el jardín que Moctezuma II tenía en Oaxtepec.

Lee el siguiente texto de cómo Moctezuma Ilhuicamina construyó su grandioso jardín en Oaxtepec.

 

Arqueología de la Tradición Herbolaria

Xavier Lozoya Legorreta

 

Cuentan los viejos que durante el tiempo en que Moctezuma llhuicamina, el Mayor, era el tlalticpactli, dueño de la tierra, Tlacaelel, su hermano y consejero, le dijo: Señor, una memoria deseo que dejes en este mundo.

 

En la provincia de tierra caliente como es Cuauhnáhuac, en el cerro de Oaxtepec, del que tengo noticias que posee abundantes fuentes y tierras muy fértiles, sería justo que mandes se haga, en la parte de arriba del cerro, una pila grande de piedra donde se recoja el agua y suba todo lo que pudiere subir para que luego, bajando por apantli (acequia) con ella se pueda regar toda la tierra que alcance en Oaxtepec y que, luego, envíes gente a la provincia de Cuetlaxtlan donde reina en tu nombre Pinotl y le hagas traer árboles de hueynacaxtli, de izquixóchitl, de cacahuaxóchitl, de xochinacaztli, de yoloxóchitl, de cocitzapotl, de ahuacatl y de todos los géneros de hierbas que en aquella costa se dan para que formen, con las plantas de Oaxtepec, un gran jardín que sirva de recreación y desenfado tuyo, y para la cura y salud de tu pueblo.

 

Al tlatoani le pareció muy bien el consejo; ordenó que en Oaxtepec se cercaran las fuentes, acarreando piedras para atrapar el agua en una gran poza desde donde el líquido fue guiado por canales en todas direcciones, y junto a ellos se construyeron terrazas grandes y chicas, como jardineras, con tierra negra y de hoja, donde cultivar las preciadas plantas. Después, despachó a sus mensajeros en varias direcciones para que trajeran con cuidado y solicitud todas aquellas plantas reconocidas por su belleza y virtudes, y que con ellas vinieran los agricultores (tlamaiti) para que ellos mismos con sus manos las plantas en conforme al tiempo y modo que en sus tierras guardaban. Estos tlalmaiti trajeron los árboles con las raíces envueltas en petates, las yerbas apretadas en tinajas de barro y las plantaron en las terrazas, distribuyéndola según su uso, su aroma, su belleza y costumbre, al tiempo que las salpicaban con sangre que se sacaron de la lengua y de los brazos, haciendo muchas ceremonias y quemando incienso, para los buenos augurios, y que todo se diera florido y hermoso como lo quería el tlatoani.

 

Cuando Tlacaelel vio lo que se había construido en Oaxtepec, quedó muy satisfecho y feliz. Las plantas crecieron por doquier y el lugar se llenó de pájaros cantores y de aves de muchos colores que se quedan en los arroyos a la sombra del ahuehuetl, y de mariposas y flores que colorean durante todo el año este jardín que parece Tlalocan.

 

Aquellos hombres que ves allá, con el pelo largo hasta los hombros y la risa en los ojos, son titici, los sanadores de la gente; ellos escogen el tiempo en que han de cortarse las plantas y cómo deberán usarse, son uei tlamatini, sabios, que dialogan con el picietl, escuchan el granizo y las voces de la montaña.

 

¡Cuidado! Sé prudente, y aléjate de la flor de cuero, que su aroma te enferma.

 

Los titici seleccionan el iztahuyátl, el epázotl, las hojas del xalxócotl, las varas de malinalli, las raíces del chilcuan, las semillas y flores de tzompantli, en fin, todos los productos que se envían en las trajineras que van a Tenochtitlan y cuidan que siempre haya flores para curar la tristeza del corazón, de yólotl.

 

Sin duda resulta interesante cómo los consejeros del Gran Tlatoani lo convencen para hacer un gran jardín para dos cosas: contra el desenfado y para curar a su gente, es decir, al pueblo.

En la antigüedad, a las personas que se dedicaban al cultivo y cuidado de plantas y hierbas se le denominaba tilci.

Conocerás seis plantas y hierbas de origen mesoamericano y sabrás para qué sirve cada una de ellas:

1. El huazontle: significa “cabello de bledo” y es una planta en forma de un pequeño arbolito alargado, con tallo y ramas gruesas, flor en forma de bolita, además tiene un alto valor nutricional, ya que contiene vitaminas A, B, B1, B2, B3, C, E; así como minerales, hierro, fósforo y calcio, incluso en cantidades similares a la leche, dicen que cada vez se consume menos. Seguramente ya lo has probado y cuando se seca, se consigue el amaranto y cuando se le agrega miel, se convierte en la famosa “alegría”.

2. El epazote: su nombre significa zorrillo, sudor u olor. Se usa en muchos platillos, como en los frijoles, esquites y caldos; en ciertas quesadillas, bebidas, infusiones y tamales, y también se emplea en algunas sopas de mariscos. Es rico en vitaminas A, B6, C; y algunos minerales como calcio, potasio, zinc y fósforo. Como puedes apreciar es una hoja larga con pequeños picos y un olor muy penetrante.

3. Las hojas de aguacate: se consideran hierba medicinal y la utilizan como antiinflamatorio, antiséptico, antidiarreico y astringente. Como puedes apreciar es una hoja semiredonda y hay que tener mucho cuidado para seleccionarla porque es parecida a las hojas del árbol común.

4. Los quelites: son hierbas comestibles y su nombre deriva del término náhuatl quilitl, que significa hierba. Los quelites eran consumidos por todas las culturas mesoamericanas y hoy tienen un rol importante en la vida cotidiana de los mexicanos igual que el maíz, los frijoles y las calabazas. Su contenido nutrimental varía de acuerdo con la especie y la tierra donde se cultive. Los quelites son buena fuente de fibra; de vitaminas A y C; minerales, como el hierro y el calcio; así como ácidos grasos Omega 3 y Omega 6. Como puedes ver tienen diferentes tamaños y formas y los deben conseguir en el mercado.

5. La flor de Cempaxúchitl: Cempoalxochitl es una palabra náhuatl que significa Veinte Flores. Como puedes ver es naranja y tiene muchos pétalos, usualmente se usa para la ofrenda de Día de Muertos, por lo mismo también es conocida como flor de muertos.

6. La prodigiosa o fresnillo, tiene forma de corazón y diferentes puntas onduladas alrededor de la hoja.

Todas las plantas que acabas de conocer son de origen mesoamericano y constituyen un aporte herbolario de México para el mundo.

Ahora observa algunas imágenes del Códice Badiano también llamado “Librito sobre hierbas indígenas medicinales”, escrito a mediados del siglo XVI y considerado el primer herbario ilustrado en el mundo.

 

 

Esta imagen representa la Xiuhhamolli o Planta de Jabón, que se utilizaba cuando se bañaban los indígenas y también la empleaban contra la caída de pelo. Como puedes ver en la ilustración era una planta con flor blanca y en la base puedes apreciar el glifo del agua, es decir, florecía cerca o en ella.

 

 

Esta otra imagen corresponde al Tlatonochtli o nopal, en el Códice Badiano se mencionan los frutos que da y su utilización para la preparación de los alimentos. Se refiere que la tuna y el xoconochtle aportan gran valor nutricional al cuerpo. Como sabes, el nopal también es la planta emblemática en el escudo nacional.

 

 

Esta otra planta se llama Nonochton Azcapanyxiua, significa la que “nace cerca de los hormigueros”, por esa razón en la raíz hay hormigas que suben a ella. Se dice que esta flor se consumía por su alto valor nutricional. Como puedes apreciar, era roja y con algunos pétalos verdes.

Ahora observa algunas imágenes del Códice Florentino donde puedes apreciar cómo se cuidaban, cultivaban y preparaban algunas hierbas y plantas.

 

 

Como puedes apreciar, en esta imagen está una mujer que lleva flores, probablemente las utilizará para bañarse, o tal vez sólo aprecia la belleza de las mismas. Recuerda que, independientemente de su ocupación o estatus social, los indígenas reconocían el valor de las hierbas y plantas.

 

 

Esta ilustración representa a un agricultor que se dedica al cultivo del maíz. La domesticación del maíz tardó siglos y se convirtió en el alimento fundamental de nuestros antepasados y hoy día lo sigue siendo. En nuestro país la variedad de ese cereal es rica y somos uno de los pocos países que acompaña la comida con tortillas.

 

 

En esta otra imagen puedes apreciar a un hombre que siembra flores y utiliza las raíces de las plantas, tal vez para comerlas o usarlas como remedio para algún dolor.

El uso de la herbolaria en los primeros años de la conquista fue relegado a un segundo plano porque los españoles establecieron boticas donde se vendían remedios traídos de Europa para malestares o enfermedades.

Sin embargo, los indígenas siguieron resguardando su conocimiento y transmitiéndolo de generación a generación. Fue tan potente la resistencia a desecharlos que los españoles decidieron mezclar la herbolaria prehispánica con la medicina europea. Este sincretismo médico logró preservar un poco el conocimiento prehispánico acerca de la herbolaria.

Como sabrás, la Santa Inquisición fue la institución colonial, de los invasores, que también se encargó de otorgar el permiso para consumir ciertas plantas curativas y de prohibir otras, sobre todo las alucinógenas.

Durante casi todo el periodo colonial, la medicina fue un oficio especializado y de ensayo y error en las familias, pero hasta el siglo XIX se estableció la industria farmacéutica y se vendieron medicamentos de patente. Esto vino a reducir el uso y conocimiento de la herbolaria tradicional.

Ahora observa la segunda parte de la entrevista realizada a la Abuelita Amalia:

 

2. Entrevista a Amalia Salas. parte 2

Los conocimientos herbolarios de la abuelita Amalia Salas, son avalados por la Organización de las Naciones Unidas para la Agricultura y la Alimentación (FAO) por sus siglas en inglés, institución que la acredita como promotora de la medicina herbolaria, sanadora y cuidadora de plantas y semillas.

Recuerda los consejos de la abuelita Amalia: “YO ME CUIDO, YO ME QUIERO Y YO ME RESPETO”.

Por tanto, nunca debes auto medicarte, ni emplees hierbas curativas sin la debida supervisión y guía de un especialista, de lo contrario corres el riesgo de hacerte daño o agravar el malestar.

Te recomendamos que siembres un pequeño jardín o un huerto con las plantas que tengas a la mano, como lo hacían los indígenas en la antigüedad. Además, que cuides las plantas que están a tu alrededor.

Al inicio de la sesión se formularon las siguientes preguntas: ¿Qué hierbas son originarias del México Antiguo? ¿Para qué se usaron y se siguen usando?

Has revisado el uso y propiedades de hierbas y plantas: algunas se comen y otras se utilizan para sanar. Casi todas las revisadas en esta sesión son de origen mexicano.

Puedes afirmar que el conocimiento herbolario se ha resistido a desaparecer ante el colonialismo europeo de los siglos XVI al XVIII, y al monopolio de las grandes farmacéuticas del siglo XIX, XX y XXI, es decir, la lucha por conservar el saber acerca de las plantas y su empleo, ha sorteado cinco siglos y sigue en pie.

Además, recuerda que las plantas con propiedades curativas deben ser recetadas por médicos homeópatas o alópatas. En la actualidad, instituciones de prestigio como la Universidad Nacional Autónoma de México y el Instituto Politécnico Nacional tienen departamentos científicos dedicados al estudio de la herbolaria.

Valorar el conocimiento herbolario es revivir una tradición ancestral que ayuda a ubicarnos en el mundo como una sociedad con un pasado rico que se niega a desaparecer, por eso es importante escuchar a nuestros abuelos acerca del uso de hierbas y plantas.

El Reto de Hoy:

Elabora un catálogo de plantas curativas y comestibles, te pueden ayudar tus familiares cercanos como tus padres o abuelos. Utiliza tu imaginación, dibuja cada planta y, al lado de cada una, escribe para qué se usa o qué malestar sana.

Ten en cuenta que tu libro de texto puede brindarte más información sobre el tema; en tu casa, seguramente tienes revistas, libros, o tal vez, un teléfono inteligente con el que pueden investigar más acerca de este tópico en Internet.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

¿De qué elementos químicos estamos formados los seres vivos?

Aprendizaje esperado: Relaciona la abundancia de elementos (C, H, O, N, P, S) con su importancia para los seres vivos.

Énfasis: Reconocer la importancia de los bioelementos en el funcionamiento de los organismos vivos.

¿Qué vamos aprender?

Lee la siguiente frase célebre de Humphry Davy:

 

“Nada es tan fatal para el progreso de la mente humana como suponer que nuestros puntos de vista sobre la ciencia son lo último, que no hay misterios en la naturaleza, que nuestros triunfos son completos, y que no hay nuevos mundos que conquistar.”

 

Reconocerás la importancia de los bioelementos en el funcionamiento de los organismos vivos. Asimismo, reflexionarás acerca de los bioelementos, que son elementos químicos indispensables para la vida, pues forman las diferentes estructuras que hacen posible que se lleven a cabo procesos vitales en los seres vivos.

Estos elementos se encuentran en la tabla periódica y forman parte de otros compuestos, sin embargo, por sus propiedades químicas permiten la formación de moléculas muy complejas que constituyen y mantienen a los organismos vivos.

Toma nota de las preguntas planteadas durante la sesión para que al final puedas contestarlas a tu propio ritmo.

Las dudas con respecto al tema de bioelementos, las puedes resolver al revisar la información y los ejemplos que aparecen en tu libro de texto.

¿Sabían que...? Se llama bromatología a la disciplina científica que se dedica al análisis de los alimentos y se centra en el estudio de las sustancias que los seres humanos necesitan ingerir para la supervivencia.

Observa con atención los porcentajes de los elementos químicos que constituyen el cuerpo humano; puedes observar los cuatro principales:

 

• El oxígeno, con 65%
• El carbono, con 18.5%
• El hidrógeno, 9.5%
• El nitrógeno, 3.3%

 

Ahora observa los porcentajes de los cuatro principales elementos químicos que constituyen la alfalfa:

 

• El oxígeno, con 77.9%
• El carbono, con 11.3%
• El hidrógeno, con 8.7%
• El nitrógeno, con 0.83%

 

Finalmente, observa los porcentajes de los cuatro principales elementos químicos que constituyen la calabaza:

 

• El oxígeno, con 85%
• El carbono, con 3.3%
• El hidrógeno, 10.7%
• El nitrógeno, 0.16%

 

• ¿Qué similitudes notas?
• ¿Y cuáles diferencias?
• ¿Crees que suceda lo mismo en todos los seres vivos?, ¿por qué?
• ¿Qué tienen de especial estos elementos?
• ¿Qué función tienen estos elementos químicos en el cuerpo?

 

Conoce más acerca de ellos para contestar las preguntas anteriores. Comienza con el carbono, que es un elemento muy especial, pues tiene la propiedad de formar largas cadenas al unirse con otros átomos de carbono, lo que permite formar una gran cantidad de compuestos.

¿Qué hacemos?

Observen con atención el siguiente video del minuto 2:38 al 3:28 y del minuto 4:40 al 5:10 para saber más de este elemento.

 

1. El agua tan conocida y tan sorprendente

El ser humano está formado de sistemas, algunos de ellos son: sistema óseo, sistema respiratorio, sistema digestivo, por mencionar algunos. A su vez, los sistemas están conformados de órganos, como son: el hígado, el páncreas, el corazón, el cerebro, entre otros.

Los órganos están constituidos de tejidos como pueden ser: el tejido adiposo, el tejido nervioso, el tejido muscular, por mencionar algunos. A continuación, se tiene que los tejidos están hechos de células, algunas de sus partes son: el núcleo, citoplasma, membrana, entre otros.

Las diferentes partes de la célula están hechas de moléculas o biomoléculas, como las proteínas, los carbohidratos, lípidos.

Por fin llegamos a la parte que analizarás. Las biomoléculas están compuestas por elementos químicos, también conocidos como bioelementos.

Ahora que sabes que tu cuerpo está formado por los llamados bioelementos, es muy importante conocer cuáles son y cómo se clasifican. Los bioelementos, para su estudio, se clasifican en elementos primarios, secundarios y terciarios.

Los elementos primarios son: carbono, hidrógeno, oxígeno, nitrógeno, fósforo y azufre. Se requieren para formar biomoléculas de carbohidratos, lípidos, proteínas y ácidos nucleicos. Estos elementos químicos ocupan aproximadamente 96% de la masa total del cuerpo.

El carbono es considerado como el elemento químico de la vida; puede formar enlaces fuertes entre sí o con otros elementos, esto permite que se organicen de diversas formas para formar moléculas complejas.

El oxígeno es un gas importante para los seres vivos, tiene un rol fundamental en la producción de energía; cuando haces ejercicio, el flujo de este elemento se requiere en cantidades mayores por la cantidad de energía que requieren para sus actividades, mejora el sistema inmunológico, acelera la cicatrización, mejora la memoria, maximiza el rendimiento físico.

El hidrógeno, al combinarse con átomos de oxígeno y carbono, producen las principales biomoléculas, todos ellos son de suma importancia para la vida.

El nitrógeno, en su forma natural, es un gas, pero en el cuerpo forma parte de compuestos denominados bases nitrogenadas, éstas las puedes encontrar en el ácido desoxirribonucleico, mejor conocido como ADN, éste es el encargado de duplicar las células en los seres vivos, contiene también la información genética.

El fósforo, refiriéndose no a los cerillos, sino al elemento químico que está presente en el adenosín trifosfato o ATP; éste es la fuente principal de energía para la mayoría de los procesos celulares.

Este elemento también lo encuentras en los fosfolípidos, que mantienen la estructura de la membrana celular.

Otro elemento muy importante para los seres vivos es el azufre, aunque su olor sea insoportable, en realidad es un componente clave en la formación de algunas proteínas, vitaminas y hormonas, promueve la formación de la queratina y el colágeno, que dan firmeza y elasticidad a la piel, elimina toxinas, ayuda al hígado en la secreción de la bilis e interviene en la síntesis de insulina para regular los niveles de azúcar en la sangre.

Los bioelementos secundarios se encuentran en menor proporción que los primarios y, entre ellos, un elemento químico que se encuentra principalmente en los lácteos, que fortalece los huesos y los dientes, el calcio, este elemento secundario aporta aproximadamente 1.5% de la masa total en el cuerpo.

El sodio, el potasio, el cloro y el magnesio intervienen en forma de iones en la distribución del agua en las células.

Finalmente están los oligoelementos o elementos terciarios. Se les llama así debido a que su cantidad en los seres vivos es muy poca, sin embargo, no por eso son menos importantes. Los principales son:

El hierro, presente en la sangre para producir las proteínas hemoglobina y mioglobina que transportan el oxígeno. La hemoglobina se encuentra en los glóbulos rojos y la mioglobina en los músculos.

El yodo, que participa en la síntesis de hormonas en la glándula tiroides para evitar su inflamación.

El litio ayuda a regular el ciclo del sueño y el estado de ánimo.

Por último, el zinc y el cobre cumplen una gran variedad de funciones importantes en el metabolismo, en la proliferación celular y en los procesos de óxido-reducción. El carbono es un elemento único en la química porque forma un número de compuestos mayor que la suma total de todos los otros elementos combinados.

El grupo más grande de estos compuestos es el constituido por carbono e hidrógeno. Se estima que se conoce un mínimo de 1 000 000 de estos compuestos. Ahora ubica estos elementos en la tabla periódica, recuerda que en sesiones anteriores aprendiste sobre los grupos y periodos, y cómo se clasifican en metales y no metales.

Elabora en tu cuaderno una tabla como la siguiente:

 

 

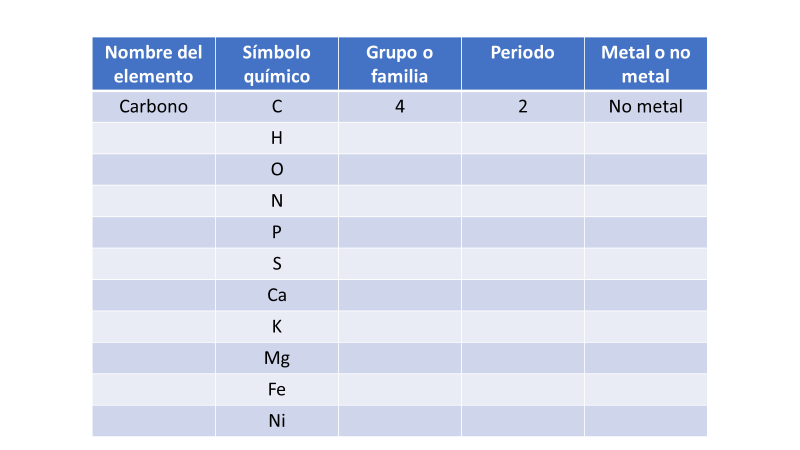
En la primera columna colocas el nombre del elemento; en la segunda, su símbolo químico; en la tercera, su grupo o familia; en la cuarta, su periodo, y finalmente, en la quinta si se trata de un metal o un no metal.

Para esta actividad necesitas la tabla periódica. Observa cómo se llena la primera fila como ejemplo:

 

Nombre: Carbono

Símbolo: C (mayúscula)

Grupo: 14

Periodo: 2

Y se clasifica como no metal.

Ahora termina de llenar el resto del cuadro.

Como actividad, calcula la masa que tienes en el cuerpo de cada uno de los bioelementos principales, ya que conoces los porcentajes. Pon mucha atención en el ejemplo para que, al término de la sesión y a tu propio ritmo, realices lo mismo con los demás elementos.

Empezarás con el carbono; recuerda el porcentaje en el cuerpo, 18.5%; toma como ejemplo la masa de una persona de 50 kg. Recuerda que debes hacerlo con tu propia masa.

El cuerpo humano lo considerarás como 100% es decir, la masa de 50 kg, y 18.5% de ese total es carbono; resuelve esa proporción con dos sencillas operaciones: una multiplicación y una división.

 

Tienes 18.5 x 50 = 925

925 ÷ 100 = 9.25

 

Es decir que una persona de 50 kg de masa tiene en su cuerpo 9.25 kg de carbono.

Realiza el cálculo de los demás elementos, recuerda utilizar tu propia masa y completa el cuadro. Los bioelementos, a su vez, constituyen compuestos complejos como carbohidratos, proteínas y lípidos. La dieta diaria, es decir, los alimentos que ingieres diariamente deben estar acordes con los requerimientos energéticos, para ello, es necesario tomar en cuenta la edad, el género y las actividades físicas que realizamos.

Un aspecto que contribuye a cuidar y mantener tu salud es la alimentación, por lo que te sugerimos llevar a cabo las recomendaciones del Plato del Bien Comer.

Observa con atención el siguiente video e identifica las ideas relevantes. Finalmente, recuerda, que se consideran bioelementos a los elementos de la tabla periódica que constituyen a los seres vivos y los principales son carbono C; hidrógeno H; oxígeno O; nitrógeno N; fósforo P; azufre S, y en los seres humanos se incluye al calcio porque es muy importante en la formación de la estructura ósea.

La falta o exceso de los bioelementos y sus compuestos pueden causar desequilibrios en el organismo y provocar serios trastornos en tu salud. Cada vez que te sientes a comer en familia, recuerda lo importante que es incluir en tu dieta aquellos alimentos que pueden aportarte nutrimentos esenciales, incluidos en las frutas, verduras, lácteos, pescado y cereales, con una alimentación correcta, de acuerdo al Plato del Bien Comer.

El Reto de Hoy:

Si quieres saber más acerca de este tema, te sugerimos la lectura del libro Triptofanito, un viaje por el cuerpo humano, del médico y escritor mexicano Julio Frenk. En sus páginas encontrarás el viaje que hacen los aminoácidos cuando un granjero come un huevo, y salen a escena los actores Triptofanito, Lisina y Glutamito, que forman a las proteínas. Es una aventura llena de emociones y peligros, con enemigos que los están acechando y otros amigos que los ayudarán a derrotarlos. Aprenderás a conocer tu cuerpo y sus funciones principales.

Y también el artículo de divulgación científica de la UNAM en la siguiente dirección electrónica:

http://blogs.ciencia.unam.mx/cienciamundo/2017/10/04/nobel-de-quimica-2017-para-la-criomicroscopia-electronica/ 

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.

Veo, escucho, siento y opino

Aprendizaje esperado: Distingue las propiedades de los elementos del arte en obras o manifestaciones artísticas para ampliar su percepción y sensibilidad hacia el arte.

Énfasis: Analizar los elementos del arte que componen una obra o manifestación artística interdisciplinaria para emitir un juicio crítico al respecto.

¿Qué vamos aprender?

Observarás, escucharás y reflexionarás sobre obras o manifestaciones artísticas a partir de algunos de los elementos que las componen y a emitir una opinión crítica de ellas.

¿Qué elementos suelen considerarse para emitir una opinión sobre una canción, película, obra dancística, teatral, museo o galería, etc.?

Recuerda tener a la mano tu libreta, lápiz o bolígrafo, para hacer cualquier anotación que desees sobre la experiencia vivida en esta actividad.

Realizarás un escudo, para ello, necesitarás cartón, ya sea de una caja vacía, la portada de un cuaderno que ya no uses o cualquier hoja firme. Para decorarla, además de los colores con los que ya cuentas, prepara diversos materiales como: plumas, listones, hilos o cordones, tijeras, marcadores; algunos elementos naturales que encuentres a tu paso, como hojas secas de árbol, piedritas, ramas, semillas, o alguna pieza natural que se te haga interesante.

¿Qué te hace pensar el tema, ver, sentir, escuchar, para después opinar?

Cuando visitas una galería de arte, un museo, presencias una obra teatral, una manifestación dancística o musical.

¿Qué es lo primero que haces?

Disfrutar de ese tiempo que se está en contacto y en comunicación con la obra. Sin embargo, al finalizar la experiencia sueles compartir tu parecer sobre lo apreciado y, posiblemente, te preguntes: ¿qué quiso decir el artista con su obra?, ¿por qué tomó un tema en particular para el desarrollo su obra o utilizó alguna técnica?, ¿y esto qué tiene que ver conmigo, con mis gustos, con mis intereses, con mi contexto, con la vida?

En ocasiones se puede pensar que la apreciación del arte es una tarea muy compleja, que requiere seriedad o rigidez. Aprenderás algunas herramientas que te ayudarán a hacerlo de una forma más dinámica y divertida.

La interpretación de una obra artística es personal y subjetiva, en donde intervienen diversos factores, por ejemplo: los gustos e intereses personales en relación con la disciplina artística, el contexto de la obra en relación con el actual, entre otros. Es más, en ocasiones podrías hacer juicios de valor dejándote llevar por los sentimientos presentes y sin tener éstos relación con la obra.

¿Cuándo es el momento para hacer un juicio crítico sobre alguna pieza artística?

Lo primero que se sugiere al apreciar una obra artística, ya sea visual, escénica o literaria, es dejarse conectar con ella: obsérvala, escúchala, contémplala, siéntela, disfrútala y dialoga con la obra; es decir, deja que los elementos que percibes en ella trasciendan tus sentidos.

Con este encuentro puedes generar diversas relaciones y reflexiones, y dar como resultado un conjunto de imágenes y sensaciones con significados propios, lo que te permitirá generar una opinión de ella. Pero ¿a qué se refiere la opinión y crítica hacia una obra?

Antes, hay que dejar claro que: “Toda persona tiene derecho a la libertad de pensamiento y expresión”. La libertad de expresión es un Derecho Humano. Sin embargo, para dar una opinión artística de mayor profundidad, después de “dialogar con la obra” date un tiempo para reflexionar sobre lo observado, escuchado y percibido en ella. Y al respecto, distingue los elementos que componen dicha obra.

Por ejemplo:

 

• ¿Cómo son las formas, líneas, trazos, colores, texturas de la obra?
• ¿Cómo son las intensidades o ritmos de los sonidos?
• ¿Cómo fueron los movimientos corporales y los desplazamientos que los artistas escénicos ejecutaron en el escenario?

 

Algunos otros aspectos de las artes que se deben distinguir son los materiales y las técnicas, pues son los medios de expresión y el lenguaje que elige el artista a través del cual se comunica. Por ejemplo, en la pintura, no es lo mismo crear una acuarela que un óleo o, en la escultura, modelar una pieza de barro que fundir una de hierro.

Y esta conjunción entre materiales, manejo de la técnica, el talento y la sensibilidad del artista son fundamentales para la creación de toda obra artística.

Todo esto se hace especialmente importante cuando varios materiales son mezclados en una misma obra, pues entonces se produce un juego de texturas ya sean visuales o auditivas de procesos de elaboración que enriquecen el lenguaje del artista.

Por otro lado, los colores tienen un lenguaje propio, muchas veces está vinculado a ciertos significados que la sociedad les atribuye.

En una obra artística muchas veces interviene más de un color, generando armonías cromáticas o, todo lo contrario.

De igual manera las formas son los elementos básicos con los que el artista crea su obra. Mientras algunos optan por una abstracción en la que juegan con figuras geométricas, ya sea con una obra pictórica o con el cuerpo humano.

Otros recurren a imágenes figurativas con elementos perfectamente reconocibles. Algunos otros, por ejemplo, utilizan formas en las que predomina la línea curva, como en la danza.

Otro punto importante a observar son los vínculos con otros artistas. Las influencias de otros artistas pueden ser más o menos conscientes en un creador y es posible que puedas establecer relaciones que van más allá de realidad.

Sin embargo, independientemente de la existencia de una influencia a la hora de crear, puede ser importante establecer estos vínculos para enriquecer su experiencia y disfrutar más de la observación de la obra.

¿Qué hacemos?

En México contamos con una amplia gama de manifestaciones artísticas y culturales. Observa el siguiente video del inicio al minuto 1:52:

 

1. Patrimonio y derechos culturales

Como observaste, el patrimonio cultural de México es muy basto en expresiones y manifestaciones artísticas y culturales. Reflexiona sobre algunas de ellas, de la mano de nuestras raíces, que orgullosamente tienes a tu alcance.

Se está en vísperas de una de las celebraciones más populares del país, el Día de muertos, que ha sido inspiración de películas, canciones, bailes o pinturas.

Esta celebración se lleva a cabo a lo largo y ancho de la República Mexicana, cada uno de los estados imprime su propia interpretación de la muerte, el recuerdo y la trascendencia del ser.

Observa el siguiente video y toma nota de los elementos que identifiques alrededor de esta festividad.

 

2. México

¿Lograste observar las imágenes, los colores, las formas, los elementos que estaban presentes en los altares?

Dependiendo del lugar, éstos pueden variar, pero el juego de luces y sombras que se observan, lo mítico de los elementos, la alegoría de los objetos y vestimentas es lo que hace de esta celebración un tema basto para otros artistas.

Un ejemplo de ello es el artista Saturnino Herrán con su obra llamada La ofrenda, elaborada en 1923. En ella puedes observar varios elementos que dan identidad nacional; de manera simbólica están representadas las 3 etapas de la vida, el niño cargado en la espalda de la mujer, a su lado derecho una niña, en el medio del cuadro la mujer de edad adulta y por último el hombre mayor que carga el puntal. Todo esto en un ambiente lleno del color del cempasúchil, flor representativa de esta temporada.

 

 

¿Qué te pareció la temática que Saturnino Herrán le imprime a la obra? ¿Pudiste observar o sentir la expresividad de sus personajes? ¿Qué elementos identificas? ¿Qué podrías opinar en torno a las relaciones que pudieras hacer sobre lo que percibiste de la obra, los elementos que distinguen en ella, y lo que sabes sobre esta manifestación artística y cultural?

En el mismo orden de ideas, está la canción de “La llorona” que proviene de una región del istmo de Tehuantepec, del estado de Oaxaca. Se ha interpretado en diversas versiones y lenguas como el zapoteco, el náhuatl y el castellano. Se dice que fue escrita en 1850, pero fue hasta la Revolución mexicana que tuvo un mayor auge. Esta pieza hace referencia a la leyenda del mismo nombre. ¿Conoces la leyenda de la llorona?

¿Te das cuenta cómo ver, escuchar y sentir, te puede abrir paso hacia opinar? Sigue desmenuzando obras y con ello, reflexiona y genera una opinión.

Y cómo no hacerlo con una de las figuras más representativas de nuestra cultura: La Catrina de José Guadalupe Posada, observa sus elementos y características.

 

 

Observa la figura, ésta es relacionada con la muerte, pero no se llamaba así en su origen, el artista Posada la nombró la Calavera Garbancera, y fue creada como una burla hacia la burguesía que predominaba en el país, ya que en ese momento se hacían de menos, se despreciaban los orígenes mexicanos por preferir la cultura europea.

 

¿En qué momento se relaciona con la muerte?

 

 

Fue hasta que Diego Rivera la utilizó en uno de sus murales más importantes, dándole así un nuevo significado a esta alegoría.

¿Has visto esculturas, figurillas de papel mache, en tu localidad? ¿te acercas a la idea original que plasmó Posada? ¿Qué sentimientos te genera el reconocer esta forma? ¿cuál sería tu opinión acerca de este personaje?

También por todo el país existen danzas con alegorías a distintos temas y son interpretadas en las fiestas patronales o celebraciones tradicionales. Como la de Los Viejitos que asemejan ancianos, la Danza del Venado de los estados al norte del país, del tigre y de la iguana en Guerrero, Veracruz y Chiapas, las calendas de Oaxaca o como en la Huasteca Potosina con el Xantolo. Se podría decir que estas manifestaciones culturales conjuntan la cosmovisión de un pueblo a través de la danza, la música, la representación escénica, personajes, vestuarios. Es una gran forma de representar la identidad, la comunidad, la cultura.

Como pudiste observar en las obras anteriores hay ejemplos, de obras y manifestaciones artísticas y culturales. Pero, además de que te des la oportunidad de conocerlas y apreciarlas, es importante reflexionar y expresar nuestro pensar y sentir entorno a tu experiencia con ellas.

Así que después de “ver, escuchar y sentir.” llega el turno de: emitir tu opinión. Ahora anota una reflexión en tu libreta.

Por ejemplo, al pensar si has participado en alguna celebración artística o cultural, ya sea como ejecutante o como espectadora o espectador ¿Qué podrías compartir sobre esas experiencias?

Es hora de realizar el escudo, así que puedes traer tus materiales, si no cuentas con ellos en este momento, puedes realizar este ejercicio posteriormente.

Esta actividad está inspirada en el escudo chimalli. ¿Sabías qué en la época prehispánica, este escudo era un símbolo del valor y el rango de los combatientes? Y sólo existen 4 en el mundo, uno de ellos pertenecía a Moctezuma.

En él se mostraban una secuencia de elementos decorativos que tenían un uso de carácter militar u ornamental. Se podía observar rostros, figuras legendarias o diseños abstractos con distintos significados.

El diseño del escudo ayudaba a identificar al portador en rango militar, jerarquía social y experiencia en combate. Los materiales utilizados variaban también a su vez con respecto al nivel del combatiente, las versiones más fuertes, estaban hechas de aleaciones de bronce con metales preciosos como el oro y plata, las cuales estaban reservadas para los altos rangos.

Ahora vas a realizar tu escudo, recuerda que todos los elementos que pongas en él son libres, deja volar tu imaginación y creatividad.

Primero haz un boceto y dibujos, símbolos, o cómo lo desees, da respuesta a las siguientes preguntas:

 

1. ¿Cuáles son tus raíces? Por ejemplo, que representes de dónde son originarios, tu comunidad, tus costumbres y tradiciones, tu familia.

 

2. ¿Cuál es tu identidad personal? Por ejemplo: cuáles son tus gustos, inquietudes e intereses particulares.

 

3. ¿Cuáles son tus sueños? ¿Cuáles son tus proyecciones hacia el futuro?

 

Todas tus respuestas, plásmalas en tu escudo con diversas formas, colores, texturas, símbolos; llénalas del corazón del artista que vive en ti, de imaginación y creatividad.

Para la elaboración del escudo, puedes utilizar cualquier material que sirva para lo que quieres expresar. Por ejemplo: puedes decorarlo con estambres, plumas, hojas de plantas o de papel; materiales que tengas a la mano en tu casa.

Ahora es tiempo de comenzar a elaborarlo.

Observa el abanico de escudos que realizaron algunas de tus compañeras y compañeros de tercero de secundaria.

 

3. Mi escudo y yo

Observaste los objetos que ocuparon tus compañeros, objetos que muestran las raíces de México y puedes adecuarlos a tu creación.

El crítico e historiador teatral Jorge Dubatti afirma que “la mejor crítica es aquella que es divertida, amorosa y refleja un espíritu inteligente y sensible”. Así que te sugerimos poner en práctica estos principios siempre que compartas alguna opinión.

 

4. Observo y opino

Al hablar de las manifestaciones artísticas y culturales del país, también lleva a reflexionar en torno a la herencia cultural. Reflexiona partir de la riqueza artística y cultural, y a continuar la experiencia en la construcción de tu propio escudo el que, como observaste en el video, está cargado de tu propia historia.

También, se revisaron algunos elementos del arte con la intención de contar con algunas herramientas que permitirán profundizar al analizar una obra, y así, dar una opinión argumentada.

Anota tus conclusiones.

Recuerda que el arte es subjetivo, por lo tanto, no hay opiniones correctas o incorrectas, y éstas están basadas en la particularidad de cada espectador. Sólo te sugerimos que indagues un poco más sobre las manifestaciones artísticas y culturales, y logres descifrar las sutilezas de cada detalle. Y, como dijo el maestro Dubatti, se espera que cada opinión o crítica que te hagas sea divertida y amorosa, como reflejo de tu espíritu inteligente y sensible.

El Reto de Hoy:

Ahora que ya sabes que elementos conforman a las obras artísticas, puedes experimentar viendo con ojo crítico las diversas manifestaciones que hay en tu estado.

Comparte en casa con tus familiares tus puntos de vista y realiza un intercambio de ideas, amoroso, inteligente y productivo.

Recuerda que el arte se vive, se siente, se interpreta y se expresa. No hay límite para la imaginación.

Descarga tu clase dando clic aquí

¡Buen trabajo!

Gracias por tu esfuerzo.






Aprende en casa II TERCERO DE SECUNDARIA 30 DE OCTUBRE