Aprende en Casa 2 SEP: 30 de octubre TAREAS y ACTIVIDADES de 2° de secundaria
A continuación dejamos los temas vistos el 30 de octubre de clases virtuales mediante el programa Aprende en Casa 2, para los alumnos de 2° de secundaria.

Para todos aquellos padres y madres de familia cuyos hijos se encuentran cursando el nivel Secundaria de educación básica y toman las clases en línea por medio del programa de la SEP Aprende en Casa 2, compartimos los temas y actividades que se abordaron este Viernes 30 de octubre, así como las dudas que se plantearon.
La información que obtendrás a continuación forma parte del material educativo que se vio en el apartado Actividades, del nivel Secundaria, publicado en la página oficial del programa Aprende en casa 2:
https://aprendeencasa.sep.gob.mx/#

Generalización de los procedimientos del cálculo del perímetro y del área
Aprendizaje esperado: Formula expresiones de primer grado para representar propiedades (perímetros y áreas) de figuras geométricas y verifica equivalencia de expresiones, tanto algebraica como geométricamente (análisis de las figuras).
Énfasis: Generalizar los procedimientos de cálculo del perímetro y área de las figuras por medio de la introducción de literales para representar las dimensiones de las figuras.
¿Qué vamos a aprender?
Hoy aprenderás a generalizar los procedimientos del cálculo del perímetro y del área de algunas figuras por medio del uso de literales. Además, resolveremos y analizaremos algunas situaciones matemáticas relacionadas con este tema.
Trabajarás con algunas figuras geométricas, así como con sus áreas y perímetros.
¿Qué hacemos?
¿Tú sabes qué es el perímetro? Y ¿qué es el área?, ¿ambos se refieren a la misma propiedad?
El perímetro es la medida del contorno de una figura poligonal que se obtiene al sumar sus lados y se mide en unidades lineales, como centímetros o metros.
El área es la medida de la superficie plana de una figura que se mide con unidades cuadradas, como centímetros cuadrados o metros cuadrados.
También sabemos que el área y el perímetro de una figura geométrica se obtienen a través de diferentes procesos y con diferentes fórmulas.
Veamos el siguiente problema para mostrarlo.
Bruno está planeando iniciar un negocio de elaboración de manteles de diferentes formas y tamaños. Ha pensado en algunas figuras que podría utilizar como plantilla, éstas son: un cuadrado, un triángulo equilátero, un rectángulo y un hexágono regular.
Para saber la cantidad de material que va a utilizar en la elaboración de cada mantel, necesita calcular el área y el perímetro de las figuras que ya seleccionó.
Ayudemos a Bruno a recordar esta información. Si Bruno decide elaborar manteles en forma de cuadrado, tiene que considerar que se trata de una figura de cuatro lados de igual tamaño.

Para calcular el perímetro, se suma cada uno de los lados de la figura, a+a+a+a; al tratarse de una suma repetida del mismo valor, el perímetro se puede expresar también como 4a, en donde la literal “a” representa el lado del cuadrado. De esta manera sabemos que con la expresión P=4a, podemos obtener el perímetro de cualquier cuadrado.
¿Qué tendría que hacer Bruno si lo que quiere saber es el área del mantel?
Una multiplicación, considerando que la superficie de una figura se mide a partir de unidades cuadradas. Para calcular el área, Bruno puede contar el número de unidades cuadradas que integran a la figura, o bien multiplicar la medida de sus lados (a) por (a), que es equivalente a la expresión a2 (a, al cuadrado).
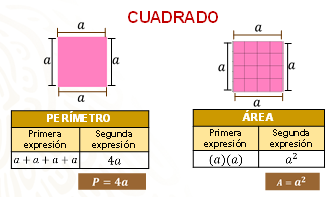
Analiza: si Bruno elabora manteles en forma de cuadrado de 4 metros de lado, para calcular el perímetro es necesario sumar los cuatro lados de la figura.
¿Y sólo sumando se puede encontrar el perímetro?
También puedes multiplicar por cuatro la medida del lado. En este ejemplo, multiplicamos 4 lados por los 4 metros que mide cada lado de la figura, así sabemos que el perímetro del mantel será de 16 metros lineales.
Para calcular el área, multiplica 4 metros por 4 metros, como lo indica la expresión, porque 4 metros es lo que mide por lado el cuadrado, así sabemos que el área del mantel será de 16 metros cuadrados.
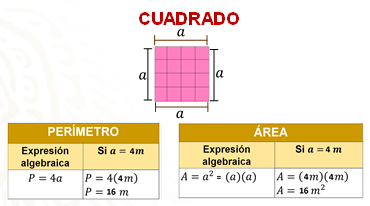
En este caso, el perímetro y el área tienen la misma magnitud, pero diferentes unidades, porque, como ya dijimos, son propiedades diferentes.
Para elaborar manteles en forma rectangular, Bruno sabe también que esta figura tiene cuatro lados con dos pares de lados iguales.
De manera que, para conocer el perímetro de un rectángulo, hay que sumar la medida de cada uno de sus lados, b+d+b+d; considerando que esta figura tiene dos pares de lados iguales, esta expresión también se puede representar como 2b+2d, en donde “b” representa el largo o base del rectángulo, y “d” el ancho o alto.
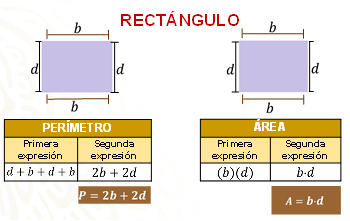
Calcular el área del rectángulo es un proceso similar a la del cuadrado. Tomando en cuenta que la superficie se mide mediante unidades cuadradas, en este caso basta con contar la cantidad de cuadrados que hay en la superficie del rectángulo, o bien multiplicar la medida del largo (b) por la medida del ancho (d), así sabemos que la expresión A= bxd (b por d) puede utilizarse para calcular el área de cualquier rectángulo.
Si Bruno decide hacer manteles en forma de rectángulo que midan 4 metros de largo y 2 metros de ancho, para calcular el perímetro se suman los cuatro lados de la figura.
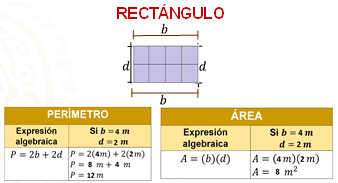
También puedes sumar los productos 2 por 4 metros y 2 por 2 metros, y de esta manera sabemos que el perímetro del mantel tendrá 12 metros de longitud.
Como sabrás, para calcular el área se utiliza la expresión A=bxd, por esta razón multiplicamos la medida del largo (4 metros) por la medida del ancho (2 metros) y así sabemos que el área de un mantel de forma rectangular de 4 metros de largo y 2 metros de ancho es de 8 metros cuadrados.
Mira a tu alrededor: ¿qué objetos tienen forma de rectángulo o de cuadrado? ¿Podrías utilizar algunas de las expresiones que acabamos de revisar con el cuadrado y el rectángulo para calcular su perímetro y área?
¿Qué pasa si Bruno necesita hacer manteles en forma de triángulo equilátero?
Debe tomar en cuenta que se trata de una figura de tres lados iguales y, para calcular su perímetro, hay que sumar la medida de cada lado, esto es, b+b+b.
También puedes expresar el perímetro de la siguiente manera: 3b (el triple del valor de b), en donde la literal “b” representa la medida de lado de cualquier triángulo equilátero.
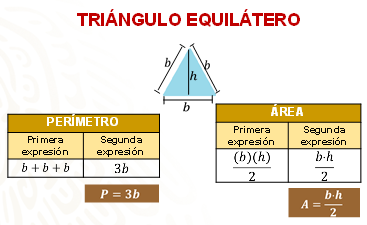
Respecto del área, recuerda que, en comparación con un rectángulo de la misma base y altura que el triángulo, éste siempre representará la mitad de su área; de esta forma, para calcular el área de un triángulo, se multiplica la base por la altura y el resultado se divide entre dos.
Este proceso se generaliza con la expresión que seguramente ya conocen: el área del triángulo es igual a base por altura sobre dos.
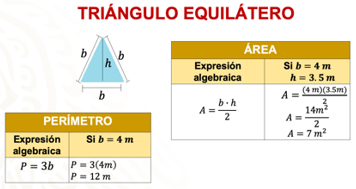
Si Bruno tiene pensado hacer una plantilla para elaborar manteles en forma de triángulo equilátero que midan 4 metros de lado, entonces puede sumar la medida de los tres lados del triángulo: 4+4+4, y al efectuar la suma obtenemos 12 metros, que corresponden a la medida del contorno o perímetro del mantel.
Es más eficiente si multiplicamos 3 por los 4 metros que mide cada lado, y también obtenemos 12 metros como resultado.
Ahora observa qué pasa con el área. ¿Qué tiene que hacer Bruno si lo que quiere saber es el área del mantel en forma de triángulo equilátero?
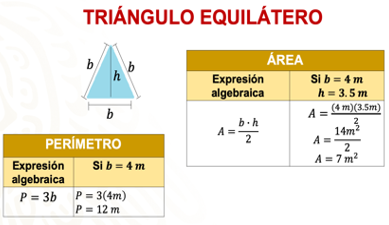
Utilizaste la expresión base por altura entre dos, multiplicando los 4 metros de la base por los 3.5 metros de altura aproximadamente y el producto lo dividiste entre 2, así sabes que el mantel tendría una superficie de 7 metros cuadrados aproximadamente.
Ahora ve qué sucede si Bruno necesita hacer manteles en forma de hexágono regular.

Como ya sabes, un hexágono regular es un polígono de 6 lados iguales y 6 ángulos interiores iguales.
¿Y cómo calculas el perímetro y el área de un hexágono?
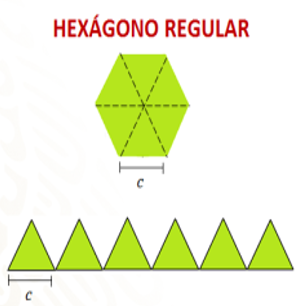
Cualquier superficie plana de lados rectos como los polígonos, y en este caso, del hexágono regular, pueden dividirse en triángulos y así calcular su área como la suma de las áreas de dichos triángulos.
Un hexágono regular se puede dividir en 6 triángulos equiláteros; observa.
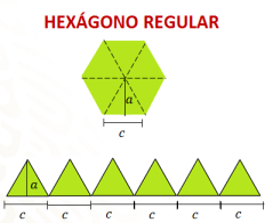
Al dividir el hexágono a partir del centro hacia sus vértices, obtenemos 6 triángulos iguales con igual medida de base y altura.
Con base en lo anterior, aun sin conocer la medida del lado del hexágono, sabemos que todos sus lados miden lo mismo, porque se trata de una figura regular. En conclusión, el perímetro se obtiene sumando c+c+c+c+c+c, o bien multiplicando 6c (seis por “c”), en donde la literal “c” representa el lado de cualquier hexágono regular.
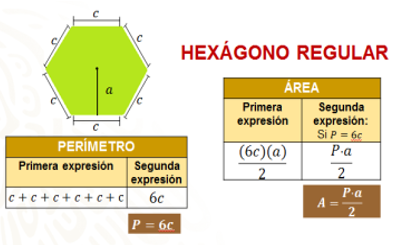
¿Y qué sucede con el área?
Hace un momento explicamos que un hexágono regular puede ser descompuesto en 6 triángulos con igual base y altura.
Esta información te ayudará a establecer una expresión que permita calcular el área del hexágono. Pero antes, debes saber que en un polígono regular la altura de los triángulos en los que se descompone se llama apotema, y es la distancia de su centro al punto medio de cualquiera de los lados del polígono regular.
Una forma de calcular el área de un hexágono regular a partir de la descomposición en triángulos, es sumar el área de los 6 triángulos obtenidos, o bien calcular el perímetro de la figura y multiplicar el resultado por la medida del apotema, dividiendo el producto obtenido entre dos.
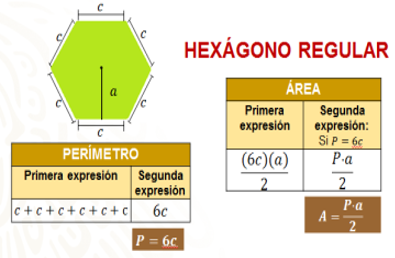
Ahora Bruno sabe que con la expresión A=p(a)/2 (área es igual al perímetro por la apotema entre dos), es posible obtener el área de cualquier hexágono regular
Verifica que las expresiones antes mencionadas nos ayudan a calcular el perímetro y el área de un hexágono regular.
Si Bruno elabora un mantel en forma de hexágono que mida 4 metros de lado y tiene 3.5 metros de apotema.
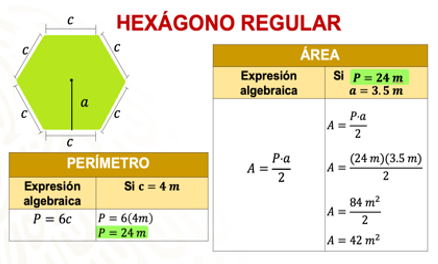
Utiliza la expresión 6c para calcular el perímetro del mantel, esto es, multiplicar 6 lados por los 4 metros que tiene cada lado del hexágono; al efectuar la multiplicación obtienes 24 metros que corresponden al perímetro del mantel.
Esto puede parecer muy fácil, pero tengo una duda: ¿esta expresión también se aplica para el área?
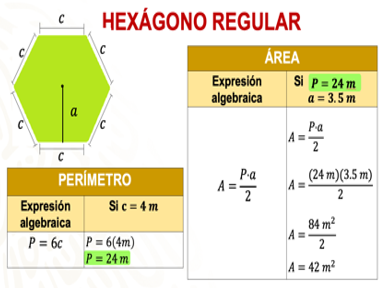
Considera que para el área usamos la expresión A = P(a)/2 (área es igual al perímetro por apotema sobre dos), multiplicamos el perímetro (24 metros) por el apotema (3.5 metros) y dividimos el producto entre 2. De esta forma, sabes que la superficie de un mantel en forma de hexágono regular de 4 metros de lado y 3.5 metros de apotema es de 42 metros cuadrados.
Ahora pon en práctica lo que has aprendido con el siguiente problema.
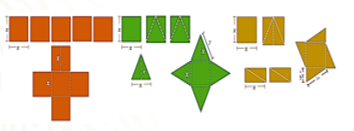
Bruno hizo los siguientes diseños para hacer algunos manteles de papel. Él dice que, si se respetan las medidas de éstos, se utilizará la misma cantidad de papel para cada uno, aunque sus formas sean diferentes. ¿Qué piensan de lo que dice Bruno?
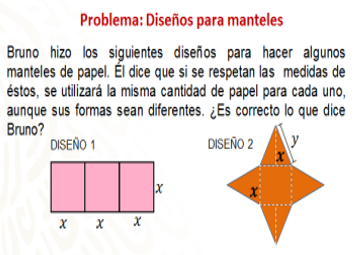
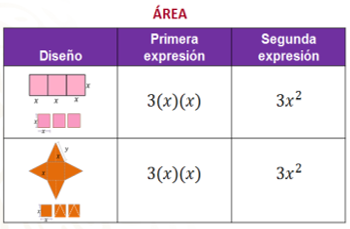
Puedes comenzar por analizar los diseños. El primero se trata de un mantel rectangular formado por tres cuadrados de lado “x”.
El segundo diseño se presenta en forma de estrella, para la que se ocupa 1 cuadrado de lado “x” y 4 triángulos de base y altura “x”. ¿Será verdad que ocupan la misma área?
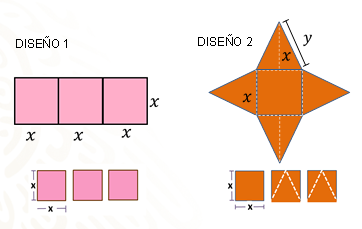
Sí ocupan la misma área, porque si observas los diseños, se ve que cada triángulo equivale a la mitad de un cuadrado.
Para estar seguros y seguras de lo que Bruno dice, es necesario comparar el área de las dos figuras.
No conocemos la medida del lado del cuadrado, pero se tomó como referencia el mismo tamaño para los dos diseños, porque están representados con la misma literal, lo que significa que se trata de la misma medida desconocida.
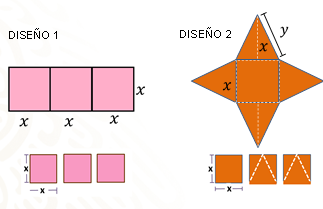
El primer diseño ocupa tres cuadrados, al igual que el segundo, porque para obtener los triángulos del segundo diseño, se requiere hacer algunos cortes que se acomodan para armar la figura del mantel.
A partir del análisis que has realizado, puedes concluir que Bruno tiene razón: si se respetan las medidas de cada uno de los diseños, se utiliza la misma cantidad de papel.
No importando el diseño, nos damos cuenta de que el área es la misma, porque las expresiones que la representan son equivalentes.
Te invitamos a poner a prueba tus conocimientos adquiridos resolviendo el nuevo reto que enfrenta Bruno.
Ahora Bruno ha decidido contribuir al cuidado del medio ambiente, tener un negocio socialmente responsable y comprometido con el cuidado del medio ambiente; por tal motivo, ha decidido hacer sus manteles con papel reciclado y, además, reducir la cantidad de papel empleado en su elaboración, esto con base en el nuevo diseño que producirá ahora.
Inicialmente el diseño se elaboraba con 5 cuadrados, posteriormente se realizaba con 3 y ahora los realizará con tan sólo 2 cuadrados, como se muestra a continuación.
¿Logrará Bruno reducir realmente la cantidad de papel que se utiliza para la elaboración de los manteles con sus nuevos diseños?
Depende de las medidas de los cuadrados que utilice Bruno.
Sabes que x representa cualquier medida para los tres diseños. Observa sus diseños.
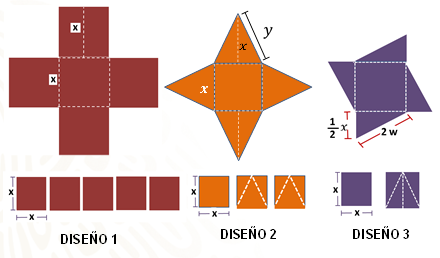
Nota que tómo como referencia nuevamente cuadrados del mismo tamaño, porque representa la medida de lado con la misma literal “x”.
Quizá nos ayude a comprobarlo si calculamos el perímetro y el área de los diseños como lo hicimos en el problema anterior.
Comencemos por analizar el perímetro de cada diseño.
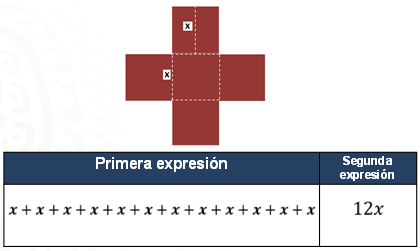
El primer mantel está compuesto por 5 cuadrados de lado “x”.
Para calcular el perímetro, se suman todos los lados de la figura, siendo el perímetro del diseño uno del mantel igual a la suma de 12 veces el valor que representa la literal “x”, o bien el producto de 12 por el valor de la literal “x”.

En el diseño dos del mantel, la medida de los lados es diferente porque se representa con la literal “y”.
Para calcular el perímetro, se suman todos los lados de la figura, y el perímetro del diseño dos del mantel es igual a la suma de 8 veces el valor que representa la literal “y”, o bien el producto de 8 por el valor de la literal “y”.
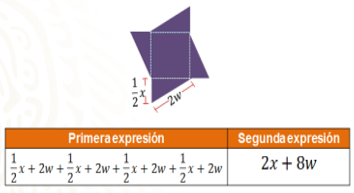
Por último, para calcular el perímetro del diseño tres del mantel, únicamente se suman cada uno de los lados de la figura, expresados como un medio de “x” y 2w; al efectuar las operaciones obtenemos la expresión 2x+8w, que representa el perímetro del mantel.
Entonces, la primera expresión y la segunda expresión en cada diseño, ¿representan lo mismo? Sí, ambas expresiones en cada diseño son equivalentes.
Ahora analiza el perímetro resultante de cada diseño con ayuda de la siguiente tabla: “Perímetro de figuras”.
Al comparar la expresión algebraica que representa el perímetro de cada diseño que Bruno elaboró, puedes notar que los tres resultados son diferentes, esto significa que las tres figuras tienen un perímetro distinto.
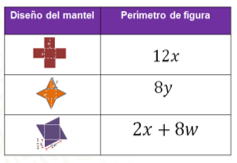
¿Qué representan las expresiones contenidas en la tabla en relación con los diseños del mantel?
Representan la medida del contorno de los manteles, es decir, el perímetro de cada diseño.
Para saber la cantidad de papel en metros cuadrados que necesita Bruno para elaborar los diseños de mantel, ¿qué necesitas calcular?, ¿área o perímetro?
Con lo que hemos visto, ahora lo que necesitamos calcular es el área, porque lo que buscamos es la medida de la superficie que ocupa cada diseño y ésta se da en metros cuadrados.
Atenta y atento a lo siguiente:
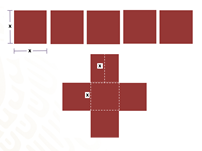
Si observas y analizas detenidamente el diseño número uno, está construido por 5 cuadrados, cuya medida del lado está representada por la literal “x”.
Para su elaboración, los cinco cuadrados se acomodan en forma de una cruz.
El diseño número 2 está compuesto por tres cuadrados, la medida de cada lado está expresada por la literal “x”; es decir que los cuadrados que se ocupan para este diseño y el anterior tienen la misma medida porque se representan con la misma literal.
En este diseño, dos de los cuadrados se cortan para dar la forma de estrella al mantel.
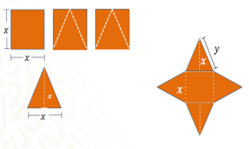
Por último, puedes ver que el diseño 3 se compone de 2 cuadrados del mismo tamaño que los cuadrados de los diseños anteriores, porque la medida de cada lado se representa con la literal “x”, pero, al igual que en el diseño dos, se hicieron cortes a las figuras originales para dar forma al mantel.
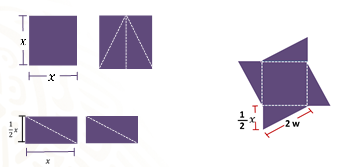
Sí, uno de los cuadrados se corta por la mitad, y los rectángulos que resultan se cortan en diagonal para obtener cuatro triángulos que se acomodan para dar forma al diseño del mantel.
Al comparar los tres diseños, y observar la cantidad de papel empleado en la elaboración de cada uno, podemos notar que Bruno logró disminuir la cantidad de papel.
Si se fuera a cubrir una mesa cuadrada de lado x, con lo que quedaría cubierta esa superficie, que es equis cuadrada, tendría cada diseño un faldón.
El diseño uno tendría cuatro faldones cuadrados de lado x; para el diseño 2, cuatro faldones en forma de triángulo de base y altura equis. El tercer diseño tendría cuatro faldones en forma de triángulo con base equis y altura 1/2 (un medio) de equis.
Al calcular el área de cada diseño a partir de la suma de los cuadrados que los componen, comprobamos que Bruno disminuyó la cantidad de papel en la elaboración de sus manteles.
Analicemos el problema de “La granja de José”.
José quiere ampliar su granja para reacomodar a sus animales. El terreno de la granja se representa de color verde. José necesita comprar los terrenos que aparecen en azul y en amarillo, como se muestra en la imagen.
Sin embargo, José tiene algunas dudas. Ayudemos a José a resolverlas.
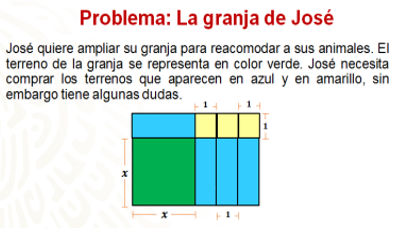
La primera pregunta que tiene José es: ¿qué forma tiene el terreno?
Como podrás notar, el terreno de José es el de color verde, al observarlo nos damos cuenta de que sus lados son iguales, en este caso, representados con la literal “x” (equis).
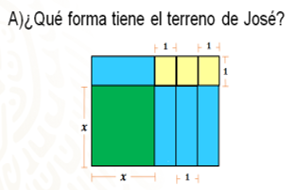
Sabes que el cuadrado es una figura geométrica que pertenece a los paralelogramos porque tiene cuatro lados que miden lo mismo y son paralelos dos a dos.
¿Recuerdas qué quiere decir dos a dos?
Que tiene dos lados paralelos e iguales entre sí, y los otros dos también son paralelos e iguales entre sí.
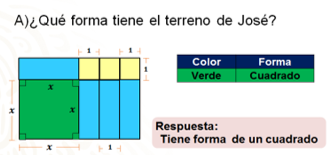
Además de los cuatro lados iguales, posee cuatro ángulos interiores que miden 90 grados, es decir, son ángulos rectos, y la suma de sus cuatro ángulos interiores es igual a 360 grados; entonces el terreno de José corresponde a la figura geométrica de un cuadrado porque cumple con todas estas características.
Al observar y analizar los terrenos que se encuentran junto al de José, identificados con color azul y amarillo, podemos notar que los de color azul corresponden a la figura del rectángulo porque sus lados son iguales dos a dos.
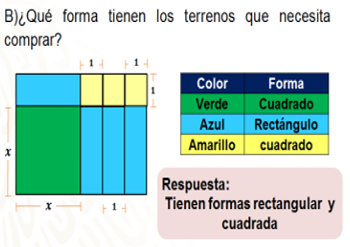
Recuerda que los rectángulos tienen dos lados opuestos paralelos que tienen la misma medida. Además, otra característica de los rectángulos es que sus ángulos son rectos.
¿Recuerdas a qué se refiere con tener ángulos rectos?
Se refiere a que un ángulo recto es igual a 90°.
Las figuras en color azul corresponden a rectángulos porque se encuentran compuestas por cuatro lados, de los cuales dos tienen una longitud y los dos restantes otra, y además forman cuatro ángulos rectos de 90°.
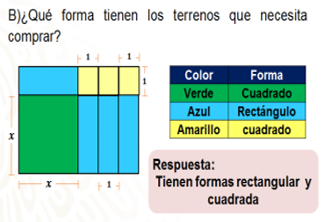
Para el caso de las figuras de color amarillo, corresponden a un cuadrado que tienen las mismas características, pero que, además, los cuatro lados del cuadrado miden lo mismo.
Al comprar los terrenos, ¿qué forma tendrá la granja? ¿Sabes la respuesta?
Tendrá forma rectangular porque tendrá mayor longitud en su largo, comparado con la longitud del ancho.
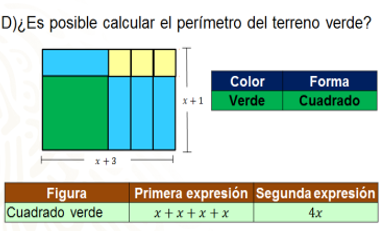
Como podrás notar, el largo del terreno de la granja estará aumentado en tres unidades, mientras que en su ancho sólo estará excedido en una; esto es, el largo está representado por la expresión de “x” más tres, y el ancho, por la expresión “x” más uno.
¿Es posible calcular el perímetro del terreno verde?
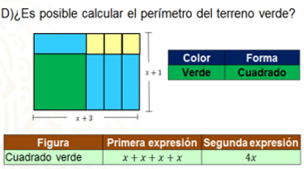
Recuerda que el perímetro de una figura plana es la medida de su contorno, para el caso de la figura verde, que corresponde a un cuadrado, es posible expresar su perímetro como 4 equis, es decir, cuatro veces el valor del lado equis.
Para poder saber las dimensiones del nuevo terreno que tendrá la granja, una vez que se han adquirido los terrenos que muestra la imagen, es necesario saber, en primer lugar, ¿cuál es el ancho del nuevo terreno? Y al mismo tiempo, ¿cuál será el largo del nuevo terreno?
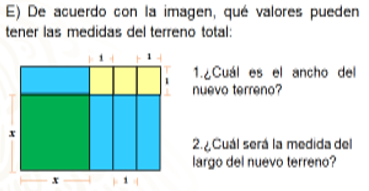
Es importante, en primer lugar, establecer la magnitud del largo y del ancho a través de la información que se proporciona mediante la imagen; en este caso, se representará cada una de las expresiones a través de una tabla.
El largo del terreno total está expresado como equis más uno, más uno, más uno. Si realizamos la reducción de términos semejantes, obtenemos una segunda expresión algebraica: equis más tres, siendo ambas expresiones equivalentes.

Entonces, para el caso del ancho, la primera expresión es equis más uno, ya que no hay términos semejantes que podamos reducir.
De acuerdo con la imagen, ¿qué valores pueden tener las medidas del terreno total?
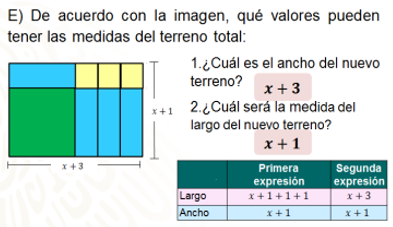
El nuevo terreno tendrá de ancho equis más tres, y de largo, equis más uno, como se observa en la imagen.
José comprará el terreno que necesita para la ampliación de su granja, irá adquiriendo de forma mensual cada uno. En primer lugar, comprará los terrenos de color azul y posteriormente los de color amarillo. El costo de cada terreno depende de su tamaño, si José desconoce las medidas de los terrenos que quiere adquirir y únicamente sabe el costo que pagará por cada metro cuadrado...
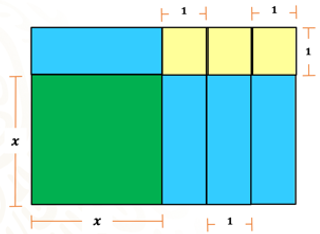
¿Qué expresión permite calcular el área de cada terreno?
Depende de la forma de cada terreno, porque si observamos, hay terrenos cuadrados y rectangulares.
Por lo que, para poder ayudar a José, es necesario analizar cada una de las figuras y expresar sus medidas con la información que se proporciona en la imagen.

Representa a través de una tabla los datos que te permiten conocer la superficie de cada figura.
Para el caso del cuadrado verde: la longitud de sus lados está representada con la literal equis, y su expresión algebraica se expresa como el producto de equis por equis (x)(x). Al realizar la multiplicación, obtenemos el área, que se representa como equis cuadrada, o bien equis elevada a la segunda potencia.
En segundo lugar, tenemos el rectángulo azul; el largo de la figura es equis, y su ancho corresponde a uno, la expresión algebraica que representa el área es el producto de equis por uno; al efectuar la multiplicación obtenemos como producto equis, que representa el área del rectángulo.
Ahora te toca: ¿cuál es el área del cuadrado amarillo?
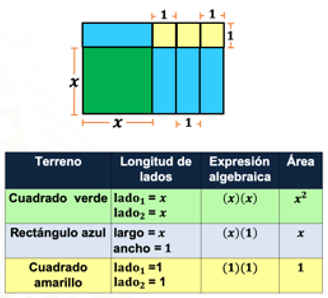
Eso está muy fácil, en el cuadrado amarillo las medidas por lado son igual a uno, de manera que la expresión que representa el área se expresa como la multiplicación de uno por uno; al final se obtiene el área, que es igual a uno.
Otra manera de representar el área del terreno total de José es analizar la forma que tiene el terreno total, como es posible observar, corresponde a un rectángulo.
Representa la longitud de su largo con la expresión equis más tres, y su ancho con la expresión equis más uno. Así obtendrás la expresión algebraica del producto de equis más tres por equis más uno.
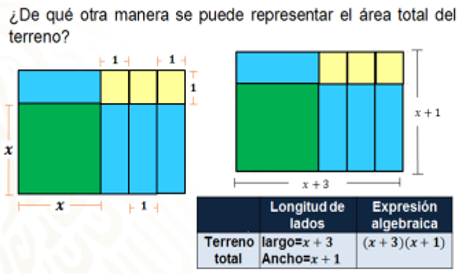
Para que José pueda saber la superficie de su terreno total, una vez adquiridos los terrenos, sólo necesitará sustituir el valor que representa la literal equis y efectuar las multiplicaciones correspondientes, y podrá hallar el valor del área total.
Analiza el siguiente problema:
El largo del campo de fútbol de la colonia mide 30 metros más que el ancho. Encuentra sus dimensiones y calcula su perímetro y su área.
Para poder resolver el problema, es necesario hacer una representación gráfica del campo de fútbol. ¿Qué forma tiene? Es un rectángulo.
Como te habrás dado cuenta, la figura que representa el campo de fútbol corresponde a un rectángulo, lo que significa que tiene dos lados iguales dos a dos, es decir, sus pares de lados paralelos son iguales.
Para obtener el perímetro es necesario sumar los cuatro lados del campo de fútbol. A través de la tabla se muestran las expresiones que representan la suma de las medidas de cada lado, se realiza la reducción de términos semejantes hasta obtener la expresión algebraica que representa el perímetro del campo de futbol, siendo ésta cuatro equis más sesenta.
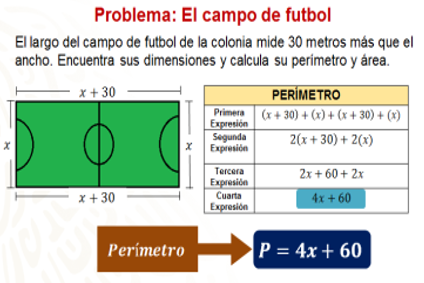
Para obtener el área del campo de fútbol es posible utilizar la expresión A=bxh. Si el largo es x+30 y el ancho es “x”, el área del rectángulo será el producto de x+30 por x (equis), así obtenemos la expresión algebraica x cuadrada + 30x, o bien equis elevada a la segunda potencia más treinta equis.
Con lo que has aprendido hoy, determina el valor del perímetro y del área del campo de fútbol si el ancho “x” tuviera un valor de 70 metros.
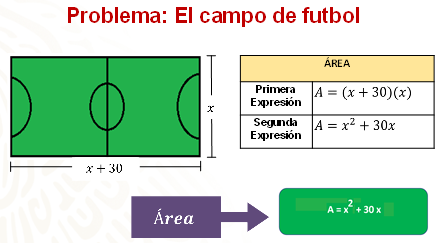
Ahora sabes que generalizar los procedimientos del cálculo del perímetro y del área de figuras geométricas, significa representar los procedimientos de resolución por medio de expresiones algebraicas o fórmulas.
Algunas de las expresiones que estudiamos son las siguientes.
Figura geométrica: cuadrado, cuya medida por lado es a.
Expresión para calcular su perímetro:
a+a+a+a=4ª
Expresión para calcular su área:
“a” cuadrada
Figura geométrica: rectángulo, la medida de su base es b y su altura mide d.
Expresión para calcular su perímetro:
d+b+b+d=2b+2d
Expresión para calcular su área:
Be por de
Figura geométrica: triángulo, la medida de su base es b y su altura mide h.
Figura geométrica: cuadrado, cuya medida por lado es a.
Expresión para calcular su perímetro:
a+a+a+a=4ª
Expresión para calcular su área:
“a” cuadrada
Figura geométrica: rectángulo, la medida de su base es b y su altura mide d.
Expresión para calcular su perímetro:
d+b+b+d=2b+2d
Expresión para calcular su área:
Be por de
Figura geométrica: triángulo, la medida de su base es b y su altura mide h.
Expresión para calcular su perímetro:
b+b+b=3b
Expresión para calcular su área:
Base por altura entre dos

¡Ahora tienen más herramientas para resolver este tipo de problemas!
El Reto de Hoy:
Revisar lo aprendido en tu libro de Matemáticas de segundo grado y resuelve algunos de los ejercicios de tu libro de texto.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

“Los pasos que siguen nuestras letras”
Aprendizaje esperado: Investiga sobre la diversidad lingüística y cultural de los pueblos hispanohablantes.
Énfasis: Reconocer el papel del español escrito.
¿Qué vamos a aprender?
En esta sesión aprenderás sobre un aspecto más de la diversidad lingüística. Nuestro idioma es diverso y tiene muchas formas para manifestarse. Éstas son una muestra de lo que somos como personas, pero también como cultura.
¿Qué hacemos?
El español es una lengua con una larga historia. Para saber más sobre las características que tiene la escritura del español y cómo ha cambiado con el paso del tiempo, revisemos el siguiente material.
El lingüista inglés Geoffrey Sampson explica que podemos caracterizar a la lengua por su lugar de origen, pero también podemos caracterizarla por el medio de representación que utiliza. Esos medios pueden ser oral, gestual o escrito.
La escritura es particular, ya que tiene ciertas características que la separan de otras maneras de representar la lengua; es decir, tiene convenciones propias, distintas de la oralidad o la gestualidad.
Por ejemplo, la puntuación entre otras cosas, contribuye en la escritura a organizar y delimitar ideas y a indicar modos e intenciones de la oralidad. Es un intento limitado por representar pausas y emociones que se hacen al hablar. A veces, hay quienes deciden usar punto y coma en vez de punto para separar, y ambas decisiones pueden ser válidas.
Ninguna lengua se escribe como se habla. La ortografía deriva de este hecho. Siempre existen discrepancias entre la cantidad de caracteres escritos y la cantidad de sonidos.
En el caso del español, tenemos varias discrepancias entre la oralidad y la escritura, por ejemplo, el uso de la letra “h”, que no representa un sonido.
Otra es la existencia de casos en que son necesarias dos letras para representar un sonido, como es el empleo de la “ll” o la “ch”. A esos grupos de letras se les denomina dígrafos.
O bien tenemos casos en que para un solo sonido se pueden utilizar dos letras diferentes, como es el caso del sonido /b/, que usa las letras” b” y “v”.
En comparación con otros idiomas con escritura alfabética, en el español hay más correspondencia uno a uno entre letras y sonidos. Ello se debe, en buena medida, a los ajustes que la escritura del español ha tenido a lo largo de su historia.
¿Alguna vez has visto cómo se escribía el español a principios del siglo XIII?
Pues acompáñame a ver y escuchar cómo era el español hace 800 años.
Cantar del Mio Cid
(fragmento)
AÅ¿ccondenÅ¿e de myo çid ca nol oÅ¿an dezir nada
El campeador adelino aſu poſada
aÅ¿i como lego a la puerta, falola bien çerrada
Observa ese signo que parece como una “f”. En realidad, es una “s”, llamada “ese larga”, y era muy común en la época.
También pueden observar una “C” con colita, llamada “ce cedilla”, que se pronunciaba como /ts/, como en /Tsid/.
La z, en “dezir”, se pronunciaba como /dz/, o sea que se pronunciaría “dedzir”.
Esas “eles” que ven en “lego” y “falola”, habría que leerlas como “llego” y “fallola”, con un sonido muy peculiar para la elle que está muy poco extendido en la actualidad. Y, como escucharon, la “n” hay que leerla como “ñ”, por eso es “adeliñó” y no “adelino”.
El uso de mayúsculas y minúsculas también era muy distinto en la época, así como el uso de las preposiciones.
En este extracto del poema, el Cid acaba de llegar con su gente al poblado de Burgos, pero el rey Alfonso había mandado una carta amenazando a la comunidad para que no le dieran albergue al Cid en dicha población. La gente, temerosa, sólo se asoma por la ventana.
Si modernizamos la ortografía, el texto seguramente será más comprensible y quedaría así:
Ascóndense [escóndense] de Mio Cid, ca [porque]
no le osan decir nada
El Campeador adeliñó [se dirigió] a su posada
Así como llegó a la puerta, hallola bien cerrada
Lo anterior es una muestra de cómo el español, con el paso del tiempo, ha sufrido grandes cambios. Siempre se ha adaptado a las necesidades de los usuarios y épocas. Pon atención.
Todavía en el siglo XVIII se conservaba el uso del dígrafo “ph” para representar el sonido /f/, igual que se utilizaba “th”, como en la palabra orthographia.
La “s” larga también era muy común. Además, la “a”, como preposición, solía llevar acento. Mientras que palabras como explicación o expresión no llevaban acento en la última sílaba. Asimismo, la equis <x> podía representar el sonido de la jota como en la palabra exercicio.
Estos cambios en la escritura son graduales, pero nos enseñan que la expresión escrita también requiere ajustes para que siga siendo una herramienta útil.
El español es hablado por alrededor de 500 millones de personas como lengua materna; según datos de la UNESCO, de 2015 a la fecha, entre 85 y 90% de estas personas saben leer y escribir en nuestra lengua, aunque estas cifras pueden variar en cada país hispanohablante.
Pareciera que el español escrito nos ofrece la posibilidad de entendernos sin dificultades, ¿cómo es esto posible?
Gracias a su convencionalidad. La escritura del español es una de las más normadas y reguladas. Esto quiere decir que busca la “homogeneidad” en el “uso escrito” de la lengua.
Pongo énfasis en el “USO ESCRITO” porque muchos tienden a pensar que esta normatividad también pretende homogenizar el “habla” de las distintas regiones hispanas y no es así. Por lo menos, no en términos de las finalidades que cumple la escritura.
Vamos a señalar tres funciones importantes que distinguen a la lengua escrita:
La primera característica es que la escritura sirve para vincular entre sí épocas y regiones alejadas. No refleja la pronunciación de todos y no corresponde exactamente a la pronunciación de alguien.
Como decía la lingüista francesa Claire Blanche-Benveniste: la escritura “no tiene nada que ver ni con la pronunciación individual, ni con la pronunciación de regiones vecinas, sino que sirve para fabricar un modelo de referencia”.
Este modelo trasciende fronteras regionales y nacionales. Y esto es lo que nos permite leer textos escritos en otras regiones de Latinoamérica e incluso de España, aunque nuestras pronunciaciones al hablar o al leer sean diferentes.
La segunda función, también siguiendo a Blanche-Benveniste, es que la escritura, y quizá con mayor precisión la ortografía y la separación entre palabras, tienen la función de dar “estabilidad” a los sentidos.
Esto quiere decir que la escritura no transcribe o copia la lengua oral de los distintos países hispanohablantes o regiones de nuestro país, sino que permite hacer comprensible un mensaje escrito para todos los hablantes de esta lengua.
La tercera y última función es el papel de la escritura como medio de pertenencia cultural.
Se trata del acceso a un uso de la lengua en el que se privilegian cualidades formales y culturales que no aparecen en la lengua oral de todos los días.
Es un registro de comunicación común entre hablantes de una misma lengua, y es lo que nos da “identidad” como hablantes del español, a pesar de que tengamos formas de habla distintas.
Es decir que la escritura es importante porque nos permite una comunicación más amplia y comprensible entre hablantes del español.
El sistema ortográfico tiene una importancia medular dentro de un idioma, entre otras razones, porque posee el carácter de normalizador y fijador de la lengua; es un instrumento esencial de cohesión y unidad del español. Además, permite establecer una secuencia histórica en la formación de un idioma.
Hay quienes piensan que la lengua escrita es una fuente de corrección que evita los errores de la lengua hablada; en pocas palabras, que no puede modificarse y es superior a la lengua oral. ¿Cuáles son tus consideraciones al respecto?
Es importante ubicar: ¿quiénes son aquéllos que piensan que la “escritura” es una fuente de corrección del “habla”? Sin temor a equivocarme, diré que son o somos aquellos sujetos alfabetizados y con experiencia y contacto con la cultura escrita. Porque somos estos sujetos para quienes la adquisición de la escritura cambió por completo la manera de concebir nuestra forma de hablar,la propia y la de otros.
Previo a incorporarnos a la cultura escrita de nuestra lengua, no percibíamos la necesidad de “corregir” la oralidad, la finalidad comunicativa se cumplía y, con ella, el objetivo buscado.
Lo que ahora identificas como fallos en la oralidad viene del hecho de que concibes a la escritura, como lo señalaba Blanche-Benveniste, como un modelo de referencia, al que instancias como la RAE se han encargado de ubicar como el “top del habla ideal”, inexistente en realidad. Porque como también lo decía Blanche-Benveniste, la escritura no representa un “habla” o “variedad” particular del español.
Por eso, si tomas a la escritura como el criterio para valorar el habla de las distintas regiones hispanas o incluso el habla de distintos estratos sociales, estarías atentando con el principio propio de la escritura y también de la oralidad. Ni la oralidad es superior a la escritura ni la escritura a la oralidad; te sorprendería cómo, en ocasiones, cada una va por caminos distintos en las comunicaciones cotidianas que entablamos.
La oralidad no puede juzgarse a partir de la escritura ni al revés. Cada una –en el caso del español– ha ido construyendo sus propias dinámicas de uso con cierta (inter)dependencia.
Utilizas un lenguaje diferente cuando vas a comunicar algo, si lo haces a través de un teléfono celular, o en persona, o a través de tu cuenta de correo o bien por escrito.
Estas ideas te llevan a reflexionar sobre las diferencias del lenguaje escrito, según cada situación.
Hay que conocer la pertinencia de escribir de cierta manera cuando se realizan trabajos escolares, y de otra, cuando se usan los medios electrónicos.
Los trabajos escolares son una buena oportunidad para aprender otros usos de la escritura, que después pueden ser reutilizados en los diferentes medios que frecuentamos, como blogs o las redes sociales en donde se comparten textos, imágenes y videos. Pero también las actividades de escritura que propone la escuela son una buena oportunidad para abrir las puertas a la escritura que circula en otros medios de la vida cotidiana de los estudiantes como las que acabo de señalar.
Las redes sociales son, hoy por hoy, uno de los principales canales/medios de comunicación. ¿Cómo impactan en los diversos usos de la escritura?
Las redes sociales son el reflejo más rápido que podemos tener de las innovaciones que se hacen con el lenguaje escrito –particularmente de adolescentes y jóvenes– y de las modificaciones generadas por los intercambios entre hablantes de distintas regiones hispanohablantes. Incluso de la influencia entre distintas lenguas. Estos cambios empiezan a observarse también de manera escrita.
¿Qué piensas del futuro uso del español escrito? ¿Cómo será empleado en los medios electrónicos?
En la historia de la escritura –por lo menos de lenguas como el español, el francés o emparentadas–, los cambios o innovaciones dependieron de los medios materiales con que se escribía. Los medios electrónicos vinieron a imponer con fuerza la necesidad de economizar la escritura porque el espacio del que disponemos es acotado.
Hay un incremento de comunicaciones donde la escritura, la imagen, el movimiento y el sonido conviven cada vez más. Y contrario a lo que se piensa, no es que la imagen y el sonido estén desplazando a las palabras escritas, están potenciándolas.
De acuerdo con el Instituto Nacional para la Evaluación de la Educación, en la publicación “La Ortografía de los estudiantes de educación básica en México”, se presentan los errores ortográficos más frecuentes en los estudiantes de nivel básico en México. Entre ellos encontramos la falta de acentuación, el uso equivocado de mayúsculas, la confusión con las letras “b” y “v”, “g” y “j”, “h”, etc.
El tema de la ortografía es bastante complejo. Retomemos las palabras del Premio Nobel de Literatura, Gabriel García Márquez, en el discurso inaugural del primer Congreso Internacional de la Lengua Española, en Zacatecas, en 1997.
“Simplifiquemos la gramática antes de que la gramática termine por simplificarnos a nosotros. Humanicemos sus leyes, aprendamos de las lenguas indígenas a las que tanto debemos lo mucho que tienen todavía para enseñarnos y enriquecernos...
Los neologismos técnicos y científicos, antes de que se nos infiltren sin digerir, negociemos de buen corazón con los gerundios bárbaros, los qués endémicos, el dequeísmo parasitario, y devuélvamos al subjuntivo presente el esplendor de sus esdrújulas: váyamos en vez de vayamos, cántemos en vez de cantemos, o el armonioso muéramos en vez del siniestro muramos.
Jubilemos la ortografía, terror del ser humano desde la cuna: enterremos las haches rupestres, firmemos un tratado de límites entre la ge y jota, y pongamos más uso de razón en los acentos escritos, que al fin y al cabo nadie ha de leer lagrima donde diga lágrima ni confundirá revólver con revolver. ¿Y qué de nuestra be de burro y nuestra ve de vaca, que los abuelos españoles nos trajeron como si fueran dos y siempre sobra una?”
Gabriel García Márquez
¿Qué opinas sobre lo anterior? ¿Qué sucedería si, en lugar de usar las convenciones gramaticales y ortográficas del español escrito, pudiéramos escribir como quisiéramos?
Los fragmentos que citan sintetizan uno de los aspectos medulares de ese discurso inaugural: el énfasis que Gabriel García Márquez hace de la “vitalidad”, la “dinámica creativa” y la “rapidez”, y capacidad de “expansión” que tiene el español gracias a tres cosas: al vasto territorio donde se habla, al contacto que nuestra lengua tiene con otras lenguas y a la amplia gama de ámbitos donde se usa.
Pero, sobre todo, hace alusión a la tremenda capacidad que tenemos de innovar, modificar y transformar todo el tiempo la lengua de la que somos hablantes, en este caso, el español. Porque algo es cierto: los cambios en la oralidad son más rápidos y fugaces de lo que son en la escritura. Sólo aquellos cambios que logran permanecer y ser transformados por los usuarios quedan registrados en la escritura. Lo cierto es que también asistimos a una serie de innovaciones y cambios propios de la escritura: las redes sociales están llenas de esto.
Respecto a la segunda parte de la pregunta (sobre si usar o no las convenciones de la gramática y la ortografía), me parece que de lo que se trata, como bien lo decía García Márquez, es de pensar la conveniencia de las reglas gramaticales y ortográficas para los USUARIOS (escritores y lectores) no desde la mirada de quien dicta la norma (la RAE, por dar un ejemplo). De ahí la frase “Humanicemos las leyes”, es decir, pensemos en los usuarios; ellos-nosotros somos quienes decidimos en la práctica la funcionalidad o caducidad de ciertas normas o reglas.
¿Qué textos recuerdas que contienen palabras, frases o modismos que son cruciales para observar el papel del español escrito?
Particularmente, la literatura del BOOM LATINOAMERICANO es sumamente rica para “ver” y “conocer” la riqueza del español en las distintas regiones, y observar cómo la escritura nos permite estos intercambios. Son textos que pueden ser comprendidos incluso fuera del entorno que les dio origen.
Hablamos de:
- Gabriel García Márquez, de Colombia
- Carlos Fuentes, de México
- Mario Vargas Llosa, de Perú
- O Julio Cortázar y Jorge Luis Borges, de Argentina, entre otros autores
Lo que caracteriza a esta generación de escritores es el intento por “reflejar” en sus historias a personajes variados de la vida cotidiana y cómo imprimían sus modos de hablar en los diálogos.
La obra de estos autores ha dado la vuelta a los países hispanohablantes y ha sido posible leerla gracias a que compartimos ciertas convenciones escritas.
Gracias a la escritura, nos es posible la lectura de textos
de distintos lugares de habla hispana.
Esto es importante destacar: gracias a la escritura, podemos comprender estas palabras, frases y modismos, por lo menos en términos de lectura, porque es cierto que se requiere conocer los distintos significados según las regiones.
Sí, por ejemplo, la palabra GUAGUA para los mexicanos no tendría sentido, pero podemos reconocer su escritura como parte del español e incluso leerla: “guagua”. Esta misma palabra puede tener distinto significado en un texto según la región latinoamericana: “camión” en Cuba y Venezuela, o “niño” en Argentina, Colombia y Chile, y a pesar de estos distintos significados, podríamos leerla, aunque no necesariamente conocer este cambio de significado. Lo que quiero resaltar con este ejemplo es que, gracias a la escritura y sus convenciones, es posible leer estos textos escritos en distintas regiones hispanohablantes, aunque requiramos de algunos datos de contexto para comprender a cabalidad.
¿Te gustaría hacer un mejor uso de la lengua escrita?
Te invitamos a acercarte a la lectura. Es una manera divertida de relacionarse con las convenciones y usos de nuestro idioma. Si les es posible, pide a tus familiares que te acompañen en esta actividad, ya que es una excelente herramienta para conocer un mundo de palabras.
La escritura, excelente herramienta para conocer un mundo de palabras
Los especialistas recomiendan que maestros y familiares o tutores den libertad a la escritura de los estudiantes. La escuela suele cohibir escrituras no escolares. Estas escrituras cumplen funciones comunicativas fundamentales y muestran los conocimientos que los estudiantes tienen del español escrito. Si les damos a nuestros estudiantes o hijos la libertad de “jugar con el lenguaje escrito”, el interés por descubrir e investigar sobre la escritura del español va a llegar paulatinamente.
Y a ti, estudiante, te invitaría a que explores con la escritura a partir de tus propios intereses. La información sobre el español escrito no viene solamente en los libros, también se encuentra en la propaganda, las revistas, los periódicos o los cómics. Los textos que circulan en la vida cotidiana están cargados de información implícita sobre la escritura de nuestra lengua.
Puedes hacerte preguntas al respecto, se observador y prueba también a jugar con las convenciones de escritura.
Para finalizar, quiero recomendarte un libro muy reciente, se llama: Ansina se dice, Ansina se escribe. Historias e histerias del habla popular, de Daniel Escorza. Búsquenlo en Internet, es un libro muy interesante para reflexionar sobre el papel de la escritura.
Recapitulemos, ¿cuál es el papel del español escrito?
Cumple una función social fundamental: permite la comunicación por escrito entre hablantes de distintas variedades del español, pero, sobre todo, brinda identidad a nuestra lengua.
No olvides que en tu libro de texto pueden localizar más información sobre el propósito trabajado en esta sesión, el cual fue: “Reconocer el papel del español escrito”.
Es importante que, para reforzar lo aprendido, busques el aprendizaje esperado y complementen el tema con los ejercicios y actividades que ahí se proponen.
El Reto de Hoy:
Con el material que tengas en casa, realiza un tríptico en el que reflejen lo revisado en la sesión de hoy. Puedes usar fragmentos de revistas, quizá alguna etiqueta publicitaria que use el lenguaje de manera particular. Recuerda que el propósito es: “Reconocer el papel del español escrito”.
Comparte tu trabajo con familiares, amigos y profesores. Quizá ellos tengan algo extra que aportarte.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Clásico, panorama general
Aprendizaje esperado: Conoce el proceso de formación de Mesoamérica y sus principales características culturales. Reconoce la ubicación de las áreas culturales que conformaron esta región e identifica las similitudes y diferencias entre ellas.
Énfasis: Conoce las características generales del Clásico y sus períodos: temprano y tardío.
¿Qué vamos a aprender?
Conocerás las características generales del Clásico y sus periodos: temprano y tardío.
Los materiales que vas ocupar son: cuaderno y pluma, así como tu libro de texto, pues es tu principal fuente de consulta.
¿Qué hacemos?
Algunos de los cambios más importantes que propició el período clásico americano fueron el crecimiento en general de las poblaciones, la construcción de enormes y fastuosas ciudades haciendo uso de un notable manejo de la piedra y un evidente avance en el dominio de las técnicas relacionadas con la cerámica, la metalurgia y la orfebrería. Además, lograron un mejor aprovechamiento de la agricultura en sus zonas de influencia.
Lee esta breve historia de Teotihuacán, que presenta el Instituto Nacional de Antropología en una de sus páginas informativas. Dice así:
Historia breve de Teotihuacán
La Zona Arqueológica de Teotihuacán se localiza en el Estado de México, es considerado uno de los sitios prehispánicos más importantes descubiertos hasta el día de hoy. Es testimonio material de una de las ciudades prehispánicas mejor planificadas y extensas del mundo antiguo.
Es símbolo de desarrollo cultural, artístico, religioso, político y social de la cultura mesoamericana, y que aún después de su abandono continúa siendo objeto de la construcción simbólica colectiva. Por sus valores históricos, culturales y educativos, no solo es el sitio arqueológico más visitado en México, sino que se ha consolidado como un destino turístico internacional.
Teotihuacán significa el “lugar donde fueron creados los dioses” y debe su nombre a los mexicas, que la llamaron así seis siglos después de su abandono. Alcanzó los 22 kilómetros cuadrados de extensión y fue uno de los polos culturales del área conocida como Mesoamérica. Su alcance abarcó desde el norte hasta el sur del México actual, así como Guatemala y Honduras, regiones con las que mantuvo un intercambio traducido en influencias estilísticas y arquitectónicas.
Su valor universal se aprecia en el diseño urbano ortogonal, definido por la calzada de Los Muertos en el eje norte-sur y las canalizaciones del río San Juan en el este-oeste, disposición que se vincula con el paisaje y sus elevaciones naturales, como el Cerro Gordo y la Sierra de Patlachique. Sobre ese plano se trazaron calles, palacios, templos y conjuntos habitacionales con una población multiétnica dedicada a la producción artesanal, el comercio, el sacerdocio y la guerra.
También se caracterizó por su cultura material, como la pintura mural o los objetos cerámicos y de piedra ofrendados en edificios y entierros de todas las clases sociales. De sus numerosas construcciones, distribuidas en tres mil hectáreas, las más importantes se hallan en la calzada de Los Muertos, entre las que destacan las pirámides del Sol y la Luna, la Ciudadela, los conjuntos Oeste y de La Ventilla, el Gran Complejo y los palacios de Tetitla, Atetelco, Tepantitla, Yayahuala y Zacuala.
¿Qué te pareció el texto? Hace que uno sienta mucho orgullo, ¿verdad?
A partir de la lectura del texto anterior espero que reconozcas la influencia cultural de Teotihuacán en el posclásico que se manifiesta en el uso de técnica y conocimiento, de elementos arquitectónicos, como el talud y tablero, y de cultos a dioses.
Los teotihuacanos construyeron pirámides de grandes dimensiones utilizando el talud y el tablero. A nivel arquitectónico, un mismo estilo se propagó por toda la ciudad: el talud-tablero.
Es importante definir “diseño urbano ortogonal” que se refiere a un PLANO ORTOGONAL; en CUADRÍCULA o DAMERO; que está formado por calles que se cortan en ángulo recto.
Se ha encontrado evidencia de este mismo estilo arquitectónico en toda Mesoamérica.

Anota las siguientes preguntas y conforme se desarrolle el tema podrás ir contestándolas:
¿Cómo estaban construidas y diseñadas las ciudades del México antiguo?
¿Qué tipo de edificaciones tenían?
Observa el siguiente video:
- Seis Ciudades Antiguas de Mesoamérica, Mito de Orígenes
Como se plantea en el video, los pueblos mesoamericanos compartieron creencias que se relacionan con el origen del mundo o del universo.
El esplendor Clásico.
A principios de la era cristiana, mientras en Roma se consolidaba el Imperio y el cristianismo empezaba a extenderse por el mundo mediterráneo, en Mesoamérica comenzaban a surgir las ciudades sagradas de los mayas en Tikal, Uaxactún, Yaxchilán, Copán y Palenque.
Fue entonces cuando en la región central de México, a unos cuarenta kilómetros al norte de la actual capital, se comenzaba a edificar la gran metrópoli de los dioses, Teotihuacán, que son sus pirámides, sus palacios, esculturas y pinturas llegaría a ser paradigma e inspiración de los demás pueblos que habrían de venir.
La ruina del Imperio Romano coincide en el tiempo con el esplendor clásico de las ciudades del mundo maya y de Teotihuacán, con sus incontables palacios cubiertos de inscripciones y frescos. Muchas de esas mismas inscripciones y representaciones de dioses habrán de encontrarse más tarde en los códices de pinturas y en el arte de los mexicas contemporáneos de la invasión europea.
Hacia los siglos IV y V aproximadamente, especialmente en el mundo maya, las inscripciones redactadas con una escritura en parte ideográfica y en parte fonética se vuelven en extremo abundantes. Son testimonios de que esos pueblos poseyeron un hondo sentido de la historia y del tiempo, como lo prueba su calendario.
A su vez, el arte de los mayas no sólo sobresale entre las grandes creaciones del México antiguo, sino que se considera hoy como extraordinaria aportación al legado universal. Ya la UNESCO ha incluido en la Lista del Patrimonio Cultural de la Humanidad a los centros clásicos mayas de Tikal, Copán, Palenque y Chichén-Itzá. También la Ciudad de los Dioses, Teotihuacán, forma parte de ese patrimonio.
La cultura clásica floreció asimismo en la región de Oaxaca, al sureste del altiplano central. En el antiguo centro conocido hoy como Monte Albán, donde se conservan las inscripciones más antiguas del Nuevo Mundo, los zapotecas edificaron suntuosos templos y palacios.
La existencia de formas más complejas de escritura muestra que, como en el caso de los mayas, también los zapotecas, inspirados en la aportación original de la cultura olmeca, continuaron perfeccionando ese arte de representar conceptos valiéndose de signos glíficos y otras figuras
Por razones en gran parte desconocidas, entre los siglos VII y IX, los grandes centros rituales de Teotihuacán y del mundo maya comenzaron a decaer y fueron al fin abandonados.
El periodo de la historia mesoamericana llamado clásico temprano (200 al 650 nuestra era aproximadamente) se caracterizó por el surgimiento de ciudades planeadas de manera cuidadosa, que fueron la sede del poder político y religioso. Estas ciudades tenían relaciones comerciales entre sí, y gracias a este contacto compartieron muchos elementos culturales, como estilos arquitectónicos, prácticas religiosas y técnicas de cultivo entre otras.
Las ciudades del Clásico eran regidas por un Estado fuerte, capaz de planificar grandes obras públicas y de movilizar a muchos hombres para construirlas. Teotihuacán llegó a dominar las redes comerciales, por donde circulaban bienes como obsidiana, jade, plumas de quetzal, cacao y algodón. El influjo de Teotihuacán se extendió hacia muchas regiones, por lo que tuvo una gran influencia en las tradiciones de otros pueblos.
En el Altiplano central territorio que hoy comprende el Estado de México, Puebla, Tlaxcala; Morelos y Ciudad de México; entre el 650 y 750 de nuestra era, aproximadamente, las grandes ciudades y particularmente Teotihuacán, entraron en un periodo de decadencia y abandono, en algunos casos. A esta época se le ha dado el nombre de Epiclásico.
Para conocer más características del Clásico, observa el siguiente video.
- Nuevas ciudades, nuevas regiones
Después de observar el video, recuerda las preguntas de inicio, ¿cómo estaban construidas y diseñadas las ciudades del México antiguo? ¿Qué tipo de edificaciones tenían? ¿Identificaste cuáles y cómo eran sus principales ciudades?
Lee este siguiente fragmento:
El libro se llama Dioses del Norte, Dioses del Sur, Religiones y cosmovisión en Mesoamérica y los Andes
Alfredo López Austin y
Luis Millones.
Se ha denominado Clásico al periodo de esplendor mesoamericano, marcado por las grandes concentraciones de una población firmemente jerarquizada.
Nació entonces el urbanismo, diferenciándose claramente la ciudad (en la que se centraron las actividades artesanales, comerciales, políticas y religiosas), del campo (gran productor de bienes de subsistencia), como una diada interdependiente.
Las grandes ciudades fueron autónomas, pero sus alianzas comerciales y políticas eran frecuentes. Las mayores irradiaron su influencia política y económica a grandes distancias, fincando su poder en ejércitos bien equipados
Controlaron así extensas redes comerciales, estableciéndose al mismo tiempo como productores y exportadores especializados. A lo largo y ancho de Mesoamérica circularon cacao, manufacturas de algodón, plumas y piedras preciosas, objetos de obsidiana, cerámica de lujo, piedras talladas y muchas otras mercancías.
Las ciudades centralizaron también la religión, y las cortes se vieron incrementadas con un sacerdocio especializado no sólo en el oficio del culto, sino en el conocimiento del calendario, la escritura, la astronomía, la arquitectura y la urbanística. Las artes tuvieron un florecimiento espectacular. Las ciudades contaban con sistemas de conducción de agua y drenaje
Algunas de ellas cuando el relieve del terreno lo permitía se edificaban bajo patrón ortogonal. En su centro se ordenaban amplias plazas limitadas por edificios templario, entre los que destacaban pirámides de gran altura. Allí también se construían palacios, mercados, canchas para el juego de pelota, y a la redonda se distribuían los barrios residenciales, también provistos de templos y plazas.
Los caminos y acueductos contemplaban aquella concentración de industria, poder y religión, poder y sabiduría.
El Clásico Temprano (200 nuestra era a 650 nuestra era, aproximadamente) se
caracteriza por un predominio comercial de Teotihuacán, la gran capital ubicada en el Centro de México.
El Clásico Tardío (650 nuestra era a 900 nuestra era aproximadamente), tras la caída de Teotihuacán, fue el esplendor de otras urbes, entre ellas Monte Albán, en Oaxaca, y toda una pléyade de ciudades mayas: Tikal, Calakmul, Palenque, Copán, Becán, Uaxactún, Uxmal, Yaxchilán, Quiriguá, Cobá y otras muchas.
 En éstas llegan a su culminación la pintura, la escultura, el calendario, la escritura, la numeración y la astronomía. Sin embargo, todos esos centros de poder van declinando uno tras otro, para dar paso a una Mesoamérica de fuerte carácter militarista. En la parte final del Clásico, denominada por algunos autores Epiclásico, florecieron El Tajín en la subárea del Golfo, y Cacaxtla, Cholula y Xochicalco en la del Centro de México.
En éstas llegan a su culminación la pintura, la escultura, el calendario, la escritura, la numeración y la astronomía. Sin embargo, todos esos centros de poder van declinando uno tras otro, para dar paso a una Mesoamérica de fuerte carácter militarista. En la parte final del Clásico, denominada por algunos autores Epiclásico, florecieron El Tajín en la subárea del Golfo, y Cacaxtla, Cholula y Xochicalco en la del Centro de México.
Observa el siguiente video sobre el militarismo de las culturas mesoamericanas del Clásico Tardío.
- Mural de la Batalla, Cacaxtla.
Es muy impresionante saber cómo en los murales representaban su vida cotidiana y las batallas, ¿ustedes han tenido la oportunidad de conocer este mural que aparece en este video?
Tal vez el cambio más reciente de opinión entre los especialistas respecto al Clásico Temprano es la aceptación de que no fue un periodo exento de enfrentamientos bélicos, como se pensó originalmente. Abunda la evidencia de simbolismos bélicos e incluso hay indicios de que se libraron guerras durante este periodo.
Mural teotihuacano

Fuente: https://www.mexicodesconocido.com.mx/escapadas/acueducto-del-padre-tembleque1.html
La dimensión y finalidad de los combates en las distintas regiones aún es objeto de controversia. Tal vez en algunos lugares se trató de incursiones en pequeña escala con miras a la glorificación personal del grupo gobernante, la eliminación de rivales, la obtención de víctimas para el sacrificio y otros propósitos similares.
Monte Albán

No obstante, en otros casos, como los de Monte Albán y Teotihuacán, la guerra o la amenaza de guerra probablemente eran parten integral del expansionismo del estado.
Esto no significa que las sociedades del Clásico Temprano estuvieran dominadas por elementos militares o por intereses y actitudes materialistas. Por el contrario, la religión era una fuerza omnipresente, como lo comprueba la existencia de sacerdotes, templos y rituales. La religión tenía que ver principalmente con mantener el orden del cosmos, la fertilidad, el bienestar general y con acontecimientos como el nacimiento, el matrimonio y la muerte.
Sin embargo, como salta a la vista en la actualidad, las sociedades con conceptos y prácticas religiosas altamente desarrollados pueden ser bastante belicosas, como sucedió con los mexicas y probablemente también durante el Clásico Temprano. Aun así, sabemos muy poco de la frecuencia, la dimensión y los objetivos de las contiendas en las distintas regiones durante esa época, y posiblemente la guerra fue más limitada de lo que llegaría a ser posteriormente.
El intercambio hizo indispensable la existencia de un ejército formal que pudiera cuidar de las caravanas de comerciantes.
En el conjunto habitacional de Atetelco aparecen representaciones de posibles órdenes militares: coyotes y águilas, probables antecedentes de los guerreros águilas y jaguar de los mexicas.
Durante el clásico hay una clara diferenciación cultural que dividió a Mesoamérica en dos grandes regiones con lo que hoy conocemos como el Istmo de Tehuantepec como línea divisoria. Tal diferenciación se reflejó en los sistemas de escritura, numeración y calendáricos.
Si bien la individualidad de las distintas regiones era manifiesta, las unía el intercambio de ideas y de objetos valiosos.
La mayoría de los pueblos mesoamericanos utilizaba un complejo calendario ritual basado en ciclos entrelazados de 260 y 365 días, mientras que los mayas y algunos pueblos vecinos utilizaban la llamada cuenta larga para registrar fechas precisas.
Durante el Clásico Temprano –aproximadamente desde el año 150 o 200 de nuestra era hasta el 650 nuestra era– estas tendencias adquirieron un grado de desarrollo aún mayor.
Para sintetizar, observa el siguiente video y toma nota ya que la información te ayudará a realizar tu reto.
- Nuevas ciudades, nuevas regiones
Hemos llegado al final de la sesión, esperemos que esta sesión haya contribuido a que valores las características del periodo clásico.
El Reto de Hoy:
El reto de la semana, que empezaste fue la elaboración de una línea del tiempo, por lo que debes colorear el Periodo Clásico, con una barra de color que prefieras. Recuerda seguir ilustrando las características de dicha época en el lugar que corresponde.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

El poder de la unión
Aprendizaje esperado: Explica los estados y cambios de estado de agregación de la materia, con base en el modelo de partículas.
Énfasis: Explicar los diferentes estados de agregación de la materia (sólido, líquido, gas).
¿Qué vamos a aprender?
Vas a aprender sobre las características de los estados de la agregación de la materia.
Los materiales que necesitaras son: cuaderno, lápiz o pluma y tu libro de texto.
¿Qué hacemos?
Te sugerimos que completes el siguiente cuadro comparativo con lo que se mencione en esta sesión.
Cuadro comparativo de los distintos estados de agregación de la materia que revisaras en esta sesión. Deberás describir como son:
|
|
Sólidos |
Líquidos |
Gases |
|
La fuerza de cohesión |
|
|
|
|
La libertad de movimiento |
|
|
|
|
El arreglo molecular |
|
|
|
|
La forma |
|
|
|
|
La masa |
|
|
|
|
El volumen |
|
|
|
|
La compresión |
|
|
|
Para completar el cuadro comparativo, pon mucha atención en lo que se mencione a lo largo de la sesión. Y no olvides que siempre puedes consultar su libro de texto y fuentes confiables de información, como páginas de Internet.
Observa el siguiente video que nos habla sobre los distintos estados de agregación en los que puedes encontrar la materia:
- Las mil formas de la materia
¿Qué fue lo que más te llamó la atención de este video?
En la sesión anterior aprendimos que todo lo que nos rodea está constituido de materia; sin embargo, considero que el video aporta 4 puntos nuevos, los cuales me gustaría mencionar:
Primero, que la materia se encuentra en diferentes formas:
- Sólida, como el suelo que pisamos o la ropa que vestimos.
- Líquida, como el agua de los ríos o del mar.
- Gaseosa, como el aire que respiramos.
- Y plasma, como los relámpagos.
A estos cuatro tipos de arreglos de la materia se les llama estados de agregación.
El plasma es el estado de agregación más abundante del universo, ya que en este estado se encuentran las estrellas, como nuestro sol. Y que las diferencias entre los estados de la materia se deben a cómo están organizadas las partículas que los conforman.
¿Recuerdas que es una partícula?
En sesiones anteriores platicamos acerca del modelo de partículas, que este nos servía para describir a la materia.
¿Recuerdas las características de ese modelo? ¿cómo es el arreglo de las partículas de un sólido, de un líquido, de un gas y del plasma?
Para tenerlo más claro, observa el siguiente video.
- La Grecia atomista
Definición formal:
Las partículas son un modelo científico, utilizado para explicar algunas características de la materia. Éstas representan a los átomos o moléculas que conforman todo lo que nos rodea.
Pero ¿cómo están unidas?
Las partículas permanecen unidas por una fuerza que las atrae, llamada fuerza de cohesión; la magnitud de esta fuerza determinará si la distancia entre ellas es corta o amplia. Recuerda que, aunque no lo podamos observar a simple vista, las partículas no están estáticas, se encuentran en constante movimiento e interaccionan entre sí con mayor o menor intensidad.
También recuerda que existe otra fuerza, la de repulsión, que hace que las partículas estén separadas.
¿Todas se mueven de igual forma en los distintos estados de agregación?
No, esto depende de la relación entre las fuerzas de cohesión y repulsión, además de la energía cinética que posean.
El arreglo que las partículas adopten es característico para cada estado de agregación.
Ahora, vas a revisar las características de cada uno.
Pon atención para que puedas completar tu cuadro comparativo.
Vas a conocer a Tsedi, Aki, Gui y Tlahuetequi, que nos van ayudar a entender las características de los estados de agregación de la materia.
- Hola, yo soy Tsedi, que en otomí significa fuerte, y me encuentro en estado sólido.
Si me miras más de cerca podrás ver las partículas que me componen.
Como puedes observar, mis partículas están muy juntas, esto es porque la fuerza de cohesión entre ellas es muy fuerte, sin embargo, la fuerza de repulsión hace que no estén totalmente amontonadas.
La energía cinética de mis partículas es baja y también su libertad de movimiento.
Todo esto hace que mi arreglo molecular sea muy ordenado.
Recuerda que la energía cinética es la que está relacionada con el movimiento. Como la energía cinética de mis partículas es baja, estas sólo pueden vibrar alrededor de su posición.
Si me ves con atención podrás notar que mi forma es definida, y si las condiciones que me rodean no varían, mi forma nunca cambia.
Por ello, mi masa y volumen también son definidos.
Si tú intentas deformarme, tendrás que aplicar una fuerza para lograrlo.
- Mi nombre es Aki, y significa acuático en náhuatl.
Me pusieron así porque soy un líquido, y quiero que conozcas el estado de agregación de mis partículas.
Mírame más de cerca y verás que mis partículas están muy separadas, esto se debe a que ellas tienen una energía cinética alta. Por eso, aunque están unidas, las fuerzas de cohesión no tienen la suficiente magnitud para que mis partículas tengan una estructura definida, como en el caso de los sólidos.
Debido a esta característica, mi arreglo molecular tiene una mayor libertad de movimiento, por lo que no puedo tener una forma definida, y tomo la forma del recipiente que me contenga.
Aunque mi forma no es definida, mi masa y mi volumen sí lo son, esto significa que siempre tengo la misma cantidad de masa y ocupo el mismo volumen.
- Mi nombre es Gui, que en otomí significa nube.
Me dieron ese nombre porque soy un gas.
Acérquense a mirarme y descubrirán que mis partículas están en constante colisión con las paredes del recipiente que me contiene. Pero si no estoy dentro de uno, me disperso por toda la atmósfera de la tierra.
Esto sucede porque mi energía cinética es muy alta, y la fuerza de cohesión es prácticamente nula.
Recuerda que la fuerza de cohesión es como el pegamento que une a las partículas.
A consecuencia de esto, mis partículas tienen una total libertad de movimiento, y sólo cuando estoy dentro de un recipiente pueden cuantificar mi masa, pero mi volumen y forma son indefinidos.
- Me llamo Tlahuetequi, que en náhuatl significa relámpago.
Me dieron este nombre porque los relámpagos son una forma de plasma que podemos encontrar en la Tierra, y yo soy un plasma.
Soy un gas que se encuentra a muy altas temperaturas, por ejemplo, la temperatura del plasma que forma un relámpago es de aproximadamente 27 mil grados Celsius.
Si me miras de cerca podrás ver que mis partículas no están unidas, de hecho, están muy separadas una de otra debido a que la energía cinética es muy alta.
Una característica muy importante es que mis átomos pierden electrones por las altas energías.
Las partículas que me componen reciben el nombre de iones, son los electrones y los átomos que los han perdido.
Mi arreglo molecular es muy parecido al del gas. Mi forma, masa y volumen no están definidos.
Después de estas breves explicaciones, ¿consideras que se han resuelto tus dudas?
Si observas tu cuadro comparativo faltaría hablar de la compresión, fenómeno que se presenta en algunos estados de agregación de la materia.
Hay que realizar un pequeño experimento para analizar la compresibilidad de los tres estados de la materia.
Para realizar este experimento necesitaras:
- Tres jeringas sin aguja.
- Una esfera pequeña de metal, que quepa en la jeringa. Si en casa no consiguen una esfera de metal, pueden usar una canica.
- Un poco de agua.
Vas a sacar el émbolo de una de las jeringas y metemos la esfera de metal, después vuelves a colocar el émbolo.
En otra jeringa, pon un poco de agua.
Y a la última, sólo le vas a jalar el émbolo.
¿Puedes decir en qué estado de agregación se encuentra cada una de las sustancias o cuerpos que están dentro de las jeringas?
En la primera jeringa tienes una bolita de metal, la cual se encuentra en estado sólido.
En la segunda tienes agua en estado líquido, y finalmente en la tercera jeringa no se observa ninguna sustancia, pues lo que contiene es aire, un gas que a simple vista no se ve.
Debemos mencionar que no podemos tener una jeringa con plasma, ya que éste necesita condiciones muy específicas, como altas temperaturas, para poder formarse.
Ahora te voy a pedir que tomes la primera jeringa y empujes el émbolo intentando deformar la esfera de metal
¿Lograste deformar la esfera?
Inténtalo ahora con la segunda jeringa, pero en esta ocasión te voy a pedir que tapes el orificio de salida, para que no se derrame el agua, y trates de comprimir el líquido que se encuentra dentro de la jeringa.
¿Lograste comprimir el líquido?
Por último, repite el experimento con la tercera jeringa, en ella tienes aire, es decir un gas. Vuelve a tapar el orificio de salida y empuja el émbolo de la jeringa.
Veremos si logras comprimir el aire que se encuentra dentro.
Si puedes ver, al recorrerse el émbolo disminuyó el volumen que estaba ocupando el aire, lo que significa que logré comprimirlo.
Lo que comprobaste con este pequeño experimento es que únicamente los gases se pueden comprimir, los líquidos y los sólidos no, pues ellos, como vimos antes, tienen una masa y volumen definido.
Te preguntarás ¿cómo aplicamos esto a nuestra vida cotidiana?
Por ejemplo, existen varios gases que son guardados a presión. Como en los tanques de oxígeno, en éstos el gas se comprime para que en un tanque pequeño quepa mucho oxígeno. Entonces en ese caso, se aprovecha la compresibilidad de los gases.
Así es, también todas las latas de productos en aerosol tienen gas comprimido.
Por ejemplo, si pudieras ver por dentro de un desodorante en aerosol, encontraríamos que una parte de la lata está ocupada por el desodorante líquido, y el resto tiene gas presurizado. Cuando accionas la boquilla de la lata, la presión del gas empuja el desodorante hacia afuera.
¿Conoces algo en donde se utilice la incompresibilidad de los líquidos o los sólidos?
¿Alguna vez has visto una prensa hidráulica?
Hay de diferentes tamaños, unas de las más grandes son las que ayudan a los mecánicos a levantar los automóviles. También el gato, el que nos sirve para cambiar las llantas cuando se ponchan, es una prensa hidráulica. De hecho, se llama gato hidráulico.
Dentro de las prensas hidráulicas, sin importar su tamaño o uso, existen unos cilindros llenos de aceite que se encuentran en estado líquido.
Como los líquidos no se pueden comprimir, cuando presionamos en uno de los extremos de los cilindros, el otro se tiene que levantar. Y es de ese modo que se levantan los autos, aunque estén muy pesados.
El Reto de Hoy:
Con esta información ya puedes completar tu cuadro comparativo de los distintos estados de agregación de la materia que revisaste en esta sesión.
Reúnete con tu familia e investiga cómo se puede pasar de un estado de agregación a otro, esto te servirá para la siguiente sesión.
Para profundizar en el tema o resolver dudas, revisa tu libro de texto o recurre a fuentes de información confiables.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.

Nada es lo que parece: de la mirada de los colores al movimiento de las palabras
Aprendizaje esperado: Explorar en colectivo el movimiento, el gesto, la forma, el color y el sonido para recrear un fragmento de distintas obras o manifestaciones artísticas de su interés.
Énfasis: Recrear por distintos medios expresivos el fragmento de una obra plástica, sonora y visual.
¿Qué vamos a aprender?
Elaborarás una producción creativa a través de la expresión artística de tu interés, para desarrollar aún más tu imaginación, tu creatividad y tu sensibilidad. Para ello, observarás los elementos cotidianos que te rodean y distinguirás sus rastros, por ejemplo, al identificar huellas corporales que nos representan, mismas que nos recuerdan quiénes somos y lo valiosos que somos.
Los materiales que vas a necesitar además de un cuaderno, lápiz o bolígrafo son: todos lo que quieras, menos lápices de colores, ni crayolas, ni pinturas vinílicas. ¡Vas a crear tus propios pigmentos!
Pregúntales a los adultos que te acompañan qué materiales podrías ocupar, por ejemplo:
- Semillas
- Cereales
- Masa
- Palillos
- Hojas secas
- Tierra (seca o húmeda).
Dependiendo de lo que decidas representar.
También, si deseas entintar algo, podrás hacerlo, por ejemplo, con café, flor de jamaica o chocolate diluido.
Echa mano de todo el poder de tu imaginación y creatividad.
Recuerda que todo lo que veas hoy, es para continuar con tu experimentación artística, así que te recomiendo dejarte llevar por las instrucciones y, al finalizar, registra los aprendizajes, encuentros, descubrimientos, hallazgos y curiosidades de la experiencia, o las inquietudes y dificultades que surjan en el proceso de esta sesión.
¿Qué hacemos?
Iniciarás a partir de la pregunta: Si un artista no tuviera a la mano materiales convencionales para trabajar, ¿con qué otros materiales se te ocurren que podrías elaborar tus obras?
Recuerda lo que realizaste la sesión anterior:
Reconociste tu vena como poeta urbano: compusiste coplas bajo el tema de labores domésticas y, te convertiste en célebre cantante en tu hogar.
El énfasis estuvo puesto en la literatura, en este caso, a través de la escritura de versos, la música y, por su puesto, en la resonancia que ésta tiene para invitar al cuerpo al movimiento
El día de hoy, el acento estará puesto en la plástica, en la apreciación de sonidos, en los aromas y sabores.
La actividad consta de 5 momentos.
Primero, realiza un ejercicio para sensibilizar tu imaginación, a partir de la observación de algunas fotografías de nubes.
Te invito a que tengas una disposición relajada, para ello, harás tres respiraciones profundas 1...2...3...
Ahora, desde esta nueva disposición, observa con mirada curiosa las fotografías que aparecerán en tu pantalla. Pon atención a sus formas, colores, sensaciones que les provocan, imaginemos sus sonidos, las distancias de los elementos. Deja libre la imaginación.






¿En estos días has observado las nubes?
¿O recuerdas cuándo fue la última vez que las viste?
¿Alguna vez creíste distinguir algunas formas…rostros… animales en las nubes?
Trata de recordar una experiencia que te haya dejado una huella positiva y que tenga relación con las nubes… Escríbela en tu cuaderno.
¿Últimamente, has observado tu entorno?
Pues, ahora es momento de hacerlo. Así que te invitamos a que, en el lugar en donde estés, busques un espacio en donde puedas estar cómodo, por ejemplo, un tapete, el sillón o incluso en el piso... y acuéstate bocarriba mirando el techo, como si se dispusieran a ver nubes...
Y con esa mirada curiosa identifica los detalles del techo de tu casa: trazos, marcas, grietas, manchas, formas, etc., y trata de indagar cómo es que esa marca apareció ¿cómo llegó ahí?
Date unos segundos para observar…
¿Logras identificar alguna forma?
¿Alguna vez habías mirado tan detenidamente el techo de tu casa? ¿Qué detalles encontraste ahora? ¿Imaginaste alguna forma? ¿Cuáles? Escríbelas en tu cuaderno.
Ahora, continúa investigando los detalles de rastros y huellas de tu casa.
Así que toma unos minutos y encuentra detalles, rastros, manchas o huellas en paredes, muebles, ventanas, etc., y escribe en tu cuaderno los que consideres que tiene alguna forma particular.
¿Cuáles sonidos identificas? ¿Cuáles llaman tu atención?
Observa el siguiente video.
- Video de Pau y Cris
¿Cuántos rastros anotaste en tu libreta?
¿Qué huellas encontraste?
Por ejemplo: sonidos...recuerdos...
- ¿Qué sonidos recuerdas?
Podemos decir que las huellas son aquellos registros que dejan una marca a partir de un suceso. En este sentido, podríamos decir que hay huellas físicas y psicológicas.
Ejemplos de huellas físicas podrían ser: alguna mancha en la pared o en el piso o las de la piel: un lunar o cicatriz, por ejemplo.
Una huella psicológica, podría ser el recuerdo de alguna canción, algún aroma o alguna situación que hayan marcado un momento de su vida
Ahora, te invito a escribir tres huellas positivas. Por ejemplo, alguna anécdota interesante, divertida, graciosa que te haya ocurrido, y escríbelas en tu cuaderno.
Piensa cómo lo representarías
Ahora te toca a ti elegir las imágenes de tus huellas.
¿Y cómo la vas a representar?
Trae tus materiales con los que consideres puedes representar tu “huella”. Así que ve con tu papá o mamá y pregúntales qué puedes tomar para realizar la imagen de tu huella.
Recuerda que no se puede emplear ningún recurso de papelería convencional, excepto su cuaderno u hojas de papel.
Acerca una base en la que sirva como lienzo de la actividad, por ejemplo: un pedazo de papel o cartón o, si lo decides, en el piso —claro, después lo limpiarán muy bien—.
Puedes apoyarte con semillas, salsas, para experimentar con las tinturas y reacciones en diferentes superficies sobre estos materiales.
En esta actividad, además de poner a prueba una vez más tu imaginación y creatividad, también te dará experiencias sensitivas con las texturas, degustativas y aromáticas.
Observa el siguiente video:
- Proceso
Mientras sigues realizando la actividad, te invitamos a mirar la obra del artista plástico Vik Muniz. Puedes tomar algunas ideas para tu trabajo.






Vik Muniz es un artista plástico brasileño. Hay quien dice que es un “artista de la ilusión”, pues juega con la mente y miradas de todas aquellas personas que admiran sus obras, mediante el uso creativo e inusitado de los materiales que emplea para ellas.
Restos de comida, juguetes, azúcar, mermeladas, chocolate, tierra, diamantes, caviar, confeti, alambres, algodón, recortes de revistas viejas, desechos, por mencionar algunas.
Sus composiciones son efímeras y de gran contenido social, quedando como evidencia de su arte el registro fotográfico.
¿Recuerdas a las nubes?
Nosotros tomamos como base esta obra, para trabajar con “la huella” como premisa, como esta nube fabricada con la estela de una avioneta que dejó su rastro en el cielo.
Azúcar, juguetes, comida, desechos… cuántas cosas se pueden crear y recrear con los materiales más insospechados y que están en nuestro entorno.
Observa el siguiente video:
- Proceso pastel
¿Tú qué hiciste?
¿Dejaste como registro una fotografía?
¿Qué material utilizaste?
El día de hoy hiciste un ejercicio de exploración, a partir de la observación de las nubes y, como exploradora y explorador, investigaste las huellas que encontraste en diversos lugares de tu casa y las registraste en tu libreta.
Posteriormente, reflexionaste sobre las huellas personales, aquellas que te permiten recordar situaciones, sensaciones, sonidos, sabores.
Por eso nombramos a esta clase de la mirada de los colores al movimiento de las palabras, en donde partimos de nuestra observación curiosa y sensible de nuestras huellas —la mirada de los colores— a la representación simbólica —al movimiento de las palabras— de alguna de nuestras huellas y a través de composiciones con materiales no convencionales. Traducimos a estos símbolos como palabras, puesto que los podemos leer.
Revisaste parte de la propuesta estética del artista plástico Vik Muniz, quien en sus obras emplea materiales no convencionales, casi insospechados, y la relacionamos con nuestras producciones.
El Reto de Hoy:
1) Registrar en tu cuaderno los hallazgos sobre las huellas que hay en los lugares de su casa, así como aquellas situaciones que les evocan recuerdos positivos.
2) Con materiales no convencionales, elabora una composición alusiva a la huella personal que elijas y hagas una foto o, de lo contrario, tíntala y fíjala con pegamento en tu cuaderno.
3) Comparte la imagen con tus compañeras, compañeros y docente, y por supuesto, con tu familia con quien, esperamos, sigan generando huellas que trasciendan positivamente toda su vida.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Aprende en casa II SEGUNDO DE SECUNDARIA 30 DE OCTUBRE










Publicar un Comentario